Combined Linear Interaction Energy and Alchemical Solvation Free-Energy Approach for Protein-Binding Affinity Computation

Abstract

Calculating free energies of binding (ΔG_bind) between ligands and their target protein is of major interest to drug discovery and safety, yet it is still associated with several challenges and difficulties. Linear interaction energy (LIE) is an efficient in silico method for ΔG_bind computation. LIE models can be trained and used to directly calculate binding affinities from interaction energies involving ligands in the bound and unbound states only, and LIE can be combined with statistical weighting to calculate ΔG_bind for flexible proteins that may bind their ligands in multiple orientations. Here, we investigate if LIE predictions can be effectively improved by explicitly including the entropy of (de)solvation into our free-energy calculations. For that purpose, we combine LIE calculations for the protein–ligand-bound state with explicit free-energy perturbation to rigorously compute the unbound ligand’s solvation free energy. We show that for 28 Cytochrome P450 2A6 (CYP2A6) ligands, coupling LIE with alchemical solvation free-energy calculation helps to improve obtained correlation between computed and reference (experimental) binding data.

Introduction

Protein–ligand binding can lead to (enhanced) activity or inhibition of a protein,¹⁻⁴ and the binding affinity of a ligand to its target or off-target can be quantitatively expressed in terms of the corresponding binding free energy (ΔG_bind).⁵ Therefore, free-energy calculations have played a prominent role from the hit-identification to lead-optimization stages of drug design and discovery^6,7 and in the screening of inhibitory potentials of molecules that can interact specifically with pharmacologically or toxicologically relevant proteins.⁸⁻¹⁰ Due to the increased availability of biomolecular off-targets and computational resources, protein-structure-based computational techniques increasingly become attractive for the pharmaceutical industry for the prediction of ΔG_bind values.¹¹⁻¹⁴

In silico approaches to calculate protein–ligand ΔG_bind values range from combined docking and scoring¹⁵ to molecular-simulation-based end-point^16,17 and alchemical free-energy methods.^18,19 Selection of the most suitable method depends on the number of compounds involved, the studied system, and the preferred levels of accuracy and efficiency.^20,21 Docking and scoring functions usually treat protein structure rigidly and are typically used for binding pose prediction and to (qualitatively) distinguish binders from nonbinders within large databases, thus filtering them into smaller sets of compounds for further processing and/or experimental validation.²² On the other hand, rigorous alchemical methods such as free-energy perturbation (FEP)¹⁸ and thermodynamic integration (TI)¹⁹ can lead to accurate free-energy estimates when sufficient sampling of the relevant conformational states is obtained. This is typically compute-intensive as it requires extensive molecular dynamics (MD) simulations of the system including MD runs of nonphysical states,²³ making these methods less suitable for use in (semi)high-throughput settings. Alternatively, end-point methods such as linear interaction energy (LIE)¹⁷ and molecular mechanics combined with Poisson–Boltzmann or generalized Born and surface area continuum solvation (MM/PBSA or MM/GBSA)¹⁶ lie between alchemical and docking/scoring-based approaches and offer a trade-off between computational efficiency and accuracy, by including protein and ligand conformational sampling but only performing MD simulation of the end states for protein–ligand (un)binding.²⁴ A plausible application of end-point methods is to reduce compounds in a large set of potential binders to a subset of promising molecules.²⁰

An advantage of LIE is that it allows for a straightforward incorporation of the contribution of multiple and/or different binding modes of ligands in its computation of (direct or “absolute”) binding free energies to the protein of interest.²⁵ This is especially relevant when quantifying affinities of binding to target receptors or off-target enzymes with large active-site conformational flexibility, including, e.g., pharmaceutically relevant proteins such as the families of Cytochrome P450s (CYPs) and kinases. In such cases, it can be especially difficult to compute binding free energies from docking/scoring or alchemical calculations, because different protein and/or ligand binding conformations may contribute to the binding free energy. As an attractive alternative, we have in recent years extended and automated a statistical-weighting-based approach to efficiently compute ΔG_bind by combining results from (short) MD simulations starting from different relevant parts of protein–ligand conformations. For that purpose, MD simulations are run per training or query compound free in solvent (free) and bound to the protein of interest in N starting configurations comprising different binding orientations and/or protein conformations (bound). From every individual MD simulation, average van der Waals (vdw) and electrostatic (ele) interaction energies of the ligand (lig) with its surrounding (surr) are used to obtain the calculated binding free energy ΔG_bind,calc, by weighting results from the N individual simulations of the protein–ligand complex in a Boltzmann-like manner^25,26

1

with

2

and

3

The weights W_i of the individual simulations i in eq 1 are calculated as²⁶

4

in which k_B is Boltzmann’s constant and T is the temperature of the simulated system. Both α and β are parameterized based on experimentally curated values of ΔG_bind, and this needs to be done in an iterative fashion when N > 1.²⁵ Note that the use of the offset parameter (γ) in eq 1 is optional, which would need to be trained along with α and β as well (albeit in an iterative fashion). In the LIE models presented in this work, γ was set to zero unless noted otherwise.

While the above-described (iterative) weighting approach can improve LIE predictions by enhancing protein–ligand sampling, we investigate here if we can further improve LIE by calculating the free energy of ligand desolvation alchemically and by including this contribution to ΔG_bind explicitly into our LIE approach. In this way, we can rigorously evaluate both the energetic and entropic contributions of desolvation to ΔG_bind, and we only have to calibrate α and β parameters associated with ligand–environment interaction energies in the simulation of the protein-bound system. We evaluate if replacing the contributions from the unbound state in LIE by alchemically computed (de)solvation free energies will improve ΔG_bind calculations when compared to experiment, by merely performing short free-energy perturbations of the ligands free in solvent. Thus, we introduce here a modified framework of LIE computation by including ligand solvation by means of FEP instead of using the second terms on the right-hand sides of eqs 2 and 3.

In particular, we present combined LIE/FEP models to compute binding to human Cytochrome P450 2A6 (CYP2A6; EC 1.14.13.−) and compare it to traditional LIE models. Cytochrome P450s (CYPs) are malleable and promiscuous heme-containing redox proteins comprising a ubiquitous superfamily of mono-oxygenases, and they act as the major drug-metabolizing enzyme in phase I of xenobiotics metabolism, converting ca. 75% of available marketed drugs.^27,28 A variety of CYPs are known to be able to accommodate substrates in different binding poses. CYP2A6 is a hepatic enzyme comprising 1–10% of total CYPs in human body²⁹ but responsible for 70–80% of nicotine metabolism,³⁰ and inhibiting nicotine metabolism may diminish the desire for smoking; hence, CYP2A6 inhibitors may help smoking cessation. Here, we calibrate LIE models for CYP2A6 based on experimental data for 28 inhibitors and take advantage of the weighted LIE scheme of eqs 1–4 to enable the inclusion of multiple binding poses in the model. We present several adapted LIE models in which (de)solvation thermodynamics is included as described above, and we show that combining LIE with FEP for that purpose can improve correlations between calculated and experimental CYP2A6–inhibitor binding affinities. In addition, we study if this conclusion can be extended toward another CYP (CYP2E1).

Methods

Protein and Ligand Structure Preparation

The crystal structure of CYP2A6 was downloaded from the Protein Data Bank (PDB)³¹ with ID 2FDV.³² After retaining the protein and heme-group atomic positions of chain A, MolProbity³³ was used to add missing hydrogen atoms, optimize hydrogen bond networks, and check for flipped Asn, Gln, and His residues. No residue was flipped. Chimera version 1.10.2³⁴ was used to define AMBER ff14SB³⁵ force field parameters for the protein and AM1-BCC charges³⁶ for the heme group and to energy-minimize the structure by 100 steps steepest descent and 10 steps conjugate gradient, and correct protonation states of His residues.

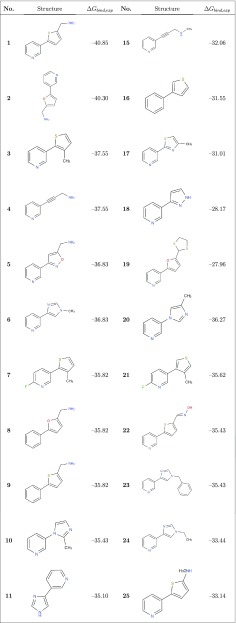
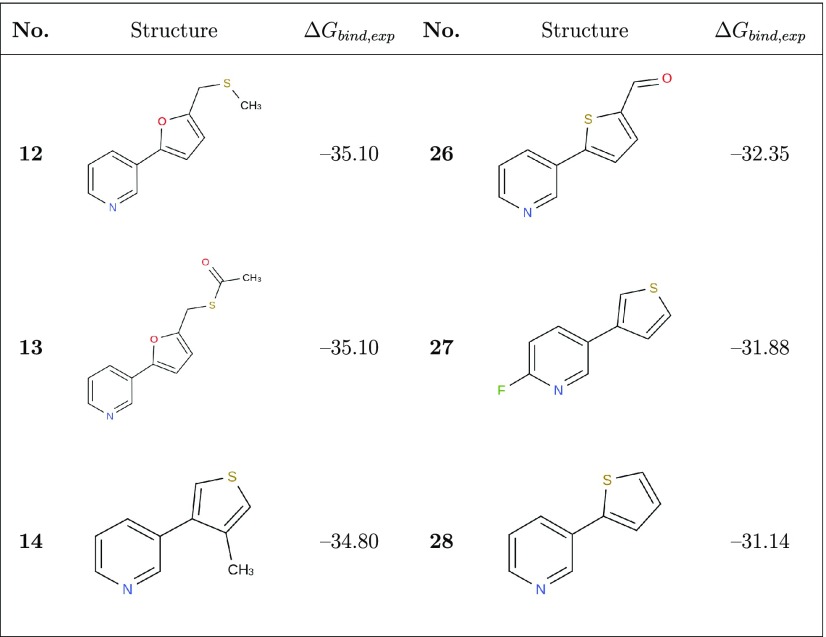
We collected a data set of experimental CYP2A6 (as well as CYP2E1) IC₅₀ or K_i values for 28 pyridine analogues of nicotine from the literature^32,37 via ChEMBL,³⁸ which was used to derive either the Cheng–Prusoff estimates of K_i and/or the observed binding free energies ΔG_bind,exp (ranging from −40.9 to −28.0 kJ mol^–1; Table 1) using³⁹

5

Table 1. Molecular Structures and Experimental Estimates for the CYP2A6 Binding Free Energy (ΔG_bind,exp in kJ mol^–1) of the 28 Compounds Considered in the Current Work.

LIE Model Parameterization

We used our eTOX ALLIES⁴⁰ pipeline to automatically perform docking and MD simulations and to employ the Boltzmann-weighted LIE method (Figure 1). Open Babel 2.3.9⁴¹ was used to prepare ligand structures (i.e., generation of three-dimensional (3D) coordinates if necessary and protonation based on pH 7.4 or neutralization, depending on model settings). Ligand topologies were created using AmberTools15⁴² based on the general Amber force field (GAFF)⁴³ and the AM1-BCC approach,³⁶ and this topology generation was automatically executed and converted to GROMACS format using ACPYPE⁴⁴ (Rev: 7828). Ligands were docked into the CYP2A6 active site by ParaDockS 1.0.1⁴⁵ with a sphere radius of 1.0 nm from the center, which was automatically determined on the basis of the heme domain atom coordinates. Docking solutions were subsequently subjected to principal component analysis (PCA) and k-means clustering to generate medoids as representative docking conformations for MD inputs, as described in our previous works.^40,46

Figure 1.

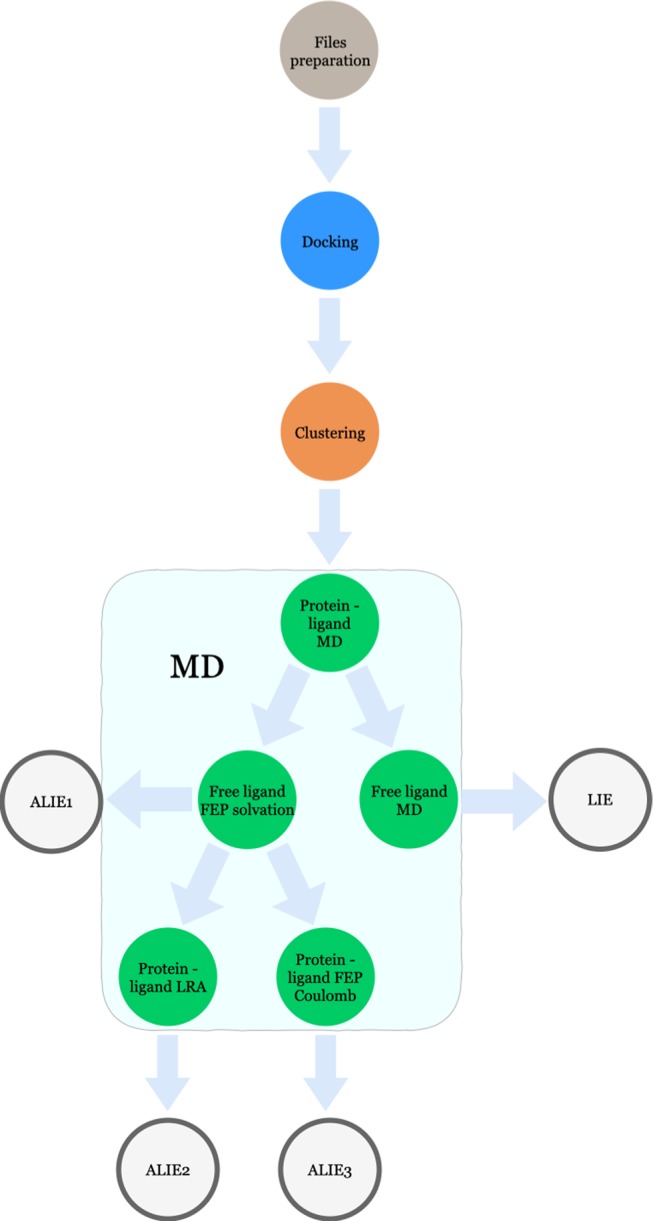
Schematic overview of LIE and ALIE workflows used in this study. The pipeline starts from the ligand and protein structure preparation, followed by docking, clustering, and MD simulations. The LIE model is obtained using eTOX ALLIES,⁴⁰ while the ALIE models are generated using in-house scripts.

The medoids (2–3 per ligand) were afterward used in combination with the protein structure as input for steepest-descent energy minimization in GROMACS 4.5.5. The minimized complex structures were in a next step solvated in approximately 16180 TIP3P water molecules,⁴⁷ and the systems were neutralized by the addition of 6 Cl^– counterions. All subsequent MD stages, including the 1 ns production runs starting from the 2–3 selected binding poses of the relatively rigid ligands, were carried out using GROMACS 4.5.5⁴⁸ and the Amber14SB force field,³⁵ in which energy and coordinate trajectories were written out to disk every 10 ps. Thermal pre-equilibration, temperature and pressure coupling (with time constants of 0.1 and 0.5 ps, respectively), grid-based pair-list update frequency, and long-range treatment of nonbonded interactions during MD were performed as described previously.⁴⁹ For the heme cofactor and coordinating cysteine residue in CYP2A6, special force field parameters were used.⁴⁰ Every ligand pose was run in duplicated simulations⁵⁰ and weighted based on Boltzmann-like statistics (eqs 1–4).²⁵ Separate duplicated 1 ns production runs for ligands free in solvent using identical MD settings as for protein–ligand complexes were conducted to obtain average interaction energies for unbound ligands for use in eq 1. Time-averaged energetic terms between the ligand and environment as obtained from MD were subsequently subjected to ordinary least-squares (OLS) fitting to train LIE models based on curated experimental ΔG_bind values, which was performed using the Python scikit-learn 0.17 package.⁵¹ Fitted LIE parameters (i.e., α and β (and γ if required)) from model creation (see Results and Discussion) were obtained in an iterative way.²⁵ All of the works from ligand preparation until LIE model generation were performed within the eTOX ALLIES pipeline.⁴⁰

Adapted Model 1: Including (De)Solvation Free-Energy Calculations

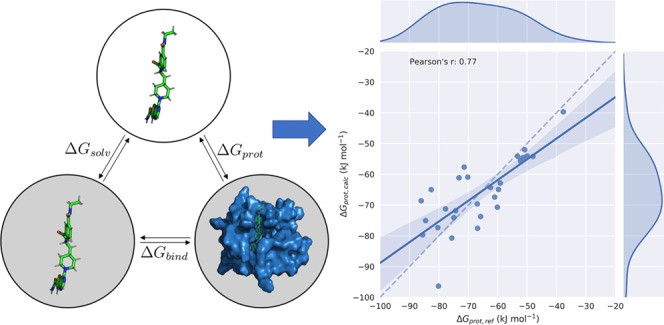
In adapted LIE model 1 (ALIE1), we separately consider the solvation free energy ΔG_solv (using rigorous alchemical computation) and the free energy of transferring a ligand from the gas phase into the bound state (ΔG_prot, Figure 2). In this way, we only need LIE parameters to scale ligand–environment interaction energies in the protein-bound state, in which ligand sampling is already enhanced compared to traditional LIE by weighting results from MD simulations starting from different ligand binding poses using eq 4. Thus, the calculation of “binding free energies” reduces in this ALIE1 model to

6

As reference data ΔG_prot,ref for the calibration of scaling parameters α and β (and optionally, offset parameter γ), we use the sum of ΔG_bind,exp and ΔG_solv, cf. Figure 2

7

To rigorously evaluate ΔG_solv from free-energy perturbation, 21 independent MD simulations were performed of the individual ligands in water. Solute–solvent (Coulomb and van der Waals) interactions were gradually activated in these simulations using equispaced λ points (ranging from 0 to 1) with λ as perturbation parameter for the Hamiltonian.^19,52,53 At every λ point, MD simulations were performed under minimum image periodic boundary conditions based on cubic computational boxes. The equations of motion were integrated using the leap-frog scheme⁵⁴ with a time step of 2 fs. All simulations were performed at a temperature of 300 K and a pressure of 1 bar; water was simulated as the TIP3P model. MD simulations were performed using the software GROMACS version 5.⁵⁵ All of the systems were previously equilibrated by performing a first minimization step (50 000 steps steepest descent algorithm) followed by 30 ns of equilibration in NPT ensemble at 300 K and at 1 bar of pressure using the v-rescale algorithm and Parrinello–Rahman algorithm for temperature and pressure coupling, respectively.^56,57 Electrostatic interactions were calculated using the fast smooth particle-mesh Ewald (SPME) algorithm.⁵⁸ For each λ point, the system was minimized (10 000 steps, steepest descent) and equilibrated for 200 ps (100 ps in NVT ensemble followed by 100 ps in NPT ensemble) before the production of MD simulation (15 ns). The final solvation free energies relied on multistate Bennett acceptance ratio (MBAR).⁵⁹ For every free energy calculated, statistical error estimation is provided as indicated by Klimovich et al.⁵² Values for and errors in the calculated free energy were obtained using an automatic analysis workflow (http://github.com/choderalab/pymbar) that systematically evaluates free-energy differences for each pair of adjacent states, as a function of simulation time in both the forward and reverse directions and from overlapping distributions.^52,59

Figure 2.

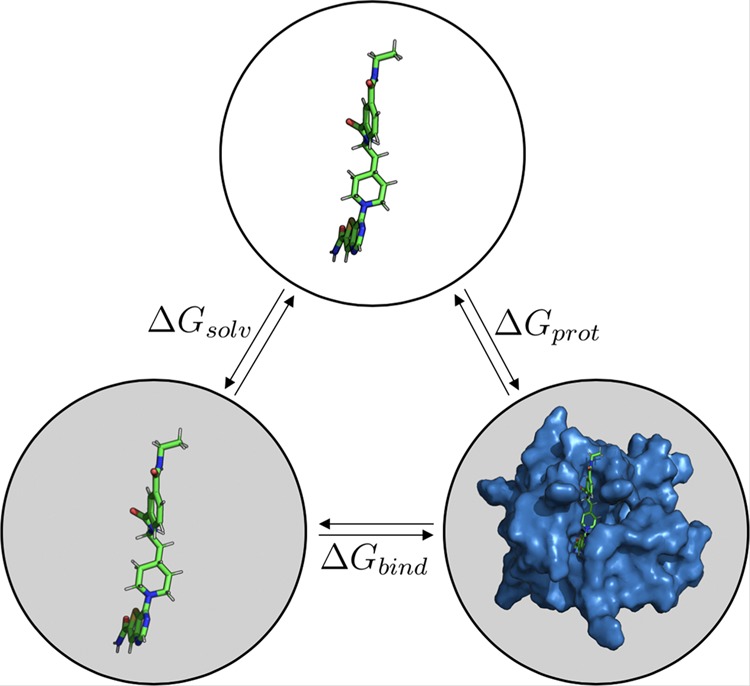
Thermodynamic cycle illustrating the calculated and reference free-energy differences considered in this study. The solvation free energy ΔG_solv is associated with the transfer of the ligand in the gas phase (top) into the water solvent (bottom left). Binding of the solvated ligand to the target protein is associated with the free energy of binding ΔG_bind. The sum of these two free energies is equal to the free-energy difference ΔG_prot for transferring the ligand from the gas phase directly to its protein-bound state in solution (bottom right).

Adapted Model 2: Extension to the Linear Response Approximation (LRA) Approach

Equation 6 does not account for possible inherent ligand interaction energies with the protein in its unbound conformation, but depending on the system of interest, such preorganization energy may be significant.⁶⁰ In that case, the assumption of the linear response in the electrostatic interactions as taken in eq 6 can break down. Here, we examined the size of the preorganization energy and if our calculations could be further improved by replacing the second term on the right-hand side of eq 6 with the original linear response approximation (LRA) of Warshel and co-workers⁶¹ to retrieve adapted model 2 (ALIE2), where

8

and

9

⟨V_lig–surr^ele⟩_off is the preorganization energy, which can be directly calculated as average ligand–surrounding interaction energy from MD simulations of the noninteracting protein–ligand complex. Thus, we only need to calibrate α (and optionally γ) in the ALIE2 models, for which values of the difference ΔG_prot,ref – ΔG_LRA for the set of compounds in Table 1 serve as reference calibration data, while the first term on the right-hand side of eq 8 was the actually calculated value during calibration. To generate the ALIE2 model, we only performed MD simulations starting from a single binding pose per ligand. This was per ligand taken to be the (thermally equilibrated) MD starting pose of the simulation used in the ALIE1 model with highest weight W_i (see Table S1 of the Supporting Information for the separate W_i values), from which ⟨V_lig–surr⟩_bound was directly obtained. Figure S1 compares selected ligand binding poses used as MD starting poses in the ALIE1 model to illustrate observed differences in these poses both among ligands for which a single simulation showed a contribution (W_i) of more than 80% in the calculated binding free energy and among poses with significant contribution to the calculated affinity of a single compound. ⟨V_lig–surr^ele⟩_off was calculated by averaging ligand–protein electrostatic interaction energies over configurations from additional duplicated 1 ns simulations in which protein–ligand interactions were turned off while otherwise utilizing identical MD settings (and starting poses) used to obtain the ⟨V_lig–surr⟩_bound values.

Adapted Model 3: Using Free-Energy Perturbation To Estimate Protein–Ligand Electrostatic Interactions

Previously, de Ruiter and Oostenbrink showed for different cases that LRA or LIE approaches for binding free-energy computation can be improved by allowing nonlinear fits to the change in electrostatic energy upon (un)binding.⁶⁰ Here, we investigate in a last step if explicitly running free-energy perturbations using a coupling λ parameter for the electrostatic ligand–protein interactions can lead to improved LRA or LIE predictions. For this purpose, 20 ps equilibration and 10 ns production MD runs were performed in one replicate, starting from the same protein–ligand complex structure as used in the additional ALIE2 simulations, at five λ points in which electrostatic interactions between the ligand and surrounding were gradually decoupled. Other MD settings were identical as those in the simulations of the bound state used for the other (A)LIE models. From these simulations, the electrostatic contribution to ΔG_prot (denoted by the subscript ele in eq 10) was obtained using the Bennett acceptance ratio (BAR) method.⁵² Similarly as in the ALIE2 model, only α had to be fitted, which was in this case done based on the difference ΔG_prot,ref – ΔG_prot,ele, as follows

10

Results and Discussion

LIE Model

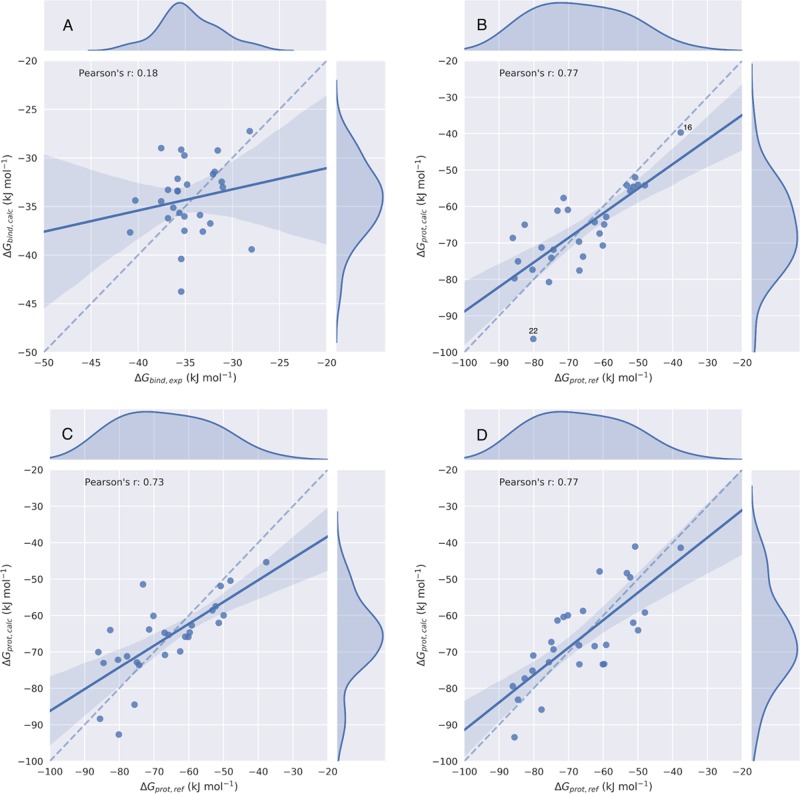
The parameterization and performance of the calibrated LIE model are summarized in Table 2. The quality of the model was evaluated by two kinds of metrics, i.e., correlation coefficients r², Pearson’s r, and Spearman’s ρ, and deviations from experimental values estimated as root-mean-square error (RMSE). The obtained correlation between observed experimental and calculated ΔG_bind values is also illustrated by the regression and kernel density plots in Figure 3A, in which the 95% confidence interval is indicated by the shaded area. From Table 2 and Figure 3A, it can be seen that ΔG_bind values as calculated with our LIE model show deviations from ΔG_bind,exp that are close to 1 kcal mol^–1 (RMSE = 4.3 kJ mol^–1), but the obtained correlation plots and coefficients indicate poor predictions of trends in binding for the considered set of compounds (r = 0.18, ρ = 0.16). This may be a result of the small spread within the experimental reference values for the employed data set, cf. Table 1 and Figure 3A.⁶²

Table 2. Model Parameters for the LIE and ALIE Models of CYP2A6, Together with Respective Root-Mean-Square Errors (RMSEs, with Respect to Experiment) and Correlation Metrics for the Set of Compounds Considered in This Work.

	LIE	ALIE1	ALIE2	ALIE3
α	0.67	0.34	0.38	0.29
β	0.13	0.66	0.50
RMSE (kJ mol–1)	4.34	8.39	8.93	8.64
r2	0.03	0.59	0.53	0.59
Pearson’s r	0.18	0.77	0.73	0.77
Spearman’s ρ	0.16	0.76	0.76	0.74

Figure 3.

Scatter and kernel density plots of the LIE (A), ALIE1 (B), ALIE2 (C), and ALIE3 (D) models for CYP2A6 binding, illustrating obtained correlations between calculated free energies ΔG_bind,calc or ΔG_prot,calc and their respective reference values. Dashed lines indicate an ideal correlation between the calculated and reference data, solid lines indicate the actually obtained correlations, and shaded areas indicate 95% confidence intervals.

Adapted LIE Models

The solvation free energies of the set of 28 CYP2A6 binders were calculated from MD simulations and free-energy perturbation. The results of these calculations, as well as their error estimates, are presented in Table S2 of the Supporting Information. The model performance and parameters of the ALIE models are summarized in Table 2 and plotted in Figure 3B–3D. Interestingly, explicitly evaluating the solvation free energy via alchemical perturbation and only parameterizing α and β parameters to compute ΔG_prot greatly improve predictions in trends in binding affinity. This is illustrated by the relatively high correlation coefficients for the ALIE1 model, especially when compared to those for the traditional LIE model (Table 2). As recently argued by one of us,⁶³ computing ΔG_prot can aid in predicting intrinsic preferences in protein–ligand interactions, regardless of the desolvation contribution as included in the experimental binding free energy. This can be of help in studying, e.g., possible effects on these intrinsic protein–ligand affinities due to protein mutations (which may, in turn, be relevant to bioengineering⁶³ or studying polymorphisms), but it should be noted that in our ALIE1 model, relatively large errors in calculated ΔG_prot values were obtained (RMSE = 8.4 kJ mol^–1). Probably, an important contribution to the approximate doubling of the RMSE when going from the LIE to the ALIE1 model is the accompanying 2- to 3-fold increase in the absolute reference values to be predicted, cf. Figure S2. In addition, the increase in RMSE in going from the LIE to the ALIE1 model may be due to a contribution from possible errors in the computed ΔG_solv value to the calculated complexation free energies in the ALIE1 model.

Besides the larger spread in ΔG_prot,ref values than for ΔG_bind,exp, the higher ALIE1 correlation coefficients (when compared to LIE) can be understood in terms of the different α and β values that we obtained when fitting separate LIE-like models for the prediction of ΔG_solv and ΔG_prot (which together constitute ΔG_bind; Figure 2). To obtain an LIE model for ΔG_solv computation, we used our FEP/MBAR values as reference data to fit parameters that directly relate the ligand–solvent van der Waals and electrostatic interaction energies in the unbound state to the solvation free energy⁶⁴

11

In this way, a model was obtained with α and β close to 0 and 0.5, respectively (Table 3). Thus, to compute ΔG_solv values, we can use a linear response model in terms of electrostatic interactions only, Figure 4. In contrast, our fitted ALIE1 model for ΔG_prot calculation has values of α = 0.34 and β = 0.66, which is also significantly closer to the theoretical value of 0.5 than obtained for our LIE model for ΔG_bind calculation, Table 2. In conclusion, by splitting up the calculation of ΔG_bind into the upper steps in the thermodynamic cycle depicted in Figure 2, an improved and significant correlation could be obtained between the computed and reference data, as illustrated by the values of Pearson’s r and Spearman’s ρ that are close to 0.8 for the ALIE1 model.

Table 3. LIE Parameters for and Performance of a Model That Linearly Relates Average Ligand–Solvent van der Waals (via α) and Electrostatic Interaction Energies (via β) As Obtained from Independent Simulations of the 28 Unbound Ligands in Water Solvent, Fitted Based on ΔG_solv Values Computed from Alchemical Perturbation^a.

	value
α	–0.04
β	0.52
RMSE (kJ mol–1)	3.40
r2	0.92
Pearson’s r	0.96
Spearman’s ρ	0.97

^aDeviations and correlation between the LIE and alchemical calculations are expressed in terms of the root-mean-square error (RMSE), and the r², Pearson’s r, and Spearman’s ρ, respectively.

Figure 4.

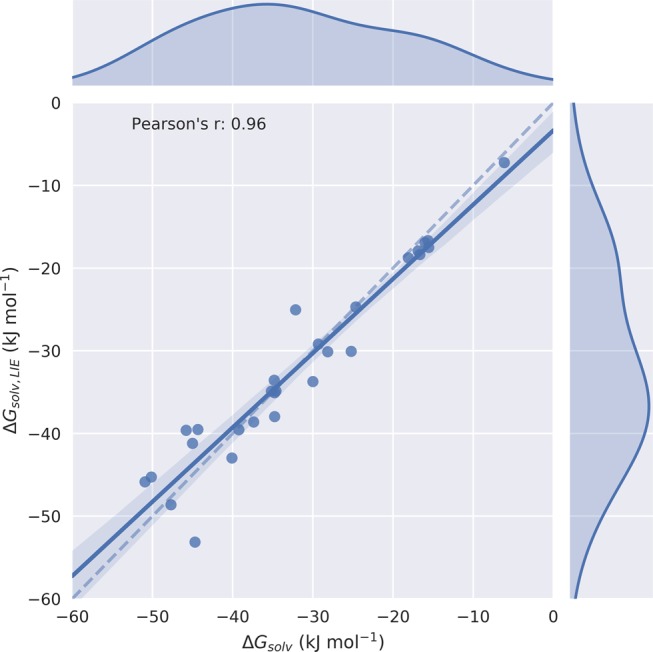
Scatter and kernel density plots of an LIE model to predict ligand solvation free energies ΔG_solv, which are linearly related to average ligand–solvent van der Waals (via LIE parameter α) and electrostatic interaction energies (via LIE parameter β) as obtained from independent simulations of the 28 unbound ligands in water solvent. Values for α and β are fitted based on ΔG_solv values computed from alchemical perturbation. The dashed line indicates an ideal correlation between the calculated and reference data, the solid line indicates the actually obtained correlations, and the shaded area indicates the 95% confidence interval.

Subsequently, we investigated if we could further improve our model by including the protein–ligand preorganization energy via the linear response approximation in the ALIE2 model. Table 2 shows that this did not lead to a further improvement in model performance when compared to the ALIE1 results, indicating that the preorganization term does not contribute significantly to trends in CYP2A6 binding for the considered compounds. This is confirmed by the relatively low values obtained for ⟨V_lig–surr^ele⟩_off (Table S3). Accounting for a possible nonlinear contribution of the electrostatic protein–ligand interaction energy to ΔG_prot (by evaluating ΔG_prot,ele via alchemical free-energy calculation in the ALIE3 model) did not lead to improved model performance compared to that of the ALIE1 model either, Table 2. We also assessed the effect of including more λ points into the calculation of ΔG_prot,ele (i.e., by going from 5 to 9 λ points with regular intervals) for three randomly chosen ligands in the data set (compounds 16, 20, and 23). By introducing more λ points in this way, we observed changes in ΔG_prot,calc ranging between 0.04 and 1.74 kJ mol^–1 only. In conclusion, the possible nonlinear change in electrostatic energy upon (de)coupling protein–ligand interactions (as we observed for several compounds, data not shown) could, in this case, still effectively be accounted by using β as a free parameter in the ALIE1 model. This is also illustrated by comparing the standard deviation error in the prediction (SDEP) of 9.3 kJ mol^–1 as obtained from leave-one-out cross-validation (LOO-CV) for ALIE1, with the corresponding SDEP values for the ALIE2 and ALIE3 models, which were with values of 9.2 and 9.0 kJ mol^–1 only 0.1 and 0.3 kJ mol^–1 lower, respectively. For these reasons, we focus below on the ALIE1 model, for which we included the SDEP and the associated LOO-CV correlation coefficient q² in Table S4 of the Supporting Information.

A Closer Look at the ALIE1 Model

To exclude a possible large effect on model performance of the data points that are outliers in the ALIE1 model in terms of their reference (compound 16) or calculated value (compound 22, Figure 3B), we generated ALIE1-like models, in which either of these two compounds was excluded from the training set (Table S4 and Figure S3). Our finding that compound 22 is an outlier in terms of ΔG_prot prediction (Figure 3B) may be due to the fact that this is the only hydroxyl-containing compound in our ligand set, and previously Åqvist and co-workers argued to calibrate different values for β for compounds with a different number of −OH groups.⁶⁵ We found that the quality of the ALIE1 model only moderately improves when excluding compound 22 from our data set: the RMSE decreases by 0.7 kJ mol^–1, whereas Pearson’s r and especially Spearman’s ρ do not change significantly (Table S4). On the other hand, LOO-CV shows a more substantial decrease of the SDEP and an increase in q² upon excluding compound 22 from the data set, Table S4. Encouragingly, when compound 16 (instead of 22) is excluded, the quality of the ALIE1 model only changes slightly. The RMSE and SDEP increase by 0.1 and 0.2 kJ mol^–1, respectively, and Pearson’s r and Spearman’s ρ are still above 0.7, while compound 16 is responsible for approximately 20% of the spread in reference data for ALIE1 model calibration (cf. Figure 3B). This implies that the model does not necessarily rely on compound 16 to show a significant correlation.

In a next step, we investigated if we could improve the ALIE1 model by including the γ offset parameter in eq 6 or by including effective corrections for the loss in ligand-configurational freedom and possible release of water molecules from the active site upon binding. We found that including γ as an additional free parameter in eq 6 does not significantly improve the model quality, which is especially apparent when comparing the obtained correlation with the ALIE1 performance, Table S4.

To account for possible differences among the considered compounds in their loss in configurational entropy upon protein binding, we added a correction term ΔG_rot to our binding free-energy calculations defined as

12

with N the number of rotatable bonds, k_B Boltzmann’s constant, and T the temperature.⁶⁶ In this way, we add a penalty per rotatable bond to the ligand binding free energies that is comparable to the corresponding estimates as reported in the literature, which range between 1.5 and 4 kJ mol^–1. In an attempt to also account for possible differences in the replacement of water molecules by the different ligands, we computed a free-energy correction ΔG_SASA for this based on the ratio of the ligand’s SASA (SASA_ligand) and the SASA of a water molecule (SASA_water), multiplied by a factor TΔS representing the entropy of a water molecule and set to 20 kJ mol^–1, as given by

13

To include ΔG_rot and ΔG_SASA into our ALIE1 model, we calibrated α and β in eq 6 based on the sum (ΔG_bind,exp + ΔG_solv + ΔG_rot + ΔG_SASA). The resulting model is presented in Table S4 and Figure S3D. Table S4 and Figure S3 also present the results for a similar model in which a value of TΔS = 6 kJ mol^–1 is used. From a comparison with Table 2 and Figure 3B, we find that incorporating the SASA term and number of rotatable bonds in this adapted model does not significantly change model performance compared to ALIE1, with (for different choices of TΔS in eq 13) maximal changes in correlation coefficients and RMSE (or SDEP) of only 0.07 and 0.25 kJ mol^–1, respectively.

LIE and ALIE1 Models for Cytochrome P450 2E1

As another test case, we calibrated and compared an LIE and ALIE1 model for a different CYP, i.e., Cytochrome P450 2E1 (CYP2E1), a hepatic enzyme responsible for alcohol metabolism.⁶⁷ We chose this protein because for the compounds of our CYP2A6 data set, we also have experimentally estimated ΔG_bind values available for CYP2E1 (ranging from −42.6 to −21.5 kJ mol^–1; Table S5). As for CYP2A6, these values were obtained using eq 5(39) and using inhibition data from Cashman and co-workers.^32,37 Obviously, for these compounds, we already have the rigorously calculated set of ΔG_solv values available from our alchemical free-energy calculations described above. The initial protein structure (with ID 3E6I(68)) was obtained from the PDB database. Missing loops were modeled with ModLoop.⁶⁹ Subsequent steps for structure preparation, docking, MD, and model calibration were identical as for our CYP2A6 modeling.

The performance and parameters of our LIE and ALIE1 models for CYP2E1 binding are summarized in Table 4 and Figure 5. As observed for CYP2A6, the ALIE1 approach led to a clearly enhanced correlation between the calculated and reference data. For our ALIE1 model for CYP2E1, Pearson’s r = 0.75 and Spearman’s ρ = 0.73, which are to be compared to LIE values of 0.36 and 0.23, respectively. Table 4 additionally shows that β is in the ALIE1 model again closer to its theoretical value of 0.5 than when using traditional LIE (0.57 vs 0.20), and we find the same ligand (compound 22) as a predicted outlier. We also find a higher RMSE value for the ALIE1 model of CYP2E1 than for its LIE model, which is, as in the case of CYP2A6, in line with the accompanying increase in the spread of absolute values for the reference calibration data, Figure S4. We note that different α and β values are obtained for the ALIE1 (and for the LIE) models for CYP2A6 and CYP2E1, cf. Tables 2 and 4. This prevented us from using a single model for CYP2E1 vs CYP2A6 binding selectivity prediction for the compounds of interest.

Table 4. Model Parameters for the LIE and ALIE1 Models of CYP2E1, Together with Respective Root-Mean-Square Errors (RMSEs, with Respect to Experiment) and Correlation Metrics for the Set of Compounds Considered in This Work.

	LIE	ALIE1
α	0.70	0.40
β	0.20	0.57
RMSE (kJ mol–1)	5.14	8.81
r2	0.13	0.56
Pearson’s r	0.36	0.75
Spearman’s ρ	0.23	0.73

Figure 5.

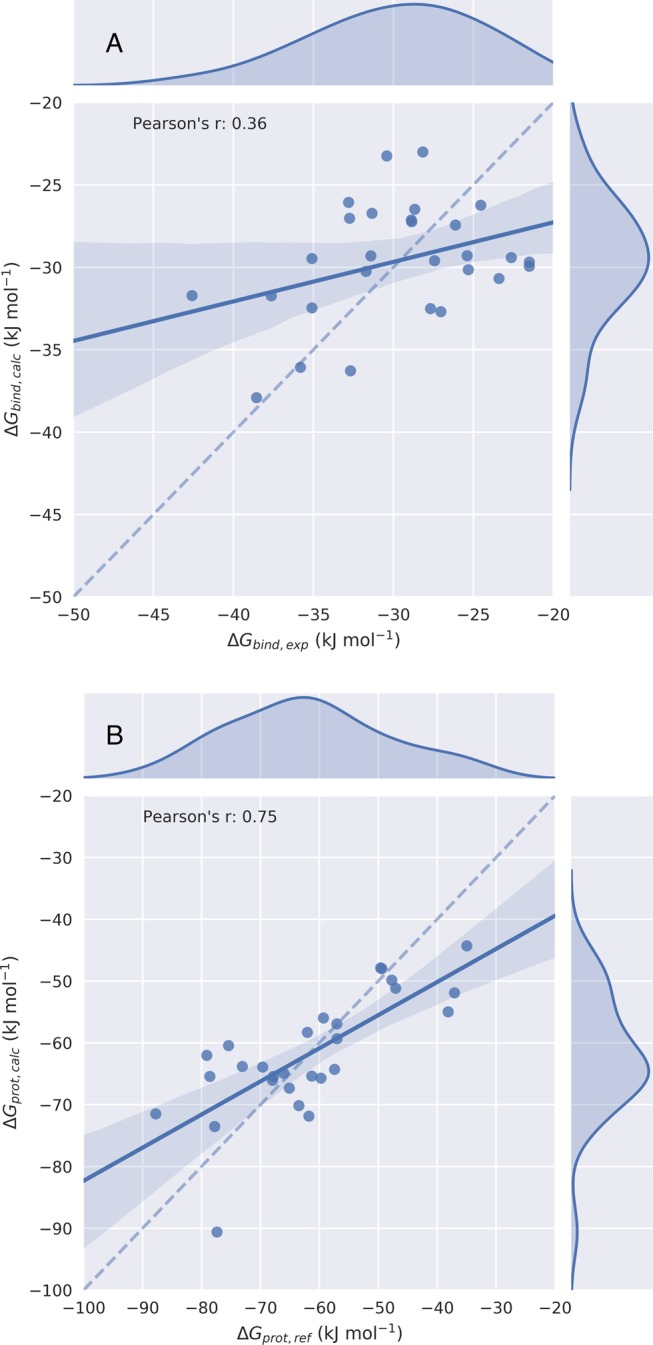
Scatter and kernel density plots of the LIE (A) and ALIE1 (B) models for CYP2E1 binding free-energy calculation, illustrating the obtained correlations between calculated free energies ΔG_bind,calc or ΔG_prot,calc and their respective reference values. Dashed lines indicate an ideal correlation between the calculated and reference data, solid lines indicate the actually obtained correlations, and shaded areas indicate 95% confidence intervals.

Conclusions

We showcase here several adapted LIE models based on modifications of a Boltzmann-like weighted LIE approach for calculating protein–ligand binding free energies. By separately computing ligand solvation free energies (using alchemical perturbation) and evaluating protein–ligand interactions from MD of the bound state, we were able to obtain an adapted LIE model with a high correlation between reference binding data and the calculated results. For that purpose, we solely needed to run short (1 ns production) MD simulations of the protein-bound state in combination with alchemical free-energy calculations of the unbound state only. Pearson’s r and Spearman’s ρ values increased from 0.18 and 0.16 for the traditional LIE model to 0.77 and 0.76, respectively. By including alchemical ligand solvation free-energy calculations into an LIE model for the same set of compounds binding to a different Cytochrome P450 (CYP2E1), a similar increase in correlation was obtained.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.9b00890.

• Weights per ligand of individual simulations in the ALIE1 model (Table S1); solvation free energies and associated error estimates as calculated for the studied molecules (Table S2); average ligand–surrounding interaction energy from MD simulations of the interacting and noninteracting protein–ligand complex (Table S3); statistics of the ALIE1 model including some parameters (Table S4); experimental ΔG_bind values of compounds used in this study against CYP2E1 (Table S5); comparison of selected ligand binding starting poses for MD simulations used in the ALIE1 model (Figure S1); comparison of distributions of calculated and reference CYP2A6 ΔG_bind values within the LIE and ALIE models (Figure S2); effect of exclusion and inclusion of several data points and parameters (Figure S3); and comparison of distributions of calculated and reference CYP2E1 ΔG_bind values within the LIE and ALIE1 models (Figure S4) (PDF)

The authors declare no competing financial interest.