Simulation of Gating Currents of the Shaker K Channel Using a Brownian Model of the Voltage Sensor

Abstract

The physical mechanism underlying the voltage-dependent gating of K channels is usually addressed theoretically using molecular dynamics simulations. However, besides being computationally very expensive, this approach is presently unable to fully predict the behavior of fundamental variables of channel gating such as the macroscopic gating current, and hence, it is presently unable to validate the model. To fill this gap, here we propose a voltage-gating model that treats the S4 segment as a Brownian particle moving through a gating channel pore and adjacent internal and external vestibules. In our model, charges on the S4 segment are screened by charged residues localized on neighboring segments of the channel protein and by ions present in the vestibules, whose dynamics are assessed using a flux conservation equation. The electrostatic voltage spatial profile is consistently assessed by applying the Poisson equation to all the charges present in the system. The treatment of the S4 segment as a Brownian particle allows description of the dynamics of a single S4 segment using the Langevin stochastic differential equation or the behavior of a population of S4 segments—useful for assessing the macroscopic gating current—using the Fokker-Planck equation. The proposed model confirms the gating charge transfer hypothesis with the movement of the S4 segment among five different stable positions where the gating charges interact in succession with the negatively charged residues on the channel protein. This behavior produces macroscopic gating currents quite similar to those experimentally found.

Significance

A, to our knowledge, new modeling approach to explore the mechanism of voltage-dependent gating, based on the description of the channel voltage sensor as a Brownian particle, is presented. The model starts from the structural, geometrical, and electrostatic properties of the voltage sensor domain of the Shaker channel to predict both the voltage sensor dynamics and the macroscopic gating current. The model qualitatively predicts all the main features of the Shaker channel voltage-dependent gating and explains them in terms of the electrostatic potential profile originating from all the charges present in the system.

Introduction

Voltage-gated K (Kv) channels promote the transmembrane flux of K ions in response to a plasma membrane depolarization. They are formed by four subunits surrounding a central permeation pore, each consisting of six transmembrane α-helical segments. The first four segments, S1–S4, form the voltage sensor domain (VSD), able to change its conformation in response to a membrane depolarization and allosterically promote the opening of the pore domain formed by the S5 and S6 segments. Mutational and electrophysiological analysis has identified the S4 segment as the main voltage-sensing structure within the VSD. In most Kv channels, this structure contains a series of six positive residues (R1–R4, K5, and R6) placed at every third position along the primary structure; the first four of the series (R1–R4), called gating charges, are thought to couple the membrane voltage changes to the transmembrane movement of the S4 segment and channel opening (1, 2, 3).

Gating charge movement along the membrane electrical gradient can be detected as a small capacitive current, known as gating current, whose time integral at large depolarizations gives a measure of the total charge being transferred that for the most studied Kv channel, the Shaker channel, amounts to 12–14 elementary charges, e₀ (1, 2, 4). Gating currents of the Shaker channel have been studied in detail in the attempt to obtain information on the mechanism underlying the voltage-sensor conformational changes in response to membrane depolarization. Although the gating current of a single channel cannot be detected directly because of technical limits, fluctuation analysis of the macroscopic gating current is consistent with the presence of “shot events” of charge movements amounting to ∼2.4 e₀ (5). At the macroscopic level, the ON and OFF gating currents recorded in response to depolarization show complex properties depending on the stimulation protocol used, decaying mono- or biexponentially for small depolarizations, and showing an initial rising phase for larger depolarizations. This complex behavior suggested the presence of multiple discrete and energetically stable conformational states for the S4 segment, separated by high energy barriers, that were interpreted using discrete Markov models (DMMs; (6, 7, 8, 9)). In the absence of structural information, these models considered the energetic landscape encountered during state transitions as a parameter rather than being assessed from structure by applying physical laws. The difficulties involved with using DMMs are larger than sometimes realized because the energetic landscape must vary substantially with conditions and transmembrane potential to satisfy the fundamental laws of electrodynamics. Neglecting this variation can produce exponentially large errors in calculations of flux (10).

The successful application of x-ray crystallography to Kv1.2 and Kv1.2/Kv2.1 chimera channels provided the first three-dimensional (3D) structure of a VSD in its activated conformation (11, 12), and indicated that the S4 segment is tilted away from the S1 and S2 helices to form an extracellular water-accessible vestibule penetrating ∼10 Å below the membrane surface. The positive residues on the S4 segment are in direct contact with the aqueous solution, and some are further stabilized by conserved (among Kv channels) external (E183 and E226) and internal (E154, E236, D259) negative clusters, separated by a water-inaccessible phenylalanine (F233) located near the midpoint of the membrane (12). Mutagenesis experiments suggest that F233, together with two negatively charged amino acids of the internal negative cluster, forms a gating charge transfer center (GCTC) that interacts in succession with the R1 to K5 positive residues of the S4 segment during channel gating (13). Based on these results, it has been proposed that the S4 segment, in addition to the activated and the resting state, can enter three more stable positions corresponding to the specific positive gating charges occupying the GCTC (13). This view would provide the structural basis for the multiple kinetic states predicted by DMMs, yet a theory consistent with electrodynamics is needed to calculate how these states vary with conditions, e.g., transmembrane potential.

The new crystallographic data of Shaker channels in the activated state soon inspired a number of different computational studies based on molecular dynamics (MD) or Rosetta modeling, aimed at predicting the movement of the S4 segment during gating and the architecture of the channel in the resting and intermediate (closed) states (14, 15, 16, 17, 18, 19, 20, 21, 22). Interestingly, these approaches, when constrained with selected experimental data, reached a consensus regarding the predicted architecture of the resting state of the channel. Namely, the S1–S3 helices virtually retain the conformation assumed in the activated state, whereas the S4 segment appears rotated and translated inward by ∼10 Å, with the R1 residue located extracellularly to F233 (23); (it needs to be stressed, however, that the resting state proposed contrasts with some experimental results that would instead place the R1 residue in the GCTC; see (13, 24)). These computational studies have also found evidence for the presence of three stable intermediate states of the voltage sensor (17, 25), confirming the conclusion previously reached using DMMs, and consistent with the more recent GCTC hypothesis. In only one case, long (hundreds of microseconds) MD simulations while applying strong voltage pulses show an S4 movement toward the resting state that follows the classical helical screw-sliding helix as the most likely mechanism, with the gating charges never exposed to the lipid hydrophobic environment but forming intermediate salt bridges with the external and internal negative clusters (23).

Although potentially very useful for understanding the physics of the voltage-dependent gating, MD simulations suffer for being computationally very expensive and hence unable to access sufficiently long timescales or report the dynamics of a population of homogeneous channels, as needed to predict the kinetics of macroscopic gating currents. To fill this gap, a number of studies have used more macroscopic models able to start from the available structural data of the VSD and predict macroscopic gating currents, with a computational effort that can be more easily achieved (26, 27). A first model of this type applied coarse-grained MD on the available Kv1.2 open crystal structure and intermediate and resting model structures to assess the energetic profile encountered by the voltage sensor during its activation. This energetic profile was then used in a Langevin dynamics to predict the macroscopic gating current in response to a depolarizing step (28, 29, 30). Notably, this multiscale modeling approach was able to predict the main kinetic features of the gating current such as the initial fast component and the rising phase present at relatively depolarized potentials. Another, more macroscopic model of voltage-dependent gating was proposed by Horng et al. (27). In this model, the gating charges attached to the S4 segment through hook springs were allowed to move through the gating pore and intracellular and extracellular vestibules using a Poisson-Nernst-Planck formalism. Namely, arginine residues were treated as particles whose diffusion inside the VSD was described by a Nernst-Planck equation, considering the movement of a particle in response to an electrical and chemical gradient. The electrostatic potential profile was self-consistently computed using the Poisson equation and considering all the charges present in the system. By adjusting the free parameters of the model (essentially represented by the spring constants and mobility of the particles), the authors were able to reproduce the main features of the gating currents experimentally observed for Shaker channels. Unfortunately, the model did not consider the fixed countercharges that are known to be very important in voltage-dependent gating, and the interaction of the VSD and protein was described with the inclusion of a potential profile.

Along the line of the above-described models, here we propose a novel voltage-gating model that treats the S4 segment as a Brownian particle moving in one dimension through a water-inaccessible gating channel pore and adjacent internal and external water-accessible vestibules, delimited by the remaining parts of the VSD (S1–S3 segments). The treatment of the S4 segment as a Brownian particle allows to describe the dynamics of a single S4 segment using the Langevin stochastic differential equation, or the behavior of a population of S4 segments using the Fokker-Planck (FP) equation to assess the probability density function of finding the particle in the various allowed positions. With these two different approaches, our model can predict the trajectory of a single S4 segment or, alternatively, the macroscopic gating currents.

Methods

Assessment of the Shaker K channel 3D structure by homology modeling

In our model, the geometrical and electrostatic properties of the VSD are derived from the 3D structure of the channel under study (cf. below). Although this structural information is presently available for the Kv1.2 and Kv1.2/Kv2.1 channel chimera, most of the functional data (i.e., gating and ionic current measurements) have been obtained from the Shaker K channel (cf. Introduction). Although these two K channels have a high degree of homology and are thus expected to have a very similar 3D structure (12), differences in charged residues in relevant positions of the VSD may well change the details of their gating behavior. We thus proceeded to generate a 3D structure of the Shaker K channel by homology modeling, using the SWISS-MODEL environment (31, 32, 33) and the Kv1.2/Kv2.1 chimera as a template.

Homology modeling, also known as comparative protein structure modeling, is a computational approach to build 3D structural models for proteins using experimental structures of related protein family members as templates. It generates the structural coordinates of the model based on the mapping between the target residues and the corresponding amino acids of the structural template. Regions of the protein for which no template information is available (i.e., insertions and deletions in loop regions) are built from libraries of backbone fragments or by de novo reconstruction by constrained dynamics. Local suboptimal geometry of the models obtained (i.e., distorted bonds, angles, and too close atomic contacts) are finally regularized by limited MD. The Shaker channel primary sequence (accession P08510.3) was first aligned to the Kv1.2/Kv2.1 chimera using the PDBviewer software v4.10 (see Fig. S1 F), and then the two aligned sequences, together with the 3D coordinates of the Kv1.2/Kv2.1 chimera, were sent to the SWISS-MODEL web site to find the 3D structure for the Shaker K channels. As shown in Fig. S1 A, the 3D structure model for the Shaker channel appears very similar to that experimentally found for the Kv1.2/Kv2.1 channel chimera, as expected from the very high similarity of the two protein sequences.

Notwithstanding, several residues predicted to reside close to the S4 segment appear to be differently charged in the VSDs of the two channels (see Fig. S1 A, where the negative and positive residues of the two structures are colored in red and yellow, respectively, and the gating charges on the S4 segment in magenta). This is especially evident in their external vestibules, with the Shaker VSD charge density profile displaying a strongly negative charge density peak not present in the chimera channel, originating from several charged residues localized in the loops connecting the helices. Diverse dynamics of the S4 segment in the two channels, due to the marked difference in the electrostatic voltage profile along their gating pores and vestibules, can thus be envisaged. This peculiar feature is expected to stabilize the S4 segment in its activated position, in accordance with a Q-V relationship shift to more hyperpolarized voltages found for the Shaker K channel as compared to the Kv1.2 channel, which has a fixed charge profile virtually identical to the Kv1.2/Kv2.1 chimera (8, 34).

The use of a homology model of the Shaker K channel is quite justified by the high similarity of its primary structure with that of the Kv1.2/Kv2.1 chimera channel (cf. Fig. S1). The reader should, however, be aware that the resulting structural features of the Shaker channel are hypothetical, and subtle differences with the real channel (whose crystal structure is not presently available) may occur.

Structure of the VSD

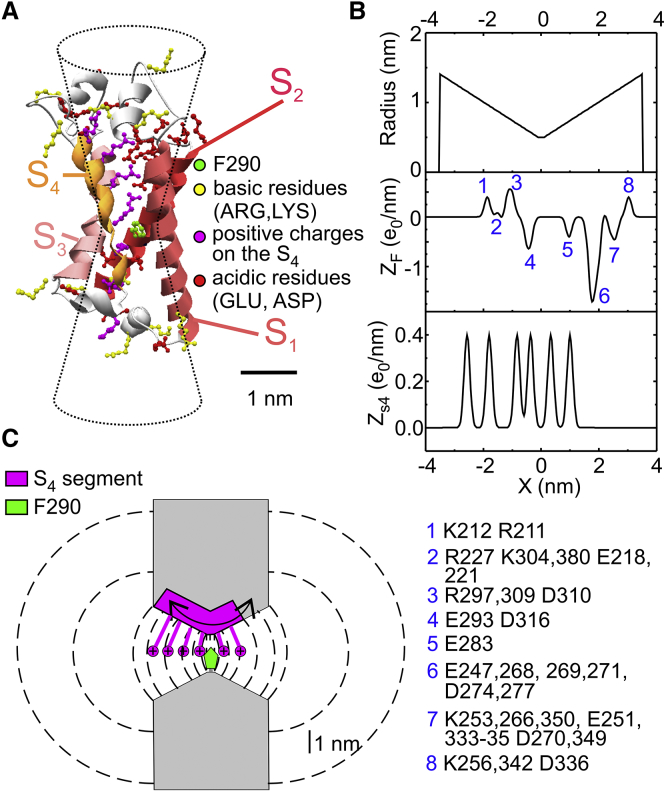
In our model, the VSD was approximated by an hourglass-shaped geometrical structure consisting of a water-inaccessible cylindrical gating pore (0.2 nm long and with a diameter of 1 nm). These spatial values were chosen on the assumption that the water-inaccessible gating pore is represented by the aromatic ring of F290, whose thickness and planar dimension are close to 0.2 and 1.0 nm, respectively. The gating pore is flanked by internal and external water-accessible vestibules (3.4 nm long each and a conical shape opening with a half angle of 15° into two hemispherical subdomains of bath solution; Fig. 1, A and B). As shown in Fig. 1 A, this geometrical shape is well-adapted to that of the vestibules inferred from the 3D crystal structure, and a vestibule length of 3.4 nm ensures that the S4 segment remains within the vestibules for all its allowed positions. The water-inaccessible gating pore was located at the level of the F290 residue, proposed to separate the internal and external vestibules of the VSD. This symmetrical geometry allows the formulation of the model in one spatial dimension, consisting of a main axis perpendicular to the membrane and passing through the gating pore. In the numerical simulation, the main axis was divided into subdomains of constant step size within the VSD and a step size increasing geometrically going outwards in the two bath solutions. Using this subdivision, the surfaces separating adjacent subvolumes were circles inside the gating pore, spherical caps in the vestibules, and hemispheres in the baths, each one perpendicularly contacting the channel wall (dashed lines in Fig. 1 C).

Figure 1.

(A) Model of the Shaker 3D structure obtained by homology modeling using the Kv1.2/Kv2.1 chimera structure (2R9R) as template. Gating charges on the S4 segment are in magenta, whereas negative and positive residues located in the remaining segments of the VSDs are in red and yellow, respectively. The residue F290 (homologous of F233 in the chimera channel) is in green. The hourglass-shaped drawing superimposed on the Shaker structure represents the geometry used in our model to delimit the gating pore and vestibules. (B) Profiles of the gating pore radius, the fixed charge density located in the S1–S3 region of the VSD (Z_F), and the charge density on the S4 segment (Z_S4), for the Shaker model structure. For symmetrical reasons, x = 0 was assumed to coincide with the center of the gating pore, where F290 is located. The blue numbers on the Z_F plot and the associated legend at the bottom identify the residues contributing to the various peaks of the profile. (C) Schematics showing the geometry of the VSD assumed in our model. The S4 segment containing the six gating charges was assumed to move perpendicular to the membrane through the gating pore (0.2 nm long) and the extracellular and intracellular vestibules (each 3.4 nm long and opening with a half angle of 15°). The dashed lines represent some of the surfaces delimiting the volume elements considered in our numerical simulations (see text for details).

As emphasized in Fig. 1 C, the S4 segment does not occupy space in either vestibule because it contributes to forming the vestibule walls together with the other parts of the VSD (S1–S3), in accordance with the available crystal structure showing that the extracellular vestibule is formed by a departure of the S3–S4 segments from the S1–S2 segments (12). With regard to the charges on the S4 segment, we explicitly consider them by letting them contribute to the charge density of the volume grids together with the charges carried by the other parts of the VSD (fixed charges) and by freely moving ions. The S4 charge profile (Z_S4, expressed in e₀ units) was built by considering six positive charges, whose mean distance was determined from the position of the charged atoms in the crystal structure and each giving rise to a charge profile normally distributed with a standard deviation of 0.1 nm (Fig. 1 B). The resulting charge spreading over a region of a few angstroms arises from the flexible locations and thermal motion of the charged residues. Notice that the charged atoms at the top of the arginine and lysine lateral chains seem to maximize their distance in the crystal structure so that the peak-to-peak distance in the Z_S4 profile is sensibly larger than the 4.5–6.0 Å expected for Cα carbons of the corresponding residues in an α (or α3–10) helix (inset to Fig. S1). The fixed charged profile (Z_F, expressed in e₀ units) was similarly built by considering all the charges of the S1-S3 segments of the VSD (Fig. 1 B). For the several charges belonging to the loop helices, we did not consider an extra flexibility in this model, although these regions are probably more unstructured and mobile. In our model, the S4 segment was assumed to be a rigid body, its position being represented by the variable x_S4, expressing the distance of the midpoint between R2 and R3 from the center of the gating pore. The position of the S4 segment in Fig. 1 B corresponds to x_S4 = 0, and during the simulation, it was allowed to move through the gating pore and vestibules up to a maximal displacement x_S4 of ±1.8 nm, a movement that enables all the gating charges (R1 to K5) to reach the GCTC.

Ion electrodiffusion

We assumed that the intracellular and extracellular faces of the VSD are bathed by ionic solutions containing 140 mM of positively and negatively charged monovalent ions that can freely move in the baths and vestibules of the VSD with a diffusion constant of 2 × 10⁻⁹ m/s² but cannot enter the gating pore (diffusion coefficient of zero there). Because of water and ion inaccessibility, the gating pore was assumed to have a relative dielectric constant (ε = 4, the value typical of protein interior) much lower than in the bathing solution (ε = 80; cf. Fig. S1 E). Ions were subject to electrodiffusion governed by the following flux conservative equation:

$$\frac{d{C}_j\left(x,t\right)}{dt}=-\mathit{\nabla }{F}_j\left(x,t\right),$$ (1)

where C_j(x, t) is the concentration of ion j, t is time, $\mathit{\nabla }$ is the spatial gradient operator, and F_j(x, t) is the flux (mole per second per unit area) of ion j given by the Nernst-Planck equation:

$$F_j\left(x,t\right)=-D_j\left(x\right)\left[\mathit{\nabla }{C}_j\left(x,t\right)+\frac{z_{j}F}{RT}{C}_j\left(x,t\right)\mathit{\nabla }V\left(x,t\right)\right],$$ (2)

where D_j(x) and z_j are the diffusion coefficient profile and the valence of ion j, respectively; F, R, and T have their usual meanings; and V(x, t) is the electrical voltage profile.

Movement of the S4 segment

The S4 segment was assumed to move in one dimension as a Brownian particle, whose dynamics is governed by the following Langevin equation:

$$m\frac{d^2{x}_{S4}\left(t\right)}{dt}=F_{ex}\left(x_{S4},t\right)-\gamma \frac{d{x}_{S4}\left(t\right)}{dt}+R\left(t\right).$$ (3)

Here, x_S4(t) represents the position of the voltage sensor (distance between the R2–R3 midpoint and the center of the gating pore), m is the mass of the particle, F_ex(x_S4, t) is the external (electrical) force acting on the particle, and R(t) is a random force due to the collision of the fluid and the rest of the protein on the S4 segment, which has a probability distribution with zero mean and second moment given by

$$\langle R\left(t\right)R\left(t^{\text{'}}\right)\rangle =2\gamma k_{B}T\delta \left(t-t\text{'}\right),$$ (4)

where k_B is the Boltzmann constant and δ is the delta function. γ, the friction coefficient of the S4 voltage sensor, was set to 4 × 10⁻⁶ kg/s, a value that provided a gating current rate similar to that experimentally observed. Notice, however, that the shape of the gating current, as well as the steady-state Q-V relationship, remains unaltered when varying γ (cf. Fig. S6).

In the very high friction limit, the acceleration of the particle may be assumed to be zero, hence the Langevin equation reduces to

$$\frac{d{x}_{S4}\left(t\right)}{dt}=\raisebox{1ex}{$F_{ex}\left(x_{S4},t\right)$}\!\left/ \!\raisebox{-1ex}{$\gamma $}\right.+r\left(t\right),$$ (5)

which may be written in the form of the following stochastic differential equation:

$$d{x}_{S4}\left(t\right)=\left(\raisebox{1ex}{$F_{ex}\left(x_{S4},t\right)$}\!\left/ \!\raisebox{-1ex}{$\gamma $}\right.\right)dt+\sqrt{\frac{2k_{B}Tdt}{\gamma }}\varphi \left(t\right),$$ (6)

where ϕ(t) represents a normally distributed random variable with zero mean and unitary variance. Based on Eq. 6, the position of the particle may be found at each time step dt, as $x_{S4}=x_{S4}^{old}$+$d{x}_{S4}$, where $x_{S4}^{old}$ represents the starting position of the particle. As already stated, the particle was allowed to freely move in the range x_S4 = ±1.8 nm by imposing elastic boundary conditions. This was achieved by using the following relationships for resetting the position of the particles moving outside the allowed region:

$$x_{S4}^r=x_{S4}+\left(-1.8\mathrm{nm}-x_{S4}\right)\text{if}{x}_{S4}<1\text{.}8\text{nm}$$

$$x_{S4}^r=x_{S4}-\left(x_{S4}-1.8\mathrm{nm}\right)\text{if}{x}_{S4}>1\text{.}8\text{nm}$$

In our model, the external force acting on the S4 segment, F_ex(x_S4, t), is represented by the electrical force due to the voltage gradient acting on the gating charges:

$$F_{ex}\left(x_{S4},t\right)=-e_0\int Z_{mS4}\left(\mathit{ϵ}\right)\left(\frac{dV\left(\mathit{\epsilon },t\right)}{d\mathit{\epsilon }}\right)d\mathit{ϵ},$$ (7)

where Z_mS4(ϵ) = Z_S4(ϵ + x_S4) represents the gating charge spatial distribution when the S4 segment is positioned at x_S4.

Assessment of the electrical voltage

The electrical voltage profile V(x) was assessed from the net charge density profile ρ(x) using the following Poisson equation (35):

$${\epsilon }_0\left[\frac{d}{dx}\left(\epsilon \left(x\right)\frac{dV\left(x\right)}{dx}\right)+\epsilon \left(x\right)\frac{dV\left(x\right)}{dx}\frac{dlnA\left(x\right)}{dx}\right]=-\rho \left(x\right),$$ (8)

where ε₀ = 8.854 × 10⁻¹² F/m is the vacuum permittivity, ε(x) is the position-dependent dielectric coefficient, V(x) is the electric potential, and A(x) is the position-dependent surface. The charge density profile was assessed by including the gating charges, the fixed charges present in the remaining part of the VSD (Z_F, Fig. 1 B), and the ions in solution:

$$\rho \left(x\right)=\frac{e_0\left(Z_F\left(x\right)+Z_{mS4}\left(x\right)\right)}{A\left(x\right)dx}+e_0\sum _j{z}_j{C}_j\left(x\right),$$ (9)

where e₀ is the elementary charge, Z_F(x) and Z_mS4(x) are the fixed and gating charge density profiles, and z_j and C_j(x) are the valence and concentration of ion j.

Simulation of the dynamics of a single S4 segment

In our simulation of a single S4 segment, Eqs. 1, 6, and 8 were discretized in space and time using a variable step size (dx = 0.33 Å in the VSD and an increasing step size dx_i = 2 × dx_{i − 1} going far in the baths) and a time step of 6 ns. Both Eqs. 1 and 8 were solved using a fully implicit method and an appropriate algorithm for tridiagonal matrix equations, whereas the stochastic differential Eq. 6. was solved using a normally distributed random number generator from (36).

The FP equation

The dynamics of the S4 segment may also be described in terms of the time evolution of the probability density function profile, given by the following FP equation:

$$\frac{\partial f_{S4}\left(x,t\right)}{\partial t}=-\frac{\partial \left(\mu \left(x\right)f_{S4}\left(x,t\right)\right)}{\partial x}+\frac{k_{B}T}{\gamma }\frac{{\partial }^2{f}_{S4}\left(x,t\right)}{\partial x^2}.$$ (10)

Here, f_S4 represents the probability density function for the position of the S4 segment and μ(x) is $\raisebox{1ex}{$F_{ex}\left(x_{S4},t\right)$}\!\left/ \!\raisebox{-1ex}{$\gamma $}\right.$. This partial differential equation was solved with elastic boundary conditions at x = ±1.8 nm to set the allowed movement of the particle to 3.6 nm. The elastic boundary condition was imposed by setting the particle flux equal to zero at the boundaries (37):

$$Flux={\left(\mu f-\frac{k_{B}T}{\gamma }\frac{\delta f\left(x,t\right)}{\delta x}\right)}_{x=\pm 1.8\mathrm{nm}}=0.$$ (11)

The solution of the FP equation relies on the possibility of finding a good description of the position-dependent drift velocity μ. This is not a trivial issue because μ will actually depend also on the relaxation time of electrolyte ions around the S4 segment, which, in turn, will affect the electrical voltage and the external force acting on the segment. For this reason, if one considers the full model that includes electrolyte ion dynamics (Eq. 1), μ will become also a function of time, making nontrivial the numerical solution of the FP equation. To solve this problem, in the solution of the FP equation, we assumed steady state for the dynamics of the electrolyte ions:

$$\frac{d{C}_j\left(x,t\right)}{dt}=0,$$ (12)

where C_j(x, t) represents the concentration of ion j. The validity of this approximation, which is based on the finding that ions relax on a timescale much faster than the movement of the S4 segment, is fully demonstrated in the Supporting Materials and Methods (cf. paragraph “Validation of the steady-state approximation for ion dynamics in the solution of the Fokker-Planck equation”). This approximation allowed us to find a steady-state solution for the ion concentration and electrical voltage profiles for each allowed position of the S4 segment within the volumes grid used in the numerical simulation. As a consequence, a μ spatial profile could easily be found with Eq. 7 and used during the time-dependent simulation of the voltage sensor.

Assessment of gating current

The dynamics of the probability density function f_S4(x, t) was then used to estimate the macroscopic gating current. Because our main goal was to compare the output of the model with the experimental results, we computed the gating current exactly as it is normally done in experiments, that is, by assessing the ionic current measured at the intracellular and extracellular electrodes positioned far from the VSD (I_gL and I_gR, respectively; the equations of electrodynamics guarantee exact equality of total current in one-dimensional series systems like ours. Thus, we can measure the current anywhere and be confident it is the current everywhere). More specifically, because the solution of the FP equation required the steady-state approximation for the electrolyte ions dynamics (cf. above), the ionic current present at position x and time t, i_ions(x, t), could not be directly obtained from Eq. 2. It was instead assessed by analyzing the net charge changes (with time) in the left (or alternatively in the right) bath, on the assumption that ions cannot pass through the gating pore, and by applying charge conservation equations (cf. also Supporting Materials and Methods, “Validation of the model: conservation of the total current”):

$$i_{ions}\left(x,t\right)=\frac{d}{dt}\underset{x}{\overset{x_{pl}}{\int }}A\left(x\right)F\left(\sum _{j=0}^{nions-1}{c}_j\left(x,t\right)z_j\right)dx=-\frac{d}{dt}\underset{x_{pr}}{\overset{x}{\int }}A\left(x\right)F\left(\sum _{j=0}^{nions-1}{c}_j\left(x,t\right)z_j\right)dx,$$ (13)

where x_pl and x_pr are the left and right edges of the gating pore, F is the Faraday constant, and z_j and C_j(s, t) are the valence and concentration of ion j. Using Eq. 13. the gating current may be assessed as the ionic current present at the extremes of the simulated region (at x = 0 and x = L) by mediating over all possible positions of the S4 segment, weighting with the density function f_S4(x₄, t):

$$I_{gL}\left(x,t\right)=\underset{-x_L/2}{\overset{x_L/2}{\int }}{i}_{ions}\left(0,t\right)f_{S4}\left(x_{S4}\right)d{x}_{S4}=\frac{d}{dt}\underset{-x_L/2}{\overset{x_L/2}{\int }}\left[\underset{0}{\overset{x_{pl}}{\int }}A\left(x\right)F\left(\sum _{j=0}^{nions-1}{c}_j\left(x,t\right)z_j\right)\right]f_{S4}\left(x_{S4}\right)d{x}_{S4},$$ (14)

$$I_{gR}\left(x,t\right)=\underset{-x_L/2}{\overset{x_L/2}{\int }}{i}_{ions}\left(L,t\right)f_{S4}\left(x_{S4}\right)d{x}_{S4}=\frac{d}{dt}\underset{-x_L/2}{\overset{x_L/2}{\int }}\left[\underset{x_{pr}}{\overset{L}{\int }}A\left(x\right)F\left(\sum _{j=0}^{nions-1}{c}_j\left(x,t\right)z_j\right)\right]f_{S4}\left(x_{S4}\right)d{x}_{S4},$$ (15)

where I_gL(x, t) and I_gR(x, t) are the gating currents assessed from the charge changes in the left and right bath, respectively. We verified in every simulation that identical results were obtained from Eqs. 14 and 15. The details in the model implementation may be found in the C code made available as Data S1.

Results and Discussion

In our model, the geometrical and electrostatic properties of the VSD have been taken from the 3D structure of the Shaker K channel derived by homology modeling, using the available Kv1.2/Kv2.1 chimera structure as a template (Fig. 1 A; see Supporting Materials and Methods). In accordance with this structure, we modeled the VSD as an hourglass-shaped geometrical structure made by a short water-inaccessible cylindrical gating pore flanked by internal and external water-accessible conical vestibules (dashed drawing in Fig. 1 A). The water-inaccessible gating pore was located at the level of the F290 residue (corresponding to F233 of the Kv1.2/Kv2.1 chimera channel), proposed to separate the internal and external vestibules of the VSD. As emphasized in Fig. 1 C, the S4 segment does not occupy space in the vestibules because it contributes to forming the vestibule walls together with the other transmembrane segments of the VSD (12).

The model explicitly considers the six positively charged residues on the S4 segment by letting them contribute to the S4 charge density profile (Z_S4, Fig. 1 B). By analogy, the fixed charge density profile (Z_F, Fig. 1 B) was built by considering the position of all the positive and negative charges of the S1–S3 segments of the VSD (marked as red and yellow residues in the 3D structure of Fig. 1 A). The S4 segment (i.e., its charge density profile) was allowed to move as a rigid body along the gating pore and vestibules by Brownian dynamics, and the electrolyte ions located in the vestibules and surrounding baths were subject to electrodiffusion governed by a flux conservative equation. Finally, both ions and the S4 segment dynamics were driven by an electrostatic potential self-consistently assessed by considering all the charges present in the system using the Poisson equation (see Supporting Materials and Methods for details of the model).

Dynamics of a single S4 segment

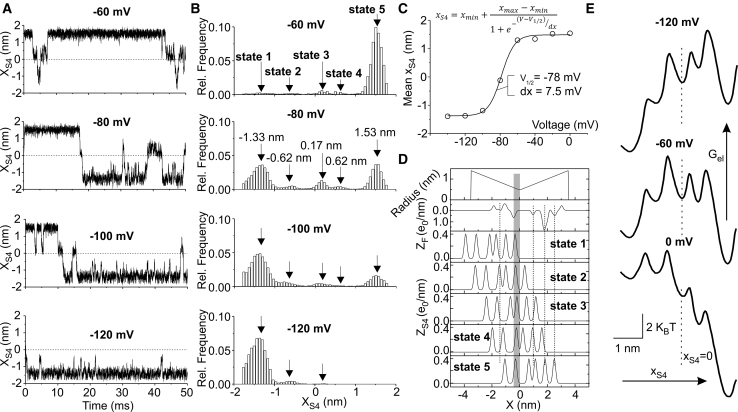
Fig. 2 A shows representative simulations of the dynamics of the S4 segment, obtained by solving the stochastic differential Langevin equation at four different applied membrane voltages. The time-dependent variable x_S4 plotted in Fig. 2 A represents the position of the S4 segment, namely the distance of the midpoint between its R2 and R3 residues from the center of the gating pore, where F290 is located. When x_S4 = 0, the S4 segment is positioned halfway along its allowed pathway from its furthest intracellular and extracellular positions (x_S4 = ±1.8 nm; Supporting Materials and Methods). Several features are evident from these stochastic simulations. First, the S4 segment tends to assume deep intracellular positions (x_S4 negative) at very negative voltages (i.e., −100/−120 mV), whereas the opposite occurs at more depolarized voltages, with the S4 segment mostly residing in the fully activated state (i.e. at −60 mV). This voltage dependence can be better appreciated in Fig. 2 C, in which the mean position of the S4 segment, assessed from 100 ms long simulations, is plotted as a function of the membrane voltage and fitted with a Boltzmann relationship (V_1/2 = −78 mV and dx = 7.5 mV; fitted curve). Second, while moving along its activation pathway, the S4 segment tends to spend most of its time around five specific positions, as evident from the five clear peaks (indicated by arrows) in the x_S4 amplitude histograms of Fig. 2 B. Fig. 2 D illustrates the position of the S4 charge density profiles (Z_S4) at the five identified preferential positions of the S4 segment. As a first approximation, these five positions correspond to the five gating charges on the S4 segment, R1–K5, occupying in turn the GCTC (marked by the gray bar in Fig. 2 D). There are, however, other fixed charges contributing to the stability of the five states, as suggested by their closeness to the gating charges (cf. dashed lines in Fig. 2 D).

Figure 2.

(A) Time courses of the position of the S4 segment (x_S4) obtained from stochastic simulations at four different applied voltages. (B) Amplitude histograms of x_S4, obtained from 100 ms simulations at the indicated voltages. The arrows, corresponding to the amplitude histogram peaks, indicate the five positions where the S4 segment spends most of its time. (C) Plot of the mean x_S4 as a function of the applied voltage, obtained from 100 ms simulations at the indicated voltages. The curve represents a fit of the model data with a Boltzmann relationship, and the best-fit parameters are indicated in the panel. (D) Plot showing the gating charge profiles for the five positions where the S4 segment spends most of its time, corresponding to x_S4 = −1.33, −0.62, 0.17, 0.62, and 1.53 nm. Also shown are the fixed charge profile (Z_F, same as that shown in Fig. 1B) and the radius profile of the VSD. The gray region represents the GCTC of (12), i.e., the region laying between F290 and the first negative peak of fixed charges corresponding to the two closest intracellular negative residues. (E) Graphs showing the electrostatic energy associated to the S4 segment, assessed as $G_{el}=\int Z_{S4}{e}_0\left(dV\left(x\right)/dx\right)dx$, as a function of the S4 segment position (x_S4) at three applied voltages (indicated). The dashed vertical lines indicate the S4 segment position corresponding to x_S4 = 0.

To further explore the origin of the five states characterizing the S4 segment, in Fig. 2 E we plotted the electrostatic energy (G_el) of the S4 segment for all its possible positions at three different applied voltages (indicated). It is evident from the G_el profiles, characterized by five electrostatic energy wells, that the electrostatics by itself is able to predict five stable positions (states) of the S4 segment. At −60 mV, intermediate adjacent states are separated by energy barriers of ∼2–4 k_BT that must be crossed by the S4 segment during the activation process. At more depolarized or hyperpolarized voltages, the G_el profile continues to display clear wells, but now the energy barriers separating adjacent wells become even lower than 2 k_BT, suggesting an almost continuous motion rather than a discrete hopping for the S4 segment. As obvious in Fig. 2 E, the G_el profile varies in complex ways with the transmembrane potential, and this complexity is an important determinant of current flow. In general, potential profiles change with conditions and must be computed by a self-consistent model that starts with charges, as done here (38).

Ion concentrations and electrical profiles

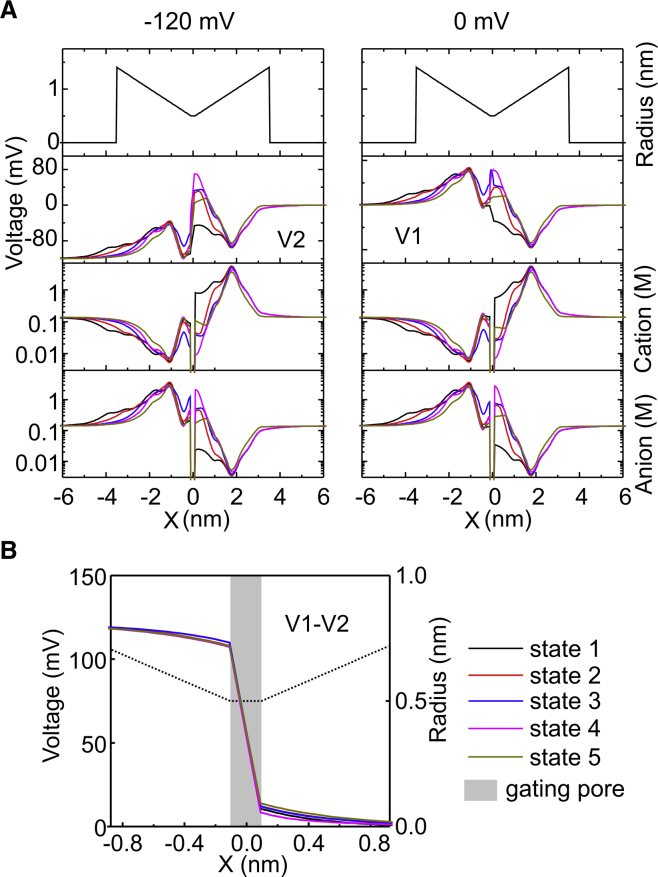
We then looked at the ion concentration and electrical voltage profiles associated with the five states at −120 and 0 mV (Fig. 3 A). Different positions of the S4 segment correspond to very different ion concentration profiles, especially in the extracellular vestibule where the number of gating charges present varies greatly (from 0 to 4) during activation. More specifically, when the S4 segment occupies the most intracellular position (black line, corresponding to state 1, R1 in GCTC), and no gating charge is in the extracellular vestibule, the cation concentration there raises well above 1 molar to screen the residing negative fixed charges. For the same reason, anion concentration in the outer vestibule under these conditions is very low. As the S4 segment moves outward, electrolyte cations tend to leave while anions concentrate there, creating a negative Debye layer to screen the gating charges. In the intracellular vestibule, the ion concentration changes in relation to the different positions of the S4 segment are much less pronounced because, unlike the extracellular vestibule, here the gating charges are added or removed much farther away from the gating pore, where volumes per unit length are much larger and the effect on the Debye screening layer is much less evident. The strong changes in ion concentration profiles in the extracellular vestibule determine, in turn, strong changes in the electrical voltage profile, which, very close to the gating pore, may change by as much as 100 mV (Fig. 3 A). Several experimental data and modeling results suggest that the structure of the VSD is optimized to focus the electrical field produced by the applied voltage within a very narrow region, a condition that would allow the transfer of several gating charges across the entire voltage drop with reduced movement of the S4 segment (39, 40, 41, 42). This high-resistance region is thought to exactly identify with the F290 residue, where the VSD becomes inaccessible to water and ions. To test this hypothesis, we looked at the voltage drop profile by assessing the voltage difference profile between −120 and 0 mV. This was done with the S4 segment positioned at the five stable states to verify whether the focusing of the electrical field changed with the position of the S4 segment. As shown in Fig. 3 B, 90/95% of the voltage drop was indeed concentrated within the gating pore (gray region in Fig. 3 B), a region 2/2.5 Å long. This is in accordance with experiments indicating a nonzero electrical field across a distance shorter than 4 Å (39). In addition, our results also indicate that the voltage drop has an essentially identical profile in the five different positions (states) of the S4 segment, suggesting that at constant applied voltage, during the activation process, the electrical field remains essentially the same.

Figure 3.

(A) Graphs showing the voltage and electrolyte ion concentration profiles. The different colors represent simulations performed with the S4 segment positioned (and not allowed to move) at the five different stable positions (states 1–5). The simulations were run until the equilibrium conditions for the voltage and ionic concentration profiles were reached. Left and right panels refer to computations performed at −120 and 0 mV of applied voltage, respectively. (B) Graph showing the voltage drop profile, assessed as the difference of the voltage profile at two different applied voltages (V2 = −120 mV and V1 = 0 mV; A). The different colors represent simulations performed with the S4 segment positioned at the five different stable positions (states 1–5). The dashed line represents the radius profile of the accessible zone of the VSD, and the gray region marks the gating pore.

The focusing of the electrical field is another example showing the importance of calculating the field rather than assuming it. The fact that the voltage drop has essentially the same profile at the five different positions of the S4 segment is striking and would have not been assumed or anticipated easily. In general, models that do not compute the field are likely to miss many effects, and simulations that may not be consistent with the laws of electrodynamics will have difficulties as well.

The macroscopic gating current

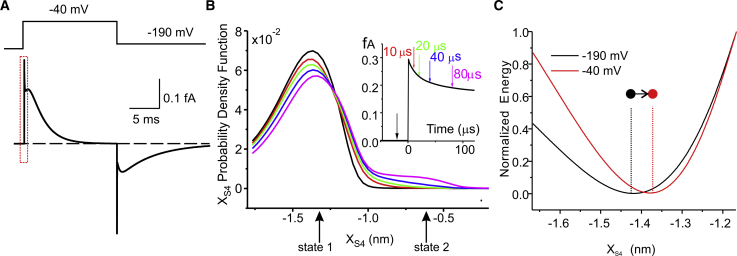
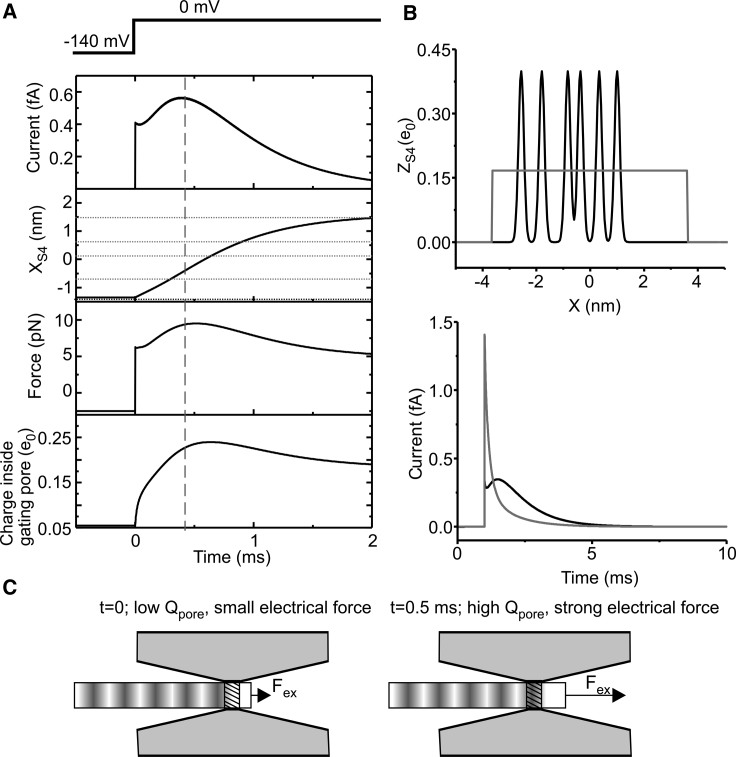
As already stated, the main advantage of treating the S4 segment as a Brownian particle is that one may alternatively predict the trajectory of a single segment, as shown above, or the behavior of a population of identical S4 segments by determining the probability density function of finding the segment in the various allowed positions. This second option is particularly attractive because it allows the prediction of the macroscopic gating currents that have been largely investigated experimentally to monitor the movement of the gating charges. Fig. 4 A shows a simulation of the macroscopic gating current obtained in response to a membrane depolarization from −190 to −40 mV (and with the tested assumption that the electrolyte ions equilibrate instantaneously; cf. Supporting Materials and Methods).

Figure 4.

(A) Simulated macroscopic gating current evoked by a voltage pulse from −190 to −40 mV (protocol indicated above). The dashed rectangle represents the part of the gating current response expanded in the inset of (B). (B) Probability density functions for the x_S4 variable, assessed at various times from the beginning of the depolarization in the same simulation shown in (A). (C) Energy landscapes for x_s4 values around state 1 at the two indicated membrane voltages. To compare the two profiles, the energy values have been normalized to their value at x_s4 = −1.2 nm.

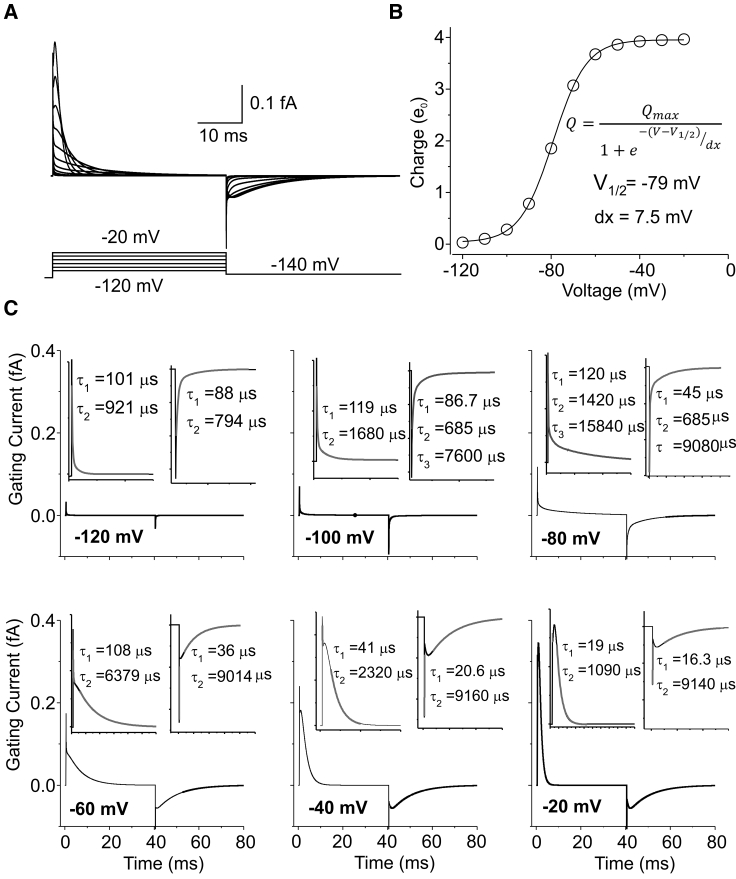
Several features of the simulated response have been also observed in experiments. First, within microseconds after the depolarizing step, a very fast gating current component appears, rising instantaneously and then falling very rapidly (cf. inset to Fig. 4 B). Notably, although this fast component was also present outside the voltage range of channel activation (i.e., with voltage steps lower than −100 mV or higher than +50 mV), voltage subtraction protocols were not able to completely eliminate it, as also observed experimentally (cf. Supporting Materials and Methods). Second, the fast gating current component was followed by a slower component starting with a plateau/rising phase and continuing with a slow decay (Fig. 4 A). The plateau phase disappeared at small depolarizations, whereas it became a prominent rising phase for larger depolarizations (cf. Fig. 6; Fig. S4). These features of the macroscopic gating currents have been observed experimentally (3, 43).

Figure 6.

(A) Family of simulated macroscopic gating currents evoked by voltage pulses from −120 to −20 mV (in steps of 10 mV) from a holding voltage of −140 mV. (B) Plot of the gating charge obtained as the integral of the simulated macroscopic gating current in (A), as a function of the applied voltage. The solid line represents the best fit of the simulated data with a single Boltzmann relationship, whose parameters are reported in the plot. (C) Each plot displays in isolation a simulated macroscopic gating current obtained in response to a single depolarization (at the indicated applied voltage). The insets are expansions of the ON and OFF gating currents, with superimposed multiexponential fits performed with the minimum number of exponentials needed to obtain a satisfactory fit. Best-fit time constants are indicated.

To understand the origin of the fast gating current component, in Fig. 4 B, we plotted the probability density function of the S4 segments position (f_S4) at various times during the current decay (10, 20, 40, and 80 μs). It is evident that within these short times, the S4 segments cannot change substantially their position. There is, however, a slight redistribution of the S4 segments within the energy well of state 1, and this very movement would give rise to the fast gating current component. This slight redistribution originates from a change in the energetic landscape due to the change in applied voltage, causing an outward movement of the energy minimum of state 1. This is evident in Fig. 4 C, in which the energy wells corresponding to state 1 at the two different voltages (−190 and −40 mV) have been superimposed.

We then looked at the slower component of the gating current, i.e., the plateau/rising phase followed by the decaying phase. Fig. 5 A shows the time course of the gating current obtained in response to a membrane depolarization from −140 to 0 mV, together with quantities that may help to understand their dynamics, namely the mean position of the S4 segment, the force acting on it, and the portion of the gating charge residing inside the gating pore, where, as we have seen, most of the electrical field is concentrated (cf. Fig. 3 B). From the time course of this last quantity, it appears that at −140 mV, a very small charge is present inside the gating pore (∼0.05 e₀), as the S4 segments mostly reside in state 1, with the R1 center of charge positioned in the GCTC. As soon as the VSDs are depolarized, the average gating charge inside the gating pore begins to increase, reaching a maximum of ∼0.25 e₀ at ∼0.5 ms from the beginning of the depolarization, and then decreases to a lower value (∼0.16 e₀) that is maintained for the rest of the depolarization. This behavior is mainly due to the coherent movement, upon depolarization, of the S4 segments. They move toward the extracellular vestibule, allowing the R1 charges to enter the gating pore quite synchronously. The resulting increase in the force active on the S4 segment would lead to its acceleration toward the extracellular side, which is responsible for the rising phase of the gating current (cf. Fig. 5 C). To test this interpretation, we performed a simulation in which the charge density along the S4 segment was kept constant so that the amount of gating charge inside the gating pore would remain constant during the whole movement of the S4 segment. As expected, in this case, the gating current did not have a rising phase (Fig. 5 B, gray).

Figure 5.

(A) Time courses of (from top to bottom) the gating current, the mean position of the S4 segment (x_S4) obtained as $\overline{x_{S4}}=\int f_{S4}{x}_{S4}dx$, the force acting on the S4 segment, and the gating charge residing inside the gating pore. The VSD was subjected to a depolarization from −140 to 0 mV (voltage protocol indicated above the plots). (B) S4 segment charge profiles (upper graph) and gating currents obtained in response to a depolarization from −140 to 0 mV (lower graph), for our model (black lines) and for a model in which the gating charge density over the S4 segment region traversing the gating pore during activation was made homogeneous (gray lines). Notice that the rising phase of the gating current disappears when considering a homogeneous charge density along the S4 segment. (C) A drawing is given showing that upon depolarization, the R1 charge enters the gating pore, causing an increase in the force acting on the voltage sensor.

Comparing gating current kinetics and Q-V relationships

Finally, we simulated a family of macroscopic gating currents evoked by depolarizations from −120 to −20 mV in 10 mV steps from a holding voltage of −140 mV and assessed the current kinetics and the Q-V relationship from the time integral of the currents at the various applied voltages (Fig. 6 A). When the kinetics of the simulated ON and OFF macroscopic gating currents were analyzed in detail, we found a surprising qualitative agreement with the kinetic features of the experimental counterparts from Shaker channels. More specifically, as observed experimentally, the ON and OFF gating currents showed complex properties depending on the level of depolarization, decaying mono- or biexponentially or showing an initial rising phase followed by a monoexponential decay (Fig. 6 C).

Fig. 6 B shows that the gating charge assessed from the gating currents increases with the applied voltage up to values close to ∼4 e₀, thus predicting a single channel gating charge of ∼16 e₀, slightly higher than the 12–14 e₀ experimentally found. It also shows that the voltage range in which the voltage sensor is predicted to move (−100 mV/−50 mV) is ∼20/30 mV more hyperpolarized than that found experimentally for the macroscopic gating charge of Shaker channels. It is important to realize that our modeling results are much more similar to the Shaker mutants in which the movement of the voltage sensor has been uncoupled from the opening of the channel (44). In accordance with this view, the correct voltage dependence of the charge movement may be recovered by simply adding to our model a spring-type force discouraging the voltage-sensor activation (see Fig. S4).

The Cole-Moore effect on gating currents

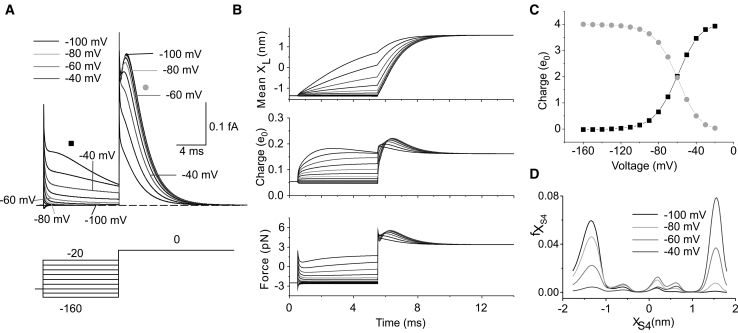
Many different types of Kv channels, including Shaker K channels, display an activation rate strongly dependent on the magnitude of the prepulse voltage, an effect often referred to as Cole-Moore shift (45). This is usually taken as a demonstration of the presence of a linear sequence of voltage-dependent closed-state transitions that the channel must undergo before opening. Because a change in the prepulse voltage alters the occupancy of the different closed states at rest, the time needed to reach the open state in response to a depolarizing step will also change, with higher rates obtained with more depolarized voltages, at which closed states proximal to the open state become more occupied. A similar Cole-Moore shift can also be observed in Shaker gating currents, in which strong depolarizations from relatively hyperpolarized voltages produce gating currents with a clear rising phase and a subsequent delayed decay, whereas identical depolarizations from less hyperpolarized voltages lead to the disappearance of the rising phase and the consequent anticipation of the decaying phase of the gating current (8).

To verify whether a Cole-Moore shift is reproduced by our model of Shaker K channel gating current, we simulated a two-pulse protocol and looked at the gating current elicited at 0 mV after applying 5 ms prepulses at different membrane voltages. As shown in Fig. 7 A, our model correctly predicts that as the prepulse voltage becomes more depolarized, the rising phase of the gating current at 0 mV gradually disappears, and the decaying phase is significantly anticipated. To understand the mechanism at the origin of the Cole-Moore shift of the macroscopic gating currents, in Fig. 7 B we plotted the time course of the mean position of the S4 segment, the amount of gating charge inside the gating pore, and the force acting on the S4 segment. With relatively hyperpolarized prepulse voltages, the S4 segment mostly occupies state 1, with a probability distribution that predicts a very small charge inside the gating pore (∼0.05 e₀). With such a small charge within the electrical field, the force pushing the S4 segment extracellularly upon stepping to 0 mV will be proportionally small. However, because the S4 segments will coherently move extracellularly, their charges inside the gating pore will gradually increase, leading to an increase in the applied force and velocity of the segments. The combination of the time-dependent increase of the gating charge traversing the pore and the velocity of the S4 segment accounts for the rising phase of the gating current at the beginning of the depolarization. As the prepulse voltage becomes more depolarized, the gating charge stably residing in the gating pore at the beginning of the test pulse will progressively increase (Fig. 7 B), and so will the force acting on the S4 segment at the beginning of the test pulse and the S4 segment acceleration. This will cause the disappearance of the rising phase in the macroscopic gating current.

Figure 7.

(A) Family of simulated macroscopic gating currents evoked by a voltage protocol consisting of a test pulse to 0 mV preceded by 5 ms prepulses ranging from −160 to −20 mV (in steps of 10 mV). (B) Time courses of the mean S4 segment position, charge inside the gating pore, and force applied on the S4 segment obtained for the simulations shown in (A). (C) Plot of the gating charge obtained as the integral of the macroscopic gating current during the test pulse (gray symbols) and during the prepulse (black symbols) as a function of the prepulse voltage, for the simulations shown in (A). (D) Profiles of the probability density function of the S4 segment at the end of the 5 ms prepulse from the simulations shown in (A).

Conclusions

In this work, we have presented a new modeling approach, to our knowledge, to investigate the voltage-dependent gating mechanism of ion channels. Starting from the structural properties of the VSD, our model is capable of accurately reproducing the experimentally determined macroscopic gating current and giving an insight into the physical mechanism at the base of channel electromechanical transduction. The model treats the charged S4 segment as a Brownian particle subject to electrodiffusion and assesses the electrical force acting on it by taking into account the externally applied voltage and the electrostatic voltage originating from the charged residues of the VSD and electrolyte ions. We verified the validity of the model by testing the conservation of the total current along the spatial domain ((46, 47); cf. Supporting Materials and Methods).

Our treatment of the S4 segment as a Brownian particle and the VSD as a set of charges from which potentials (i.e., electrical forces) are calculated is in striking contrast to Markov models and other models in the spirit of chemical kinetics that assume potential profiles and how those profiles vary with conditions, e.g., transmembrane potentials. The assumptions underlying these kinetic models may lead to large errors in potentials that may translate into exponentially larger errors in the predicted gating current, especially if they are determined by large barriers, given the (roughly) exponential dependence between flow rate and barrier height (10, 38). For these reasons, we believe that our model represents a significant improvement in the understanding of voltage-dependent gating.

Our model predicts a maximal S4 displacement of 28.6 Å (as assessed from the mean distance between the S1 and S5 stable states of the segment, cf. Fig. 2 B). Although this displacement may appear too large, it must be considered that the S4 segment is tilted by ∼40–60° with respect to the membrane axis (12), giving a vertical maximal displacement of the voltage sensor of 14–22 Å, values close to the 15–20 Å vertical displacement assessed in some experiments (48).

The model predicts and explains most of the experimentally determined features of the macroscopic gating current. First, it predicts the existence of stable intermediate states of the S4 segment, corresponding to the various positions the S4 segment can take and the different number of gating charges exposed in the intracellular and extracellular vestibules. The presence of multiple closed states in Shaker K channels has long been suggested (6, 7, 8, 9). More recently, MD simulations (17) and mutagenesis experiments (13) have confirmed the presence of five states assumed by the S4 segment along its activation pathway. Our numerical simulations predict that these stable states are separated by energy barriers of 2–4 k_BT at a membrane voltage close to the activation V_1/2. Notably, theoretical calculations performed using Kramer diffusion theory suggest that well-defined Markovian states (that can be well-described by DMMs) are delimited by barriers at least 4–5 k_BT high (43, 49). The energetic landscape resulting from our model is even more divergent from those described by DMMs when the applied voltage is outside the range for channel activation. As we have shown in Fig. 2 E, in this range a clear distinction of the energy profile into multiple stable states is somewhat loosened, and the energetic landscape suggests a continuous drift motion of the S4 segment along its activation pathway. These results suggest that channel gating properties not expected on the basis of DMMs may well appear in channel gating under particular conditions. It may be of interest to point out, however, that DMMs can be extended to barriers that are not large without further approximation, resulting in expressions that are nearly as simple to compute and understand as the large barrier approximations (38, 50).

The model also predicts a very fast component in the macroscopic gating current at the beginning of a depolarizing and repolarizing step. In accordance with previous numerical simulations performed using continuous models of channel gating (43), our model suggests that this fast component mainly originates from a redistribution of the S4 segment population within the most extreme energy wells (fully activated or fully deactivated) because of the sudden change in the electrical force acting on the voltage sensors after a step change in the applied voltage. However, when the applied voltage step falls in the channel activation range, the occupancy of the adjacent stable state along the activation pathway may also contribute to this fast component, likely because of the relatively low energy barrier separating the two stable states.

A third property of the voltage sensor dynamics well-reproduced by our model is the peculiar shape of the macroscopic gating current time course for relatively high depolarizing steps, consisting of a rising phase followed by a slower decay. Using DMMs, this behavior has been previously interpreted with initial transitions carrying less charge than later transitions along a chain of voltage sensor conformational states. This interpretation is not supported by currently available structural and functional data, which indicate that the various closed states of the channel correspond to different positions of the voltage sensor relative to the gating pore, whereas its charges interact sequentially with the GCTC (13). In this view, each transition from one closed state to the next should carry exactly the same—one—positive charge along the entire voltage drop (i.e., through the gating pore), and no gating transition carrying a different amount of charge could be postulated. Within this framework, our model was able to reproduce the initial rising phase of the macroscopic gating current by simply considering the discreteness of the charge density along the S4 segment because of the discrete nature of the gating charge residues and the electrical field dropping almost entirely within the short gating pore. In this framework, only the charge effectively present within this region (the gating pore) moves in response to the electric field. Given that the gating pore is relatively short as compared to the distance between the gating charges along the S4 segment, the charge density residing within the gating pore as the S4 segment moves along the activation pathway, and thus the force acting on it, will be subjected to strong oscillations. This scheme could well explain the rising phase of the macroscopic gating current under certain conditions. Consider, for example, the response to a depolarization from a highly negative holding voltage that has concentrated virtually all the S4 segments within only one (the most inward) state. At the beginning, the small charge density within the gating pore will result in a small force applied on the S4 segments and their small acceleration. The increasing charge getting inside the gating pore will, however, cause a bigger and bigger acceleration of all S4 segments, which will, in turn, determine a rising macroscopic gating current. The oscillating behavior of the gating current disappears after the passage of the first gating charge through the gating pore because the thermal diffusion soon desynchronizes the S4 segment populations.

Our model is also able to predict the complex time course of the OFF gating currents in response to repolarization from different prepulse voltages, namely a monotonically decaying OFF gating current for prepulses below the channel activation V_1/2 and the presence of a second, slower exponential component or a rising phase preceding the gating current decay for higher prepulse voltages. We found that this rising phase present in the OFF gating current has the same origin of the rising phase in the ON gating current at high depolarizing voltages that we have described above. Although early mutagenesis experiments seemed to suggest that the initial slow rising phase of the OFF gating current represented an open-state stabilization after the cooperative transition of the four channel subunits to the activated state (51), more recent data have clarified that the slow onset and decay of the OFF gating current are preserved in the absence of pore opening and thus represent an intrinsic property of the S4 segment dynamics (52). Our model fully agrees with this view, as a rising phase of the OFF gating current can be predicted in the complete absence of a coupling of the S4 voltage sensor with the channel pore.

A shortcoming of all reduced physical models, including the one presented in this work, is the presence of free parameters whose exact quantitative values are unknown. They need however to be included to take into consideration the effects of what has not been explicitly considered. In our Brownian model of voltage gating, although the geometrical features and the charge locations do not represent free parameters because we have estimated them from the experimentally available crystal structure, we still have several free parameters. One of them is the frictional coefficient γ appearing in the stochastic differential and FP equations, describing the frictional effect that water and surrounding protein structures have on the S4 segment. Understandably, for this parameter we had no idea, so we set it by an eye-fitting procedure to obtain a rate of the macroscopic gating current similar to that observed experimentally (cf. Methods; Supporting Materials and Methods). However, we could verify that the value chosen was reasonable by comparing it with the internal friction estimated for other proteins undergoing conformational changes. For example, the VS viscosity assessed from the chosen frictional coefficient and from Stokes’ law is ∼20 mPa/s, a value well within the range found for other proteins such as trypsin or electron transport enzymes (53). Another free parameter of our model is the relative dielectric constant ε, whose presence is necessary to account for the effect of structural charges on the electrostatic forces acting on the voltage sensor. We chose to set the relative dielectric constant inside the water-inaccessible gating pore to 4, a value typical of the interior of proteins (54). By contrast, a relative dielectric constant of 80, typical of aqueous solutions, was chosen for the intracellular and extracellular water-accessible regions. It needs to be considered, however, that in the vestibules of the voltage sensor, the regions occupied by water and ions (high dielectric regions) are surrounded by the protein (low dielectric region), which, in our one-dimensional model, is not considered. The presence of a separation surface between different dielectric constants may well impact on the electrostatic potential that is calculated by solving the Poisson equation, and this effect is particularly severe in confined regions (26, 55). A higher-dimensional version of our model addressing this issue is under way.

Our simplified model cannot obviously account for several other features of the gating mechanism because provisions for them have not been included. First, being developed in one dimension, the model is not able to predict possible tilting and rotations of the S4 segment during its trip along the activation pathway. Many experimental data suggest that while translating in the direction perpendicular to the membrane plane, the S4 segment undergoes a 180° counterclockwise rotation, a movement that allows the positioning of the gating charges always close to the countercharges present in the S1–S3 segments of the VSD, thus maximizing their electrostatic interaction (56, 57, 58). This rotation is coherently predicted by MD simulations, which also suggest a tilting of the S4 segment, changing from 60 to 35° the angle with the plane of the membrane during its activation (15). Based on these data, future development of a 3D Brownian model will better describe the conformational changes of the S4 segment during voltage-dependent gating. Second, our model only includes electrostatic interactions between the S4 segment and the rest of the VSD. However other types of interactions such as van der Waals, π-cation, etc., may significantly contribute to the stability of the various kinetic states of the VSD. Notably, the contribution of nonelectrostatic interactions may easily be introduced in the Langevin and FP equations as an additional external force contributing to the drift term. Finally, the Brownian model presented in this work considers only one of the four VSDs contributing to the gating of an ion channel, and thus, it cannot be used to explore cooperative interactions between the different channel subunits. Interestingly, intersubunit cooperativity has long been postulated in Shaker K channels on observing that their DMM kinetic schemes had to include a cooperative step preceding channel opening to explain the steep Q-V and G-V relationships at relatively depolarized voltages (6, 7, 8, 9). In addition, mutagenesis experiments indicate that the N-terminal part of the S4–S5 linker of each Shaker K channel subunit interacts with the C-terminal part of the adjacent S6 segment of another subunit during channel opening (44), suggesting that a full understanding of the voltage-dependent gating should include intersubunit interactions. In accordance with this view, we think that the failure of our model to predict a double Boltzmann, as found in experimental Q-V relationships, is due to the lack of a cooperative, intersubunit conformational change. Our model may easily be expanded to include four interacting VSDs controlling a single channel gate. This expansion of the model may allow prediction of ionic currents in addition to gating currents, thus increasing the available experimental data that can be used to understand the physics of the voltage-dependent gating in ion channels.

Author Contributions

L.C. conceived the Brownian model and performed the theoretical simulations. L.C. and F.F. discussed model results and wrote the manuscript.

Editor: Chris Chipot.