Abstract
Longitudinal‐ordered categorical data, common in clinical trials, can be effectively analyzed with nonlinear mixed effect models. In this article, we systematically evaluated the performance of three different models in longitudinal muscle spasm adverse event (AE) data obtained from a clinical trial for vismodegib: a proportional odds (PO) model, a discrete‐time Markov model, and a continuous‐time Markov model. All models developed based on weekly spaced data can reasonably capture the proportion of AE grade over time; however, the PO model overpredicted the transition frequency between grades and the cumulative probability of AEs. The influence of data frequency (daily, weekly, or unevenly spaced) was also investigated. The PO model performance reduced with increased data frequency, and the discrete‐time Markov model failed to describe unevenly spaced data, but the continuous‐time Markov model performed consistently well. Clinical trial simulations were conducted to illustrate the muscle spasm resolution time profile during the 8‐week dose interruption period after 12 weeks of continuous treatment.
Study Highlights.
WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?
☑ Pharmacometric models with diverse structures have been applied to analyze longitudinal‐ordered categorical data. Although the proportional odds model is the first model for such data, the continuous‐time Markov model and the discrete‐time Markov model have been widely used given their unique Markov properties. Systematic comparisons of those models are currently lacking.
WHAT QUESTION DID THIS STUDY ADDRESS?
☑ This study provides direct comparisons of the three models mentioned previously using muscle spasm data from vismodegib clinical study with varying observation frequencies to enable model selections under specific conditions.
WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?
☑ This study provides model selection recommendations for analyzing longitudinal‐ordered categorical data. It also suggests ways to handle the delay between pharmacokinetics and adverse events in different models and reset adverse event compartments for continuous‐time Markov models.
HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?
☑ The model selection recommendations will help with making rational decisions for analyzing longitudinal‐ordered categorical data. The model outcomes also support the recent US label change for vismodegib pertaining to dose interruptions for safety reasons.
In clinical trials, longitudinal data for ordered categorical end points are routinely collected either by spontaneous reporting or by scheduled repeated assessments. A common approach for analyzing the exposure response of discrete data is to apply simple logistic regression methodology, disregarding the ordinal and longitudinal nature of the end points.1 This can be a fit‐for‐purpose approach to provide an understanding of the relationship between exposure and the incidence of end points and any impact of covariates. However, if the aim is to understand the dynamics of these end points over time, models that can handle longitudinal‐ordered categorical data are essential. Such models make full use of the ordinal structure of the end points and the change in response over time and have the potential to inform the dosing regimen and individualization.
Methodologies for analyzing longitudinal‐ordered categorical data have been extensively investigated. The proportional odds (PO) model was introduced in the pharmacometric area in 1994 to analyze pain scores in an analgesic trial.2 It is essentially a logistic regression model incorporating the time component for both the explanatory and response variables and allowing for interindividual variability of the probability of the event. It can estimate the probability of reaching a certain category as a function of time and explanatory variables. The effect parameter for an explanatory variable is assumed to be the same for all the cumulative probabilities regardless of categories (such as grade ≥ 1 or grade ≥ 2). The PO model structure ignores the autocorrelation between serial observations in the same individual, although the subject‐level random effect might contribute to the correlation of observations within individual. To explicitly account for the autocorrelations, a Markov component can be added to PO model3, 4, 5, 6, 7; it was first applied in 2000 to model sleep stage data in an insomnia clinical trial.3 Those models, referred to as a discrete‐time Markov model (DTMM), assume that the influence of the preceding observation on the current one is independent of time between the two observations. Thereafter, the continuous‐time Markov model (CTMM) was introduced to accommodate data with varying time intervals between observations, where the influence of the preceding state decreases as time between observations increases. It was first proposed in 2009 to model tablet transit in gastrointestinal tract8 and thereafter adopted widely to characterize various types of ordered categorical data.9, 10, 11, 12, 13, 14
Some other approaches are available to analyze such data: the latent variable approach for the efficacy end points in rheumatoid arthritis and Crohn's disease,15, 16, 17 the repeated time‐to‐categorical event approach for heartburn in gastroesophageal reflux disease,18 and hypoglycemia in type 1 diabetes mellitus.19 There has been an extensive discussion surrounding the Markov and the latent variable models,4, 10 which is not the focus of this article.
Schindler and Karlsson20 recently proposed a minimal CTMM (mCTMM), assuming that the transition rate between consecutive states is independent of the state. The results indicated that the mCTMM outperformed the PO model, but could not describe the data as well as the DTMM; the PO model showed consistently poor performance.
Given the variety of model structures for analyzing longitudinal‐ordered categorical data, there is a lack of systematic comparison of these models, especially between the CTMM and DTMM. The PO model also warrants further evaluations, as its performance can depend on the data set. In this article, we present a direct comparison of the PO model and the DTMM and CTMM by analyzing data sets with varying observation frequencies using longitudinal muscle spasm (MS) data from a phase II trial of vismodegib.21 The assessment of the mCTMM is not included in this article. The purpose of this analysis is to provide recommendations on the ideal model for analyzing longitudinal‐ordered categorical data under specific conditions. The resolution time‐profile for MS during the 8‐week dose interruption was simulated using Markov models. The results obtained support the recent label change regarding the dose interruption of vismodegib.22
Methods
Clinical study design and MS data
Vismodegib (ERIVEDGE; Genentech, South San Francisco, CA) is a first‐in‐class, small‐molecule inhibitor of the Hedgehog signaling pathway through binding to and inhibiting the smoothened, a seven‐transmembrane protein involved in hedgehog signal transduction. Abnormal activation of hedgehog pathway signaling is a key driver in the pathogenesis of basal cell carcinoma (BCC).23 Vismodegib was approved by the US Food and Drug Administration (FDA) in 2012 for the treatment of adults with metastatic BCC or with locally advanced BCC.22 The inhibition of smoothened will also lead to MS via increased membrane calcium channel activation and uptake, which is the most common treatment‐emergent adverse event (AE) for vismodegib.21, 24
The MS AE data were collected from a phase II trial evaluating the efficacy and safety of vismodegib in operable BCC (SHH4812g; ClinicalTrials.gov identifier NCT01201915).21 The study was approved by each site's Institutional Review Board or the medical ethics committee, and carried out in accordance with the International Conference on Harmonization Guideline for Good Clinical Practice. Patients gave written informed consent. One of the primary objectives of this study was to assess the safety and tolerability of vismodegib in the intermittent dosing regimen. A total of 74 patients were enrolled into three cohorts (24, 25, and 25 patients, respectively), with 150 mg daily dose of vismodegib following varying regimens (12 weeks on for cohort 1, 12 weeks on/24 weeks off for cohort 2, and 8 weeks on/4 weeks off/8 weeks on for cohort 3; the patients in all cohorts were followed by Mohs surgery; Figure 1A). The AEs were monitored until 30 days after Mohs surgery or the last dose of vismodegib if Mohs surgery did not occur.21 Patients spontaneously reported the start and end dates of each MS episode (1–3; 1 as mild pain, 2 as moderate pain with limiting instrumental activities of daily living, 3 as severe pain with limiting self‐care activities of daily living) based on the National Cancer Institute Common Terminology Criteria for adverse effects (version 4.0).25 The incidence of MS was evenly distributed across cohorts (72 ~ 79%). Grades 2 and 3 MS were grouped together as “grade 2/3” because only 3 of 74 patients developed grade 3 MS. Treatment interruptions or discontinuations were allowed for AE reasons. The treatment discontinuation as a result of MS occurred in only 2 of 74 patients.21 No recommended treatment was defined in the protocol to manage MS.
Figure 1.
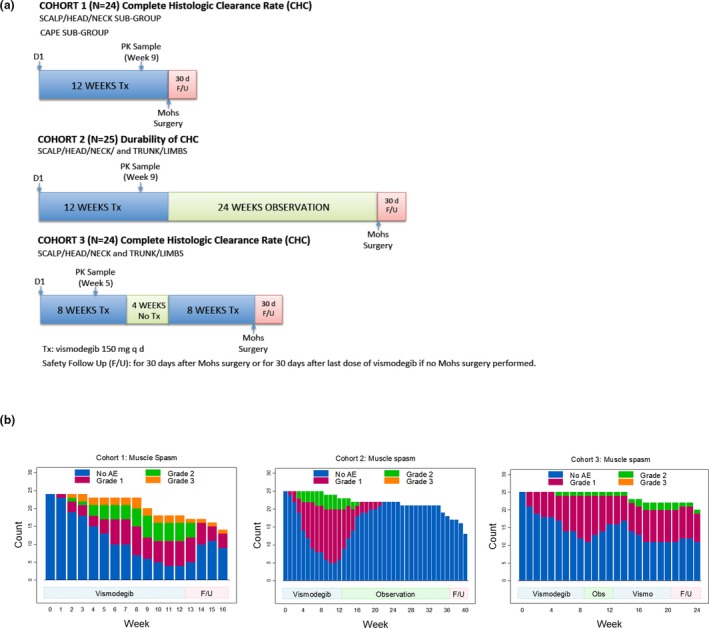
Schematic representation of the clinical study design for SHH4812g (a) and the stacked bar plots for the observed longitudinal profiles of muscle spasm in SHH4812g based on weekly spaced data set (b). AE, adverse event; CHC, complete histologic clearance; d, days; F/U, follow‐up; PK, pharmacokinetics; Tx, treatment.
The original MS data set was constructed based on the start and end dates of each grade in the source database. A weekly spaced data set was derived from the original data set (day 1 as week 0, day 8 as week 1, etc.). The possibility of missing MS events in the weekly data set was negligible given that only six MS episodes had a duration of 7 days or shorter. To investigate the impact of observation frequencies on model performance, daily data set was generated from weekly data set, and unevenly spaced data set was further generated from daily data set by repeating the order of rich (every other day for 2 ~ 3 weeks), sparse (every week for 2 ~ 3 weeks), and very sparse (every other week for 2 ~ 3 weeks) sampling in each cohort.
Software
The data were analyzed with nonlinear mixed‐effect modeling (NONMEM) version 7.3.026 on a Linux cluster using the first‐order conditional estimation (FOCE) method for the PO model and the DTMM or the Monte Carlo importance sampling (IMP) method for the CTMM, with LAPLACE and Likelihood options. Model evaluations were conducted using perl‐speaks‐NONMEM version 4.8.127 and the Xpose4 package.28 Mrgsolve version 0.9.029 was used for the simulation of individual AE time profiles. R version 3.5.530 was used for data management.
Model structure
The pharmacokinetics (PK) of vismodegib (total and unbound) was previously described by a one‐compartment population PK model with first‐order absorption, first‐order elimination of unbound drug, and saturable binding to α1‐acid glycoprotein with fast equilibrium.31 The unbound drug was considered as the driving force for the efficacy and safety of vismodegib.31 Because the steady‐state total drug was the only PK data collected that were not available for all patients in SHH4812g, the model‐predicted unbound PK profiles based on typical model estimates,31 individual average dose, and demographics (age, body weight, and typical value of α1‐acid glycoprotein (30 µM)) were used in the analysis. The simulated PK profiles are shown in Figure S1 for the total and unbound drug. The average dose for each patient based on individual pill count was used to account for dose interruptions without documented dates. The mean average dose level across individuals was 136 mg (data on file).
All 74 subjects were included in the analysis. The models were first developed using the weekly data set. Subsequently, the same structures and initial values were applied to analyze the data sets with daily and uneven intervals unless modifications were needed. No dropout model was considered because only two patients had discontinued treatment as a result of MS.21
Given the time delay between MS and unbound vismodegib PK in plasma (Figure S1 ), the need of biophase compartment was tested in all models. As shown in Eq. 1, and were the unbound concentrations in biophase or plasma for the i th individual at the j th time point; was the first‐order rate constant for biophase distribution. The default function for drug effect was a linear model. The Emax model was also tested.
| (1) |
PO model
The logit for the probability of a patient having MS greater or equal to a specific grade was modeled as a linear function of unbound vismodegib exposure in plasma or biophase compartment (Eq. 2).
| (2) |
is the MS grade for the i th patient at the j th time point; m is the MS grade (m = 1, 2/3); is the baseline of logit probability for ; slope represents the population mean increase in per unit increase in exposure; describes the random effect in slope for the i th individual, with mean zero and variance . The value of slope was the same regardless of categories (grade ≥ 1 or ≥ 2), reflecting the PO assumption.
The probability for can be back calculated as shown (Eq. 3):
| (3) |
The probability of achieving certain MS grade (0, 1, or 2/3) can be calculated as shown (Eqs. (4), (5), (6)):
| (4) |
| (5) |
| (6) |
DTMM
The DTMM is the implementation of the Markov component using a PO model structure (Eq. 7).
| (7) |
is the logit probability for without drug, conditioning on the preceding grade k. In a specific data set, changed with m (current grade) and k (preceding grade, shown as PDV in the code), but was constant for a given m and k regardless of the time interval between them (discrete Markov feature). The preceding grade PDV was derived directly in the control stream, making it possible to use the same data set as for PO model (Data S1 , Model S1 ).
CTMM
The CTMM is based on a compartmental structure with one compartment for each possible state. The amount in each compartment was the probability for the corresponding state. The probability transferred between states continuously via first‐order processes, reflecting the Markov property. At the time of an observation, the probability of the corresponding state (compartment) was set to 1 and all other compartments were set to 0. This was achieved by event identification 3 in the data set and A0_FLG in the control stream to empty out the entire system and then reset to the right amount for PK and AE compartments (Model S1 ). The sum of the amount in all compartments will always be equal to 1. The initial state included the amount of 1 in the “grade 0” compartment (no MS before treatment) and 0 in other compartments.
Generally, the transition rates between neighboring states are included in the CTMM; however, in this study, we allowed the flexibility to model the transitions for both neighboring and nonneighboring states (Eqs. (8), (9), (10), (11), (12), (13); Figure S2 ) based on the available data.
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
, , are probabilities of MS grades 0, 1, and 2/3, respectively. is the first‐order transfer rate constant, with as the preceding grade and as the current grade. can be defined as and , which describe the transitions from low to high grade () and from high to low grade (), respectively. is the baseline of without treatment. is the drug effect for transition in the i th individual at the j th time point. The slope can be different for different transitions, if identifiable . described the random effect for , with mean zero and variance .
Model evaluation
Several model evaluations were conducted:
Visual predictive check (VPC) for the proportion of MS grade (0, 1, and 2/3) over time.
Posterior predictive check for the number of transitions for every transition scenario (0–0, 0–1, 0–2/3; 1–0, 1–1, 1–2/3; 2/3–0, 2/3–1, and 2/3–2/3) by comparing the histogram frequency between simulations and observed.
VPC for the proportion of transitions over time for each transition scenario.
VPC of Kaplan‐Meier plots for the time to first MS event (any grade or grade 2/3).
All of the aforementioned simulations were conducted 500 times and stratified by cohort. A 95% prediction interval was used for VPCs.
Nonparametric bootstrapping for parameter uncertainty. Both the relative standard error (%RSE) (bootstrap standard deviation/median) and 95% confidence intervals (bootstrap percentile confidence interval (CI)) were provided.
Model‐simulated individual AE time profiles for representative subjects.
Clinical trial simulations
Clinical trial simulations (CTS) were performed to calculate the proportion of patients with any or grade 2/3 MS at weeks 12 and 20, after 12‐week daily treatments of 150 mg vismodegib. A total of 500 trials with 200 patients each (sampling with replacement using the 74 patients) were simulated based on bootstrapped parameters. The median and 95% CI were derived. CTS were applied to the data set with weekly or daily intervals using the models developed from weekly intervals.
Results
PO model
The PO model for MS was originally developed by Lu et al. 32 A biophase compartment was necessary to account for the delay between MS and profiles. A linear drug effect model was selected over the Emax model based on a chi‐square test at the 0.05 level. Random effect interindividual variability (IIV) was tested for either slope or . Allowing IIV for slope resulted in better model performance. The estimates based on the weekly data set are listed in Table 1 with good precision (≤15% RSE from bootstrapping). Given that “B 1” can take either a positive or negative value, the RSE by “SE/THETA” is not a proper measure of uncertainty, and standard error (SE) was presented instead. “B 2–B 1” was estimated and constrained to be negative to ensure the probability of grade ≥ 2 MS is smaller than that for grade ≥ 1. was estimated to be 0.03/day with half‐life of 23 days.
Table 1.
Model estimates for three models based on the weekly spaced data set
| Model | Parameters | Estimate | SE, covariance step | RSE (%), covariance step | SE, bootstrapping | RSE (%), bootstrapping | Median (95% CI), bootstrapping | |
|---|---|---|---|---|---|---|---|---|
| POa | k eo | 0.034 | 4.9 | 13.8 | 0.034 (0.026, 0.046) | |||
| B 1 | −4.03 | 0.20 | 0.36 | −4.09 (−4.90, −3.49) | ||||
| B 2–B 1 | −4.33 | 4.9 | 13.8 | −4.37 (−5.72, −3.39) | ||||
| Slope | 20.0 | 12.1 | 14.3 | 20.4 (15.4, 26.5) | ||||
| CV% (slope) | 78.9 | 12.4 | 15.0 | 78.0 (57.8, 101.3) | ||||
| DTMMb | B 1,0 | −5.48 | 0.40 | 0.43 | −5.54 (−6.53, −4.83) | |||
| B 2,0–B 1,0 | −1.58 | 15.5 | 15.8 | −1.60 (−2.17, −1.19) | ||||
| B 1,1 | 1.35 | 0.22 | 0.19 | 1.33 (0.97,1.71) | ||||
| B 2,1–B 1,1 | −9.86 | 7.7 | 18.5 | −9.88 (−19.90, −8.53) | ||||
| B 1,2 | 0.394 | 0.33 | 0.38 | 0.352 (−0.454, 1.083) | ||||
| B 2,2–B 1,2 | −0.0966 (fix) | NA | NA | NA | ||||
| Slope | 18.8 | 12.4 | 13.2 | 19.1 (14.8, 24.9) | ||||
| CV% (slope) | 21.1 | 28.7 | 23.7 | 20.4 (9.63, 29.95) | ||||
| CTMMc | Slope01 | 0.053 | 21.6 | 23.4 | 0.053 (0.031, 0.077) | |||
| Slope10 | 32.14 | 50.1 | 40.8 | 36.60 (14.30, 75.19) | ||||
| Slope02 | 0.014 | 39.3 | 35.6 | 0.013 (0.006, 0.024) | ||||
| Slope20 | 8.94 | 41.3 | 23.0 | 9.87 (5.99, 14.88) | ||||
| Slope12 | 0.1 × Slope01 | NA | NA | NA | ||||
| K 10 | 0.115 | 44.6 | 45.5 | 0.141 (0.068, 0.368) | ||||
| K 20 | K10 | NA | NA | NA | ||||
| K 21 | 0.01 × K10 | NA | NA | NA | ||||
| CV% (slope01) | 86.0 | 35.9 | 68.3 | 87.8 (41.6, 199.8) | ||||
| CV% (slope10) | 97.5 | 39.2 | 39.1 | 100.5 (71.7, 183.4) | ||||
| CV% (slope02) | 146.3 | 17.6 | 18.4 | 139.3 (89.3, 189.8) | ||||
| CV% (slope20) | 80.4 | 33.4 | 39.5 | 79.7 (19.2, 139.8) | ||||
Only the parameter estimates related to the adverse event analysis were included in the table. The parameter estimates related to the pharmacokinetics of vismodegib was included in Model S1 .
CI, confidence interval; Median (95% CI) bootstrapping, median and 95% CI from “percentile confidence intervals” (bootstrap_results.csv); NA, not applicable; RSE, relative standard error; SE, standard error.
a K eo is shown on a normal scale but was estimated in the log domain. The RSE% presented in “RSE (%) covariance step” or “RSE% bootstrapping” is the SE of the logged parameter *100 that is approximately equal to the RSE% of the parameter on the normal domain. , baseline of logit probability for AE ≥ m (m = 1, 2/3); coefficient of variation (CV%) (parameter), standard deviation of the interindividual variability for certain parameter that derived by “sqrt(omega)*100”; PO, proportional odds model; RSE% bootstrapping, relative standard error from bootstrapping that was derived by “(bootstrap SD/median)*100”, bootstrap SD is the standard deviation of parameter estimates that is “standard.errors”; RSE% for CV% are derived by RSE% for omega/2 for the RSE% from covariance step and bootstrapping; RSE (%) covariance step, relative standard error from nonlinear mixed‐effect modeling (NONMEM) covariance step; SE bootstrapping, “standard.errors” from bootstrapping results (bootstrap_results.csv) (same as SE covariance step, only apply to B1); SE covariance step, standard error from NONMEM covariance step (only apply to B1 as it can take either positive or negative value; RSE by SE/THETA is not a proper measure of uncertainty in this case); Slope, population mean increase in per unit increase in exposure. bSE covariance step and SE bootstrapping were only applied to B 1,0, B 1,1, B 1,2, as they can take either positive or negative value (same as B1 for the PO model). , baseline of , given the preceding grade ; B 2,2–B 1,2, the transition probability in logit scale from grade 2/3 to 1, which was fixed to the estimated value (−0.0966) with no change in the objective function values; DTMM, discrete‐time Markov model. cAll of the slope parameters and K 10 are shown on normal scale but were estimated in the log domain. The RSE% presented in “RSE (%) covariance step” or “RSE% bootstrapping” are the SE of the logged parameter *100 that is approximately equal to the RSE% of the parameter on the normal domain. CTMM, continuous‐time Markov model; , slope for transition , with as the preceding grade and as the current grade; K g1g2, baseline of without treatment (, first‐order transfer rate constant from high to low grade ()).
DTMM
Different sets of baseline parameters () were estimated depending on the current and preceding AE state. The model could describe the gradual increase in probability, and no improvement was seen upon adding a biophase. The estimates based on the weekly data set are listed in Table 1. “B 2, k–B 1, k” was estimated and constrained to be negative. The precision was in general good (<24% RSE from bootstrapping). Similar to B 1 from the PO model, SE was presented for “B 1,0,” “B 1,1,” and “B 1,2.” The 95% CI from bootstrapping was relatively wide for “B 1,2” (−0.454, 1.083), with a median value of 0.352, which might be the result of a limited number of grade 2/3 events. “B 2,2–B 1,2,” the transition probability in logit scale from grades 2/3 to 1, was estimated to be −0.0966 with 97.5% RSE, reflecting the very limited transitions from 2/3 to 1. It was fixed to −0.0966 in the final model.
CTMM
Of all the transitions recorded in the weekly data set, there were 3 transitions from grade 1 to grade 2/3 and 1 transition from grade 2/3 to grade 1; however, there were 14 transitions from grades 0 to 2/3 and 2/3 to 0, respectively (Figure S2 ). The reason could be because of the incomplete recording of grade 1 during the transitions between grades 0 and 2/3. The CTMM, including mass transfer between compartments of neighboring states only, could not predict the observed higher number of transitions between 0 and 2/3 compared with 1 and 2/3. A direct linkage between 0 and 2/3 was tested and included in the model (Figure S2 ). Similar to the DTMM, no biophase compartment was needed in the CTMM. The estimates based on the weekly data set are listed in Table 1 with reasonable precision (<46% RSE for fixed effect parameters; <69% RSE for random effect parameters as coefficient of variation (CV%); from bootstrapping). Certain parameters were set to share the same value or have fixed relations to keep a parsimonious and identifiable model (Table 1, Model S1 ), such as K 21 = 0.01 × K 10. Allowing each slope parameter (slope01, slope10, slope02, slope20) to have separate IIV improved model performance. The Emax model was tested, but did not improve the objective function value. The FOCE method was sensitive to initial values and also failed the covariance step. The IMP method was selected to overcome these issues.
Model evaluation
There was a gradual decrease in the proportion of patients with grade 2/3 MS from cohorts 1 to 3 (Figure 1 b), which cannot be explained by covariate effects on PK as indicated by VPC (Figure S3 ). The sequential nonrandomized enrollment of the three cohorts could be the reason for the discrepancy, as the VPC for the pooled first 8‐week data performed well overall in all models (data on file). Among the cohorts, the model predictions in cohort 2 were reasonable and distinguishable across models (Figure S3 ). Therefore, cohort 2 was selected for model comparisons.
This section only included evaluations from modeling the weekly data. VPC for the proportion of patients on each MS grade captured the observed profile reasonably well in all models (Figure 2), with a slight underprediction of grade 1 for the PO model. The PO model greatly underpredicted the number of transitions within grade and overpredicted the number of transitions between grades (except that the transitions between 2/3 and 0 were underestimated because of a large number of direct transitions between 2/3 and 0 observed); both the DTMM and CTMM accurately predicted the number of transitions (Figure 3). This was further supported by VPC for the proportions of transitions over time (data on file), and the simulation of the individual AE time profile (Figure S4 ). For any grade or grade 2/3 of MS, the PO model significantly overpredicted the cumulative probability with an observed value outside the 95% prediction interval and also predicted early event occurrence; both the DTMM and CTMM performed well (Figure 4). For all models, bootstrapping has a 100% minimization rate. The %RSE from the NONMEM covariance step were similar or slightly smaller than those from bootstrapping.
Figure 2.
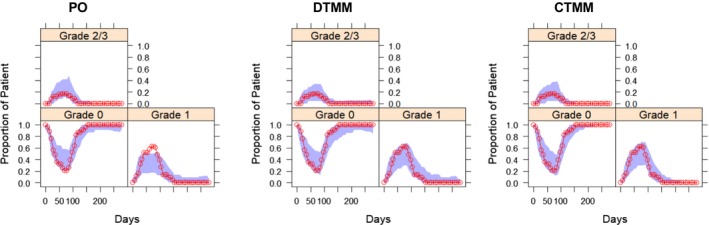
Visual predictive check for proportion of patients on each muscle spasm grade in cohort 2 based on the weekly spaced data set. Circles depict the observed proportion, and shaded areas are 95% confidence interval of model predictions. CTMM, continuous‐time Markov model; DTMM, discrete‐time Markov model; PO, proportional odds model.
Figure 3.
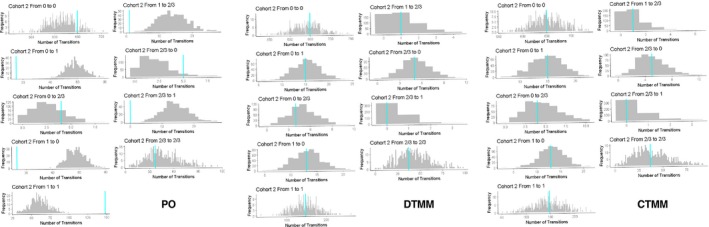
Posterior predictive check for total number of transitions in each transition scenarios in cohort 2 based on the weekly spaced data set. The gray bars are the frequency distribution of number of transitions from 500 model simulations. The vertical bar is the observed number of transitions. CTMM, continuous‐time Markov model; DTMM, discrete‐time Markov model; PO, proportional odds model.
Figure 4.
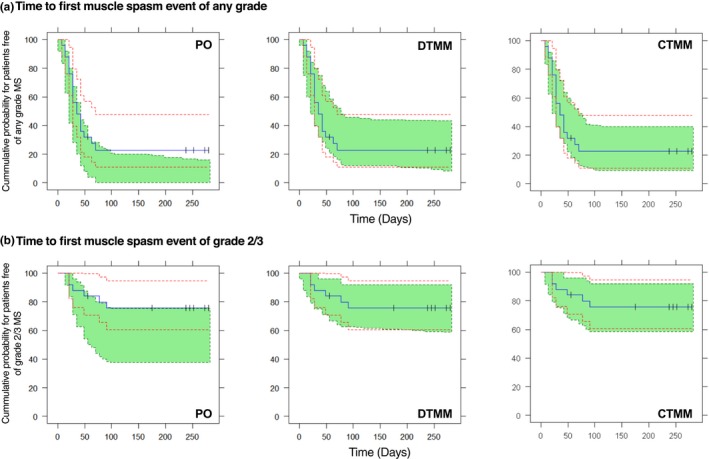
Visual predictive check for Kaplan‐Meier plot for time to first MS event of any grade (a) and or grade 2/3 (b) in cohort 2 based on the weekly spaced data set. Blue lines are the observed curve, green area is 95% prediction interval of model predictions, and red dash lines are the 95% confidence interval of the observed curve. CTMM, continuous‐time Markov model; DTMM, discrete‐time Markov model; MS, muscle spasm; PO, proportional odds model.
CTS
After a daily dosing for 12 weeks, the CTS of the CTMM indicated that the proportion of patients with any MS decreased from 73% (95% CI, 62 ~ 82%) at week 12 to 10% (95% CI, 4 ~ 17%) at week 20, and patients with grade 2/3 MS decreased from 20% (95% CI, 12 ~ 29%) to 0% (95% CI, 0 ~ 1%). The DTMM generated similar outcomes. The PO model generated higher proportion with grade 2/3 at week 12 (29%) and less proportion with any MS at week 12 (64%) (Table 2 “Estimation Weekly, Simulation Weekly”; Figure S5 , “Weekly Interval”).
Table 2.
Proportion of muscle spasms at week 12 and week 20 after 12‐week treatment based on clinical trial simulations
| Data frequency | Model | Any grade, median (95% CI) | Grade: 2/3, median (95% CI) | |||
|---|---|---|---|---|---|---|
| Estimation | Simulation | Week 12 | Week 20 | Week 12 | Week 20 | |
| Weekly | Weekly | PO | 0.64 (0.52–0.76) | 0.09 (0.05–0.18) | 0.29 (0.19–0.39) | 0.01 (0.00–0.02) |
| DTMM | 0.69 (0.59–0.80) | 0.14 (0.07–0.21) | 0.20 (0.10–0.31) | 0.01 (0.00–0.04) | ||
| CTMM | 0.73 (0.62–0.82) | 0.10 (0.04–0.17) | 0.20 (0.12–0.29) | 0.00 (0.00–0.01) | ||
| Weekly | Daily | PO | 0.63 (0.51–0.76) | 0.09 (0.04–0.17) | 0.29 (0.18–0.39) | 0.01 (0.00–0.02) |
| DTMM | 0.86 (0.75–0.95) | 0.02 (0.00–0.05) | 0.32 (0.14–0.51) | 0.00 (0.00–0.01) | ||
| CTMM | 0.73 (0.62–0.81) | 0.10 (0.04–0.16) | 0.20 (0.13–0.28) | 0.00 (0.00–0.02) | ||
CI, confidence interval; CTMM, continuous‐time Markov model; DTMM, discrete‐time Markov model; PO, proportional odds model.
Impact of observation frequency on model performance
The model estimates and VPCs for models based on varying observation frequencies are shown in Table S1 and Figure S6 . With increasing frequency, the PO model estimated a trend of decreased drug effect along with decreased model performance. For daily frequency, the PO model significantly underestimated proportion at grade 1 and overestimated grade 0. The estimates for the DTMM differed greatly for daily and weekly frequencies, reflecting the stronger correlation from day to day than week to week, which was supported by the different profiles in the CTS for daily and weekly frequencies. As expected, the DTMM could not handle unevenly spaced observations well, as shown in VPC. The CTMM performed consistently well with similar parameter estimates for all observation frequencies, which agreed with the similar profiles in the CTS for daily and weekly frequencies (Table 2; Figure S5 ).
Discussion
For analyzing longitudinal‐ordered categorical data, the benefit of adding the complexity of Markov components may not be obvious if without direct comparisons. In this article, we compared the performance of the PO model and the DTMM and CTMM based on MS data sets with various observation frequencies. The goal was to provide recommendations on the ideal model(s) for specific conditions.
As Markov models depend on neighboring observations, it is important to document any change in state during the deterioration and resolution phase of AE, if spontaneously reported. Missing intermittent states may impact parameter identifiability or even model structures, such as adding direct transitions between nonneighboring grades in the CTMM (0 and 2/3 in this case). Medical interventions for AE management also need to be documented and assessed in the model.12, 33 As the major AE for vismodegib, no recommended treatment is available to manage MS other than dose withholding.22
We have summarized the recommendations for method selection in Table 3. For the weekly data set, the PO model reasonably captured the AE time profile at the population level (proportion of AE grade over time), although not as well as Markov models. Theoretically, the independency of the PO model with regard to the consecutive observations would provide more flexibility to model data with diverse observation intervals. However, the performance of the PO model was found to decrease with an increase in observation frequencies (stronger Markov properties). We do not have a good explanation for this observation. Schindler and Karlsson20reported the consistent misprediction of the PO model in three examples and commented that applying PO models to data with Markov properties may lead to potential model misspecification. Because the Markov properties in a given data set might not be obvious, and moreover, it is a case‐by‐case scenario whether a PO model can provide a good fit, our suggestion is to always test the DTMM in case of evenly spaced data even if the PO model fit the analysis purpose (such as to derive the AE incidence over time at trial level). Whether PO models from Schindler and Karlsson20incorporated the delay between PK and AE is not clear. The impact of such a delay mechanism can be significant for a PO model, as drug exposure is the only dynamic element driving AE probability and has to have a similar profile (Figure S7 ). It is recommended that a delay compartment model is always tested for a PO model to account for the potential delay between PK and AE. The Markov models have an inherent capability of handling delayed response without requiring a delay compartment. The transition probabilities are described as a function of exposure in both Markov models. In the CTMM, the change in exposure will instantaneously affect the transition rate of the probability, but the change in probability of certain AEs is delayed. In the DTMM, the probability of AEs without drug effect () changes along with treatment depending on the preceding grade , which reduces the impact of the drug exposure change on the probability of AEs, leading to the delayed increase and decrease of the AE probability time profile compared with PK.
Table 3.
Recommendations for model selections
| Modeling exercise | Scenario | PO | DTMM | CTMM |
|---|---|---|---|---|
| Model building | Based on evenly spaced data | Case by casea | OK | OK |
| Based on unevenly spaced data | Case by casea | NO | OK | |
| Model application | Derive the proportion of AE grade over time | Case by casea | OK | OK |
| Derive the cumulative probability, and the time to first AE event of interest | NO | OK | OK | |
| Conduct CTS | OK with exceptionsb | OK with exceptionsc | OK |
AE, adverse event; CTMM, Continuous‐time Markov model; CTS, clinical trial simulations; DTMM, discrete‐time Markov model; PO, proportional odds model.
The performance might deteriorate with more frequent intervals when the Markov properties became stronger. bExceptions applied: need to first pass a visual predictive check for “proportion of AE grade over time”; only for simulating the clinical trials without dose adaptation based on individual AE prediction. cExceptions applied: only for simulating the data set with the same frequencies as the model‐building data set.
The PO model cannot describe data at the individual level well as it does not account for the dependency between adjacent observations explicitly. The dependency was partly accounted for by the interindividual variability on the drug effect parameter (slope), showing as a better accordance between adjacent observations for individual with stronger drug effect. Under a similar drug effect, the PO model tended to predict transitions between states too frequently as compared with the DTMM, leading to an overpredicted incidence rate and early occurrence. Therefore, the PO model cannot be used for adaptive CTS, where dose adjustment is based on the predicted individual response. The PO model may also lead to inflated type 1 error rate of (falsely) including a covariate as a result of the ignoring of serial correlation between observations.34 By considering dependency between adjacent observations, the Markov models can capture the AE time profile at both the population and individual levels and are capable of describing time to first AE profile and conducting adaptive CTS.
The estimates for the DTMM are sensitive to observation frequency and cannot be used directly to simulate the outcomes for data set with different frequency (e.g., using the model from weekly data to simulate outcomes for daily data). The misfit of unevenly spaced data confirmed the inappropriateness of using the DTMM for such data, as it violated the discrete feature of Markov property. For spontaneously reported AEs, one can always interpolate evenly spaced data based on the start and end dates of each grade. However, for end points measured at specific time points during clinical visits, unevenly spaced data are very common.
Of the three models compared, the CTMM is the most universally applicable model. Without modification to model structure, it can describe very well the MS data sets with different observation frequencies at both the population and individual levels. As the CTMM can naturally account for the change of dependency over time between adjacent observations, very similar parameter estimates could be obtained regardless of the observation frequencies, as opposed to the distinct estimates in the DTMM. For this reason, the CTMM can be used to simulate outcomes for data sets with any frequency. However, it is challenging to develop a parsimonious and identifiable CTMM, as the function format of transfer rate can be very versatile. In this study, because of the estimation challenges for the CTMM, the IMP method was selected instead of FOCE to combine with the LAPLACE and Like options to provide optimal estimations with reliable covariance and better VPC. In general, the DTMM would be sufficient in most cases (Table 3). It is recommended to start with the DTMM when both the DTMM and CTMM are appropriate, considering the comparable performance in the two Markov models and the less development time for the DTMM. The challenges for developing the CTMM in this study might be because of the small data set (n = 74) with few grade ≥ 2 AEs and the unique model structure with direct transitions between nonneighboring states, which might not be generalized to more general situations. In any case, the CTMM is necessary to deal with unevenly spaced data sets or simulate trials with new observation frequency. When needed, the mCTMM can be a good alternative to the CTMM with a parsimonious structure.20
The US label of vismodegib was updated recently to allow treatment interruption for up to 8 weeks in metastatic or locally advanced BCC.22 The purpose is to achieve long‐term treatment by reducing the AE incidence without compromising efficacy. Simulations with tumor growth inhibition models were used directly to support the label change (data on file). In this study, the CTS of MS using Markov models confirmed that 8‐week treatment interruption following 12‐week daily treatment reduced the MS incidence substantially (from ~ 73% to 10%). The incidence of MS for any duration of treatment interruption can be derived when necessary.
Funding
The analysis was funded by Genentech, Inc., a member of the Roche group.
Conflict of Interest/Disclosure
T.L., J.Y.J. and M.K. are full‐time employees of Genentech, Inc., and own Roche stock. Y.Y. was supported by a Genentech summer internship when the analysis was initially conducted.
Author Contributions
T.L., Y.Y., and M.K. wrote the manuscript. T.L., Y.Y., M.K., and J.Y.J. designed the research. T.L., Y.Y., and M.K. analyzed the data.
Supporting information
Figure S1-S7.
Parameter table (Table S1).
NONMEM code (Model S1).
Mock dataset (Data S1).
Acknowledgments
The authors acknowledge the investigators, patients, and their families who participated in the clinical trials. The authors thank Dr. Russ Wada (Certara) for helping with the initial version of proportional odds model and discrete‐time Markov model, and Dr. Mats Karlsson (Uppsala University) and Drs. Pascal Chanu, Laurent Claret, Rene Bruno, and Ivor Caro (Genentech) for scientific discussions and input.
References
- 1. Mould, D.R. , Walz, A.C. , Lave, T. , Gibbs, J.P. & Frame, B. Developing exposure/response models for anticancer drug treatment. Special considerations. CPT Pharmacometrics Syst. Pharmacol. 4, e00016 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Sheiner, L.B. A new approach to the analysis of analgesic drug trials, illustrated with bromfenac data. Clin. Pharmacol. Ther. 56, 309–322 (1994). [DOI] [PubMed] [Google Scholar]
- 3. Karlsson, M.O. et al A pharmacodynamic Markov mixed‐effects model for the effect of temazepam on sleep. Clin. Pharmacol. Ther. 68, 175–188 (2000). [DOI] [PubMed] [Google Scholar]
- 4. Lacroix, B.D. et al A pharmacodynamic Markov mixed‐effects model for determining the effect of exposure to certolizumab pegol on the ACR20 score in patients with rheumatoid arthritis. Clin. Pharmacol. Ther. 86, 387–395 (2009). [DOI] [PubMed] [Google Scholar]
- 5. Zingmark, P.H. , Kagedal, M. & Karlsson, M.O. Modelling a spontaneously reported side effect by use of a Markov mixed‐effects model. J. Pharmacokinet Pharmacodyn. 32, 261–281 (2005). [DOI] [PubMed] [Google Scholar]
- 6. Ito, K. et al Exposure‐response analysis for spontaneously reported dizziness in pregabalin‐treated patient with generalized anxiety disorder. Clin. Pharmacol. Ther. 84, 127–135 (2008). [DOI] [PubMed] [Google Scholar]
- 7. Niebecker, R. , Maas, H. , Staab, A. , Freiwald, M. & Karlsson, M.O. Modeling exposure‐driven adverse event time courses in oncology exemplified by afatinib. CPT: Pharmacometrics Syst. Pharmacol. 8, 230–239 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Bergstrand, M. , Soderlind, E. , Weitschies, W. & Karlsson, M.O. Mechanistic modeling of a magnetic marker monitoring study linking gastrointestinal tablet transit, in vivo drug release, and pharmacokinetics. Clin. Pharmacol. Ther. 86, 77–83 (2009). [DOI] [PubMed] [Google Scholar]
- 9. Keizer, R.J. et al A model of hypertension and proteinuria in cancer patients treated with the anti‐angiogenic drug E7080. J. Pharmacokinet Pharmacodyn. 37, 347–363 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Lacroix, B.D. , Karlsson, M.O. & Friberg, L.E. Simultaneous exposure‐response modeling of ACR20, ACR50, and ACR70 improvement scores in rheumatoid arthritis patients treated With certolizumab pegol. CPT: Pharmacometrics Syst. Pharmacol. 3, e143 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Pilla Reddy, V. et al Pharmacokinetic‐pharmacodynamic modeling of severity levels of extrapyramidal side effects with Markov elements. CPT: Pharmacometrics Syst. Pharmacol. 1, e1 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Xu, C. et al A continuous‐time multistate Markov model to describe the occurrence and severity of diarrhea events in metastatic breast cancer patients treated with lumretuzumab in combination with pertuzumab and paclitaxel. Cancer Chemother. Pharmacol. 82, 395–406 (2018). [DOI] [PubMed] [Google Scholar]
- 13. Maringwa, J. et al Pharmacokinetic‐pharmacodynamic modeling of fostamatinib efficacy on ACR20 to support dose selection in patients with rheumatoid arthritis (RA). J. Clin. Pharmacol. 55, 328–335 (2015). [DOI] [PubMed] [Google Scholar]
- 14. Niebecker, R. , Maas, H. , Staab, A. , Freiwald, M. & Karlsson, M.O. Modeling exposure‐driven adverse event time courses in oncology exemplified by afatinib. CPT: Pharmacometrics Syst. Pharmacol. 8, 230–239 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Hu, C. Exposure‐response modeling of clinical end points using latent variable indirect response models. CPT Pharmacometrics Syst. Pharmacol. 3, e117 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Hu, C. , Randazzo, B. , Sharma, A. & Zhou, H. Improvement in latent variable indirect response modeling of multiple categorical clinical endpoints: application to modeling of guselkumab treatment effects in psoriatic patients. J. Pharmacokinet. Pharmacodyn. 44, 437–448 (2017). [DOI] [PubMed] [Google Scholar]
- 17. Hutmacher, M.M. , Krishnaswami, S. & Kowalski, K.G. Exposure‐response modeling using latent variables for the efficacy of a JAK3 inhibitor administered to rheumatoid arthritis patients. J. Pharmacokinet. Pharmacodyn. 35, 139–157 (2008). [DOI] [PubMed] [Google Scholar]
- 18. Plan, E.L. , Karlsson, K.E. & Karlsson, M.O. Approaches to simultaneous analysis of frequency and severity of symptoms. Clin. Pharmacol. Ther. 88, 255–259 (2010). [DOI] [PubMed] [Google Scholar]
- 19. Pérez‐Pitarch, A. et al Empagliflozin as adjunct to insulin in patients with type 1 diabetes mellitus: modelling rate and severity of hypoglycemic events. Abstract 5743. <http://www.page-meetingorg/?abstract=5743> (2016).
- 20. Schindler, E. & Karlsson, M.O. A minimal continuous‐time Markov pharmacometric model. AAPS J. 19, 1424–1435 (2017). [DOI] [PubMed] [Google Scholar]
- 21. Sofen, H. et al A phase II, multicenter, open‐label, 3‐cohort trial evaluating the efficacy and safety of vismodegib in operable basal cell carcinoma. J. Am. Acad. Dermatol. 73, 99–105 e101 (2015). [DOI] [PubMed] [Google Scholar]
- 22. Labeling-Package Insert for Erivedge (Vismodegib) – Food and Drug Administration. <https://www.accessdata.fda.gov/drugsatfda_docs/label/2019/203388s012lbl.pdf> (2019).
- 23. Von Hoff, D.D. et al Inhibition of the hedgehog pathway in advanced basal‐cell carcinoma. N. Engl. J. Med. 361, 1164–1172 (2009). [DOI] [PubMed] [Google Scholar]
- 24. Sekulic, A. et al Efficacy and safety of vismodegib in advanced basal‐cell carcinoma. N. Engl. J. Med. 366, 2171–2179 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Cancer Therapy Evaluation Program, National Cancer Institute (NCI) Division of Cancer Treatment and Diagnosis . Common terminology criteria for adverse events, version 4.0. <https://ctepcancergov/protocolDevelopment/electronic_applications/ctchtm#ctc_40> (2010).
- 26. Beal, S.L. , Sheiner, L.B. , Boeckmann, A.J. & Bauer, R.J. (Eds). NONMEM 7.3 users guides. <https://nonmem.iconplc.com/nonmem730/> (1989–2013).
- 27. Lindbom, L. , Pihlgren, P. & Jonsson, E.N. PsN‐Toolkit–a collection of computer intensive statistical methods for non‐linear mixed effect modeling using NONMEM. Comput. Methods Programs Biomed. 79, 241–257 (2005). [DOI] [PubMed] [Google Scholar]
- 28. Jonsson, E.N. & Karlsson, M.O. Xpose–an S‐PLUS based population pharmacokinetic/pharmacodynamic model building aid for NONMEM. Comput. Methods Programs Biomed. 58, 51–64 (1999). [DOI] [PubMed] [Google Scholar]
- 29. Baron, K.T. mrgsolve: simulate from ODE‐based models. R package version 0.9.0. <https://CRAN.R-project.org/package=mrgsolve> (2019).
- 30. R Core Team . R: a language and environment for statistical computing. <http://www.R-project.org> (2014).
- 31. Lu, T. et al Semi‐mechanism‐based population pharmacokinetic modeling of the hedgehog pathway inhibitor vismodegib. CPT: Pharmacometrics Syst. Pharmacol. 4, 680–689 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Lu, T. et al Longitudinal safety modeling and simulation for regimen optimization of vismodegib in operable basal cell carcinoma. Abstract 3254. <http://www.page-meetingorg/?abstract=3254> (2014).
- 33. Lu, T. , Claret, L. , Bruno, R. , Ware, J. & Jin, J. Joint longitudinal ordered categorical model for drug‐induced diarrhea and colitis: a case example in oncology. Abstract w‐75. <https://www.go-acop.org/assets/Legacy_ACOPs/ACoP7/Abstracts/w-75.pdf> (2017).
- 34. Silber, H.E. , Kjellsson, M.C. & Karlsson, M.O. The impact of misspecification of residual error or correlation structure on the type I error rate for covariate inclusion. J. Pharmacokinet Pharmacodyn. 36, 81–99 (2009). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1-S7.
Parameter table (Table S1).
NONMEM code (Model S1).
Mock dataset (Data S1).


