Persistent and polarised global actin flow is essential for directionality during cell migration

Abstract

Cell migration is hypothesised to involve a cycle of behaviours beginning with leading edge extension. However, recent evidence suggests that the leading edge may be dispensable for migration, raising the question of what actually controls cell directionality. Here we exploit the embryonic migration of Drosophila macrophages to bridge the different temporal scales of the behaviours controlling motility. This reveals that edge fluctuations during random motility are impersistent and weakly correlated with motion. In contrast, flow of the actin network behind the leading edge is highly persistent. Quantification of actin flow structure during migration reveals a stable organisation and asymmetry in the cell-wide flowfield that strongly correlates with cell directionality. This organisation is regulated by a gradient of actin network compression and destruction, which is controlled by myosin contraction and cofilin-mediated disassembly. It is this stable actin-flow polarity, which integrates rapid fluctuations of the leading edge that controls inherent cellular persistence.

Introduction

Cell migration is hypothesised to involve a stepwise cycle of behaviours starting with protrusion of the leading edge¹. At the same time the cell must maintain polarity, which is hypothesised to be controlled by a combination of reaction-diffusion modules and membrane tension to maintain an asymmetry in these behaviours^2–5. The integration of these stages leads to coherent motion whereby cells have an inherent persistence in speed and direction⁶.

Since the first postulation of the migratory cycle, we now understand many of its molecular components. Protrusion of the leading edge is driven by Arp2/3-mediated actin polymerisation^{7, 8}. Pushing of the actin filaments against the leading edge, along with myosin-II contraction, subsequently induces a retrograde motion of the crosslinked actin-network^9–11. When integrins are engaged, these points of friction with the extracellular matrix lead to a slowing of the retrograde flow allowing for transmission of the forces of the flowing actin network into extracellular traction stresses^{12, 13}. Finally, asymmetric release of integrin adhesions at the rear allows for net cell translocation¹⁴.

This model of migration is predicated on the idea that it is a linear stepwise process starting at the leading edge^{1, 15}. Therefore, with regards to the control of cell directionality, a major focus has been on the actin polymerisation machinery at the front¹⁶. However, evidence has arisen to bring this leading edge centric view into question. Loss of leading edge lamellipodia does not grossly inhibit chemotaxis^{17, 18} and the presence of actin protrusions, rather than being essential for cell translocation, may actually destabilise migration and enhance exploratory behaviour^{19, 20}. Additionally, recent data revealed that cell shape is a predictor of migratory dynamics,^{21, 22} suggesting that global cellular processes are also important in controlling motility. However, the idea that cell movement may not be directly controlled by extensions at the cell edge is still controversial²³ as the stepwise view of migration has remained nearly unchanged for decades²⁴.

What is currently lacking is a holistic understanding of how the hypothesised steps of motility are integrated in space and time to give a cell its inherent persistence and directionality. The complexity in bridging the stages of migration is partly due to the different time and lengthscales of these behaviours²⁵. For instance, it is difficult to understand how rapid fluctuation of the leading edge, which oscillates on the order of seconds^26–28, controls overall cell persistence that decays on the order of minutes to hours⁶. To resolve such questions requires migration to be imaged at sufficiently high spatiotemporal resolution for long time periods to correlate edge fluctuation, actin dynamics, and overall cell motion. However, correlating behaviours on such different timescales is both experimentally and quantitatively challenging.

In previous work, we exploited the embryonic migration of Drosophila macrophages (hemocytes), which are highly amenable to live imaging during their developmental dispersal²⁹, to develop tools to image cell-wide actin flows during their migration in vivo³⁰. Here we use this system to quantify, and correlate in time, the various behaviours of motility during both random and directed migration. This reveals that edge fluctuation is a weak predictor of directionality during random motility, with a persistence that is less than the overall persistence of the cell. In contrast, the retrograde flow of the actin network behind the leading edge, which has recently been revealed to couple cell speed and persistence³¹, is highly organised and stable in time. Through the development of approaches to quantify global actin flow organisation we reveal that cell migration involves network-wide coordination and an intrinsic asymmetry in the flowfield that highly correlates with cell directionality. This asymmetry is controlled by a stable gradient of actin network compression and destruction towards the rear of the lamellae, which is driven by myosin contraction and cofilin-mediated disassembly. It is this destruction/contraction gradient that leads to a stable cell-wide polarity within the flowing actin network, which likely integrates the rapid fluctuations of the leading edge to control overall cell persistence.

Results

Leading edge fluctuations are a weak predictor of cell directionality

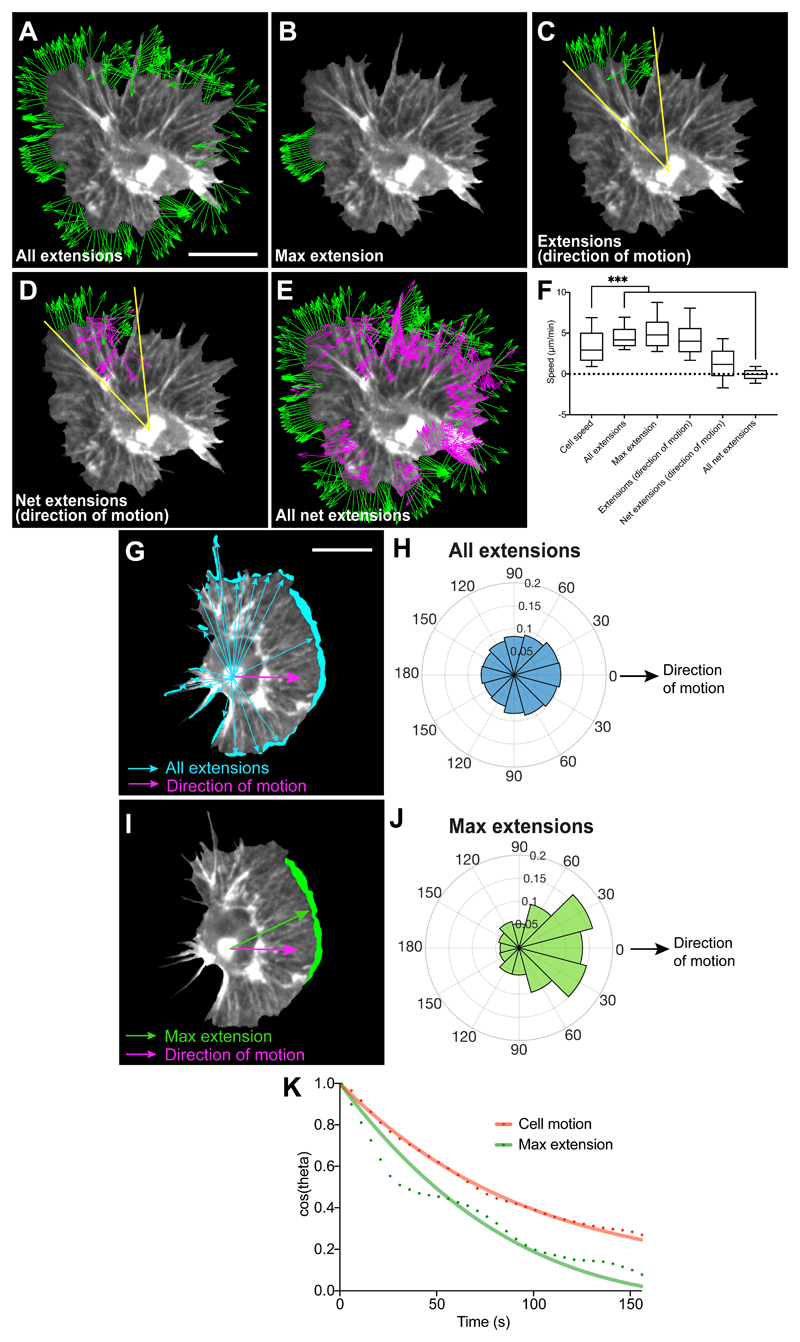
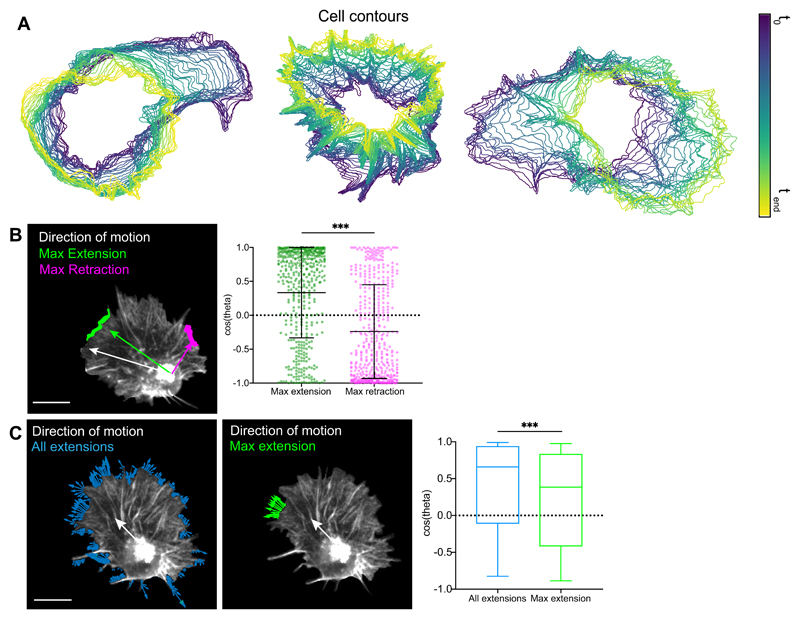
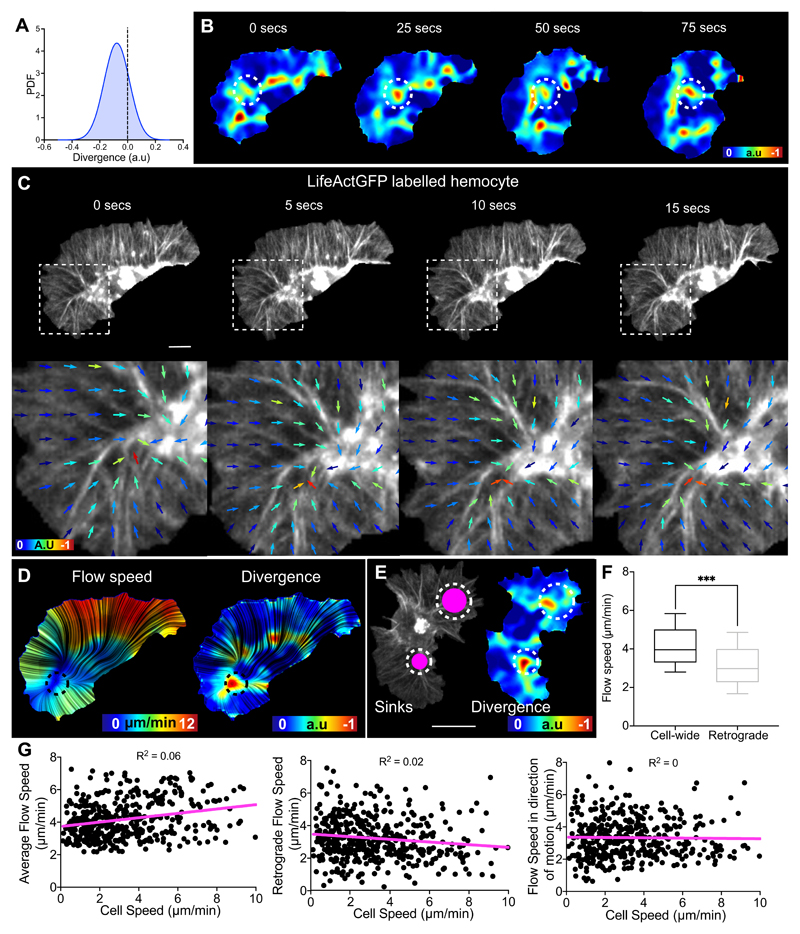
Hemocytes can be automatically and precisely tracked during their embryonic migration using the nucleus as a fiducial marker, which is more accurate than tracking cell centroid at high temporal resolution (Supplementary Video 1). We first used the natural variation in the fluctuation of hemocyte contours (Extended Data Fig. 1A) to highlight a relationship between edge activity and cell motion at high temporal resolution (5 s/frame). However, morphodynamic analysis revealed that edge fluctuations are largely disconnected from cell speed (Fig. 1A-F). We next quantified the positions of edge extensions during random migration with respect to the instantaneous direction of motion to determine how protrusions are correlated with cell directionality. Normalising the position vectors of edge extensions or retractions to hemocyte directionality revealed that edge fluctuations are weakly correlated with motion (Fig. 1G-J; Extended Data Fig. 1B; Supplementary Video 2). These data are surprising considering the high persistence of hemocytes (directionality ratio 0.7 ± 0.1 SEM, this work)³². Interestingly, taking into account both direction and speed of extensions (resultant velocity) revealed that all extensions around the cell collectively showed stronger correlation to motion than the maximum extension alone (Extended Data Fig. 1C); this suggests that minor extensions that individually are not correlated to motion are integrated to provide directional information. Finally, comparing the persistence of cell trajectory and the maximum extension revealed that the leading edge was less persistent than overall cell motion (Fig. 1K). These data highlight that randomly patrolling hemocytes spend significant effort generating extensions independent of motion in a mode of motility that has been termed ‘inefficient’^{27, 33}, suggesting that other behaviours must be involved to provide their high migratory persistence.

Figure 1. Leading edge fluctuations are a weak predictor of cell directionality.

(A-E) Morphodynamic analysis of edge fluctuation in hemocytes by quantifying the speed of: (A) all edge extensions, (B) the maximum edge extension (longest contiguous extension of perimeter), (C) extensions in the direction of motion (30° cone), (D) edge extensions and retractions in the direction of motion, and (E) all edge extensions and retractions (green, extension; magenta, retraction; for display purposes ‘A-E’ show unit vectors; scale bar 10 μm).

(F) Comparison of cell speed with the speed of edge fluctuations as measured in ‘A-E’. ***P < 0.0001, Kruskal-Wallis and Dunn’s multiple comparison test. Boxplot shows medians, 25^th and 75^th percentiles as box limits, 10^th and 90^th as whiskers (n = 443, 9 biologically independent samples). Note that cell speed is not correlated with edge extension speed, and that net extensions (extensions – retractions) sum to zero showing that cells maintain a constant area over time.

(G) A representative snapshot of a randomly migrating hemocyte with edge extensions automatically segmented. Vectors are drawn from the nucleus to each individual extension (blue arrows) and correlated with the direction of cell motion (magenta arrow) in panel ‘H’. Scale bar 10 μm.

(H) A rose plot showing the direction of all extension vectors, as highlighted in ‘G’, normalised to the direction of cell motion (n = 16379, 9 biologically independent samples).

(I) A representative snapshot of a randomly migrating hemocyte with the maximum edge extension (by area) automatically segmented. Vectors are drawn from the nucleus to the centroid of the maximum extension (green arrow) and correlated with the direction of cell motion (magenta arrow) in ‘J’.

(J) A rose plot showing the direction of the maximum extension vectors, as highlighted in ‘I’, normalised to the direction of cell motion (n = 443, 9 biologically independent samples).

(K) Directional autocorrelation comparing the persistence of cell motion and maximum edge extension showing that the maximum edge extension is less persistent than overall cell motion (note that a slower decay represents an increased persistence). Dotted lines are real data and solid lines represent fitted decay curves (n = 9 biologically independent samples).

Actin flow is globally organised in migrating cells

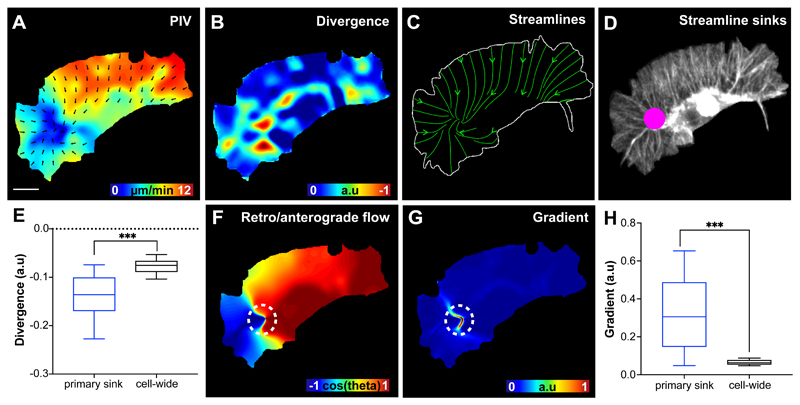
Recent mathematical modelling has suggested that actin flow may help establish the inherent persistence of migrating cells³¹. To examine cell-wide actin flows in hemocytes we performed Particle Image Velocimetry (PIV) of LifeAct-GFP expressing cells. Global PIV analysis suggested an overall organisation to the actin flow with vectors showing a high degree of alignment and a gradient of high to low flow speed from the leading edge to the cell body (Fig. 2A; Supplementary Video 3). As LifeAct-GFP binds actin indirectly, we wanted to confirm that PIV was actually highlighting internal motion of the network. We therefore labelled directly with Actin-GFP, and photobleached spots in the network, which allowed us to examine network transit. Photobleached spots at the leading edge moved in a retrograde fashion toward the cell body and mimicked the flowfield of LifeAct-GFP expressing cells, suggesting PIV analysis was indeed tracking actin motion (Supplementary Video 4). In order to understand how actin flow was structured we first calculated its divergence, which highlights sources and sinks in the network. While there was little positive divergence (Extended Data Fig. 2A), the network showed large regions of high negative divergence at the rear of the lamella immediately adjacent to the hemocyte cell body (Fig. 2B; Extended Data Fig. 2B; Supplementary Video 3), which correlated with zones of actin fibre deformation (Extended Data Fig. 2C). In contrast to the rapid fluctuation of the leading edge, these negatively divergent regions were persistent on the order of 30-60 seconds (Extended Data Fig. 2B).

Figure 2. Actin retrograde flow is globally organised in migrating hemocytes.

(A) Particle Image Velocimetry (PIV) analysis performed on a LifeAct-GFP expressing cell to highlight the direction and magnitude of actin flow. The region of the flowfield without vectors represents the soma of the hemocyte, which has no observable actin flow, and this information was removed for all subsequent quantification. Scale bar 10 μm.

(B) Divergence calculated from the actin flowfield to highlight sinks within the network. In this image only negatively divergent regions are highlighted.

(C) Streamlines calculated from the actin flowfield in which streamlines were seeded along the boundary of the cell.

(D) The confluence of streamlines quantified by calculating the number of streamlines ending in any location within the cell. In this image, the size of the spot is normalised to the number of streamline endpoints.

(E) The actin flow divergence calculated at the primary sink and compared to the divergence values averaged across the entire cell. ***P < 0.0001, Mann-Whitney two-tailed test. Boxplot shows medians, 25^th and 75^th percentiles as box limits, 10^th and 90^th as whiskers (n = 443, 9 biologically independent samples).

(F) A correlation map in which the direction of cell motion was correlated to the direction of every actin flow vector within the cell. Note that a positive correlation highlights anterograde flow while a negative correlation denotes retrograde flow. The dashed circle indicates the location of the primary sink in this frame of the movie.

(G) Quantification of the gradient of the correlation map in ‘F’ reveals sharp transition regions within the flowfield. The dashed circle indicates the location of the primary streamline sink in this frame of the time-lapse movie.

(H) Quantification of the gradient of the retrograde/anterograde flow correlation, as highlighted in ‘F’ and ‘G’, at the primary streamline sinks compared to the gradient values averaged across the entire cell. ***P < 0.0001, Mann-Whitney two-tailed test. Boxplot representation as in ‘E’ (n = 443, 9 biologically independent samples).

In order to examine the global organisation of actin flow we seeded streamlines at each point along the edge of migrating hemocytes. The evolution of streamlines during migration showed an overall organisation in the actin flowfield with many streamlines ending within a region of the lamella anterior to the cell body in the direction of cell travel (Fig. 2C; Supplementary Video 3). We calculated the strength of streamline confluence, which revealed a predominant streamline endpoint that was asymmetrically distributed within the cell (Fig. 2D; Supplementary Video 3). Interestingly, this streamline endpoint was highly negatively divergent and tended to represent a region of low actin flow speed (Fig. 2E; Extended Data Fig. 2D; Supplementary Video 3), showing that it represents a large sink within the actin flowfield. Additionally, the number of sinks appeared to correlate with the number of hemocyte lamellae suggesting that they may contribute to maintaining cell polarity (Extended Data Fig. 2E; Supplementary Video 5).

The primary streamline sink appeared to represent some transition in the actin flow as its location was strongly correlated with sharp transition from retrograde to anterograde actin motion (Fig. 2F-H). We hypothesise that these transition regions are analogous to the retrograde/anterograde transitions observed in migrating cells in vitro^{18, 34–36} and the transition of actin network gripping to slipping. When we calculated the actin flow speed in the retrograde region, this revealed that the actin flow was indeed slower anterior to the primary sink (Extended Data Fig. 2F), suggesting that this is where extracellular friction is highest. While this is consistent with the actin-clutch hypothesis, we observed no relationship between actin flow speed and cell speed as has been hypothesised should occur³¹, suggesting that this linear relationship may not be valid on shorter timescales (Extended Data Fig. 2G).

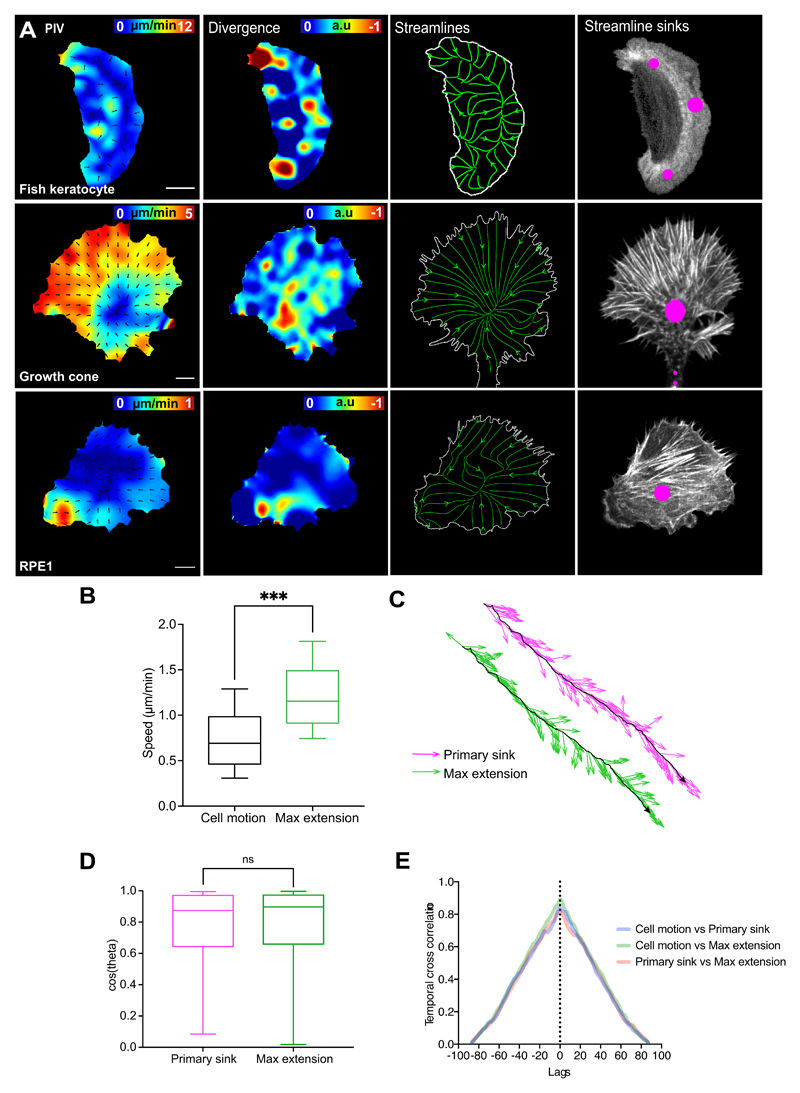
In order to examine whether actin flow organisation can be observed in other migrating cells we examined fish keratocytes, growth cones^{28, 37}, and retinal pigmented epithelial cells (RPE1) (Extended Data Fig. 3A, Supplementary Videos 6-8). All cell types showed similar global organisation of actin flow with streamlines converging at a large network sink deep within the cell, suggesting that this is a conserved feature of migrating cells.

During random migration, the polarity of global actin flow is highly correlated with hemocyte directionality

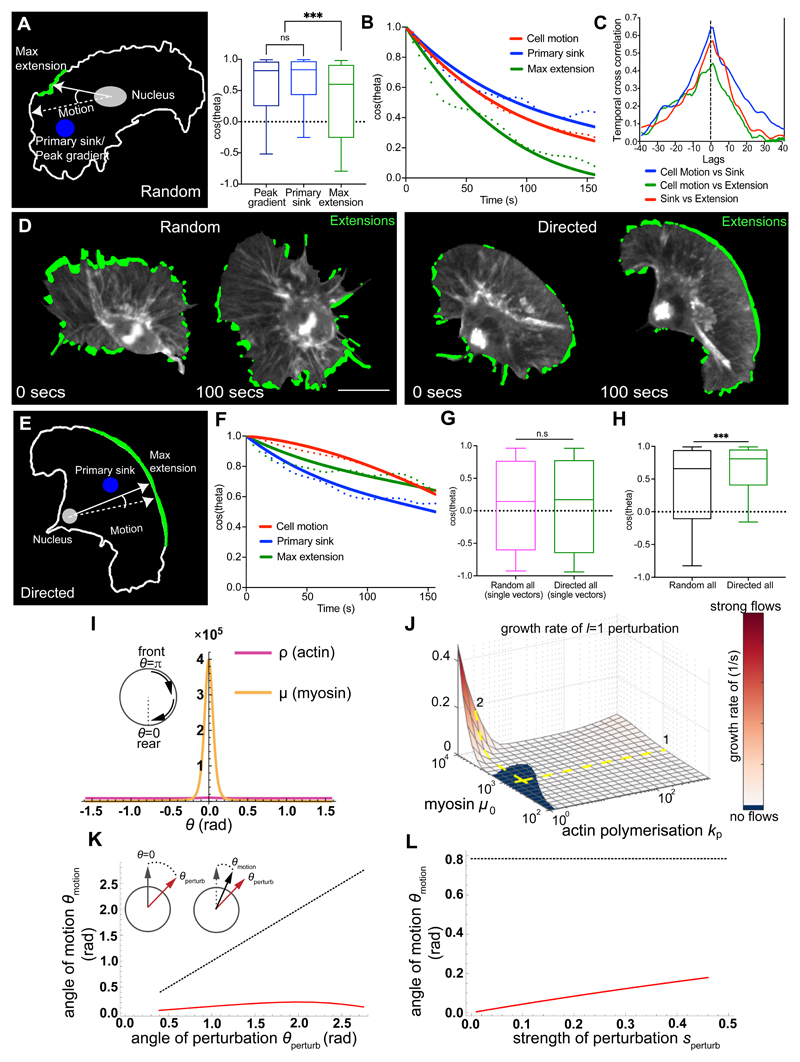
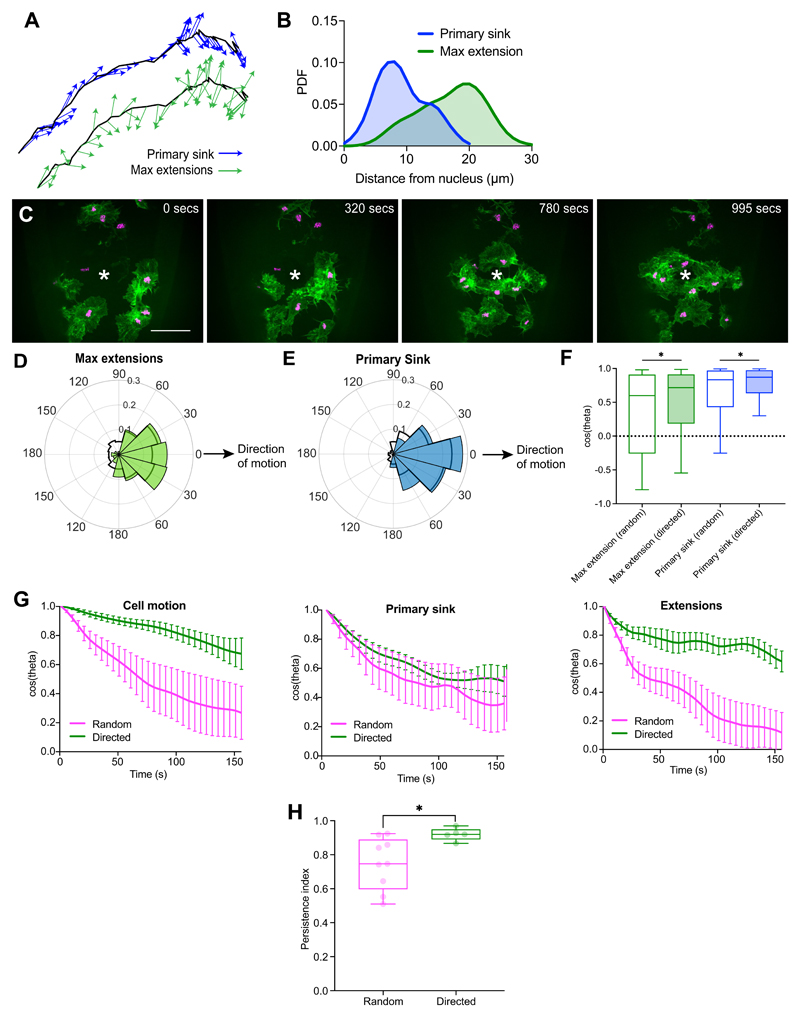
We next examined how actin flow organisation correlated with leading edge dynamics and cell directionality. In order to correlate leading edge extension and flow polarity with cell motion, we calculated vectors from the nucleus to defined points within the cell and correlated the direction of these vectors with the cell’s direction of motion. This revealed that the primary streamline sink and the retrograde/anterograde transition region were more correlated with cell motion than edge extension/retraction (Fig. 3A; Extended Data Fig. 4A; Supplementary Video 9). Furthermore, the persistence of the primary sink was higher than the persistence of the leading edge (Fig. 3B). These data suggest that the coordinated flow of actin may be integrating leading edge activity to provide an inherent persistence to randomly migrating hemocytes.

Figure 3. The polarity of global actin flow is highly stable and correlated to hemocyte motion during random and directed migration.

(A) Schematic depicting the regions correlated to cell motion. ***P < 0.0001, (n.s) P = 0.4471, Kruskal-Wallis and Dunn’s multiple comparison test. Boxplot shows medians, 25^th and 75^th percentiles as box limits, 10^th and 90^th as whiskers (n = 443, 9 biologically independent samples).

(B) Directional autocorrelation of behaviours during random migration. Dotted lines, real data; solid lines, fitted decay curves (n = 9 biologically independent samples, same data as in ‘1K’).

(C) Temporal cross-correlation of migratory behaviours revealing a peak at 0-lag (n = 9 biologically independent samples).

(D) Visualisation of all hemocyte edge extensions (green) during random and directed migration.

(E) Schematic of a directly migrating cell correlating behaviours as in ‘A’.

(F) Directional autocorrelation of behaviours during directed migration. Dotted lines, real data; solid lines, fitted decay curves (n = 4 biologically independent samples).

(G) Correlation to motion of edge extension unit vectors (i.e. direction only) during random (n = 33617, 9 biologically independent samples) versus directed migration (n = 19486, 4 biologically independent samples). (n.s) P = 0.4155, Mann-Whitney two-tailed test. Boxplot representation as in ‘A’.

(H) Correlation to motion of the resultant edge extension velocities (i.e. direction and magnitude) during random (n = 443, 9 biologically independent samples) versus directed migration (n = 272, 4 biologically independent samples). ***P = 0.0002, Mann-Whitney two-tailed test. Boxplot representation as in ‘A’.

(I) A minimal one-dimensional fluid-mechanical model shows myosin contraction spontaneously leads to acto-myosin cortical flows with a sink at the rear (θ = 0), corresponding with a peak in Myosin-II concentration.

(J) Linear stability analysis shows the emergence of flows is sensitive to Myosin-II levels (steep dependence in path 2) and insensitive to polymerisation rate (flat dependence in path 1).

(K) Angular location of Myosin-II peak and hence direction of cell migration (red solid line) versus the angle of actin perturbation (black dashed line).

(L) Angular location of Myosin-II peak and cell motion versus the strength of actin perturbation. Angle of perturbation (black dashed line) was kept constant while varying its strength.

We next tested if there was a temporal hierarchy of these various migratory behaviours. Interestingly, even at our rapid temporal resolution of 5 s/frame we observed a maximum correlation at 0-lag, highlighting that edge extension, actin flow polarity, and cell directionality are precisely correlated in time (Fig. 3C). This is despite the fact that these different phenomena are separated by relatively large distances within the cell (Extended Data Fig. 4B).

We next examined the correlation of leading edge activity and the streamline sink with cell directionality in RPE1 cells. Similar to hemocytes, edge speed in RPE1 cells was uncorrelated with cell speed (Extended Data Fig. 3B). Furthermore, both the direction of the maximum extension and the primary sink were correlated with cell motion (Extended Data Fig. 3C,D; Supplementary Video 10). Additionally, the direction of the velocities of the maximum extension, primary sink, and cell motion showed a maximum correlation at 0-lag, highlighting that, similar to hemocytes, these behaviours were strongly coordinated (Extended Data Fig. 3E). However, in contrast to hemocytes the maximum extension and primary sink were equivalently correlated with cell motion (Extended Data Fig. 3D) suggesting that RPE1 cells are more efficient with regards to the production of edge protrusions.

During directed migration, leading edge persistence controls hemocyte directionality

While the organisation of global actin flow appeared more important than edge fluctuations in defining the persistence of randomly patrolling hemocytes, we wondered whether the same would be true during directed migration. Hemocytes can be rapidly induced to migrate to epithelial wounds through hydrogen peroxide release³⁸. When migration behaviours were examined during a wound response (Extended Data Fig. 4C; Supplementary Videos 11,12) there was an increase in the correlation of the maximum extension and primary sink with cell motion (Fig. 3D; Extended Data Fig. 4D-F). Furthermore, there was an increase in leading edge persistence, which unlike randomly moving cells, closely matched the persistence of other migratory behaviours (Fig. 3E,F; Extended Data Fig. 4G). Interestingly, cells undergoing directed and random migration showed equivalent distributions of extensions around the cell perimeter when normalised to the direction of motion (Fig. 3G). However, the resultant edge velocity of these extensions was more correlated to motion in directionally migrating cells (Fig. 3H), suggesting that the wound cue may be increasing the speed of edge extensions in the direction of the wound site. These changes in leading edge activity were also correlated with an increase in the persistence of cells migrating to the wound (Extended Data Fig. 4H). These data suggest that the leading edge in hemocytes is more critical for driving migration during chemotactic responses, which is similar to what has been reported for mammalian dendritic cells²⁰.

Nonequilibrium fluid-mechanical model spontaneously breaks symmetry, resulting in highly stable actin flows and persistent motion

To gain insight into the connections between actin flows, sinks, and persistent cell motion, we built a minimal one-dimensional fluid-mechanical model with active processes based on only four coupled partial differential equations (see Supplementary modelling details and related models for more information^{39, 40}). This minimal model leads to an emergent actin flow profile with a gradient of myosin intensity and a sink at the rear (Fig. 3I). The induction of stable flow was relatively insensitive to changes in actin polymerisation (as long as a threshold was reached; Fig. 3J) or depolymerisation (see Supplementary modelling details) but sensitive to changes in myosin levels, suggesting the flow was remarkably robust (Fig. 3J). Additionally, it was relatively difficult to reorient the flow by perturbation of cortical actin density. When we simulated a single pulse of actin at a new region of the cortex, the angle of actin flow – and hence cell motion – was hardly deflected (Fig. 3K). However, increasing the strength of the perturbation had an increased capacity to reorient the flow (Fig. 3L), suggesting that an external cue could steer cell motion by increasing the strength of actin polymerisation. Indeed, this mechanism of cell steering may be occurring in hemocytes migrating towards wounds as their increase in resultant edge velocity in the direction of motion is likely driven by increased actin polymerisation (Fig. 3G,H). Nevertheless, this minimal model suggests that actin flow organisation is inherently stable and strongly dependent on myosin contraction.

Negatively divergent regions of the actin flowfield represent regions of actin network strain and disassembly

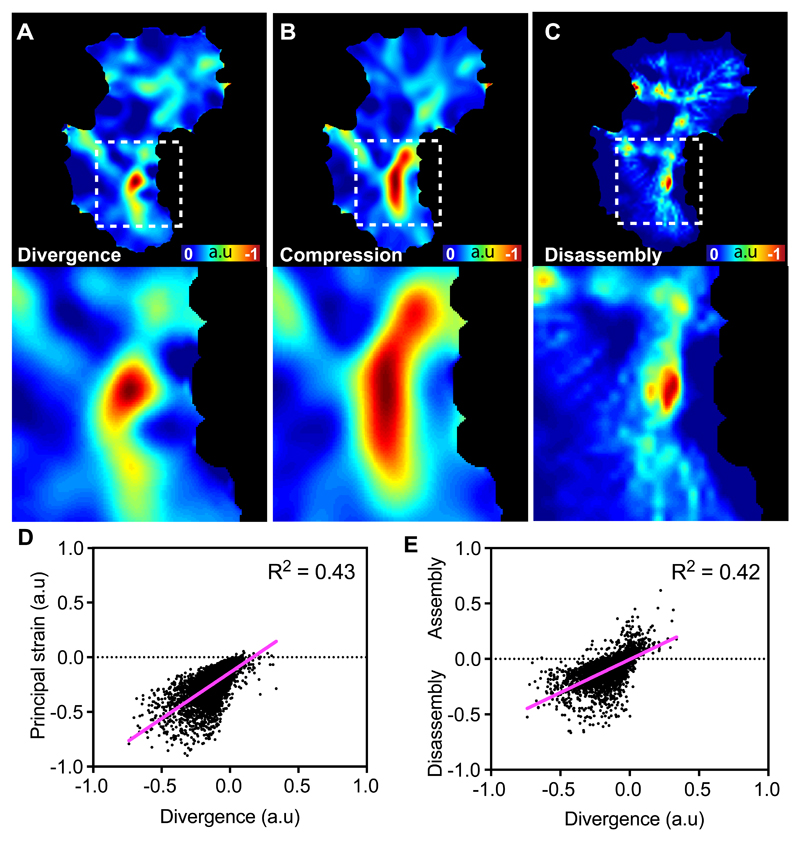
Due to the presence of stable, negatively divergent regions within the actin flowfield, we hypothesised that global actin flow may be coordinated by these points within the network. There are two, non-mutually exclusive mechanisms hypothesised to contribute to actin flows: motor-driven contraction and actin network destruction. We therefore examined how the negatively divergent regions of the network correlated with measures of compression and disassembly. We first calculated the principal component of the strain rate, which is quantified from the spatial changes in the actin velocity field; this analysis of network deformation highlighted that the negatively divergent regions were correlated with high rates of compression (Fig. 4A,B,D; Supplementary Video 13). We also modelled the assembly/disassembly within the network by taking into account the actin intensity and flow information as previously described¹⁰. This revealed that the negatively divergent regions were also correlated with regions of disassembly (Fig. 4A,C,E; Supplementary Video 13). These data suggest that the negatively divergent regions of the network are controlled by a combination of both contraction and disassembly of actin filaments.

Figure 4. Negatively divergent regions of the actin flowfield represent regions of actin network strain and disassembly.

(A-C) Heatmaps comparing the quantification of divergence (A), network compression (B), and actin network disassembly (C) in an individual hemocyte. Bottom panels are high magnification images of the boxes outlined in the upper panels. Note the partial overlap of these parameters.

(D) Scatter plot comparing a random sample of points in the actin flowfield for divergence and principal strain. Note the positive relationship between negative divergence and the negative values of the principal strain (i.e. compression) (n = 5000 random points, 9 biologically independent samples).

(E) Scatter plot comparing a random sample of points in the actin flowfield for divergence and amount of assembly/disassembly within the actin network. Note the positive relationship between negative divergence and the amount of disassembly (n = 5000 random points, 9 biologically independent samples).

Myosin-II driven contraction and cofilin-mediated disassembly are essential for actin flow

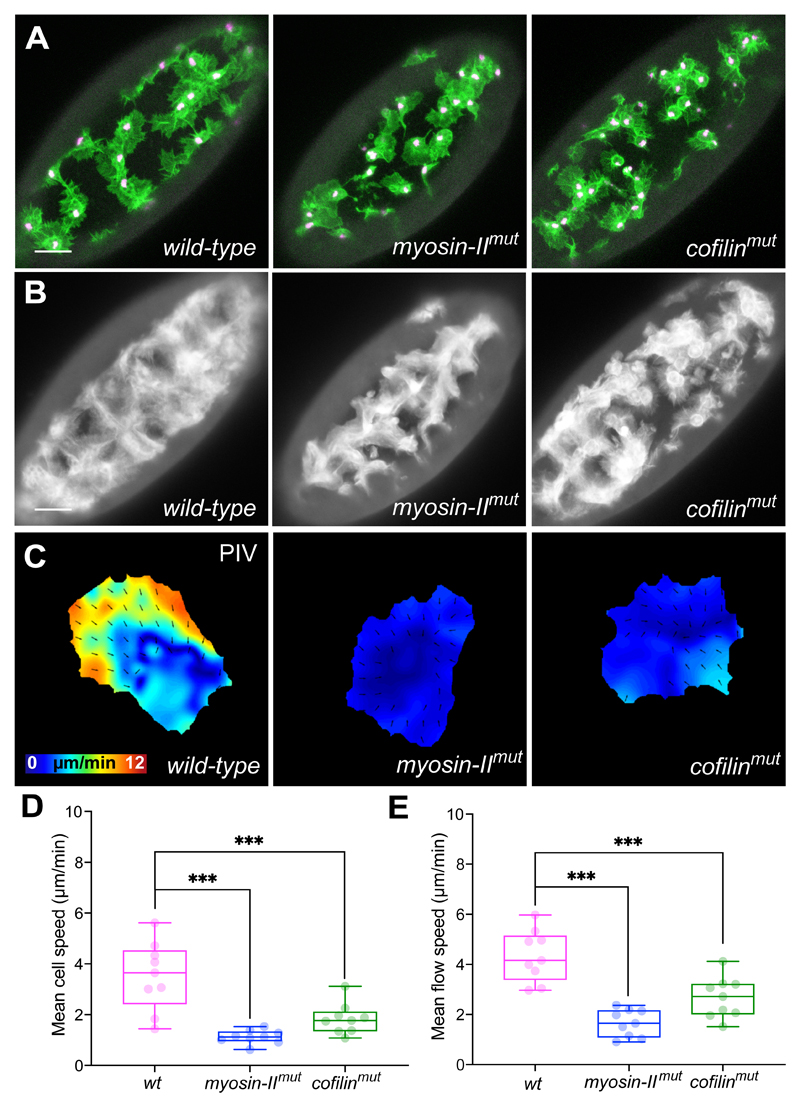
We next examined zygotic mutations in non-muscle myosin-II and cofilin, which have both been hypothesised to regulate actin flow through contraction and severing, respectively^{10, 41–43}. Indeed, homozygous mutation of either myosin-II or cofilin led to defects in hemocyte dispersal (Fig. 5A,B; Supplementary Video 14). Furthermore, both mutations showed a reduction in cell speed, and similar to what has been observed in cultured cells in vitro, a reduction in actin flow velocity^{10, 41, 42, 44} (Fig. 5C-E; Supplementary Video 15).

Figure 5. Loss of myosin-II and cofilin lead to reduced actin flow and cell speed.

(A) Images of hemocytes on the ventral surface of Drosophila embryos in wild-type, myosin-II, and cofilin mutant embryos. LifeAct-GFP is shown in green, nuclei are labelled in magenta. Scale bar 30 μm.

(B) Temporal average projection of wild-type, myosin-II, and cofilin mutant embryos, highlighting domains occupied by migrating hemocytes. Note that the mutant embryos display a less homogenous domain distribution. Scale bar 30 μm.

(C) PIV analysis of actin flow in wild-type, myosin-II, and cofilin mutant cells.

(D) Quantification of mean cell speed in wild-type and mutant cells showing that both myosin-II and cofilin mutant hemocytes are slower than wild-type cells. ***P < 0.001, ordinary one-way ANOVA test and Holm-Sidak’s multiple comparison test. Boxplot shows medians, 25^th and 75^th percentiles as box limits, minimum and maximum values as whiskers; each datapoint is displayed as a dot (n = 9 biologically independent samples for each genotype).

(E) Quantification of mean actin flow speed in wild-type and mutant cells. Both myosin-II and cofilin mutant hemocytes are slower than wild-type cells. ***P < 0.001, ordinary one-way ANOVA test and Holm-Sidak’s multiple comparison test. Boxplot representation as in ‘D’ (n = 9 biologically independent samples for each genotype).

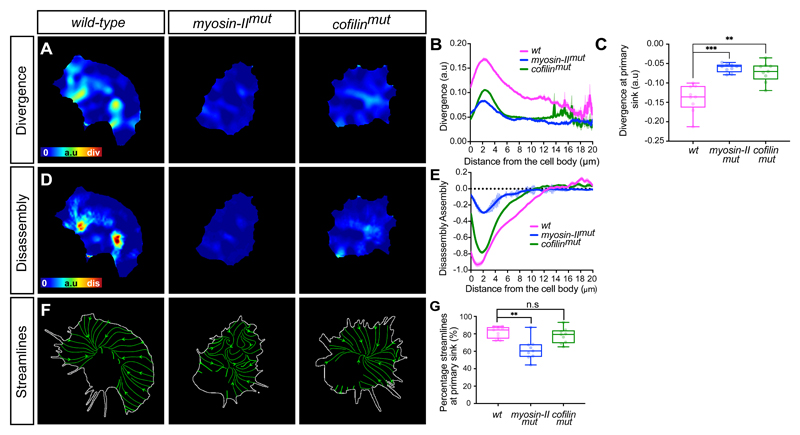
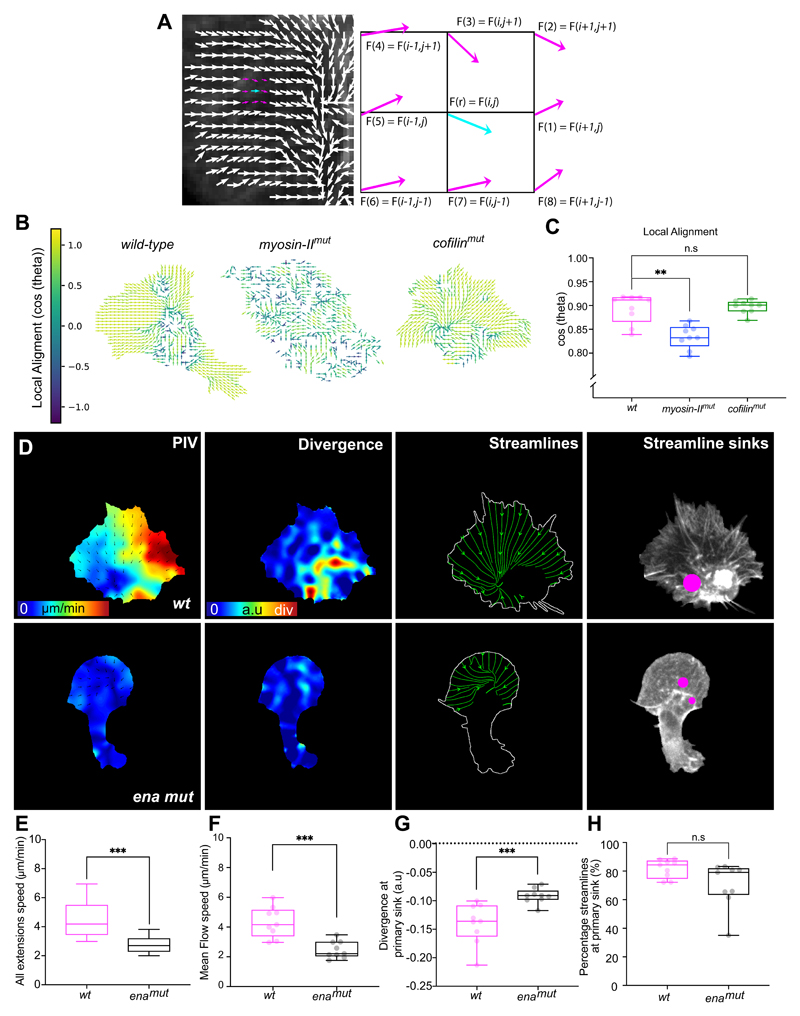
We subsequently examined how organisation of the actin flow was affected by the absence of either Cofilin or Myosin-II. As mechanical gradients across the cytoplasm are hypothesised to be a property of polarised motility^{31, 45, 46}, we first determined if there was a gradient of negative divergence. Wild-type cells showed a gradient of network divergence starting a few microns from the cell edge, which increased until peaking just before reaching the cell body (Fig. 6A,B). In contrast, in both myosin-II and cofilin mutant cells, the overall divergence values increased and there was no obvious gradient from front to rear (Fig. 6A,B; Supplementary Video 16). Furthermore, the primary streamline sink, which was negatively divergent in wild-type cells, showed an increase in divergence values in the mutants (Fig. 6C) suggesting that myosin-II and cofilin are both playing some role in generating sinks within the actin network.

Figure 6. A gradient of myosin-II driven contraction is essential for global organisation of actin flow.

(A) Heatmaps comparing the quantification of divergence in wild-type, myosin-II, and cofilin mutant hemocytes.

(B) Quantification of the mean divergence values in wild-type and mutant cells calculated by drawing linescans from the cell body to the edge (wild-type, n = 1329 lines, 9 biologically independent samples; myosin-II mutant, n = 657 lines, 4 biologically independent samples; cofilin mutant, n = 1480 lines, 7 biologically independent samples). Error bars = SEM.

(C) Quantification of the mean divergence at primary sink in wild-type and mutant cells, which reveals that mutants have an increase in divergence values highlighting a reduction in network compression. ***P = 0.0002, **P = 0.004, Kruskal-Wallis and Dunn’s multiple comparison test. Boxplot shows medians, 25^th and 75^th percentiles as box limits, minimum and maximum values as whiskers; each datapoint is displayed as a dot (n = 9 biologically independent samples for all genotypes).

(D) Heatmaps comparing the quantification of actin disassembly in wild-type and mutant cell

(E) Quantification of the mean assembly/disassembly values in wild-type and mutant cells calculated by drawing linescans from the cell body to the edge (wild-type, n = 1328 lines, 9 biologically independent samples; myosin-II mutant, n = 657 lines, 4 biologically independent samples; cofilin mutant, n = 1538 lines, 7 biologically independent samples). Error bars = SEM.

(F) Images highlighting an analysis of streamlines through the actin flowfield in wild-type and mutant cells. Note the disorganised streamlines in myosin-II mutants.

(G) Quantification of the percentage of streamlines that end at the primary sink in wild-type and mutant cells. Note that myosin-II mutants show a significant reduction in their streamline confluence compared to wild-type or cofilin mutant cells. **P = 0.0018, (n.s) P = 0.6840, Kruskal-Wallis test and Dunn’s multiple comparison test. Boxplot representation as in ‘C’ (n = 9 biologically independent samples for each genotype).

While the divergence profiles appeared similar in myosin-II and cofilin mutants, they showed other phenotypes suggestive of unique roles in the regulation of actin flow when we compared rates of assembly/disassembly. Wild-type cells displayed a gradient of disassembly that peaked at the rear of the network in a region similar in location to the peak in negative divergence (Fig. 6A,B,D,E). In cofilin and myosin-II mutant cells, overall disassembly was reduced suggesting that they both play a role in network destruction (Fig. 6D,E; Supplementary Video 16), however, the profile of the disassembly rates was not identical. In the absence of myosin-II, net disassembly of the network was relatively flat until reaching the rear of the network. In contrast, in the absence of cofilin there was a similar profile of net disassembly to wild-type cells, with a peak at the rear of the network that failed to reach levels observed in controls (Fig. 6D,E). These data suggest that both cofilin-mediated severing and myosin-II contraction are essential to regulate disassembly, however, cofilin is setting a baseline level of actin depolymerisation across the network while myosin-II is controlling its graded destruction.

Streamline analysis also revealed that the myosin-II mutants showed a much more disorganised actin flow. Quantifying the strength of the streamline sink revealed that the maximum streamline endpoint in myosin-II mutants accumulated far fewer streamlines than either wild-type or cofilin mutants (Fig. 6F,G; Supplementary Video 16). Furthermore, quantifying local alignment of the flowfield revealed that myosin-II mutants specifically had a more disorganised actin flow profile (Extended Data Fig. 5A-C).

We also examined how changing polymerisation dynamics altered global actin flow organisation. As loss of actin polymerisation factors (e.g. Scar and Arp2/3) results in a severe and near complete loss of lamellae^{47, 48} it was not possible to analyse their role in controlling actin flow. However, Drosophila Ena/Vasp, which enhances leading edge dynamics, plays a more subtle role in regulating hemocyte lamellipodia^{49, 50}, allowing us to examine how changing edge activity affects actin flow. Ena mutant hemocytes showed a reduction in edge activity, and consequently a reduction in actin flow speed and an increase in divergence values (Extended Data Fig. 5D-G; Supplementary Video 17). However, we observed no obvious change in actin flow organisation (Extended Data Fig. 5H). Therefore, as predicted by the modelling, the emergence of a stable flow profile is likely insensitive to changes in actin polymerisation.

A gradient of Myosin-II indirectly leads to actin network contraction

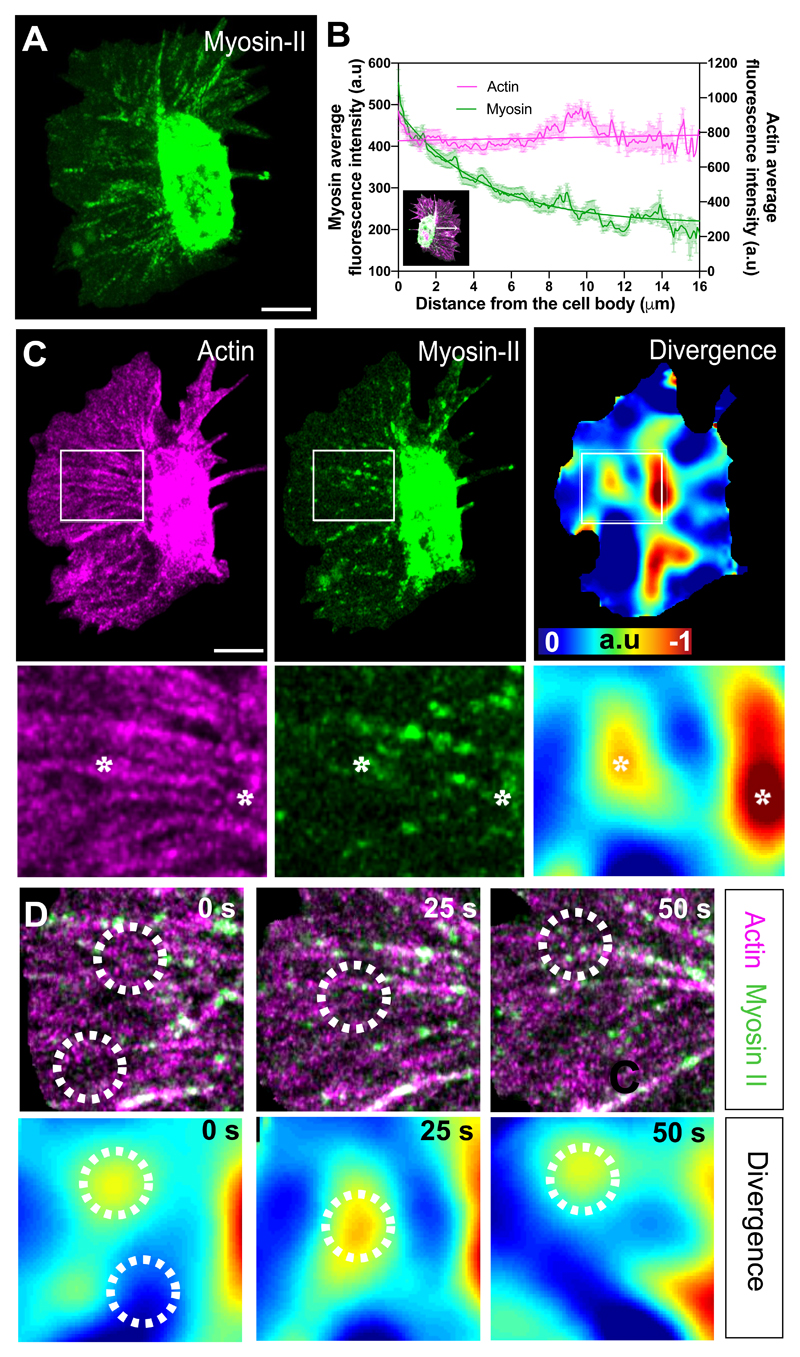
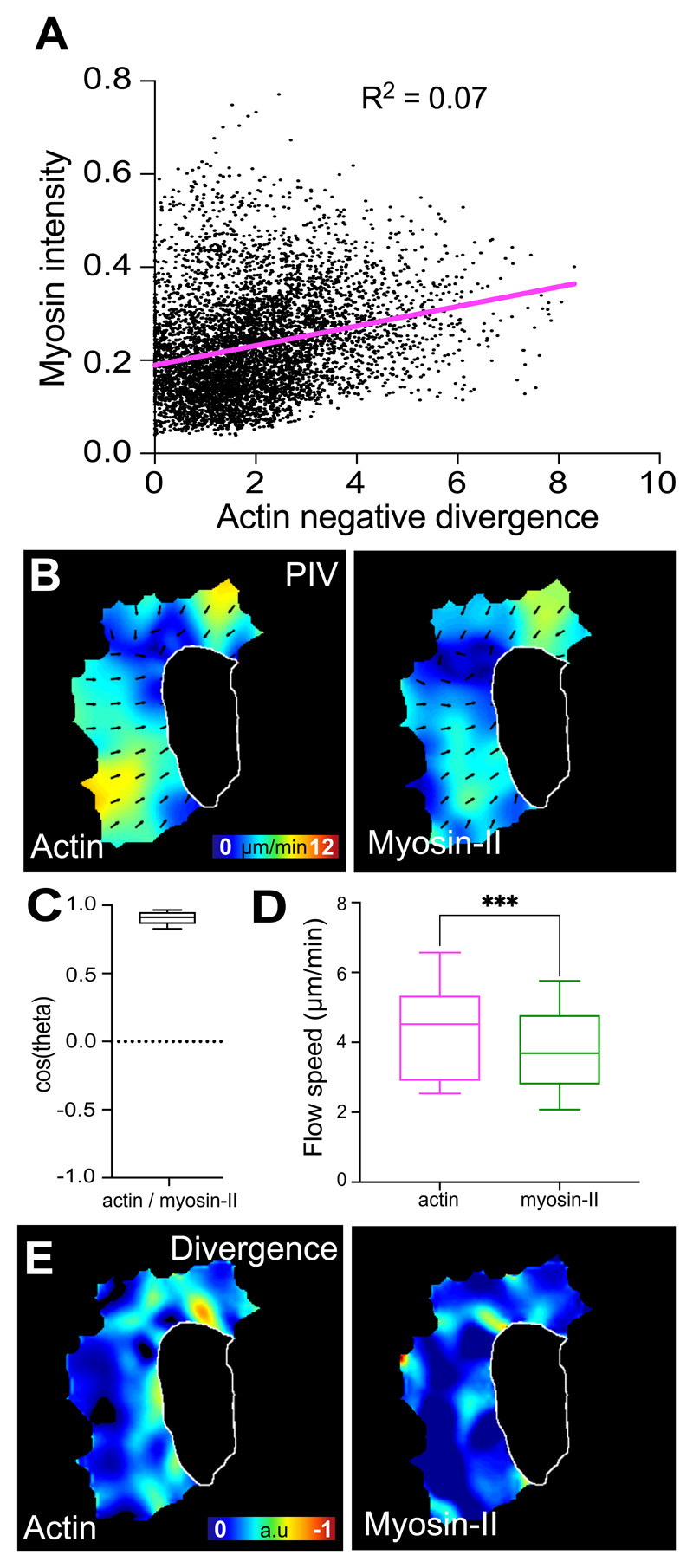
As myosin-II mutants showed a more perturbed organisation in actin flow, myosin-II may be driving long-range coordination of the network. Indeed, GFP-tagged Myosin-II revealed a front to rear gradient of puncta flowing within the hemocyte lamella (Fig. 7A,B; Supplementary Video 18). We therefore hypothesised that myosin-II may directly control the stable regions of network compression. We simultaneously analysed actin and myosin-II flows while also calculating the divergence within the actin flowfield. To our surprise, we observed no correlation of Myosin-II puncta with divergent hotspots (Fig. 7C; Extended Data Fig. 6A). Indeed, dynamic analysis of the divergence revealed that the divergent hotspots often developed adjacent to Myosin-II puncta and in between dense actin fibres within the network (Fig. 7D). Furthermore, while the negatively divergent regions appeared to be fixed points within the network, Myosin-II puncta flowed through these regions suggesting that these stable sites of network compression and disassembly are helping drive the flowfield (Supplementary Video 19). Consistent with this, we observed that Myosin-II puncta, while moving in the same direction as the overall actin flow, showed a statistically lower speed, and concomitantly a distinct divergence profile (Extended Data Fig. 6B-E; Supplementary Video 20), which is similar to what was observed in migrating fish keratocytes⁴⁴. These data suggest that myosin-II is not directly responsible for generating local contractile stresses within the actin network sinks; instead, the points of actin network divergence are likely an emergent behaviour driven by a stable gradient of actin network tension and disassembly of the network.

Figure 7. A gradient of myosin-II indirectly leads to actin network contraction.

(A) Temporal maximum projection of a Myosin-II-GFP expressing hemocyte highlighting that Myosin-II puncta within the lamellae are predominantly toward the rear of the network surrounding the cell body. Scale bar 10 μm.

(B) Linescan analysis of Actin and Myosin-II localisation within hemocytes. The plot profile of mean fluorescence intensity was performed on randomly chosen lines within the lamellae from the cell body towards the edge (see insert). Note that the average intensity of Myosin-II is high toward the cell body and decreases in a gradient approaching the edge, whereas Actin intensity remains constant (n = 63 lines, 12 independent samples). Error bars = SEM.

(C) Comparison of Actin and Myosin-II localisation with actin flow divergence. Bottom panels are high magnification images of the boxes outlined in upper panels. Asterisks highlight regions of strong negative divergence, which show no obvious colocalisation with Myosin-II. Scale bar 10 μm.

(D) Time-lapse series comparing Actin and Myosin-II localisation with actin flow divergence. Circles highlight example regions of strong negative divergence. Note that the negatively divergent regions are adjacent to Myosin-II puncta.

Discussion

Here, we have taken advantage of hemocyte dispersal to examine stereotypical behaviours hypothesised to control motility and determine how these processes correlate with cell directionality. Contrary to the previous lamellipodial-centric model of cell motility, the leading edge is poorly correlated with cell motion with a persistence that is less than the overall persistence of the cell. Hemocytes spend significant energy using extensions to explore their environment rather than directly inducing motion. While this mode of motility has been termed ‘inefficient’^{27, 33}, this does not mean that these seemingly extraneous edge fluctuations are non-functional; indeed, hemocytes are necessary to engulf apoptotic debris⁵¹ and evenly deposit extracellular matrix⁵², and the decoupling of extensions from motion may be necessary for hemocytes to efficiently explore their environment to carry out these critical tasks. Nevertheless, the term ‘leading edge’ is a misnomer as it is not obviously playing a leading role during hemocyte random migration; however, nor is it completely uncorrelated with motion. Edge fluctuations in hemocytes are still weakly correlated to motion, and therefore cells must have an intrinsic capacity to integrate this activity to ‘decide’ on a direction of travel, which we speculate occurs through the flow of actin. Furthermore, edge extensions, actin flow, and cell motion are highly integrated behaviours with no obvious temporal hierarchy. The migratory process is not stepwise and, in the future, only a holistic approach to understanding motility may explain how these behaviours are coordinated in such a precise fashion to control coherent cell motion.

Our global view of actin flow revealed a structure that is coordinated across the entire cell, both for hemocytes and other cell types. Indeed, this is consistent with what was reported in one of the first publications of actin flow³⁴; it is also interesting to note that the authors of this work presciently noted that organisation of the flow, in contrast to the leading edge, “is time persistent over minutes”, and we hypothesise that this stable organisation of the actin flowfield may be a consistent feature of motility. The network sink also represents a transition from retrograde to anterograde actin flow. While actin flows within migrating cells are often generally termed ‘retrograde flow’ (due to the focus on the leading edge), there is significant anterograde motion observed from the rear of numerous cell types^{18, 34–36}. Furthermore, modelling has predicted that retrograde flow at the front of a migrating cell will transition to anterograde flow as the adhesions switch from gripping (within the retrograde region) to slipping (within the anterograde region)^{53, 54}.

One outstanding question is, what is controlling the formation and stability of these network sinks? As the motion of the leading edge and the sinks are correlated, it is possible that there is information being transmitted between these two sites. Recent work has suggested that actin flow mediates a coupling between cell speed and persistence through the advection of polarity cues from the leading edge³¹ and it is possible that these cues may converge on the network sink. Another possibility is that the flowing actin network is inherently stable and flow patterns may develop spontaneously in the absence of any direct regulation. Indeed, our minimal model of actin flow, in which flows emerge primarily through myosin-II contraction, leads to a highly stable ‘sink’ at the rear.

The destruction of the actin network, which is occurring at these network sinks may also be directly providing forces for locomotion. Disassembly of cytoskeletal networks can generate force in the absence of motors through entropic contraction^55–57. Due to the absence of a time lag between the direction of nuclear movement and the primary streamline sink, we hypothesise that the sink may provide the force for motion of the trailing cell body. The actin network on the retrograde side of this sink is experiencing high friction while the anterograde side is slipping. This would imply that the retrograde region is anchored to the substrate, allowing the forces generated by the reorganisation of the actin network at the sink to drive unidirectional retraction of the rear of the cell. This mechanism is also consistent with the network-contraction model that has been hypothesised to drive rear retraction in other cell types⁵⁸.

This organisation of actin flow may have wide-ranging implications for how cells interpret and respond to cues. Due to the extreme stability of actin flow, it is possible that in some cells a complete loss of polarity may be required to reset flow direction and redirect cell motion (e.g. during run and tumble modes of migration⁵⁹). The stable actin flow may also be providing a stable polarity to the cell that enhances the discrimination of guidance cues. While internal amplification through reaction-diffusion signalling modules are hypothesised to be required to accurately chemotax towards low concentrations of guidance cues^{4, 60}, this may be unnecessary. The stable flow of actin itself may be sufficient to provide the directional memory that allows the leading edge to rapidly sample external cues with subtle biases in the edge fluctuations stabilised and integrated by the actin flow. Indeed, directional memory can make chemotaxis more efficient and discriminatory^{61, 62}, and while reaction-diffusion modules have been hypothesised to control this memory⁶³, recent work suggests that it may also come from the cytoskeleton itself⁶⁴; our work suggests that it may originate from the highly coordinated and stable flow of the actin network.

Materials and methods

Fly genetics

The following fly stocks were used in this study: w¹¹¹⁸ strain as wild-type (Bloomington Drosophila Stock Center (BDSC), BL3605); myosin-II mutant (BDSC, BL4199); cofilin mutant (BDSC, BL9107), ena mutant (BDSC, BL8569). Hemocytes were labelled using the promoters, Srp-Gal4 (BDSC7, BL78565) or Sn-Gal4⁶⁵. The following fluorescent probes were used to label: nuclei [UAS-RedStinger, (BDSC, BL8546 and 8547]; actin [UAS-LifeAct-GFP⁶⁵ or UAS-Moesin-Cherry⁶⁶, or UAS-Act5C-GFP (BDSC, BL9275)]; Myosin-II heavy chain [(UAS-Zip-GFP)⁶⁷]. Flies were left to lay eggs on grape juice/agar plates overnight at 25°C. Embryos were dechorionated in bleach and the appropriate genotype was identified based on the presence of fluorescent markers.

Cell lines

Zebrafish lines expressing LifeAct-GFP (Tg(actb1:lifeact-GFP)) were generated and fish keratocytes cultured as previously described⁶⁸. Keratocytes were prepared from adult zebrafish scales, plucked from sacrificed animals and washed three times with Dulbecco’s Modified Eagle’s Medium (DMEM) (Gibco). Scales were incubated in START medium at room temperature for one or two days to allow the keratocytes to migrate off in a monolayer. The monolayer was then washed three times in PBS, incubated for 40 min with Running Buffer with 1 mM EGTA and the scales removed. The remaining cells were washed three times with PBS, trypsinised for 2 min with 0.25% Trypsin-EDTA (Gibco) at room temperature, resuspended in the same volume of trypsin inhibitor (Sigma) and transferred to a coverslip coated with 0.5mg/ml PLL(20)-g[3.5]-PEG(2)/PEG(3.4)-RGD (Surface Solutions) for 50min. Live cell imaging of migrating keratocytes was performed at room temperature in START medium. Confocal microscopy was performed with an inverted microscope (Zeiss), equipped with a Spinning disk system (Yokogawa X1, iXon897, Andor), a C-Apochromat 100x/1.4 Oil Objective, a motorised stage and a 488nm laser.

RPE1 cells expressing LifeAct-TagRFP (a gift from Buzz Baum)⁶⁹ were cultured in DMEM/F12 media containing HEPES and sodium bicarbonate (Sigma) supplemented with 10% Fetal Bovine Serum (HyClone, Fisher Scientific), 1% penicillin-streptomycin (Sigma) and 2 mM L-glutamine (Sigma). Imaging was carried out in 35 mm dishes that had been coated with 10μg/ml fibronectin for 1 hour at 37 °C. RPE1 cells were plated and allowed to adhere and spread overnight before imaging. Cells were imaged using an LSM 880 confocal microscope using airyscan with a 40x NA 1.3 Plan-Apochromat oil objective at 1.8x zoom. Images were acquired every 30 seconds. Nuclei were labelled with SiR-DNA (Spirochrome) at 0.5 mM to enable cell tracking.

Embryo microscopy

Embryos were mounted as previously described⁴ and time-lapse images were acquired every 5 s with a PerkinElmer Ultraview spinning disk microscope equipped with a 63x NA 1.4 Plan-Apochromat oil objective during developmental dispersal (stages 15–16). Whole embryo snapshots were taken using the LSM 880 confocal microscope (Carl Zeiss) equipped with a 40x NA 1.3 Plan-Apochromat oil objective.

Data analysis

For the characterisation of control hemocyte migratory parameters (i.e. directional autocorrelation, retrograde flow speed, streamline analysis, divergence, principal strain, assembly/disassembly, and flow alignment) data were gathered on a per/frame basis from 9 individual cells each imaged over approximately 4-5 minutes at intervals of 5 s/frame, representing an n number of 443 time-points. When comparing control and mutant genotypes, statistical tests were performed on a per cell basis due to the partial penetrance of the various mutant phenotypes. Here, comparisons were made between the 9 control cells, 9 myosin-II mutants, and 9 cofilin mutants. The specific statistical test, as well as the thresholds for significance are noted in the respective figure legends. The computational analysis was performed in MATLAB (Mathworks®) using custom code, which can be obtained from the corresponding author upon reasonable request [BS].

Wounding

Laser wounding was performed using an ablation laser (MicroPoint; Andor Technology) as previously described⁷⁰ and imaged using a Perkin Elmer spinning disk microscope.

Photobleaching

Photobleaching experiments were performed on hemocytes labelled with Actin-GFP. Images were acquired every 5 s using airyscan imaging on an LSM 880 confocal microscope (Carl Zeiss), equipped with a 63x NA 1.4 Plan-Apochromat oil objective and a 1.8X zoom. Laser power was set at 100% to bleach a region of 25 x 25 pixels for 2 s, with a pixel dwell time of 66 μs.

Quantification of Moesin-Cherry and Myosin-GFP fluorescence

In order to quantify the spatial distribution of Actin and Myosin-II within hemocytes, cells expressing Moesin-Cherry and Myosin-II-GFP were sampled by linescan analysis to measure average fluorescence intensity. Fiji line and profile functions were used to draw and record 2 μm wide lines from the cell body boundary to the cell edge in 12 different cells.

Cell tracking

Hemocytes containing labelled nuclei were first thresholded in Fiji. Tracking was then performed in MATLAB by calculating the positions of the centroid of the nucleus through time.

Particle Image Velocimetry

Time-lapse images of freely moving hemocytes were acquired at 5 s/frame. Actin was labelled with LifeAct-GFP for all figures with the exception of Fig. 7 and Extended Data Fig. 6, which used Moesin-Cherry in conjunction with Myosin-II-GFP (Drosophila non-muscle Myosin heavy chain) Cells were then manually segmented prior to PIV analysis.

There is no grossly observable actin flow behaviour within the cell body of the hemocytes, therefore information from the cell body was removed by manually segmenting the cell body region and using this as a mask to remove PIV values. The actin flow PIV information is therefore entirely from within the lamellae. To observe myosin-II flow in the lamellae, the signal from the cell body was oversaturated. For this reason, no PIV information could be obtained from the cell body region and it was excluded from the myosin flow PIV analysis and its actin flow counterpart (Extended Data Fig. 6D-G).

A 2D cross-correlation algorithm adapted from classical PIV was implemented³⁰. In brief, this method compares a region of interest in an image (source image) with a larger region of a subsequent image (search image). The sizes of the source and search regions are determined on the basis of the feature size to be tracked and the area of their expected displacement (i.e. actin bundles). For this analysis, source and search images encompassing areas of 1.2 μm² and 2 μm² were used. A cross-correlation map was computed by analysing the cross-correlation coefficient between the source image and the search image, by shifting the source across the search one pixel at a time. Network displacement was measured by finding the maximum coefficient within the resulting cross-correlation map. To filter anomalous tracking data, only displacements that had a cross-correlation coefficient above a certain threshold, c₀, were kept. For the present work, the threshold was set at c₀ = 0.5. Finally, a spatial convolution with a Gaussian kernel (size of 5 μm, sigma of 1 μm), and temporal convolution with temporal kernel of 20 s (sigma 10 s) were used to interpolate the measured displacements to cover all the pixels within the cell outline. The complete algorithm for this analysis was implemented in MATLAB.

Defining retrograde and anterograde flow regions

Retrograde and anterograde flow were defined with respect to their respective alignment to cell motion. The direction of the actin flow at every point within the lamellae was correlated with the instantaneous direction of cell motion using the cosine of the angle between these velocity vectors. Retrograde flow was defined as a negative correlation while anterograde flow was a positive correlation to cell motion.

Streamlines

Streamlines were used to assess the global organisation of the actin flowfield. Here each line is drawn tangent to a local velocity vector and describes a path that a massless particle would take if entering the actin flowfield at that point (MATLAB stream2 function). The seed points for the streamlines were placed at every pixel along the cell boundary. For visualisation purposes streamlines were represented at regular intervals (MATLAB streamslice function). Line Integral Convolution was employed to represent global streamline activity (Figure S2D) utilising an open source vector field visualisation toolkit (http://sccn.ucsd.edu/~nima/). Streamline sinks were defined by quantifying the frequency of streamline termini within non-overlapping 2.5 μm² regions of the cell image and the coordinates of these endpoints were set at the centre of the boxes. For position vector analysis of these endpoints, vectors were constructed from the centroid of the nucleus to the endpoint coordinates.

Principal strain

Local deformation of the actin network can be quantified by evaluation of the principal strains which are derived from local velocity changes obtained by PIV. The relative positional changes of points within a deforming body are described with a velocity tensor, which is computed based on a central difference estimation over 2.5 μm in both spatial dimensions.

$$V=\left(\begin{array}{ll}\frac{\partial V_x}{\partial x}\hfill & \frac{\partial V_x}{\partial y}\hfill \\ \frac{\partial V_y}{\partial x}\hfill & \frac{\partial V_y}{\partial y}\hfill \end{array}\right)$$

Decomposition of the velocity gradient provides a symmetric and an antisymmetric component, with the symmetric part being the strain rate tensor. This strain rate tensor is defined as $S=\frac{1}{2}\left(V+V^T\right).$ Decomposition of S yields the eigenvalues and eigenvectors of the deformation, where eigenvectors denote the principle axes of the deformation and eigenvalues the principle components of the strain rate tensor. The eigenvalues sign accounts for compressive (negative) or tensile (positive) strain. We observed very little tensile strain inside the network along the major axis. Therefore, for visualisation purposes, only the principal strain denoting compression was shown. For visual representation of control cells the principal strain field was normalised between -1 and 0. For comparing the principal strain field between genotypes, no normalisation was performed because of the reduction of the strain values in the mutant conditions, however the colourmap scaling was fixed between genotypes.

Divergence and network turnover analysis

For quantification of divergence a central difference scheme was implemented to compute the spatial derivatives of the actin flow velocities (∇ · V). This method of calculating divergence was also utilised in the computation of network turnover, to determine the spatial distribution of network assembly and disassembly which was calculated using the equation below.

$$\mathit{\text{turnover}}=\frac{\partial I}{\partial t}+\left(I\ast \left(\nabla \cdot V\right)\right)+\left(V\ast \left(\nabla \cdot I\right)\right)$$

The temporal derivative of the fluorescence intensity $\left(\frac{\partial I}{\partial t}\right)$ was computed using a forward difference scheme between two consecutive frame of the time-lapse. As with the spatial gradients of flow velocity (∇ · V) the fluorescence intensity (∇ · I) was computed using a central difference scheme. As there was not much assembly information inside the lamellae of hemocytes, only the disassembly data were visually represented and normalised to the maximum value in the field. However, both assembly and disassembly was included in the quantification.

For visualisation purposes in control cells, normalised disassembly or negative divergence maps were shown normalised to the maximum value in the field, providing values between -1 and 0. For comparing the disassembly or negative divergence between genotypes, no normalisation was performed because of the reduction of these values in the mutant conditions, however the colourmap scaling was fixed between genotypes.

Linescans were used to show the contractile and destructive gradients of the flowing actin network (MATLAB improfile function) by drawing three random lines of 1 pixel width per frame. Lines originate from the centroid of the nucleus and extend through the lamella to the cell edge. Data points within the cell body were discarded.

Flow alignment

For determining the average alignment of actin flows, the cosine similarity between all velocity vectors and their 8 nearest neighbours was computed using cosθ = v₁ · v₂/|v₁||v₂|, and subsequently averaged to give flowfield alignment.

Extension/retraction analysis

For the extension/retraction analysis, segmented time-lapse images of freely moving hemocytes were subtracted from the subsequent frames in the time-lapse series to highlight regions of extension or retraction. The MATLAB regionprops function was used to filter extensions and retractions by their respective area, and to attain their centroid for the purpose of tracking these regions with respect to the position of the nucleus. Maximum extensions and retractions were defined as the regions for each frame with the largest area.

Edge velocity analysis

To evaluate edge dynamics, segmented time-lapse images of hemocytes were analysed using a Segmentation and Windowing package²⁶, calculating edge extensions and retractions at each pixel along the cell boundary. Custom scripts implemented in MATLAB were used to calculate extension speed globally, and locally within specific regions of the cell boundary. To calculate the edge velocity in the direction of cell motion, the edge was segmented within a region bounded by a 30° cone centred on the direction of motion. To calculate the edge velocity within the maximum extension, the longest uninterrupted region along the perimeter of the cell edge was segmented. To quantify the average net edge activity, positive and negative sign was assigned to velocity vectors depending on whether they were classified as extension or retractions.

Temporal cross-correlation

Temporal cross-correlation was employed to evaluate whether there was any temporal hierarchy governing the dynamics of the considered migratory parameters (i.e. cell motion, primary sink, maximum edge extension). This analysis involves the directional correlation of two vectors at all potential time lags. The temporal cross-correlation function is described as DC = 〈v_i (t) · v_j (t + τ) 〉, where DC is the time averaged cosine similarity between vector i (v_i) and parameter j (v_j) at time and lagged time intervals (t + τ).

Statistics and reproducibility

When example images are shown in figures, these represent similar results obtained from 9 independent biological samples for wild-type (Fig. 1-7, Extended Data Fig. 1,2,5,6), myosin-II (Fig. 5,6), cofilin (Fig. 5,6), and ena mutants (Extended Data Fig. 5); from 4 independent biological samples for directed migration (Fig. 3, Extended Data Fig. 4); from 5 independent biological samples for actin and myosin-II analysis (Fig. 7, Extended Data Fig. 6); from 3 independent biological samples for RPE1 cells (Extended Data Fig. 3); from 3 independent biological samples for neuronal growth cones (Extended Data Fig. 3); from 2 independent biological samples for fish keratocytes (Extended Data Fig. 3).

Extended Data

Extended Data Fig. 1. Leading edge fluctuations are a weak predictor of cell directionality.

(A) Three examples of cell contour analysis during hemocyte migration revealing highly dynamic edge activity.

(B) Left panel reveals a representative snapshot of a randomly migrating hemocyte with the maximum edge extension (green) and retraction (magenta) automatically tracked and compared to the direction of cell motion (white). Right panel shows that the maximum extension and retraction are positively and negatively correlated to motion. Note the high variance in the distribution. ***P < 0.0001, Mann-Whitney two-tailed test. The graph shows mean and SD as bars; each datapoint is displayed as a dot (n = 443, 9 biologically independent samples).

(C) Left panel shows a representative snapshot of all extension vectors around the cell perimeter (green) and maximum extension vectors based on the longest contiguous extension (blue). White arrow shows the direction of cell motion. Right panel shows the correlation of the resultant velocity of extension vectors to the direction of motion, showing that the resultant of all extensions is better correlated than maximum extension alone. ***P < 0.0001, Mann-Whitney two-tailed test. Boxplot shows medians as central lines, 25^th and 75^th percentiles as box limits, 10^th and 90^th as whiskers (n = 443, 9 biologically independent samples).

Extended Data Fig. 2. Actin retrograde flow is globally organised in migrating hemocytes.

(A) Probability density function of the divergence within the actin flowfield. Note that most of the measured divergence is negative.

(B) Time-lapse of divergence within the actin flowfield during hemocyte migration. Dashed circle highlights a region of strong negative divergence that is persistent in time.

(C) Time-lapse of a LifeAct-GFP labelled hemocyte (top panel). High magnification image showing the direction of the actin flowfield (arrows) colour-coded for the strength of the negative divergence (bottom panel). Note that in the centre of the flowfield is a region of actin network deformation, which correlates with strong negative divergence.

(D) Comparison of streamlines with the speed and divergence of global actin flow. The dashed circle highlights the streamline sink which correlates with a region of low flow speed and high negative divergence.

(E) Example image of a hemocyte with sustained bipolar protrusions and opposing streamline sinks. Note the strong negative divergence within both sinks. Scale bar 10 μm.

(F) Quantification of the mean cell-wide versus retrograde actin flow speed. Note the significant reduction in the retrograde region. ***P < 0.0001, Mann-Whitney two-tailed test. Boxplot shows medians as central lines, 25^th and 75^th percentiles as box limits, 10^th and 90^th as whiskers (n = 443, 9 biologically independent samples).

(G) Comparison of instantaneous cell speed with average global actin flow speed (left, linear regression goodness-of-fit R² = 0.06), flow speed within the retrograde region only (middle, R² = 0.02), and flow speed in the direction of motion (right, R² = 0). Note that there is no significant correlation in any of these comparisons (n = 443, 9 biologically independent samples).

Extended Data Fig. 3. Actin retrograde flow is globally organised in migrating cells.

(A) PIV, divergence, streamline analysis, and quantification of streamline sinks of cultured cells containing labelled actin. Representative snapshots are displayed for a fish keratocyte (scale bar 10 μm), a neural growth cone (scale bar 5 μm), and a Retinal Pigment Epithelium (RPE1) cell (scale bar 10 μm).

(B) Comparison of cell speed with the speed of the maximum edge extension in RPE1 cells reveals that protrusion speed is significantly higher than instantaneous cell speed. ***P < 0.0001, Mann-Whitney two-tailed test. Boxplot shows medians as central lines, 25^th and 75^th percentiles as box limits, 10^th and 90^th as whiskers (n = 247, 3 biologically independent samples).

(C) Example cell track of an RPE1 cell in which the unit vectors of the maximum edge extension or the primary streamline sink were superimposed.

(D) Correlation of the primary streamline sink and the maximum edge extension vectors to the direction of cell motion in RPE1 cells. Note that that both are strongly correlated with the direction of cell motion. Mann-Whitney two-tailed test. Boxplot representation as in ‘B’ (n = 247, 3 biologically independent samples).

(E) Temporal cross correlation comparing the direction of cell motion, maximum edge extension, and the maximum streamline sink in RPE1 cells, which reveals a peak correlation at 0-lag showing no obvious temporal hierarchy in these migratory behaviours (n = 3 biologically independent samples).

Extended Data Fig. 4. The polarity of global actin flow is highly stable and correlated to hemocyte motion during random and directed migration.

(A) Example cell track of a randomly migrating hemocyte in which the unit vectors of the maximum extension or the primary sink are superimposed, showing better correlation to motion for the primary sink.

(B) Probability density function of the distance from the nucleus to the maximum extension and to the primary sink.

(C) Time-lapse of hemocytes migrating directionally to a laser wound (asterisk) in the embryo. LifeAct-GFP in green, nuclei in magenta. Scale bar 30 μm.

(D) Rose plot showing the direction of maximum extensions normalised to motion comparing random (black outline, n = 443, 9 biologically independent samples, same data shown in ‘1J’) to directed migration (green, n = 272, 4 biologically independent samples).

(E) Rose plot showing the direction of the primary sink normalised to motion comparing random (black outline) to directed migration (blue). Sample size as in ‘D’.

(F) Correlation to motion of the direction of the maximum extension (*P = 0.0339) and primary sink (*P = 0.0240). Note that both parameters are more correlated in directly migrating cells. Mann-Whitney two-tailed tests. Boxplot shows medians as central lines, 25^th and 75^th percentiles as box limits, 10^th and 90^th as whiskers (sample size as in ‘D’).

(G) Comparison of the directional autocorrelations of cell motion (left), primary sink (middle), and maximum extension (right) during random (n = 9) and directed migration (n = 4 biologically independent samples). Note the slower decay during directed migration suggesting increased persistence. Error bars = SEM.

(H) Quantification of the directionality ratio shows higher persistence in directly migrating cells (walking average over 60 s intervals). *P < 0.05, Mann-Whitney two-tailed test. Boxplot shows medians as central lines, 25^th and 75^th percentiles as box limits, minimum and maximum values as whiskers; each datapoint is displayed as a dot (sample size as in ‘D’).

Extended Data Fig. 5. Loss of myosin-II, cofilin and ena lead to reduced actin flow and cell speed.

(A) Schematic of the actin flow alignment analysis. The average cosine similarity between each velocity vector (F(r)) and its 8 nearest neighbours (F(n)) is calculated to reflect the organisation of the actin flow.

(B) Colour-coded flowfield alignment representation for each genotype (1 meaning perfect alignment).

(C) Average alignment of the actin flowfield showing that flow in myosin-II mutants is most disorganised. **P = 0.0014, (n.s) P > 0.99, Kruskal-Wallis test and Dunn’s multiple comparison test. Boxplot shows medians as central lines, 25^th and 75^th percentiles as box limits, minimum and maximum values as whiskers; each datapoint is displayed as a dot (n = 9 biologically independent samples for all genotypes).

(D) PIV, divergence, streamline, and streamline sink analysis of LifeAct-GFP expressing wild-type and ena mutant cells. Scale bar 10 μm.

(E) Comparison of the speed of extensions in wild-type (n = 443, 9 biologically independent samples) and ena mutants (n = 50, 9 biologically independent samples) reveals significantly lower speed in mutants. ***P < 0.0001, Mann-Whitney two-tailed test. Boxplot shows medians as central lines, 25^th and 75^th percentiles as box limits, 10^th and 90^th as whiskers.

(F) Quantification of mean actin flow speed in wild-type and ena mutant cells reveals lower speed in mutants. ***P = 0.0005, Mann-Whitney two-tailed test. Boxplot representation and sample size as in ‘C’ (n = 9 biologically independent samples for both genotypes).

(G) The primary sink is more negatively divergent in wild-type cells. ***P = 0.0003, Mann-Whitney two-tailed test. Boxplot representation as in ‘C’, sample size as in ‘F’.

(H) Quantification of the percentage of streamlines at the primary sink in wild-type and ena mutant cells shows a similar level of streamline confluence. (n.s) P = 0.0625. Mann-Whitney two-tailed test. Boxplot representation as in ‘C’, sample size as in ‘F’.

Extended Data Fig. 6. A gradient of myosin-II driven contraction is essential for global organisation of actin flow.

(A) Scatter plot of Myosin-II intensity and actin divergence for each point in the lamella of a hemocyte reveals no relationship between Myosin-II levels and strength of divergence (linear regression goodness-of-fit R² = 0.07, n = 5985 values from 5 biologically independent samples).

(B) PIV analysis of actin and myosin-II flow performed simultaneously in a migrating hemocyte.

(C) Comparison of the direction of actin and myosin-II flow from simultaneous PIV analysis reveals that their direction of motion is nearly identical. Boxplot shows median as central lines, 25^th and 75^th percentiles as box limits, 10^th and 90^th percentiles as whiskers (n = 147, 5 biologically independent samples).

(D) Comparison of actin and myosin-II flow speed from simultaneous PIV analysis reveals that myosin-II motion is significantly slower. ***P < 0.0001, Wilcoxon matched-pairs signed rank two-tailed test. Boxplot representation and sample size as in ‘C’.

(E) Comparison of actin and myosin-II divergence from simultaneous PIV analysis reveals that they have distinct profiles.

Supplementary Material

Movie 1

Automatic tracking of a hemocyte comparing tracking of the cell centroid (magenta) or the nucleus (green). Note that in hemocytes at this temporal resolution (5 s/frame), tracking the cell centroid reflects overall shape changes more than cell motion. In contrast, the nucleus represents a fixed fiducial marker within the cell that more accurately reflects cell movement. Similar results obtained in 9 biologically independent samples.

Movie 2

Time-lapse movie of a randomly migrating hemocyte in which edge extensions were automatically segmented. Vectors (green arrows) were drawn from the nucleus to either each individual extension or the maximum extension (extension of the largest contiguous area), while simultaneously tracking the cell direction of travel (magenta arrow). Similar results obtained in 9 biologically independent samples.

Movie 3

Time-lapse movie of a randomly migrating hemocyte in which analysis of the actin flowfield was conducted using PIV, divergence, streamlines, and streamline sinks (the size of the spots are normalised to the number of streamlines ending within a defined region). Similar results obtained in 9 biologically independent samples.

Movie 4

Time-lapse movie of a hemocyte expressing Actin-GFP (left panel) to directly label the actin network. A region within the network was photobleached (highlighted by the circle) and subsequently tracked as it transited through the lamella. Note that the bleached spot moves through the lamella in a direction predicted by the PIV (middle panel) and begins to disappear at the rear of the network, which shows an increase in negative divergence (right panel). Similar results obtained in 9 biologically independent samples.

Movie 5

Time-lapse movies of a randomly migrating bipolar hemocyte in which the sinks colocalise with the negative divergent regions. Note that two independent sinks develop at the time when the cell develops a bipolar shape.

Movie 6

Time-lapse movie of a fish keratocyte in which analysis of the actin flowfield was conducted using PIV, divergence, streamlines, and streamline sinks. Similar results obtained in 2 biologically independent samples.

Movie 7

Time-lapse movie of a neural growth cone in which analysis of the actin flowfield was conducted using PIV, divergence, streamlines, and streamline sinks. Similar results obtained in 3 biologically independent samples.

Movie 8

Time-lapse movie of an RPE1 cell in which analysis of the actin flowfield was conducted using PIV, divergence, streamlines, and streamline sinks. Similar results obtained in 3 biologically independent samples.

Movie 9

Time-lapse movie of a randomly migrating hemocyte comparing the direction of motion (white arrow) to either the direction to the maximum extension (green arrow) or the primary sink (magenta arrow). Similar results obtained in 9 biologically independent samples.

Movie 10

Time-lapse movie of an RPE1 cell in which cell motion, edge extensions, and streamline sink were automatically tracked. Vectors were drawn from the nucleus to the maximum extension (green arrow), and the primary sink (magenta arrow), while simultaneously showing the cell’s direction of motion (white arrow). Similar results obtained in 3 biologically independent samples.

Movie 11

Time-lapse movie of hemocytes migrating towards a laser wound (asterisk). LifeAct-GFP is shown in green, nuclei are labelled in magenta. Similar results obtained in 4 biologically independent samples.

Movie 12

Time-lapse movie of a randomly and a directionally migrating hemocyte highlighting the vector to their maximum edge extension (green) along with their direction of travel (white arrow). Asterisk denotes the wound site. Similar results obtained in 9 (random) and 4 (directed) biologically independent samples.

Movie 13

Time-lapse movie of a randomly migrating hemocyte comparing negative divergence, compression, and actin disassembly. Similar results obtained in 9 biologically independent samples.

Movie 14

Time-lapse movies of wild-type, myosin-II, and cofilin mutant hemocytes undergoing developmental dispersal (LifeAct-GFP is shown in green, nuclei are labelled in magenta). Similar results obtained in 9 biologically independent samples for all genotypes.

Movie 15

Time-lapse movies of PIV analysis of actin flow on wild-type, myosin-II and cofilin mutant haemocytes expressing LifeAct-GFP. Similar results obtained in nine biologically independent samples for all genotypes.

Movie 16

Time-lapse movies wild-type, myosin-II, and cofilin mutant cells analysed for divergence, disassembly, and streamlines of the actin flow. Similar results obtained in 9 biologically independent samples for all genotypes.

Movie 17

Time-lapse movie of an ena mutant cell in which analysis of the actin flowfield was conducted using PIV, divergence, streamlines, and streamline sinks. Similar results obtained in 9 biologically independent samples.

Movie 18

Time-lapse movie of a hemocyte containing fluorescently labelled Actin and Myosin-II. Similar results obtained in 5 biologically independent samples.

Movie 19

Time-lapse movie of a hemocyte showing divergence of the actin flow and the location of Actin and Myosin-II. Crosses highlight transient regions of strong negative divergence. Note that the Myosin-II puncta do not accumulate at regions of negative divergence and instead continue to flow through. Similar results obtained in 5 biologically independent samples.

Movie 20

Time-lapse movie of PIV analysis and divergence of actin and myosin-II flow performed simultaneously in a migrating hemocyte. Similar results obtained in 5 biologically independent samples.