Abstract
Chromatin compaction and gene accessibility are orchestrated by assembly and disassembly of nucleosomes. Although the disassembly process was widely studied, little is known about the structure and dynamics of the disordered histone tails, which play a pivotal role for nucleosome integrity. This is a gap filling experimental FRET study from the perspective of the histone H3 N-terminal tail (H3NtT) of reconstituted mononucleosomes. By systematic variation of the labeling positions we monitored the motions of the H3NtT relative to the dyad axis and linker DNA. Single-molecule FRET unveiled that H3NtTs do not diffuse freely but follow the DNA motions with multiple interaction modes with certain permitted dynamic transitions in the μs to ms time range. We also demonstrate that the H3NtT can allosterically sense charge-modifying mutations within the histone core (helix α3 of histone H2A (R81E/R88E)) resulting in increased dynamic transitions and lower rate constants. Those results complement our earlier model on the NaCl induced nucleosome disassembly as changes in H3NtT configurations coincide with two major steps: unwrapping of one linker DNA and weakening of the internal DNA - histone interactions on the other side. This emphasizes the contribution of the H3NtT to the fine-tuned equilibrium between overall nucleosome stability and DNA accessibility.
INTRODUCTION
The nucleosome, consisting of two copies of each of the four histone proteins H2A, H2B, H3 and H4, is the basic unit of chromatin compaction and key to gene regulation (1–4). Single nucleosomes are connected by short linker DNA stretches (10–90 bp) to a bead-on-a-string like structure, which allows for dynamic compaction into higher order chromatin with two intertwined stacks of nucleosomes and compact tetranucleosomes as basic units (5–7). Each of the four histone proteins consists of a core domain – the histone fold domain, which is well characterized by X-ray crystallography – and a less well characterized tail that protrudes from the core particle in an unknown manner (1,8). A wide range of experiments and computer simulations give a complex view on the factors contributing to nucleosome stability, revealing that the histone tails play a pivotal role for nucleosome integrity, e.g. through posttranslational modifications (PTMs) which mediate structural changes and modulate gene accessibility (9–11). Even though the nucleosome disassembly process (12–15) and the effects of PTMs (16–18) have been discussed widely, studying the histone tails in the context of the nucleosome revealed to be challenging. Hence, many studies focused on isolated tails or tailless nucleosomes (e.g. (3,9,19–21)). Hitherto, surprisingly little is known about the actual tail conformations, their dynamics and their role during the nucleosome disassembly process (22–25). Circular dichroism and NMR showed that the H3 and H4 tails are not completely unstructured but have significant α-helical content and that post-translational modifications influence these structures (26). Results from various molecular dynamics simulations and NMR studies suggest that histone tails have a propensity to form α-helical segments and are capable (21,27) to explore a wide conformational space in the nucleosome with large sections of the histone tails not perpetually bound to DNA (9,20,28–30). This agrees with experimental observations that cross-linking efficiency depends on the linker DNA length (31) and an NMR study showing that histone tails bind to the linker DNA (32). Additionally, recent Förster Resonance Energy Transfer (FRET) experiments and Molecular Dynamics (MD) simulations revealed that removal of the H3 N-terminal Tail (H3NtT) leads to a more open conformation and decreased thermal stability of reconstituted mononucleosomes, most likely accompanied by an altered electrostatic environment within the core particle (27,33–36). Those results further emphasized the importance of the H3NtT for nucleosome integrity.
Hitherto, several major questions concerning the H3NtT remained unanswered, which we address in this experimental study:
(I) Where is the H3NtT preferentially localized and is it possible to monitor its distance relative to other parts of the nucleosome? (II) Does the H3NtT arrest in certain static conformations or is the H3NtT entirely dynamic? (III) Are the H3NtT conformations and dynamics sensitive to modifications, e.g. charge-modifying mutations in the nucleosome core? (IV) How are the H3NtT conformations and dynamics affected by the NaCl induced disassembly process?
To answer these questions, mononucleosomes were reconstituted on the strong positioning Widom 601 DNA sequence (37) and possible conformations and dynamics of the H3NtT were analyzed at different NaCl concentrations. Conformational changes were measured by ensemble and single-molecule (sm) FRET also studied by dynamic Photon Distribution Analysis (dynPDA) which has already been applied earlier to various aspects of nucleosome structure and dynamics (12,14,38–41). Nucleosomes used in this study were labeled with donor fluorophores on the H3NtT at position K9C and by an acceptor fluorophore at one of four different positions on the core DNA or on the linker DNA with a total DNA length of 170 bp or 210 bp. The systematic variation of the DNA labeling position allowed us to localize the H3NtT with respect to the outer or inner DNA gyre and to compare these observations with all atom molecular dynamics simulations. Moreover, we compared wild type (wt) and mutated (mut) nucleosomes – bearing charge-modifying mutations in helix α3 within the helix-strand-helix motif of the H2A histone fold domain, namely H2A R81E/R88E – to unravel long-range interactions affecting H3NtT conformation and dynamics. Finally, we monitored distance changes under nucleosome destabilizing conditions using different NaCl concentrations to study intermediate disassembly steps. We exploit the non-palindromic nature of the Widom 601 sequence and the recently described asymmetric opening of the respective 601 mononucleosomes (13,15,42) to analyze the vicinity and dynamics of the H3NtT to the two opposing halves of the inner DNA gyre.
MATERIALS AND METHODS
DNA preparation
DNA fragments were prepared via PCR from the pGEM3z vector containing the Widom 601 nucleosome positioning sequence (Supplementary Methods) (43). Alexa 594 or Cy5 was used as acceptor dye for DNA labeling and was attached through amino-C6 linker to a thymine at appropriate positions on the primers (IBA, Germany). Subsequently, DNAs were purified on Gen-Pak HPLC (Waters, USA). The DNA labeling efficiency was determined to >95% by absorption spectroscopy.
Histone protein expression and purification
To allow for specific labeling of the H3NtT we used an H3 recombinant Xenopus laevis histone variant bearing two point-mutations, namely K9C as label position and C110A to avoid unwanted binding of fluorophores. Plasmids containing the mutated H3 K9C/C110A sequence were designed in the lab of Jennifer Nyborg (Colorado State University, USA) and provided by Planet Protein (Colorado State University, USA). The H3 K9C/C110A sequence was subcloned into pET3 vector using XbaI and NheI. Overexpression of mutated H3 proteins was performed in Escherichia coli BL21(DE3) for 3 h after induction with IPTG (0.2 mM final concentration). Isolation and purification of the protein comprises three major steps as described in (44): (i) preparation of the isolated inclusion bodies, (ii) size exclusion chromatography under denaturing conditions and (iii) ion-exchange chromatography under denaturing conditions. Lyophilized proteins were stored at −80°C (44).
The inserted cysteine of histone H3 K9C/C110A was used for specific labeling with Alexa 488 C5 maleimide as previously described (12). Labeling reaction was conducted with 10-fold excess of TCEP under unfolding conditions (7 M guanidine hydrochloride, 20 mM Tris–HCl, pH 7.5).
The mutated recombinant X. laevis histone H2A R81E/R88E, bearing two arginine to glutamic acid mutations (RE) at position 81 and 88, was obtained from overlap extension PCR as described in (34). Any other recombinant, wild type X. laevis histones were purchased from Planet Protein (Colorado State University, USA).
Octamer reconstitution
For histone octamer reconstitution equimolar concentrations of H2A (wt or R81E/R88E mutant) and H2B with 20% excess of H3 (wt or labeled H3K9C mutant) and H4 were mixed under unfolding conditions (7 M guanidine hydrochloride, 20 mM Tris–HCl, 10 mM dithiothreitol). Octamers self-assembled during an overnight dialysis against refolding buffer (10 mM Tris–HCl, 0.1 mM EDTA, 5 mM β-mercaptoethanol, 2 M NaCl) at 4°C in Slide-A-Lyser cassettes (MWCO 7000, Pierce, Thermo Fisher Scientific, USA). After dialysis, octamers were purified via size exclusion with FPLC (Superdex 200HR 10/10, GE Healthcare, USA) and fractions were analyzed via Triton X-100/acetic acid/urea (TAU) gel analysis. Only fractions containing all four histone proteins in best proportion were selected for nucleosome reconstitution.
Nucleosome reconstitution
Nucleosomes were reconstituted via salt dialysis as described in (12,45) on 170 bp or 210 bp long DNAs containing the 601 Widom sequence (43). Molar mixing proportions for DNA:octamers were optimized between 1:1.7 and 1:1.9 to avoid aggregation and to minimize excess free DNA. Nucleosomes were reconstituted in mini dialyzing tubes (Pierce, Thermo Fisher Scientific, USA) via gradual salt dialysis from high salt (10 mM Tris–HCl, 0.1 mM EDTA, 2 M NaCl) to low salt (to 10 mM Tris–HCl, 0.1 mM EDTA, 5 mM NaCl). Successful nucleosome reconstitution was validated by gel electrophoresis on 6% polyacrylamide gels (60:1 acrylamide:bisacrylamide) in a TBE buffer with pH 7.5 at 10 V/cm. For FRET experiments nucleosomes with less than 5 % free DNA and fluorescence anisotropy of the attached dyes of <0.2 were used.
The two halves of the nucleosome where assigned with α- and β-side to account for the non-palindromic character of the Widom 601 sequence. DNA basepairs are counted from the dyad axis with − and + in the direction of the α- and β-side, respectively. The sequences of all fragments used are listed in Supplementary Methods. The two copies of the histones closer to one or the other halves of the DNA are assigned with α and β as well.
The donor dye (Alexa488) was always attached to K9C on each copy of the H3 histones. The nomenclature for the four nucleosome types used here is related to the position of the acceptor on the DNA: Dyx: close to the dyad; Ex: at the end of the DNA; Lx(170): on the linker DNA at the same position as Ex, but on a 210 bp long DNA. The indices α and β indicate to which side of the DNA the fluorophore is attached.
| Dyα | Alexa594 at – 9 bp, DNA length 170 bp |
| Dyβ | Alexa594/Cy5 at + 21 bp, DNA length 170 bp |
| Eα | Alexa594/Cy5 at – 77 bp, DNA length 170 bp |
| Lα(170) | Alexa594 at – 77 bp, DNA length 210 bp |
Replacement of Alexa594 by Cy5 was necessary in case of single-molecule experiments with Pulsed Interleaved Excitation (PIE) and Multiparameter Fluorescence Detection (MFD). Nucleosomes containing the histone mutation H2A R81/88E are referred to as mutDyx, mutEx and mutLx(170). Unlabeled nucleosomes from the same DNA sequences and histone octamers were prepared and used to adjust the total nucleosome concentration in single-molecule experiments
Ensemble FRET measurements
A Typhoon 9400 multimode imager (GE Healthcare, USA) was used for ensemble FRET experiments as described in (45). The concentration of the labeled nucleosomes was set to 300 pM and measurements were performed in a freshly cleaned and passivated 384-well microplate. To induce nucleosome disassembly, samples were incubated for 60 min in 0.02 μm-filtered TE buffer (10 mM Tris, 0.1 mM EDTA, pH 7.5) containing 5–1200 mM NaCl, 1 mM ascorbic acid (Sigma-Aldrich, USA) and 0.01 % Nonidet P40 (Roche Diagnostics, Germany) and the FRET signal was measured to track nucleosome disassembly.
After excitation at 488 nm, donor emission between 500 and 540 nm, IDDex, and via FRET excited acceptor emission between 595 and 625 nm, IADex, were recorded. After acceptor direct excitation at 532 nm, an emission between 595 and 625 nm, IAAex, was recorded. A donor-only, acceptor-only, double labeled DNA fragments with very low or no FRET, and the buffer solutions were measured in parallel as control samples to correct for background, crosstalk of Alexa488 emission into the acceptor channel and direct excitation of the acceptor dye at 488 nm excitation as described in (45).
The proximity ratio (P) was calculated from the corrected fluorescence intensities.
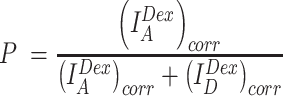 |
(1) |
Samples were measured in technical triplicates to calculate average P and standard deviation for each salt concentration of the nucleosome disassembly assay. Average P values were plotted against NaCl concentration and where possible fitted with a sigmoidal or a sum of up to three sigmoidal functions, beginning from their plateau to calculate c1/2-values as a measure of nucleosome stability.
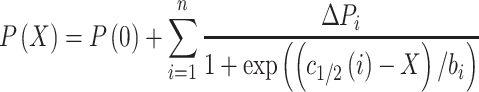 |
(2) |
X represents the salt concentration in mM, P(0) and ΔPi are maximum amplitude and step height(s) of the fit curve. Data were then normalized to P(0) = 1 and P(0) + Σ(ΔPi) = 0 of the fit. c1/2(i) is the inflection point of the curve at each step and the transition width bi is related to the slope at the respective inflection point. If not stated otherwise, the nucleosome disassembly assay was repeated with three independent replicates to calculate average P(X)-values and standard errors of the data points.
Multi-parameter fluorescence detection (MFD)
MFD measurements with pulsed interleaved excitation (MFD-PIE) were carried out as shown in (46) employing a confocal epi-illuminated setup based on an Olympus IX71 inverted microscope as described in (47–51). In PIE measurements, donor and acceptor dyes are sequentially excited by rapidly alternating laser pulses. MFD can be performed on both dyes, allowing computation of the donor-acceptor ratio (stoichiometry, SPIE) for each particle. Excitation is achieved using 485 and 635 nm pulsed diode lasers (LDH-D-C 485 and LDH-P-C-635B, respectively; both PicoQuant, Germany) operated at 32 MHz and focused into the sample solution by a 60×/1.2NA water immersion objective (UPLAPO 60×, Olympus, Germany). Laser powers in the samples were 55 and 9 μW, respectively. After separating the fluorescence signal by dual-edge dichroic beamsplitter (FF500/646, Semrock, USA), it was further divided into its parallel and perpendicular components by a polarizing beamsplitter cube (VISHT11, Gsänger, Germany) and then into spectral ranges below and above 595 nm by a dichroic beamsplitter (595 LPXR, AHF, Germany). Later each of the four channels was split again using 50/50 beam splitters, which allows us to get dead time free filtered FCS curves, resulting in a total of eight detection channels. Photons were detected by avalanche photodiodes (green channels: τ-SPAD-100, PicoQuant, Germany; red channels: SPCM-AQR-14, Perkin Elmer, USA). Additionally, green (HQ 530/43 nm for Alexa488) and red (HQ 720/150 nm for Cy5) bandpass filters (AHF, Germany) in front of the detectors ensured that only fluorescence from the acceptor and donor molecules was registered, while residual laser light and Raman scattering from the solvent were blocked. The detector outputs were recorded by a TCSPC module (HydraHarp 400, PicoQuant, Germany) and stored on a PC. Analysis of the single photon data stream was done using threshold criteria as described in (52).
The selection of FRET bursts (to be used in MFD-plots (Figure 3) and PDA (Figure 5)) in SPIE versus EFRET plots (Figure 2A) applying a 0.2 < SPIE < 0.8 threshold was based on the following arguments: particles with (i) only acceptor dye are distributed around 〈SPIE〉 = 0, (ii) one donor and two acceptor dyes—around 〈SPIE〉 = 0.33, (iii) equal number of donor and acceptor dyes—around 〈SPIE〉 = 0.5, (iv) with two donor and one acceptor dyes—around 〈SPIE〉 = 0.67 and (v) only donor dye—around 〈SPIE〉 = 1. The lower limit of 0.2 for selection is between 0 and 0.33 values to separate particles of type (i) and (ii). With the selected value of 0.2 (0.165 < 0.2) we prefer to lose some particles of type (ii) instead of including acceptor only labeled particles into the FRET population. Similarly, the upper limit of 0.8 for selection, i.e. between 0.67 and 1, separates particles of types (iv) and (v). With the selected value of 0.8 (0.8 < 0.835) we prefer to lose some particles of type (iv) instead of including donor only labeled particles into FRET population. These selection criteria were applied to all samples.
Figure 3.
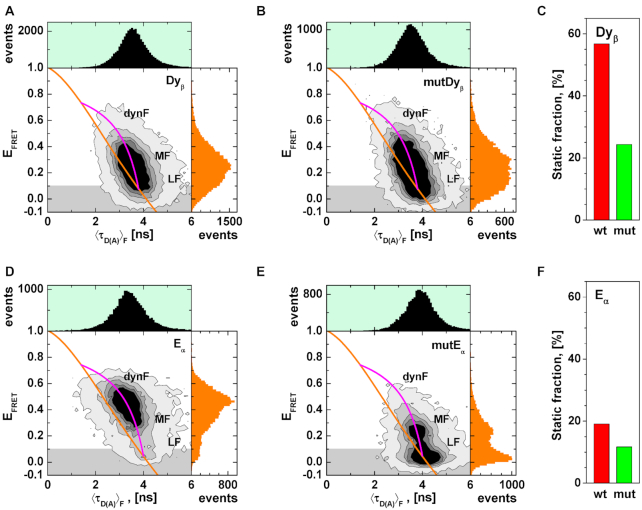
MFD analysis of H3NtT:DNA interactions in presence of FRET. (A) Dyβ: FRET efficiency (EFRET) plotted versus fluorescence weighted average donor lifetime (〈τD(A)〉F). (B) FRET efficiency (EFRET) versus fluorescence weighted average donor lifetime (〈τD(A)〉F) for mutDyβ nucleosomes. (C) Total static fractions of wt Dyβ (red bar) and mutDyβ (green bar) nucleosome samples obtained by dynPDA. (D) Eα: FRET efficiency (EFRET) plotted versus fluorescence weighted donor lifetime (〈τD(A)〉F). (E) FRET efficiency (EFRET) versus fluorescence weighted average donor lifetime (〈τD(A)〉F) for mutEα nucleosomes. (F) Total static fractions of wt Eα (red bar) and mutEα (green bar) nucleosome samples obtained by dynPDA. The orange line represents the EFRET–〈τD(A)〉F relation for static FRET species (all parameters for the FRET lines are described in Supplementary Note 1). The magenta line represents the EFRET–〈τD〉F relation for dynamic FRET species. The comparison of the total static fractions in Dyβ and Eα nucleosome samples demonstrates the fast dynamics of the DNA arm.
Figure 5.
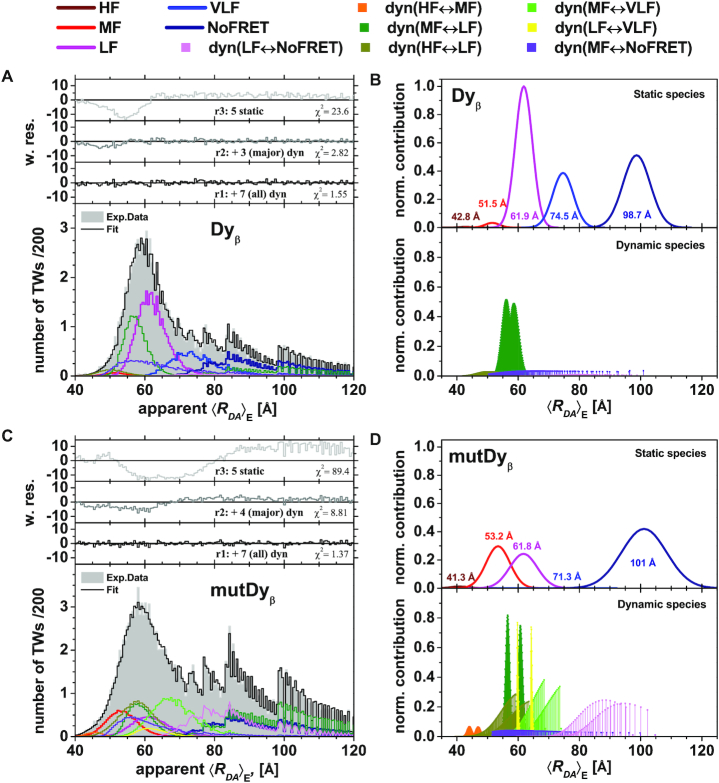
Dynamic Photon Distribution Analysis (dynPDA) of Dyβ and mutDyβ nucleosomes reveals frequency of conversion between H3NtT conformations and allosteric effects. Bursts were divided into 1, 2 and 3 ms (presented here) time windows and the resulting three apparent donor-acceptor distance histograms were used for global fitting. Their distribution function was approximated by seven interconverting, dynamic species (dyn(HF↔MF), dyn(MF↔LF), dyn(HF↔LF), dyn(MF↔VLF), dyn(LF↔VLF), dyn(MF↔NoFRET) and dyn(LF↔NoFRET), lower panels B and D) and five static states (HF, MF, LF, VLF and NoFRET, top panels B and D). Donor-acceptor distances (x-axis) were calculated from integer photon counts and are affected by photon shot noise, leading to not entirely smooth distributions. Normalized contribution: the area of each distribution on these model plots is proportional to the fraction of the corresponding species. The total area of all species multiplied by the total number of time windows in the histogram represents the area under the experimental data histogram. (A) (dyn)PDA of 40 pM Dyβ plus 1960 pM unlabeled nucleosomes at 100 mM NaCl (corresponding MFD–PIE plot shown in Figure 2A). Best fit quality is shown as weighted residuals (w. res.) in the upper panel (black line). In order to demonstrate contribution of dynamic species, weighted residuals are presented (gray line) with only three major (dyn(MF↔LF), dyn(MF↔VLF) and dyn(MF↔NoFRET)) and without all (light gray line) dynamic species in the top two panels. (B) Model distribution of 〈RDA〉E distances for Dyβ nucleosomes. For the limit of large photon counts (i.e. no shot noise), the distance distribution is calculated by a sum of five Gaussian-distributed probabilities of donor-acceptor distances (top panel) and seven allowed dynamic transitions between pairs of those static species (lower panel) (56). (C) dynPDA of 40 pM mutDyβ plus 1960 pM unlabeled nucleosomes at 100 mM NaCl (corresponding MFD–PIE plot is shown in Supplementary Figure S2B). Best fit quality is shown by weighted residuals (w. res.) in the upper panel (black line). In order to demonstrate contribution of dynamic species, weighted residuals are presented (gray line) with only four major (dyn(MF↔LF), dyn(MF↔VLF), dyn(MF↔NoFRET) and dyn(LF↔NoFRET)) and without any dynamic species (light gray line) in top two panels. (D) Model distribution of 〈RDA〉E distances for mutDyβ nucleosomes. The shot noise free distance distribution is calculated by a sum of five Gaussian-distributed probabilities of donor-acceptor distances (top panel) and seven allowed dynamic transitions between pairs of those static species (lower panel, pathways see Figure 4B) (56).
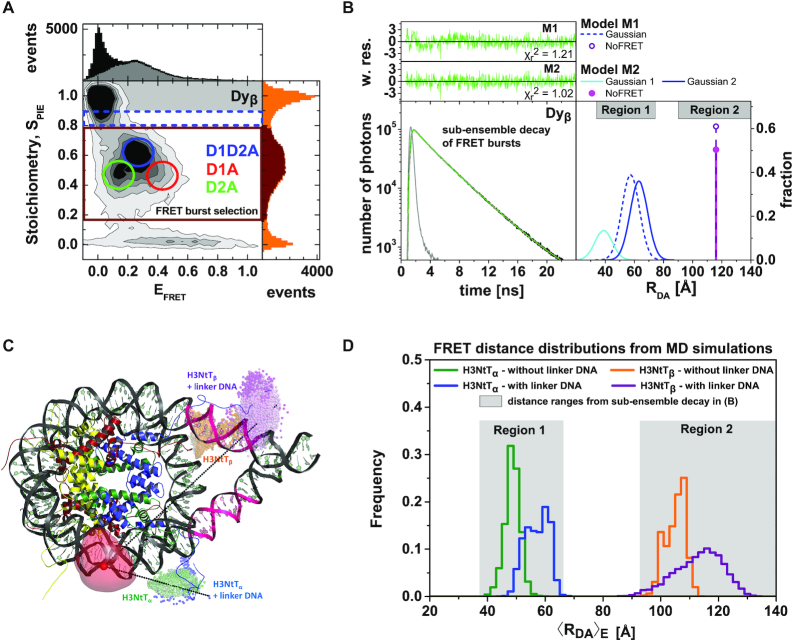
Figure 2.
MFD-PIE analysis of H3NtT:DNA interactions and sub-ensemble donor decay analysis in presence of FRET based on donor–acceptor distance distribution. Data for all plots are obtained at 100 mM NaCl from 40 pM Dyβ nucleosomes in the presence of 1960 pM or 260 pM unlabeled nucleosomes. (A) MFD-plot for stoichiometry, SPIE (Equation 6) versus FRET efficiency EFRET (Equation 5). Subspecies (D1A, D2A and D1D2A) are identified according to their position in the 2D distribution and indicated with circles. (B) Sub-ensemble histogram of the donor fluorescence intensity decay (lower left panel) from the selected FRET bursts (wine box in Figure 2A) and best fit model curve (green line). The decay histogram was analyzed by two models composed of two and three species (lower right panel): (M1) one Gaussian distributed distance (blue dashed line) and a donor-acceptor NoFRET-species (purple dashed line, corresponding to the distances larger than 95 Å), and (M2) two Gaussian distributed distances (cyan and blue lines) and a donor-acceptor NoFRET-species (magenta vertical line, corresponding to the distances larger than 95 Å) (see Material and Methods: Sub-ensemble TCSPC). The weighted residuals shown on top with the reduced sum of the weighted squared deviation between the model and the data of the decay histogram, 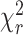 , demonstrate that higher fit quality was achieved by model M2. (C) Visualization of the dye accessible volume mean positions (spheres) for donors on both H3NtTs estimated from two distinct MD simulations: nucleosome without linker DNA (147 bp) (34): green—H3NtTα, orange—H3NtTβ, and nucleosome with linker DNA (187 bp) (25): blue—H3NtTα, purple—H3NtTβ (lighter shades indicate later simulation time). The accessible volume of the acceptor position +21 bp is shown as transparent red surface, the corresponding mean position is shown as a sphere. The preferential interaction areas of the linker DNA with the histone tails that were identified by crosslinking studies (31) are highlighted in magenta. (D) 〈RDA〉E distance distributions from two distinct MD traces in (C) computed by FPS (45) for the four cases. Two separate populations are clearly visible for H3NtTα (38–68 Å) and H3NtTβ (95–120 Å). These distance ranges agree well with the two distance ranges of experimental observations (gray regions) obtained by sub-ensemble time correlated single photon counting (seTCSPC) decay histogram analysis, Table 1.
, demonstrate that higher fit quality was achieved by model M2. (C) Visualization of the dye accessible volume mean positions (spheres) for donors on both H3NtTs estimated from two distinct MD simulations: nucleosome without linker DNA (147 bp) (34): green—H3NtTα, orange—H3NtTβ, and nucleosome with linker DNA (187 bp) (25): blue—H3NtTα, purple—H3NtTβ (lighter shades indicate later simulation time). The accessible volume of the acceptor position +21 bp is shown as transparent red surface, the corresponding mean position is shown as a sphere. The preferential interaction areas of the linker DNA with the histone tails that were identified by crosslinking studies (31) are highlighted in magenta. (D) 〈RDA〉E distance distributions from two distinct MD traces in (C) computed by FPS (45) for the four cases. Two separate populations are clearly visible for H3NtTα (38–68 Å) and H3NtTβ (95–120 Å). These distance ranges agree well with the two distance ranges of experimental observations (gray regions) obtained by sub-ensemble time correlated single photon counting (seTCSPC) decay histogram analysis, Table 1.
We used 40 pM of labeled nucleosomes for smFRET and added up to 1960 pM unlabeled nucleosomes to adjust the overall nucleosome concentration. Measurements were performed in a freshly cleaned and passivated 384-well microplate. To induce nucleosome disassembly, samples were incubated for 60 min in 0.02 μm-filtered TE buffer (10 mM Tris, 0.1 mM EDTA, pH 7.5) containing 5–600 mM NaCl, 1 mM ascorbic acid (Sigma-Aldrich, USA) and 0.01% Nonidet P40 (Roche Diagnostics, Germany). Data were taken for at least 90 min per sample.
Calculation of FRET efficiency EFRET and stoichiometry SPIE
For PIE, the FRET efficiency EFRET and stoichiometry SPIE (53) are defined as:
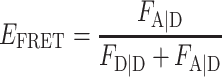 |
(3) |
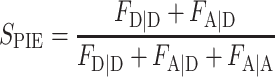 |
(4) |
FXem|Xex corresponds to a fully corrected fluorescence intensity computed from observed signal obsS considering background intensities and other experimental correction factors α, β, γ and δ defined below. The meaning of the indices is as follows: (D|D) is the donor intensity if the donor was excited, (A|D) is the acceptor intensity if the donor was excited (A|A) is the acceptor intensity if the acceptor was excited. EFRET and SPIE are computed from the observed signals obsS in two steps: (i) The registered primary signal obsS was corrected for the mean background 〈B〉 signal contribution in the green and red channels, respectively, to obtain the background corrected signal 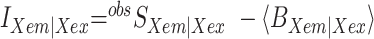 . (ii) Based on the definitions in Equations (3) and (4), the background corrected signals I were used together with four correction factors α, β, γ and δ to compute EFRET and SPIE according to (54):
. (ii) Based on the definitions in Equations (3) and (4), the background corrected signals I were used together with four correction factors α, β, γ and δ to compute EFRET and SPIE according to (54):
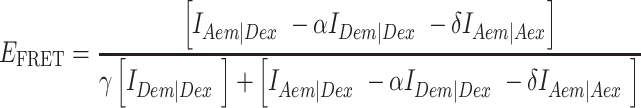 |
(5) |
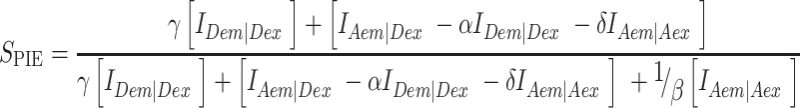 |
(6) |
The parameter α is a correction factor for the spectral donor fluorescence crosstalk (leakage) into the red ‘acceptor’ detection channel 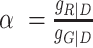 with the corresponding detection efficiencies gXem|Xex. The parameter
with the corresponding detection efficiencies gXem|Xex. The parameter 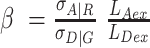 normalizes the acceptor delayed direct excitation rate to the donor prompt excitation rate in the PIE experiment defined by the absorption cross-sections for D σD|G and A σA|R, respectively, and the direct excitation irradiances [photons/cm2] LDex and LAex for the donor and acceptor lasers at the wavelengths Dex (G) and Aex (R) so that donor and acceptor dyes direct excitation rates are set equal providing SPIE= 0.5 for double DA labeled molecules. The parameter
normalizes the acceptor delayed direct excitation rate to the donor prompt excitation rate in the PIE experiment defined by the absorption cross-sections for D σD|G and A σA|R, respectively, and the direct excitation irradiances [photons/cm2] LDex and LAex for the donor and acceptor lasers at the wavelengths Dex (G) and Aex (R) so that donor and acceptor dyes direct excitation rates are set equal providing SPIE= 0.5 for double DA labeled molecules. The parameter 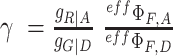 corrects for the effective fluorescence quantum yields, effΦF = ab.ΦF, and detection efficiencies, g, of A and D detection channels. ab is the fraction of molecules in the bright state and ΦF is the fluorescence quantum yield without photophysical (saturation) effects. The parameter
corrects for the effective fluorescence quantum yields, effΦF = ab.ΦF, and detection efficiencies, g, of A and D detection channels. ab is the fraction of molecules in the bright state and ΦF is the fluorescence quantum yield without photophysical (saturation) effects. The parameter 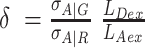 normalizes the acceptor excitation rate in the FRET PIE experiment by D laser to that defined by the acceptor absorption cross-sections σA|G and σA|R, and the laser irradiances [photons/cm2] LDex and LAex for donor and acceptor lasers at the wavelengths Dex (G) and Aex (R).
normalizes the acceptor excitation rate in the FRET PIE experiment by D laser to that defined by the acceptor absorption cross-sections σA|G and σA|R, and the laser irradiances [photons/cm2] LDex and LAex for donor and acceptor lasers at the wavelengths Dex (G) and Aex (R).
For the smFRET studies with the dye pair Alexa488-Cy5, we used the following parameters for the computation of EFRET and SPIE via Equations (5) and (6): α = 0.017, β = 0.667, γ, = 0.50 (based on gG|D/gR|A = 0.8, effΦF,A= 0.32 with ab,A = 0.8 and ΦF,A = 0.40, and effΦF,D= 0.80 with ab,D = 1.0 and ΦF,D = 0.80) and δ = 0.02. We applied the laser powers measured at the objective: LDex(485 nm) = 55.1 μW and LAex(635 nm) = 9.2 μW and registered the following background count rates 〈BDem|Dex〉 = 0.368 kHz, 〈BAem|Dex〉 = 0.223 kHz, 〈BAem|Aex〉 = 0.223 kHz.
Sub-ensemble TCSPC (seTCSPC)
The selected model function was fit to the experimental fluorescence intensity decays using the iterative re-convolution approach. Here, the model-decay curves were convoluted with the experimental instrument response function (IRF). Furthermore, a constant offset c of the fluorescence intensity was considered. The experimental time-resolved fluorescence intensities of the FRET-sample and the donor-only reference sample are presented as:
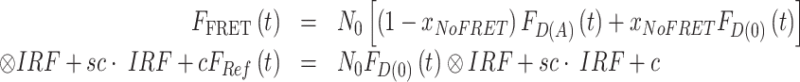 |
(7) |
Here, sc takes scattered light from the sample into account. The normalized to unit area model functions were scaled by the experimentally measured total photon number N0. This reduces the number of free fitting parameters by 1.
Due to local quenching the fluorescence decay of the donor in the absence of FRET is already often multi-exponential. Thus, the time resolved fluorescence intensity decays of donor-/acceptor-labeled nucleosomes (FRET-population) were fitted globally with the decays of the donor-/unlabeled nucleosomes (donor-only sample, D-only) as reference sample.
Due to local quenching the fluorescence decay FD(0)(t) of the donor-only reference sample in the absence of FRET is already often multi-exponential with the species fractions xD(i) and fluorescence lifetimes τD(0)(i) (55):
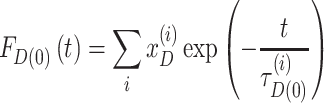 |
(8) |
FD(0)(t) was also used to describe the NoFRET-species.
It is reasonable to assume that local quenching of the donor radiative lifetime is not changed by quenching by FRET. Hence, the FRET-rate (kFRET) is only determined by the donor–acceptor distance and their relative orientation. In the presence of FRET, the donor fluorescence decay can be expressed using the donor-acceptor distance distribution p(RDA).
We assumed Gaussian distribution of donor–acceptor distances 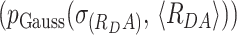 with a mean of 〈RDA〉 and a standard deviation of
with a mean of 〈RDA〉 and a standard deviation of 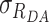 , which is a good approximation within the framework of an accessible volume (AV) (55). For Gaussian distributed donor–acceptor distances the lifetime-decay of single FRET species is expressed as follows:
, which is a good approximation within the framework of an accessible volume (AV) (55). For Gaussian distributed donor–acceptor distances the lifetime-decay of single FRET species is expressed as follows:
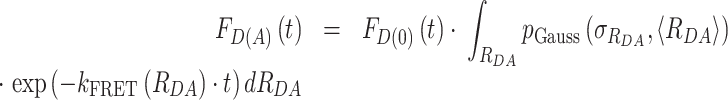 |
(9) |
In general FD(A)(t) model function is represented as a weighted sum of decays with different mean 〈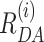 〉 Gaussian distance distributions corresponding to different FRET species.
〉 Gaussian distance distributions corresponding to different FRET species.
To distinguish FRET populations from D-only one can demonstrate the existence of a bright acceptor (interleaved direct acceptor excitation in PIE) in nucleosomes via building sub-ensemble fluorescence decay histograms for donor and acceptor, for example generated from bursts between D-only (grayed region) and FRET (wine rectangle) populations on Figure 2A (dashed blue rectangle), which indicate a very low average FRET efficiency per burst while delayed acceptor decay is clearly visible (see Supplementary Figure S3).
Photon distribution analysis (PDA)
Samples were measured at various NaCl concentrations under single-molecule conditions. The signals of the full trace or selected FRET bursts were split into equal time windows (TW). The FRET efficiency was calculated from photon numbers emitted by donor and acceptor dyes in the prompt TDC (time-to-digital converter) channels defined by the donor excitation (TDC channels before acceptor excitation pulse). In MFD-PIE experiments the acceptor excitation laser pulse is delayed by ∼16 ns, which defines the delayed TDC window for computation of the stoichiometry SPIE value (see next section: Calculation of RDA distances).
For each TW (only full-length time windows were used and incomplete pieces at the end were excluded from analysis) the values for the FRET parameters (RDA, EFRET) were calculated as described in Calculation of RDA distances below and plotted in a frequency histogram with 201 bins (Supplementary Figure S5A–F). The main idea in PDA is computation of the distribution of the chosen FRET indicator at a given FRET efficiency (or FRET-averaged donor-acceptor distance, 〈RDA〉E) (56) taking photon shot-noise into account. Due to the flexibility of the dye linker, FRET pairs exhibit a distribution of FRET efficiencies or apparent distances even on rigid molecules (52). This distance distribution was well approximated by a Gaussian distribution with a standard deviation σ ∼6 Å.
Calculation of RDA distances
Based on fluorescence signals, the FRET-averaged distance 〈RDA〉E between the dyes can be calculated from the mean FRET efficiency as defined (for ideal dyes) by
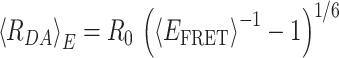 |
(10) |
In this work we calculated 〈RDA〉E directly from the observed, background-corrected intensities and corresponding correction parameters α, γ and δ (Equations 5 and 6) using the FRET pair specific Förster radius for Alexa488 and Cy5 of R0 = 52 Å.
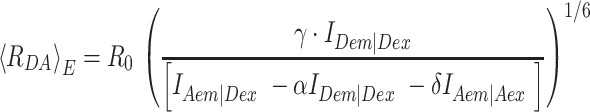 |
(11) |
Dynamic PDA
To find a global fit model that can accurately distinguish a dynamic system from a static one, we have tried different models on our data. A joint model with static Gaussian distributions indicates that a model without dynamic exchange terms cannot describe all data sets appropriately, since the exchange dynamics influences the width of the distributions in parameter histograms as a function of used TW duration (data not shown). One of the key advantages of our PDA technique is generation of non-smooth (spiky) model histograms for any given smooth (noise free) model at any given binning and any given time window size. Spiky photon counting histograms with few hundred photons are a digital fingerprint of single-molecule experiments originating from a convolute of Poisson statistics for photon counting and binomial statistics for FRET (57). Fitting this fingerprint directly is far superior to fitting smooth model functions. For this reason dynPDA is very a powerful analysis technique that can safely extract unusual high numbers of independent parameters from the data.
Therefore, we have used dynamic PDA (56) in the subsequent analysis, which can describe exchange dynamics in the nucleosome. For each data set histograms of apparent interdye distances were created for three different TWs (1, 2 and 3 ms). All FRET-parameter histograms created for each NaCl concentration and for every TW (number of [NaCl]  number of TWs; here: 3 × 3 = 9) were globally fitted by the kinetic models described below.
number of TWs; here: 3 × 3 = 9) were globally fitted by the kinetic models described below.
Each static FRET species was modeled by a Gaussian distribution of donor–acceptor (DA) distances, RDA, approximated by 51 bins. To describe the histograms by dynamic mixing between two Gaussian distributed FRET species (e.g. species 1, species 2), the model distribution can be approximated with the sum of two dynamic mixing distributions with distances between (〈R(1)〉 – σ1 and 〈R(2)〉 – σ2) and (〈R(1)〉 + σ1 and 〈R(2)〉 + σ2) where σ represents the standard deviation of the respective Gaussian distributions (5).
All FRET-parameter histograms from MFD data were then globally fitted using dynamic PDA and assuming a kinetic model. The dynamic PDA model assumed a number of co-existing individual FRET species (static nucleosome fractions: static 1, static 2, …) showing no dynamics on the timescale of diffusion (relaxation times, tR > 20 ms), with populations of molecules which exchange between those FRET species (dynamic fractions: dyn(1↔2), dyn(2↔3), …). The mean interdye distances of the static FRET species(1-5) were assumed to be invariant to NaCl concentration. Thus, a sum of Gaussian distributed FRET species (〈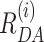 〉, xi, σi—as fraction of 〈
〉, xi, σi—as fraction of 〈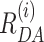 〉) and dynamically mixing pairs of those Gaussian distributed FRET species, dyn(i↔j), defined by the selected kinetic model was used to globally fit the group of histograms from all NaCl concentrations. Importantly, global fits were employed to evaluate the NaCl dependencies, assuming a linear relationship (with slope mij) between the logarithm of the rate constants (kij) and the ionic strength within the investigated NaCl concentration range:
〉) and dynamically mixing pairs of those Gaussian distributed FRET species, dyn(i↔j), defined by the selected kinetic model was used to globally fit the group of histograms from all NaCl concentrations. Importantly, global fits were employed to evaluate the NaCl dependencies, assuming a linear relationship (with slope mij) between the logarithm of the rate constants (kij) and the ionic strength within the investigated NaCl concentration range:
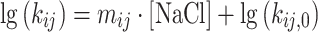 |
(12) |
similar to observations in protein folding (58).
With these two assumptions we have significantly reduced the number of free fit parameters. For each dynamic exchange term at three investigated NaCl concentrations, instead of 3  2 = 6 transition rate constants and 3
2 = 6 transition rate constants and 3 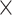 2 = 6 limiting distances only two pairs of
2 = 6 limiting distances only two pairs of 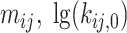 constants and one pair of distances were needed. This leads to a total of 6 free parameters instead of 12.
constants and one pair of distances were needed. This leads to a total of 6 free parameters instead of 12.
Finally, a generalized dynamic PDA model accounting for donor only, five static species (Gaussian distributed distances) and all possible dynamic mixing distributions between them (10 pairs) has been generated. Based on structural limitations (see in Results and Discussion: Structural model for H3NtT conformations and their multiple interaction modes) we could exclude 3 out of 10 possible mixing pairs (Figure 4A). Overall, nine FRET-parameter histograms were globally fitted considering seven two-species exchange equilibria (i.e. 14 pairs of 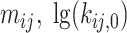 constants) and five static FRET-species (Figure 4B, C). Each static FRET-species was described by a mean distance and a standard deviation of Gaussian distributed distances as fraction of 〈RDA〉 defined by one global fraction parameter. Taking together in our approximate model these (2
constants) and five static FRET-species (Figure 4B, C). Each static FRET-species was described by a mean distance and a standard deviation of Gaussian distributed distances as fraction of 〈RDA〉 defined by one global fraction parameter. Taking together in our approximate model these (2 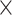 14+5+1) = 34 were global fit parameters while donor only, five static and seven dynamic species fractions were free fit parameters for each NaCl concentration (overall 3
14+5+1) = 34 were global fit parameters while donor only, five static and seven dynamic species fractions were free fit parameters for each NaCl concentration (overall 3  (5+7) = 36, since for each concentration the amplitude of one static Gaussian is fixed to 1). Notably simpler models with fewer static and/or dynamic states could not describe the data (see residuals r3 and r2 in Figure 5A, C). We performed this global dynamic PDA fit to decipher: (i) which states are connected by transitions, (ii) time ranges of the associated kinetic rate constants and (iii) steady state concentrations of all species.
(5+7) = 36, since for each concentration the amplitude of one static Gaussian is fixed to 1). Notably simpler models with fewer static and/or dynamic states could not describe the data (see residuals r3 and r2 in Figure 5A, C). We performed this global dynamic PDA fit to decipher: (i) which states are connected by transitions, (ii) time ranges of the associated kinetic rate constants and (iii) steady state concentrations of all species.
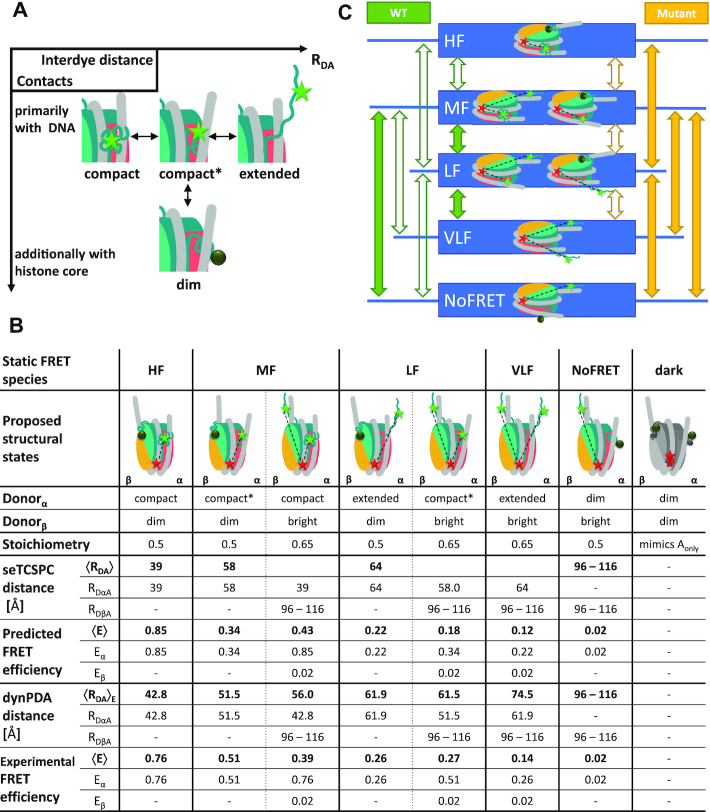
Figure 4.
Structural model for H3NtT conformations and observed transitions in nucleosomes. (A) Proposed four conformational states for each H3NtT. The dynPDA model reveals three possible transitions between them: (i) compact ↔ compact*, (ii) compact* ↔ extended and (iii) compact* ↔ protein associated/dim state. (B) Assignment of all possible combinations of the assumed H3NtT conformations (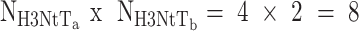 ) to the five static FRET states. The dynPDA model with five static states was defined based on sub-ensemble donor decay analysis results. The states are named with respect to their corresponding FRET efficiency level. The RDA distances were extracted from the MFD measurements by dynPDA analysis. The average FRET efficiencies, 〈E〉, for species with two bright donors were calculated as arithmetical mean of two FRET efficiencies corresponding to the shown RDαA and RDβA distances (67). Bright donor and acceptor fluorophores are shown as green or red stars, respectively. Dim donor fluorophores are shown as dark green circles. (C) dynPDA model containing five static states and seven dynamics species. Green and orange arrows correspond to possible transitions in wt nucleosomes and mutated nucleosomes, respectively. Filled arrows indicate that transitions are significantly populated (>7%), whereas open arrows refer to transitions, which are allowed in the dynPDA model, but are not significantly populated according to the PDA global fit. Three transitions are generally excluded based on direct structural transition defined in (A): HF↔NoFRET, HF↔VLF and VLF↔NoFRET.
) to the five static FRET states. The dynPDA model with five static states was defined based on sub-ensemble donor decay analysis results. The states are named with respect to their corresponding FRET efficiency level. The RDA distances were extracted from the MFD measurements by dynPDA analysis. The average FRET efficiencies, 〈E〉, for species with two bright donors were calculated as arithmetical mean of two FRET efficiencies corresponding to the shown RDαA and RDβA distances (67). Bright donor and acceptor fluorophores are shown as green or red stars, respectively. Dim donor fluorophores are shown as dark green circles. (C) dynPDA model containing five static states and seven dynamics species. Green and orange arrows correspond to possible transitions in wt nucleosomes and mutated nucleosomes, respectively. Filled arrows indicate that transitions are significantly populated (>7%), whereas open arrows refer to transitions, which are allowed in the dynPDA model, but are not significantly populated according to the PDA global fit. Three transitions are generally excluded based on direct structural transition defined in (A): HF↔NoFRET, HF↔VLF and VLF↔NoFRET.
Estimation of possible RDA distances from molecular dynamics trajectory
We used two all atom molecular dynamics (MD) simulation trajectories based on PDB 1KX5 to explore H3NtT conformations and determine interdye distance distributions. One was a 250 ns trajectory by Lehmann et al. (34) of a core nucleosome with 147 bp DNA and the second was a 1 μs trajectory by Shaytan et al. (25) of a nucleosome with linker DNA extended to 187 bp. We calculated interdye distance distributions and determined mean dye positions by AV simulations (Supplementary Note 2) that were performed with the FRET-restrained positioning and screening (FPS) toolkit (59).
RESULTS AND DISCUSSION
Salt induced nucleosome disassembly monitored from the perspective of the H3NtT by ensemble FRET
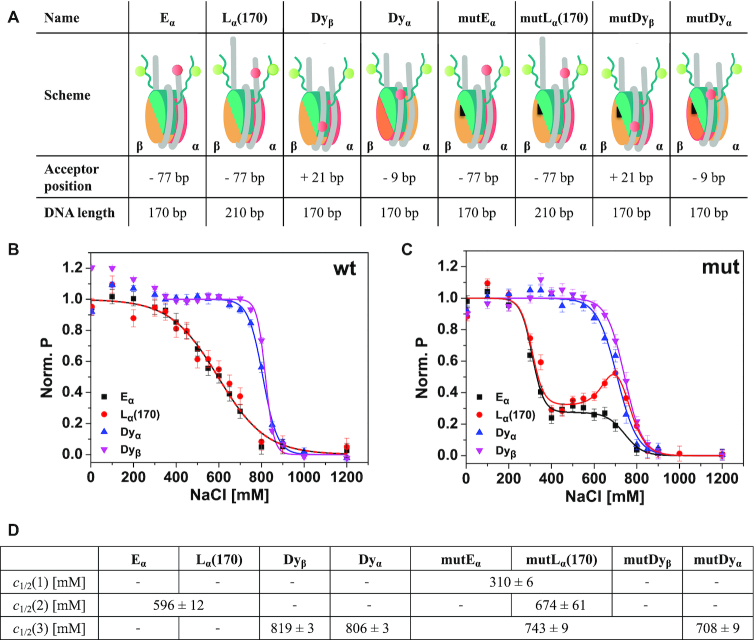
To investigate the localization of the protruding N-terminal tail of H3 histones (H3NtT) in reconstituted 601 mononucleosomes, we designed four fluorescently labeled wild type and four H2A R81E/R88E mutated nucleosome constructs (Figure 1A, see Materials and Methods, Supplementary Methods); all labeled with donor fluorophores on the H3NtTs at position K9C and an acceptor fluorophore at various DNA positions. The systematic variation of DNA labeling positions allowed us to monitor proximity or interactions between H3NtT and the nucleosomal DNA to unravel the distance preferences and dynamics of the H3NtT. First, we performed fast, well-established ensemble FRET measurements using a Typhoon multimode imager (34,41,45) to monitor changes in proximity ratio as a function of the NaCl concentration in wild type and mutated nucleosomes. We either tracked averaged proximity changes between the H3NtT and the DNA linker arm (constructs Eα and Lα(170)) or the H3NtT and the inner DNA gyre close to the dyad axis (constructs Dyα and Dyβ) (Figure 1B, C). Data sets were fitted with one- or multi-sigmoidal functions (Equation 2), yielding c1/2-values for the NaCl concentrations where the averaged proximity ratio P reaches 50% of the corresponding step height (global fit is presented in Figure 1B and C, independent fits are shown in Supplementary Figure S4A and B, complete table of global fit results can be found in Supplementary Table S1).
Figure 1.
Schematic representation of the used labeled constructs and ensemble analysis of salt-induced proximity changes between H3NtT and the nucleosomal DNA. (A) In the cartoon representations H2A–H2B dimer on α-side is shown in orange, H2A–H2B dimer on β-side is shown in yellow, (H3–H4)2 tetramer in turquoise, DNA in gray. The black triangle on the H2A–H2B dimers indicates mutated nucleosomes bearing two point mutations in the α3 domain of H2A, namely H2A R81E/R88E. The donor on H3K9C is shown as a green circle. The acceptor is shown as a red circle and labeling positions on the DNA are given as relative base shifts to the dyad axis. Dyα: acceptor close to dyad axis at position −9, Dyβ: acceptor close to dyad axis at position +21, Eα: acceptor at the end of a 170 bp long DNA at position −77, Lα(170): acceptor at position −77 on a 210 bp long DNA, mut: nucleosomes bearing the H2A R81E/R88E mutation. (B) Ensemble FRET analysis of distance changes between wild type H3NtT and various positions on the DNA. For visualization, data were normalized to the maximal and minimal amplitude of the sigmoidal fit (Equation 2). Labeled nucleosomes were measured at 300 pM total concentration after 1 h incubation in buffers with different NaCl content. (C) Ensemble FRET analysis of distance changes between H3NtT and the DNA in mutated nucleosomes. Inflection points of the proximity curves are significantly lower in mutDα and mutDyβ nucleosomes; curve progression is changed to two-step behavior in Eα and Lα(170), indicating allosteric effects induced by the mutation. (D) Results of global fit of Equation (2) to the data in B, C (for full set of fit parameters and individual fits see Supplementary Table S1 and Figure S4, respectively). Empty fields: parameter not needed in the fit, joint fields: global parameter.
The ensemble FRET measurements revealed that in all samples the average distances between the donor on H3NtT and the acceptor on the DNA were within a FRET-sensitive range (<100 Å) at low NaCl concentrations. The decrease of the normalized proximity ratio as a function of the NaCl concentration shows, that in wt nucleosomes the contact between the H3NtT and the DNA linker arm is disrupted at rather low NaCl concentrations with c1/2 = 596 ± 12 mM for Eα and Lα(170). In contrast, the contact between the H3NtT and the inner DNA gyre is disrupted at higher NaCl concentrations (Dyα: c1/2 = 806 ± 3 mM, Dyβ: c1/2 = 819 ± 3 mM). This finding is in good agreement with previous studies focusing on nucleosome stability, utilizing labeling positions in the core particle (12,14,34). However, a comparison between the curve progression for the sample with acceptor on the inner DNA gyre ((Dyα and Dyβ) and the sample with acceptor on the DNA linker arm (Eα and Lα(170)) reveals significant differences. While the averaged proximity between the H3NtT and the DNA linker arm decreases gradually (increase in distance) with a broad transition width (Eα and Lα(170): b = 112 ± 11 mM, Supplementary Table S1; the parameter b is used as a measure for the half-width of the transition), the proximity between the H3NtT and the inner DNA gyre is stable till 700 mM and decreases very fast thereafter with a narrow transition width (Dyα: b = 34 ± 2 mM, Dyβ: b = 20 ± 2 mM, Supplementary Table S1). This rather abrupt change in distance leads to the assumption that the loss of the contact between H3NtT and the inner DNA gyre (Dyα and Dyβ) is coupled to the internal weakening of the DNA β-side (c1/2 = 783 ± 5 mM (13)) and initializes the release of the second, more weakly bound β-dimer (c1/2 = 866 ± 33 mM (13)) (for a comprehensive disassembly scheme see Conclusion). The almost linear curve progression for the H3NtT:DNA linker arm contact instead (Eα and Lα(170)) can be explained by a successive loss of the protein:DNA contacts (TA steps) described earlier (60). Accordingly, a progressive opening of the outer DNA gyre occurs, i.e. DNA ends are gradually moving away from the dyad axis and from H3NtT. Despite the electrostatic interaction between the negatively charged linker DNA arm and the positively charged histone tails, no differences were detected for different total DNA lengths (Lα(170) with 210 bp and Eα with170 bp total length, both labeled at position −77), i.e. 20 bp DNA overhanging on each side have no detectable effect on the average H3NtT conformation. This finding corroborates the results of cross-linking experiments (31) suggesting that a certain linker length of the nucleosomal DNA is important for the binding of the H3NtT to the linker DNA where crosslinking yields increased between 147 and 170 bp, reaching a saturation level at 170 bp. Taken together, our study is in line with their suggestion, that contacts between H3NtT and linker DNA could be concentrated within the first ≈12 bp of linker DNA on each side of their symmetric constructs. The similar c1/2-values of the two opposing sides of the inner gyre (Dyα/Dyβ) lead us to hypothesize that the reported asymmetric opening of 601 nucleosomes, which was observed for the H2A-H2B dimer release (13,15,42), plays only a subordinate role in respect to the interactions between H3NtT and the inner DNA gyre. Hence, the local geometry of the nucleosome particle in the inner gyre is only weakly affected by the described asymmetry even though the weaker bound H2A:H2B dimer (on the α-side) is already evicted.
Next, we analyzed how mutations in helix α3 of H2A may affect H3NtT:DNA interactions (Figure 1C). Initially, the importance of this region was predicted from molecular dynamics simulations which aimed at unraveling the impact of H3 tail removal on the structure of the nucleosome core particle (27). A structural comparison between wt and H3 tailless nucleosomes suggested an altered orientation and thus a more negatively charged helix α3 (27), even without direct interactions between the H3NtT and the H2A helix α3 (1,61). We have recently shown by all atom MD simulations of mutated nucleosomes that charge-modifying mutations in helix α3 of H2A at positions R81 and R88 play a fundamental role for nucleosome core stability (34). H2A R81 is centrally important for stabilizing the H3 αN-helix and the H2A C-loop (N89–V100) while R88 is important for maintaining the intact structure of the H2A C-loop and for interaction with the H2A C-tail (34). Ensemble and single-molecule FRET experiments revealed a destabilizing effect of those mutations and an allosteric influence on the H3 tail interactions and dynamics was hypothesized (34). In the present study we choose the H2A R81E/R88E mutant (simultaneous exchange of two positively charged arginines by negatively charged glutamic acids), which was shown to lead to a pronounced destabilization of the nucleosome core. The comparison of the results from ensemble FRET measurements with wt nucleosomes shows that the c1/2-values for interactions between the inner DNA gyre and H3NtT (mutDyα: c1/2 = 708 ± 9 mM, mutDyβ: c1/2 = 743 ± 9 mM) were slightly, but significantly weakened by the H2A mutations (Figure 1C and D). This long-range, allosteric effect of the H2A R81E/R88E mutation is even more prominent for interactions between H3NtT and the outer DNA gyre/linker DNA, as both c1/2-value and curve shape are significantly altered upon mutations within the nucleosome core (mutEα and mutLα(170)). Here, in comparison to wt nucleosomes the linear regression for the contact probability is changed to a multi-step progression. Note, that the NaCl range of the first step (mutEα and mutLα(170), c1/2 = 310 ± 6 mM) coincides with the already reported very early release of the mutated H2A proteins (c1/2 = 336 ± 3 mM (34)). After the release of both mutated H2A–H2B dimers the remaining mutEα tetrasome ((H3–H4)2-tetramer and DNA) rests in the second plateau (between 400 and 600 mM). At higher NaCl concentrations the decrease of P is similar for mutEα and wt Eα samples. The unique increase in proximity ratio for mutLα(170) between 600 and 800 mM NaCl suggests the existence of residual interactions between the H3NtT and the longer linker DNA (DNA length 210 bp). Thus, an increased linker DNA might facilitate the interaction of the H3NtT with the linker DNA after dimer release. Altogether, these results show that the H3NtT is localized within the FRET sensitive regime from the core and linker DNA and that distance changes during salt-induced nucleosome disassembly can be tracked. This way we can determine distance ranges between histone tails and the nucleosomal DNA which are not deducible from the crystal structures. To analyze the H3NtT interactions and its dynamics further, we performed single-molecule FRET (smFRET) measurements.
smFRET unveils H3NtT:DNA configurations and allostery between the H2A helix α3 and H3NtT
FRET-based single-molecule techniques can be used for a detailed structural and kinetic analysis of transient structures in an ensemble and have already been applied to various aspects of nucleosome structure and dynamics (13,14,34,39,40,62–64). Combining PIE and MFD, the fluorescence signal can be classified according to e.g. spectral response, lifetime and polarization. smFRET enables the separation of conformational states of the H3NtT and thereby elucidates its structural dynamics. To unravel the H3NtT interactions we focus on the Dyβ nucleosomal constructs where the acceptor label is on the core DNA and both H3 tails are labeled with donor. A total nucleosome concentration of 2 nM (40 pM labeled nucleosomes) was chosen to avoid spontaneous, unwanted nucleosome disintegration. An example for a two-dimensional burst histogram (PIE plot) of stoichiometry SPIE versus intensity-based FRET efficiency EFRET at 100 mM NaCl is shown in Figure 2A.
Three distinct FRET species with different stoichiometry ratios and FRET efficiency levels can be distinguished in the plot: (i) D1A: SPIE = 0.5, EFRET = 0.43, (ii) D1D2A: SPIE = 0.65, EFRET = 0.27 and (iii) D2A: SPIE = 0.5, EFRET = 0.13. The species were named according to their intrinsic stoichiometry of bright fluorophores, as a stoichiometry ratio SPIE = 0.5 corresponds to molecules with only one donor and one acceptor, whereas SPIE = 0.65 is related to the particles with two donors and one acceptor. Keeping in mind nearly 100% labeling efficiency of H3NtT and DNA molecules, intact nucleosomes should always contain two donor and one acceptor dyes (SPIE = 0.65, Figure 2A and Supplementary Figure S1A).
Reasons for the observed three SPIE-values in presence of FRET can be deduced from donor seTCSPC fluorescence decay analysis (or sub-ensemble time-resolved FRET analysis) (Figure 2B). For the sub-ensemble analysis, we selected the FRET bursts highlighted in Figure 2A as described in Materials and Methods: Multi-parameter Fluorescence Detection. As the structural fluctuations of the molecular backbone should be small on the fluorescence lifetime scale of the dyes (ns), we applied a two-step incremental sub-ensemble time-resolved FRET analysis to resolve which FRET species contribute to a selection of FRET bursts so that a minimum number of FRET species is revealed. In the first step, the specific donor decay was generated (Figure 2B) from all FRET bursts (wine rectangle of Figure 2A) and fitted with two different models: (M1) a single FRET species with a Gaussian distance RDA distribution and a NoFRET species, and (M2) two FRET species with a Gaussian 〈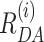 〉 distance distribution and a NoFRET species. (Equations 7–9). In both models the half-widths of Gaussian distributed distances were fixed to 6 Å. The residuals and corresponding parameter for the goodness-of-fit (
〉 distance distribution and a NoFRET species. (Equations 7–9). In both models the half-widths of Gaussian distributed distances were fixed to 6 Å. The residuals and corresponding parameter for the goodness-of-fit (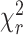 ) are presented for both fits on the top panel of Figure 2B. As the fit quality of the second model was significantly better, judged by a
) are presented for both fits on the top panel of Figure 2B. As the fit quality of the second model was significantly better, judged by a 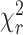 value much closer to the optimal value of 1 and flat weighted residuals, we subsequently used it for independent sub-ensemble time-resolved FRET analysis of wt and mutated samples. In the next step, specific donor decays were generated from selected bursts for each of the three shown populations (Figure 2A: D1A, D1D2A and D2A) and fitted with the second model (M2) with fixed half-widths (6 Å) of the Gaussian distance distribution to find heterogeneities between populations within the considered FRET bursts selection. The results of the independent sub-ensemble time-resolved FRET analysis (Table 1) for Dyβ and mutDyβ nucleosomes reveal the existence of a broad and complex fluorescence lifetime distribution. Based on Table 1 (ignoring distances shorter than 34 Å due to the large error in this distance range), up to three distinct ranges of 〈
value much closer to the optimal value of 1 and flat weighted residuals, we subsequently used it for independent sub-ensemble time-resolved FRET analysis of wt and mutated samples. In the next step, specific donor decays were generated from selected bursts for each of the three shown populations (Figure 2A: D1A, D1D2A and D2A) and fitted with the second model (M2) with fixed half-widths (6 Å) of the Gaussian distance distribution to find heterogeneities between populations within the considered FRET bursts selection. The results of the independent sub-ensemble time-resolved FRET analysis (Table 1) for Dyβ and mutDyβ nucleosomes reveal the existence of a broad and complex fluorescence lifetime distribution. Based on Table 1 (ignoring distances shorter than 34 Å due to the large error in this distance range), up to three distinct ranges of 〈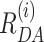 〉 distances become evident from all results: (i) 34–42 Å, (ii) 57–60 Å and (iii) 61–68 Å. Additionally, all populations contain a significant fraction of donor that is not quenched by FRET (32–62%), even though we have selected the double labeled population in Figure 2A. This NoFRET species is characterized by the same bi-exponential fluorescence decay as the donor only sample (4.08 ns (87%) and 1.3 ns (13%)).
〉 distances become evident from all results: (i) 34–42 Å, (ii) 57–60 Å and (iii) 61–68 Å. Additionally, all populations contain a significant fraction of donor that is not quenched by FRET (32–62%), even though we have selected the double labeled population in Figure 2A. This NoFRET species is characterized by the same bi-exponential fluorescence decay as the donor only sample (4.08 ns (87%) and 1.3 ns (13%)).
Table 1.
Mean interdye distances 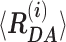 and their relative fractions (xi) estimated from sub-ensemble time-resolved FRET analysis for Dyβ and mutDyβ (Supplementary Note 3).
and their relative fractions (xi) estimated from sub-ensemble time-resolved FRET analysis for Dyβ and mutDyβ (Supplementary Note 3).
| Sample | Population |
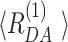 [Å] [Å] |
x 1* |
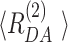 [Å] [Å] |
x 2* | x3, NoFRET |
|---|---|---|---|---|---|---|
| Dyβ | All FRET bursts | 38.9 | 0.08 | 63.1 | 0.37 | 0.56 |
| D1A | 41.3 | 0.15 | 63.8 | 0.53 | 0.32 | |
| D2A | 28.0 | 0.05 | 67.7 | 0.33 | 0.62 | |
| D1D2A | 38.9 | 0.06 | 63.1 | 0.46 | 0.48 | |
| mutDyβ | All FRET bursts | 27.0 | 0.21 | 59.6 | 0.29 | 0.49 |
| D1A | 33.8 | 0.19 | 57.0 | 0.45 | 0.36 | |
| D2A | 23.9 | 0.27 | 62.9 | 0.23 | 0.50 | |
| D1D2A | 35.3 | 0.11 | 60.8 | 0.43 | 0.46 |
*
To relate the distances found by sub-ensemble time-resolved FRET analysis to potential H3NtT conformations and to estimate possible interdye distances for Dyβ nucleosomes, we used the trajectories from all atom molecular dynamics (MD) simulations of a nucleosome (147 bp DNA, 250 ns) by Lehmann et al. (34) and of a nucleosome with linker DNA (total length 187 bp, 1 μs) by Shaytan et al. (25). The computed accessible volume and the respective mean positions for both donors on the H3NtTs at position K9C and for the acceptor on the DNA near the dyad axis (+21 bp) are shown in Figure 2C. The mean positions of K9C in each frame of the trajectories are represented by small spheres. Notably, each H3NtT seems to prefer a rather extended conformation in presence of linker DNA. To visualize this relationship we computed 〈RDA〉E distances by FPS (59) from both simulation trajectories, yielding a distribution of FRET-averaged donor to acceptor distances (Figure 2D). Now, two separate main populations are clearly visible, which nicely match the seTCSPC derived distance ranges (H3NtTα: ∼38–68 Å and H3NtTβ: 95–120 Å). The distance between the donor on H3NtTβ and the acceptor is beyond the distance resolvable by FRET (∼100 Å for the A488–Cy5 dye pair). Recalling the observed two SPIE values (0.5 and 0.65), we hypothesize a conformational state of H3NtT in which the donor dye is trapped on the nucleosome core surface so that it can be quenched and its brightness drops dramatically (Supplementary Figure S2). Consequently, the observed high fraction of NoFRET lifetime is caused by a configuration in which the donor on H3NtTα is dim and the donor on H3NtTβ is bright, but RDA > 100 Å. As the H3NtT is supposed to be highly dynamic, we use two dimensional MFD plots where two FRET indicators, the intensity-based FRET efficiency and the fluorescence weighted average lifetime of the donor in presence of acceptor (〈τD(A)〉F) are plotted versus each other, (Figure 3A, B, D, E) to distinguish between FRET populations that are static or dynamic during the burst duration. While the orange line represents the EFRET–〈τD(A)〉F relation for static FRET species, the magenta line represents the EFRET–〈τD(A)〉F relation for dynamic FRET species (all parameters for the FRET lines are described in Supplementary Note 1). Static species would be localized on the orange line, whereas dynamic species are on the magenta line (5,56). Considering Dyβ nucleosomes at 100 mM NaCl, a significant fraction of bursts deviate from the static line and fall on the dynamic line (Figure 3A). Furthermore, no clearly separated populations are detectable, which gives rise to the assumption of a highly dynamic system with multiple interaction modes. By comparing wild type nucleosomes (Dyβ, Figure 3A) with those mutated on H2A histones (mutDyβ, Figure 3B), we observe an even broader distribution with an increased fraction of species with low FRET efficiency. Moreover, dynamic Photon Distribution Analysis (dynPDA) detects a decreased fraction of static FRET species (a detailed discussion follows below in the section: Multiple FRET species are needed to describe H3NtT dynamics). The sum of static species in Dyβ nucleosomes is ∼55 % in contrast to ∼25 % in mutDyβ nucleosomes (Figure 3C).
Corresponding MFD-PIE experiments and analyses were done for Eα and mutEα nucleosomes (Figure 3D and E) to study the distances between the linker DNA and the H3NtT. By changing the acceptor labeling position from the dyad axis to the linker DNA end, we can clearly demonstrate the existence of a species with a high FRET efficiency in Eα nucleosomes. The corresponding dynamic transitions lead to a broadened dynF peak (Figure 3D), which is diminished in mutEα nucleosomes (Figure 3E). We therefore conclude that this high FRET species can be attributed to an interaction of the H3NtT with the linker DNA arm which vanishes upon H2A R81E/R88E mutation. DynPDA results also show that the prevalence of the static species is decreased due to H2A R81E/R88E mutation (Figure 3F, Eα: ∼19 %, mutEα: ∼12 %). For Eα nucleosomes both fluorophores, donor and acceptor, are attached to highly dynamic parts of the nucleosome (H3 tail and linker DNA arm, respectively). Thus, the increased fraction of dynamic species of Eα in comparison to Dyβ nucleosomes can be assigned to the additional dynamics of the linker DNA.
The comparison between Dyβ and mutDyβ as well as between Eα and mutEα nucleosomes directly shows that the H3NtT dynamics are affected by the mutations within the nucleosome core which confirms the assumed long-range effects. This, in fact, is a conclusive proof of the proposed allostery between the helix α3 of H2A and H3NtT.
Structural model for H3NtT conformations and their multiple interaction modes
Based on the results of the sub-ensemble time-resolved FRET analysis combined with MD simulations and FRET screening (Figure 2C) (59), and quenching (analog to PIFE, but rhodamines are rather quenched and not enhanced (65)), we propose a structural model (Figure 4A), assuming four conformational states for each H3NtT independently. These four states can be divided into two groups based on donor dye quenching. Group I consists of three states where the donor is bright because the tail is primarily associated with DNA so that quenching is prevented (66). Group II has one state where the donor is dim because the tail is in proximity to quenching amino acid residues on the histone core (Supplementary Figure S2). To account for the distance ranges found in seTCSPC decay histogram analysis of Dyβ and mutDyβ nucleosomes, we denote the three bright FRET species in group I as: (i) compact with 〈RDA〉≈ 39 Å, (ii) compact* with 〈RDA〉≈ 58 Å and (iii) extended with 〈RDA〉≈ 64 Å. Note that all three distances fit into the first gray region defined by the MD simulations (Figure 2D). All possible combinations of tail conformers within the whole nucleosome (Figure 4C) result in multiple interaction sites with at least eight fluorescent species (Figure 4B).
As the H3NtT appeared to be highly dynamic (see section: smFRET unveils H3NtT:DNA configurations and allostery between the H2A helix α3 and H3NtT), our dynPDA model accounts for both static and dynamic FRET species. Moreover, we assume three reversible conformational transitions (Figure 4A) for each H3NtT, two with a stepwise distance increase and one leading to a dim donor state: (i) compact ↔ compact*, (ii) compact* ↔ extended and (iii) compact* ↔ protein associated/dim state. We also assume that both H3NtT (on the α- and β-side) can adopt these conformations independently. While we expect significant FRET for H3NtTα, the expected FRET efficiency of H3NtTβ is approximately zero (〈RDA〉 > 100 Å in Figure 2C and D, see Materials and Methods: Estimation of possible RDA distances from molecular dynamics trajectory). Thus, for H3NtTβ we can only distinguish between two donor states: bright and dim.
In Figure 4B, all possible combinations of the proposed H3NtT structural states are assigned to the estimated distances 〈RDA〉 (calculated by seTCSPC decay analysis) and the corresponding mean FRET efficiencies, 〈E〉. The average FRET efficiencies for species with two bright donors correspond to the arithmetical mean of two FRET efficiencies, Eα and Eβ (67). While different conformations of H3NtTβ in combination with a dark H3NtTα donor exhibit only a negligible FRET efficiency (0.02 (NoFRET)), the three bright conformers of H3NtTα in combination with a dark H3NtTβ donor result into significantly different FRET efficiencies: 0.26 (LF), 0.51 (MF) and 0.76 (HF). In this way, altogether five apparent FRET species and a completely dark species are expected (see below section: Multiple FRET species are needed to describe H3NtT dynamics) that are grouped into five average FRET efficiency levels: HF (0.85), MF (0.34, 0.43), LF (0.22, 0.18), VLF (0.12) and NoFRET (0.02). For comparison, the 〈RDA〉E distances obtained from dynPDA by a global fit assuming 5 static species are also presented in Figure 4B.
Multiple FRET species are needed to describe H3NtT dynamics
As a next step, we analyzed the dynamics of the H3NtT relative to the dyad axis of the nucleosome by dynPDA and studied the influence of the H2A R81E/R88E mutations on this. Based on the structural (Figure 4A) and the spectroscopic assignment (Figure 4B), we identified seven potential transitions (open and filled arrows in Figure 4C) between the five static FRET species identified above (blue boxes in Figure 4C) and we could exclude three transitions dyn(HF↔VLF), dyn(HF↔NoFRET) and dyn(VLF↔NoFRET). We used this general unbiased kinetic model for the dynPDA analysis in Figure 5 to address three main questions: (i) Are all seven transitions between the FRET species actually needed for a good fit of wt (green) and mutated (orange) nucleosomes? (ii) Which FRET species are involved and to which conformational states do they correspond? (iii) Which species are dynamic and which rate constants do the transitions have?
DynPDA has been especially developed recently for fitting these spiky and broad parameter histograms of single-molecule FRET measurements (56,57) because it explicitly considers the stochastic and digital nature of photon emission, background signal, spectral crosstalk and dynamic exchange between states that further broadens the histogram (further details see Material and Methods: Dynamic PDA). The recovered FRET efficiencies are directly expressed as apparent 〈RDA〉E distribution histograms (see Material and Methods: Calculation of RDA distances) for the discussion of their structural features.
To differentiate between the distinct FRET species representing different H3NtT conformers in dynPDA, we use a two-dimensional analysis approach by fitting data with distinct chemical conditions (three NaCl concentrations) and with distinct temporal resolution (data integration in three time windows of 1, 2 and 3 ms). Representative plots for Dyβ and mutDyβ nucleosomes at 100 mM NaCl and 2 nM total nucleosome concentration are shown in Figure 5A and C, respectively.
With respect to the number of FRET species, we found for both nucleosome variants that the highest fit quality (black residuals r1 in top panel of Figure 5A and C) was achieved by the dynPDA model with 5 static and 7 dynamic species. In Dyβ nucleosomes three of the static species (LF: 〈RDA〉E = 61.9 Å, VLF: 〈RDA〉E = 74.5 Å, and NoFRET: 〈RDA〉E = 98.7 Å) and only three dynamic species dyn(MF↔LF), dyn(LF↔VLF) and dyn(MF↔NoFRET) are significantly populated (Figure 5B, see also Figure 6C and E). Notwithstanding the miniscule contribution of the other four dynamic species (dyn(HF↔MF), dyn(HF↔LF), dyn(MF↔VLF), and dyn(LF↔NoFRET)), the fit quality already drops significantly when contributions of those four dynamic species are excluded from the dynPDA model (gray residuals r2 in Figure 5A and C, top panels) by setting their fractions equal to 0. Fit quality drops dramatically (light gray residuals r3 in Figure 5A and C, top panels) if all dynamic species are excluded, which corroborates the presence of significant fractions of dynamic nucleosome species seen also on the MFD plots in Figure 2.
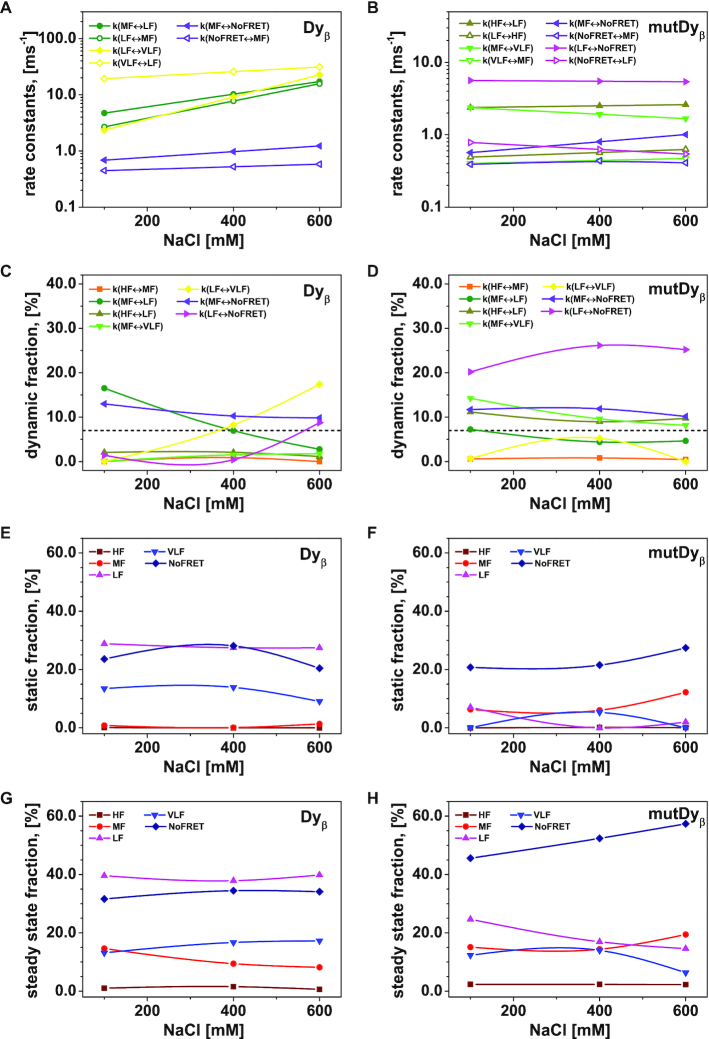
Figure 6.
The interconversion between possible H3NtT conformations depends on the NaCl concentrations and can be altered by allosteric effects. Considering different NaCl concentrations, rate constants from dynPDA fits are displayed only for dynamic species with an average fraction larger than 7% in (A) Dyβ and (B) mutDyβ nucleosomes. The fractions of dynamic species in (C) Dyβ and (D) mutDyβ nucleosomes at different NaCl concentrations are shown (the 7% limit is indicated by dashed line) together with the static species fractions in (E) Dyβ and (F) mutDyβ nucleosomes. The resulting total fractions of static states in (G) Dyβ and (H) mutDyβ nucleosomes are also presented. The dynamic fractions 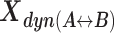 are redistributed to the limiting A and B states proportional to the residence time in each state via rate constants (kAB, kBA) as
are redistributed to the limiting A and B states proportional to the residence time in each state via rate constants (kAB, kBA) as 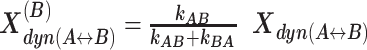 and
and 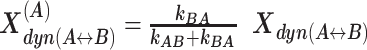 The total fractions of the static states are calculated as a sum of static fraction and contributions from all considered dynamic fractions.
The total fractions of the static states are calculated as a sum of static fraction and contributions from all considered dynamic fractions.
In conclusion, even though all transitions in Figure 4C are present, the distinct fits by dynPDA show that only certain transitions are significantly populated (>7%) and are visible as dynamic species (filled arrows in Figure 4C), which are distinct for Dyβ and mutDyβ nucleosomes.
Assigning FRET species to conformational states
To address the second question on the structural features of the FRET species, we consider the introduced structural model in Figure 4A and the corresponding assignment to FRET species in Figure 4B. From this, it is evident that the three prominent static fluorescence species (LF, VLF and NoFRET in Figure 5B) can be attributed to various conformational states of the H3NtTα. Thus, the majority of the wt H3NtTα seems to be in dynamic exchange between extended/compact* and dim states. We hypothesize that the compact* and the dim state are enabled by spontaneous DNA opening that is accompanied by a structural rearrangement of the H3 tail as previously suggested by MD simulation results by Voltz et al. (68). They proposed a turn-like structure of the H3 tail within the gap between nucleosome core and the detached DNA (68). Additionally, mononucleosomes reconstituted on the Widom 601 DNA sequence are asymmetric due to the DNA sequence, which was seen in mechanical and salt induced dissociation (13,15,42,69). We find that the dim conformational state is less favored in H3NtTβ than in H3NtTα as static MF and HF species are only sparsely populated (Figure 5B, see also Figure 4C). Hence, the dim donor state is more favorable on the less stable α-side H3NtT where the DNA opens more easily. This leads to the assumption that upon DNA opening the H3NtT is trapped within the gap between nucleosome core and the detached DNA in both the compact* and the protein associated state (dim donor state) (see Figure 4A). The extended state can be assigned to an association of the H3NtT to the linker DNA, as a high FRET species was found for Eα (Figure 3D). The middle FRET (MF) species is the most prominent one at very low salt concentration (5 mM NaCl) (Figure 5B), where nucleosomes are supposed to be in the closed conformation (D1D2A in Supplementary Figure S1A). Thus, we assume that both H3NtTs are in compact conformation.
The comparison of the normalized contributions of fitted distance distributions for Dyβ and mutDyβ nucleosomes (Figure 5B and D) shows two salient differences: (I) Different static and dynamic species are populated in mutDyβ nucleosomes as compared to wt. The most populated static species in mutDyβ are MF, LF, NoFRET together with four (dyn(HF↔LF), dyn(MF↔VLF), dyn(MF↔NoFRET), dyn(LF↔NoFRET)) out of the seven permitted dynamic species (Figure 5D, see also Figure 6D and F). (II) The dynamic species are generally more populated at expenses of the static ones in mutDyβ. This increase of H3NtT dynamics is a further confirmation of the proposed allostery between the helix α3 of H2A within the nucleosome core on the H3NtT dynamics. The H2A R81E/R88E mutations in mutDyβ nucleosomes seem to stabilize the transient MF species and simultaneously destabilize the LF and VLF species, and to significantly increase dynamic transition from LF into HF and NoFRET (dyn(HF↔LF), dyn(LF↔NoFRET)). Based on these findings, we conclude that the destabilizing effect of the H2A R81E/R88E is accompanied by an increased probability of DNA breathing/unwrapping and H3NtTs dynamics, leading to a significant loss of the extended H3NtT conformation in mutated nucleosomes (see Figure 3E).
NaCl concentration and mutations in H2A helix α3 affect conversion between H3NtT conformations
To tackle the third question on the time scale of the dynamics and the associated species, we analyzed the influence of increasing NaCl concentrations on the different FRET species of Dyβ and mutDyβ nucleosomes. An overview of the dynPDA results for 100 mM, 400 mM and 600 mM NaCl concentrations can be found in Figure 6. For Dyβ nucleosomes only three dynamic species (dyn(MF↔LF), dyn(LF↔VLF) and dyn(MF↔NoFRET)) have average fractions >7% (Figure 6C) and their rate constants are increasing with NaCl concentration (see Figure 6A). The mutDyβ nucleosomes instead exhibit four relevant dynamic species, namely dyn(HF↔LF), dyn(MF↔VLF), dyn(MF↔NoFRET) and dyn(LF↔NoFRET) (Figure 6D) and their corresponding rate constants appear to be rather stable in the chosen NaCl concentrations range (Figure 6B). The rate constants for Dyβ range from 400 to 40000 s−1 i.e. differ by a factor of ∼100. In contrast, the rate constants for mutDyβ range from 400 to 1600 s−1, and hence only differ by a factor of ∼15. Overall, the dynamic exchange processes in mutDyβ are slower than in wt nucleosomes but the dynamic population is significantly higher (75% versus 43 %).
A direct comparison between the dynamic fraction of Dyβ and mutDyβ nucleosomes (Figure 6C and D) reveals, that the largest difference can be observed for dyn(LF↔NoFRET). In Dyβ the fraction of dyn(LF↔NoFRET) is negligible up to 400 mM NaCl and is only significantly populated at 600 mM NaCl concentration, whereas it is strongly populated with a fraction of ∼ 20–25 % for mutDyβ. However, in general the dynamic fractions increase in Dyβ nucleosomes with increasing NaCl concentration, while mutDyβ nucleosomes show an opposing behavior. The increase of total static fraction in mutDyβ at 600 mM NaCl concentration (Figure 6F) coincides with the early loss of the mutated H2A-H2B dimers (c1/2 = 336 ± 3 mM (34)), which initially triggers the more dynamic behavior at low NaCl concentration (see conclusion).
In the last step, we calculated the total steady-state fraction of each FRET species as a sum of the contributions of static species plus those from all seven considered dynamic species (Figure 6G and H). The steady-state fractions of Dyβ nucleosomes remain rather constant (Figure 6G), which indicates that the H3NtT conformations are independent from the NaCl concentration in the studied range. Only the MF species drops from ∼15% at 100 mM to ∼10% with increasing NaCl concentration. As other FRET experiments showed that salt-induced nucleosome disassembly under the chosen conditions starts at NaCl concentrations above 550 mM (12,45), nucleosome integrity can be safely assumed for low NaCl concentrations (100 mM and 400 mM NaCl). Thus, we might detect some initial nucleosome disassembly at 600 mM in Dyβ nucleosomes.
However, for mutDyβ all steady-state fractions appear to be dependent on the NaCl concentration (Figure 6H). The NoFRET species fraction in mutDyβ is significantly increased (Dyβ: 30%, mutDyβ ∼ 45–55 %) and the LF species is decreased (Dyβ: ∼40%, mutDyβ: 25% to ∼15%). These findings agree well with the previous results showing that the H2A R81E/R88E strongly destabilizes the core mutDyβ nucleosomes (34) along with salt-induced release of H2A–H2B heterodimers >400 mM NaCl, so that we detect much more incomplete nucleosomes at 600 mM NaCl.
CONCLUSION
Compaction into higher genome structures and gene accessibility is orchestrated by assembly and disassembly of nucleosomes. The structural details and kinetic parameters of nucleosome disassembly have been widely studied (12–14,24,38,41,42,70). Even though, the physiological importance of the H3NtT for maintaining nucleosome stability (27,35,36,71) and its role as a target site for posttranslational modifications (72–75) has been shown, H3NtT interactions and its dynamics during nucleosome disassembly remained unsolved. Here, we systematically studied proximity changes between the H3NtT and certain positions on either the nucleosomal inner DNA gyre or the linker DNA during NaCl induced disassembly. Thus, we could obtain some answers to the initially raised questions related to the H3NtT:
With respect to the localization of H3NtT, we revealed that the wt H3NtT has multiple interaction modes with at least four distinguishable configurations in which they may arrest on the millisecond time scale (Figure 4C). Three of these conformations are DNA associated and one is considered as histone protein associated. The dynamic properties of H3NtT are inconsistent with the fast ns-chain dynamics characteristic for a free and mainly unstructured protein chain (76). Thus, we conclude that the tail, as a whole, is mainly not free and is located leastwise partially within the FRET resolvable distance from the nucleosomal DNA. The found huge dynamic range of timescales ranging from quasi static (on the ms time scale) to highly dynamic species (down to 10 μs) is indicative for a rich and complex energy landscape with multiple interaction sites. With respect to the whole nucleosome with two H3NtTs, we observe at least eight fluorescent species (Figure 4B), which reflect the intercombination of tail configurations. It is important to note that only certain dynamic transitions between these conformations were detectable (Figure 4C).
Importantly, the population proportions are influenced by the ionic conditions and internal modifications of the nucleosomes. Mutations within the H2A helix α3 alter the fraction of dynamic transitions, while the possible conformations are not sensitive to the mutation. The importance of the H2A helix α3 for nucleosome stability was first predicted by MD simulations on H3 tailless nucleosomes (27) and confirmed by FRET experiments, revealing a destabilizing effect of charge-modifying mutations within the helix α3 (34). Notably, this charge-modifying mutation, namely H2A R81E/R88E, is not only affecting stability (34) of the nucleosome core and enhancing the asymmetry of the linker DNA unwrapping (77) but is also accelerating the dynamics of the H3 tail. This indicates that the multiple interaction modes of H3NtT are subject to allosteric effects at a distance of >2–3 nm from the mutation. A possible transmission pathway might be that the mutation abolishes several stable hydrogen bonds with the surrounding residues (34) allowing higher flexibility of the tail. As suggested by Biswas et al. (78) alternative structures – resulting from histone variants, mutations or PTMs – were shown to be of key relevance to our understanding of nucleosome (dis)assembly pathways (12,13,34).
Finally, we elucidate how the nucleosome core affects H3NtT configuration and its dynamics by studying the effects of increasing NaCl concentrations, which is a valuable approach to study the effect of small influences on the nucleosome structure: sites (79) and kinetics (42) of DNA release from the core particle, the origin of histones (41), single histone mutations (34) or PMTs (80), which could not be detected otherwise. Therefore we inspected the NaCl-induced distance changes during the nucleosome disassembly process from different perspectives through systematic variation of labeling positions on the nucleosome core and the nucleosomal DNA that we monitored over the past decades. To this end, NaCl concentrations of 5 mM to 1.2 M are used to cover not only the physiologically important range but also higher concentrations, which may reveal potential in vivo transitions as well. In Figure 7 we combine our observations presented here with earlier results (12,13) into a comprehensive scheme of nucleosome disassembly. All results were obtained from freely diffusing mononucleosomes (concentration of 300 pM to 2 nM) reconstituted on the asymmetric Widom 601 DNA sequence and are subject to change with DNA sequences, showing a delicate dynamic equilibrium of tail and core particle conformations easily being influenced by NaCl and mutations.
Figure 7.
Comprehensive nucleosome disassembly scheme including the multiple interaction modes of the H3NtT. Considering similarly reconstituted nucleosomes with different dye labeling positions, this scheme is based on disassembly steps that were observed under similar conditions. This comprehensive scheme summarizes consistent results from: [a] this paper in Fig. 1B and D, [b] Ref. (13), [c] Ref. (12), and [d] so far unpublished data (K. Tóth). The nomenclature of the labeled constructs refers to the position of the donor and the acceptor. H2B: labeled at T112C, H3: labeled at H3 K9C, H4: labeled at H4 E63C, E: labeled at the end of the DNA, Dy: labeled close to the dyad axis (either −9 bp or +21 bp away from the dyad axis), I: labeled internally (either at +41 bp and −53 bp away from the dyad axis). α- and β-side refer to the two halves of the nucleosome (see Material and Methods). c1/2-values correspond to NaCl concentrations where the averaged proximity ratio P reaches 50% of the corresponding step height. The transition width b was calculated from the sigmoidal fit that is related to the slope at the respective inflection point (see Equation (2)). Trackable disassembly steps are visualized in the last column. The transparent green clouds indicate the accessible space of the H3NtTα and the black crosses point to the four proposed conformational state positions of the donor dye on it. The opening of the linker DNA can be detected in the dynamic octasome (Eβ–Eα), but the DNA is not yet significantly unwrapped. The first prominent event is the α-dimer release (H2Bα–Dyα) that results in the formation of dynamic hexasomes. Further NaCl increase leads to a stepwise asymmetric unwrapping of the DNA ends: starting from the α-side (Dyβ–Eα). Under the same conditions, we observe the weakening of the H3 tail linker DNA interaction (H3–Eα) followed by loosening of the β side (Dyα-Eβ). Next, DNA opening within the hexasome (Iβ-Iα) together with the weakening of the H3 tail inner DNA interaction (H3-Dyα, H3-Dyβ) and formation of the tetrasome with extended DNA through release of the second dimer (H2Bβ–Dyα) occurs. The final step is the release of the tetramer (H4–Dyα).
Taken together, we propose the following model with a unified nomenclature for the location of the donor/acceptor positions (D-A) monitoring the transition. The NaCl induced nucleosome disassembly starts with a dynamic octasome (Eβ–Eα) in which the dimer:tetramer interface opens at the weaker α-side into a metastable intermediate that is in rapid equilibrium with a conformation having a disrupted dimer:tetramer interface at the β-side (13). This process is coupled to nucleosome breathing, i.e. the linker DNA opens and closes dynamically but is not yet significantly unwrapped. In this NaCl regime no significant change in dynamics of the H3NtT were detected, which indicates that the H3NtT is following the movements of the DNA. The disassembly process proceeds with the release of the α-dimer (H2Bα–Dyα) that results in the formation of dynamic hexasomes (13). Further NaCl increase leads to weakening of the H3NtT:linker DNA interaction (H3–Eα) that is accompanied by an increase in the dynamics of the H3NtT probed at the dyad (H3-Dyβ) (Figure 1). Almost simultaneously a stepwise unwrapping of the α-DNA end (DyβEα) is detectable, indicating that weakening of the H3NtT:linker DNA contact facilitates unwrapping of the DNA α-end. The asymmetric DNA opening continues with unwrapping of the DNA β-end (Dyα–Eβ) followed by an internal DNA loosening on the β-side (Iβ–Iα) and a coupled reduction of the H3 tail inner DNA interaction (H3–Dyα,β) within the hexasome. The subsequent release of the second dimer (H2Bβ–Dyα) leads to the formation of the tetrasome. The disassembly process is completed by the release of the tetramer (H4–Dyα) (12).
This comprehensive nucleosome disassembly scheme unveils that the changes in H3NtT configurations coincide with two major steps of the nucleosome disassembly process: (I) unwrapping of the α-DNA end and (II) weakening of the internal DNA on the β-side. These findings reveal that the H3NtT is indeed following the movements of the DNA and is thereby anchoring the linker DNA. This confirms the suggested role of the H3NtTs as ‘close pins’ that traps the DNA against the histone core (33). Mutations in the histone core (such as the mutant (R81E/R88E) of histone H2A) can be sensed by the H3-tail in an allosteric manner leading to a ‘loss of function’ of the H3 tail that is comparable to the in vivo observed destabilization of nucleosomes due to enzymatic cleavage of the H3NtT (81,82) and to the effect of PTMs (16–18,83).
In conclusion, our FRET-based approach can be used to complement imaging and scattering methods to interrogate the complex interplay between histone variants, mutations and PTMs on the stability and dynamics of the nucleosomal core and the histone tails.
DATA AVAILABILITY
The datasets generated and/or analyzed during the current study are available from the corresponding authors on reasonable request.
Supplementary Material
ACKNOWLEDGEMENTS
We dedicate this contribution to the memory of Jörg Langowski, a brilliant pioneer in studying chromatin in silico, in vitro and in live cells. He had the courage to follow his heart and intuition in life and research. The authors thank Anja Riedel, Jana Tünnermann and Christina Schneider for conducting initial FRET experiments, Ruihan Zhang for providing the MD trajectory.
Author contributions: K.L. designed, conducted and analyzed biochemical and biophysical experiments, prepared Figures 1A, 4 and 7. S.F. performed and analyzed smFRET experiments, prepared Figures 2, 4–6, Supplementary Tables S2–S3 and Figures S1–S3 and S5. R.K. analyzed data and prepared Figure 1B–D and Supplementary Figure S4 and Table S1. M.D. analyzed the trajectories by our FPS toolkit to compute interdye distances (Figure 2C, D). All authors wrote the manuscript and supplementary information. K.T., J.L. and C.A.M.S. supervised the work.
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
FUNDING
K.L. acknowledges support by the German-Israeli Helmholtz Graduate School for Cancer Research, the Heidelberg Biosciences International Graduate School and the DFG [Le 3910/2-1]; DFG grants [La 500/18-1 to J.L., Se 1195/15-1 to C.A.M.S.]; European Research Council through the Advanced Grant 2014 hybridFRET [671208 to C.A.M.S.]. Funding for open access charge: H2020 European Research Council Advanced Grant [2014, 671208].
Conflict of interest statement. None declared.
REFERENCES
- 1. Davey C.A., Sargent D.F., Luger K., Maeder A.W., Richmond T.J.. Solvent mediated interactions in the structure of the nucleosome core particle at 1.9 Å resolution. J. Mol. Biol. 2002; 319:1097–1113. [DOI] [PubMed] [Google Scholar]
- 2. Kornberg R.D. Chromatin structure: a repeating unit of histones and DNA. Science. 1974; 184:868–871. [DOI] [PubMed] [Google Scholar]
- 3. Luger K., Mäder A.W., Richmond R.K., Sargent D.F., Richmond T.J.. Crystal structure of the nucleosome core particle at 2.8 Å resolution. Nature. 1997; 389:251–260. [DOI] [PubMed] [Google Scholar]
- 4. Olins A.L., Olins D.E.. Spheroid chromatin units (ν bodies). Science. 1974; 183:330–332. [DOI] [PubMed] [Google Scholar]
- 5. Kilic S., Felekyan S., Doroshenko O., Boichenko I., Dimura M., Vardanyan H., Bryan L.C., Arya G., Seidel C.A.M., Fierz B.. Single-molecule FRET reveals multiscale chromatin dynamics modulated by HP1α. Nat. Commun. 2018; 9:235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Schalch T., Duda S., Sargent D.F., Richmond T.J.. X-ray structure of a tetranucleosome and its implications for the chromatin fibre. Nature. 2005; 436:138–141. [DOI] [PubMed] [Google Scholar]
- 7. Song F., Chen P., Sun D., Wang M., Dong L., Liang D., Xu R.M., Zhu P., Li G.. Cryo-EM study of the chromatin fiber reveals a double helix twisted by tetranucleosomal units. Science. 2014; 344:376–380. [DOI] [PubMed] [Google Scholar]
- 8. Mersfelder E.L., Parthun M.R.. The tale beyond the tail: Histone core domain modifications and the regulation of chromatin structure. Nucleic Acids Res. 2006; 34:2653–2662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Erler J., Zhang R., Petridis L., Cheng X., Smith J.C., Langowski J.. The role of histone tails in the nucleosome: a computational study. Biophys. J. 2014; 107:2911–2922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Kouzarides T. Chromatin modifications and their function. Cell. 2007; 128:693–705. [DOI] [PubMed] [Google Scholar]
- 11. Peterson C.L., Laniel M.-A.. Histones and histone modifications. Curr. Biol. 2004; 14:R546–R551. [DOI] [PubMed] [Google Scholar]
- 12. Böhm V., Hieb A.R., Andrews A.J., Gansen A., Rocker A., Tóth K., Luger K., Langowski J.. Nucleosome accessibility governed by the dimer/tetramer interface. Nucleic Acids Res. 2011; 39:3093–3102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Gansen A., Felekyan S., Kühnemuth R., Lehmann K., Tóth K., Seidel C.A.M., Langowski J.. High precision FRET studies reveal reversible transitions in nucleosomes between microseconds and minutes. Nat. Commun. 2018; 9:4628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Gansen A., Valeri A., Hauger F., Felekyan S., Kalinin S., Tóth K., Langowski J., Seidel C.A.M.. Nucleosome disassembly intermediates characterized by single-molecule FRET. Proc. Natl. Acad. Sci. U.S.A. 2009; 106:15308–15313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Ngo T.T.M., Zhang Q.C., Zhou R.B., Yodh J.G., Ha T.. Asymmetric unwrapping of nucleosomes under tension directed by DNA local flexibility. Cell. 2015; 160:1135–1144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Bowman G.D., Poirier M.G.. Post-translational modifications of histones that influence nucleosome dynamics. Chem. Rev. 2015; 115:2274–2295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Tóth K., Brun N., Langowski J.. Chromatin compaction at the mononucleosome level. Biochemistry. 2006; 45:1591–1598. [DOI] [PubMed] [Google Scholar]
- 18. Zhou K.D., Gaullier G., Luger K.. Nucleosome structure and dynamics are coming of age. Nat. Struct. Mol. Biol. 2019; 26:3–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Liu H.G., Duan Y.. Effects of posttranslational modifications on the structure and dynamics of histone H3N-terminal peptide. Biophys. J. 2008; 94:4579–4585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Morrison E.A., Bowerman S., Sylvers K.L., Wereszczynski J., Musselman C.A.. The conformation of the histone H3 tail inhibits association of the BPTF PHD finger with the nucleosome. eLife. 2018; 7:e31481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Potoyan D.A., Papoian G.A.. Energy landscape analyses of disordered histone tails reveal special organization of their conformational dynamics. J. Am. Chem. Soc. 2011; 133:7405–7415. [DOI] [PubMed] [Google Scholar]
- 22. Banères J.L., Martin A., Parello J.. The N tails of histones H3 and H4 adopt a highly structured conformation in the nucleosome. J. Mol. Biol. 1997; 273:503–508. [DOI] [PubMed] [Google Scholar]
- 23. Ikebe J., Sakuraba S., Kono H.. H3 histone tail conformation within the nucleosome and the impact of K14 acetylation studied using enhanced sampling simulation. PLoS Comput. Biol. 2016; 12:e1004788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Li Z., Kono H.. Distinct roles of histone H3 and H2A tails in nucleosome stability. Sci. Rep. 2016; 6:31437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Shaytan A.K., Armeev G.A., Goncearenco A., Zhurkin V.B., Landsman D., Panchenko A.R.. Coupling between histone conformations and DNA geometry in nucleosomes on a microsecond timescale: atomistic insights into nucleosome functions. J. Mol. Biol. 2016; 428:221–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. du Preez L.L., Patterton H.-G.. Kundu TK. Epigenetics: Development and Disease. 2013; Netherlands: Springer; 37–55. [Google Scholar]
- 27. Biswas M., Voltz K., Smith J.C., Langowski J.. Role of histone tails in structural stability of the nucleosome. PLoS Comput. Biol. 2011; 7:2–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Kastenholz M.A., Hünenberger P.H.. Computation of methodology-independent ionic solvation free energies from molecular simulations. II. The hydration free energy of the sodium cation. J. Chem. Phys. 2006; 124:224501. [DOI] [PubMed] [Google Scholar]
- 29. Mangenot S., Leforestier A., Vachette P., Durand D., Livolant F.. Salt-induced conformation and interaction changes of nucleosome core particles. Biophys. J. 2002; 82:345–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Roccatano D., Barthel A., Zacharias M.. Structural flexibility of the nucleosome core particle at atomic resolution studied by molecular dynamics simulation. Biopolymers. 2007; 85:407–421. [DOI] [PubMed] [Google Scholar]
- 31. Angelov D., Vitolo J.M., Mutskov V., Dimitrov S., Hayes J.J.. Preferential interaction of the core histone tail domains with linker DNA. Proc. Natl. Acad. Sci. U.S.A. 2001; 98:6599–6604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Stützer A., Liokatis S., Kiesel A., Schwarzer D., Sprangers R., Söding J., Selenko P., Fischle W.. Modulations of DNA contacts by linker histones and post-translational modifications determine the mobility and modifiability of nucleosomal H3 tails. Mol. Cell. 2016; 61:247–259. [DOI] [PubMed] [Google Scholar]
- 33. Andresen K., Jimenez-Useche I., Howell S.C., Yuan C., Qiu X.. Solution scattering and FRET studies on nucleosomes reveal DNA unwrapping effects of H3 and H4 tail removal. PLoS One. 2013; 8:e78587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Lehmann K., Zhang R., Schwarz N., Gansen A., Mücke N., Langowski J., Tóth K.. Effects of charge-modifying mutations in histone H2A α3-domain on nucleosome stability assessed by single-pair FRET and MD simulations. Sci. Rep. 2017; 7:13303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Nurse N.P., Jimenez-Useche I., Smith I.T., Yuan C.. Clipping of flexible tails of histones H3 and H4 affects the structure and dynamics of the nucleosome. Biophys. J. 2013; 104:1081–1088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Iwasaki W., Miya Y., Horikoshi N., Osakabe A., Taguchi H., Tachiwana H., Shibata T., Kagawa W., Kurumizaka H.. Contribution of histone N-terminal tails to the structure and stability of nucleosomes. FEBS Open Biol. 2013; 3:363–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Lowary P.T., Widom J.. Nucleosome packaging and nucleosome positioning of genomic DNA. Proc. Natl. Acad. Sci. U.S.A. 1997; 94:1183–1188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Kim J., Wei S., Lee J., Yue H., Lee T.H.. Single-molecule observation reveals spontaneous protein dynamics in the nucleosome. J. Phys. Chem. B. 2016; 120:8925–8931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Koopmans W.J.A., Brehm A., Logie C., Schmidt T., Van Noort J.. Single-pair FRET microscopy reveals mononucleosome dynamics. J. Fluoresc. 2007; 17:785–795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Lovullo D., Daniel D., Yodh J., Lohr D., Woodbury N.W.. A fluorescence resonance energy transfer-based probe to monitor nucleosome structure. Anal. Biochem. 2005; 341:165–172. [DOI] [PubMed] [Google Scholar]
- 41. Tóth K., Böhm V., Sellmann C., Danner M., Hanne J., Berg M., Barz I., Gansen A., Langowski J.. Histone- and DNA sequence-dependent stability of nucleosomes studied by single-pair FRET. Cytometry A. 2013; 83:839–846. [DOI] [PubMed] [Google Scholar]
- 42. Chen Y., Tokuda J.M., Topping T., Meisburger S.P., Pabit S.A., Gloss L.M., Pollack L.. Asymmetric unwrapping of nucleosomal DNA propagates asymmetric opening and dissociation of the histone core. Proc. Natl. Acad. Sci. U.S.A. 2017; 114:334–339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Lowary P.T., Widom J.. New DNA sequence rules for high affinity binding to histone octamer and sequence-directed nucleosome positioning. J. Mol. Biol. 1998; 276:19–42. [DOI] [PubMed] [Google Scholar]
- 44. Luger K., Rechsteiner T.J., Richmond T.J.. Expression and purification of recombinant histones and nucleosome reconstitution. Methods Mol. Biol. 1999; 119:1–16. [DOI] [PubMed] [Google Scholar]
- 45. Gansen A., Hieb A.R., Böhm V., Tóth K., Langowski J.. Closing the gap between single molecule and bulk FRET analysis of nucleosomes. PLoS One. 2013; 8:e57018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Kudryavtsev V., Sikor M., Kalinin S., Mokranjac D., Seidel C.A.M., Lamb D.C.. Combining MFD and PIE for accurate single-pair Förster resonance energy transfer measurements. Chem. Phys. Chem. 2012; 13:1060–1078. [DOI] [PubMed] [Google Scholar]
- 47. Al-Soufi W., Reija B., Novo M., Felekyan S., Kühnemuth R., Seidel C.A.M.. Fluorescence correlation spectroscopy, a tool to investigate supramolecular dynamics: inclusion complexes of pyronines with cyclodextrin. J. Am. Chem. Soc. 2005; 127:8775–8784. [DOI] [PubMed] [Google Scholar]
- 48. Eggeling C., Berger S., Brand L., Fries J.R., Schaffer J., Volkmer A., Seidel C.A.M.. Data registration and selective single-molecule analysis using multi-parameter fluorescence detection. J. Biotechnol. 2001; 86:163–180. [DOI] [PubMed] [Google Scholar]
- 49. Felekyan S., Kühnemuth R., Kudryavtsev V., Sandhagen C., Becker W., Seidel C.A.M.. Full correlation from picoseconds to seconds by time-resolved and time-correlated single photon detection. Rev. Sci. Instrum. 2005; 76:1–14. [Google Scholar]
- 50. Kühnemuth R., Seidel C.A.M.. Principles of single molecule multiparameter fluorescence spectroscopy. Single Mol. 2001; 2:251–254. [Google Scholar]
- 51. Widengren J., Kudryavtsev V., Antonik M., Berger S., Gerken M., Seidel C.A.M.. Single-molecule detection and identification of multiple species by multiparameter fluorescence detection. Anal. Chem. 2006; 78:2039–2050. [DOI] [PubMed] [Google Scholar]
- 52. Kalinin S., Sisamakis E., Magennis S.W., Felekyan S., Seidel C.A.M.. On the origin of broadening of single-molecule FRET efficiency distributions beyond shot noise limits. J. Phys. Chem. B. 2010; 114:6197–6206. [DOI] [PubMed] [Google Scholar]
- 53. Lee N.K., Kapanidis A.N., Wang Y., Michalet X., Mukhopadhyay J., Ebright R.H., Weiss S.. Accurate FRET measurements within single diffusing biomolecules using alternating-laser excitation. Biophys. J. 2005; 88:2939–2953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Hellenkamp B., Schmid S., Doroshenko O., Opanasyuk O., Kühnemuth R., Adariani S.R., Ambrose B., Aznauryan M., Barth A., Birkedal V. et al.. Precision and accuracy of single-molecule FRET measurements-a multi-laboratory benchmark study. Nat. Methods. 2018; 15:669–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Peulen T.O., Opanasyuk O., Seidel C.A.M.. Combining graphical and analytical methods with molecular simulations to analyze time-resolved FRET measurements of labeled macromolecules accurately. J. Phys. Chem. B. 2017; 121:8211–8241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56. Kalinin S., Valeri A., Antonik M., Felekyan S., Seidel C.A.M.. Detection of structural dynamics by FRET: A photon distribution and fluorescence lifetime analysis of systems with multiple states. J. Phys. Chem. B. 2010; 114:7983–7995. [DOI] [PubMed] [Google Scholar]
- 57. Antonik M., Felekyan S., Gaiduk A., Seidel C.A.M.. Separating structural heterogeneities from stochastic variations in fluorescence resonance energy transfer distributions via photon distribution analysis. J. Phys. Chem. B. 2006; 110:6970–6978. [DOI] [PubMed] [Google Scholar]
- 58. Song B., Cho J.-H., Raleigh D.P.. Ionic-strength-dependent effects in protein folding: analysis of rate equilibrium free-energy relationships and their interpretation. Biochemistry. 2007; 46:14206–14214. [DOI] [PubMed] [Google Scholar]
- 59. Kalinin S., Peulen T., Sindbert S., Rothwell P.J., Berger S., Restle T., Goody R.S., Gohlke H., Seidel C.A.M.. A toolkit and benchmark study for FRET-restrained high-precision structural modeling. Nat. Methods. 2012; 9:1218–1227. [DOI] [PubMed] [Google Scholar]
- 60. Wang D., Ulyanov N.B., Zhurkin V.B.. Sequence-dependent kink-and-slide deformations of nucleosomal DNA facilitated by histone arginines bound in the minor groove. J. Biomol. Struct. Dyn. 2010; 27:843–859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Vasudevan D., Chua E.Y.D., Davey C.A.. Crystal structures of nucleosome core particles containing the ‘601’ strong positioning sequence. J. Mol. Biol. 2010; 403:1–10. [DOI] [PubMed] [Google Scholar]
- 62. Blosser T.R., Yang J.G., Stone M.D., Narlikar G.J., Zhuang X.. Dynamics of nucleosome remodelling by individual ACF complexes. Nature. 2009; 462:1022–1027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Chen J., Miller A., Kirchmaier A.L., Irudayaraj J.M.K.. Single-molecule tools elucidate H2A.Z nucleosome composition. J. Cell Sci. 2012; 125:2954–2964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Gansen A., Tóth K., Schwarz N., Langowski J.. Structural variability of nucleosomes detected by single-pair Förster resonance energy transfer: Histone acetylation, sequence variation, and salt effects. J. Phys. Chem. B. 2009; 113:2604–2613. [DOI] [PubMed] [Google Scholar]
- 65. Hwang H., Myong S.. Protein induced fluorescence enhancement (PIFE) for probing protein-nucleic acid interactions. Chem. Soc. Rev. 2014; 43:1221–1229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Sindbert S., Kalinin S., Nguyen H., Kienzler A., Clima L., Bannwarth W., Appel B., Müller S., Seidel C.A.M.. Accurate distance determination of nucleic acids via Förster resonance energy transfer: implications of dye linker length and rigidity. J. Am. Chem. Soc. 2011; 133:2463–2480. [DOI] [PubMed] [Google Scholar]
- 67. Corry B., Jayatilaka D., Rigby P.. A flexible approach to the calculation of resonance energy transfer efficiency between multiple donors and acceptors in complex geometries. Biophys. J. 2005; 89:3822–3836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Voltz K., Trylska J., Calimet N., Smith J.C., Langowski J.. Unwrapping of nucleosomal DNA ends: a multiscale molecular dynamics study. Biophys. J. 2012; 102:849–858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Chodaparambil J.V., Edayathumangalam R.S., Bao Y., Park Y.J., Luger K., McGinty R.K., Tan S.. Nucleosome structure and function. Chem. Rev. 2015; 115:2255–2273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Rhee H.S., Bataille A.R., Zhang L., Pugh B.F.. Subnucleosomal structures and nucleosome asymmetry across a genome. Cell. 2014; 159:1377–1388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71. Ferreira H., Somers J., Webster R., Flaus A., Owen-Hughes T.. Histone tails and the H3 αN helix regulate nucleosome mobility and stability. Mol. Cell. Biol. 2007; 27:4037–4048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72. Melcher M., Schmid M., Aagaard L., Selenko P., Laible G., Jenuwein T.. Structure-function analysis of SUV39H1 reveals a dominant role in heterochromatin organization, chromosome segregation, and mitotic progression. Mol. Cell Biol. 2000; 20:3728–3741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Nakayama J., Rice J.C., Strahl B.D., Allis C.D., Grewal S.I.. Role of histone H3 lysine 9 methylation in epigenetic control of heterochromatin assembly. Science. 2001; 292:110–113. [DOI] [PubMed] [Google Scholar]
- 74. Rea S., Eisenhaber F., O’Carroll D., Strahl B.D., Sun Z.W., Schmid M., Opravil S., Mechtier K., Ponting C.P., Allis C.D. et al.. Regulation of chromatin structure by site-specific histone H3 methyltransferases. Nature. 2000; 406:593–599. [DOI] [PubMed] [Google Scholar]
- 75. Tachibana M., Sugimoto K., Fukushima T., Shinkai Y.. SET domain-containing protein, G9a, is a novel lysine-preferring mammalian histone methyltransferase with hyperactivity and specific selectivity to lysines 9 and 27 of histone H3. J. Biol. Chem. 2001; 276:25309–25317. [DOI] [PubMed] [Google Scholar]
- 76. Brucale M., Schuler B., Samori B.. Single-molecule studies of intrinsically disordered proteins. Chem. Rev. 2014; 114:3281–3317. [DOI] [PubMed] [Google Scholar]
- 77. Würtz M., Aumiller D., Gundelwein L., Jung P., Schütz C., Lehmann K., Tóth K., Rohr K.. DNA accessibility of chromatosomes quantified by automated image analysis of AFM data. Sci. Rep. 2019; 9:12788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78. Biswas M., Langowski J., Bishop T.C.. Atomistic simulations of nucleosomes. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2013; 3:378–392. [Google Scholar]
- 79. Yager T.D., McMurray C.T., van Holde K.E.. Salt-induced release of DNA from nucleosome core particles. Biochemistry. 1989; 28:2271–2281. [DOI] [PubMed] [Google Scholar]
- 80. Gansen A., Tóth K., Schwarz N., Langowski J.. Opposing roles of H3-and H4-acetylation in the regulation of nucleosome structure-a FRET study. Nucleic. Acids. Res. 2015; 43:1433–1443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81. Santos-Rosa H., Kirmizis A., Nelson C., Bartke T., Saksouk N., Cote J., Kouzarides T.. Histone H3 tail clipping regulates gene expression. Nat. Struct. Mol. Biol. 2009; 16:17–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82. Yi S.J., Kim K.. Histone tail cleavage as a novel epigenetic regulatory mechanism for gene expression. BMB Rep. 2018; 51:211–218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83. Bussiek M., Tóth K., Schwarz N., Langowski J.. Trinucleosome compaction studied by fluorescence energy transfer and scanning force microscopy. Biochemistry. 2006; 45:10838–10846. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets generated and/or analyzed during the current study are available from the corresponding authors on reasonable request.