Greenhouse gas emissions from lakes and impoundments: upscaling in the face of global change

Abstract

Lakes and impoundments are important sources of greenhouse gases (GHG: i.e., CO₂, CH₄, N₂O), yet global emission estimates are based on regionally-biased averages and elementary upscaling. We assembled the largest global dataset to date on emission rates of all three GHGs and found they covary with lake size and trophic state. Fitted models were upscaled to estimate global emission using global lake size inventories and a remotely-sensed global lake productivity distribution. Traditional upscaling approaches overestimated CO₂ and N₂O emission but underestimated CH₄ by half. Our upscaled size-productivity weighted estimates (1.25–2.30 Pg of CO₂-equivalents annually) are nearly 20% of global CO₂ fossil fuel emission with ~75% of the climate impact due to CH₄. Moderate global increases in eutrophication could translate to 5–40% increases in the GHG effects in the atmosphere, adding the equivalent effect of another 13% of fossil fuel combustion or an effect equal to GHG emissions from current land use change.

Introduction

Lakes and other surface waters are globally significant emitters of CO_2, CH₄, and N₂O to the atmosphere (Cole et al. 2007; Tranvik et al. 2009; Bastviken et al. 2011; Deemer et al. 2016; Soued et al. 2016). Accurate estimates of greenhouse gas (GHG) fluxes to and from the atmosphere are important to understanding the global carbon (C) budget as well as making projections of the trajectory of climate change. Improvements in sensor technology (e.g., Eugster et al. 2011; Gonzalez-valencia et al. 2014; Maeck et al. 2014; Delwiche et al. 2015) and the use of statistically robust survey designs (Beaulieu et al. 2016; Wik et al. 2016) have improved the accuracy of GHG emission rate measurements in aquatic systems over the last decade. These advancements and the increasing number of observations made around the world have allowed limnologists to identify environmental variables that control GHG emission rates across a broad range of spatial scales. Despite improvements in our understanding of GHG emission rates and factors influencing them, this information has not been combined to inform estimates of global GHG emissions from lakes and impoundments (hereafter referred to as ‘lakes’).

Most traditional analyses of the global role of lakes as sources of GHGs to the atmosphere have scaled local or regional measurements to the globe by multiplying an average emission rate by the global area covered by lentic systems (Cole et al. 2007; Tranvik et al. 2009; Bastviken et al. 2011). For example, Tranvik et al. (2009) multiplied an average rate of CO₂ emission from lakes and impoundments, as determined from a literature review, by the global area of those systems (Downing et al. 2006) to calculate a global emission rate of 0.81 Pg C y⁻¹. Bastviken et al. (2011) attempted a similar analysis for CH₄ emission by calculating mean emission rates and lentic area within four latitude zones. This global analysis indicated lake and impoundment CH₄ emissions of 69 Tg y⁻¹ of CH₄-C or about 0.85 Pg of C as CO₂ emission equivalents (using a 34-times conversion factor for a 100-yr time-scale; Myhre et al. 2013). N₂O is another, more potent GHG emitted from aquatic systems. Soued et al. (2015) offered a first-order approximation of the global emission of N₂O by all inland waters using a similar traditional upscaling approach and suggested that lakes and impoundments could be emitting 0.63 Tg of N₂O-N per year. In CO₂ equivalents, this is approximately 0.08 Pg of C (using a 298 conversion factor for a 100-yr time-scale; Myhre et al. 2013).

Estimates of global GHG emissions based on this ‘traditional’ average emission-extrapolated approach can be strongly biased if the emission rates are not derived from a representative sample of lakes, however. For example, estimates of CH₄ flux from northern latitude lakes (i.e., Wik et al. 2016) were substantially reduced when more recent data from large glacial lakes in Alaska were included (Stackpoole et al. 2017). Moreover, studies are increasingly finding that aquatic GHG fluxes are related to certain local drivers, which could be used to improve upscaled emission estimates. For example, Lapierre et al. (2017) found that 31% of summer CO₂ concentration variability in lakes of the United States is explained by chlorophyll a (chla), a proxy for system productivity, as well as color and alkalinity. Therefore, traditional regional estimates of CO₂ emissions from these systems would be biased if the average value was not derived from lakes with a distribution of those variables similar to that of all lakes in the U.S. Similarly, Rasilo et al. (2015) report that diffusive CH₄ emission rates are inversely related to lake size in boreal Canada. Estimates of diffusive CH₄ emissions for lakes across this biome would therefore be biased unless the published data were derived from a collection of lakes with a size distribution that mirrors the true size distribution of lakes in the boreal landscape. Ultimately, upscaling with models that explicitly incorporate such environmental drivers (i.e., size and productivity) is likely to produce more accurate regional or global emission estimates (see Downing 2009).

A longstanding challenge to upscaling based on environmental covariates is the limited availability of spatially explicit data sets on lake characteristics at the global scale. Recent advances in satellite imagery are beginning to address this issue, however. For example, Sayers et al. (2015) report the frequency distribution of chla in 80,000 lakes around the world, covering the northern and southern hemispheres. Since some metrics of productivity, such as chla and nutrients, are potentially good predictors of CO₂, CH₄ and N₂O in lakes and impoundments (Beaulieu et al. 2015; Deemer et al. 2016; DelSontro et al. 2016; Lapierre et al. 2017), the Sayers et al. (2015) data set provide a powerful tool for upscaling GHG emission rates. Similarly, improved satellite imagery and analytical approaches have allowed for several estimates of the distribution of lake and impoundment sizes across the globe (Downing et al. 2006; Verpoorter et al. 2014; Messager et al. 2016).

In this research, we address several gaps in our current knowledge of GHG emissions from lakes and impoundments. First, we estimate GHG emissions from these systems by combining data on the global distribution of lake size and productivity with new empirical models linking GHG emission rates with these variables. Second, we provide global estimates of all three major GHGs (i.e., CO₂, CH₄, and N₂O). This is important because, although they may be reported less frequently than CO₂ fluxes, N₂O and CH₄ are more potent GHGs. On a 100-year time horizon, N₂O and CH₄ have ~265- and 28-times the effect of CO₂ on atmospheric warming, respectively, and these values increase to 298 and 34 when indirect effects of these GHGs on the climate are considered (Myhre et al. 2013). Finally, we use this new analytical approach to assess the sensitivity of lentic GHG emission to expected future changes in lake and impoundment productivity.

Methods

The general approach was to perform a secondary analysis (sensu Kiecolt and Nathan 1985) of GHG fluxes and the factors influencing them (i.e., lake size and trophic status) and to upscale these relationships to global estimates following Downing (2009), while using a global, joint lake size and productivity distribution. Although several global size distributions have been published (Downing et al. 2006; Verpoorter et al. 2014; Messager et al. 2016), global productivity distributions are less well constrained so we derived a distribution using remotely sensed lake chla data from the best available source (Sayers et al. 2015).

Data collection

We collected previously published GHG flux and ancillary data from 223 different studies for a total of 8233 system measurements from at least 54 countries (Table S1 in Supporting Information (SI)). About 7637 systems were natural lakes and 596 were considered impoundments of some type. More data were available for CO₂ than for CH₄ and N₂O (7824 unique systems for CO₂ versus 561, 144 and 166 with diffusive, ebullitive and total CH₄ estimates, respectively, and 309 for N₂O). Because we aimed to upscale based on the premise that productivity and lake-size impact emissions, we also collected nutrient (total phosphorus (TP) and total nitrogen (TN)), chla, and surface area (SA) data when available. The vast majority of collected water quality and gas flux measurements were made during the warm, open water season and fluxes were in daily areal units of mg m⁻² d⁻¹. Flux data, sources, and ancillary variables are available in the SI or at figshare.com/s/c6a4133f3595b67a9816. Our compilation dataset should not be considered exhaustive as we chose to use data from studies with large and/or easily accessible datasets as well as containing the ancillary data necessary for our approach (Table S1 in SI).

Data treatment

All CH₄ and N₂O flux data we compiled from the literature were used in our analysis. The compiled CO₂ data set contained an order of magnitude more observations than the other GHG data sets, however, and was pruned prior to analysis to reduce the effect of outliers. There are two main concerns in data mining that results in large data sets: (1) analyzing the bulk of a dataset to determine “large patterns” (sensu Ramaswamy et al. 2000) and (2) determining outliers that represent aberrant observations (Yu et al. 2002; e.g., detect credit card fraud or irregularities in gene expression). Because we were interested in determining characteristic patterns exhibited in a significant portion of the CO₂ emission rates, we pruned this large dataset using the approach of Ramaswamy et al. (2000). This approach defines outliers not by the distance from the mean but based on the distance defined by the kth nearest neighbor to the mean, where k is defined as a fraction of the dataset, above and below the mean observation. We thus limited the CO₂ data to those observations within the 5^th and 95^th percentiles of the distribution.. The efficacy of the Ramaswamy et al. (2000) pruning approach is illustrated by the fact that fitting to the CO₂ outliers (i.e., using unpruned data) resulted in a biased regression analysis that predicted the three largest lake size bins to be net CO₂ sinks, which is clearly unrealistic (c.f., Alin and Johnson 2007). To reduce heteroskedasticity and normalize model residuals, all data were log₁₀-transformed prior to analysis and a constant was added to data sets containing flux values less than or equal to zero prior to log transformation.

We analyzed the relationship between emission rates and predictor variables using simple and multiple linear regression. Candidate predictor variables were lake size, chla, TP, and TN. For each gas and emission mechanism, multivariate models were constructed for all combinations of size and one other predictor variable, including their interaction. Variable selection was conducted using the partial t-statistic at a significance level of 0.05. The model with the greatest explanatory power (i.e., r²) and smallest model error (i.e., mean absolute error, root mean squared error) for each gas and emission mechanism was selected as the ‘best’ model and used for all subsequent analysis and upscaling.

Global lake size and productivity distribution

In order to upscale gas fluxes to global rates, it is necessary to know the worldwide joint distribution of lake size and production. Three size analyses are available that quantify the global size distribution and abundance of lakes and impoundments (Downing et al. 2006; Verpoorter et al. 2014; Messager et al. 2016). These analyses were done with different methods and yield slightly different global surface area and size distributions. Downing et al. (2006) estimated the global size and abundance distribution of lakes using data on the largest systems and a Pareto function to model the remaining systems. This analysis covered 9 logarithmic size categories from 0.001 to >100,000 km² (Table S2). The Verpoorter et al. (2014) estimate was created by applying an automated algorithm to high resolution satellite imagery of lakes and impoundments, covered 8 logarithmic size categories, did not include the Caspian Sea, and could not resolve the smallest (< 0.002 km²) water bodies. We determined the total lake surface area within each of the 8 size categories by digitizing Figure 2b of Verpoorter et al. (2014). We then added a new category for the Caspian Sea using data from Downing et al. (2006) (Table S3). Messager et al. (2016) estimated the number and area of lakes and impoundments in 6 logarithmic size-categories (0.1 to >10,000 km²) from their “HydroLAKES” database created by unifying several GIS databases and calculating areas of smaller lakes from Pareto distributions. We calculated the area of lakes < 0.1 km² to match the previous two distributions by subtracting the area listed for lakes from 0.1 to >10,000 km² in Table 1 of Messager et al. (2016) (2,672,900 km²) from their estimate of the total area of lakes >0.01 km² (3,232,200 km²). We further modified the Messager et al. (2016) distribution by substituting the data in the largest size category (> 10,000 km²) with the canonical area of the largest systems reported in Table 2 of Downing et al. (2006) (Table S4).

Figure 2.

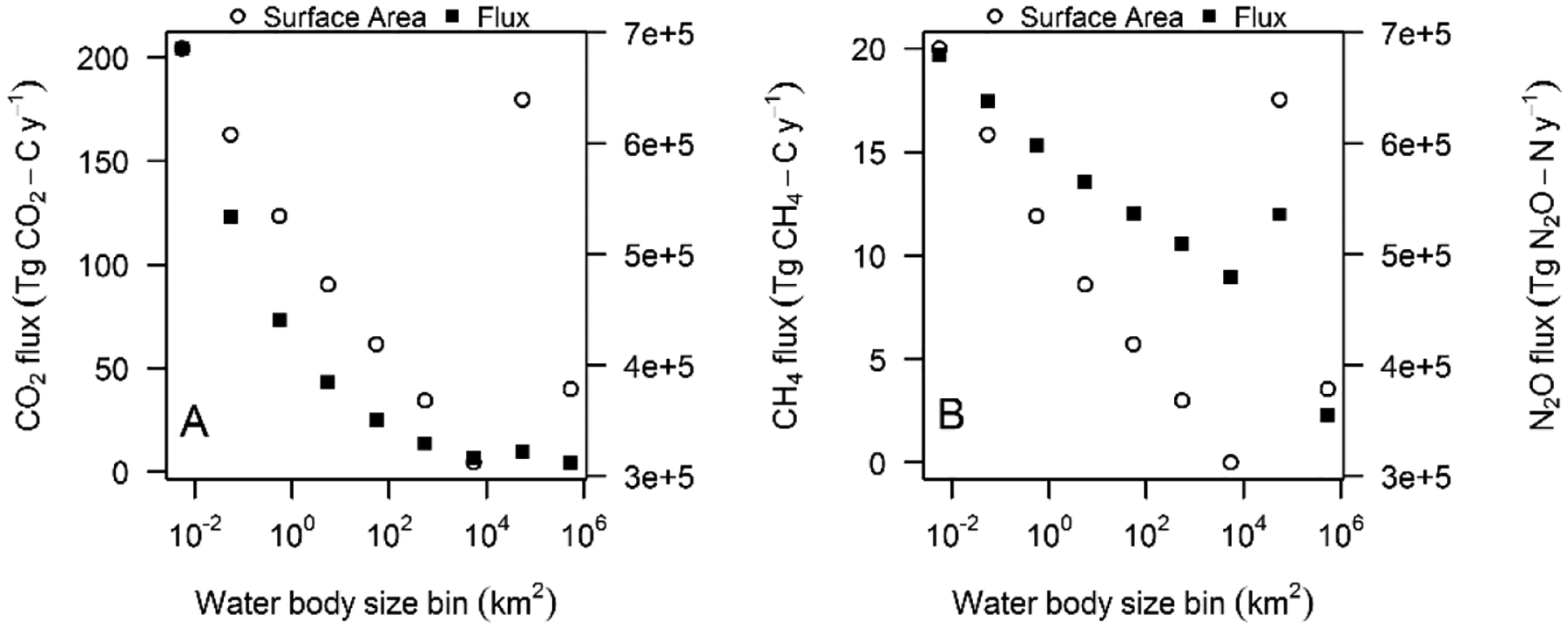
Annual emissions (Tg Gas y⁻¹) and total surface area (km²) per lake size bin according to the Downing et al. (2006) distribution using the size-productivity weighted (SPW) approach for (A) CO₂, (B) total CH₄, and (C) N₂O.

Table 1.

Global annual GHG gas emissions according to the traditional and size-productivity weighted (SPW) approaches and three different global lake and impoundment size distributions.

			Lake Size Distribution
Gas	Data source	Upscaling approach1–†emission mechanism	Downing et al. 2006	Verpoorter et al. 2014	Messager et al. 2016
CO2 (Tg CO2-C y−1)	Tranvik et al. (2009)	Traditional	810	--	--
	This work	Traditional	740	899	542
		SPW	503 (468–541)	525 (491–562)	244 (227–262)
CH4 (Tg CH4-C y−1)	Bastviken et al. (2011)	Traditional - Diffusion	7	--	--
		Traditional – Ebullition	41	--	--
		Traditional - Total	69	--	--
	This work	Traditional - Diffusion	43	52	32
		Traditional - Ebullition	140	170	102
		Traditional - Total	204	248	149
		SWP - Diffusion	28 (17–48)	34 (21–57)	18 (11–13)
		SWP - Ebullition	67 (39–115)	84 (49–144)	47 (28–81)
		SPW - Total	112 (71–177)	139 (89–221)	78 (50–124)
N2O (Tg N2O-N y−1)	Soued et al. (2015)	Traditional	0.63	--	--
	This work	Traditional	0.22	0.27	0.16
		SPW	0.3 (0.19–0.45)	0.38 (0.24–0.55)	0.26 (0.16–0.38)

¹SPW estimates include lower and upper 95% confidence intervals in parentheses.

^†If not reported, emission mechanism is diffusion.

Table 2.

Global carbon emissions (Pg C-CO₂eq y⁻¹ for each GHG) from lakes and impoundments and individual contributions to total radiative forcing from aquatic water bodies

Lake Size Distribution	Total Area (x 106 km2)	Literature Totala	Traditional Approach	SWP (95% CI)b	CO2c (%)	CH4c (%)	N2Oc (%)
Downing et al. 2006	4.42	1.74	3.29	1.92 (1.37–2.79)	26.1	71.8	2.0
Verpoorter et al. 2014	5.36	--	4	2.30 (1.62–3.36)	22.9	75.0	2.1
Messager et al. 2016	3.23	--	2.41	1.25 (0.86–1.84)	19.6	77.8	2.6

^aSum of estimates for CO₂ from Tranvik et al. (2009), CH₄ from Bastviken et al. (2011), and N₂O from Soued et al. (2016) (also listed in Table 1) and converted to CO₂-equivalents.

^bSize-productivity weighted (SPW) estimate with lower and upper 95% confidence intervals (CI) in parentheses.

^cIndividual GHG contributions based on SPW approach estimates.

We estimated the global distribution of lake productivity using satellite-based remote sensing measurements of chla on 80,000 lakes around the world, covering the northern and southern hemispheres (Sayers et al. 2015). The data divide the world’s lakes into productivity bins of 5 μg L⁻¹ width (e.g., 0–5, 5–10, etc.; up to 100+). We used these data to calculate the proportion of global lake and impoundment surface area within each chla bin. We then propagated this chla distribution across the Downing et al. (2006), Verpoorter et al. (2014), and Messager et al. (2016) global size distributions mentioned above, except for the two largest size bins. We therefore assumed that each size bin would have the same chla distribution as derived for the world’s lakes, which is also supported by the lack of correlation globally between lake size and both chla and TP in our collected dataset (Figure S1 in SI). For the two largest size bins, however, we used literature data to determine the size and chla of the world’s 17 largest systems (Table S1). The joint size-productivity distribution is insensitive to error in individual lake chla estimates because the bins are of 5 μg L⁻¹ breadth. We defined the joint distribution of TP and system size by converting chla bins to TP bins using a regression relationship between TP and chla calculated using the global data of McCauley et al. (1989). The resulting joint size-productivity distributions for the Downing et al. (2006), Verpoorter et al. (2014), and Messager et al. (2016) lake and impoundment size distributions are presented in Tables S2–S4 in the SI .

Upscaling procedures

Size-Productivity Weighting (SPW) approach.

We used the size and/or productivity model that best explained the emission rates of the individual GHGs in our datasets to predict an areal emission rate and 95% confidence interval (CI) for each unique combination of lake size and productivity represented in the three joint size-productivity distributions (i.e., Tables S2–S4). Next, we multiplied the predicted areal emission rate for each size-productivity bin by the total surface area of the bin, then summed across productivity bins to find the total amount of gas emitted daily from each size class. Finally, summing daily emissions from all size classes and multiplying by 365 provided an annual global estimate of GHG emissions from lakes and impoundments according to the three different size distributions. These calculations were repeated using the lower and upper 95% CI of the predicted emission rates, resulting in a 95% CI for the emission estimate for each gas and lake size distribution. This 95% CI reflects uncertainty in the statistical models used to predict emission rates, but does not account for uncertainty in the flux estimates reported in the literature. Spatiotemporal variability (Tranvik et al. 2009; Bastviken et al. 2011) and the use of different measurement approaches (Deemer et al. 2016) can add multiple levels of uncertainty to flux estimates. This uncertainty is rarely quantified, however, and is not reflected in the 5 and 95% CI of the statistical models used in this secondary analysis.

Traditional approach.

The traditional approach to upscaling entails multiplying an average areal emission rate by a global lentic surface area estimate (e.g., Cole et al. 2007; Tranvik et al. 2009; Bastviken et al. 2011). We applied this approach to each GHG using the mean emission rate calculated from the collection of measurements used to derive the models described above and scaled that rate to the globe using each of the three global lake and impoundment size distributions described above (Downing et al. 2006; Verpoorter et al. 2014; Messager et al. 2016).

Results and Discussion

Nutrients and lake size drive aquatic CO₂ emissions

Out of the diverse candidate models (Table S5), the model that best explained CO₂ flux included lake size and TP as well as their interaction (Table S6). CO₂ emission rates decreased with size across all productivity levels. CO₂ flux was positively correlated with TP in the smallest systems (Figure 1a) and negatively correlated with TP in medium to large-sized systems, but chla was not included in the best CO₂ model (Table S5). TP is likely serving as a proxy for watershed inputs of terrestrial materials. High TP concentrations in smaller lakes typically reflect large watershed inputs of water and solutes (Arbuckle and Downing 2001) including terrestrially-sourced CO₂ and/or dissolved organic carbon (DOC) (Palviainen et al. 2016). Indeed, others have found that TP tends to covary with DOC in lakes (Lapierre and del Giorgio 2012) and that direct inputs of CO₂ (Maberly et al. 2013; Weyhenmeyer et al. 2015) from the surrounding watershed, as well as inputs of biologically- and photochemically-degradable DOC (Lapierre et al. 2013), drives CO₂ concentration in lakes. Thus, the positive correlation between CO₂ flux and TP that we observed in the smallest lakes and impoundments could merely represent the impact of nutrient and C runoff from the watershed on C dynamics in the smaller systems, and the negative effect of TP in larger systems reflects enhanced primary production in pelagic waters that tends to be more important in those systems. Our results support previous findings that CO₂ dynamics in the world’s lentic waters are directly impacted by activities in their watersheds (Tranvik et al. 2009; Regnier et al. 2013) and that future changes in watershed properties, such as climate-induced changes to runoff (Milly et al. 2005), can alter the C balance of the world’s lakes and impoundments.

Figure 1.

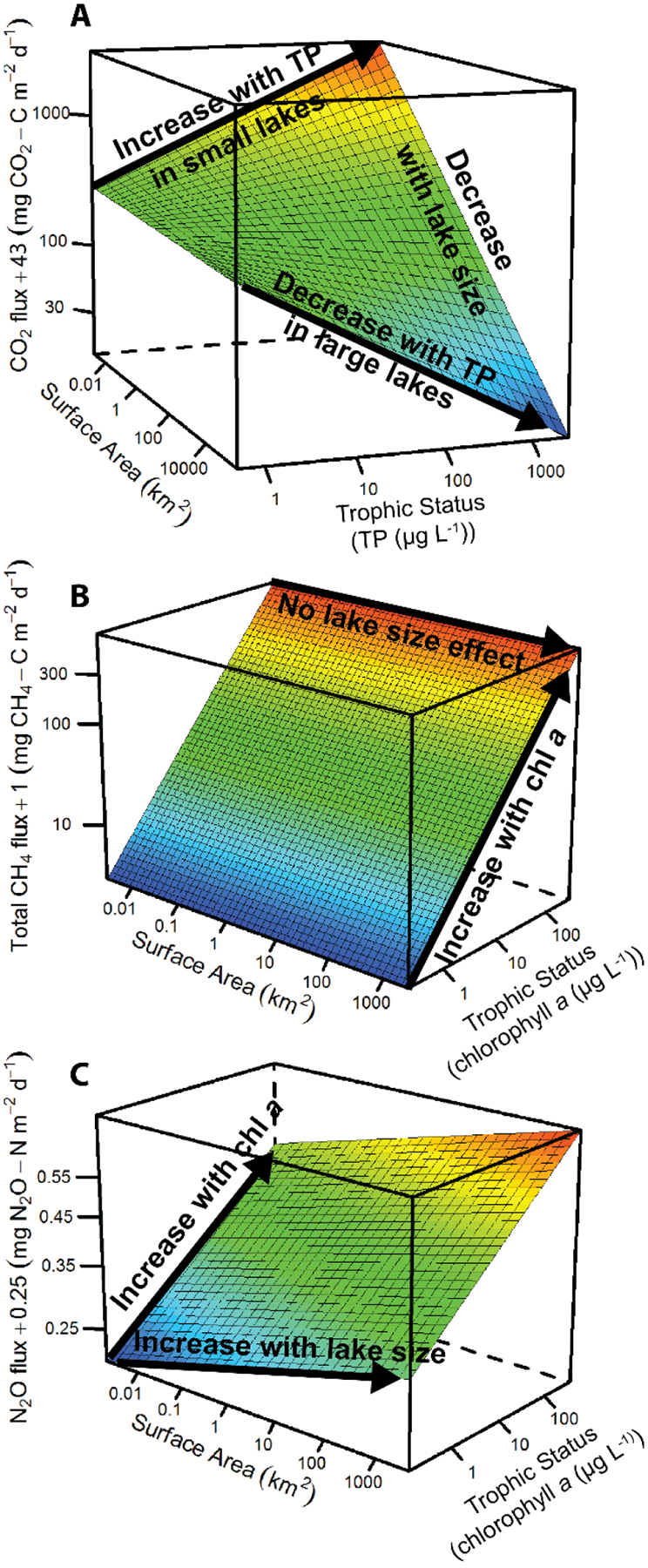
Size-productivity weighted (SPW) models for GHG emissions from lakes and impoundments. (A) CO₂ emissions best explained by surface area (SA), trophic status via TP, and the interaction between the two. (B) A linear relationship with chla, also a trophic state proxy, is the best model for total CH₄. (C) SA and chla (but no interaction) best explain N₂O emissions.

Productivity-driven aquatic CH₄ emissions

The only factor retained in the best models for ebullitive and total (i.e., diffusive + ebullitive) CH₄ emission rates was a positive effect of chla (Figure 1B; Table S6). Chla was also positively related to the diffusive CH₄ emission rate, though the strength of the effect was stronger for large rather than small systems. While previous studies have reported a positive relationship between chla and CH₄ emissions for lakes (Bastviken et al. 2004) and impoundments (Deemer et al. 2016), this is the first study to generalize the finding to lentic systems across the globe. This relationship could arise through several mechanisms, including the correlation between chla and the oxygen-poor and C-rich environments that favor CH₄ production and often develop in eutrophic systems. There is also evidence that the labile C derived from autochthonous production is more readily converted to CH₄ than more recalcitrant allochthonous C sources (West et al. 2012). Our findings suggest that the eutrophication of the world’s lentic ecosystems could increase global CH₄ emissions.

Productivity and lake size influence N₂O emissions

In aquatic ecosystems, N₂O is produced primarily by the oxidation and reduction of nitrogen (N) via microbial nitrification and denitrification, respectively. Nitrous oxide is one of several N-species that can be produced by these processes and rates of N₂O production are determined by the overall rates of de/nitrification and the fraction of de/nitrified N converted to N₂O (i.e., the N₂O yield; Davidson et al. 2000). In this study, we found that N₂O emission rates exhibited a positive relationship with lake size and chla (Figure 1C, Table S6). Chla is a proxy for algal biomass which can serve as a labile carbon source for denitrification and consequent N₂O production (Sirivedhin and Gray 2006; McMillan et al. 2010; Chen et al. 2012). High algal biomass can also result in hypoxia in the hypolimnia of stratified lakes, further stimulating denitrification, an anaerobic process. Finally, chla may serve as an indicator of N loading, which can stimulate both algal growth (McCauley et al. 1989) and denitrification (Beaulieu et al. 2011). The positive relationship between N₂O emission rate and lake size has not been previously reported and may be related to differences in the relative abundance of littoral and pelagic habitats along the lake size continuum. In general, well oxygenated pelagic habitats will favor nitrification, the aerobic oxidation of ammonium, and will be relatively more abundant in large lakes, whereas carbon rich littoral zones will be relatively more abundant in small lakes. Systematic differences in the rates of de/nitrification and/or the N₂O yield among these habitats could account for the effect of lake size on N₂O emissions. For example, the denitrification N₂O yield decreases as the relative availability of C to N increases (Miller et al. 2008); therefore, littoral habitats, which represent a larger area in smaller lakes, may yield less N₂O than pelagic habitats, which dominate larger lakes. Regardless of the mechanisms driving the relationship with lake size and chla, our analysis illustrates that these covariates can be used to improve global estimates of N₂O emissions from lakes and impoundments.

Upscaling global GHG emissions with size-productivity weighting (SPW)

The global lake and impoundment size distribution chosen for upscaling impacted the global emission estimates for all three GHGs. With the traditional upscaling approach, the Verpoorter et al. (2014) distribution produced global emission rates ~22% higher for each gas than when using the Downing et al. 2006 distribution, which in turn produced rates ~35% higher than when using the Messager et al. (2016) distribution (Table 1). This pattern is consistent with the total surface areas predicted by each distribution. We found a similar pattern when comparing the SPW approach across the three size distributions, except for CO₂ emissions. Despite the fact that Verpoorter et al. (2014) reports ~22% more total lake and impoundment area than Downing et al. (2006), there is only a 4% difference in the global CO₂ emissions estimated by SPW from these two distributions. This is because the Verpoorter et al. (2014) distribution estimates less surface area in the smallest class (<0.01 km²) than the Downing et al. (2006) distribution, and these small systems support the highest CO₂ emission rates (Figure 1A). The surface area discrepancy in the small size bins between Verpoorter et al. (2014) and the other distributions made more of a difference in the CH₄ and N₂O emission estimates, with the Verpoorter et al. (2014) model reporting significant emission peaks around the 1 km² size bin that are not present in the other models (Figures 2, S2 and S3). Ultimately, all three distributions have their limitations and criticisms (Verpoorter et al., 2014; Messager et al., 2016; Feng et al. 2016); therefore, as the Downing et al. (2006) size distribution provides estimates falling between the two other distributions, we used it in the following sections for comparison between our upscaling approaches and with literature values that also used the Downing et al. (2006) distribution.

We found differing trends for each GHG when comparing the traditional upscaling approach to the SPW approach (Table 1). The traditional approach, when applied to our data, produced annual emissions ~50 and ~80 % higher than the SPW approach for CO₂ and CH₄, respectively. Even the upper 95% CI of the SPW approach was lower than the corresponding traditional approach estimate for these two gases, except for diffusive emission of CH₄ (Table 1). For N₂O, the SPW approach predicted ~35% higher annual emissions than the traditional approach. Differences between the SPW and traditional approaches can be attributed to the effect of lake size and productivity on GHG emission rates. These relationships are explicitly incorporated into the SPW approach, whereas they are ignored by traditional published calculations. Consequently, we would expect that a simple multiplication of an average emission rate by global lake and impoundment area (i.e., the traditional approach) would yield an inaccurate GHG emission estimate unless the systems sampled to calculate the average emission rate exhibited a size and productivity distribution identical to that of the true distribution that exists worldwide.

Lack of a representative mean emission rate is likely what caused previous global estimates to diverge from that found using the SPW approach. Tranvik et al.’s (2009) estimate of 810 Tg y⁻¹ CO₂ is 62% higher than our mean CO₂ estimate, suggesting that lakes in their dataset were smaller and more productive than those in our global dataset. Soued et al.’s (2015) N₂O emission estimate of 0.63 Tg y⁻¹ is nearly twice the mean rate we calculated, suggesting that the lakes in their dataset must have been larger and more productive than those in our global dataset. Contrary to the other gases, our SPW approach resulted in a mean total CH₄ emission rate double that of the literature-derived CH₄ emission rate of 69 Tg y⁻¹ from Bastviken et al. (2011), although our lower 95% CI estimate is equivalent to their estimate. The difference in estimates thus suggests that systems included in the Bastviken et al. (2011) emission rate were much less productive than those in our global dataset. Our new estimate of CH₄ emissions from lakes exacerbates the discrepancy between top-down estimates of natural global CH₄ emissions, derived from atmospheric sampling, and bottom-up estimates that are derived from in situ flux measurements, with bottom-up exceeding top-down estimates by ~60% (Saunois et al. 2016). Saunois et al. (2016) suggests that much of the discrepancy could be attributed to uncertainty in the areal extent of inland waters, as demonstrated by the difference in SPW emission estimates from the three lake-size distribution models (Table 2). Furthermore, difficulty in differentiating wetlands from small/shallow lakes may lead to those systems being double counted in bottom-up estimates. Finally, the accuracy of reported CH₄ emission rates for lakes is sensitive to how ebullition, the dominant CH₄ emission pathway in many systems, is measured and integrated into a system-scale estimate. System-scale ebullition rates can be greatly overestimated if investigators focus on emission hot spots without accounting for lake areas with low ebullition rates. This highlights a major limitation of using the traditional approach for global estimates in which point measurements are merely averaged and scaled upwards. In general, CO₂ and CH₄ fluxes can vary by a few orders of magnitude with size or productivity (Figure 1) so that a few divergent fluxes could easily skew a predicted global rate using the traditional approach (Table 1). Upscaling emissions based on predictors of GHG emission rates, as we did with the SPW approach, should result in a more accurate estimate of global fluxes and one that can be upscaled to diverse regions with divergent lake size and productivity distributions.

Our analysis implies an evolving view of the “active pipe” model (sensu Cole et al. 2007), which describes how lakes and impoundments store terrestrially-carbon in sediments and emit CO₂ to the atmosphere (Figure 3). As traditional approaches used improved databases for the calculation of CO₂ emissions, the global role of lakes was amplified substantially (i.e., Cole et al 2007 vs Tranvik et al. 2009). Application of the SPW approach used here modulates the estimated role in emissions from 0.81 Pg y⁻¹ (Tranvik et al. 2009) to 0.5 Pg y⁻¹ when weighting global estimates by the size- and productivity-distributions of the world’s lentic systems. Although the difference between the SPW estimate and the estimate of Tranvik et al (2009) seems small, it is 1.5-times the amount of C buried annually by the world’s oceans and ⅓ of the C delivered annually to the world’s oceans from the continents. Accounting for important drivers of GHG fluxes can make a substantial difference in the evaluation of the role of lakes and impoundments in global GHG flux and atmospheric effects.

Figure 3.

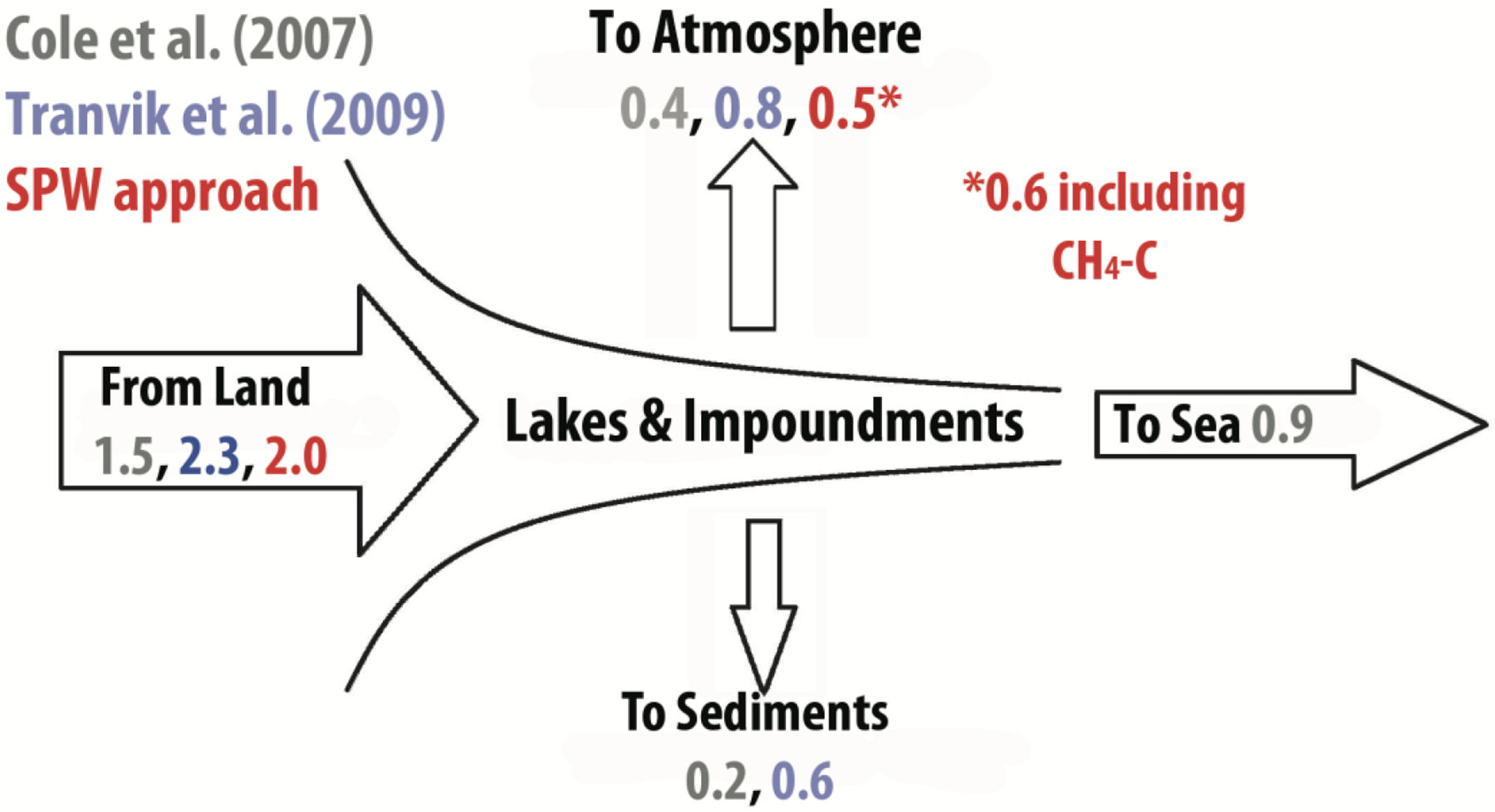
Evolving view of the ‘active pipe’ model first proposed by Cole et al. (2007). Values represent annual transport of C (Pg) and emissions to atmosphere are for lakes and impoundments.

The relative contribution of different lake size classes to GHG emissions differed among the three gases. The smaller size classes had greatest global CO₂ emissions, which can be attributed to the large cumulative surface area of small systems and the negative relationship between CO₂ emission rates and lake size (Figures 1A and 2). Areal CH₄ emissions were predicted by chla, which has a similar distribution across most lake sizes (Figure S1), therefore global CH₄ emissions scale with the total surface area in each size class (Figure 2B). Areal N₂O emission rates, on the other hand, increased with system size, so global N₂O emissions were positively related to productivity and size, which explains why the SPW approach produced a higher emission estimate than the traditional approach for that GHG. Finally, in all GHG emission distributions, the size bin in which the US Great Lakes fall is easily visible by the spike in emissions in the second to largest size class (Figure 2). Previous studies have reported that GHG emissions are greatest for large systems (Alin and Johnson 2007) or small ones (Holgerson and Raymond 2016), yet the nature of these relationships had not been heretofore thoroughly resolved. Our analysis shows that, in terms of GHG emissions, the relative importance of large and small aquatic systems depends upon which gas is being considered.

Global C emissions from lakes and impoundments and their atmospheric potential

We combined the traditional and SPW emission results of the three GHGs, as well as those from the literature, into total CO₂-equivalent (CO₂eq) emissions (using 100-yr timeframes for CH₄ and N₂O conversions, including indirect effects; Myhre et al. 2013) in order to evaluate the role that lakes and impoundments play in the global C cycle and their potential impact on atmosphere and climate. While the traditional approach suggested a doubling of the literature value for aquatic CO₂eq emissions, global CO₂eq emissions based on our SPW approach were remarkably similar to the previously reported estimates (Table 2). The combined literature total of 1.74 Pg C y⁻¹ falls within the 95% CI range of the SPW estimate for each lake size distribution, but is closest to (just 10% lower than) the Downing et al. (2006) estimate of 1.92 Pg C y⁻¹ (Table 2). Moreover, the 95% CI for all three lake size distributions overlap suggesting (1) that we are close to constraining the true aquatic C emission value, and (2) that using the middle estimate found with the Downing et al. (2006) distribution is justified for comparative purposes.

Interestingly, even though the upscaling estimates using the Verpoorter et al. (2014) and Messager et al. (2016) distributions were somewhat higher and lower than the Downing et al. (2006) estimate, respectively, all three distributions revealed that CH₄ has the greatest atmospheric influence of the GHGs being emitted from lakes and impoundments. On average, CH₄ accounts for 75% of total CO₂eq emissions, while CO₂ and N₂O account for 23% and 2%, respectively (Table 2). Despite CO₂ being emitted from lakes and impoundments at rates about four times higher than CH₄ (Table 1), the enhanced climate change potential of CH₄ implies that it is responsible for three times more of the radiative forcing by lentic systems globally than CO₂. Although N₂O is about 300-times more potent in the atmosphere than CO₂ (on a 100-yr time scale), aquatic N₂O emissions from lakes and impoundments appear to have a small effect.

Ultimately, we found a global CO₂eq emission estimate similar to that reported in the literature, but the traditional approach used to calculate those literature values misattributed the majority of the CO₂eq emission to CO₂. By using an approach based on the drivers of GHG emission rates, we found that CH₄ may be the dominant climate change-related gas being emitted from lentic systems. Similar results were indicated in a recent global synthesis of emissions of all three GHGs from impoundments (Deemer et al. 2016) and together these findings support the conclusion that the productivity of lakes and impoundments plays an important role in the alteration of Earth’s climate. However, because productivity enhances GHG emissions but the global chla distribution used in our analysis did not exceed 100 μg L⁻¹ (Tables S2–S4), our estimate of the global role of lakes and impoundments is conservative. Furthermore, as a result of ongoing global change, the warming of lakes globally has already been observed (O’Reilly et al. 2015), as has the continued eutrophication of inland waters, despite concerted efforts to thwart it (Smith et al. 2014). If eutrophication leads to shifts in the GHG balance of lentic systems towards the more potent CH₄, then we will consequently see an increase in the impact that these systems have on the climate.

To estimate the potential impact of continued eutrophication on the GHG emissions of lakes and impoundments, we incremented our joint size-chla distributions (Tables S2–S4) by 1, 5 and 10 μg L⁻¹ and calculated the CO₂eq emission of these simulated conditions using the SPW models. This analysis suggests that these moderate levels of enhanced eutrophication could increase the atmospheric effect of GHGs emitted from lakes and impoundments by 5, 26 or 42 %, respectively (Table S7). This increased emission would be equivalent to around 1 Pg CO₂eq y⁻¹ or about 13% of the effect of the current global emission of CO₂ by the combustion of fossil fuels, and about equal to the excess CO₂ emissions to the atmosphere from global land use change (Ciais et al. 2013).

Further improvement of aquatic C emission upscaling

The accuracy of our predicted GHG emissions from lentic systems is limited in part by the availability of data on the global distribution of key limnological variables. For example, while the Sayers et al. (2015) chla distribution represents an important advancement in the mapping of limnological variables at the global scale, the distribution has a maximum chla value of 100 ug L⁻¹, whereas GHG flux rates have been reported from hypereutrophic systems with chla concentrations in excess of 700 μg L⁻¹ (Figure S1). Therefore, we are likely underestimating GHG emissions because the most eutrophic lentic systems are not accounted for. This bias could be significant for some regions, such as the 1.1 million km² Southern Plains ecoregion of the United States where 25% of the lakes have chla in excess of 100 ug L⁻¹ (USEPA 2017). This effect is also likely to be more important for N₂O and CH₄ than CO₂ emissions because chla was a stronger covariable for those GHGs. In this study, we estimated TP from the Sayers et al. (2015) chla distribution, thereby allowing us to upscale CO₂ emissions using the CO₂~TP model, which explained more of the variation in CO₂ emission rates than the CO₂~chla model. However, CO₂ emission estimates could be improved by better global mapping of TP in lakes and impoundments. Another source of variability in modeled global emission estimates arises because of the disagreement among published global lake and impoundment distributions. We used three distributions for our analyses, but others can be found in the literature (e.g., Feng et al. 2016). Further, these distributions tally only permanently wetted environments and ignore the likely large influence of seasonally flooded ecosystems. Until a consensus is reached on the global area and size distribution of lakes and impoundments, the global lentic GHG emission estimate will remain sensitive to the chosen surface area distribution model.

The accuracy of the emission estimate is also limited by methodological constraints, particularly for CH₄. Ebullition can be the dominant CH₄ emission pathway, especially in smaller systems, yet our ability to accurately measure this flux is hampered by its spatiotemporal variability and difficulty in assessing system-wide estimates of it (e.g., Beaulieu et al. 2016). Much work is still needed to sufficiently address this issue. The geographic distribution and temporal resolution of reported GHG emission rates also limits the representativeness of global annual estimates. A substantial fraction of the global data is from studies in the boreal biome, and more measurements are needed across a range of lake sizes and trophic levels from poorly-studied regions of the world. In addition, the global flux models we found may not be the best ones for lakes or impoundments on a regional basis. For example, differing emission drivers have been found for CO₂ emissions from lakes across various regions of Canada (Lapierre and del Giorgio 2012) and the United States (Lapierre et al. 2017). Another important gap is the relative lack of data that represent annual emissions (cf., Jones et al. 2016). Most available data in our analysis represent the open water/summer season and do not include large emissions that can occur during ice-out (Michmerhuizen et al. 1996; Striegl et al. 2001; Karlsson et al. 2013) or turnover (Kankaala et al. 2007; Schubert et al. 2012; Beaulieu et al. 2015). For example, the ventilation of accumulated gases during ice-out constitutes 18% and 27% of annual emissions for CO₂ and CH₄, respectively (Denfeld et al. In revision). While not directly considered here, our approach for scaling daily rates to annual rates may somewhat compensate for this. As previous publications have done, we multiplied daily rates by 365 to arrive at annual rates, which implicitly assumes that emissions continue to occur during periods of ice cover. While this assumption is likely inaccurate, ice-out emissions represent GHGs that were produced and stored during periods of ice cover; therefore, our assumption that emission occurs year-round may compensate for the poor coverage of ice-out emission in the literature. Nevertheless, improved temporal resolution of measurement campaigns will reduce uncertainty in upscaled emission estimates. Finally, predictive models may be further improved through the inclusion of other environmental covariables that predict GHG emission rates from lakes and impoundments at the global scale. For example, global maps of climate, land use, and soil variables are available and could be used for upscaling if empirical relationships with GHG emissions could be demonstrated.

Conclusions

Here we offer the first joint global analyses of all GHGs emitted from both lakes and impoundments. We found that lake size and productivity are important drivers of emission rates and used these drivers in creating new, global estimates of GHG fluxes from lakes and impoundments. This analysis indicates that lentic systems are important sources of GHGs driving climate change, but concludes that CH₄ emissions may be of disproportionate importance due to their link with lake/impoundment productivity and the high potency of CH₄ as a GHG. Although we expect improvements in a global understanding as data availability evolves, we suggest that linking emission rates with important drivers is a path to a more accurate understanding of the global GHG role of lentic waters. Our study shows that GHG emissions from lakes and impoundments are equivalent to ~20% of global fossil fuel CO₂ emission (9.3 Pg C-CO2 y-1; Le Quéré et al. 2016) and that emissions will rise even further with the continued eutrophication of Earth’s lentic ecosystems.

Scientific Significance Statement.

Releases of greenhouse gases (GHG; carbon dioxide, methane and nitrous oxide) into the atmosphere drive global climate change. Knowing the amount of GHGs released is important for predicting how much and how fast the climate will change. GHGs are released from natural and constructed lakes but current knowledge ignores differences in emission rates from lakes of differing size and productivity. Our challenge was to estimate the effects of lake size and productivity on GHG emission and combine this with global lake size and productivity distributions to calculate accurate annual GHG emissions. We found that past estimates have been inaccurate and that the effects of aquatic GHG emissions on the atmosphere is nearly 20% that of fossil fuel emissions, but will increase as waters become more productive.