The Interplay Between Cell-Cell and Cell-Matrix Forces Regulates Cell Migration Dynamics

Abstract

Cells in vivo encounter and exert forces as they interact with the extracellular matrix (ECM) and neighboring cells during migration. These mechanical forces play crucial roles in regulating cell migratory behaviors. Although a variety of studies have focused on describing single-cell or the collective cell migration behaviors, a fully mechanistic understanding of how the cell-cell (intercellular) and cell-ECM (extracellular) traction forces individually and cooperatively regulate single-cell migration and coordinate multicellular movement in a cellular monolayer is still lacking. Here, we developed an integrated experimental and analytical system to examine both the intercellular and extracellular traction forces acting on individual cells within an endothelial cell colony as well as their roles in guiding cell migratory behaviors (i.e., cell translation and rotation). Combined with force, multipole, and moment analysis, our results revealed that traction force dominates in regulating cell active translation, whereas intercellular force actively modulates cell rotation. Our findings advance the understanding of the intricacies of cell-cell and cell-ECM forces in regulating cellular migratory behaviors that occur during the monolayer development and may yield deeper insights into the single-cell dynamic behaviors during tissue development, embryogenesis, and wound healing.

Significance

Exploring the coordinated roles of cell-cell and cell-extracellular matrix forces in regulating single-cell migration in a multicellular environment has critical implications during tissue development, embryogenesis, and wound healing. Yet, establishing a comprehensive picture that incorporates and elucidates the mechanistic basis of these forces and migratory behaviors remains a pressing and challenging task. Here, using an integrated mechanobiology platform, we map the spatiotemporal dynamics of single-cell traction and intercellular forces as well as migration trajectories within an endothelial monolayer. The multiscale measurement and modeling approach proposed here highlights the intricacies of cell-cell and cell-extracellular matrix forces in regulating cellular migratory behaviors, such as cell translation and rotation, and thus provides a direct link between single-cell processes and collective cell migration behaviors.

Introduction

Single-cell migration behaviors within a tissue are critical for tissue development, embryogenesis, and wound healing and may also present insight into disease progression (1, 2, 3). As cells progress through their cycle within the tissue, they demonstrate dynamic processes, such as active translational motion, stationary reorientation, and cell division (4, 5, 6). During these stages, cells physically interact with the surrounding extracellular matrix (ECM) and neighboring cells through adhesions formed between cells and the ECM and between neighboring cells (7, 8, 9, 10, 11, 12). The forces from the cell-ECM interaction (traction force) (13,14) and cell-cell interaction (intercellular force) (15,16) individually and cooperatively play a vital role in guiding cell migration and cell/tissue homeostasis (17,18). The dynamics of traction and intercellular forces are distinct in healthy and diseased tissue, and the distribution and magnitude of those forces reflect the overall tissue integrity (19,20). For example, cancer cells that exhibit an increase in cell traction force and loss of intercellular force may acquire metastatic characteristics in a tumor colony (21, 22, 23). With respect to the endothelial cell (EC) monolayer in blood vessels, intercellular forces are important to maintain the integrity of the EC monolayer and prevent damage from flow shear stress of circulating blood (24,25). However, previous studies have either focused on the study of cell migratory behaviors of isolated single cells or the influence of ECM or the collective cell behaviors without single-cell resolution (26, 27, 28, 29, 30, 31). Hence, the regulatory roles of intercellular and cell-ECM traction forces during the cell migration in the endothelial layer have never been reported.

Techniques for investigating cellular traction forces, such as traction force microscopy (TFM) (32, 33, 34), confocal TFM (35), and elastic micropillars (36, 37, 38, 39, 40), are well developed and widely used. By applying these techniques, researchers have shown that physiological changes in cell-ECM interactions affect cell functions, including migration behaviors, morphological features, biomechanical properties, and gene expressions (41, 42, 43, 44, 45, 46, 47, 48, 49). However, unlike traction force studies, there are methodological limitations in the direct measurement of intercellular force from experimental observation of cell colonies, preventing studies from probing the importance of intercellular forces in mechanobiology. In the case of cells arranged in a linear configuration, intercellular forces can be measured using the residual forces acting in the cellular region of interest and the mechanical imbalances of traction forces between cells (15,26,50, 51, 52). However, in the case in which cells are arranged so that their intercellular interactions result in a mechanically redundant system, as is the case in most monolayers, traction forces can provide us with an inferential method of calculation of intercellular forces within cellular monolayers (8,53,54). Many methods based on stress determination using the traction forces measured by TFM, such as monolayer stress microscopy (53,55, 56, 57, 58, 59, 60, 61, 62, 63) and Bayesian inversion stress microscopy (8), have been widely used in past studies. Monolayer stress analysis has revealed that intercellular adhesion propagates cell stress over multiple cell diameters because of cell-cell adhesion, and the minimization of intercellular shear stress directs cell migration (53) within cohesive cell monolayers through cell-cell junctions (64). Further, the existence of a tensile state in the monolayer inferenced using traction forces has been confirmed with E-cadherin-mediated tension measurements performed using Förster resonance energy transfer systems (65). Intercellular forces can be calculated using inferential mechanical stresses obtained in the monolayer and have been successfully correlated with E-cadherin localization in small cellular colonies, further confirming their applicability in monolayers (51). Although features of intercellular stresses can be obtained using these analytical models of a cell monolayer, the overall interplay between traction force and intercellular force in cellular monolayers remains poorly understood. Furthermore, there are gaps in knowledge about how single-cell migration behaviors within a tissue are affected by the presence of multiple forces inside the monolayer.

To explore how traction and intercellular forces individually and cooperatively regulate single-cell migratory behaviors within a multicellular environment, we developed an integrated mechanobiology platform to simultaneously examine cell traction and intercellular forces acting on individual cells within an EC colony and their roles in guiding cell migratory dynamics. Our system can report high-resolution and spatiotemporal dynamics of single-cell traction and intercellular forces within an endothelial monolayer and precisely map single-cell migratory behaviors. We demonstrated that cell traction and intercellular forces affect cellular migration dynamics in various stages and highlighted their distinct roles in regulating migratory behaviors when cells experience translating, rotating, and dividing processes. Combined with multipole (66) and moment analysis, our results revealed that traction force dominates in regulating cell active translation, whereas intercellular force actively modulates cells in rotation. We showed that there was a lack of correlation in both forces and cell migration in the case of dividing cells, in which cell machinery is otherwise engaged (67,68). Our findings advance the understanding of traction and intercellular forces in dictating cell migration during monolayer development and may yield deeper insights into characterizing the dynamics of single cells during tissue development, embryogenesis, and wound healing.

Materials and Methods

Cell culture

Mouse ECs (C166; ATCC, Manassas, VA) were cultured in Dulbecco’s Modified Eagle’s Medium (Gibco; Thermo Fisher Scientific, Waltham, MA) supplemented with 10% fetal bovine serum (Gibco; Thermo Fisher Scientific), 100 U/mL penicillin G, and 100 g/mL streptomycin (Gibco; Thermo Fisher Scientific). Human umbilical vascular ECs (C2519A; Lonza, Basel, Switzerland) were cultured in EGM-2 EC Growth Medium-2 (CC-3162; Lonza) and used in experiments between passages 3 and 8. Cells were maintained at 37°C in a humidified atmosphere containing 5% CO₂.

Gel substrate preparation

Polyacrylamide (PA) hydrogels were created using a previously adopted method (69). Briefly, PA gels with a stiffness of 16.2 kPa were manufactured by the mixing of 40% acrylamide and 2% bisacrylamide (Sigma-Aldrich, St. Louis, MO). Before casting the gel, coverslips (18 mm; Thermo Fisher Scientific) were treated with 0.1 M NaOH (Sigma-Aldrich) for 4 h. The coverslips were then functionalized with 3-aminopropyltriethoxysilane (Sigma-Aldrich) for 20 min, rinsed three times with distilled water, incubated with 0.5% glutaraldehyde (Sigma-Aldrich) for 30 min, and then washed three times with distilled water. The activated coverslips were then dried at room temperature. To initiate the reaction, 0.1% ammonium persulfate (Sigma-Aldrich) and 0.1% tetramethylethylenediamine (Sigma-Aldrich) were added to the acrylamide and bisacrylamide mixtures with orange fluorescent (540/560) microbeads (Thermo Fisher Scientific). 40 μL of the gel solution was sandwiched between the activated coverslip and a glass slide hydrophobically treated with dichlorodimethylsilane (Sigma-Aldrich). The gel-coated coverslips were gently detached after 30 min of polymerization. The PA gel substrates were activated by treating with 100 μL of 1 mM sulfo-SANPAH(succinimidyl-6-[4'-azido-2'-nitrophenylamino] hexanoate) (Pierce Biotechnology, Waltham, MA) in phosphate-buffered saline (pH 7.4; Thermo Fisher Scientific) under ultraviolet light (UMV-57; Analytik Jena, Jena, Germany) for 10 min and followed by washing with distilled water thrice.

Microcontact printing of cells

Microcontact printing of ECs was done using a protocol described before (70). Briefly, circular patterns, 600 μm in diameter, were fabricated using SU-8 (MicroChem, Westborough, MA) photolithographic technique on silicon wafers. Polydimethylsiloxane (Dow Corning, Midland, MI) stamps were made by the replica molding of the SU-8 mask. The polydimethylsiloxane stamps were coated with fibronectin (Sigma-Aldrich) for an hour and pressed onto the functionalized PA gel substrate to develop a patterned adhesive surface. ECs were then plated on the micropatterned culture substrates to form a cell colony monolayer within the defined patterns.

TFM

Live cells and embedded fluorescent microbeads in PA gels were imaged with an inverted fluorescent microscope (Zeiss Axio Observer.Z1) employing a 40× objective in an enclosed 37°C and 5% CO₂ incubation chamber. After the experiments, cells were removed from the PA gel by adding 100 μL of 1 N NaOH (Sigma-Aldrich), and the fluorescent images of the same locations were recorded again as a control. A phase contrast image together with two sets of fluorescence microscopic images pre- and post-cell lysis were used to measure bead displacement using particle image velocimetry. The resultant displacements were then used to calculate the traction force using Fast Fourier transform cytometry (71).

Intercellular force calculation

Intercellular force was calculated using a previously established finite element method (FEM) for the modeling of a cellular monolayer as a thin sheet (51,53). In brief, the cell monolayer was treated as a thin sheet and the stresses were calculated using the stress-strain relationship. Cellular boundaries, position, and orientation of the cellular nuclei were manually selected using the phase-field images of the cells. The calculated stresses were used in conjugation with the cellular boundary to infer the intercellular forces. For details, see Supporting Materials and Methods.

Box and whisker plot

Box and whisker plots were made using OriginPro software (OriginLab, Northampton, MA). Each separate box represents a separate y column. The x axis tick labels represent the column names. The upper and lower edges of the box represent the 75th and 25th percentiles, respectively. The upper and lower whiskers are determined by the 95th and 5th percentiles, respectively. The line inside the box determines the median, and the point inside the box determines the mean. Any outliers are shown as separate points.

Statistics

All experiments were repeated at least thrice for each condition. Data with an error bar represent the mean values, and the error bars are the standard errors. All statistical correlations were calculated using two-tailed Student’s t-test. For all comparisons, p < 0.05 was considered statistically significant.

Results

Spatiotemporal mapping of single-cell forces and migration in a monolayer

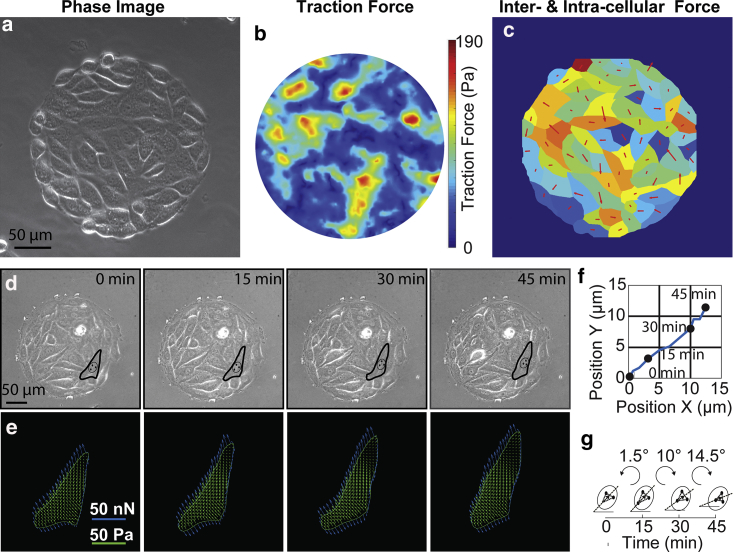
As a model to investigate single-cell migration due to traction and intercellular forces in a multicellular context, we first established our micromechanical system by growing micropatterned mouse EC (C166) colonies on a PA hydrogel substrate embedded with fluorescent beads (Fig. 1 a). In this configuration, single cells in the monolayer would exhibit migratory behaviors and, at the same time, experience physical interactions with its surrounding ECM and neighboring cells. Traction force exerted by the C166 colonies on the substrate can be readily obtained using the established TFM method (71) by tracking the displacements of the embedded fluorescent beads (Fig. 1 b; Fig. S1 a). We also applied a FEM model (51,53) to determine the intercellular forces exerted by neighboring cells in the monolayer based on the measured traction forces (Fig. 1 c; Fig. S1 b; for details, see Supporting Materials and Methods). We assumed that the cell monolayer could be approximated as a thin sheet, an assumption used and verified in numerous studies on inferential stress determination under multiple frameworks (8,51,53,56,72, 73, 74); hence, stresses across the sheet can be calculated using the traction force data with a FEM analysis. The sheet was then divided into regions containing single cells (Figs. S1, c and d and S2). Intercellular force along the cell boundary was calculated as the product of the stress tensor at a location on the section and the length of the infinitesimal section directed normal to the section line, pointing toward the center of the cell. Therefore, we could successfully map both traction and intercellular forces with spatiotemporal resolution for a single cell in a colony (Fig. 1 c).

Figure 1.

Spatiotemporal mapping of single cell traction and intercellular forces in a monolayer. (a) Phase-field image of the cells on a TFM substrate. (b) Traction force exerted by the cellular colony. (c) Traction and intercellular forces of individual cells: the color of the cells corresponds to the magnitude of the average traction force, and the size of the arrow represents the magnitude of the intercellular force. (d) Phase-field images show an outline of the cell as it migrates over a period of 45 min. (e) Images show the traction force field (yellow arrows) exerted by the cell and the corresponding intercellular forces (blue arrows). (f) The trajectory of the cell as it moves over the course of 45 min. (g) Cellular rotation quantified by the nuclear orientation, in which the black arrows determine the orientation at a given time.

Our study showed that the cell density drastically affects various morphological and dynamic properties of the cells in the monolayer (Fig. S3; for details, see Supporting Materials and Methods). The cellular velocity decreased significantly with an increase in cell density, and cells became virtually inert (Fig. S3 d), which may be a result of increased intercellular friction (75, 76, 77). Further, we found that cells morphologically regularized themselves with increasing density (Fig. S3 e). We used the order parameter defined in Eq. 1 (78,79) to measure the morphological regularization and confirmed a decrease in order parameter with increasing cell density.

$$Orderparameter=\frac{Perimeter}{\sqrt{Area}}.$$ (1)

Our study deals with cells in low-density confluent states that are a transition between the subconfluent individual cells and the solid-like and inert, high-density confluent states (Fig. S3). The characteristics of single-cell traction and intercellular forces in the low-density confluent monolayers, which were dependent on the area, order parameter, number of neighbors, and perimeter of the cell, are shown in Fig. S4.

Next, we applied our established system to study how these forces individually and cooperatively direct cell migratory behaviors in a multicellular context. To account for the migratory behaviors of single cells within cell colonies, we monitored the spatiotemporal dynamics of nuclear translation and rotation behaviors. The cell nucleus has long been documented to undergo both translation and rotation, and the switch between these two modes mediates cell migration (4,80). We showed that the cell nuclear translation is intimately linked with cellular translation (Fig. S5) and centrosome translation (Fig. S6) and that the nuclear orientation is linked with cellular orientation (Fig. S7). Thus, we were able to simultaneously track cell translation and rotation based on cell nucleus. As shown, for a representative cell in a colony (Fig. 1 d), we can easily map both the spatiotemporal dynamics of cell translation and rotation (Fig. 1, e–g). As indicated (Fig. 1 e), traction forces were indicated by yellow vectors inside the cell, whereas intercellular forces were indicated by blue vectors acting on the cell along the cell boundary. Together, we have established an analytical mechanobiology system in which the translation and rotation behaviors of a cell and single-cell mechanical forces (traction and intercellular forces) can be readily characterized for a migrating single cell within cell colonies.

Cell translation is dominantly regulated by cell-matrix force

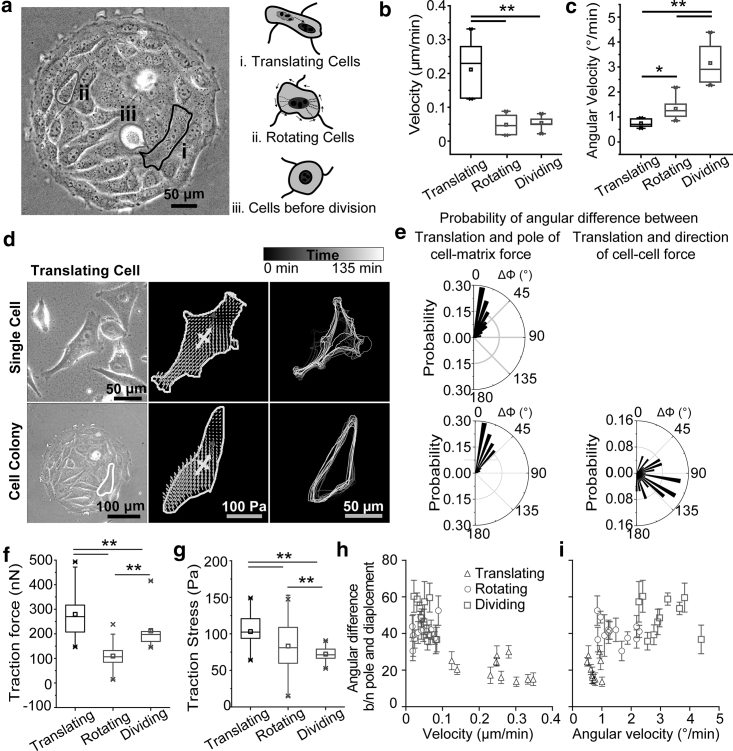
When inspecting cells in a multicellular context, we found that cells displayed distinct migratory behaviors. By quantifying the translation velocity and angular rotation velocity, we defined the cell migratory behaviors into three phenotypes: translating, rotating cells and nonmigrating, dividing cells (Fig. 2 a). We identified dividing cells by tracking cell division using phase-field images (Fig. S8). Translating cells exhibited a significantly larger translation velocity compared to rotating and dividing cells (Fig. 2 b), whereas rotating cells displayed a significantly larger unregulated angular rotation (Fig. 2 c). The dividing cells showed some similarity in their behavior with rotating cells by demonstrating minimal translation but differed from them owing to their unusually large angular rotation velocity (Fig. 2, b and c).

Figure 2.

Effect of forces in guiding translation in cells in a monolayer. (a) Different types of cells inside a colony, translating, rotating, and dividing cells. (b) Graph shows the distribution of angular difference between the pole of traction force and the displacement of the cells with (b) cellular velocity and (c) angular velocity, for translating, rotating, and dividing cells. (d) Cellular translation in Single cell and translating cells in a cellular colony. The image on the extreme left shows the phase-field images of the cells; the middle image corresponds to the traction force (light gray arrows), matrix eigenvectors of traction field depicting the poles (white arrows), and the displacement of the nucleus between two time frames, 5 min apart (dark gray arrow); and the image on the extreme right corresponds to the trajectory of the cells over a period of 135 min. (e) Graph depicts the probability of the angle between the pole of the force and the cellular translation (left) and the probability of the angle between cell translation and the direction of intercellular force (right). (f) Box and whisker plot of the total cell-ECM force exerted by translating, rotating, and dividing cells. (g) Average traction stress (total traction force divided by total cell area) exerted by translating, rotating, and dividing cells shown by a box and whisker plot. (h) Error plot shows the angular difference between the pole of traction field and the cellular translation, plotted against the cellular velocity (left) and, (i) angular velocity (right). Data represent the mean ± error. The p-values were calculated using the Student’s paired sample t-test. ^∗p < 0.05, ^∗∗p < 0.001. Number of cells ≥10, and the number of experiments = 4 for each condition.

After observing distinct cell migratory behaviors, we first explored the regulatory role of multiple forces for translating cell behaviors within cell colonies. To this end, an accurate description of the relation between mechanical force and cell translation is necessary. Single cells migrate directionally, at a small scale, and in a quasistatic way, where the sum of all vector forces acting on the cells at each time point usually cancels out, hence, the magnitude of force alone cannot provide us with the necessary information to account for the cell translation. A multipole analysis that explores the orientation and directionality of the force field has been previously described in determining the trajectory of cell migration (66). We adopted the analytical method to describe the translational dynamics of cells in a monolayer using nuclei centers to represent cell migration centers (80, 81, 82). We used the first order moment (M_ij) of the traction field, dubbed as the “force dipole,” which is defined as follows:

$$M_{ij}=\underset{S}{\int }{x}_i{T}_{j}dS;$$ (2)

where x_i and T_j are the ith and jth components of the position and the traction stress, respectively, on the substrate surface to relate the spatiotemporal coordination of mechanical forces with cell translation. A dipole matrix was generated using this analysis. Hence, we could accurately describe cell translation behaviors using dipole analysis and coordinate it with mechanical forces.

As shown in Fig. 2, d and e, the orientation of the force dipole for a single cell can be analyzed based on its matrix eigenvectors (white arrows), and the cell translation direction can be evaluated by measuring the displacement of the nucleus between two time frames. We can then correlate the force dipole with translation direction by calculating the angular difference (ϕ) between them. For single cells undergoing translation without intercellular forces (Fig. 2, d and e, top panel), we found that the pole of the force aligns strongly with the migration direction. Similar results were observed regarding cell-matrix force for translating cells in a monolayer (Fig. 2, d and e, bottom panel). However, no significant correlation was found between the intercellular force and the direction of translation for translating cells (Fig. 2, d and e, bottom panel), implying that forces from cell-cell interactions may not have a direct influence on translational motion. Traction forces indicated minimal effects on regulating the behaviors of rotating and dividing cells as we did not observe a correlation between the angular difference (ϕ) between force dipole and translational direction (Fig. S9). When considering the regulation of cell-matrix forces in cell translational motion, we also observed that traction forces for migrating cells are significantly larger than that of rotating and dividing cells (Fig. 2 f), regardless of cell spreading area (Fig. 2 g). Dividing cells demonstrated minimal traction forces compared to translating and rotating cells (Fig. 2, f and g). Moreover, we found that the plotting probability of angular difference between force dipole and translational direction (φ) for translating cells demonstrated a strong alignment between force dipole direction and translational motion direction (Fig. 2 e). As a result, cells showed distinctly higher translating velocity and lower angular velocity (Fig. 2, h and i), revealing that cell translational motion is largely regulated by traction force. Interestingly, although substrate stiffness has been shown to regulate the behaviors of cells, we did not see a significant change in the roles of traction and intercellular forces in guiding cellular translation and rotation behaviors on substrates of different stiffness (Fig. S10).

Intercellular torque change actively regulates cell rotation behavior

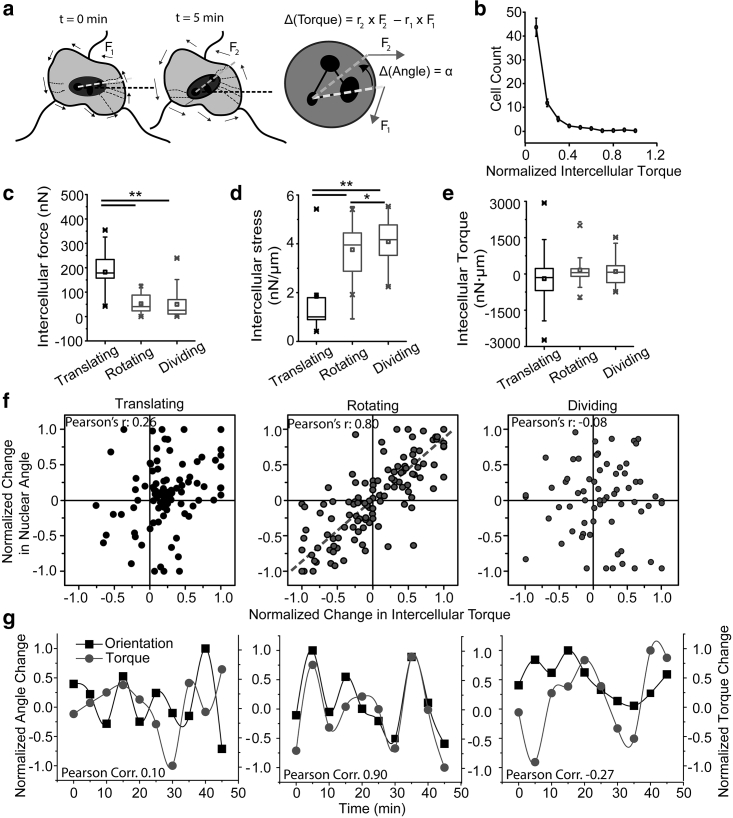
The second dynamic migratory behavior of cells observed in a monolayer is rotation. To understand the mechanism behind nuclear rotation, we used the first moment of the intercellular force to describe the effects of intercellular force on cell rotation (Fig. 3 a). In this situation, the force exerted on the cells is the intercellular force, and the point of action is the nucleus. We showed a tight coupling between the nuclear orientation and cellular orientation in translating cells (Fig. S7). Thus, the nucleus orientation is related to and can indicate the orientation of a cell during its rotation. To calculate the change in orientation of the nucleus, the nuclear bodies (black ellipsoids) on the nucleus were used to calculate the angle that the nucleus subtends along the laboratory axis. The laboratory x axis was defined as the horizontal axis of the cell image, and the y axis was defined as the vertical axis of the cell image, and they were kept constant throughout the experiment. The change in the nucleus angle characterizes the reorientation of the nucleus and the cell. By analyzing the intercellular torque for single cells in a monolayer, we found that most cells are subjected to minimal intercellular torque (Fig. 3 b). Comparing the three subtypes of cells, translating cells demonstrated higher total intercellular force acting on them (Fig. 3 c) yet had a lower intercellular stress as compared to rotating and dividing cells (Fig. 3 d). This is a result of the perimeter of the cells being directly correlated with the intercellular force acting on the cell (Fig. S4 e). We further found that there is no significant difference in the magnitude of torque acting on the cells (Fig. 3 e). To explore the relationship between cell rotation and intercellular torque, we closely monitored and mapped the dynamic changes of intercellular torque for the three cell subtypes. When plotting the normalized change of the nucleus angle against intercellular torque, we found that there is a strong correlation for rotating cells, whereas no correlation was found for migrating and dividing cells (Fig. 3, f and g). Overall, our results suggest that cell rotation behavior is dominated by intercellular torque.

Figure 3.

Intercellular torque change regulates cell angular velocity and has a more significant effect on rotating cells. (a) The concept of torque and the calculation of nuclear rotation. Here, forces are intercellular forces, and the distance is calculated between the nuclear centroid and the point of action of the force. (b) Plot shows the distribution of intercellular torque in a cellular colony. (c) Box and whisker plot shows the intercellular force acting on translating, rotating, and dividing cells. (d) Intercellular stress acting on translating, rotating, and dividing cells, signifying the force per unit interface length, as depicted by a box and whisker plot. (e) Box and whisker plot shows the distribution of intercellular torque acting on translating, rotating, and dividing cells. (f) Scatter plot shows the normalized change in nuclear angle versus the normalized change in intercellular torque in translating, rotating, and dividing cells. (g) Representative curves of normalized change in nuclear orientation and the normalized change in nuclear torque over a period of 45 min in translating, rotating, and dividing cells, and measurements were taken every 5 min. Data represent the mean ± error. The p-values were calculated using the Student’s paired sample t-test. ^∗p < 0.05, ^∗∗p < 0.001. Number of cells ≥10, and the number of experiments = 4 for each condition.

Conclusions

Cells in vivo are physically constrained by their neighboring cells, and intercellular signaling is a fundamental biochemical and biophysical cue that may influence cell/tissue behaviors along with cell-ECM interactions. For multicellular tissues, understanding the mechanobiology of the collective behaviors of cell colonies has been established using micropatterning techniques (83, 84, 85, 86, 87). Methods to measure intercellular forces in such systems have also been explored with variations in the distribution of traction forces and velocity correlations (50,51,53). However, these studies have a limited focus on the collective behaviors of cells and fail to consider mapping intercellular and traction forces at a single-cell resolution. Hence, we applied a mechanobiological system (51) that could characterize the mechanical forces of cells in a colony at a single-cell scale from cell-matrix and cell-cell interactions to study their regulatory effects on different cellular migratory behaviors. We performed our analysis on confluent confined monolayers (Fig. 1 a) with well-established intercellular contacts that can be approximated as a flat plate for the purpose of analysis (53,88). In addition, cells during this phase undergo significant rearrangements, which make it feasible to observe the roles of forces in directing single-cell migration. The studies of single-cell migration have shown two different modes in normal cells, in which cells are elongated and move in a directional manner (translocation), whereas cells that are round are associated with rotational behaviors (rotation) (4, 5, 6). Drawing parallels from this, we hypothesized three different types of cell modes in a colony: two migrating, translating and rotating, cell types and one nonmigrating (dividing) cell type. Indeed, our results showed that there was a significant difference in the translational velocity and angular velocity of the cells from different groups (Fig. 2, b and c). Furthermore, single-cell studies have previously shown differences in forces exerted by the cells of different morphologies, with elongated cells exerting more forces as compared to rounded cells (49). We found that the traction force (Fig. 2 f) and intercellular force (Fig. 3 d) acting on translating cells was significantly larger than the other two groups, respectively, owing to the dynamic nature of the cells. However, the intercellular stress (i.e., the intercellular force acting on a cell divided by the length of the interface between two cells) (Fig. 3 f) acting on translating cells was significantly lower than on stationary and dividing cells. This points to the fact that intercellular adhesion between translating cells is weaker than that of stationary cells. Furthermore, our results demonstrate that, in accordance with the trend found in single cells in which traction force is the primary mediator of the displacement, traction force is reasoned to be the primary cause of cell migration (Fig. 2 e). In addition, intercellular force does not correlate with the cell displacement (Fig. 2 e), which shows that cells are not undergoing collective migration in this phase but rearrangement. However, intercellular forces have been intimately linked with the organization of forces in a cell colony, shown by the fact that the absence of intercellular forces results in an uncharacteristic traction force distribution in patterned cellular colonies (20). During collective cell migration, we observed that forces in the colony were concentrated on the edge, displaying intact intercellular force transmission (Fig. S3 b; (30)).

Hence, the question remains: how does intercellular force affect cell organization in a multicellular colony? To determine its regulatory role, we used the intercellular torque acting on the nuclear center of the cell (dubbed “torque of the intercellular force”) and correlated it to cell rotation (Fig. 3 a), which is a key mediator in cell directionality (80,89). Previous studies have shown that translating cells have a well-established actin network in the form of an actin cap, prompting directional migration. Furthermore, the nucleus is coupled to cytoskeleton (CSK) filaments and exposed to dynamic mechanical forces from the CSK that may actively regulate nucleus dynamics (90). Previous studies have revealed that the migratory dynamics of the nucleus are mediated by CSK filaments (microtubules and F-actin) and linkers of nucleoskeleton and CSK complex proteins (91). Thus, intercellular force should not influence the directionality of translating cells (Fig. 3, g and h; (80,92,93)). Similarly, dividing cells undergo significant changes in their actin network and, therefore, cannot use mechanical inputs to activate proper or feedback-appropriate changes (Fig. 3 g; (94)). We determined that translating cells had an insignificant angular velocity, whereas dividing cells had a distinctly large angular velocity (Fig. 2 c). Furthermore, our results indicated no correlation between the change in the torque of the intercellular force and the angular rotation of the nucleus in the case of translating or dividing cells (Fig. 3 h). However, for rotating cells, we saw a strong correlation between the change in torque and the angular rotation, emphasizing that the intercellular forces are affecting single-cell migration through cell reorientation (Fig. 3 h).

Our study conclusively illustrated the effects of cell forces on reconfiguring cell organization in a confluent confined pattern, in which cell-generated forces have a direct effect, whereas the intercellular forces have an indirect effect in determining cell migration. By applying this integrated mechanobiology system, we clearly distinguished between the effects of the traction and intercellular force on different types of cells and showed that intercellular forces play a guiding role in migratory dynamics. This can help us in differentiating between cells, in which more individualistic cells (e.g., cancer cells) may have less correlation with intercellular forces, whereas more organotypic cells will be more susceptible to them. Our study is currently focused on cells that form monolayers inside the body, like endothelial and epithelial cells. It would be interesting to see how three-dimensional ensembles (e.g., blood vessels, tumors, etc.) affect changes in forms due to cellular forces and how promoting or inhibiting intercellular forces in these collectives can result in differentiated modes of migration in the future. Further, it may also be interesting to see if we can use external impulses (e.g., fluid shear stresses) and assess their effect in altering the cellular forces and how these forces help in tissue reorganization in such conditions.

Author Contributions

A.B., J.T., W.Q., and W.C. designed research. A.B., J.T., W.Q., and Y.P. performed experiments and modeling. A.B., J.T., W.Q., and W.C. analyzed data and wrote the manuscript. W.C. supervised the project. All authors edited and approved the final manuscript.

Editor: Cynthia Reinhart-King.