Highlights
-
•
Statistical Process Control metrics can assess linac operational performance.
-
•
Linacs produced in series have statistically different operating parameters.
-
•
Although having different operating parameters, linacs have similar performance.
Keywords: Statistical process control, Medical linear accelerator, Performance, Quality assurance
Abstract
The purpose of this study was to determine if medical linear accelerators (linac) produced by the same manufacturer exhibit operational consistency within their subsystems and components. Two linacs that were commissioned together and installed at the same facility were monitored. Each machine delivered a daily robust quality assurance (QA) irradiation. Linacs and their components operate consistently, but have different operational parameter levels even when produced by the same manufacturer and commissioned in series. These findings have implications on the feasibility of true clinical beam matching.
Introduction
A medical linear accelerator (linac) requires meticulous checks of internal components to ensure that its output is consistent for daily operation. Internal components are subjected to various tests to ensure that they are consistent. Linacs built by the same manufacturer should be similar both internally and externally: internal components behave in a similar fashion and external radiation output measurements yield the same desired result. The purpose of this study was to determine if linacs produced by the same manufacturer exhibit operational consistency within their subsystems and components. Operational consistency facilitates detection of performance changes. Establishing universal operating parameter standards should allow for more efficient and uniform linac commissioning and maintenance processes. We hypothesize that linacs of the same model that operate with similar performance characteristics will have similar and consistent subsystem parameters.
Methods and materials
Linac performance testing
Two linacs produced by the same manufacturer that were commissioned in series and installed at the same facility were monitored. Each machine delivered a daily robust quality assurance (QA) irradiation designed to assess the interplay between gantry angle, multi-leaf collimator (MLC) position, and fluence delivery in a single delivery [1]. The QA irradiation consisted of delivering dose at narrow angular sectors by maximum gantry acceleration and deceleration. In turn, MLC position could be analyzed due to the delayed displacement of the MLC gap from one position to the other before coming to an abrupt halt at the moment of delivery [1]. Each QA irradiation generated trajectory and text log files that were used to monitor various operational components and subsystem performance. The resulting log files from the irradiation were transferred, decoded, analyzed, regrouped, and subjected to Statistical Process Control (SPC) analytics [2], [3], [4], [5], [6], [7], [8]. All computer code was written in MATLAB (Mathworks, Inc. Natick, MA, USA) [9]. The QA irradiation delivery parameters reported here are representative of the 525 performance parameters being monitored.
The performance parameters investigated belong to two major subsystems: beam generation and monitoring (BGM) and motion control (gantry, collimator, MLC, etc.). The BGM subsystem is responsible for setting the operating values for beam generation components. Motion control subsystems control the movements of the machine and consist of the various motion axes that move the machine and support the delivery of the beam [10], [11], [12], [13].
The BGM subsystem consists of a central controller board and five subnode boards. The central controller board monitors all beam functions to ensure that the beam remains within manufacturer tolerance [14], [15], [16]. The board will interlock the linac when the beam is outside of these limits [10], [11], [12], [13]. The BGM-Pulse Width Modulation (PWM) subnode controls the coils that steer the beam [10], [11], [12], [13], [17]. Thus, differences in performance parameters in this subnode can show that linacs deliver a similar beam at varying operational performance values. Performance parameters within each subnode of the BGM subsystem were investigated in greater detail to determine how differently they performed within each linac.
Subsystem motion is controlled through the Supervisor (SPV) by motors that drive motion axes and sensors that provide feedback [10], [11], [12], [13]. Based on information from the treatment plan, the SPV determines the required positions of each of the axes and the dose to be delivered. The SPV then sends commands for all motions to the nodes for each of the axes. If the SPV does not receive a feedback reply from the nodes or the nodes do not receive instructions from the SPV, the subsystem issues a communication fault interlock, and stops the treatment [15], [16], [17].
Statistical testing
SPC analytics consisted of calculating the individual grand mean, moving range and grand mean (I/MR) chart values. They were determined as follows:
| (1) |
| (2) |
| (3) |
where T = 20, It is the individual value of the performance parameter, and MR is the moving range. Control chart limits were calculated as follows:
| (4) |
| (5) |
| (6) |
where d2 is a normality constant that is dependent upon the sample size.
Each operating performance parameter was subjected to a ranked analysis of variance (ANOVA) to determine if there were differences between each of their parameter means [18]. The distributions of the outcomes were analyzed and due to outliers we used non-parametric approaches for the analysis. The use of non-parametric methods is needed due to data outliers having a non-normal distribution. We believe the statistical approach used is correct due to the highly skewed distributions in the data and do not believe these are due to error in measurement. A ranked ANOVA was performed because each accelerator had an unequal amount of QA irradiation deliveries. Each original data point value is ranked from 1 for the smallest to N for the largest. Ranking improves the data set by adding robustness to non-normal errors (due to unequal sample sizes) and resistance to outliers [18]. Parameters were also graphically compared using their parameter medians and performance operating window. The median is reported because it is a better measure of centrality than the mean when outliers are present [4], [5], [6], [8]. The “range” is the minimum and maximum median of a parameter.
To depict the differences, the medians of the “I” chart values were plotted for each performance parameter within each subnode. Another visual investigation to further test this theory was examining how each performance parameter deviated from its overall median value. This interpretation provides a method of determining whether a performance parameter operates at a single, specific value. An overall median value was determined for each performance parameter in each subnode for each linac. A final investigation used the calculated limits of each performance parameter. This procedure depicts the operating window in which the parameter is performing for each linac [3], [4], [5], [6], [7], [8], [19], [20], [21], [22], [23].
Results
As detailed in the subsections below, linacs produced by the same manufacturer and commissioned in series were found to be statistically and operationally different (p-value < 0.00001). Each monitored performance parameter was statistically different and operated at a unique, distinct value. Yet, each linac met clinical treatment performance specifications as recommended by TG-142 with no output changes observed during the monitoring process.
Beam generation and monitoring
Table 1 shows performance parameters contained within the BGM-PWM subnode. It is representative of all subnodes and their respective performance parameters contained within the BGM subsystem. The results of the ranked ANOVA indicate that performance parameters monitored within each subnode of the BGM subsystem were statistically different between linacs (p-value < 0.00001). The initial results indicate that each performance parameter operate collectively at a distinct and consistent value.
Table 1.
Statistics for BGM-PWM performance parameters in two linacs.
| Performance parameter | Range | P-value |
|---|---|---|
| Buncher Radial Current (A) – BRC | −0.110 to 0.125 | <0.00001 |
| Buncher Transverse Current (A) – BTC | 0.065 to 0.115 | <0.00001 |
| Angle Radial Current (A) – ARC | −0.064 to 0.006 | <0.00001 |
| Angle Transverse Current (A) – ATC | −0.007 to 0.011 | <0.00001 |
| Position Radial Current (A) – PRC | −0.847 to 0.273 | <0.00001 |
| Position Transverse Current (A) – PTC | 0.296 to 0.759 | <0.00001 |
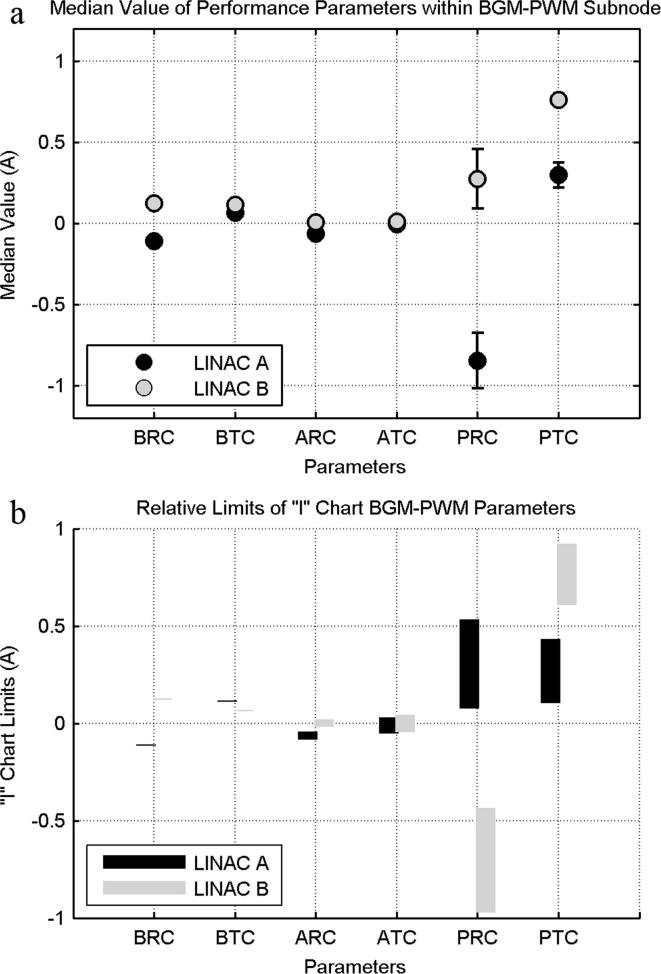
It was visually determined that for each performance parameter, each linac had distinct median values (Fig. 1). Performance parameters related to beam symmetry or flatness in the radial and transverse planes had median values that were consistently different (Fig. 1a). The median values in the Position coils were larger than those in the Buncher and Angle steering coils. Each parameter had a unique operating window characteristic of that particular linac; i.e., there was minimal overlap when comparing against each other (Fig. 1b). Thus, linacs and their components operate consistently but perform at different operational values even when produced by the same manufacturer and commissioned in series.
Fig. 1.
Graphical analysis of the BGM-PWM subnode. (a) Median values for the BGM-PWM parameters of the two linacs in this study. The median values show that each linac performance parameter is distinct. (b) The control limits of the “I” chart for BGM-PWM parameters of two linacs. The control limits show that each linac has its own operating window.
Motion control
Table 2 reports the important linac delivery parameters contained within the motion control subsystem. The results of the ranked ANOVA indicate that performance parameters monitored within the motion control subsystem were also statistically different (p-value < 0.00001). This suggests that each performance parameter operates at a distinct value. Although it appears that the maximum difference of certain parameters is zero, the distribution of the ranks shows the parameters are statistically different between the machines. Leaf Speed 2 in MLC Bank A and Leaf Speed 1 in MLC Bank B had statistical values greater than other parameters within this subsystem; however, they were still statistically different (p-value < 0.01).
Table 2.
Statistics for motion control performance parameters in two linacs.
| Performance parameter | Range | P-value |
|---|---|---|
| Gantry speed 1 | 4.994 to 4.993 | <0.00001 |
| Gantry speed 2 | 5.679 to 5.672 | <0.00001 |
| MLC bank A speed 1 | 1.8287 to 1.8283 | <0.00001 |
| MLC bank A speed 2 | 2.400 to 2.400 | 0.006 |
| MLC bank B speed 1 | 2.417 to 2.417 | 0.01 |
| MLC bank B speed 2 | 2.279 to 2.417 | <0.00001 |
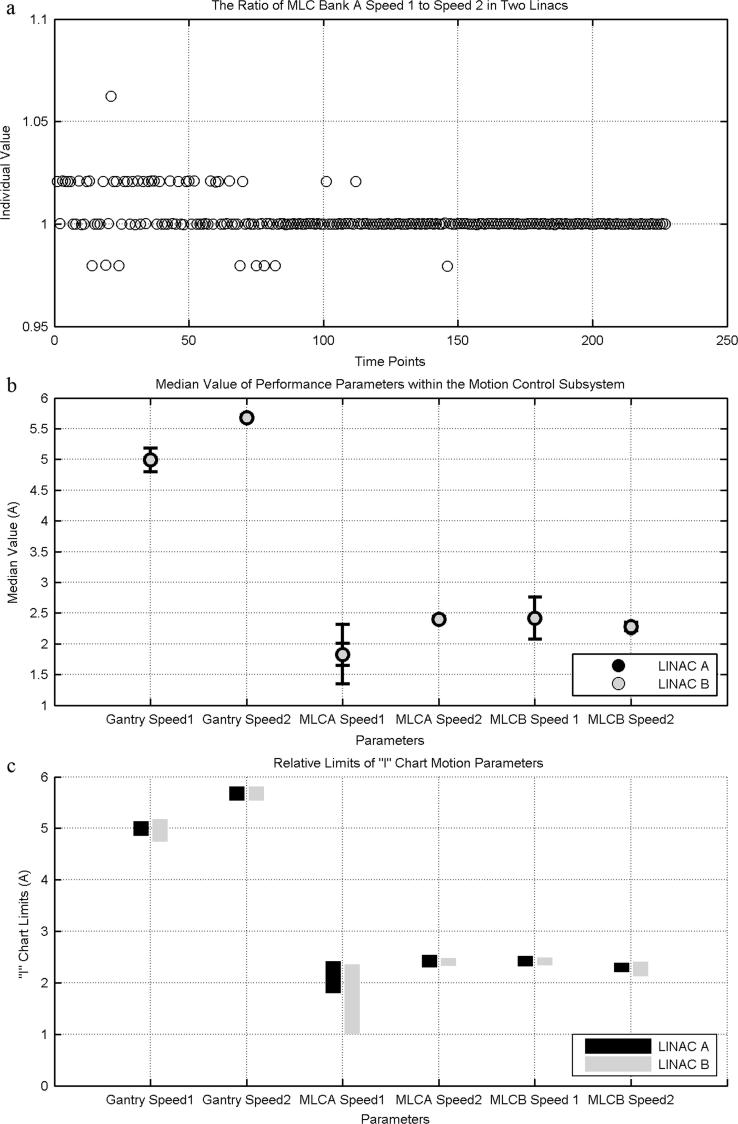
As in the BGM-PWM subnode, each linac had distinct median values (Fig. 2). Gantry and MLC speeds were depicted for their importance to beam delivery [1], [11], [24], [25], [26], [27], [28], [29], [30], [31], [32], [33], [34], [35], [36], [37]. Speeds were calculated by assessing sectors of the delivery that used maximal gantry acceleration (Speed 1) and deceleration (Speed 2). Gantry and MLC speeds had median values that were consistently different between linacs; however, beam delivery was unaffected by these changes within clinical tolerances.
Fig. 2.
Graphical analysis of Motion Control parameters. (a) The ratio of MLC speeds in Bank A of two linacs. The spread of the data shows that these parameters are different from each other. (b) Median values for Motion Control parameters of the two linacs in this study. The median values show that each linac performance parameter is distinct. (c) The control limits of the “I” chart for the Motion Control parameters of two linacs. The control limits show that each linac has its own operating window.
Discussion
Linacs manufactured and commissioned in series do exhibit overall operational consistency within their subsystems. Both linacs produced the same beams, within clinical tolerances as prescribed by TG-142, despite their differences in performance parameters and subsystems having different values. The more important subsystems exhibited variations which highlighted the differences between these two linacs manufactured and commissioned in series. The causes of these variations stem from a number of factors, both internal, such as the assembly of each individual component, and external, such as the design procedure by mechanical and/or human processes [4], [5], [6], [8]. The magnitudes of differences of the various performance parameters are small. The magnitudes of these parameters do not directly correlate to a specific performance function rather they are indicators that performance may be changing. The goal was that the operating parameters were close enough to each other so that a universal standard could be applied to all similar linacs when being commissioned.
Linac performance variation can be affected by each individual component, each with its own performance tolerance. Although these components may only vary slightly, the subtle differences can affect the overall performance. Thus, each individual component has a tolerance level set forth by the manufacturer which deems the product acceptable for use. Since each subsystem is comprised of several components, the total variation grows larger due to propagation in quadrature of each individual component variation. Even if individual components are performing differently from each other, if the operation of the final product yields the desired result, then operational consistency of the final product is favored over the performance consistency of its internal components.
SPC techniques can offer a solution in identifying variation within a process [4], [5], [6], [7], [8], [19], [20], [21], [22], [23], [25], [28], [34], [35], [36], [37], [38], [39], [40], [41]. Statistical and graphical analysis using SPC metrics revealed that each performance parameter had its own operating window in which operational consistency of linacs was maintained. Although the median values and performance windows were relatively similar to each other, these metrics can be used to establish a universal configuration file for commissioning and identify an overall tolerance level for each subsystem. The importance of identifying this tolerance level is that it can then be used to detect undesirable values before malfunctions occur. These tolerance levels can also be used to justify a course of action to return the subsystem to optimal levels [4], [5], [6], [7], [8], [19], [20], [21], [22], [23], [25], [28], [34], [35], [36], [37], [38], [39], [40], [41]. There are also interdependencies between the parameters measured such that if one changed, one would expect that change to affect other parameters. Determining correlations between the various parameters and the corresponding subsystem tolerances with respect to clinically observable deviations in beam delivery is an intended aim of future work.
Conclusion
Linacs are highly complex machines that consist of many subsystems. Similar linacs that were manufactured and commissioned sequentially were found to have unique operational parameters, but consistently had similar performance with each other while collectively meeting all clinical delivery specifications as prescribed by TG-142. SPC techniques were used to identify results and can further be implemented to identify similarities and differences in performance and operation.
Conflict of interest
All authors claim they do not have a conflict of interest.
Acknowledgments
This work was supported in part by a research grant from Varian Medical Systems, Inc (Palo Alto, CA). The authors thank Alois Ndlovu, Ph.D. and Irene Rebo, Ph.D. of John Theurer Cancer Center at Hackensack University Medical Center in Hackensack, NJ for providing the log files used in this work.
Footnotes
Supplementary data associated with this article can be found, in the online version, at https://doi.org/10.1016/j.tipsro.2018.05.001.
Contributor Information
Callistus M. Nguyen, Email: canguyen@wakehealth.edu.
Alan H. Baydush, Email: abaydush@wakehealth.edu.
James D. Ververs, Email: jververs@wakehealth.edu.
Scott Isom, Email: sisom@wakehealth.edu.
Charles M. Able, Email: cable@flcancer.com.
Michael T. Munley, Email: mmunley@wakehealth.edu.
Appendix A. Supplementary material
References
- 1.Van Esch A. Implementing RapidArc into clinical routine: a comprehensive program from machine QA to TPS validation and patient QA. Med Phys. 2011;38(9):5146–5166. doi: 10.1118/1.3622672. [DOI] [PubMed] [Google Scholar]
- 2.Burr I.W. The effect of non-normality on constants for X-bar and R charts. Ind Qual Control. 1967;23(11):563–568. [Google Scholar]
- 3.Montgomery D. 6th ed. John Wiley & Sons Inc.; Hoboken, New Jersey: 2009. Introduction to statistical quality control. [Google Scholar]
- 4.Oakland J., Control Statistical Process. ButterWorth-Heinemann; Oxford, UK: 2008. Jordan hill. [Google Scholar]
- 5.Robert T, Amsden HEB, Amsden Davida M. SPC: simplified practical steps to quality, 2nd ed. New York, NY, USA: Productivity Press; 1998.
- 6.Stapenhurst T., Control Mastering Statistical Process. UK ButterWorth-Heinemann; Oxford: 2005. Jordan hill. [Google Scholar]
- 7.Wheeler D.J. SPC Press; Knoxville: 2000. Normality and the process control chart. [Google Scholar]
- 8.Wheeler D.J., Chambers D.S. 2nd ed. TN SPC Press; Knoxville: 1992. Understanding statistical process control; p. 401. [Google Scholar]
- 9.MATLAB and Statistics Toolbox Release 2013a. The Mathworks, Inc.: Natick, Massachusetts, United States; 2013.
- 10.Karzmark CJ, Nunan Craig S., Tanabe E. Medical electron accelerators. McGraw-Hill, Inc.; 1993. p. 336.
- 11.Dyk J.V. Medical Physics Publishing; Madison, Wisconsin: 1999. The modern technology of radiation oncology; p. 1073. [Google Scholar]
- 12.Karzmark C.J., Morton R.J. 2nd ed. Medical Physics Publishing; Madison, WI: 1998. A primer on theory and operation of linear accelerators in radiation therapy; p. 50. [Google Scholar]
- 13.Loew GA, Talman R. Elementary principles of linear accelerators, vol. 91; 1983. http://doi.org/10.1063/1.34235.
- 14.Varian Medical Systems I. TrueBeam high-intensity energy configurations: performance and operational characteristics; 2012.
- 15.Varian Medical Systems I. TrueBeam administrators guide; 2014.
- 16.Varian Medical Systems I, TrueBeam technical reference guide; 2015.
- 17.Khan F. Lippincott Williams & Wilkins; PA, USA: 2003. The physics of radiation therapy. [Google Scholar]
- 18.Conover W.J., Iman R.L. Rank transformations as a bridge between parametric and nonparametric statistics. Am Stat. 1981;35(3):124–129. [Google Scholar]
- 19.Able C., Baydush A. Effective control limits for predictive maintenance (PdM) of accelerator beam uniformity. Med Phys. 2013;40(6):1. [Google Scholar]
- 20.Able C., Baydush A., Hampton C. Statistical process control methodologies for predictive maintenance of linear accelerator beam quality. Med Phys. 2011;38(6) p. 3497-3497. [Google Scholar]
- 21.Able C.M. Initial investigation using statistical process control for quality control of accelerator beam steering. Radiat Oncol. 2011;6:180. doi: 10.1186/1748-717X-6-180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Duncan A.J. 4th ed. Richard D. Irwin Inc.; Hornewood, Illinois: 1974. Quality control and industrial statistics. [Google Scholar]
- 23.Roberts S.W. Properties of control chart zone tests. Bell Syst Tech J. 1958;37(1):83–114. [Google Scholar]
- 24.Able C. MLC predictive maintenance using statistical process control analysis. Med Phys. 2012;39(6) doi: 10.1118/1.4735265. p. 3750-3750. [DOI] [PubMed] [Google Scholar]
- 25.Agnew A. Monitoring daily MLC positional errors using trajectory log files and EPID measurements for IMRT and VMAT deliveries. Phys Med Biol. 2014;59(9):N49–N63. doi: 10.1088/0031-9155/59/9/N49. [DOI] [PubMed] [Google Scholar]
- 26.Bai S. Effect of MLC leaf position, collimator rotation angle, and gantry rotation angle errors on intensity-modulated radiotherapy plans for nasopharyngeal carcinoma. Med Dosim. 2013;38(2):143–147. doi: 10.1016/j.meddos.2012.10.002. [DOI] [PubMed] [Google Scholar]
- 27.Basran PS, Woo MK. An analysis of tolerance levels in IMRT quality assurance procedures. Med Phys 2008;35(6 Part 1):2300–7. [DOI] [PubMed]
- 28.Breen S.L. Statistical process control for IMRT dosimetric verification. Med Phys. 2008;35(10):4417–4425. doi: 10.1118/1.2975144. [DOI] [PubMed] [Google Scholar]
- 29.Fraass B. American Association of Physicists in Medicine radiation therapy committee task group 53: Quality assurance for clinical radiotherapy treatment planning. Med Phys. 1998;25(10):1773–1829. doi: 10.1118/1.598373. [DOI] [PubMed] [Google Scholar]
- 30.Gérard K. A comprehensive analysis of the IMRT dose delivery process using statistical process control (SPC) Med Phys. 2009;36(4):1275–1285. doi: 10.1118/1.3089793. [DOI] [PubMed] [Google Scholar]
- 31.Greene D, Williams PC. Linear accelerators for radiation therapy, 2nd ed. Medical science. New York, NY: Taylor & Francis Group; 1997.
- 32.Klein E.E. Task Group 142 report: quality assurance of medical accelerators. Med Phys. 2009;36(9):4197–4212. doi: 10.1118/1.3190392. [DOI] [PubMed] [Google Scholar]
- 33.Kutcher G.J. Comprehensive QA for radiation oncology – report of AAPM radiation-therapy committee task-group-40. Med Phys. 1994;21(4):581–618. doi: 10.1118/1.597316. [DOI] [PubMed] [Google Scholar]
- 34.Pawlicki T., Mundt A.J. Quality in radiation oncology. Med Phys. 2007;34(5):1529–1534. doi: 10.1118/1.2727748. [DOI] [PubMed] [Google Scholar]
- 35.Pawlicki T., Whitaker M., Boyer A.L. Statistical process control for radiotherapy quality assurance. Med Phys. 2005;32(9):2777–2786. doi: 10.1118/1.2001209. [DOI] [PubMed] [Google Scholar]
- 36.Pawlicki T. Process control analysis of IMRT QA: implications for clinical trials. Phys Med Biol. 2008;53(18):5193–5205. doi: 10.1088/0031-9155/53/18/023. [DOI] [PubMed] [Google Scholar]
- 37.Pawlicki T. Moving from IMRT QA measurements toward independent computer calculations using control charts. Radiother Oncol. 2008;89(3):330–337. doi: 10.1016/j.radonc.2008.07.002. [DOI] [PubMed] [Google Scholar]
- 38.Able C., Hampton C., Baydush A. Flatness and symmetry threshold detection using statistical process control. Med Phys. 2012;39(6) doi: 10.1118/1.4735268. p. 3751-3751. [DOI] [PubMed] [Google Scholar]
- 39.Hampton C.J., Able C.M., Best R.M. Statistical process control: quality control of linear accelerator treatment delivery. Int J Radiat Oncol Biol Phys. 2010;78(3):S71. [Google Scholar]
- 40.Jennings I.D. Predictive maintenance for process machinery. Min Technol. 1990;72:111–118. [Google Scholar]
- 41.Rah J.-E. Feasibility study of using statistical process control to customized quality assurance in proton therapy. Med Phys. 2014;41(9) doi: 10.1118/1.4893916. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.