An Electrophysiological Approach to Measure Changes in the Membrane Surface Potential in Real Time

Abstract

Biological membranes carry fixed charges at their surfaces. These arise primarily from phospholipid headgroups. In addition, membrane proteins contribute to the surface potential with their charged residues. Membrane lipids are asymmetrically distributed. Because of this asymmetry, the net-negative charge at the inner leaflet exceeds that at the outer leaflet. Changes in surface potential are predicted to give rise to apparent changes in membrane capacitance. Here, we show that it is possible to detect changes in surface potential by an electrophysiological approach; the analysis of cellular currents relies on assuming that the electrical properties of a cell are faithfully described by a three-element circuit (i.e., the minimal equivalent circuit) comprised of two resistors and one capacitor. However, to account for changes in surface potential, it is necessary to add a battery to this circuit connected in series with the capacitor. This extended circuit model predicts that the current response to a square-wave voltage pulse harbors information, which allows for separating the changes in surface potential from a true capacitance change. We interrogated our model by investigating changes in the capacitance induced by ligand binding to the serotonin transporter and to the glycine transporters (GlyT1 and GlyT2). The experimental observations were consistent with the predictions of the extended circuit. We conclude that ligand-induced changes in surface potential (reflecting the binding event) and in true membrane capacitance (reflecting the concomitant conformational change) can be detected in real time even in instances in which they occur simultaneously.

Significance

The plasma membrane of a cell possesses fixed charges on both surfaces. Surface charges play an important role in many biological processes. However, the mechanisms, which regulate the surface charge densities at the plasma membrane, are poorly understood. This is in part due to lack of experimental approaches that allow for detecting changes in surface charges in real time. Here, we show that it is possible to track alterations in the electric potential at the membrane surface with high temporal resolution by an electrophysiological approach. Importantly, the described method allows for discriminating between a change in surface potential and a change in true membrane capacitance (e.g., a change in membrane area), even if these occur in parallel.

Introduction

Membrane capacitance recordings are primarily suited for measuring the plasma membrane surface area and changes thereof, with exquisite sensitivity (1, 2). For instance, techniques to measure the capacitance are ideally suited for this purpose; it is possible to detect a change in surface area resulting from the fusion of a single vesicle with the plasma membrane (3). However, it has long been known that membrane proteins can also contribute to the measured membrane capacitance (4, 5). For instance, in membranes containing a large number of voltage-gated ion channels, the measured capacitance is comprised of two components: a voltage-independent component that can be ascribed to the membrane and a voltage-dependent component that arises from mobile charges present in the voltage-sensing domains of the channels. Similarly, capacitance measurements also allow for monitoring conformational rearrangements that occur in membrane transporters. It has, for instance been possible to infer the conformational transition associated with phosphorylation of the Na⁺/K⁺-pump or to track the conformational rearrangement associated with Cl⁻ binding to the inward facing conformation of the γ-aminobutyric acid transporter 1 (6).

In all of the above cases, the observed changes were assumed to reflect true changes in the membrane capacitance arising from alterations in the polarizability of membrane-embedded proteins. Macroscopically, these alterations can be described as a result of changes in relative permittivity of the protein (i.e., dielectric constant). Theoretical estimates for the relative permittivity of folded proteins fall into the range between 2.5 and 4 (7). Different conformations of a protein may exhibit differences in their polarizability; if this is the case, the conformational rearrangement is expected to be measurable by capacitance recordings. However, alterations in the permittivity of a protein are not the only cause for a protein-associated capacitance change. We previously reported that the application of cocaine to HEK293 cells stably expressing the human SERT (hSERT) resulted in a reduction of membrane capacitance. We hypothesized that the change evoked by cocaine originated from a change in the outer surface potential caused by the binding of the charged ligand to serotonin transporter (SERT) rather than from a true capacitance change. Accordingly, we referred to this alteration as an apparent change in capacitance (8).

Cellular currents are usually assumed to be produced by a three-element circuit comprised of a capacitor (C_M) representing the membrane and two resistors (R_S and R_M) representing the series resistance and membrane resistance, respectively (i.e., minimal equivalent circuit of a cell) (9). However, the three-element circuit cannot account for the apparent change in capacitance that occurs as a consequence of charged ligand binding to a membrane protein. Here, we show that cellular currents are better described by an extended circuit, which contains an additional battery. This battery, which is connected in a series with the capacitor, can account for the ligand-induced change in surface potential. This allows for modeling the apparent capacitance change. Importantly, the extended circuit also predicts differences in the currents produced by a true and an apparent capacitance change. We verified these predictions by documenting that ligand-induced alterations and true capacitance changes can be differentiated based on information contained in current responses to a square-wave voltage stimulus. Importantly, our findings show that the measured current responses reveal information that allows for monitoring changes in the surface potential of the cell and in membrane capacitance and also in those instances in which they occur simultaneously.

Methods

Cell culture

hSERT tagged with GFP was stably expressed in a tetracycline-inducible HEK293 cell line. HEK293 cells have been previously authenticated by short tandem repeat profiling at the Medical University of Graz (Cell Culture Core Facility, Graz, Austria). Cercopithecus aethiops SV40-transformed kidney (Cos-7) cells were obtained from American Type Culture Collection (CRL-1651; Manassas, VA). Cos-7 were transfected with a plasmid encoding N-terminally GFP-tagged hGlyT1b or hGlyT2a, respectively; the complementary DNAs of hGlyT1b in eGFP-C-1 and hGlyT2b in pcDNA3.1(+)-N-eGFP were bought from GenScript (New York, NY). The transfection was performed with jetPRIME (0.8 μg DNA/dish) according to the manufacturer’s protocol. All cells were maintained in Dulbecco's Modified Eagle’s Medium containing 10% fetal bovine serum. Twenty-four hours before the experiment, the cells were seeded at low density onto poly-D-lysine-coated dishes (35 mm Nunc Cell culture dishes, Thermo Fisher Scientific, Waltham, MA).

Membrane capacitance measurements using voltage square-wave stimulation

Recordings were performed in the whole-cell configuration using an Axopatch 200B amplifier and pClamp 10.2 software (MDS Analytical Technologies, Downingtown, PA). A train of bipolar square-wave voltage pulses was applied with an amplitude ±40 mV and a frequency of 200 Hz. Currents were recorded at room temperature (20–24°C). In the protocol, the holding potential was set to 0 mV. Exponential current responses were low-pass filtered by a 10 kHz Bessel filter and digitized at 100 kHz using a Digidata 1440 (MDS Analytical Technologies). The cross talk between R_S and C_M was suppressed by the following procedure; the acquired current traces were first deconvoluted with the transfer function of the recording apparatus. Passive membrane parameters of a cell were calculated from the theoretical function as described elsewhere (10). The pipette capacitance was recorded in the cell-attached mode first and subtracted from the currents recorded in the whole-cell configuration before further analysis. The patch pipettes used had a resistance of 2–4 MΩ. To stabilize the level of stray capacitance, the pipettes were coated with hydrophobic resin Sylgard184 (Dow Corning, Midland, MI). The sensitivity of the method to changes in stray capacitance, series, and membrane resistance were scrutinized in great detail in (10). In the measurements, the cells were continuously superfused with an external solution containing 140 mM NaCl, 3 mM KCl, 2.5 mM CaCl₂, 2 mM MgCl₂, 20 mM glucose, and 10 mM HEPES (pH adjusted to 7.4 with NaOH). In experiments with Cl⁻-free external solution, NaCl⁻ was replaced by Na⁺MES⁻ (methanesulfonate). The internal solution in the patch pipette contained 152 mM NaCl, 1 mM CaCl₂, 0.7 mM MgCl₂, 10 mM HEPES, and 10 mM EGTA (ethylenglycol-bis(aminoethylether)-N,N,N′,N′-tetra-acidic-acid) (pH 7.2 adjusted with NaOH). Ligands were applied via a four-tube or eight-tube ALA perfusion manifold using the OctaFlow perfusion system (ALA Scientific Instruments, Farmingdale, NY), which allowed for complete solution exchange around the cells within 100 ms. We want to point out, however, that the solution exchange rate is immaterial to the method itself. The only effect of slow solution exchange is to misrepresent the true rate of the measured change. A detailed description of the method can be found in (11).

Membrane capacitance measurements with a dual-phase lock-in amplifier

Recordings were made using a dual-phase lock-in patch-clamp amplifier (SWAM-2C; Celica, Ljubljana, Slovenia). Signals were low-pass filtered at 10 Hz with a six-pole Bessel filter and digitized at 250 Hz by an analog to digital converter (CED 1401, Cambridge, UK) utilizing whole cell program software for acquisition (Dempster, University of Strathclyde, Glasgow, U.K.). HEK293 cells stably expressing hSERT were voltage clamped at a holding potential of 0 mV, on which a sine-wave voltage (111 mV rms, 1600 Hz) was superimposed. In the compensated mode of recording, one of two outputs of the dual-phase lock-in amplifier signal is directly proportional to changes in C_M. The correct phase angle was adjusted based on recordings elicited by the application of 1 pF calibration pulses. The patch pipettes used were coated with Sylgard184 and had a resistance of 2–4 MΩ. The employed solutions were the same as described above. For solution exchange, we used the OctaFlow perfusion system (see above).

Analysis of electrical circuits

Equivalent circuits were solved by loop analysis using Laplace transform. Below, we show the analytical solutions for current differences before and after the addition of a ligand in which inverse Laplace transform is indicated only formally. For the sake of space and clarity, we used substitutions.

Inverse Laplace transform of a difference of two analytical solutions of the circuit shown in Fig. 2 B and 6 A is as follows:

$$\mathit{\Delta }{I}_M={\mathcal{L}}^{-1}\left\{\left(\frac{\frac{V_M}{s}}{R_S+R_M\left(1-A\right)}+\frac{B·R_M}{R_S+R_M\left(1-A\right)}\right)-\left(\frac{\frac{V_M}{s}}{R_S+R_M\left(1-A_2\right)}+\frac{B_2·R_M}{R_S+R_M\left(1-A_2\right)}\right)\right\},$$

where,

$$A=\frac{R_M}{R_M+\frac{1}{C_{M\cdot }s}};B=\frac{\frac{V_S}{s}}{R_M+\frac{1}{C_{M\cdot }s}};A_2=\frac{R_M}{R_M+\left(\frac{1}{C_{M\cdot }s}-\frac{1}{\mathit{\Delta }{C}_{M\cdot }s}\right)};B_2=\frac{\left(\frac{V_S}{s}-\frac{\mathit{\Delta \Delta }{V}_S}{s}\right)}{R_M+\left(\frac{1}{C_{M\cdot }s}-\frac{1}{\mathit{\Delta }{C}_M·s}\right)}.$$

Figure 2.

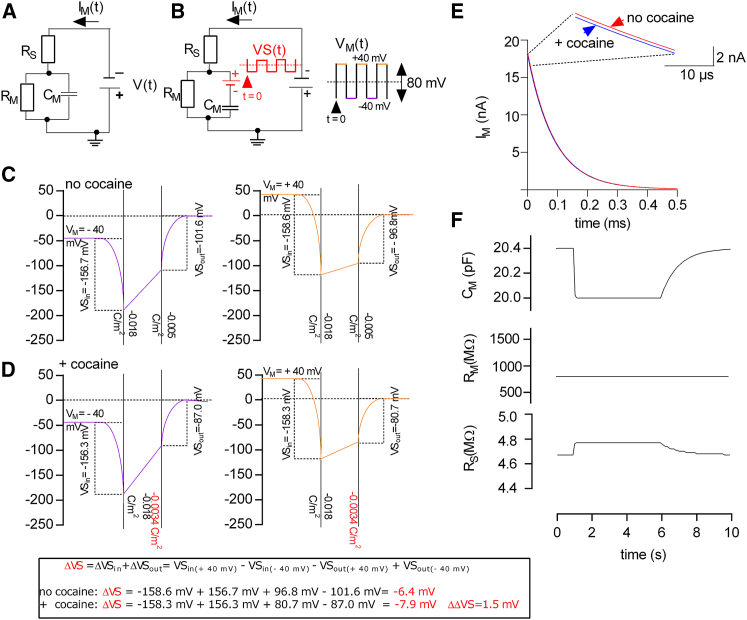
The apparent change in membrane capacitance can be accounted for by an extended equivalent circuit of the cell. (A) Schematic representation of the minimal circuit of a cell is shown. (B) Shown is a schematic representation of an extended equivalent circuit of the cell; a battery (in red) was added to the minimal equivalent circuit shown in (A). The depicted voltage square-wave stimulus V_M(t) was applied to the cell to elicit the recordings shown in Fig. 1A. V_M was stepped from −40 to +40 mV in time increments of 5 ms. The resulting changes in voltage VS(t) at the added battery were calculated by utilizing the Gouy-Chapman model and are shown as red traces. (C) Shown is a voltage profile over the membrane in the absence of cocaine. The potential at the inner and outer surface was calculated utilizing the Gouy-Chapman model as adapted by (15). For the simulation, we assumed that both the inner and outer solution contained 150 mM NaCl. Initial surface charge densities for a HEK293 cell were taken from (16). The left- and right-hand panel in (B) show the voltage profile for voltage differences (V_M) between the outer and inner bulk solution of −40 and +40 mV, respectively. (D) Voltage profile over the membrane in the assumed presence of a saturating concentration of cocaine is shown. The left and the right panel show the voltage profile at −40 and +40 mV, respectively. The potential at the membrane surfaces in (C) are different from that in (B). This is because in (C), the outer surface charge density was assumed to change to −0.0034 C/m² as a consequence of cocaine binding. The inserted box at the bottom of (C) shows the calculation of the voltage step, which occurs at the added battery according to the Gouy-Chapman model. (E) Simulated current responses of a cell expressing SERT in the assumed absence (red trace) and presence (blue trace) of cocaine are shown. The inset shows that the current amplitude of the response in the absence of cocaine is slightly larger than in the presence of cocaine. (F) Simulated current responses were analyzed by employing the minimal equivalent circuit of the cell (A). This analysis misinterprets the change at the battery as a change in the other circuit parameters. The parameters that are most affected are R_S and C_M. To see this figure in color, go online.

Figure 6.

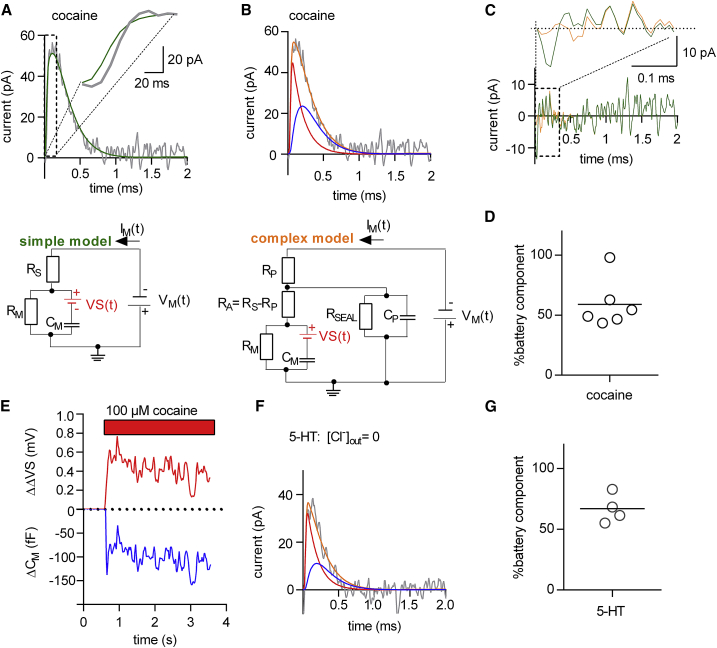
Residuals measured from HEK293 cells stably expressing SERT cells challenged with cocaine or 5-HT can be decomposed into a battery and a capacitive residual. (A) The upper panel shows a residual obtained from recordings of a HEK293 cell stably expressing SERT, which was superfused with cocaine binding (gray trace). The measured residual was fitted to the simple circuit shown in the lower panel. The inset shows the magnified rising phase of the residual. The fit (in green) did not adequately account for the initial phase of the residual. The lower panel depicts the simple model. (B) The upper panel shows the same residual as in (A) fitted to the analytical solution of a more complex circuit displayed in the lower panel of (B). The fit (in orange) allowed for decomposing the measured residual into a battery (in red) and a capacitive residual (in blue). The lower panel depicts the complex model (C). Shown is a comparison of the fitted residuals of the simple model (in green) and the complex model (in orange). The inset shows the magnified initial phase of the fit. In the initial phase, the more complex model better accounted for the data. (D) Shown is the contribution of the battery component in percentage to the total change in C_M induced by cocaine. Shown is the summery of six independent experiments. In average, the contribution of the battery component was 60 ± 20%. (E) Change in ΔΔVS over time as a result of cocaine binding is plotted along with the simultaneous change in C_M. (F) Shown is the measured residual of a HEK293 cell stably expressing SERT, which was challenged with 30 μM serotonin (5-HT) in the absence of extracellular Cl⁻ (in gray). The residual was fitted to the complex model. The fit (orange trace) decomposed the measured residual into a battery (in red) and a capacitive residual (in blue). (G) Shown is a summary of four independent experiments in which 5-HT was applied. Plotted in percentage is the contribution of the battery residual to the total change in capacitance (67.0 ± 11.9%). To see this figure in color, go online.

Inverse Laplace transform of a difference of two analytical solutions of the complex equivalent circuit shown on Fig. 6 B is as follows:

$$\mathit{\Delta }{I}_M={\mathcal{L}}^{-1}\left\{\left(\frac{R·G}{1-S·G}+\frac{H}{1-S·G}\right)-\left(\frac{R_2·G}{1-S_2·G}+\frac{H}{1-S_2·G}\right)\right\},$$

where,

$$A=\frac{\frac{V_S}{s}}{R_M+\frac{1}{C_{M\cdot }s}};B=\frac{R_M}{R_M+\frac{1}{C_{M\cdot }s}};C=\frac{R_M}{R_M+R_{Seal}+R_A};D=\frac{R_{Seal}}{R_{Seal}+R_A+R_M};E=\frac{R_{Seal}}{R_{Seal}+R_{Cp}+\frac{1}{C_P·s}};$$

$$F=\frac{R_{Cp}+\frac{1}{C_P·s}}{R_{Seal}+R_{Cp}+\frac{1}{C_{P\cdot }s}};G=\frac{R_{Cp}+\frac{1}{C_{P\cdot }s}}{R_P+R_{Cp}+\frac{1}{C_{P\cdot }s}};H=\frac{\frac{V_M}{s}}{R_P+R_{Cp}+\frac{1}{C_{P\cdot }s}};A_2=\frac{\left(\frac{V_S}{s}-\frac{\mathit{\Delta \Delta }{V}_S}{s}\right)}{R_M+\left(\frac{1}{C_{M\cdot }s}-\frac{1}{\mathit{\Delta }{C}_M·s}\right)};$$

$$B_2=\frac{R_M}{R_M+\left(\frac{1}{C_{M\cdot }s}-\frac{1}{\mathit{\Delta }{C}_{M\cdot }s}\right)};P=\frac{-A·C}{1-B·C};Q=\frac{D}{1-B·C};R=\frac{E·P}{1-E·Q};S=\frac{F}{1-E·Q};P_2=\frac{-A_2·C}{1-B_2·C};$$

$$Q_2=\frac{D}{1-B_2·C};R_2=\frac{E·P_2}{1-E·Q_2};S_2=\frac{F}{1-E·Q_2}.$$

Fitting procedure

Fitting of the residuals was performed with MATLAB (The MathWorks, Natick, MA). We used the constrained version of the MATLAB build-in function fminsearch (i.e., “fminsearchbnd.m” (D’Errico, 2012: https://de.mathworks.com/matlabcentral/fileexchange/8277-fminsearchbnd-fminsearchcon)) in which the fitted parameter ΔΔVS and ΔC_M were constrained to positive and negative values, respectively. The remaining parameters were set, fixed, and obtained from the individual recordings (C_M, R_M, R_A, R_P) and separate measurements (Cp = 3 pF). R_SEAL was assumed to be 3 GΩ.

Sensitivity analysis

We estimated the sensitivity of the method to changes in ΔΔVS by simulating a set of residuals produced by various surface charge changes. We then added the noise from an actual measurement to the simulated residuals and fitted them to the analytical solution of the complex equivalent circuit shown in Fig. 6 B. The fit was able to accurately resolve ΔΔVS changes down to 0.1 mV. At smaller values, the error rose exponentially (data not shown).

Results

Cocaine binding to SERT reduces the membrane capacitance

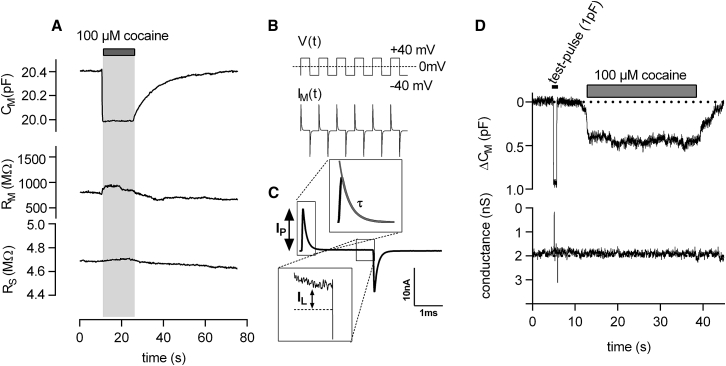
We previously showed that it is possible to monitor ligand binding to membrane proteins in real time by utilizing measurements of the cell membrane capacitance (C_M) (8). We investigated the ligand-induced capacitance change in HEK293 cells stably expressing hSERT. Binding of a SERT ligand (e.g., cocaine) to the transporter resulted in a decrease in the total membrane capacitance (see Fig. 1 A, also shown in the figure is the time-dependent evolution of the circuit parameters R_M and R_S). The circuit parameters in Fig. 1 A were obtained by the analysis of the current responses to a train of voltage square-wave pulses (Fig. 1, B and C). More often, however, membrane capacitance measurements are conducted utilizing a sinusoidal-voltage stimuli in combination with a hardwired (12) or a software-based lock-in amplifier (13). We thus asked the question whether the ligand-induced change in capacitance is also detectable by approaches that rely on sinusoidal voltage stimuli. To test this, we used a dual-phase lock-in amplifier (see Methods) and we recorded the membrane capacitance of a cell expressing hSERT, which we challenged with cocaine. As can be seen, with this method, we were also able to detect the cocaine-induced reduction in membrane capacitance. Fig. 1 D shows the two outputs of the amplifier. The upper panel displays the output that is directly proportional to changes in C_M. It is evident that there is no cross talk between the two channels. This shows that both approaches (square-wave pulse and sinusoid) are equally suited for monitoring ligand binding to membrane proteins.

Figure 1.

Cocaine binding to SERT reduces the total membrane capacitance (C_M). (A) A saturating concentration of cocaine (100 μM) was applied to a HEK293 cell stably expressing SERT, and the change in membrane capacitance was recorded in the whole-cell patch-clamp configuration. The application of cocaine reduced the membrane capacitance. After 15 s, the drug was removed from the bath solution, upon which C_M returned to initial values. Also shown is the time-dependent evolution of the other circuit parameters (membrane resistance R_M and series resistance R_S). Data are from a representative experiment, which was reproduced 47 times. (B) The method relies on the application of a train of square-wave voltage pulses. (C) The circuit parameters are extracted by fitting a monoexponential function to the measured current decay. The fit (in gray) yields three parameters (I_P, τ, and I_L). I_P is the current amplitude at time point zero, τ is the time constant of the current decay, and I_L is the leak current after relaxation of the displacement current. With these parameters, it is possible to obtain R_S (R_S = ΔV_M/(I_P + I_L)), R_M (R_M = ΔV_M/I_L − R_S), and C_M (C_M = τ^∗(1/R_S + 1/R_M)). (D) The change in membrane capacitance C_M was recorded in the whole-cell patch-clamp configuration from a HEK293 cell stably expressing hSERT using a hardwired lock-in amplifier. Application of 100 μM cocaine (indicated by the gray bar) led to a reduction of C_M. Upon cocaine washout, C_M relaxed to initial values.

Ligand-induced changes in capacitance are apparent changes

In Burtscher et al., we posited that this change in capacitance was caused by charged ligand binding to the protein. Upon adsorption to the binding site, the charge on the ligand becomes a surface charge (i.e., a fixed charge at the interface between the membrane and the surrounding aqueous solution). This offsets the electric potential at the outer surface of the membrane. As a consequence, the voltage difference between the inner and the outer membrane surface (ф_TRANS) changes. This affects the number of capacitive charges at the surface. Accordingly, the ligand-induced change in membrane capacitance (C_M) does not result from a true capacitance change. It can rather be rationalized as follows. Approaches to measure the membrane capacitance rely on the assumption that the three-element circuit displayed in Fig. 2 A can model the electrical response of a cell to a voltage stimulus (e.g., a square-wave voltage pulse, Fig. 1, B and C). However, one additional circuit component is needed in the equivalent circuit of the cell to represent changes induced by the adsorption of the charged ligand. This component is a battery, which must be added to account for changes of the charge densities at the inner and/or outer membrane surfaces. Omission of the battery from the circuit leads to an erroneous inference; the ligand-induced change in surface potential is misinterpreted as a change in the estimates of the other circuit components, most prominently of C_M. This point is illustrated in Fig. 2. The figure shows an expanded circuit in which we incorporated an additional battery in series with the capacitor (Fig. 2 B). The voltage (VS) at the battery (highlighted in red) was specified by the Gouy-Chapman model, which relates the potentials at the inner and outer membrane surfaces to the corresponding surface charge densities (Fig. 2, C and D; (14, 15)); Fig. 2 C shows the voltage profile over the membrane in the absence of cocaine at −40 and +40 mV, respectively. In this calculation, the initial inner and outer surface charge densities were assumed to be −0.018 C/m² and −0.005 C/m², respectively (16). The Gouy-Chapman model predicts that–because of the asymmetry of the inner and outer surface charge densities–VS increases by 6.4 mV (ΔVS) when the membrane potential (V_M) is switched from −40 to +40 mV (i.e., by a voltage step of 80 mV). Importantly, the VS step is predicted to be oppositely directed to the V_M step (see Fig. 2 B). Binding of cocaine to SERT adds one positive charge per occupied binding site and thus reduces the density of negative charges on the outer leaflet. Fig. 2 D shows the voltage profile over the membrane in the presence of cocaine, again at −40 and +40 mV, respectively. The calculation is based on the assumption that, upon the binding of cocaine, the outer surface charge density drops to −0.0034 C/m². The difference of 0.0016 C/m² is accounted for by the number of SERT moieties (i.e., 2 × 10⁷) expressed on the surface of our stable cell line (8), to which cocaine binds in a 1:1 stoichiometry at saturating concentrations. The Gouy-Chapman model predicts that ΔVS in the presence of cocaine is 7.9 mV, which differs by 1.5 mV from that in the absence of cocaine. The other circuit parameters (i.e., C_M, R_M, and R_S) were chosen to closely approximate the circuit parameters of the experiment displayed in Fig. 1 A. Fig. 2 E shows the simulated current response of this circuit before (blue trace) and after (red trace) the application of a saturating concentration of cocaine. The evolution of the current over the first 10 μs was magnified in the inset to Fig. 2 E to show that the amplitude of the current response is slightly larger in the absence of cocaine. The simulated currents produced by the four circuit elements were then analyzed with the three-element circuit in Fig. 2 A (Fig. 2 F). Because the simulated current decay was not fitted to the circuit that produced it, this analysis erroneously inferred that all three circuit parameters had changed upon cocaine binding. Accordingly, the cocaine-induced alterations of the circuit parameters displayed in Fig. 2 F are all apparent. Whereas the apparent change in R_M was minute and not visible at the chosen scaling, the apparent changes in C_M and R_S were more pronounced. In actual measurements, we frequently observed an increase in R_M upon cocaine application (see Fig. 1 A). However, because we also observed a cocaine-induced R_M change in control cells (data not shown) and because cocaine is known to inhibit ion channels, we attribute this small change to a block of endogenous channels, which are present at low levels in our HEK293 cell line (17). Our model does not account for the presence of endogenous ion channels. For this reason, the change in R_M is not seen in the simulation (see Fig. 2 F). We also simulated the current response of our extended equivalent circuit to a sinusoidal voltage stimulus (Fig. 3 A). In the simulation, we assumed that the cell was held at a holding potential of −40 mV. At this holding potential, we superimposed a sinusoidal voltage stimulus with a frequency of 1 kHz and a peak-to-peak amplitude of 40 mV (see Fig. 3, A and B). The Gouy-Chapman model was employed to calculate the voltage at the battery (ΔVS) in response to the sinusoidal change in V_M, in time steps of 1 μs (i.e., 1 MHz). The other circuit parameters were set to the values used in Fig. 2. Notably, the Gouy-Chapman model predicts that the voltage at the battery (ΔVS) is shifted by 90° with respect to the stimulating voltage (V_M) (see Fig. 3 A). Fig. 3 B shows the current response (I_M) of this circuit to V_M (black trace) before (red trace) and after the application of cocaine (blue trace). As can be seen from the magnified traces in the inset to Fig. 3 B, the simulation predicts a reduction in the amplitude of I_M upon cocaine binding. When subjected to admittance analysis, this change translated into a reduction in C_M. Importantly, the calculated changes in the circuit parameters C_M, R_M, and R_S were exactly the same as predicted for the square-wave pulse method (Fig. 2 F).

Figure 3.

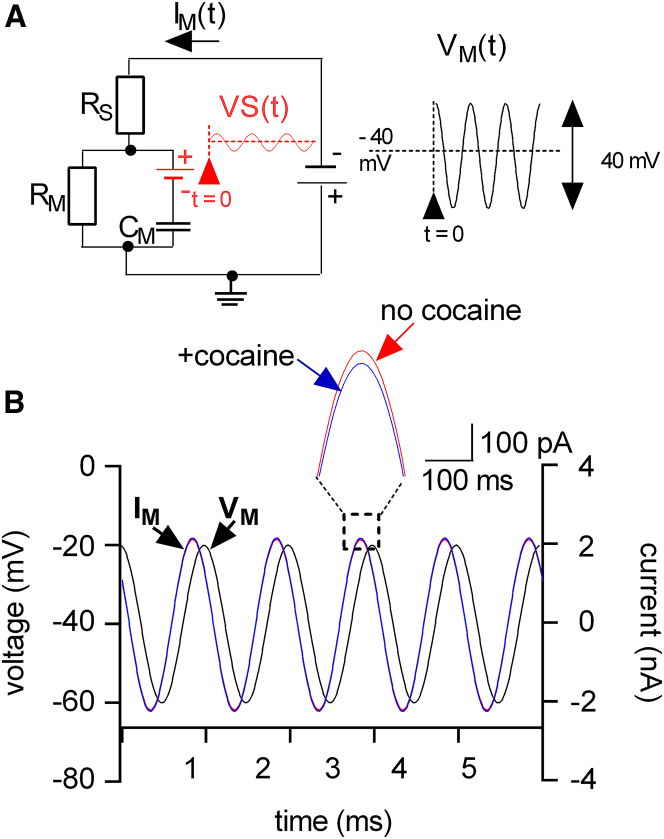
Effect of a sinusoidal voltage stimulus on the extended equivalent circuit. (A) The voltage change at the battery VS(t) (red trace) was calculated using a simulation. This simulation assumed that a sinusoidal voltage V_M(t) (black trace) with a peak-to-peak amplitude of 40 mV and superimposed on a holding potential of −40 mV was applied to the extended equivalent circuit. The frequency of the applied sinusoid was 1 kHz. The voltage at the battery VS(t) was specified by the Gouy-Chapman model, which predicted a shift in VS by 90° with respect to V_M. (B) The current response (I_M) to the stimulating voltage (V_M, black trace) was extracted from simulations assuming the absence (red trace) and the presence (blue trace) of cocaine. The inset shows a magnified section of the currents (I_M); the amplitude of the current in the absence is larger than in the presence of cocaine. To see this figure in color, go online.

The simulated current response to a voltage square pulse differs depending on whether the change is a true or an apparent capacitance change

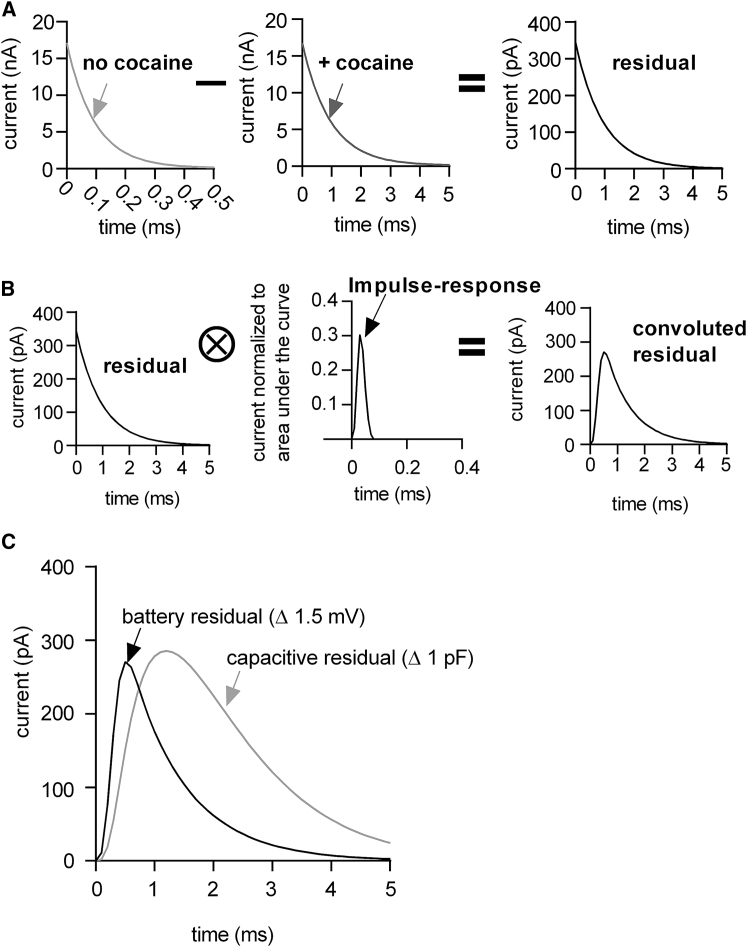
A change in any of the circuit parameters defining the equivalent circuit of the cell must result in a shape change of the current response to a square-wave voltage pulse. However, the characteristics of this shape change depend on the underlying alteration in the circuitry. This point is illustrated in Fig. 4; the left-hand and the middle panel of Fig. 4 A show the simulated current response to a square-wave voltage pulse in the absence and presence of cocaine, respectively. In this simulation, cocaine binding was accounted for by a 1.5 mV change in the voltage (ΔΔVS) supplied by the battery. The right-hand panel shows the subtraction of the two traces, which for the following description will be referred to as the “residual.” The residual corresponds to the cocaine-induced change in current, which we denote as the “battery residual.” In Fig. 4 B, we convoluted the battery residual with the impulse response function of our recording apparatus to emulate the residual of an actual measurement. The impulse response function was acquired as described in (10, 11). In Fig. 4 C, we show the overlay of the battery residual with the simulated residual of a true capacitance change (referred to as “capacitive residual” henceforth), which was obtained by changing C_M in the simulation (i.e., ΔC_M = 1 pF). It is evident from the overlay of the two residuals that they differ in their kinetics. For instance, the rising phase of the “battery residual” is faster than the rising phase of the “capacitive residual.” The reason for this is as follows: changes of the voltage supplied by the battery give rise to residuals that are only subject to the intrinsic filters of the recordings apparatus and not of the filter constituted by the cell (i.e., τ∼R_S^∗C_M, cutoff frequency = 1/τ). In contrast, in patch-clamp experiments, the current required to charge the membrane (i.e., the displacement current) must pass through R_S, which results in a slow rise of the “capacitive residual.”

Figure 4.

The shape of the differential current (i.e., residuals) produced by square-wave voltage pulses depends on the underlying alteration in the circuitry. (A) The left-hand and the middle panel show the simulated current response of the extended circuit depicted in Figs. 2A and 3A in the absence (light gray trace) and presence of cocaine (gray trace), respectively. The right-hand panel shows the subtraction of the two traces (i.e., the residual). (B) Shown is the convolution of the simulated residual (left) with the impulse response function obtained from the recording apparatus employed (middle panel). The right-hand panel shows the convoluted residual produced by the change at the battery. (C) Shown is a comparison of the residual produced by the change at the battery (i.e., the battery residual) with the simulated residual of a true capacitance change (light gray trace).

Model residuals measured utilizing the compensation circuitry of the patch-clamp amplifier

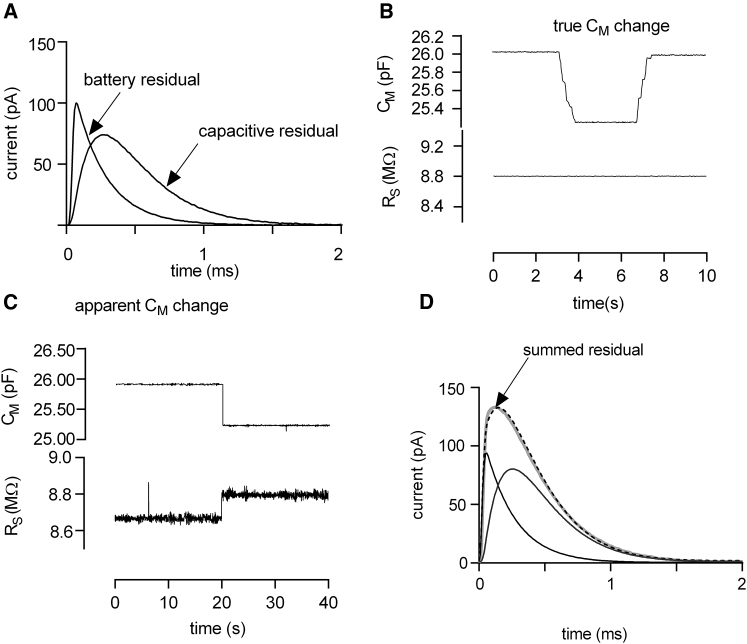
Fig. 5 A shows an overlay of two residuals measured with our recording apparatus; one is a residual of a true capacitance change and the other of an apparent capacitance change. We generated the residual of the true capacitance change by using the compensation circuitry of the patch-clamp amplifier (Axopatch 200B). We emulated the current response of a typical HEK293 cell by setting the whole-cell capacitance and series resistance compensation to 26 pF and 8 MΩ, respectively. Currents were elicited by the application of voltage steps (V_M = 80 mV). The capacitive residual was obtained by changing the compensation setting to 25.5 pF and subtracting the resulting current from a current recorded at the prior setting (i.e., 26 pF). The battery residual was recorded as follows: we kept the compensation circuitry settings at 26 pF and 8 MΩ and recorded the current in response to an 80-mV step pulse. We then changed the stimulus voltage by 1 mV (i.e., 79 mV) to mimic the ligand-induced change in ф_TRANS. The displayed residual (red trace) was obtained by subtracting the two current responses (i.e., V_{M, 80 mV} − V_{M, 79 mV}). It is evident that the measured residuals match the simulated residuals shown in Fig. 4 C. We analyzed the currents produced by the compensation circuitry utilizing the three-element circuit. As expected, the modeled true capacitance change was correctly identified as a sole change in C_M (Fig. 5 B). However, the analysis showed that the error made by assuming an unchanged V_M (i.e., 80 mV instead of 79 mV) had translated into a change in R_S and C_M (Fig. 5 C). R_M in both measurements was infinite.

Figure 5.

Measured residuals utilizing the compensation circuitry of the patch-clamp amplifier. (A) Modeled battery and capacitive residual is shown (see text for a detailed description of the approach employed to obtain the parameters). (B) Shown is an analysis of the recorded true capacitance change using the minimal equivalent circuit of the cell. (C) Shown is an analysis of the modeled apparent capacitance change using the minimal equivalent circuit of the cell. (D) The summed measured residuals of (A) (gray trace) were fitted to an analytical solution of the extended circuit (dashed line). The fit allowed for decomposing the summed residual into a battery and capacitive residual.

Analysis of mixed responses

So far, we assumed that a measured capacitance change can either originate from a true change in capacitance or from an apparent change (i.e., from alterations in surface potential). However, a scenario can be envisaged in which a manipulation (e.g., application of a ligand or a voltage change) triggers a mixed response. We reasoned that–because of the distinct shape of the two types of residuals–each individual component can be isolated even in those instances in which they occur simultaneously. We tested our ability to decompose a mixed response by summing the measured residual displayed in Fig. 5 A and subjected the sum to the following fitting procedure; an analytical expression describing the response of the extended equivalent circuit to a square pulse was derived from the Laplace transformation (18). The sum of the residuals was fitted by using the difference of two analytical solutions. To take into account the filters in our signal path, we transformed this difference into the frequency domain using fast Fourier transformation and convolved it with the impulse response of the recording apparatus. The filtered difference of the analytical solutions was then back transferred into the time domain using inverse fast Fourier transform and was fitted to the experimental data with only two fitting parameters: 1) ΔC_M, which describes a difference in C_M and 2) ΔΔVS, which accounts for the change in surface potential. The other circuit parameters (C_M, R_S, R_M) were fixed, and the corresponding values were estimated by fitting the current responses to the three-element circuit. As can be seen from Fig. 5 D, the fit (shown in magenta) was able to decompose the summed residual (gray trace) into its original elements (i.e., the battery residual (in red) and the capacitive residual (in blue)). Thus, this approach provides the means for monitoring both processes and their evolution over time in instances in which true capacitance changes and changes in surface potential occur in parallel.

Analysis of the current responses recorded from mammalian cells

In the upper panel of Fig. 6 A, we show a residual (gray trace) recorded from a HEK293 cell stably expressing SERT, which originated from cocaine binding. The noise level in the residual acquired from the cell was higher than in the residuals produced by the compensation circuitry (cf. Fig. 5 A). This was presumably due to the higher impedance noise and due to spontaneous fluctuations in the circuit parameters, both of which seem inherent to recordings conducted on cells. There is an additional difference between the residual produced by the compensation circuitry and the recorded data from the cell; in contrast to the former, the cellular residual was recorded utilizing a glass electrode, which acted as a capacitor because it was immersed into the bath solution. This introduced an additional low-pass filter into the signal path. As a result, the circuit shown in the lower panel of Fig. 6 A (i.e., simple model) failed to adequately account for the time course of the rising phase of the residual. This is evident from the inset in Fig. 6 A in which we show the first 100 μs of the recording; in this time interval, the fit (green trace) deviates considerably from the data.

In protocols utilizing voltage square-wave pulses, the frequency richness allows for modeling the cellular current response by more complex equivalent circuits (19). In the circuit shown in the lower panel of Fig. 6 B (i.e., complex model), we introduced additional circuit elements that influence cellular recordings. These are the stray capacitance of the electrode (C_P), its resistance (R_P), and the seal resistance (R_SEAL). We derived an analytical solution of this circuit (see Methods) using Laplace transform. We fitted the residual, which had resulted from the cocaine-induced change by the same procedure as outlined before, except that we employed the model shown in the lower panel of Fig. 6 B instead of the model in the lower panel of Fig. 6 A. We emphasize, however, that–regardless of the model employed–we only allowed two parameters to vary (i.e., ΔC_M and ΔΔVS). The other parameters were fixed in both models. In the case of the complex model, we obtained the required circuit parameter values as follows; initial values for C_M, R_M, and R_S were extracted by analyzing the current response in the absence of cocaine with the three-component circuit shown in Fig. 1 B. R_P was measured before every experiment by the application of a square-wave voltage pulse to an electrode immersed into the bath solution. For estimating C_P, we recorded the current responses to square-wave voltage pulses from three different Sylgard-coated pipettes immersed into Vaseline to emulate a gigaOhm seal. C_P values were calculated by integrating the current responses to obtain the charge (Q) and by the division of Q with the applied voltage (C_P = 3 pF). R_A is the difference between R_S and R_P. R_SEAL was assumed to be 3 GΩ. In Fig. 6 B, we show the fit of the complex model (orange trace) to the data. In Fig. 6 C, we plotted the fitted residuals of the simple model (in green) and the complex model (in orange) for comparison. Both models were able to adequately account for the larger part of the recorded residual; however, the complex model was superior in fitting the rising phase of the residual (see inset in Fig. 6 C).

The fit revealed that the residual, which had originated from cocaine binding to SERT, is comprised of a battery (red trace) and a capacitive component (blue trace) (Fig. 6 B, upper panel). This was unexpected and disproved our original claim that the cocaine-induced change in C_M was fully attributable to changes in surface potential (8). However, in partial exoneration of this claim, we found that the battery residual accounted in average for a slightly larger part of the change. In Fig. 6 D, we show the analysis of six independent experiments. This figure indicates the relative contribution of the apparent capacitance change of each experiment to the total capacitance change. In average, we found that ∼60% of the change had been caused by a ligand-induced alteration in the outer surface charge density. The remaining 40% represented a true capacitance change. It is currently unclear why cocaine binding also gave rise to a true capacitance change. We surmise that cocaine binding to SERT may have induced conformational rearrangements, which reduced the polarizability of the protein. In Fig. 6 E, we show the time-dependent evolution of the cocaine-induced true capacitance change (ΔC_M) and of the transmembrane potential change (ΔΔVS). This figure demonstrates that our analysis allows for individually tracking both changes when they occur simultaneously. In Fig. 6 F, we show another example of a residual recorded from a cell stably expressing hSERT. In this experiment, we applied 30 μM of the endogenous substrate 5-hydroxytryptamine (5-HT) in the absence of extracellular Cl⁻. Extracellular Cl⁻ was omitted because this prevented conversion from the outward- to the inward-facing conformation while still allowing for binding of the substrate to SERT (8). The fit (in orange) decomposed the residual that had originated from the binding of 5-HT to SERT into a battery (in red) and a capacitive component (in blue). Fig. 6 G summarizes the analysis of four independent experiments showing that the C_M change induced by 30 μM 5-HT is to the larger part (65%) caused by adsorption of the charged ligand to SERT. We note that a limitation of the method is its reliance on the stability of C_M. In cells, we frequently observed a linear decline in C_M, the reason of which is currently unknown. Because of the inevitable contamination of the residual, we refrained from analyzing cells with a drift in C_M but restricted our analysis to those 15% of the recordings, in which C_M had remained stable over the entire time span of the measurement.

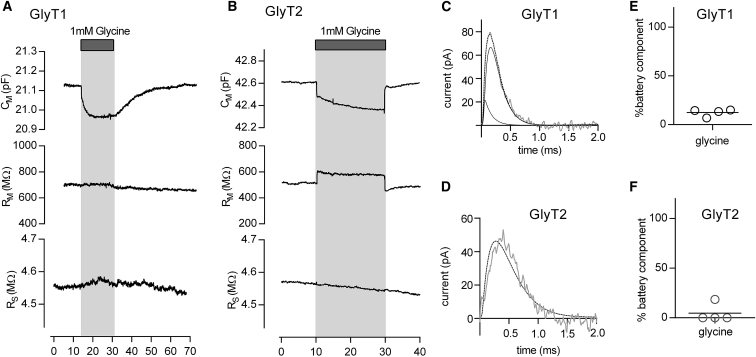
It is implicit to our model that ligand-induced changes in surface potential occur as a consequence of charged ligand binding. In contrast, the binding of an uncharged ligand is expected to be ineffective in altering the outer surface potential and consequently in producing a “battery residual.” This prediction is difficult to verify utilizing HEK293 cells expressing SERT because all ligands known to bind to this transporter harbor a positive charge. However, other solute carrier transporters exist that bind neutral (i.e., zwitter-ionic) ligands. Notable examples are the transporters for glycine (i.e., GlyT1 and GlyT2). Accordingly, in this study, we employed Cos7 cells transiently expressing GlyT1 and GlyT2, respectively. We used Cos7 cells because unlike HEK-293 cells, they did not express endogenous glycine transporters. We then asked the question of how the binding of an uncharged ligand (i.e., glycine) to glycine transporters impinges on the measured membrane capacitance. Accordingly, we recorded the capacitance of cells expressing GlyT1 and GlyT2, which were challenged by 1 mM glycine. Fig. 7, A and B show the result of typical measurements obtained from cells expressing GlyT1 and GlyT2; the application of glycine led to a reduction in membrane capacitance in cells expressing either of the two glycine transporter subtypes. Upon subsequent removal of glycine from the bath solution, the capacitance relaxed to initial values. Plotted in these figures is also the evolution of R_M and R_S over time. When tested in control cells, the application of glycine did not result in an appreciable change in the membrane capacitance (data not shown).

Figure 7.

Application of glycine reduces the membrane capacitance of COS-7 cells expressing GlyT1 and GlyT2. (A and B) The change in membrane capacitance C_M was recorded in the whole-cell patch-clamp configuration of a COS-7 cell transiently expressing GlyT1 (A) or GlyT2 (B), which were challenged by the application of 1 mM glycine. The time-dependent evolution of the circuit parameters is shown; in both GlyT1 (A) and GlyT2 expressing cells, the application of 1mM glycine gave rise to a reduction in C_M. However, R_S and R_M were not affected by glycine in (A) but glycine increased R_M in (B). After 15 s, glycine was removed from the bath solution. Upon removal of the amino acid, C_M and R_M relaxed to initial values. (C) Shown is a measured residual produced by the application of glycine to a COS-7 cell expressing GlyT1. The fit (dashed line) of the data (gray trace) to the complex model shown in Fig. 6B decomposed the residual into a small battery and into a large capacitive residual. (D) Shown is a measured residual of a COS-7 cell expressing GlyT2 produced by binding of 1 mM glycine (gray trace). The complex model only inadequately accounted for the data (dashed line). The fitted parameter–ΔΔVS–converged to zero. Accordingly, there is no battery residual. (E and F) show in percentage the contribution of the battery residual to the total change in capacitance for GlyT1 (12.4 ± 3.8%) and GlyT2 (4.6 ± 9.3%), respectively (n = 4).

Inspection of the residual produced by the application of 1 mM glycine to cells expressing GlyT1 revealed that the underlying change had mostly been caused by a true change in C_M (see Fig. 7 C). The contribution of the battery residual amounted to only ∼12%, suggesting that glycine binding had only minimally affected the outer surface potential (see Fig. 7 E). This result was in line with the net zero charge of glycine in the physiological pH range.

In cells expressing GlyT2, the observations were similar (see Fig. 7, D and F). However, the residuals derived from GlyT2-expressing cells challenged with glycine were even slower than predicted for a true change in C_M (see Fig. 7 D). It was reported that GlyT2 but not GlyT1 bound extracellular Na⁺ in a voltage-dependent manner. Voltage jumps from negative (i.e., −60 mV) to more positive potentials, resulted in outwardly directed transient currents, which were presumably carried by dissociating Na⁺ ions (20, 21). Our data suggest that the voltage at the membrane settles faster than Na⁺ can unbind. However, the model does not consider Na⁺ binding. We surmise that it is for this reason that the fit failed to adequately account for the data. We note that the application of glycine led to an increase in R_M (Fig. 7 B). This effect of glycine was absent in control cells (data not shown). We therefore also attribute this change to slow Na⁺ dissociation from GlyT2. Slow dissociation of Na⁺ is expected to affect the fit parameter I_L (see Fig. 1 D) and, thereby, R_M. Synchronized Na⁺ unbinding from GlyT2 is prevented by glycine binding, which we believe is the reason why R_M is increased in the presence of the amino acid (20).

Discussion

We previously showed that it is possible to detect changes of the surface potential at the plasma membrane by measurements of the membrane capacitance (8). In this study, we demonstrate that, in addition, it is also possible to distinguish between a change in surface potential (i.e., apparent capacitance change) and a true capacitance change. Capacitance measurements rely on the assumption that the electric properties of a recorded cell are adequately described by a three-element electric circuit. However, this minimal equivalent circuit of the cell cannot account for a change in the cellular surface potential. To model the latter, it is necessary to use a more complex circuit that contains a battery connected in series with the capacitor. This complex circuitry predicts that the shape of the differential current (i.e., residual) produced by a true and an apparent capacitance change, respectively, differ. We experimentally verified this prediction and we confirmed that the cocaine- and 5-HT-induced changes measured in cells expressing SERT were indeed and, to a larger part, caused by alterations in the surface potential. We also showed that the electrically neutral ligand glycine only minimally affected the surface potential of the plasma membrane when bound to glycine transporter 1 or glycine transporter 2 (i.e., GlyT1 and GlyT2). These findings are consistent with the concept that–upon binding to a membrane protein–the charge of the ligand becomes a surface charge and thereby offsets the outer surface potential.

The electrical potentials at the inner and the outer surface of the plasma membrane are to a large extent defined by fixed charges at the interface between the membrane and the surrounding aqueous solution (22). These arise primarily from the net-negative charge of phospholipid headgroups but also from water-accessible acidic or basic amino acid residues within membrane proteins. In addition, charged molecules, which bind to the plasma membrane or to membrane proteins, also contribute to the surface charge. Although both membrane surfaces carry a negative net charge, the net-negative charge on the inner surface normally exceeds that on the outer surface (23). This is mainly due to the asymmetric distribution of membrane lipids between the inner and the outer membrane leaflet (e.g., the inner membrane leaflet shows a higher content of phosphatidylserine). This asymmetry is maintained by specialized proteins, which are tasked with moving phospholipids from the inner to the outer membrane layer (i.e., flippases) or in the opposite direction (i.e., floppases) (24, 25). These proteins harness the energy required to maintain the lipid/charge asymmetry from the hydrolysis of ATP (26). The energy stored in this lipid gradient can be readily dissipated by scramblases, which are proteins that facilitate diffusive lipid crossing between the two membrane leaflets (27, 28).

Surface charges play an important role in many biological processes. For instance, because of their net-negative surface charge, cells tend to repel each other. This ζ potential prevents cell aggregation (29). In fact, the ζ potential is the basis for the single file mode of capillary transit in vivo and the slow sedimentation of red blood cells ex vivo; the erythrocyte sedimentation rate has been used for more than a century as a sensitive–albeit nonspecific–parameter to detect inflammation and other abnormalities in people. The net-negative surface charge of cells is also one of the reasons why specific interactions between cell surface proteins are required for establishing cell contacts. The adhesive forces provided by these proteins are needed to overcome the electrostatic repulsion. Moreover, surface charges greatly affect the concentrations of charged solutes in the vicinity of the membrane. Within a perimeter of ∼1 nm, the concentrations of positively charged or negatively charged molecules are much higher or lower, respectively, than in the bulk solution (30). In addition, the asymmetric distribution of surface charges (i.e., excess of negative charge on the inner surface) increases the driving force for cellular uptake of positively charged solutes but reduces the driving force for the uptake of negatively charged solutes. Both effects are expected to shape the intra- and extracellular concentration of signaling molecules, such as monoamines or glutamate. In addition, surface charges are known to impinge on the voltage dependence of voltage-gated ion channels (31). By virtue of this action, they gauge the excitability of cells, such as cardiomyocytes, skeletal muscle cells, and neurons (32).

It is evident from this nonexhaustive list of examples that many cellular functions are affected by changes of the inner and/or the outer surface charge densities. However, the mechanisms, which regulate the surface charge densities at the plasma membrane, are poorly understood. This is in part due to a lack of experimental approaches that allow for detecting changes in surface charges in real time. Here, we show that it is possible to track alterations in the surface potential by an electrophysiological approach. Importantly, the method described in this study allows for discriminating between a change in surface potential and a change in true capacitance, even if these occur in parallel. This can be of relevance if a process is monitored that gives rise to simultaneous changes in the surface area of the plasma membrane and the surface charge density. This can plausibly be the case during mitosis, apoptosis, T-cell activation, etc. (33, 34, 35). Likewise, changes in the surface charge density may also occur in parallel with changes that affect the polarizability of a membrane protein. In this context, it is worth noting that cocaine binding and 5-HT binding to SERT also resulted in a true capacitance change. Specifically, the capacitance was reduced when cocaine/5-HT was bound to SERT. This implies that the polarizability of the ligand-bound state of SERT is lower than that of the apo state. It is unclear, however, how the macroscopically observed change can be explained on the microscopic level. At the current stage, the underlying conformational changes in SERT remain elusive and difficult to address by an experimental approach. However, we anticipate that this will be amenable to computational studies in the near future because of the continuous progress in structural studies of SERT.

Author Contributions

V.B., M.H, M.F., and W.S. designed the experiments and wrote the article. V.B. performed the experiments shown in Figs. 1, 5, 6, and 7. M.H and W.S. performed the simulations in Figs. 2, 3, 4, and 6. M.H. scripted the fitting routine used in Figs. 5, 6, and 7. All authors reviewed the results and approved the final version of the manuscript.

Editor: Baron Chanda.