Abstract
Efficient water use assessment and irrigation management is critical for the sustainability of irrigated agriculture, especially under changing climate conditions. Due to the impracticality of maintaining ground instrumentation over wide geographic areas, remote sensing and numerical model-based fine-scale mapping of soil water conditions have been applied for water resource applications at a range of spatial scales. Here, we present a prototype framework for integrating high-resolution thermal infrared (TIR) and synthetic aperture radar (SAR) remote sensing data into a soil-vegetation-atmosphere-transfer (SVAT) model with the aim of providing improved estimates of surface- and root-zone soil moisture that can support optimized irrigation management strategies. Specifically, remotely-sensed estimates of water stress (from TIR) and surface soil moisture retrievals (from SAR) are assimilated into a 30-m resolution SVAT model over a vineyard site in the Central Valley of California, U.S. The efficacy of our data assimilation algorithm is investigated via both the synthetic and real data experiments. Results demonstrate that a particle filtering approach is superior to an ensemble Kalman filter for handling the nonlinear relationship between model states and observations. In addition, biophysical conditions such as leaf area index are shown to impact the relationship between observations and states and must therefore be represented accurately in the assimilation model. Overall, both surface and root-zone soil moisture predicted via the SVAT model are enhanced through the assimilation of thermal and radar-based retrievals, suggesting the potential for improving irrigation management at the agricultural sub-field scale using a data assimilation strategy.
Keywords: data assimilation, thermal remote sensing, radar, evapotranspiration, soil moisture, high-resolution, irrigation management
1. Introduction
Optimizing crop water usage efficiency and maintaining water sustainability are challenging under rapidly changing natural conditions. In recent years, California has experienced periods of extreme drought characterized by seasonal precipitation deficits and elevated air temperature [Diffenbaugh et al., 2015; Griffin and Anchukaitis et al., 2014]. Reduced surface water availability during these droughts has led to increased groundwater withdrawals for satisfying irrigation demands and resulted in prominent groundwater depletion [Famiglietti et al., 2011; Borsa et al., 2014].
Spurred by the high economic value of wine-grape production in California, the increasing acreage of vineyards and their irrigation requirements pose a challenge given limited irrigation water availability and policies devoted to ensuring sustainable groundwater management [Escriva-Bou et al., 2016]. In addition, the yield and quality of wine grapes are often closely linked to available soil water content. Typically, intensified vine water stress in the early grape growing season (from bud break to fruit set) can reduce vine foliage growth, berry size and yield. In contrast, moderate amount of water stress is desirable in the later growing season (from veraison to harvest) for improving grape quality and composition [Salón et al., 2005; Sivilotti et al., 2005; van Leeuwen et al., 2009].
Recently, there has been increased interest in the application of variable rate drip irrigation systems as testbeds for precision irrigation management over vineyards [Sanchez et al., 2017]. In such systems, an accurate characterization of the time/space heterogeneity in soil moisture at the sub-field-scale (30-m) can be used to guide the application of spatially varying irrigation rates – targeting enhanced water applications to sub-areas within the vineyard where soil moisture deficits are highest. The goal of these practices is to develop optimal irrigation management strategies, improve wine-grape yield, quality, and homogeneity across the vineyard [Oliveira, 2001; Valdés-Gómez et al., 2009; Acevedo-Opazo et al., 2010] and increase the sustainability of agricultural production [Scanlon et al., 2012; Amos et al., 2014]. However, to reach their full potential, these approaches require access to high-quality descriptions of soil moisture and/or evapotranspiration (ET) at the sub-field-scale.
Ground-based instrumentation has been applied to characterize soil moisture, ET and crop water stress conditions at local scales [Dorigo et al., 2011; Baldocchi et al., 2001]. In addition, various conceptual or physical numerical models have been developed that quantify and track surface water and energy fluxes at different spatial and temporal scales using water and energy balance principles [Olioso et al., 1999; Courault et al., 2003]. Finally, with the development of satellite-based sensors, certain land surface hydrological and biophysical variables can be retrieved remotely to complement ground-based observations and models [Bastiaanssen et al., 2000; Dorigo et al., 2007; Kustas and Anderson, 2009].
Among various satellite-based microwave sensors, Synthetic Aperture Radar (SAR) instruments, such as the C-band SAR onboard the Sentinel-1 constellation [Torres et al., 2012], enable the highest resolution (1-m to 1-km) retrieval of surface soil moisture conditions. SAR sensor have revisit times ranging from days to weeks. In addition, SAR signals are highly sensitive to surface roughness conditions and biomass, especially for spatially heterogeneous land cover types, introducing complexities for retrieving reliable soil moisture information [Hornacek et al., 2012]. Moreover, SAR sensors penetrate only the top couple of centimeters of the soil profile (0–5 cm), limiting their value for agricultural (i.e., root-zone) applications.
Likewise, using land surface temperature (LST) retrievals from satellite-based thermal infrared (TIR) imagery, terrestrial ET can be derived by contrasting radiometric surface temperature and aerodynamic temperature [Norman et al., 1995; Kustas and Norman, 1996]. One widely applied ET estimation approach is the Atmosphere-Land Exchange Inverse (ALEXI) model [Anderson et al., 2007] and its associated disaggregation algorithm (DisALEXI) [Norman et al., 2003; Anderson et al., 2004], which allows multi-scale applications from coarse-resolution global-scale down to fine-scale (30-m) at the sub-field level. By normalizing the atmospheric demand for water vapor, the ratio of actual-to-potential ET or fractional potential ET (referred to as fPET hereinafter) reflects soil water availability for soil evaporation and canopy transpiration [Pereira et al., 2015]. This ratio has been widely applied as an indicator of evaporative stress [Anderson et al., 2007; Yang et al., 2018], crop yield [Anderson et al., 2016a, b; Semmens et al., 2016; Mladenova et al., 2017], drought conditions [Anderson et al., 2011a; 2013], and root-zone soil moisture [Hain et al., 2011; Fang et al., 2016]. In particular, Hain et al. [2012] linked fPET to the volumetric soil water content at different vertical depths by taking into account the vegetation density. Over bare soil or lightly vegetated conditions, ET mainly comes from direct soil evaporation which, like microwave sensors, reflects soil water availability in only the first several centimeters of soil. However, when ET is dominated by canopy transpiration over a dense vegetation canopy, fPET represents integrated soil moisture conditions within the entire effective vegetation rooting zone [Fang et al., 2016].
Surface- and root-zone soil moisture information derived from various satellite sensors can be integrated with numerical physical models via data assimilation techniques [Crow et al., 2008; Brocca et al., 2012; Lievens et al., 2017; Reichle et al., 2017]. Through data assimilation, instantaneous remotely-sensed measurements are used to sequentially update continuous model simulations of water and energy fluxes. However, both microwave- and TIR-based soil moisture estimates have significant limitations as a source of such measurements. For example, realizing improvement in root-zone soil moisture via the assimilation of microwave-based surface soil moisture requires an accurate model representation of the vertical coupling between surface- and root-zone soil moisture [Chen et al., 2011; Lievens et al., 2015]. Likewise, the TIR-based fPET can reflect the integrated root-zone water availability — but only under water-limited conditions [Anderson et al., 2007; Joiner et al., 2018]. Therefore, the best operational approaches for monitoring root-zone soil water content will likely integrate multiple sources of information. Motivated by the recent availability of high-resolution TIR-based root-zone soil moisture information product from ALEXI/DisALEXI and SAR-based surface soil moisture retrievals from Sentinel-1 [Pasolli et al., 2015; Attarzadeh et al., 2018], this paper describes the construction and evaluation of a data assimilation system designed to simultaneously assimilate both SAR- and TIR-based soil moisture information into a continuous, fine-scale water-energy-balance soil-vegetation-atmosphere transfer (WEB-SVAT) model with the eventual goal of improving agricultural irrigation management over California vineyards.
For current geoscience applications, the ensemble Kalman filter (EnKF) and particle filter (PF) are perhaps the most widely used sequential data assimilation techniques for integrating sporadic observations into a continuous background model. The EnKF relies on the evolution of an ensemble of model realizations to predict the model prior probability distribution function [Evensen, 2003]. However, the nonlinearity of hydrological and land surface models and the bounded nature of various geophysical variables (e.g., soil moisture) can violate the linear model and/or Gaussian error assumption in the EnKF and lead to suboptimal estimates [Moradkhani et al., 2005]. Unlike the EnKF, which assumes Gaussian distribution properties and only tracks the first and second moments of the state distribution, the PF uses an ensemble of random particles to characterize the entire probability density function and, therefore, does not require a linearity assumption in either its model forecast or analysis steps [van Leeuwen, 2010]. Considering the likely nonlinear relationship between soil moisture and fPET [Seneviratne et al., 2010], the PF is potentially superior to the EnKF when assimilating fPET. However, the comparison of EnKF versus PF in handling nonlinear relationships between observations and model states has not been examined closely for the assimilation of both microwave and thermal-based soil moisture information.
Here, the efficacy of different data assimilation algorithms is explored for the fine-scale mapping of soil moisture within a highly heterogeneous vineyard landscape in California. Our study area, remote sensing data products, model and data assimilation framework are described in Section 2. Results from synthetic and real data assimilation experiments are presented in Section 3 and discussed in Section 4. Conclusions are presented in Section 5.
2. Materials and Methods
2.1. Study Area
Our high-resolution data assimilation framework is implemented over a 780-m by 420-m (32.8 ha) Pinot Noir (Vitis vinifera) vineyard located in the California Central Valley near Lodi, CA (38.29° N, 121.12° W, Figure 1a) — hereinafter referred to as the “Sierra Loma” site (the name of this site has recently been updated and has been referred to as either “Lodi” or “Borden” in previously published studies). Beginning in 2013, the Grape Remote Sensing Atmospheric Profile and Evapotranspiration eXperiment (GRAPEX) project has conducted extensive satellite and field measurements at the site to improve water management strategies for vineyards. These measurements include satellite and airborne-based water and energy fluxes estimates (e.g., ET and LST), crop physiological properties (e.g., leaf area index and LAI), and in-situ meteorological conditions and surface fluxes validation data [Kustas et al., 2018].
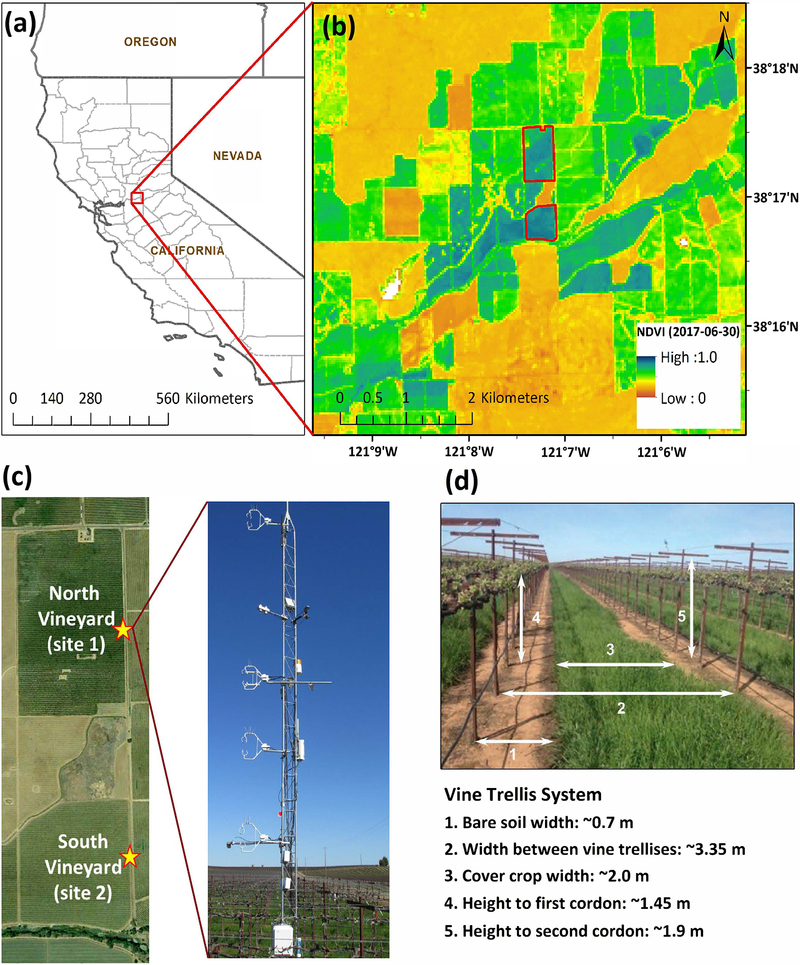
Figure 1.
Study site information, a) the location of the Sierra Loma Pinot Noir vineyards near Lodi, California, b) a Landsat normalized difference vegetation index (NDVI) map showing the boundaries of the vineyards, and c) the flux tower in north vineyard, and d) vine trellising system.
Figure 1b shows two adjacent vineyards at the GRAPEX Sierra Loma site, of which the north block is selected here as the main test field. An eddy covariance micro-meteorological system is mounted on a 10-m tower at the east side of vineyard (Figure 1c). Continuous meteorological and radiation measurements are recorded at the 15 min interval, allowing for the estimation of ET and other energy fluxes as described in Alfieri et al. [2019]. Specifically, a four-component net radiometer (CNR-1, Kipp and Zonen, Delft, Netherlands1) mounted at 6 m above ground level (a.g.l) measures the full radiation budget. Air temperature and humidity are measured using three combined temperature and humidity probes (HMP45C, Vaisala, Helsinki, Finland) mounted at 2.5, 5, and 8 m a.g.l. Other meteorological measurements collected at 5 m a.g.l of the tower include wind velocity measured using a three-dimensional sonic anemometer (CSAT3, Campbell Scientific) and air pressure measured using barometric pressure sensor (CS-106, Campbell Scientific). A tipping bucket rain gauge (TE-525, Texas Electronics, Dallas, Texas) was originally mounted at 5.5 m a.g.l and then lowered to 3 m after the 2016 growing season.
The average annual precipitation and mean temperature of this study site are about 190 mm and 16 °C, respectively. The vineyard soil texture is roughly clay loam, with an average texture content of 29% sand and 32% clay. The perennial grapevine root depth is approximately 1 m with dense roots gathered at 0.3–0.6 m below ground level (b.g.l.). Profile soil water content is measured using probes (HydraProbe, Stevens Water Monitoring Systems) installed under the vines at three locations near the flux tower at depths of 30, 60, and 90 cm. A cross-row transect characterization of soil water content has been conducted using five soil moisture probes at a depth of 5 cm since 2013, with two sensors at the center of vine-rows, one sensor at the middle of inter-row, and two more sensors at either side between vine-row and inter-row centers.
The Sierra Loma vineyard contains a highly-structured vine canopy and the shoot positioning trellis system is illustrated in Figure 1d. Vines are planted 1.5 m apart along an east-west orientation, with 3.35-m spacing between vine rows. The main vine stems are trained to the first cordon at a height of 1.45 m a.g.l, and vine shoots are maintained at 1.9 m a.g.l. The vine buds normally start to swell (bud break) and sprout during April, with peak growing season from June to August and harvest in September. Vine shoots can reach a maximum height at 2.0–2.5 m a.g.l with the majority of vine biomass concentrated in the upper half of this height. Pruning of vines is conducted to remove shoots growing significantly into the inter-row and maintain a nominal canopy width of 1 m during the growing season. The grass cover crop in the inter-row extends about 2 m in width and can reach a height of approximate 50 cm before vine bud break. It is mowed when vines start to develop in late April or early May. When viewed at nadir, the field is (approximately) covered by 40% of the vine-row and 60% of the inter-row [Kustas et al., 2019]. This geometry of vine-row and inter-row spaces is explicitly considered in the modelling process described below in Section 2.4.
The timing and amount of applied irrigation vary between years depending on pre-growing season soil water storage, precipitation conditions, and the applied vine water stress management protocol. Occasional irrigation is commonly applied to replenish the soil profile between bud break in early April and flowering in late May. Intensive irrigation (i.e., 5–6 daily applications per week) does not begin in earnest until early June and lasts until late August or early September. After harvest, the soil water profile is intermittently recharged by irrigation before the arrival of winter precipitation. Drip irrigation pipes run parallel with row trellis at 0.3 m a.g.l, with two drip emitters between each vine. Irrigation is recorded in gallons of water per vine per hour and converted into mm hour−1 using the vine areal unit (1.5 m by 3.35 m).
2.2. ALEXI/DisALEXI Fractional Potential Evapotranspiration
High-resolution ET estimates are derived through the multi-scale ALEXI and DisALEXI framework [Anderson et al., 2007; 2011a] based on the Two-Source Energy Balance (TSEB) model [Norman et al. 1995; Kustas and Norman 1999]. The TSEB is applied to LST imagery acquired from the polar-orbiting Landsat and the Moderate Resolution Imaging Spectroradiometer (MODIS) sensors. Specifically, the DisALEXI spatial disaggregation scheme is utilized for ensuring reaggregated ET flux based on Landsat (30-m, sharpened with reflectance band data) and MODIS (500-m) resolution simulations matches ALEXI ET estimates at the continental-scale (4-km). This ALEXI/DisALEXI framework facilitates the implementation of TSEB to the scalable flux and moisture stress mapping for multi-scale applications [Anderson et al., 2011b]. Furthermore, a data fusion algorithm developed by Gao et al. [2006], the Spatial and Temporal Adaptive Reflectance Fusion Model (STARFM), is integrated with the ALEXI/DisALEXI to combine daily, MODIS-scale (500-m) retrievals with biweekly, Landsat-scale (30-m) retrievals and generate a daily, 30-m ET time series [Cammalleri et al., 2013]. Additional background on ALEXI/DisALEXI ET estimates can be found in Appendix A.
To minimize the impact of temporal variations in available energy and atmospheric demand for evaporative rate, retrieved ET is normalized by the potential rate of ET under unstressed conditions over grass [Allen et al., 1998]. This ratio, fPET, helps to isolate the impact of soil water limitations on ET [Anderson et al., 2011a; Yang et al., 2018]. More specifically, when soil water content lies between wilting point and field capacity, canopy transpiration is constrained by water availability and atmospheric evaporative demand cannot be fully satisfied. Since ET composites both surface evaporation and canopy transpiration, fPET reflects the signal of the integrated surface to root-zone soil water profile as a constraining factor for ET under water-limited condition. The potential ET is estimated at the MODIS 500-m resolution using the Penman-Monteith equation [Allen et al., 1998] and meteorological inputs obtained from the Climate Forecast System Reanalysis [Saha et al., 2010] — the same data source utilized in ALEXI/DisALEXI to estimate ET. 30-m LAI images acquired at Landsat acquisition dates are derived using the 4-day MODIS LAI product through an upscaling process and a regression tree analysis [Gao et al., 2012]. Landsat LAI are then smoothed and gap-filled using the Savitzky-Golay filter approach to generate daily 30-m LAI. Over the Sierra Loma site, daily fPET time series at 30-m spatial resolution, as well as LAI, are generated through ALEXI/DisALEXI and the STARFM fusion scheme from January 1, 2014 to December 31, 2017 [Knipper et al., 2019].
2.3. Sentinel-1 Surface Soil Moisture
Using C-band Synthetic Aperture Radar (C-SAR, 5.405 GHz) instruments onboard the Sentinel-1 satellites operating in both dual and single polarizations, high-resolution surface soil moisture retrievals are generated. As a constellation of two polar-orbiting satellites (Sentinel-1A and 1B), this product covers the entire global land surface on a 6-day repeat cycle with an ascending overpass at 6:00 pm local solar time. The interferometric wide swath mode of Sentinel-1 allows for a geometric resolution of 5 m by 20 m, facilitating the fine-scale mapping of soil moisture. Here, an algorithm based on the inversion of an analytical electromagnetic model through a feed-forward multilayer perceptron neural network (ANN) is employed to retrieve temporal changes in the surface soil moisture signal [Paloscia et al., 2013]. Although the retrieving process is challenged by the high complexity of SAR signal introduced by surface roughness and dynamic vegetation cover (particularly within structured agricultural fields) [Cunha et al., 2010], ground validation results have demonstrated promising accuracies of this approach over different land cover types [Gao et al., 2017; El Hajj et al., 2017; Attarzadeh et al., 2018].
Specifically, 2017 Sentinel-1 afternoon data are utilized to generate 20-m surface soil moisture imagery, referred to as θSSM, over the Sierra Loma site. For consistency with the ALEXI/DisALEXI fPET data, 20-m Sentinel-1 θSSM imagery is resampled onto a 30-m grid via drop-in-bucket averaging.
2.4. Water-Energy-Balance Soil-Vegetation-Atmosphere Transfer Model
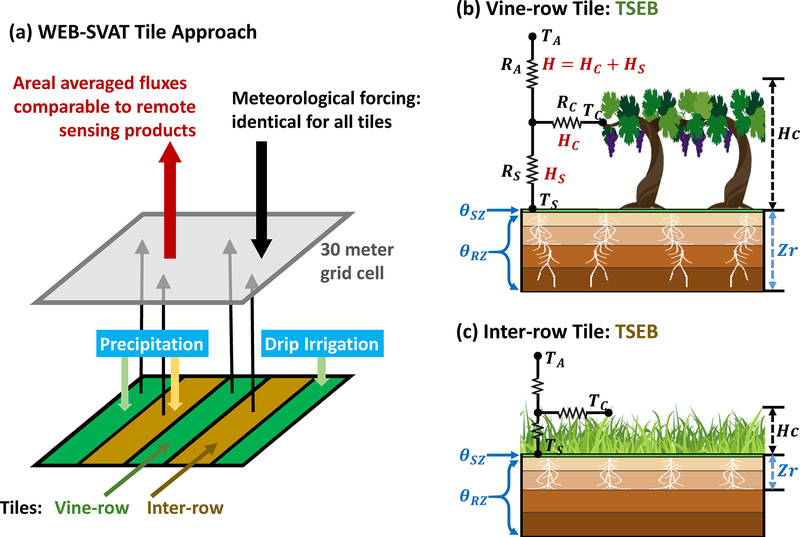
The fine-scale WEB-SVAT model is applied to continuously track soil moisture evolution via a water balance approach. To facilitate a multiple soil layer configuration, the original force-restore model employed in Crow et al. [2008] is adapted to a simple conceptual representation of soil water source-sink processes [Hashemian et al., 2015]. One surface layer at 0–0.05 m depth, and four subsurface layers are defined at 0.05–0.3, 0.3–0.6, 0.6–0.9, and 0.9–1.2 m, respectively. The predicted total ET comprises soil evaporation from the surface layer and canopy transpiration from deeper layers. Typically, about 60% of grapevine roots are in the top 60 cm of the soil profile [Smart et al., 2006]. An exponential root water uptake module [Li et al., 2001] is incorporated into the canopy transpiration term, leading to a nonlinear relationship between model-predicted soil moisture states and fPET. In addition to solving soil water balance equations, WEB-SVAT solves a surface energy balance to derive ET. Note that, to maximize the consistency of WEB-SVAT and ALEXI/DisALEXI ET predictions, WEB-SVAT uses a surface resistance scheme that is structurally equivalent to that applied in the TSEB (see Figure 2b and 2c). For additional details on WEB-SVAT water- and energy-balance calculations, see Appendix B.
Figure 2.
Basic components of the Water-Energy-Balance Soil-Vegetation-Atmosphere Transfer (WEB-SVAT) model and the new sub-grid tiling approach.
To accommodate the high-resolution data assimilation of thermal and radar-based remote sensing products, the WEB-SVAT is implemented on the same 30-m by 30-m grid as the ALEXI/DisALEXI data described above (Figure 2a). The model is run on an hourly time step from January 1, 2014 to December 31, 2017.
2.4.1. Tile Approach for Structured Vineyard
To account for the unique canopy distribution of a vineyard, a sub-grid tile approach is adopted to statistically represent sub-grid heterogeneity in vegetation cover within each 30-m grid cell (see Figure 2). Specifically, an inter-row tile and a vine-row tile are defined to represent the cover crop (grass) and the vine canopy sub-grid fractions, respectively. As described in Section 2.1, when viewed at nadir, about 40% of each grid cell is covered by the vine-row and 60% by the inter-row [Kustas et al., 2019]. Thereby, estimated WEB-SVAT water and energy fluxes are weighted averages for each grid based on these areal fractions. This averaging is performed primarily to maximize the compatibility of WEB-SVAT flux and states estimates with (area-averaged) remote sensing products. Meteorological forcing inputs are assumed to be identical for both tiles, and the same physical underlying processes are utilized (Figure 2).
30-m LAI values are sub-divided into two tiles by introducing a conceptual coefficient determining the LAI fraction of vine-row tile, which changes with different vine growth stages [Fraga et al., 2016]. Maximum canopy height and maximum root depth for vine-row and inter-row are 3 and 1.2 m, and 0.5 and 0.6 m a.g.l, respectively. The fraction of root density within the first 10-cm soil layer for determining profile root density is set to 0.2 [−] for both perennial vine and cover crop. Minimum canopy stomatal resistance values for vine-row and inter-row tiles are 400 and 200 s m−1, respectively. The same soil texture and soil hydraulic parameters are applied in both tiles based on clay loam lookup table values in Clapp and Hornberger [1978] — as well as the same vertical soil layer discretization scheme. Specifically, porosity is 0.47 m3 m−3 and residual soil water content is 0.08 m3 m−3. Soil moisture at field capacity and wilting point are estimated by assuming matrix potentials of −2.1 and −100 Mb, respectively.
2.4.2. Drip Irrigation Consideration
Drip irrigation is concentrated around drip emitters along irrigation pipes at the center of each vine row. Here, the impact of drip irrigation is simulated by separating vine-row and inter-row tiles as described in Section 2.4.1. Particularly, precipitation is the same for both tiles, but drip irrigation only infiltrates into the vine-row tile (Figure 2a). In addition, a dimensionless rescaling factor of 2.5 [−] is applied to irrigation values to account for the concentration of area-averaged irrigation applications into only the vine row which occupies only 40% of the total area. Lateral flow between vine-row and inter-row tiles is neglected.
2.5. Data Assimilation Method and Framework
In our approach, fPET and θSSM are simultaneously assimilated into the WEB-SVAT model to improve root-zone soil moisture state estimates. Since the relationship between modelled soil moisture states and fPET observations is typically nonlinear [Seneviratne et al., 2010; Hain et al., 2012; Kustas et al., 2018], two different filter-based data assimilation algorithms — an ensemble Kalman filter (EnKF) and a particle filter (PF) — are examined to explore their relative efficacy for this nonlinear estimation problem. A brief overview of both approaches is presented below. For additional details, see Appendix C.
2.5.1. Data Assimilation Setting
Based on the discussion presented in Gruber et al. [2015], the integration of model states and observations is conducted separately for each modelling grid. The model states in our application of WEB-SVAT consist of soil moisture states within five vertical soil layers for both the vine-row and inter-row tiles in each grid cell. Model-predicted observations are area-weighted averages of WEB-SVAT θSSM and/or fPET estimates for each tile. More specifically, when assimilating observations of daily fPET, the model-predicted observation is the ratio of tile-averaged daytime ET and potential ET, and the state vector contains the hourly soil moisture states at five layers of two tiles for a single day. To match with the overpass time of Sentinel-1, only states and model-predicted observations at 6 pm local solar time are considered in the assimilation of θSSM (Section 2.3).
Typically, the PF requires more particles than EnKF ensemble members to obtain estimates of comparable accuracy [Weerts and Serafy, 2006]. This tendency is explored in the synthetic data assimilation experiments (Section 2.5.3) for determining the optimal particle number and ensemble size to utilize as a meaningful compromise between accuracy and computation cost.
2.5.2. Error Assumptions and Evaluation Metrics
Both the PF and EnKF require an accurate statistical representation of error in the assimilated observations. Here, the observation error variance of fPET is estimated by comparing daily DisALEXI data against the flux tower-based measurements. To accommodate the spatial footprint of flux tower measurements, DisALEXI fPET time series are extracted by averaging over a 90-m by 90-m box located to the west of the tower (based on predominant wind direction in the field). Likewise, the Sentinel-1 θSSM error variance is derived by comparing SAR retrievals against transect-averaged soil moisture measurements acquired across the row at the depth of 5 cm (see Section 2.1). Based on these comparisons, the observation error standard deviations of fPET and θSSM are fixed as 0.1 (unit-less) and 0.05 m3 m−3, respectively. These errors are assumed to be constant in both space and time, and the impact of varying them (on data assimilation results) is discussed in Section 4.
In addition, both the PF and EnKF are ensemble-based and require a Monte Carlo representation of modelling uncertainty. To capture such uncertainty, precipitation and irrigation inputs into the WEB-SVAT are perturbed at an hourly time step via multiplicative rescaling with mean-unity lognormally distributed random errors that have a standard deviation equal to 20% of the corresponding input amount. In addition, direct perturbations to soil moisture states at all depths of two tiles are applied to each daily time step without consideration of spatial or temporal autocorrelation. Both sub-grid tiles are perturbed independently with random errors sampled from a mean-zero, normal distribution with temporally varying standard deviation equal to 10% of the state value. Following Kumar et al. [2009], a vertical cross-correlation matrix is utilized to introduce vertical auto-correlation into perturbations applied to soil moisture states at different depths. In addition, at the start of the analysis on January 1, 2014, initial values of soil moisture at five layers are sampled from bounded uniform (U) distributions of U(0.25, 0.45), U(0.30, 0.40), U(0.35, 0.45), U(0.28, 0.37), U(0.28, 0.37) for the vine-row, and U(0.15, 0.40), U(0.25, 0.35), U(0.25, 0.35), U(0.30, 0.40), U(0.30, 0.40) for the inter-row, respectively. These perturbation error assumptions are held constant in all the synthetic and real data assimilation experiments described below. All experiments are repeated 50 times to reduce the impact of varying initial conditions and random number sequences.
Two metrics are used here to evaluate the efficacy of data assimilation, including the root-mean-square-error (RMSE) and the normalized error reduction (NER) defined as the difference between unity and ratio of posterior and prior RMSEs of data assimilation [Chen et al., 2011]. NER varies from negative infinity to 1.0, with 1.0 indicating a perfect match between true values and updated states after assimilation and negative values indicating degradation upon assimilation.
2.5.3. Synthetic Twin Experiment
To first explore the merits of the EnKF and PF algorithms in assimilating daily fPET and biweekly θSSM for improving root-zone soil moisture states, synthetic twin data experiments are conducted to determine the optimal ensemble size or particle number. These experiments follow the structure of a typical identical twin experiment with four key components. First, a single model run with in-situ meteorological forcing data and calibrated parameters is defined as the synthetic benchmark “TRUE” scenario. This scenario is further used for generating synthetic observations consistent with pre-defined observation error assumptions (Section 2.5.2). A single-member open loop run (“OL”) is then generated based on the model state and forcing perturbations as specified above. Next, synthetic observations of fPET and θSSM are either separately or simultaneously (depending on the case) assimilated into the model for correcting random errors in forcing and states (“DA”). Resulting state predictions are evaluated based on their ability to recover the TRUE scenario.
The optimal ensemble size or particle number is determined by exploring a range of choices. Using resulting optimized values of ensemble size or particle number, the relative advantages of PF versus EnKF are investigated for handling non-linearities in our estimation problem. The time range for all synthetic experiments is from January 1, 2014 to December 31, 2017.
2.5.4. Real Data Experiment
In addition to these synthetic experiments, a real data assimilation experiment is performed to test the efficacy of assimilating actual remote sensing observations. Here, the open loop (“OL”) scenario is the model run with calibrated parameters and flux tower meteorological data. Perturbations of precipitation/irrigation and soil moisture states are the same as those applied during the synthetic twin experiments. Likewise, the observation error assumptions for fPET and θSSM are fixed in both time and space at values used above. Following Hain et al. [2012], both Sentinel-1 θSSM and DisALEXI fPET observations are rescaled to match the first (mean) and second (standard deviation) statistical moments of the model soil moisture climatology. The temporal range of real data experiments is constrained by the availability of Sentinel-1 θSSM from January 1, 2017 to December 31, 2017. Note that, unlike the synthetic twin experiments described above, the evaluation of these runs is limited to a single, 30-m grid cell where ground-based soil moisture observations are available during the 2017 growing season. Generally, there are no significant differences in meteorological conditions across the study area, and this selected validation pixel is representative of vineyard-wide irrigation management, vine biomass and maturity conditions.
Since soil moisture and fPET are de-coupled during energy-limited conditions in the winter, the assimilation of DisALEXI fPET is limited to the summertime period of April 1 to September 10 for the real data experiment. The relationship between soil moisture and fPET is further investigated in Section 4.1. Likewise, since the accuracy of SAR-based retrievals is known to vary as a function of biomass, an additional real data assimilation experiment is described in Section 4.2 where retrieval errors in Sentinel-1 θSSM estimates are scaled as a function of LAI.
3. Results
3.1. Modelling of Vine-row and Inter-row Tiles
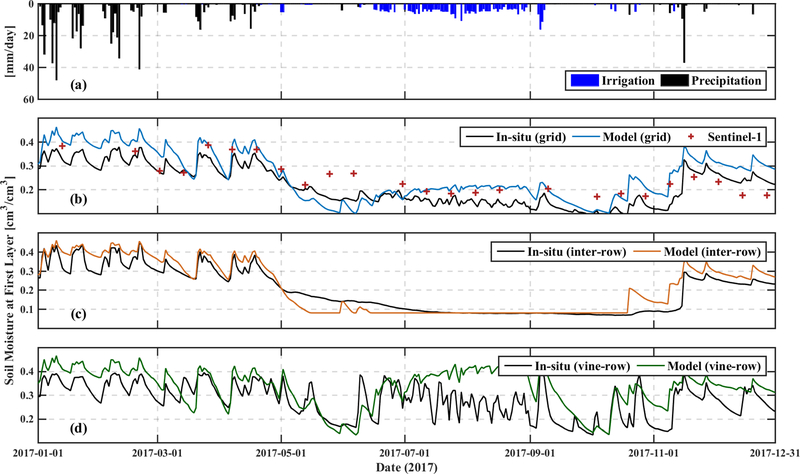
Prior to any data assimilation experiments, WEB-SVAT surface (0–0.05 m) soil moisture estimates are evaluated against in-situ ground measurements in Figure 3. Since precipitation at the Sierra Loma site generally occurs during the spring and winter seasons (Figure 3a), the soil is kept wet with mean value greater than 0.3 m3 m−3 from January to March. Since vines are dormant in this period, bare soil evaporation and transpiration from the inter-row cover crop are the primary processes depleting soil moisture. Vine canopies start to emerge and develop in April when soil moisture is still relatively high. Starting in May, the soil starts to dry out with rapid vine growth and mowing of the inter-row cover crop. Surface soil water content in the inter-row falls to almost residual levels soon afterwards and does not recover until precipitation returns in late fall or winter (see Figure 3c). In contrast, within the vine-row, occasional irrigation starts in May and intensive irrigation runs between June and grape harvest in September.
Figure 3.
(a) Daily precipitation and irrigation for 2017 and 0–5 cm surface soil moisture at the (b) grid-level from transect-averaged in-situ measurements, tile-averaged model simulation, and Sentinel-1 retrievals; and observed and model-simulated within the (c) inter-row and (d) vine-row tiles, respectively.
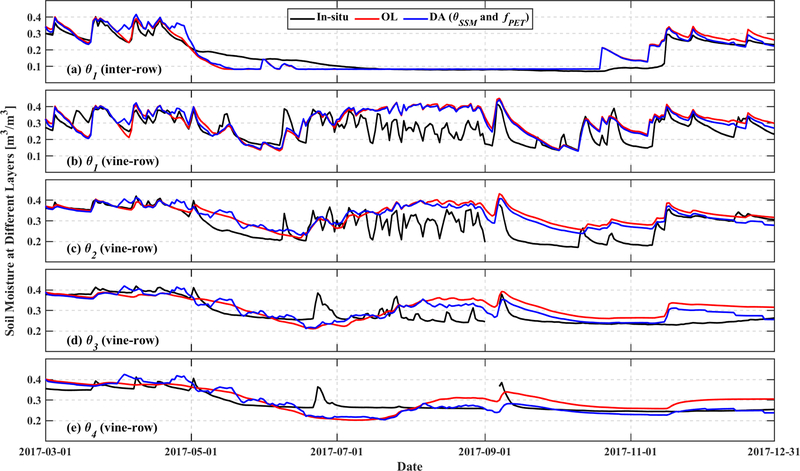
As a result, from May to November, large horizontal contrasts in surface soil moisture are observed between the inter-row and vine-row (Figure 3c and 3d) due to localized drip irrigation along the vine-row. These contrasts are reflected in our application of WEB-SVAT soil moisture states in the vine-row and inter-row. Nevertheless, WEB-SVAT slightly overpredicts surface soil moisture within the vine-row prior to March when vines are in dormancy and not transpiring. Moreover, model-predicted vine-row soil moisture stays at a relatively constant high level throughout the June to September intensive irrigation period, while in-situ observations show stronger temporal fluctuations during this period. This may be partially attributable to subtle differences in the support of each estimate. The vine-row soil moisture probes are installed directly underneath the irrigation drip line. As a result, ground-based measurements represent localized signals and capture quick responses to irrigation. In contrast, model-predicted soil moisture states are representative of a more areal-averaged signal and therefore evolve in a somewhat smoother manner.
3.2. Synthetic Twin Experiments
In the synthetic twin experiment, the model simulation (Section 3.1) with ground-based forcing inputs is deployed as the “TRUE” simulation and used for generating synthetic observations as described in Section 2.5.3. Therefore, the OL and DA scenarios are compared against the TRUE simulation to quantify the net impact of data assimilation. See Section 2.5.3 above for details. The primary goals of the synthetic data assimilation experiments are to: (1) examine sample size requirements for the PF and EnKF, (2) cross-compare PF and EnKF performance for a constant sample size, and (3) explore factors affecting the degree to which data assimilation improves root-zone soil moisture estimation.
3.2.1. Impact of Sample Size
Figure 4 plots NER values for grid-level soil moisture states (obtained via the weighted averaging of vine-row and inter-row values) within the first and root-zone layers as a function of ensemble size for the EnKF and particle sample size for the PF. Note that root-zone estimates are based on the weighted averaging of soil moisture in the second, third and fourth modelled layers (i.e., mean soil moisture between 5 and 90 cm).
Figure 4.
Normalized error reduction (NER) of the grid-level soil moisture states for the first (0– 5 cm; θ1) and root-zone (5 − 90 cm; θrz) soil layers. Either daily fPET or biweekly θSSM is assimilated into the model using different ensemble sizes or particle numbers for the ensemble Kalman filter (EnKF) and particle filter (PF), respectively. Median values of NER from 50 separate synthetic experiments are shown as circles, and error bars indicate the full range of NER from minimum to maximum values.
All EnKF and PF results indicate improved data assimilation performance (higher NER values) with increasing sample size, especially for root-zone soil moisture. In addition, the impact of initial conditions and random number sequences is reduced (i.e., error bars are narrowed) when sample sizes are increased from 10 to 500. For the EnKF, increasing ensemble size enhances the robustness of data assimilation (smaller error bars) but introduces only marginal improvements (slightly increased median NER) for the surface soil moisture when daily fPET is assimilated. In contrast, the estimation of root-zone soil moisture is consistently improved by increasing ensemble size (see Figure 4a). For the PF, moderate improvement is achieved by increasing the sample size from 10 to 25 (Figure 4c), and NER gradually increases with larger particle numbers from 50 to 500. However, additional NER improvements are marginal when ensemble size/particle number is larger than 100 for both surface and root-zone soil moisture for both the assimilation of daily fPET (Figure 4a and 4c) or biweekly θSSM (Figure 4b and 4d). Therefore, as a compromise between DA performance and computational cost, a sample size of 100 is applied in all subsequent experiments.
3.2.2. Particle Filter Versus Ensemble Kalman Filter
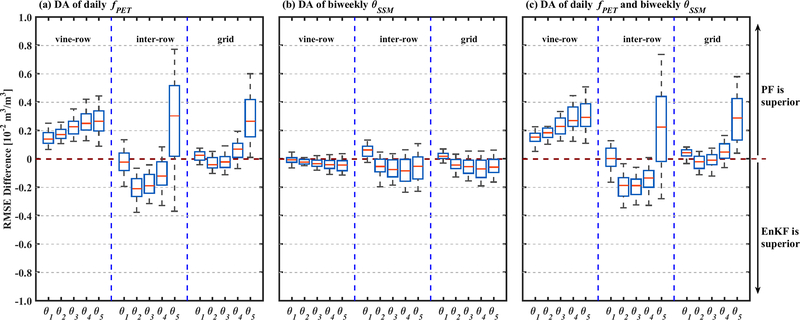
Figure 5 shows the soil moisture RMSE differences (i.e., EnKF RMSE minus PF RMSE) based on the synthetic twin experiment results for the two data assimilation methods (EnKF and PF) at five different soil moisture depths. For the assimilation of daily fPET in Figure 5a, positive RMSE difference values indicate that the PF performs better for vine-row soil moisture states. In contrast, the EnKF yields greater error reductions (i.e., smaller RMSEs and therefore negative RMSE differences) for the inter-row states, especially in the top four soil layers. However, in terms of overall results at the grid-level (based on the weighted averaging of vine-row and inter-row results), the PF outperforms EnKF for most multi-layer soil moisture states at different depths. Overall, smaller differences between the EnKF and PF are noted when assimilating biweekly θSSM (Figure 5b). In this case, EnKF results are generally only slightly superior.
Figure 5.
Box plots of the root-mean-square-error (RMSE) differences (EnKF minus PF) between the EnKF and PF for soil moisture estimates of all five soil layers. Plotted cases are based on the assimilation of: (a) only daily fPET, (b) only biweekly θSSM and (c) both daily fPET and biweekly θSSM. Median values of RMSE differences from 50 separate synthetic experiments are plotted in red. Boxes represent 25–75 quantiles and whiskers represent 5–95 quantiles of replicated experiment results. Positive values indicate superior PF performance.
The difference in the relative performance for the EnKF versus PF for the fPET and θSSM assimilation cases are consistent with our a priori expectations concerning the linearity of their relationship with updated soil moisture states. The relationship between soil moisture states and fPET is nonlinear (as characterized via Eq. B5). In contrast, θSSM is linearly related to surface soil moisture. Especially for the vine-row tile, reductions in soil moisture are linked to the exponential root water uptake through transpiration, and thus nonlinearly related to fPET values. For inter-row tile, this nonlinearity is weaker since the cover crop is senescent from May to October and transpiration is limited to superficial soil layers due to the shallower rooting depth for inter-row cover crops. Therefore, cases with strong nonlinearity (e.g., fPET assimilation into the vine-row) tend to favor the PF while the EnKF performs better in more linear cases (e.g., θSSM assimilation and fPET assimilation into the inter-row). Note that the nonlinearity can also originate from the boundary truncation imposed on soil moisture states. Such truncation can lead to a non-Gaussian distributed state ensemble. When fPET is assimilated, the relative merit of PF versus EnKF for solving stronger nonlinearity between model states and observation is identified.
Nevertheless, for the same level of computation demand (i.e., 100 ensemble members versus 100 particles) and the simultaneous assimilation of both daily fPET and biweekly θSSM (Figure 5c), the PF demonstrates overall superior performance — particularly in the vine-row (which is naturally our primary concern for irrigation scheduling). Accordingly, a 100-particle PF is utilized in all subsequent data assimilation experiments.
3.2.3. Spatial Patterns in NER
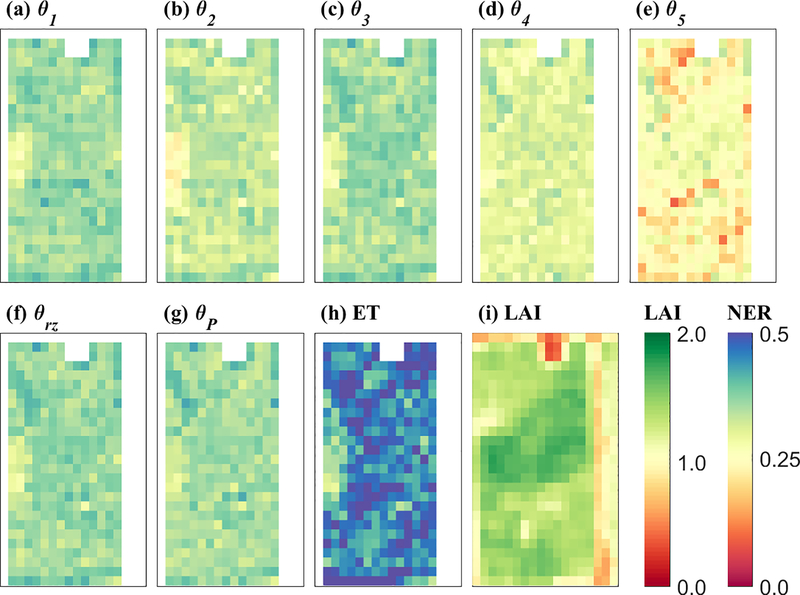
As described above, the performance of any data assimilation algorithm is fundamentally related to the strength of the relationship between observations and model states. Figure 6i shows the mean annual LAI for the study area. LAI is relatively high in the central part of the vineyard from its northeast to southwest corner and relatively low in its northwest and southeast corners. Enhancements to both root-zone soil moisture (Figure 6f) and ET (Figure 6h) associated with fPET assimilation (and a synthetic twin experiment) are moderately larger for areas of high LAI — likely reflecting the tighter coupling of soil moisture states and fPET in these areas.
Figure 6.
For the assimilation of daily fPET (from January 1, 2014 to December 31, 2017), the spatial distribution of NER for the: (a) first layer θ1 (0–5 cm); (b) second layer θ2 (5–30 cm), (c) third layer θ3 (30–60 cm), (d) fourth layer θ4 (60–90 cm), (e) fifth layer θ5 (90–120 cm), (f) root-zone layer θrz (5–90 cm), (g) profile θP (0–120 cm)—represented as the weighted averages over all five layers and (h) evapotranspiration (ET) of the vine-row tile. (i) is the mean-annual leaf area index (LAI).
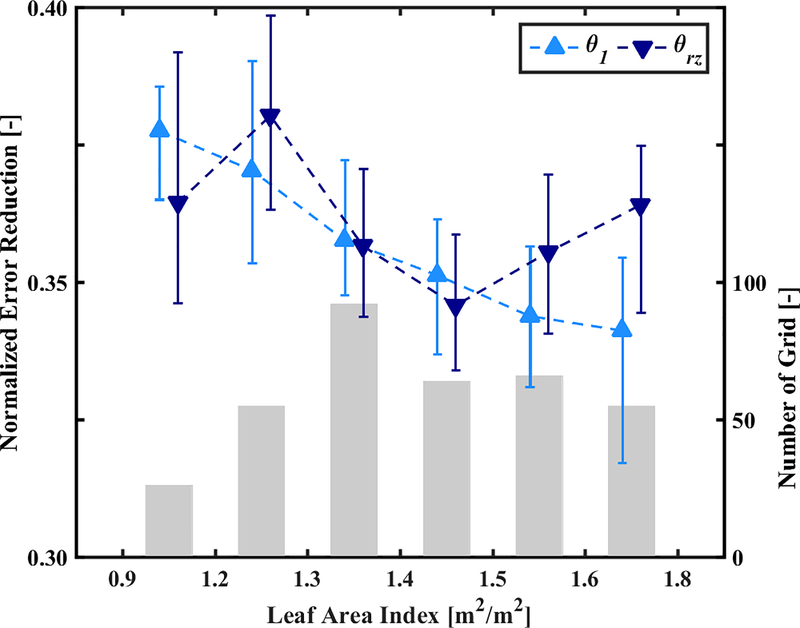
Figure 7 summarizes aggregate NER values for vine-row surface and root-zone soil moisture estimates as a function of LAI. For grid cells with LAI less than 1.3 m2 m−2, soil moisture values in deeper soil layers tend to be higher due to less ET extraction of soil water. This leads to stronger PF updates, and thus higher NER, since the variance of model perturbations (and thus the strength of PF updates) increases as a function of soil moisture.
Figure 7.
For the assimilation of daily fPET, spatially averaged NER values of soil moisture states for grids with different LAI levels within the surface-zone (θ1) and root-zone (θrz). Results are shown for the vine-row tile only. Median values are shown as triangles with 10–90 quantiles as vertical bars. The number of 30-m grids with a given time-averaged LAI value are indicated by the grey bars.
Another factor related to LAI is the coupling strength between fPET and multi-layer soil moisture states. For example, the increase in NER for LAI greater than 1.4 m2 m−2 (Figure 7) appears to be a response to stronger coupling between root-zone soil moisture and fPET for higher biomass areas (i.e., larger LAI) where transpiration dominates total ET. For areas of high transpiration/LAI, this increased coupling between fPET and root-zone soil moisture comes at the expense of coupling between fPET and surface soil moisture — note the decrease in soil moisture NER for the top-most soil layer for higher LAI conditions where bare soil evaporation is minimal (light blue line in Figure 7). As described in Section 2.4, soil evaporation extracts water directly from the surface soil layer — so higher LAI (and less bare soil evaporation) decreases our ability to constrain surface soil moisture through fPET. Therefore, for cases where model error covariances are comparatively similar, improvements in root-zone soil moisture states in vine-row tiles are larger for regions with larger LAI values.
3.3. Real Data Experiments
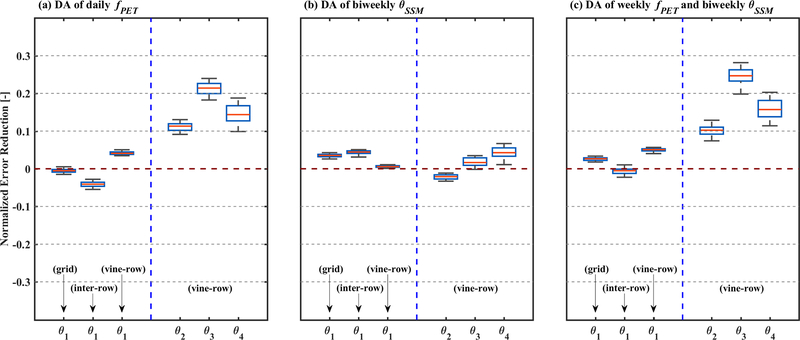
In addition to the synthetic experiments described above, the assimilation of remotely-sensed DisALEXI fPET and Sentinel-1 θSSM observations is validated against the ground-based soil moisture measurements via the real-data assimilation experiment outlined in Section 2.5.4. The same flux tower-based meteorological data and irrigation forcing data are applied in both the OL and DA scenarios — allowing for an objective examination of net benefits introduced by the assimilation of remote sensing data. Real data assimilation experiments provide, of course, the most comprehensive test for a data assimilation system; however, their evaluation is limited only to sites containing actual ground-based soil moisture observations. Figure 8 shows the in-situ soil moisture observations acquired near the flux tower (black lines) for inter-row surface and four upper layers within the vine-row. Model-simulated soil moisture states based on flux tower meteorological inputs from the OL scenario are shown in red lines, and DA results are shown in the blue lines. The assimilation of both θSSM and fPET slightly improves estimates of surface soil moisture states at both tiles (Figure 8a and 8b). More prominent improvements are found for soil moisture states in deeper soil layers (Figure 8d and 8e). Specifically, based on the NER values shown in Figure 9, improvements are limited for surface soil moisture — with NER values below 0.06 [-] for all three DA scenarios. NER values get larger (i.e., greater than 0.1) for deeper soil layers, especially when fPET is assimilated. The simultaneous assimilation of both Sentinel-1 θSSM and DisALEXI fPET (Figure 9c) is generally associated with the largest improvement in soil moisture accuracy.
Figure 8.
Time series of soil moisture estimates based on in-situ measurements, the open loop (OL) simulation and the assimilation (DA) of both θSSM and fPET (between January 1, 2017 to December 31, 2017) for the: (a) first layer θ1 of the inter-row (0–5 cm), (b) first layer θ1 of the vine-row (0–5 cm), (c) second layer θ2 of the vine-row (5–30 cm), (d) third layer θ3 of the vine-row (30–60 cm), and (e) fourth layer θ4 of the vine-row (60–90 cm).
Figure 9.
Box plots of NER values for soil moisture states as validated against in-situ measurements for the cases of assimilating: (a) daily DisALEXI fPET, (b) biweekly Sentinel-1 θSSM, and (c) both fPET and θSSM.
4. Discussion
4.1. Relationship Between Soil Moisture and fPET
The updating of model soil moisture states in response to fPET observations is a direct function of the assumed dependence of fPET on soil moisture within the assimilation model. Both over- and under-dependence can lead to degraded data assimilation performance [Kumar et al., 2009; Crow et al., 2015; Lei et al., 2018]. Therefore, it’s important to evaluate this dependence in models.
For the WEB-SVAT model utilized in this work, the relationship between profile soil moisture and fPET varies as a function of LAI and meteorological conditions. Lines in Figure 10 are generated via the WEB-SVAT model for the vine-row profile soil moisture and daily fPET under different LAI conditions. Specifically, minimum (0.3) and maximum (3.0) LAI values are assumed for a single day (August 1, 2017) with typical summer meteorological conditions. The model clearly predicts stronger coupling between soil moisture and fPET for denser vegetation cover. However, note that this exact relationship changes with the meteorological conditions, including insolation, wind speed, air pressure, temperature, and relative humidity.
Figure 10.
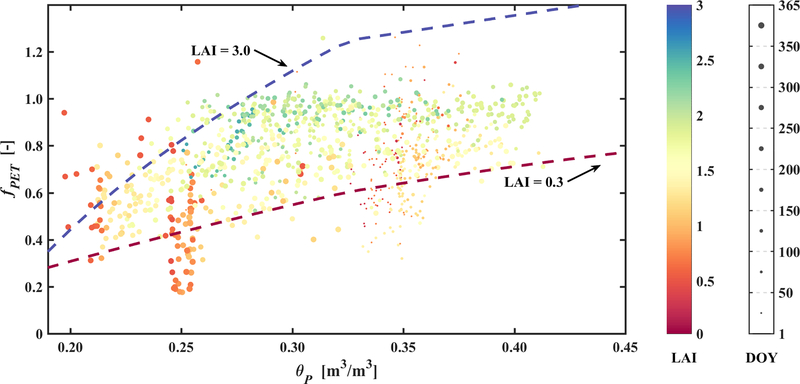
The relationship between daily mean profile soil moisture (θP) averaged over ground-based vine-row profile soil moisture sensors at 30, 60, 90 cm depths and fPET obtained from flux tower ET measurement and potential ET using the Penman-Monteith equation, shown as scattered points with color representing LAI levels and size representing the Day-Of-Year (DOY). Lines are generated with the model by assuming minimum (0.3) and maximum (3.0) LAI bounds and August 1, 2017 meteorological conditions.
In contrast, the scattered points in Figure 10 demonstrate the observed relationship between the averaged soil moisture from three vine-row profile sensors at depths of 30, 60, 90 cm and daily fPET obtained by taking the ratio of flux tower ET and potential ET using the Penman-Monteith equation [Allen et al., 1998]. Overall, the observed coupling between profile soil moisture and fPET starts to decrease when soil moisture gets higher and above 0.35. Most noticeably, these observations show little dependence of fPET on soil moisture for days with low air temperature (Day-Of-Year; DOY<100 or DOY>250) and light vegetation cover (reddish points with small LAI).
Comparing the model intrinsic coupling and ground observation-based relationship reveals large variations in the degree of dependence. For spring and winter conditions, there is marginal dependence of fPET on soil moisture as indicated by observations. As a result, the assimilation of DisALEXI fPET for the entire year (as opposed to only the growing seasons) leads to deteriorated results in the real data experiment (not shown here). Therefore, in addition to accurately characterizing the observation errors in fPET retrievals, the (dynamic) relationship between fPET and profile soil moisture needs to be better understand before we can fully utilize fPET observations in data assimilation systems. Indeed, a multi-year analysis by Wilson et al. [2019] using the flux tower measurements of ET along with the soil moisture profile measurements over the Sierra Loma site indicates that the fPET – root zone soil moisture relationship changes throughout the spring and summer months due to advancing phenological stages and management practices. There is also evidence that vines have access to water beyond the 90-cm maximum depth measured by the profile soil moisture sensors.
4.2. Uncertainties in Remote Sensing Retrievals
The main challenge for Sentinel-1 θSSM retrievals is adequately compensating for the sensitivity of radar signals to surface roughness and vegetation cover. For highly clumped row crops, the low signal-to-noise ratio in SAR data degrades the accuracy of soil moisture retrievals and will reduce the magnitude of potential data assimilation improvements. These effects will naturally be more pronounced for high vine biomass conditions. Therefore, data assimilation systems that accurately capture temporal variations in θSSM retrieval accuracy should also provide more accurate output.
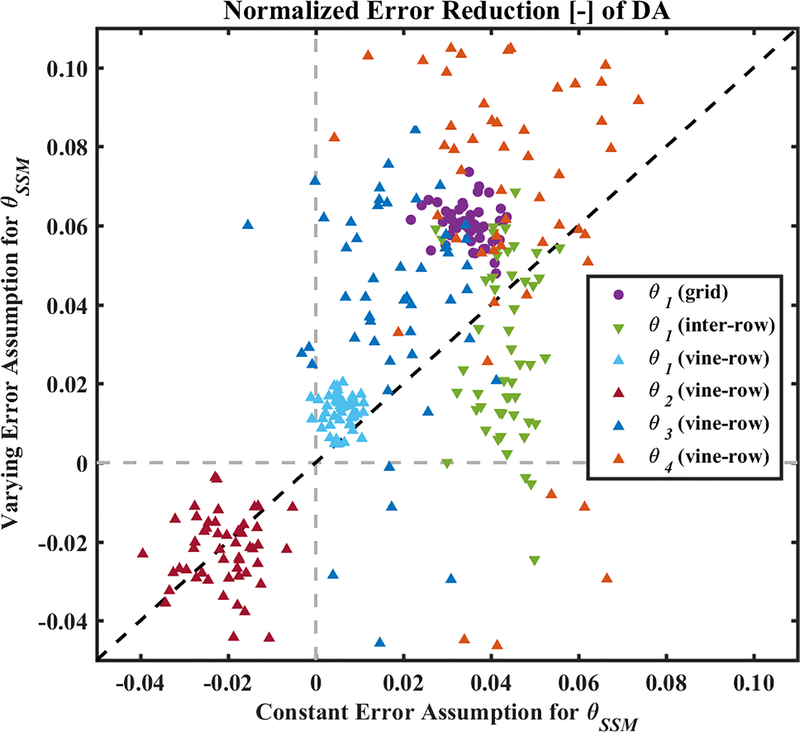
Therefore, an additional real data experiment is conducted for the assimilation of Sentinel-1 θSSM as described in Section 2.5.4. In this new experiment, a time-varying function (defined as the product of 0.03 m3 m−3 and unitless LAI) — with the consideration of vegetation density impact on SAR backscatter signals — is used to described uncertainty (i.e., error standard deviation) in the assimilated Sentinel-1 θSSM data. Results from this new experiment are compared to earlier real data assimilation results — derived using a temporally constant representation of retrieval uncertainty (0.05 m3 m−3). Figure 11 compares NER values between these two cases. In most cases, vine-row tile estimates of soil moisture states are improved with the time-varying error assumption (i.e., produces slightly higher NERs). The exception being the second soil layer where no significant differences are found. However, despite this overall improvement, DA performance is somewhat less stable for the time-varying case — with larger observed variations in NER values corresponding to random initial conditions and individual error sequence replicates. Nevertheless, it is promising that the assimilation of Sentinel-1 θSSM can generally be improved via the application of a realistic time-varying error assumption.
Figure 11.
Comparison between the NER values for the assimilation of Sentinel-1 θSSM with a constant error assumption (x-axis) and a time-varying error function (y-axis). Each experiment is repeated 50 times with different initial conditions and random number sequences.
5. Conclusions
In this work, a high-resolution (30-m) data assimilation framework is constructed for modelling soil moisture in a vineyard in California. With the recent availability of TIR-based ET products and SAR-based surface soil moisture retrievals at sub-field scale, modelled soil moisture states at different soil depths can be improved via the integration of both remote sensing data types. Modifications, such as the tile approach for row and inter-row regions, are made to the WEB-SVAT model to accommodate its application within highly structured vineyards (Section 3.1). Starting from the synthetic twin experiments, the optimal sampling size is determined (Section 3.2) for the data assimilation of daily fPET and biweekly θSSM. A performance comparison between PF and EnKF suggests that a PF approach is superior to an EnKF when assimilated observations are nonlinearly related with the model states to be updated. This is particularly important since observed fPET data are nonlinearly linked to soil moisture states in the model, as well as observed from ground-based measurements (Section 4.1). Moreover, the impact of biophysical conditions (i.e., LAI) on data assimilation performance is explored for soil moisture states at different depths. Overall, high LAI conditions seem to enhance the ability of fPET assimilation to constrain vine-row root-zone soil moisture.
Furthermore, to examine the capability of real remote sensing data assimilation for improving soil moisture estimation, 30-m daily DisALEXI fPET and biweekly Sentinel-1 θSSM retrievals are individually and simultaneously assimilated into the model (Section 3.3). Validation against in-situ soil moisture measurements in the real data experiment suggests that the simultaneous assimilation of both fPET and θSSM has the largest potential for accurately constraining root-zone soil moisture. However, it should be stressed that the advantages of dual fPET and θSSM assimilation are relatively marginal compared to the case of assimilating only fPET (Figure 9). Therefore, further study of this point using additional real data experiments is likely warranted.
To facilitate improved validation of real data experiments, more ground-based soil moisture measurements are required. To this end, the GRAPEX experiment has improved the spatial sampling of ground-based soil moisture within multiple E&J Gallo production vineyards during the 2018 and 2019 growing seasons. Enhanced ground-based soil moisture observations from these sites will be utilized in future research. Likewise, future satellite-based, L-band SAR instruments like the NASA-Indian Space Research Organization Synthetic Aperture Radar (NISAR), Argentina’s space agency CONAE (Satélite Argentino de Observación COn Microondas) SAOCOM satellite constellation, and German Tandem-L [Moreira et al., 2015] missions will provide more frequent and accurate SAR-based retrievals of surface soil moisture observations. Simultaneously, new LST products from the Visible Infrared Imaging Radiometer Suite (VIIRS) onboard the NASA Suomi-NPP satellite, ECOsystem Spaceborne Thermal Radiometer Experiment on Space Station (ECOSTRESS), and Sentinel satellite constellation will be synergistically deployed in the ALEXI/DisALEXI framework to produce daily 30-m products at higher accuracy. Future work will focus on utilizing these new data sources to further optimize our data assimilation system at fine spatio-temporal resolutions.
Through incorporating thermal and radar information into the data assimilation system described here, spatially high-resolution (30-m) and temporally continuous (at a short data latency, <3–5 days) soil moisture map can be provided and distributed to vineyard irrigation managers. In operation, this root-zone soil water content information will help optimize irrigation allocation and enhance water conservation efforts. During early growing season, the onset of irrigation is typically based on either point observations or growers experience estimating plant available water threshold of ~50%. With the proposed modelling system, this threshold can be determined spatially by incorporating the current water content map in conjunction with short-term weather forecasts. The enhanced spatial and temporal characterization of root-zone water availability, in combination with the variable rate drip irrigation system, will allow vineyard managers to identify blocks with water inadequacy or irrigation inefficacy. Accordingly, appropriate amounts of irrigated water can be determined by growers and vineyard managers to optimize irrigation strategies, target uniform grape quality, and yield.
Highlights.
30-m soil moisture variation is described via model, thermal and radar remote sensing
A PF is superior to an EnKF in solving the nonlinear estimation problem
Soil moisture monitoring can be improved via assimilating thermal and radar data
Acknowledgments
Funding and logistical support provided by E. & J. Gallo Winery Viticulture, Chemistry and Enology Division made possible the installation and acquisition of the micrometeorological and soil moisture profile data at the vineyard site used in this study. In addition, this project would not have been possible without the cooperation of Mr. Ernie Dosio of Pacific Agri Lands Management, along with the Sierra Loma vineyard staff, for logistical support of GRAPEX field and research activities. Financial support for this research was provided by a grant from the NASA Applied Sciences–Water Resources Program (Grant Award NNH17AE39I, P-I W. Kustas).
Appendix A —. ALEXI/DisALEXI
The core of the ALEXI/DisALEXI is the TSEB land surface scheme developed by Norman et al. [1995] and further refined by Kustas and Norman [1999]. In the TSEB scheme, surface energy fluxes are explicitly represented for canopy (C) and soil (S) sources
| (A1) |
where RN is net radiation, H sensible heat flux, LE latent heat flux, and G the soil heat flux. The soil and canopy heat fluxes are constrained by partitioning the remotely sensed LST or surface radiometric temperature, TRAD, into effective canopy (TC) and soil (TS) temperatures
| (A2) |
where fC(θ) refers to the directional vegetation cover fraction derived as a function of LAI and the sensor view angle (θ). The components for the energy balance system in Eq. A1 are solved simultaneously with the radiometric temperature balance Eq. A2. Net radiation for the soil and canopy components (RN,S and RN,C) is estimated via the radiative transfer model of Campbell and Norman [1998]. Sensible heat fluxes are predicted through the surface-to-air temperature gradient by using air temperature (TA) at the reference height above canopy as a boundary layer, mediated by an in-canopy node as in the series formalism presented by Norman et al. [1995]. Soil heat flux (GS) is computed as a fraction of the net radiation at the soil surface (RN,S). Using a modified Priestley-Taylor approach [Priestley and Taylor, 1972], an initial estimate of canopy transpiration (LEC) is firstly derived assuming unstressed water condition. Thus, soil evaporation LES is computed as the residual to the energy balance Eq. A1. Considering the daytime soil condensation (i.e., LES < 0) is unlikely, LEC is iteratively adjusted downward to ensure LES prediction is non-negative. ET (mass flux in units of mm d−1) is computed from LE (energy flux in units of W m−2 or MJ m−2 d−1) using the latent heat of vaporization.
For the regional implementation of TSEB in the ALEXI framework, an atmospheric boundary layer module is coupled with the TSEB scheme to relate the morning temperature rise in the mixing layer to the time-integrated sensible heat flux from the surface [Anderson et al., 2007]. This configuration employs the time-differential signal provided by geostationary satellites like GOES, thereby reducing the reliance on the accurate retrieval of absolute, instantaneous LST from remote sensing platforms. To further enhance the spatial resolution of the ET products, thermal LST imageries from polar-orbiting satellites of Landsat and MODIS are utilized for finer resolution mapping. The spatial disaggregation scheme, namely DisALEXI, is implemented to ensure the spatially reaggregated DisALEXI ET flux (MODIS and Landsat) matches the ET estimate at the regional ALEXI scale. All ET estimates are upscaled from the sensor overpass time to daytime-integrated values for representing daytime ET amount by assuming the ratio of latent heat flux to insolation is constant during the daylight hours.
Due to cloud cover and sensor issues, spatiotemporal discontinuities in thermal-based LST observations can lead to gaps in ALEXI/DisALEXI ET estimates. A simple gap-filling technique is applied to the ALEXI ET retrievals through conserving a ratio of actual ET to a predetermined scaling flux. This ratio is temporally filtered, smoother and gap-filled for each pixel grid using a Savitzky-Golay filter with a second-order smoothing polynomial. Gaps in ET estimates are recovered by applying this ratio to the scaling flux. For ALEXI ET, the daily insolation is proven to be robust as the scaling flux at global scale. While DisALEXI algorithm aims to ensure the consistency between ET estimates at different spatial scales, the ALEXI ET is used as the scaling flux for filling gaps in MODIS DisALEXI ET. Gaps in Landsat DisALEXI ET for overpass dates are filled through an extension of the STARFM algorithm [Gao et al., 2006] that fuses daily 500-m MODIS ET maps with periodic (16-day) 30-m Landsat ET maps to generate a daily 30-m ET product.
Appendix B —. WEB-SVAT
In WEB-SVAT model, surface (θsz) and root-zone (θrz,i) soil moisture at layer i are predicted as
| (B1) |
| (B2) |
where Pg is the precipitation through-fall after canopy interception and/or drip irrigation, ρw the density of water, λ the latent heat of vaporization for water, Qi→i+1 the downward diffusive water flux from layer i to i + 1, dt the hourly time step, dzsz the depth of surface soil layer, and dzrz,i the depth of root-zone layer i.
Assuming Darcy’s law for the unsaturated water flow, Qi→i+1 can be estimated as
| (B3) |
here Kθ is the hydraulic conductivity at soil moisture θ, and ψm the matrix potential.
In contrast to ALEXI/DisALEXI, soil evaporation LES is predicted as
| (B4) |
where Cp is the specific heat of air, γ the slope of the saturation vapor pressure versus temperature curve, es and ea saturation and actual vapor pressure, RA,S the within-canopy aerodynamic resistance, RA the above canopy aerodynamic resistance, and RS the soil resistance as an empirical function of θsz.
Taking into account variations in the vertical root distribution of grapevines, an exponential root water uptake module [Li et al., 2001] is deployed to estimate canopy transpiration LEC,i at root-zone i as
| (B5) |
where αi is a dimensionless soil water availability factor as a function of θrz,i, Fi the dimensionless fraction of the root length density in soil layer i as a function of the fraction in top 10% of the root zone F10, η an empirical parameter controlling the water uptake distribution within the soil profile, and n the number of root-zone layers. The maximum total canopy transpiration LEC,max is estimated assuming an unstressed water condition with minimum canopy stomatal resistance (RC,min)
| (B6) |
From Eq. B5 and B6, it is clear that the model-predicted fPET as a function of integrated LEC,i and LEC,max is nonlinearly related to soil moisture via the factor αi. For the consistency with ALEXI/DisALEXI, other energy components in the WEB-SVAT are calculated using the same equations as described in Appendix A. Therefore, given the initial estimates of θsz and θrz, all flux terms in Eq. A1 can be directly expressed in terms of TS and TC and solved via a numerical root finder method. The estimated LES and LEC,i are subsequently used to update soil moisture states in time via Eq. B1 and B2. For more details on WEB-SVAT, see Crow et al. [2008] and Hashemian et al. [2015].
Appendix C —. Data Assimilation Algorithms
C.1. Generic Data Assimilation System
Given a model transition function F(·), the model state vector xt−1 evolves from time step t − 1 to the next step t as
| (C1) |
where μt is the forcing data, ξ a time-invariant parameter vector, and ωt represents the model forecast error which is typically assumed to be Gaussian distributed with mean zero and variance of Qt.
The model state vector xt and observation vector yt are related through a nonlinear observation operator H(·)
| (C2) |
where vt is the Gaussian distributed random observation error with mean zero and variance of Rt. Model error ωt and observation error vt are generally assumed to be statistically independent.
C.2. Ensemble Kalman Filter
In EnKF, the model background forecast error covariance information is represented through an ensemble of model replicates with perturbed forcing data, parameters, and/or model states in a Monte Carlo manner [Evensen, 2003]. When observation yt becomes available at time t, the state vector of ith ensemble member is updated as follows
| (C3) |
where is the posterior state vector after integration of yt, the prior state vector, vi the observation error, H(·) the observation operator for projecting state vector from model space to observation space, and Kt the Kalman gain which weighs the relative uncertainties of model and observation
| (C4) |
where Pt represents the prior model state error covariance, Rt the observation error covariance, the cross-covariance between model-predicted state and the corresponding predicted observation , and the error covariance of in observation space.
C.3. Particle Filter
Given temporally independent observations y1:t, the posterior distribution of the model state of jth particle in PF can be written recursively as [Vrugt et al., 2013]
| (C5) |
where is the transition probability of model states, the likelihood of observations given model states, and p(yt|y1:t−1) the normalization factor. By integrating , the marginal distribution is derived as
| (C6) |
where prior distribution is expressed as
| (C7) |
In practice, the posterior distribution is difficult to obtain and thus is usually approximated as
| (C8) |
where is the weight for jth particle, δ(·) the Dirac delta function, and N the particle number. Using the importance sampling strategy, the unnormalized importance weight can be expressed as
| (C9) |
where is the proposal distribution which is usually assumed as transition prior and thereby
| (C10) |
Generally, the likelihood is estimated as
| (C11) |
where n is the number of observations. Therefore, the normalized weight is
| (C12) |
For PF, equal weights are assigned to particles in prior and updated based on likelihood when observations are available using Eq. C10. In practice, resampling is required to avoid particle degeneration whereby most particles have negligible weights. Here, resampling is conducted after each step of assimilating observations [Moradkhani et al., 2005]. Therefore, particle weights are updated when observations become available and particles are resampled based on these weights. After resampling, weights are reset to equal as 1/N for the next time step.
Footnotes
The use of trade, firm, or corporation names in this article is for the information and convenience of the reader. Such use does not constitute official endorsement or approval by the US Department of Agriculture or the Agricultural Research Service of any product or service to the exclusion of others that may be suitable.
References
- Acevedo-Opazo C, Ortega-Farias S and Fuentes S, 2010. Effects of grapevine (Vitis vinifera L.) water status on water consumption, vegetative growth and grape quality: An irrigation scheduling application to achieve regulated deficit irrigation. Agricultural Water Management, 97(7), pp.956–964. [Google Scholar]
- Alfieri JG, Kustas WP, Prueger JH, McKee LG, Hipps LE and Gao F, 2019. A multi-year intercomparison of micrometeorological observations at adjacent vineyards in California’s central valley during GRAPEX. Irrigation Science, 37(3), pp.345–357. [Google Scholar]
- Allen RG, Pereira LS, Raes D and Smith M, 1998. Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56. FAO, Rome, 300(9), D05109. [Google Scholar]
- Amos CB, Audet P, Hammond WC, Bürgmann R, Johanson IA and Blewitt G, 2014. Uplift and seismicity driven by groundwater depletion in central California. Nature, 509(7501), pp.483–486. [DOI] [PubMed] [Google Scholar]
- Anderson MC, Norman JM, Mecikalski JR, Torn RD, Kustas WP and Basara JB, 2004. A multiscale remote sensing model for disaggregating regional fluxes to micrometeorological scales. Journal of Hydrometeorology, 5(2), pp.343–363. [Google Scholar]
- Anderson MC, Norman JM, Mecikalski JR, Otkin JA and Kustas WP, 2007. A climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 1. Model formulation. Journal of Geophysical Research: Atmospheres, 112, D10117, doi: 10.1029/2006JD007506. [DOI] [Google Scholar]
- Anderson MC, Hain C, Wardlow B, Pimstein A, Mecikalski JR and Kustas WP, 2011a. Evaluation of drought indices based on thermal remote sensing of evapotranspiration over the continental United States. Journal of Climate, 24(8), pp.2025–2044. [Google Scholar]
- Anderson MC, Kustas WP, Norman JM, Hain CR, Mecikalski JR, Schultz L, González-Dugo MP, Cammalleri C, d’Urso G, Pimstein A and Gao F, 2011b. Mapping daily evapotranspiration at field to continental scales using geostationary and polar orbiting satellite imagery. Hydrology and Earth System Sciences, 15(1), pp.223–239. [Google Scholar]
- Anderson MC, Hain C, Otkin J, Zhan X, Mo K, Svoboda M, Wardlow B and Pimstein A, 2013. An intercomparison of drought indicators based on thermal remote sensing and NLDAS-2 simulations with US Drought Monitor classifications. Journal of Hydrometeorology, 14(4), pp.1035–1056. [Google Scholar]
- Anderson MC, Zolin CA, Sentelhas PC, Hain CR, Semmens K, Yilmaz MT, Gao F, Otkin JA and Tetrault R, 2016a. The Evaporative Stress Index as an indicator of agricultural drought in Brazil: An assessment based on crop yield impacts. Remote Sensing of Environment, 174, pp.82–99. [Google Scholar]
- Anderson MC, Hain CR, Jurecka F, Trnka M, Hlavinka P, Dulaney W, Otkin JA, Johnson D and Gao F, 2016b. Relationships between the evaporative stress index and winter wheat and spring barley yield anomalies in the Czech Republic. Climate Research, 70(2–3), pp.215–230. [Google Scholar]
- Attarzadeh R, Amini J, Notarnicola C and Greifeneder F, 2018. Synergetic Use of Sentinel-1 and Sentinel-2 Data for Soil Moisture Mapping at Plot Scale. Remote Sensing, 10(8), 1285, doi: 10.3390/rs10081285. [DOI] [Google Scholar]
- Baldocchi D, Falge E, Gu L, Olson R, Hollinger D, Running S, Anthoni P, Bernhofer C, Davis K, Evans R and Fuentes J, 2001. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bulletin of the American Meteorological Society, 82(11), pp.2415–2434. [Google Scholar]
- Bastiaanssen WG, Molden DJ and Makin IW, 2000. Remote sensing for irrigated agriculture: examples from research and possible applications. Agricultural water management, 46(2), pp.137–155. [Google Scholar]
- Borsa AA, Agnew DC and Cayan DR, 2014. Ongoing drought-induced uplift in the western United States. Science, 345(6204), pp.1587–1590. [DOI] [PubMed] [Google Scholar]
- Brocca L, Moramarco T, Melone F, Wagner W, Hasenauer S and Hahn S, 2012. Assimilation of surface-and root-zone ASCAT soil moisture products into rainfall–runoff modeling. IEEE Transactions on Geoscience and Remote Sensing, 50(7), pp.2542–2555. [Google Scholar]
- Cammalleri C, Anderson MC, Gao F, Hain CR and Kustas WP, 2013. A data fusion approach for mapping daily evapotranspiration at field scale. Water Resources Research, 49(8), pp.4672–4686. [Google Scholar]
- Campbell GS, and Norman JM, 1998. An Introduction to Environmental Geophysics. New York: Springer-Verlag; pp. 286. [Google Scholar]
- Chen F, Crow WT, Starks PJ and Moriasi DN, 2011. Improving hydrologic predictions of a catchment model via assimilation of surface soil moisture. Advances in Water Resources, 34(4), pp.526–536. [Google Scholar]
- Clapp RB and Hornberger GM, 1978. Empirical equations for some soil hydraulic properties. Water resources research, 14(4), pp.601–604. [Google Scholar]
- Courault D, Seguin B and Olioso A, 2003. Review to estimate evapotranspiration from remote sensing data: some examples from the simplified relationship to the use of mesoscale atmospheric models. In ICID workshop on remote sensing of ET for large regions, Vol. 17, pp. 1–18. [Google Scholar]
- Crow WT, Lei F, Hain C, Anderson MC, Scott RL, Billesbach D and Arkebauer T, 2015. Robust estimates of soil moisture and latent heat flux coupling strength obtained from triple collocation. Geophysical Research Letters, 42(20), pp.8415–8423. [Google Scholar]
- Crow WT, Kustas WP and Prueger JH, 2008. Monitoring root-zone soil moisture through the assimilation of a thermal remote sensing-based soil moisture proxy into a water balance model. Remote Sensing of Environment, 112(4), pp.1268–1281. [Google Scholar]
- Cunha M, Marçal AR and Rodrigues A, 2010, March. A comparative study of satellite and ground-based vineyard phenology. In Proc. 29th Symp EARSeL pp. 68–77. [Google Scholar]
- Diffenbaugh NS, Swain DL and Touma D, 2015. Anthropogenic warming has increased drought risk in California. Proceedings of the National Academy of Sciences, 112(13), pp.3931–3936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorigo WA, Wagner W, Hohensinn R, Hahn S, Paulik C, Xaver A, Gruber A, Drusch M, Mecklenburg S, Oevelen PV and Robock A, 2011. The International Soil Moisture Network: a data hosting facility for global in situ soil moisture measurements. Hydrology and Earth System Sciences, 15(5), pp.1675–1698. [Google Scholar]
- Dorigo WA, Zurita-Milla R, de Wit AJ, Brazile J, Singh R and Schaepman ME, 2007. A review on reflective remote sensing and data assimilation techniques for enhanced agroecosystem modeling. International journal of applied earth observation and geoinformation, 9(2), pp.165–193. [Google Scholar]
- El Hajj M, Baghdadi N, Zribi M and Bazzi H, 2017. Synergic use of Sentinel-1 and Sentinel-2 images for operational soil moisture mapping at high spatial resolution over agricultural areas. Remote Sensing, 9(12), 1292, doi: 10.3390/rs9121292. [DOI] [Google Scholar]
- Escriva-Bou A, McCann H, Hanak E, Lund J and Gray B, 2016. Accounting for California Water. California Journal of Politics and Policy, 8(3), doi: 10.5070/P2cjpp8331935. [DOI] [Google Scholar]
- Evensen G, 2003. The ensemble Kalman filter: Theoretical formulation and practical implementation. Ocean dynamics, 53(4), pp.343–367. [Google Scholar]
- Famiglietti JS, Lo M, Ho SL, Bethune J, Anderson KJ, Syed TH, Swenson SC, De Linage CR and Rodell M, 2011. Satellites measure recent rates of groundwater depletion in California’s Central Valley. Geophysical Research Letters, 38, L03403, doi: 10.1029/2010GL046442. [DOI] [Google Scholar]
- Fang L, Hain CR, Zhan X and Anderson MC, 2016. An inter-comparison of soil moisture data products from satellite remote sensing and a land surface model. International journal of applied earth observation and geoinformation, 48, pp.37–50. [Google Scholar]
- Fraga H, Santos JA, Moutinho-Pereira J, Carlos C, Silvestre J, Eiras-Dias J, Mota T and Malheiro AC, 2016. Statistical modelling of grapevine phenology in Portuguese wine regions: observed trends and climate change projections. The Journal of Agricultural Science, 154(5), pp.795–811. [Google Scholar]
- Gao F, Masek J, Schwaller M and Hall F, 2006. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Transactions on Geoscience and Remote sensing, 44(8), pp.2207–2218. [Google Scholar]
- Gao F, Anderson MC, Kustas WP and Wang Y, 2012. Simple method for retrieving leaf area index from Landsat using MODIS leaf area index products as reference. Journal of Applied Remote Sensing, 6(1), 063554, doi: 10.1117/1.JRS.6.063554. [DOI] [Google Scholar]
- Gao Q, Zribi M, Escorihuela M and Baghdadi N, 2017. Synergetic use of Sentinel-1 and Sentinel-2 data for soil moisture mapping at 100 m resolution. Sensors, 17(9), 1966, doi: 10.3390/s17091966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffin D and Anchukaitis KJ, 2014. How unusual is the 2012–2014 California drought?. Geophysical Research Letters, 41(24), pp.9017–9023. [Google Scholar]
- Gruber A, Crow W, Dorigo W and Wagner W, 2015. The potential of 2D Kalman filtering for soil moisture data assimilation. Remote Sensing of Environment, 171, pp.137–148. [Google Scholar]
- Hain CR, Crow WT, Mecikalski JR, Anderson MC and Holmes T, 2011. An intercomparison of available soil moisture estimates from thermal infrared and passive microwave remote sensing and land surface modeling. Journal of Geophysical Research: Atmospheres, 116, D15107, doi: 10.1029/2011JD015633. [DOI] [Google Scholar]
- Hain CR, Crow WT, Anderson MC and Mecikalski JR, 2012. An ensemble Kalman filter dual assimilation of thermal infrared and microwave satellite observations of soil moisture into the Noah land surface model. Water Resources Research, 48, W11517, doi: 10.1029/2011WR011268. [DOI] [Google Scholar]
- Hashemian M, Ryu D, Crow WT and Kustas WP, 2015. Improving root-zone soil moisture estimations using dynamic root growth and crop phenology. Advances in water resources, 86, pp.170–183. [Google Scholar]
- Hornacek M, Wagner W, Sabel D, Truong HL, Snoeij P, Hahmann T, Diedrich E and Doubková M, 2012. Potential for high resolution systematic global surface soil moisture retrieval via change detection using Sentinel-1. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 5(4), pp.1303–1311. [Google Scholar]
- Joiner J, Yoshida Y, Anderson M, Holmes T, Hain C, Reichle R, Koster R, Middleton E and Zeng FW, 2018. Global relationships among traditional reflectance vegetation indices (NDVI and NDII), evapotranspiration (ET), and soil moisture variability on weekly timescales. Remote Sensing of Environment, 219, pp.339–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knipper KR, Kustas WP, Anderson MC, Alfieri JG, Prueger JH, Hain CR, Gao F, Yang Y, McKee LG, Nieto H and Hipps LE, 2019. Evapotranspiration estimates derived using thermal-based satellite remote sensing and data fusion for irrigation management in California vineyards. Irrigation Science, 37(3), pp. 431–449. [Google Scholar]
- Kustas W and Anderson M, 2009. Advances in thermal infrared remote sensing for land surface modeling. Agricultural and Forest Meteorology, 149(12), pp.2071–2081. [Google Scholar]
- Kustas WP, Anderson MC, Alfieri JG, Knipper K, Torres-Rua A, Parry CK, Nieto H, Agam N, White WA, Gao F and McKee L, et al. , 2018. The grape remote sensing atmospheric profile and evapotranspiration experiment. Bulletin of the American Meteorological Society, 99(9), pp.1791–1812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kustas WP, Alfieri JG, Nieto H, Wilson TG, Gao F and Anderson MC, 2019. Utility of the two-source energy balance (TSEB) model in vine and interrow flux partitioning over the growing season. Irrigation Science, 37(3), pp.375–388. [Google Scholar]
- Kustas WP and Norman JM, 1999. Evaluation of soil and vegetation heat flux predictions using a simple two-source model with radiometric temperatures for partial canopy cover. Agricultural and Forest Meteorology, 94(1), pp.13–29. [Google Scholar]
- Kustas WP and Norman JM, 1996. Use of remote sensing for evapotranspiration monitoring over land surfaces. Hydrological Sciences Journal, 41(4), pp.495–516. [Google Scholar]
- Kumar SV, Reichle RH, Koster RD, Crow WT and Peters-Lidard CD, 2009. Role of subsurface physics in the assimilation of surface soil moisture observations. Journal of hydrometeorology, 10(6), pp.1534–1547. [Google Scholar]
- Lei F, Crow WT, Holmes TR, Hain C and Anderson MC, 2018. Global investigation of soil moisture and latent heat flux coupling strength. Water Resources Research, 54(10), pp.8196–8215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lievens H, Reichle RH, Liu Q, De Lannoy GJM, Dunbar RS, Kim SB, Das NN, Cosh M, Walker JP and Wagner W, 2017. Joint Sentinel-1 and SMAP data assimilation to improve soil moisture estimates. Geophysical research letters, 44(12), pp.6145–6153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lievens H, Tomer SK, Al Bitar A, De Lannoy GJ, Drusch M, Dumedah G, Franssen HJH, Kerr YH, Martens B, Pan M and Roundy JK, 2015. SMOS soil moisture assimilation for improved hydrologic simulation in the Murray Darling Basin, Australia. Remote Sensing of Environment, 168, pp.146–162. [Google Scholar]
- Li KY, De Jong R and Boisvert JB, 2001. An exponential root-water-uptake model with water stress compensation. Journal of hydrology, 252(1–4), pp.189–204. [Google Scholar]
- Mladenova IE, Bolten JD, Crow WT, Anderson MC, Hain CR, Johnson DM and Mueller R, 2017. Intercomparison of soil moisture, evaporative stress, and vegetation indices for estimating corn and soybean yields over the US. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 10(4), pp.1328–1343. [Google Scholar]
- Moradkhani H, Hsu KL, Gupta H and Sorooshian S, 2005. Uncertainty assessment of hydrologic model states and parameters: Sequential data assimilation using the particle filter. Water resources research, 41, W05012, doi: 10.1029/2004WR003604. [DOI] [Google Scholar]
- Moreira A, Krieger G, Hajnsek I, Papathanassiou K, Younis M, Lopez-Dekker P, Huber S, Villano M, Pardini M, Eineder M and De Zan F, 2015. Tandem-L: A highly innovative bistatic SAR mission for global observation of dynamic processes on the Earth’s surface. IEEE Geoscience and Remote Sensing Magazine, 3(2), pp.8–23. [Google Scholar]
- Norman JM, Kustas WP and Humes KS, 1995. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agricultural and Forest Meteorology, 77(3–4), pp.263–293. [Google Scholar]
- Norman JM, Anderson MC, Kustas WP, French AN, Mecikalski J, Torn R, Diak GR, Schmugge TJ and Tanner BCW, 2003. Remote sensing of surface energy fluxes at 101-m pixel resolutions. Water Resources Research, 39(8), 1221, doi: 10.1029/2002WR001775. [DOI] [Google Scholar]
- Olioso A, Chauki H, Courault D and Wigneron JP, 1999. Estimation of evapotranspiration and photosynthesis by assimilation of remote sensing data into SVAT models. Remote Sensing of Environment, 68(3), pp.341–356. [Google Scholar]
- Oliveira MT, 2001. Modeling water content of a vineyard soil in the Douro Region, Portugal. Plant and Soil, 233(2), pp.213–221. [Google Scholar]
- Paloscia S, Pettinato S, Santi E, Notarnicola C, Pasolli L and Reppucci A, 2013. Soil moisture mapping using Sentinel-1 images: Algorithm and preliminary validation. Remote Sensing of Environment, 134, pp.234–248. [Google Scholar]
- Pasolli L, Notarnicola C, Bertoldi G, Bruzzone L, Remelgado R, Greifeneder F, Niedrist G, Della Chiesa S, Tappeiner U and Zebisch M, 2015. Estimation of soil moisture in mountain areas using SVR technique applied to multiscale active radar images at C-band. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 8(1), pp.262–283. [Google Scholar]
- Pereira LS, Allen RG, Smith M and Raes D, 2015. Crop evapotranspiration estimation with FAO56: Past and future. Agricultural Water Management, 147, pp.4–20. [Google Scholar]
- Priestley CHB and Taylor RJ, 1972. On the assessment of surface heat flux and evaporation using large-scale parameters. Monthly weather review, 100(2), pp.81–92. [Google Scholar]
- Reichle RH, De Lannoy GJ, Liu Q, Koster RD, Kimball JS, Crow WT, Ardizzone JV, Chakraborty P, Collins DW, Conaty AL and Girotto M, 2017. Global assessment of the SMAP level-4 surface and root-zone soil moisture product using assimilation diagnostics. Journal of hydrometeorology, 18(12), pp.3217–3237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saha S, Moorthi S, Pan HL, Wu X, Wang J, Nadiga S, Tripp P, Kistler R, Woollen J, Behringer D and Liu H, 2010. The NCEP climate forecast system reanalysis. Bulletin of the American Meteorological Society, 91(8), pp.1015–1058. [Google Scholar]
- Salón JL, Chirivella C and Castel JR, 2005. Response of cv. Bobal to timing of deficit irrigation in Requena, Spain: water relations, yield, and wine quality. American Journal of Enology and Viticulture, 56(1), pp.1–8. [Google Scholar]
- Sanchez LA, Sams B, Alsina MM, Hinds N, Klein LJ and Dokoozlian N, 2017. Improving vineyard water use efficiency and yield with variable rate irrigation in California. Advances in Animal Biosciences, 8(2), pp.574–577. [Google Scholar]
- Scanlon BR, Faunt CC, Longuevergne L, Reedy RC, Alley WM, McGuire VL and McMahon PB, 2012. Groundwater depletion and sustainability of irrigation in the US High Plains and Central Valley. Proceedings of the national academy of sciences, 109(24), pp.9320–9325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Semmens KA, Anderson MC, Kustas WP, Gao F, Alfieri JG, McKee L, Prueger JH, Hain CR, Cammalleri C, Yang Y and Xia T, 2016. Monitoring daily evapotranspiration over two California vineyards using Landsat 8 in a multi-sensor data fusion approach. Remote Sensing of Environment, 185, pp.155–170. [Google Scholar]
- Seneviratne SI, Corti T, Davin EL, Hirschi M, Jaeger EB, Lehner I, Orlowsky B and Teuling AJ, 2010. Investigating soil moisture–climate interactions in a changing climate: A review. Earth-Science Reviews, 99(3–4), pp.125–161. [Google Scholar]
- Sivilotti P, Bonetto C, Paladin M and Peterlunger E, 2005. Effect of soil moisture availability on Merlot: from leaf water potential to grape composition. American Journal of Enology and Viticulture, 56(1), pp.9–18. [Google Scholar]
- Smart DR, Schwass E, Lakso A and Morano L, 2006. Grapevine rooting patterns: a comprehensive analysis and a review. American Journal of Enology and Viticulture, 57(1), pp.89–104. [Google Scholar]
- Torres R, Snoeij P, Geudtner D, Bibby D, Davidson M, Attema E, Potin P, Rommen B, Floury N, Brown M and Traver IN, 2012. GMES Sentinel-1 mission. Remote Sensing of Environment, 120, pp.9–24. [Google Scholar]
- Valdés-Gómez H, Celette F, de Cortázar-Atauri IG, Jara-Rojas F, Ortega-Farías S and Gary C, 2009. Modelling soil water content and grapevine growth and development with the STICS crop-soil model under two different water management strategies. OENO One, 43(1), pp.13–28. [Google Scholar]
- van Leeuwen C, Trégoat O, Choné X, Bois B, Pernet D and Gaudillère JP, 2009. Vine water status is a key factor in grape ripening and vintage quality for red Bordeaux wine. How can it be assessed for vineyard management purposes?. OENO One, 43(3), pp.121–134. [Google Scholar]
- van Leeuwen PJ, 2010. Nonlinear data assimilation in geosciences: an extremely efficient particle filter. Quarterly Journal of the Royal Meteorological Society, 136(653), pp.1991–1999. [Google Scholar]
- Vrugt JA, ter Braak CJ, Diks CG and Schoups G, 2013. Hydrologic data assimilation using particle Markov chain Monte Carlo simulation: Theory, concepts and applications. Advances in Water Resources, 51, pp.457–478. [Google Scholar]
- Weerts AH and El Serafy GY, 2006. Particle filtering and ensemble Kalman filtering for state updating with hydrological conceptual rainfall-runoff models. Water Resources Research, 42, W09403, doi: 10.1029/2005WR004093. [DOI] [Google Scholar]
- Wilson TG, Kustas WP, Alfieri JG, Anderson MA, Prueger JH, McKee LG, Alsina Mar M, Sanchez L, 2019. Relationships between soil water content, evapotranspiration, and irrigation measurements in a California drip-irrigated pinot noir vineyard. (submitted to Water Resources Research) [Google Scholar]
- Yang Y, Anderson MC, Gao F, Wardlow B, Hain CR, Otkin JA, Alfieri J, Yang Y, Sun L and Dulaney W, 2018. Field-scale mapping of evaporative stress indicators of crop yield: An application over Mead, NE, USA. Remote Sensing of Environment, 210, pp.387–402. [Google Scholar]