Bootstrap analysis of diffusion tensor and mean apparent propagator parameters derived from multiband diffusion MRI

Abstract

Purpose:

To directly compare diffusion metrics derived from multiband (MB) imaging sequences to those derived using a single-band acquisition.

Methods:

In this work, diffusion metrics from DTI and mean apparent propagator MRI derived from a commercial MB sequence with an acceleration factor of 3 are compared with those derived from a conventional diffusion MRI sequence using a novel bootstrapping analysis scheme on oversampled diffusion MRI data. The average parameter values for fractional anisotropy and mean diffusivity derived from DTI, as well as propagator anisotropy and return to origin probability derived from mean apparent propagator MRI, are compared.

Results:

Fractional anisotropy and propagator anisotropy are very similar when computed from data collected with and without MB, but show minor differences at low and high values of fractional anisotropy/propagator anisotropy. Mean diffusivity values are generally lower in the MB-derived maps, and return to origin probability is generally higher. The coefficient of variation of each parameter is shown to be slightly higher on average from the maps derived from MB versus single band when the TR is short, and slightly lower when the TR of the MB and single-band experiments is equal.

Conclusion:

These results demonstrate that the MB sequence tested in this work provides very similar results to a conventional diffusion MRI sequence. The MB sequence is affected minimally by the slight decrease in SNR associated with the parallel reconstruction and reduced TR, and there are relaxation effects associated with the reduced TR.

1 |. INTRODUCTION

Simultaneous multislice MRI, also known as multiband (MB) imaging, is able to greatly reduce long scan times associated with diffusion MRI (dMRI) experiments.^1–4 By exciting and collecting data from multiple slices in a single repetition, total acquisition time can be reduced by several orders, and can make complex diffusion experiments clinically feasible. Diffusion tensor imaging (DTI)⁵ requires a minimum of 7 measurements with at least 6 noncollinear directions, but typically at least 30 directions⁶ are required to reliably estimate the diffusion tensor. For high angular resolution diffusion imaging methods, such as q-ball imaging⁷ and constrained spherical deconvolution,⁸ a minimum of 45 directions are recommended,⁹ but more than 60 are generally collected. For diffusion propagator imaging methods, such as q-space imaging and mean apparent propagator MRI (MAP-MRI),¹⁰ 100 or more directions are required with multiple b-values. Using non-slice-accelerated diffusion imaging, or single-band (SB) imaging, the scan times for these more advanced diffusion imaging methods far exceed those required for clinical imaging. Multiband not only makes advanced diffusion imaging more practical in both research and clinical settings, but it also reduces the likelihood of significant motion and subject discomfort.

Although the time-saving benefits of using MB in dMRI are obvious, it is critical to quantitatively compare the results of MB and SB acquisitions to establish what differences, if any, MB and SB acquisitions impart to dMRI results. In previous work using a bootstrap analysis,³ it was demonstrated that primary and secondary fiber orientations, as determined by q-ball imaging, are similar, although the fiber orientations estimated from the MB data suffered from increased uncertainty (measured as an increase in the 95% confidence interval). In the same work, orientation distribution functions and tractograms produced from both MB and SB sequences were compared and shown to be qualitatively similar. The bootstrap analysis used in that work was not used to compare scalar indices such as the fractional anisotropy (FA) or mean diffusivity (MD), however, nor were other scalar metrics from other diffusion analysis techniques, such as MAP-MRI, considered. Instead, a region of interest–based analysis was used to demonstrate that the FA derived from MB and SB experiments were not statistically different. In other work, Duan et al¹¹ examined the test–retest reliability of DTI-based metrics, as well as tractography-derived connectivity metrics,¹² and demonstrated moderate to good repeatability in MB-derived DTI parameters, but did not compare MB results to SB results. Yet another study¹³ investigated the effects of a MB sequence on diffusion parameters derived from data collected on a 1.5T system with a 12-channel head coil. It reported that the results from the MB sequences with large acceleration factors^3,4 did not reliably reproduce FA, MD, or tractography results.

Here, a novel bootstrapping-based analysis is performed to provide a more detailed, voxel-wise comparison of dMRI parameters derived from SB and MB acquisitions. This bootstrapping scheme allows for the analysis of large diffusion data sets with a more reasonable acquisition time by subsampling a single, oversampled data set collected during 1 imaging session. In this way, the impact of misalignment of data due to registration errors is minimized when performing a direct, voxel-by-voxel comparison of dMRI-derived metrics, and multiple, long acquisitions are not necessary. In addition, a controlled analysis on the effects of reduced TR on dMRI metrics is included in the context of MB imaging. Furthermore, a multiple q-shell acquisition scheme with a large number of non-collinear diffusion-sensitizing gradients has been used to allow an analysis of the effects of MB techniques on higher-order models of diffusion, namely MAP, which has not been considered previously. Briefly, MAP-MRI is a technique that efficiently estimates the full, 3D diffusion probability distribution (or propagator) of water diffusion in complex media, such as tissue. By finding an analytic approximation of the 3D propagator, many different microstructural parameters can be estimated, such as the return to origin probability (RTOP), which provides a metric related to the average compartment size within a given voxel, or the propagator anisotropy (PA), which provides a measure of tissue anisotropy, similar to FA, but accounts for the increased complexity of the 3D propagator when compared with the simpler diffusion tensor.¹⁰

2 |. METHODS

2.1 |. Data acquisition

Two healthy volunteers were scanned with approval from the institutional review board at the University of Arizona. All data were collected on a 3T Skyra MRI scanner (VE 11A; Siemens Medical Solutions, Erlangen, Germany) using a commercial 32-channel head coil for reception. A T₁-weighted data set (MPRAGE parameters: TR = 2530 ms, TE = 3.3 ms, TI = 1000 ms, resolution = 1 × 1 × 1 mm, matrix = 256 × 256) was acquired for anatomical reference. The standard SB dMRI experiment used pulsed gradient spin-echo Stejskal-Tanner EPI with TR/TE = 10 700/115 ms; matrix size = 128 × 128 and 69 slices; FOV = 256 × 256 mm; 2-mm isotropic resolution; in-plane GRAPPA factor of 2; 6/8 partial Fourier; and 14 b = 0 s/mm² images, 20 b = 1000 s/mm² images, 32 b = 2000 s/mm² images, and 64 b = 3000 s/mm² images, sampled evenly around the sphere using a multishell electrostatic repulsion scheme similar to that described by Caruyer et al.¹⁴ This produced a direction set that was both evenly distributed on each shell and noncollinear between shells. In addition, a single b = 0 s/mm² was collected with the phase encoding direction reversed for use in distortion correction. Two MB data sets were also collected with identical parameters except for the TR and a 3-times MB acceleration factor. The first MB data set used the minimum TR possible (3700 ms), whereas the second used a TR = 10 700 ms to match the SB data set. Each MB data set also included a matching b = 0 s/mm² with the phase-encoding direction reversed. The diffusion acquisition was designed to provide more than enough measurements to fit DTI (minimum 6 directions, 2 b-values) as well as MAP-MRI (minimum 22 measurements across multiple q-values for an order 4 fit) after subsampling the data sets when performing statistical comparison.

2.2 |. Data preprocessing

Gibbs ringing correction was first performed on the original dMRI images using the method described by Kellner.¹⁵ Echo planar imaging distortion correction was then performed using FSL’s TOPUP algorithm using all b = 0 s/mm² images collected.¹⁶ Eddy current and motion correction was then performed using FSL’s eddy algorithm,¹⁷ and the diffusion-encoding directions were rotated to adjust for head motion. In this step, all images were registered to the first b = 0 s/mm² in the SB data set, to correct for intrascan and interscan motion. Next, local principal component analysis was used to denoise the data set.¹⁸

2.3 |. Bootstrapping

Each of the 3 dMRI data sets were randomly sampled 100 times to generate 100 unique subsets of the data with 2 b = 0 s/mm² images, 10 b = 1000 s/mm² images, 19 b = 2000 s/mm² images, and 39 b = 3000 s/mm² images. These numbers were selected to provide enough measurements to fit the data to higher-order diffusion models, while avoiding significant overlap of the measurements in each subsampled data set. Although each of the 100 subsampled sets has a unique set of directions, the directions are identical across the 3 sets of data.

2.4 |. Microstructure processing

Diffusion tensor imaging fitting for each set of subsampled data was carried out using weighted linear least squares fitting, and FA and MD were estimated from the derived eigenvalues using in-house Python code.⁵ The MAP was also estimated for each subsampled set using the Laplacian-regularized linear fitting technique described in Fick et al,¹⁹ using basis functions up to order 4 (22 coefficients). Propagator anisotropy (PA) and RTOP were estimated from the fit MAP coefficients as described by Özarslan et al,¹⁰ using in-house Python code.

2.5 |. Analysis

The results of the DTI and MAP fits were compared on a voxel-wise basis. Using the 100 unique samples of DTI and MAP parameters, voxel-wise probability distributions were estimated. The mean and the coefficient of variation (CV, σ/μ) were calculated for each measured parameter distribution, in which σ is the SD of each estimated parameter, and μ is the mean. The CV provides a comparable measure of variation in the presence of differences in mean values. The mean and CV for each parameter derived from both MB experiments were then compared with the mean and CV for each parameter derived from the SB experiment, which served as the “gold standard” for this work. Voxel-wise difference maps were computed for each parameter’s mean and CV. Additionally, the T₁-weighted image was segmented into white matter, gray matter, and CSF using FSL’s FAST routine,²⁰ to perform tissue type–specific analysis.

3 |. RESULTS

Figure 1 shows dMRI parameter maps derived from both DTI and MAP-MRI, using MB or SB sequences. Each image displays the average of the estimated probability distributions for each parameter, which appear qualitatively very similar. Patterns of high and low anisotropy are maintained in both the FA (Figure 1A–C) and PA (Figure 1G–I) maps across all acquisition schemes. The inverse relationship between MD (Figure 1D–F) and RTOP (Figure 1J–L) is also maintained and apparent in the images displayed. In regions where diffusion is highly restricted, such as at the genu of the internal capsule, the MD is low and the RTOP is high. The RTOP also demonstrates high contrast between white and gray matter, and this contrast is preserved in images from both MB and SB sequences.

FIGURE 1.

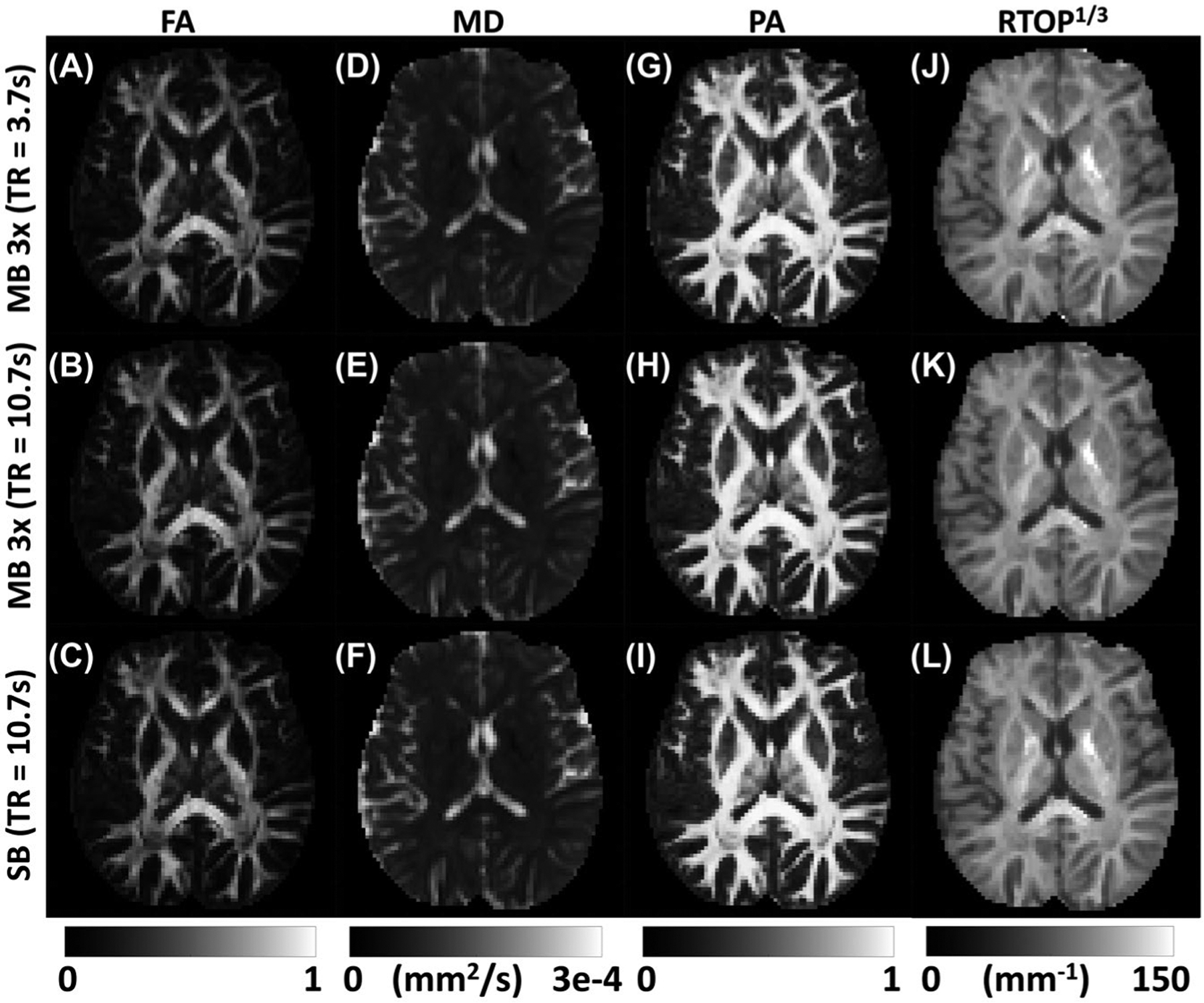
Visualization of the average parameter maps derived from DTI and mean apparent propagator (MAP) MRI for 3 different collection schemes. The top row displays the maps derived from the minimum TR (i.e., 3.7 seconds) 3-times multiband (MB) sequence, followed by the 10.7-second TR 3-times MB sequence, and finally the parameter maps derived from the standard single-band (SB) sequence with minimum TR (10.7 seconds) for full-brain coverage. The first and second column show fractional anisotropy (FA) and mean diffusivity (MD, mm²/s) derived from DTI analysis. The third and fourth column show propagator anisotropy (PA) and return to origin probability maps (RTOP^1/3, mm⁻¹) derived from the MAP-MRI analysis

The scatter plots in Figure 2 plot the average value of a dMRI parameter derived from the SB sequence in a particular voxel versus the average of the same parameter for that voxel derived from the MB sequence. Voxels from the entire brain are included in each plot and have been categorized as gray matter, white matter, and CSF with different colors. If the parameters generated from the MB data were identical to those generated from the SB data, they would lay perfectly along the dashed line. Any consistent deviations from the dashed line are indicative of a bias, and the larger the spread about the dashed line, the larger the variability when estimating a given parameter.

FIGURE 2.

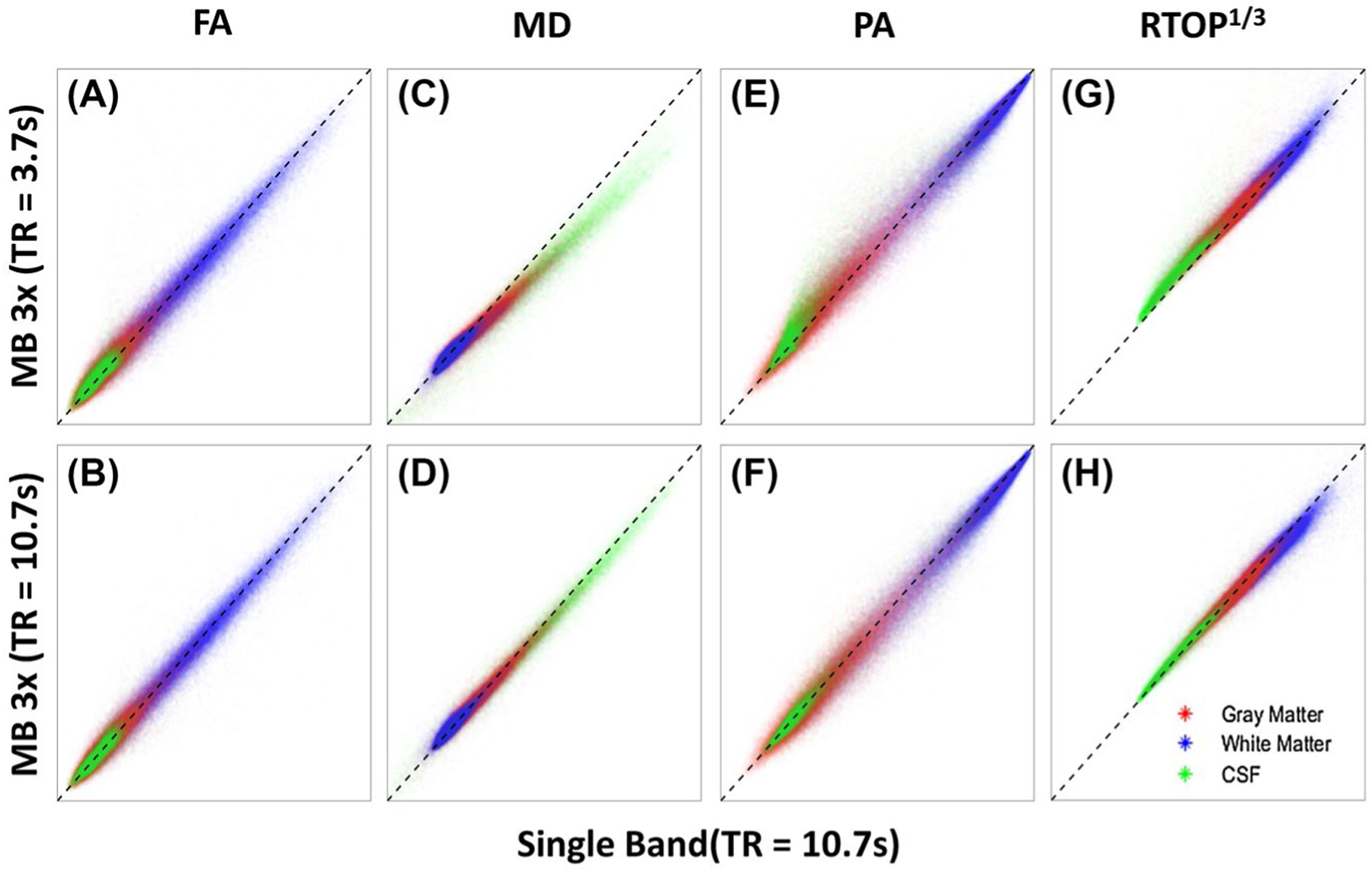
Scatter plots of MB-derived parameter values plotted against SB-derived parameter values on a voxel-by-voxel basis for the entire brain. Voxels are categorized as either gray matter (red), white matter (blue), or CSF (green). The black, dashed line has a slope of 1.0 and is plotted for reference. The top row shows parameters derived from the MB sequence using a minimal TR (3.7 seconds) plotted against the same parameters derived from the SB sequence. The bottom row shows the parameters derived from the MB sequence using a matched TR (10.7 seconds) plotted against the same parameters derived from the SB sequence. The range for both the x-axis and y-axis is 0–1 for FA, 0–0.003 mm²/s for MD, 0–1 for PA, and 0–100 mm⁻¹ for RTOP^1/3

Figure 2A shows that there is very little bias in the estimation of FA when using MB with a short TR relative to a SB sequence. The FA in CSF is slightly overestimated (on average) by the short TR MB sequence, and is very slightly underestimated on average in the white matter. These small biases are almost completely gone in the data from the TR-matched MB sequence (Figure 2B). The largest, most obvious bias comes from the estimation of MD in the CSF when using the short-TR MB sequence (Figure 2C). Here, the MB sequence underestimates the MD relative to the SB sequence. The bias is also present in gray and white matter, but to a much smaller extent than that found in the CSF. When the TR of the MB sequence is matched to that of the SB sequence, the bias is reduced (Figure 2D). When using the short-TR MB sequence, the PA measured in CSF is overestimated in general, and that of white matter tends to be very slightly underestimated relative to the SB values (Figure 2E). Although the slight white matter bias does not appear to change when the TR of the MB sequence is matched to the SB sequence, the bias of the CSF goes away (Figure 2F). Finally, the RTOP estimated by the fully accelerated MB sequence is almost always overestimated in the CSF, but is normalized when the TR of the MB sequence is set to match that of the SB sequence (Figure 2G,H). A slight bias appears for white matter and gray matter in the matched TR data sets in which the MB value is slightly lower than that of the SB.

Looking at the averages demonstrates potential biases caused by collecting diffusion data with 1 scheme or the other, but it does not provide any information about the uncertainty in the data. To quantify the variability, we performed a similar analysis using the CV. Figure 3 shows maps of the CV for all of the derived parameter maps from each acquisition scheme. As shown, the FA (Figure 3A–C) has the highest CV, followed by the PA (Figure 3G–I), the MD (Figure 3D–F), and finally the RTOP (Figure 3J–L). For FA and PA, the CV is lowest in the white matter, and highest in the CSF. For MD and RTOP, however, the CV appears to be higher in the central portion of the image, and lower on the periphery, without any obvious relationship to tissue type.

FIGURE 3.

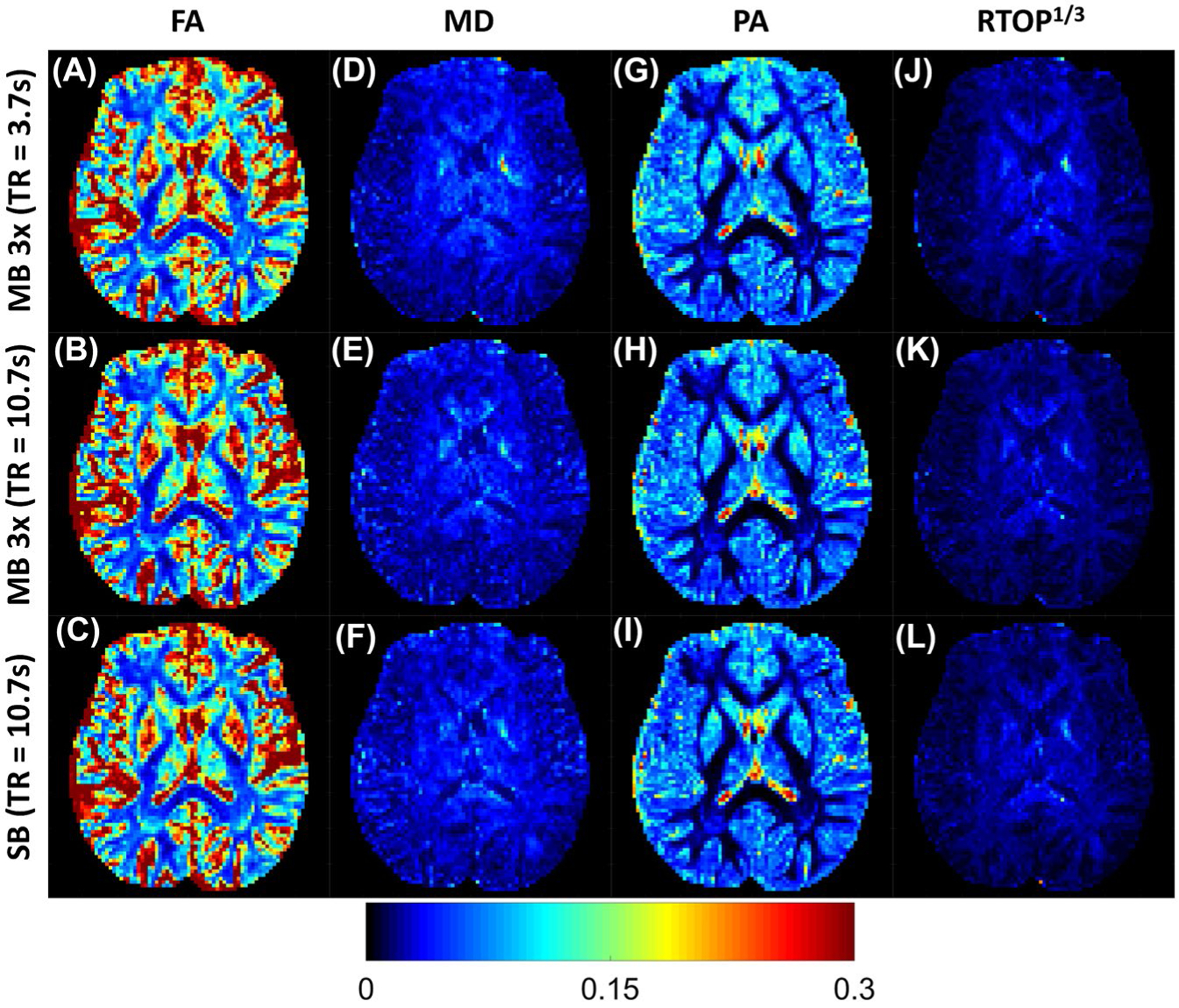
Maps of the coefficient of variation (CV) of the parameter maps derived from both DTI and MAP for all 3 collection schemes. The top row displays the maps derived from the minimum TR simultaneous multislice sequence, followed by the 10-second TR simultaneous multislice sequence, and finally the parameter maps derived from the standard SB sequence with minimum TR for full-brain coverage

Finally, Figure 4 shows a difference map between the CV of parameters derived from MB and SB sequences. Figure 4A demonstrates that in white matter, the short-TR MB sequence estimates the FA with higher uncertainty than the SB sequence. Furthermore, the effect appears to be greater in the anterior portion of the image than the posterior. This effect is more pronounced when the TRs are matched between the MB and SB sequences (Figure 4B), in which the variability of the FA measurement is lower in the MB image than in the SB image at the posterior portion of the image. In fact, this pattern of higher uncertainty in the anterior portions of the image and lower uncertainty in the posterior of the image can be seen in the MD and RTOP difference maps as well. The variability in the MD estimates does not appear to be dependent on tissue type, but more by location within the FOV of the image (Figure 4C,D). The CV is lower in the TR-matched MB image than in the SB MD image almost everywhere. This is also the case in the TR-matched RTOP image (Figure 4H). An analysis of the SNR in raw dMRI images produced from MB and SB acquisitions is presented in the Supporting Information.

FIGURE 4.

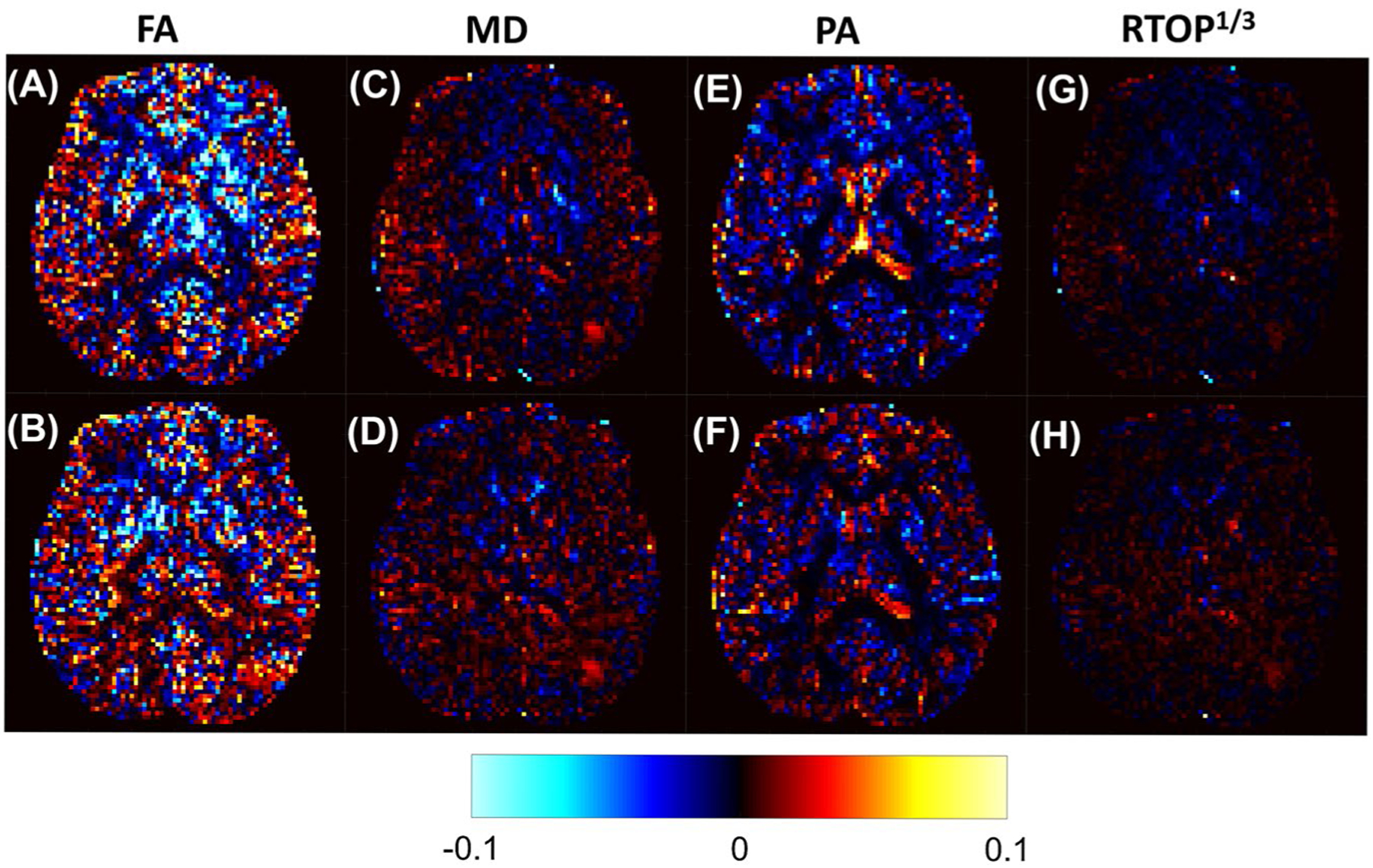
Difference maps between the CVs of parameters derived from MB and SB acquisitions. The top row displays the CV of the short TR MB (TR = 3.7 seconds)–derived parameter values subtracted from the CV of the SB-derived parameter values. The bottom row shows the CV of the TR-matched MB (TR = 10.7 seconds)–derived parameter values subtracted from the CV of the SB-derived parameter values. All CV maps are plotted on the same scale, where red and yellow indicate that the MB CV is lower than the SB CV, and blue indicates that the MB CV is larger than the SB CV

4 |. DISCUSSION

In this study, the similarities and differences of several dMRI parameters estimated using MB and SB imaging sequences are compared using a bootstrapping analysis. This bootstrapping analysis was designed to accommodate the comparison of multiple diffusion MR analysis techniques (DTI and MAP-MRI) without the need for repeated scans, which could take several hours and be susceptible to significant subject motion. In addition to DTI-derived parameters, analysis has been extended to include diffusion parameters derived from MAP-MRI, which more completely characterize the diffusion propagator. Finally, T₁ effects were studied by collecting MB data with both a minimal TR and a TR that matches the required TR of the SB data set. In this way, differences in estimated values between the MB and SB data sets can be attributed to either T₁-related effects and/or MB scheme-related effects.

Overall, there is very high degree of agreement between the parameters derived from MB and SB sequences, as visualized in Figure 1. However, there are measurable differences that are worth noting. First, there is a slight increase, in general, in the CV of parameters derived from the fully accelerated MB sequence when compared with those derived from the SB sequence. If this increased uncertainty was due to the MB pulse sequence and parallel reconstruction alone, the same increase in CV would be expected in the MB sequence with a matched TR, which is not the case. The increased uncertainty may be due, at least in part, to the slightly reduced SNR associated with the reduced TR. When the TR is decreased, signal from tissues with a long T₁ do not recover as much and are decreased. In fact, when the TR is matched between the MB and SB sequences, the CV is generally smaller for the MB-derived parameters. The CV also tends to be further increased in the center of the FOV in the MB-derived parameter maps when compared with the SB-derived parameter maps, as shown in Figure 4, which is particularly evident in the CV difference maps of the MD. This pattern tends to follow the pattern seen in the g-factor maps discussed by Setsompop et al.³ It makes sense that increased acceleration will lead to an increased g-factor penalty, and we believe that this can largely explain the spatial dependence of the CV.

Second, some of the dMRI parameters tend to be slightly biased when estimated from the MB data, particularly the short-TR data, which can also be explained by a combination of T₁ effects and SNR differences. It has been reported previously²¹ that in instances of low SNR, low values of FA tend to be artificially increased, and high values of FA tend to be artificially decreased. This is the pattern displayed by the FA and PA data in this study, suggesting that the MB sequence itself may not be responsible for the slight biases in FA and PA, but rather the slightly decreased SNR is causing minor deviations in FA and PA.

The bias displayed by the estimation of MD by the accelerated MB sequence appears to be explained, in large part, by T₁ effects. Voxels with a significant volume fraction of CSF show decreases in MD when estimated with the accelerated MB sequence relative to the SB sequence. With a short TR, CSF cannot fully relax between RF excitations. The signal fraction of tissue with shorter T₁ values (which also have lower MDs) is therefore increased, and the MD of those voxels is decreased overall. Interestingly, the bias in MD and RTOP does not completely disappear when the TRs are matched, so there are likely other mechanisms at play.

One of the challenges of this study was developing a bootstrapping scheme that allowed for the comparison of dMRI parameters derived from both DTI and MAP-MRI that did not require multiple acquisitions of the same data sets. In the bootstrapping scheme used, each subsampled data set contains a different set of diffusion directions than all of the other subsampled data sets. This subsampling scheme likely adds another source of variation to the derived parameter maps. This variation, however, is consistent across the SB and MB acquisitions, and thus does not affect the final interpretation of the results. Other bootstrapping strategies, such as the residual and wild bootstrap, were considered, but ultimately rejected as the results are model-dependent. Thus, a separate bootstrapping must be completed for both DTI and MAP-MRI, making it difficult to harmonize the results across multiple dMRI fitting techniques.

The results of the current work suggest that dMRI data of very similar quality can be expected when using a MB sequence compared with that collected using a traditional SB sequence. Furthermore, dMRI parameter maps generated from MB and SB sequences are very similar. Although there are biases introduced in several parameters by the shorter TR and the resulting reduction in SNR afforded by accelerated MB acquisitions, they are small and consistent. These differences may lead to issues if trying to directly compare dMRI parameter values derived from data acquired with MB sequences to those estimated from SB data, but they should not be an issue when comparing data collected using only MB.

Supplementary Material

supporting information

FIGURE S1 Pipeline for estimating the relative contribution of noise from each acquired sequence. Panel 1 shows the representative (9 of 130) DWIs acquired for the SB sequence. Panel 2 shows example components (9 of 130) from the phase contrast angiography decomposition of the DWIs. Panel 3 shows the resulting noise map (approximated as the least significant principle component), and local SD estimation depicted as a small, 3 × 3 × 3 moving red box. Finally, panel 4 shows an example of the resulting SD map

FIGURE S2 A–C, Noise maps derived from a phase contrast angiography decomposition of the data: fully accelerated MB sequence (A), TR-matched MB sequence (B), and SB sequence (C). D–F, Maps of the local SD of the noise, estimated from a 3 × 3 × 3 moving window throughout the noise maps in (A)–(C). D, Fully accelerated MB sequence. E, Repetition time-matched MB sequence. F, Single-band sequence. Panels (A)–(C) have the same gray scale (arbitrary units), and (D)–(F) are shown on the same color scale (arbitrary units)