Parameter estimation for sigmoid E_max models in exposure-response relationship

Abstract

The purpose of this simulation study is to explore the limitation of the population PK/PD analysis using data from a clinical study and to help to construct an appropriate PK/PD design that enable precise and unbiased estimation of both fixed and random PD parameters in PK/PD analysis under different doses and Hill coefficients. Seven escalating doses of virtual drugs with equal potency and efficacy but with five different Hill coefficients were used in simulations of single and multiple dose scenarios with dense sampling design. A total of 70 scenarios with 100 subjects were simulated and estimated 100 times applying 1-compartment PK model and sigmoid E_max model. The bias and precision of the parameter estimates in each scenario were assessed using relative bias and relative root mean square error. For the single dose scenarios, most PD parameters of sigmoid E_max model were accurately and precisely estimated when the C_max was more than 85% of EC₅₀, except for typical value and inter-individual variability of EC₅₀ which were poorly estimated at low Hill coefficients. For the multiple dose studies, the parameter estimation performance was not good. This simulation study demonstrated the effect of the relative range of sampled concentrations to EC₅₀ and sigmoidicity on the parameter estimation performance using dense sampling design.

Introduction

The role of pharmacokinetic (PK) and pharmacodynamic (PD) modeling and simulation is expanding in almost all drug development processes, from non-clinical to different phases of clinical trials.[1] The number of regulatory decisions, including new drug approval and labeling, that were effected by pharmacometric analysis increased from 45 submissions between 2000 and 2004 to 87 submissions between 2007 and 2008.[2,3] The population approach or pharmacometric analysis based on computational methods is being applied to bridging studies, proof of concept studies for go/no-go decision, simulation for dose selection or study design, and extension to other indications (drug repositioning), among many others.[1] PK/PD modeling and simulation is also used for individualized pharmacotherapy based on relevant demographic factors including race, age, sex, weight, height and genotype.[4,5]

Pharmacometric analysis usually relies on non-linear mixed effect models to explain and quantify time-varying PK/PD parameters, disease progression, and their relationships based on population data. Pharmacokinetic models describe the change of drug concentration over time and pharmacodynamic models quantify the relationship between concentration and effect. PK/ PD models link PK models to PD models using direct effect models, effect compartment models, or indirect response models.[6,7] This mathematical method is also used for constructing disease progression models comprising the natural history of a disease and drug effect.[8] E_max models play important roles in describing excitatory or inhibitory exposure-response relationship. Sigmoid E_max models, also known as Hill equations, have successfully explained pharmacodynamics of many drugs with Hill coefficients determining sigmoidicity or sensitivity between exposure and response.[9] However, drug exposure often does not cover the higher range of values required to estimate maximum effect (E_max) since higher concentrations can either result in toxicity or the testing doses in dose escalation study have little information on dose-response surface. This leads to potentially biased or imprecise PD parameter estimates or overly-simplified models such as linear or log-linear models that are not useful for extrapolation.

The purpose of this simulation study is to explore the limitation of the population PK/PD analysis using data from a clinical study and to help to construct an appropriate PK/PD design that enable precise and unbiased estimation of both fixed and random PD parameters in PK/PD analysis under different doses and Hill coefficients.

Methods

PK/PD Simulation and Estimation

In this simulation study, seven doses of virtual drugs with equal potency and efficacy but different Hill coefficients were used for generality of interpretation and comparison among virtual drugs and for easy application to PK/PD modeling and simulation of various drugs in clinical use or development. The seven doses were 12.5, 25, 50, 100, 200, 400, and 800 mg, where each succeeding dose was double the preceding dose. The Hill coefficients were 0.5, 1, 2, 5 and 10. Single and multiple-dose studies were simulated with each of the doses and Hill coefficients. A total of 70 (=7 x 5 x 2) scenarios each with 100 subjects were simulated and then estimated 100 times using SSE (Stochastic simulation and estimation) of PSN (Perl-speaks-NONMEM, version 3.7.6, http://psn.sourceforge.net) and first order conditional estimation with interaction (FOCE-I) method in NONMEM (version 7.2, ICON Development Solutions, Ellicott City, MD, USA). Pharmacokinetic and pharmacodynamic data were simultaneously simulated and estimated using the same model. A one-compartment model with first-order absorption and elimination was used as the PK simulation model. The true values (θ) of the structural PK parameters for k_a, CL/F and V/ F were: θ_ka = 1 hr^-1, θ_CL/F = 5 L/hr, θ_V/F = 100 L, where k_a, CL/F and V/F was absorption rate constant, clearance and volume of distribution, respectively.

$$C=\frac{F·D}{V}·\frac{k_a}{\left(k_a-k_e\right)}·(e^{-k_e·\mathrm{t}}-e^{-k_a·\mathrm{t}})$$

where C is drug concentration, k_e is elimination rate constant, obtained by CL over V, F is bioavailability and D is dose, respectively. The approximate values of the T_max (the time at which the maximum concentration was observed) for single- and multiple-dose study were 3.15 and 2.78 h, respectively and the half-life was around 13.9 h. The blood sampling time points for dense sampling schedules were 0 (predose), 0.25, 0.5, 0.75, 1, 2, 3, 4, 5, 6, 8, 12, 24, and 48 h after drug administration. The samples at 24 and 48 h were not included for multiple-dose scenarios. The PD measurement time points were equal to those of PK.

A sigmoid E_max model was used for PD simulation based on an assumption that plasma concentration is directly linked to the drug effects, as below.

$$E=E_0+\frac{E_{max}\times C^{\mathrm{\gamma }}}{E{C}_{50}^{\mathrm{\gamma }}+C^{\mathrm{\gamma }}}$$

where E is drug effect. The true values (θ) of PD parameters for baseline (E₀), efficacy (E_max), potency (EC₅₀) and Hill coefficients (γ) were: θ_E0 = 1000, θ_Emax = 10000, θ_EC50 = 1000 ng/mL, and θ_γ = 0.5, 1, 2, 5 or 10, respectively. The coefficient of variation (CV%) of random effect for inter-individual variability (IIV) and residual variability (RV) were set at 30% for all PK/PD parameters and 20% for PK/PD observations, respectively. An exponential error model for IIV and RV was applied as follows:

θ_i=θ×exp(ŋi)

$$y_{ij}=\widehat{y_{ij}}\times \mathrm{e}\mathrm{x}\mathrm{p}\left({\epsilon }_{ij}\right)$$

where θ_i is the i^th individual PK/PD parameter, θ is the population mean value, η_i is an instance of a normally distributed random variable η with mean zero and variance of ω² which represent IIV, γ_ij is the observed concentrations or effect for the i^th subjects at time j, is the individual predicted observations for the for the i^th subjects at time j, $\widehat{y_{ij}}$ and ɛ_ij is an instance of a normally distributed random variable ɛ with mean zero and variance of σ² which represents RV.

The simulated effect versus concentration plots were used to explore the relationship between concentration and EC₅₀ and whether E_max was attained in each study or not. Simulated concentrations were normalized by true EC₅₀ (=1000 ng/mL) to identify the generalized exposure-response relationship and then “EC₅₀” was used as a unit to express normalized concentra-tions.[10,11]

To evaluate the estimation performance for PD parameters at each dosing scenario, the median values and ranges of normalized maximum concentration (C_max) (normalized by EC₅₀) for single-dose study and normalized steady-state minimum concentration (C_min,ss) and C_max,ss for multiple-dose study at each dose level at all values of γ were obtained using individual predicted values, which were calculated from the parameter estimates from 100 simulated subjects and the simulation time points in each scenario.

To evaluate the estimation performance for PD parameters at each dose, the following statistics were obtained using individual predicted values.

1) Median values and range of normalized maximum concentration (C_max) (normalization using EC₅₀) for single-dose studies

2) Normalized steady-state minimum concentration and C_max,ss for multiple-dose studies at each dose level at all values of gamma.

Individual predicted values were calculated from the parameter estimates from 100 simulated subjects and simulated time points in each scenario.

Bias and Precision of Parameter Estimates

The bias and precision of the parameter estimates in each scenario were assessed using relative bias and relative root mean square error (RMSE) (instead of bias and RMSE) to compare estimation performance between parameters with different scales.

$$\mathrm{r}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{ }\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}=100\mathrm{\%}\frac{1}{N}\sum _i^{}\frac{P_{est}-P_{sim}}{P_{sim}}$$

$$\mathrm{r}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{ }\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=100\mathrm{\%}\sqrt{\frac{1}{N}\sum _i^{}\frac{{(P_{est}-P_{sim})}^2}{P_{sim}^2}}$$

where P_est is the fixed or random effect parameter estimate and P_sim is the true fixed and or random effect parameters (θ, ω², σ²) value used for each simulation. The criteria for accuracy and precision were less than or equal to 15% and 35%, respectively. [10,11,12]

Results

Eight scenarios out of total seventy scenarios failed stochastic simulation and estimation (SSE), in spite of numerous attempts. The failed scenarios were: four scenarios of 12.5 and 25 mg at high Hill coefficients (γ = 5, 10) in single-dose study and four scenarios of 100, 200, 400 and 800 mg at low Hill coefficients (γ = 0.5) in multiple-dose study. Among the remaining sixty two scenarios which were successful, one scenario in single-dose studies had 1 failure and eight scenarios in multiple-dose studies had 1 to 3 failure(s) during 100 simulations and estimations for each scenario.

PK simulation and estimation

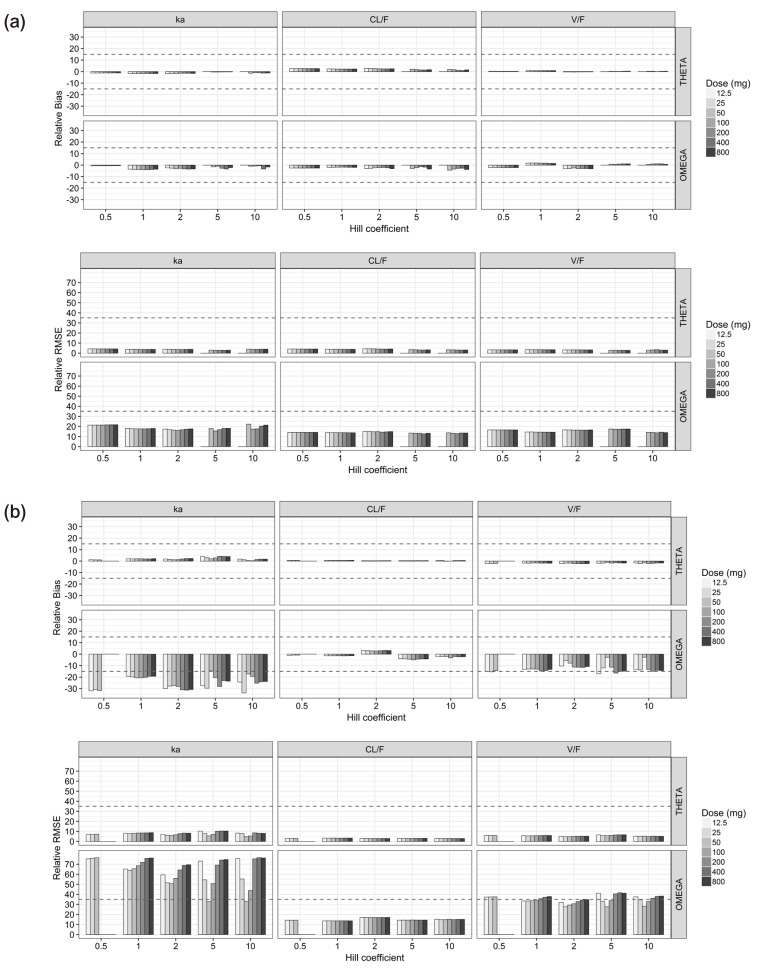
For the single-dose studies, all the PK parameters (θ and ω²) for k_a, CL/F and V/F were unbiased and precise (Fig. 1a), while ω_ka² was considerably biased and imprecise for the multiple-dose studies (Fig. 1b). The CL/F was estimated at best and V/ F was the next in the multiple-dose scenarios (Fig. 1b). The relative bias and RMSE of σ² for the PK observations were less than 0.8% and 5% for single-dose study and 1.4% and 5.1% for multiple-dose study, respectively.

Figure 1. Relative bias (upper) and relative root mean square error (lower) of pharmacokinetic parameters estimates for the single-dose scenarios (a) and the multiple-dose scenarios (b).

The median ratios of the individual predicted C_max and C_max,ss to EC₅₀ represented, respectively, near two-fold increases from 0.11 to 6.8 EC₅₀ units for the single-dose studies and from 0.25 to 16 EC₅₀ units for the multiple-dose studies with the increase in doses. The median ratio of the individual predicted C_min,ss to EC₅₀ for the multiple-dose studies also increased to double from 0.16 to 10 EC₅₀ units (Table 1).

Table 1. Normalized C_min and C_max by EC50 at each dose scenario.

Dose (mg)	Single dose		Multiple Doses
	Cmax/EC50 (Range) *		Cmin,ss/EC50 (Range)†		Cmax,ss/EC50 (Range)‡
12.5	0.11	(0.10 - 0.11)	0.16	(0.14 - 0.18)	0.25	(0.23 - 0.26)
25	0.21	(0.20 - 0.23)	0.32	(0.28 - 0.35)	0.49	(0.46 - 0.53)
50	0.42	(0.39 - 0.45)	0.63	(0.57 - 0.71)	0.99	(0.92 - 1.1)
100	0.85	(0.78 - 0.91)	1.3	(1.1 - 1.4)	2.0	(1.9 - 2.1)
200	1.7	(1.5 - 1.8)	2.5	(2.3 - 2.8)	3.9	(3.7 - 4.2)
400	3.4	(3.1 - 3.6)	5.1	(4.6 - 5.6)	7.9	(7.4 - 8.4)
800	6.8	(6.3 - 7.2)	10	(9.1 - 11)	16	(15 - 17)

^*, the median values and ranges of normalized maximum concentration for single-dose study, ^†, the median values and ranges of normalized minimum concentration for multiple-dose study, ^‡, the median values and ranges of normalized maximum concentration for multiple-dose study.

PD simulation and estimation

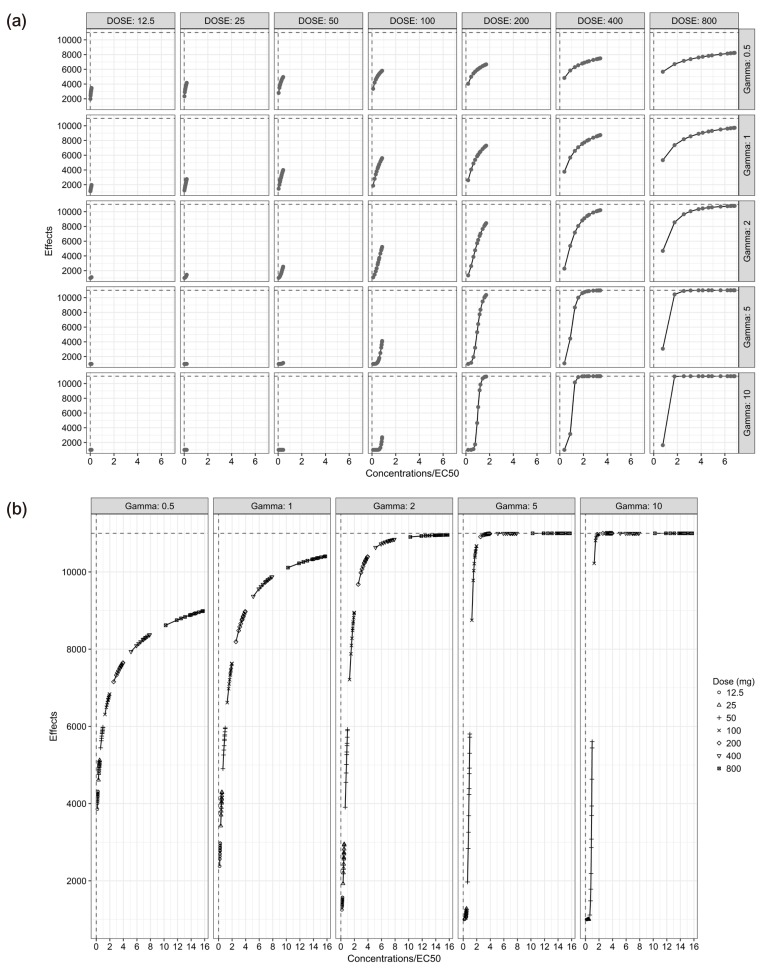
In single-dose studies, E_max was not attained at γ of 0.5 and 1, while it was attained at higher doses with γ of 2, 5 and 10. In case of multiple-dose studies, only a small part of a full sigmoid E_max curve was obtainable (Fig. 2).

Figure 2. Effects versus concentrations/EC50 plots relevant to each simulation scenario for the single-dose scenarios (a) and the multiple-dose scenarios (b).

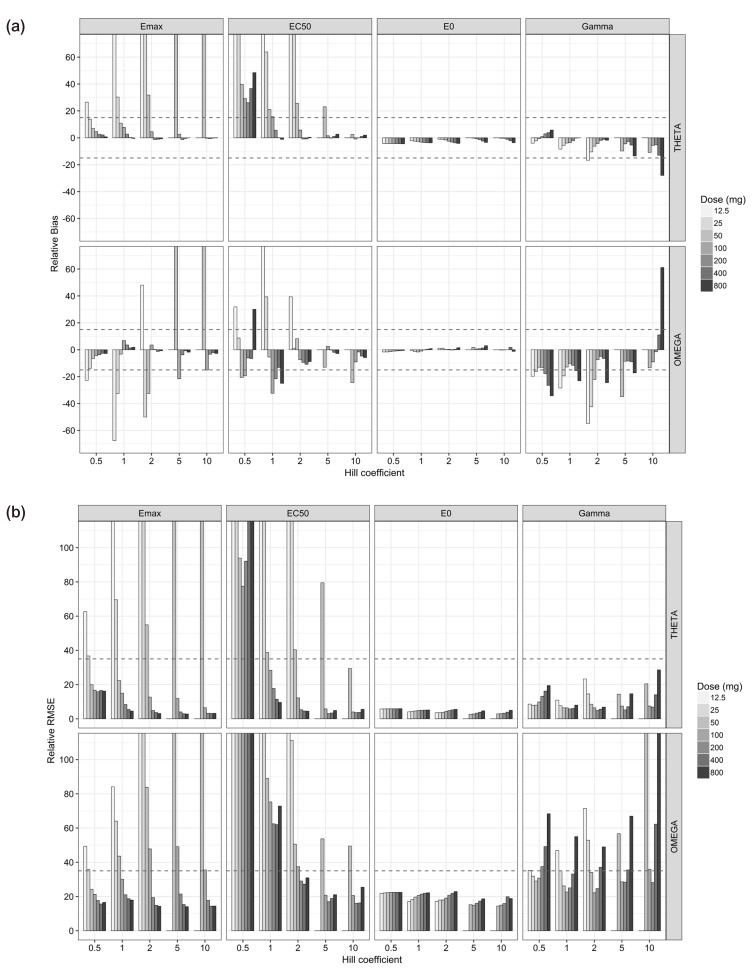
For the single-dose scenarios (Table 2, Fig. 3), estimated θ_Emax and ω_Emax² were mostly biased at lower doses, while most of them were unbiased and precise when the doses and the C_max were, respectively, more than or equal to 100 mg and 0.42 EC₅₀ units, except for the biased ω_Emax² at 100 mg doses (C_max = 0.42 EC₅₀ units) with γ of 5 and 10 and the imprecise ω_Emax² at 100 mg doses (C_max = 0.42 EC₅₀ units) with γ of 2, 5, and 10. θ_EC50 and ω_EC50² were reliably estimated at more than or equal to 100 mg doses with γ of 2 and 5 except the imprecise ω_EC50² at 100 mg dose with γ of 2. The scenarios with γ of 0.5 and 1 resulted in poor estimates of EC₅₀ in most doses, while estimates of θ_EC50 were reliable at more than or equal to 200 mg doses or C_max of 0.85 EC₅₀ units with γ of 1. With regard to E₀, the parameter estimates from all single-dose scenarios were precisely estimated with little bias. Parameter estimates of θγ were mostly accurate and precise except for those at 12.5 mg dose (C_max=0.11 EC₅₀ units) with γ of 2 and 800 mg dose (C_max=6.8 EC₅₀ units) with γ of 10, whereas the parameter estimates of ωγ² were reliably estimated only when the doses were 50 mg (C_max=0.21 EC₅₀ units) with γ of 0.5 and 1 or 100 (C_max=0.85 EC₅₀ units) and 200 mg (C_max= 1.7 EC₅₀ units) with all γ except for 100 mg dose (C_max=0.85 EC₅₀ units) with γ of 0.5 and 200 mg (C_max= 1.7 EC₅₀ units) dose with γ of 10. The relative bias and RMSE of σ² for the PD observations were less than 0.9% and 5% for single-dose study, respectively.

Table 2. Bias and Precision for PD parameters in Single-Dose Scenarios (All values are rounded off to have 3 figures to allow for better readability.

Gamma		relative BIAS (Accuracy: ≤15%, shaded)								relative RMSE (Precision: ≤35%, shaded)
	Dose (mg)	Emax		EC50		E0		γ		Emax		EC50		E0		γ
		θ	ω2	θ	ω2	θ	ω2	θ	ω2	θ	ω2	θ	ω2	θ	ω2	θ	ω2
0.5	12.5	26.5	−23.0	316	31.9	−4.20	−1.60	−4.00	−20.0	62.6	49.3	1140	225	5.78	21.7	8.56	35.3
	25	13.8	−14.0	113	8.67	−4.30	−1.60	−2.20	−16.0	36.7	35.9	410	209	5.82	22.1	7.83	31.9
	50	7.02	−6.50	39.8	−21.0	−4.30	−1.40	−0.50	−13.0	19.9	24.3	94.0	166	5.85	22.3	8.05	29.0
	100	4.67	−4.50	29.3	−19.0	−4.40	−1.10	0.94	−13.0	16.7	21.3	77.5	166	5.87	22.4	9.86	30.8
	200	2.55	−3.80	26.1	−6.10	−4.40	−0.90	2.97	−18.0	15.8	17.7	92.1	165	5.89	22.5	13.2	37.5
	400	2.18	−2.70	36.7	−6.50	−4.40	−0.70	3.86	−26.0	16.6	15.6	141	167	5.91	22.4	16.2	49.2
	800	0.74	−2.80	48.5	30.0	−4.50	−0.50	5.78	−34.0	16.2	16.6	287	287	5.92	22.5	19.4	68.4
1	12.5	120	−68.0	346	85.8	−2.20	−0.50	−8.40	−28.0	398	84.1	1520	241	4.09	17.1	10.9	46.9
	25	30.3	−33.0	63.9	39.3	−2.50	−1.40	−5.60	−19.0	69.6	64.1	159	136	4.30	18.2	7.73	35.0
	50	10.9	−3.30	21.0	−5.50	−2.90	−1.70	−3.90	−13.0	22.4	43.6	38.8	89.0	4.60	19.7	6.42	26.3
	100	7.80	6.88	15.7	−32.0	−3.30	−1.00	−3.70	−10.0	15.0	30.1	28.4	75.3	4.88	20.6	6.41	22.6
	200	2.73	3.55	5.60	−22.0	−3.50	−0.10	−2.10	−12.0	8.43	21.0	17.8	62.5	5.04	21.4	5.77	25.1
	400	0.16	1.37	0.07	−13.0	−3.60	0.43	−0.20	−16.0	5.47	18.7	11.5	62.0	5.11	21.9	6.14	33.2
	800	−0.40	1.89	−1.20	−25.0	−3.70	0.81	0.00	−23.0	4.58	18.0	9.61	72.9	5.16	22.2	8.00	55.0
2	12.5	1420	48.0	1320	39.4	−1.00	1.03	−17.0	−55.0	6820	328	6170	258	3.59	17.1	23.3	71.5
	25	824	−50.0	390	1.08	−1.20	1.13	−10.00	−42.0	3290	153	1650	111	3.56	18.0	14.6	52.9
	50	31.8	−33.0	25.6	8.20	−1.60	0.10	−6.20	−22.0	54.9	83.9	40.4	50.6	3.78	18.0	8.54	34.1
	100	4.57	3.52	5.79	−7.40	−2.60	0.25	−4.30	−7.50	12.7	47.8	12.2	37.5	4.35	19.1	6.45	22.2
	200	−1.30	0.16	−0.90	−9.00	−3.20	−0.20	−1.90	−5.00	4.89	19.4	5.33	29.0	4.80	20.8	4.97	24.7
	400	−1.10	−1.20	−0.80	−11.0	−3.80	0.34	−1.30	−6.50	3.68	14.9	4.60	27.2	5.23	21.9	5.66	37.1
	800	−0.80	−0.80	0.36	−8.80	−4.20	1.50	−1.80	−24.0	3.17	14.3	4.45	30.9	5.53	22.9	6.85	49.0
5	50	800	99	23.0	−13.0	−0.20	1.69	−10.00	−35.0	4400	492	79.5	53.7	2.68	15.2	14.4	56.7
	100	2.66	−22.0	1.56	2.56	−0.70	0.56	−4.50	−8.60	11.9	49.1	5.81	20.8	2.85	15.0	7.47	28.6
	200	−1.40	−3.80	−0.20	−0.20	−1.50	0.76	−2.90	−8.40	4.02	21.5	3.11	17.0	3.30	16.1	5.21	28.4
	400	−0.50	−0.80	1.12	−2.00	−2.40	1.33	−5.40	−8.90	3.01	15.3	3.43	18.9	3.85	17.4	7.09	35.6
	800	0.00	−1.80	2.71	−2.90	−3.40	3.02	−13.0	−17.0	2.81	14.1	4.88	21.1	4.68	18.6	14.7	67.0
10	50	302	175	2.60	−24.0	−0.30	−0.20	−11.0	−13.0	1600	792	29.4	49.5	2.89	14.4	20.5	118
	100	−0.30	−15.0	−0.90	−9.00	−0.30	−0.10	−5.60	−9.00	6.50	35.5	3.99	20.5	3.11	15.0	7.48	35.9
	200	−0.60	−3.30	0.00	−1.60	−1.20	0.00	−5.20	−1.50	3.25	17.8	3.63	16.1	3.31	15.9	6.87	28.2
	400	−0.20	−2.10	1.03	−4.70	−2.10	1.78	−13.0	11.0	3.18	14.4	3.79	16.3	3.92	19.9	14.1	62.3
	800	0.05	−2.80	2.04	−5.90	−3.60	−1.20	−28.0	61.2	3.20	14.4	5.58	25.4	5.00	18.9	28.6	132

Figure 3. Relative bias (a) and relative root mean square error (b) of pharmacodynamic parameters estimates for the single-dose scenarios.

For the multiple-dose scenarios (Table 3, Supplementary Fig. 1), it was very difficult to estimate accurate and precise PD parameters. The estimates of θ_Emax and ω_Emax² met the acceptance criteria of bias and precision when the doses were within the range of 50 (C_min=0.63 and C_max=0.99 EC₅₀ units) and 200 mg (C_min=2.5 and C_max=3.9 EC₅₀ units) and γ was either 5 or 10. This was not true, however, for 50 mg dose (C_min=0.63 and C_max=0.99 EC₅₀ units) with γ of 5 and 200 mg dose (C_min=2.5 and C_max=3.9 EC₅₀ units) with γ of either 5 or 10. Estimates corresponding to these doses resulted in high imprecision. With regard to the estimates of θ_EC50 and ω_EC50², the results from designs at 100 mg dose 50 (C_min=1.3 and C_max=2.0 EC₅₀ units) with γ of 5 and 50 mg dose (C_min=0.63 and C_max=0.99 EC₅₀ units) with γ of 10 were reliable. Contrary to the results of single-dose studies, the performance of estimating E₀ represented considerably poor accuracy and precision. θ_E0 and ω_E0² were estimated with accuracy and precision, when the doses were in the range of 12.5 and 50 with γ of 5 and 10, except for the imprecise ω_E0² at 50 mg dose (C_min=0.63 and C_max=0.99 EC₅₀ units) with γ of 5. Some θ_γ were estimated with accuracy and precision, while most ω_γ² were unreliable. The relative bias and RMSE of σ² for the PD observations were less than 0.9% and 5.1% for multiple-dose study, respectively.

Table 3. Bias and Precision for PD parameters in Multiple-Dose Scenarios (All values are rounded off to have 3 figures to allow for better readability.).

Gamma		relative BIAS (Accuracy: ≤15%, shaded)								relative RMSE (Precision: ≤35%, shaded)
	Dose (mg)	Emax		EC50		E0		γ		Emax		EC50		E0		γ
		θ	ω2	θ	ω2	θ	ω2	θ	ω2	θ	ω2	θ	ω2	θ	ω2	θ	ω2
0.5	12.5	106	−1.90	1.E+03	144	−10.0	42700	55.3	−19.0	833	83.5	3.E+03	607	137	4.E+05	157	126
	25	134	14.9	718	88.0	19.2	2.E+06	85.4	−29.0	1.E+03	102	4.E+03	540	192	2.E+07	177	136
	50	13.7	25.1	644	86.6	41.4	−410	91.5	−3500	154	95.0	2.E+03	526	257	1.E+04	165	3.E+04
1	12.5	283	−40.0	1.E+03	22.6	−22.0	−46.0	−13.0	−20.0	2.E+03	79.4	5.E+03	200	40.3	108	26.6	80.4
	25	80.7	−23.0	741	3.87	−27.0	2.E+04	−6.60	−27.0	178	64.0	4.E+03	143	60.2	1.E+05	32.0	92.6
	50	16.0	1.54	68.2	−8.70	−21.0	4.E+04	12.3	−33.0	57.8	49.6	304	150	138	4.E+05	51.0	106
	100	10.4	14.8	0168	−7.30	−5.40	4.E+03	17.5	−17.0	63.7	64.1	974	195	210	4.E+04	50.1	174
	200	9.97	16.9	195	57.4	−38.0	1.E+03	19.5	18.7	51.4	80.0	1.E+03	426	318	8910	57.1	260
	400	10.6	25.0	780	278	−9.00	−60.0	26.0	122	58.3	96.8	4.E+03	1.E+03	453	141	74.4	453
	800	5.38	60.9	1.E+03	415	69.9	6700	48.2	349	51.9	204	6.E+03	2.E+03	389	5.E+04	165	1.E+03
2	12.5	806	−15.0	599	−13.0	−3.70	−4.30	−15.0	−44.0	2330	179	1870	135	12.1	46.8	25.9	70.6
	25	127	−24.0	107	−12.0	−4.80	−16.0	−9.00	−27.0	304	108	295	73.5	14.8	66.1	17.9	64.7
	50	14.5	5.91	18.3	−17.0	−6.00	−33.0	−3.50	−29.0	41.2	55.2	54.1	57.4	34.2	128	20.8	68.6
	100	2.45	3.74	3.69	−24.0	−11.0	3.E+03	2.48	−42.0	24.2	35.6	29.7	56.3	117	3.E+04	25.1	97.0
	200	−4.30	17.0	15.0	−40.0	51.2	1.E+04	9.67	25.8	30.8	68.3	36.8	96.6	268	1.E+05	38.6	243
	400	−24.0	101	84.7	−34.0	269	1.E+05	69.5	200	42.2	222	232	203	402	1.E+06	256	777
	800	−14.0	299	1.E+04	297	228	83100	77.0	134	49.5	1450	81700	2.E+03	434	8.E+05	230	541
5	12.5	881	544	104	62.2	−1.90	1.63	−5.80	24.7	5.E+03	1690	365	693	5.68	17.6	67.9	284
	25	319	79.6	20.7	−7.00	−1.00	4.13	−13.0	−59.0	2.E+03	380	59.8	50.5	4.98	20.2	18.8	74.3
	50	0.57	−5.60	0.70	−0.80	−1.80	−11.0	−5.30	−30.0	11.2	51.3	6.22	21.1	7.82	39.6	10.8	58.8
	100	−0.30	0.58	2.01	−15.0	−6.90	−65.0	−5.40	−14.0	4.87	20.0	5.08	27.1	19.3	82.9	12.3	74.4
	200	−4.80	8.54	9.55	−24.0	47.7	−29.0	2.64	15.0	23.1	48.1	19.5	65.7	224	193	51.2	246
	400	−20.0	96.0	654	253	254	5940	98.2	174	66.7	284	6420	2.E+03	579	3.E+04	299	790
	800	−22.0	141	3350	−42.0	245	68.7	60.8	165	58.9	445	3.E+04	176	593	930	222	804
10	12.5	865	25.5	93.9	−41.0	−1.10	−2.10	94.4	191	4.E+03	646	643	142	4.99	14.5	218	1.E+03
	25	23.1	116	2.37	−13.0	0.00	−3.00	−19.0	−31.0	90.0	749	16.6	38.9	3.24	16.6	23.4	111
	50	−1.00	−2.20	−0.20	−4.20	0.48	−3.50	−7.20	−33.0	7.11	32.6	3.81	20.5	4.43	29.1	9.88	60.4
	100	−0.10	−2.50	3.64	−18.0	−1.10	−24.0	−11.0	−15.0	3.85	18.7	5.51	29.1	11.7	59.4	14.0	63.6
	200	−4.10	6.78	5.98	−3.90	41.1	−31.0	−3.90	235	15.0	48.4	20.1	134	141	182	36.5	777
	400	−8.20	132	4.E+04	7.E+03	259	−24.0	46.1	663	157	645	4.E+05	4.E+04	543	130	161	2.E+03
	800	−24.0	137	217	−48.0	263	1820	2.75	42.3	58.6	606	1.E+03	72.8	586	1.E+04	74.7	422

Discussion

This simulation study assumes a typical human pharmacology study design where plasma concentration and effect are frequently measured in order to characterize PK and/or PD. Dense sampling strategies are used in all phases of clinical trials for changing dose, indication, or target population as well as phase 1 clinical trials in new drug development, and pharmacometric analyses are frequently done for these studies. However, not all analyses are successful and the quality of population approach depends on the quality of study design as well as the quantity of data. Therefore, this study aims to specifically investigate the estimation performance of PD parameters based on different data properties given the same quantity of data. In case of sparse sampling, it is natural that parameters are poorly estimated.

Ette et al. suggested a data supplementation (PK/PD knowledge creation or discovery) method to characterize an unknown target region of the response surface, which is very useful in finding appropriate new doses in a completed clinical study with limited information on exposure-response relationship.[13] Dutta et al. found that E_max, EC₅₀, and γ of sigmoid E_max model were poorly estimated if the maximum concentration was not attained up to 95% of E_max applying clinical data simulation. Seven escalating C_max levels with five different Hill coefficients (γ=0.2, 0.5, 1, 2 or 5) were used in simulations. The number of blood samples was ten in each scenario. However, the concentrations were derived from sigmoid E_max curve and pharmacokinetics was not considered.[14] The parameter estimation of sigmoid E_max model is an important part in dose-finding study. Dragalin et al. found that the adaptive designs with the selected dose applying Fisher information matrix were superior in finding target dose compared to the common designs with the doses allocated by equal interval.[15] Wang et al. also compared the performance of the adaptive design to the uniform design.[16] The purpose of these two studies was to show the performance of adaptive optimal designs for dose-finding studies, (corresponding to phase 2 clinical studies) and pharmacokinetics was not considered. On the other hand, the next two studies used pharmacokinetic sampling designs to investigate pharmacodynamic parameter estimation, as is done in this study. Girgis et al.[10] found that the accuracy and precision of the PD parameter estimates got worse as the number of subjects decreased from 100 to 25 with sparse sampling design. Pai et al.[11] performed a series of studies that evaluated the effect of octreotide on the insulin-like growth factor-1and the effect of remifentanil on electroencephalogram, which were successfully described using sigmoid E_max model with moderate sigmoidicity (γ=2.51) and simple E_max model (γ=1), respectively, while the previous study of theophylline-induced eosinopenia was described using a model of high sigmoidicity. The latter study investigated the change in bias and precision in relation to Hill coefficient using 100 subjects in each scenario and 4 to 5 sparse samplings based on the former study and found that the plasma concentration of two to three times EC₅₀ was needed to get reliable parameter estimates if the drug exhibited high Hill coefficient, and that the plasma sampling near EC₅₀ was important with simple E_max model. In the two studies, all the estimated ω_γ² were biased and imprecise, whereas ω_γ² of 10 scenarios, including doses of 50 (C_max=0.42 EC₅₀ units) and 100 mg (C_max=0.85 EC₅₀ units) with γ of 0.5, 50 to 200 mg with γ of 1, 100 and 200 mg with γ of 2 or 5 and 200 mg (C_max=1.7 EC₅₀ units) with γ of 10, among 31 single-dose scenarios were accurately and precisely estimated in this study with dense sampling design.

In this study, the number of subjects was set to 100 in each scenario and dense sampling design was adopted based on the results of the previous studies to investigate the estimation performance with regard to differing concentration and Hill coefficients while fixing the number of subjects and sampling points. Using virtual drugs with different Hill coefficients and ratios of concentration to EC₅₀ would facilitate general interpretation and easy application to the real drugs.

For the single-dose studies, the SSE processes failed when the doses were 12.5 (C_max=0.11 EC₅₀ units) and 50 mg (C_max=0.42 EC₅₀ units) and γ was either 5 or 10, because the simulated concentrations were located at lower flat area of the sigmoid E_max curve (Fig. 2). The accuracy and precision of θ_Emax and ω_Emax² were getting better with the increase in dose, regardless of γ, while those of θ_EC50 and ω_EC50² gradually improved with increase in both dose and γ (Fig. 3). In single-dose studies, since the baseline of effects before dosing was measurable, all the θ_E0 and ω_E0² were estimated with accuracy and precision. The estimated θ_γ showed various trends at different values of γ. The absolute values of relative bias for θ_γ were represented by a U-shaped curve when γ was 0.5, 5 or 10, while they grew with increase in dose when γ was either 1 or 2 (Fig. 3). The relative RMSE for θ_γ and the relative bias and relative RMSE for ω_γ² also represented U-shape trends regardless of γ (Fig. 3), because the bottom area of the effects were measured with lower doses and the ceiling area were measured with higher doses. Sampling enough concentrations corresponding to the whole range of the effect curve must be crucial to estimate reliable θ_γ and ω_γ² (Fig. 2).

The estimation capabilities of the PD parameters except for θ_E0 and ω_E0² with different Hill coefficients (γ) in single-dose scenarios are as follows (Fig. 3). For the γ of 0.5, all the estimates of θ_Emax and ω_Emax² were reliable when the dose was at least 50 mg or C_max was more than 0.42 EC₅₀ units. The estimates of θ_γ and ω_γ² were accurate and precise only under doses of 50 (C_max=0.42 EC₅₀ units) and 100 mg (C_max=0.84 EC₅₀ units). However, θ_EC50 and ω_EC50² were poorly estimated in all dosing scenarios. The reason seemed that the range of concentration-effect relationships was not enough to describe whole shape of sigmoid E_max model as shown in the multiple-dose scenarios. The effect-concentration profiles obtained from various doses seem to be needed to estimate accurate and precise θ_EC50 and ω_EC50². For the γ of 1, all the estimates of θ_Emax and ω_Emax² were reliable when the dose was at least 100 mg or C_max was more than 0.85 EC₅₀ units. θ_EC50 was accurately and precisely estimated when the dose was at least 100 mg (C_max=0.84 EC₅₀ units), while ω_EC50² was hardly estimated, as shown in a previous study.[11] The estimates of θ_γ and ω_γ² were accurate and precise when the doses were within the range of 50 to 400 mg (C_max=0.42 to 3.4 EC₅₀ units). This was not true, however, for 800 mg dose (C_max=6.8 EC₅₀ units) owing to lack of information on sigmoidicity in concentration-effect relationship. For the γ of 2 to 10, all the parameter estimates for E_max and EC₅₀ met the acceptance criteria of bias and precision when the doses were more than or equal to 200 mg (C_max=1.7 EC₅₀ units). This is a relatively smaller value than the result form a study which reported that the 2 to 3 EC₅₀ region is needed to get an unbiased and precise estimate of ω_Emax², when γ was 6.22 and blood sampling was sparse.[10] A dense sampling design is recommended to get a precise ωE_C502, because it was impossible with sparse sampling design.[11]

Both the θ_γ and ω_γ² met the criteria for accuracy and precision at 100 (C_max=0.84 EC₅₀ units) and 200 mg (C_max=1.7 EC₅₀ units) with γ of 2, 100 to 400 mg (C_max=0.84 to 3.4 EC₅₀ units) with γ of 5, and 200 mg (C_max=1.7 EC₅₀ units) with γ of 10. On the other hand, Girgis et al. found that all θ_γ and ω_γ² were biased and imprecise when the Hill coefficient was high (γ=6.22), 4 to 5 blood samples were gathered[10] and Pai et al. also reported similar results from spare sampling design, when γ were 1 or 2.51.[11] These results suggest that dense sampling design may be essential to get accurate and precise estimates of θ_γ and ω_γ².

These results can be applied to clinical trials and PK/PD modeling of resultant data. When a clinical study is performed to evaluate the PK/PD of an investigational product with Hill coefficients of 2, an investigator can use 200 mg (C_max=1.7 EC₅₀ units) to get the best results of parameter estimation or 100 mg (C_max=0.84 EC₅₀ units) to get useful parameter estimates with less toxicity. On the other hand, an investigator can interpret the reliability of the results from PK/PD modeling based on the results of this study.

For the multiple-dose studies (Table 3, Supplementary Fig. 1), the parameter estimation performance was not good. In this simulation setting, the accumulation index was 2.22 with the half-life of 14 hours and 12 hour dosing interval. The concentration-effect profile obtained from this setting could not include the whole range of effects and resulted in poor performance. If the dosing interval was longer than 12 hours or the drug had lower accumulation rate than 2.22, wider range of concentration-time profiles could be gathered. The worse performance of PK parameter estimation in multiple-dose settings than in single-dose settings might play a role in the poor estimates of PD parameter. On the other hand, errors in PD parameter estimates might have negatively affected PK parameter estimation, and this is hinted from different levels of bias and precision with different combinations Hill coefficients and doses, although the Hill coefficient had no relation to pharmacokinetics. If PK/PD modeling is performed with data from multiple-dose studies, the sampled concentrations may include at least 0.63 EC₅₀ and at most 3.9 EC₅₀ corresponding to the doses of 50 to 200 mg in this study.

This study has some limitations. Since the PK profiles were simulated under the assumption of dose proportionality, the relationship between dose and EC₅₀ units might change if investigational drugs have nonlinear PK properties. However, the exposure-response relationship can be easily understood and applied, if concentrations are normalized by EC₅₀. Another limitation is that only one dosing interval was used for simulation in the multiple-dose scenarios. Since a different dosing interval may yield a different steady-state fluctuation, the parameter estimation performance can be better or worse than this study according to the dosing interval. A further limitation stems from the limited range of variability parameters of this study. Since all CV% of IIV and RV were set at moderate values of 30% and 20%, respectively, prediction of exposure-response relationship of a drug with larger variability might show deviations from our findings. Simultaneous modeling of PK/PD is one of the causes of poor IIV estimation, and certain types of sequential approaches may result in better performance.[17]

This simulation study demonstrated the effect of the relative range of sampled concentrations to EC₅₀ and sigmoidicity (or sensitivity) between exposure and response on the parameter estimation performance using dense sampling design. In single-dose studies, most PD parameters of sigmoid E_max model were accurately and precisely estimated when the C_max was more than 0.85 EC₅₀ units, except for typical value and IIV of EC₅₀ which were poorly estimated at low Hill coefficients (γ=0.5 and 1) regardless of doses. The PK/PD modeling results using only steady-state data may be carefully interpreted. This study can be useful in designing a clinical study to evaluate PK/PD relationship for new drug development or drug repositioning.

Supplementary Materials

Supplementary Figure 1

Relative bias (a) and relative root mean square error (b) of pharmacodynamic parameters estimates for the multiple-dose scenarios.