UK Biobank Whole-Exome Sequence Binary Phenome Analysis with Robust Region-Based Rare-Variant Test

Abstract

In biobank data analysis, most binary phenotypes have unbalanced case-control ratios, and this can cause inflation of type I error rates. Recently, a saddle point approximation (SPA) based single-variant test has been developed to provide an accurate and scalable method to test for associations of such phenotypes. For gene- or region-based multiple-variant tests, a few methods exist that can adjust for unbalanced case-control ratios; however, these methods are either less accurate when case-control ratios are extremely unbalanced or not scalable for large data analyses. To address these problems, we propose SKAT- and SKAT-O- type region-based tests; in these tests, the single-variant score statistic is calibrated based on SPA and efficient resampling (ER). Through simulation studies, we show that the proposed method provides well-calibrated p values. In contrast, when the case-control ratio is 1:99, the unadjusted approach has greatly inflated type I error rates (90 times that of exome-wide sequencing $\mathit{\alpha }$ = 2.5 × 10⁻⁶). Additionally, the proposed method has similar computation time to the unadjusted approaches and is scalable for large sample data. In our application, the UK Biobank whole-exome sequence data analysis of 45,596 unrelated European samples and 791 PheCode phenotypes identified 10 rare-variant associations with p value < 10⁻⁷, including the associations between JAK2 and myeloproliferative disease, HOXB13 and cancer of prostate, and F11 and congenital coagulation defects. All analysis summary results are publicly available through a web-based visual server, and this availability can help facilitate the identification of the genetic basis of complex diseases.

Introduction

With the decreased cost of sequencing, big biobanks have started to whole-exome or whole-genome sequence large numbers of participants to identify the role of rare variants in complex diseases.1, 2, 3 By combining rich phenotypic information in electronic health records (EHRs),⁴ these sequence data will illuminate the phenome-wide association patterns of rare variants. Since most diseases and symptoms have low prevalence, the binary phenotypes in biobanks generally have unbalanced case-control ratios (1:10 or 1:100, for example).⁵ For example, in the UK Biobank data, nearly 99% of PheCode-based binary phenotypes have case-control ratios less than 1:10.⁶ Substantial challenges are posed when analyzing the associations between rare variants and unbalanced phenotypes.

Since single-variant tests are underpowered for identifying disease-associated rare variants,⁷ gene- or region-based multiple-variant tests, including the burden test,^8,9 SKAT,¹⁰ and SKAT-O,¹¹ are commonly used to identify rare-variant associations. To evaluate the association signals in multiple variants, these methods aggregate single-variant score statistics. However, as shown in our simulation studies and elsewhere,12, 13, 14 these methods suffer from the inflation of type I error rates when case-control ratios are unbalanced. For single-variant tests, the recently developed saddle point approximation (SPA) based approach provides accurate p values under such a case-control imbalance.^5,15 Although a few methods exist that adjust for unbalanced case-control ratios for gene- or region-based tests, including moment-based adjustment (MA)¹⁶ and efficient resampling (ER),¹⁶ these methods are not scalable or accurate for biobank data. When the case-control ratio is extremely unbalanced, MA can still have inflated type I error rates. ER is computationally expensive when minor allele counts (MAC) are moderate or large.

To address these problems, we propose a robust region-based test that adjusts single-variant score statistics through the use of SPA and ER and then aggregates the adjusted statistics. The SPA and ER help to precisely calculate the reference distribution of the single-variant score statistics, thereby properly controlling for type I error rates. The computation cost of the proposed approach is comparable to those of unadjusted tests, and the proposed approach can thus be applied to large biobank data. Using extensive simulation studies, we demonstrate that our robust burden, SKAT, and SKAT-O tests have proper type I error rates even when the case-control ratio is 1:99 and our tests exhibit larger power compared to the unadjusted burden, SKAT, and SKAT-O test. In addition, this method can be applicable not only to rare-variant tests but also to the joint association test of common and rare variants.

The UK Biobank resource² completed the first tranche of whole-exome sequencing (WES) data for 49,960 participants.¹ We performed robust gene-based rare-variant tests of 45,596 unrelated European samples on 791 phenotypes with at least 50 cases, and we identified 10 rare-variant associations with p value < 10⁻⁷, including the associations between JAK2 (MIM: 147796) and myeloproliferative disease (MIM: 254700), HOXB13 (MIM: 604607) and prostate cancer (MIM: 610997), and F11 (MIM: 264900) and congenital coagulation defects (MIM: 134520). These results anticipate the discoveries we can make with the full 500,000 WES samples, which will be available in the near future. In addition, the analysis results can be used as a community resource and facilitate the identification of the genetic basis of complex diseases.

Material and Methods

Gene- and Region-based Rare-Variant Tests for Binary Traits

Assume $n$ individuals are sequenced in a region, which has $m$ rare variants. For the $i$-th individual, let $y_i$ denote a binary phenotype, $G_i=\left(g_{i1},g_{i2},\dots ,g_{im}\right)\text{'}$ the hard call genotypes $\left(g_{ij}=\mathrm{0,1,2}\right)$ or dosage values of the $m$ genetic variants in the target gene or region, and $X_i=\left(X_{i1},X_{i2},\dots ,X_{is}\right)\text{'}$ the covariates, including the intercept. To model a binary outcome, the following logistic regression model can be used:

$$logit\left({\pi }_i\right)=X_i^{\text{'}}\alpha +G_i^{\text{'}}\beta ,$$

where ${\pi }_i$ is the disease probability for the $i$-th individual, $\alpha$ is an $s\times 1$ vector of regression coefficients of covariates, and $\beta$ is an $m\times 1$ vector of regression coefficients of genetic variants. Suppose $S_j={\sum }_{i=1}^n{g}_{ij}\left(y_i-\widehat{{\pi }_i}\right)$ is the score statistic for the variant $j$, where $\widehat{{\pi }_i}$ is the estimated disease probability under the null hypothesis of no association (i.e., $\beta =0)$. Burden and SKAT test statistics can be written as

$$Q_B={\left(\sum _{j=1}^m{\omega }_j{S}_j\right)}^2,Q_s=\sum _{j=1}^m{\omega }_j^2{S}_j^2,$$

where w_j is the weight for each variant.¹⁰ In the simulation and real data analysis, we used beta(1,25) weights, which upweight rarer variants.¹⁰ The SKAT-O method combines the burden test and SKAT with the following framework:

$$Q_{\rho }=\left(1-\rho \right)Q_B+\rho Q_s,$$

where $\rho$ is a tuning parameter with range [0,1]. Since the optimal $\rho$ is unknown, SKAT-O applies the minimum p values over a grid of $\rho$ as a test statistic.

Under the null hypothesis, $S={\left(S_1,\dots ,S_m\right)}^T$ asymptotically follows the multivariate normal distribution, $MVN\left(0,V^{\frac{1}{2}}C{V}^{\frac{1}{2}}\right)$, where $C$ is the correlation matrix among m variants and $V$ is a diagonal matrix where the diagonal elements are the asymptotic variances of $S$. In the presence of a case-control imbalance, however, the distribution of score statistics is skewed, which causes the inflation of type I error rates. To address this problem, we will utilize SPA and ER to adjust the variance matrix $V$.

SPA and ER

SPA is a statistical method for calculating the distribution function through the use of the cumulant-generating function (CGF). Since it utilizes all the cumulants, SPA is more accurate than normal approximation, which only uses the first two cumulants (mean and variance). From the work of Dey et al.,⁵ suppose $K_j\left(t\right)$ is the CGF of the score statistic $S_j$, which can be derived based on the fact that $Y_i\sim \text{Bernoulli}\left({\pi }_i\right)$ under the null. Then the distribution function of the score statistic $S_j$ can be approximated by

$$\mathrm{Pr}\left(S_j<\text{s}\right)=\tilde{F}\left(s\right)=\text{Ö}\left\{d+\frac{1}{d}\log \left(\frac{v}{d}\right)\right\},$$

where $d=sgn\left(\hat{t}\right)\sqrt{2\left(\hat{t}s-K_j\left(\hat{t}\right)\right)}$, $\text{v}=\hat{t}\sqrt{K_j^{\text{'}\text{'}}\left(\hat{t}\right)}$, $\hat{t}$ is the solution to the equation $K_j^{\text{'}}\left(\hat{t}\right)=s,$ and $\text{Ö}$ is the distribution function of the standard normal distribution.⁵

Although SPA performs better than normal approximation, because it is still an asymptotic-based approach, SPA can result in inaccurate p values when MAC is very low. To address this issue, we use ER for low-MAC variants. ER is a resampling method that resamples the case-control status of individuals with a minor allele at a given variant and disease risk ${\pi }_i$ instead of permuting case-control status across all individuals. This is done because only individuals with minor alleles contribute to the score statistics S. Because ER is resampling-based, it can provide an accurate p value for a very rare variant. When MAC is low (ex. MAC ≤ 10), ER can rapidly calculate the exact p value by numerating all possible configurations of case-control statuses. The detailed derivations of ER can be found in Lee et al.¹⁶

Robust Burden Test, Robust SKAT and Robust SKAT-O

For each variant $j$, when the score statistic $S_j$ lies within two standard deviations of the mean, the normal approximation generally performs well.⁵ Otherwise, due to the skewed distribution, the normal approximation causes inflated type I error rates. Hence, when $S_j$ is beyond two standard deviations of the mean, we apply SPA (when MAC > 10) or ER (when MAC ≤ 10) to calculate the p value ${\tilde{p}}_j$, which will be used to calibrate the variance of $S_j$.

Let $S_j^2/{\hat{V}}_j$ be a square-standardized test statistic in which ${\hat{V}}_j$ is the estimated variance of $S_j^2$. When $S_j$ follows the normal distribution, $S_j^2/{\hat{V}}_j$ follows the chi-square distribution with one degree of freedom. We adjust the variance so that the p value is the same as ${\tilde{p}}_j$, in which the adjusted variance is

$${\tilde{V}}_j=S_j^2/{\chi }_{quantile}^2\left(1-{\tilde{p}}_j\right),$$

where ${\chi }_{quantile}^2$ is the quantile function of the chi-square distribution with one degree of freedom. Note that if $S_j$ lies within two standard deviations of the mean, ${\tilde{V}}_j={\hat{V}}_j$. Suppose $\tilde{V}={\left({\tilde{V}}_1,{\tilde{V}}_2,\dots ,{\tilde{V}}_m\right)}^T$, then the p value of the region can be calculated based on the assumption that

$$S\sim MVN\left(0,{\tilde{V}}^{\frac{1}{2}}C{\tilde{V}}^{\frac{1}{2}}\right).$$

These adjustments overcome the inflated type I error rates for common variants, but they are insufficient to address the inflation issue for rare variants (4.87 times of exome-wide alpha = 2.5 × 10⁻⁶ when the case-control ratio is 1:99). Details can be found in Table S1. We apply additional adjustment by using the fact that the burden test can be presented as a single-marker test with collapsed variants, and SPA performs very well for single-marker tests. From the above equation, the variance estimate of the burden test is ${\tilde{V}}_{burden}=w^T{\tilde{V}}^{\left(1/2\right)}C{\tilde{V}}^{\left(1/2\right)}w$, where $w={\left(w_1,\dots ,w_m\right)}^T$ is an $m\times 1$ vector of the weight. Suppose $g_i^{burden}={\sum }_{j=1}^m{w}_j{g}_{ij}$, and then the burden test statistic (i.e., $Q_B$) is identical to $S_{burden}^2$, where $S_{burden}={\sum }_{i=1}^n{g}_i^{burden}\left(y_i-\widehat{{\pi }_i}\right)$, and the p value ${\check{p}}_{S_{burden}}$ of $S_{burden}$ can be calculated from SPA. Using the similar approximation as above, we estimate the variance $S_{burden}$ as ${\check{V}}_{sum}=S_{burden}^2/{\chi }_{quantile}^2\left(1-{\check{p}}_{S_{burden}}\right)$. Suppose $r={\tilde{V}}_{sum}/{\check{V}}_{sum}$. In order to control type I error inflation, we suggest utilizing a more conservative variance. Let $\tilde{r}=\min \left(1,r\right),$ then

$$S\sim MVN\left(0,{\left(\frac{\tilde{V}}{\tilde{r}}\right)}^{\frac{1}{2}}C{\left(\frac{\tilde{V}}{\tilde{r}}\right)}^{\frac{1}{2}}\right).$$

With this formula, robust burden, SKAT, and SKAT-O tests can be performed.

Extension to the Joint Test of Common and Rare Variants

Our robust method can be extended to the joint test of common and rare variants. Consider the following model

$$logit\left({\pi }_i\right)=X_i^{\text{'}}\alpha +G_{1i}^{\text{'}}{\beta }_1+G_{2i}^{\text{'}}{\beta }_2.$$

For the individual $i$, ${\pi }_i$ is the disease probability; $X_i$ is the vector containing all the covariates, including the intercept; $G_{1i}\mathrm{is}\mathrm{the}\mathrm{genotype}\mathrm{vector}\mathrm{of}\mathrm{rare}\mathrm{variants}\mathrm{with}\mathrm{length}{m}_r;$ and $G_{2i}$ is the vector of common variants with length $m_c$. To test the hypothesis of no genetic effects $H_0:{\beta }_1=0,{\beta }_2=0$, the test statistic $Q_{\phi }$ can be written as

$$Q_{\phi }=\left(1-\phi \right)Q_{rare}+\phi Q_{common}$$

$$=\left(1-\phi \right)S_1^{\text{'}}{W}_1{W}_1^{\text{'}}{S}_1+\phi S_2^{\text{'}}{W}_2{W}_2^{\text{'}}{S}_2,$$

where $S_1\text{and}{S}_2$ are the vectors of score statistics for rare and common variants, respectively, and $W_1\text{and}{W}_2$ are diagonal weight matrices for rare and common variants.

Under the null, $S=\left(S_1,S_2\right)\sim MVN\left(0,V^{\frac{1}{2}}C{V}^{\frac{1}{2}}\right)$. Using the approach described in the previous section, we apply SPA and ER to calibrate variance estimates in order to perform a robust SKAT method.

Numerical Simulations

We conducted extensive simulation studies to evaluate the performance of the proposed methods for dichotomized traits. The sequence data of mimicking European ancestry over 200 kb regions were generated using the calibrated coalescent model.¹⁷ We randomly selected regions with lengths of 1, 2, and 3 kb and tested for associations in all simulation settings. On average, each simulated dataset had 16.33 (SD: 4.05), 32.69 (SD: 5.65), and 49.05 (SD: 6.71) rare variants for 1, 2, and 3 kb regions, respectively, when the sample size was 50,000.

We generated datasets with sample size 50,000. We included two covariates for the analysis. The first one followed a Bernoulli distribution with $\mathit{\text{p}}=0.5$ and the other followed the standard normal distribution, corresponding to the gender and normalized age. Four case-control ratios were considered, 1:1, 1:9, 1:49, and 1:99, and the binary phenotypes were simulated from

$$\text{logit}\left({\pi }_i\right)={\gamma }_0+{\gamma }_1{X}_{1i}+{\gamma }_2{X}_{2i}+{\beta }_1{g}_{1i}+\dots +{\beta }_m{g}_{mi},$$

where ${\beta }_1={\beta }_2=\dots ={\beta }_m=0$; ${\gamma }_1$ and ${\gamma }_2$ were chosen to let the odds ratio (OR) of $X_1$ and $X_2$ equal 1.2 and 1.5, respectively, and ${\gamma }_0$ was chosen based on disease prevalence. Seven different methods were applied to each of the generated datasets. For all variants in the region, we applied the unadjusted and robust joint test of common and rare variants. For rare-variant tests (minor allele frequency [MAF] ≤ 0.01), we applied (1) burden test; (2) robust burden test; (3) SKAT; (4) robust SKAT; (5) SKAT-O; (6) robust SKAT-O; and (7) the hybrid method. The hybrid method,¹⁶ developed by Lee, selects a method among ER, quantile adjusted moment matching (QA), and moment matching adjustment (MA) based on MAC and the degree of case-control imbalance. A total of 10⁷ phenotypes were generated, and type I error rates were estimated based on the proportion of p values smaller than the given $\alpha$ level divided by given $\alpha .$

For power simulations, 30% of variants were randomly selected as causal. Two settings were considered: (1) 80% causal variants were risk-increasing variants and 20% were risk-decreasing variants; and (2) all causal variants were risk-increasing variants. For each setting, 10,000 datasets were generated, and the power was estimated as the proportion of p values smaller than the empirical $\alpha$ level, which was calculated in the type I error simulation.

Analysis of WES Data in the UK Biobank

We analyzed the first tranche of UK Biobank WES data with 49,960 participants.¹ Due to the quality issues in the Regeneron pipeline,¹⁸ we analyzed genotype data processed from the functional equivalence (FE) pipeline.¹⁹ The details of sample selection and QC procedures are described elsewhere.¹ We excluded one individual in each related pair (up to second-degree relatives) to identify a set of unrelated individuals. To preserve cases, we first selected a maximal set of unrelated cases, then removed controls that were related to the unrelated cases and kept a maximal set of unrelated controls. Because of the missing values in the phenotypes, the individuals included in the analysis varied across phenotypes. We performed gene-based tests on 45,596 independent European participants whose phenotype data were available in the UK Biobank.

Following a previously published scheme,²⁰ we defined disease-specific binary phenotypes by combining hospital ICD-9 codes into hierarchical PheCodes, each representing a specific disease group. ICD-10 codes were mapped to PheCodes through the use of a combination of maps available through the Unified Medical Language System, manual review, and other sources. Study participants were labeled with a PheCode if they had one or more of the PheCode-specific ICD codes. “Cases” were defined as all study participants with the PheCode of interest, and “controls” were defined as all study participants without the PheCode of interest. Gender checks were performed so that PheCodes specific for one gender could not be assigned to the other gender by mistake.¹⁵

There were 791 binary phenotypes with at least 50 cases based on PheCodes, in which 551 phenotypes had case-control ratios smaller than 1:99. Because our robust methods would cause a certain inflation for extremely unbalanced case-control ratios (Table S1), and using more controls than those from a case-control ratio of 1:99 would not improve power (Figure S1), we did matching on these 551 traits by using the first four genotype principal components. Specifically, for each case, we found the closest controls in Euclidean distance to make the case-control ratio be 1:99. We used principal components calculated by UK Biobank, which were calculated from 147,551 LD-pruned SNPs with missing rate < 0.015 and MAF > 0.01.²¹

We focused on the rare variants (MAF ≤ 0.01) of the nonsynonymous and splicing variants in the exon and neighboring regions. In particular, we used annotation of frameshift deletion, frameshift insertion, nonframeshift deletion, nonframeshift insertion, nonsynonymous SNV, splicing, stopgain, and stoploss from ANNOVAR (Version built on 2018-04-16) with refGene database (hg38).²² A total of 18,360 genes were used for the analysis. The number of variants in genes ranged from two to 7,439 and the distribution was highly skewed (Figure S2). The six methods discussed in the simulation study, unadjusted, and robust versions of the burden test, SKAT, and SKAT-O methods were applied to the data. Age, gender, and the first four principal components were used as covariates to adjust for population stratification.

Results

Type I Error and Power Simulation Results

We generated 10⁷ datasets to compare type I error rates of the proposed approaches (robust burden, SKAT, and SKAT-O), unadjusted approaches (burden, SKAT, and SKAT-O) and a hybrid approach for SKAT-O.¹⁶ The hybrid approach applies several adjustment methods based on MAC. Table 1 shows that the unadjusted approaches had substantial inflation of type I error rates when the case-control ratio was unbalanced and the region length was 1 kb. In contrast, the robust approaches controlled type I error rates much better and had only a slight inflation when the case-control ratio was 1:99. Interestingly, the existing hybrid approach showed substantially inflated type I error rates when case-control ratios were extremely unbalanced (case-control ratio = 1:49 and 1:99). This may be due to the fact that the MAC-based method selection rule in the hybrid approach does not perform well under extremely unbalanced case-control ratios. When the case-control ratios were more extreme than 1:99, the robust SKAT and SKAT-O showed some inflation of type I error rates (Table S1). Simulation studies with 2 and 3 kb regions show that empirical type I error rates of robust SKAT-O are generally similar regardless of region length (Table S2). Additionally, when testing both common and rare variants, robust SKAT can control type I error rates well compared with unadjusted SKAT (Table S3). Overall, the type I error simulation results confirmed that the proposed robust approaches provide substantially improved type I error rates compared to the unadjusted and existing hybrid approaches.

Table 1.

Type I Error Rates of Unadjusted and Robust Versions of Burden, SKAT, and SKAT-O and Hybrid Method

Case: Control	Burden	Robust Burden	SKAT	Robust SKAT	SKAT-O	Robust SKAT-O	Hybrid SKAT-O
$\alpha ={10}^{-2}$
1:1	1.00	1.00	0.99	0.99	1.11	1.11	1.09
1:9	0.99	1.00	1.01	1.01	1.13	1.13	1.09
1:49	1.02	0.95	1.44	1.22	1.44	1.23	1.27
1:99	1.07	0.91	1.92	1.41	1.82	1.33	1.53
$\alpha ={10}^{-4}$
1:1	1.02	1.00	0.99	1.03	1.27	1.32	1.27
1:9	1.12	0.99	1.39	1.14	1.65	1.40	1.52
1:49	2.43	0.97	6.31	1.65	6.16	1.79	4.54
1:99	3.95	1.02	13.48	2.13	12.77	2.17	8.89
$\alpha =2.5\times {10}^{-6}$
1:1	1.11	1.03	1.24	1.54	1.38	1.38	1.40
1:9	1.29	0.77	2.47	1.45	2.51	1.49	2.23
1:49	6.88	1.06	28.27	1.91	23.70	1.98	16.69
1:99	16.34	0.90	89.53	1.81	71.32	1.60	42.59

A total of 10⁷ datasets of 1 kb regions were generated to estimate type I error rates. Each cell represents an empirical type I error rate divided by significance level $\alpha$. The sample size was 50,000.

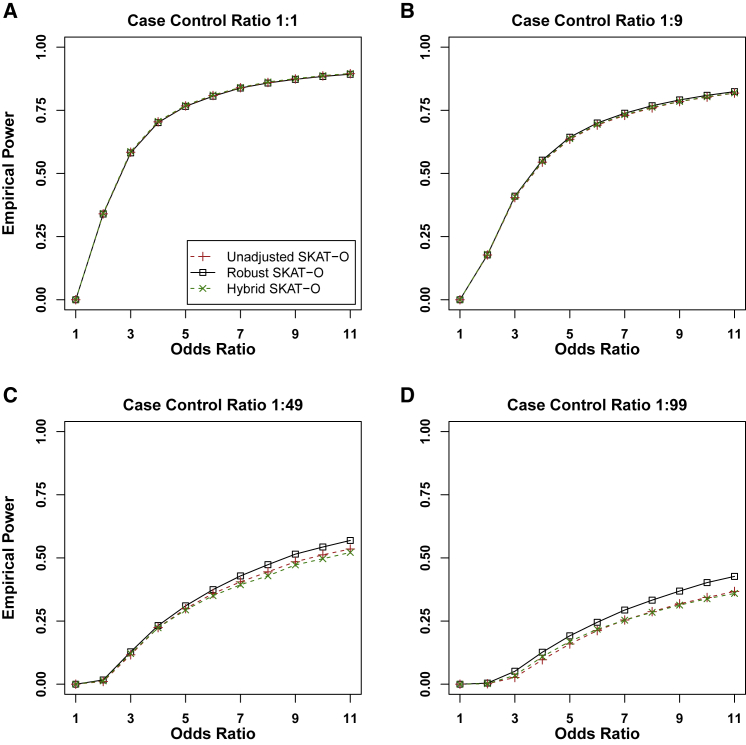
Figure 1 shows the empirical powers of the hybrid, unadjusted, and robust versions of SKAT-O methods, when 80% of causal variants were risk-increasing variants and 20% were risk-decreasing variants. The empirical powers of unadjusted and robust versions of the burden tests and SKAT can be found in Figure S3. Because unadjusted and hybrid methods had severely inflated type I error rates, for the fair comparison, we used the empirical significance level estimated from type I error simulation studies. Assuming that the type I error rates could be properly controlled for all methods, robust SKAT-O had similar power to that of unadjusted SKAT-O in balanced and moderately unbalanced case-control ratios (1:1 and 1:9) and was more powerful than unadjusted SKAT-O in extremely unbalanced ratios (1:49 and 1:99). Robust burden tests had the same power as unadjusted burden tests across all four case-control ratios. Robust SKAT had similar power to that of unadjusted SKAT in balanced ratios and was more powerful than unadjusted SKAT in unbalanced ratios. If the number of cases was fixed, more controls (1:49 and 1:99) increased power greatly compared to case-control ratio 1:1 for all three robust methods (Figure S1). In addition, we found that 1:99 had slightly more power than 1:49, where we could infer that 1:99 is sufficient to achieve the maximum power and more controls can hardly increase the power. The power simulation results with different region lengths (Figure S4) and power simulation results with all causal variants being risk-increasing variants (Figure S5) were quantitatively similar.

Figure 1.

Empirical Power Estimates for the Unadjusted and Robust Versions of Skat-O, and Hybrid Method

Power was calculated at the empirical $\alpha$ levels estimated from Type I error simulations with adjusting type I error rate at 2.5 × 10⁻⁶. A total of 10,000 datasets were generated with region length 1kb. 30% of variants were causal variants, and 80% of causal variants were risk-increasing while 20% were risk-decreasing. The sample size was 50,000. The x axis represents the genetic effect odds ratio, and the y axis represents the empirical power.

In summary, the robust methods had similar or more power than the unadjusted methods in all scenarios. Among the three robust methods, robust SKAT-O generally performed better than robust SKAT and robust burden tests because robust SKAT-O combined the two tests (Figure S6).

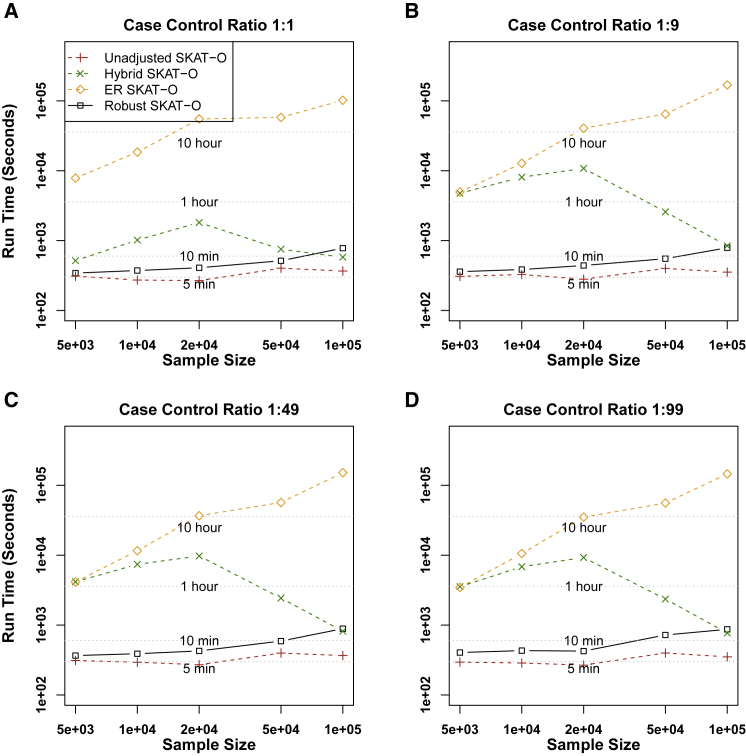
Comparison of Computational Times

To compare the computation times, we generated 1,000 datasets (Figure 2). Because SKAT-O combines the burden and SKAT tests, we only considered the SKAT-O test. As the sample sizes increased, the computation time of ER increased and required ∼16.1 CPU h for analyzing 1,000 genes for 50,000 individuals. In contrast, unadjusted methods required 140× less computation time (∼6.7 min), and the computation times barely changed based on sample size (5,000–100,000 individuals). Our robust method performed similarly to unadjusted SKAT-O (∼8.5 min). Because the hybrid approach selects its methods based on MAC and case-control ratios, the computation cost of the hybrid approach is not determined by the sample size. Overall, the hybrid approach was slower than the proposed method. The computation time for analyzing UK Biobank data of 791 binary phenotypes with robust SKAT-O was 453 CPU days, i.e., ∼13.7 CPU h per one phenotype.

Figure 2.

Comparison of Computation Time of Unadjusted, Hybrid, ER, and Robust Approaches for SKAT-O

The rare-variant region-based tests were performed on randomly selected 1 kb regions of 1,000 resamples. The x axis represents the sample size and the y axis represents the run time of 1,000 resamples.

Analysis of WES Data in the UK Biobank

We applied six methods (unadjusted and robust versions of burden, SKAT, and SKAT-O) to the analysis of WES data in the UK Biobank. We restricted our analysis to the rare nonsynonymous and splicing variants with MAFs < 0.01 in exon regions. A total of 18,360 genes were analyzed based on 45,596 independent European samples across 791 binary phenotypes with at least 50 cases each. For phenotypes with case-control ratios more extreme than 1:99, we identified the ancestry-matched control samples to make the case-control ratios 1:99 (see Material and Methods).

With the cutoff of $\alpha =2.5\times {10}^{-6}$, unadjusted SKAT-O detected 73,723 significant associations, most of which would be false positives, while our robust methods detected 34 significant associations for the burden test, 99 for SKAT, and 111 for SKAT-O (Table S4). Because we were testing many phenotypes, the usual exome-based cutoff of $2.5\times {10}^{-6}$ could have produced spurious associations. Following Hout et al.,¹ we used a more stringent level $\alpha$ = 10⁻⁷, and we identified that 10 gene-phenotype pairs had robust SKAT-O p values smaller than 10⁻⁷ (Table 2). Among 10 phenotype-gene pairs, only two had a single SNP p value < 5 $\times {10}^{-8}$; this result indicates that gene- and region-based approaches are more powerful than single-variant analyses. For each gene, the top three smallest p value variants are reported in Table S5, and single-variant p values are presented in Figure S7. Quantile-quantile (Q-Q) plots for those 10 phenotypes show that unadjusted SKAT-O had greatly inflated type I error rates, but our robust approach provided relatively well-calibrated results (Figure S8).

Table 2.

Significant Gene-Phenotype Associations in the UK Biobank WES Data

Phenotype (PheCode)	Gene Name	Case: Control	Number of SNPs	Case MAC	Control MAC	Robust SKAT-O p Values	Lowest P SNP	Conditional p Value (SKAT-O)	p Value of the Most Significant Nearby Variant
Myeloproliferative disease (200)	JAK2	94:9,306	73	27	442	1.36E-33	1.81E-41	1.06E-35	2.30E-17
Unspecified monoarthritis (716.2)	OGG1	1728:41,060	117	118	1643	7.73E-09	4.67E-04	7.79E-09	4.28E-04
Menopausal and postmenopausal disorders (627)	NFE2L3	1345:21,226	171	145	1358	2.54E-08	2.72E-05	3.94E-08	2.14E-04
Cancer of prostate (185)	HOXB13	741:18,940	37	18	154	3.00E-08	5.24E-08	2.50E-08	1.17E-04
Other aneurysm (442)	P3H1	164:16,236	110	17	497	5.76E-08	1.71E-05	4.03E-07	1.22E-03
Heartburn (530.9)	USP45	189:18,711	103	24	649	6.34E-08	5.39E-05	1.46E-09	4.08E-02
Fracture of hand or wrist (804)	GSDMC	382:37,818	109	25	761	7.12E-08	8.17E-05	1.49E-07	1.84E-02
Congenital coagulation defects (286.1)	F11	76:7,524	38	8	84	7.40E-08	4.52E-05	4.09E-08	6.30E-03
Congenital anomalies of great vessels (747.13)	SLC46A1	134:13,266	28	11	255	9.38E-08	1.86E-08	3.87E-08	2.29E-03
Peptic ulcer (excl. esophageal) (531)	LMNB2	773:44,818	171	24	508	9.89E-08	3.83E-06	9.54E-08	1.31E-03

Lowest P SNP means the lowest p value of all single variants contained in the gene-phenotype association. Conditional p value (SKAT-O) means the robust SKAT-O p value after conditioning on the most significant nearby common variant (±100 Kbp up- and downstream). p value of the most significant nearby variant was from SAIGE single-variant analysis results¹⁵ of the UK Biobank imputed datasets of 400,000 British samples.

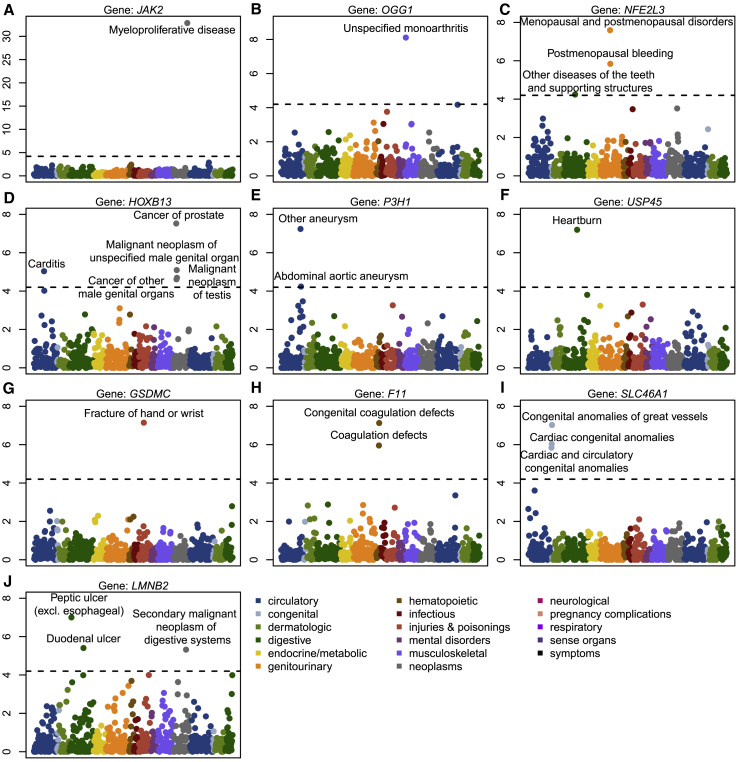
Rare-variant associations between JAK2 and myeloproliferative disease (number of cases = 94),²³ and HOXB13 (MIM: 604607) and prostate cancers (MIM: 610997) (number of cases = 741)²⁴ have been previously reported, which demonstrates that our analysis can replicate known signals even when the number of case samples is very small. A PheWAS plot of HOXB13 shows that there is an additional association signal between HOXB13 and Carditis (p value = 9.18 × 10⁻⁶) (Figure 3), and this may be due to the fact that Carditis is a complication of prostate cancer biopsy and treatment.²⁵

Figure 3.

PheWAS Plots of 10 Rare-Variant Associations with p Value < 10⁻⁷

The x axis represents 791 binary traits, and the y axis represents the negative log10 p values. The dashed line represents the cutoff of 0.05/791 = 6.32 × 10⁻⁵.

Among other genes, P3H1 (MIM: 610339), also known as Prolyl 3-Hydroxylase 1, was observed to be associated with other aneurysm (p value = 5.76 × 10⁻⁸) and possibly associated with abdominal aortic aneurysm (p value = 5.79 × 10⁻⁵). P3H1 is involved in collagen metabolism and was found to be present in the pulmonary artery.²⁶ F11 (MIM: 264900), also known as Coagulation Factor XI, was observed to be associated with congenital coagulation defects (p value = 6.13 × 10⁻⁸), and this observation is consistent with the fact that Factor XI participates in blood coagulation as a catalyst in the conversion of factor IX to factor IXa in the presence of calcium ions.²⁷ SLC46A1 (MIM: 611672), which encodes a transmembrane folate transporter protein, is associated with congenital anomalies of great vessels (p value = 9.38 × 10⁻⁸), and this is consistent with the role of folate in cardiovascular disease.²⁸ PheWAS shows the close association between SLC46A1 and two other blood diseases: cardiac congenital anomalies (p value = 9.16 × 10⁻⁷) and cardiac and circulatory congenital anomalies (p value = 1.44 × 10⁻⁶).

We carried out conditional analysis to evaluate whether the rare-variant association signals were independent of the nearby common variant association signals (±100 Kbp up and down stream) (Table S6). To identify most significant nearby variants, we used SAIGE single-variant analysis results of the UK Biobank imputed datasets of 400,000 British samples.¹⁵ All 10 associations remained significant after the conditional analysis (Table 2).

We have generated summary statistics for all gene-phenotype association results by using our robust approach, and we have made those summary statistics available in a PheWEB-like visual server (see Web Resources).

Discussion

In this paper, we present a robust approach that can address case-control imbalance in region-based rare-variant tests. The proposed approach uses recently developed ER and SPA to calibrate the variance of single-variant score statistics to accurately calculate region-based p values. The computation cost of the proposed approach is similar to that of the unadjusted approach; this makes our approach scalable for large analysis. Simulation studies show that unadjusted methods suffer severe inflation of type I error rate in unbalanced case-control ratios but also show that robust methods can successfully address it. The UK Biobank exome data analysis shows that the method provides calibrated p values and contributes to the identification of true association signals.

The proposed robust methods combine SPA and ER to recalibrate variances of single-score statistics. SPA can be thought of as a higher-order asymptotic approach with error bound $O\left(n^{-3/2}\right)$,⁵ where n is the sample size, which is much smaller than the error bound of normal approximation, $O\left(n^{-1/2}\right)$. However, SPA is still asymptotic-based and cannot perform well when MAC is small. Because ER is a resampling-based approach and can calculate the exact p value when MAC is small, it can complement SPA.

Our UK Biobank WES data analysis of 45,596 European samples and 791 binary phenotypes has identified 10 rare-variant associations with p value < 10⁻⁷, including the replication of two known signals. Currently UK Biobank is carrying out WES for 500,000 individuals. Our analysis presents an early snapshot of the discoveries that can be made with full UK Biobank samples.

All the UK Biobank analysis summary statistics are publicly available and so can be a useful community resource to show detailed results of the UK Biobank. Due to the large scale of the data, for labs not specialized in big data analysis, it is very challenging to analyze UK Biobank exome data. The analysis results will make the data more accessible and facilitate the identification of the genetic bases of complex diseases. For example, researchers could utilize our results for meta-analysis to combine samples from different studies. Our results can also be used to validate novel signals from other studies.

There are several limitations to the proposed method. Currently, the robust methods require that all individuals are unrelated. Restricting analysis to unrelated samples reduces sample size and case counts in many situations.²⁹ For example, some rare phenotypes within a health system may be clustered in a few families. Analysis based on independent samples may significantly decrease the power. When there are related individuals, generalized linear mixed model (GLMM) based approaches^15,30 should be used to incorporate the relatedness. Recently Chen et al. developed an efficient mixed-effect model approach for gene-based tests,³¹ and Zhou et al. expanded scalable single-variant GLMM to gene-based tests that can handle the full size of the UK Biobank data of 500,000 samples.³² Since these methods are also based on single-variant score statistics, the robust approach can be applied to them with modifications for GLMM. We leave it for a separate work. Second, when the case-control ratios are more extreme than case: control = 1:99, the method suffers type I error inflation. Because of this, our UK Biobank exome analysis used the matching scheme in which, if the case-control ratios are more extreme than 1:99, we use the matching to reduce the number of controls. Third, novel findings are not validated from independent datasets, so we cannot rule out the possibility that they are false positives. Lack of replication can be alleviated as more sequencing studies are conducted in biobanks.

In summary, we have proposed a robust region-based method and showed that the method can accurately analyze UK Biobank exome data. With the continuous decrease of sequencing cost and a growing effort to build large biobanks and cohorts,³³ rare-variant association analysis will be increasingly applied to binary phenomes. Our method will provide accurate results for binary phenome analysis and contribute to identifying the role of rare variants in complex diseases.

Declaration of Interests

The authors declare no competing interests.

Published: December 19, 2019

Web Resources

• OMIM, https://www.omim.org

• Robust gene-based test, https://github.com/leeshawn/SKAT/tree/Sparse_Version

• SKAT (version 1.3.2.1), https://cran.r-project.org/web/packages/SKAT

• UK Biobank, https://www.ukbiobank.ac.uk/

• UK Biobank analysis results (gene-based test for binary phenome), http://ukb-50kexome.leelabsg.org/

• Unified medical language system, https://www.nlm.nih.gov/research/umls