Computational Approaches for Inferring 3D Conformations of Chromatin from Chromosome Conformation Capture Data

Abstract

Chromosome conformation capture (3C) and its variants are powerful experimental techniques for probing intra- and inter-chromosomal interactions within cell nuclei at high resolution and in a high-throughput, quantitative manner. The contact maps derived from such experiments provide an avenue for inferring the 3D spatial organization of the genome. This review provides an overview of the various computational methods developed in the past decade for addressing the very important but challenging problem of deducing the detailed 3D structure or structure population of chromosomal domains, chromosomes, and even entire genomes from 3C contact maps.

INTRODUCTION

Eukaryotic chromosomes are made up of chromatin, a fibrous complex of DNA and histone proteins.¹ Understanding how the chromatin fiber is spatially organized inside the cell nucleus has become an increasingly important topic of study.^2-4 The reasons for the growing interest include: a greater appreciation for the biological roles of chromatin organization in all cellular and nuclear processes;⁵ an increasing numbers of cancers,^6-8 developmental defects,^{9, 10} and neurological disorders^{11, 12} being linked to defects in chromatin organization; and recent developments in powerful microscopy and DNA sequencing technologies providing a wealth of new data.^13-16 The most obvious role of chromatin organization is in packaging the enormously long genomic DNA into the tiny confines of the cell nucleus, while enabling ready access to genes and regulatory elements on demand.^{17, 18} Chromatin organization also plays critical roles in DNA transcription and recombination by bringing into proximity multiple functional DNA elements that are otherwise distant on the DNA sequence. Two striking illustrations of such long-range interactions, mediated by chromatin looping, include the classical case of promoter-enhancer interactions required for initiating transcription¹⁹ and the fascinating rosette-like organization of the immunoglobulin heavy chain locus that appears in developing B-cells to facilitate V(D)J recombination.^{20, 21} Lastly, chromatin organization enables physical segregation of genomic elements based on their function. For instance, mammalian genomes are organized into topologically associating domains (TADs) harboring common epigenetic marks at the 100 kb to 1 Mb scale,^22-24 into tissue-specific compartments of active and inactive chromatin at ~5 Mb scales,^25-27 and into the well-known chromosome territories at the largest scale.²⁸

Biology has traditionally relied on light and electron microscopy for studying intracellular organelles and structures. However, these approaches are not ideal for visualizing the 3D organization of chromatin in vivo, owing to the low, diffraction-limited resolution of light microscopy (~200 nm) and to the highly invasive and non-specific nature of electron microscopy.²⁹ Typically, chromatin folding has been visualized by multicolor fluorescence in situ hybridization (FISH), which can simultaneously provide the 3D positions of multiple genomic loci separated by >100 kb along DNA sequence or >200 nm in space,³⁰ though discerning the folded configuration of chromatin remains challenging. While limitations in resolution can be overcome by super-resolution microscopy techniques,^{31, 32} these lack the throughput necessary to study more than a few chromatin regions at once.

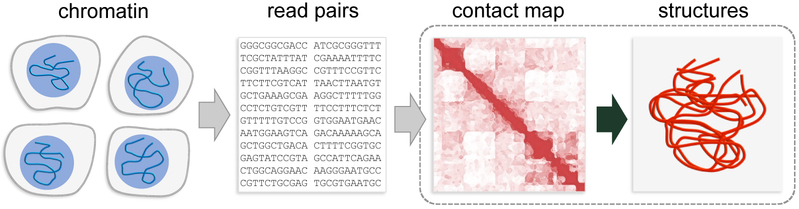
A recently developed set of experimental methods, known as chromosome conformation capture (3C), has enabled researchers to study chromatin interactions and conformations at an unprecedented resolution and throughput (Fig. 1).^{33, 34} These methods begin by treating the chromatin inside cell nuclei with chemicals like formaldehyde. In this manner, DNA loci that are in close spatial proximity to each other become cross-linked, typically via intervening proteins. Next, the cross-linked DNA is digested using a restriction enzyme, yielding two kinds of DNA fragments: isolated and cross-linked fragments, with only the latter kind containing information about the interacting genomic loci. These loci are identified and quantified from the cross-linked fragments through a series of biochemical and bioinformatic steps. Then, by counting the number of times that each pair of loci is observed in cross-linked fragments collected from millions of cells, one can construct a 2D contact map that quantifies the frequency of interactions between all pairs of loci. While the original 3C method detected interactions between only a few preselected pairs of loci,³⁵ the latest and most advanced 3C variant, known as Hi-C, takes advantage of high-throughput sequencing to provide a comprehensive map of interactions across the entire genome at resolutions of up to ~1 kb.^{36, 37} Importantly, because the frequencies of interactions between genomic loci must on average be related to their spatial proximity in some reciprocal manner, the contact maps also contain valuable information about the 3D conformation of the underlying chromatin fiber. Inferring such structural information from contact maps is however a challenging task, because many unknowns are associated with the underlying chromatin fiber, including its physical properties, its variability across populations of cells, and the uncertainties in the measured contact counts, and because of the high dimensionality of the configurational space. To tackle this multidimensional structure-determination problem, different strategies, assumptions, and approximations have been proposed to develop a variety of ingenious computational approaches, which have been described by many excellent reviews.^38-45

Figure 1:

Schematic of the overall pipeline for studying 3D organization of chromatin using 3C technology. The primary topic of this review article on computational methods for recovering 3D structure and structure populations of chromatin from 2D contact maps is highlighted by the dashed box. The maps themselves are generated from the sequences of read pairs, which are in turn collected from crosslinked chromatin in a large ensemble of cells.

In this review, we provide our perspective on these computational approaches, which can be generally categorized into three classes. The first class assumes a functional relationship between spatial distance and interaction frequency, enabling the optimization of chromatin conformation directly in the distance space. The second class does not invoke any such functional relationship, but uses polymer models to directly predict chromatin interactions, thus enabling the optimization of structures in the interaction frequency space. The third class also uses a distance-frequency relationship, but describes the measured interaction frequencies in probabilistic terms, thus enabling the optimization of structures within the statistical parameter space. The three classes of approaches are not completely mutually exclusive, as some approaches aptly combine features of different classes. For instance, some aspects of polymer modeling may also be used in the first and third class of methods. Nevertheless, such classification serves to organize the several possible components of a computational protocol for obtaining 3D chromatin conformation from 3C data. This review article does not cover other interesting aspects of 3C experiments, such as the experimental protocols, the computational pipelines for generating contact maps, and the vast amount of chromosome biology and physics learnt from such maps using de-novo polymer models. For information on these topics we refer the reader to several pertinent reviews.^46-52

PROBLEM DEFINITION

All computational methods considered in this review take as input a 2D contact map and generate as output one or more 3D conformations of chromatin. Before describing these methods, we define their input and output in mathematical terms.

Hi-C experiments can generate up to ~10⁹ sequence reads.⁵³ However, even such large numbers of reads are insufficient to cover all possible inter-fragment interactions, whose number is much larger. For instance, the MboI enzyme generates ~10⁶ fragments from the human genome, involving ~10¹² possible inter-fragment interactions. Therefore, contact maps are typically constructed by dividing the genome into “bins” that are larger than the fragments⁴⁶ Interactions are then counted across genomic bins rather than fragments. Denoting the total number of bins by N, a Hi-C contact map is represented as a symmetric N × N matrix

$$\mathbf{C}\equiv \left[\begin{array}{ccc}\hfill c_{11}\hfill & \hfill \dots \hfill & \hfill c_{1N}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill c_{N1}\hfill & \hfill \dots \hfill & \hfill c_{NN}\hfill \end{array}\right]$$ (1)

where c_ij represents the count of fragment pairs with one fragment in bin i and the other in bin j. The contact maps are then corrected for various experimental biases such as those arising from sequence mappability, density of restriction sites, and GC content.⁵⁴ The contact maps of 3C and 5C experiments, which probe only selected pairs of interactions and can afford to probe them at much higher precision, are however best described in terms of the original inter-fragment interaction counts.⁵⁵ In 5C, which relies on distinct sets of forward and reverse oligonucleotide probes that may also differ in numbers, only interactions between fragments associated with oppositely oriented primers can be probed, and hence the contact matrix is no longer symmetric and is also not square in most cases. Nevertheless, the computational approaches developed for Hi-C maps may be adapted for maps obtained from 3C and 5C, and vice versa, as long as differences in the definition and resolution of the interacting loci (fragments versus bins) between the two types of techniques are taken into account.⁵⁶ The contacts in Eq. 1 are often converted to interaction frequencies (IFs) or contact probabilities via f_ij = c_ij/∑_i,jc_ij and the resulting “normalized” matrix is denoted by F.

Given a contact map C, or F, as input, the desired computational output consists of one or more 3D conformations of the chromatin fiber that are consistent with that contact map. One such conformation, or structure, can be described by a 3 × N matrix

$$\mathbf{R}\equiv [{\mathbf{r}}_1,{\mathbf{r}}_2,\cdots ,{\mathbf{r}}_N]$$ (2)

where r_i ≡ [x_i,y_i,z_i]^T represents the position vector of genomic bin i = 1,…,N in terms of Cartesian coordinates.

DISTANCE-OPTIMIZATION METHODS

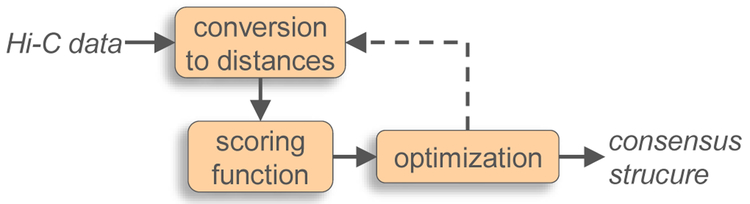
The underlying idea in these methods is to convert the contact frequencies f_ij in the contact map into suitable spatial, or Euclidean, distances δ_ij between the interacting loci, and then determine the locus coordinates r_i of the chromatin conformation whose internal Euclidean distances d_ij ≡ ∣r_i – r_j∣ best match the target distances δ_ij derived from the maps. The single solution for the chromatin conformation obtained in this manner is often referred to as the “consensus structure” (Fig. 2).

Figure 2:

General scheme for computational methods that rely on distance-optimization to generate a consensus structure that is consistent with an experimental contact map. Blocks represent the main components common to these methods. Arrows represent the main flow of information. Not all methods attempt to optimize the parameters of the relation used to convert contact frequencies into inter-locus distances.

There are two key assumptions inherent in these methods. The first deals with the existence of a functional relationship for converting frequencies into distances. Certainly, such relationships are available for simple models of polymers. For instance, in ideal chains, where segments are connected by freely-rotatable joints, the frequency f_ij of overlap of two segments i and j decays as $f_{\mathit{ij}}~s_{\mathit{ij}}^{-3∕2}$ with respect to their separation s_ij ≡ ∣i – j∣ along the chain, while their spatial distance increases as $d_{\mathit{ij}}~s_{\mathit{ij}}^{1∕2}$.⁵⁷, ⁵⁸ Combining the two results yields the simple inverse relationship $d_{\mathit{ij}}~f_{\mathit{ij}}^{-1∕3}$ between frequency and distance. Chromosomes are however considerably more complex than ideal chains due to energetic interactions and heterogeneity of the underlying chromatin fiber and due to confinement and molecular crowding effects. Furthermore, the interactions observed in 3C maps arise not only from random collisions between loci, but also from protein-mediated loops with unknown lifetimes. The d_ij-f_ij relationship in chromosomes is generally far too complex to be described by any tangible model. Nevertheless, studies have employed various functions to at least capture the reciprocal dependence of locus distances on frequency, often with adjustable parameters to obtain the best agreement with experimental data.

The second assumption is that the obtained consensus structure is a reasonable approximation of the “average” conformation of chromatin exhibited by the ensemble of cells from which the 3C data were derived. Chromosomes, on the other hand, are highly dynamic entities and the conformation of chromatin likely varies from cell to cell. This conclusion may in fact be directly deduced from the non-binary nature of the interaction frequencies.⁴⁹ Nonetheless, consensus structures may still provide valuable information on the overall structure of chromosomes, and on differences in chromosome organization between different populations of cells examined by 3C.

Scoring Function and Constraints.

The consensus structure is obtained by minimizing the deviation of its internal distances d_ij from the corresponding distances ${\delta }_{\mathit{ij}}=\mathcal{F}(f_{\mathit{ij}})$ inferred from the 3C contact map via a suitable function $\mathcal{F}$ that converts frequencies to distances. In its simplest formulation, this deviation is quantified as a weighted sum of squares of the individual deviations of the internal distances from the distance restraints

$$S(\mathbf{R})={\sum }_{i=1}^{N-1}{\sum }_{j=i+1}^N{w}_{ij}(d_{ij}-{\delta }_{ij}{)}^2$$ (3)

where w_ij are weights and S(R) is the objective or scoring function that needs to be minimized to attain the consensus structure denoted by R₀. Without w_ij, the scoring function would be dominated by pairs of loci with large δ_ij. Since the largest distances are inferred from the smallest f_ij values, the largest δ_ij represent the least reliable inter-locus distances. Thus, to ensure that the scoring function is appropriately weighted based on the reliability of each restraint, w_ij should ideally decrease with δ_ij (or increase with f_ij). A popular weighting function is $w_{\mathit{ij}}=1∕{\delta }_{\mathit{ij}}^2$, ^59-61 though w_ij = 1/δ_ij,⁶² w_ij = 1,^63-65 and w_ij ∝ ∣Zscore(f_ij)∣^p, with p = 0.5 or 2,^{66, 67} have also been used. Interestingly, the latter approach assigns larger weights to frequencies that deviate from its average value in the map, irrespective of whether f_ij is smaller or larger than the average. Instead of using a functional form for w_ij(δ_ij), one approach used two different values of w_ij, a large value for all δ_ij smaller than some cutoff distance and a small one for larger distances.⁶⁸ In some cases, the nature of the weighting function is restricted by the optimization approach. For instance, the multidimensional scaling approach discussed below generally requires w_ij = 1,^{45, 69, 70} though using log-transformed distances may allow $w_{\mathit{ij}}=1∕{\delta }_{\mathit{ij}}^2$ to be used.⁷¹ The quadratic form of the above scoring function implies that even small deviations of the structure from the targeted distances δ_ij get penalized. Hence, any uncertainties in the function $\mathcal{F}$ used to derive the δ_ij’s propagate to the obtained consensus structure. To alleviate some of the inherent bias introduced through the uncertain function $\mathcal{F}$, several approaches have attempted to use “flat-bottomed” restraints that do not penalize deviations from δ_ij until they become larger than a cutoff.^72-74 Another approach devised a bell-shaped Lorentzian scoring function that assigns larger weights to consistent distance restraints whose values are not affected by the violation of inconsistent restraints.⁷⁵

The scoring functions discussed above constrains the path of the chromatin fiber based purely on the distance restraints obtained from 3C data. However, because of the two assumptions and the data reliability issues discussed above, the consensus structures obtained after optimization may not be physically or biologically realistic. In addition, as this scoring function lacks an associated length scale, all structures proportional to R₀ are equally valid solutions. Hence, the scoring function is often accompanied by additional structural constraints based on physical properties of chromatin and biological data. Chain connectivity and excluded volume represent two commonly implemented physical constraints. The first constraint, which accounts for the physical connectivity of adjacent loci i and i + 1, is usually implemented as an upper-bound limit d_max on the spatial distance between the two loci given their lengths and the linear density of chromatin.^{61, 63, 72} The second constraint, accounting for the excluded volume of each locus, is typically implemented as a lower-bound limit d_min on the spatial distance between all locus pairs i and j, where d_min is either the diameter of the chromatin fiber for high-resolution structures, or a suitable larger value for coarser models.^{63, 72, 73, 76} Two common biological constraints include confinement and position restraints. The confinement constraint ensures that every locus in the genome is located inside the cell nucleus, usually approximated as a sphere of size consistent with that obtained from microscopy.^{61, 63} Confinement constraints may also be imposed on individual chromosomes, as they are known to occupy specific territories within the nucleus.²⁸ In this case, the size of the confinement domain may be obtained from whole-chromosome FISH painting or estimated by scaling down the size of the nucleus with the ratio of the chromosome to genome length.⁶⁰ Microscopy also provides information on the positioning of specific chromosomal regions, such as centromeres, telomeres, and lamin-associated domains, thus allowing related constraints to be implemented.^{61, 63, 76}

Frequency-Distance Conversion.

The relationship used for converting frequencies into distances plays a key role in these methods. The simple relationship ${\delta }_{\mathit{ij}}=\gamma f_{\mathit{ij}}^{-1∕3}$ obtained from the polymer physics of ideal chain and fractal-globule models provides one possible option.^{61, 73} A softer version of this inverse relationship, δ_ij = γ/f_ij, has also been used, especially in some of the earlier methods.^{59, 63} The unknown prefactor γ that sets the scale of the system is generally chosen or optimized so that the strongest frequencies yields an appropriate contact distance, e.g., thickness of chromatin fiber, or that the resulting structure exhibits a more or less uniform density in the nucleus.⁶¹ Recognizing that chromosomes are complex and likely not to follow any single, tangible relationship between frequency and distance, many recent methods have begun to use a more open relationship ${\delta }_{\mathit{ij}}=\gamma f_{\mathit{ij}}^{-\alpha }$, where parameter α is used as an unknown parameter that also needs to be optimized.^{62, 65, 75, 77-79} Values of α obtained in this manner have been found to range between 0.5 and 1.4, highlighting the variable and complex nature of chromatin. Extending the concept of variability even further, one study assigned locus-dependent α’s to account for the tendency of some loci to co-cluster.⁸⁰ Several approaches have also considered using linear relationships, e.g., δ_ij = −mf_ij +c (with m > 0), to only assign $\mathcal{F}$ within a select range of frequencies deemed to be sufficiently reliable.^{60, 66}

A more robust alternative to assuming relationships for $\mathcal{F}$ is to derive such a function directly from a combination of 3D-FISH and 3C measurements, which respectively provide inter-locus distances and corresponding interaction frequencies. Such a strategy has been used by several researchers,^{64, 67, 70, 81} yielding various different kinds of calibration curves. In some cases, the δ_ij vs. f_ij data could be well described by the power-law function ${\delta }_{\mathit{ij}}~f_{\mathit{ij}}^{-\alpha }$ with α = 0.25⁷⁰ and α = 0.39–0.49,⁸¹ while in other cases it was better described by a decaying exponential function⁶⁴ and a 5th-degree polynomial.^{67, 82} An alternative approach is to derive the embedding function itself during optimization via nonlinear dimensionality reduction.^{69, 83} One of these studies⁶⁹ recovered a reciprocal relationship between δ_ij and f_ij that could in fact be described by the power-law ${\delta }_{\mathit{ij}}~f_{\mathit{ij}}^{-\alpha }$. However, the recovered exponent α was found to vary across different Hi-C data sets, attesting to the large variability in chromatin behavior or in Hi-C experiments, and to the inaccuracy inherent in using a single function $\mathcal{F}$.

Structure Determination.

The last aspect of these approaches involves optimizing chromatin conformation by minimizing the scoring function, often subject to the additional constraints mentioned earlier. A variety of optimization approaches have been employed, which may be roughly classified into two categories: (i) methods that use classical numerical optimization algorithms, which smartly traverse the multidimensional vector space R to locate the global minimum R₀, and (ii) methods that use the established mathematical formalism of multidimensional scaling to obtain R₀ through matrix algebra operations.

Classical numerical optimization offer flexibility, easy integration of a wide variety of weights and constraints, and the opportunity to observe intermediate structural solutions. While gradient-descent (or gradient-ascent) optimization provide a simple and efficient approach for optimizing scoring functions containing a few distance restraints and no constraints,^{59, 74, 75} more sophisticated optimization methods are required when analyzing contact maps involving hundreds of loci (bins) with an even larger number of constraints. A number of studies have used the open-source IPOPT software for such optimization.^{63, 64, 68, 80} IPOPT is an interior-point gradient-based algorithm that is especially adept at tackling high-dimensional, nonlinear constrained optimization problems.⁸⁴ Another commonly used optimization approach is simulated annealing.⁸⁵ Here, the loci are represented by particles that interact with each other via harmonic potentials representing each of the distance restraints, i.e., particles i and j interact with a harmonic spring of equilibrium length δ_ij and spring constant 2w_ij, whereupon the scoring function simply becomes the total energy of this system of interacting particles. The particle positions are sampled stochastically or deterministically using Monte Carlo (MC)^{66, 82, 86} or molecular dynamics (MD)^{65, 72, 73} simulations at a fictitious temperature. This temperature is set to a high value at the beginning of the simulation and is gradually lowered in steps during the simulation, enabling both rapid exploration of the configuration space and increased chance of trapping a configuration at or at least near the global minimum. In addition, multiple copies of simulations are performed to collect many possible candidates for the global minimum. Such candidates can then be clustered based on structural similarity to identify the consensus structure.⁶⁶ While external constraints are easily handled in MC methods, they typically need to be converted into stiff potentials and moved into the scoring function in MD simulations.

Multidimensional scaling (MDS)⁸⁷ provides a more elegant and efficient alternative to determining the consensus structure, though this approach works best with quadratic scoring functions without constraints and with equal weights. Given a complete set of pairwise distances between points in some vector space of high dimension K, MDS allows one to infer the vector coordinates of those points in a space of dimension k ≤ K so that the cumulative deviation in the inferred distances from the given distances is minimized. This approach has found applications in sensor network localization⁸⁸ and in determining molecular structures based on interatomic distances obtained from nuclear magnetic resonance.⁸⁹ More recently, MDS has been use to determine chromatin conformations that best satisfy distance restraints. While the most general forms of MDS scoring, or stress, functions require numerical algorithms known as stress majorization to obtain optimal structures,⁹⁰ the simplest form of MDS (with w_ij = 1) can be solved algebraically. This involves formulating a suitably centered N × N “Gram” matrix from distances δ_ij inferred from the contact map, and then determining the largest three eigenvalues and corresponding eigenvectors of the Gram matrix. Simple rescaling of normalized eigenvectors by the square-root of their corresponding eigenvalues then yields the desired consensus structure.⁴⁵ Such an approach was first applied by the developers of the original 3C technique on the limited number of interactions they obtained.³⁵ Since then, the approach has been applied to the more exhaustive Hi-C contact maps, which pose additional challenges. One of the main challenges in dealing with Hi-C data, especially from single cells, is that the contact maps are often quite sparse, i.e., contain many zero c_ij’s. Furthermore, due to low reliability of some interactions, pairs of inferred distances may not satisfy the triangle inequality (δ_ij + δ_jk ≥ δ_ik for any loci i, j, and k). Hence, significant efforts have been devoted to assigning more reliable distances to missing or low frequency data using shortest-path approaches (e.g., the Floyd-Warshall algorithm) adopted from graph theory,^{45, 78, 91} recurrence plots adopted from non-linear time-series analysis,⁹² and regularization terms that account for missing data.⁶² Another strategy for dealing with map sparseness is multi-staged implementation of MDS, where MDS is first applied at high resolution to strongly interacting domains with large c_ij, e.g., TADs, and then applied at a lower resolution to weaker interactions across these domains.⁷⁰ Researchers have also begun to consider optimization on distance manifolds to reduce the importance of distances derived from low frequencies⁸⁶ or to entirely eliminate the use of the function $\mathcal{F}$.^{69, 83}

POLYMER PHYSICS-BASED METHODS

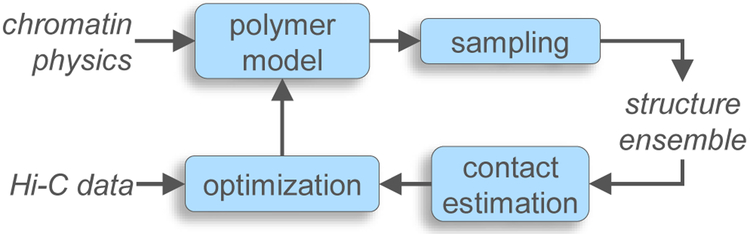
Approaches based on polymer physics involve optimizing the parameters of a polymer-chain model of the chromatin fiber, whose conformational ensemble best recapitulates the experimentally-derived 3C contact maps. As shown in Fig. 3, such “training” of the model is usually accomplished via an iterative process involving three components: a polymer model, a sampling algorithm, and a parameter optimizer. The polymer model captures the physical properties of chromatin fiber, using a few known and unknown parameters. The sampling algorithm generates a thermodynamic ensemble of chromatin conformations consistent with the parameters of the model. These conformations are used for generating a “predicted” version of the contact map. The parameter optimizer compares the predicted map against the experimental map to suggest parametric refinements to the model in order to improve the agreement between the two maps. This process is repeated until the best possible agreement is achieved. Since all information about inter-locus interactions is embedded in the polymer model, which is assumed to accurately capture the conformational behavior of the chromatin fiber, these methods do not need to invoke any specific functional relationship between spatial distance d_ij and interaction frequency f_ij. Furthermore, it is not necessary to generate conformations that are individually consistent with the contact map; only the conformation ensemble as a whole should be consistent. Therefore, these approaches by construction incorporate variability in chromatin structures and interactions across members of the conformational ensemble, mimicking the population nature of the interactions derived from 3C experiments.

Figure 3:

General scheme for computational methods that use polymer physics to generate an ensemble of structures that is consistent with an experimental contact map. Blocks represent the main components common to these methods. Arrows represent the main flow of information.

Polymer Model.

The interaction frequencies probed by the 3C method arise from a combination of specific interactions, usually attributed to protein-mediated looping of chromatin, and non-specific interactions, associated with random collisions between loci. A polymer model representing chromatin should capture both kinds of interactions in its ensemble of conformations.

The frequencies of non-specific interactions between loci are dictated by the separation distance between the loci along the chromatin fiber, by the physical properties of the fiber, and by its confinement. Each of these effects can be captured in a bead-chain model, where each bead represents a segment of the chromatin fiber. Usually the beads represent segments of fixed length, which can be as short as ~3 kb^93-95 to as long as ~500 kb,⁹⁶ depending on the desired resolution. Adjacent beads along the fiber are connected by rigid bonds,^{94, 95} harmonic springs,^{93, 97} or finite extensible nonlinear elastic springs^98-100 to account for the stretching resistance of the fibers. Such “connectivity” restraints are already sufficient to produce polymer-like conformations. Chromatin fibers, however, are also resistant to bending, and their bending rigidity is often treated using harmonic⁹³ or cosine potentials⁹⁹ in the bending angle subtended by three adjacent beads along the fiber. The excluded volume of the beads prevents them from penetrating each other, and can be represented by hard-sphere¹⁰¹ or short-range repulsive potentials^{93, 99} between non-adjacent beads. The above polymer representation is often referred to as the self-avoiding wormlike chain (SA-WLC). Confinement effects arising from nuclear boundaries can also be incorporated using excluded-volume potentials.^{95, 96, 98, 99} When modeling individual chromosomes or chromosomal domains, these confinement effects may arise from other chromosomes or domains whose boundaries are not known. Such unknown effects can be implicitly included in the models for specific interactions.

The choice of interaction potentials depends on the resolution of the model. At high resolutions, where beads represent the actual thickness of the chromatin fiber, i.e., ~30 nm, stiff bonded and excluded-volume potentials are used. Since the bead sizes are shorter than the persistence length of chromatin, a bending potential is also required to obtain realistic fiber conformations.⁹³ Most parameters in these potentials can be fixed based on experimental estimates of chromatin thickness, elastic modulus, and persistence length.⁹³ At lower resolutions, where beads represent folded-up balls of the fiber, much softer bonded and excluded-volume potentials need to be used, and the bending potential becomes redundant.⁹⁷

The specific interactions arising from chromatin looping and the confinement effects described earlier are the primary unknowns of the model. These interactions can be approximated by looping restraints between pairs of beads. Possible implementations of the restraints include harmonic spring potentials,^{93, 101} a square-well potential,⁹⁴ or its smoother differentiable form.⁹⁸ Then, the unknown parameters, to be determined by the optimization procedure, are the locations of the looping restraints along the fiber, together with the stiffness and equilibrium lengths of the harmonic restraints, or the depth and width of the square-well restraints. These restraints can be established across all pairs of beads, thus counting on the optimization algorithm to identify the true looping partners, while converging the strengths of unnecessary restraints to zero values.^{94, 98} Alternatively, researchers have applied restraints only across those locus pairs exhibiting strong peaks in the contact maps.^{93, 95} To further reduce the number of adjustable parameters, the equilibrium lengths of the harmonic restraints are set to zero,⁹³ as excluded-volume interactions can enforce a minimum distance even between strongly looped segments, and the widths of the square-well restraints are often set to a physically reasonable value.⁹⁹

Conformational Sampling.

A key step in these methods involves generating at each optimization step an ensemble of bead-chain conformations consistent with its parameters at that step. In theory, a molecular system at equilibrium should exhibit conformations consistent with its thermodynamic state, or, more technically, its statistical-mechanical ensemble. In the canonical ensemble with fixed number of molecules, volume, and temperature, the probability ρ of observing a specific conformation R should follow the Boltzmann distribution ρ(R) ∝ exp ( −U(R)/k_BT), where U (R) is the total potential energy of the conformation, k_B is the Boltzmann constant, and T is the temperature. Whether chromosomes obey such a distribution or even represent an equilibrium system is debatable, but in the absence of any concrete alternatives, this distribution at least provides a useful starting point for obtaining physically-realistic conformations.⁹⁹ Ideally, to obtain the most realistic ensembles, U and T should be quantitatively described. This may however be unfeasible in the case of low-resolution models that use more ad-hoc energy potentials and temperature.^{96, 97}

Various sampling methods have been used in the context of generating Boltzmann-distributed conformations of chromatin. Monte Carlo (MC) simulations provide a computationally efficient and flexible strategy for sampling conformations.^{94, 95} In the most common implementation, the Metropolis-Hastings algorithm,¹⁰² conformations are sampled through simple trial “moves”, such as translation of randomly chosen beads, which are accepted with a probability P_acc = min [1,exp ( −ΔU/k_BT)], where ΔU is the change in the potential energy associated with each move. Such an approach, repeated over millions of trial moves, eventually yields the desired ensemble of conformations. However, this approach becomes inefficient for sampling the conformations of long polymer chains, especially those strongly confined and possessing looping restraints. More efficient sampling of chains has been achieved through biased regrowth of chains via geometric sequential importance sampling,⁹⁵ or through use of quaternions, instead of Euler angles, for implementing rotational moves on rigid clusters of beads within chains.¹⁰³ Molecular dynamics (MD) simulations provide an easily implementable approach for sampling conformations.⁹⁶ A number of freely-available MD simulation software such as LAMMPS¹⁰⁴ and GROMACS¹⁰⁵ work well with user-supplied interaction potentials. Other sampling methods such as Langevin dynamics⁹⁹ and Brownian dynamics simulations^{93, 97} provide a good compromise between efficiency and usability.

The sampled conformations are used to compute the predicted interaction frequencies denoted by ${\widehat{f}}_{\mathit{ij}}$. Though the spatial distance at which two segments of chromatin get crosslinked in 3C experiments is not known, it is reasonable to assume that crosslinking occurs at small distances on the order of the fiber diameter. By setting a reasonable distance threshold ξ for contact, typically 30 nm or smaller, ${\widehat{f}}_{\mathit{ij}}$ calculation simply boils down to counting the fraction of conformations in the ensemble with d_ij,k ≤ ξ, where d_ij,k is the shortest of the distances between pairs of beads representing loci i and j in structure k. In other words, ${\widehat{f}}_{\mathit{ij}}=\frac{1}{n}{\sum }_{k=1}^n\Theta (\xi -d_{\mathrm{ij},k})$, where Θ is the Heavyside step function and n is the size of the ensemble.^{93, 94} Some approaches use the smoother sigmoidal function for counting contacts.⁹⁹ Two particularly attractive approaches for obtaining ${\widehat{f}}_{\mathit{ij}}$ involves estimating them from distributions of inter-bead distances,¹⁰⁶ or their mean-square values,⁹⁷ which can both be more reliably measured from the ensemble than the direct counting method for loci exhibiting very small ${\widehat{f}}_{\mathit{ij}}$.

Parameter Optimization.

The last component in the optimization loop adjusts the parameters P^(m) of the polymer model (where m is the iteration number) based on differences in ${\widehat{f}}_{\mathit{ij}}^{(m)}$ predicted from the simulated conformations and the 3C map f_ij to obtain a new set of parameters P^{(m + 1)} that should achieve better agreement between the two maps in the next iteration. The optimization stops when the difference between the maps becomes smaller than some specified tolerance, yielding the desired ensemble of conformations.

The original 3C or ChIP-chip techniques can probe interactions between only a handful of loci. If the interactions are sufficiently independent of each other, i.e., changing one interaction does not influence other interactions, then the imposed looping restraints can be optimized independently via simple rules that increase or decrease a restraint strength when its predicted interaction frequency is weaker or stronger than the experimental counterpart. For instance, one study optimized the stiffnesses k_ij of harmonic restraints via $k_{\mathit{ij}}^{(m+1)}=k_{\mathit{ij}}^{(m)}{\left[\epsilon (f_{\mathit{ij}})∕\epsilon \left({\widehat{f}}_{\mathit{ij}}^{(m)}\right)\right]}^a$, where ε is an inverse error function and a is a parameter that governs the accuracy and speed of convergence¹⁰¹. The chosen function not only ensured that k_ij’s were correctly up- or down-scaled based on the relative magnitudes of the predicted and experimental frequencies, but that strong restraints were adjusted more aggressively than the weaker ones.

More formal approaches are required for carrying out optimization of systems involving the large numbers of interactions probed by 5C or Hi-C experiments, where interactions are also more likely to be correlated. This requires defining an error function $S(\mathbf{k})=\frac{1}{2}{\Vert \widehat{F}(k)-F\Vert }^2$ that quantifies the difference between the predicted and experimental maps, where k is a vector of all imposed restraint stiffnesses k_ij. The objective is then to minimize this error under the condition that all k_ij > 0. This is most naturally achieved through a gradient-descent algorithm wherein the stiffnesses are updated via k^{(m + 1)} = k^(m) −h ∇S^(m)/∥∇S^(m)∥, where h is a step size and ∇S^(m) is the gradient of the scoring function with respect to each restraint stiffness.⁹⁷ Alternatively, a reweighting scheme may be used to update restraint strengths, as done recently for optimizing the depths B_ij of square-well restraints.⁹⁴ Here, the existing ensemble of conformations is used for predicting how the existing set of interactions might change with small perturbations in B_ij via ${\widehat{f}}_{\mathit{ij}}^{(m)}={\sum }_{k=1}^n\Theta (\xi -d_{\mathrm{ij},k}^{(m)})\text{exp}(-\Delta E_k∕k_{B}T)∕{\sum }_{k=1}^n\text{exp}(-\Delta E_k∕k_{B}T)$, where ΔE_k is the change in the energy of all restraints in the k^th conformation in the ensemble due to the change in B_ij and Θ is the previously defined function for counting contacts. A Monte Carlo search in B_ij’s is carried out to minimize the deviation between the reweighted and experimental frequencies. These locally optimized parameters are then used in the next iteration to generate a new ensemble of conformations, and the process is repeated until convergence.

Instead of directly optimizing restraints, an alternative strategy involves optimizing the elements of a transformation matrix W that relates the interaction frequencies of the restrained pairs of beads to the strengths of their restraints via the linear relationship k = Wf.⁹³ The approach boils down to determining the elements of W that yield a set of restraint stiffnesses, such that the simulated ensemble of conformations using these stiffnesses reproduces the experimental interaction frequencies of the restrained loci. Within the optimization algorithm, this requires using the current elements of the matrix W^(m) to predict two sets of stiffnesses: one set is obtained from the experimental frequencies, via k^(m) = W^(m)f, and the other set is obtained from the frequencies of the current ensemble, via ${\widehat{k}}^{(m)}={\mathbf{W}}^{(m)}{\widehat{f}}^{(m)}$. The difference between the two stiffnesses ${\epsilon }^{(m)}={\mathbf{k}}^{(m)}-{\widehat{k}}^{(m)}$ is then used to update the matrix via the least mean-square algorithm: ${\mathbf{W}}^{(m+1)}={\mathbf{W}}^{(m)}+2{\mu }_m{\epsilon }^{(m)}\cdot {\widehat{f}}^{(m)}$, where μ_m is a “gain factor” that governs the stability and speed of convergence. The above iteration is repeated until the matrix predicts similar stiffnesses from the predicted and experimental frequencies, implying that both maps are also similar. A key advantage of this approach is that the converged matrix provides an explicit relationship between restraints and frequencies, revealing how each restraint affects the interactions between all pairs of restrained loci. This allows one to distinguish true looping partners from “secondary” interactions that yield peaks in the contact map due to the looping of neighboring loci.

Researchers have also attempted to optimize restraint strengths using the maximum entropy principle.^{98, 99} The underlying concept here is to impose the fewest or softest possible restraints to a “baseline” polymer model that still allows the restrained system to reproduce the experimental contact maps. If the potential energy of the baseline model is denoted by U₀(R), then the potential energy of the optimally restrained system is given by U(R) = U₀(R) + ∑_i,jα_ijf_SW(r_ij), where f_SW (r) is a smooth square-well potential of a prescribed width defining contact distance and unit depth that simultaneously defines the potential energy of the restraint and counts interactions between loci i and j since ${\widehat{f}}_{\mathit{ij}}$ is simply the ensemble average ⟨f_SW(r_ij)⟩. The parameters α_ij represent Lagrange multipliers that define the strengths of the restraints, whose values are obtained by maximizing the free energy associated with imposing the constraint that the predicted contact map must match the experimental map.⁹⁸ This is typically achieved using an optimization scheme involving cumulant expansion of the free energy. The maximum-entropy approach can be extended further to include other kinds of experimental data into the model, including the local structure of chromatin and the association tendency between similar types of chromatin, i.e., loci exhibiting similar histone modifications.⁹⁹

A few methods using polymer models do not strictly follow every aspect of the optimization scheme described in Fig. 3. For instance, in one approach, the simulated ensemble of conformations were required to satisfy only one-sided constraints arising from excluded volume interactions and nuclear confinement, without following any specific thermodynamic distribution.⁹⁶ Another approach used simulations of a confined polymer model without any looping restraints to model the Hi-C “background” contacts arising from non-specific interactions, i.e., random collisions between loci and confining obstacles.⁹⁵ The remaining contacts that were not accounted for by the unrestrained polymer model were assigned to specific looping interactions, which were then added to the model as distance constraints in the second stage of the optimization. A third approach used a polymer model with essentially no constraints, and generated Boltzmann-distributed conformations using a fictitious energy given by U(R) = ∑_i,jf_ijd_ij, rather than the characteristic potential energy of polymer chains.¹⁰³

MAXIMUM LIKELIHOOD AND BAYESIAN METHODS

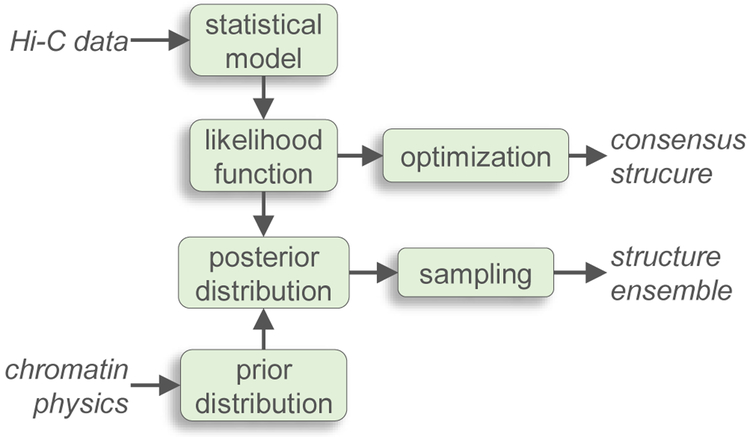
The statistical methods known as maximum likelihood (ML) and Bayesian inference can be used to estimate the unknown parameters of a system by processing some data D with an appropriate statistical model. Whereas ML yields point estimates of the desired parameters, Bayesian inference yields their probability distribution and can also take advantage of prior knowledge or beliefs about the system under study. Both methods have been applied to the problem of inferring 3D conformations of chromatin from contact maps. In this context, the data D are obtained from 3C experiments, and the unknown parameters include the chromatin conformation R and the parameters θ of a statistical model that describes the production of the data D. Common to both methods is the construction of a likelihood function, denoted by P(D∣R,θ), which describes the probability of observing the data given the parameters. ML involves maximizing P(D∣R,θ) to obtain the best estimates of R and θ, thus yielding a “consensus” structure R₀ consistent with the available data D. On the other hand, Bayesian inference also requires defining the prior distribution of the parameters, P(R,θ), and sampling the posterior distribution, P(R,θ∣D), thus yielding an ensemble of structures R consistent with the underlying population (Fig. 4).

Figure 4:

General scheme for computational methods that use maximum likelihood or Bayesian inference to generate a consensus structure or an ensemble of structures, respectively, that is consistent with an experimental contact map. Blocks represent the main components common to these methods. Arrows represent the main flow of information.

Likelihood function.

Formulating the likelihood function P(D∣R,θ) requires choosing (i) a representation for the system, (ii) the form of the observed data, and (iii) a statistical model describing the behavior of the system. To represent the 3D conformation of a chromosome, various formulations have been adopted. A simple representation involves points or beads corresponding to the restriction fragments generated by 5C or Hi-C experiments.^56,107 Another natural choice is a chain of points or beads matching the genomic segments used to define the bins of the contact matrix. Such segments are typically of equal length,^{71, 108-112} but can also be defined by hierarchical clustering of the contact matrix¹¹³ or by matching the extents of TADs.^{108, 114} The volume of each bead may be proportional to the length of the genomic segment represented by the bead.¹¹³ Actual bead diameters can be determined from values of chromatin density in the nucleus.¹¹¹ Also, each bead may have both a hard-core radius, to enforce excluded volume, and a larger soft-core radius, to detect contacts between beads.¹¹³ Although chromosomes are suitably represented as continuous chains of beads, contact matrices often include gaps due to poor mappability of reads. Beads that fall in those gaps are omitted from some optimization procedures.^{71, 109, 110}

The second requirement of the likelihood function is an appropriate form for the data D. A possible choice is the matrix C of contact counts c_ij.^{56, 71, 108-111, 115} In some cases, matrices from multiple experiments are used simultaneously, allowing integration of data from different restriction enzymes.¹¹⁵ Using contact counts from Hi-C experiments requires some care in regard to experimental biases.⁵⁴ These can be ignored for simplicity,⁵⁶ or can be explicitly modeled by including appropriate covariates in the likelihood function.^{108-110, 115} Alternatively,^{71, 112, 113} the contact matrix may be corrected using published procedures^{54, 116-118} before computing the likelihood function. Further conversion of contact counts c_ij to frequencies f_ij may be required for some likelihood formulations.^{56, 113} The likelihood function can also be defined using data D in the form of distances δ_ij between pairs of loci i and j.^{107, 112} These distances may be obtained from c_ij by assuming δ_ij = γc_ij^−α. Here, γ can be set arbitrarily¹¹² or estimated from published data, such as the average spatial distance between genomic loci,¹⁰⁷ and α can be treated as an unknown parameter.¹⁰⁷ In one study, α was varied within a specified range and, to choose the best value, the inferred structures were compared to a known structure using the Spearman correlation coefficient of the internal distances.¹¹² The likelihood function may also rely on data from other types of experiments. For example, FISH measurements have been used to constrain the radius of gyration of the inferred chromosome structure.¹¹¹

The last requirement is a statistical model that yields the probability of observing each data point. For example, each contact count c_ij, may be assumed to obey a binomial distribution, which in turn is approximated by a normal distribution with an unknown mean μ_ij and standard deviation σ_ij equal to the mean plus a small constant.⁵⁶ On the other hand, the discrete nature of c_ij suggests they be modeled as independent Poisson random variables, thus yielding

$$P(\mathbf{D}\mid \mathbf{R},\theta )={\prod }_{1\le i<j\le N}\frac{e^{-{\mu }_{ij}}{{\mu }_{ij}}^{c_{ij}}}{c_{ij}!}$$ (4)

where each mean contact count μ_ij is in turn related to the spatial distance d_ij between the interacting loci i and j. The relation is an inverse power law, log μ_ij = α₀ + α₁ log d_ij, where α₁ < 0, and α₀ > 0 determines the scale of the 3D structure.^{56, 71, 108} Because such scale cannot be derived from contact counts alone, the value of α₀ may be set arbitrarily,^{56, 109, 110} deduced by assuming d_1,n = 1,¹⁰⁸ or inferred using non-metric MDS.⁷¹ The definition of mean contact counts μ_ij can also be refined to include experimental biases inherent in the Hi-C data. In this case log μ_ij = α₀ + α₁ log d_ij + v^T_ijβ, where v_ij is a vector of covariates quantifying the biases, and β is a vector of corresponding coefficients.^{108, 109, 115}

Although convenient for modeling contact counts, the Poisson distribution may not be adequate for contact maps containing many zero entries. To overcome this issue, the use of a zero-truncated Poisson model was proposed,^{109, 110} where the log likelihood is computed by excluding the terms associated with zero c_ij’s. Another potential problem is that the c_ij’s may not be truly independent, because neighboring loci along a chromosome may form similar contacts with farther loci. Moreover, the actual variance of the c_ij’s may be larger than allowed by the Poisson distribution. These problems can be addressed by including additional random variables in log μ_ij that account for variance over-dispersion and interdependency of contact counts.¹¹⁰

Instead of using contacts c_ij in the likelihood function, one can use distances δ_ij = γc_ij^−α, which can be assumed to follow a normal distribution with mean d_ij and variance σ^{2107, 112}:

$$P(\mathbf{D}\mid \mathbf{R},\theta )={\prod }_{1\le i<j\le N}\frac{1}{\sigma \sqrt{2\pi }}\text{exp}\left\{-\frac{1}{2{\sigma }^2}({\delta }_{ij}-d_{ij}{)}^2\right\}$$ (5)

The parameters α and σ can be inferred together with the distances d_ij.¹⁰⁷ Another option is to keep α constant and to eliminate the variance from Eq. 5 by assuming that σ² ∝ ∑(δ_ij – d_ij)².¹¹² Although the above examples of likelihood functions are generally applicable to data from bulk Hi-C experiments, analysis of data from single-cell Hi-C experiments requires different statistical models. One approach is to express the log-likelihood as a sum of logistic functions of d_ij, thus introducing adjustable parameters for the contact distance and the steepness of the step.¹¹¹

The likelihood function can be pushed even further. For example, the need for an explicit relation between c_ij and d_ij can be avoided, and a population of conformations for an entire diploid genome can be inferred at once via a single likelihood maximization. These ambitious requirements were met by expressing the likelihood function in terms of two large matrices: a 2N × 2N × M matrix R containing the coordinates of the beads for all diploid genome structures in the population, and a 2N × 2N × M binary matrix W assigning contacts to pairs of beads that overlap within each estimated structure, where N is the number of beads per haploid genome and M is the population size.¹¹³ Estimating M genomic structures simultaneously also allows estimation of interaction frequencies, which are compared directly to the contact map F. The resulting likelihood function is thus P(F∣R) = P(F∣W)P(W∣R), i.e., a product of the probability of observing the assigned contacts W given the estimated structures R, and the probability of observing the Hi-C interaction frequencies F given the contact assignments W.

Likelihood maximization.

Having defined the likelihood function, one can proceed to determine a consensus structure R₀ that recapitulates the observed data D. Assuming such structure to be the most probable given the data, then the task is to find R and θ that maximize P(D∣R,θ). To achieve this goal, several optimization techniques can be employed with various tradeoffs in computational efficiency and reliability. A sufficiently simple likelihood function that depends only on R can be maximized using the gradient ascent method or the adaptive gradient algorithm.¹¹² More complex scenarios can be handled with appropriate iteration schemes. For instance, optimization of both R and the parameters α₀ and α₁ can be performed through a coordinate-descent algorithm that randomly initializes R and then alternates between (i) maximizing the likelihood with respect to α₀ and α₁ with a fixed conformation R, and (ii) maximizing the likelihood with respect to R while keeping α₀ and α₁ fixed.⁷¹ The individual optimization problems can be solved by using the interior point filter algorithm implemented in the IPOPT code.⁸⁴

Even more challenging functions require iteration at multiple levels. For example, maximizing the likelihood function P(F∣R) = P(F∣W)P(W∣R), used in Ref. ¹¹³, entails optimizing a structure matrix R and a contact assignment matrix W that are both very large. Here, one iteration level involves two steps: (i) updating the contact assignments in W by maximizing P(F∣W), and (ii) estimating R by maximizing P(W∣R).¹¹³ Specifically, P(F∣W) is maximized by comparing inter-bead distances to appropriate thresholds determined from R, while P(W∣R) is maximized through simulated annealing and conjugate gradient algorithms in IMP.¹¹⁹ Another iteration level takes advantage of the idea that enforcing frequent contacts before infrequent ones can efficiently guide the search for an optimal structure. Thus, the above procedure is repeated by incrementally populating the matrix F with sets of contact probabilities arranged from largest to smallest.¹¹³

One advantage of using ML is that additional constraints can be introduced without complicating the likelihood function. For example, the excluded volume of beads, the confinement of beads within the nuclear volume, and the distance of certain beads from the nuclear periphery based on FISH data can all be enforced by using constrained optimization methods.¹¹³

Bayesian inference.

An alternative to ML is Bayesian inference, which explicitly recognizes the existence of probability distributions for chromatin structures and auxiliary parameters. This approach, named inferential structure determination, was previously shown to be effective in obtaining the structure of macromolecules from nuclear magnetic resonance data.¹²⁰ The general scheme is derived from Bayes’ theorem to yield the posterior distribution of conformation R and parameters θ given the observed data D, i.e., P(R,θ∣D) = P(D∣R,θ)P(R,θ)/P(D), where the now familiar likelihood function P(D∣R,θ) is multiplied by P(R,θ), which is the prior distribution of R and θ based on some assumed behavior of R. The normalizing constant P(D) ensures that 0 ≤ P (R,θ∣D) ≤ 1, but is usually not needed to estimate R and θ from P(R,θ∣D). Thus, to evaluate the posterior distribution P(R,θ∣D), it is only necessary to define an appropriate prior distribution P (R,θ). This requirement can be sidestepped by assuming a uniform distribution, i.e., a non-informative prior, so that P(R,θ∣D) ∝ P(D∣R,θ),^{56, 108-110} or one can take advantage of the prior to obtain conformations R that are more physically realistic. For example, the dependency between the 3D positions of neighboring genomic loci can be modeled with a normal distribution, thus yielding the prior $P(R,\theta )\propto {\prod }_{i\ge 2}\text{exp}\left\{-\lambda (l_i-l_{i-1})d_{l_i,l_{i-1}}^2\right\}$, where the l_i’s are integer indices of the genomic loci for which contact counts are available, and the tunable parameter λ determines the smoothness of the chain.¹¹⁵ Another option is to assume that the potential energy U of a conformation obeys the Boltzmann distribution,^{107, 111} yielding P(R,θ) ∝ exp(−U(R,θ)/k_BT). Such a formulation affords great flexibility in choosing relevant physical properties of chromatin. For instance, U may include potentials for stretching, bending, and excluded volume, using physical parameters θ similar to those used in polymer models.^{107, 111}

Once the likelihood function and priors are defined, the posterior distribution P(R,θ∣D) can be sampled to infer conformations R and model parameters θ from the observed data D. The purpose of sampling may be to find a single consensus structure that maximizes the posterior,^{108-110, 115} or to obtain an ensemble of conformations that can be further studied, e.g., via clustering methods.^56,107 A general approach for sampling the posterior distribution is to employ Markov chain Monte Carlo (MCMC) with the Metropolis-Hastings algorithm,¹⁰² which draws conformations from the posterior without requiring evaluation of P(D). Specific refinements of this strategy may be required based on the complexity of the posterior. When the latter lacks adjustable model parameters, MCMC may be adequate by itself to produce a conformation ensemble.⁵⁶ In this case, starting with a random initial structure, each MC step generates a proposal structure by randomly displacing a randomly chosen point in the chain.

The presence of unknown model parameters requires more elaborate schemes. A possible solution is to use Gibbs sampling,¹²¹ which alternates between chromosome structures and model parameters.^108-111 In regards to chromosome structures, the Hamiltonian, or Hybrid, MC method¹²² can be used to efficiently sample the posterior distribution of R while keeping θ fixed.^108-111 In this case, each MC step produces a proposal conformation by performing a short MD simulation, where the 3D coordinates are updated by numerical integration.^{109, 110} Complicated posteriors may lead the Gibbs sampler to become trapped in local peaks. A smart solution to this problem is to combine he Gibbs sampler with replica exchange MC,¹²³ where a fictitious inverse temperature determines the weight of the likelihood function on the posterior distribution.^{111, 124} Additional improvements are possible: the model parameters can be initialized using Poisson regression and then refined using adaptive rejection sampling.¹⁰⁸ Moreover, the initial conformations R can be obtained using sequential importance sampling with a rejection control technique that improves efficiency.¹⁰⁸

Besides the Gibbs sampler, other schemes have been proposed. For example, a posterior that includes a distance penalty to enforce the connectivity of the chain¹¹⁵ can be maximized by iterating over two steps: (i) fitting a generalized linear model (GLM) obtained from the log likelihood function by omitting the terms for α₁ and the distance penalty, and (ii) minimizing the distance penalty by adjusting groups of sequential coordinates to obtain an initial structure, followed by updating the GLM coefficients through simulated annealing with Hamiltonian dynamics.¹¹⁵ Another iterative scheme uses the expectation maximization algorithm¹²⁵ to estimate the model parameters while also generating an ensemble of conformations.¹⁰⁷ After initializing the model parameters and generating an initial ensemble of structures through Brownian dynamics, the computation alternates between two steps. In the expectation step, a gradient ascent algorithm is used to refine each structure by maximizing its likelihood, which is calculated from the posterior using the current estimates of model parameters. In the maximization step, a grid search is performed to estimate the model parameters that maximize the likelihood of the ensemble of conformations refined in the previous step.¹⁰⁷

CONCLUSION

In this review, we have provided an overview of available methods for converting 2D contact data from Hi-C experiments into 3D chromatin conformations that are consistent with such data. We have found it expedient to group such methods into three classes. The first class includes methods that covert contact frequencies into internal distances and feed the latter to a scoring function whose optimization yields a single consensus structure. The second class includes methods that avoid the conversion from contact frequencies to internal distances and instead use polymer models to obtain conformation ensembles that recapitulate the experimental contact frequencies. The third class includes methods that relate the contact frequencies to internal distances through a statistical model, whose parameters are then optimized to agree with the contact frequencies.

Each class of methods includes a variety of techniques and refinements that enable structural recovery at different scales, ranging from domains, to chromosomes, to whole diploid genomes. The large number of proposed methods creates opportunities for further research and improvement. For example, choosing the method most appropriate for a given biological question will benefit from efforts to assess objectively the strengths and weaknesses of the available methods.¹²⁶ Also, careful evaluation and comparison of present and future methods will benefit from the availability of standardized test cases where the solution structure or ensemble is known in advance. This practice is well established in the Critical Assessment of Structure Prediction (CASP) experiments, which are periodically performed to track the progress of computational methods for predicting protein structure from amino acid sequence.¹²⁷ However, CASP relies on experimental data that are currently unavailable to provide the ground truth for chromatin conformation inference, which is therefore more difficult to validate than protein structure prediction. The variety of available methods for 3D genome structure determination and their likely complementary strengths and weaknesses also suggest the possibility to apply such methods simultaneously in order to obtain a consensus solution based on suitable criteria. Similar strategies have been proposed, for example, to improve the reliability of protein-ligand predictions,^{128, 129} protein structure alignments,¹³⁰ protein structure comparison,¹³¹ and protein secondary structure prediction.^132-134

There are also opportunities for further improvement of the current methods and their specific implementations. For example, a major area of concern is computational efficiency, especially when attempting to reconstruct the structure of whole diploid genomes at high resolution. Execution speed and complexity of the reconstructed structures may both increase by exploiting high-performance hardware, such as large computer clusters and GPUs, which have already been used for 3D genome visualization.⁷⁷ Efficiency could also be improved through the use of multi-resolution models, where increasingly refined models of chromatin are threaded through structural solutions obtained from lower-resolution models and then locally optimized at higher resolution. Such approaches have found applications in building high-resolution models of bacterial genomes,^{82, 135, 136} and similar ideas could be applied to obtaining refined structures of eukaryotic genomes using available high-resolution models of chromatin.^137-140 Also, the accuracy of the reconstructed structures may be improved by deriving constraints from additional experimental techniques such as super-resolution microscopy and soft X-ray tomography.¹⁴¹ This trend has already begun with the integration of epigenetic data from ChIP-seq and DNase-seq experiments toward the prediction of chromatin conformation.^142-144 Lastly, it remains to be explored whether the reconstruction of 3D genomic structure from experimental data can be improved by taking advantage of increasingly popular, data-greedy machine learning algorithms. For example, deep neural networks¹⁴⁵ have been applied to predict transcription factors binding sites,¹⁴⁶ protein secondary structure,¹⁴⁷ and protein-protein interactions.¹⁴⁸ Indeed, as the quantity of experimental data continues to grow, such strategies are already finding their way into predicting 3D chromatin architecture.¹⁴⁹

HIGHLIGHTS.

• Computational methods can infer 3D genome structure from 3C contact maps.

• Distance-optimization methods convert contact maps to internal distances.

• Polymer physics methods recapitulate contact maps from polymer model simulations.

• Maximum-likelihood and Bayesian methods infer parameters of statistical models.