Exact inference on the random-effects model for meta-analyses with few studies

Abstract

We describe an exact, unconditional, non-randomized procedure for producing confidence intervals for the grand mean in a normal-normal random effects meta-analysis. The procedure targets meta-analyses based on too few primary studies, ≤ 7, say, to allow for the conventional asymptotic estimators, e.g., DerSimonian and Laird (1986), or non-parametric resampling-based procedures, e.g., Liu et al. (2017). Meta-analyses with such few studies are common, with one recent sample of 22,453 heath-related meta-analyses finding a median of 3 primary studies per meta-analysis (Davey et al., 2011). Reliable and efficient inference procedures are therefore needed to address this setting. The coverage level of the resulting CI is guaranteed to be above the nominal level, up to Monte Carlo error, provided the meta-analysis contains more than 1 study and the model assumptions are met. After employing several techniques to accelerate computation, the new CI can be easily constructed on a personal computer. Simulations suggest that the proposed CI typically is not overly conservative. We illustrate the approach on several contrasting examples of meta-analyses investigating the effect of calcium intake on bone mineral density.

1 ∣. INTRODUCTION

The random effects model is often used to account for between-study heterogeneity when conducting a meta-analysis. When the distribution of the primary study treatment effect estimates is approximately normal, the simple normal-normal model is commonly used, and the DerSimonian-Laird (“DL”) method and its variations are the most popular approach to estimating the model’s parameters and performing statistical inference (DerSimonian and Laird, 1986). However, the DL method is based on an asymptotic approximation and its use is only justified when the number of studies is large. In many fields, the number of studies used in a meta-analysis or sub-meta-analysis rarely exceeds 20 and is typically fewer than 7 (Davey et al., 2011), leaving inferences based on the DL estimator questionable. Indeed, extensive simulation studies have found that the coverage probability of the DL-based confidence interval (CI) can be substantially lower than the nominal level in various settings (Kontopantelis et al., 2010; IntHout et al., 2014), leading to false positives. One reason for this poor performance is that the asymptotic approximation ignores the variability in estimating the heterogeneous variance, which can be substantial when the number of studies is small (Higgins et al., 2009).

Various remedies have been proposed to correct the under-coverage of DL-based confidence intervals. Hartung and Knapp (2001) proposed an unbiased estimator of the variance of the DL point estimator explicitly accounting for the variability in estimating the heterogenous variance. Sidik and Jonkman (2006) used the heavy-tailed t-distribution to approximate the distribution of a modified Wald-type test statistic based on the DL estimator. Using the more robust t- rather than normal distribution has also been proposed (Raghunathan, 1993; Berkey et al., 1995; Follmann and Proschan, 1999). Hardy and Thompson (1996), Vangel and Rukhin (1999), Viechtbauer (2005), and Raudenbush (2009) proposed procedures based on maximum-likelihood estimation. Noma (2011) further improved the performance of the likelihood-based inference procedure when the number of studies is small by using a Bartlett-type correction. Zeng and Lin (2015) describe a resampling procedure to approximate the “large cluster” asymptotic distribution, i.e., as the primary study sizes all grow. Bayesian approaches incorporating external information have been developed by many authors (Smith et al., 1995; Higgins and Whitehead, 1996; Bodnar et al., 2017). However, with few exceptions, most of these methods still depend on an asymptotic approximation and their performance with very few studies has only been examined by specific simulation studies. To overcome these difficulties, potentially conservative but “exact” inference procedures for the random effects model have been proposed (Follmann and Proschan, 1999; Wang et al., 2010; Liu et al., 2017; Wang and Tian, 2017). A permutation rather than the asymptotic limiting distribution is used to approximate the distribution of the relevant test statistics and thus the validity of the associated inference is guaranteed for any number of studies. However, due to the discreteness of the permutation distribution, the highest significance level that may be achieved without randomization depends on the number of studies. For example, a 95% confidence interval can only be constructed with more than 5 studies. While Bayesian methods also permit statistical inference with fewer studies, the results are correspondingly sensitive to the choice of the prior distributions.

The main contribution of this paper is to propose a set of new methods for constructing exact, unconditional, non-randomized frequentist CIs for the location parameter of the normal-normal model by inverting exact tests. The coverage level of the resulting CI is guaranteed to be above the nominal level, up to Monte Carlo error, as long as the meta-analysis contains more than 1 study. After employing several techniques to accelerate computation, the new CI can be easily constructed on a personal computer. Simulations suggest that the proposed CI typically is not overly conservative. In Section 2, we present our procedure for constructing exact CIs for the population mean; in Section 3, we report results from comprehensive simulation studies; in Section 4, we illustrate the proposed method with a real data example; and in Section 5 we conclude the paper with additional discussion.

2 ∣. METHOD

The observed data consist of ${\mathcal{Y}}_0=\{Y_k,k=1,\dots ,K\}$, where Y_k follows a random effects model,

$$Y_k\mid {\theta }_k\stackrel{ind.}{\sim }N({\theta }_k,{\sigma }_k^2),{\theta }_k\stackrel{ind.}{\sim }N({\mu }_0,{\tau }_0^2),k=1,\dots ,K,$$

with the variances ${\sigma }_k^2>0$, k = 1, … , K, assumed known. The random effects model implies the simple parametric model

$$Y_k\stackrel{ind.}{\sim }N({\mu }_0,{\sigma }_k^2+{\tau }_0^2),k=1,\dots ,K.$$ (1)

In the context of a meta-analysis, the pairs (Y_k, ${\sigma }_k^2$), k = 1, … , K, are interpreted as observed effects and known within-study variances drawn from K studies, respectively. The unobserved population effect and between-study variance are μ₀ and ${\tau }_0^2$, respectively. The goal is inference on the location parameter μ₀, viewing ${\tau }_0^2$ as a nuisance parameter. The typical number of studies depends on the area of research and can be small, e.g., K ≤ 10.

With ${\tau }_0^2$ known, the uniformly minimum variance unbiased estimator of μ₀ under (1) is given by

$$\frac{{\sum }_{k=1}^K{Y}_k({\tau }_0^2+{\sigma }_k^2{)}^{-1}}{{\sum }_{k=1}^K({\tau }_0^2+{\sigma }_k^2{)}^{-1}}.$$

As ${\tau }_0^2$ is unknown, DerSimonian and Laird (1986) propose substituting a simplified method of moments estimator,

$${\widehat{\tau }}_{DL}^2=\max \left\{0,\frac{{\sum }_{k=1}^K(Y_k-{\widehat{\mu }}_F{)}^2∕{\sigma }_k^2-(K-1)}{{\sum }_{k=1}^K{\sigma }_k^{-2}-({\sum }_{k=1}^K{\sigma }_k^{-4})∕({\sum }_{k=1}^K{\sigma }_k^{-2})}\right\},$$

where

$${\widehat{\mu }}_F=\frac{{\sum }_{i=1}^K{Y}_k{\sigma }_k^{-2}}{{\sum }_{i=1}^K{\sigma }_k^{-2}}$$

is the minimum variance unbiased estimator of μ₀ under a fixed effects model, i.e., when ${\tau }_0^2=0$. The resulting estimator is known as the “DerSimonian-Laird” estimator of μ₀:

$${\widehat{\mu }}_{DL}=\frac{{\sum }_{k=1}^K{Y}_k({\widehat{\tau }}_{DL}^2+{\sigma }_k^2{)}^{-1}}{{\sum }_{k=1}^K({\widehat{\tau }}_{DL}^2+{\sigma }_k^2{)}^{-1}}.$$

By an analogous substitution, a level 1 − α confidence interval for μ₀ is given by

$$\{{\widehat{\mu }}_{DL}-z_{1-\alpha ∕2}{\left(\sum _{k=1}^K({\widehat{\tau }}_{DL}^2+{\sigma }_k^2{)}^{-1}\right)}^{-1∕2}\phantom{\}},\phantom{\{}{\widehat{\mu }}_{DL}+z_{1-\alpha ∕2}{\left(\sum _{k=1}^K({\widehat{\tau }}_{DL}^2+{\sigma }_k^2{)}^{-1}\right)}^{-1∕2}\}.$$ (2)

The justification of the CI given in (2) relies on the asymptotic approximation

$$T_0({\mu }_0;\mathcal{Y})=({\widehat{\mu }}_{DL}-{\mu }_0{)}^2\sum _{k=1}^K({\widehat{\tau }}_{DL}^2+{\sigma }_k^2{)}^{-1}⇝{\chi }_1^2$$ (3)

as the number of studies, K, grows to infinity and max{σ_k}/ min{σ_k) is uniformly bounded. However, the exact distribution of $T_0({\mu }_0;\mathcal{Y})$ depends on ${\tau }_0^2$ and may be very different from a ${\chi }_1^2$ distribution when K is moderate or small (Hoaglin, 2016). Consequently, the finite-sample performance of the CI given by (2) is often unsatisfactory. We propose constructing an exact CI for μ₀ by first constructing an exact confidence region for (μ₀, ${\tau }_0^2$). To this end, let $T\{(\mu ,{\tau }^2);{\mathcal{Y}}_0\}$ denote a scalar test statistic, which may depend on the null parameter (μ, τ²), for the simple hypothesis $({\mu }_0,{\tau }_0^2)=(\mu ,{\tau }^2)$. The specific choice of $T\{(\mu ,{\tau }^2);{\mathcal{Y}}_0\}$ will be discussed later and here we only assume that a high value of $T\{(\mu ,{\tau }^2);{\mathcal{Y}}_0\}$ represents grounds for rejection. For a given choice of $T\{(\mu ,{\tau }^2);{\mathcal{Y}}_0\}$, a 1 − α level CI for μ₀ can be constructed as follows:

1. Obtain bounds [μ_min, μ_max] and [${\tau }_{min}^2$, ${\tau }_{max}^2$] for μ₀ and${\tau }_0^2$.

2. For each pair of μ and τ² in an R × R grid of points on $[{\mu }_{min},{\mu }_{max}]\times [{\tau }_{min}^2,{\tau }_{max}^2]$,

   1. Compute the null distribution of $T\{(\mu ,{\tau }^2);\mathcal{Y}(\mu ,{\tau }^2)\}$, where

      $$\mathcal{Y}(\mu ,{\tau }^2)=\left\{{\tilde{Y}}_k,k=1,\dots ,K\right\}$$

      with ${\tilde{Y}}_k\stackrel{ind.}{~}N(\mu ,{\sigma }_k^2+{\tau }^2)$, k = 1, … , K.
   2. Compute the p-value $p_{\mu ,{\tau }^2}({\mathcal{Y}}_0)≔P[T\{(\mu ,{\tau }^2);{\mathcal{Y}}_0\}>T\{(\mu ,{\tau }^2);\mathcal{Y}(\mu ,{\tau }^2)\}]$.

3. Obtain a confidence region for (μ₀, ${\tau }_0^2$) as${\Omega }_{1-\alpha }({\mathcal{Y}}_0)≔\{(\mu ,{\tau }^2):p_{\mu ,{\tau }^2}({\mathcal{Y}}_0)>\alpha \}$.

4. Project ${\Omega }_{1-\alpha }({\mathcal{Y}}_0)$ onto the μ axis to obtain a CI for ${\mu }_0:\{\mu :(\mu ,{\tau }^2)\in {\Omega }_{1-\alpha }({\mathcal{Y}}_0)\}$.

We discuss below the selection of appropriate bounds for the first step; here, we assume their existence for purposes of illustration.

This method generates the exact CI for μ₀ in the sense that

$$\text{pr}\left({\mu }_0\in \{\mu :(\mu ,{\tau }^2)\in {\Omega }_{1-\alpha }({\mathcal{Y}}_0)\}\right)\ge 1-\alpha .$$

This is due to the fact that

$$\begin{gathered} \text{pr}\left({\mu }_0\in \{\mu :(\mu ,{\tau }^2)\in {\Omega }_{1-\alpha }({\mathcal{Y}}_0)\}\right) \\ \ge \text{pr}\{({\mu }_0,{\tau }_0^2)\in {\Omega }_{1-\alpha }({\mathcal{Y}}_0)\} \\ =\text{pr}\left\{p_{{\mu }_0,{\tau }_0^2}({\mathcal{Y}}_0)\ge \alpha \right\} \\ =\text{pr}(U\ge \alpha )=1-\alpha , \end{gathered}$$

where the random variable U follows the unit uniform distribution. Here, we assume that ${\tau }_0\in [{\tau }_{min}^2,{\tau }_{max}^2]$. If ${\tau }_{min}^2$ and ${\tau }_{max}^2$ are chosen depending on the data in such a way that $\mathrm{pr}({\tau }_{min}^2<{\tau }^2<{\tau }_{max}^2)\ge 1-\beta$, then the guaranteed coverage probability of the proposed CI is 1 − α ≈ 1 − α for very small β. The error of the approximation, i.e., the magnitude of β, can be made arbitrarily small by methods described further below.

The cumulative distribution function of $T\{(\mu ,{\tau }^2);\mathcal{Y}(\mu ,{\tau }^2)\}$ may not be analytically tractable, but it is well defined for any given grid point (μ, τ²) and can always be approximated by a Monte Carlo simulation. To be specific, given (μ, τ²), we may approximate the distribution of $T\{(\mu ,{\tau }^2);\mathcal{Y}(\mu ,{\tau }^2)\}$ in 2a as follows:

2(a) For b = 1, … , B,

1. Generate $e_{1b}^{\ast }$, … , $e_{Kb}^{\ast }\stackrel{ind.}{~}N(0,1)$.

2. Let $Y_{kb}^{\ast }=\mu +({\sigma }_k^2+{\tau }^2{)}^{1∕2}{e}_{kb}^{\ast }$, k = 1, … , K, and let ${\mathcal{Y}}_b^{\ast }=\{Y_{kb}^{\ast },k=1,\dots ,K\}$.

3. Let $T_b^{\ast }=T\{(\mu ,{\tau }^2);{\mathcal{Y}}_b^{\ast }\}$ be the corresponding test statistic based on the generated data ${\mathcal{Y}}_b^{\ast }$. The empirical distribution of {$T_1^{\ast }$, … ,$T_B^{\ast }$} can be used to approximate the distribution of $T\{(\mu ,{\tau }^2);\mathcal{Y}(\mu ,{\tau }^2)\}$.

Since the estimation of the null distribution in 2a does not depend on any asymptotic approximation, both the p-value, $p_{\mu ,{\tau }^2}({\mathcal{Y}}_0)$, and the confidence region, ${\Omega }_{1-\alpha }({\mathcal{Y}}_0)$, are “exact” if we can safely ignore the errors of the grid approximation and the Monte Carlo simulation above, which can be controlled by increasing the grid density and B in step 2a, respectively.

Because the data Y_k, k = 1, … , K, are distributed as $\mathcal{N}(\mu ,{\sigma }_k^2+{\tau }_0^2)$, k = 1, … , K, whenever the shifted data Y_k − μ, k = 1, … , K, are distributed as $\mathcal{N}(0,{\sigma }_k^2+{\tau }_0^2)$, k = 1 … , K, we restrict our focus to equivariant statistics (Lehmann and Romano, 2006), that is, T satisfying $T\{(\mu ,{\tau }^2);{\mathcal{Y}}_0\}=T\{(0,{\tau }^2);{\mathcal{Y}}_0-\mu \}$, where ${\mathcal{Y}}_0-\mu =\{Y_k-\mu ,k=1,\dots ,K\}$. In this situation, testing the null $H_0:({\mu }_0,{\tau }_0^2)=(\mu ,{\tau }^2)$ based on the data ${\mathcal{Y}}_0$ is the same as testing the null $H_0:({\mu }_0,{\tau }_0^2)=(0,{\tau }^2)$ based on the shifted data ${\mathcal{Y}}_0-\mu$. When the test statistic is equivariant, the computations in step (2)(a) need only be performed once for each τ² in the grid rather than each pair (μ, τ²). Thus, although a 2-dimensional grid is used in the algorithm, the computational complexity remains linear in the grid size, R. More specifically, steps (2)–(3) become:

2′.For each τ² of an R-sized grid on [${\tau }_{min}^2$, ${\tau }_{max}^2$],

1. Compute the distribution of $T\{(0,{\tau }^2);\mathcal{Y}(0,{\tau }^2)\}$.

2. Compute q_1−α;τ², the 1 − α quantile of $T\{(0,{\tau }^2);\mathcal{Y}(0,{\tau }^2)\}$.

3. Compute ${\Omega }_{1-\alpha }({\tau }^2;{\mathcal{Y}}_0)=\{(\mu ,{\tau }^2)\mid T\{(\mu ,{\tau }^2);{\mathcal{Y}}_0\}=T\{(0,{\tau }^2);{\mathcal{Y}}_0-\mu \}<q_{1-\alpha ;{\tau }^2}\}$.

3′.Compute a (1 − α)-level confidence region for (μ₀, ${\tau }_0^2$) as

$$\bigcup _{{\tau }^2\in [{\tau }_{min}^2,{\tau }_{max}^2]}{\Omega }_{1-\alpha }({\tau }^2;{\mathcal{Y}}_0).$$

We propose the test statistics

$$T\left\{(\mu ,{\tau }^2);\mathcal{Y}\right\}=T_0(\mu ;\mathcal{Y})+c_0{T}_{lik}\left\{(\mu ,{\tau }^2);\mathcal{Y}\right\},$$ (4)

where $T_0(\mu ;\mathcal{Y})$ is the sameWald-type test statistic used in the Dersimonian-Laird procedure,

$$\begin{gathered} T_{lik}\left\{(\mu ,{\tau }^2);\mathcal{Y}\right\}= \\ -\frac{1}{2}\sum _{k=1}^K\left[\frac{(Y_k-{\widehat{\mu }}_{DL}{)}^2}{{\widehat{\tau }}_{DL}^2+{\sigma }_k^2}+\log \{2\pi ({\widehat{\tau }}_{DL}^2+{\sigma }_k^2)\}\right] \\ +\sum _{k=1}^K\frac{1}{2}\left[\frac{(Y_k-\mu {)}^2}{{\tau }^2+{\sigma }_k^2}+\log \{2\pi ({\tau }^2+{\sigma }_k^2)\}\right], \end{gathered}$$

and c₀ is a tuning parameter controlling the relative contributions of these two statistics. While $T_0(\mu ;\mathcal{Y})$ directly focuses on the location parameter μ₀, $T_{lik}\{(\mu ,{\tau }^2);\mathcal{Y}\}$, similar to the likelihood ratio test statistic, targets the combination of μ₀ and ${\tau }_0^2$ and helps to construct a narrower CI of μ₀ when the number of studies is small. The proposed test statistics satisfy the equivariance condition, ensuring speedy computation when carrying out the procedure on a typical personal computer.

A further simplification afforded by this choice of test statistics is that step 2′c may be carried out by solving the quadratic inequality

$$A(\tau ){\mu }_0^2+B(\tau ){\mu }_0+C(\tau )<0,$$

where

$$\begin{gathered} A(\tau )=\sum _{k=1}^K\left\{\frac{1}{{\widehat{\tau }}_{DL}^2+{\sigma }_k^2}+\frac{c_0}{2({\tau }^2+{\sigma }_k^2)}\right\}>0, \\ B(\tau )=-\sum _{k=1}^K\left\{\frac{2{\widehat{\mu }}_{0DL}}{{\widehat{\tau }}_{0DL}^2+{\sigma }_k^2}+\frac{c_0{Y}_k}{{\tau }^2+{\sigma }_k^2}\right\}, \\ C(\tau )=\sum _{k=1}^K\frac{c_0}{2}\left[\frac{Y_k^2}{{\tau }^2+{\sigma }_k^2}+\log \frac{{\tau }^2+{\sigma }_k^2}{{\widehat{\tau }}_{DL}^2+{\sigma }_k^2}-\frac{(Y_k-{\widehat{\mu }}_{DL}{)}^2}{{\widehat{\tau }}_{DL}^2+{\sigma }_k^2}\right] \\ +{\widehat{\mu }}_{DL}^2\sum _{k=1}^K\frac{1}{{\widehat{\tau }}_{DL}^2+{\sigma }_k^2}-q_{1-\alpha ;{\tau }^2}. \end{gathered}$$ (5)

As a result, the confidence interval of μ₀ when τ₀ = τ, ${\Omega }_{1-\alpha }({\tau }^2;{\mathcal{Y}}_0)$, is simply the segment with endpoints

$$\left(\frac{-B(\tau )-\Delta (\tau {)}^{1∕2}}{2A(\tau )},\frac{-B(\tau )+\Delta (\tau {)}^{1∕2}}{2A(\tau )}\right),$$

when Δ(τ) = B(τ)² − 4A(τ)C(τ) ≥ 0, and an empty set, otherwise.

To choose ${\tau }_{min}^2$ and ${\tau }_{max}^2$ in step (1) of the algorithm, we may use the endpoints of a 100(1 – β)%, e.g., 99.9%, confidence interval of ${\tau }_0^2$. This CI can be constructed by inverting the pivotal statistic

$$T_3({\tau }^2)=(\mathbf{W}\mathbf{Y}{)}^{\prime }{\left\{\mathbf{W}\Sigma (\tau ){\mathbf{W}}^{\prime }\right\}}^{-1}(\mathbf{W}\mathbf{Y}),$$

where Y = (Y₁, … , Y_K)′, $\Sigma (\tau )=\mathrm{diag}\{{\sigma }_1^2+{\tau }^2,\dots ,{\sigma }_K^2+{\tau }^2\}$, and

$$\mathbf{W}=\left(\begin{array}{cccc}\hfill {\sigma }_1^{-2}∕{\sum }_{i=1}^K{\sigma }_i^{-2}-1\hfill & \hfill {\sigma }_2^{-2}∕{\sum }_{i=1}^K{\sigma }_i^{-2}\hfill & \hfill \cdots \hfill & \hfill {\sigma }_K^{-2}∕{\sum }_{i=1}^K{\sigma }_i^{-2}\hfill \\ \hfill {\sigma }_1^{-2}∕{\sum }_{i=1}^K{\sigma }_i^{-2}\hfill & \hfill {\sigma }_2^{-2}∕{\sum }_{i=1}^K{\sigma }_i^{-2}-1\hfill & \hfill \cdots \hfill & \hfill {\sigma }_K^{-2}∕{\sum }_{i=1}^K{\sigma }_i^{-2}\hfill \\ \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill {\sigma }_1^{-2}∕{\sum }_{i=1}^K{\sigma }_i^{-2}\hfill & \hfill {\sigma }_2^{-2}∕{\sum }_{i=1}^K{\sigma }_i^{-2}\hfill & \hfill \cdots \hfill & \hfill {\sigma }_K^{-2}∕{\sum }_{i=1}^K{\sigma }_i^{-2}-1\hfill \end{array}\right).$$

The pivot follows a ${\chi }_{K-1}^2$ distribution when ${\tau }^2={\tau }_0^2$.

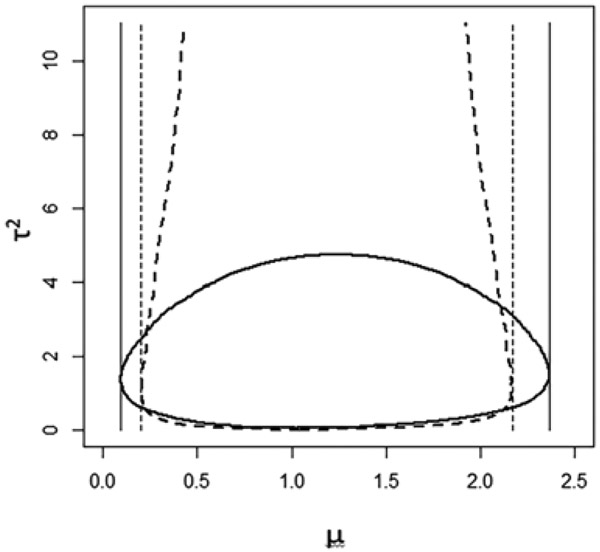
Since our goal is a CI for μ₀, the shape of the confidence region is crucial to its performance: the projection of ${\Omega }_{1-\alpha }({\mathcal{Y}}_0)$ onto the μ axis should be as small as possible, relative to the area of the confidence region. Figure 1 plots two confidence regions with the same confidence coefficient, but substantially different projected lengths. To avoid an overly conservative CI, we prefer a confidence region with boundaries parallel to the τ-axis, or nearly so. The shape of ${\Omega }_{1-\alpha }({\mathcal{Y}}_0)$ is determined by the way we combine $T_0(\mu ;\mathcal{Y})$ and $T_{lik}\{(\mu ,{\tau }^2);\mathcal{Y}\}$ or, more generally, by the choice of $T\{(\mu ,{\tau }^2);\mathcal{Y}\}$. Because the proposed statistics (4) are quadratic in μ, the resulting confidence regions are a union of intervals with similar centers and tend not to produce overly conservative CIs when the tuning parameter c₀ is chosen appropriately.

FIGURE 1.

The projection of the confidence region; the solid and dashed thick lines are boundaries of two confidence regions.

The proposed test statistic was chosen to balance performance and computation costs. For example, the true likelihood ratio test statistic under model (1) may be more informative than $T_{lik}\{(\mu ,{\tau }^2);\mathcal{Y})$, but its evaluation involves computing the maximum likelihood estimate and is substantially slower. The proposed algorithm is easily parallelized, so further gains in computing speed are available.

3 ∣. NUMERICAL STUDY

In this section, we study the small-sample performance of the proposed method through a comprehensive simulation study. Observed data are simulated under the random effects model

$$Y_k\sim N({\mu }_0,{\tau }_0^2+{\sigma }_k^2),k=1,\dots ,K,$$

where σ₁, … , σ_K, are K equally spaced points in the interval [1, 5], that is, σ_k = 1 + 4(k − 1)/(K − 1), k = 1, … , K. The population variance ${\tau }_0^2$ takes values 0, 12.5, and 25 to mimic settings with low, moderate, and high study heterogeneity, respectively. The corresponding I² measures of heterogeneity are approximately 0, 50%, and 70%, respectively.

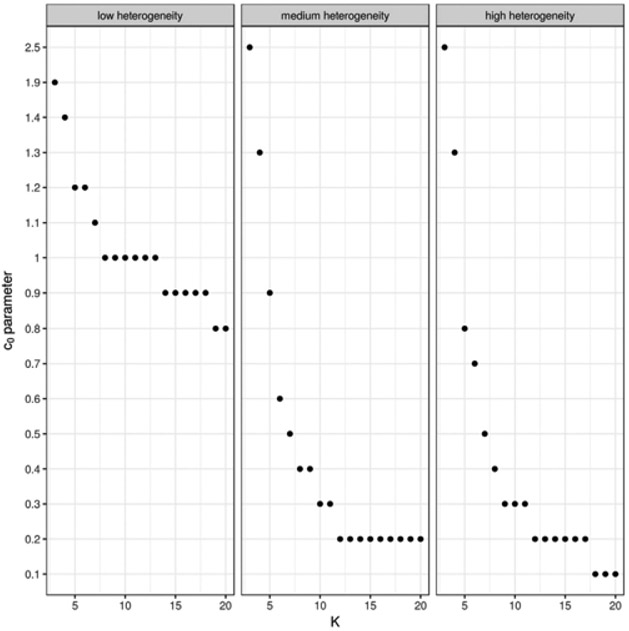
In the first set of simulations, we examine the effect of the tuning parameter c₀ on the performance of the proposed method. For each set of simulated data, we construct a series of CIs using the proposed method with c₀ ranging from 0 to 2.5 in increments of 0.1, and the number of studies K ranges from 3 to 20. Based on results from 10,000 simulated datasets under each combination of settings, we calculate the empirical coverage levels and average lengths of the resulting 95% CIs. In all settings, the empirical coverage levels of the proposed CIs are above the nominal level and therefore we optimize power by selecting the value of c₀ with the shortest CI lengths. When K ≥ 10, the choice of c₀ does not have a pronounced effect on CI length. When K is between 3 and 6, the setting of primary interest, assigning more weight to the likelihood ratio-type statistic typically reduces the length of the CIs. We summarize the value of c₀ achieving the minimum mean 95% CI length in Figure 2. Based on these results, we suggest for a tuning parameter c₀ = 1.2 for meta-analyses with fewer than 6 studies, c₀ = 0.6 for meta-analysess with 6–10 studies, c₀ = 0.2 for meta-analysis with 10–20 studies, and c₀ = 0 for analysis with more than 20 studies.

FIGURE 2.

The choice of c₀ achieving the minimum mean 95% CI length is plotted against the number K of studies, at 3 levels of between-study heterogeneity.

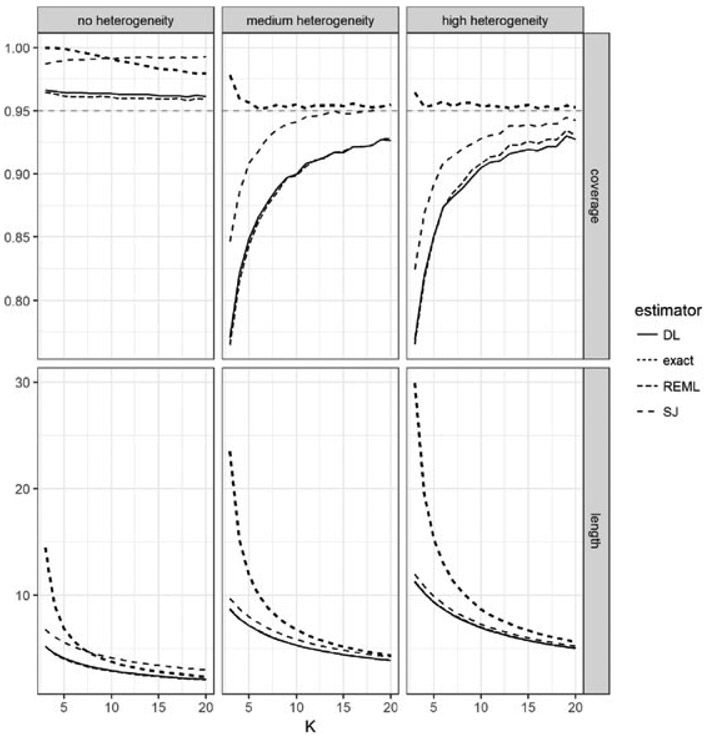
In the second set of simulations, we compare the performance of the proposed CIs with existing alternatives. For 10,000 replicates at each data-generation setting described above, we construct CIs using the DerSimonian-Laird, Sidik-Jonkman, and restricted maximum likelihood asymptotic variance estimates, as well as the proposed CI with the recommended tuning parameter. In Figure 3 we summarize the average coverage and lengths of these CIs. In the presence of moderate heterogeneity, I₂ = 0.5, the empirical coverage level of the DL method is below 90% when K ≤ 10, with the lowest coverage ~ 75% when the number of studies is 3. The CIs based on the Sidik-Jonkman estimator have better coverage, but still drop below 90% when K ≤ 5. In contrast, the proposed exact CIs using the recommended tuning parameter settings do not fall below the nominal 95% coverage level. Morover, the coverage level is not overly conservative even for small Ks. The length of the 95% CI is comparable to the lengths of the asymptotic CIs, when these match the nominal coverage level, e.g., K = 20. When I² = 0, i.e., the random effects model degenerates to the fixed effects model, all methods, including the asymptotic estimators, control the Type 1 error. Sidik-Jonkman’s CI is overly conservative even for moderate K values, while the proposed CIs, also overly conservative at lower values of K, improve steadily as K increases. When I² = 0.70, only the proposed CIs maintain the proper coverage level, while other methods fall below the nominal level for K as large as 10–20.

FIGURE 3.

Comparison by 95% CI coverage and length of the proposed estimator with 3 commonly used estimators based on asymptotic approximations. Data was generated according to model (1) with the number of studies K varying between 3 and 20 and the ratio of between- to average within-variance adjusted to give 3 levels of between-study heterogeneity. The proposed estimator achieves the nominal size at all configurations, with overcoverage evident where the heterogeneity is low or the studies is very few (3-4).

Several other common estimators, including Hedges-Olkin, Hunter-Schmidt, and maximum likelihood, were also tested, with performance found to be generally intermediate between the performance of the DerSimonian-Laird and Sidik-Jonkman estimators. These other comparisons are reported in the Supplementary Materials. Also reported in the Supplementary Materials are results for a Bayesian estimator using a non-informative prior, as recently implemented by Röver (2017). The simulation results of the Bayesian estimator are on the whole comparable to our estimator but slightly more conservative. However, its theoretical basis is somewhat incomplete and our evaluation of its performance is limited to the investigated simulation settings.

In a third set of simulations, we compare the performance of the proposed estimator to other common estimators under misspecifications of the model, such as a skew or heavy-tailed distribution. Specifically, rather than using a normal distribution, we used a centered chi-square variable (Supplementary Material, Table 2), a Cauchy distribution (Supplementary Material, Table 3), a centered exponential distribution (Supplementary Material, Table 4), and a uniform distribution on the interval [−5, 5] (Supplementary Material, Table 5) to generate θ_k. We typically find that the coverage rate of the proposed estimator is somewhat conservative, whereas the asymptotic estimators fall below the nominal level, sometimes significantly so. The bayesian estimator with non-informative prior performs similarly to the proposed estimator, though somewhat more conservatively, at least under the default parameters of the selected implementation.

4 ∣. EXAMPLE

Tai et al. (2015) conduct a random effects meta-analysis of 59 randomized controlled trials to determine if increased calcium intake affects bone mineral density (“BMD”). Altogether, these trials measured the changes in BMD at five skeletal sites over three time points and measured the effect of calcium intake on BMD from dietary sources and from calcium supplements. We illustrate the proposed method using four meta-analyses. The first meta-analysis investigates changes in BMD of the lumbar spine and is based on the findings of 27 trials that lasted fewer than 18 months. As shown in Table 1, the 95% CI produced by the proposed exact method does not differ very much from the 95% CI based on the DL method. The two intervals have a similar length and are centered around a BMD difference of about 1.2. We also construct the exact CI by permuting a Hodge-Lehman type estimator (Liu et al., 2018). The resulting interval is very similar to the interval produced by the proposed method. These similarities are to be expected since the normality assumptions of the DL estimator may not be too unreasonable for a meta-analysis based on this number of primary studies.

TABLE 1.

Random effects meta-analyses of the effect of calcium supplements on percentage change in bone mineral density (Tai et al. (2015), Figs. 1, 3, and 7). The meta-analyses were carried out using the DerSimonian-Laird variance estimator (as in Tai et al. (2015)), the permutation test of Wang and Tian (2018), applicable to meta-analyses with 6 or more studies, and the proposed exact method. A nominal 95% CI is reported, with the length in parentheses. On the two smaller meta-analyses (K = 3, 5) the proposed exact method fails to reject the null of no change, whereas the asymptotic DL method does reject.

Study	K	DerSimonian-Laird	Permutation	Proposal
Lumbar spine	27	0.828–1.669 (0.841)	0.788–1.758 (0.970)	0.768–1.726 (0.958)
Total hip	6	0.502–1.847 (1.345)	0.000–2.298 (2.298)	0.159–2.246 (2.087)
Forearm	5	0.209–3.378 (3.169)		−0.459–4.124 (4.583)
Total body	3	0.268–1.778 (1.511)		−0.740–2.796 (3.536)

Two of the other random effects meta-analyses investigate changes in BMD in the hip and forearm for trials of size six and five, respectively, that lasted for more than two years. The fourth analysis we consider here is the meta-analysis of three trials that lasted fewer than 18 months and measured changes in BMD for the total body of subjects. For these three meta-analyses, however, the number of studies is small, and the DL method may be expected to fall short of the nominal level. In the hip study, the proposed exact method and the DL method both yield the same conclusion, producing 95% confidence intervals rejecting the null of no change in BMD, although the exact method produces confidence intervals that are wider than their DL counterparts. In contrast, the DL 95% confidence intervals for the forearm and total body studies find a significant change in BMD whereas the exact method does not, suggesting that the DL method may be giving a false positive in these two cases. The intervals and their lengths are given in Table 1. Note that the exact 95% CI based on the permutation method is not available for the last two meta analyses, since the number of studies is fewer than 6.

A table including confidence intervals obtained using other common estimators of τ² is included in the Supplementary Materials.

5 ∣. DISCUSSION

We have proposed a method to construct an exact CI for the population mean under the normal-normal model commonly used in meta-analysis. Appropriate coverage is guaranteed, up to Monte Carlo error, even when the number of studies used in the meta-analysis is as small as 2. As an important limitation, the proposed “exact” inference procedure is developed under stringent parametric assumptions, which cannot be effectively examined from the data when the number of studies is small. We have examined by simulation a few common misspecifications, but the results still need to be interpreted with extreme caution. On the other hand, there is a practical need for meta-analyses with few studies, where unverifiable assumptions are unavoidable. The main objective of this paper is to propose a valid statistical method when those assumptions hold true. This incremental contribution is arguably warranted by the frequency with which meta-analyses with few studies are conducted using existing methods making the same parametric assumptions.

While convenient, the normal assumption for the study-specific treatment effect estimate may not be valid in other settings. For example, the treatment effect estimate may be an odds ratio from a 2 × 2 contingency table. If the total sample sizes are small or if cell entries are close to 0, the normal assumption for the odds ratio may be inappropriate. More generally, Y_k may be a quantity relevant to a treatment effect with Y_k∣θ_k following a non-normal, e.g., hypergeoemtric, distribution depending on the study-specific parameter θ_k. In such a case, the model for θ_k and the corresponding inference procedure warrant further research. More recently, there have been several new developments on confidence distribution and related generalized fiducial inference that have facilitated new inference procedures for meta-analysis (Xie and Singh, 2013; Claggett et al., 2014). These developments may also be promising directions for developing exact inference procedures for meta-analysis.