The phase stability network of all inorganic materials

Inorganic materials seen through the lens of complex network theory reveal insights into material reactivity.

Abstract

One of the holy grails of materials science, unlocking structure-property relationships, has largely been pursued via bottom-up investigations of how the arrangement of atoms and interatomic bonding in a material determine its macroscopic behavior. Here, we consider a complementary approach, a top-down study of the organizational structure of networks of materials, based on the interaction between materials themselves. We unravel the complete “phase stability network of all inorganic materials” as a densely connected complex network of 21,000 thermodynamically stable compounds (nodes) interlinked by 41 million tie line (edges) defining their two-phase equilibria, as computed by high-throughput density functional theory. Analyzing the topology of this network of materials has the potential to uncover previously unidentified characteristics inaccessible from traditional atoms-to-materials paradigms. Using the connectivity of nodes in the phase stability network, we derive a rational, data-driven metric for material reactivity, the “nobility index,” and quantitatively identify the noblest materials in nature.

INTRODUCTION

Several diverse complex systems are modeled as networks of discrete components linked together: man-made systems such as electrical power grids and the World Wide Web (1, 2), social systems such as friendship and scientific collaborations (3, 4), and natural systems such as metabolism in a cell and food webs (5, 6). Despite substantial variation in the nature of individual components and interconnections, many of these networks show notable similarities in their topology (7, 8), often providing new insights into each respective domain of knowledge. For instance, disparate systems such as the world wide web and metabolic reactions in cellular organisms both have been shown to follow the organizational principles of robust, error-tolerant scale-free networks, with implications for the resilience of the internet and the design of therapeutics (8, 9), respectively.

Recent developments in high-throughput density functional theory (HT-DFT) (10) have resulted in massive computational databases of materials properties (11–15), containing the calculated properties of hundreds of thousands of experimentally reported and hypothetical materials. Such databases have led to new data-driven approaches toward understanding materials. Here, we introduce a previosuly unexplored paradigm for viewing materials in general, and equilibrium phase diagrams in particular, using the lens of complex network theory. This approach uses the study of similarities and interactions between materials themselves, in notable contrast to the traditional bottom-up approaches toward unlocking structure-property relationships in materials (16, 17).

We use the Open Quantum Materials Database (OQMD) (11, 12), an HT-DFT database containing calculations of nearly all crystallographically ordered, structurally unique materials experimentally observed to date [as collected in the Inorganic Crystal Structure Database (18) repository] and a large number of hypothetical materials constructed using commonly occurring structural prototypes—a total of more than half a million materials—to extract the “universal phase stability network” or the “universal T = 0 K phase diagram”. We accomplish this by using all the phase data in the OQMD within a convex-hull formalism, and identifying all thermodynamically stable materials and all two-phase equilibria between them. We then represent stable materials as nodes and two-phase equilibria (tie-lines) as edges, thus describing a T = 0 K phase diagram as a network encoding thermodynamic stability (illustrated with schematics in Fig. 1).

Fig. 1. Network representation of T = 0 K materials phase diagrams.

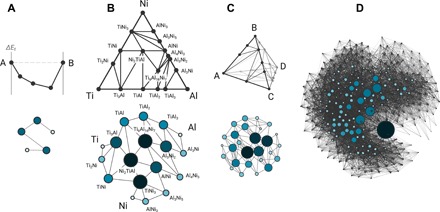
Stable phases and two-phase equilibria (tie-lines) in a phase diagram are represented as nodes and edges, respectively, to create the corresponding network: (A) Schematic A-B binary system represented as a typical two-dimensional convex hull of compound formation energies. (B) Ti-Ni-Al as an example ternary system, with the T = 0 K phase diagram shown as a Gibbs triangle. (C) Schematic A-B-C-D quaternary phase diagram shown as a Gibbs tetrahedron. (D) The 3d transition metal-chalcogen (i.e., 14-dimensional chemical space) materials network. No conventional visual representations of phase diagrams exist at higher than four dimensions. Node sizes shown are proportional to node degree.

RESULTS

Overall network connectivity

We find that the phase stability network of all inorganic materials consists of ∼21,300 nodes and is remarkably dense with a total of nearly 41 million edges, and extremely well connected with ∼3850 edges per node on average (“mean degree” 〈k〉). This means that every stable inorganic compound can form a stable two-phase equilibrium with 3850 other compounds on average. For comparison, 〈k〉 for other widely studied networks range from 1.4 (network of email messages) to 113.4 (collaboration network of film actors) (19). The connectance of the materials network, or the fraction of the maximum possible number of edges that are actually present, is 0.18. This is an important statistic for the design of “systems of materials”, such as electrodes and electrolytes making up batteries (20), or coating materials separating two reactive components (21), where the longevity of the system relies on stable coexistence of such components. Using a lithium-ion intercalation battery as an example “system of materials”, a common approach to tackling electrode degradation is to apply protective coatings on electrode particles. In such a battery, the material in the electrode coating should not react with/be consumed by materials in the electrode as well as those in the electrolyte (22, 23). Thus, the coating-electrode and the coating-electrolyte material pairs must both have tie-lines with each other to stably coexist in the system. In other words, both pairs must be neighboring, connected nodes in the materials network.

The degree distribution in the complete phase stability network, specifically the probability p(k) that a material has a tie-line with other k materials in the network, follows a lognormal form (Fig. 2A and fig. S1). While many widely studied networks are known to have scale-free power-law degree distributions, lognormal distributions are another member of the “heavy-tail” family, are also relatively common, and behave quite similar to power laws (24). Sparsity has been shown to be a necessary condition for the emergence of an exact power law behavior (25), and densification in sparse, scale-free networks leads to distributions that deviate from a power law and become closer to lognormal. Thus, the lognormal behavior of the materials network can be understood to result from its extremely dense connectivity, in contrast to the general sparsity of commonly studied networks.

Fig. 2. Overall structure and topology of the materials network.

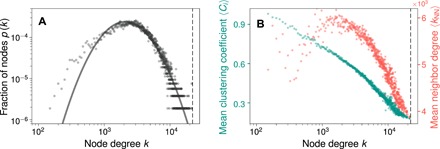
(A) The distribution of node degree in the materials network (gray circles) shows a heavy tail; i.e., a sizeable fraction of materials have tie-lines with nearly all other materials. A lognormal fit is shown as a solid gray line. (B) The mean local clustering coefficient 〈𝒞_i〉 (green) decreases with node degree k, indicating that stable materials form local, highly connected communities. The mean neighbor degree 〈k_NN〉 (red) also decreases with k, implying a weakly dissortative network behavior; i.e., materials with a large number of tie-lines connect with those with fewer tie-lines in the network. In both subplots, the vertical dashed line represents the total number of nodes (stable materials) in the network.

Network topology

The characteristic path length or mean node-node distance in a network, L, is defined as the number of edges in the shortest path between two nodes, averaged over all pairs of nodes. The longest node-node distance in the network defines its diameter, L_max. The characteristic path length of the materials network L = 1.8, and its diameter L_max = 2. This remarkably short path length indicates that the materials network has “small-world” characteristics (1); i.e., despite its large size, the number of edges that need to be traversed from a given node to any other node is relatively small. The extremely small L for the materials network can be intuitively understood to be a consequence of the almost complete lack of reactivity of noble gases. The nonparticipation of noble gases in the formation of compounds (and thus having tie-lines with nearly all materials in the network) places an upper bound of 2 on L_max, and since some material pairs already have tie-lines that connect them immediately, the mean path L is slightly smaller than 2. Even if noble gases are disregarded, the mean path length and diameter of the materials network remain small because of the presence of a few other very highly connected nodes corresponding to extremely stable and nonreactive materials, e.g., binary halides.

Another metric of interest in a real-world network is transitivity or clustering, quantified by its clustering coefficient, 𝒞, which is the probability that two nodes connected to the same third node are themselves connected. In other words, given that there exist stable two-phase equilibria A–C and B–C, what is the probability that A and B can stably coexist? Depending on how the averaging is performed, a global (C_g) or mean local ($\overline{{\mathrm{C}}_{\mathrm{i}}}$) cluster coefficient of a network can be defined (1, 19). For the materials network, the clustering coefficients are C_g = 0.41 and $\overline{{\mathrm{C}}_{\mathrm{i}}}=0.55$, comparable to other real-world networks, and much higher than random networks of the same density. The mean local clustering coefficient of the materials network decreases with increasing node connectivity (Fig. 2B), indicating that stable materials form local highly connected communities in the network, and such behavior often suggests a hierarchical network structure (26). The assortativity coefficient or the Pearson correlation coefficient of degree between pairs of connected nodes in the materials network is −0.13, indicating weakly dissortative mixing behavior. This is also confirmed by the distribution of the mean degree of neighbors of a node of degree k being a decreasing function of k (Fig. 2A). In other words, materials with a high k (i.e., large number of tie-lines) tend to connect with materials with a lower k (i.e., smaller number of tie-lines). This weakly dissortative behavior of the materials network is similar to that observed in most other technological, information, and biological networks and is likely a virtue of such networks being simple graphs (27).

Hierarchy in the materials network

The mean degree or the average number of tie-lines per material 〈k〉 decreases with the number of components, 𝒩 (𝒩 = 2 for binary, 𝒩 = 3 for ternary, etc.; see Fig. 3A), indicating a chemical hierarchy in the materials network. This can be understood to result from an inherent competition for tie-lines that high-𝒩 materials face with low-𝒩 materials in their chemical space, but not vice versa. In other words, ternary compounds X_aY_bZ_c compete not only with other compounds in the X-Y-Z chemical space but also with binary compounds in the X-Y, Y-Z, and Z-X spaces for tie-lines.

Fig. 3. Hierarchy in the materials network and underlying energetic considerations.

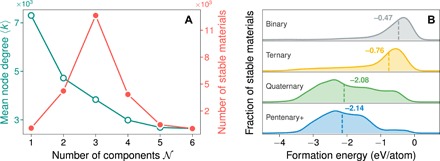
(A) The mean node degree or average number of tie-lines 〈k〉 (green, open) decreases as a function of number of components 𝒩 (i.e., binary, ternary, and so on), which results from high-𝒩 materials having to compete with low-𝒩 materials for stability. The number of known stable 𝒩-ary materials (red) itself actually peaks at 𝒩 = 3 (ternaries). (B) Gaussian kernel density estimates of compound formation energies for all stable materials separated by number of components in the material. Dashed vertical lines indicate the respective median of each distribution. High-𝒩 materials need notably lower formation energies than low-𝒩 materials to become stable, e.g., −2.08 versus −0.47 eV per atom for quaternary and binary materials, respectively.

We note that this decrease in 〈k〉 with 𝒩 is distinct from the distribution of number of stable 𝒩-ary materials itself (Fig. 3A), which shows a peak at 𝒩 = 3. Does this peak in the distribution of stable materials imply the existence of infinite, underexplored space for the discovery of previously unknown materials beyond ternaries? The distribution of formation energies of materials as a function of number of components 𝒩 (Fig. 3B) reflects the consequence of competition between low- and high-component materials: high-𝒩 compounds appear to need substantially lower formation energies than low-𝒩 ones to become stable. Since there is no obvious underlying reason for the distribution of T = 0 K formation energies (with entropic effects neglected) to differ substantially with 𝒩, only a few high-𝒩 materials can “survive” as stable phases if the corresponding lower-𝒩 systems already have several stable phases. This is consistent with the recent reports of a “volcano plot” that emerges for stable inorganic ternary nitrides as a function of energetic competition with their corresponding binary nitrides (28), and an increased probability of phase separation with increasing number of components in a material system (29). Widom (30) further argued that the peak near 𝒩 = 3 or 4 in such distributions arises from a competition between combinatorial explosion and diminishing volume-to-surface ratio in the composition simplex, as 𝒩 increases. Thus, although we do not know of a fundamental law limiting access to thermodynamically stable materials with higher components, a combination of the hierarchy observed in the phase stability network, the distribution of formation energies, and the topology of the convex energy surface all suggest that the scarcity of known high-𝒩 stable materials is not merely a consequence of those chemical spaces being underexplored.

Knowledge extraction: Material nobility index

Since the phase stability network practically encompasses all known inorganic crystalline materials as well as a large number of predicted hypothetical materials, the number of tie-lines emerges as a natural metric of nobility of a crystalline material—it is simply the count of other materials it is determined to have no reactivity against. Thus, while material reactivity or nobility has no standard definitions, a network representation of materials enables us to tackle the chemical nobility of inorganic materials in solid-solid and solid-gas reactions in a completely data-driven fashion, instead of the traditional intuitive or heuristic approaches. Since the number of tie-lines in the materials network is lognormally distributed, we devise a new standard score of material nobility, the “nobility index”

$${\mathrm{Z}}_n=\frac{\mathit{\text{ln}} (k)-\mathrm{\mu }}{\mathrm{\sigma }}$$ (1)

where k is the node degree or the number of tie-lines a material has and μ = 8.06 and σ = 0.65 are the mean and standard deviation of the underlying lognormal distribution, respectively. The nobility index is thus agnostic of textbook classifications such as metal, nonmetal, metalloid, ionic, covalent, and so on and works equally well for any given material. Since the tie-lines in the network are as computed with DFT, the nobilities of materials predicted herewith are only limited by DFT accuracy in estimating relative stabilities of inorganic materials (12, 29, 31).

First, we tackle the reactivity or nobility of elements. Noble gases and fluorine form the bounds of the nobility index (Fig. 4), as the noblest and the most reactive, respectively, not only among the elements but in fact among all materials in the network. The most reactive elements following F are P, S, and Cl. Alkali and alkaline earth metals, often considered to be highly reactive metals, are relatively noble in solid-solid and solid-gas reactions, in comparison to early d-block or lanthanide elements, which are, along with Al, the most reactive metals. The nobility index increases down a group for metals and increases (decreases) from left to right along a row of the periodic table within the d-block (s-block). But what is the noblest metal of them all? Ag emerges as the noblest of all elements after noble gases, followed closely by Hg, Os, Re, W, and Cu, all having more than 14,000 tie-lines. Gold, traditionally considered the noblest element (32), despite being relatively densely connected with 10,000 tie-lines, is less noble in solid-state reactions. Last, we find that 𝒵_n is not correlated with other common elemental properties such as electronegativity, atomic radii, melting point, and others (33), indicating that the nobility index encodes information not readily captured by those properties (fig. S2).

Fig. 4. Nobility index of all elements.

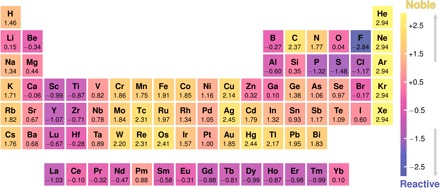
The standard score, 𝒵_n, derived in this work using material connectivity in the phase stability network, as a measure of nobility against solid-solid and solid-gas reactions. Nobility increases up the scale. Numerical values of elemental 𝒵_n are given below the respective symbols.

Beyond elements, what are the noblest inorganic compounds of all? The compounds at the top of the nobility list are IA/IIA-VIIA compounds such as LiF, NaCl, KCl, CsCl, KBr, CsBr, KI, RbI, CaF₂, SrF₂, CsYbF₃, RbYbF₃, and others, their inertness likely due to stability from strong ionic bonding between their constituents. We exclude rare earth– and actinide-containing compounds from the previous analysis of compound nobility to account for any shortcomings in the DFT description of f-block elements and compounds containing them.

DISCUSSION

While some of our findings above are in line with chemical intuition, relative nobilities in certain cases, e.g., silver versus gold, deviate from it. This deviation is, in part, due to the historical context in which these materials have been considered noble or reactive, e.g., whether an element oxidizes or corrodes readily in air, reacts with water and/or certain acids, and dissolves in water or electrolytes, and how vigorous such reactions seem. More fundamental approaches to finding descriptors for reactivity go back to electronegativity-related concepts, followed by interrelated theories based on perturbation theory, derivatives of electronic energy such as hardness and softness, and others largely developed for molecules (34–37). In contrast, the nobility index, 𝒵_n, as derived from the tie-lines in the network of all inorganic materials, represents a general metric emerging directly from bulk thermodynamic data.

High-throughput experimental and computational techniques are leading to an explosive growth in the size of materials databases. Representation and interpretation of the data at a large scale, however, remain a challenge. Here, we show that tools from complex network theory enable us to access otherwise difficult-to-extract information from such large datasets. In other words, the emergence of material reactivity from the collective behavior of all materials in the phase stability network serves as a simple, preliminary example of knowledge extraction out of complex networks of materials. Other similar approaches can be used to discover other hidden knowledge; e.g., analysis of “communities” or “cliques” in the network of all materials can uncover hitherto-unknown relationships between various known materials.

Further, there are various ways our graph theoretic approach to materials data can be used to be immediately applied to materials discovery and design: (i) Direct techniques, e.g., metrics from network theory such as local clustering and similarity, can be used to identify “holes” in the current network—where nodes (i.e., materials) are expected to exist but currently do not. (ii) Indirect techniques, e.g., using the extracted knowledge or quantities derived from the network as input to other approaches such as in materials informatics. For example, using temporal materials discovery information in combination with thermodynamic phase stability networks can help predict synthesizability (38). Furthermore, while some of its features resemble other complex networks, the extremely high connectance and the lognormal degree distribution of the presented phase stability network imply that its underlying generative mechanisms may be unique, and developing generative models for such materials networks can have substantial impact on the knowledge discovery of materials in the future.

METHODS

All convex hull constructions were performed using the Qhull library (39) as implemented in the qmpy (pypi.org/project/qmpy) package. All network analyses were performed using the graph-tool (40) and powerlaw (41) packages, and comparison of heavy-tailed distributions was done according to the method of log likelihood ratios as described by Clauset et al. (42). Details of the divide-and-conquer approach used to tackle the combinatorial explosion in calculating the universal phase diagram, the related exponential increase in the time complexity to construct convex hulls in higher dimensions (43), its network representation, and determining the node degree distribution are provided in the Supplementary Materials.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/9/eaay5606/DC1

Section S1. Calculation of the T = 0 K universal phase diagram

Section S2. Degree distribution of the network of all materials

Section S3. New information encoded in the nobility index

Table S1. Sample compute times for calculating the existence of a tie-line between two phases.

Fig. S1. Fitting node connectivity data to candidate distributions.

Fig. S2. Comparison of nobility index versus common elemental properties.

Fig. S3. Comparison of number of compounds formed by an element versus its node degree.