Abstract
Introduction
The adhesion of tumor cells to vessel wall is a critical stage in cancer metastasis. Firm adhesion of cancer cells is usually followed by their extravasation through the endothelium. Despite previous studies identifying the influential parameters in the adhesive behavior of the cancer cell to a planer substrate, less is known about the interactions between the cancer cell and microvasculature wall and whether these interactions exhibit organ specificity. The objective of our study is to characterize sizes of microvasculature where a deformable circulating cell (DCC) would firmly adhere or roll over the wall, as well as to identify parameters that facilitate such firm adherence and underlying mechanisms driving adhesive interactions.
Methods
A three-dimensional model of DCCs is applied to simulate the fluid-structure interaction between the DCC and surrounding fluid. A dynamic adhesion model, where an adhesion molecule is modeled as a spring, is employed to represent the stochastic receptor-ligand interactions using kinetic rate expressions.
Results
Our results reveal that both the cell deformability and low shear rate of flow promote the firm adhesion of DCC in small vessels (). Our findings suggest that ligand–receptor bonds of PSGL-1-P-selectin may lead to firm adherence of DCC in smaller vessels and rolling-adhesion of DCC in larger ones where cell velocity drops to facilitate the activation of integrin-ICAM-1 bonds.
Conclusions
Our study provides a framework to predict accurately where different DCC-types are likely to adhere firmly in microvasculature and to establish the criteria predisposing cancer cells to such firm adhesion.
Electronic supplementary material
The online version of this article (10.1007/s12195-020-00610-7) contains supplementary material, which is available to authorized users.
Keywords: Cancer cell, Cell deformability, Microvasculature, Selectins, Adhesion, Firm adhesion, Rolling, Metastasis, Vessel diameter, Hemodynamics, Survival time, Detach, Critical dissociation rate
Introduction
The extravasation of a deformable circulating cancer cell is a highly dynamic process that involves the modulation of tumor cell adhesion to the endothelium and intravascular cell migration through the endothelial cells lining the vascular wall.10,14,29,40,45 In order to exit the circulatory system, a cancer cell must first bind to a blood vessel wall through the formation of adhesive bonds associated with ligand–receptor reactions between the cell and endothelial cells.10,14,40 Firm adhesion is a key transition for the transmigration process because it ends the rolling process and starts positioning cells on the endothelium in preparation for transmigration.2,5,10,16 Dynamic adhesive and mechanical interactions between the cancer cell and the endothelium are critical to the biophysical processes of adhesion and transmigration.10,14,40 Thus, the focus of this study is on understanding the metastatic process by identifying the vessel sizes for which deformable cells have a higher probability of adherence and the biophysical criteria that facilitate firm adhesion of cells to the vessel wall.
The location of firm adhesion in vessels has been shown to be based partly on the anatomy of the vascular structure and the local hemodynamic conditions.7,9,13,14,18,23,29,38–40,42,44,45,49 Reference 14 reported that most deformable cancer cells are entrapped in capillaries, postcapillary, venule intersections, and in postcapillary venules. Although adhesion of cancer cells and leukocytes has been studied extensively, studies focused mostly on ligand–receptor interactions between the cells and a planar substrate.2–5,16–19,22,24,31,46,50 To best of our knowledge, References 49 and 44 investigated the adhesion of cells to vessels. Reference 49 applied a 2D model in which a cell was idealized as a disk to study the effect of local hemodynamics on the cell adhesion whereas Reference 44 used a 3D model of capillaries with diameters comparable or smaller than the cell diameter.
The mechanical properties of cancer cells has been shown to influence their malignancy.9,13,14, 29, 40,45 Stiff cancer cells have lower migration and invasion potential compared with cells that are five times less stiff.43 Reference 14 observed more invasive, malignant, and metastatic behavior of cancer cells with greater deformability. In addition, rigid beads were arrested and adhered in different locations compared with tumor cells for which mechanical trapping was responsible for almost all the arrest of beads. Reference 18 demonstrated in a 3D computational model that the average number of bonds per leukocyte decreases with increasing leukocyte stiffness because of higher hydrodynamic forces experienced by the stiffer leukocytes.
Local hemodynamics has also been shown to play a key role in determining locations of cancer cell adhesion to the vasculature wall.7,13,14,38, 40, 42, 45, 49 Reference 14 observed in vivo that local hemodynamic factors may modulate the interactions between the cancer cell and the endothelium. However, they did not investigate how hemodynamic factors could affect both the cell-endothelium interactions and trajectory of the cell in the microvasculature. Reference 44 modeled the cancer cell adhesion in smaller vessels and reported that the rolling velocity of the cell and the number of adhesive bonds formed vary with the shear rate, which is directly related to blood velocity, in the capillaries. Other investigators have similarly reported that the interactions between tumor cells and the endothelium vary with local hemodynamics.7,38
Despite previous identification of key parameters that affect adhesive interactions between cancer cells and microvasculature wall, we still lack the ability to predict the locations in the vascular network where different cancer cell types may firmly adhere, roll, or detach. Further, we do not understand how the local microenvironment affects adhesive behavior of deformable cancer cells. In this study, we developed a computational model to investigate the functions of the microvasculature size, local hemodynamics, adhesion molecular properties, and cell stiffness on the dynamic adhesive interactions between the deformable cell and the microvasculature wall. We performed simulations with HARVEY, an in-house developed computational fluid dynamics solver based on the lattice Boltzmann method.33–35 We used fluid-structure interaction functionality implemented via the immersed boundary method to couple a finite element model for the deformable circulating cell (DCC) to the fluid model.11 A kinetic-based stochastic, dynamic adhesion model, appropriate for modeling of an adhesion molecule as a spring, was implemented in HARVEY to simulate the stochastic receptor-ligand interactions. We investigated the adhesion of DCCs to wall of vessels with wide range of diameters (comparable to or larger than the cell diameter). We quantified the effect of the microenvironment on the number of ligand–receptor bonds between the DCC and the wall, the lifetime of the bonds, the DCC’s velocity, the adhesion force on the bonds, the critical disassociation rate for transition from firm-adhesion-to-detachment and rolling-adhesion-to-detachment, and the critical capillary number for transition from rolling-adhesion-to-firm-adhesion. Taken together, we investigated the mechanisms underlying the adhesive behavior of the deformable cells circulating in different regions of the microvasculature. The results of our study enable precise prediction of spots of the microvasculature prone to firm adherence of different cancer cell types. Our findings will facilitate development of more efficient targeted therapeutic strategies.
Methods
Figure 1 displays a schematic of the computational domain in which the adhesive interaction between a deformable cancer cell and a vessel wall coated by P-selectin was studied. Several in vivo studies suggest that rolling interactions of leukocytes with vascular endothelial cells are mediated primarily by endothelial P-selectin that binds P-selectin glycoprotein ligand-1 (PSGL-1) expressed on the surface of leukocytes.17,20,31 The initial cancer cell was spherical with a diameter of 8 ; the cell migrated within the vessel with a diameter comparable to or larger than the cell diameter. We accounted for the fluid-structure-interaction (FSI) between the cancer cell and fluid flow by coupling the finite element model for the cell (defined on a Lagrangian grid) with the lattice Boltzmann method (defined on a Eulerian grid).32
Figure 1.
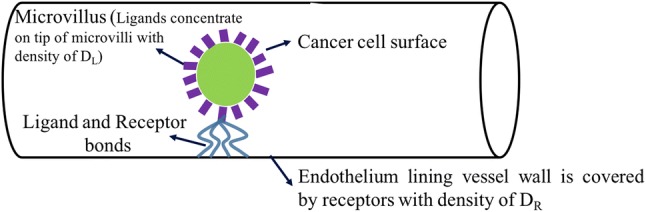
Schematic illustration of adhesive ligand–receptor interaction between cancer cell PSGL-1 and endothelial P-selectin. Deformable, circulating cancer cell which initially has spherical shape migrates through a vessel.
Lattice Boltzmann
As the backbone of our mathematical model, we used HARVEY, a parallel computational fluid dynamics solver that implements the lattice Boltzmann method (LBM) to perform computational simulations of flow in complex 3D geometries.33–35,41 The LBM is a deterministic, mesoscopic approach to numerically solve the Navier–Stokes equations governing fluid flows. Discretizing space and velocity with a fixed Cartesian lattice, LBM models the fluid with a particle distribution function that denotes the probability of finding a particle at time t and lattice point with the discrete velocity . The evolution of distribution f is governed by the lattice Boltzmann equation:
| 1 |
The local equilibrium is the second-order expansion of the local Maxwellian-Boltzmann distribution. The distribution corresponds to external force being applied to the fluid. HARVEY implementation of LBM made use of the standard D3Q19 velocity discretization, BGK collision operator , and kinematic viscosity with lattice speed of sound . A no-slip boundary condition was enforced on the geometry surfaces by the halfway bounce-back boundary, whereas Zou-He boundary conditions were used at the inlets and outlets with a fixed velocity profile at the inlet and a fixed pressure at the outlet.11 The BGK collision kernel from previous HARVEY implementations was extended to include an external force distribution derived from an external force .11 The external force was used in the immersed boundary method to couple fluid and cancer cell dynamics. The hydrodynamic moments, density and momentum , in this kernel were computed as
| 2 |
| 3 |
The velocity, , is used to compute the Maxwell–Boltzmann equilibrium distribution. Further, and were applied to compute the components of external force distribution. Additional details about the HARVEY implementation, parallelization, and scaling may be found in References 33–35.
Deformable Cell Finite Element Model
Cell circulation and deformation due to the effects of different parameters (e.g. membrane mechanical properties) have been widely studied.11,14,17–19,23,24,31,40,44,46,50 A two-dimensional rigid sphere model has been systematically applied for cell motion modeling.5,49 Immersed boundary (IBM)11,17,31,44,50 or the volume-of-fluid (VOF)19,20 methods have been applied for three-dimensional simulations of circulating cells where cells are modeled as fluid-filled capsules surrounded by a single zero-thickness11,12,17,25,31,44,50 or finite thickness membrane.8 We followed the approach described by Reference 28 that applied a front-tracking method to study the deformation of an elastic compound capsule in shear flow. In the present study, the cancer cell was represented as a compound capsule with a zero-thickness outer cell membrane.28 Major cellular elements were incorporated into the model including the outer cell membrane and the cytoplasm. Flat triangular elements were used as a numerical representation of the cell membrane. The triangular grid, using 20480 elements, for the cell membrane was created by taking successive subdivisions of an icosahedron, which produces favorable regularity and isotropy. The grid was then projected onto the cell’s initially spherical shape.11,25 The shear and dilational elastic responses to strain of cell membrane were governed by a Skalak constitutive law,
| 4 |
where were strain invariants, G was shear elastic modulus, and C was the ratio of dilational to shear elastic moduli. The membrane forces from the strain energy function were computed using a simple finite element model.37 Furthermore, the membrane bending resistance was considered with a bending modulus of .27,44,51 Cytoplasm and palsma were assumed as Newtonian fluid44 with viscosity of Pa s.44 Red blood cells were not included in the current model, but their presence may not impact the adhesion of circulating cancer cells in the vessel sizes applied in the present study.47
Immersed Boundary
We accounted for interaction between the cancer cell and fluid flow by coupling the finite element model for the cell (defined on a Lagrangian grid) with the LBM (defined on a Eulerian grid).32 The IBM enforced the no-slip condition on the capsule surface and allowed the cell to exert a force on the surrounding fluid. Physical values between the two grids were transferred using a discrete delta function . In this implementation, the discrete delta function was defined by the one-dimensional delta function
| 5 |
using the spatial step of the fluid grid. Three components of the IBM were used in our implementation: spreading, interpolation, and updating. The force defined on the cell vertex was spread onto the fluid grid by the equation
| 6 |
and fluid velocity was updated with the lattice Boltzmann algorithm. In the interpolation step, the updated velocity of the capsule vertex was computed at time with the sum
| 7 |
Finally, the position of the capsule vertex was updated using the no-slip condition:
| 8 |
A general discussion of the coupling of LBM and finite element methods with IBM may be found in Reference 25. In the present study, the mesh size of LBM was set to be 150 nm, and that of FEM was approximately 150 nm (an unstructured mesh with 20480 elements for cancer cell). The grid resolution of both LBM and FEM methods were determined by comparing the deformation of an initially spherical cancer cell located at the center of a vessel with diameter of where the ratio of diameter of cell () to diameter of vessel () is 0.77 (Fig. S1A–S1B), with the results of References 44 and 26. The comparison was examined with grid spacing varying in the range of 120, 125, 130, 140, 150, 160, 170, 180, 190, and 200 nm. Consistency in cell deformation magnitude was observed in range of 125–180 nm. We set the grid spacing to 150 nm. Figures S1C show the comparison between our results, References 44 and 26 on deformed shape of the DCC subjected to the shear rates corresponding to Ca=0.02 and 0.052, with the grid resolution size of 150 nm (for more detail, see Appendix).
Kinetic Models of Ligand–Receptor Interactions
We modeled the interaction between receptors and ligands using the kinetic-based stochastic, dynamic adhesion model proposed by Reference 6 for modeling an adhesion molecule as a spring. P-selectin glycoprotein ligand-1 (PSGL-1) was assumed as the ligand (and the adhesion molecule) on the cell membrane where P-selectin was considered as the receptor (and the adhesion molecule) on the vessel wall. Ligands concentrate on the tip of microvilli whose average length is 0.5 .44 Microvilli were uniformly distributed over the cell membrane with the density whereas each microvillus had 50 ligands.30,44 Receptors, on the surface of the endothelium lining the vessel wall, were uniformly distributed with the density of (Fig. 1). The ligand–receptor parameters applied in the model are summarized in Table 1. We computed explicitly, at each time step, the formation probability of each bond between the ligands and the receptors. After the bond was formed, its survival or rupture probability was computed. Kinetic properties of the receptor-ligand adhesion bonds, PSGL-1-P-selectin, were quantified using Monte Carlo simulations.2,3,5,16–19,22,31,44,50 We applied the following rules to examine PSGL-1-P-selectin binding: (1) one ligand can bind to one receptor, (2) ligands from one microvillus can bind to several receptors. In our stochastic kinetic-based dynamic, adhesion model, when an unbound PSGL-1 and an unbound P-selectin were separated by a length less than a microvillus, a test for forming a bond was performed. A PSGL-1-P-selectin bond was modeled as a linear spring. The probability of formation or rupture of the bond in a time interval of was calculated by:
| 9 |
| 10 |
where was the probability of formation, was the probability of an existing bond’s disassociation, was the association rate, and was the disassociation rate. and were given by:
| 11 |
| 12 |
where L was the bond length and was the reference length of the spring which was assumed as the length of the microvillus. and were the forward and reverse rate constants at equilibrium distance. was the spring constant whereas represented the transition state spring constant. (1.38e-23 J/K) was the Boltzmann constant and T (310 K) was the absolute temperature. At a given time instance, two random numbers were generated between 0 and 1. A PSGL-1-P-selectin bond was formed if was greater than the first number whereas an existing bond was ruptured if was greater than the second. The adhesion force of the PSGL-1-P-selectin bond was calculated using a spring model as follows44:
| 13 |
where Lij was the relative position of an adherent point (ligand) on cell membrane to its paired point (receptor) on the vessel wall.
Table 1.
Model parameters in the simulations.
| Definition | Parameters | Value | References |
|---|---|---|---|
| Cancer cell diameter | 8 | 14,44,49 | |
| Capillary diameter | 8.82, 9, 10, 10.4,12, 14, 16 | 14,21,49 | |
| Cell surface shear elastic modulus | G | 30, 3, 0.3 N/m | 14,17–19, 31,44,49 |
| Bending modulus | J | 44 | |
| Association constant rate | 50 | ||
| Dissociation constant rate | 0.35, 3.5, 35,350,3500,35000 | 50 | |
| Microvilli density | 5 / | 30 | |
| Ligand (PSGL-1) density | 50/microvillus | 44 | |
| Receptor (P-selectin) density | 30 | 48 | |
| Spring constant | 0.35 mN/m | 50 | |
| Transition state spring constant | 7 N/m | 50 | |
| Palsma viscosity | Pa s | 11 | |
| Palsma density | Kg/m | 44 | |
| Unstressed microvilli length | 0.5 | 44 |
Model Parameters
Test ranges and the reference values of geometric and the mechanical parameters of deformable cell and the vessel applied in the model are summarized in Table 1. The properties of the receptor, ligand, and microvilli are also given in Table 1. We quantified the cell adhesive behavior with the cell velocity, the cell deformation, the number of ligand–receptor bonds, the average lifetime of each ligand–receptor bonds, and the average adhesion force of each ligand–receptor bonds. Note that result of one run is shown our data were consistent over five independent runs. We defined the dimensionless parameter, capillary number (Ca) as for shear rate and outer membrane radius R. was defined as , where U was the mean fluid velocity at the inlet.
Results and Discussion
Effects of Microvasculature Geometry, Local Hemodynamics, and Cell Stiffness on Adhesive Behavior of the Deformable Cell
Tumor cell metastasis relies on continuous cross-talk between the tumor cells and their local microenvironment.13,40,45 In this part, we investigated how the microenvironment conditions of the vasculature and the mechanical properties of the DCC may affect its migration, deformation, and dynamic adhesive interactions with the microvasculature wall. Three distinctive values of DCC surface shear elastic modulus (G) were examined: 30, 3, and 0.3 N/m.14,17,26,44,50 A DCC with the diameter of 8 14,17,26,44,50 migrated within a vessel with diameters of 8.82, 9, 10, 12, 14, and 16 .14,44 The range of vessel diameter was selected based on the findings in Reference 14 regarding the geometrical characteristics of vessels where deformable cancer cells mostly extravasate. Here, we evaluated the effect of cell stiffness, vascular anatomic geometry, and local hemodynamics on the adhesive behavior of the DCC, velocity of the DCC, and the deformation of the DCC. In this part, the formation constant of PSGL-1-P-selectin bond was and the dissociation rate was .5,22,49,50
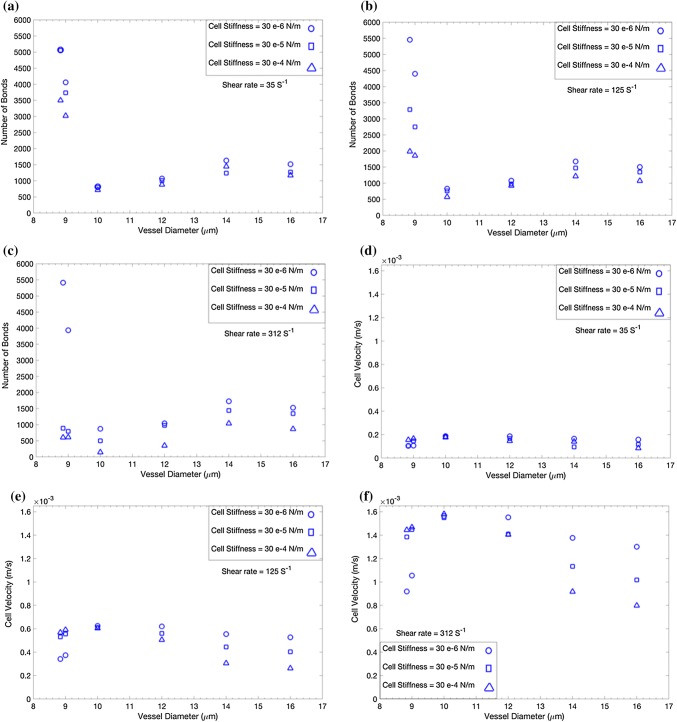
In Figs. 2a–2c, we demonstrate the number of ligand–receptor bonds between the DCC and the microvasculature wall vs. the vessel diameter under three physiological shear rates as = 312 , = 125 , and = 35 in Figs. 2a–2c, respectively.17,18,31,44,50 It was evident from Figs. 2a–2c that the number of ligand–receptor bonds depends on the diameter of the vessel, mechanical properties of the DCC, and the hemodynamic condition within the vessel. The number of bonds for the DCC migrating in a vessel with was in the range of data reported by References 17 and 50, considering that 1000 microvilli were present over the DCC surface in our study vs. 250 in Reference 17 and 600 ligands cover the DCC in Reference 50. Figures 2a–2c showed a significant difference in the number of bonds for vessel sizes and . In both vessel size categories, the stiffness of the DCC had a notable effect on the number of ligand–receptor bonds under higher shear rates. The mechanical properties of DCCs had a larger effect in smaller capillaries. We confirmed that the influence of cell stiffness is hindered under lower shear rates, as previously reported by References 17 and 50. Figures 2d–2f demonstrate the velocity of the DCC, under = in Fig. 2d, = in Fig. 2e, and = in Fig. 2f. The velocity shown in Fig. 2 is the translational velocity of the center of the tumor cell along the axial direction of a vessel. The calculated velocity of the DCC in the present study was in good agreement with the data reported by References 21 and 49. We observed a significantly distinct effect of DCC stiffness on DCC velocity in both smaller () and larger () capillaries. Softer cancer cells migrated slowly in smaller vessels, whereas softer cells moved faster in larger capillaries. In addition, the stiffness of the DCC had a higher impact on the cell velocity under higher shear rates, in both vessel size categories.
Figure 2.
Effect of vascular anatomic geometry, hemodynamics, and cell stiffness on adhesive behavior of a deformable cancer cell. (a–c) The number of bonds between the cancer cell and the endothelium vs. the vessel diameter under shear rate of 312, 125, and respectively. (d–f) Cancer cell velocity vs. the vessel diameter under shear rate of 312, 125, and respectively.
The aspect ratio of the DCC was measured with the Taylor deformation parameter, defined as and using the major and minor axes L and B of the ellipsoid with the same moment of inertia as the DCC.11 Figures 3a–3c demonstrates that the aspect ratio changes as shear rate was varied. Figure 3a presents the DCC aspect ratio vs. shear elastic modulus of DCC for six different vessel diameters, under = 312 , where = 125 in Fig. 3b and = 35 in Fig. 3c. It is evident from Figures 3a–3c that DCCs displayed larger deformations in smaller vessel diameters whereas stiffer DCCs underwent smaller deformations. Larger deformations were observed under higher shear rates. Under a lower shear rate of , only DCCs migrating within the vessel with of exhibited distinct deformation. Moreover, Fig. 3c demonstrates that DCCs show a small change in its aspect ratio over a two-fold change in cell stiffness, under lower shear rates. Further investigation of DCC shape change demonstrated that the DCC exhibits bullet motion during migration within the vessel with as (Figs. 4a and 4b). The deformation of DCCs to bullet-like shape was previously observed by Reference 44 in the subset of vessels whose diameter was comparable to cell diameter. Here, we show that in of , DCCs also deformed to the bullet-like shape. We also demonstrate that, in of , DCCs deformed to the bullet-like shape at lower shear rates whereas stiffer cells exhibited the bullet-like shape at higher shear rate of . Figure 4a demonstrates that the DCC bullet-like shape occurred for of 8.82 whereas Fig. 4b shows a DCC rolling shape observed when was . In Figs. 4a–4b, the stiffness of DCC was and the shear rate was .
Figure 3.
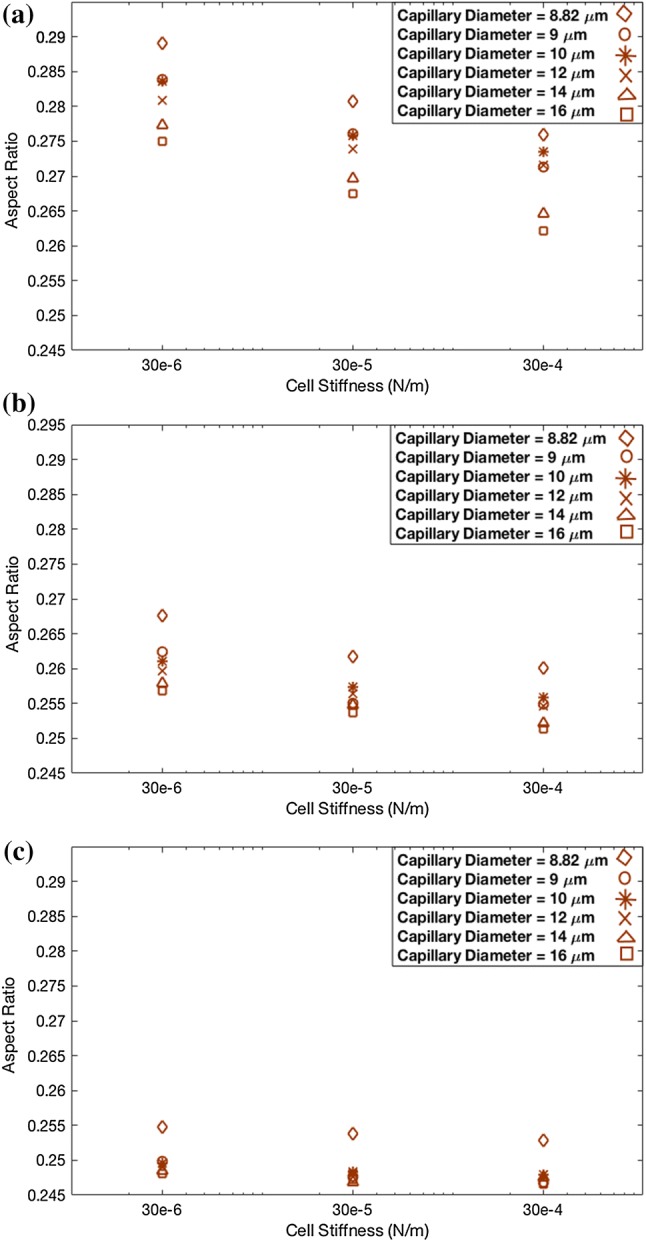
Deformation of deformable cell migrating in vessels with different diameters. (a) shear rate is . (b) shear rate is . (c) shear rate is .
Figure 4.
Snapshot of a deformable, circulating cancer cell: (a) in vessel with diameter of 8.82 , a cell with stiffness of 30 N/m exhibits bullet motion. (b) in vessel with diameter of 14 , a cell with stiffness of 30 N/m exhibits rolling. Flow direction is from left to right. The colored points on cell surface show the microvilli involved in binding.
Furthermore, we examined the behavior of DCCs in the vessels with a in the range of 8.82 to 16 . A state diagram of DCC motion vs. and the capillary number, Ca, is depicted in Fig. 5. A stiffer DCC exhibited bullet motion for , particularly at lower shear rate, whereas a softer DCC exhibited rolling in all vessel sizes except as 8.82 and 9 . The motion of DCC in different vessels sizes can explain the discrepancy in the number of ligand–receptor bonds in Figs. 2a–2c and cell velocity in Figs. 2d–2f. When a DCC exhibited the bullet motion, its shape provided more ligands capable of forming adhesive bonds with the receptors over the vessel wall. During DCC rolling in larger capillaries, softer DCCs presented more bonds as they can be more flattened over endothelium that is covered with receptors.
Figure 5.
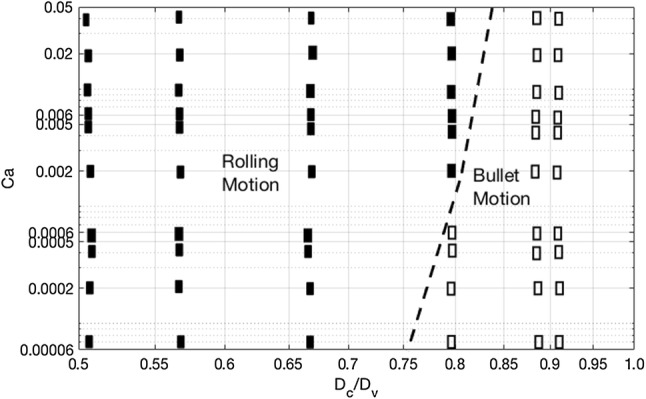
State diagram of deformable cancer cell motion in capillaries as a function of the capillary number Ca and normalized capillary radius(/). The closed squares represent rolling motion of the cell and the open squares are bullet motion.
Effect of Bond Affinity on Adhesive Behavior of Cancer Cell
In this section, we investigated the conditions that predispose different cell types to firmly adhere on the vessel wall, roll over the wall, or detach from the wall of the vessel. Tumor cells may express different ligand types when residing at different regions of the vasculature and under discrepant microenvironmental conditions.36,40 Then, the bonds between these ligands and their pair receptors will in turn affect the dynamic interactions between the cancer cells and the endothelium.15,36,44,50 To explain why different metastatic cell types adhere to specific locations of the vasculature, there is a need to determine how DCC affinity is associated with the cell adhesion in these regions under local microenvironment conditions. Here, we examined how the affinities of ligand–receptor pairs influence the adhesive interactions of DCC-wall. We quantified the effect of disassociation rate on the number of adhesive bonds between the DCC and endothelium, the average lifetime of ligand–receptor bonds, the average adhesion force on ligand–receptor bonds, and the critical off rate for transition from firm-adhesion-to-detachment and rolling-adhesion-to-detachment. The disassociation (off) rate has been shown to impact the adhesive behavior of cells.44,50 State diagrams of DCC adhesive states vs. capillary number and the disassociation rate constant are presented to determine the critical capillary number for transition from rolling-adhesion to firm-adhesion. We focused on DCC migration within two vessel diameters of and The formation constant was and the off rate varied as 0.35, 3.5, 35, 350, 3500, and 35000 .50
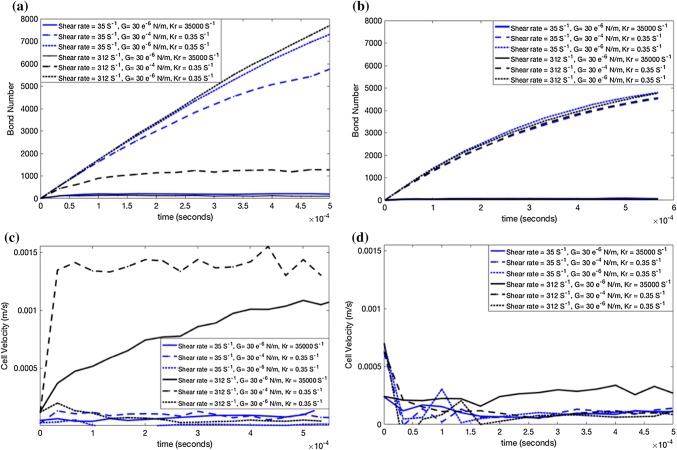
Figures 6a–6c demonstrate the number of ligand–receptor bonds, the average lifetime of each bond, and the average adhesion force of each bond for the as 8.82 , where Figs. 6d–6e stand for the of . It is evident from Figs. 6a–6e that the DCC formed a higher number of bonds when ligand–receptor pairs had a lower off rate, whereas the number of bonds dropped dramatically with an increase in the off rate. This result was consistent with previous experiments that indicated the ligand–receptor types (e.g., L-selectin) with higher off rates form lower number of bonds with shorter lifetime.1 For the DCCs migrating in the vessel with set as , the hemodynamic conditions and cell stiffness significantly affected the bond number, the bond lifetime, and the bond adhesion force, whereas a greater effect was observed at lower off rates under higher shear rates (Figs. 6a–6c). In addition, Fig. 6c shows that less deformable cells, which are subject to larger torques and drag forces, experienced larger adhesion forces. The fact that less deformable cells under high shear rates were subject to larger torque, drag, and adhesion forces can explain why these cells formed a lower number of bonds with higher rupture probability (shorter lifetime) as observed for stiffer DCC in Figs. 6a–6b. Note that the probability of rupturing a ligand–receptor bond increased under larger forces. Adhesive behavior of the DCC under lower shear rates was not significantly sensitive to the cell stiffness and even stiff cells could form a higher number of long surviving bonds. Thus, cell stiffness and cell deformation did not alter the cell adhesive behavior under low shear rates. Under lower shear rates, adhesive behavior of the DCC was also not significantly sensitive to the magnitude of the off rate. Our findings revealed that not only softer cancer cells but stiffer DCCs which exhibit bullet motion can firmly adhere to the endothelial cells of smaller vessels. This observation gives a new perspective to the study by Reference 44 that suggested that the bullet motion enables the firm adhesion of cell. Note that Reference 44 studied only adhesive behavior of very soft cells at one specific rate of formation and off constant rate. Like our results, they observed a slight decrease in the number of bonds under lower shear rates (Fig. 5B in Reference 44 and Figs. 2a and 2c of our study). However, our further investigation showed that the number of bonds for the cells circulating in small vessels under low shear was sufficient for firm cell adherence even at greater off rates. For of , a higher number of bonds with longer lifetimes was observed at lower off rates (Figs. 6d–6e). We observed that a stiffer DCC under high shear rate was subject to higher adhesion force, even in low off rates and that a DCC exposed to lower shear rates was subject to lower adhesion force independent of the cell stiffness. The maximum bond force was observed (in Fig. 6e) in the ligand–receptor bond before its rupture.
Figure 6.
Effect of cell affinity on dynamic adhesive interaction between the cancer cell and the endothelium. (a–c) Vessel diameter is 8.82 . (d–f) Vessel diameter is 14 . The number of bonds, average lifetime of each ligand–receptor bond, and average adhesion force are shown, respectively.
We further examined the effect of the off rate on adhesive states between the DCC and the vessel wall. Several disassociation rates and capillary numbers were examined to determine the suitable range of parameters for the discrepant adhesive states of the DCCs. Figure 7 identifies three conditions that exhibit three different adhesive states between the DCC and the vessel wall, where firm adhesion was defined as the condition in which the formed bonds is increased with decreasing the cell velocity. Figures 7a and 7b demonstrate the number of bonds vs. time, when the cell was circulating within a vessel with the set to 8.82 and , respectively. Figures 7c and 7d demonstrate the cell velocity for the vessel diameter of 8.82 and , respectively. In the smaller capillary and at lower shear rates, firm adhesion occurred for DCCs independent of cell stiffness at lower off rates whereas DCCs detached at higher off rates. At higher shear rate, softer DCCs with lower off rates firmly adhered to the vessel wall whereas the soft DCCs detached at higher off rates. Stiffer cells, under a high shear rate, exhibited intermittent bullet motion even at lower off rates. In the larger capillary, the DCCs experienced the rolling at lower shear rates and softer DCCs detached at the higher off rates. In a rolling state, the existing bonds ruptured and formed continuously according to local microenvironmental conditions. In this case, the number of bonds remained relatively constant even though fluctuations in the bond number were observed. In the detached state, the number of bonds decreased gradually to finally dislodge the cell from the vessel wall to migrate within the blood stream. In contrast to the detachment state, under the firm adhesion state, the number of bonds increased gradually to enable the cancer cell to spread over the endothelium. Our observations of cell adhesive states in large vessels agree well with the data reported by Reference 50, who investigated the probability of adhesive bond formation between PSGL-1 and P-selectin of a spherical cell and a planer substrate.
Figure 7.
Three adhesion state of cancer cell. Time evolution of bound numbers between the deformable, circulating cancer cell and the endothelium of vessel with diameters of: (a) 8.82 and (b) 14 . Detachment occurs at high dissociation rate. At lower off rate, softer cells firmly adhere whereas stiffer cell exhibit rolling adhesion in a smaller vessel. In a larger vessel, cells show a rolling sate at lower off rate.
Figure 8 shows the state diagram of DCCs adhesive states vs. capillary number and disassociation rate constant. In Fig. 8a, was set to under the shear rate of . In Fig. 8b, was set to under shear rate of . For is , the DCCs exhibited intermittent bullet motion over the the vessel wall with off rates below and the detachment occurred with off rates greater than . The shear rate magnitude did not affect the adhesive behavior of DCC in larger vessels. Therefore, it can be concluded that DCCs may not adhere firmly in vessels with larger diameters, a result that agrees with the finding of Reference 44. Figures 8a–8b reveal that the critical off rate for the DCC to transition from firm-adhesion-to-detach or intermittent bullet motion-to-detach depended on capillary number. In a small vessel, the critical off rate for transition from firm adhesion /intermittent bullet motion to detachment increased with increasing Ca. Thus, the DCC detachment was facilitated by the cell rigidity. We observed that the critical off rate for cell detachment was higher for softer DCC. This finding may be explained by the fact that the deformation of softer cells in the direction of flow, which causes a bullet shape for the cell under high shear or the cell elongation under low shear, leads to smaller drag force. Under high capillary numbers, the DCC detached only under very large off rates. The critical capillary number for the transition from intermittent bullet motion to firm adhesion depended on the shear rate whereas rolling to firm-adhesion transition occurred at low Ca under low shear rate (see Figs. 8a–8b).
Figure 8.
State diagram of deformable cancer cell adhesion to the endothelium as a function of capillary number, Ca, and dissociation number, Kr. (a) Vessel diameter is 8.82 and shear rate is . (b) Vessel diameter is 8.84 and shear rate is . Closed squares represent rolling-adhesion state, open squares show the detachment state, closed circles represent the firm-adhesion state.
Conclusions
Mechanisms driving adhesion of tumor cells in the microvasculature have not been completely understood, despite several studies that focused on the adhesion of leukocytes and cancer cells in planer substrates or small capillaries. In the present study, we aimed to first identify the sizes of the microvasculature where deformable cells are likely to firmly adhere or exhibit rolling adhesion and then explain the mechanisms of cell adhesion to the vessel wall in these vessels. Our main goal was to explore the criteria that predisposes a deformable cell in the microvasculature to firm adhesion. We applied a computational method based on a lattice Boltzmann method-immersed boundary coupling to investigate the dynamic adhesive interactions between a deformable, circulating cell and the wall of vessels whose diameters were comparable to, or larger than, the diameter of the cancer cell. This range of vessel diameters is more susceptible to the adhesion of deformable cells. We introduced a kinetic-based dynamic adhesion model to simulate the stochastic receptor-ligand interactions. We quantified the effect of cell properties, adhesion molecule properties, anatomical structure of microvasculature, and local hemodynamic conditions on the dynamic adhesive interactions between DCCs and the vessel wall.
The size of vessels where circulating deformable cells firmly adhere was identified. Deformable, circulating cells form a higher number of bonds in vessels with a diameter . In these vessels, the adhesive state of cells depends significantly on the cell deformability and local hemodynamic conditions. Softer cells typically adhere firmly to the vessel wall and move slowly. The critical disassociation rate for the rupture of ligand–receptor-bonds is strongly related to the DCC deformability and the local hemodynamics. In the firm-adhesion state, the detachment of DCCs with larger deformability was observed at a higher critical off rate. It is because the bullet (or elongated) shape that the DCC has a larger contact area that allows a greater number of bonds to form. Moreover, more deformable cells are subjected to a smaller drag force from the flow, which increases the bond lifetime. In addition, bond force increases with raising both the shear rate and the stiffness of cells. We also observed that the critical off rate decreases the likelihood moving from rolling-to-detachment of stiffer cells. The critical capillary number for the transition from rolling to firm adhesion is higher under larger shear rates. Alternatively, in larger capillaries, DCC exhibits the rolling motion whereas the critical off rate for rolling-to-detachment is not associated with cell deformability and the local hemodynamics.
We studied adhesive interactions between the deformable, circulating cell and the vessel wall to identify both the requirements that predispose cancer cells to firm adhesion in the microvasculature and the regions of microvasculature where cells firmly adhere. Our method can be applied to model different cell types and different receptor-ligand types in microvasculature with discrepant anatomical geometry, under a wide range of physiological hemodynamic conditions. In the present study, we found that cell deformability and local hemodynamic conditions facilitate the firm adhesion of cells in small arteries. Our findings suggest that a weak ligand–receptor interaction between PSGL-1 and P-selectin will lead to firm adhesion for deformable cancer cells in smaller vessels, and slow down the cell motion in larger vessels, which, in turn, can facilitate the activation of integrin-ICAM-1 bonds. Therefore, strong ligand- receptor bonds of integrins are necessary for the firm adherence of DCC in larger vessels. In summary, (a) the cell deformability and low shear rate facilitate the firm adhesion of cancer cells in small vessels, (b) the ligand–receptor interaction between PSGL-1 and P-selectin promotes the firm adhesion of cancer cell in smaller vessels (), (c) DCC deformability and local hemodynamics do not affect the cell adhesive behavior in larger vessels (), and (d) ligand–receptor interaction between PSGL-1 and P-selectin promotes the cell rolling in larger vessels. Our study provides a straightforward prospective for understanding of the mechanisms of adhesive interactions between different cancer cell types and endothelium in microvasculature. These interactions are important in determining the survival and extravasation of different cancer cell types in a specific organ. Our findings can guide development of more efficient therapeutics to block extravasation in the microvasculature of different organs.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Electronic supplementary material 1 (PNG 43 kb)
Acknowledgments
Research reported in this publication was supported by the Office of the Director, National Institutes of Health of the National Institutes of Health under Award Number DP5OD019876. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. This work was also supported by the Duke University Quantitative Initiative and the Big Data Scientist Training Enhancement Program (BD-STEP) of the Department of Veterans Affairs. Authors acknowledge the support of Duke Research Computing and specifically, Mr. Tom Milledge during the running of the simulations on the Duke Compute Cluster.
Conflict of interest
Mahsa Dabagh, John Gounley, , Amanda Randles declare that they have no conflicts of interest.
Ethical Standards
No human and no animal studies were carried out by the authors for this article.
Appendix: Validation
Our FSI framework was validated through a comparison with results from References 44 and 26. We compared the deformation of an initially spherical cancer cell located at the center of a vessel with diameter of where the diameter of the cell ()/ diameter of vessel () = 0.77 (Figs. S1A-B). The cell is freely flowing in the vessel and the deformation of the cell was examined under capillary numbers and 0.052. Ca is defined as , for shear rate and outer membrane radius R. is defined as , where U is the fluid velocity at the inlet. We applied similar mechanical properties for cancer cell as used in Reference 44: the surface shear elastic modulus was set to and the viscosity of the plasma and the cell cytoplasm was set to Pa s. It is evident from Fig. S1C that our results agree with results reported by References 44 and 26. To determine the optimized grid resolution, we compared deformed shape of cell with simulation of References 44 and 26 where the grid spacing was set to 120, 125, 130, 140, 150, 160, 180, and 200 nm. The cell deformation magnitude was consistently observed in the range of 125–180 nm. Fig. S1C shows the deformed shapes of the cell subjected to the shear rates corresponding to Ca=0.02 and 0.052, with the grid resolution size of 150 nm.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Alon R, Chen S, Puri KD, Finger EB, Springer TA. The kinetics of l-selectin tethers and the mechanics of selectin-mediated rolling. J. Cell Biol. 1997;138(5):1169–1180. doi: 10.1083/jcb.138.5.1169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bhatia SK, King MR, Hammer DA. The state diagram for cell adhesion mediated by two receptors. Biophys. J. 2003;84(4):2671–2690. doi: 10.1016/S0006-3495(03)75073-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Brunk DK, Hammer DA. Quantifying rolling adhesion with a cell-free assay: E-selectin and its carbohydrate ligands. Biophys. J. 1997;72(6):2820–2833. doi: 10.1016/S0006-3495(97)78924-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Caputo KE, Hammer DA. Adhesive dynamics simulation of g-protein-mediated chemokine-activated neutrophil adhesion. Biophys. J. 2009;96(8):2989–3004. doi: 10.1016/j.bpj.2008.12.3930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chang K-C, Tees DF, Hammer DA. The state diagram for cell adhesion under flow: leukocyte rolling and firm adhesion. Proc. Natl. Acad. Sci. 2000;97(21):11262–11267. doi: 10.1073/pnas.200240897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dembo M, Torney D, Saxman K, Hammer D. The reaction-limited kinetics of membrane-to-surface adhesion and detachment. Proc. R. Soc. Lond. B. 1988;234(1274):55–83. doi: 10.1098/rspb.1988.0038. [DOI] [PubMed] [Google Scholar]
- 7.Dong C, Slattery MJ, Liang S, Peng H-H. Melanoma cell extravasation under flow conditions is modulated by leukocytes and endogenously produced interleukin 8. Mol. Cell. Biomech. MCB. 2005;2(3):145. [PMC free article] [PubMed] [Google Scholar]
- 8.Fai TG, Griffith BE, Mori Y, Peskin CS. Immersed boundary method for variable viscosity and variable density problems using fast constant-coefficient linear solvers i: Numerical method and results. SIAM J. Sci. Comput. 2013;35(5):B1132–B1161. [Google Scholar]
- 9.Fidler IJ. The pathogenesis of cancer metastasis: the’seed and soil’hypothesis revisited. Nat. Rev. Cancer. 2003;3(6):453. doi: 10.1038/nrc1098. [DOI] [PubMed] [Google Scholar]
- 10.Fu BM, Yang J, Cai B, Fan J, Zhang L, Zeng M. Reinforcing endothelial junctions prevents microvessel permeability increase and tumor cell adhesion in microvessels in vivo. Sci. Rep. 2015;5:15697. doi: 10.1038/srep15697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gounley J, Draeger EW, Randles A. Numerical simulation of a compound capsule in a constricted microchannel. Procedia Comput. Sci. 2017;108:175–184. doi: 10.1016/j.procs.2017.05.209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gounley J, Peng Y. Computational modeling of membrane viscosity of red blood cells. Commun. Comput. Phys. 2015;17(4):1073–1087. [Google Scholar]
- 13.Gout S, Huot J. Role of cancer microenvironment in metastasis: focus on colon cancer. Cancer Microenviron. 2008;1(1):69–83. doi: 10.1007/s12307-008-0007-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Guo P, Cai B, Lei M, Liu Y, Fu BM. Differential arrest and adhesion of tumor cells and microbeads in the microvasculature. Biomech. Model. Mechanobiol. 2014;13(3):537–550. doi: 10.1007/s10237-013-0515-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Haier J, Korb T, Hotz B, Spiegel H-U, Senninger N. An intravital model to monitor steps of metastatic tumor cell adhesion within the hepatic microcirculation. J. Gastrointest. Surg. 2003;7(4):507–515. doi: 10.1016/S1091-255X(03)00023-4. [DOI] [PubMed] [Google Scholar]
- 16.Hammer DA. Adhesive dynamics. J. Biomech. Eng. 2014;136(2):021006. doi: 10.1115/1.4026402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Jadhav S, Eggleton CD, Konstantopoulos K. A 3-d computational model predicts that cell deformation affects selectin-mediated leukocyte rolling. Biophys. J. 2005;88(1):96–104. doi: 10.1529/biophysj.104.051029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Jadhav S, Eggleton CD, Konstantopoulos K. Mathematical modeling of cell adhesion in shear flow: application to targeted drug delivery in inflammation and cancer metastasis. Curr. Pharm. Des. 2007;13(15):1511–1526. doi: 10.2174/138161207780765909. [DOI] [PubMed] [Google Scholar]
- 19.Khismatullin DB, Truskey GA. Three-dimensional numerical simulation of receptor-mediated leukocyte adhesion to surfaces: effects of cell deformability and viscoelasticity. Phys. Fluids. 2005;17(3):031505. [Google Scholar]
- 20.Khismatullin DB, Truskey GA. Leukocyte rolling on p-selectin: a three-dimensional numerical study of the effect of cytoplasmic viscosity. Biophys. J. 2012;102(8):1757–1766. doi: 10.1016/j.bpj.2012.03.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kienast Y, Baumgarten L, Fuhrmann M, Klinkert W, Goldbrunner R, Herms J, Winkler F. Real-time imaging reveals the single steps of brain metastasis formation. Nat. Med. 2010;16(1):116–123. doi: 10.1038/nm.2072. [DOI] [PubMed] [Google Scholar]
- 22.King MR, Hammer DA. Multiparticle adhesive dynamics. Interactions between stably rolling cells. Biophys. J. 2001;81(2):799–813. doi: 10.1016/S0006-3495(01)75742-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Konstantopoulos K, Thomas SN. Cancer cells in transit: the vascular interactions of tumor cells. Annu. Rev. Biomed. Eng. 2009;11:177–202. doi: 10.1146/annurev-bioeng-061008-124949. [DOI] [PubMed] [Google Scholar]
- 24.Krasik EF, Yee KL, Hammer DA. Adhesive dynamics simulation of neutrophil arrest with deterministic activation. Biophys. J. 2006;91(4):1145–1155. doi: 10.1529/biophysj.105.070706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Krüger T, Varnik F, Raabe D. Efficient and accurate simulations of deformable particles immersed in a fluid using a combined immersed boundary lattice boltzmann finite element method. Comput. Math. Appl. 2011;61(12):3485–3505. [Google Scholar]
- 26.Lefebvre Y, Barthes-Biesel D. Motion of a capsule in a cylindrical tube: effect of membrane pre-stress. J. Fluid Mech. 2007;589:157–181. [Google Scholar]
- 27.Li J, Dao M, Lim C, Suresh S. Spectrin-level modeling of the cytoskeleton and optical tweezers stretching of the erythrocyte. Biophys. J. 2005;88(5):3707–3719. doi: 10.1529/biophysj.104.047332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Luo ZY, He L, Bai BF. Deformation of spherical compound capsules in simple shear flow. J. Fluid Mech. 2015;775:77–104. [Google Scholar]
- 29.Mack GS, Marshall A. Lost in migration. Nat. Biotechnol. 2010;28(3):214. doi: 10.1038/nbt0310-214. [DOI] [PubMed] [Google Scholar]
- 30.Moore KL, Patel KD, Bruehl RE, Li F, Johnson DA, Lichenstein HS, Cummings RD, Bainton DF, McEver RP. P-selectin glycoprotein ligand-1 mediates rolling of human neutrophils on p-selectin. J. Cell Biol. 1995;128(4):661–671. doi: 10.1083/jcb.128.4.661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Pappu V, Bagchi P. 3d computational modeling and simulation of leukocyte rolling adhesion and deformation. Comput. Biol. Med. 2008;38(6):738–753. doi: 10.1016/j.compbiomed.2008.04.002. [DOI] [PubMed] [Google Scholar]
- 32.Peskin CS. The immersed boundary method. Acta Numer. 2002;11:479–517. [Google Scholar]
- 33.Randles A, Draeger EW, Bailey PE. Massively parallel simulations of hemodynamics in the primary large arteries of the human vasculature. J. Comput. Sci. 2015;9:70–75. doi: 10.1016/j.jocs.2015.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Randles, A., E. W. Draeger, T. Oppelstrup, L. Krauss, and J. A. Gunnels. Massively parallel models of the human circulatory system. In: Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis. ACM, 2015, p. 1.
- 35.Randles, A. P., V. Kale, J. Hammond, W. Gropp, and E. Kaxiras. Performance analysis of the lattice Boltzmann model beyond Navier–Stokes. In: 2013 IEEE 27th International Symposium on Parallel & Distributed Processing (IPDPS). IEEE, 2013, pp. 1063–1074.
- 36.Schlüter K, Gassmann P, Enns A, Korb T, Hemping-Bovenkerk A, Hölzen J, Haier J. Organ-specific metastatic tumor cell adhesion and extravasation of colon carcinoma cells with different metastatic potential. Am. J. Pathol. 2006;169(3):1064–1073. doi: 10.2353/ajpath.2006.050566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Shrivastava S, Tang J. Large deformation finite element analysis of non-linear viscoelastic membranes with reference to thermoforming. J. Strain Anal. Eng. Des. 1993;28(1):31–51. [Google Scholar]
- 38.Slattery MJ, Liang S, Dong C. Distinct role of hydrodynamic shear in leukocyte-facilitated tumor cell extravasation. Am. J. Physiol. Cell Physiol. 2005;288(4):C831–C839. doi: 10.1152/ajpcell.00439.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Stoletov, K., H. Kato, E. Zardouzian, J. Kelber, J. Yang, S. Shattil, and R. Klemke. Visualizing extravasation dynamics of metastatic tumor cells. J. Cell Sci., 2010, pp. jcs–069443. [DOI] [PMC free article] [PubMed]
- 40.Stroka KM, Konstantopoulos K. Physical biology in cancer. 4. Physical cues guide tumor cell adhesion and migration. Am. J. Physiol. Cell Physiol. 2013;306(2):c98–c109. doi: 10.1152/ajpcell.00289.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Succi S, Succi S. The Lattice Boltzmann Equation: For Fluid Dynamics and Beyond. Oxford: Oxford University Press; 2001. [Google Scholar]
- 42.Sundd P, Pospieszalska MK, Cheung LS-L, Konstantopoulos K, Ley K. Biomechanics of leukocyte rolling. Biorheology. 2011;48(1):1–35. doi: 10.3233/BIR-2011-0579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Swaminathan, V., K. Mythreye, E. T. O’Brien, A. Berchuck, G. C. Blobe, and R. Superfine. Mechanical stiffness grades metastatic potential in patient tumor cells and in cancer cell lines. Cancer Res. pp. canres–0247, 2011. [DOI] [PMC free article] [PubMed]
- 44.Takeishi N, Imai Y, Ishida S, Omori T, Kamm RD, Ishikawa T. Cell adhesion during bullet motion in capillaries. Am. J. Physiol.-Heart Circ. Physiol. 2016;311(2):H395–H403. doi: 10.1152/ajpheart.00241.2016. [DOI] [PubMed] [Google Scholar]
- 45.Wirtz D, Konstantopoulos K, Searson PC. The physics of cancer: the role of physical interactions and mechanical forces in metastasis. Nat. Rev. Cancer. 2011;11(7):512. doi: 10.1038/nrc3080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wu Z, Xu Z, Kim O, Alber M. Three-dimensional multi-scale model of deformable platelets adhesion to vessel wall in blood flow. Phil. Trans. R. Soc. A. 2014;372(2021):20130380. doi: 10.1098/rsta.2013.0380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Xiao L, Liu Y, Chen S, Fu B. Effects of flowing rbcs on adhesion of a circulating tumor cell in microvessels. Biomech. Model. Mechanobiol. 2017;16(2):597–610. doi: 10.1007/s10237-016-0839-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Yago T, Leppänen A, Qiu H, Marcus WD, Nollert MU, Zhu C, Cummings RD, McEver RP. Distinct molecular and cellular contributions to stabilizing selectin-mediated rolling under flow. J. Cell Biol. 2002;158(4):787–799. doi: 10.1083/jcb.200204041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Yan W, Cai B, Liu Y, Fu B. Effects of wall shear stress and its gradient on tumor cell adhesion in curved microvessels. Biomech. Model. Mechanobiol. 2012;11(5):641–653. doi: 10.1007/s10237-011-0339-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Zhang Z, Du J, Wei Z, Wang Z, Li M. Effects of membrane deformability and bond formation/dissociation rates on adhesion dynamics of a spherical capsule in shear flow. Biomech. Model. Mechanobiol. 2018;17(1):223–234. doi: 10.1007/s10237-017-0956-9. [DOI] [PubMed] [Google Scholar]
- 51.Zhelev DV, Needham D, Hochmuth RM. Role of the membrane cortex in neutrophil deformation in small pipets. Biophys. J. 1994;67(2):696–705. doi: 10.1016/S0006-3495(94)80529-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Electronic supplementary material 1 (PNG 43 kb)