Radiation damage and dose limits in serial synchrotron crystallography at cryo- and room temperatures

Significance

Macromolecular X-ray crystallography (MX) is the most prolific structure determination method in structural biology but is limited by radiation damage. To reduce damage progression, MX is usually carried out at cryogenic temperatures, sometimes blocking functionally important conformational heterogeneity. Lacking this shortcoming, room temperature MX has gained momentum with the recent advent of serial crystallography, whereby distribution of the X-ray dose over thousands of crystals mitigates damage. Here, an approach to serial crystallography is presented allowing visualization of specific damage to amino acids at room temperature and determination of a dose limit above which structural information from electron density maps decreases due to radiation damage. This limit provides important guidance for the growing number of synchrotron room temperature MX experiments.

Abstract

Radiation damage limits the accuracy of macromolecular structures in X-ray crystallography. Cryogenic (cryo-) cooling reduces the global radiation damage rate and, therefore, became the method of choice over the past decades. The recent advent of serial crystallography, which spreads the absorbed energy over many crystals, thereby reducing damage, has rendered room temperature (RT) data collection more practical and also extendable to microcrystals, both enabling and requiring the study of specific and global radiation damage at RT. Here, we performed sequential serial raster-scanning crystallography using a microfocused synchrotron beam that allowed for the collection of two series of 40 and 90 full datasets at 2- and 1.9-Å resolution at a dose rate of 40.3 MGy/s on hen egg white lysozyme (HEWL) crystals at RT and cryotemperature, respectively. The diffraction intensity halved its initial value at average doses (D_1/2) of 0.57 and 15.3 MGy at RT and 100 K, respectively. Specific radiation damage at RT was observed at disulfide bonds but not at acidic residues, increasing and then apparently reversing, a peculiar behavior that can be modeled by accounting for differential diffraction intensity decay due to the nonuniform illumination by the X-ray beam. Specific damage to disulfide bonds is evident early on at RT and proceeds at a fivefold higher rate than global damage. The decay modeling suggests it is advisable not to exceed a dose of 0.38 MGy per dataset in static and time-resolved synchrotron crystallography experiments at RT. This rough yardstick might change for proteins other than HEWL and at resolutions other than 2 Å.

Macromolecular X-ray crystallography (MX) is the workhorse in structural biology yet suffers from radiation damage to the crystalline molecules (1). Global radiation damage manifests itself in reciprocal space as a reduction in diffraction power (decrease in diffraction resolution, worsening of merging statistics, increase in Wilson B factor), whereas specific damage is typically detected in real space as changes in the electron density as dose increases. Specific damage has been extensively studied at 100 K where it mainly manifests as breakage of disulfide bonds, decarboxylation of acidic amino acid residues (2–4), modifications in chromophore moieties (5), and photoreduction of metal centers (6), portending challenges in biological interpretation. The introduction of cryocooling methods (7, 8) mitigated the extent and progression of global radiation damage by about two orders of magnitude (9, 10) because liquid-like diffusive motions in the protein and the solvent are suppressed below 200 K (10), where solvent and protein motions have undergone glass and dynamical transitions, respectively (11). The decreased rates of radiation damage at 100 K explains the fact that cryocrystallography has largely replaced data collection at room temperature (RT) over the past two decades (12). Even at cryogenic temperatures, however, the crystal lifetime remains limited, explaining why investigators have sought to determine dose limits that should not be exceeded. Based on the lifetime of two-dimensional protein crystals in electron microscopy at 77 K, a value of 20 MGy was suggested by Henderson (13), at which the total diffraction intensity from a cryocooled macromolecular crystal would have decreased to one-half of its initial value (D_1/2). A similar D_1/2 value (43 MGy) was experimentally determined for apo- and holo-ferritin crystals at 2.2-Å resolution at 100 K, but a limit of 30 MGy was suggested (corresponding to D_0.7), considering that beyond that dose, radiation damage may compromise biological interpretation of macromolecular crystal structures (14). For diffraction data collected on tetragonal crystals of hen egg white lysozyme (HEWL) at 100 K and extending to 1.6-Å resolution, analysis of diffraction data quality indicators showed deviation from linear behavior above 10 MGy, which was interpreted as secondary and tertiary radiation damage becoming significant (15). Since D_1/2 depends on the diffraction limit of the crystals (14–17) (see also discussion in ref. 18) and on the criteria used to determine the resolution cutoff, the 30-MGy limit provides only rough guidance for safe data collection strategies in cryocrystallography. Depending on the biological question asked, much lower limits may need to be respected, e.g., in studies of proteins featuring metal centers since photoreduction of these entities occurs at doses one to two orders of magnitude lower (6, 19).

Notwithstanding the fact that the first study of radiation damage, more than half a century ago, was based on RT crystallographic data (20), radiation damage in RT crystallography has been less studied and is therefore less understood than that occurring at 100 K. In their seminal paper, Blake and Phillips (20) reported that the total diffraction intensity from myoglobin crystals had decreased to one-half of its initial value after a dose of 0.59 MGy, providing an experimental dose limit for the global damage to these crystals. The observed nonexponential intensity decay has been explained by various models describing sequential processes of local crystal damage (20–22). Recently, however, it has been shown that the nonexponential intensity decay at RT could be explained by the nonuniform irradiation resulting from exposure to a Gaussian profile X-ray beam and the resulting “hole burning” effect (23). In contrast to cryocrystallography, where no dose rate effect for global radiation damage has been found (24, 25), there is evidence that global radiation damage at RT decreases when collecting data at higher dose rates (23, 26–28).

Based on their observation that the intensity of some diffraction peaks decreased while that of others increased, Blake and Phillips suggested that specific structural damage to particular amino acids must occur (20), a postulate verified in another RT study more than 25 y later (29). Since then, specific damage to disulfide bonds at RT has been observed in a traditional oscillation study performed on a rotating anode X-ray generator (26), in a serial synchrotron crystallography (SSX) experiment (30) and in two multicrystal investigations (31, 32). Also classifying as specific damage, the iron–water bond in a metalloprotein has been shown to elongate as a consequence of RT radiation damage at a dose as low as 0.033 MGy (33). In contrast, another multicrystal RT study on insulin did not detect any specific damage to disulfide bonds (maximum dose was 0.5 MGy) (34). Likewise, multiple sequential RT datasets collected on single large crystals of the fluorescent protein Cerulean, AtPhot2LOV2, and lysozyme, respectively, hardly showed signs of specific radiation damage in Fourier difference maps, although Raman spectroscopy did show spectral changes characteristic of damage to disulfide bonds (35). Specific damage at RT remains challenging to probe because of the high rate at which global radiation damage destroys diffraction quality.

RT crystallography presents a certain number of advantages over cryocrystallography. First, functionally relevant conformational heterogeneity, which may be modified during flash-cooling in cryocrystallography, is preserved at RT (36). The resulting RT structural models are thus biologically more meaningful. Second, the functional flexibility maintained at RT allows time-resolved crystallography experiments to be carried out, with the aim of following macromolecular activity in real time, and third, addition of cryoprotectants is unnecessary. However, the greatly increased radiation sensitivity of crystals at RT compared to at cryotemperatures (9, 10), exacerbated by the ever-increasing photon flux density of modern synchrotron sources, has translated into RT crystallography being employed much less frequently than cryocrystallography over the past two decades. Nevertheless, with the recent advent of serial techniques, RT crystallography is experiencing a renaissance and is again becoming more widely used.

Serial crystallography consists of sequentially collecting a large number of single diffraction patterns, each from either a microcrystal or a small previously unexposed part of a large crystal that remains stationary during exposure. Based on multicrystal data collection strategies, used in the late 1970s when investigating highly radiation-sensitive virus crystals (37), serial crystallography has realized its full potential at X-ray free-electron lasers (XFELs), where the extremely high peak brilliance of femtosecond pulses requires the sample to be constantly replenished (38). This data collection mode, dubbed serial femtosecond crystallography [SFX (39)], enables collection of a diffraction pattern before disintegration of the exposed area or crystal [so-called diffraction-before-destruction (40)]. Inspired by SFX, serial helical line scans were carried out at a synchrotron source on microcrystals of cathepsin B at 100 K (41), paving the way for the implementation of SSX. Since then, various sample presentation methods have been developed, diversifying the means by which SSX data can be collected at RT. Briefly, crystals can be flowed through quartz capillaries (42) or a microfluidic flow-focusing device (43), or embedded in lipidic cubic phase (44) or other viscous media (45), and then slowly extruded across the X-ray beam. Alternatively, crystals can be presented on fixed targets, such as silicon nitride wafer sandwiches (30), silicon chips (46, 47), or Mylar sheet-on-sheet sandwiches (48), and X-ray data collected by raster scanning. As an in-between the injection and fixed-target approaches, tape drives carrying microcrystals are yet another way of delivering crystalline samples to the X-ray beam (49, 50). Together with the availability of fast readout detectors and of X-ray microbeams with increasing flux densities, these various SSX methods provide the potential to systematically study and compare both global and specific radiation damage at RT and at 100 K. Common to all of these SSX approaches is that the per-crystal X-ray radiation damage is reduced, but not eliminated, by distributing the absorbed energy per dataset over a multitude of crystals (33), as opposed to being accumulated in oscillation-based approaches.

Here, we performed fixed-target raster-scanning SSX at one of the most brilliant microfocus synchrotron beamlines currently available to investigate specific and global radiation damage in HEWL microcrystals at both RT and 100 K. The questions we address include whether or not specific radiation damage can be observed at RT, and if yes, in which respect it differs from that observed at 100 K and at what rate it develops compared to global RT radiation damage. The combination of a high photon flux density, the use of an EIGER-X 4M detector framing at close to 500 Hz, and distribution of the dose over ∼20,000 (RT) and ∼9,000 (100 K) microcrystals through a raster-scanning SSX approach (30) allowed data collection at high dose rates with 2.01-ms exposure time per frame. At an average dose rate of 40.3 MGy/s, 40 (RT) and 90 (100 K) datasets could be assembled sequentially and D_1/2 values (used here to define the global radiation damage limit of HEWL crystals diffracting to 2-Å resolution) were determined to be 0.57 MGy at RT and 15.3 MGy at 100 K. The signal in sequential Fourier difference maps, reflecting specific damage, increased up to 0.5 MGy in the RT study before decreasing with increasing average dose, a phenomenon that can be explained by nonuniform illumination with a beam whose shape can be well approximated with a Voigt function (i.e., a convolution of a Gaussian and a Lorentzian beam, or alternatively, a Gaussian beam with significant tails). Furthermore, we collected RT data at 2.4 MGy/s using the same methodology and provide evidence that the gain in crystal D_1/2 dose tolerance at 40.3 MGy/s is at most 58% compared to the 2.4 MGy/s data. Our study contributes to extending to RT the vast knowledge of radiation damage manifestations and implications gained over the past two decades at 100 K (1) and sets a framework for future SSX experiments.

Results

Raster-Scanning Serial Crystallography Allows Radiation Damage Studies with Dose Fine Slicing.

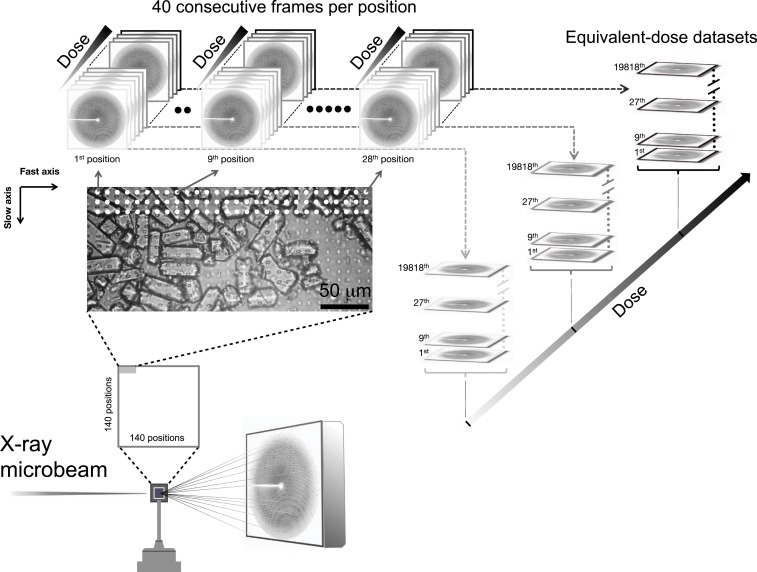
The combination of the highly brilliant microfocus X-ray beam available at the European Synchrotron Radiation Facility (ESRF) beamline ID13, a fast readout EIGER-X 4M detector (51), and a raster-scanning approach to serial crystallography (30) enabled the collection of up to 90 full datasets with minimum dose increments on HEWL crystals (Fig. 1). For RT (22 °C in our study) data collection, the crystals were sandwiched between two Si₃N₄ membranes as reported earlier (30) while they were deposited, for the control cryo- data collection, on a microporous silicon chip (52) that was flash-cooled after blotting of excess solvent, and maintained in the gaseous-nitrogen stream of a cryocooler operating at 100 K. The membranes and chips were raster-scanned in lines from left to right across the micrometer-sized X-ray beam (3.0 μm [horizontal (h)] × 1.5 μm [vertical (v)] [full width at half-maximum (FWHM)]) of 2.67 × 10¹² photons/s if unattenuated. Positions at which data were collected were spaced by 10 μm in both the horizontal and the vertical directions, and at each position, 40 to 90 consecutive still diffraction patterns (i.e., without rotation during exposure) were acquired using about a 500-Hz data collection rate. For assessing a potential dose rate effect at RT, the flux of the X-ray beam was decreased 17-fold and a low-dose rate series also acquired. Patterns of equivalent dose collected at each spot were then assembled into equivalent-dose datasets by processing of still diffraction images using serial-crystallography protocols (see Materials and Methods section for details). In this serial approach, the dose increment for each of the above equivalent-dose datasets was low (5 kGy for the RT low-dose rate series and 81 kGy for the RT high-dose rate and cryo- series) while the high-frame rate data collection in combination with the brilliant X-ray beam minimized the total data collection time. Progression of global and specific radiation damage as a function of dose was then monitored by inspecting the decrease in diffraction intensities and by analyzing Fourier difference maps calculated with respect to the lowest-dose dataset, respectively. We refer to this experimental approach as sequential serial raster-scanning (SSRS) crystallography.

Fig. 1.

Serial radiation damage raster-scanning approach. Protein crystals (cf. photo) are sandwiched between two Si₃N₄ membranes and presented to the X-ray beam on a solid support (30) for RT data collection or deposited on a microporous silicon chip (52) for data collection at 100 K maintained by a stream of gaseous nitrogen. As an example, the scheme shows the RT high-dose rate series for which two Si₃N₄ sandwiches were used. The support was raster scanned across the micrometer-sized X-ray beam from the upper left to the lower right with each line being scanned from left to right. Each Si₃N₄ membrane is sampled at a total number of 140 (x) × 140 (y) positions, i.e., at 19,600 positions. At each position sampled (indicated in the photo by white circles for the first three lines), 40 consecutive still diffraction patterns are retained from the 50 collected by truncating the first 5 and last 5 as noted in the text, each for a 2.01-ms exposure time with an increasing average X-ray dose on a high-frame rate EIGER-X 4M detector. The 1st, 9th, and 28th positions are highlighted. Sampled positions are spaced by 10 μm, horizontally and vertically. The small whitish dots uniformly observed along the x and y axes of the Si₃N₄ membrane (see photo) are marks left by the X-ray beam. They provide an estimate of the extent to which visual radiation damage spreads. Patterns of equivalent dose collected at 19,818 positions (i.e., corresponding to 19,818 indexed hits, from multiple membranes) are then assembled into 40 equivalent-dose serial-crystallography datasets from which protein structures at increasing dose are solved.

Global Radiation Damage, Dose Limits, and Characteristic Decay Constants at RT and at 100 K.

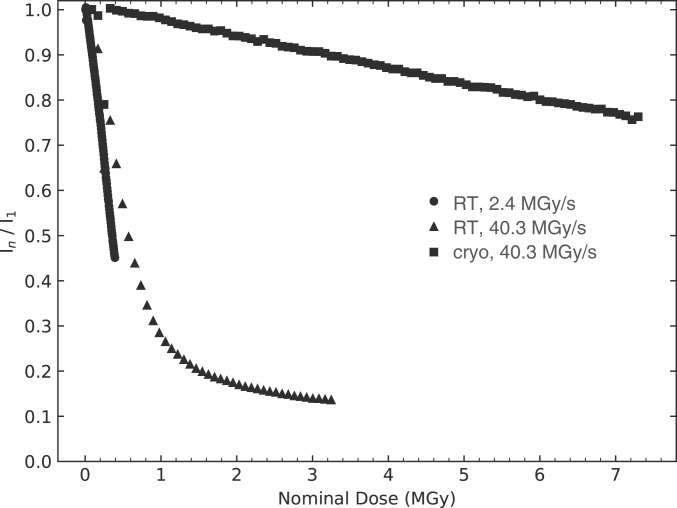
We recorded SSRS series at RT at two different dose rates (2.4 and 40.3 MGy/s) and a control series at 100 K at a dose rate of 40.3 MGy/s. Calculation of dose and dose rates was carried out with RADDOSE-3D (53) and the “average dose” metric (AD_G95) reported here corresponds to the average dose delivered by a Gaussian beam over the region of the crystal where 95% of the energy is deposited. Of important note, the latest version of RADDOSE-3D takes into account the dose reduction originating from photoelectron escape from small irradiated volumes (54); hence this effect was accounted for in our dose calculation. Indeed, the horizontal and vertical dimensions of the used X-ray beam (3.0 μm [h] × 1.5 μm [v] for the high-dose rate SSRS series, and 2.5 μm [h] × 1.5 μm [v] for the low-dose rate SSRS series) are smaller than the range of photoelectrons at the incident energy used (2 μm at 13.45 keV), so that the latter transport a fraction of the deposited X-ray energy out of the irradiated volume. At this energy and for these crystals, the photoelectron median range is calculated to be 2 μm, so that taking their escape into account, the calculated average dose is reduced by 47% in the high-dose rate series (40.3 instead of 76.0 MGy/s). In order to monitor global radiation damage as it progresses from dataset to dataset, intensities of all predicted Bragg reflections on the detector, i.e., including those that extended beyond the resolution limit of the highest-dose dataset in each series (2.04 and 1.9 Å for both RT series and the cryo- series, respectively), were summed for all indexed patterns of dataset n and added to yield a total intensity I_n. Normalized by the total intensity of the first dataset (I₁) and plotted as a function of dose, the I_n/I₁ ratio reflects the dose-dependent decrease in diffraction power for consecutive datasets (Fig. 2). The average dose at which the diffracted intensity decreases to one-half of its initial value (D_1/2) was determined to be 0.36 and 0.57 MGy for the RT SSRS series at 2.4 and 40.3 MGy/s, respectively, indicating a marginal dose rate effect on the rate of global radiation damage of 58%, which might be fully or partially explained by the estimated error in beam dimensions (Materials and Methods). In contrast to an earlier report (55), we do not observe a lag phase for the onset of global radiation damage at high dose rates that would have indicated the possibility of outrunning radiation damage at RT at the detector’s 0.5-kHz repetition rate.

Fig. 2.

Decrease in diffraction power as a function of increasing average dose. The sum of the intensities of all reflections up to the detector edges in all indexed diffraction patterns of a dataset, normalized by the sum of the first (i.e., lowest dose) dataset are shown as a function of the average dose delivered by a Gaussian beam (AD_G95, average over the region of the crystal where 95% of the energy is deposited) for dose rates of 2.4 MGy/s (circles) and 40.3 MGy/s (triangles) at RT and of 40.3 MGy/s (squares) at 100 K. The dose at which the diffracted intensity decreased to one-half of its initial value (D_1/2) was determined to be 0.36, 0.57, and 15.3 MGy for the RT series at 2.4 and 40.3 MGy/s and the cryo- series at 40.3 MGy/s, respectively.

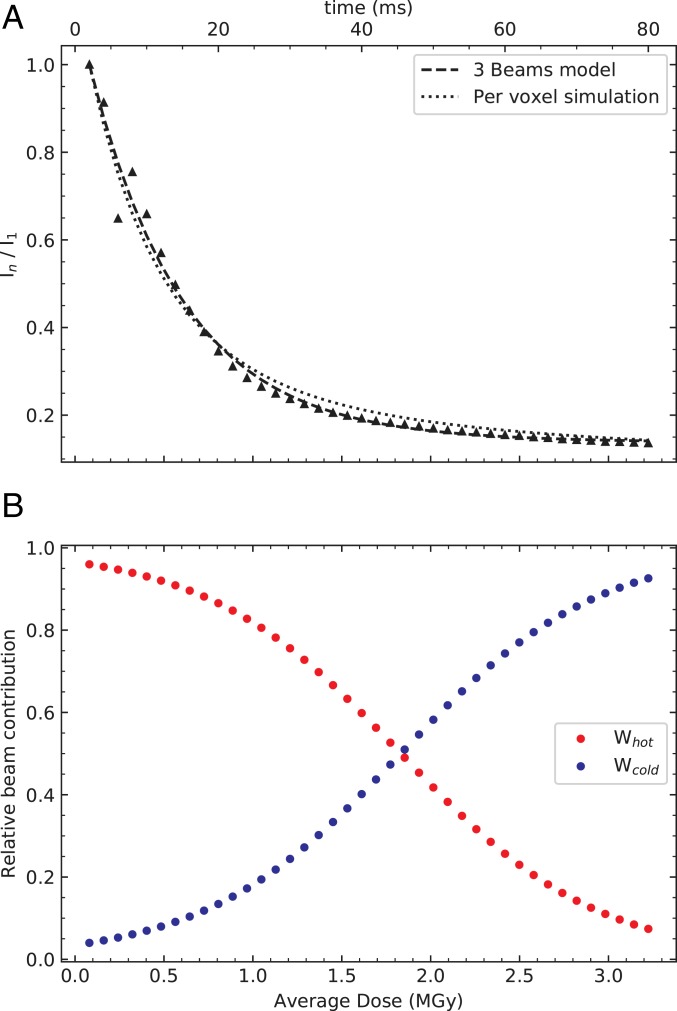
The intensity decay at RT (Fig. 2) cannot be fitted with a single-exponential function, because of the nonuniform irradiation within the X-ray beam (23). Elaborating on a two-beam model presented earlier (56), we approximated the Voigt-shaped beam (Materials and Methods) by a three-beam model, composed of a hot inner, a cold outer beam, and an additional very weak beam; only the two first beams, which respectively display a cylindrical and a ring shape, produce observable damage, whereas the additional very weak beam does not generate observable damage (see SI Appendix, Supplementary Text S1 for details). Assuming that the decay of the diffraction intensity in the hot and cold beams is exponential, the experimental intensity decay I_n/I₁ can be fitted according to SI Appendix, Eq. S6 with a single-exponential parameter D_1/2,g for global damage as shown in Fig. 3A for the RT high-dose rate series, corresponding to D_1/2,g = 0.38 MGy. With increasing dose, the contribution to diffraction of the hot beam decreases (SI Appendix, Eq. S9), while that of the cold beam increases (SI Appendix, Eq. S10 and Fig. 3B). If there is no intensity decay model in the calculation of the average dose, the true average dose (here called diffraction decay weighted dose) is overestimated (SI Appendix, Eq. S8) and, perhaps counterintuitively, becomes nearly independent of dose as it increases, as reported earlier (23) (SI Appendix, Fig. S1B). In an alternative approach to the three-beam model, the dose rate at each position in the crystal (represented by a cubic voxel of dimensions 0.2 μm per side) was computed and this distribution was subsequently used to simulate the expected fading of each voxel with dose (see SI Appendix, Supplementary Text S2 for details). The resulting simulation-predicted diffraction decay well reproduces the experimental I_n/I₁ decay (Fig. 3A). The dose dependence of I_n/I₁ at 100 K differs from that at RT (Fig. 2) and the decrease at 100 K can be well explained by a linear fit, but it can also be well fitted according to SI Appendix, Eq. S6 (SI Appendix, Fig. S3). Linear extrapolation indicates a half-dose D_1/2 of 15.3 MGy for the cryo- dataset at 40.3 MGy/s—a value that is similar to the D_1/2 reported earlier for lysozyme crystals assessed at 100 K at similar resolution [12.5 MGy (57), 9.2 MGy (35)] but 27 times larger than the corresponding value at RT at the same dose rate. In contrast to the cryotemperature (SI Appendix, Fig. S3) and RT high-dose rate series (Fig. 3A and SI Appendix, Fig. S1), the intensity decay I_n/I₁ of the RT low-dose rate series cannot be well fitted according to SI Appendix, Eq. S6 (SI Appendix, Fig. S2), because the beam profile deviated considerably more from a Gaussian function for the collection of the RT low-dose rate than for the RT high-dose rate series.

Fig. 3.

Modeling and simulation of the decrease in diffraction power for the RT series at 40.3 MGy/s. (A) The sum of the intensities of all predicted reflections for each indexed pattern of a dataset n was averaged and normalized by the sum of the first (i.e., lowest dose) dataset (triangles, same data as in Fig. 2). The fit to these data according to a three-beam model (hot, cold, and nondamaging beams; see SI Appendix, Supplementary Text S1 for details) approximating the Voigt-shaped beam is shown as a dashed line. The dotted line is the per-voxel simulation of I_n/I₁, with the Voigt-shaped beam represented by the sum of a Gaussian and a Lorentzian profile (see SI Appendix, Supplementary Text S2 for details). (B) Relative contributions of the hot (SI Appendix, Eq. S9) and cold (SI Appendix, Eq. S10) beams of the three-beam model as a function of average dose. Only these two beams have been used in the weight computation that will further be used in the model of the specific damage (SI Appendix, Eq. S11). Indeed, as the third-beam contribution to the diffraction intensity is assumed to be constant in the dose range studied, it does not generate features in F_o^RT-HDRn – F_o^RT-LDR1 maps.

Specific Radiation Damage at Room Temperature and at 100 K.

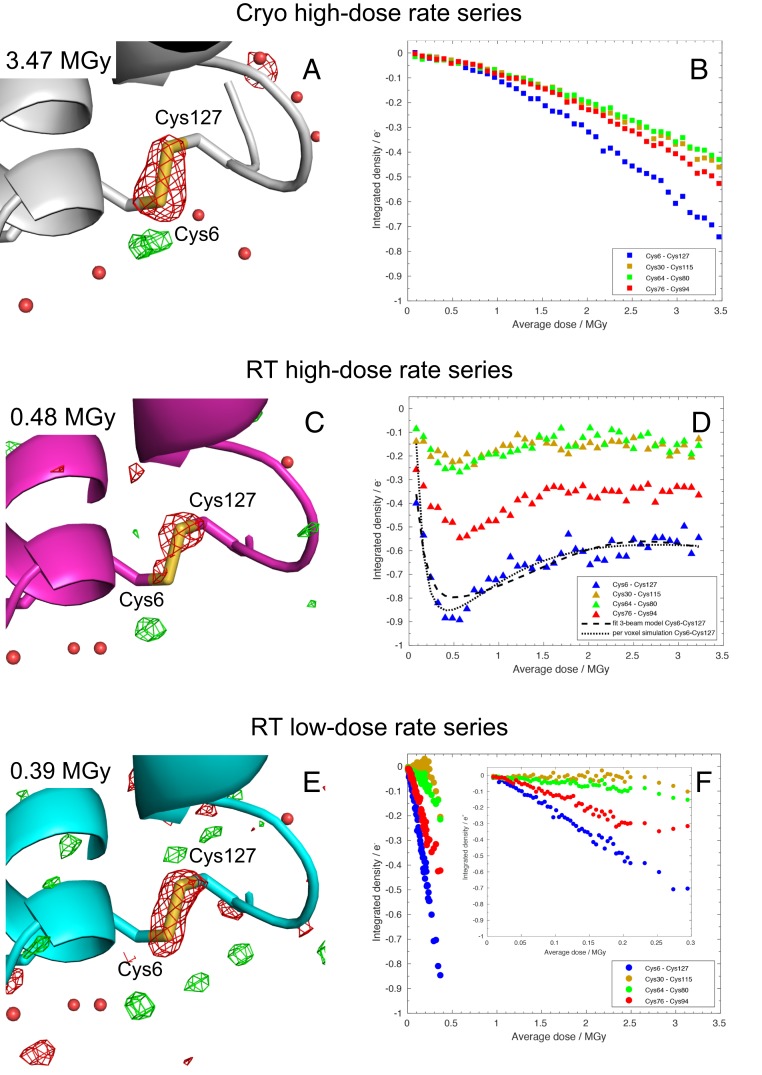
The progression of specific structural and chemical radiation damage is best visualized in Fourier difference maps calculated between datasets collected with different average doses (2–4). Sequential difference Fourier maps were calculated for the RT series with respect to the lowest-dose dataset of the RT low-dose rate (2.4 MGy/s) series (i.e., dataset RT-LDR1), i.e., F_o^RT-XDRn – F_o^RT-LDR1 with X representing the high (H)- or low (L)-dose rate series, and n being datasets 2 to 80 for the RT low-dose rate (2.4 MGy/s) series (i.e., datasets RT-LDR2 to RT-LDR80), and datasets 1 to 40 for the RT high-dose rate (40.3 MGy/s) series (i.e., datasets RT-HDR1 to RT-HDR40). For the cryo- series, sequential-difference Fourier maps were calculated with respect to its lowest-dose dataset (CR1), i.e., F_o^CRn – F_o^CR1, with n being datasets 2 to 90 for the cryo- (40.3 MGy/s) series (i.e., datasets CR2 to CR90) (Fig. 4). As an example, Fig. 4A shows difference electron density at the disulfide bond Cys6–Cys127 in the F_o^CR43 – F_o^CR1 map. The negative density highlights specific damage to this disulfide bond in the 43rd dataset of the cryo- series (3.47 MGy), with indications of damage on Cys6 being larger than on Cys127. In order to follow specific radiation damage as a function of dose, difference peaks around each sulfur in a disulfide were integrated within a sphere of radius proportional to its isotropic atomic displacement parameter, i.e., B factor (ref. 58; see Materials and Methods for details). Fig. 4B shows the sum of the integrated difference density around both sulfur atoms within a disulfide bond as a function of dose. Starting from zero, the sum monotonically decreases for all four disulfide bonds with increasing dose, reflecting previously well-described radiation-induced bond rupture at 100 K (2–4). The radiation sensitivity of the four disulfide bonds differ, with Cys6–Cys127 being the most sensitive and Cys64–Cys80 being the least sensitive, as already documented previously (3, 59).

Fig. 4.

Specific radiation damage to disulfide bonds as a function of increasing average dose. Sequential difference Fourier maps at the disulfide bond Cys6–Cys127 (A) between the 43rd (3.47 MGy) and the 1st datasets in the cryo- high-dose rate series contoured at ±0.06 e⁻/ų (negative and positive peaks are in red and green, respectively), (C) between the 6th dataset (0.48 MGy) in the RT 40.3 MGy/s series and the 1st dataset in the RT 2.4 MGy/s series (at ±0.06 e⁻/ų), and (E) between the 80th (0.39 MGy) and the 1st dataset in the RT 2.4 MGy/s series (at ±0.06 e⁻/ų). Sum of the integrated density in Fourier difference maps around both sulfur atoms in the disulfide bonds as a function of average dose (B) for the cryo- 40.3 MGy/s, (D) RT 40.3 MGy/s and (F) RT 2.4 MGy/s series. Note, only every fifth data point is shown at doses above 0.24 MGy in F. In D, the dashed line indicates the fit result according to a “weighted specific damage” model (SI Appendix, Eq. S11) based on the Voigt-shaped beam being represented by a three-beam model (see SI Appendix, Supplementary Text S1 for details), and the dotted line, the per-voxel simulation of specific damage, with the Voigt profile describing the microbeam approximated by the sum of a Gaussian and a Lorentzian profile (see SI Appendix, Supplementary Text S2 for details). The Inset in F focuses on a reduced dose scale. Models of the cryo- 40.3 MGy/s series dataset 1 (Protein Data Bank [PDB] ID code 6Q8T) and of the RT 2.4 MGy/s series dataset 1 (PDB ID code 6Q88) are superimposed on the difference Fourier maps in A and in C and E, respectively.

Our SSRS approach also allows the observation of specific radiation damage at RT, owing both to the fine-slicing of the dose and to the collection of an ultralow-dose dataset (5 kGy, RT-LDR1) as a reference RT dataset for the calculation of F_o^RT-LDRN – F_o^RT-LDR1 difference maps. Fig. 4 C and E shows difference electron density at the disulfide bond Cys6–Cys127 in the F_o^RT-HDR6 – F_o^RT-LDR1 and the F_o^RT-LDR80 – F_o^RT-LDR1 maps, respectively. Specific damage to the disulfide bond is clearly evident, even at the lowest probed dose (F_o^RT-LDR2 – F_o^RT-LDR1), with damage on Cys127 being larger than on Cys6, i.e., the reverse of that seen at 100 K. At RT and high-dose rate (40.3 MGy/s), the evolution of the sum of the integrated difference density in Fourier difference maps around both sulfur atoms in the disulfide bonds shows a peculiar dose dependence (Fig. 4D) that is very different from that at 100 K (Fig. 4B). The negative difference density decreases down to a minimum at 0.5 MGy and then increases again. Based on the Voigt-shaped beam being approximated by the three-beam model (SI Appendix, Supplementary Text S1), the integrated difference density around each of the four disulfide bonds can be fitted (Fig. 4D) as a function of the average dose according to a “weighted specific damage” model (SI Appendix, Eq. S11); this fit yields a characteristic half-dose D_1/2,s of 0.08 MGy for the Cys6–Cys127 disulfide bridge. The alternative per-voxel simulation (SI Appendix, Supplementary Text S2) reproduces the peculiar dose dependence equally well (Fig. 4D). The characteristic half-dose of specific disulfide damage D_1/2,s (0.08 MGy) is five times lower than the characteristic half-dose of global damage D_1/2,g (0.38 MGy), suggesting that global and specific damage evolve at different rates at RT. Despite being composed of 80 datasets, our RT low-dose rate series does not extend in dose beyond 0.4 MGy, so we cannot conclude that collection at a lower dose rate would result in a better preservation of structural differences. However, we note that peak heights in F_o^RT-HDRn – F_o^RT-LDR1 and F_o^RT-LDRn – F_o^RT-LDR1 Fourier difference maps are of similar heights at 0.4 MGy (Fig. 4 D and F), suggesting that there is no, or at most a small dose rate effect in the progression of specific radiation damage at RT. The order of disulfide-bond radiation sensitivities in the RT series (high and low dose rate) is the same as in the cryo- series, contrary to our previous observations at higher average doses (30).

Whereas specific damage to disulfide bonds is evident at both RT and 100 K (Fig. 4), negative peaks in sequential Fourier difference maps on glutamic and aspartic acids residues are visible at 100 K but not at RT. Surprisingly, sequential difference Fourier maps at RT show negative peaks on the main-chain atoms of Pro70, sandwiching a positive peak on one of the crystal symmetry axes (SI Appendix, Fig. S6). Specific damage to proline residues has not been reported in the literature and is indeed absent from the cryo- high-dose rate control series (SI Appendix, Fig. S6B). It is possible this proline peak is due to noise accumulating on the symmetry axis. Concerning tryptophan residues, we observe no peaks in sequential difference Fourier maps in the cryo- and RT low-dose rate series, but in the RT high-dose rate series, a negative peak is already seen at the five-membered pyrrole ring of Trp108 and Trp111 in the F_o^RT-HDR1 – F_o^RT-LDR1 map (−0.063 e⁻/A³ [−3.5 σ] and −0.067 e⁻/A³ [−3.7 σ], respectively).

Discussion

The SSRS approach described here is based on the combination of a highly brilliant microfocus X-ray beam, a fast readout detector (EIGER-X 4M) (51), and a raster-scanning approach to serial crystallography (30). The protocol allowed SSX data to be collected at RT and 100 K with 2-ms exposure time per frame, and a total dose per dataset as low as 81 kGy for the high-dose rate series (RT and cryotemperature) and 5 kGy for the RT low-dose rate series. The serial approach used here inherently allows the dose to be distributed over a multitude of crystals (here, several thousand per dataset), minimizing the total dose per dataset. By collecting several (up to 90) consecutive diffraction images at each sample position, equivalent-dose datasets were assembled. This enabled a fine-sliced monitoring of global and specific radiation damage on HEWL crystals at both RT and 100 K, and allowed dose limits to be determined at both temperatures.

The dose at which the diffracted intensity of the dose-equivalent datasets decreased to one-half of its initial value (D_1/2) was 0.36 MGy for the SSRS series collected at RT at a dose rate of 2.4 MGy/s. At a 17-fold increased dose rate (40.3 MGy/s), D_1/2 at RT increased by 58% to 0.57 MGy. Thus, the D_1/2 value reflecting global radiation damage in RT SSX is only marginally dependent on dose rate. Earlier studies have reported the absence of a RT dose rate effect, based on data collected at rates between 3 and 680 kGy/s (27), and that D_1/2 increases by a factor of 1.5 to 2 at 33 MGy/s relative to data collected at dose rates of less than 100 kGy/s (23). Regardless, similar D_1/2 values for global radiation damage at RT were reported in the original Blake and Phillips study on myoglobin (0.59 MGy) (20) and in more recent RT studies on HEWL [0.18 to 0.26 MGy (23); 0.11 MGy (35)], insulin (0.15 MGy) (34), thaumatin (0.4 MGy) (32), Cerulean (0.13 MGy), AtPhot2LOV2 (0.17 MGy) (35), and other model proteins (0.10 to 1.18 MGy) (60), with the last study revealing a clear dependence of D_1/2 on solvent content (60). It should be noted, however, that a variety of methods were used to estimate the dose in these publications, illustrating both the complexity of radiation damage at RT and that a sufficiently robust approach for properly weighting dose has not yet emerged. Also, the variation in resolution of the reported studies affect D_1/2 (14–17). The SSRS control series at 100 K collected at 40.3 MGy/s on HEWL crystals yielded a D_1/2 of 15.3 MGy, thus evidencing a 27-fold reduced global radiation damage sensitivity at 100 K compared to RT for HEWL crystals.

Positions at which data were collected were spaced by 10 μm both in the horizontal and the vertical directions—a distance more than double that across which global radiation damage has been measured to spread (4 μm at 18.5 keV) beyond a micrometer-sized beam at 100 K (61), and more than four times that across which photoelectrons are calculated to travel in this experiment [∼2 μm at 13.45 keV (53)]. Since there have been no equivalent systematic studies at RT, we cannot exclude the possibility that the 10-μm spacing was insufficient and that global or specific radiation damage affected unexposed positions, in particular in the vertical direction where damaging species had more time to diffuse between probing neighboring spots than in the horizontal direction. However, no indication of data degradation was visible during data collection time. Also, an indication that global radiation damage at RT might not spread beyond 10 μm has been reported in a study using a 2.5 μm (FWHM, v) × 5.1 μm (FWHM, h) beam (23). However, we expect that the broad tails of the Voigt-shaped beam that was used in our study have preexposed neighboring positions on the crystals.

Visualizing the buildup of specific radiation damage at RT was made possible by the dose fine-slicing inherent in the SSRS approach and by the assembly of full datasets, all constituted from data originating from the same crystals, for each sequential dose point. In the RT 40.3 MGy/s series, sequential Fourier difference maps show the appearance and progression of specific damage to disulfide bonds up to a dose of about 0.5 MGy, above which the summed integrated difference electron density decreases again. Three different explanations can be offered to rationalize the peculiar dose dependence of disulfide bond damage at RT (Fig. 4D). The decrease of signal in Fourier difference maps above 0.5 MGy might reflect X-ray–induced repair of damaged disulfide bonds (62). Another explanation could be that global radiation damage might have generated sufficient nonisomorphism to swamp peaks in Fourier difference maps. A third possibility is hole burning by the intense beam center (23), resulting, as dose increases, in the recorded diffraction signal becoming dominated by scattering from the less damaged material that is illuminated by the weaker tails of the X-ray beam, leading to the specific damage observed at disulfide bonds apparently running backward with dose (Fig. 4D). We favor this third possibility since the dose dependence of specific damage at the Cys6–Cys127 disulfide bond can be well fitted by a “weighted specific damage” model (SI Appendix, Eq. S11) based on the Voigt-shaped beam being approximated by a three-beam model (see fit in Fig. 4D). The dose at which specific damage in the RT 40.3 MGy/s series is maximum (0.5 MGy, Fig. 4D) corresponds to the limit above which the information content originating from the central, hot part of the beam does not dominate anymore in difference Fourier maps. Diffraction intensities originating from the central, hot part of the beam decreased to one-half of their initial values at a slightly lower average dose, i.e., at D_1/2,g = 0.38 MGy. We advise that the 0.38-MGy dose limit not be exceeded when global damage is to be minimized. This dose limit holds strictly true only for tetragonal HEWL crystals at 2-Å resolution, but RT studies on other protein crystals (see above) reported D_1/2 values of the same order of magnitude ranging from 0.10 to 1.18 MGy at various resolutions and employing a variety of techniques to estimate the dose (20, 23, 26, 32, 34, 35, 60).

Negative peaks in sequential difference Fourier maps are observed on Pro70 at RT but not at 100 K (SI Appendix, Fig. S6). These peaks could reflect specific radiation damage to proline residues, so far reported neither for RT nor for 100 K structures. Alternatively, they could be due to an artifact of the Fourier synthesis, generated by preferential orientation of the crystals on the silicon nitride wafers observed at RT (see photo in Fig. 1) and not on the silicon chips at 100 K. However, such a missing cone of reflections would be the same for all time points and is therefore inconsistent with the dose dependence of difference Fourier peaks observed in SI Appendix, Fig. S6B. A third explanation might be X-ray-induced nonisomorphism, specifically deformation along the twofold axis—possibly because this interface is the weakest point of crystal contact in tetragonal lysozyme crystals (buried surface area at this interface is 60 Ų). The latter hypothesis could be tested by carrying out a RT SSRS study on HEWL crystals belonging to a different space group than the ones used here and analyzing features in difference Fourier maps near Pro70.

It is intriguing that Fourier difference maps at RT did not show any negative peaks at carboxyl groups of Glu and Asp residues, in contrast to the cryo- control series. The absence of peaks does not stem from large side-chain disorder at RT that could have prevented dose-dependent changes in electron density from being observed, because all Glu and Asp side chains are well ordered from the beginning to the end of the two RT series (SI Appendix, Fig. S4 as an example). Possibly, specific damage to the residues might not be observable at RT, in contrast to the well-documented decarboxylation occurring at 100 K (2–4). By analogy with observations in irradiated dilute aqueous solutions of simple amino acids (63), we expect that decarboxylation follows an oxidative event. The oxidizing agents will be holes created by an absorbed X-ray and, thereafter, the more numerous ionization events triggered by the released photoelectrons. In RT aqueous solutions, the hole carrier is the hydroxyl radical; however, in the presence of 1.75 M chloride ions, the hole would be rapidly [second-order rate constant is 4.3 × 10⁹ L⋅mol^–1⋅s^–1 (64)] transferred to give the chlorine atom, which presumably lacks the potential to oxidize the carboxylate. Although hydroxyl radicals are thought to be immobile at cryotemperatures (specifically, 100 K), decarboxylation is observed. Hole transport along the protein chain is a possible explanation inferred by the above low-temperature findings. Again at RT, this transport may be disrupted by thermal fluctuations or the reactivity of radicals formed in the mother liquor, protecting Glu and Asp residues from being decarboxylated.

Our study provides evidence that, at RT, specific damage to disulfide bonds occurs at a five times higher rate than does global damage to the crystal (characteristic half-dose of global damage D_1/2,g is 0.38 MGy and of specific disulfide damage D_1/2,s is 0.08 MGy). This is somewhat at variance with a recent systematic study (35) that determined the decoupling factor between global and specific damage of lysozyme crystals at RT to be of only 1.3, although in significantly different experimental conditions (e.g., oscillation datasets obtained from unique large crystals). At 100 K, the decoupling factor has been determined to be 12.4 (35). Whereas specific damage to disulfide bonds is easier to observe at 100 K than at RT (35), our study shows it can readily be observed at RT in dose fine-sliced SSRS using a highly intense microbeam.

The experimentally determined dose limit of 0.38 MGy (D_1/2,g) provides guidance for the growing number of RT SSX experiments being conducted (see SI Appendix, Table S2 for a summary of all D_1/2 values determined in this study). Note that the fitted D_1/2,g, characterizing the intensity decay due to the central, hot part of the X-ray beam, is smaller than the measured D_1/2 (0.57 MGy, Fig. 2) that relates to the entire beam and thus includes a contribution from the cold tails of the Voigt-shaped beam. The dose should be kept even below 0.08 MGy (D_1/2,s) if specific damage to disulfides is to be avoided. The increasing availability of high frame-rate photon counting detectors and of highly brilliant microfocus beamlines will make dose minimization in SSX experiments to below 0.38 MGy (minimizing global damage) or 0.08 MGy (minimizing specific damage to disulfides) more accessible. As outlined above, these limits are mere yardsticks as they are expected to vary between protein crystals of different compositions, solvent contents, and/or diffracting to different resolutions. Also, the dose limit estimates are based on the fit of I_n/I₁ data as a function of the dose averaged over the region of the crystal where 95% of the energy is deposited (AD_G95). In the presence of a strong dose contrast, as is the case for the intense microbeam (here, a 2.5 to 3.0 [h] × 1.5 [v] µm² FWHM impinging on ∼20 × 20 × 20-µm³ crystals) with considerable tails used here, the AD₉₅ is prone to large variations depending on crystal size and average spacing of crystals (and thus hit rate). A possibility would be to report the maximum dose, which is not prone to these variations and is experienced by the part of the crystal being exposed to the beam center in the beginning of the experiment and this part yields the most useful data—i.e., those collected before the dose limits are reached and hole burning (23) occurred. Another possibility would be to report the dose averaged over the FWHM of the beam, which would be most appropriate for crystals that are the same size as the beam FWHM. Independently of which average dose is being reported, one should keep in mind that for crystals larger than the beam most of the illuminated crystal volume experiences a dose that is not the average dose, due to the high dose contrast and the time-dependent hole burning (23).

It is anticipated that time-resolved (TR) SSX experiments (65–68) will gain importance following the current upgrade to (or building of) fourth-generation synchrotron sources (e.g., ESRF-EBS, NSLS II, and Max IV), and experimenters will be advised to respect the 0.38-MGy limit. Indeed, structural changes in TR-SSX experiments are visualized in Fourier difference maps calculated between datasets obtained with and without reaction triggering. Inasmuch as the Fourier difference peaks in SSRS series decrease above 0.38 MGy, our data suggest that the dynamic range of TR-SSX difference maps will decrease above that limit, rendering the detection of structural changes difficult, if not impossible, due to degradation of the structural information by global radiation damage in the central, intense part of the Voigt-shaped beam. Likewise, experimental phasing experiments at RT, requiring the accurate measurement of small changes in structure factor amplitudes, will be in danger of failing above 0.38 MGy.

Materials and Methods

Crystallization and Data Collection.

HEWL (Roche) was crystallized as described previously (69). Briefly, crystallization was achieved using the batch method by mixing 10 µL of HEWL solution (20 mg/mL) in 150 mM ammonium acetate, pH 4.5, and 10 µL of precipitant solution consisting of 3.5 M NaCl, 6% PEG 6000, and 150 mM ammonium acetate, pH 4.0. Crystals of 25 × 15 × 15 μm³ grew within a few hours and were subsequently centrifuged in a benchtop centrifuge at 2,000 × g and a 0.5-μL drop of the pellet deposited on solid supports for X-ray data collection. For RT data collection, the drop was sandwiched between two 2.5 mm × 2.5 mm × 0.5-μm silicon nitride wafers (Silson) and sealed with cyanoacrylate adhesive (Super Glue; Locktite). For data collection at 100 K, the drop was deposited on a 5- to 10-μm-thick microporous silicon chip [SUNA Precision (52)] and excess precipitant solution was blotted. The chip was then flash-cooled in a gaseous nitrogen stream of a cryocooler (Oxford Cryosystems) operating at 100 K.

Data collection was performed on the microbranch of the ESRF “Microfocus Beamline” (ID13) using the raster-scanning serial crystallography approach (30). The temperature in the experimental hutch was controlled by air conditioning and set to 22 °C and is referred to as RT in this study. In the focal plane, the shape of the X-ray beam can be accurately represented using a Voigt profile: similar to a Gaussian with weak but broad tails caused by parasitic scattering and aberrations of the X-ray optics. For the collection of high-dose rate series datasets at RT and at 100 K, an unattenuated beam with 2.7 × 10¹² photons/s and a FWHM of 3.0 μm (h) × 1.5 μm (v) was used. In order to collect a RT low-dose rate series, the beam was attenuated by adjusting the gap of the beamline’s u18 in-vacuum undulator (giving then 1.5 × 10¹¹ photons/s) resulting in FWHM dimensions of 2.5 μm (h) × 1.5 μm (v). The photon flux of the beam was measured using a silicon diode (type CANBERRA 300–500CB) which had been cross-calibrated with a diode of the same type certified by “Physikalisch-Technische Bundesanstalt.” The beam profile was measured via X-ray absorption of a gold-wire (50-µm diameter; Cambridge Ltd.), which was mounted on the scanner instead of the sample and was scanned through the beam in the horizontal and the vertical directions. The error in beam dimensions was estimated to be less than 300 nm in the horizontal, and less than 150 nm in the vertical directions. The X-ray beam energy was 13.45 keV (0.9219 Å) with a divergence of 0.67 mrad (h) and 0.7 mrad (v). We took advantage of the EIGER X 4M capability (51) to carry out shutterless data collection at a frame rate of close to 500 Hz (497.5 Hz, i.e., one frame every 2.01 ms) over a period of 100.5 ms (50 images, RT high-dose rate series), 160.8 ms (80 images, RT low-dose rate series), or 201 ms (100 images, cryo- high-dose rate series) at each sample position. The detector readout time was 10 μs, so that the total exposure time per frame was 2.01 ms, whereas the recording time per frame was 2.0 ms. The data acquisition periods included shutter opening and closing times (∼10 ms each, before and after translation to a new position). Thus, the first five and the last five frames were discarded. The fifth frame corresponded to a faint image acquired during shutter opening, with an intensity corresponding to 7.8% of the total intensity of the following full frames (i.e., corresponding to an average dose of 6.2 kGy for the RT and cryo- series collected at 40.3 MGy/s and of 0.37 kGy for the RT series collected at 2.4 MGy/s) that has been taken into account in the dose calculation. As a consequence, the 100.5-, 160.8-, and 201-ms series are composed of 40, 80, and 90 consecutive diffraction patterns at each sample position, respectively. Data collection positions were spaced by 10 μm, horizontally and vertically. After having moved to a new position, a settling time of 100 ms was allowed before the start of data collection so that sample oscillations owing to motor movements had ceased.

Dose Calculation.

The program RADDOSE-3D (53, 70) was used to estimate the average dose, corresponding to the average over the region of the crystal where 95% of the energy is deposited by a Gaussian beam (AD_G95). For sufficiently small crystals and/or small beams, the probability that photoelectrons will escape the irradiated volume is higher than the probability of being absorbed (54), thus reducing the dose. This phenomenon, known as photoelectron escape, is significant for the microbeams used in this study and needs to be considered in dose calculations. The most recent version of RADDOSE-3D (53) takes photoelectron escape into account as well as the entry into the crystal of photoelectrons from irradiation of surrounding liquid. For the crystals and incident X-ray energy used, the median range of photoelectrons is predicted to be 2 μm. The high-dose rate series, both at RT and at 100 K, were collected at 40.3 MGy/s, while the RT low-dose rate series was collected at 2.4 MGy/s. If photoelectron escape had not been taken into account, apparent average dose rates would have been 76.0 and 5.0 MGy/s, respectively.

Data Reduction and Processing and Structure Refinement.

NanoPeakCell (30) was used for processing of SSRS data. Selected hits were indexed and integrated with CrystFEL 0.6.2 (71). Indexing relied on MOSFLM (72), XDS (73), and Dirax (74). Real-space refinement was carried out in Coot (75) and reciprocal space refinement in Phenix (76). Details can be found in SI Appendix.

Difference Map Calculation and Integration in Real Space.

Structure factor amplitude Fourier difference maps were calculated for all three series with respect to the lowest-dose dataset of the RT low-dose rate and the cryo- series, i.e., F_o^RT-LDRn – F_o^RT-LDR1, F_o^RT-HDRn – F_o^RT-LDR1, and F_o^CRn – F_o^CR1, with RT-LDRn, RT-HDRn, and CRn being the 80 RT low-dose rate, the 40 RT high-dose rate, and the 90 cryo- datasets, respectively. Because of a high structure factor isomorphism between the two RT series, the lowest-dose dataset of the RT low-dose rate (RT-LDR1; corresponding to a dose of 5 kGy) could be used as the reference dataset for both RT low- and high-dose rate series. Q-weighted difference maps were calculated as described earlier (77), using custom-made scripts (78) implemented in CNS (79). Maps were calculated on an absolute scale (e⁻ per cubic angstrom) at a resolution of 2.04 and 1.9 Å for both RT series and the cryo- series, respectively. The resolution cutoff of each series was set to that of the highest-dose dataset in each series.

In order to quantify specific radiation damage, a custom-made Python script was used to integrate electron density in the difference maps around all atoms of the model (58). The integration volume was a sphere with a radius r proportional to the square root of the refined B factor of the respective atom of the first dataset in each series used for the calculation of difference maps (LDR1 or cryo1): $r=\left(1/2\pi \right)\sqrt{B/2}$, as described in ref. 80. For disulfide bonds, integration was performed over the two sulfur atoms and summed (Fig. 4). For Pro70, it was carried out over all modeled atoms (SI Appendix, Fig. S6). As a control for the RT high-dose rate series (Fig. 4D), we integrated over a sphere with a radius proportional to the square root of the refined B factor of the respective atom of the nth dataset. In the resulting graph, the dose at which the integrated signal in Fourier difference maps was maximum (about 0.5 MGy) remained unchanged.

Code Availability.

All Python scripts have been deposited on GitHub and are accessible at https://github.com/coquellen/RADDAM_2019 (58).