Continual evolution through coupled fast and slow feedbacks

Significance

Continual evolution refers to the unceasing evolution of at least one trait involving at least one organism. Van Valen’s Red Queen Hypothesis is a particular example that represents the unceasing evolution of organisms in response to each other. In spite of the intense research on the topic from macroevolutionary and microevolutionary perspectives, the conditions that guarantee continual evolution remain elusive. Here, we provide mathematical proof for conditions that lead to continual evolution, which essentially requires interaction between fast positive and slow negative feedbacks between environment, population, and evolving traits. Our general framework allows for a polymorphic population and mutations of large effect, properties typically found in microbial systems, and therefore our results help bridge theory and experimental results.

Abstract

Continual evolution describes the unceasing evolution of at least one trait involving at least one organism. The Red Queen Hypothesis is a specific case in which continual evolution results from coevolution of at least two species. While microevolutionary studies have described examples in which evolution does not cease, understanding which general conditions lead to continual evolution or to stasis remains a major challenge. In many cases, it is unclear which experimental features or model assumptions are necessary for the observed continual evolution to emerge, and whether the described behavior is robust to variations in the given setup. Here, we aim to find the minimal set of conditions under which continual evolution occurs. To this end, we present a theoretical framework that does not assume any specific functional form and, therefore, can be applied to a wide variety of systems. Our framework is also general enough to make predictions about both monomorphic and polymorphic populations. We show that the combination of a fast positive and a slow negative feedback between environment, population, and evolving traits causes continual evolution to emerge even from the evolution of a single evolving trait, provided that the ecological timescale is sufficiently faster than the timescales of mutation and the negative feedback. Our approach and results thus contribute to a deeper understanding of the evolutionary dynamics resulting from biotic interactions.

The evolutionary dynamics of a species in a complex ecosystem can be driven by the properties of the species, by the interaction with coexisting species and their environment, and/or by external factors. To better understand to what extent the emerging ecological and evolutionary dynamics are caused by the species or by (intraspecific or interspecific) biotic interactions, it is essential to study systems in the absence of any abiotic drivers. Isolating a system from all abiotic factors may lead to a static adaptive landscape, where adaptation follows a path toward a peak in that landscape—reachable or not (1, 2). However, since a major part of any individual’s environment is typically composed of other (evolving) species, any species’ environment will normally change even without external abiotic variation, through both ecological and evolutionary changes. Hence, the resulting adaptive landscape is expected to be dynamic, potentially leading to continual coevolutionary dynamics, where traits are oscillating or changing continually in a directional manner over evolutionary time (3).

Continual evolutionary dynamics are evolutionary dynamics that do not result in stasis, because the evolving traits eventually show significant changes over time. This means that, although the evolutionary dynamics could be apparently stable for some period, eventually sustained fluctuations (i.e., either periodic or irregular changes over time) will materialize for genotypes and phenotypes over long timescales. Continual evolutionary dynamics may involve one or more evolving traits and one or more evolving species and includes both arms race and fluctuating dynamics. Therefore, these dynamics are more general than Red Queen (RQ) dynamics, as the latter typically refers to systems of at least two species, whereas the former includes systems with a single species.

The RQ dynamics (4) is a concept that has had a major influence on microevolutionary and macroevolutionary theory. The analysis of macroevolutionary models has led to the conclusion that the emergence of either RQ dynamics or stasis depends upon the nature of the within-system biotic interactions (5–8). This body of work, however, has not been able to translate into ecological terms what the conditions for the emergence of the RQ are, although recent research found that symmetric competitive interactions are more likely to lead to stasis (9).

From the microevolutionary perspective, theoretical work has focused on mechanistic descriptions of specific examples where the RQ can emerge (3). Theoretical studies of microevolutionary RQ dynamics mostly use methods based on adaptive dynamics and quantitative genetics (10–16). The adaptive dynamics approach assumes that the ecological dynamics have reached an equilibrium before evolution can occur, and studies the attempts of invading this stationary state of the resident by mutants (defined as individuals with a value of the adaptive trait that is slightly deviating from that of the resident). These assumptions enable a rigorous theoretical analysis of the system, and are often still a good approximation even if those assumptions are not strictly met. The quantitative genetics approach, on the other hand, does not require an ecological equilibrium, but also requires the timescale separation between evolutionary adaptation and ecological dynamics. Genetic variation is sometimes incorporated in the quantitative genetics approach as affecting the speed of evolution, with the mean trait value affecting the ecological dynamics (e.g., ref. 17). If the rate of evolutionary change is very slow, the quantitative genetics approach becomes similar to adaptive dynamics. Both methods assume that adaptive traits evolve along a fitness gradient. Following these theoretical frameworks, studies focusing on predator–prey or host–parasite systems have been able to reach conclusions about the conditions that increase or decrease the chance of RQ dynamics under the specific circumstances defined in the study [e.g., fast adaptation is less likely to lead to RQ dynamics (11), and RQ dynamics require an intermediate harvesting efficiency of the prey (10)].

With exceptions [e.g., evolutionary branching models (18)], most of the work mentioned above constrains the evolving population to be monomorphic, and therefore there is no guarantee that the same examples will lead to RQ dynamics in a polymorphic setting, which includes coexistence of subpopulations with different trait values. A polymorphic trait distribution arises easily with asexual reproduction or traits that are determined by a few loci, but can also arise when assortive mating develops (see the discussion in ref. 18). Hence, the conditions that lead to the emergence of the RQ, or, more generally, continual evolution, in polymorphic populations remain elusive. Since most evolution experiments concern microorganisms, which are prone to showing polymorphic populations, this knowledge gap can prevent linking theoretical results to experimental data. Here, we fill this gap by studying the mechanisms leading to continual evolution without constraining the distribution of phenotypes that may be present in the population, and therefore the emergent continual evolutionary dynamics do not rely on the assumption of a monomorphic population. Additionally, we allow for interactions with (possible abiotic parts of) the environment (19) and for mutations of small and large effects, which can be expected in such populations (20–22).

Most of the theoretical microevolutionary RQ studies use specific functional forms for their analysis, hampering the generalization of the obtained results. Metaanalyses and reviews [such as the one by Abrams (23)] can provide some more general insights, but, since many of these studies use similar equations, the breadth of their conclusions is still limited. To obtain general results and a broad understanding of what ecological interactions can cause evolutionary patterns such as continual evolution, we need as general models as possible. Here, we aim at extending the theoretical understanding of the conditions that lead to either continual evolution or stasis. For this purpose, we use a general model with a reduced set of assumptions regarding the form of the model functions. We find that a system with slow and fast feedback interactions in a polymorphic setting exhibits continual evolutionary dynamics in the presence of a timescale separation between the ecological and evolutionary dynamics, regardless of the size or effect of mutations. Note that the separation of timescales can result from either ecological processes that are much faster than evolutionary ones or from differential rates for different evolutionary processes.

Generic Model and Emerging Ecoevolutionary Dynamics

General Model Description.

We model a population with genetic variation using differential equations that allow for mutations that are not constrained to be infinitesimal changes in the trait value. Note that, although, for simplicity, we focus on one trait for most of this study, our framework for continual evolution is generalizable to any number of traits. In order to focus our argument, we use a general model of a population density distribution $u\left(x,t\right)$ over the trait space $x$ and the distribution of environmental factors (i.e., abiotic factors and nonevolving species here, but the coevolving species in a RQ scenario), $\phi \left(y,t\right)$, over the space of values for the environment $y$,

$$\begin{array}{c}\frac{\partial }{\partial t}u\left(x,t\right)=u\left(x,t\right)\cdot f\left(u,\phi \right)+{ϵ}_m\cdot g\left(u\right)\\ \frac{\partial }{\partial t}\phi \left(y,t\right)={ϵ}_e\cdot h\left(u,\phi \right).\end{array}$$ [1]

In this general case, the evolving trait is not specified, and therefore its trait space could have any shape and dimensionality (i.e., any number of evolving traits). Distinct peaks for $u\left(x,t\right)$ in the trait space, for example, represent a polymorphic trait distribution within a species if there can be exchange of individuals between these distinct peaks, or different species if there is no exchange between peaks (or very low exchange, in a macroevolutionary setting). Similarly, the environment space, $y$, which consists of all nonevolving parts of the system, could have any form. The functional $f$ describes the growth of the population, which can depend on the population density distribution $u\left(x,t\right)$ as well as on the environmental factors $\phi \left(y,t\right)$. The functional $g$ describes the change in the population density due to mutations, which could reasonably be represented by a diffusion process (9). This change due to mutations is modeled in an unbiased manner, with the benefits of a mutation resulting from the relative performance of its associated population. The functional $h$ encodes the rate of change in environmental factors, which can again depend on $u\left(x,t\right)$ and $\phi \left(y,t\right)$. Timescale differences between growth, environmental factors, and mutations are represented with ${ϵ}_e$ and ${ϵ}_m$. More subtle differences in timescales can be incorporated through the individual parameters, but the timescale differences captured in the ${ϵ}_e$ and ${ϵ}_m$ suffice to derive the results in this paper.

Continual Evolutionary Dynamics and the Role of Feedbacks.

In this paper, we show the conditions that guarantee continual evolutionary dynamics in the generic model above, Eq. 1. These conditions include a fast positive feedback and a slow negative feedback. The former is incorporated in the model through a positive effect of the trait density $u$ on the population growth $f$ (essentially, an Allee effect). For the latter, the negative effect is implemented through how the dynamics of the environmental factors depend on the population density (i.e., how the functional $h$ depends on $u$) and how environmental factors affect the growth of the population (i.e., how $\phi$ affects $f$). The negative feedback is either a much slower process or a process that only affects population growth once it has changed by a large amount; in other words, it occurs within a much longer time frame, which can be encoded through ${ϵ}_e<<1$.

A biological example of the slow negative feedback could be a predator–prey interaction where the generation time of the predator is much longer than that of the prey, and where the predator targets preferentially a specific prey phenotype or prey type [e.g., bears preferring large salmon (24) or zooplankton preferring phytoplankton with a certain nitrogen-to-phosphorus ratio (16)]. For the former example (predator that feeds on prey with a specific size), the evolving trait would be the body size, and, therefore, $u$ would indicate the density of prey with a specific size value, $x$; the environment space $y$ would represent the preference of predators for each different size, and, therefore, the function $h$ would represent the growth of predators which depends on the density of their specific target prey. Prey growth is represented by function $f$, which incorporates the negative effect caused by (their specific) predators, but also a positive effect due to, for example, cooperation in defense or feeding (when the evolving population is foraging on a certain vegetation area with sufficient resources, the more individuals forage in the same place, the better they are protected against predation). Evolutionary changes in size would be encoded in the $g$ function.

A predator–prey system with only a single evolving trait and with positive and negative feedbacks could be a predator that adapts not to a prey trait but to the prey population size, as in adaptive foraging (25). The positive feedback originates from an increase in prey population size that leads to decreased selection on a foraging trait of the predator, leading to a stronger increase in prey population size. The slower but stronger negative feedback results from a very high prey population that, through density dependence (e.g., intraspecific competition), leads to a rapid decline of the prey population. Here, $x$ is the combination of the foraging trait of the predator and the prey population size, such that the positive feedback is contained in this variable, while only the foraging trait of the predator evolves. Then $u$ would indicate the density of predators with specific foraging traits and the prey population size. The environment $y$ consists of the factor that causes the prey collapse, for example, the resource level for the prey. The function $h$ describes the change in prey resource level, and the function $f$ describes both the growth of the predator population (which depends on the foraging trait and the prey population size) and the change of prey population size (which depends on the predators and the prey resource level, $\phi$).

Another system that is a potential example is a species with a complex life cycle that switches to a different habitat at a specific age (e.g., ref. 26). In this case, the trait space $x$ is a one-dimensional space representing the age at which the individual moves to the second habitat; the environment space $y$ consists of resource densities at the two different habitats; the function $h$ signifies how the resource densities in both habitats depend on 1) the density of the species and 2) the distribution of ages at which the species changes habitats: As the switching age increases, the risk of depleting resources in the current habitat increases. The function $f$ signifies the growth of the species, which depends on the distribution of switching ages and resource density. This function includes a positive effect provided by more individuals shifting at the same time (e.g., increased protection or reduced founder effect), and the negative effect of competition for resources. The evolution of the switching age is encoded by the $g$ function. More examples of the fast positive and slow negative feedbacks are listed in Box 1.

Box 1: Nonexhaustive list of processes that could potentially lead to the type of fast positive and slow negative feedbacks considered by our framework.

These feedbacks operate at the level of the trait; that is, after an increase of the number of individuals with a certain trait value, a slow negative feedback leads to a negative effect on the selection for that trait value over time. Note that “fast” and “slow” refer to the relative rates of the respective ecological processes, also relative to the evolution of the trait of interest.

Fast Positive Feedbacks.

• •Increased mating opportunities in larger groups of individuals with similar trait values.
• •Increased fitness of offspring when mating occurs between individuals with trait values approaching the same extremal trait.
• •Increased survival/protection from predation when forming groups with individuals of similar trait value.

Slow Negative Feedbacks.

• •Microbial byproduct formation that inhibits growth for cells with a similar trait value when their population density reaches high concentrations.
• •Viruses that evolve as a result of a vaccination campaign (devised seasonally due to the virulence of the virus the previous season).
• •Slowly evolving predator/parasite that specializes on a specific prey/host trait value.
• •Prey/host population changes in response to a predator/parasite population with a specific trait value.

We use the slow negative feedback in the proofs below to ensure that, when one type is abundant, over time other types will grow faster, and there will be trait changes and not an equilibrium at one extreme of the trait values. The fast positive feedback translates into trait changes from the vicinity of one extreme to the other that occur quickly enough, ensuring that the system does not relax to an equilibrium at an intermediate trait value or an equilibrium with a coexistence of two subpopulations with more extreme trait values. In some systems, it will be unlikely that the system goes to such an equilibrium, and, therefore, the fast positive feedback will not be required in every model.

Results

General Conditions for Continual Dynamics.

We now prove the existence of continual evolution for the generic model represented by Eq. 1. The main idea of the proof holds independently from context, and works in arbitrary trait spaces, both continuous and discrete.

We assume the existence of one-dimensional projections $u\mapsto M\left(u\right)$ and $\phi \mapsto \mathrm{\Phi }\left(\phi \right)$, both taking real values, and focus on studying the evolutionary dynamics in the $\left(M,\mathrm{\Phi }\right)$ plane. In general, it will not be possible to determine the values of $\partial M/\partial t$ and $\partial \mathrm{\Phi }/\partial t$ without knowing $u$ and $\phi$. However, to prove continual evolution, one merely needs to know how the signs of the two derivatives behave in suitable regions in the $\left(M,\mathrm{\Phi }\right)$ plane.

In the most general scenario, there is no specification on the projections $M\left(u\right)$ and $\mathrm{\Phi }\left(\phi \right)$, nor is there any information on the dynamics in $\left(u,\phi \right)$ coordinates. The assumptions refer directly to the signs of $\partial M/\partial t$ and $\partial \mathrm{\Phi }/\partial t$ in different parts of the dynamical plane. In this scenario, there is no reference to how these conditions can be obtained from knowledge of the dynamics in the $\left(u,\phi \right)$ coordinates; the conditions are taken as given.

A fast positive feedback is modeled directly, by assuming that a sufficiently large value of $M$ implies that $\partial M/\partial t$ is positive and, similarly, that a sufficiently small value of $M$ implies that $\partial M/\partial t$ is negative. We also assume the existence of a slowly reacting, negative feedback, modeled indirectly via $\mathrm{\Phi }$: for large $M$, the external factor $\mathrm{\Phi }$ will slowly increase, and, for sufficiently large $\mathrm{\Phi }$, the value of $M$ will slowly decrease (this implies a feedback loop through the environment as in the biological examples above). Similar assumptions are stated for small $M$ and small $\mathrm{\Phi }$. While the value of $\mathrm{\Phi }$ adapts to the value of $M$ very slowly, we assume that the negative feedback eventually dominates the positive feedback: for sufficiently large $\mathrm{\Phi }$, the rate $\partial M/\partial t$ is negative, regardless of the value of $M$.

These feedback assumptions are stated more formally in Box 2, conditions PF1, PF2, NF1, and NF2. The following result, which guarantees continual evolution, is proved in SI Appendix, section S1 under these feedback assumptions, provided there is a sufficiently strong separation of timescales between the ecological dynamics in $M$, on the one hand, and between the ecological dynamics in $\mathrm{\Phi }$ and the effects of mutations, on the other hand.

Box 2: Assumptions on the positive and negative feedbacks required for the proof.

We assume that there exist values $0<{\mathrm{\Phi }}_{-}<{\mathrm{\Phi }}_{+}<1$ such that the rates of change due to ecology only satisfy the following feedback conditions:

• •Positive feedback, assumption 1 (PF1): When $\mathrm{\Phi }<{\mathrm{\Phi }}_{+}$, we assume that $\partial M/\partial t>0$ whenever $M$ is unequal to, but sufficiently close to, 1, and, similarly:
• •Positive feedback, assumption 2 (PF2): When $\mathrm{\Phi }>{\mathrm{\Phi }}_{-}$, we assume that $\partial M/\partial t<0$ whenever $M$ is unequal to, but sufficiently close to, 0.
• •Negative feedback, assumption 1 (NF1): When $\mathrm{\Phi }\ge {\mathrm{\Phi }}_{+}$ and $M<1$, we assume that $\partial M/\partial t<0$. When $M=1$ and $\mathrm{\Phi }\le {\mathrm{\Phi }}_{+}$, we assume that $\partial \mathrm{\Phi }/\partial t>0$, and, similarly:
• •Negative feedback, assumption 2 (NF2): When $\mathrm{\Phi }\le {\mathrm{\Phi }}_{-}$ and $M>0$, we assume that $\partial M/\partial t>0$. When $M=0$ and $\mathrm{\Phi }\ge {\mathrm{\Phi }}_{-}$, we assume that $\partial \mathrm{\Phi }/\partial t<0$.

Note that, for simplicity, this list and the proofs in SI Appendix use a normalized version of $M$ and $\mathrm{\Phi }$, but they could more generally be phrased in terms of an $M$ and $\mathrm{\Phi }$ within any arbitrary (but constrained) range.

Theorem. If the feedback assumptions above are satisfied, then there exist initial values $\left(u,\phi \right)$ for which $M\left(t\right)$ will fluctuate indefinitely between values arbitrarily close to both a maximum and a minimum value.

Let us emphasize that, when the spaces for the variable $u$ or $\phi$ (i.e., $x$ or $y$, respectively) are multidimensional, there is no reason to expect strictly periodic dynamics. When $x$ and $y$ are one-dimensional, we expect periodic dynamics due to the Poincaré–Bendixson theorem, but, as we show below, higher-dimensional $x$ and $y$ can also show nonperiodic continual evolution (see Continual Dynamics in the Case of Two Evolving Traits: An Example).

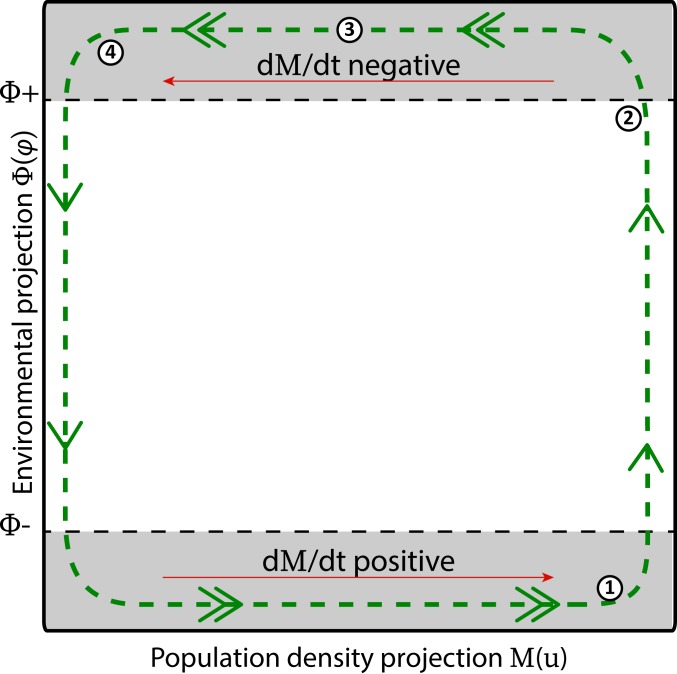
Fig. 1 illustrates the emerging behavior in the $\left(M,\mathrm{\Phi }\right)$ plane. When $M$ is sufficiently close to (but, due to mutations, never equal to) its maximum value, $\mathrm{\Phi }$ increases until it gets very close to a sufficiently large value ${\mathrm{\Phi }}_{+}$ (step 1). When $\mathrm{\Phi }$ is near ${\mathrm{\Phi }}_{+}$, the value of $M$ decreases due to the dominant negative feedback (step 2). Initially, the decrease in $M$ is slow, and, during that time, $\mathrm{\Phi }$ continues to increase. However, because the dynamics of $M$ are much faster than the dynamics of $\mathrm{\Phi }$, eventually, $M$ decreases very quickly toward its minimum value while $\mathrm{\Phi }$ remains effectively constant (step 3). After a limited amount of time, $M$ eventually reaches a value arbitrarily close to its minimum, and $\mathrm{\Phi }$ decreases (step 4). Due to the timescale separation assumption, the decrease in $\mathrm{\Phi }$ is arbitrarily small in the time interval in which $M$ decreases, and hence the decrease in $M$ is not prevented by $\mathrm{\Phi }$. The symmetry in the feedback conditions (i.e., the fact that PF1 and NF1 can be obtained by replacing $M\to 1-M$ and $\mathrm{\Phi }\to 1-\mathrm{\Phi }$ in PF2 and NF2) guarantees that the process repeats itself.

Fig. 1.

Sketch of emerging behavior in a one-dimensional projection: the dynamics in the ($M\left(u\right)$, $\mathrm{\Phi }\left(\phi \right)$) plane, where $M\left(u\right)$ is a one-dimensional projection from the population density space and $\mathrm{\Phi }\left(\phi \right)$ is a one-dimensional projection from the environmental space. Because of the assumptions on the sign of the derivatives of these projections (red arrows), there will be continual dynamics (green arrows). The numbers correspond to the steps of the dynamics as described in the main text.

Note that the simple formulation of the negative feedback conditions (NF1 and NF2) is not realistic on the whole $\left(u,\phi \right)$ space. For example, when the population density $u$ is concentrated around a single trait, one cannot expect any dynamics due to ecology, regardless of $\mathrm{\Phi }$, because, near such a single trait, the rate of change $\partial M/\partial t$ is governed almost entirely by mutations, which, by assumption, act at a much slower timescale. Also, in the proof sketched above, it is essential that the time interval needed for $M$ to decrease to a value close to its minimum is independent of the slower timescale. It is sufficient, however, if the feedback conditions hold in the region of $\left(u,\phi \right)$ space reached by the dynamics. In the more explicit case discussed below, we exploit this observation to obtain more realistic feedback assumptions.

Continual Dynamics with a Single Evolving Trait.

Let us discuss a more explicit case involving a continuous one-dimensional trait space, $x$ (representing, for example, a continuous trait such as length), and a single environmental factor, $\phi$. For this case, we will use as the one-dimensional projection $M\left(u\right)$ the average trait value,

$$M\left(u\right)=\frac{{\int }_{x}x\cdot u\left(x,t\right)}{{\int }_{x}u\left(x,t\right)}.$$ [2]

As explained in SI Appendix, section S1, suitable feedback conditions in the $\left(u,\phi \right)$ space determine, to a large extent, the dynamical behavior in the $\left(M,\phi \right)$ plane. While it will generally not be possible to deduce $\partial M/\partial t$ and $\partial \phi /\partial t$ from only knowing $M$ and $\phi$, it will be possible to determine the signs of these rates in large regions of the plane. As discussed in the previous section, this can be sufficient for deducing continual evolution.

As a practical example, let us consider the logistic growth model, that is, that the growth function in Eq. 1 is given by

$$f\left(u,\phi \right)=\mu \left(u,\phi \right)\left(1-\frac{\int u\left(x\prime ,t\right)dx\prime }{K}\right)-d,$$

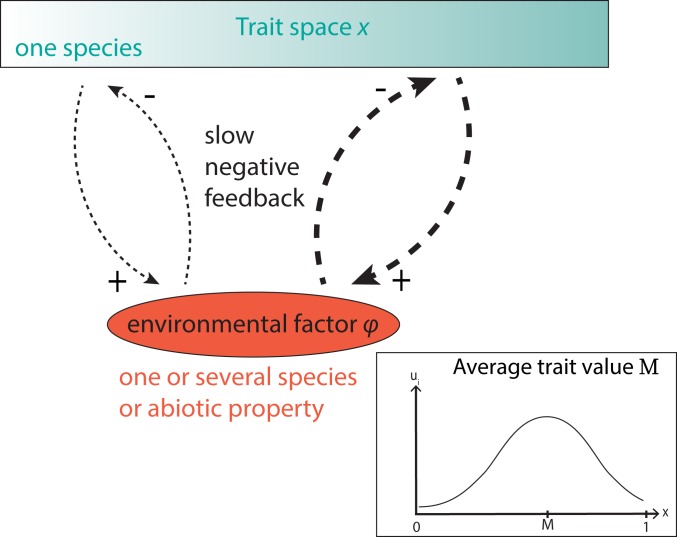
where $d$ represents a mortality rate, $K$ is the carrying capacity, and the growth rate $\mu$ depends on the populations density $u$ and environmental factor $\phi$. The positive feedback is incorporated directly through the effect of $u$ on the growth rate $\mu$, while the negative feedback is incorporated indirectly through the effect of $u$ on $\phi$ and the (opposite) effect of $\phi$ on $\mu$. Fig. 2 illustrates the indirect negative feedback.

Fig. 2.

A single evolving trait with a range of possible trait values. One species has a single evolving trait, with a phenotype ranging from $x=0$ to $x=1$. Dashed lines indicate the negative feedback, which originates from the interaction with the environment $\phi$ (which can be a species, an abiotic factor, or a property of the ecosystem). Thicker lines denote a stronger interaction with the environment, and therefore a stronger negative feedback. Inset illustrates that $M$ is calculated by taking the average trait value in the population, thus weighing the trait values by the density of that phenotype (Eq. 2).

The logistic equation is a simplistic model, but it helps represent biological examples for which continual evolution can occur. For instance, a plausible biological example would be a species whose growth is determined by a trait that affects the environment (e.g., food choice), while the carrying capacity and death rate are determined by other factors (e.g., space and predation, respectively). This trait could have a positive effect on growth when the resource is spatially localized.

As we show in SI Appendix, section S1, given the mean trait value $M$ (Eq. 2), the sign of $\partial M/\partial t$ can be determined from the values of $M$ and $\phi$ when $\mu$ is assumed to be either constant or strictly monotonic for all relevant parameters. Therefore, under the corresponding feedback assumptions and timescale separation assumptions, the logistic model can satisfy continual evolutionary dynamics.

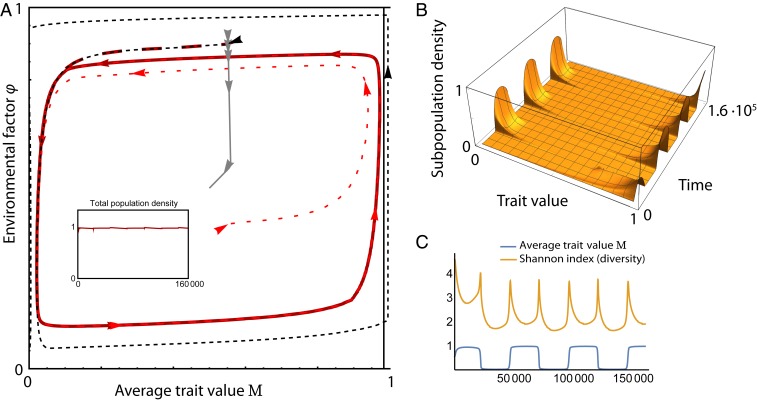
To simulate this example numerically, we split the population into discrete groups with similar trait values. Fig. 3A shows that forcing the absence of evolution leads to extinction of all but one group; fast evolution (i.e., large ${ϵ}_e$) leads to an equilibrium, that is, to a static $u\left(x,t\right)$ that shows one single, well-defined mean value $M$; slow evolution, on the other hand, leads to continual evolutionary fluctuations where the average trait value approaches one of the two extremal values in an alternating way. Fig. 3B shows the distribution of phenotypes over time for the latter case. The population is centered around one of the extreme trait values most of the time, but intermediate phenotypes are also seen in the transition periods. Fig. 3C shows that the diversity of phenotypes, measured by the Shannon index (SI Appendix, section S2), peaks at shifts of the mean trait value due to the flattening of $u$ during the transition period, which increases the standard deviation of the distribution (see ref. 27).

Fig. 3.

Example of evolutionary dynamics with a single evolving trait: behavior of a system following the outline of Fig. 2. (A) System behavior for no mutation (thin dashed lines, resulting in the extinction of the population), fast evolution (gray dashed line, leading to an equilibrium), and slow evolution (dashed red lines; continual evolutionary dynamics from different initial values). Inset shows that the total population remains approximately constant. (B) Phenotype abundances obtained in the continual evolution case. (C) Mean trait value and Shannon diversity index for the same case, showing the emerging fluctuations. Simulation is of 100 phenotypes equally distributed over the range of trait values; see SI Appendix, section S2 for the exact equations and parameter values.

Conditions for Continual Dynamics in the Case of a Single Evolving Trait Consisting of Two Phenotypes.

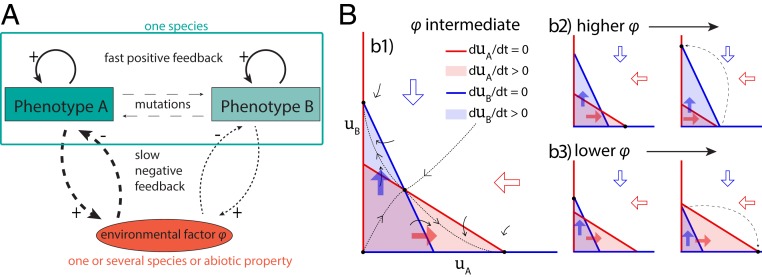
To understand, in more detail, the role of a fast positive and a slow negative feedback in the emergence of the evolutionary oscillations, we reduced the system to a simpler version. In this case, the trait space $x$ consists of only two points, $A$ and $B$, representing a trait with only two main values (i.e., only two phenotypes are possible). One of the phenotypes is interacting with an external factor, and the other one either interacts less strongly or not at all (Fig. 4A). This representation reflects a biological system where a trait value is either present or not, for example, a parasite choosing one host type over another. When the trait also affects mate choice (for example, because they will be located near the same host), the trait shows a positive feedback. The slow negative feedback could result from the fact that one of the hosts can develop defenses.

Fig. 4.

Continual evolution with a single evolving trait consisting of two phenotypes. (A) A species with only two possible phenotypes, $A$ and $B$, which both show fast positive feedbacks on their own phenotype. The arrows signify the different processes/feedbacks, with thickness representing the strength of the interaction, and the number of dashes representing the timescale. Continuous arrows are the fast positive feedback. Phenotype $A$ shows a strong negative feedback on an external factor $\phi$ (thick dashed line), while phenotype $B$ shows a weaker (or nonexistent), negative feedback (thin dashed line); this feedback could result from the phenotype having a positive effect on the environment and the environment having a negative effect on the phenotype (as in the figure), or vice versa. Mutations are represented with the thinnest and most spaced dashed lines, because they are the weakest and slowest interactions; they are only possible between the two phenotypes, although rates are low. (B) Approximate phase planes. Block arrows and colored areas show the sign of the derivatives. Blue and red lines show the isoclines where the derivatives are 0. The isoclines for $d{u}_A/dt=0$ and $d{u}_B/dt=0$ cross as shown, because the fast positive feedback ensures that the growth of the subpopulation $u_B$ decreases faster with increasing $u_A$ than the growth of the subpopulation $u_A$, and vice versa. Black dashed lines show the direction of change over time. Different phase planes with black solid lines above show how the phase planes will change over time.

We analyzed this system, where individuals with both phenotypes ($u_A$ and $u_B$) and the environmental factors ($\phi$) change over time. Phenotype $A$ could represent the parasite phenotype choosing the host that can develop defenses; the (less) interacting phenotype $B$ could represent the phenotype choosing the host that cannot develop defenses, and the external factors $\phi$ would therefore refer to the amount of defense (for the host that can develop defenses). Thus, $\phi$ is positively affected by $u_A$ and negatively affected by $u_B$,

$$\begin{array}{l}\frac{d}{dt}{u}_A\left(t\right)=u_A\cdot f_A\left(u_A,u_B,\phi \right)+{ϵ}_m\cdot m\left(u_A,u_B\right)\\ \frac{d}{dt}{u}_B\left(t\right)=u_B\cdot f_B\left(u_A,u_B,\phi \right)-{ϵ}_m\cdot m\left(u_A,u_B\right)\\ \frac{d\phi }{dt}={ϵ}_e\cdot h\left(u_A,u_B,\phi \right).\end{array}$$ [3]

This set of equations directly results from Eq. 1 by splitting the population density distribution $u\left(x,t\right)$ into two subpopulations: $u_A$ (for individuals showing trait value $A$, i.e., phenotype $A$) and $u_B$. Because the only relevant mutations in this case are mutations that change the phenotype from $A$ to $B$ and vice versa, the evolution function $g$ can be simplified into a function $m$ that describes the net mutations from one trait value to the other (hence the opposite sign). The dependency of the functions $f_A$ and $f_B$ on the subpopulations $u_A$ and $u_B$ is assumed to cause a positive feedback (see conditions PF1 and PF2 in Box 2), while the dependency on $\phi$ of the functions $f_A,f_B$, and $h$ generate a negative feedback, given by conditions NF1 and NF2, assumed to eventually dominate over the positive feedback. In SI Appendix, section S1, we prove that, under the additional, mild “unique stable value assumptions” (USV1 and USV2), sufficiently small ${ϵ}_m$ and ${ϵ}_e$ lead to the emergence of continual evolution. It is both natural and necessary to assume that the effect of evolution is relatively small (but never zero), as large values of ${ϵ}_m$ typically cause convergence to an equilibrium. The detailed proof can be found in SI Appendix, section S1.

The idea of the proof for a variable population size is illustrated in Fig. 4B. The diagrams show an approximation of the dynamics in the ($u_A,u_B$) phase planes. This approximation is without the mutation term, but, since mutations are rare (in our case the mutation term is small), the actual phase plane will not be very different. The assumptions above guarantee that the phase plane for intermediate $\phi$ resemble the one shown in Fig. 4 B, b1. When the environmental strength $\phi$ is intermediate, there are four intersections of the lines $d{u}_A/dt=0$ and $d{u}_B/dt=0$, that is, four equilibria, where one is repelling (the origin), another one is a saddle point (the point in the middle), and the other two are attractors. The nature of the equilibria can be seen from the sign of the derivatives. Depending on the initial value for $u_A$ and $u_B$, the system converges to an attractor near the $u_A$ axis or the $u_B$ axis. When the system is near the former, $u_B$ will be almost 0, and, since $u_A$ has a positive effect on $\phi$, $\phi$ will increase. The change in $\phi$ will, in turn, change the phase plane diagram, and the intersection near the $u_A$ axis will become repelling (Fig. 4 B, b2). When $\phi$ is high enough, there will be only one attracting intersection (near the $u_B$ axis), and the system will approach that state. As $u_B$ increases (and $u_A$ decreases), $\phi$ decreases, but, since the fast–slow condition guarantees that the dynamics in $\phi$ are slower than in $u_A$ and $u_B$, the system will come close to the intersection near the $u_B$ axis before $\phi$ changes significantly. When $\phi$ does change, the system will pass by the phase plane depicted in Fig. 4 B, b1 (figure for intermediate $\phi$), but now $\phi$ will continue to decrease, and the intersection near the $u_B$ axis will eventually disappear (Fig. 4 B, b3). This cycle will continue indefinitely, giving rise to continual evolution.

The proof of continual dynamics above only required some restrictions on the functions $f$, $m$, and $h$, and did not use any functional forms. However, to give an indication of the expected dynamics, we constructed an example that follows these restrictions (see Fig. 5 and SI Appendix, section S2 for details and additional example). Our proof states that stable continual evolutionary cycles will emerge for almost all initial values if ${ϵ}_e$ and ${ϵ}_m$ are chosen to be sufficiently small. Fig. 5 shows that this is the case, by using two different initial states. On the other hand, a high mutation rate and/or a fast feedback lead to a stable equilibrium (i.e., stasis), whereas the absence of mutations causes one of the two phenotypes to go extinct.

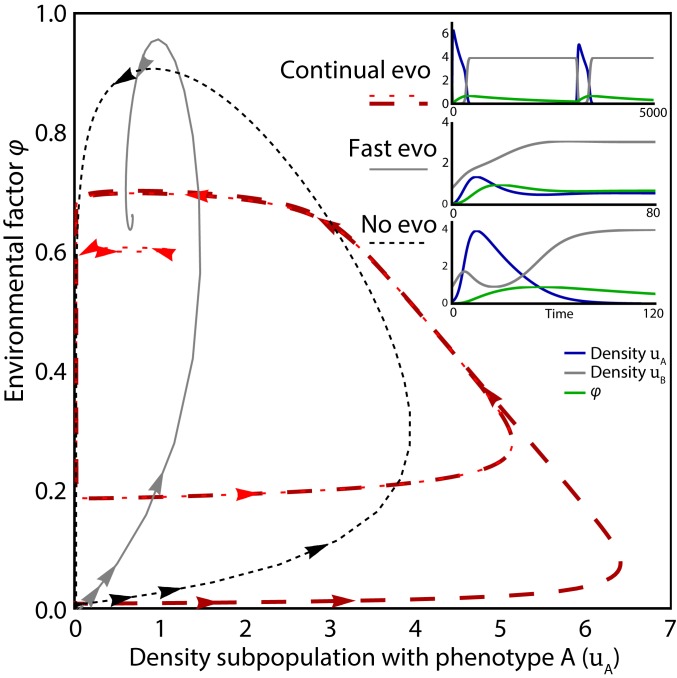
Fig. 5.

Example of evolutionary dynamics with a single evolving trait consisting of two phenotypes: behavior of a specific system following the outline of Fig. 4A. Phase plane diagram of the density of individuals with phenotype A and environment $\phi$ shows the possible system behavior for different values for the relative timescales of population dynamics, feedbacks, and mutation (evo). Slow feedback and mutations (${ϵ}_m=0.00005$ and ${ϵ}_e=0.0005$) lead to continual cyclic evolutionary dynamics (red lines and Top Inset), almost independent of initial conditions (two initial conditions shown). With fast feedback and mutations (${ϵ}_m=0.01$ and ${ϵ}_e=0.1$), an equilibrium is reached (gray line and Middle Inset). No mutation (${ϵ}_m=0$ and ${ϵ}_e=0.01$) leads to the extinction of one of the traits (black dashed line and Bottom Inset). See SI Appendix, section S2 for equations and parameter values. Note that Continual evo refers to continual evolution, whereas Fast evo and No evo refer to fast and no mutations, respectively.

Continual Dynamics in the Case of Two Evolving Traits: An Example.

In natural systems, multiple traits determine the fitness of an individual. An extension of our model to more traits can thus provide a more realistic picture of the dynamics expected in natural populations. We extended the system to a species with two evolving traits, each associated with a different environmental factor through a negative feedback. In other words, the trait space $x$ is now a two-dimensional space and, since both traits are associated with a different environmental factor, the space of external factors $y$ is also a two-dimensional space. A biological example would be a species having two of the feedbacks mentioned before (e.g., both a habitat shift and size-dependent interaction with a predator).

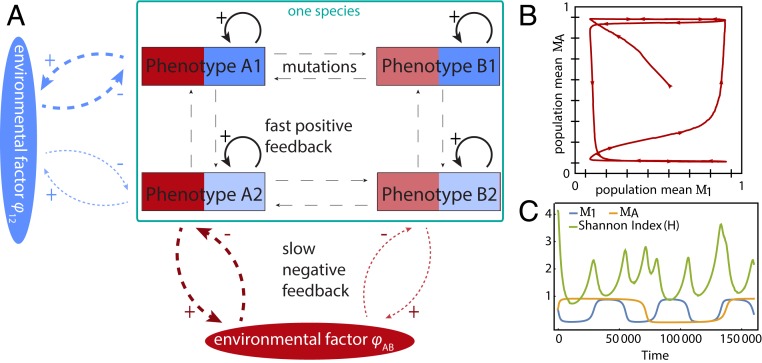
For the sake of simplicity, we discretized the trait space, and therefore the number of possible phenotypes is now the product of the number of possible values for each of the traits. In the simplest case, which we only use for a schematic representation of the population, there are only two values per trait, thus defining four possible phenotypes in the population (Fig. 6A): high susceptibility for both feedbacks (A1 in that figure), low susceptibility for both feedbacks (B2), and high susceptibility for one and low for the other feedback (A2 and B1). For our simulations, we extended the system to eight possible values per trait, and therefore 64 possible phenotypes in total. Our results show that this system can lead to continual evolution. Interestingly, the emerging evolutionary fluctuations generally become irregular (in Fig. 6B, shown through the mean trait value $M$ for each trait of the population). Moreover, looking at the change of the diversity index over time, we can conclude that there is no fixed period in the dynamics (Fig. 6C). Based on the example with two traits, we do not expect a natural system to come back to exactly the same state recurrently (i.e., to show periodic dynamics). Moreover, while we cannot prove that/whether there is a projection to one-dimensional $M$ and $\mathrm{\Phi }$, our simulations indicate that the combination of the feedbacks proposed here still induces continual large fluctuations. See SI Appendix, section S2 for more details.

Fig. 6.

Example of evolutionary dynamics with two evolving traits. (A) We consider two environmental factors (${\phi }_{12}$ and ${\phi }_{AB}$, where the character of the subscript refers, respectively, to the phenotype the factor affects strongly and weakly). In the simplest case, each trait consists of two trait values, leading to four phenotypes in total (more phenotypes per trait are also possible, leading to a total number of phenotypes as the product of the possible values per trait). The arrows signify the different processes, where the thickness denotes the strength of the interaction and the dashes denote the timescale. Continuous arrows are the fast positive feedback, dashed arrows are the slower but potentially stronger (thicker lines) negative feedbacks, and thin lines with large spaced dashes are the slowest process of mutations. (B) The change in the subpopulation-level mean value for each trait ($M_1$ for one trait and $M_A$ for the other trait) in time for an example with eight possible phenotypes per trait (indicated by the tics on the axes) and therefore 64 phenotypes in total. (C) Mean trait values and diversity over time. With more than one trait, periods are irregular, as can be seen from the nonperiodic Shannon index ($H$). Equations and parameters for the figure are given in SI Appendix, section 2.

Discussion

We have shown that, when allowing for phenotypic variation in the population, a simple motif of fast positive and slow (but eventually dominant) negative feedbacks leads to continual evolution regardless of whether mutations have small or large effects. Our results are general because the evolutionary dynamics do not depend on specific equations, parameter values, or dependencies between traits (trade-offs). Our results are also robust to small temporal change in the population density distribution (e.g., migration, random effects). Previous work has shown that continual evolution can be found in specific (and typically simple) models. In the literature, generality is typically claimed by showing that the reported results remain for a range of parameter values or different equations (11, 28). Here, we avoided the use of specific equations and parameter values to obtain truly general results that are robust across parameter values and functional forms. On the other hand, previous examples that have avoided using specific functional forms to explain some aspect of continual evolution required additional restrictions on the models. For example, Dercole et al. (28) focused on predator–prey interactions, Nordbotten and Stenseth (9) considered bilinear species interactions (i.e., interactions between species that are linear in both species’ densities, like in the Lotka–Volterra model), and Bonachela et al. (27) considered a fixed set of three species that interact, forming a nontransitive cycle. Our proofs are accompanied by specific examples for the sake of concreteness, but our results are not restricted to those examples.

In all our examples, continual evolutionary dynamics stem from switching between multiple ecological attractors that are nodes [ecogenetically driven RQ dynamics (29)]. Our conclusions remain the same when these attractors are limit cycles instead. An example of this type of dynamics is given in Khibnik and Kondrashov’s (29) figure 4. Interestingly, including a polymorphic population in their example eliminates the evolutionary oscillations, and only ecological cycles remain, that is, ecologically driven RQ dynamics (fluctuations in traits that are fast and small in amplitude and only follow ecological population density oscillations). However, when we made their negative feedback slower by decreasing the parameters for the predator dynamics 10-fold (their parameters r4 and $\gamma$), ecogenetically driven RQ dynamics were retrieved, which supports the applicability of our claims to existing examples.

Some of our results are in line with and extend previous conclusions. The dynamics of continual evolution are very similar to microevolutionary RQ dynamics; the difference is that continual evolution does not require coevolution. Khibnik and Kondrashov (29) mention that RQ dynamics with a single evolving trait are possible when the dynamics are ecologically driven (the traits follow ecological dynamics), or ecogenetically driven and switching between two different ecological attractors. Continual evolution of a single trait might be quite prevalent, and examples include predator–prey systems in which the prey evolves but the predator does not (or evolves much more slowly, as might be relatively common; see, e.g., ref. 30) and contest competition (20). Moreover, our case of a single evolving trait with two phenotypes reproduces previous results by Mougi and Iwasa (11) showing that fast adaptation is less likely to lead to RQ dynamics. In Bonachela et al. (27), we also found that biotic drivers that respond too fast to the environment do not lead to RQ dynamics, and, similarly to that paper, the dynamics in this work are not linked to population density fluctuations (Fig. 3A). Also, as observed before (e.g., ref. 27), we show, for a one-dimensional trait space, that evolution should not be too slow relative to the negative feedback, and that ecology and evolution have to interact to guarantee continual dynamics. The average population trait has to change drastically while the negative feedback changes relatively little. If a trait evolved gradually, evolution should not be much slower than the dynamics of the feedback, or otherwise the feedback would “catch up” with the average population trait while this average is near the equilibrium value. An example of such a kind of dynamics could be found in predator–prey systems with a slowly evolving predator [due to, e.g., generation times that are much longer for the predator than for the prey, like in the laboratory system of an algae and a rotifer (31)]. In these cases, nonoptimal predator phenotypes might stay in the population and not go extinct. Thus, the species does not need de novo mutations for continual evolution to emerge, as the trait space can be explored through selection and recombination. This type of RQ dynamics where the traits stay in the population are more common in higher organisms. Faster evolutionary change through mutations might also occur when species are regularly exposed to different environments and evolve adaptability (32, 33).

We included the possibility of polymorphism (often left out of RQ studies, typically focused on cycling monomorphic populations), which can have a pronounced effect on the results. As shown in SI Appendix, section 2, existing examples of models showing RQ dynamics can lose these evolutionary oscillations when the more general setting of a polymorphic population is considered. Even when the original models do not seem to be directly linked to the motif described in this paper, including our fast positive–slow negative feedback combination leads to recovering continual evolution. This is the case for models such as the one in Mougi and Iwasa (11), where the RQ dynamics remain when polymorphism is introduced but become ecologically driven (i.e., evolution just follows the population’s ecological predator–prey cycles). Other cases that do include polymorphic populations are the stochastic model by Dieckmann et al. (10); models of evolutionary branching and extinction using adaptive dynamics (summarized in ref. 18); and a Lotka–Volterra predator–prey model with a polymorphic population that, similarly to our results, shows examples of RQ dynamics (34).

Our results are an important addition for linking theoretical to experimental observations of evolutionary dynamics. Collecting evidence of continual evolution from natural systems is a difficult task (23), and, in experiments, the need for long-term measurements is a problem. Experiments show the effect of evolution on predator–prey dynamics (e.g., ref. 35), with at least one suggesting RQ dynamics (11), but, due to the limited measurement time, it cannot be excluded that the cycles will eventually dampen. On the other hand, there is an increase in the number of long-term adaptation experiments, but these are usually in bacterial systems, whereas most of the modeling has focused on sexually reproducing predator–prey communities. Here, microbial systems are included by allowing for polymorphism and larger mutation effect sizes. In bacterial systems, polymorphic populations are common even under reasonably constant conditions, as recently shown in the long-term evolution experiment with Escherichia coli (36). A polymorphic trait distribution might result from density-dependent dynamics, as shown theoretically in a chemostat (37).

We see several interesting directions for further research. First, we show that, under specific assumptions, we can guarantee the emergence of continual evolution. It would be interesting to investigate whether systems that do not follow some of these assumptions (e.g., fast negative feedbacks, no positive feedback, not enough timescale separation) can be proven to lead to stasis. Second, the methods used in this paper with a polymorphic population to link the ecological and evolutionary timescales could be combined with individual-based models (26). Third, our results are limited to only one evolving species, although the feedbacks we describe could come from another evolving species or be a result of a more complex ecosystem. A next step would thus be extending our study to more than one evolving species. Fourth, our results can be extended to systems with nonsymmetric feedback assumptions and systems where the negative feedback does not operate through an environmental factor, such as in contest competition (21, 38). Finally, the results in this paper are constrained to microevolutionary dynamics, but the general model (Eq. 1) allows for extension to macroevolutionary phenomena. In this respect, our results are in line with the results in Doebeli and Ispolatov (39), which show that most coevolutionary dynamics are found with intermediate diversity, for a fixed phenotypic space. Here we see that, if diversification emerges (and, therefore, a phenotypically polymorphic population that fills more niches), the coevolutionary dynamics cease (SI Appendix, Fig. S3).

In conclusion, our general framework shows, without constraining functional forms or phenotypic diversity within the system, that a fast positive feedback combined with a slow negative feedback leads to continual dynamics if there is enough separation between the timescales involved. By doing so, we have improved the understanding of continual evolution and coevolution in a large class of systems. Importantly, our general framework may be used to study and predict evolutionary dynamics without knowledge of the exact equations describing the system, and thus assess what likely happens and has happened in nature.