Abstract
The composition of the cell nucleus is highly heterogeneous, with different constituents forming complex interactomes. However, the global patterns of these interwoven heterogeneous interactomes remain poorly understood. Here we focus on two different interactomes, chromatin interaction network and gene regulatory network, as a proof of principle to identify heterogeneous interactome modules (HIMs), each of which represents a cluster of gene loci that is in spatial contact more frequently than expected and that is regulated by the same group of transcription factors. HIM integrates transcription factor binding and 3D genome structure to reflect “transcriptional niche” in the nucleus. We develop a new algorithm, MOCHI, to facilitate the discovery of HIMs based on network motif clustering in heterogeneous interactomes. By applying MOCHI to five different cell types, we found that HIMs have strong spatial preference within the nucleus and show distinct functional properties. Through integrative analysis, this work shows the utility of MOCHI to identify HIMs, which may provide new perspectives on the interplay between transcriptional regulation and 3D genome organization.
The cell nucleus is an organelle that contains heterogeneous components such as chromosomes, proteins, RNAs, and subnuclear compartments. These different constituents form complex organizations that are spatially and temporally dynamic (Lanctôt et al. 2007; Bonev and Cavalli 2016). Interphase chromosomes are folded and organized in three-dimensional (3D) space by compartmentalizing the cell nucleus (Cremer and Cremer 2001; van Steensel and Belmont 2017), and different chromosomal loci also interact with each other (Bonev and Cavalli 2016). The development of whole-genome mapping approaches such as Hi-C (Lieberman-Aiden et al. 2009) to probing the chromatin interactome has enabled comprehensive identification of genome-wide chromatin interactions, revealing important nuclear genome features such as loops (Rao et al. 2014; Tang et al. 2015), topologically associating domains (TADs) (Dixon et al. 2012; Nora et al. 2012), and A/B compartments (Lieberman-Aiden et al. 2009). Nuclear genome organization has intricate connections with gene regulation (Cremer and Cremer 2001; Misteli 2007). In particular, correlations between higher-order genome organization (including chromatin interactions and chromosome compartmentalization) and transcriptional activity have been shown (Guelen et al. 2008; Rao et al. 2014; Chen et al. 2018).
Systems-level transcriptional machinery can often be represented by gene regulatory networks (GRNs), which are dynamic in different cellular conditions (Gerstein et al. 2012; Marbach et al. 2016). GRN models the phenomena of selective binding of transcription factors (TFs) to cis-regulatory elements in the genome to regulate target genes (Davidson 2006; Lambert et al. 2018). Transcription of coregulated genes in GRN can be facilitated by long-range chromosomal interactions (Fanucchi et al. 2013), and the chromatin interactome shows strong correlations with GRN (Kosak et al. 2007; Neems et al. 2016; Zhang et al. 2019). Indeed, network-based representation of both the chromatin interactome and GRN has been suggested to analyze different subnuclear components holistically (Rajapakse et al. 2010; Chen et al. 2015). The paradigm of viewing the nucleus as a collection of interacting networks among various constituents can also be extended to account for other types of interactomes in the nucleus. However, whether these interactomes, in particular the chromatin interactome and GRN, are organized to form functionally relevant, global patterns remains to be explored. Insights derived from such analysis would also be imperative to better understand the interplay between TFs and 3D genome organization, which has been postulated to play important roles in the formation of nuclear genome condensates (Kim and Shendure 2019; Stadhouders et al. 2019), possibly through phase separation with the involvement of super-enhancers and “3D cliques” (Hnisz et al. 2017; Boija et al. 2018; Petrovic et al. 2019).
In this work, as a proof of principle, we specifically consider two different types of global interactomes in the nucleus: (1) the chromatin interactome, a network of chromosomal interactions between different genomic loci, and (2) a GRN in which TFs bind to cis-regulatory elements to regulate target genes’ transcription. Many studies in the past have analyzed the structure and dynamics of chromatin interactomes and GRNs, as well as cases of coordinated binding of transcription factors on folded chromatin (Rao et al. 2014; Tang et al. 2015; Marbach et al. 2016; Belyaeva et al. 2017; Cortini and Filion 2018; Ma et al. 2018; Petrovic et al. 2019; Zhang et al. 2019). However, the global network level patterns between chromatin interactome and GRN are still unclear, and algorithms that can simultaneously analyze these heterogeneous networks in the nucleus to discover intricate network structures have not been developed.
Here we aim to identify network structures in which nodes representing TFs (from GRN) and gene loci (from both chromatin interactome and GRN) cooperatively form distinct types of modules (i.e., clusters). We develop a new algorithm, MOCHI (motif clustering in heterogeneous interactomes), that can effectively uncover such network modules, which we call heterogeneous interactome modules (HIMs), based on network motif clustering using a four-node motif specifically designed to reveal HIMs. HIMs integrate TF binding and 3D genome structure to reflect global “transcriptional niches” in the nucleus. Each identified HIM represents a collection of gene loci and TFs for which (1) the gene loci have higher than expected chromatin interaction frequencies and (2) the gene loci are regulated by the same group of TFs. To show the utility of MOCHI to identify HIMs based on complex heterogeneous interactomes in the nucleus, we apply MOCHI to five different human cell types, identifying patterns of HIMs and their functional properties through integrative analysis. HIMs have the potential to provide new insights into the nucleome structure and function, in particular, the interwoven interactome patterns from different components of the nucleus.
Results
Overview of the MOCHI algorithm
The overview of our method is illustrated in Figure 1. Our goal is to reveal network clusters in a heterogeneous network such that certain higher-order network structures (e.g., the network motif M in Fig. 1A) are frequently contained within the same cluster. The input heterogeneous network in this work considers two types of interactomes: a GRN (directed) between TFs and target genes; and a chromatin interaction network (undirected) between gene loci on the genome. For a chromatin interactome, for each pair of gene loci within 10 Mb, we use the “observed over expected” (O/E) quantity in the Hi-C data (we use O/E > 1 as the cutoff in this work, but we found that our main results are largely consistent with different cutoffs) (see Supplemental Results) to define the edges in the chromatin interaction network. For GRNs, we use the transcriptional regulatory networks from Marbach et al. (2016), which were constructed by combining the enrichment of TF binding motifs in enhancer and promoter regions and the coexpression between TFs and genes. If a TF regulates a gene, we add a directed edge from the TF to the gene. We then merge the chromatin interaction network and the GRN from the same cell type to form a network G with nodes that are either TFs or gene loci together with the directed and undirected edges defined above (Fig. 1B).
Figure 1.
Workflow of our MOCHI algorithm and output examples of HIMs. The network has both gene–gene spatial proximity and TF–gene regulation relationships. (A) A four-node motif M represents the smallest HIM. Here a directed interaction represents a TF–gene regulation relationship, and an undirected interaction represents that the two genes are spatially more proximal to each other than expected. (B) Given a heterogeneous network G, we find HIMs by minimizing the motif conductance (see Equation 2). (C) We compute the subgraph adjacency matrix WM, with [WM]ij being the number of occurrences of M that have both nodes i and j. (D) The weighted network GM is defined from adjacency matrix WM. (E) Spectral clustering will find clusters in GM. We recursively apply the method to find multiple HIMs and overlapping HIMs. (F,G) Two HIMs as examples in GM12878. (H) Example of two overlapping HIMs in GM12878 sharing seven TFs (the group with pink nodes in the middle). TFs in orange and pink nodes form one HIM with their target genes (bottom left). TFs in pink and blue nodes form another HIM with their target genes (bottom right). Note that the directed interactions from TFs to their target genes are bundled.
We specifically consider the network motif M with four nodes, namely, two gene loci and two TFs in the heterogeneous network with two genes whose genomic loci are spatially more proximal to each other (than expected) in the nucleus and that are also coregulated by the two TFs (see the later section for the justification of this motif) (Fig. 1A). Our goal is to reveal higher-order network clusters based on this particular network motif. In other words, we want to partition the nodes in the network such that this four-node network motif occurs mostly within the same cluster. Based on the motif, our MOCHI algorithm, which extends the original algorithm by Benson et al. (2016), constructs an undirected, weighted network GM (Fig. 1D) based on the subgraph adjacency matrix, WM, whose elements are the number of times that two nodes are in the same occurrence of motif M in the heterogeneous network G (Fig. 1C). We then apply recursive bipartitioning in GM to find multiple clusters (Fig. 1E). We call such clusters HIMs, which, in this work, represent network structures containing the same group of TFs that regulate many target genes whose spatial contact frequencies are higher than expected. Because TFs can regulate multiple sets of genes that may belong to different clusters, different HIMs may overlap by sharing TFs. The algorithm details of MOCHI are in the Methods section.
MOCHI identifies HIMs in multiple cell types
We applied MOCHI to five different human cell types: GM12878, HeLa, HUVEC, K562, and NHEK. The input heterogeneous network of each cell type has 591 TFs, approximately 12,000 expressed genes, and approximately 1 million regulatory interactions (Supplemental Table S1). A few examples of HIMs identified in GM12878 are shown in Figure 1, F through H, including overlapping HIMs in Figure 1H (for the full list of HIMs, see Supplemental File S1). We found that the identified HIMs in five cell types cover a majority (62.1%–77.2%) of the genes in the heterogeneous networks and share several basic characteristics, including the number of HIMs, the proportion of HIMs sharing TFs with other HIMs, and the number of genes and TFs in HIMs (Supplemental Tables S1, S2). In addition, we found that the identified HIMs in different cell types share similar connections to 3D genome features (Supplemental Results; Supplemental Table S2).
Note that the four-node motif M was chosen specifically for uncovering HIMs derived from TFs and genes based on 3D genome organization. Specifically, we compared the four-node motif M against its subgraphs bifan and triangle motifs (Supplemental Fig. S1A). The bifan and triangle motifs do not explicitly and simultaneously encode the spatial proximity between genes and the coregulation between TFs. We found that the clusters based on the four-node motif M have better clustering features, including triangle density and motif M density (see Supplemental Results; Supplemental Figs. S1, S2; Supplemental Table S3). These advantages highlight the necessity of using the four-node motif M to identify HIMs.
To further assess that the genes in a HIM are indeed coregulated by the same TFs, we used the available ChIP-seq data of 26 TFs in GM12878 and K562 cells from the ENCODE portal (Davis et al. 2018; https://www.encodeproject.org). We found that for all the HIMs in GM12878 or K562 with these 26 TFs, more than half (55.85%) of them have ≥50% of their genes with corresponding TF ChIP-seq peaks within 10 kb of the transcription start site, further suggesting that the genes in HIMs identified by MOCHI share regulatory TFs. Note that TF ChIP-seq data were not used to infer the input GRNs. In addition, MOCHI can robustly identify HIMs with different parameters in various cell types (Supplemental Results; Supplemental Fig. S3). These results show that MOCHI can reliably discover HIMs across multiple cell types.
HIMs show advantages over conventional GRN clusters in multiple aspects
Conceptually, one key difference between HIMs and clusters in conventional GRN (using GRN data only) is that HIMs have spatial constraints such that genes in HIMs are in spatial contact more frequently than expected. To investigate potential advantages of HIMs with a fair comparison between HIMs and GRN clusters, we modified the MOCHI framework to identify GRN clusters from GRN data used in this study (see Supplemental Results). We first sought to assess the connections with fundamental genome functions, including replication timing and gene expression. We found that, compared with genes in GRN clusters, genes in HIMs replicate earlier and replicate with more similar timing (Supplemental Figs. S4A,B, S5). Genes in HIMs also express at higher levels and at more similar levels (Supplemental Fig. S5). These results suggest the stronger connection between HIMs and fundamental genome functions compared with GRN clusters.
We next compared HIMs with GRN clusters in terms of the enrichment of genes affected by eQTLs using the GEUVADIS data set (The 1000 Genomes Project Consortium 2015). Here we call a cluster enriched with an eQTL if (1) the cluster has more than five genes, (2) the cluster and eQTL share at least two genes, and (3) the number of shared genes is significantly higher than those of randomly selected equal-sized expressed gene sets on the same chromosome (P < 0.05, hypergeometric test). We found that nearly half (49.44%) of GM12878 HIMs are enriched in genes affected by eQTLs, which is significantly higher than the enrichment (36.5%) based on GRN clusters (P = 0.001) (Supplemental Fig. S4C), suggesting that genes in HIMs are more likely to share eQTLs. Similar enrichment analysis for genes affected by SNPs in GWAS (based on the NHGRI-EBI GWAS Catalog) revealed that HIMs have significantly higher proportions of gene clusters that are affected by GWAS SNPs than GRN clusters (P ≤ 7.38 × 10−4) (Supplemental Figs. S4D and S6). In addition, we extracted a subset of GWAS SNPs that is associated with blood-related disorders and assessed their enrichment in HIMs in blood-related cell lines GM12878 and K562. We found that HIMs have higher proportion of genes affected by such SNPs than GRN clusters (P ≤ 0.035) (Supplemental Figs. S4E, S6). In particular, there are four blood-related disorders in which genes affected by their associated SNPs are enriched in HIMs but not in GRN clusters (Supplemental Table S4). On the other hand, there is no blood-related disorder in which genes affected by their SNPs are enriched in GRN clusters but not in HIMs. These results further show the greater functional relevance of HIMs compared with GRN clusters.
We then assessed the level of involvement of long-range enhancer–gene interactions in HIMs and in conventional GRN clusters (also see Supplemental Results). We specifically focused on the clusters in which the majority (≥50%) of genes are connected to enhancers that are located within the wide genomic region covered by the HIM through long-range enhancer–gene interactions (example HIMs in Supplemental Fig. S4F–H). The proportion of such HIMs is significantly higher than that of conventional GRN clusters across cell types (Supplemental Fig. S7; Supplemental Results). These results indicate that HIMs have stronger connection with long-range enhancers, which also reflects the advantage of HIMs that integrate TF binding and 3D genome organization.
Taken together, the comparison with conventional GRN clusters highlights the importance of having 3D genome spatial constraints to identity HIMs. In addition, these analyses also show that HIMs have overall stronger significance in biological functions compared with GRN clusters. For the rest of this paper, we characterize structural and functional properties of HIMs and investigate the dynamics of HIMs across different cell types.
HIMs show strong preference in spatial localization relative to subnuclear structures
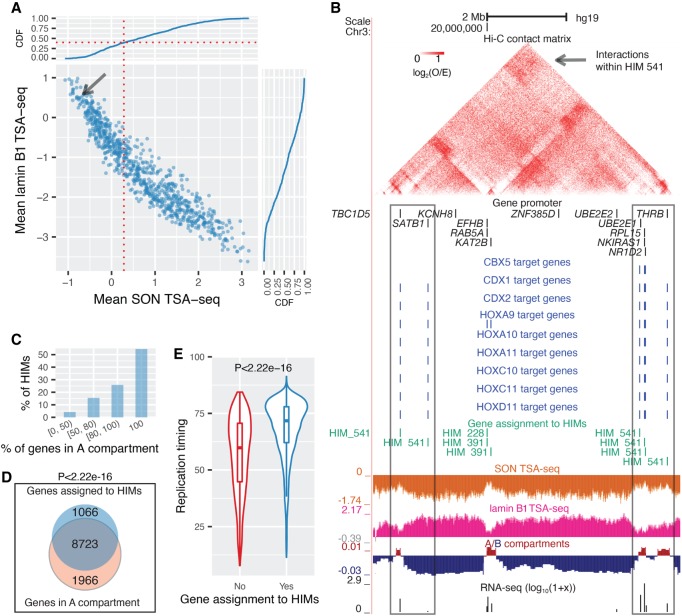
Next, we analyzed the spatial localization of HIM in the nucleus. Recently published SON TSA-seq and lamin B1 TSA-seq data sets quantify cytological distance of chromosome regions to nuclear speckles and nuclear lamina, respectively (Chen et al. 2018). In K562, which is currently the only cell type with published TSA-seq data, 60.7% of the HIMs have a mean SON TSA-seq score higher than 0.284 (80th percentile of the SON TSA-seq score), suggesting that the genes in these HIMs, on average, are within 0.518 µm (estimated by Chen et al. 2018) of nuclear speckles (Fig. 2A). Compared with the genes in the K562 heterogeneous network but not assigned to HIMs, the genes in HIMs have a higher mean SON TSA-seq score and a lower mean lamin B1 TSA-seq score (P < 2.22 × 10−16) (Supplemental Fig. S8).
Figure 2.
HIMs tend to be close to the nuclear interior, in particular, speckles. (A) Scatter plot shows the mean SON TSA-seq score and mean lamin B1 TSA-seq score of the genes in each HIM. Each dot represents a HIM. The curves on the top and on the right are cumulative density functions (CDFs). The red vertical dotted line represents the mean SON TSA-seq at 0.284 (approximately within 0.518 µm of nuclear speckles) (Chen et al. 2018). The black arrow points to HIM #541. (B) HIM #541 with low mean SON TSA-seq (pointed by the arrow in A). The heatmap shows the upper-triangle part of the Hi-C contact matrix (O/E) of the 10-kb-sized bins in the chromosome region that covers the genes in this HIM. Target genes of different TFs, gene members of HIM, SON TSA-seq, lamin B1 TSA-seq, A/B compartments, and RNA-seq signals are shown in different tracks. (C) Barplot shows the proportion of HIMs with a varied proportion of genes in the A compartment. (D) Venn diagram shows that the genes assigned to HIMs are enriched in the A compartment. (E) Violin and boxplot compare the replication timing of the genes assigned to HIMs and the other genes in the heterogeneous network of K562. Here the HIMs are identified in K562. The spatial localization features of HIMs in other cell types are in Supplemental Figure S9.
We specifically looked at those HIMs that are away from the nuclear interior. Figure 2B shows one HIM (#541) that is close to nuclear lamina (mean lamin B1 TSA-seq score 0.593, mean SON TSA-seq score −0.642). This HIM has nine TFs coregulating six genes that span 6.78 Mb on Chromosome 3. The Hi-C edge density (see Supplemental Methods) among these genes is 0.667, suggesting that these six genes as a group are spatially closer to each other than expected through chromatin interactions. The SON TSA-seq scores of the six genes are low but tend to be the local maxima (i.e., small peaks within valleys), whereas the lamin B1 TSA-seq scores are high but tend to be the local minima (i.e., small valleys within peaks), suggesting that these gene loci are localized more toward the nuclear interior than their surrounding chromatin. Five out of the six genes are expressed with FPKM ≥ 3.4. The gene RPL15 in this HIM is a K562 essential gene (Wang et al. 2015). The TFs CDX1, HOXA9, and HOXA10 are involved in leukemia and hematopoietic lineage commitment according to GeneCards (Safran et al. 2010). This suggests that even though HIM #541 is a HIM away from nuclear speckles, it may play relevant functional roles in K562.
Recently, Quinodoz et al. (2018) reported that inter-chromosomal interactions are clustered around two distinct nuclear bodies, nuclear speckles and nucleoli, as hubs. By comparing with the genomic regions organized around the nucleolus based on data from the SPRITE method in GM12878 (Quinodoz et al. 2018), we found that a vast majority (85.4%) of the GM12878 HIMs do not have genes close to the nucleolus. Earlier work estimated that only 4% of the human genome is within nucleolus-associated domains (Németh et al. 2010). It is therefore expected that only a small number of HIMs would be close to the nucleolus. Indeed, we found that there are only 30 (4.62%) GM12878 HIMs with all their genes near the nucleoli. Sixteen out of these 30 HIMs have at least one TF protein located close to nucleoli according to protein subcellular locations from the human protein atlas (Thul et al. 2017). For example, HIM #267 has four TF regulators: ETS1, ETV6, PPARG, and PTEN, in which ETV6 is known to localize to the nucleoli.
Earlier work from Hi-C data showed that at megabase resolution, the interphase chromosomes are segregated into A and B compartments that are largely active and inactive in transcription, respectively (Lieberman-Aiden et al. 2009). Chromosome regions in B and A compartments have nearly identical agreements, respectively, with lamina-associated domains (LADs) and inter-LADs (i.e., more toward interior) (van Steensel and Belmont 2017). Compartment A regions also replicate earlier than compartment B regions (Pope et al. 2014). We found that the genes in HIMs are preferentially in A compartments and replicated earlier across cell types. Specifically, 57.4% of HIMs have genes that are all in A compartments in K562 (Fig. 2C). We also found that the genes in HIMs as a whole are more enriched in A compartments (P < 2.22 × 10−16, hypergeometric test) (Fig. 2D). Compartment A can be further subdivided into A1 and A2 subcompartments in GM12878 (Rao et al. 2014) at a finer scale. Among the 369 GM12878 HIMs with genes all in A compartments, 198 (53.66%) HIMs have ≥80% of their genes in A1 subcompartments, 60 (16.26%) HIMs are in A2 subcompartments, and the remaining 111 HIMs span both A1 and A2 compartments. Additionally, we found that the genes assigned to HIMs have much earlier replication timing than the other genes (P < 2.22 × 10−16) (Fig. 2E). We also observed that the genes (on the same chromosome) that are in HIMs tend to have more similar replication timing compared with the genes (on the same chromosome) that are not in HIMs (Supplemental Fig. S9). These patterns can also be observed in other cell types (Supplemental Fig. S9).
Taken together, these results have revealed that HIMs have a strong preference to localize toward the nuclear interior in active compartments, with the majority of them being in proximity of the nuclear speckles and replicating earlier.
HIMs are enriched in essential genes, super-enhancers, and PPIs
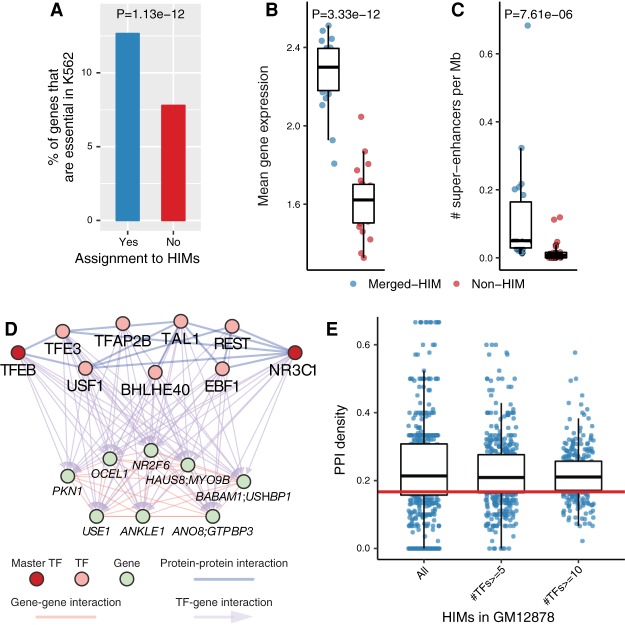
Next, we explored the functional properties of HIMs. We grouped the genes assigned to HIMs into one set and the genes in the heterogeneous network that are not assigned to HIMs into another set. For a fair comparison, we group the gene sets by chromosome number. We call these clusters merged-HIM clusters and non-HIM clusters accordingly. We first looked at gene essentiality (Supplemental Methods; Wang et al. 2015). We found that genes assigned to HIMs are enriched with essential genes across all five cell types. For example, 12.7% of the genes assigned to HIMs in K562 are K562 essential genes, which is significantly higher than the proportion (7.79%) of the genes not assigned to HIMs (P = 1.13 × 10−12) (Fig. 3A). This observation is also present on different chromosomes (Supplemental Fig. S10A). Across the cell types, genes assigned to HIMs consistently have higher proportions of essential genes than those not assigned to HIMs (P ≤ 2.17 × 10−6) (Supplemental Fig. S10B). Regarding gene expression level, we found that genes assigned to HIMs are more highly expressed and expressed at more similar levels (Fig. 3B; Supplemental Fig. S11).
Figure 3.
HIMs are enriched with essential genes, super-enhancers, and protein–protein interactions. (A) Barplots show the proportions of genes that are K562 essential genes among the genes assigned to HIMs and those not assigned to HIMs. (B,C) Functional properties of the genes in the identified HIMs in K562. To make a fair comparison, we group the genes assigned to HIMs by chromosome number and called the resulting clusters as merged-HIM clusters. Similarly, we derive non-HIM clusters from the genes in the heterogeneous networks but not assigned to HIMs. P-values are computed by the paired two-sample Wilcoxon rank-sum test. (B) Boxplot shows the average gene expression level of the genes in a cluster. (C) Boxplot shows the normalized number of super-enhancers related to a cluster. (D,E) TFs in HIMs are enriched with protein–protein interactions (PPIs) among themselves. (D) One example of HIM from GM12878 shows that nine TFs in the HIM are connected by 14 PPIs. The sub-PPI network has a density at 0.389. The TFs NR3C1 and TFEB are master TFs in GM12878. (E) Boxplots show the distribution of the sub-PPI network density of the HIMs and the subsets of HIMs with at least n TFs, n = 5, 10. The medians are significantly (P < 2.22 × 10−16) higher than the expected density (0.158; red line) of the sub-PPI networks induced by randomly sampled TFs.
Super-enhancers are known to be associated with many cell type–specific functions (Hnisz et al. 2013). To study the connections between HIMs and super-enhancers, we computed the cluster-size normalized number of super-enhancers annotated by Hnisz et al. (2013) that (1) have Hi-C contacts with and (2) are close to (window size = 50 kb) at least one gene in each cluster. We found that HIMs are enriched with spatial contacts with super-enhancers. Specifically, the merged-HIMs have at least a sixfold higher normalized number of super-enhancers than the non-HIMs across cell types (Fig. 3C; Supplemental Fig. S12). This significant pattern is consistent with varied window sizes from 20 kb to 1 Mb (Supplemental Fig. S12).
Protein–protein interactions (PPIs) can further stabilize TF-DNA binding of the interacting TFs (Lambert et al. 2018). We asked whether TFs in the same HIM tend to have more PPIs with each other. We computed the density of the sub-PPI network induced by the TFs in a HIM, in which the PPI network is based on 591 TF proteins used in this study (Supplemental Methods). We found that TFs within HIMs are enriched with PPIs among themselves compared with random cases selected from the 591 TFs. For example, in GM12878, TFs NR3C1 and TFEB, which are master regulators (Hnisz et al. 2013), coregulate eight genes with the other seven TFs in a HIM (Fig. 3D). The density of this particular sub-PPI network is 0.389, which is 2.46 times higher than the average density (0.158) of the random cases. Overall, the median density of the sub-PPI networks induced by TFs in the identified HIMs in GM12878 is 0.214, much higher than the random cases (P < 2.22 × 10−16) (Fig. 3E). This observation also holds in other cell types in this study (Supplemental Fig. S13). We also found that the significance is not affected by the different number of TFs across HIMs (Supplemental Fig. S13).
These results suggest that the genes and TFs involved in HIMs likely perform critical roles, which are manifested by the level of gene essentiality of target genes, engagement of super-enhancers, and enrichment of PPI among TFs.
Genes in HIMs show stability and variability across cell types
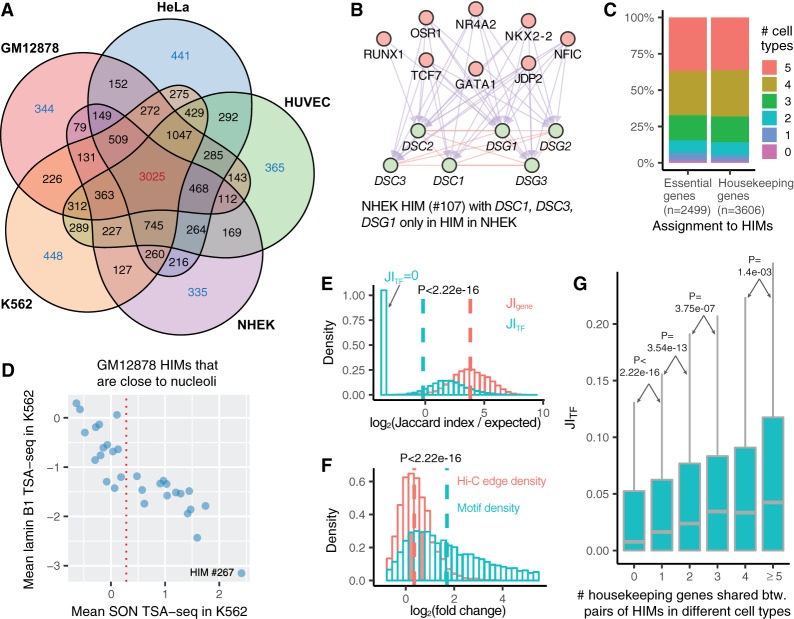
To study how HIMs change among different cell types, we first focused on the assignment of genes to HIMs in different cell types. Through pairwise comparison, we found that the genes assigned to HIMs have the highest degree of overlap between GM12878 and K562 compared with the other cell types, which is consistent with the fact that both GM12878 and K562 are from human hematopoietic cells (Supplemental Fig. S14A). Comparisons among all five cell types showed that 3025 genes are consistently assigned to HIMs, accounting for 30.91%–40.06% of genes that are in the HIMs in each cell type (Fig. 4A). In contrast, only a small fraction (≤5.93%) of genes are uniquely assigned to HIMs in each cell type.
Figure 4.
HIM comparisons in terms of genes and TFs across the cell types. (A) Venn diagram shows the assignment of genes in HIMs across five cell types. Numbers in each facet represent the gene number in each possible intersection relationship across five cell types. (B) A NHEK HIM with three genes only assigned to HIMs in NHEK. All of its genes are involved in the keratinization pathway. Here the top and bottom nodes are the TFs and genes in the HIM, respectively. (C) Barplot shows the assignment of essential genes and housekeeping genes to HIMs across five cell types. (D) Scatter plot shows the mean SON TSA-seq and lamin B1 TSA-seq scores (in K562) (Chen et al. 2018) of the 30 GM12878 HIMs that are inferred as close to nucleoli in GM12878 (Quinodoz et al. 2018). The red vertical dotted line represents the mean SON TSA-seq score at 0.284. (E) The log-transformed ratio of the Jaccard index on the genes/TFs between paired HIMs from different cell types over the expected Jaccard index between random control sets. (F) Fold changes of motif M density and Hi-C edge density of each HIM between the cell type in which it is identified and another cell type. Here a vertical dash line represents the median of a variable. (G) Boxplots represent the distribution of the Jaccard index on the TFs of paired HIMs with different numbers of shared housekeeping genes.
The genes consistently and uniquely assigned to HIMs are enriched with distinct functional terms using DAVID (Supplemental Table S5; Huang da et al. 2009). The genes consistently assigned to HIMs are strongly enriched with functions related to essential cellular machinery, whereas the genes uniquely assigned to HIMs in a particular cell type are enriched with more cell type–specific functions. An example is NHEK HIM #107 (Fig. 4B). Among the six genes in this HIM, DSC1, DSC3, and DSG1 are not assigned to HIMs in the other cell types. These six genes are involved in the keratinization pathway based on GeneCards (Safran et al. 2010). We further assessed the assignment of housekeeping genes (Eisenberg and Levanon 2013) and essential genes to HIMs. We found that for both sets of genes, the majority (≥84%) of them are assigned to HIMs consistently in at least three out of the five cell types (Fig. 4C), suggesting that the genes with crucial functions tend to form spatial clusters across multiple cell types.
We next analyzed the variability of HIMs in terms of spatial proximity to subnuclear compartments. We found that 15 out of the 30 HIMs close to nucleoli in GM12878 (based on the data from Quinodoz et al. 2018) have mean SON TSA-seq score ≥0.284 in K562 (based on the data from Chen et al. 2018; Fig. 4D). In other words, these HIMs are involved in a change of spatial position from nucleoli to speckles between GM12878 and K562. One example is HIM #267 in GM12878, which has the highest mean SON TSA-seq score (2.41) in K562. The 10 genes (in HIM #267 in GM12878) together with another eight genes form a new HIM (#628) in K562. This GM12878 HIM #267 has four TFs: ETS1, ETV6, PPARG, and PTEN. On the other hand, the K562 HIM #628 has four different TFs: KLF4, NFKB1, STAT3, and WT1.
To compare the detailed membership changes of HIMs across cell types, we computed Jaccard indices, denoted by JITF and JIgene, of the TF members and gene members between HIMs from two different cell types, respectively. We found that the gene members undergo a moderate change from one cell type to another, whereas the TF members change at a much higher rate. JIgene has a median of 0.096, and it is higher than the expected JIgene between random gene sets while controlling the set size and chromosome number (median ratio = 14.12) (Fig. 4E). On the other hand, JITF has a median of 0.017, which is close to the expected JITF between randomly selected control TF sets (median ratio = 0.878) (Fig. 4E). There are at least two factors jointly contributing to these observations. First, the Hi-C interaction networks and GRNs are highly cell type–specific, as 66% chromatin interactions and 31.4% GRN interactions only exist in one cell type (Supplemental Table S6). Second, given a HIM identified in a cell type, the motif M density of the HIM (see Supplemental Methods) has a higher fold change than the Hi-C edge density of the HIM in another cell type (P < 2.22 × 10−16) (Fig. 4F). In other words, the coregulation relationships of the TFs on the genes within HIMs change more often across cell types than the spatial proximity relationships between the gene loci. However, we observed that if HIMs from two different cell types share a higher number of housekeeping genes, they tend to have a higher JITF (Fig. 4G). We found a similar pattern for essential genes (Supplemental Fig. S14B).
Conserved and cell type–specific HIMs have distinct properties
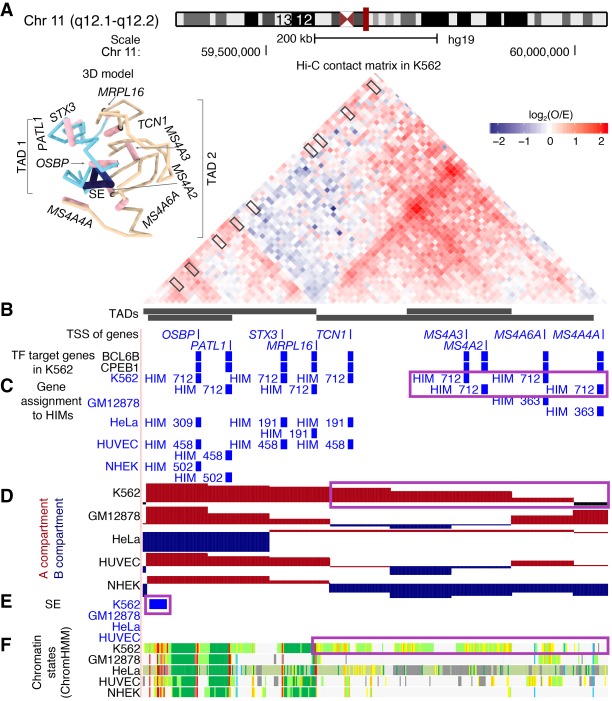
Motivated by the gene membership dynamics of HIMs across cell types, we further classified HIMs into conserved and cell type–specific HIMs. For HIMs in a given cell type, we call a HIM conserved if it shares a significantly high proportion of genes (JIgene ≥1/3, P ≤ 0.001, Bonferroni adjusted hypergeometric test) with at least one HIM in other cell types (i.e., the HIM is recurrent). Note that JIgene ≥1/3 represents that two equal-sized gene sets share more than half of their genes. The rest are called cell type–specific HIMs. Figure 5 shows a cell type–specific HIM, HIM #712, in K562 and its changes in other cell types. This HIM covers nine genes on Chromosome 11. These genes spatially contact each other at higher frequencies than expected (Fig. 5A) and are coregulated by TFs BCL6B and CPEB1 in K562 (Fig. 5B). In other cell types, at most four out of the nine genes are assigned to HIMs (Fig. 5C). We found that this HIM has K562-specific chromosomal structures and functional annotations. The genomic region covering the genes in the HIM is in the A compartment in K562 but switches to the B compartment in other cell types (Fig. 5D). One nearby upstream region is annotated as a super-enhancer only in K562 (Fig. 5E; Hnisz et al. 2013). Many genomic loci are annotated as transcriptionally active states, such as enhancers, promoters, or transcribed states in K562, but not in other cell types based on ChromHMM (Fig. 5F; Ernst and Kellis 2012). The genes MRPL16, OSBP, and PATL1 are essential genes in K562. We compared the 3D structural representations of the chromosome region centered on genes in HIM #712. We ran Chrom3D (Paulsen et al. 2018) 100 times to construct 100 possible 3D structures in each cell type to enable statistical comparisons. One possible 3D structure in K562 is shown in Figure 5A. We found that the chromosome region covering the genes in the HIM has a specific 3D structure in K562. The upstream super-enhancer is spatially closest to the genes in HIM #712 in K562 (Supplemental Fig. S15A). The chromosome region covering the super-enhancer and the genes in HIM #712 are spatially more proximal to each other compared with the flanking regions (±500 kb) in 3D space in K562 (Supplemental Movie S1; Supplemental Fig. S15B). This example illustrates that the K562-specific HIM has specific chromatin organization and potential biological functions. Together, our comparisons reveal that in general conserved HIMs have stronger cluster features, tend to be closer to nuclear interior, and have higher expression levels. On the other hand, cell type–specific HIMs have a higher proportion of cell type–specific genes (Supplemental Results; Supplemental Figs. S16, S17).
Figure 5.
A K562-specific HIM with K562-specific chromatin interactome and functional annotations. (A) The 45° rotated upper triangle part of the contact matrix between the 10-kb-sized bins in a chromosome region in K562. The region is segregated into four nested TADs. The 3D model on top left is inferred by Chrom3D using 10-kb resolution Hi-C data. (B) Thin bars represent the transcriptional start sites (TSSs) of the genes that are in the heterogeneous networks. Thick bars represent the genes that are regulated by BCL6B or CPEB1 in K562. (C) The assignment of the genes to HIMs in K562 and the other cell types. (D) The assignment of the bins to A/B compartments. (E) The regions that are annotated as super-enhancers (SEs). (F) The chromatin states inferred by ChromHMM based on multiple histone modification marks, where red and purple colors represent promoters, orange and yellow stand for enhancers, green represents transcribed regions, and gray represents other types of regions such as repressed regions.
Discussion
To better understand the heterogeneous nature of different components in the nucleus, new computational models are needed to jointly consider different types of molecular interacting networks. In this work, we developed MOCHI to specifically consider two types of different interactomes in the nucleus: (1) a network of chromosomal interactions between different gene loci, and (2) a GRN where TFs bind to the genomic loci with cis-regulatory elements to regulate target genes. MOCHI is able to identify network patterns in which nodes of TFs (from GRN) and gene loci (from both chromatin interactome and GRN) cooperatively form distinct network clusters, which we call HIMs, by using a new motif clustering framework for heterogeneous networks. To the best of our knowledge, this is the first algorithm that can simultaneously analyze these heterogeneous networks within the nucleus to discover important network structures and properties. By applying MOCHI to five different human cell types, we made new observations to show the biological relevance of HIMs in the 3D nucleome.
Our method has multiple methodological contributions. We further extended the motif conductance clustering method (Benson et al. 2016) to find overlapping HIMs in heterogeneous networks. Our work shows the utility of our new algorithm to identify HIMs based on complex heterogeneous molecular interactomes. In addition, our method can be further modified to identify other types of potential HIMs in heterogeneous networks by replacing the four-node motif M with relevant motifs, especially when additional types of interactomes are included. For example, in addition to considering chromatin interactions and protein–DNA interactions as we did in this work, it would be of interest to incorporate other types of relevant interactomes in the nucleus, such as the RNA–chromatin interactome (Nguyen et al. 2018).
How can we explain the formation of HIMs? In Figure 6, we illustrate a possible model of HIMs within the nucleus. HIMs (light pink domains) are toward the interior with a group of interacting TFs and chromatin loci as “transcriptional niche.” The set of TFs in a HIM cooperatively regulate target genes, which also have higher contact frequency than expected. Note that this is conceptually consistent with recently reported colocalized TF pairs (Ma et al. 2018), condensates (Chong et al. 2018; Sabari et al. 2018; Kim and Shendure 2019), and 3D cliques (Petrovic et al. 2019). Some of these TF clusters may be related to the localization preferences of TFs in nuclear compartments, such as nuclear speckles that are enriched with various transcriptional activities (Spector and Lamond 2011; Chen et al. 2018). Indeed, we found that the majority of the identified HIMs are close to nuclear speckles. The definitions of HIMs may also have intrinsic connections with the emerging findings on the mechanism of nuclear subcompartment formation, in which TFs and their potential target genes/chromatin are trapped by localized liquid-like chambers through phase separation (Hnisz et al. 2017; Shin and Brangwynne 2017; Chong et al. 2018). It has been suggested that phase separation may help explain the formation of super-enhancer-mediated gene regulation (Hnisz et al. 2017; Boija et al. 2018), although the exact roles of TFs in this process remain elusive (Kim and Shendure 2019; Stadhouders et al. 2019). From our analysis, we found that genes assigned to HIMs are enriched with contacts with super-enhancers. The genes consistently assigned to HIMs are enriched with essential biological processes related to chromosomal organization and transcription. However, the detailed formation mechanisms for HIMs, which may involve both cis-elements and trans-factors, remain to be investigated. It would also be important to delineate the different roles of both different TFs and different genes in forming the HIMs, as some of them may be necessary and others may be redundant for the stability of HIMs. In addition, more experimental data are needed to further evaluate the functional significance of HIMs. For example, although we observed connections between HIMs and 3D genome organization features, the intricate functional relevance among these different higher-order nucleome units that jointly contribute to gene regulation in different cellular conditions has yet to be revealed. Nevertheless, HIMs may become a useful type of nuclear genome unit and an informative resource in integrating heterogeneous nucleome mapping data, which has the potential to provide new insights into the interplay among different constituents in the nucleus and their roles in 3D nucleome structure and function.
Figure 6.
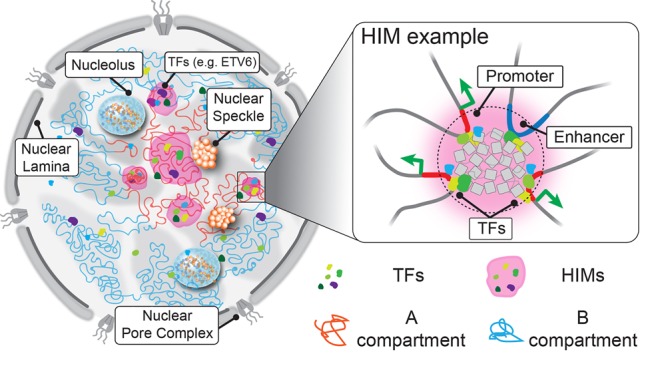
Illustration of the spatial organization of HIMs inside the nucleus. The cartoon on the left shows how chromosomes (curved lines) are intertwined in 3D space. Each chromosome can be primarily partitioned into an active A compartment (red) and an inactive B compartment (blue). Active and inactive genomic regions are formed in 3D space through cis- and trans-contacts, revealing shared localization relative to subnuclear structures, such as nuclear speckles and nuclear lamina. Similarly, the spatial localization of TFs within the nucleus is not randomly distributed but shows a great level of heterogeneity, probably affected by the distribution of binding sites on the 1D genome and the chromatin openness. As an example, ETV6 is highlighted. The MOCHI algorithm developed in this work is able to identify HIMs (shaded in pink), putative functional modules that transiently or stably exist in the nucleus, in which a group of TFs show an elevated concentration in a “transcriptional niche” and colocalize with genes in proximity in 3D. For example, a zoom-in view on the right reveals a potential scenario of a HIM in which the enhancer and its target genes located far away share binding by a group of TFs and are likely to be pulled together by TFs and cofactors. However, the exact interplay between TFs and 3D genome features and the global formation mechanisms of HIMs have yet to be revealed.
Methods
Brief introduction to homogeneous network clustering by motif conductance
We first review a higher-order network clustering method that can identify a cluster of nodes S based on motif conductance (defined below). We then introduce our algorithm MOCHI in the next subsection. Let G be an undirected graph with N nodes and let A be the adjacency matrix of G. [A]ij ∈ {0,1} represents the connection between nodes i and j. The conductance of a cut, where S is a subset of the nodes and the complementary set of S is defined as
| (1) |
where is the number of edges connecting nodes in S and . is the sum of the node degree in S. Moreover, the conductance of the graph G, φG, is defined as minS φG(S). The S that minimizes the function is the optimal solution. Finding the optimal S is NP-hard, but spectral methods such as Fiedler partitions can obtain clusters effectively (Chung 2007). Recently, the conductance metric has been generalized to motif conductance (Benson et al. 2016; Tsourakakis et al. 2017), in which a motif refers to an induced subgraph. The motif conductance computes and VolG(S) based on a chosen n-node motif. When n = 2, the motif is an interaction that reduces the motif conductance to conductance in Equation 1. When n ≥ 3, the motif conductance may reveal new higher-order organization patterns of the network (Benson et al. 2016). A more recent network clustering method that incorporates network higher-order structures has been developed in the setting of hypergraph clustering (Li and Milenkovic 2017), which includes the motif conductance as a special case. However, one key limitation of the aforementioned methods is that they cannot identify overlapping clusters, which is a crucial feature of the heterogeneous networks that we want to achieve in this work.
MOCHI: higher-order network clustering to identify HIMs in a heterogeneous network
We developed a higher-order network clustering method based on network motif to identify overlapping HIMs in a heterogeneous network by extending the approach by Benson et al. (2016). We call our method MOCHI (motif clustering in heterogeneous interactomes). We illustrate the workflow of MOCHI in Figure 1. First, we select a specific heterogeneous four-node network motif, M (Fig. 1A). In M, two nodes are TFs, and the other two nodes are genes. Both TFs regulate the two genes, and the two genes are spatially more proximal to each other than expected. The motivation for choosing the subgraph M is that it is the building block of HIMs given that our goal is to discover a group of genes that have contact with each other more frequently than expected and also share TF regulators. Compared with simpler motifs (e.g., three-node motif in which one node is TF), our four-node motif defined here has the advantage of simultaneously considering a pair of genomic loci that interact with each other and are coregulated by the same pair of TFs.
Conceptually, our method searches for HIMs with two goals. The TFs and genes in the same HIM should be involved in many occurrences of M. Additionally, HIM should avoid cutting occurrences of M, where a cut of occurrences of M means that only a subset of TFs and genes in the occurrences of M is in the HIM node set. More formally, our method aims to find HIMs with the node set S that minimizes the motif conductance:
| (2) |
We first introduce some notations before we explain φM(S) and provide definitions of in Equation 3 and VolM(S) in Equation 4. Let G be the given heterogeneous network (e.g., Fig. 1B). Let be the set of occurrences of the motif M in G. For simplicity and without confusion, we also denote an occurrence of the motif M as M. Let VM be the node set of the two TFs and two genes in M ∈ . In Equation 2, is the number of occurrences of the subgraph M that are cut by S. Formally,
| (3) |
where is an indicator function. Here, distinguishes the number of nodes of the four-node motif M being assigned to S and . Specifically, it adds a higher penalty for the cut to the cases in which two nodes in M are assigned to S and two nodes are assigned to (i.e., in Equation 3), compared with the cases in which one node or three nodes are assigned to S (i.e., in Equation 3), by letting α > 1 in Equation 3. This is because the one-versus-three split could still keep interaction information from both the GRN and chromatin interaction network, and the two-versus-two split will lose either of the information. We show that when α = 4/3 in Equation 3, the clustering results would be near optimal (Supplemental Methods). Thus, α is set to 4/3 in this work. VolM(S) is the sum of the number of occurrences of M containing nodes in S, which is defined as
| (4) |
Similarly, we define the subgraph conductance of the graph G based on the motif M, as minS φM(S). Note that the notation G is excluded from the notations cutM, VolM, , and φM(S) that are dependent on both heterogeneous network G and motif M. This is because including G would likely confuse this set of notations with a set of notations related to homogeneous network GM derived from heterogeneous network G and network motif M later in this section. In the following procedures of the algorithm, we show that the motif conductance is equivalent to the normal conductance in a projection of the graph by calculating the subgraph adjacency matrix. Thus, finding the set S that achieves the minimum subgraph conductance is also NP-hard, following that it is NP-hard to find the minimal φG(S). We describe our algorithm MOCHI to find HIMs that approximate the solution.
1. Calculate subgraph adjacency matrix WM(G)
We first calculate the subgraph adjacency matrix WM(G) by
| (5) |
where [WM(G)]ij is the number of occurrences of the subgraph M in G that cover both i and j (for an example, see Fig. 1C). For example, if both i and j are TFs, [WM]ij reflects the number of paired gene loci that are spatially more proximal to each other and that are also coregulated by TFs i and j. If both i and j are genes, [WM]ij = 0 if i and j are not spatially more proximal to each other. Otherwise, [WM]ij is the number of paired TFs that coregulate i and j. Generally, WM(G) is symmetric and [WM(G)]ij ≥ 0. Thus WM(G) can be viewed as the adjacency matrix of an undirected weighted network. Let GM denote the network with WM(G) as the adjacency matrix (for an example, see Fig. 1D). It is important to note that there are genes or TFs that may not be in any occurrence of M, which would lead to zero vectors in the corresponding rows and columns in WM(G). These singleton nodes in GM would be removed before the next step.
2. Apply Fiedler partitions to find a cluster in GM
We use Fiedler partitions similar to the algorithm by Benson et al. (2016) to find a cluster S in graph GM, where is close to the global optimal conductance of the graph: φ(GM). Recall that φ(GM) is the minimum of over all possible sets S1. The method is described as follows:
Calculate the normalized Laplacian matrix of WM(G),
| (6) |
where is an identity matrix, and where with is the diagonal degree matrix of GM.
Calculate the eigenvector v of the second smallest eigenvalue of .
Find the index vector (α1, …, αN), where αk is the kth smallest value of .
, where , 1 ≤ k ≤ N.
The sets S and are two disjoint clusters for the heterogeneous network G.
3. Apply recursive bipartitioning to find multiple HIMs
We then use recursive bipartitioning to find multiple HIMs. We use a very different strategy than the one by Benson et al. (2016) to select which cluster to split at each iteration in order to specifically allow overlapping motif clusters (HIMs) with shared TFs. At each iteration, we split one HIM into two child HIMs. After iteration ℓ − 1, there are ℓ HIMs: S1, S2, …, Sℓ.
At the next iteration ℓ, one HIM Sk is selected if the graph it forms, Gk, has the lowest subgraph conductance value among , 1 ≤ j ≤ ℓ. We set a threshold t1 for . If , Sk will be split into two child HIMs Sk(c) and by treating the induced heterogeneous subnetwork as a new network Gk and repeating Steps 1 and 2 for graph Gk. However, if the partition of graph Gk would lead to zero motif occurrences in either of its child graphs, we would stop partitioning this graph, add a large enough penalty value to its conductance value (to make sure it would not be selected to partition again), and move on to the next iteration. Otherwise, when , the recursive bipartitioning process will stop as all the HIM's subgraph conductance values pass the threshold.
4. Find overlapping HIMs
Finally, we reconcile the HIMs from the clustering history tree to find overlapping HIMs. This step is added because the HIMs after Step 3 share no TFs. To resolve this, we first trace back the ancestral HIMs up to certain generations for each HIM based on the conductance value of its ancestor , where denotes for the timing of ancestors (e.g., “parent,” “grandparent”) of the HIM. We trace along the tree until , where t2 denotes another threshold. Clearly, t2 has to be smaller than t1 to make this process practical. Next, we pool together the TFs from the HIM and from its ancestor HIMs. We sequentially remove the pooled TFs from the HIM. Each time, we remove the TF that contributes the least number of occurrences of the subgraph M in the graph that this HIM represents. We stop the process when removing a TF would significantly decrease the number of occurrences of the subgraph M.
Pseudocode and runtime analysis of our algorithm
The pseudocode of our MOCHI algorithm is presented in Supplemental Methods. The runtime of MOCHI is bounded by O(t2c2), where t and c (t ≪ c) are the number of TFs and the number of gene loci in the input heterogeneous network, respectively (for detailed analysis, see Supplemental Methods).
Summary of the algorithm
Given a heterogeneous network from chromatin interactome network and GRN, our algorithm MOCHI identifies multiple and overlapping HIMs, which represent clusters of genes and TFs in which the genes are interacting more frequently than expected and are also coregulated by the same set of TFs. MOCHI has a few key differences compared with the subgraph conductance method of Benson et al. (2016). First, the input of our algorithm is a heterogeneous network with different types of nodes (TFs and gene loci), which are treated differently, whereas the input network for the method of Benson et al. (2016) is rather homogeneous. Second, the algorithm of Benson et al. (2016) will not explicitly identify multiple overlapping clusters. In MOCHI, we further developed a recursive bipartitioning method to find multiple HIMs that may overlap. Specifically, we selected a HIM to split if it has the smallest motif conductance among the HIMs at each iteration. In other words, we split the HIM that has the clearest pattern of multiple clusters. HIMs with overlapping TFs will be split in the late stage of iterations, and the overlapping information is encoded in the clustering history tree.
The recent method on hypergraph clustering (Li and Milenkovic 2017) can be applied to identify nonoverlapping HIMs in which a hyperedge is defined as the motif M. However, similar to the method of Benson et al. (2016), it was not designed to identify overlapping clusters; that is, the method would not be able to find multiple overlapping HIMs. Our method also has clear differences compared with previous works on multilayer network clustering (for review, see Kivelä et al. 2014). First, the inputs are different. A multilayer network typically has only one type of nodes and different types of interactions connecting nodes within the same layer and between layers. The heterogeneous network in this work has different types of nodes (TFs and gene loci) and also different types of edges. Previous multilayer network clustering methods are therefore not directly applicable to identify HIMs. Second, the outputs are different. The majority of multilayer network clustering methods aim to find clusters that either are consistently observed across multiple layers or are observed only in a specific layer, which are conceptually different from HIMs.
Software availability
The source code of our MOCHI method is available as Supplemental Code and at GitHub at https://github.com/ma-compbio/MOCHI.
Competing interest statement
The authors declare no competing interests.
Supplementary Material
Acknowledgments
This work was supported in part by the National Institutes of Health Common Fund 4D Nucleome Program grant U54DK107965 (J.M.), National Institutes of Health grant R01HG007352 (J.M.), and National Science Foundation grant 1717205 (J.M.). We thank Bas van Steensel, Zhijun Duan, and members of the laboratory of J.M. (Ben Chidester, Tianming Zhou, Kyle Xiong, and Yang Yang) for helpful comments to improve the manuscript. J.M. thanks Michael Levine for suggesting the term “transcriptional niche” as a property of HIMs.
Author contributions: Conceptualization was by J.M. Methodology was by D.T., R.Z., and J.M. Software was contributed by D.T. and R.Z. Investigation was done by D.T., R.Z., Y.Z., X.Z., and J.M. Writing of the original draft was done by D.T., R.Z., and J.M. Review and editing were done by D.T. and J.M. Funding acquisition was by J.M.
Footnotes
[Supplemental material is available for this article.]
Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.250316.119.
References
- The 1000 Genomes Project Consortium. 2015. A global reference for human genetic variation. Nature 526: 68–74. 10.1038/nature15393 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belyaeva A, Venkatachalapathy S, Nagarajan M, Shivashankar GV, Uhler C. 2017. Network analysis identifies chromosome intermingling regions as regulatory hotspots for transcription. Proc Natl Acad Sci 114: 13714–13719. 10.1073/pnas.1708028115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benson AR, Gleich DF, Leskovec J. 2016. Higher-order organization of complex networks. Science 353: 163–166. 10.1126/science.aad9029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boija A, Klein IA, Sabari BR, Dall'Agnese A, Coffey EL, Zamudio AV, Li CH, Shrinivas K, Manteiga JC, Hannett NM, et al. 2018. Transcription factors activate genes through the phase-separation capacity of their activation domains. Cell 175: 1842–1855.e16. 10.1016/j.cell.2018.10.042 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonev B, Cavalli G. 2016. Organization and function of the 3D genome. Nat Rev Genet 17: 661–678. 10.1038/nrg.2016.112 [DOI] [PubMed] [Google Scholar]
- Chen H, Chen J, Muir LA, Ronquist S, Meixner W, Ljungman M, Ried T, Smale S, Rajapakse I. 2015. Functional organization of the human 4D nucleome. Proc Natl Acad Sci 112: 8002–8007. 10.1073/pnas.1505822112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y, Zhang Y, Wang Y, Zhang L, Brinkman EK, Adam SA, Goldman R, van Steensel B, Ma J, Belmont AS. 2018. Mapping 3D genome organization relative to nuclear compartments using TSA-Seq as a cytological ruler. J Cell Biol 217: 4025–4048. 10.1083/jcb.201807108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chong S, Dugast-Darzacq C, Liu Z, Dong P, Dailey GM, Cattoglio C, Heckert A, Banala S, Lavis L, Darzacq X, et al. 2018. Imaging dynamic and selective low-complexity domain interactions that control gene transcription. Science 361: eaar2555 10.1126/science.aar2555 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung F. 2007. Four Cheeger-type inequalities for graph partitioning algorithms. In Proceedings of ICCM, II (ed. Ji L, et al. ), pp. 751–772. International Press, Boston. [Google Scholar]
- Cortini R, Filion GJ. 2018. Theoretical principles of transcription factor traffic on folded chromatin. Nat Commun 9: 1740 10.1038/s41467-018-04130-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cremer T, Cremer C. 2001. Chromosome territories, nuclear architecture and gene regulation in mammalian cells. Nat Rev Genet 2: 292–301. 10.1038/35066075 [DOI] [PubMed] [Google Scholar]
- Davidson EH. 2006. The regulatory genome: gene regulatory networks in development and evolution. Academic Press, San Diego. [Google Scholar]
- Davis CA, Hitz BC, Sloan CA, Chan ET, Davidson JM, Gabdank I, Hilton JA, Jain K, Baymuradov UK, Narayanan AK, et al. 2018. The Encyclopedia of DNA elements (ENCODE): data portal update. Nucleic Acids Res 46: D794–D801. 10.1093/nar/gkx1081 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dixon JR, Selvaraj S, Yue F, Kim A, Li Y, Shen Y, Hu M, Liu JS, Ren B. 2012. Topological domains in mammalian genomes identified by analysis of chromatin interactions. Nature 485: 376–380. 10.1038/nature11082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eisenberg E, Levanon EY. 2013. Human housekeeping genes, revisited. Trends Genet 29: 569–574. 10.1016/j.tig.2013.05.010 [DOI] [PubMed] [Google Scholar]
- Ernst J, Kellis M. 2012. ChromHMM: automating chromatin-state discovery and characterization. Nat Methods 9: 215–216. 10.1038/nmeth.1906 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fanucchi S, Shibayama Y, Burd S, Weinberg MS, Mhlanga MM. 2013. Chromosomal contact permits transcription between coregulated genes. Cell 155: 606–620. 10.1016/j.cell.2013.09.051 [DOI] [PubMed] [Google Scholar]
- Gerstein MB, Kundaje A, Hariharan M, Landt SG, Yan KK, Cheng C, Mu XJ, Khurana E, Rozowsky J, Alexander R, et al. 2012. Architecture of the human regulatory network derived from ENCODE data. Nature 489: 91–100. 10.1038/nature11245 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guelen L, Pagie L, Brasset E, Meuleman W, Faza MB, Talhout W, Eussen BH, de Klein A, Wessels L, de Laat W, et al. 2008. Domain organization of human chromosomes revealed by mapping of nuclear lamina interactions. Nature 453: 948–951. 10.1038/nature06947 [DOI] [PubMed] [Google Scholar]
- Hnisz D, Abraham BJ, Lee TI, Lau A, Saint-André V, Sigova AA, Hoke HA, Young RA. 2013. Super-enhancers in the control of cell identity and disease. Cell 155: 934–947. 10.1016/j.cell.2013.09.053 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hnisz D, Shrinivas K, Young RA, Chakraborty AK, Sharp PA. 2017. A phase separation model for transcriptional control. Cell 169: 13–23. 10.1016/j.cell.2017.02.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang da W, Sherman BT, Lempicki RA. 2009. Bioinformatics enrichment tools: paths toward the comprehensive functional analysis of large gene lists. Nucleic Acids Res 37: 1–13. 10.1093/nar/gkn923 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S, Shendure J. 2019. Mechanisms of interplay between transcription factors and the 3D genome. Mol Cell 76: 306–319. 10.1016/j.molcel.2019.08.010 [DOI] [PubMed] [Google Scholar]
- Kivelä M, Arenas A, Barthelemy M, Gleeson JP, Moreno Y, Porter MA. 2014. Multilayer networks. J Complex Netw 2: 203–271. 10.1093/comnet/cnu016 [DOI] [Google Scholar]
- Kosak ST, Scalzo D, Alworth SV, Li F, Palmer S, Enver T, Lee JS, Groudine M. 2007. Coordinate gene regulation during hematopoiesis is related to genomic organization. PLoS Biol 5: e309 10.1371/journal.pbio.0050309 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lambert SA, Jolma A, Campitelli LF, Das PK, Yin Y, Albu M, Chen X, Taipale J, Hughes TR, Weirauch MT. 2018. The human transcription factors. Cell 172: 650–665. 10.1016/j.cell.2018.01.029 [DOI] [PubMed] [Google Scholar]
- Lanctôt C, Cheutin T, Cremer M, Cavalli G, Cremer T. 2007. Dynamic genome architecture in the nuclear space: regulation of gene expression in three dimensions. Nat Rev Genet 8: 104–115. 10.1038/nrg2041 [DOI] [PubMed] [Google Scholar]
- Li P, Milenkovic O. 2017. Inhomogeneous hypergraph clustering with applications. In NIPS'17: Proceedings of the 31st international conference on neural information processing systems (ed. Guyon I, et al. ), pp. 2305–2315. Curran Associates Inc., Red Hook, NY. [Google Scholar]
- Lieberman-Aiden E, van Berkum NL, Williams L, Imakaev M, Ragoczy T, Telling A, Amit I, Lajoie BR, Sabo PJ, Dorschner MO, et al. 2009. Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science 326: 289–293. 10.1126/science.1181369 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma X, Ezer D, Adryan B, Stevens TJ. 2018. Canonical and single-cell Hi-C reveal distinct chromatin interaction sub-networks of mammalian transcription factors. Genome Biol 19: 174 10.1186/s13059-018-1558-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marbach D, Lamparter D, Quon G, Kellis M, Kutalik Z, Bergmann S. 2016. Tissue-specific regulatory circuits reveal variable modular perturbations across complex diseases. Nat Methods 13: 366–370. 10.1038/nmeth.3799 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Misteli T. 2007. Beyond the sequence: cellular organization of genome function. Cell 128: 787–800. 10.1016/j.cell.2007.01.028 [DOI] [PubMed] [Google Scholar]
- Neems DS, Garza-Gongora AG, Smith ED, Kosak ST. 2016. Topologically associated domains enriched for lineage-specific genes reveal expression-dependent nuclear topologies during myogenesis. Proc Natl Acad Sci 113: E1691–E1700. 10.1073/pnas.1521826113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Németh A, Conesa A, Santoyo-Lopez J, Medina I, Montaner D, Péterfia B, Solovei I, Cremer T, Dopazo J, Längst G. 2010. Initial genomics of the human nucleolus. PLoS Genet 6: e1000889 10.1371/journal.pgen.1000889 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen TC, Zaleta-Rivera K, Huang X, Dai X, Zhong S. 2018. RNA, action through interactions. Trends Genet 34: 867–882. 10.1016/j.tig.2018.08.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nora EP, Lajoie BR, Schulz EG, Giorgetti L, Okamoto I, Servant N, Piolot T, van Berkum NL, Meisig J, Sedat J, et al. 2012. Spatial partitioning of the regulatory landscape of the X-inactivation centre. Nature 485: 381–385. 10.1038/nature11049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paulsen J, Liyakat Ali TM, Collas P. 2018. Computational 3D genome modeling using Chrom3D. Nat Protoc 13: 1137–1152. 10.1038/nprot.2018.009 [DOI] [PubMed] [Google Scholar]
- Petrovic J, Zhou Y, Fasolino M, Goldman N, Schwartz GW, Mumbach MR, Nguyen SC, Rome KS, Sela Y, Zapataro Z, et al. 2019. Oncogenic Notch promotes long-range regulatory interactions within hyperconnected 3D cliques. Mol Cell 73: 1174–1190.e12. 10.1016/j.molcel.2019.01.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pope BD, Ryba T, Dileep V, Yue F, Wu W, Denas O, Vera DL, Wang Y, Hansen RS, Canfield TK, et al. 2014. Topologically associating domains are stable units of replication-timing regulation. Nature 515: 402–405. 10.1038/nature13986 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quinodoz SA, Ollikainen N, Tabak B, Palla A, Schmidt JM, Detmar E, Lai MM, Shishkin AA, Bhat P, Takei Y, et al. 2018. Higher-order inter-chromosomal hubs shape 3D genome organization in the nucleus. Cell 174: 744–757.e24. 10.1016/j.cell.2018.05.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rajapakse I, Scalzo D, Tapscott SJ, Kosak ST, Groudine M. 2010. Networking the nucleus. Mol Syst Biol 6: 395 10.1038/msb.2010.48 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao SS, Huntley MH, Durand NC, Stamenova EK, Bochkov ID, Robinson JT, Sanborn AL, Machol I, Omer AD, Lander ES, et al. 2014. A 3D map of the human genome at kilobase resolution reveals principles of chromatin looping. Cell 159: 1665–1680. 10.1016/j.cell.2014.11.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabari BR, Dall'Agnese A, Boija A, Klein IA, Coffey EL, Shrinivas K, Abraham BJ, Hannett NM, Zamudio AV, Manteiga JC, et al. 2018. Coactivator condensation at super-enhancers links phase separation and gene control. Science 361: eaar3958 10.1126/science.aar3958 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Safran M, Dalah I, Alexander J, Rosen N, Iny Stein T, Shmoish M, Nativ N, Bahir I, Doniger T, Krug H, et al. 2010. GeneCards Version 3: the human gene integrator. Database 2010: baq020 10.1093/database/baq020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shin Y, Brangwynne CP. 2017. Liquid phase condensation in cell physiology and disease. Science 357: eaaf4382 10.1126/science.aaf4382 [DOI] [PubMed] [Google Scholar]
- Spector DL, Lamond AI. 2011. Nuclear speckles. Cold Spring Harb Perspect Biol 3: a000646 10.1101/cshperspect.a000646 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stadhouders R, Filion GJ, Graf T. 2019. Transcription factors and 3D genome conformation in cell-fate decisions. Nature 569: 345–354. 10.1038/s41586-019-1182-7 [DOI] [PubMed] [Google Scholar]
- Tang Z, Luo OJ, Li X, Zheng M, Zhu JJ, Szalaj P, Trzaskoma P, Magalska A, Wlodarczyk J, Ruszczycki B, et al. 2015. CTCF-mediated human 3D genome architecture reveals chromatin topology for transcription. Cell 163: 1611–1627. 10.1016/j.cell.2015.11.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thul PJ, Åkesson L, Wiking M, Mahdessian D, Geladaki A, Ait Blal H, Alm T, Asplund A, Björk L, Breckels LM, et al. 2017. A subcellular map of the human proteome. Science 356: eaal3321 10.1126/science.aal3321 [DOI] [PubMed] [Google Scholar]
- Tsourakakis CE, Pachocki J, Mitzenmacher M. 2017. Scalable motif-aware graph clustering. In WWW'17: Proceedings of the 26th international conference on world wide web, pp. 1451–1460. International World Wide Web Conferences Steering Committee, Republic and Canton of Geneva, Switzerland. [Google Scholar]
- van Steensel B, Belmont AS. 2017. Lamina-associated domains: links with chromosome architecture, heterochromatin, and gene repression. Cell 169: 780–791. 10.1016/j.cell.2017.04.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang T, Birsoy K, Hughes NW, Krupczak KM, Post Y, Wei JJ, Lander ES, Sabatini DM. 2015. Identification and characterization of essential genes in the human genome. Science 350: 1096–1101. 10.1126/science.aac7041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, Chen H, Li R, Taft DA, Yao G, Bai F, Xing J. 2019. Spatial clustering and common regulatory elements correlate with coordinated gene expression. PLoS Comput Biol 15: e1006786 10.1371/journal.pcbi.1006786 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.