Efficient triple-VENC phase-contrast MRI for improved velocity dynamic range

Abstract

Purpose

To evaluate the utility of an efficient triple velocity-encoding (VENC) 4D flow MRI implementation to improve velocity unwrapping of 4D flow MRI data with the same scan time as an interleaved dual-VENC acquisition.

Methods

A balanced 7-point acquisition was used to derive 3 sets of 4D flow images corresponding to 3 different VENCs. These 3 datasets were then used to unwrap the aliased lowest VENC into a minimally aliased, triple-VENC dataset. Triple-VENC MRI was evaluated and compared with dual-VENC MRI over 3 different VENC ranges (50–150, 60–150, and 60–180 cm/s) in vitro in a steadily rotating phantom as well as in a pulsatile flow phantom. In vivo, triple-VENC data of the thoracic aorta were also evaluated in 3 healthy volunteers (2 males, 26–44 years old) with VENC = 50/75/150 cm/s. Two triple-VENC (triconditional and biconditional) and 1 dual-VENC unwrapping algorithms were quantitatively assessed through comparison to a reference, unaliased, single-VENC scan.

Results

Triple-VENC 4D flow constant rotation phantom results showed high correlation with the analytical solution (intraclass correlation coefficient = 0.984–0.995, P < .001) and up to a 61% reduction in velocity noise compared with the corresponding single-VENC scans (VENC = 150, 180 cm/s). Pulsatile flow phantom experiments demonstrated good agreement between triple-VENC and single-VENC acquisitions (peak flow < 0.8% difference; peak velocity < 11.7% difference). Triconditional triple-VENC unwrapping consistently outperformed dual-VENC unwrapping, correctly unwrapping more than 83% and 46%−66% more voxels in vitro and in vivo, respectively.

Conclusion

Triple-VENC 4D flow MRI adds no additional scan time to dual-VENC MRI and has the potential for improved unwrapping to extend the velocity dynamic range beyond dual-VENC methods.

1 |. INTRODUCTION

Four-dimensional flow MRI enables visualization of complex hemodynamics over the cardiac cycle. However, the measurement of blood flow velocity (v) with phase-contrast (PC) MRI is inherently limited by the need to set a velocity-encoding sensitivity (VENC). This single-VENC acquisition results in either velocity aliasing for unexpectedly high blood flow velocities (v > VENC), or elevated noise for slow flow (v << VENC), as velocity noise (σ_v) is directly proportional to VENC (σ_v ~ VENC).¹ However, the evaluation of cardiac and vascular disease often requires measurement of blood flow across a wide range of velocities, such as in patients with aortic valve stenosis who present with high-velocity flow jets (up to 400 cm/s) and adjacent regions of low circulating flow (as low as 10 cm/s).

Many groups have investigated using extra velocity encodings to provide additional information to unwrap phase aliasing and increase the velocity-to-noise ratio (VNR).^2–6 Johnson et al implemented 5-point balanced flow encoding to reduce noise and velocity aliasing in phase images,⁷ while more recently, a multidimensional high-moment method was proposed that used 6 velocity encodings arranged as an icosahedron to produce high-efficiency unwrapping.⁸ Schnell et al previously developed a dual-VENC 4D flow MRI sequence using a shared reference scan followed by 2 successive interleaved, 3D (low-VENC and high-VENC) scans, which allowed for the encoding of 3D blood flow velocities within 7 TRs.^9–11 Dual-VENC unwrapping resulted in a single dataset with the favorable VNR of the low-VENC scan but without velocity aliasing, enabling the in vivo assessment of both fast arterial flow and slow venous flow as seen in intracranial hemodynamics. However, dual-VENC 4D flow techniques are still limited by inherently long scan times. For example, even an optimized dual-VENC 4D flow sequence (7 TRs for interleaved dual-VENC) has a 75% longer scan time than a standard single-VENC 4D flow acquisition (4 TRs for single-VENC encoding).^12,13 Moreover, current multi-VENC unwrapping algorithms are limited in their velocity dynamic range and typically use a high to low VENC ratio of 2:1 to avoid multiple phase wraps, which can complicate velocity anti-aliasing. Specifically, Zwart et al found that increased v relative to low-VENC increased noise sensitivity and limited the reconstruction algorithm.⁸

Thus, we propose a novel method for reconstruction of a 3-VENC 4D flow dataset from a 7TR dual-VENC sequence without additional scan time. The aim of this study was to systematically evaluate the utility of a prototype 7-point triple-VENC implementation by (1) evaluating and validating the unconventionally reconstructed intrinsic third VENC (iVENC), (2) evaluating 2 unwrapping algorithms for triple-VENC reconstruction, and (3) comparing these techniques to available dual-VENC methods. We hypothesized that triple-VENC unwrapping algorithms would correctly unwrap more voxels than dual-VENC methods when evaluated over the same velocity-sensitivity range.

2 |. METHODS

2.1 |. Dual-VENC theory and beyond

Velocity sensitivity is achieved in PC-MRI using bipolar gradients. The change in the gradient first moment, ΔM₁, applied in the direction of a moving spin, and the velocity of that spin determines the accrued MR-signal phase, Φ, as follows:

$$\mathrm{\Phi }=\gamma \mathrm{\Delta }{M}_{1}v,$$ (1)

where γ is the gyromagnetic ratio and v is the spin velocity. The reconstructed MR-signal phase is limited to a range of [−π, π] radians; thus, the VENC describes the maximum measurable velocity as

$$\mathrm{VENC}=\frac{\mathrm{\Pi }}{\gamma \mathrm{\Delta }{M}_1}.$$ (2)

Lee et al stated that both phase and magnitude noise have the same fundamental thermal origin; therefore, phase noise, σ_Φ, can be expressed as

$${\mathrm{\sigma }}_{\mathrm{\Phi }}\sim \frac{{\mathrm{\sigma }}_{mag}}{mag}=\frac{1}{\mathrm{SNR}}{.}^{(9)}$$ (3)

In combining Equations 1–3,

$${\mathrm{\sigma }}_v=\frac{{\mathrm{\sigma }}_{\mathrm{\Phi }}}{\mathrm{\Pi }}\mathrm{VENC}\sim \frac{\mathrm{VENC}}{\mathrm{SNR}\mathrm{\Pi }}.$$ (4)

Thus, the VNR can be expressed as

$$\mathrm{VNR}=\frac{v}{{\mathrm{\sigma }}_v}=\frac{\mathrm{\Pi }v}{\sqrt{2}\mathrm{VENC}}\mathrm{SNR}.$$ (5)

Equation 5 indicates that the VNR is inversely proportional to the VENC of the PC-MRI measurement.

Dual-VENC reconstruction algorithms combine information from both the low-VENC and high-VENC acquisitions in an attempt to reduce the tradeoffs among VENC, VNR, and velocity dynamic range. Given a low-VENC and high-VENC set of phase-difference images, the phase values in the high-VENC dataset can be converted to phase values corresponding to the low-VENC by multiplying the high-VENC phase by the ratio of the 2 VENCs as follows:

$${\varphi }_{\mathrm{est},\mathrm{low}-\mathrm{VENC}}=\frac{{\mathrm{VENC}}_{\mathrm{high}-\mathrm{VENC}}}{{\mathrm{VENC}}_{\mathrm{low}-\mathrm{VENC}}}{\mathrm{\Phi }}_{\mathrm{high}-\mathrm{VENC}},$$ (6)

where Φ_high−VENC represents the measured high-VENC phase values and Φ_{est,low−VENC} is the estimated high-VENC measurement in the low-VENC phase domain. For velocities between VENC_low and VENC_high, the phase will be aliased in low-VENC images but within the range of [−Π, Π] in high-VENC phase values, such that

$$\left|\frac{{\mathrm{VENC}}_{\mathrm{high}-\mathrm{VENC}}}{{\mathrm{VENC}}_{\mathrm{low}}-\mathrm{VENC}}{\mathrm{\Phi }}_{\mathrm{high}-\mathrm{VENC}}-{\mathrm{\Phi }}_{\mathrm{aliased},\mathrm{low}-\mathrm{VENC}}\right|\approx 2\mathrm{\Pi }n,$$ (7)

where n is an integer and varies with the number of phase wraps. For example, in the case of 1–2 wraps, where VENC<Velocity≤3*VENC, n = 1. in the case of 3–4 wraps, where 3*VENC<Velocity≤5*VENC, n = 2. This relationship can be used to unwrap the aliased low-VENC voxels while preserving the favorable velocity noise (see Equations 4 and 5) of the low-VENC dataset.

2.2 |. Intrinsic triple-VENC 4D flow MRI

2.2.1 |. Encoding scheme

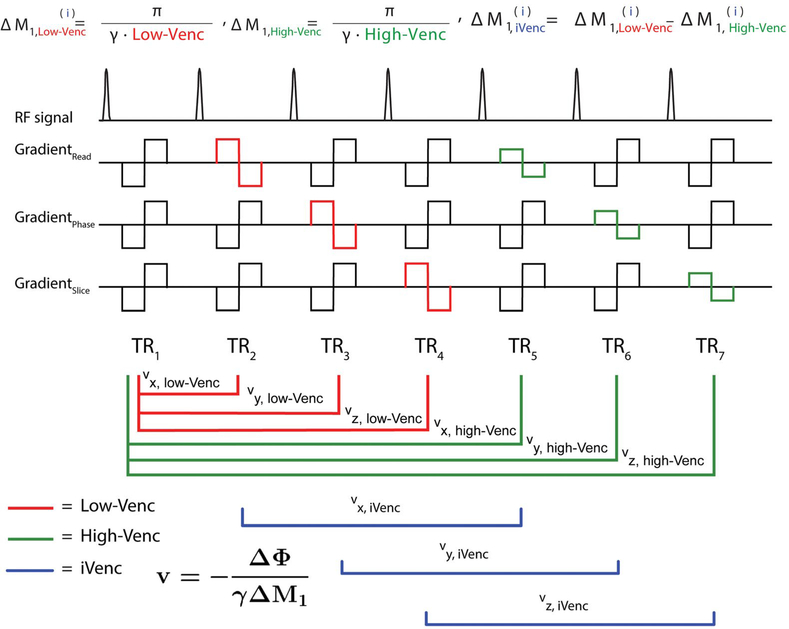
A triple-VENC scheme for reconstruction of a triple-VENC 4D flow dataset was acquired based on a previously described 7-TR dual-VENC 4D flow MRI sequence.¹ As shown in Figure 1, gradient waveforms were implemented using balanced 7-point velocity encoding. The first gradient moment, $M_1^{\mathrm{TR1}}$, for the first TR (“reference”) scan was calculated based on the total desired change in the first-gradient moment ΔM_1,low-VENC for low-VENC encoding of velocities along the x, y, and z directions in TRs 2–4. First-gradient moments $M_1^{\mathrm{TR2}}$, $M_1^{\mathrm{TR3}}$, and $M_1^{\mathrm{TR4}}$ were calculated as for traditional balanced 4-point velocity encoding (Figure 1, TRs 1–4)¹⁴ as follows:

$$\mathrm{\Delta }{M}_{1,\mathrm{low}-\mathrm{VENC}}^{\mathrm{n}}=M_1^{\mathrm{TRi}}-M_1^{\mathrm{TR1}},n=\mathrm{x},\mathrm{y},\mathrm{z},i=2,3,4.$$ (8)

FIGURE 1.

Triple velocity-encoded sensitivity (VENC) acquisition and reconstruction. Triple-VENC phase-contrast (PC) MRI sequence with a shared reference scan between low-VENC and high-VENC in the read, phase, and slice (i = x, y, z) directions, and combined use of low-VENC and high-VENC scans for reconstruction of the implicit VENC (iVENC) data. Imaging gradients are omitted for clarity. The red lines indicate the paired scans used to calculate low-VENC phase-difference images; the green lines indicate the high-VENC pairs; and the blue lines indicate the iVENC pairs. The first moments of each TR are described for all VENCs

To minimize the total acquisition time, the reference scan, TR1, was shared for the high-VENC data acquisition, in which the high-VENC gradient moments (encoding of high-VENC velocities along the x, y, and z directions in TRs 5–7) were calculated based on $M_1^{\mathrm{TR1}}$ as follows:

$$\mathrm{\Delta }{M}_{1,\mathrm{high}-\mathrm{VENC}}^{\mathrm{n}}=M_1^{\mathrm{TRi}}-M_1^{\mathrm{TR1}},n=\mathrm{x},\mathrm{y},\mathrm{z},i=5,6,7.$$ (9)

Although conventional dual-VENC reconstruction enables the reconstruction of 2 VENCs, as shown in Figure 1, the proposed triple-VENC reconstruction uses these 7 TRs to calculate an additional set of time-resolved phase-difference images. This additional iVENC phase-difference image set wasreconstructed using 6 TRs (TRs 2–7, blue lines in Figure 1), where

$$\begin{gathered} \mathrm{\Delta }{M}_{1,\mathrm{iVENC}}^{\mathrm{x}}=M_1^{\mathrm{TR2}}-M_1^{\mathrm{TR5}},\mathrm{\Delta }{M}_{1,\mathrm{iVENC}}^{\mathrm{y}} \\ =M_1^{\mathrm{TR3}}-M_1^{\mathrm{TR6}},\mathrm{and}\mathrm{\Delta }{M}_{1,\mathrm{iVENC}}^{\mathrm{z}}=M_1^{\mathrm{TR4}}-M_1^{\mathrm{TR7}}. \end{gathered}$$ (10)

The resulting third VENC is intrinsic to the dual-VENC acquisition and depends on the change in first moment between the low-VENC and high-VENC scans (Supporting Information Figure S1); thus,

$$\begin{gathered} \mathrm{the}\mathrm{iVENC}=\frac{\pi }{\gamma \left(M_{1i}^{(\mathrm{low}-\mathrm{VENC})}-M_{1i}^{(\mathrm{high}-\mathrm{VENC})}\right)} \\ =\frac{\mathrm{low}-\mathrm{VENC}*\mathrm{high}-\mathrm{VENC}}{(\mathrm{high}-\mathrm{VENC}-\mathrm{low}-\mathrm{VENC})}. \end{gathered}$$ (11)

2.2.2 |. Triple-VENC unwrapped reconstruction

Following the logic of dual-VENC algorithms, the 3 sets of PC images can be used to identify aliased voxels in the lowest VENC images. For the purposes of this study, the high-VENC and low-VENC images were chosen such that the iVENC corresponded to the highest VENC (low-VENC < high-VENC < iVENC) (Figure 1B). A biconditional unwrapping algorithm was used to reconstruct an unwrapped triple-VENC dataset based on a simple extension of Equation 7, where if assuming a nonaliased iVENC dataset, the aliased velocities fell into 2 categories:

1. If v > low-VENC and v < high-VENC, unwrap if a, where a is

   1. $\left|\frac{{\mathrm{VENC}}_{\mathrm{high}-\mathrm{VENC}}}{{\mathrm{VENC}}_{\mathrm{low}-\mathrm{VENC}}}{\mathrm{\Phi }}_{\mathrm{high}-\mathrm{VENC}}-{\mathrm{\Phi }}_{\mathrm{aliased},\mathrm{low}-\mathrm{VENC}}\right|\approx 2\mathrm{\Pi }\mathrm{n}$
2. v > high-VENC, unwrap if (a||b), where a and b are

   1. $\left|\frac{Ven{c}_{\mathrm{iVENC}}}{{\mathrm{VENC}}_{\mathrm{low}-\mathrm{VENC}}}{\mathrm{\Phi }}_{iVenc}-{\mathrm{\Phi }}_{\mathrm{aliased},\mathrm{low}-\mathrm{VENC}}\right|\approx 2\mathrm{\Pi }\mathrm{n}$
   2. $\left|\frac{{\mathrm{VENC}}_{\mathrm{iVENC}}}{{\mathrm{VENC}}_{\mathrm{high}-\mathrm{VENC}}}{\mathrm{\Phi }}_{\mathrm{iVENC}}-{\mathrm{\Phi }}_{\mathrm{aliased},\mathrm{high}-\mathrm{VENC}}\right|\approx 2\mathrm{\Pi }\mathrm{n},$

where n is an integer, then Φ_{aliased,low−VENC} was unwrapped by subtracting or adding 2πn (in the case of 1–2 wraps, where VENC<Velocity≤3*VENC, n = 1; in the case of 3–4 wraps, where 3*VENC<Velocity≤5*VENC, n = 2).¹⁵ This algorithm was previously shown to improve unwrapping compared with just the use of the iVENC and low-VENC comparison alone and compares the lower VENC(s) to the highest, regardless of how each set of phase difference images are calculated (Supporting Information Figure S2).¹⁵

A second, simple triconditional reconstruction algorithm also considered the relationship between the low-VENC and high-VENC images, using the same 2 aliased velocity categories:

1. If v > low-VENC and v < high-VENC, unwrap if a, where a is

   1. $\left|\frac{{\mathrm{VENC}}_{\mathrm{high}-\mathrm{VENC}}}{{\mathrm{VENC}}_{\mathrm{low}-\mathrm{VENC}}}{\mathrm{\Phi }}_{\mathrm{high}-\mathrm{VENC}}-{\mathrm{\Phi }}_{\mathrm{aliased},\mathrm{low}-\mathrm{VENC}}\right|\approx 2\mathrm{\Pi }\mathrm{n}$
      For v < high-VENC, traditional dual-VENC algorithms have shown effective unwrapping for high-VENC ≤ 2*low_VENC. Most of the aliased velocities of interest will fall under the next category.
2. v > high-VENC, unwrap if [(a||b) && c], where a, b, and c are

   1. $\left|\frac{{\mathrm{VENC}}_{\mathrm{iVENC}}}{{\mathrm{VENC}}_{\mathrm{low}-\mathrm{VENC}}}{\mathrm{\Phi }}_{\mathrm{iVENC}}-{\mathrm{\Phi }}_{\mathrm{aliased},\mathrm{low}-\mathrm{VENC}}\right|\approx 2\mathrm{\Pi }\mathrm{n}$
   2. $\left|\frac{{\mathrm{VENC}}_{\mathrm{iVENC}}}{{\mathrm{VENC}}_{\mathrm{high}-\mathrm{VENC}}}{\mathrm{\Phi }}_{\mathrm{iVENC}}-{\mathrm{\Phi }}_{\mathrm{aliased},\mathrm{high}-\mathrm{VENC}}\right|\approx 2\mathrm{\Pi }\mathrm{n}$
   3. $\left|\frac{{\mathrm{VENC}}_{\mathrm{high}-\mathrm{VENC}}}{{\mathrm{VENC}}_{\mathrm{iVENC}}}{\mathrm{\Phi }}_{\mathrm{aliased},\mathrm{high}-\mathrm{VENC}}-\frac{Ven{c}_{\mathrm{low}-\mathrm{VENC}}}{Ven{c}_{\mathrm{iVENC}}}{\mathrm{\Phi }}_{\mathrm{aliased},\mathrm{low}-\mathrm{VENC}}\right|\approx 2\mathrm{\Pi }\mathrm{n}.$
      This last condition brings the high-VENC and low-VENC into the same VENC domain and adds an additional constraint to prevent incorrect unwrapping of aliased voxels. This constraint was chosen because the dual-VENC phase-difference reconstruction of conventional low-VENC and high-VENC data have been well explored, and the high-VENC:low-VENC values used in this experiment are in ratios of within 2:1. Although the low-VENC and high-VENC were both compared with the highest VENC (iVENC) in the biconditional algorithm, this triconditional algorithm assumes valid unwrapping of VENC ratios within 2:1 (thus, [a||b] and c) and uses the novel iVENC reconstruction as an additional constraint.

For both biconditional and triconditional algorithms, in the case of 1–2 wraps, as was the case for all in vitro experiments, where VENC<Velocity≤3*VENC, n = 1. In the case of 3–4 wraps, where 3*VENC<Velocity≤5*VENC, n was equal to 2.

“Triconditional” refers to the use of 3 conditions in the range of velocities where v > high-VENC. Unwrapped low-VENC images using either the biconditional or triconditional algorithm are referred to as triple-VENC data. The performance of both algorithms was evaluated and compared in vitro and in vivo.

Dual-VENC and triple-VENC reconstructions were directly implemented in the MR scanner online reconstruction software. Concomitant gradient terms as a consequence of Maxwell’s equations were calculated for all 3 reconstructed sets of phase-difference images (low-VENC, high-VENC, and iVENC) and corrected during image reconstruction.¹⁶

2.2.3 |. In vitro experiments

Constant rotation phantom

An MRI-compatible air-driven rotation phantom consisting of a cylindrical canister filled with gadolinium contrast–doped agarose gel was used for in vitro validation. The top of the cylinder was designed as a centrifugal impeller with 12 blades, allowing rotation of the cylinder using a constant pressure compressed air source. An optical sensor was used to measure the rotations per minute in real time. The velocity at each point in the phantom was calculated analytically as

$$v_{x,analytic}=2\mathrm{\Pi }\omega \mathrm{x}$$ (12)

and

$$v_{y,analytic}=2\mathrm{\Pi }\omega \mathrm{y},$$ (13)

where ω is the rotational speed and x and y are the horizontal and vertical distance from the central axis of rotation.

A ring (double cylinder wall) filled with gadolinium-doped gel provided a static material surrounding the rotating cylinder to serve as a reference for background phase correction. This phantom is described in more detail in Supporting Information Figure S3. Triple-VENC reconstruction was evaluated using a coronally oriented imaging plane (spatial resolution = 2.0 × 2.0 × 8.0 mm³, TE = 2.4–3.0 ms, TR = 4.7–5.3 ms, temporal resolution = 36.4–42.4 ms, 8 cardiac phases, flip angle = 15°, bandwidth = 455 Hz/px, parallel imaging GRAPPA acceleration factor R = 2. Three different sets of VENCs wereevaluated: low-VENC = 50/high-VENC = 75/iVENC = 150 cm/s; low-VENC = 60/high-VENC = 100/iVENC = 150 cm/s; and low-VENC = 60/high-VENC = 90/iVENC = 180 cm/s. For comparison, 7 conventional 4-point encoded single-VENC scans corresponding to all reconstructed VENCs were acquired with matched spatial coverage and imaging parameters (VENC = 50, 75, 150, 60, 100, 90, and 180 cm/s). The same VENC value was used for all 3 velocity directions for all phase-difference reconstructions. The corresponding 7-point dual-VENC scans with acquired low and high VENCs corresponding to the widest velocity ranges tested were also acquired (VENC = 50/150, 60/100, and 60/180 cm/s). While dual-VENC scans with these wide velocity ranges can result in a third set of reconstructed VENC images, these dual-VENC scans served as a proof-of-concept comparison and only a conventional shared reference low-VENC and high-VENC set of images were reconstructed for simplicity.

Constant rotation data analysis

Four-dimensional flow MRI data offline preprocessing included noise filtering and second-order eddy current correction, in which a second-order polynomial was fitted to the phase of segmented static material.¹⁷ All acquired cardiac phases of the rotation phantom were averaged, and velocities were compared among low-VENC, high-VENC, iVENC, and unwrapped triple-VENC reconstructions. Four-dimensional flow velocities were compared with analytic velocities calculated from Equations 12 and 13. Cross-sectional horizontal and vertical lines were drawn through the center of the phantom for velocity comparisons of the acquired data with the calculated ground truth (horizontal lines are shown in Figure 2.II,III). Velocity noise was quantified over the static ring using the SD of the velocities over all time frames and compared among low-VENC, high-VENC, iVENC, and unwrapped dual-VENC and triple-VENC scans.

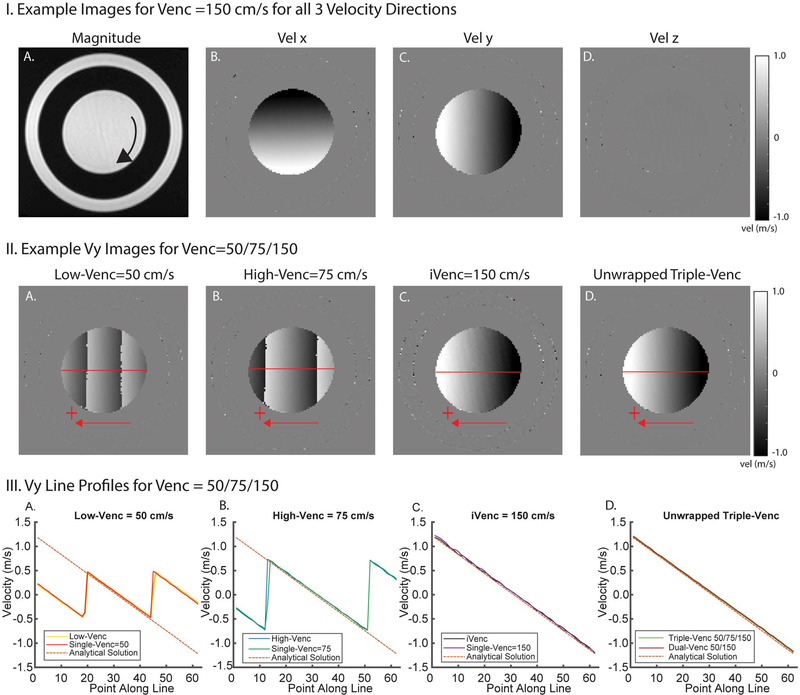
FIGURE 2.

Example rotation phantom images and results. I, Example images for all 3 velocity directions (Vx, Vy, Vz) showing velocity gradients in in-plane velocity encoding directions (x, y). II, Example Vx images from a triple-VENC acquisition. Low-VENC and high-VENC images show different degrees of velocity aliasing. The unwrapped image has the benefit of decreased velocity noise from the low-VENC image and no velocity aliasing. This reduced noise can be seen in comparing the triple-VENC and iVENC images (IIC,D). III, Velocity profiles along a horizontal line (illustrated in red) in the Vx images, showing the velocity values in reconstructed low-VENC, high-VENC, and iVENC phase difference images compared with their corresponding single-VENC acquisitions. Unwrapped triple-VENC velocity profiles are also in agreement with those of the corresponding dual-VENC acquisition

Pulsatile flow phantom

A flow phantom (U-shaped pipe representing a simplified aorta) was integrated into an MRI-compatible pulsatile flow circuit as described previously.¹⁸ Pulsatile flow was generated using a pneumatically driven ventricular assist device driven by a pressure pump control unit (MEDOS, Germany) located outside the MR room. The device was directly attached to the simple U-phantom to mimic pulsatile flow entering the thoracic aorta and used to generate flow rates of 3 L/min at a frequency of 69 “beats” per minute. Water doped with gadolinium-based contrast material was used as fluid in all experiments. All in vitro 4D flow measurements were gated to the pulsatile flow by a trigger signal generated by the pump control unit.

In vitro 4D flow scans used the same sets of VENCs as rotating phantom experiments with the following imaging parameters: spatial resolution = 2.3 × 3.5 × 2.3 mm³, TE = 2.5–3.2 ms, TR = 4.9–5.6 ms, temporal resolution = 38.5–44.0 ms, flip angle = 15°, FOV = 270 × 278 × 55 mm³, bandwidth = 455 Hz/px, and k-t GRAPPA R = 5. As with the rotating phantom, 7 corresponding single-VENC conventional 4D flow scans and 3 sets of dual-VENC scans were acquired with the same spatial coverage, temporal resolution, and imaging parameters.

Pulsatile flow data analysis

Four-dimensional flow MRI data preprocessing included noise filtering and slice-by-slice second-order eddy current correction using a manually segmented static tissue mask.¹⁹ A 3D PC-MRA was calculated from the 4D flow data and used to create a 3D segmentation of the U-phantom (Mimics; Materialise, Leuven, Belgium). For both triple-VENC and single-VENC acquisitions, ten 2D analysis planes were placed orthogonally along the entire “aorta” for quantification of regional peak velocities and time-resolved flow (Figure 3.IA). All ten 4D flow acquisitions were acquired with the same spatial resolution and location, and all analysis planes were placed at identical locations. Systolic blood flow (where “systole” was chosen as the time frame with the highest average velocity) of the entire phantom was visualized using time-resolved 3D streamlines and pathlines (EnSight; CEI, USA) (Figure 3.I.A,B). The triple-VENC unwrapping algorithms were compared with the traditional dual-VENC scans. Incorrectly unwrapped/still aliased voxels were identified by temporally interpolating the unaliased, reference, single-VENC data to the unwrapped dual-VENC and triple-VENC timepoints and performing a voxel-by-voxel comparison of phase values.

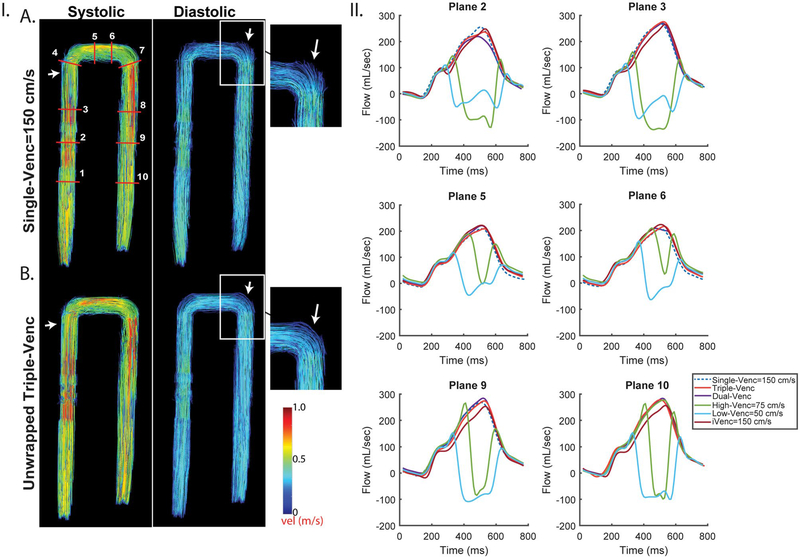
FIGURE 3.

Pulsatile in vitro results for VENC set 50/75/150 cm/s. I, Systolic and diastolic streamlines for a single-VENC acquisition (A) and the triple-VENC (B) dataset. Systolic streamlines show reduction in velocity noise in the unwrapped triple-VENC (triconditional) compared with single-VENC datasets (white arrows, zoomed in); however, this effect is seen more prominently in diastole, where the streamlines are noticeably more collinear at the more complex bends in the phantom. IA, Location of ten 2D analysis planes for quantification of peak velocities and flow time curves. White rectangle indicates location evaluated for number of voxels unwrapped in Table 3. II, Flow time curves over 6 representative planes show agreement between the iVENC unwrapped triple-VENC and unwrapped dual-VENC, and the corresponding single-VENC scan

2.2.4 |. In vivo experiment

Triple-VENC 4D flow MRI was tested in vivo in 3 healthy volunteers (2 males, ages 26, 38, and 44 years old).All volunteers received one 7-point triple-VENC scan (VENC = 50/75/150 cm/s), one 7-point dual-VENC scan (VENC = 50/150 cm/s), and one single VENC scan (VENC = 150 cm/s, TR/TE = 4.9/2.5 ms). All scans were acquired with matched spatial and temporal resolution (dual and triple-VENC TR/TE/flip angle = 5.5–5.6 ms/3.1 ms/7°, spatial resolution = 2.4–2.5 × 3.6–3.8 × 2.4–2.6 mm³) on a 1.5T MAGNETOM Aera system (Siemens Healthcare, Erlangen, Germany). Four-dimensional flow data were acquired in a sagittal-oblique 3D slab with full coverage of the thoracic aorta using prospective ECG gating and a respiratory navigator placed on the lung–liver interface.²⁰ All scans were acquired with k-t GRAPPA, R = 5.²¹ This study was approved by Northwestern University’s Institutional Review Board, and written informed consent was obtained from all volunteers.

2.2.5 |. In vivo flow analysis

A similar workflow was applied to the in vivo data, in which 4D flow preprocessing included noise filtering, first-order eddy current correction, and segmentation of the thoracic aorta using a calculated 3D PC-MRA. Nine 2D analysis planes were placed along the thoracic aorta for time-resolved depiction of flow (Figure 4.I, top). Systolic and diastolic blood flow were visualized using 3D streamlines and pathlines, and the triple-VENC and dual-VENC unwrapping algorithms were compared for each volunteer.

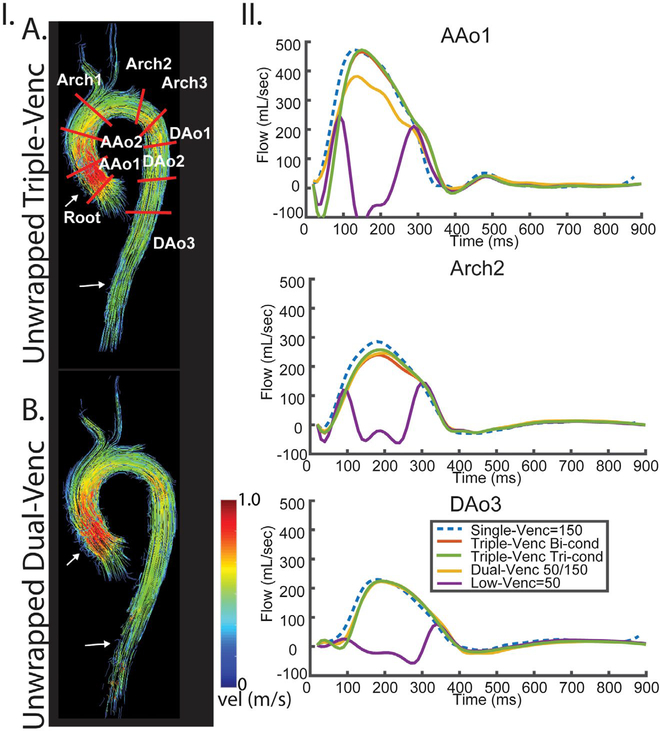
FIGURE 4.

Systolic streamlines comparing the triple-VENC triconditional dataset (A, 50/70/150 cm/s) and dual-VENC acquisition (B, 50/150 cm/s) in 1 healthy volunteer. I, streamlines show improved integrity in the ascending aorta and descending aorta (white arrows) in the triple-VENC dataset compared with dual-VENC. IA, Placement of 9 planes along the aorta. II, Flow curves for 3 representative planes depict agreement of the triple-VENC dataset with the single-VENC flow curves. Abbreviations: AAo, ascending aorta; and DAo, descending aorta

2.3 |. Statistical analysis

All numeric results are reported as mean ± SD or percentages relative to conventional single-VENC 4D flow values. Horizontal and vertical line profile velocities were compared between unwrapped triple-VENC and analytical velocities for the rotation phantom experiment. A Bland-Altman analysis was used to establish the mean difference and limits of agreement between the 4D flow techniques. Coefficients of variation were also calculated for all 4D flow values. Agreement between the 2 methods was assessed using orthogonal regression and intraclass correlation coefficient. A P-value of less than .05 was considered statistically significant.

3 |. RESULTS

3.1 |. In vitro rotation phantom

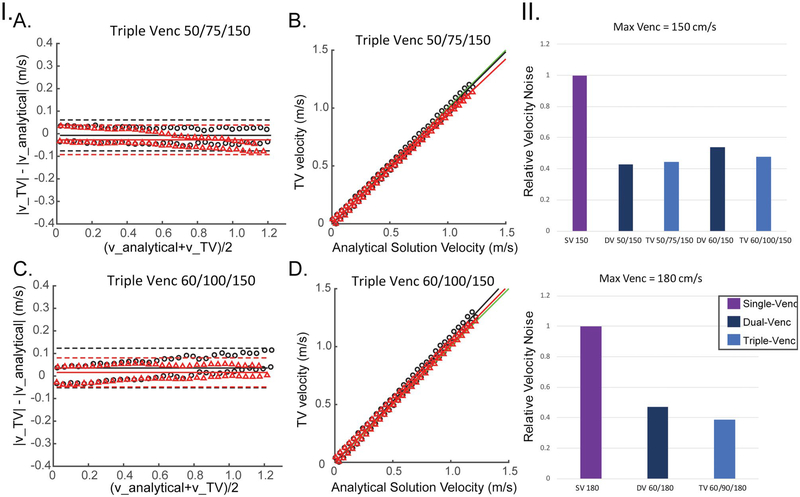
Rotation phantom results validated triple-VENC imaging reconstruction and are summarized in Figures 2 and 5 and Table 1. Example phase difference images at VENC = 150 cm/s are shown in Figure 2.I, where the constant rotation of the phantom results in a linear gradient of velocities in the x and y-directions and zero velocity in z-direction. Figure 2. II depicts representative rotation phantom phase difference images for the x-velocity direction from a 50/75/150-cm/s triple-VENC scan. The dual-VENC and triple-VENC biconditional and triconditional unwrapping algorithms successfully unwrapped all voxels without any residual velocity aliasing; thus, only triconditional results are shown for simplicity (Figure 2.II). Triple-VENC reconstructions showed excellent agreement with their corresponding single-VENC scans and analytical velocities (Figure 2.III). Similar results were found for all other VENC combinations. As shown in Figure 5 and Table 1, Bland-Altman analysis revealed good to excellent agreement between the reconstructed triple-VENC images and the analytical solution (|mean difference| < 3 cm/s for Vx, and < 5 cm/s for Vy). In addition, correlation analysis indicated strong correlation of the unwrapped triple-VENC with the estimated velocities, with high intraclass correlation coefficient values (0.988–0.997) and slopes close to unity (0.941–1.081). Furthermore, both dual-VENC and triple-VENC unwrapping resulted in a 46%−57% reduction in velocity noise for a highest VENC of 150 cm/s (VENCs 50–150 and 60–150 cm/s) and a 53%−61% reduction for a highest VENC of 180 cm/s (VENCs = 60–180 cm/s) compared with the standard unaliased single-VENC acquisition, in which the single-VENC velocity noise for VENC = 150 cm/s and VENC = 180 cm/s was 1.3 cm/s and 1.6 cm/s, respectively (Figure 5.II).

FIGURE 5.

I, Rotation phantom Bland-Altman (A,C) and correlation (B,D) analysis results of the absolute velocity for unwrapped triple-VENC (TV) 50/75/150 and 60/100/150 data using the triconditional algorithm. Red triangles represent the x-velocities plotted along a vertical line, and black circles represent the y-velocities. Red and black lines represent the lines calculated by orthogonal regression for x and y velocities, respectively. Green lines represent a line with slope of 1 (perfect correlation). II, Noise analysis for all 3 sets of VENCs relative to a single-VENC scan corresponding to the iVENC. Noise values are normalized to the separate single-VENC scan noise values. A, experiments using a maximum VENC of 150 cm/s. B, Experiments using a maximum VENC of 180 cm/s

TABLE 1.

Results for the rotating phantom: Bland-Altman and correlation analysis of the absolute velocity for all 3 sets of VENCs for both x and y velocities

	Line	Mean velocity (m/s)	Mean difference (m/s)	LOA (m/s)	CV (%)	Slope (m/s)	Intercept (m/s)	ICC
SV 150	x	0.59 ± 0.34	−0.03	0.07	22.1	0.961	0.008	0.994a
	y	0.62 ± 0.36	0.02	0.08	25.4	1.018	−0.004	0.994a
Triple-VENC 50/75/150	x	0.59 ± 0.35	−0.03	0.07	24.8	0.945	0.006	0.992a
	y	0.60 ± 0.35	−0.01	0.07	25.3	0.992	−0.003	0.995a
Dual-VENC 50/150	x	0.58 ± 0.33	−0.02	0.07	21.9	0.951	0.006	0.992a
	y	0.60 ± 0.35	−0.02	0.07	23.5	0.994	−0.003	0.994a
Triple-VENC 60/100/150	x	0.62 ± 0.36	0.03	0.07	22.7	1.017	0.006	0.995a
	y	0.65 ± 0.38	0.04	0.09	24.5	1.064	−0.003	0.988a
Dual-VENC 60/150	x	0.58 ± 0.34	−0.02	0.06	24.3	0.959	0.005	0.995a
	y	0.62 ± 0.36	0.03	0.04	18.1	1.042	0.005	0.995a
SV 180	x	0.63 ± 0.36	0.03	0.04	22.7	1.041	0.006	0.995a
	y	0.66 ± 0.38	0.05	0.09	24.6	1.081	−0.003	0.984a
Triple-VENC 60/90/180	x	0.57 ± 0.33	−0.03	0.07	24.7	0.941	0.006	0.991a
	y	0.60 ± 0.35	−0.01	0.07	24.0	0.985	−0.003	0.995a
Dual-VENC 60/180	x	0.57 ± 0.33	−0.04	0.07	24.6	0.931	0.006	0.988a
	y	0.59 ± 0.35	−0.02	0.07	23.7	0.974	−0.003	0.993a

Note: Bland-Altman analysis is presented with the mean difference and limits of agreement (LOAs).

Abbreviations: CV, coefficient of variation; and SV, single VENC.

^aDepicts statistical signficance of P < .001 for correlation analyses of intraclass correlation coefficient (ICC).

3.2 |. In vitro pulsatile phantom

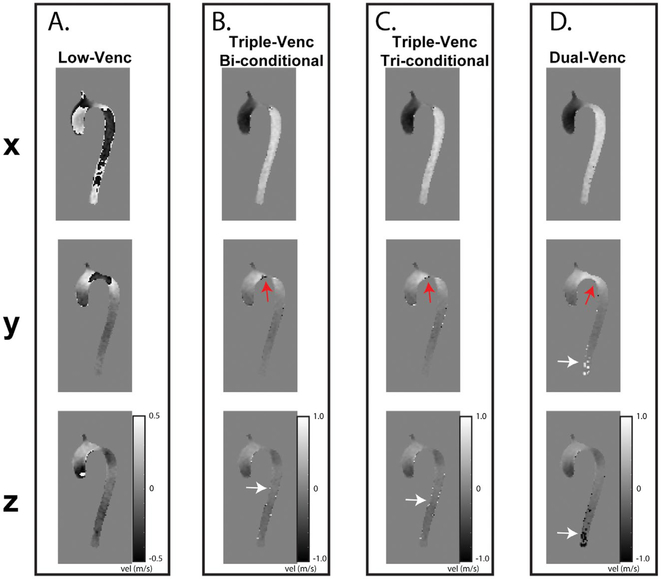
Pulsatile flow phantom results are summarized in Tables 2 and 3 and Figures 3 and 6. Unwrapping the lowest VENC using triconditional triple-VENC unwrapping resulted in greater than 83% fewer incorrectly unwrapped/missed voxels after unwrapping compared with dual-VENC unwrapping (Figure 6 and Table 3) when evaluated over the same VENC range. Figure 3 depicts the representative 4D flow MRI results for a VENC of 50/75/150 cm/s. Systolic and diastolic streamlines indicate good visual agreement between the unwrapped triple-VENC reconstruction and the corresponding single-VENC scan (Figure 3.IA,B). Time-resolved flow curves over 4 representative 2D analysis planes show similar patterns among unaliased iVENC, single-VENC, and triple-VENC data. Triple-VENC flow curves further demonstrate successful unwrapping of aliased low-VENC voxels. Flow and velocity quantification indicate good to excellent agreement between unaliased single-VENC and triple-VENC measurements. Although all 3 unwrapping methods performed well (Figure 6), the triconditional triple-VENC acquisition outperformed dual-VENC unwrapping. (The triple-VENC quantification results are presented for triconditional unwrapping in Table 2). Table 2 indicates good agreement between all triple-VENC and single-VENC reconstructions. Unwrapped triple-VENC quantification over all 10 planes was within 10% of unaliased single-VENC values, except in planes 4–6 at the outer edges of the FOV (Figure 3.II). Net flow over these planes deviated by up to 29.3% from single-VENC measurements. Peak flow of triple-VENC datasets was within 0.2% to 0.8%, and peak velocity within 0.3% to 11.7%, of the corresponding single-VENC values. Dual-VENC data tended to deviate further from single-VENC values, potentially due to acquisition-related background-phase effects (Discussion and Supporting Information Figure S4), with peak velocities varying as much as 54% from single-VENC values.

TABLE 2.

Pulsatile in vitro velocity and flow quantification over ten 2D analysis planes

		Peak flow (mL/s, %)
VENC combination	VENC component	Plane 1	Plane 2	Plane 3	Plane 4	Plane 5	Plane 6	Plane 7	Plane 8	Plane 9	Plane 10
VENC 150	Single VENC 150 (mL/cycle)	275.9	255.1	269.0	223.0	209.1	205.7	234.4	270.8	268.8	278.1
Range 50–150	Triple VENC 50/75/150 tri-conditional (%)	1.2	−6.9	2.7	6.5	1.5	7.6	−4.8	3.2	2.5	−2.2
	Dual VENC 50/150 (%)	−1.0	−14.0	0.5	16.4	5.7	1.2	8.6	6.4	5.8	2.1
Range 60–150	Triple VENC 60/100/150 (%)	−0.3	3.6	2.0	8.6	2.6	4.3	−0.8	1.2	1.5	−0.2
	Dual VENC 60/150 (%)	−2.7	−1.7	−0.9	12.6	5.7	9.1	6.2	6.8	6.4	1.9
VENC 180	Single VENC 180	277.1	251.3	267.6	219.5	213.0	204.6	234.9	271.9	269.8	276.9
Range 60–180	Triple VENC 60/90/180 (%)	−1.5	4.5	2.3	8.9	1.0	8.0	3.5	1.4	1.7	0.8
	Dual VENC 60/180 (%)	−3.1	−0.3	−0.7	14.2	5.8	12.1	7.4	5.2	6.0	2.5
		Net flow (mL/cycle, %)
VENC combination	VENC component	Plane 1	Plane 2	Plane 3	Plane 4	Plane 5	Plane 6	Plane 7	Plane 8	Plane 9	Plane 10
VENC 150	Single VENC 150 (mL/cycle)	87.3	75.5	83.9	71.0	55.3	54.7	80.9	94.0	91.8	86.9
Range 50–150	Triple VENC 50/75/150 triconditional (%)	1.2	4.3	4.8	9.5	24.3	29.3	−2.9	−6.1	−6.8	−5.5
	Dual VENC 50/150 (%)	−6.1	−7.7	−2.4	12.0	24.6	26.6	4.7	−1.0	−1.2	2.3
Range 60–150	Triple VENC 60/100/150 (%)	−1.5	8.3	3.4	8.5	23.9	25.1	−4.8	−9.7	−8.2	−0.3
	Dual VENC 60/150 (%)	−6.9	−3.4	−2.6	9.1	30.6	34.5	8.3	3.2	3.5	6.2
VENC 180	Single VENC 180	84.3	78.8	85.2	66.8	63.9	63.6	76.5	86.4	86.2	87.9
Range 60–180	Triple VENC 60/90/180 (%)	0.6	3.0	1.2	13.3	8.0	9.7	0.9	−0.3	−0.1	−0.1
	Dual VENC 60/180 (%)	−3.3	−7.3	−4.0	17.9	15.0	16.9	16.1	11.4	9.0	5.6
		Peak velocity (m/s, %)
VENC combination	VENC component	Plane 1	Plane 2	Plane 3	Plane 4	Plane 5	Plane 6	Plane 7	Plane 8	Plane 9	Plane 10
VENC 150	Single VENC 150 (mL/cycle)	0.9	1.1	1.1	0.9	0.9	0.8	1.1	1.0	0.9	0.9
Range 50–150	Triple VENC 50/75/150 triconditional (%)	−2.7	−1.8	0.6	3.4	7.5	7.0	−1.8	2.4	0.6	−4.3
	Dual VENC 50/150 (%)	−3.4	30.3	0.0	37.8	25.2	23.4	45.3	7.0	3.8	0.1
Range 60–150	Triple VENC 60/100/150 (%)	−9.6	−5.8	−2.1	7.0	11.7	2.4	1.3	−6.4	−9.8	−6.8
	Dual VENC 60/150 (%)	−2.7	−4.1	1.1	11.7	16.9	18.2	26.5	10.3	6.7	2.2
VENC 180	Single VENC 180	0.8	1.1	1.1	1.0	1.0	0.9	1.1	1.0	0.9	0.9
Range 60–180	Triple VENC 60/90/180 (%)	−2.7	0.4	0.9	0.9	5.7	2.1	7.0	2.1	−0.7	−0.3
	Dual VENC 60/180 (%)	−4.7	−5.6	−1.1	53.9	23.7	29.4	45.6	6.8	3.2	1.0

Note: Quantified values are shown for the unwrapped triple-VENC dataset of each VENC combination. Differences from the corresponding unaliased single-VENC comparison are depicted in percentages.

TABLE 3.

Evaluation of unwrapping algorithms

	Aliased voxels after unwrapping (N [%])
	In vitro	In vivo
Dataset	Pulsatile phantom	Subject 1	Subject 2	Subject 3
50/75/150 biconditional	108 [0.02]	1609 [0.72]	695 [0.25]	1305 [0.35]
50/75/150 triconditional	51 [0.01]	1353 [0.61]	670 [0.24]	1199 [0.32]
50/150 dual VENC	306 [0.06]	3947 [1.78]	1279 [0.47]	2541 [0.62]
60/100/150 biconditional	51 [0.01]
60/100/150 triconditional	0 [0.00]
60/150 dual VENC	22 [0.004]
60/90/180 biconditional	61 [0.01]
60/100/180 triconditional	0 [0.00]
60/180 dual VENC	3 [0.000]

Note: Aliased number of voxels after the unwrapping algorithm is performed are depicted as pure numbers as well as a percentage of the segmented voxels over all phases (in brackets).

FIGURE 6.

Evaluation of dual-VENC and triple-VENC unwrapping algorithms. A-C, Representative 50/75/150 cm/s phase-difference images. All phase-difference images are shown for the same slice location and time point. D, The dual-VENC, triple-VENC biconditional (E) and triple-VENC triconditional (F) datasets shows successful unwrapping of most voxels, but some residual ones near the vessel wall (red arrows). Red arrows depict residual aliasing in the dual-VENC and triple-VENC unwrapped datasets

3.3 |. In vivo

The 4D flow data were successfully acquired in all 3 volunteers with a total scan time of 4:53–6:06 minutes for the single-VENC, 10:53–12:45 minutes for triple-VENC (50/75/150 cm/s), and 10:42–14:46 minutes for the dual-VENC acquisitions. For in vivo data, the biconditional and triconditional algorithm resulted in improved velocity anti-aliasing compared with dual-VENC unwrapping, unwrapping 45%−60% and 48–66% more voxels, respectively. Figure 7 shows an example of unwrapping using the 2 triple-VENC algorithms compared with the conventional dual-VENC acquisition and unwrapping. Although the triple-VENC algorithms perform similarly in vivo, dual-VENC algorithms incorrectly unwrap noticeably more voxels (Figure 7, white arrows). These effects are further seen in example systolic streamlines, where unwrapped Triple-VENC data appear more collinear in the descending aorta, and denser in the ascending aorta (Figure 4). Triconditional example images are shown for simplicity. Representative flow curves over three 2D analysis planes show successful recovery of aliased flow dynamics in the unwrapped triple-VENC dataset.

FIGURE 7.

In vivo application of dual-VENC and triple-VENC unwrapping algorithms for the representative 50/75/150 cm/s phase-difference images. All phase-difference images are shown for the same slice location and time point. Low-VENC data show significant velocity aliasing throughout the volunteer. The unwrapped dual-VENC dataset indicates more incorrect unwrapping in the descending aorta than the triple-VENC algorithms (white arrows), which shows successful unwrapping of most voxels, but some residual ones near the vessel wall (red arrows)

4 |. DISCUSSION

We demonstrated that (1) efficient triple-VENC 4D flow MRI enables acquisition of 3 datasets corresponding to 3 different VENCs in less than 10 minutes; (2) In vivo and in vitro results indicate that triconditional triple-VENC algorithms proved superior to dual-VENC algorithms in correctly unwrapping aliased voxels; and (3) 7-point triple-VENC reconstruction and unwrapping schemes require further investigation, but have the potential to extend the velocity dynamic range beyond those of traditional dual-VENC algorithms within the same scan time.

Constant rotation phantom experiments validated the imaging gradients and the triple-VENC and dual-VENC unwrapping algorithms. However, Bland-Altman plots showed a potential increase in bias with increasing velocities. This bias may have been due to insufficient background phase correction, causing offsets in velocity values, as well as artifacts that arise from imaging a rotation phantom, as pressurized air can cause some sinusoidal fluctuations in the speed. These experiments further confirmed that unwrapped triple-VENC and dual-VENC datasets inherit the improved VNR of their lowest VENC dataset compared with their corresponding single-VENC scans, in which unwrapped triple-VENC and dual-VENC datasets showed a 53%−61% reduction in velocity noise compared with the corresponding nonaliased single-VENC scans (VENC = 150, 180 cm/s) for a highest to lowest VENC ratio of 3:1 (VENC 50–150, 60–180 cm/s) (Figure 5), within range of an expected reduction of 66%. Slight differences may be due to a comparison with a separate, nonaliased single-VENC scan. The simplicity of the rotation phantom, high SNR, and constant rotation likely contributed to the success of all dual-VENC and triple-VENC algorithms in unwrapping all voxels. Although the pulsatile flow in in vitro experiments introduced additional flow complexity, these results nonetheless demonstrated the superiority of the triconditional triple-VENC over the dual-VENC unwrapping algorithm. Unwrapped triple-VENC flow curves and streamlines showed good to excellent agreement in qualitative and quantitative hemodynamic agreement with single-VENC acquisitions, except in planes near the 4D flow data volume boundary. This discrepancy is likely caused by the location of these planes at the edge of the imaging volume, along with increased background phase error in the calculation of net flow. These differences are even more pronounced in the dual-VENC dataset, potentially due to even more pronounced background phase effects associated with the necessary reversal of the high-VENC gradients (TR5-TR7) for a net ΔM_1,high-VENC < 2*ΔM_1,low-VENC. Background phase effects in the dual-VENC acquisitions could also have contributed to increased residual aliasing compared with the triple-VENC triconditional algorithm. Although these effects were outside the scope of this study, the calculation of these dual-VENC gradients and their effects on background phase are explored and explained in Supporting Information Figures S4 and S5.

In vivo experiments further demonstrated the feasibility of the triple-VENC acquisition and reconstruction; however, these experiments further complicated unwrapping. Although the proposed 7-point acquisitions increase scan time by about 75% compared with single-VENC acquisitions, scan times varied between volunteers based on breathing pattern and heart rate during the scans. Moreover, while in vivo results also demonstrated improved unwrapping with the triconditional triple-VENC unwrapping algorithm, the in vivo data showed some incorrect unwrapping of voxels that were not aliased in the low-VENC data. Although in vitro data follow more controlled and predictable behavior, in vivo data are influenced by respiration blurring and patient movement, potentially disrupting the relationship between the 3 VENCs. Moreover, these incorrectly unwrapped timepoints tended to be clustered around systole, potentially caused by slight differences in time stamps between VENCs due to the 7-point encoding. Because the triconditional algorithm tries to consider all 3 VENCs in unwrapping, it inherently adds more constraints on unwrapping, potentially accounting for fewer incorrectly unwrapped voxels compared with dual-VENC acquisitions. Future explorations in unwrapping will include additional constraints to limit the incorrect unwrapping, as well as evaluation of the effects of temporal shifts on multi-VENC reconstruction.

Previous studies have explored similar unwrapping algorithms. Nett et al evaluated dual-VENC reconstruction with 3-directional velocity encoding.²² However, their study used 2 separately acquired single-VENC PC-VIPR (vastly under-sampled isotropic-voxel radial projection imaging) scans, unwrapping the low-VENC data in a postprocessing step. Due to the 3D radial nature of PC-VIPR, Nett et al were able to undersample the high-VENC data up to 25% (R = 4) compared with the fully sampled low-VENC data to achieve reasonable velocity unwrapping for a high to low VENC ratio of 2:1 in vivo. However, this sequential acquisition is limited by patient motion between scans, which increases the potential of registration errors in unwrapping. Moreover, a recent 4D flow consensus statement suggested that despite the tradeoffs in temporal resolution, interleaved velocity encoding is preferred to avoid intercycle variability.²⁰

The volunteer findings in this study suggest that in vivo data may benefit from reconstruction using more sophisticated algorithms to either unwrap or combine data. For example, Ha et al used multiple VENC measurements in separate acquisitions to combine phase information into an overlapped velocity field.²³ Ha’s in vitro experiments used 5 VENCs, whereas his in vivo experiments used 3 VENCs. Comparisons between VENCs were made in a stepwise fashion from the highest to the lowest VENC. Aliased voxels were identified by finding high-VENC data with higher velocities than those of the compared lower VENC, and subsequent replacement of aliased velocities with the velocities of the higher VENC. In vivo experiments using partial Fourier and conventional GRAPPA (R = 2) acceleration resulted in a total scan time of 9 minutes for 3 separate VENCs, which is similar to the in vivo scans of this study, but Ha covered a 2D FOV of only 252 × 252 × 8 mm. In addition, Ha used 3 separate acquisitions, resulting in potential misregistrations in vivo. The k-t acceleration, interleaved sequence, and triple-VENC reconstruction used in our study could be combined with the stepwise assembly used in Ha’s study for improved registration and unwrapping.

Existing automatic and semi-automatic phase-unwrapping algorithms could also be applied after triple-VENC reconstruction to correct residual aliased voxels. For example, Loecher et al previously proposed a single-step Laplacian algorithm using continuity in all 3 spatial directions and time for automated unwrapping of low SNR 4D flow data.²⁴ Loecher subsequently expanded this concept by incorporating a Laplacian term into a technique using velocity reconstruction as a nonconvex optimization problem, and applied this method to dual-VENC and 6-point multidimensional high-moment datasets.²⁵ This approach allowed the use of regularization terms to aid unwrapping (such as penalizing large discontinuities or weighting signal magnitude, to consider partial volume effects and signal dephasing). Nonconvex optimization resulted in lower velocity errors for both multidimensional high moment and dual-VENC acquisitions in simulations and flow phantoms. This approach could be combined with the proposed triple-VENC reconstruction by expanding Loecher’s encoding matrix to include a third VENC.

In addition, the 7-point acquisition used in the proposed study may benefit from incorporating advanced acceleration techniques to further offset the increased scan time. Recent advances in Cartesian acquisition techniques and hardware advances have allowed even higher acceleration of 4D flow imaging than those used in this study.^26–30 While Nett’s and Ha’s studies were based on separate single-VENC acquisitions, a PC-VIPR implementation of 7-point balanced velocity encoding could combine the advantages of a radial acquisition with the proposed triple-VENC 7-point encoding method. Because radial k-space imaging intersects the center of k-space with each projection, radial imaging could be used to improve limitations in temporal resolution, as well as increase the extent of performed undersampling.

This study was limited by a small in vivo sample size, limiting statistical comparisons and comparisons to conventional single-VENC reference standards. However, the thorough in vitro experiments showed the feasibility of the proposed methods, and the small in vivo study confirmed the potential of a novel triple-VENC reconstruction for improved velocity unwrapping. Larger cohorts and patient studies are nonetheless needed to improve the capability of unwrapping and to demonstrate the benefit of a high-velocity dynamic range. In addition, evaluating the success of unwrapping algorithms is inextricably linked to accurate identification of aliased voxels. Validation of unwrapping methods becomes even more complicated without knowledge of an actual “ground truth.” Although this study used a conventional, single-VENC, nonaliased 4D flow dataset with matched imaging parameters as a reference, differences in intravoxel dephasing, flow artifacts, and partial-volume effects made it necessary to erode segmentations before voxel-by-voxel comparisons. However, side-by-side comparison of representative phase difference images between dual-VENC and triple-VENC datasets supported the quantification results. Despite some limitations, this semi-automated method was superior to counting aliased voxels for each slice over all time frames, which in addition to being time-consuming, can introduce human miscount errors due to the hundreds of thousands of considered voxels. Finally, this study was limited to simple conditional unwrapping algorithms and triple-VENC reconstruction and initial feasibility. While this conditional comparison used for biconditional unwrapping does not fully address the issues associated with traditional dual-VENC unwrapping (i.e., the effects of severe noise), this algorithm was chosen as a simple extension of traditional unwrapping. To address some of the uncertainty in this algorithm, a triconditional algorithm was included, with specific conditions that were tailored to velocity ranges relative to the 3 VENCs. Although we demonstrated that the triconditional algorithm outperformed the even simpler biconditional algorithm, more complex unwrapping techniques are often entire studies in themselves; thus, we limited this study to simple conditional algorithms. Future work will explore advanced acceleration techniques, advanced unwrapping methods, and optimized ratios of VENCs in vivo.

5 |. CONCLUSIONS

We have demonstrated that efficient 7-point encoding 4D flow MRI allows the reconstruction of 3 VENCs within the same scan time as an interleaved dual-VENC acquisition. This technique has the potential to push the velocity dynamic range beyond the current limitations in unwrapping algorithms and is a promising extension of 7-point velocity encoding, producing 3 VENCs in the same scan time.

Supplementary Material

supporting material

FIGURE S1 Relationship of the VENCs in triple-VENC encoding. As the high-VENC to low-VENC ratio increases, the iVENC approaches the low-VENC. As the VENCs get closer together, iVENC approaches infinity. The blue dots indicate ratios used in this study

FIGURE S2 Evaluation of dual-VENC and triple-VENC unwrapping algorithms. I, Representative 50/75/150 phase-difference images. All phase-difference images are shown for the same slice location and time point. Both low-VENC (LV) and high-VENC (HV) data show significant velocity aliasing throughout the phantom. The unwrapped dual-VENC (UDV) dataset (B) shows more residual aliasing than the unwrapped triple-VENC (UTV) dataset, which shows successful unwrapping of most voxels, but some residual ones near the vessel wall (red arrows)

FIGURE S3 Rotation phantom consisting of a rotating cylinder and a static ring. Compressed air from an external source and the centrifugal impeller drive the rotation of the inner cylinder. A static ring of gadolinium-doped gel is used for background phase correction. An optical counter with a display screen provides real-time updates on the rotational speed in rotations per minute

FIGURE S4 Brief explanation of gradient polarity flipping for high-VENC > 2*low-VENC. (Refer to Figure 1 in the text for corresponding pulse sequence diagram)

FIGURE S5 Pulsatile flow phantom background phase/eddy-current effects. I, magnitude image of a central slice in the pulsatile phantom (A) with corresponding manually segmented static tissue mask (yellow, B). II, Histograms of pulsatile phantom background phase quantified over a manually segmented static tissue mask. II and III depict histograms without additional offline second-order background phase correction (B,C, left), and the right histograms represent the velocity distribution in the static tissue after background phase correction. Note that after background phase correction, more velocities are corrected toward static 0 m/s velocity; however, the dual-VENC acquisition histogram is wider with less velocities in the most central bins (red arrows). Note that correction for Maxwell terms was performed on the scanner