Unfolded states under folding conditions accommodate sequence-specific conformational preferences with random coil-like dimensions

Significance

The tools of structural biology afford high-resolution descriptions of folded states of proteins. However, an atomic-level description of unfolded states under folding conditions has remained elusive. Challenges arise from the pronounced conformational heterogeneity and the very low population of unfolded states under folding conditions. We have combined a series of time-resolved biophysical experiments with all-atom simulations and polymer theory to obtain a high-resolution description of unfolded ensembles under folding conditions. These unfolded states are characterized by discernible sequence-specific conformational preferences. These preferences are averaged over by conformational fluctuations, giving rise to ensemble-averaged properties that are consistent with those of canonical random coils. Our findings are relevant to understanding functional and pathological interactions involving unfolded forms of proteins.

Abstract

Proteins are marginally stable molecules that fluctuate between folded and unfolded states. Here, we provide a high-resolution description of unfolded states under refolding conditions for the N-terminal domain of the L9 protein (NTL9). We use a combination of time-resolved Förster resonance energy transfer (FRET) based on multiple pairs of minimally perturbing labels, time-resolved small-angle X-ray scattering (SAXS), all-atom simulations, and polymer theory. Upon dilution from high denaturant, the unfolded state undergoes rapid contraction. Although this contraction occurs before the folding transition, the unfolded state remains considerably more expanded than the folded state and accommodates a range of local and nonlocal contacts, including secondary structures and native and nonnative interactions. Paradoxically, despite discernible sequence-specific conformational preferences, the ensemble-averaged properties of unfolded states are consistent with those of canonical random coils, namely polymers in indifferent (theta) solvents. These findings are concordant with theoretical predictions based on coarse-grained models and inferences drawn from single-molecule experiments regarding the sequence-specific scaling behavior of unfolded proteins under folding conditions.

The mechanisms of protein folding remain a topic of intense interest (1–4). Recently, there has been substantial progress in characterizing folding pathways using a combination of novel experimental approaches and improved computational methods (5–7). However, the initial stages of protein folding, specifically the nature of unfolded states under folding conditions, remain a source of controversy, even for simple single-domain globular proteins that undergo an apparent two-state folding transition (8–12). There is convergence regarding the nature of unfolded states under highly denaturing conditions. These states are well described by statistics of self-avoiding walks that are congruent with polymers in good solvents. These highly denatured states are expanded with reduced local and long-range interactions compared with the native state (13, 14). In contrast, the nature of the unfolded state under folding conditions remains enigmatic and the topic of intense debate. A convergent description of unfolded states under folding conditions would be of direct relevance to understanding the mechanisms of protein folding and interactions involving unfolded proteins in cellular settings.

The folded states of globular proteins are typically compact, and their global dimensions are on average well described as polymers in poor solvents (15). Upon dilution from high concentrations of denaturant into native conditions, a foldable yet unfolded and expanded protein must undergo a collapse transition to progress to its compact and folded (native) state (16). Rapid contraction or collapse upon dilution has been observed in refolding experiments for some, but not all proteins (8, 9, 11, 17). Determining the position of the collapse transition along the folding reaction coordinate and characterizing the conformational properties of unfolded ensembles before and following this collapse are essential steps toward deciphering folding mechanisms and for developing a clear understanding of how the amino acid sequence determines the solution behavior of proteins (16).

Proteins are marginally stable molecules. Accordingly, folded and unfolded states are accessible via spontaneous fluctuations even under folding conditions. Fluctuations into and out of unfolded states under folding conditions have been demonstrated using single-molecule spectroscopies (12, 18–22). Further, in physiologically relevant milieus, the interactions within and between unfolded proteins are of functional relevance. These interactions are likely to be influenced by the amplitudes of conformational fluctuations that define unfolded ensembles under folding conditions. As an example, it is now well established that the properties of unfolded states influence the tendencies of proteins to aggregate, and this has important implications for human disease and biotechnology (23, 24). While our focus here is on the unfolded states of foldable proteins, numerous functional proteins are characterized by significant conformational heterogeneity even under native conditions. For these intrinsically disordered proteins (IDPs), a better understanding of the unfolded states under native conditions of intrinsically foldable proteins could provide a set of complementary insights that have the potential of improving our understanding of sequence-to-conformation relationships in systems defined by conformational heterogeneity (25–28).

Under native conditions, the free energy balance strongly favors the folded state. Accordingly, unfolded states are accessible via spontaneous albeit low-likelihood fluctuations (29). Characterization of the resultant low-likelihood states requires the use of methods with high temporal resolution that can “catch” short-lived transitions into and out of the unfolded state. The combination of rapid mixing techniques and spectroscopic measurements has allowed the direct interrogation of unfolded states under near native conditions in the absence of strongly destabilizing mutations (30–32). Small-angle X-ray scattering (SAXS) integrated with stopped-flow or microfluidic mixing has also been used to study the early stages of protein folding upon dilution out of high concentrations of denaturant. SAXS experiments have often, but not always, failed to detect collapse before the folding transition for proteins of <150 residues (9, 11, 33, 34). Förster resonance energy transfer (FRET) experiments, also in combination with stopped-flow or microfluidic techniques, suggest that contraction of the unfolded state can occur before the folding transition (8, 35–38). Single-molecule fluorescence experiments provide the clearest evidence for some proteins undergoing continuous contraction of their unfolded states as a function of decreasing denaturant concentration (19–22, 39–41).

Theoretical studies predict that the nature of the collapse transition is governed by the ratio of the two- to three-body interaction coefficients (42). Below a critical value of this ratio, the collapse transition is abrupt and pseudo-first order. Conversely, above a critical value for the ratio of the two- to three-body interaction coefficients, the collapse transition is continuous and will be governed by sequence-specific interactions (3, 29, 43). While there has been a growing consensus regarding the nature of the unfolded state under native conditions, some experiments have yielded seemingly conflicting views regarding chain compaction. This may reflect the fact that different proteins behave differently, based on the sequence-specific ratio of two- to three-body interaction coefficients. There may also be a contribution from the inherent limitations of each method. SAXS provides a label-free method to obtain insights regarding global dimensions such as R_g, and with high enough signal-to-noise can also provide information about overall shapes and scaling behavior (44–47). However, SAXS also has its limitations: It offers limited structural resolution, requires high protein concentrations, is more sensitive to expanded conformations as a direct consequence of the nature of the averaging involved, and can be insensitive to the presence of low-likelihood, long-range contacts and local structure (48, 49). These limitations are of particular importance when characterizing unfolded proteins under low concentrations of denaturant in equilibrium experiments. Under these conditions the fraction of unfolded proteins is very small and the ensemble averaging inherent to SAXS will prevent the discrimination of subpopulations. An alternative is to perform time-resolved ensemble experiments where the folding time is much longer than the dead time of the experiment—a strategy we pursue in this work.

Single-molecule experiments, especially single-molecule FRET, afford the important advantage of being able to directly access specific pairwise distance distributions—a feature of single-molecule detection (18, 50). This provides a direct way to monitor the evolution of populations of distinct substates in equilibrium experiments as a function of denaturant concentration. In the past, extraction of pairwise distances and global properties from FRET data relied on simple models to translate transfer efficiencies into distances (51–56). Recent advanced approaches have replaced simplified models with sophisticated methods that are aided by atomistic computer simulations and Bayesian methodologies (37, 38, 41, 53, 54). If multiple pairwise interresidue distances can be probed (19, 54), albeit in different constructs, then the discrepant inferences due to the decoupling of end-to-end distances and R_g values that arise due to the heteropolymeric, finite-size nature and the significant contributions from three-body interactions (53, 57) can be overcome to generate coherent insights regarding the dimensions of unfolded polypeptides in the absence of denaturants—a feature that is unique to single-molecule experiments (37, 38, 50, 58). Single-molecule FRET studies do rely on the use of bright dyes, which are invariably large and have large (58) Förster radii (R₀). Appending large dyes connected by flexible linkers might perturb the system and may facilitate dye–protein interactions, although recent work suggests that the effects of dyes are not generic and their sequence-specific interactions can be quantified and accounted for either by changing dyes or by accounting for their effects in data analysis (37, 53, 57–60).

To obtain a high-resolution description of the unfolded state under native conditions we pursued a different approach that combined minimally invasive, time-resolved FRET with time-resolved SAXS, all-atom simulations, and analyses guided by polymer theory. The N-terminal domain of the ribosomal protein L9 (NTL9) was used as a model system, as it shows well-defined two-state folding behavior and has been extensively characterized in the context of protein folding (7, 48, 61–63). NTL9 is 56 residues long and is one of the simplest examples of a common α–β fold (Fig. 1A). The domain has been shown to contain residual structure in the unfolded state populated under native conditions (62, 63). We monitored chain contraction in real time using a sensitive and minimally perturbing FRET method that exploits p-cyanophenylalanine (F_CN) and Trp residues as FRET pairs. F_CN is the cyano analog of Tyr and it represents a minimal perturbation to the original sequence, thus making it unlike large dyes used in single-molecule experiments. F_CN acts as the donor to Trp with an R₀ of 16 Å (64). The residue can be incorporated into proteins using solid-phase peptide synthesis or recombinantly using the 21st pair technology of Schultz and Mehl (65, 66). F_CN fluorescence can be excited selectively in the presence of Trp and Tyr and the fluorescence decay of F_CN is single exponential, facilitating the analysis of time-resolved studies.

Fig. 1.

The structure of NTL9 and the accuracy of distance calculations in the folded state. (A) Ribbon diagram of NTL9 native state (PDB code: 2HBB) showing the location of Trp-25. The N terminus is labeled. (B) The FRET-derived distances for the native state of NTL9 compared with the ring-to-ring distances taken from the crystal structure, demonstrating the precision with which distances can be determined by Phe_CN-Trp FRET. Error bars were determined by rigorous error analysis (SI Appendix). Both continuous-flow and equilibrium data are reported. (C) Primary sequence of NTL9. (C, Bottom, first row) The location of Tyr-25, which was mutated to Trp for FRET studies, is shown in red and the location of the five F_CN substitutions which are paired with Trp-25 is colored blue. (C, Bottom, second row) Residues 2 and 33 as well as residues 2 and 51 were used to prepare additional F_CN–Trp pairs and the position of these Trp residues is colored green. (C, Top) The schematic diagram above the sequence illustrates the secondary structure.

We used time-resolved FRET to measure multiple pairwise distance distributions for the unfolded state populated under strongly denaturing conditions [10 molar (M) urea] and under native conditions (1 M urea). Continuous-flow methods interfaced with time-resolved detection were used to measure pairwise distance distributions for the unfolded protein in 1 M urea, after rapid dilution out of high denaturant. The FRET studies were complemented by continuous-flow SAXS measurements by leveraging the fact that the folding time for NTL9 is on the order of 2.4 ms, while the dead times for FRET and SAXS measurement are 40 μs and 200 μs, respectively. Finally, a globally consistent ensemble of conformations was generated using all-atom simulations. The data reveal that for NTL9, modest contraction occurs rapidly, on a timescale that is faster than that of folding. The global ensemble-averaged dimensions of the chain are consistent with those of a finite-sized Flory random coil, i.e., a flexible polymer in an indifferent or theta solvent. Despite this statistical feature, the ensembles accommodate long-range interactions and fluctuations into and out of native and nonnative elements of structure. These structural preferences are more persistent than the corresponding contacts sampled in high concentrations of urea (48). This study highlights the power of minimally perturbing fluorescence probes for following rapid conformational changes and the importance of combining multiple pair positions as well as methods to construct accurate descriptions of conformational properties of unfolded ensembles.

Results

The folding time constant of wild-type NTL9 in 1 M urea, pH 5.5, is 2.4 ms, allowing much of the folding process to be accessed using continuous-flow methods. To obtain a high-resolution description of the unfolded state, we introduced a series of point mutations that allowed us to obtain pairwise distance distributions using data from FRET measurements.

Mutations to Introduce FRET Pairs Are Minimally Perturbing to Stability and Folding Rates.

A set of seven variants of NTL9 containing F_CN and Trp were prepared using 21st pair technology. The native Tyr at position 25 was replaced by Trp and F_CN sites were selected to probe a range of through-space distances and to ensure that FRET pairs span a range of sequence separations (Fig. 1C). The Trp and F_CN residues are on the surface of the protein. The sequence separation between donor and acceptor varies from 8 to 49 residues, while the distance between the sites (C_β–C_β) varies from 8 Å to 21 Å in the native state. All seven mutants were well folded, displayed sigmoidal unfolding profiles as a function of denaturant, and showed similar circular dichroism (CD) profiles to that of the wild-type protein (SI Appendix, Figs. S1 and S2 and Tables S1–S4). The folding rate of each mutant was comparable to the wild-type rate (SI Appendix, Table S5). The distances derived from equilibrium FRET measurements of the folded protein under native conditions show nearly perfect agreement with the expected distances derived from the crystal structure (Fig. 1B and SI Appendix, Tables S6–S8), demonstrating that the dyes do not perturb the tertiary structure of the folded state of NTL9. The analysis also shows that precise and accurate distance information can be derived from the FRET studies. These data confirm that the dyes are minimally perturbing and are useful as probes for the evolution of through-space distances.

The Unfolded State Is Expanded in 10 M Urea.

We first characterized the equilibrium folded- and denatured-state ensembles under 1 M urea and 10 M urea, respectively. This helps establish baselines for comparisons to data collected in continuous-flow mode. Measurements for the folded state were made in 1 M urea since this corresponds to the final conditions in the continuous-flow mixing studies and represents a facsimile of native conditions inasmuch as the protein population is greater than 99% folded (SI Appendix, Fig. S1). The fluorescence lifetime data were fitted to extract distance distributions between donor and acceptor in the folded state and in the high urea unfolded state (Fig. 2 A and B and SI Appendix, Fig. S3). Interresidue distance distributions in the folded state were fitted to a Gaussian distribution. These distributions are, in general, narrow (Fig. 3 and SI Appendix, Table S6) and they agree well with the distances expected from the crystal structure (Fig. 1B). The highly denatured state ensemble was fitted separately to both a Gaussian distribution and a wormlike chain (WLC) model with diffusion, with both methods yielding nearly identical results (SI Appendix, Tables S9 and S10). The distance distributions for the denatured state ensemble in 10 M urea are much broader and show a monotonic increase in mean distance vs. sequence separation. This is to be expected for an expanded chain in high denaturant (Fig. 4).

Fig. 2.

Representative fluorescence lifetime measurements. Data are shown for the F_CN10–W25 pair. For A and B, fits to donor-only curves are in blue, and fits to donor plus acceptor are in red. Residuals are shown below. (A) Equilibrium data in 10 M urea. (B) Equilibrium data in 1 M urea. In C and D, continuous-flow fluorescence decays as a function of folding time are shown. Decays were fitted globally to a two-population model. (C) Donor only. (D) Donor/acceptor. F_CN was preferentially excited at 240 nm and fluorescence was detected by utilizing a Semrock 292/27 bandpass filter, which has a bandwidth of 27 nm centered at 292 nm. Donor-only decays (A and B, blue) were fitted to a double-exponential model reconvoluted with the instrument response function. The donor/acceptor decay in 10 M urea (A) was fitted using a wormlike chain model with a parameter for diffusion. The donor/acceptor decay in 1 M urea (B) was fitted to a Gaussian distribution. Donor/acceptor decays from continuous-flow experiments were fitted globally using a Gaussian distribution for the folded state and a wormlike chain model, with a parameter for diffusion between donor and acceptor during the fluorescence lifetime, for the unfolded state.

Fig. 3.

(A–F) FRET provides evidence for compaction. Ribbon diagrams illustrating the location of the FRET pairs are shown together with the distance distributions. Red, unfolded state in 10 M urea; green, unfolded state in 1 M urea; black, folded state in 1 M urea. The folded and unfolded distributions in 1 M urea were extracted from the global fit to the FRET data. The unfolded-state distance distribution was modeled using a wormlike chain with a parameter for diffusion between donor and acceptor during the fluorescence lifetime, while a Gaussian distribution was used to model the folded-state distribution.

Fig. 4.

The 1-M unfolded state is more compact than the 10-M unfolded state. The unfolded state is expanded in high denaturant but is more compact in low denaturant, as quantified by average through-space distances between pairs of residues as a function of sequence separation. The folded state and the unfolded ensemble in 1 M urea both show a nonmonotonic relationship between sequence separation and spatial separation, while the 10-M urea ensemble shows a monotonic increase in distance with sequence separation. See SI Appendix, Fig. S7C for the same data which include standard polymer models.

The Unfolded-State Ensemble Under Folding Conditions Is Contracted Compared with the Denatured State in 10 M Urea.

We performed fluorescence lifetime measurements in combination with continuous-flow mixing to enable the collection of fluorescence decays as a function of refolding time (Fig. 2 C and D and SI Appendix, Fig. S4). We observed chain contraction within the dead time of the instrument, indicating that contraction occurs on a timescale that is considerably faster than that of folding. Singular-value decomposition (SVD) analysis yields a maximum of two components, the amplitudes of which can be fitted to a single exponential model. This is consistent with two-state folding (SI Appendix, Fig. S3) and it allowed us to perform a global analysis using a two-state model. A Gaussian distribution was used to describe the folded state and either a WLC model or a Gaussian distribution was used for the unfolded state. Both models indicate contraction of the unfolded state upon dilution to 1 M urea. Most notably, the two pairs at greatest sequence separation (F_CN2-Trp25 and F_CN2-Trp33) suggest a 40% contraction of the unfolded state in 1 M urea relative to the 10 M urea unfolded state. The degrees of contraction suggested by the other FRET pairs range from 12% to 31% (SI Appendix, Tables S11–S13). Since highly denatured proteins are well described by the physics of polymers in good solvents, we asked whether similar polymer models would be able to describe the unfolded state under native conditions.

Fig. 4 describes the relationship between sequence separation and spatial separation for the protein in 1 M and 10 M urea, respectively. In 10 M urea the pairwise-distance profiles are largely consistent with that of a polymer in a good solvent, with a monotonic increase in spatial separation with increasing sequence separation. In contrast, in 1 M urea the distances show a nonmonotonic increase with sequence separation. In fact, we observed a stronger correlation between the distances from the 1-M unfolded state and the folded state than between the unfolded states in 1 M and 10 M urea (Pearson r = 0.73 vs. 0.62). Importantly, the nonmonotonic changes in intermolecular distances with sequence separation would, on the surface, seem to be inconsistent with the fractal behavior that is expected of homopolymers in good or indifferent (theta) solvents.

Continuous-flow SAXS data were also collected for wild-type NTL9. A major challenge with these experiments originates from the small dimensions of the protein and the presence of urea, meaning the contribution of the protein to the total scattering is low. The R_g value of NTL9 in 10 M urea was determined from equilibrium experiments to be 23.5 ± 0.7 Å, which agrees with prior equilibrium SAXS studies of the urea-unfolded state (48). The measured R_g value for the folded state in 1 M urea is 12.8 ± 0.2 Å. For comparison, the R_g for the unfolded state in 1 M urea is 19.1 ± 0.9 Å (Fig. 5). This is indicative of ∼20% contraction upon dilution out of high denaturant. The Kratky plot for the folded state shows a peak that is characteristic of compact globules (SI Appendix, Fig. S5). Conversely, a monotonic increase with increasing scattering angle is seen for the unfolded state in 10 M urea, indicating a highly expanded chain (SI Appendix, Fig. S5). Similar behavior has been observed for other globular proteins in high concentrations of urea and for IDPs with high proline and/or charge contents (67–69). The Kratky plot for the unfolded protein in 1 M urea is very different, and a plateau is observed at increasing q values, indicating a fundamentally different ensemble from the highly denatured state ensemble.

Fig. 5.

Guinier analysis of SAXS data. (A) Continuous-flow data for the native state in 1 M urea. (B) Continuous-flow data for the unfolded state in 1 M urea. (C) Equilibrium data for the unfolded state in 10 M urea. Data were also analyzed using an independent empirical molecular form factor, which yielded near identical results (SI Appendix, Table S15). (D) Comparison of average radii of gyration across the folded and unfolded states. Error bars are those calculated from the Guinier fits.

All-Atom Simulations Show That SAXS and FRET Measurements Yield Mutually Consistent Results.

At first glance, the time-resolved FRET and SAXS results for NTL9 in 1 M urea might appear to point toward conflicting views of the unfolded state under folding conditions. The FRET data may be interpreted to imply a substantial collapse and/or the presence of interactions that cause significant deviations of intrachain distances from the expected behavior for polymers in theta or good solvents. In contrast, SAXS results demonstrate modest contraction, and given that the R_g value is considerably higher than that of the folded protein, the data are inconsistent with a sharp collapse of the unfolded states. To make sense of the totality of the data, we used all-atom Metropolis Monte Carlo simulations with the ABSINTH implicit solvent model to generate a series of unfolded-state ensembles. We used these simulations to assess the mutual compatibility of results from FRET vs. SAXS experiments. The atomistic descriptions used in these simulations allow us to preserve the sequence-specific interactions that give rise to heterogeneous contact patterns (below) that are easily glossed over if one were to use coarse-grained, single bead per residue descriptions. Importantly, these simulations capture the sidechain-specific backbone conformational preferences and they enable the explicit inclusion of the interplay between two- and three-body interactions, which are nonexistent in preparameterized coarse-grained models.

We generated a set of unfolded-state ensembles for NTL9 at different simulation temperatures. We previously used this approach to show that the ensemble generated at 390 K serves as a good proxy for the solution behavior of NTL9 in 8 M urea (48). Accordingly, we sought to identify an ensemble where the derived C_β–C_β pair distance distributions taken from the set of donor/acceptor pairs used for FRET matched the experimentally obtained distance distributions. While several ensembles yielded pair distance distributions that were qualitatively similar to the FRET distance distributions, none were quantitatively identical. To alleviate this issue we used a χ² minimization and entropy maximization approach (COPER) to reweight each ensemble to match the FRET data for the unfolded state in 1 M urea (70). We then selected the reweighted ensemble that maximized the ensemble entropy while generating the best agreement with the FRET data (see SI Appendix for further details). Reweighting was performed based on C_β–C_β distances extracted from the simulated ensembles and distances extracted from analysis of the FRET experiments.

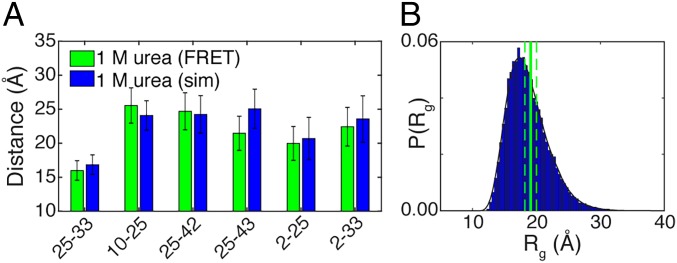
The ensemble that best fitted the data while undergoing minimal perturbations was generated by reweighting the unfolded ensemble generated at 375 K (Fig. 6A and SI Appendix, Fig. S6). An independent assessment of the accuracy of this ensemble comes from the observation that the mean R_g obtained from this reweighted ensemble (referred to hereafter as the 1 M urea unfolded-state ensemble) is 18.9 Å, which agrees very well with the value for R_g derived from the SAXS data (19.1 Å, Fig. 6B). Furthermore, a formal comparison between the scattering profile from the simulation of the 1 M urea unfolded-state ensemble and that from the experimentally measured unfolded state in 1 M urea shows good agreement (SI Appendix, Fig. S5). It is worth emphasizing that the SAXS data were not used to obtain the optimized unfolded-state ensembles, yet reweighting improves the χ² of the 375-K ensemble with respect to the full scattering curve, formally demonstrating that reweighting using data from our FRET measurements enhances agreement between simulations and SAXS. Our results indicate that inferences based on FRET and SAXS data do in fact yield mutually consistent descriptions for the unfolded-state ensembles.

Fig. 6.

Comparison between experimental results from the 1-M urea unfolded state and the 375-K reweighted ensemble (unfolded-state ensemble in 1 M urea). (A) Intrachain distances obtained from FRET experiments (green) compared with the C_β–C_β distance extracted from the unfolded ensemble (blue). The error bars reflect the SDs of the underlying distribution associated with each measurement. (B) Radius of gyration obtained from SAXS with error bars compared with the distribution of radii of gyration obtained from simulation. The simulation data in both A and B were extracted from the same ensemble, demonstrating that FRET, SAXS, and simulation are mutually compatible.

The Unfolded-State Ensemble Under Folding Conditions Contains Extensive Native and Nonnative Interactions.

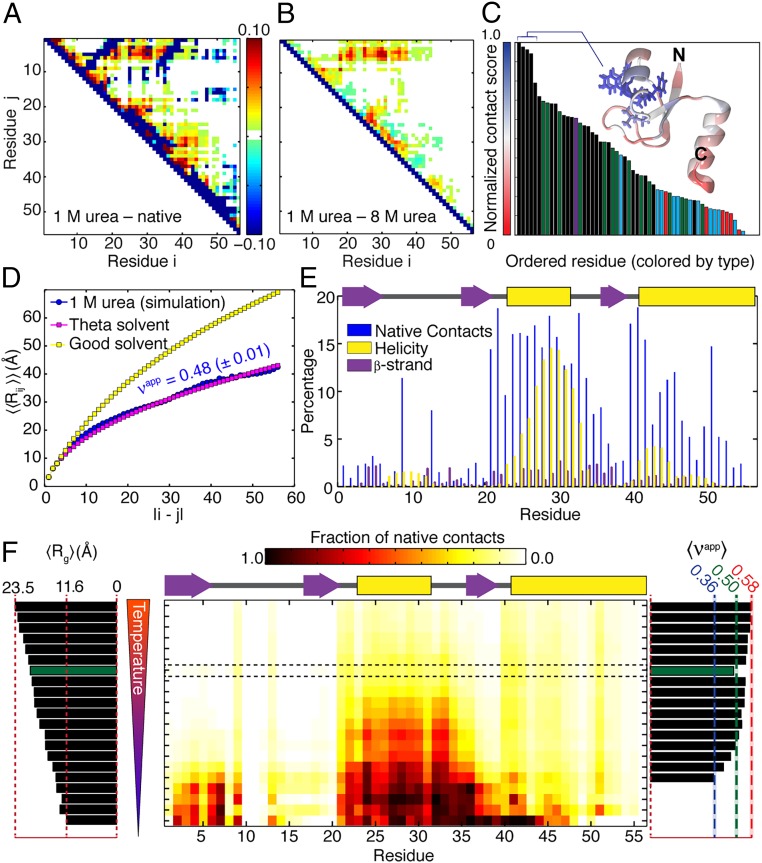
The computationally derived atomic-level description of the ensemble for the unfolded state in 1 M urea correctly reproduces the FRET and SAXS results, suggesting that it represents a reasonable, high-resolution description of the unfolded ensemble under folding conditions for NTL9. Accordingly, we examined additional features within the ensemble to gain insights regarding conformational features of the unfolded state under folding conditions. The ensemble is characterized by the presence of native and nonnative contacts, as shown in Fig. 7 A and E. Pairwise contacts primarily involve hydrophobic residues (Fig. 7C), with a notable local cluster formed by aromatic and hydrophobic residues around residue 30. The ensemble also accommodates the formation of secondary structure (Fig. 7E) and long-range interactions that have finite likelihoods associated with them (Fig. 7B). These features have higher probabilities of being observed compared with the ensemble generated to match data for NTL9 in 8 M urea (Fig. 7B). Unfolded-state ensembles under refolding conditions show a significant increase in the extent of native and nonnative structural preferences while remaining expanded (Fig. 7F). Taken together, these results indicate that the unfolded state under refolding conditions can accommodate pronounced sequence-specific native and nonnative conformational and structural preferences that are enhanced compared with the highly denatured-state ensembles.

Fig. 7.

Simulation results and analysis using polymer theory reveal the details of the unfolded state under refolding conditions. (A) Difference contact map generated by taking the 1-M urea ensemble contact map and subtracting the native-state contact map. Positive values correspond to nonnative interactions, while negative values reflect missing native contacts. (B) Difference contact map generated by taking the 1-M urea ensemble contact map and subtracting the 8-M urea contact map (48). Positive values correspond to contacts observed at 1 M urea that are not observed under strongly denaturing conditions. Specifically, we observe extensive contacts involving a cluster of N-terminal hydrophobic residues (V3, I4, F5, L6) and a cluster of central hydrophobic residues (F29, L30, F31). (C) The normalized per-residue contact score reflects the extent to which each residue is in direct contact with any other residue. Intramolecular interactions are driven by hydrophobic and aromatic residues, as shown by ordering all residues and coloring by their physicochemical properties (black, hydrophobic/aromatic; green, polar; purple, proline; blue, positive; red, negative). In particular, a cluster of hydrophobic residues (F31, F29, L30, Y25, L35) engages in extensive intramolecular interactions in the unfolded state and forms a hydrophobic cluster in the native structure. (D) Comparison of internal scaling profiles for NTL9 in a good solvent (yellow), in a theta solvent (pink), and from the 1-M urea ensemble (blue). In a globally averaged analysis, the 1-M urea ensemble shows scaling behavior consistent with a polymer in a theta solvent with an apparent scaling exponent of 0.48 ± 0.01, despite the presence of local structure and long-range interactions. (E) Presence of native contacts and secondary structure in the 1-M urea unfolded-state ensemble. The native-state secondary structure map is shown above for reference. (F) For denatured-state ensembles generated between 500 K and 280 K we quantify ensemble-averaged radius of gyration (Left), the residue-specific density of native contacts (Center), and apparent scaling exponent $\nu$^app (Right). The reweighted ensemble is highlighted in the dashed box and with green bars.

Ensemble-Averaged Conformational Properties of Unfolded-State Ensembles Under Native Conditions Are Concordant with Random Coils in Theta Solvents.

For flexible homopolymers, a scaling exponent $v$ quantifies the length scale for correlations among fluctuations between pairs of interresidue distances. The value of $v$ depends on solution conditions. It quantifies the interplay between intrachain and chain–solvent interactions and is governed by the correlation length for conformational fluctuations and the distance to the theta point. Given the connection between interresidue distances and R_g, it follows that the R_g value and degree of polymerization (chain length) are related by a simple scaling relationship of the form

$$\sqrt{\langle R_g^2\rangle }=R_0{N}^v.$$ [1]

Here, $\langle R_g^2\rangle$ is the mean-squared radius of gyration, N is the number of residues in the protein, and R₀ is a prefactor that is determined by the average strength of solvent-mediated interresidue interactions, the thickness of the chain, and the average size of an individual residue. Note the R₀ in this context is not the Förster radius.

In a poor solvent, ν = 1/3 with chain–chain interactions being preferred over chain–solvent interactions, leading to compact and globular ensembles (71). In a theta solvent, polymer–polymer and polymer–solvent interactions are counterbalanced and $v$ = 1/2, leading to large conformational fluctuations and a maximally heterogeneous ensemble (72). A chain in a theta solvent behaves as a Flory random coil (73). In a good solvent, $v$ is ∼3/5 and the chain is highly expanded due to favorable chain–solvent interactions. Under strongly denaturing conditions proteins show global dimensions consistent with a chain in a good solvent, while folded proteins can, on average, be described by a scaling relationship consistent with a chain in a poor solvent (13, 15, 16, 48). These scaling relationships describe the behavior of infinitely long homopolymers, although they are often used to characterize finite-sized heteropolymeric sequences (19, 27, 37, 38, 41, 45, 48, 53, 74–77). Consequently, for finite-sized heteropolymers we recast $v$ to be $v$^app, which we define to be an apparent scaling exponent that best describes the apparent correlation length for a heteropolymer sequence of a specific, finite length that is at a certain distance from the theta temperature. We stress that the value of $v$^app should not be conflated with well-established universal exponents, which are fixed points for infinitely long homopolymers.

We analyzed the scaling of interresidue distances as a function of sequence separation (Fig. 7D). This scaling behavior was compared with the scaling profile extracted from simulations of NTL9 in a bona fide theta solvent, i.e., Gaussian chain, in which all interresidue interactions are explicitly turned off and the intrinsic conformational preferences are modeled using a specific implementation of Flory’s rotational isomeric approximation (27). Interestingly, despite the discernible presence of local structure and nonlocal interactions, the scaling profiles calculated for the unfolded-state ensemble in 1 M urea are consistent with that of a polymer in a theta solvent, with an apparent scaling exponent of $v$^app = 0.48 (Fig. 7D). This result implies that conformational fluctuations lead to a screening whereby the effects of intrachain attractions and repulsions counterbalance one another, on average, to yield an ensemble that has the statistical features of a finite-sized homopolymer in an apparent theta solvent. Fluctuations into and out of specific types of local secondary structures and the sampling of specific patterns of local and nonlocal contacts highlight the contributions of sequence-specific effects in the unfolded ensemble. The amplitudes of and correlations among conformational fluctuations within the ensemble will lead to a counterbalancing of intrachain repulsions by attractions and vice versa. As a result, the internal distance distributions and the overall dimensions end up in the same universality class as infinitely long homopolymers in theta solvents. In summary, the observed congruence between the Flory random coil and the unfolded-state ensemble in 1 M urea is a form of screening that is achievable in polymers whereby overcompensatory conformational fluctuations screen one another, leading to ensemble averages that are concordant with properties of canonical random coils.

We compared our results here with those from previous studies to show that the unfolded state of NTL9 under folding conditions undergoes a modest contraction as a function of decreasing urea concentration. We reach this conclusion by comparing the R_g values of 23.5 Å in 10 M urea and 21.3 Å in 8 M urea to the R_g value of 19.1 Å in 1 M urea (Fig. 8A) (48). The relative extent of contraction from high to low concentrations of urea is 19%. This level of contraction is consistent with values reported previously for ACTR (18%), R17 (23%), and ubiquitin (16%) (SI Appendix, Table S16) (9, 37, 38). The R_g values obtained for NTL9 in 10 M, 8 M, and 1 M urea are well described by simulations, from which additional parameters such as the scaling exponent and end-to-end distance can be directly calculated. For highly denatured states in 10 M and 8 M urea, the R_g value can also be accurately inferred from the end-to-end distance (Fig. 8A). However, for the unfolded state under folding conditions the R_g inferred from the end-to-end distance underestimates the true R_g. Similarly, if we estimate ν^app by extrapolating from the global dimensions assuming a fixed prefactor (SI Appendix, SI Materials and Methods) or by directly calculating from simulations, we obtain good agreement under denaturing conditions, but a range of values for the unfolded state under folding conditions (Fig. 8B). These results are consistent with a general model in which sequence-specific interactions introduce significant deviations from idealized homopolymer models under native conditions, whereby the end-to-end distance and R_g can become decoupled for finite-sized heteropolymers that are not approximated as bead-spring polymers. This raises a cautionary note about using generic conversions between R_g and end-to-end distance based on observations for homopolymers in theta or good solvents or relying on simulations that map proteins to equivalent homopolymers (53, 55, 56) or coarse-grained heteropolymers. In contrast, under strongly denaturing conditions, the strong and approximately sequence-independent solvent–chain interactions overpower sequence-specific intrachain interactions such that homopolymer models appear to be effective and appropriate models for describing polypeptides.

Fig. 8.

The unfolded-state ensemble (USE) undergoes a continuous reduction in chain dimensions as a function of decreased denaturant concentration. (A) SAXS shows a continuous reduction in chain dimensions (red triangles), a trend that is matched by simulated unfolded-state ensembles. The ensemble-averaged R_g can be estimated from the end-to-end distance, assuming $R_g=\frac{R_e}{\sqrt{6}}.$ This approximation works reasonably well under strongly denaturing conditions but underestimates the R_g under native conditions. (B) ν^app can be estimated from global dimensions or calculated directly from the unfolded-state ensemble. As with R_g, these approximations for ν^app work well under strongly denaturing conditions, but under native conditions a range of ν^app values are obtained.

Discussion

Our work provides a high-resolution description of the unfolded state of NTL9 under refolding conditions. This is obtained through a combination of multiple, minimally invasive FRET probes in time-resolved FRET measurements, time-resolved SAXS, all-atom simulations, and polymer theory. Taken together, our results demonstrate that the unfolded state under refolding conditions is more compact than the fully denatured state, but still relatively expanded vis-à-vis the folded state. The unfolded state under refolding conditions is conformationally heterogeneous and is characterized by the formation of secondary and tertiary structures of the native and nonnative variety. Interresidue contacts are congruent with inferences from experiments, suggesting the importance of electrostatic and hydrophobic interactions in the unfolded state of NTL9 under highly denaturing and near native conditions (48, 78). The unfolded ensemble contains residual native helical structure in regions corresponding to the first and second α-helices. Experiments performed on peptide fragments corresponding to the first and second α-helices have shown that the second helix partially forms in isolation while the first one does not (79). Helical structure in the C-terminal helix thus requires only local contacts to form, while the first helix appears to be stabilized by tertiary interactions.

Udgaonkar and coworkers (80–83) have followed the evolution of multiple pairs of interresidue distances as a function of denaturant, using the quenching of Trp fluorescence by DTNB, and arrived at conclusions that support continuous contraction as a function of dilution from denaturant. Although the short R₀ of the F_CN-Trp pair may be considered a drawback for some applications, in the current study it offers the advantage of allowing accurate distances to be determined (Fig. 1) (53). The attachment of large fluorescent dyes to single-domain proteins has led to the oft-quoted concern that fluorophores must be inducing chain collapse (84). While the impact of dyes on the unfolded state will undoubtedly be a function of the physicochemical properties of the dyes and the specific sequences in question, our studies demonstrate that contraction of the unfolded state is observed even when using minimally perturbative probes—a finding that is concordant with observations made in single-molecule studies using larger dyes (19).

The distinctive nature of the unfolded state populated under native conditions is shown by the nonmonotonic relationship between sequence separation and spatial separation in Fig. 4. This behavior highlights the importance of probing multiple regions within the chain to obtain a more complete description of the ensemble (38). By combining multiple FRET pairs, each of which queries a relatively short distance, we have been able to construct a high-resolution and consistent description of the unfolded-state ensemble in 1 M urea. It has been proposed that hydrophobic clusters of Leu, Ile, Val, and Phe occur in the unfolded state because they are formed early in folding (85). Consistent with this hypothesis, we identified a specific cluster of residues that appear to form extensive native and nonnative contacts (Fig. 7C). Similarly, two clusters of hydrophobic residues separated in sequence by ∼25 residues engage in long-range contacts in the unfolded state. These residues also form a contiguous cluster in the folded core (residues 3–5 and residues 29–31) (Fig. 7B). Studies have reported that certain nonnative interactions can lower the free energy barrier for folding and increase the folding rate, that nonnative contacts can act to constrain the formation of native contacts, and that they may modulate folding rates without influencing the mechanism (86–91). Nonnative interactions involving hydrophobic residues may also reduce the likelihood of these residues forming intermolecular interactions that can lead the protein to aggregate.

Recent work has suggested that the unfolded state under folding conditions behaves as a polymer with an apparent scaling exponent of 0.54 (45). The unweighted simulated unfolded ensemble for NTL9 at 375 K (the ensemble that, before reweighting, most closely matched the FRET distances) has a scaling exponent of 0.55. However, upon reweighting to achieve congruence with the totality of the FRET data, the apparent scaling exponent drops to 0.48. This ensemble also reproduces the R_g value measured using SAXS. The apparent scaling exponent for the ensemble that matches all of the experimental data is actually in closer agreement to the value of 0.45 ± 0.03 from work by Hoffmann et al. (19). This is noteworthy because the scattering profiles calculated using the weighted and unweighted ensembles are essentially identical to one another (SI Appendix, Fig. S5G). Therefore, despite a minor change between the unweighted and reweighted ensembles, we observe a shift of ∼0.07 in the apparent scaling exponent. This observation highlights the fact that relying exclusively on scattering profiles can yield incomplete insights because the overall profile is insensitive to the effects of fluctuations and low-likelihood contacts. These can be gleaned only by directly probing contacts or preferred distances across multiple length scales without the confounding effects of averaging across all of the distances that happen in SAXS. In the context of our studies, values of 0.48 and 0.55 for the apparent scaling exponent are almost indistinguishable from one another as evaluated by different metrics for probing interresidue contacts and distances (Fig. 8). Moreover, differences in the methods used for estimating $v$^app from simulations can introduce differences of ±0.05, while assumptions made for estimating this value using experimental data can have similar consequences. Our results here and elsewhere paint a picture in which polypeptides with $v$^app between 0.45 and 0.55 are consistent with expanded, heterogeneous ensembles with ensemble-averaged properties being congruent with polymers in theta solvents while supporting the presence of extensive, sequence-specific local and long-range interactions. We propose that it is erroneous to assert very precise universal values for $v$^app because the inferred value for $v$^app is influenced by the resolution of the experimental techniques used and by underlying assumptions regarding polymer behavior that one makes to analyze the acquired data. In a similar vein, while we (and others) have found a modest contraction of the unfolded-state ensemble from high to low denaturant of around 20%, we do not necessarily expect this value to hold true for every protein, since sequence-specific effects will determine the consequences of the interplay between intrachain and chain–solvent interactions, an expectation borne out in numerous experimental examples (19, 27, 37, 41, 53, 92–94).

Conclusions

The combination of multiple time-resolved FRET, time-resolved SAXS, and computational results shows that the unfolded state under folding conditions is conformationally heterogeneous; certain regions of the protein undergo significant collapse while others remain relatively expanded. The overall ensemble-averaged properties such as the scaling of internal distances, the dimensions of the unfolded state under folding conditions, and the inferred apparent scaling exponent are concordant with properties of polymers in theta solvent. Similar results have been reported for several other proteins that were studied using single-molecule FRET and/or SAXS (37, 38, 95). However, the observation that the global dimensions of the unfolded ensemble for NTL9 in 1 M urea resemble those of chains in theta solvents does not mean that unfolded ensembles are ideal chains devoid of long-range interactions. The Flory-style models provide a way to describe the endpoint of conformational averaging and they say nothing about how the averaging actually comes about. Further, the results presented here highlight the difficulty in using inferred apparent scaling exponents as the sole device for defining the properties of unfolded states. Our results suggest that the apparent scaling exponent of ν^app = 0.48 is the result of counterbalancing the effects of intrachain repulsions. This is evident in the observation of segment-specific expansion coexisting with segment-specific contraction. The former should result from intrachain repulsions whereas the latter should result from intrachain attractions. It seems plausible that unfolded states characterized by amplitudes of and correlations among conformational fluctuations that are reminiscent of polymers in theta states may facilitate the search for the folded state more effectively than an expanded self-avoiding random walk or compact globular ensemble that hinders conformational diffusion (16, 19, 72, 96, 97). Our ability to uncover atomistic descriptions of unfolded ensembles under folding conditions opens the door to designing features into unfolded states without impacting the properties of folded states to interrogate the effects of such designs on folding, function, and cellular phenotypes.

Materials and Methods

Preparation and Characterization of p-cyanoPhe-Labeled NTL9.

Seven distinct variants of NTL9 containing F_CN and Trp were designed and generated. Matrix-assisted laser desorption ionization time-of-flight (MALDI-TOF) mass spectrometry was used to confirm the molecular weight of each species (SI Appendix, Fig. S8). Variants containing the donor only and the donor in the presence of acceptor were prepared recombinantly using 21st pair technology developed by the Schultz and Mehl laboratories. All of the mutants are folded as judged by CD, are minimally destabilized compared with the wild-type protein, and display sigmoidal unfolding transitions (SI Appendix, Fig. S1 and Tables S1–S4). The stability measurements demonstrate that F_CN is a minimally perturbative substitution in NTL9, not only for Tyr and Phe, but also for Lys and Gln. Only one of the variants, N43F_CN, is destabilized by >1 kcal/mol relative to wild type; however, the CD spectrum of this mutant is very similar to that of wild-type NTL9, indicating that overall native secondary structure is not perturbed. Observed relaxation rates in 1 M urea were determined for the variants from continuous-flow experiments and do not deviate significantly from that of the wild-type protein (SI Appendix, Fig. S3 and Table S5).

Analysis of Time-Resolved FRET Data.

The folded-state fluorescence lifetime data were fitted using a Gaussian distribution, where the mean distances range from 8 Å for the 33F_CNTrp25 pair to 21 Å for the 42F_CNTrp25 and 25F_CNTrp33 pairs. The high-denaturant unfolded state was fitted separately using a Gaussian distribution and a WLC model, taking into account diffusion during the excited-state lifetime (SI Appendix, Tables S9 and S10). Both models have been used to fit FRET data, but our results here show no dependence on which of the models is used, providing confidence that the underlying model is not biasing the derived distances (51, 52, 98).

SVD analysis of the continuous-flow data in 1 M urea gives a maximum of two components along both the folding and the time-correlated single-photon counting (TCSPC) axis. The amplitude of the major and minor SVD components along the folding time axis fitted well to a single exponential model, consistent with two-state folding (SI Appendix, Fig. S3). This allowed us to globally analyze the continuous-flow data using a two-population model, folded and unfolded. The observation that the data are well fitted using two SVD components does not mean that the unfolded-state properties are independent of urea, and clear differences between the 10-M and 1-M unfolded states are observed. As before, the unfolded states were fitted using a Gaussian distribution and the WLC model with diffusion. The WLC model contains only the amplitude and persistence length as fitting parameters and this allows a diffusion parameter to be introduced without overparameterizing the fits. Although the absolute value of the distances is slightly different between the Gaussian distribution and WLC models, fits to both models with and without diffusion indicate significant compaction of the protein upon dilution out of high denaturant. The greatest extent of collapse is seen for the two variants that probe the largest sequence separation, 2–25 and 2–33 (Fig. 3). The mean distance in the unfolded state derived from WLC analysis of the F_CN2–Trp25 pair is 36.5 Å in 10 M urea and 21.4 Å in 1 M urea, while the mean distances observed for the F_CN2–Trp33 pair are 40.1 Å in 10 M urea and 24.1 Å in 1 M urea. For additional information on the details associated with the fitting and interpretation of FRET data, please see SI Appendix.

Recording and Analysis of Time-Resolved SAXS Data.

Four refolding experiments were performed and averaged in the analysis. The earliest time point included in the analysis was 200 µs. Scattering curves as a function of refolding time were fitted globally to a two-state kinetic model and extrapolated to time = 0 and time = ∞ to determine the scattering curve for the unfolded and native states, respectively. The population of folded molecules in 8 M urea was accounted for in the analysis. The pair distribution function, P(r), for the folded and unfolded states in 1 M urea was also determined (SI Appendix, Fig. S5).

Generation, Reweighting, and Analysis of Denatured-State Ensembles.

Starting from the NTL9 crystal structure we generated 22 unconstrained ensembles for a range of temperatures (240–500 K) and then filtered out conformations where more than 50% native contacts were observed to ensure we had true “denatured-state” ensembles (SI Appendix, Table S14). To generate each ensemble, 10 independent simulations were run for 8 × 10⁷ Monte Carlo steps, with the first 2 × 10⁷ steps discarded as equilibration. To ensure the reproducibility and convergence of simulations, we compared two sets of 40 simulations, with each set started either from the folded state or from a randomly generated unfolded state (80 simulations total). The ensemble averages computed across the different sets were similar to one another, thus highlighting the high quality and convergence of Monte Carlo importance sampling (SI Appendix, Fig. S9).

Polymer Scaling Analysis in Finite Chains.

The apparent scaling exponent (ν^app) was estimated by fitting the results of simulations using the following expression:

$$\ln \left(\sqrt{{\langle r_{ij}\rangle }^2}\right)={\nu }^{\text{app}}\ln \left(\left|i-j\right|\right)+A_0.$$ [2]

All sequence separations, |i − j|, that are greater than 15 and up to n_res – 5 were used. Here, n_res is the number of residues in NTL9. The lower bound of 15 corrects for deviation from scaling behavior at short distances, while the upper bound of n_res – 5 corrects for the effects “dangling ends” that introduce deviations from the infinitely long chain limit (the limit under which scaling theory was developed). Points were distributed such that they are evenly spaced in log–log space, avoiding common pitfalls associated with fitting linear models to log–log plots.