Antagonistic pleiotropy conceals molecular adaptations in changing environments

Abstract

The importance of positive selection in molecular evolution is debated. Evolution experiments under invariant laboratory conditions typically show a higher rate of nonsynonymous nucleotide change than that of synonymous change, demonstrating prevalent molecular adaptations. Natural evolution inferred from genomic comparisons, however, almost always exhibits the opposite pattern even among closely related conspecifics, indicative of a paucity of positive selection. We hypothesize that this apparent contradiction is at least in part attributable to ubiquitous and frequent environmental changes in nature, causing nonsynonymous mutations beneficial at one time deleterious soon after because of antagonistic pleiotropy and hindering their fixations relative to synonymous mutations despite continued population adaptations. To test this hypothesis, we performed yeast evolution experiments in changing and corresponding constant environments, followed by genome sequencing of the evolving populations. We observed a lower nonsynonymous to synonymous rate ratio in antagonistic changing environments than in the corresponding constant environments, and the population dynamics of mutations supports our hypothesis. These findings and the accompanying population genetic simulations suggest that molecular adaptation is consistently underestimated in nature due to the antagonistic fitness effects of mutations in changing environments.

The role of positive selection in molecular evolution is a central theme of evolutionary biology, yet has remained controversial after 50 years of investigation^1–9. Experimental evolution under controlled conditions may offer otherwise hard-to-gain insights into this fundamental question. For instance, Lenski’s long-term experiment of Escherichia coli adaptation to an invariant environment showed a gradual decline of the genome-wide number of nonsynonymous changes per nonsynonymous site relative to the genome-wide number of synonymous changes per synonymous site (ω) over time, but even the overall ω in the first 50,000 generations exceeds 3, demonstrating prevalent molecular adaptations¹⁰. Similar observations have been made in other evolution experiments under invariant conditions^11–13. Because the environment varies more frequently in nature than in these studies, positive selection is expected to be more abundant in nature. Surprisingly, natural evolution inferred from genomic comparisons almost always exhibits ω that is substantially below 1 even among closely related conspecifics, indicative of a paucity of positive selection^14–16. We hypothesize that nonsynonymous mutations beneficial in one environment may become deleterious in subsequent environments owing to antagonistic pleiotropy^17,18, hindering their fixations and lowering ω even when the population continuously adapts. Pleiotropy refers to the widespread observation of one mutation influencing more than one trait^17,19. That a mutation has fitness effects in multiple environments is also a phenomenon of pleiotropy^18,20–22 because the organismal fitness in each environment may be considered a trait. In this context, antagonistic pleiotropy means opposite fitness effects of a mutation in different environments.

Here we test the above hypothesis by respectively conducting Saccharomyces cerevisiae evolution experiments in two sets of changing environments as well as the corresponding constant environments. The first set of five environments, referred to as concordant environments, are relatively similar to one another such that antagonistic pleiotropy should be rare. The second set of five environments, referred to as antagonistic environments, are highly dissimilar to one another and are expected to have abundant antagonistic pleiotropy. Hence, the extent of antagonistic pleiotropy is expected to increase and ω is predicted to decline from constant to concordant to antagonistic environments (Fig. 1a). The experimental evolution was followed by genome sequencing of the evolving populations sampled at multiple time points. Analyses of ω and population dynamics of mutants in the experimental evolution, coupled with computer simulations that help to understand the underlying population genetic processes, provide unambiguous support to our hypothesis that antagonistic pleiotropy can conceal molecular adaptations in changing environments.

Figure 1. Experimental evolution of yeast in constant and changing environments.

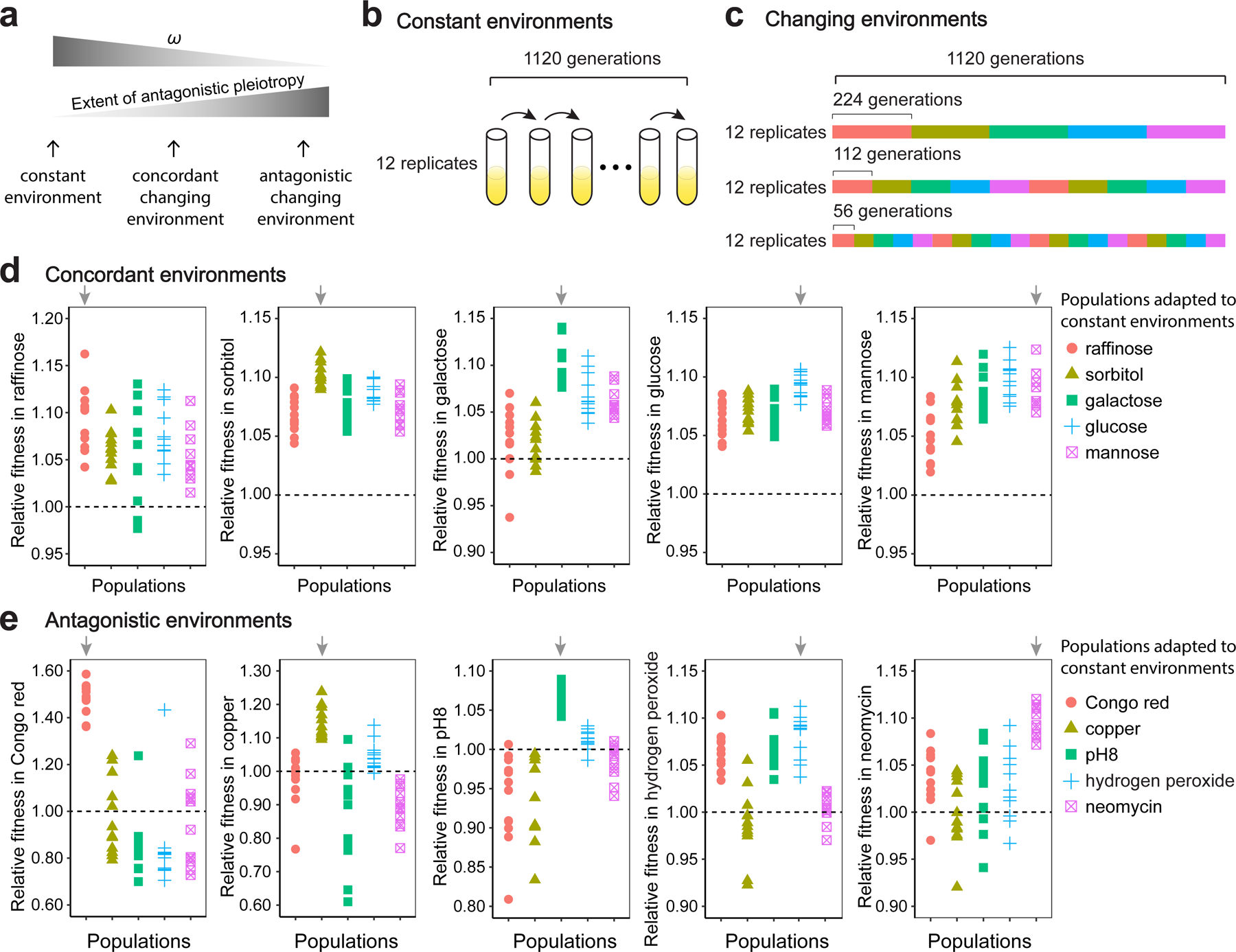
(a) Schematics showing predictions on the extent of antagonistic pleiotropy and ω in different environments. (b) Schematics showing experimental evolution in a constant environment for 1,120 generations. This experiment is performed with 12 replicates for each of the 10 environments shown in (d) and (e). (c) Schematics showing experimental evolution in a changing environment that rotates among five antagonistic or five concordant conditions with three different frequencies (each condition lasted for 224, 112, or 56 generations). Each scheme has 12 replicates. Colors indicate various environments described in (d) or (e). (d) Fitness of each adapted population relative to the progenitor in the constant environment where the adaptation occurred or in the other four concordant, constant environments. (e) Fitness of each adapted population relative to the progenitor in the constant environment where the adaptation occurred or in the other four antagonistic, constant environments. In (d) and (e), each symbol represents mean fitness of an adapted population (based on three measurements) relative to the mean fitness of the progenitor (based on 12 measurements). A total of 1920 measurements (120 populations × 5 assayed environments × 3 replicates + 1 progenitor population × 10 assayed environments ×12 replicates) were performed here. Arrows indicate populations for which the adaptation and fitness measurement occurred in the same environment.

RESULTS

Experimental evolution in two sets of constant vs. changing environments

To identify environments where mutations tend to have opposite fitness effects, we took advantage of growth rate estimates of over 1000 segregants from a cross between two yeast strains in 47 laboratory conditions²³. Five conditions were chosen to represent a set of antagonistic environments because segregant fitness tends to be negatively correlated between any two of these conditions (Supplementary Fig. 1a; see Methods). We similarly chose five conditions to represent a set of concordant environments where antagonistic mutations are rarer, because segregant fitness tends to be positively correlated between any two of these conditions (Supplementary Fig. 1b). We performed two groups of evolution experiments with a total of 192 populations, all initiated from the same haploid progenitor (see Methods). The first group examined yeast evolution in each of the 10 constant environments from the above two sets of five conditions (10 ×12 replicates = 120 populations) (Fig. 1b). The second group examined yeast evolution in changing environments that rotated among either the five antagonistic or five concordant conditions with three different frequencies of environmental switches (2×3×12 replicates = 72 populations) (Fig. 1c). The frequency of environmental switches could affect the probability of fixation of beneficial mutations and ω, so it was investigated here. The evolution lasted for 1,120 generations for each population, and a large fraction of each population was frozen per 56 generations as the “fossilized” record of the yeast evolution.

To assess the extent of antagonism among the five antagonistic (or concordant) environments, we measured the fitness of the end populations adapted to each constant environment, relative to the fitness of the progenitor, in their adapted environment as well as in the other four environments in the set of antagonistic (or concordant) environments. We found that populations adapted to each of the concordant environments tend to have higher fitness than the progenitor in all five concordant environments (Fig. 1d). Specifically, the mean fitness of the end populations is 1.096±0.005 (± indicates the 95% confidence level) when measured in the environments they are adapted to. When measured in the other concordant environments, the average fitness is 1.065±0.004 and only 8 of the 240 fitness values are below 1 (P < 10⁻¹⁵, two-sided binomial test). By contrast, populations adapted to each of the antagonistic environments tend to have lower fitness than the progenitor in the other antagonistic environments (Fig. 1e). The average fitness of the end populations is 1.174±0.042 when measured in the environments they are adapted to. When measured in the other antagonistic environments, the average fitness is 0.975±0.014, and 124 of the 240 fitness values are below 1 (P = 0.65, two-sided binomial test). The fraction of cases with fitness < 1 (i.e., antagonistic pleiotropy) is significantly greater for antagonistic environments than concordant environments (P < 10⁻¹⁵, chi-squared test), confirming that the antagonistic environments we used impose stronger contrasting effects on yeast growth when compared with the set of concordant environments.

Lowered ω in the antagonistic changing than corresponding constant environments

To estimate ω in the experimental evolution, we genome-sequenced the progenitor and all end populations to an average of 100× coverage. By comparing with the progenitor genome, we identified from each end population all single nucleotide variants (SNVs) with a frequency of at least 0.1, because a mutation must be beneficial by itself or hitchhike a beneficial mutation to reach this frequency in the short evolutionary time. A total of 1,745 SNVs were detected, of which 212 were fixed (Supplementary Dataset 1). Spontaneous diploidization of haploid yeast is known to be favored in a variety of conditions²⁴. We determined the yeast genome size in each end population by SYTOX Green staining followed by flow cytometry (see Methods), which showed that 89 of 96 populations in the constant or changing concordant environments converged to diploidy (Supplementary Fig. 2). In the constant antagonistic environments, 28 of the 60 populations became diploid, but in the changing antagonistic environments, all 36 populations remained haploid (Supplementary Fig. 3), probably because diploidy became disfavored in some of the antagonistic environments upon other genetic changes.

We computed ω for each population (see Methods), and found no significant variation in ω among the three experiments with different frequencies of antagonistic (or concordant) environmental switches (all P > 0.05, bootstrap test followed by Bonferroni correction) (Supplementary Table 1). We thus combined the data from different frequencies of environmental switches in subsequent analyses. For the set of antagonistic environments, ω is significantly lower in changing than constant environments (Fig. 2a). This disparity remained qualitatively unchanged when we further computed ω by considering a subset of SNVs with minimum allele frequencies of 0.2, 0.4, 0.6, or 0.8 (Fig. 2a). Similar results were obtained when only haploid populations were considered (Supplementary Fig. 4a). For the set of concordant environments, although ω is lower in the changing than constant environments under each minimum allele frequency cutoff examined, the difference is not statistically significant, regardless of whether the SNVs are considered to have occurred before (Fig. 2b) or after the diploidizations (Supplementary Fig. 4b). This result may not be unexpected given the rare antagonistic pleiotropy among the five concordant environments used (Fig. 1d); we may have chosen too similar conditions in the set of concordant environments for the impact of environmental changes on ω to be detectable. Note that comparing ω between the changing antagonistic environments and changing concordant environments is not meaningful, because the two sets of environments have different selective strengths.

Figure 2. The rate of molecular evolution in constant and changing environments.

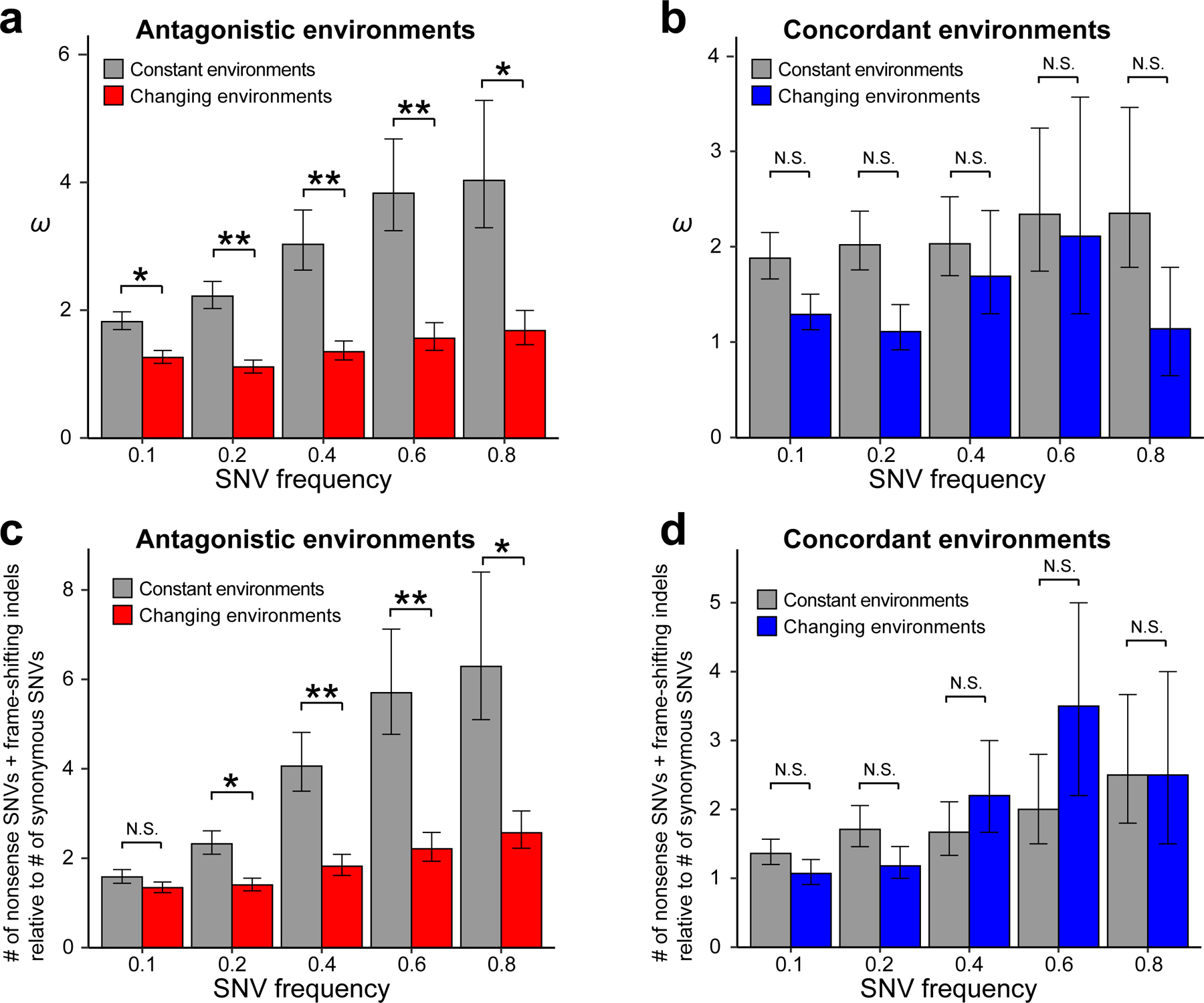
(a) The rate ratio (ω) of nonsynonymous to synonymous nucleotide changes is significantly lower in the antagonistic changing environments than in the corresponding constant environments, regardless of the minimum frequencies of single nucleotide variants (SNVs) considered in the evolved populations. (b) ω is not significantly different between the concordant changing environments and the corresponding constant environments. (c) The ratio of the total number of nonsense SNVs and frame-shifting insertions/deletions (indels) to the number of synonymous SNVs is significantly lower in the antagonistic changing environments than in the corresponding constant environments. (d) The above ratio is not significantly different between the concordant changing environments and the corresponding constant environments. P-values are determined by bootstrapping the relevant populations 10,000 times and are indicated by * (P < 0.05), ** (P < 0.01), or N.S. (P > 0.05). Error bars indicate the first and third quartiles from bootstrapped data.

Nonsense and frame-shifting mutations cause greater protein sequence alterations than nonsynonymous mutations and have been repeatedly reported to be a source of advantageous mutations in experimental evolution²⁵. Because such mutations are not included in computing ω, we estimated the ratio of the total number of nonsense SNVs and frame-shifting insertions/deletions to the number of synonymous SNVs for each population. This ratio is significantly lower in antagonistic changing environments than in the corresponding constant environments (Fig. 2c). Similar results were obtained when only haploid populations were considered (Supplementary Fig. 4c). No such significant difference was observed between concordant changing environments and the corresponding constant environments, regardless of whether the SNVs are considered to have occurred before (Fig. 2d) or after the diploidizations (Supplementary Fig. 4d). These results indicate similar impacts of environmental changes on nonsynonymous SNVs and on nonsense SNVs and frame-shifting insertions/deletions.

Population dynamics of mutations in antagonistic changing vs. constant environments

Because a significant difference in ω was observed in the comparison between the changing and constant antagonistic environments, but not in the comparison between the changing and constant concordant environments, we focus on the former comparison in all subsequent analyses in an attempt to understand why ω is lower in the changing than the constant antagonistic environments. To this end, we genome-sequenced the 12 populations frozen right before each environmental switch in the experiment with the lowest frequency of antagonistic environmental changes (12×4 = 48 samples in total; Fig. 1c). For comparison, we also genome-sequenced three frozen populations per environment at each corresponding evolutionary time under the five corresponding constant environments (3×5×4 = 60 samples in total; Fig. 1b). These data allow us to examine the population dynamics of mutations through five periods of 224 generations (Fig. 3a, b; Supplementary Figs. 5 and 6). A nonsynonymous mutation that rises to a high frequency in a population may precipitously drop in frequency at a later time. In addition to its occurrence by clonal interference¹², this phenomenon is expected to be common when the environment changes. Indeed, it was more frequently observed in changing environments (Fig. 3a; Supplementary Fig. 5) than in constant environments (Fig. 3b; Supplementary Fig. 6). Consequently, compared with constant environments, changing environments harbor more beneficial SNVs that are unaccounted for when only the end population is compared with the progenitor. To quantify this effect, we used i to represent the number of nonsynonymous SNVs reaching the frequency of 0.1 in the end population when compared with the progenitor, and used j to represent the number of new nonsynonymous SNVs reaching the frequency of 0.1 at the end of each period, summed over all five periods. The fraction of missing nonsynonymous SNVs equals (j-i)/j. We found that this fraction is significantly greater for populations in the changing environments than those in the constant environments, and the same is true regardless of the specific minimum allele frequency required (Fig. 3c). By contrast, the fraction of missing synonymous SNVs is not significantly greater in the changing than constant environments (Fig. 3d).

Figure 3. Population dynamics of individual nonsynonymous mutant alleles in the antagonistic changing or constant environments.

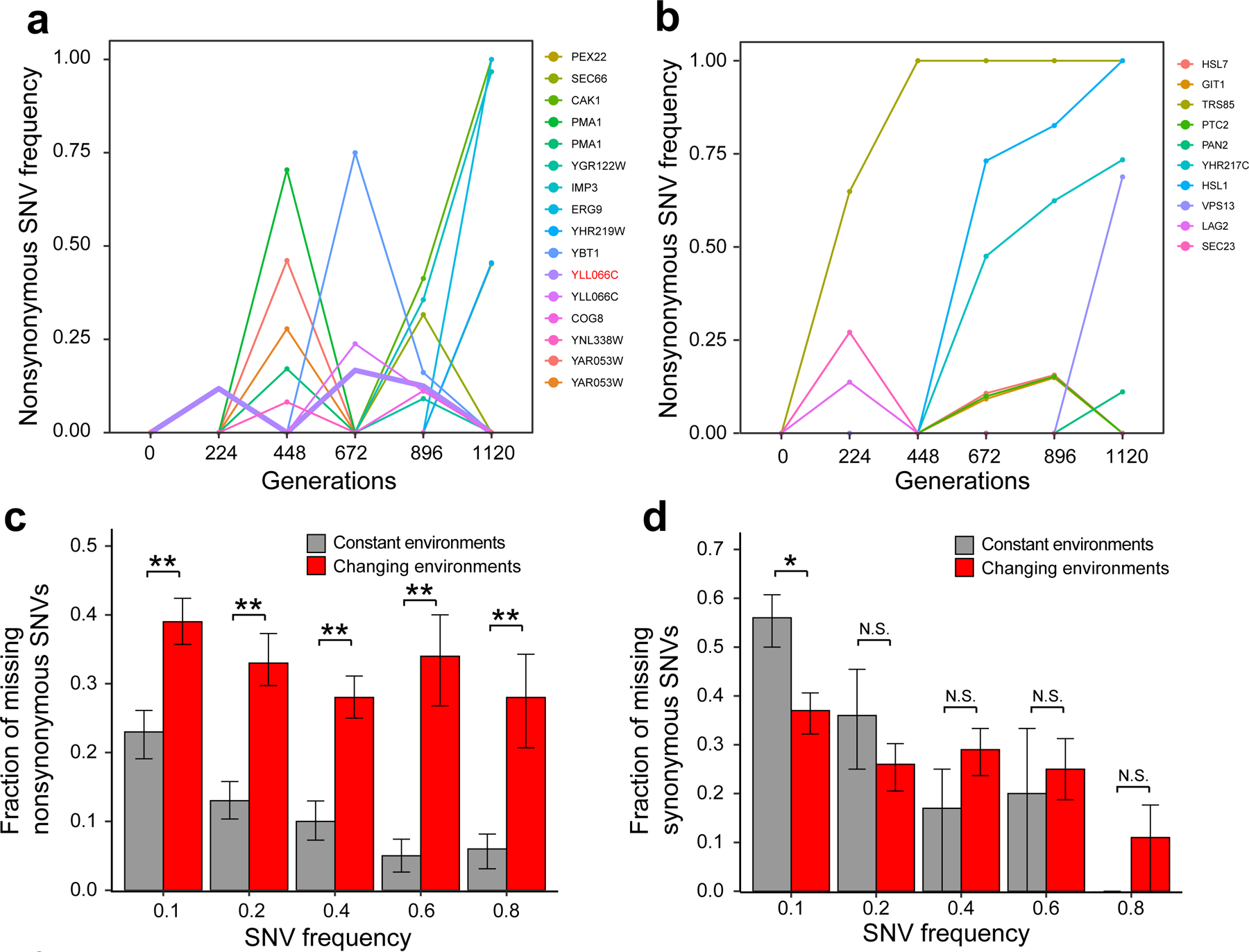
(a-b) Increases and decreases of mutant alleles in a representative population in the antagonistic changing environments (a) or in a constant environment (neomycin) (b). Different SNVs are shown by different colors; each line shows the trajectory of a SNV that attains a frequency of at least 0.05 at one or more examined time points. The name of the gene in which the SNV lies is provided on the right of the plot. A bold line indicates a mutant allele whose frequency increased in a period after a decrease in an earlier period, with the corresponding gene name shown in red. (c-d) Fraction of nonsynonymous (c) or synonymous (d) SNVs reaching an indicated minimal frequency that are uncounted when only the end populations are compared with the progenitor (see main text for details). P-values are determined by bootstrapping the relevant populations 10,000 times and are indicated by * (P < 0.05), ** (P < 0.01), or N.S. (P > 0.05). Error bars indicate the first and third quartiles from bootstrapped data.

Because synonymous mutations must hitchhike on beneficial nonsynonymous mutations to reach detectable frequencies in the short evolutionary time considered here, one wonders why the antagonistic environmental changes increased the fraction of missing nonsynonymous SNVs but not that of missing synonymous SNVs. The reason is that, the more nonsynonymous SNVs a genotype has, the higher the likelihood that it will be subject to antagonistic pleiotropy and purifying selection upon an environmental change. In other words, the environmental changes preferentially purged genotypes with more nonsynonymous SNVs. Because the expected number of synonymous SNVs of a genotype is independent of its number of nonsynonymous SNVs, this bias does not impact synonymous SNVs.

Computer simulation explains SNV and ω differences between antagonistic changing and corresponding constant environments

Some authors suggested that, for a population evolving in an changing environment, its adaptation is better measured by the integral of fitness changes over time instead of the final fitness relative to the initial fitness^26,27. Similarly, molecular adaptation is better reflected by ω estimated using the above introduced j instead of i, because a mutation beneficial in an environment may become deleterious when the environment changes and be missing from the final population. Hence, summing up new SNVs of each time period (i.e., j) captures a more complete picture of mutation dynamics than only comparing between the progenitor and the end population (i.e., i). Let us denote the ω estimated from j by ω’. As expected, the ratio (0.74) of ω’ in the antagonistic changing environments to ω’ in the constant environments significantly exceeds the corresponding ratio (0.41) of ω (P < 0.002, bootstrap test). Because the missing SNVs due to environmental changes were added back in the calculation of ω’, we expected that the ratio of ω’ in changing environments to that in constant environments should be close to 1. Nevertheless, the ratio of ω’ is still below 1, which prompted us to examine the data more thoroughly.

Contrary to our expectation, the numbers of nonsynonymous (Fig. 4a) and especially synonymous (Fig. 4b) SNVs per population are greater in the antagonistic changing environments than in the corresponding constant environments. This trend is particularly obvious when j instead of i is considered (Supplementary Fig. 7). This unexpected outcome for nonsynonymous SNVs is probably related to the common phenomenon of diminishing returns epistasis, which lowers the benefits of the same advantageous mutations in fitter genotypes and slows their accumulations as the fitness of the population rises^13,28,29. Because the fitness of the population continues to rise in a constant environment but drops when the environment changes to an antagonistic one, diminishing returns is severer in constant environments than in antagonistic changing environments. As a result, fewer nonsynonymous SNVs are expected in constant than changing environments. That the number of synonymous SNVs also differs between constant and changing environments is because the number of synonymous SNVs observed are partially determined by the number of nonsynonymous SNVs due to the hitchhiking effect aforementioned. In other words, diminishing returns also causes an excess of synonymous SNVs in antagonistic changing environments when compared with the constant environments.

Figure 4. Computer simulation explains observations from the experimental evolution in the antagonistic changing or constant environments.

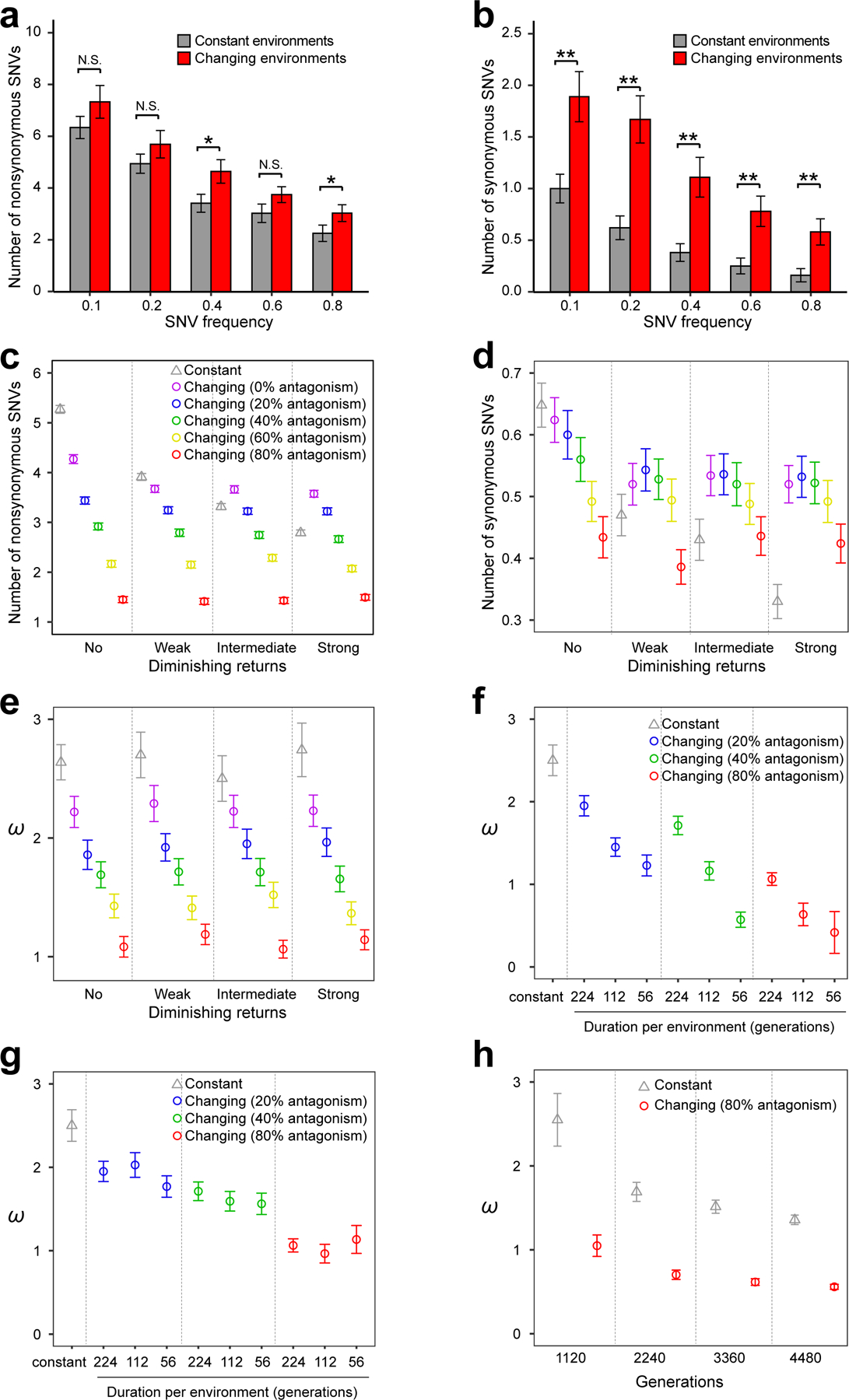
(a-b) Numbers of nonsynonymous (a) and synonymous (b) SNVs per population observed in experimental evolution are greater in the antagonistic changing environments than in the corresponding constant environments. Diploid lines are excluded. P-values are determined by bootstrapping the relevant populations 10,000 times and are indicated by * (P < 0.05), ** (P < 0.01), or N.S. (P > 0.05). Error bars indicate standard errors estimated by bootstrapping the populations. (c-e) Simulation shows that diminishing returns epistasis can reverse the relationship between constant and changing (antagonistic) environments in the numbers of nonsynonymous (c) and synonymous (d) SNVs but not in ω (e). X-axis shows the level of diminishing returns epistasis, whereas different colors represent different degrees of antagonism among environments (see Methods). Here the simulation lasted for 1,120 generations, with an environmental change every 224 generations. (f) Simulation reveals that ω decreases in antagonistic changing environments as the duration of each environment gets shorter. Simulation was performed by changing the environment to a new antagonistic condition every 224, 112, or 56 generations for a total of 1,120 generations, under the intermediate level of diminishing returns epistasis. (g) Simulation reveals no significant difference in ω among three different frequencies of environmental changes when the environment rotates among five fixed antagonistic conditions, under the intermediate level of diminishing returns epistasis. (h) Simulation shows that the estimated ω falls below 1 after a sufficient time of evolution under changing environments. The environment is changed to a new antagonistic condition every 224 generations, and the intermediate level of diminishing returns epistasis is considered. It takes longer for the estimated ω to fall below 1 under a lower degree of antagonism (e.g., 20% or 40%). In (c)-(h), under each parameter set, the mean from 1000 simulated populations is presented. Error bars indicate standard errors, estimated by bootstrapping the simulated populations 1000 times. All SNVs with a minimal allele frequency of 0.8 are considered.

Furthermore, for a hitchhiking mutation to be counted as a SNV, the mutation must occur sufficiently early relative to the selective sweep so that its frequency could reach the level used for calling SNVs. In a constant environment, the selective pressure gradually weakens as the population adapts. Thus, selective sweeps are expected to be fewer and fewer as the adaptation proceeds. By contrast, in antagonistic changing environments, every environmental change imposes a new selective pressure that could be as strong as that at the beginning of the adaptation in a constant environment; hence, selective sweeps do not become rarer later in the evolution. Because of this disparity in the temporal distribution of selective sweeps, especially when diminishing returns is at work, more hitchhiking SNVs are expected in the antagonistic changing environments than in the constant environments. Note that neutral nonsynonymous mutations can also hitchhike on beneficial nonsynonymous mutations. But, because neutral nonsynonymous mutations in an environment are also more likely than synonymous mutations to become deleterious upon an environmental change, there are fewer observed nonsynonymous hitchhikers relative to synonymous hitchhikers in changing environments than in constant environments. This difference may explain why the environmental changes caused a greater fold increase in the number of synonymous SNVs (Fig. 4b) than that of nonsynonymous SNVs (Fig. 4a) and why ω’ is still lower in the changing than constant environments.

To verify these explanations, we conducted computer simulations of 1,120 generations of evolution that incorporates mutation, drift, selection (including clonal interference and hitchhiking), and diminishing returns. Note that, while our simulation can illustrate theoretical predictions, it is not meant to be an exhaustive survey of the parameter space under which each prediction is true. We found that the inclusion of diminishing returns in the simulation could indeed reverse the relative numbers of nonsynonymous SNVs in changing and constant environments under certain parameters (Fig. 4c); the same is true for synonymous SNVs (Fig. 4d). Irrespective of diminishing returns, ω is lower in changing environments than in constant environments (Fig. 4e); the same is true for ω’ (Supplementary Fig. 8). Similar results were obtained under various population sizes (Supplementary Fig. 9).

Contrasting the observation of ω < 1 in most natural evolution, ω is not significantly below 1 in our experimental evolution (Fig. 2a; Supplementary Fig. 4a) or simulation (Fig. 4e) even under changing environments. We predict that ω will gradually decrease as the duration of each environment gets shorter in changing environments, because the probability for a beneficial mutation to reach a high frequency is lower as the time becomes shorter. We simulated evolution by changing the environment to a new antagonistic condition every 224, 112, or 56 generations and observed that ω gradually decreases as the duration of each environment reduces, regardless of the presence (Fig. 4f) or absence (Supplementary Fig. 10a) of diminishing returns. Note that, unlike our experimental evolution, each environment appeared only once in the above simulation. When mimicking our experimental evolution by simulating the rotation among five environments, we found no significant difference in ω among the three frequencies of environmental switches (Fig. 4g; Supplementary Fig. 10b), as was discovered experimentally. Even when each environment lasts for 224 generations, we predict that ω will fall below 1 if we observe the evolution for a longer time, because each beneficial mutation in an environment will eventually become deleterious in a later environment given enough time. Indeed, when we simulated evolution by changing the environment to a new antagonistic condition every 224 generations, ω falls below 1 (P < 0.0001, bootstrap test) after 2,240 generations, regardless of the presence (Fig. 4h) or absence (Supplementary Fig. 10c) of diminishing returns. This mechanism may have contributed to the widespread observation that ω generally declines with the divergence of the genomes compared^14,15.

DISCUSSION

Our experimental evolution and associated simulations demonstrate that antagonistic pleiotropy causes undercounting of beneficial nonsynonymous SNVs relative to synonymous SNVs in changing environments. Because the environment inevitably varies in nature, our results suggest that ω and consequently positive selection have been consistently underestimated in natural evolution. The amount of underestimation is determined by the frequency of environmental changes and the prevalence of antagonistic pleiotropy among the varying environments. An earlier yeast study showed that antagonistic pleiotropy is common among six laboratory conditions examined¹⁸. We note that although our experiment used the five most antagonistic conditions from a set of 47 previously studied conditions, because most of these 47 conditions are concordant rather than antagonistic³⁰, the five conditions used are not strongly antagonistic to one another (Supplementary Fig. 1a; Fig. 1e). One can certainly find more antagonistic natural environmental variations than those used here (e.g., high vs. low temperature, acidity, or humidity). The same can be said about the recent report of paucity of antagonistic pleiotropy in E. coli among 11 laboratory environments that differ only by the carbon source³¹. Such environments are likely concordant according to our data (Supplementary Fig. 1b; Fig. 1d), and they represent only one dimension of myriad environmental variations in nature. Although the prevalence of antagonistic pleiotropy among natural environments requires more studies, the observation of much lower ω in nature than in constant laboratory conditions (even with the possibility of ecological variations in a constant condition³²) suggests the possibility that the underestimation of molecular adaptation in natural evolution is substantial. While our study focuses on intraspecific evolution, the same can be said of interspecific evolution owing to the same processes involved.

While demonstrating the role of environmental variation-associated antagonistic pleiotropy in masking molecular adaptations, our study neither assumes nor concludes that this is the only reason why the estimated ω is lower in natural evolution than in experimental evolution under constant environments. Other potential reasons include, for example, population structure and small population sizes in nature. Nevertheless, it seems unlikely for their impacts to be so large and widespread that ω becomes much lower than 1 in almost all species examined at the genomic scale. By contrast, environmental changes are virtually universal so the impact of antagonistic pleiotropy is likely ubiquitous although the size of the impact undoubtedly varies. It is thus tempting to suggest that antagonistic pleiotropy is a more important and general explanation than these other factors for the observed disparity in ω. The validity of the above suggestion and the potential roles of these other factors await future studies.

We unexpectedly observed more synonymous and nonsynonymous nucleotide changes during the yeast adaptations in the antagonistic changing environments than in the corresponding constant environments, and explained this phenomenon by diminishing returns epistasis coupled with a difference in the timings of selective sweeps under the two selection schemes. A recent mutation accumulation study in seven different benign environments showed that yeast mutation rate per generation tends to be lower in environments where yeast grows faster³³. If this trend applies to the environments considered here, mutation rate is expected to decline more in the constant environments than in the antagonistic changing environments during yeast adaptations, which could also result in more synonymous and nonsynonymous changes in the changing than constant environments. Note that our two proposed explanations are not mutually exclusive and they may simultaneously contribute to the observation. Future studies are needed to help fully understand this phenomenon.

One could argue that Lenski’s E. coli populations as well as all of our yeast populations experienced cyclic environmental changes, because the media were changed every 24 hours. But, this cyclic environmental change is of a different nature than the environmental change that our study focuses on, which involved qualitative changes of nutrients and/or stresses and had much lower frequencies. Rapid cyclic environmental changes are expected to drive the evolution of plasticity to cope with the cyclic changes instead of a specific genetic adaptation to each instantaneous environment. Another dimension of environmental variation is spatial heterogeneity. Previous studies suggested that a spatially homogenous environment favors different mutations in terms of pleiotropy than does a spatially heterogeneous environment^34,35. How spatial heterogeneity in the environment impacts molecular adaptation is a question worth pursuing in the future.

METHODS

Strains and media

In an earlier experiment, we evolved the diploid yeast strain BY4743 in yeast extract peptone dextrose (YPD) media for 1,200 generations. After sporulation, we randomly picked ten haploid segregants and measured their growth rates in YPD using Bioscreen C (Growth curves Oy, Finland). The strain with the highest growth rate was used as the progenitor in the present experimental evolution. The ten conditions used were Congo red (YPD with 70 μg/ml Congo red), copper (YPD with 9 mM copper sulfate), pH8 (YPD with 50 mM HEPES buffer, NaOH for pH adjustment), hydrogen peroxide (YPD with 1.875 mM hydrogen peroxide), neomycin (YPD with 50 μg/ml neomycin), raffinose (YP with 2% raffinose), galactose (YP with 2% galactose), glucose (YP with 2% glucose), sorbitol (YPD with 1M sorbitol), and mannose (YP with 2% mannose). Because the progenitor was preadapted to YPD, subsequent beneficial mutations accumulated in the present experimental evolution are expected to be related to the specific ingredients of the 10 conditions rather than the common YP.

Experimental evolution

The 192 parallel serial transfer experiments were all initiated from the same overnight culture from a clone of the progenitor strain. In each parallel experiment, we grew 500 μl of yeast culture in an incubating shaker at 220 revolutions per minute (rpm) and 30°C. We used four 96-well plates to perform the experimental evolution. To minimize cross-contamination, we placed yeast samples in odd-numbered wells in row A, even-numbered wells in row B, and so on. This way, we used only 48 wells per plate, leaving one well empty between every two wells that had yeast samples. Every 24 hr, after culture had reached the stationary phase, we transferred 2 μl of stationary culture (~2×10⁵ cells) into 500 μl fresh culture medium. We carried out 140 such transfer cycles for a total of 1,120 generations (each transfer cycle had 8 generations). Every 56 generations, the remaining cells after the transfer were frozen in 20% glycerol and stored at −80°C for future analysis. We periodically used microscopy to examine the cultures for potential contamination.

The lack of cross-contamination was verified from our genome sequence data. Specifically, we found 15 SNVs that were shared between two populations, nine of which occurred between different plates and six occurred within plates. Cross-contamination should render the probability of SNV sharing between populations higher on the same plate than on different plates. But we cannot reject the null hypothesis of equal probabilities of SNV sharing within and between plates (P = 0.2, chi-squared test), suggesting that cross-contamination was minimal if any, and that SNV sharing between populations was largely or exclusively due to parallel evolution.

Fitness assays

Cells from frozen cultures were inoculated in 500 μl YPD and incubated for 24 hr at 30°C. The cells were then precultured in the medium to be tested overnight until saturation. Cultures were diluted to an optical density (OD) of 0.03–0.05 in 350 μl of fresh medium and cultivated for 36 hr using a Bioscreen C analyzer. OD was measured every 20 min using a wide band (450–580 nm) filter. The non-linear relation between OD and population density at high population densities was compensated for by converting each OD measurement to OD’ following standard procedures³⁶. Slopes were calculated between every two measurements spaced 40 min apart along the growth curve by Δln(OD’)/40 (no slopes were calculated from the eight initial time points). The two highest slopes were discarded to exclude possible artifacts, and a mean slope representing the growth rate per min (r) was calculated from the third to the eighth highest slopes. Population doubling time was calculated by ln2/r. The fitness of a population relative to the progenitor is estimated by 2^r/R−1, where R is the growth rate of the progenitor. The fitness of each population was measured three times, and the mean and standard error were reported.

Library construction and genome sequencing

A total of 302 populations (192 end populations + 108 intermediate populations + 2 replicates of the progenitor) were genome-sequenced. For each population, genomic DNA was extracted from ~10⁷ yeast cells using MasterPure™ Yeast DNA Purification Kit (Lucigen; Cat. No. MPY80200). Sequencing libraries were constructed using Nextera DNA Flex Library Prep (Illumina; Cat. No. 20018705). Samples were sequenced using an Illumina HiSeq 4000 with a paired-end (PE) 150 strategy. Approximately 5 million read pairs were generated from each library, corresponding to an average sequencing depth of ~100×.

Identification of mutations and estimation of ω

Sequencing reads were aligned to the S. cerevisiae reference genome (version R64-2-1) by Burrows-Wheeler Aligner³⁷ with default parameters, and duplicated reads were removed by Picard tools (http://broadinstitute.github.io/picard/). SNVs and indels were called on the Genome Analysis Toolkit (GATK) platform³⁸. Each variant must be supported by at least five reads. By comparing with the progenitor genome, we identified SNVs from each population meeting a minimum allele frequency requirement (0.1, 0.2, 0.4, 0.6, or 0.8). We also used the cutoff of 0.95 and observed qualitatively similar results despite a substantial reduction in the number of SNVs that could be analyzed. Using the SNVs, we computed ω, which is the number of nonsynonymous SNVs per nonsynonymous site, relative to the number of synonymous SNVs per synonymous site. To estimate the potential number of synonymous and nonsynonymous sites in the yeast genome, we used the modified Nei-Gojobori method³⁹, which considers the transition bias, or the number of transitional mutations relative to the number of transversional mutations (Ts/Tv). A recent mutation accumulation study³³ of yeast in multiple environments reported an average Ts/Tv of 0.84, which we used in our computation. We estimated that there are 6,839,923 potential nonsynonymous sites (N) and 2,218,694 potential synonymous sites (S) in the yeast genome. Our way of estimating ω is similar to that in Lenski’s E. coli study mentioned¹⁰ except that we identified SNVs from population sequencing while they considered the mean number of SNVs observed from two clones sequenced per population¹⁰. When comparing ω between changing and the corresponding constant environments, we bootstrapped replicate populations 10,000 times to test the significance of their difference. Note that a previous study⁴⁰ on the behavior of ω of segregating polymorphisms is not related to the problem studied here, because we consider ω between the progenitor and a descent population or between two populations whereas this previous study considered two alleles sampled from the same population at the same time. Furthermore, when the true ω < 1, its estimate tends to decrease with the divergence between the genome compared, as a result of the time lag of the effect of purifying selection in removing deleterious nonsynonymous mutations¹⁴. Conversely, when the true ω > 1, its estimate tends to increase with the genome divergence because it takes time for the expected value to settle⁴¹. These models cannot explain why the estimated ω is generally below 1 in natural evolution but exceeds 1 in experimental evolution under constant environments. Neither can recombination explain this contrast⁴².

Genome size determination

Cells were grown in YPD in 96-well plates to mid-log phase. Approximately 10⁷ cells were harvested, washed with 1.5 ml of water and fixed by gently adding 3.5 ml of 95% ethanol and incubated for 2 hr at room temperature. Fixed cells were collected by centrifuging for 15 sec at 10,000 g, followed by resuspension of the pellet in 1 ml water and transferred to a 1.5 ml microcentrifuge tube. After brief centrifuging, we resuspended cells in 0.5 ml RNase solution (2 mg/ml RNase A in 50 mM Tris pH 8.0, 15 mM NaCl, boiled for 15 min and then cooled to the room temperature) and incubated them for ≥ 2 hr at 37°C. We then collected cells from the RNase solution by centrifuging them for 15 sec at 10,000 g. Cells were incubated in 0.2 ml protease solution (5 mg/ml pepsin, 4.5 μl/ml concentrated HCl, in H₂O) for 20 min at 37°C. After incubation, cells were collected by centrifugation and then resuspension in 0.5 ml 50 mM Tris pH 7.5, after which they were either stored at 4°C for a few days or analyzed immediately. For analysis, 50 μl of cell suspension were transferred to 1 ml of 1 μM SYTOX Green staining solution. All samples were analyzed using the iQue Screener Plus flow cytometry platform. First, we used forward scatter area (FSC.A) and side scatter area (SSC.A) with a clustering package to remove non-cell particles. Second, we used FSC.A and forward scatter height (FSC.H) to remove doublets. Third, we plotted DNA content histograms showing the distribution of the amount of DNA per cell. We used haploid (BY4741) and diploid (BY4743) yeast cells as controls to determine genome sizes. In each of these two control profiles, there are two peaks, respectively representing cells in the G1 and G2/M cell-cycle stages (1C and 2C DNA content for haploids and 2C and 4C for diploids).

Computer simulation

We conducted computer simulation of evolution in constant environments as well as antagonistic changing environments. Simulation was initiated from a population of 10⁴ individuals with the same genotype and fitness (the progenitor fitness = 1). This population size was chosen because it allows the simulation to be completed in a reasonable amount of time and because the simulation results are robust to the variation in population size (see below). In each generation, nonsynonymous and synonymous mutations occur with a probability equal to the SNV mutation rate multiplied by N and S, respectively. We used the SNV mutation rate of 4.04×10⁻¹⁰ per nucleotide per generation, estimated previously by mutation accumulation in haploid yeast⁴³. We assumed that synonymous mutations are neutral, whereas 10% and 90% of nonsynonymous mutations are respectively beneficial and deleterious. The fitness effects of beneficial mutations follow an exponential distribution, whereas those of deleterious mutations follow another exponential distribution. A recent yeast study estimated that beneficial mutations with fitness effects (s) larger than 5% and 2% occur at a rate of 1×10⁻⁶ and 5×10⁻⁵ per cell per generation, respectively⁴⁴. To match these rates, for beneficial mutations, the average fitness effect ($\overline{s}$) was set to be 0.0095. Because detrimental mutations are more likely to have larger absolute fitness effects, we set their absolute mean fitness effect at 0.02, which is approximately twice the average fitness effect of beneficial mutations mentioned. When diminishing returns epistasis is considered, the fitness effect of a beneficial mutation should decrease as the individual’s fitness increases. Specifically, for a beneficial mutation with effect s, we set its effect to $\frac{s}{1+\left(f-1\right)\alpha }$ when it occurs to an individual whose fitness f exceeds 1.05, where α was set at 5, 10, and 20 in weak, intermediate, and strong diminishing return epistasis, respectively. An individual’s fitness was calculated by 1 plus the fitness effects of all beneficial and deleterious mutations. In each generation, the number of offspring produced by an individual followed a Poisson distribution with mean equals to 2f (and the mother cell was removed after reproduction). We then randomly chose 10⁴ individuals of the next generation to keep the population size constant. In constant environments, the fitness effects of all mutations remained unchanged throughout the evolution. By contrast, in the setting of changing antagonistic environments, a certain proportion (0%, 20%, 40%, 60%, or 80%) of beneficial mutations in any environment became deleterious in the next environment, and this proportion is referred to as the degree of antagonism. For example, when 20% of beneficial mutations (i.e., 0.1×20% = 2% of all nonsynonymous mutations) became deleterious in a new environment, 2.22% of deleterious mutations (i.e., 0.9×2.22% = 2% of all nonsynonymous mutations) became beneficial to keep the proportion of beneficial mutations unchanged. Briefly, we randomly sampled 20% of beneficial mutations and assigned them with negative fitness effects randomly sampled from the exponential distribution of negative fitness effects mentioned. For the remaining 80% of beneficial mutations, we assigned them with positive fitness effects randomly sampled from the corresponding exponential distribution mentioned. The same applied to deleterious mutations. We performed this simulation for 1,120 generations, calculated the number of nonsynonymous mutations and synonymous mutations with a minimum frequency of 0.8 in the population, and estimated ω. The simulation was repeated 500 times under each parameter set. To examine the potential impact of population size on ω, we performed simulations at a smaller (5 ×10³) and two larger (2 ×10⁴ and 4 ×10⁴) population sizes with three different agrees of antagonism (20%, 40%, and 80%), under the intermediate level of diminishing returns (α = 10) as well as no diminishing returns. Under each parameter set, we repeated the simulation 500 times.

To examine how the frequency of environmental changes impacts ω, we performed a simulation by changing the environment to a new antagonistic condition every 56, 112, or 224 generations for a total of 1,120 generations. We used three different degrees of antagonism (20%, 40%, and 80%), under the intermediate level of diminishing returns (α = 10) or no diminishing returns. The simulation was repeated 500 times under each parameter set. We also performed another simulation in which the environment rotated among five antagonistic conditions with each condition lasted for 56, 112, or 224 generations, mimicking our experimental evolution. This simulation was repeated 500 times under each parameter set.

To investigate if ω falls below 1 when the evolution lasts longer, we performed a simulation of evolution in 25 different antagonistic environments each lasting for 224 generations, with the degree of antagonism being 20%, 40%, or 80%, under the intermediate level of diminishing returns (α = 10) or no diminishing returns. For comparison, we also performed a simulation in a constant environment for the same number of generations. The simulations were repeated 200 times under each parameter set.