Transitioning from Basic toward Systems Pharmacodynamic Models: Lessons from Corticosteroids

Abstract

Technology in bioanalysis, -omics, and computation have evolved over the past half century to allow for comprehensive assessments of the molecular to whole body pharmacology of diverse corticosteroids. Such studies have advanced pharmacokinetic and pharmacodynamic (PK/PD) concepts and models that often generalize across various classes of drugs. These models encompass the “pillars” of pharmacology, namely PK and target drug exposure, the mass-law interactions of drugs with receptors/targets, and the consequent turnover and homeostatic control of genes, biomarkers, physiologic responses, and disease symptoms. Pharmacokinetic methodology utilizes noncompartmental, compartmental, reversible, physiologic [full physiologically based pharmacokinetic (PBPK) and minimal PBPK], and target-mediated drug disposition models using a growing array of pharmacometric considerations and software. Basic PK/PD models have emerged (simple direct, biophase, slow receptor binding, indirect response, irreversible, turnover with inactivation, and transduction models) that place emphasis on parsimony, are mechanistic in nature, and serve as highly useful “top-down” methods of quantitating the actions of diverse drugs. These are often components of more complex quantitative systems pharmacology (QSP) models that explain the array of responses to various drugs, including corticosteroids. Progressively deeper mechanistic appreciation of PBPK, drug-target interactions, and systems physiology from the molecular (genomic, proteomic, metabolomic) to cellular to whole body levels provides the foundation for enhanced PK/PD to comprehensive QSP models. Our research based on cell, animal, clinical, and theoretical studies with corticosteroids have provided ideas and quantitative methods that have broadly advanced the fields of PK/PD and QSP modeling and illustrates the transition toward a global, systems understanding of actions of diverse drugs.

Significance Statement

Over the past half century, pharmacokinetics (PK) and pharmacokinetics/pharmacodynamics (PK/PD) have evolved to provide an array of mechanism-based models that help quantitate the disposition and actions of most drugs. We describe how many basic PK and PK/PD model components were identified and often applied to the diverse properties of corticosteroids (CS). The CS have complications in disposition and a wide array of simple receptor-to complex gene-mediated actions in multiple organs. Continued assessments of such complexities have offered opportunities to develop models ranging from simple PK to enhanced PK/PD to quantitative systems pharmacology (QSP) that help explain therapeutic and adverse CS effects. Concurrent development of state-of-the-art PK, PK/PD, and QSP models are described alongside experimental studies that revealed diverse CS actions.

I. Introduction

The application of pharmacokinetic/pharmacodynamic (PK/PD) modeling in drug development and pharmacotherapy is well established across the pharmaceutical industry (Lalonde et al., 2007; Kimko and Pinheiro, 2015), government regulation (Peck et al., 1994; Gobburu and Marroum, 2001), and academia (Danhof et al., 2008; Mager and Jusko, 2008). By integrating the time course of drug concentrations (PK), the nature of drug-target interaction (pharmacology), and turnover processes reflecting the relevant physiology and disease, PK/PD modeling has advanced from an empirical and descriptive endeavor into a mechanistic science. In addition to providing a systematic framework for understanding in vivo pharmacology and systems biology by separating drug- and system-specific parameters, the implications of mechanism-based PK/PD modeling are far reaching in areas such as: 1) drug candidate selection and lead optimization, 2) the design of early proof-of-concept trials using information from preclinical studies, 3) informing dose optimization for Phase II and III trials, and 4) explaining sources of intra- and interindividual variability and disease progression.

Systems biology, another firmly established discipline, comprises a broad spectrum of computational methods to understand physiology and disease at levels of molecular pathways, regulatory networks, cells, tissues, organs, and, ultimately, the whole organism (Butcher et al., 2004). A systems approach to modeling biologic networks is crucial for unraveling complex signaling mechanisms, which often exhibit emergent properties such as signal integration across multiple time scales, generation of distinct outputs depending on input strength and duration, and self-sustaining feedback loops (Bhalla and Iyengar, 1999). There has been growing interest in the complementary adoption of PK/PD and systems biology approaches toward the development of integrative quantitative systems pharmacology (QSP) models to understand more fully the complex interactions of drugs and disease biology and consequently improve drug development and pharmacotherapy. As a multidisciplinary science, QSP promises a framework for integrating information obtained from studying biologic (normal and aberrant) pathways and pharmacological targets to predict clinical efficacy and adverse events through iterations between mathematical modeling and experimentation (Mager and Kimko, 2016). The National Institutes of Health sponsored two workshops bringing together PK/PD modelers and systems biologists and pharmacologists to consider the state-of-the-art and future of quantitative and systems pharmacology. This resulted in an extensive “white paper” (https://www.nigms.nih.gov/training/documents/systemspharmawpsorger2011.pdf), along with National Institutes of Health support for the emergence of the discipline (Rogers et al., 2013).

Our experimental and theoretical efforts to understand diverse aspects of corticosteroid (CS) actions span the spectrum from “basic” (“top-down”) PK/PD studies in animals and humans to systems modeling of an array of plasma and tissue biomarker and response data and demonstrate the concepts and elements of horizontal and vertical integration of molecular to whole body processes. This review will describe how five decades of various animal, clinical, and theoretical studies with CS have provided numerous insights into the major determinants governing steroid disposition and responses as well as general ideas that have advanced the fields of PK/PD for CS and diverse drug classes. Our continuing efforts to decipher the complex pharmacogenomic and biochemical mechanisms of CS action have resulted in an assimilative and natural transition toward a more mechanistic, global, and multiscale systems understanding of CS actions. The development and insights gained from studies leading to three systems models examining the properties of methylprednisolone (MPL) are described. Our studies seeking understanding of the PK/PD properties of CS will be summarized within the broader context of: 1) major concepts and advances in PK, PD, and mechanism-based PK/PD modeling; 2) challenges and opportunities for moving basic PK/PD toward systems modeling; and 3) model-building approaches leading to enhanced PK/PD and QSP models.

II. The Corticosteroids

A. Clinical Use

The CS represent a class of immunomodulatory agents with appreciable anti-inflammatory and immunosuppressive efficacy. These drugs are synthetic analogs of glucocorticoids, adrenal steroid hormones that extensively regulate development, metabolism, and immune function. Therapy with CS dates back to the late 1940s when cortisone was discovered (Burns, 2016). Today, their therapeutic applications span diverse clinical contexts: as frontline therapy for autoimmune diseases (Kirwan, 1995; Rhen and Cidlowski, 2005), for preventing the rejection of solid organ transplants (Bergmann et al., 2012), in the combinatorial therapy of certain cancers (Moreno et al., 2000), and as antenatal therapy for stimulating fetal lung maturation before preterm birth (El-Sayed et al., 2017). Despite the development of targeted antibody-based therapies for autoimmune diseases such as rheumatoid arthritis, inflammatory bowel disease, and systemic lupus erythematosus, CSs such as prednisolone, MPL, and dexamethasone remain a critical component in the management of such diseases (Li et al., 2017a). Beneficial effects derived from immunosuppression are, however, accompanied by a plethora of metabolic disturbances, which upon long-term steroid usage are manifested as osteoporosis, insulin resistance, steroid diabetes, obesity, and muscle wasting (Schäcke et al., 2002). Despite such issues, CSs are among the most widely prescribed drugs in developed countries, taken by up to 1.2% of the adult population (van Staa et al., 2000; Overman et al., 2013).

B. Corticosteroid Pharmacokinetics

The study of the PK of diverse CS in humans and animals, like for many modern drugs, was enabled by the development of high-pressure liquid chromatographic methodology that allowed sensitive and specific measurement of several corticosteroids, including cortisol in plasma and tissues (Rose and Jusko, 1979; Jusko et al., 1994). The preferred assay method for the CS is now LC/MS/MS (Frerichs and Tornatore, 2004). The systemically used CSs are generally well absorbed when given orally, distribute rapidly to all body tissues, and are extensively metabolized with only 5%–10% of an intravenous dose excreted unchanged in urine (Rose et al., 1981; Szefler et al., 1986). The CS exhibit monoexponential or biexponential disposition with terminal plasma half-lives of 2–4 hours in most adult humans (shorter in rodents). Although hepatic metabolism of CS is generally assumed to occur, studies with perfused rat kidneys have shown a renal contribution to biotransformation of prednisolone (Rocci et al., 1981). Several hydroxylated metabolites of prednisone and prednisolone are excreted in urine and the renal clearance of the parent compounds are nonlinear (Wald et al., 1992).Transporter-mediated membrane influx and efflux mechanisms are deemed relevant for some steroids in tissues such as the liver and brain (Schinkel et al., 1995; Lackner et al., 1998; Crowe and Tan, 2012). The synthetic CSs, prednisolone, MPL, and dexamethasone show greater uptake in the liver compared with other tissues in animals (Khalafallah and Jusko, 1984; Ayyar et al., 2019d). Cortisol (corticosterone in the rat) and prednisolone bind moderately to albumin but strongly to transcortin (Rocci et al., 1980, 1982; Ko et al., 1995), a transport globulin protein of high affinity and low capacity, which is easily saturated at therapeutic doses of binding steroids (Xu et al., 2008). Cortisol and prednisolone are bound to a similar degree and compete for binding to corticosteroid binding globulin (CBG) (Rocci et al., 1982). There is also modest binding of prednisolone to α₁-acid glycoprotein (Milsap and Jusko, 1983). The capacity-limited binding to CBG produces volumes of distribution and clearances of total plasma prednisolone that increase with dose, but these are constant for unbound prednisolone (Rose et al., 1981; Wald et al., 1992) as well as for MPL. The latter is bound at a constant percentage, predominantly to albumin, with some species differences (60% in rats and 77% in rabbits and humans) (Ebling et al., 1986; Ayyar et al., 2019d). Dosing rats with CBG results in altered distribution and elimination of prednisolone, whereas the PK of non-CBG bound MPL is not affected (Ko et al., 1995) in accordance with the classic “free hormone” hypothesis as relevant to PK. Salivary cortisol is monitored in many psychobiological studies as it approximates the “bioactive” unbound concentration in plasma (Levine et al., 2007). This is reasonable as the CS are neutral compounds; assessing salivary concentrations of ionized drugs is more complicated owing to variability in salivary pH (Jusko and Milsap, 1993).

MPL undergoes minor interconversion with its metabolite methylprednisone (Ebling et al., 1985), while more extensive reversible metabolism occurs between prednisolone and the inactive prodrug/metabolite, prednisone (Garg and Jusko, 1994) similar to the metabolism between cortisol and cortisone (Colburn et al., 1980). These interconversions are nonlinear with dose for both prednisolone (Huang and Jusko, 1990) and MPL (Haughey and Jusko, 1992) in rats. This reversible metabolism process complicates the use and interpretation of PK parameters of these CS when calculated by traditional methods such as NCA and compartmental modeling because the exposure (area under the curve) of the active forms of the CS are increased by the reconverting metabolite. Therefore, alternative methods of PK analysis and modeling were established during the study of CS disposition (described in section III.A).

The corticosteroids, largely metabolized by CYP 3A enzymes, are sensitive to a variety of metabolic drug interactions, particularly induction from anticonvulsants (Jusko and Rose, 1980) and inhibition from oral contraceptives (Slayter et al., 1996) and ketoconazole (Kandrotas et al., 1987), among others. The array of metabolic drug interactions and physiologic (sex, age, obesity) and disease effects known to affect CS PK has been reviewed (Jusko and Ludwig, 1992).

A key determinant of differences in the PK among the commonly administered CS is lipid solubility as measured by log P and a quantitative structure-activity relationship factor Connolly Molecular Surface Area. The clearances and volumes of distribution (and consequently the half-life) of the CS increase with log P and Connolly Molecular Surface Area, whereas bioavailability decreases owing to more rapid metabolism in humans (Mager and Jusko, 2002a). Binding to plasma proteins and to the glucocorticoid receptor (GR) also increases with log P, a common phenomenon for many classes of drugs.

C. Mechanisms of Action

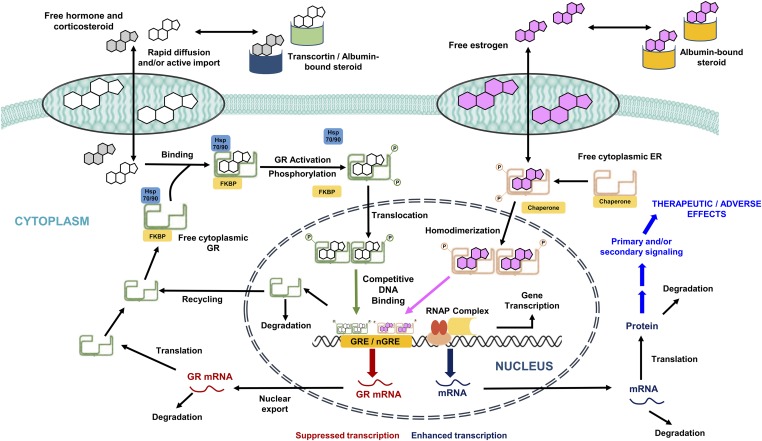
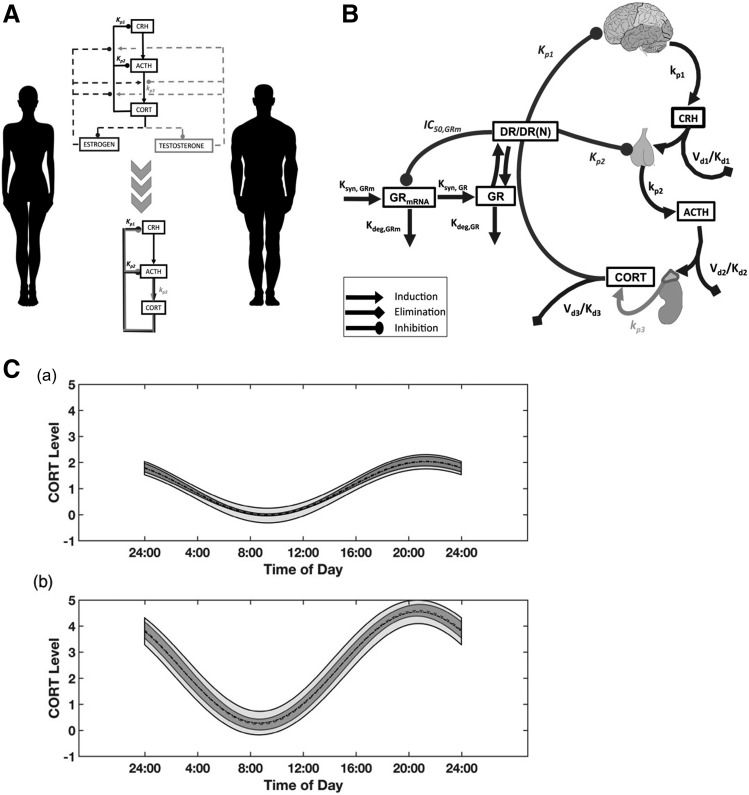
The CS exert their pharmacologic effects through diverse nongenomic (rapid) and genomic (delayed) mechanisms. Upon binding the GR, the CS can cause systemically measurable effects that are rapid in onset, such as cell trafficking and adrenal suppression (Yao et al., 2008). In contrast, pharmacogenomic regulation by the drug-receptor complex occurs in a delayed manner (Jusko, 1995) due to a series of intracellular transduction steps, including gene regulation (transactivation and transrepression) and consequent mRNA and protein synthesis. Figure 1 presents a general schematic of the receptor-mediated pharmacogenomic mechanisms of CS. The CSs are moderately protein bound in plasma, associating with albumin and sometimes CBG. Classic theory holds, in accordance with the “free hormone” hypothesis (Mendel, 1989), that unbound steroids rapidly diffuse into intracellular spaces where the GRs reside. The inactive receptor in cytosol is a heterocomplex comprised of the receptor, various heat shock protein subunits, and the FK506-binding immunophilins. The CSs bind to cytoplasmic GR and cause a dissociation of the chaperone complex by inducing a conformational change in the receptor. Upon dissociation from chaperone proteins, activated drug-receptor complexes rapidly translocate into the nucleus and homodimerize. Nuclear GR dimers then bind specific DNA sequences known as glucocorticoid-response elements (GRE) in the 5′-upstream promoter regions of target genes, leading to transcriptional changes by altering chromatin structure (Newton, 2000; Barnes, 2006). This interaction positively or negatively regulates the synthesis rates of numerous target mRNA, including homologous downregulation of new GR synthesis. In this manner, CS dosing elicits widespread changes in gene expression with both increases and decreases found in multiple rat tissues (Almon et al., 2005a,c, 2007). Circadian production of the endogenous glucocorticoid hormone (cortisol in humans, corticosterone in animals) and control by the hypothalamic-pituitary-adrenal (HPA) axis and the turnover of GR and its mRNA introduce nonstationarities in the receptor-mediated control of tissue gene expression. Two major elements are needed for gene-mediated effects of CS in various tissues; the GR and the biochemical machinery for altered synthesis or degradation of particular mRNA and proteins responsible for specific steroid actions.

Fig. 1.

Schematic representation of the genomic mechanism of corticosteroids in tissues and the influence of estrogens on glucocorticoid signaling. ER, estrogen receptor; FKBP, FK506 binding protein; GR, glucocorticoid receptor; hsp 70/90, heat shock protein 70/90; nGRE, negative glucocorticoid response element; RNAP, RNA polymerase. Figure adapted from (Ayyar et al., 2017b).

Interactions between multiple endogenous steroid hormones (e.g., sex hormones and glucocorticoids) as well as exogenous CS can occur and represent complex phenomena. In a manner similar to the CS, estradiol (E₂), the major female sex hormone, can rapidly equilibrate within tissues (Puig-Duran et al., 1979), interact with cytoplasmic estrogen receptors (ER), form activated ER complexes, and, consequently, translocate into the nucleus and modulate its own sets of target genes (Stossi et al., 2004). Cooperative binding of two different steroid hormone receptors at single target enhancer elements has been demonstrated (Tsai et al., 1989). In the presence of both CS and estrogens, GR and ER complexes in the nucleus can interact within the promoter regions of several CS-regulated target genes (Tynan et al., 2004; Whirledge et al., 2013). Such interactions result in a competitive antagonism of CS gene regulation by E₂.

The genomic actions of CS, often divided into categories of transactivation and transrepression, have been extensively reviewed (De Bosscher et al., 2003). The GR is considered a transcription factor with others that include NF-κB, activator protein-1, and STAT5. After distribution and receptor binding, the time course of changes in gene and protein expression vary considerably, but it is difficult to resolve which transcription factor is involved without direct measurements of these factors. Classic dogma (Adcock and Caramori, 2001; Barnes, 2006) contends that the anti-inflammatory effects of CS are mediated predominantly by transrepression, while the undesired metabolic side-effects primarily stem from transactivation. However, this traditional view has been challenged (Newton and Holden, 2007; Vandevyver et al., 2013), ensuing the discovery of novel transactivated genes that encode proteins such as the glucocorticoid-induced leucine zipper (GILZ) (D’Adamio et al., 1997). The therapeutic (advantageous) relevance of transactivation remains largely unestablished and remains an important question in CS pharmacology. Recent studies (Ayyar et al., 2015, 2017b, 2019a) have quantitatively measured and examined the integrative physiology and pharmacology of GILZ regulation by endogenous and exogenous CS.

Our studies and models have contributed unique insights into the dynamics of the GR and their control of CS actions. In particular, while the CS have been well appreciated to differ in their PK and affinities to the GR (Mager et al., 2003d), additional key controlling factors that determine their PD and are components of models are the type of transcription factor, translocation of the CS-bound GR from cytosol into the nucleus, its binding to GRE on DNA, control of the expression of hundreds of genes, recycling of free GR from the nucleus, and feedback downregulation of the GR mRNA. Both the full occupation and depletion of cytosolic receptors and the mRNA feedback mechanism account for tolerance to CS, namely lesser effects on repeated dosing. Capturing these processes in studies of tissues of large numbers of animals (“giant rat” experiments) led to our first- through fifth-generation CS models that were premised on several basic PK/PD principles (Ramakrishnan et al., 2002). In turn, this multicomponent receptor model serves as the backbone of more complex systems models to be described in section IV. Our recent and continued assessments of CS pharmacology involved the expansion of our “giant rat” experimental paradigm to consider both sexes. Carefully controlled animal studies and systematic measurements of PK, receptor dynamics, and gene (biomarker) expression combined with advanced systems PK/PD analysis led us to unravel a unique and natural PD interaction between CS and estrogens occurring in vivo in a time-, sex-, and tissue-dependent manner (to be described in section IV).

III. Arenas of Mechanistic Modeling in PK/PD

A. Pharmacokinetic Models

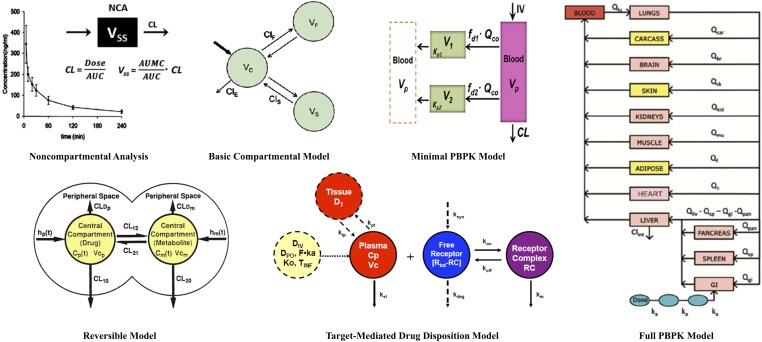
PK serves as the driving force for drug access to target sites. Drug input rates, distribution, and elimination processes control both the duration of drug exposure and, in turn, part of the duration of drug action. Since its inception, efforts in theoretical and applied PK have emphasized and evolved based on an appreciation of physiology, pharmacology, biochemistry, physicochemical, analytical methodology, mathematics, and statistics. Although the term "pharmacokinetics" was first introduced in 1953 (Dost, 1953), a systems approach to describe the processes of drug absorption, metabolism, distribution, and elimination was put forth as early as 1937 (Teorell, 1937). As displayed in Fig. 2, the major types of PK analysis methods and models now include: noncompartmental (NCA), basic and advanced compartmental, reversible compartmental, fully physiologic (PBPK), and minimal physiologic (mPBPK) approaches. Basic NCA aims to yield, as a useful starting point, information regarding the systemic clearance and steady-state volume of distribution, prime PK parameters summarizing the major elimination and distribution properties of drugs. Simple compartmental models represent semimechanistic frameworks based on a “tissue cluster” concept (Riegelman et al., 1968), which permit multiple-dose analyses and extrapolation, incorporate time-dependent and concentration-dependent processes, and provide added insights into distribution properties of drugs and organisms. More advanced compartmental models have been developed in PK, bearing complexities such as reversible systems (e.g., parent-metabolite interconversion, maternal-fetal disposition, enterohepatic recycling) and target-mediated drug disposition (TMDD). Drugs that bind to their pharmacological targets with high affinity and to a significant extent (relative to dose), such as antibodies (Wang et al., 2008) and some small molecules (Mager and Jusko, 2001a; An, 2017), can exhibit TMDD, where the drug-target interaction can be reflected in their dose-dependent PK profiles (Levy, 1994; Mager and Jusko, 2001a). The PBPK models are systems models developed based on anatomic constructions and functions such as tissue masses, blood flow, organ metabolism, specific drug absorption sites, and the processes of partitioning, binding, and transport. Such models have shown considerable success in characterizing and predicting the concentration-time profiles of small molecules (Rowland et al., 2011) and, more recently, large molecules (Garg and Balthasar, 2007; Shah and Betts, 2012) in plasma, tissues, and other body fluids. The “lumped” minimal physiologically based pharmacokinetic (mPBPK) models were introduced recently for small and large molecules and provide more useful assessments than do traditional mammillary models (Cao and Jusko, 2012; Cao et al., 2013). These mPBPK models provide a realistic basis for describing plasma PK data and differ from the traditional mammillary models in ways of initial distribution space (plasma), physiologic assignments, and restrictions (blood flow and tissue sizes), as well as flexibilities in handling different clearance mechanisms. These models have since been extended and applied to account for various physiologic complexities including the TMDD of large molecules (Cao and Jusko, 2014), kinetics of circulating target antigens (recombinant human TNF-α) (Chen et al., 2017), role of nonlinear binding of naproxen in plasma and extracellular fluid (Li et al., 2017b), and the sex-specific hepatic metabolism of MPL (Ayyar et al., 2019b). Recently, an extended “population mPBPK” approach was applied to study the plasma PK of levonorgestrel in women, considering known alterations in physiology that occur in obesity (Molins et al., 2018). Both full PBPK and minimal models have been successfully applied for the interspecies scaling of PK from animals to humans (Kawai et al., 1998; Meno-Tetang et al., 2006; Shah and Betts, 2012; Zhao et al., 2015). To date, there appear to be no fully elaborated PBPK models for any of the CS with direct measurements of tissue concentrations. The nonlinear complexities related to CBG binding and reversible metabolism will be challenging for constituting PBPK models for prednisolone and MPL. However, the PBPK of the less complex CSs, dexamethasone and betamethasone, have been simulated for pregnant women using the commercial software Simcyp (Ke and Milad, 2019).

Fig. 2.

Array of modeling approaches for pharmacokinetic data and systems, including noncompartmental analysis (NCA), basic compartmental (mammillary) models, reversible PK models, TMDD models, minimal PBPK, and full PBPK models. PBPK, physiologically-based pharmacokinetic; TMDD, target-mediated drug disposition.

The mathematical formalism relating to more complex PK phenomena such as reversible metabolism (Ebling and Jusko, 1986; Cheng and Jusko, 1990, 1993) and maternal-fetal disposition (Samtani et al., 2004, 2006a; Schwab et al., 2006) were established during studies of CS disposition (Fig. 2). For CS and an appreciable number of other drugs (e.g., spironolactone, estradiol, dapsone, lovastatin) (Cheng and Jusko, 1993), some metabolites may be enzymatically converted back to the administered parent compound, a phenomenon recognizable upon either direct administration of both the parent and metabolite or assessment of their stabilities in relevant body fluids. The reversible metabolic properties of prednisolone, MPL, and their keto metabolites were assessed extensively in the rat (Haughey and Jusko, 1992), rabbit (Ebling et al., 1985), and humans (Garg and Jusko, 1994). Simple models for the interconversion between cortisol and cortisone used area under the curve values to calculate interconversion and elimination clearances (Gurpide et al., 1963). Premised on understanding the underlying determinants of drug disposition including nonlinearities, analytical solutions for calculating the true clearance and volume of distribution at steady-state as well as two useful metrics, the exposure enhancement and the recycled fraction, were derived for parent drug and their reversible metabolites (Ebling and Jusko, 1986; Cheng and Jusko, 1991). Current software for making PBPK predictions do not account for the reversible metabolism that affects a large number of drugs.

Antenatal use of CS to induce fetal lung maturation in women at risk of preterm delivery is common in clinical practice. The PK of the common treatment CS, betamethasone and dexamethasone, were analyzed in ovine and rodent models of pregnancy to assess maternal-fetal disposition and factors controlling fetal exposure (Samtani et al., 2004). These studies developed and applied area/moment analysis and compartmental PK modeling techniques involving models with maternal-fetal distribution, exchange, and elimination of drugs, requiring the simultaneous analysis of paired maternal-fetal data obtained after both maternal and fetal drug dosing. Mechanistic PK/PD modeling studies were conducted in a rat model of pregnancy to link fetal exposures of free dexamethasone and corticosterone to their receptor/gene-mediated effects on stimulating fetal expression of lung surfactant mRNA and protein, with a goal of designing an optimal approach for dose-sparing antenatal CS therapy (Samtani et al., 2006a,b).

B. Mechanism-Based Pharmacodynamic Models

The area of PK/PD modeling has evolved based on an appreciation of basic pharmacological principles mostly applied to static or in vitro systems (Jusko, 2013). Over several decades, PD has grown from an empirical to a mechanistic and quantitative endeavor that resulted from improved analytical methods to measure various biomarkers of drug effects, advances in computer hardware, software, and statistical algorithms for parameter estimation, increased regulatory and academic interest, and the continued refinement of PK/PD models based on underlying physiologic mechanisms (Mager et al., 2003e). It was in the mid-1960s when Gerhard Levy, who is now viewed as the “Father of Pharmacodynamics” (Fung and Jusko, 2015), proposed the first PK/PD (“k∙m”) equation linking the in vivo time course of a drug response (m representing the linear slope of effect vs. the log of drug concentration) to the drug’s first-order elimination rate constant (k) (Levy, 1964, 1966). Wagner subsequently proposed direct effect models (Wagner, 1968), which employed the Hill equation reflective of the law of mass action for drug-receptor binding as a means to describe the full (nonlinear) behavior of responses. Such direct effect models are premised on the fundamental assumption that drug responses are directly proportional to receptor occupancy (i.e., with linear transduction), that plasma drug concentrations are in rapid equilibrium with the effect site, and that receptor binding is extremely rapid. In accordance with these assumptions, the maximum or peak effects should occur simultaneously with peak drug concentrations. This basic PK/PD situation is applicable for drugs affecting measured circulating enzymatic activity such as the ACE inhibitory effects of benazeprilat (Toutain et al., 2000) and the direct immunosuppression of lymphocyte proliferation by various CSs (Magee et al., 2002) where the drug and target are interacting in blood.

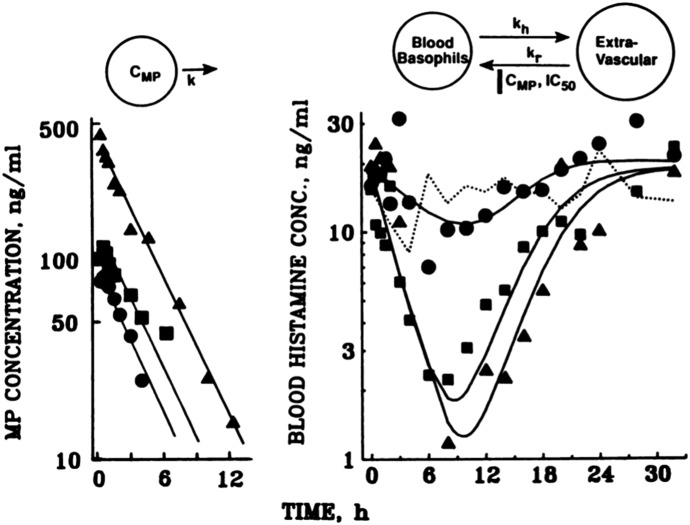
Most in vivo responses, however, lag observed plasma concentrations, a phenomenon resulting in hysteresis in plots of response versus concentration (Levy et al., 1969). This temporal displacement can result from various physiologic and/or pharmacological causes. The field of mechanism-based PK/PD modeling has advanced greatly with the appreciation and development of relationships between plasma drug exposure and mechanisms of delayed drug action. Delayed responses were first rationalized (Segre, 1968) as rate-limiting drug distribution to a hypothetical “biophase” compartment where the PD effect was assumed to occur. This concept was later popularized (Sheiner et al., 1979) with application of an “effect compartment” model, accounting for hysteresis between drug concentrations in plasma and responses using a diffusion-like transfer rate-constant (k_eo). This model, however, has been misapplied in some cases where alternative mechanisms producing delayed effects are plausible (Jusko and Ko, 1994). Many therapeutic agents can interfere with body homeostasis via indirect mechanisms affecting the natural turnover of biologic substances, structures, or their functions. Four basic indirect response models were developed and have been widely applied to characterize numerous delayed PD responses where the production (k_in) or loss (k_out) of the measured factor are rate-controlling (Dayneka et al., 1993; Jusko and Ko, 1994; Sharma and Jusko, 1998). These models embrace two basic tenets of PD: capacity limitation in target binding or action of the drug and the presence of turnover and homeostasis in physiology and disease. This type of model was conceptualized and applied in describing the suppressive effects of MPL on basophil cell trafficking from the extravascular space into blood (Kong et al., 1989) before it was extended to describe the time course of many other drug responses. Figure 3 depicts the PK/PD model and effects of 0, 10, 20, and 40 mg doses of intravenous MPL on basophils in blood, measured as whole blood histamine. After dosing, blood basophils began to fall immediately, owing to their movement into extravascular sites (k_h) as the return (k_r) process was essentially fully inhibited. When MPL concentrations fall below the IC₅₀ value of about 2 ng/ml, the cells return to the blood and gradually to the baseline value. Similar response patterns were found for plasma cortisol and blood lymphocytes. The indirect models have since been expanded to consider complexities such as depletion or accretion of precursor substances (Sharma et al., 1998), circadian input (Chakraborty et al., 1999b), circadian removal (Ayyar et al., 2019c), multicompartment responses (Krzyzanski and Jusko, 2001), cell life span loss (Krzyzanski et al., 1999), drug interactions (Earp et al., 2004), baseline variability (Sun and Jusko, 1999; Woo et al., 2009), physiologic limits (Yao et al., 2006b), role of drug infusions (Krzyzanski and Jusko, 1997), and optimization of dosage regimens (Gobburu and Jusko, 2001). Recently, linear combinations of engineering feedback control terms were incorporated into classic indirect response models as a simple means for modeling PD processes subject to autoregulation (Zhang and D’Argenio, 2016).

Fig. 3.

(Top) Schematics of the pharmacokinetic (left) and two-compartment cell distribution and direct suppression model for basophils (whole blood histamine) (right) in relation to methylprednisolone (C_MP) concentrations where IC₅₀ is the C_MP producing 50% inhibition of basophil return to blood (k_r). (Bottom) Methylprednisolone concentrations (left) and blood basophils as whole blood histamine concentrations (C_B) vs. time in a normal male subject at baseline and after 10 (●), 20 (■) and 40 (▲) mg of intravenous methylprednisolone sodium succinate. Solid lines depict joint model fittings. Figure modified from Kong et al., 1989 with permission of John Wiley & Sons, Inc.

The majority of rapid effects of CS, such as leukocyte and lymphocyte dynamics (Wald and Jusko, 1994; Chow et al., 1999; Mager et al., 2003a), blood histamine (Kong et al., 1989), and cortisol suppression (Magee et al., 2001), are well described by simple indirect response models. Clinical PD responses of CS have been examined extensively in relation to chronotherapy (Fisher et al., 1992), design of steroid-sparing regimens (Reiss et al., 1990), drug-drug interactions (Kandrotas et al., 1987; Slayter et al., 1996), sex (Lew et al., 1993), obesity (Dunn et al., 1991), and renal failure (Jusko et al., 1995b), utilizing indirect response-based modeling approaches. Whereas the basic indirect response models assume a constant steady-state baseline value in the absence of drug, some biomarkers may exhibit non-stationarity or a time-dependent baseline. Periodic production rates ranging from a simple cosines to asymmetric ramp functions have been incorporated for the indirect response modeling of diverse CS responses, such as cortisol suppression (Rohatagi et al., 1996; Chakraborty et al., 1999b), lymphocyte trafficking (Magee et al., 2002), and the receptor-mediated stimulation or inhibition of target mRNA (Sukumaran et al., 2011b). The Derendorf laboratory has also extensively used indirect response models to capture the PK/PD of various CS. One such study found that the time of day of dosing affected responses such as cortisol suppression and lymphocyte trafficking (Xu et al., 2008). The model comprehensively included the joint effects of free prednisolone and cortisol on inhibition of k_in for lymphocyte suppression. The modeling was based on the PK of free prednisolone, but it is difficult to discern whether free or total prednisolone best controls the pharmacodynamics, as both concentrations have generally similar washout profiles after single doses (Wald et al., 1992).

In extending our interests in structure-activity relationships and dose equivalencies for CS, Mager et al. (2003a) compared the PK of cortisol, prednisolone, MPL, and dexamethasone in healthy volunteers and assessed the effects of these CS on endogenous plasma cortisol, T-helper and T-suppressor lymphocytes, and neutrophils in blood. Indirect response models were employed that allowed joint assessment of the system variables (turnover) while resolving EC₅₀ values for the four CSs. The latter values differed for each of the biomarkers, but showed excellent correlations with relative receptor affinities of the four CS. These studies demonstrated both the modeling rigor of indirect response models to capture relatively rapid CS effects as well as confirmed classic expectations that PK, receptor binding, and turnover (the three “pillars”) are advantageous in describing common effects across multiple CSs.

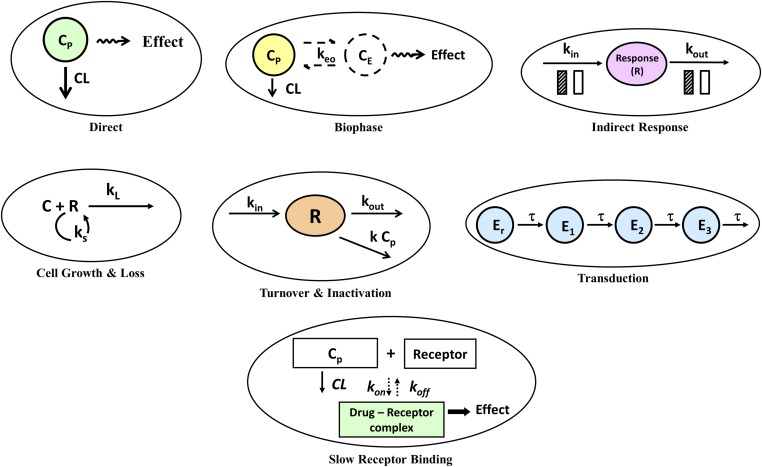
Figure 4 demonstrates the seven primary mechanism-based PKPD models that are often employed as a starting point in the “top-down” analysis of the time course of drug responses (Jusko, 2013). The figure includes the direct effect, biophase, and indirect response models already described. All models except the direct effect and biophase models include a turnover process along with a pharmacologic function for the mechanism of action. Figure 4, middle left, depicts a basic model with self-replication of cells (k_s) and a drug-induced loss process (k_L). Originally proposed to account for the actions of cytotoxic anticancer drugs (Jusko, 1971), this type of model has also been applied to some antibiotics (Zhi et al., 1988) and antimalarial drugs (Gordi et al., 2005). Figure 4, middle center, displays a basic model with zero-order production (k_in), first-order loss (k_out), and an irreversible second-order inactivation of the response variable. This type of model has been used to account for the anti-platelet inactivation of cyclooxygenase-1 by aspirin (Yamamoto et al., 1996) and effects of proton pump inhibitors (Puchalski et al., 2001). Drug response may be the result of a signaling cascade controlled by secondary messengers as well as transcripts and proteins. These post-receptor events may be rate-limiting, producing additional time delays distinguished most readily from biophase or turnover delays by a latency in the onset of drug response relative to drug concentrations. Transduction processes can be rapid or slow, single or multiple, linear or nonlinear. A general time-dependent transduction model has been proposed (Sun and Jusko, 1998; Mager and Jusko, 2001b), which introduces a series of transit compartments with equal time-constants (τ). These models (Fig. 4, middle right) offer a simplistic and flexible method to capture relatively long-onset delays for applicable drug responses in the absence of measurements of the true biologic mediators. Many applications of this model have been reported (Mager and Jusko, 2001b), including the delayed chemotherapeutic effects of methotrexate (Lobo and Balthasar, 2002).

Fig. 4.

Seven major PK/PD models based on mechanisms of drug action and primary rate-limiting steps in the kinetic, target-binding, or physiologic process.

Added to these basic PD models should be consideration that the rates of binding and dissociation of drug with their receptors may be either contributory, rate limiting, or account for delayed responses (Fig. 4, bottom center). This process is often found in TMDD models and is a component of our complex receptor models, although these rates tend to be relatively fast for CS compared with later steps in the receptor/gene-mediated transduction chain. For example, the half-life for the k_off dissociation of prednisolone from hepatic GR receptors is about 2 minutes (Boudinot et al., 1986). Of interest, the k_on and k_off rates of 8 calcium channel blockers were used as the rate-determining factors controlling delayed effects on blood pressure in hypertensive subjects (Shimada et al., 1996).

Combinations of the basic PD models have served to provide a mechanistic appreciation of drug interactions compared with empirical methods such as Loewe additivity and isobolograms. In particular, Earp et al. (2004) provided equations describing dual drug effects occurring in the four basic indirect response models. The long-mysterious concept of drug synergy could be explained as the natural multiplicative consequence of two drugs having opposite effects on each side of a turnover process (e.g., drug A inhibiting production and drug B stimulating removal). Chakraborty et al. (1999a), in assessing immunosuppressive interactions of IL-10 and prednisolone for lymphocyte proliferation, introduced a drug interaction factor, psi (ψ), which was attached to an IC₅₀ value to describe deviations from expectations of joint additive responses to two drugs using classic direct relationships such as competitive and noncompetitive inhibition.

As basic PK/PD modeling moves toward dealing with biologic and pharmacologic problems of ever-increasing complexity, more comprehensive systems models can be developed through the assembly of the basic components outlined in this section. Such has been our approach in evolving several generations of increasingly mechanistic PK/PD models to decipher the genomic mechanisms of CS actions (Boudinot et al., 1986; Nichols et al., 1989; Xu et al., 1995; Sun et al., 1998a; Ramakrishnan et al., 2002; Jin et al., 2003; Mager et al., 2003d; Hazra et al., 2007) (highlighted in section IV).

C. Enhanced Pharmacokinetic/Pharmacodynamic and Systems Pharmacology Models

1. The Systems Approach

Modeling as a scientific endeavor for assimilating knowledge embodies the process of human cognition itself, to wit “the entire breadth and depth of the human understanding of our perceived world is based on models” (Westwick and Kearney, 1998). As such, parallels may be drawn among two widely adopted philosophies in psychology and the systems approach. In attempting to rationalize human perception, Gestalt philosophy emphasized that perceptual organization involved the processing of wholes and whole processes possessed of defined intrinsic laws. In considering the living organism as an open, nonlinear, and highly dynamic system, the general systems theory (von Bertalanffy, 1950) was advanced, a scientific dogma concerned with the principles that apply to systems in general. The major goal of a systems approach in biology was to develop theories (mathematical models) to serve as “gestalts” for interpreting experimental observations and pave the way to establish biology as an “exact” science. These ideals are consonant with the works of pioneering systems physiologists such as Yates et al. (1968), who stated that “a system of coupled, connected and interacting biological components has properties beyond those that can be discovered by analysis of the components in isolation” and, relatedly, that “the objective of systems biology is to determine the dynamic attributes of a biosystem of interest, and to rationalize these attributes in terms of particular properties of the components, signals, and connections involved”. Many modern conceptions of physiologic control are deeply rooted in systems theories ranging from feedback and homeostasis (Cannon, 1929) to allometry and ontogenic growth (Adolph, 1949; von Bertalanffy, 1950).

2. Systems Biology and Enhanced Pharmacokinetic/Pharmacodynamic Modeling

Systems biology is a multi-disciplinary endeavor, borrowing from genomics, transcriptomics, proteomics, metabolomics, and network modeling, geared toward integrating the interactions of biomolecules across various scales of biologic organization (Oltvai and Barabasi, 2002). As such, systems modelers tend to seek holistic models that assemble all the known components of the biologic system of interest to simulate interrelationships and outcomes upon perturbing various components within the system. With such extensive networks, the dynamic models often operate in a simulation mode with some degree of subjective calibration of parameters made with available experimental data. Complex systems models have been developed for understanding inflammation (Dong et al., 2010), the immune system (Palsson et al., 2013), and for control of calcium homeostasis and bone remodeling (Peterson and Riggs, 2010). Building such models and data repositories often requires a team approach utilizing the input of experts from various disciplines. Once developed, they offer a platform for common understanding, enlightened discussion, efficient experimentation, and continual advancement of improved quantitative models (Jusko, 2013). Of note, the successful application of a computational model of the ErbB signaling network informed the discovery of MM-111, a bispecific antibody targeting ErbB2/ErbB3 receptor signaling, developed by Merrimack Pharmaceuticals (Schoeberl et al., 2009). The model predicted superior efficacy upon dual targeting of ErbB2 and ErbB3 compared with ErbB3-targeted monotherapy in the treatment of ErbB2-amplified breast cancers (McDonagh et al., 2012).

The basic mechanism-based PK/PD models (Fig. 4) tend to incorporate one or more of the major rate-limiting processes, including PK, receptor binding, and/or homeostatic mechanisms controlling drug responses. Unlike systems biology approaches that employ multiscale network-based structures, basic PK/PD models often rely on a single end-point (biomarker) response, and typically seek parsimony and robust statistical reliability of model parameters. Throughout most of the 20th Century, systems biology and PK/PD have largely evolved in parallel as distinct disciplines. There is now an appreciation for synergistically merging the fields of systems biology and PK/PD (Iyengar et al., 2012) to enhance the rapidly growing discipline of QSP, which aims to discover and understand therapeutic molecules at the levels of target engagement, changes in cellular biochemistry, impact on human pathophysiology, and optimal clinical use (https://www.nigms.nih.gov/training/documents/systemspharmawpsorger2011.pdf). In practice, QSP focuses on the quantitative modeling of dynamic interactions among individual elements within a system and serves to guide drug discovery and clinical development by developing formal mathematical models that incorporate data at multiple scales. The development and application of multiscale PK/PD models, therefore, forms an integral facet of the discipline.

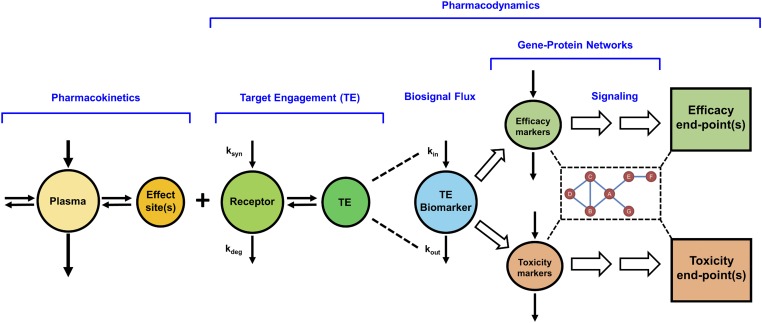
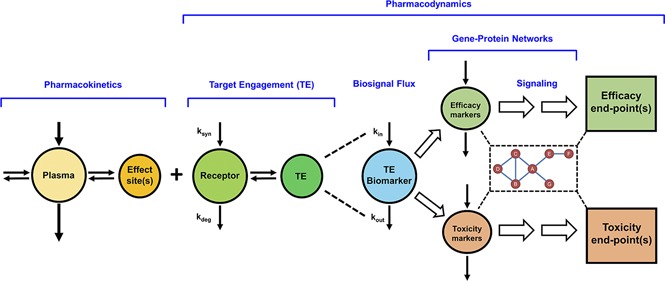
The major components of systems PK/PD models for drugs altering genomic and/or proteomic signaling networks, such as the CS, are depicted in Fig. 5. This paradigm incorporates the basic determinants linking drug exposure in plasma to response (Jusko et al., 1995a; Mager et al., 2003e) and comprises a more elaborate representation of post-receptor signaling events occurring through gene-protein networks. Drug in plasma distributes to various body spaces, including the effect-site or “biophase.” Unbound drug concentrations at the target site serve as the driving force for engaging free receptors, resulting in the formation of the drug-receptor complex (target engagement), which in turn stimulates or inhibits the production or loss (turnover) of endogenous biomarkers or mediators (biosignal flux). For drugs with complicated mechanisms, such as CSs, the drug-receptor complex evokes a polygenic response at the subcellular to organ levels, primarily by altering the turnover rates of numerous primary target genes as well as secondary messengers. Some of the altered mRNA and proteins mediate pharmacologic effects of the drug, whereas others represent mediators of toxicities associated with drug exposure. The signaling pathways perturbed by drug may not transduce in a linear manner to mediate efficacious and toxic responses but can act through intertwined transduction networks, complicating safety-efficacy relationships, as exemplified by genomic steroid actions. Additional complexities such as nonstationary baselines (Sukumaran et al., 2011b), multiple receptors (Ayyar et al., 2019a), feedback/tolerance/rebound phenomena (Sun et al., 1998a), drug interactions (Li et al., 2017c), sex differences (Ayyar et al., 2019a,b), pathophysiological changes (Earp et al., 2008a), and genetic polymorphisms (Iyengar et al., 2012) may be encountered for one or more processes included within this systems PK/PD framework.

Fig. 5.

Basic components of systems pharmacokinetic/pharmacodynamic models of genomic drug action. The PK is reflected by the concentration of drug in the central (plasma) compartment and its distribution to the effect site(s) in tissues. Local concentrations of unbound drug bind with free receptors that are synthesized (k_syn) and degraded (k_deg) over time in tissues. Target engagement and occupancy serves as the driving force for the inhibition and/or stimulation of the production (k_in) or removal (k_out) of multiple target gene biomarkers. Genomic markers and mediators of both therapeutic and adverse drug effects signal through interconnected gene (mRNA and protein) networks to mediate clinically measurable PD end-point responses. For drugs with genomic mechanisms, such as corticosteroids, signaling proteins related to efficacy and toxicity often do not transduce in a linear manner but interact through intertwined signaling networks.

3. Challenges and Opportunities

Considerable opportunities and challenges exist in moving from basic toward systems PK/PD models. Questions regarding model granularity (holism vs. reductionism), optimal approaches between robust model fitting and simulation, multidimensional data requirements, and scaling of drug responses from in vitro and animal models to patient outcomes frequently arise. Such issues are of ongoing research (and debate) among systems biologists and PK/PD modelers. Diverse receptor-related and post-receptor signaling mechanisms require further elucidation. Homeostatic mechanisms present at the whole body to intracellular scales feature a broad array of feedback loops and compensatory controls (Brandman and Meyer, 2008), some of which describe drug tolerance and rebound phenomena. Homologous desensitization is known to occur when a receptor decreases its response upon prolonged and/or supraphysiologic exposure to an agonist, causing an uncoupling of the receptor from the signaling cascade, attenuating drug response. Post-receptor transduction cascades involving multiple horizontally and vertically signaling protein networks may represent rate-controlling factors that introduce considerable lags between drug exposure and response. Transduction delays are often accounted for using multiple transit steps in basic PK/PD modeling (Mager and Jusko, 2001b). Substitution of empirical transit delay steps with the measured dynamics of mechanism-based biomarkers and signaling biomolecules (mRNA, proteins, phosphoproteins, and enzymes) along with their inter-connections represent a current and future area of opportunity in evolving more mechanistic systems pharmacology models.

Both basic PK/PD and QSP modelers should bear in mind that the major goal of mechanistic modeling is a translational one (Mager et al., 2009); measurements in cell lines and animal models need to reflect relevant processes in humans. Although it is somewhat commonplace for a conserved model structure to be applicable across species (Mager and Jusko, 2002b; Mager et al., 2003c), factors such as species differences in the cross-reactivity of drug to target and varying time scales of physiologic phenomena (e.g., 4-day rodent estrous vs. 28-day human menstrual reproductive cycle) should be considered. While allometric and PBPK strategies are relatively well-established and routinely applied for the interspecies scaling of PK (Lin, 1998), species-dependent variability in key determinants beyond general anatomy (blood/lymph flows, organ volumes, renal filtration) must be accounted for with distinct considerations for small molecules (e.g., protein binding, metabolic enzymes, transporters) and large molecule therapeutics (e.g., circulating soluble target antigen, FcRn expression, and target abundance in tissue sites of action and catabolism). The challenges of scaling entire systems PK/PD models remain considerable, although some success has been met with use of mechanistic PK/PD models (Kagan et al., 2010). Whenever possible, the ability to correlate parameters relating to drug-receptor binding (k_on, k_off, or K_D), drug efficacy (E_max and EC₅₀), growth (k_g), and turnover (k_in and k_out) between in vitro measurements and in vivo estimates from preclinical and clinical data must be evaluated.

Measurement of the inhibition of mitogen-stimulated lymphocyte proliferation, either in isolated cells or in whole blood, has been a frequently used method to assess the ex vivo immunosuppressive activity of CS. Whole blood from male human subjects was used to obtain IC₅₀ values of 10 common CSs (Mager et al., 2003b). There was excellent (r² = 0.95) correlation of the reciprocal of the IC₅₀ values with the relative receptor affinity of these compounds. This is a type of “direct effect” that has relevance in vivo. Studies in both rats (Meno-Tetang et al., 1999) and humans (Magee et al., 2002) showed that prednisolone had dual effects on circulating lymphocytes: a cell trafficking effect with reduction of cell numbers (similar to the profiles in Fig. 2) and inhibition of their ability to respond to mitogen stimulation. This work demonstrated the complexity of CS effects, the insightful application of mechanistic PK/PD modeling to unravel the relative contributions of these dual effects, and the correspondence of these animal and human systems.

IV. Pharmacokinetic/Pharmacodynamic/Systems Modeling of Corticosteroids

The receptor/gene-mediated actions of CS have been of interest to us for over three decades. Several generations of increasingly mechanistic PK/PD models of gene-mediated steroid actions have been developed, with each successive model evolving based upon on an increasing knowledge of pharmacogenomics and advancements in bioanalysis. These models have thus far demonstrated that the major determinants of genomic steroid responses include: 1) disposition characteristics of the steroid, 2) relative receptor affinity of the steroid, 3) availability of cytosolic receptors, and 4) secondarily induced mediators. Improved QSP models were developed in parallel with advances in our experimental “giant-rat” studies, where groups of animals are given various doses of CS and blood and multiple tissues sampled at sacrifice to assess PK, tissue receptor content, tissue gene expression (both specific and with gene arrays), proteomics, tissue enzyme activities, various circulating biomarkers, and sometimes measurable structures or functions.

The earliest studies in our laboratory examined literature data for effects of prednisolone on TAT induction in rat liver (Boudinot et al., 1986) and then employed the adrenalectomized (ADX) male rat model to examine steroid actions (Nichols et al., 1989). The use of ADX animals obviated complicating factors such as the influence of endogenous glucocorticoids. Tyrosine aminotransferase (TAT) was studied as a classic biomarker for genomic effects of CSs in rat liver (De Bosscher et al., 2003). This experimental paradigm subsequently evolved to examine the PK/PD effects of MPL in intact (non-ADX) rats, with consideration of endogenous steroid effects and circadian rhythms (Hazra et al., 2007).

Several aspects of CS-induced changes in metabolic functioning were explored in our animal studies, leading to new insights into the diversity of receptor/gene-mediated changes. Extensive studies were undertaken to examine the mechanisms by which CSs alter glucose metabolism and induce insulin resistance in rats. The effects of acute and chronic MPL on glucose homeostasis were investigated, and a series of mechanistic PK/PD models were proposed to explain the time course of systemic glucose changes (Jin et al., 2004; Almon et al., 2005b; Yao et al., 2006a; Jin and Jusko, 2009a,b; Fang et al., 2011; Sukumaran et al., 2011b). By appreciating that CS-induced glucose dysregulation results from the interplay of multiple target organs (whole body metabolic syndrome), a meta-modeling analysis was performed to integrate many of the key biochemical processes and roles and interrelationships of the liver, muscle, adipose, and pancreas in the development of steroid diabetes (Fang et al., 2013). The developed systems model jointly incorporated multiscale experimental measurements including drug PK, receptor binding components, target gene mRNA perturbations in multiple tissues after MPL dosing (e.g., hepatic PEPCK, leptin in adipose, and ILR1 and IRS-1 in muscle), plasma hormones and biomarkers (e.g., leptin, insulin, glucose, and free fatty acids), and food intake. This multi-organ model facilitated our understanding of how well an array of hypotheses on how CSs alter glucose metabolism explained the overall experimental data sets obtained in rats tested at multiple dose levels, dosage regimens, and over time.

The integrated effects of circadian rhythms, MPL PK, and the glucose/free fatty acids/insulin system on the regulation of two important adipokines, adiponectin and leptin, were evaluated using systems PK/PD modeling (Sukumaran et al., 2011b). The model simultaneously captured the time course of adiponectin and leptin mRNA in adipose tissue and associated changes in their circulating protein concentrations as well as glucose, insulin, and free fatty acid concentrations in plasma, under homeostatic (circadian) and perturbed (MPL-dosed) conditions. The receptor-mediated enhancement of leptin mRNA and protein by MPL were well-described based on the fifth-generation model alone. Unlike the case for leptin, MPL dosing elicited a complex, biphasic response profile for adiponectin over time (sharp rise, fall below baseline, and eventual return). Evidence from various literature reports indicated the influence of multiple hormones and transcription factors (e.g., insulin effects) on adiponectin gene regulation in adipose tissues (Sukumaran et al., 2012). Therefore, the model incorporated measured MPL effects on glucose/free fatty acids/insulin dynamics and linked the secondarily induced stimulation of insulin on adiponectin. This enhanced model enabled a more complete and mechanism-based description of the multi-factorial control of MPL on adipokine regulation and, consequently, was able to characterize the biphasic profile of adiponectin.

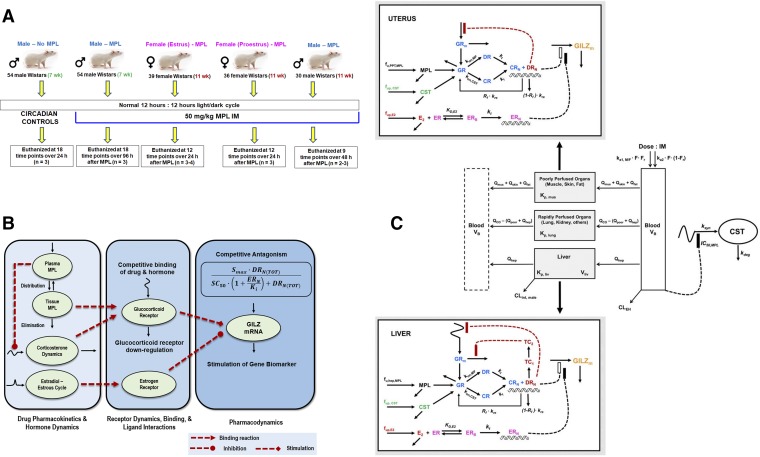
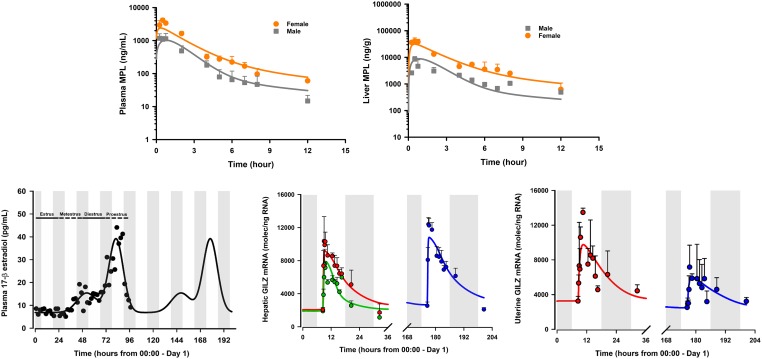
Our early CS PK/PD studies were confined to male rats. Sex is a relevant factor influencing the PK/PD of many drugs. Despite this recognition, very few preclinical PK/PD studies to date include sex as a variable. We often examined sex differences in the disposition and pharmacology of CS in humans, animals, and cell systems. Sex differences in the PK (clearance) and PD (sensitivity to adrenal suppression) of MPL have been observed in healthy subjects (Lew et al., 1993). Females exhibited faster clearances and lower IC₅₀ values than males. Ex vivo assessments of sex-related differences in the sensitivity of prednisolone to inhibit lymphocyte proliferation in whole blood have been reported in humans, rabbits, and rats (Ferron and Jusko, 1998). Modest-to-pronounced sex differences were recently observed in collagen-induced arthritis (CIA) disease progression, in the PK of dexamethasone, and in the anti-inflammatory efficacy of the drug in CIA rats (Song et al., 2018). Our understanding of CS systems pharmacology was recently broadened by extending experimental and pharmacogenomic modeling assessments from the intact male rat model to females with consideration of female reproductive cycles (as described section IV.3). These studies are consonant with recent emphasis (Clayton and Collins, 2014; Danska, 2014) that translational studies of sex differences should be expanded.

Pathophysiological changes in the system arising from disease progression represents another crucial component that must be taken into consideration while evaluating PK/PD. The fifth-generation model of CS developed from our studies of MPL (Ramakrishnan et al., 2002) was incorporated into a larger systems model to describe inflammatory disease progression in a male rat model of collagen-induced rheumatoid arthritis (paw edema) and the effects of dexamethasone on inhibition of pro-inflammatory cytokine genes in inflamed rat paws (Earp et al., 2008a,b). The systems model comprised an assembly of several components: the fifth-generation PK-receptor model, multiple transit steps reflecting the slowly evolving underlying arthritis disease progression, turnover of pro-inflammatory cytokine mRNA, and the contribution of three cytokines to the observed paw edema. The pronounced suppression of multiple pro-inflammatory genes (TNF-α, IL-6, IL-1β) by dexamethasone demonstrated the key mechanism of CS action and distinct “clinical” advantage of such broad effects. This comprehensive model was subsequently expanded by incorporating a systems model of bone remodeling (Lemaire et al., 2004) to further explore the molecular effects of arthritis and dexamethasone on bone mineral density (Lon et al., 2015). This study incorporated dynamic measurements of IL-6 and IL-1β protein concentrations in arthritic paws as well as protein concentrations of two key regulators of bone turnover, receptor activator of nuclear factor kappa-B ligand (RANKL), and osteoprotegerin (OPG). The gradual and sustained increase in RANKL:OPG ratios in CIA rats during disease progression indicated the presence of active bone resorption, which was confirmed by direct measurement of bone mineral density. The extended systems model successfully captured both the progression of RANKL and OPG in rheumatoid arthritis as well as the therapeutic PD effects of dexamethasone dosing. Studies are ongoing to extend our PK/PD/PG/DIS assessments of dexamethasone from arthritic male rats to females. Initial indications are that, like in humans, female rats develop rheumatoid arthritis more readily and quickly and are less sensitive than males to the anti-inflammatory effects of dexamethasone (Song et al., 2018).

Systems PD modeling that integrates “horizontal” and “vertical” aspects of drug actions are critical for gaining quantitative insights into drugs, such as CS, with complex mechanisms. Since hundreds of steroid-target genes are regulated in an organ, the “horizontal” can be captured by studying large-scale gene expression changes within tissues (Yang et al., 2008). Our early pharmacogenomic assessments of CS effects in rat tissues used our “giant rat” paradigm and employed early microarray platforms to demonstrate that MPL caused both increased and decreased expression of hundreds of genes in the liver (Almon et al., 2005a), skeletal muscle (Almon et al., 2007), kidney (Almon et al., 2005c), and lung (Sukumaran et al., 2011a). These findings were accompanied by development of new data-mining techniques for assessing time-series data and by identification of affected metabolic pathways that helped underscore why CS produce such extensive metabolic derangements in the body, especially on chronic use (Acevedo et al., 2019). Subsequent bioanalytical developments in proteomics involved highly sensitive and specific LC/MS/MS methodology that could measure hundreds of proteins in livers from our “giant rat” experiments (Qu et al., 2006; Nouri-Nigjeh et al., 2014). Questions regarding the complementarity (or lack thereof) between mRNA and proteins have been of general interest in molecular and systems pharmacology, as protein expression is often cited as being more reflective of drug efficacy and toxicity than mRNA expression. While some researchers believe that changes in transcript expression are seldom accompanied by concomitant alterations in protein profiles, these are often based on same-time single samples. This general question, along with improved bioanalytical capabilities, led to our comparisons of tandem and temporal genomic and proteomic effects of MPL. Hierarchical clustering based on temporal directionality of the common genes quantifiable at both the mRNA and protein levels revealed two dominant patterns: one of these patterns exhibited complementary mRNA and protein expression profiles (both changing in the same direction), whereas a second pattern indicated that changes in the mRNA were accompanied by changes in associated proteins in the reverse direction (Kamisoglu et al., 2015). Our previous studies using microarrays provided the basis to model the possible receptor-mediated mechanisms controlling the time course of several mRNAs (Jin et al., 2003). Expanding upon this work, a series of mechanism-based pharmacogenomic models were developed that jointly captured the emergent temporal transcript and protein expression patterns of over 120 mRNA and proteins perturbed by MPL (Ayyar et al., 2018a). Together, our bioinformatics (Kamisoglu et al., 2015) and model-based analyses (Ayyar et al., 2018a) indicate that transcript expression recapitulated protein dynamics for approximately 40%–50% of the genes for which both transcript and protein information were available within the -omics data sets. Our studies have demonstrated that collection of time-series PD data allows the connectivity between mRNA and proteins to be readily revealed, although the changes may occur with complex (and often opposite) directionalities.

When assessing CS effects on the multiplicity of biomarkers, genes, and proteins affected in both normal and drug-treated rat models, it is essential to consider the endogenous and often circadian behavior of these PD variables. We enacted “giant-rat” studies under carefully controlled light/dark conditions and euthanized normal rats at various times over the 24-hour light/dark cycle and used microarrays to assess gene expression in various tissues. Circadian changes of dozens of genes in rat liver, lung, muscle, and fat were identified and compared showing peaks and nadirs at differing times of the 24-hour clock for various clusters of genes with only partial concordance across tissues (Mavroudis et al., 2018a). Several known core-clock genes were found in all tissues and an integrated model for control of natural circadian rhythms was applied across the four tissues (Mavroudis et al., 2018b). Systems models for CS effects in both animals and humans need consideration that corticosterone (rats) and cortisol (humans) plus large numbers of genes and biomarkers are controlled by circadian rhythms that serve as time-varying endogenous baselines and may reflect both normal and deranged physiologic functioning. Several of our enhanced PK/PD models have these complexities accounted for.

The “vertical” in systems modeling is reflected by the intermediary mechanisms linking drug PK and receptor binding to resulting pharmacogenomic changes at the level of mRNA (Ramakrishnan et al., 2002) and proteins, and ultimately, to clinically-relevant PD outcomes (Earp et al., 2008a; Ayyar et al., 2018b). Our most recent efforts showcase the application of combined systems (experimental and modeling) approaches to decipher the “horizontal” and “vertical” PK/PD/pharmacogenomic (PK/PD/PG) relationships of MPL in relation to: 1) circadian gene expression and tissue-specific responses, 2) biologic signaling networks, and 3) sex differences, utilizing systems pharmacology approaches supported with data from microarray and proteomics analysis, systemic physiologic measurements, and/or more focused quantitation of useful biomarker(s). The development and basis of the animal model systems, modeling strategies employed, major results, and lessons learned from these studies are summarized.

A. Lesson 1: Multi-Tissue Modeling of the Glucocorticoid-Induced Leucine Zipper Gene Delineates Major System Determinants of Genomic Steroid Response

The genomic response to MPL was examined in various tissues from intact male rats by employing GILZ (Ayroldi and Riccardi, 2009), an important mediator of the anti-inflammatory actions of CSs, as a genomic biomarker. Important early steps involved the identification, assay development, and application of a sensitive, ubiquitously expressed, and pharmacologically relevant biomarker of CS actions. Literature reports and available in-house tissue microarray data (Almon et al., 2003, 2004; Sukumaran et al., 2010, 2011a) were mined to identify a subset of candidate genes, of which GILZ was pursued for further study. Features making GILZ a more robust biomarker compared with other routine gene markers of interest [e.g., tyrosine aminotransferase (TAT), glutamine synthetase, and phosphoenolpyruvate carboxykinase (PEPCK)] included: 1) ubiquitous expression in multiple tissues in humans (Cannarile et al., 2001) and rats (Ayyar et al., 2015), 2) exquisite sensitivity to glucocorticoids due to the presence of multiple functional GREs in its promoter region, and 3) its relation, in part, to anti-inflammatory CS efficacy.

In addition to quantifying the basal presence of GILZ in multiple rat tissues (Ayyar et al., 2015), robust circadian oscillations were identified in lung, muscle, and adipose tissue (Ayyar et al., 2017b) over the light:dark cycle in rats, a pattern entrained to that of endogenous corticosterone release in rats. Expression of GILZ was strongly enhanced (500%–1080%) in a time-dependent manner in the same tissues upon dosing 50 mg/kg i.m. MPL. In all three tissues, GILZ returned to its nonstationary baseline beyond 24 hours after MPL. Mild circadian rhythms in GR mRNA and robust downregulation by MPL (40%–80%) were quantified.

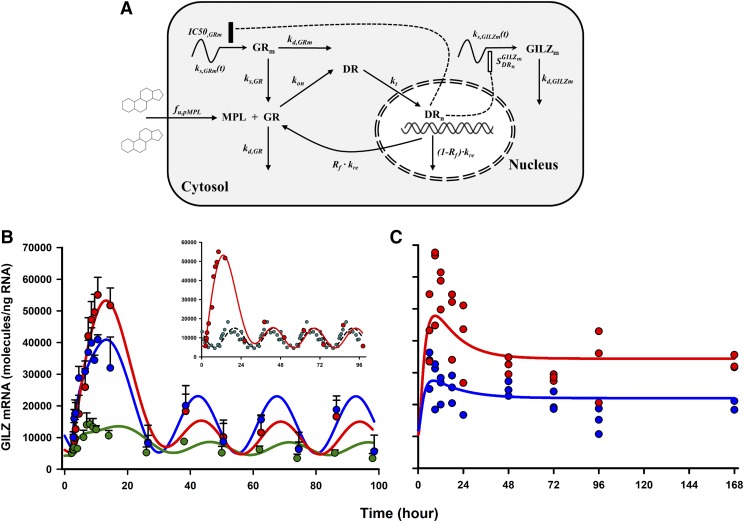
Simultaneous modeling of circadian and treatment tissue data sets was performed to: 1) analyze the PD profiles of MPL-enhanced GILZ within the context of its nonstationary baselines, 2) delineate determinants controlling the tissue-specific dynamics of GILZ, and 3) predict GILZ dynamics under different dosing regimens. The fifth-generation model for CS (Ramakrishnan et al., 2002) was adapted to include circadian production rates for GR and GILZ mRNA using a harmonics-based approach (Krzyzanski et al., 2000) to account for circadian oscillations in both biomarkers (Fig. 6A). The overall model was constructed with a series of differential equations linking MPL PK (free drug in plasma), free and bound receptors, receptor mRNA dynamics, and GILZ mRNA dynamics in rats. A transduction compartment model was used to describe the time course of the active drug-receptor complex in the nuclei of cells, coupled with a first-order partial recycling of free receptors. The nuclear concentrations of the complex in tissues were used to stimulate the production of GILZ mRNA. An inhibitory indirect response model was used to describe the downregulation of the production of the receptor mRNA, also driven by the nuclear drug-receptor complex density. Simultaneous modeling of control and bolus MPL data elucidated mechanistic features of GILZ regulation in tissues and jointly captured the baseline and PD profiles in muscle, lung, and adipose tissue (Fig. 6B). Next, the quantitative model, along with the estimated parameter values, was applied to predict GILZ dynamics a priori upon chronic steroid dosing. A follow-up in vivo study confirmed that the model successfully and quantitatively predicted the dynamics of GILZ in adipose and lung during 0.3 mg/kg/h s.c. dosing of MPL over 1 week (Fig. 6C). Of importance, the model was able to predict accurately the tolerance behavior developed upon chronic drug exposure in both tissues, resulting in a lower steady-state of GILZ mRNA beyond 48 hours and throughout the 7-day infusion. These observations are consistent with previous repeated-dose studies of MPL, which demonstrated tolerance in the hepatic profiles of TAT mRNA and activity due to decreased free cytosolic receptors (Sun et al., 1998b). This analysis indicated that absolute baseline expression of GILZ and GR dynamics (especially feedback inhibition of receptor mRNA resulting in reduced free receptor densities) remained important, global, system-specific determinants of genomic GILZ response to MPL. Collectively, these studies provided a quantitative and mechanistic framework for the application of GILZ as a tissue-wide PD marker of an anti-inflammatory mediator of CSs.

Fig. 6.

Pharmacodynamic scheme for receptor/gene-mediated corticosteroid action (A); measured data (circles) and model-fitted GILZ mRNA dynamics (lines) in skeletal muscle (green), lung (blue), and adipose tissue (red) after 50 mg/kg i.m. doses of methylprednisolone were given to male rats (B); and measured data (circles) and model-predicted (simulated) dynamics of GILZ mRNA (lines) in lung (blue) and adipose tissue (red) upon 0.3 mg/kg/h s.c. infusion of methylprednisolone administered to male rats over 1 week (C). The inset in (B) jointly depicts the mean PD profiles of GILZ in adipose tissue from dosed (red, solid line) and circadian control (cyan, dashed line) animals. Figure adapted from (Ayyar et al., 2017b).

B. Lesson 2: Simple to Complex Mechanisms of Hepatic Receptor/Gene/Protein-Mediated Signaling Connect Methylprednisolone Exposure to Metabolic and Immune-Related Pharmacodynamic Actions

This body of work extended previous generation receptor/gene-mediated models of CS by demonstrating that MPL elicited pharmaco/toxico-dynamic responses through simple-to-more complex downstream signaling mechanisms controlled by receptor/gene/protein-mediated signaling. In our experiments to model the receptor-mediated, transcriptomic, and proteomic determinants of CS effects on whole body PD responses, male ADX rats were given a 50 mg/kg bolus of MPL and in vivo measurements included steroid in plasma, microarray-based transcriptomics (Jin et al., 2003), nano-LC/MS based proteomics (Nouri-Nigjeh et al., 2014), and relevant physiologic measurements including hepatic TAT activity, plasma glucose and insulin concentrations, and blood lymphocyte counts. Recognizing that proteins, rather than mRNA, represent more direct mediators of biologic effects, a critical step involved studying steroid actions at the level of the “proteome” is understanding protein function(s), relationships to transcriptional circuitry, interactive signaling mechanisms, and contributions to drug response.

One challenging aspect of this endeavor was developing a holistic systems framework or model that incorporated the totality of “-omics” information gained though high-throughput experiments. Current knowledge gaps in the precise gene regulatory networks connecting the vast array of CS-regulated mRNA and proteins precluded the development of a unifying-yet-meaningful model. In addition, the vastly “horizontal” nature of steroid action on genes affecting diverse physiologic end-points made the incorporation of every gene infeasible. Thus, complementary and iterative approaches were evaluated to decipher the signaling mechanisms controlling select steroid responses. Functional proteomics analysis (Ayyar et al., 2017a) provided a rich biologic context for the observed changes in protein dynamics by MPL, serving as a foundational step preceding mechanistic modeling of the -omics data. Numerous signaling proteins mediating CS actions in liver were identified, annotated, and clustered. This analysis, in addition to isolating critical protein clusters, revealed that functionally clustered proteins displayed a marked diversity in temporal profiles, underscoring inherent complexities in the dynamic modeling of such systems. Next, a series of extended (Jin et al., 2003) mechanism-based pharmacogenomic models were developed that jointly captured the emergent temporal transcript and protein expression patterns of over 60 genes (120 mRNA and proteins) perturbed by MPL (Ayyar et al., 2018a). The tandem indirect response-based models used transit compartments (rationalized as secondarily-regulators) based on plausible biologic mechanisms (e.g., direct gene regulation, microRNA regulation or destabilization, and post-translational modification) to offer mechanistic hypotheses on how mRNA and protein turnover is controlled by direct and secondary mechanisms.

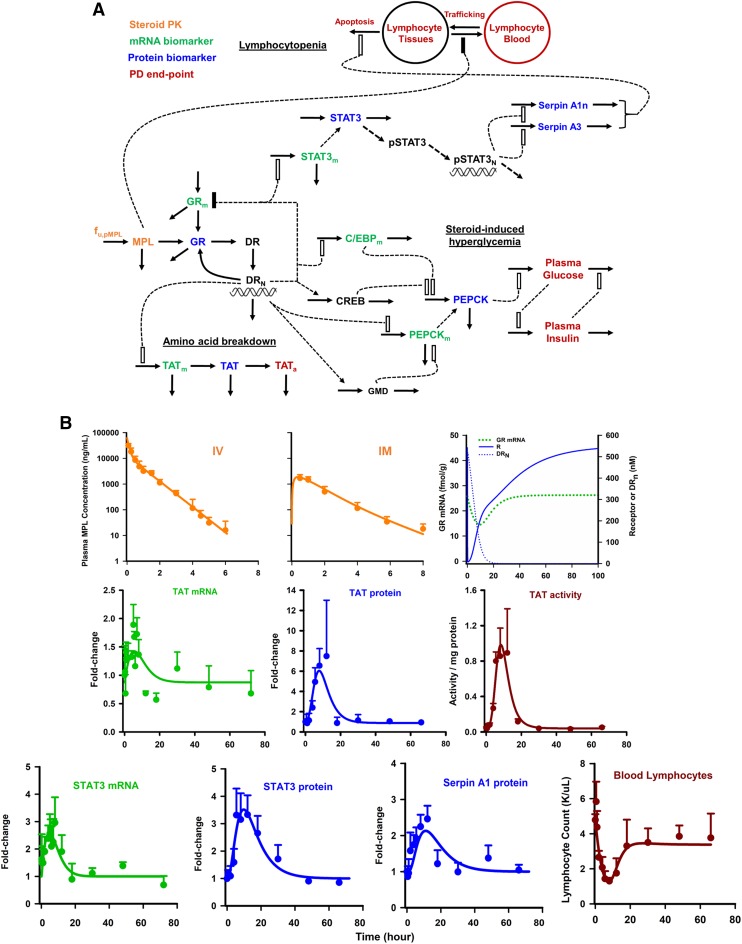
The ultimate goal of this work was the development of a QSP model platform (Ayyar et al., 2018b) that integrated and applied knowledge gained from functional proteomics (Ayyar et al., 2017a) and tandem mRNA-protein analyses (Ayyar et al., 2018a) to connect steroid kinetics, hepatic receptor dynamics, and temporal changes in important mRNA and proteins with clinically relevant responses (Fig. 7A). Our efforts focused on modeling the actions of CS on: 1) TAT regulation at the levels of mRNA, protein, and enzyme activity; 2) regulation of systemic glucose homeostasis, as controlled via hepatic gluconeogenesis; and 3) blood lymphocyte modulation via direct (trafficking) and indirect (genomic) mechanisms. The entire systems model reflects an assembly of a wide array of the basic PK/PD components: direct effects, single and tandem (precursor-dependent) indirect responses (inhibitory and stimulatory), time-dependent transduction, feedback, irreversible cell loss, and cell redistribution processes. Culminating from the modeling of the chosen biologic systems were quantitative descriptions of three distinct modes of molecular CS actions. These mechanisms included 1) simple, direct transcription-mediated signaling as employed for describing the TAT pathway; 2) secondary post-transcriptional regulation of mRNA and protein expression, as used to characterize the elevation in PEPCK protein, the rate-limiting step in hepatic gluconeogenesis, by CCAAT-enhancer binding protein and an assumed secondary mediator (reflecting the CREB transcription factor in the absence of data); and 3) activation of effector proteins lacking direct GREs via downstream signaling (i.e., serpin activation via STAT3) (Fig. 7B). The signaling model for TAT, comprising three precursor-like indirect response compartments (for measurements of mRNA, protein, and activity), naturally accounted for the post-genomic onset delays in TAT protein and activity, providing a mechanism-based description of transduction, advancing the traditional transit step approach. Another novel aspect of the model involved the coupling of rapid, direct effects of MPL on cell trafficking with delayed receptor/gene/protein (acute phase response) mediated (second-order) cell apoptosis in tissues to model lymphocyte dynamics, which, together accounted for the incomplete return of lymphocytes to baseline after steroid dosing in rats (Fig. 7B). Addressed in the development of this systems model, which combined systems structures with fundamental PK/PD principles (Mager and Kimko, 2016) and some of our earlier models, was finding a suitable “middle ground” between parsimony and an incisive recapitulation of mechanistic complexity within the system.

Fig. 7.

(A) Schematic of systems pharmacodynamic model linking methylprednisolone pharmacokinetics, glucocorticoid receptor dynamics, and hepatic mRNA and protein biomarkers to select efficacy and toxicity end-points in rats. Stimulation is denoted as open rectangles, and inhibition is denoted by closed rectangles. Heavy lines reflect turnover while broken lines reflect effects. (B) Measured and model-fitted profiles of steroid PK after 50 mg/kg i.v. (top-left) and i.m. (top-middle) doses, fitted profiles of receptor (mRNA, free cytosolic, and nuclear complex) dynamics (top right), TAT signaling pathway (middle row), and acute phase response and lymphocyte dynamics (bottom). Orange, PK; green, mRNA; blue, protein; and red, physiologic PD end-point. Figure adapted from Ayyar et al., 2018b with permission by Springer Nature.

C. Lesson 3: Combined Systems (Experimental and Modeling) Approaches Dissect Sex-Based Pharmacokinetic and Pharmacodynamic Variability in Genomic Steroid Responses

A series of experiments were undertaken to extend the “giant-rat” study paradigm of CS PK/PD/PG from male to female rats to investigate the determinants of possible sex differences in CS response (Fig. 8). Carefully controlled animal study designs where female rats were dosed with MPL within discrete phases of the rodent reproductive cycle enabled the examination of estrous (sex hormone-related) variability in MPL disposition and actions (Ayyar et al., 2019a,b,d). Prominent sex differences were observed in both plasma and hepatic drug concentration-time profiles after 50 mg/kg i.m. MPL, with higher drug exposures in females, regardless of estrous stage, compared with males (Fig. 9). Robust suppression of plasma corticosterone occurred in both sexes upon dosing. In vitro studies examining hepatic stability of steroid in homogenates as well as plasma and tissue protein binding properties (Ayyar et al., 2019d) informed important mechanistic aspects toward the development of an extended mPBPK/PD model for MPL (Ayyar et al., 2019b). Message expression of GILZ was chosen as a multi-tissue biomarker of GR-mediated drug response. Potential time-dependent interplay between sex hormone and glucocorticoid signaling in vivo was assessed by experiments comparing the time profile of enhancement of GILZ by MPL in uterus (high ER density) and in liver (lower ER density) from males (liver only) and females (liver and uterus) dosed within the proestrus (high estradiol/progesterone) and estrous (low estradiol/progesterone) phases of the rodent estrous cycle. Of translational importance, we hypothesized, based upon mechanistic in vitro data (Whirledge and Cidlowski, 2013; Whirledge et al., 2013), that elevated estradiol production during proestrus in females would antagonize the CS-enhanced genomic response in tissues with ERs. A conceptual summary of the multistep drug, hormone, and receptor interactions that were considered within our experimental and computational paradigms are depicted in Fig. 8B.

Fig. 8.

Systems modeling of sex differences in methylprednisolone action. (A) Diagrammatic summary of the various animal cohorts and general experimental study design. (B) General scheme of the multiscale modeling approach which provides the basis for the development of the systems PK/PD/PG model. (C) Schematic of the mPBPK/PD/PG systems model for corticosteroid actions in male and female rats. Lines with arrows indicate blood flows, binding interactions, conversion of species, or turnover of responses. Dashed lines ending in closed boxes indicate inhibition whereas dashed lines with open boxes depict a stimulation of turnover exerted by the connected factors.

Fig. 9.

Model fittings of the concentration-time profiles of total MPL in plasma (top left) and liver (top right) of male and female rats that received 50 mg/kg i.m. doses of MPL. Shown on the (bottom left) is the plasma concentration-time profile of E₂ in female rats over the 4-day estrous cycle; symbols are measurements from individual rats, and the solid line depicts the model-fitted profile shown to repeat for a second cycle. (Bottom middle) depicts GILZ mRNA in liver from male rats (green), estrus-phased female rats (red), and proestrus-phased female rats (blue) given 50 mg/kg i.m. MPL. The GILZ mRNA in uterus from estrus-phased female rats (red) and proestrus-phased female rats (blue) given 50 mg/kg i.m. MPL is shown (bottom right). Symbols represent the mean ± S.D. Dark (shaded) and light (unshaded) periods are indicated. Figure adapted from (Ayyar et al., 2019a and 2019b).

After accounting for PK differences using an mPBPK modeling approach, an expanded systems PD model of MPL considering circadian rhythms, multi-receptor (estrogen and glucocorticoid receptor) control, and estrous variations was developed to delineate the multi-factorial control of genomic steroid responses (Ayyar et al., 2019a). The systems mPBPK/PD model accounted for the kinetics of unbound CS in tissues, free plasma concentrations of corticosterone (including adrenal suppression) and endogenous estradiol (as a function of the rodent estrous cycle), binding of the free ligands to the GR (competitive interactions of drug and hormone) or estrogen receptor (ER) in tissues, and the antagonistic coregulation of GILZ gene synthesis by the concentrations of activated GR and ER complexes in the nucleus (Fig. 8C). The general structure of our fifth-generation model was retained for describing GR dynamics in both sexes and in different tissues. Hepatic GILZ response was about threefold higher in females, regardless of estrous stage, compared with males, driven predominantly by increased drug exposure in females (Fig. 9, top) and a negligible influence of estrogen interaction (Fig. 9). In contrast, GILZ response in uterus during proestrus in females was 60% of that observed in estrus-phased females (Fig. 9), despite no PK or receptor differences, providing in vivo support to the hypothesis of an estrogen-mediated antagonism of glucocorticoid signaling.

The developed model offered a mechanistic platform to assess the system-dependent factors contributing to PD variability in CS actions and, in turn, revealed a unique PD interaction between two different steroid receptors occurring in vivo. The modeling efforts and approaches examined CS actions across multiple time scales, including 24-hour circadian and longer 4-day reproductive biorhythms and can serve as a paradigm for the use of combined PK/PD and systems (experimental and modeling) approaches to gain a quantitative understanding of complex drug-system interactions in vivo and its impact on inter-individual variability in PK/PD. This mechanistic systems model may also form the basis for explaining the interactions of estrogens with other drugs and xenobiotics acting via nuclear receptors.

D. Lesson 4: Basic Components of the Corticosteroid Receptor Models Are Readily Incorporated within Diverse Models of Systems Biology

The CS receptor models have provided a powerful, generalizable formalism for modeling a wide range of physiologic and biochemical systems. Based on the concept of indirect responses, this paradigm has enabled numerous and seamless extensions, resulting in more expansive systems models. An early example of such an extension through the development of a receptor-mediated, indirect response-based model of Toll-like receptor 4-stimulated inflammation described the sequence of inflammatory events connecting extracellular signals and transcriptional dynamics (Foteinou et al., 2009b). Model-based simulations were performed to identify possible critical targets either upstream of the activated signaling, such as endotoxin elimination rate, or downstream, such as those associated with modulating the Toll-like receptor signaling pathway. The resulting temporal profiles further indicated the potential importance of early effective therapeutic interventions. This model was expanded further by incorporating the fifth-generation CS model to account for the receptor- and NF-κB-mediated role of synthetic CS on inflammation (Foteinou et al., 2009a). Further extensions of CS receptor models introduced basic elements of circadian regulation of the inflammatory response (Scheff et al., 2010). Built upon the hypothesis that the observed circadian variations in the inflammatory response are governed by cortisol and melatonin and their interactions with immune cells, the model provided qualitatively accurate predictions of circadian variability in the strength of the inflammatory response (Scheff et al., 2010).

The central role of CS receptor dynamics was identified in modeling the signal transduction of photic information from the systemic level, the central clock of the suprachiasmatic nucleus and HPA axis to the molecular level, peripheral clock genes (Mavroudis et al., 2012). Their model demonstrated the importance of circadian cortisol interactions with its receptor in peripheral tissues in synchronizing and entraining peripheral clock genes and predicted the loss of intercellular synchrony when cortisol moves out of its homeostatic amplitude and frequency range, as observed clinically in chronic stress and cancer (Mavroudis et al., 2012, 2014). Such integrative modeling efforts enabled the coupling of intrinsic oscillation in the HPA axis, the peripheral clock genes, and external zeitgebers (light).

As a final example, our model for GR dynamics was recently incorporated within a mathematical model that characterized sex-dependent differences and inter-individual variability in the HPA axis response to stress (Rao and Androulakis, 2017). As depicted in Fig. 10A, the semi-mechanistic light-entrained model of the HPA axis accounted for circadian rhythmicity in the response of its primary mediators, corticotropin-releasing hormone, adrenocorticotropic hormone, and corticosterone (CORT). The model was developed to evaluate the hypothesis that differential sensitivity and negative feedback of the HPA axis network are causal factors for the observed sex differences in its activity. Figure 10B shows a complete schematic representation of the model variables, with negative feedback of CORT captured by the fifth-generation model for CS, where feedback inhibition is assumed to occur at the transcriptional level in the pituitary gland. The model, in qualitative agreement with experimental results (Atkinson and Waddell, 1997), captured the significant differences in circadian amplitude between males and females based on the CORT profiles generated by the parameters sets within the spaces for each sex (Fig. 10C). These models exemplify the broad applicability of the GR model and concepts within the context of developing more elaborate systems biology and QSP models.

Fig. 10.

(A) General schematic of the physiologic model considering sex-related variability on the HPA axis to occur on the strength of glucocorticoid-mediated negative feedback (K_p1 and K_p2) and adrenal sensitivity (k_p3) within the HPA network. (B) Schematic representation of the signaling mediators in the mathematical model incorporating the fifth-generation model for corticosteroids. (C) Simulated and experimental circadian CORT profiles generated by (a) male and (b) female parameter sets. For both (male and female), the dashed line represents the mean of simulated CORT circadian profiles generated by the parameter sets. The dark gray-shaded area represents the S.D. of the simulated CORT circadian profiles. The black dashed and dotted line represents the scaled mean experimental cosinor for the CORT profile. The light gray shaded area represents the scaled S.D. of the experimental CORT cosinors. ACTH, adrenocorticotrophic hormone; CORT, corticosterone; CRH, corticotropin releasing hormone. Figure adapted from Rao and Androulakis, 2017 with permission by Oxford University Press.

V. Conclusions and Future Perspectives

The CSs remain important therapeutic agents with diverse endocrinologic, immunologic, and pharmacologic effects, and they have been particularly intriguing compounds used in seeking improved PD concepts (Jusko, 1990) as well as systems models. Studies of properties of drugs such as steroids have helped evolve PK from empirical NCA and compartment analyses to mechanistic and physiologically based models. The principles of capacity-limitation in PK and target occupancy as well as types and rates of turnover processes serve as tenets for PD and systems models. By considering multiple system components and biologic network structures rather than single transduction pathways as the basis of drug action, systems pharmacology modeling represents an extension of mechanism-based PK/PD modeling, a field premised on many basic laws of nature, biology, and pharmacology (Jusko, 2016). Efforts in QSP modeling should continue to focus and build upon the “three pillars” of drug action: 1) achieving the desired drug exposure at the site of action, 2) optimal engagement of the target or receptor over time, and 3) understanding the relevant pharmacological and physiologic post-receptor signaling mechanisms that give rise to efficacious and/or toxic responses. Principles of PBPK, receptor theory and dynamics, and systems biology modeling enable the quantitative integration of these “pillars.”

The corticosteroid systems PK/PD models described in this article highlight the integration of fundamental PK/PD principles, the stepwise measurements of intermediary events, mediators, and biomarkers in vivo, and the “current state” of biologic mechanisms found in the literature. The investigations of CS PK, PD, and systems biology across multiple scales of physiologic organization exemplify the transition from basic toward systems PK/PD approaches. The approaches taken for modeling in vivo systems pharmacology in our work are generalizable to other drugs acting through receptor and genomic mechanisms. Future efforts in evolving more global and mechanistic models for CS will include the integration of the circadian systems biology of glucocorticoid hormones, HPA feedback, and tissue-specific peripheral clock gene regulation (Mavroudis et al., 2018b) with the multi-tissue receptor-mediated pharmacogenomic actions of exogenous corticosteroids (Ayyar et al., 2017b), further reducing empiricism (e.g., use of data-driven cosine fitting) within current models. With continual advances in basic knowledge on genomics, epigenomics, and proteomics, it is anticipated that future models (Iyengar et al., 2012) will build upon current concepts and methodology to further integrate the disciplines of PK/PD and systems biology for fully describing the quantitative systems pharmacology of existing and future compounds.

Abbreviations

ADX

adrenalectomized

AP-1

activator protein-1

CBG

corticosteroid binding globulin

CIA

collagen-induced arthritis

CORT

corticosterone

CS

corticosteroid

E₂

estradiol

ER

estrogen receptor

GILZ

glucocorticoid-induced leucine zipper

GR

glucocorticoid receptor

GRE

glucocorticoid-response elements

HPA

hypothalamic-pituitary-adrenal

IL

interleukin

LC/MS

liquid chromatography/mass spectrometry

mPBPK

minimal PBPK

MPL

methylprednisolone

NCA

noncompartmental analysis

NF-κB

nuclear factor kappa B

OPG

osteoprotegerin

PBPK

physiologically based pharmacokinetic

PEPCK

phosphoenolpyruvate carboxykinase

PD

pharmacodynamics

PK

pharmacokinetics

QSP

quantitative systems pharmacology

RANKL

receptor activator of nuclear factor kappa-B ligand

STAT

signal transducer and activator of transcription

TAT

tyrosine aminotransferase

TMDD

target-mediated drug disposition

Authorship Contributions

Wrote or contributed to the writing of the manuscript: Ayyar, Jusko.