Analytical distributions for detailed models of stochastic gene expression in eukaryotic cells

Significance

The random nature of gene expression is well established experimentally. Mathematical modeling provides a means of understanding the factors leading to the observed stochasticity. In this article, we extend the classical two-state model of stochastic mRNA dynamics to include a considerable number of salient features of single-cell biology, such as cell division, replication, mRNA maturation, dosage compensation, and growth-dependent transcription. By means of biologically relevant approximations, we obtain expressions for the time-dependent distributions of mRNA and protein numbers. These provide insight into how fluctuations are modified and controlled by complex intracellular processes.

Abstract

The stochasticity of gene expression presents significant challenges to the modeling of genetic networks. A two-state model describing promoter switching, transcription, and messenger RNA (mRNA) decay is the standard model of stochastic mRNA dynamics in eukaryotic cells. Here, we extend this model to include mRNA maturation, cell division, gene replication, dosage compensation, and growth-dependent transcription. We derive expressions for the time-dependent distributions of nascent mRNA and mature mRNA numbers, provided two assumptions hold: 1) nascent mRNA dynamics are much faster than those of mature mRNA; and 2) gene-inactivation events occur far more frequently than gene-activation events. We confirm that thousands of eukaryotic genes satisfy these assumptions by using data from yeast, mouse, and human cells. We use the expressions to perform a sensitivity analysis of the coefficient of variation of mRNA fluctuations averaged over the cell cycle, for a large number of genes in mouse embryonic stem cells, identifying degradation and gene-activation rates as the most sensitive parameters. Furthermore, it is shown that, despite the model’s complexity, the time-dependent distributions predicted by our model are generally well approximated by the negative binomial distribution. Finally, we extend our model to include translation, protein decay, and auto-regulatory feedback, and derive expressions for the approximate time-dependent protein-number distributions, assuming slow protein decay. Our expressions enable us to study how complex biological processes contribute to the fluctuations of gene products in eukaryotic cells, as well as allowing a detailed quantitative comparison with experimental data via maximum-likelihood methods.

In the past two decades, advances in the real-time measurement of single-cell dynamics have revealed the stochastic nature of gene expression (1) and spurred a huge interest in the construction, simulation, and analytic solution of stochastic models of intracellular processes (2–4). Many experiments report the measurement of messenger RNA (mRNA), and, hence, there is a general need for stochastic models which can realistically predict the temporally varying distribution of mRNA molecule numbers in single cells. The word “realistically” is key because while there are a number of stochastic models of mRNA fluctuations in the literature, nevertheless, because of the complexity of the mRNA life cycle, currently very few of these models incorporate some of the detailed biological knowledge gleaned from single-cell experiments—this is particularly true for eukaryotic cells, where the transcription process is more complex than in prokaryotes and where compartmentation plays an important role (5).

The simplest stochastic model of mRNA fluctuations assumes that the gene is continuously ON, producing mRNA at some constant rate, followed by mRNA decay or its dilution due to cell division (often referred to as a constitutive expression model). If all these processes are approximated by effective first-order reactions, then the model is easy to solve and predicts a Poisson distribution of mRNA molecule numbers in cells (6). However, there is a large body of experimental evidence showing that the distribution of molecule-number fluctuations is typically non-Poisson (7–10) [except for housekeeping genes (11)], and, hence, modifications of this model are clearly needed. Adding an intermediate state which can either represent nascent mRNA or nuclear mRNA leads to the same Poisson distribution (12) (M1 in Fig. 1A). In contrast, assuming that a gene can switch between an ON and an OFF state (M2 in Fig. 1A) does lead to non-Poissonian mRNA fluctuations. The model has also been solved exactly analytically (13), and, in certain limits, it predicts bursty mRNA expression (8), a phenomenon which has been measured experimentally (14). This model, commonly called the two-state or telegraph model, has thus been widely adopted in the literature as the standard model of stochastic mRNA dynamics in eukaryotic cells (15–17). A recent application of the model is its use to infer the promoter-switching rates and the transcription rate of thousands of genes in mouse and human fibroblasts (10) from single-cell RNA-sequencing data. However, it is clear that this model is still far from including well-known processes, such as mRNA maturation, cell division, gene replication, dosage compensation, and growth-dependent transcription, all of which have been shown to have significant effects on the mRNA molecule numbers inside cells.

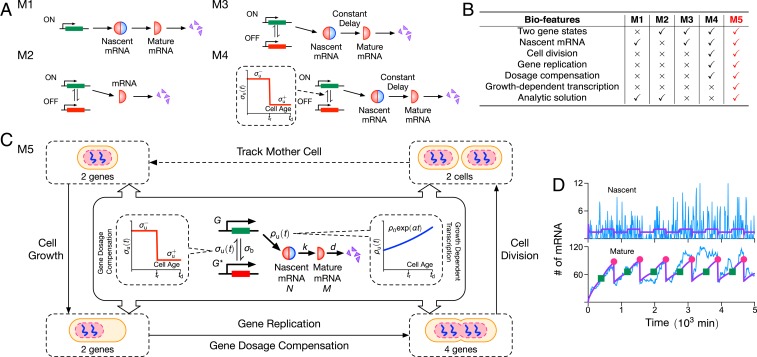
Fig. 1.

(A) Illustration of four models of stochastic mRNA dynamics in the literature. Note that nascent mRNA is shown as joined blue and red semicircles, illustrating its unspliced nature (blue for introns and red for exons), while mature mRNA being composed of only exons is shown as red semicircles. The models describe transcription (constitutive, e.g., M1; or intermittent, e.g., M2, M3, and M4), mRNA maturation (M1, M3, and M4), and details of the cell cycle (M4); their biological features are compared in B and discussed in the main text. Only the simplest of these two models (M1 and M2) have been analytically solved. The model (M5) proposed in this article is illustrated in C: It builds upon model M4 by adding growth-dependent transcription, describes maturation as a stochastic process, and has the major advantage of being analytically solvable. The model is composed of nonreactive components (dosage compensation, replication, cell division, and growth-dependent transcription) and reactive components; the latter are shown in the central boxes where $G,G^{*}$ denote genes in the ON, OFF states; $N$ is nascent mRNA; and $M$ is mature mRNA. (D) We show stochastic simulations of M5 using the SSA (25), where the purple lines denote the mean, and a typical time series is shown in blue. The green squares and red dots indicate the gene-replication time ($t_{\text{r}}$) and cell-division time ($t_{\text{d}}$), respectively. We use parameters measured for Nanog in mouse embryonic stem cells from ref. 26: ${\rho }_{\text{u}}=2.11\hspace{0.17em}{\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$, $d=0.00245\hspace{0.17em}{\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$, ${\sigma }_{\text{b}}=0.609\hspace{0.17em}{\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$, and ${\sigma }_{\text{u}}^{-}=\hspace{0.17em}0.0282\hspace{0.17em}{\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$. The gene-replication time $t_{\text{r}}=400$ min, cell-division time $t_{\text{d}}=780$ min, maturation rate $k=0.1299\hspace{0.17em}{\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$, and gene-dosage parameters ${\sigma }_{\text{u}}^{+}=\hspace{0.17em}0.71{\sigma }_{\text{u}}^{-}$ are reported in ref. 19 for the same type of cells. Note that we set $\alpha =0$, meaning that there is no growth-dependent transcription. Each realization is initiated with zero nascent and mature mRNAs and the gene in the ON state.

There are few studies which have modified the standard model of stochastic mRNA dynamics to include some of the mentioned biological processes: Senecal et al. (18) modified the standard model by including the conversion of nascent mRNA to mature mRNA after a constant time delay (model M3 in Fig. 1A), while Skinner et al. (19) extended this model further by including cell division, gene replication, and dosage compensation (model M4 in Fig. 1A). Note that there are also models which explicitly account for cell division (20, 21) or for replication (22), but have no description for promoter switching or other detailed features of the mRNA life cycle.

The disadvantage of the last two models (M3 and M4) compared to the previous two (M1 and M2) is that there is no known analytic solution to them. Hence, they have been explored purely via stochastic simulations. In Fig. 1B, we summarize the features of the models that we have discussed. In this paper, we develop an analytically tractable stochastic model of mRNA dynamics in diploid cells, which includes all of the processes in the most advanced simulation model (M4) developed thus far, while also additionally including growth-dependent transcription (the scaling of transcription with cellular volume) (23), a mechanism maintaining mRNA concentration homeostasis (24) irrespective of changes in cellular volume and DNA content. We also extend the model to include protein dynamics. The advantage of our theory is that it leads to intuitive insight that cannot be easily obtained from stochastic simulations. In addition, our model provides a framework which can be easily extended to include more intricate biological phenomena.

Results

Model Specification.

The dynamic biochemical processes described by our model are illustrated in Fig. 1C and are as follows:

• 1)In the prereplication stage of the cell cycle, two gene copies can independently switch from ON ($G$) to OFF state ($G^{*}$) with rate ${\sigma }_{\text{b}}$ and from OFF to ON with rate ${\sigma }_{\text{u}}^{-}$. Gene-copy independence has been shown experimentally (19).
• 2)In the ON state, there is the production of nascent (unspliced mRNA) denoted by $N$ which subsequently becomes mature (spliced; denoted by $M$) with rate $k$. We assume that the maturation time is exponentially distributed rather than a deterministic time delay as assumed in previous studies (18, 19). This assumption is used because it makes the model analytically tractable (since then the model is Markov) and also since it has been shown (28) that the distribution of nascent mRNA numbers is insensitive to whether the delay is deterministic or exponentially distributed with identical mean maturation time, provided that ${\rho }_{\text{u}}\gg {\sigma }_{\text{b}},{\sigma }_{\text{u}}$, which is the case experimentally (Table 1).
• 3)The mature mRNA decays with rate $d$ via first-order kinetics, which is a common assumption supported by experiments (29).
• 4)Growth-dependent transcription whereby the transcription rate is proportional to the volume of the cell—this models the mRNA-concentration homeostasis mechanism reported in ref. 23. We assume that the cell volume increases exponentially with cell age $t$ (where $0\le t\le t_{\text{d}}$ and $t_{\text{d}}$ is the cellular interdivision time); this assumption is supported by experimental evidence for a variety of mammalian cells (30). Hence, the effective transcription rate follows the equation ${\rho }_{\text{u}}\left(t\right)\hspace{0.17em}=\hspace{0.17em}{\rho }_0\exp \left(\alpha t\right)$, where ${\rho }_0$ is the transcription rate at the start of the cell cycle, $\alpha =\left(1/t_{\text{d}}\right)\ln \left(V_{\text{f}}/V_0\right)$; $V_0$ is the cell volume at the beginning of the cell cycle; and $V_{\text{f}}$ is the cell volume just before the cell divides. If there is no growth-dependent transcription, then ${\rho }_{\text{u}}\left(t\right)$ is a time-independent constant and corresponds to setting $\alpha =0$.
• 5)Replication results in a doubling of the gene copies from two to four at cell age $t_{\text{r}}$ (replication time). We assume that this occurs instantaneously—i.e., replication occurs over a period which is much shorter than the length of the cell cycle. We shall refer to the gene which is replicated as the mother copy and the duplicated gene as the daughter copy. The daughter copy can either inherit the gene state from the mother copy (31), or else all copies (mother and daughter) are reset to the OFF state upon replication. One plausible explanation for the latter case is that to avoid the potential risk of conflict between replication and transcription (and the resulting DNA damage), it is highly likely that in the region where replication is actively ongoing or just completed, there is no transcription, indicating an OFF state (figure 2C in ref. 32).
• 6)Dosage compensation is modeled as a change in the value of the rate at which the gene switches from OFF to ON upon replication, specifically ${\sigma }_{\text{u}}={\sigma }_{\text{u}}^{-}$ if $0\le t<t_{\text{r}}$ and ${\sigma }_{\text{u}}={\sigma }_{\text{u}}^{+}$ if $t_{\text{r}}\le t\le t_{\text{d}}$. This assumption can explain experimental data (19). Note that dosage compensation is another mechanism (besides growth-dependent transcription) which results in approximate mRNA concentration homeostasis (24) over the duration of the cell cycle (33).
• 7)Binomial partitioning of nascent and mature mRNA at cell division. We here assume that nascent and mature mRNA segregate independently of each other with a probability $1/2$ of ending up in one of the two daughter cells. The time between successive cell divisions is assumed to be fixed. This is a simplification, since a number of experiments show interdivision time variability (34, 35). The assumption of a fixed cell-cycle length is made to make the mathematical analysis of the model tractable. We will also show later how the theory can be modified to describe the effect of cell-cycle-length variability.

Table 1.

Kinetic parameters reported in various experimental papers

Cell type (gene)	${\sigma }_{\text{u}}\left({\text{min}}^{-1}\right)$	${\sigma }_{\text{b}}\left({\text{min}}^{-1}\right)$	${\rho }_{\text{u}}$ $\left({\text{min}}^{-1}\right)$	$d$ $\left({\text{min}}^{-1}\right)$	Burst size $\left({\rho }_{\text{u}}/{\sigma }_{\text{b}}\right)$	Fraction ON time $\left({\sigma }_{\text{u}}/\left({\sigma }_{\text{u}}+{\sigma }_{\text{b}}\right)\right)$	Timescale ratio $\delta$	Reference
Yeast (POL1)	0.0700	0.680	2.00	0.0693	2.9	0.093	9.71	(11)
Yeast (PDR5)	0.3000	5.300	11.30	0.0495	2.1	0.054	17.67	(11)
Mouse embryonic stem cells (Oct4)	0.0092	0.018	1.90	0.0023	105.6	0.338	1.96	(19)
Mouse embryonic stem cells (Nanog)	0.0019	0.007	0.80	0.0022	115.9	0.216	3.63	(19)
Mouse embryonic stem cells (Nanog)	0.0282	0.609	2.11	0.0025	3.5	0.044	21.60	(26)
Human osteosarcoma (c-Fos)	0.1075	0.313	7.30	0.0462	23.4	0.256	2.91	(18)
Mouse hepatocytes (Acly)	0.0010	0.002	0.25	0.0004	129.3	0.337	1.97	(27)
Mouse hepatocytes (Actb)	0.0013	0.036	2.52	0.0004	70.1	0.034	28.77	(27)
Mouse hepatocytes (Srebf1)	0.0015	0.013	1.80	0.0022	137.7	0.102	8.82	(27)
Mouse hepatocytes (Insr1)	1.6$\times {10}^{-5}$	3.5$\times {10}^{-4}$	0.03	3.3$\times {10}^{-5}$	81.0	0.045	21.00	(27)
Mouse fibroblasts (3,575 genes)	0.0022	0.236	0.69	0.0035	6.9	0.092	101.73	(10)
Human fibroblasts (1,609 genes)	0.2173 (d)	6.752 (d)	272.11 (d)	N/A	134.5	0.102	34.86	(10)
Mouse fibroblasts (16 genes)	0.0136	0.167	2.48	0.0109	17.2	0.074	20.11	(14)

The transcription rate (${\rho }_{\text{u}}$), the mRNA degradation rate (d), the rate at which the gene switches from ON to OFF (${\sigma }_{\text{b}}$), and the rate at which it switches from OFF to ON (${\sigma }_{\text{u}}$) have been estimated from experimental data by using various models of stochastic mRNA dynamics (mostly using the standard model M2 in Fig. 1A). The data reveal that gene expression is bursty (gene is ON for short times, and, in that time, a large burst of mRNA produced). The large values of the ratio $\delta ={\sigma }_{\text{b}}/{\sigma }_{\text{u}}$ show that gene-inactivation events occur far more frequently than gene-activation events. Note that 1) estimates for the last three rows represent averages over genes; 2) human fibroblast estimates for ${\sigma }_{\text{u}},{\sigma }_{\text{b}},{\rho }_{\text{u}}$ are in terms of d, and the latter was not measured; and 3) we do not report the value of ${\sigma }_{\text{u}}$ before and after replication because the vast majority of studies do not take into account replication and, hence, report a single value. See SI Appendix, Section 2 for details. N/A, not applicable.

Approximate Solution of the Model.

A master equation can be written which describes the exact stochastic dynamics of the above model with the replication and cell-division processes modeled via appropriate boundary conditions (see SI Appendix, section 1 for details). Given the myriad complex biological functions described by the model, it should come as no surprise that we were unable to find an exact solution to this master equation (indeed, much simpler models often cannot be solved exactly; see ref. 4 for a review of the state of the art in solutions of chemical master equations). Our approach will consist of breaking the model into submodels, where each considers only a subset of bioprocesses, followed by solving each submodel approximately and then integrating the results to obtain a solution to the full model.

We note from Table 1 that the vast majority of eukaryotic genes are characterized by a large value of the ratio $\delta ={\sigma }_{\text{b}}/{\sigma }_{\text{u}}$ (gene-inactivation rate divided by the gene-activation rate), i.e., genes spend most of their time in the OFF state. For the moment, we ignore the processes of cell division and replication and focus on nascent mRNA dynamics due to promoter switching, growth-dependent transcription, and maturation for a single gene copy. As we show in SI Appendix, Section 3.1, in this case for large $\delta$, the generating function corresponding to the time-dependent marginal distribution of nascent mRNA numbers of a single gene $P\left(n_{\text{N}},t\right)$ can be written (by a slight abuse of notation) as:

$$\begin{array}{ll}\hfill G\left(u,t\right)& =\sum _{n_{\text{N}}=0}^{\infty }{\left(1+u\right)}^{n_{\text{N}}}P\left(n_{\text{N}},t\right)\hfill \\ \hfill & =g\left(u{\text{e}}^{-kt}\right){\left(\frac{{\rho }_0{\text{e}}^{-kt}u-{\sigma }_{\text{b}}}{{\rho }_0{\text{e}}^{\alpha t}u-{\sigma }_{\text{b}}}\right)}^{\frac{{\sigma }_{\text{u}}}{\alpha +k}}.\hfill \end{array}$$ [1]

Here, we have assumed that the initial marginal distribution of $i$ nascent mRNA molecules is $P\left(i\right)=p_i$, which implies $g\left(u\right)={\sum }_i{p}_i{\left(u+1\right)}^i$. It can be shown that Eq. 1 implies that for large $\delta$, the stochastic reaction dynamics stemming from the combined processes of promoter switching and nascent mRNA production with a time-dependent transcription rate to account for growth-dependent transcription can be described by a simpler system of one effective reaction. In this reaction, nascent mRNA is produced at rate ${\sigma }_{\text{u}}$ in bursts whose size are distributed according to a negative binomial distribution with a time-dependent mean burst size $\left({\rho }_0/{\sigma }_{\text{b}}\right)\exp \left(\alpha t\right)$ (SI Appendix, Section 3.2). The major advantage of this effective reaction description is that it dispenses with an explicit gene-state description which considerably simplifies the calculations to follow. In particular, the issue of how to choose the gene state at the beginning of replication is circumvented—intuitively, this is possible because since the gene spends most of its time in the OFF state, the two mechanisms described in point 5 in Model Specification cannot be distinguished in practice.

$$G_{\text{A}}\left(u,t\right)=\left\{\begin{array}{cccc}\hfill & {\left(\frac{{\rho }_{0}u{\text{e}}^{-kt}-{\sigma }_{\text{b}}}{{\rho }_{0}u{\text{e}}^{\alpha t}-{\sigma }_{\text{b}}}\right)}^{\frac{{\sigma }_{\text{u}}^{-}}{\alpha +k}}\hfill & \hfill & t\in \left[0,t_{\text{r}}\right),\hfill \\ \hfill & {\left(\frac{{\rho }_{0}u{\text{e}}^{-kt}-{\sigma }_{\text{b}}}{{\rho }_{0}u{\text{e}}^{-k\left(t-t_{\text{r}}\right)+\alpha t_{\text{r}}}-{\sigma }_{\text{b}}}\right)}^{\frac{{\sigma }_{\text{u}}^{-}}{\alpha +k}}{\left(\frac{{\rho }_{1}u{\text{e}}^{-k\left(t-t_{\text{r}}\right)}-{\sigma }_{\text{b}}}{{\rho }_{1}u{\text{e}}^{\alpha \left(t-t_{\text{r}}\right)}-{\sigma }_{\text{b}}}\right)}^{\frac{{\sigma }_{\text{u}}^{+}}{\alpha +k}}\hfill & \hfill & t\in \left[t_{\text{r}},t_{\text{d}}\right),\hfill \end{array}\right.$$ [2A]

$$G_{\text{B}}\left(u,t\right)=\left\{\begin{array}{cccc}\hfill & 1\hfill & \hfill & t\in \left[0,t_{\text{r}}\right),\hfill \\ \hfill & {\left(\frac{{\rho }_{1}u{\text{e}}^{-k\left(t-t_{\text{r}}\right)}-{\sigma }_{\text{b}}}{{\rho }_{1}u{\text{e}}^{\alpha \left(t-t_{\text{r}}\right)}-{\sigma }_{\text{b}}}\right)}^{\frac{{\sigma }_{\text{u}}^{+}}{\alpha +k}}\hfill & \hfill & t\in \left[t_{\text{r}},t_{\text{d}}\right).\hfill \end{array}\right.$$ [2B]

Next, we include the processes of replication and dosage compensation. Specifically, let $G_{\text{A}}\left(u,t\right)$ and $G_{\text{B}}\left(u,t\right)$ be the generating functions describing the dynamics of nascent mRNAs born within a cell cycle for a single mother and daughter copy, respectively. By using Eq. 1, it follows that the generating functions of nascent mRNA produced by mother and daughter copies are piece-wisely defined and given by Eqs. 2A and 2B. The first part $t\in \left[0,t_{\text{r}}\right)$ of $G_{\text{A}}\left(u,t\right)$ describes the stochastic dynamics of nascent mRNA born in the prereplication time. Note that the initial condition is zero, and ${\sigma }_{\text{u}}={\sigma }_{\text{u}}^{-}$. The second part $t\in \left[t_{\text{r}},t_{\text{d}}\right)$ of $G_{\text{A}}\left(u,t\right)$ describes the stochastic dynamics of nascent mRNA born in the postreplication time. This is given by Eq. 1, with $g$ replaced by the initial condition which is the generating function at replication time (from the expression for $t\in \left[0,t_{\text{r}}\right)$); also note that ${\sigma }_{\text{u}}={\sigma }_{\text{u}}^{+}$ (due to dosage compensation), ${\rho }_0$ is replaced by ${\rho }_1={\rho }_0{\text{e}}^{\alpha t_{\text{r}}}$ since this is the transcription rate at replication time, and time $t$ is replaced by $t-t_{\text{r}}$. Note that, intuitively, the second part $t\in \left[t_{\text{r}},t_{\text{d}}\right)$ of $G_{\text{A}}\left(u,t\right)$ (which describes postreplication dynamics) can be written as a product of two factors because there is independence between nascent mRNA inherited from the prereplication stage and the nascent mRNA born in the postreplication stage. Since there is no transcription activity in the prereplication time for the daughter copy, the generating function $G_{\text{B}}\left(u,t\right)$ is trivially equal to 1 for $t\in \left[0,t_{\text{r}}\right)$. The second part $t\in \left[t_{\text{r}},t_{\text{d}}\right)$ of $G_{\text{B}}\left(u,t\right)$ can be found similarly as for $G_{\text{A}}\left(u,t\right)$. Note that the individual factors in the generating-function expressions can be written as a product of the generating functions for the binomial and negative binomial distributions (SI Appendix, section 3).

Finally, we add the details of cell division and the associated binomial partitioning. There are two processes contributing to the number of mRNAs at a particular cell age $t$ of a given cell cycle $n$: 1) the decay of mRNAs inherited from the previous cycle, and 2) the production of new mRNAs in cell cycle $n$. These processes are independent from each other when the gene spends most of its time in one state (as in our case), and, hence, it follows that we can write:

$$\begin{array}{ll}\hfill P_n\left(n_{\text{N}},t\right)& ={\left.\frac{1}{n_{\text{N}}!}\frac{d^{n_{\text{N}}}{G}_n\left(u,t\right)}{d{u}^{n_{\text{N}}}}\right|}_{u=-1},\hfill \\ \hfill G_n\left(u,t\right)& =\underset{\text{death process}}{\underbrace{G_n\left(u{\text{e}}^{-kt},0\right)}}\underset{\text{new born mRNA}}{\underbrace{G_{\text{A}}^2\left(u,t\right)G_{\text{B}}^2\left(u,t\right)}}\hspace{0.17em}\forall t\in \left[0,t_{\text{d}}\right),\hfill \end{array}$$ [3]

where $P_n\left(n_{\text{N}},t\right)$ is the marginal distribution of nascent mRNA numbers at time $t$ in cell cycle $n$. Note that the power of 2 on the right-hand side of Eq. 3 arises from the diploidy of gene copies and from assuming that they are independent of each other (as mentioned in point 1 of Model Specification). Binomial partitioning at cell age $t_{\text{d}}$ leads to a relationship between the initial conditions for the generating function of the $n^{\text{th}}$ cycle and the generating function of the ${n-1}^{\text{th}}$ cycle at time $t_{\text{d}}$, which can be shown (SI Appendix, section 3.3) to lead to the condition:

$$G_n\left(u,0\right)=G_{n-1}\left(\eta u,0\right)G_{\text{A}}^2\left(\frac{u}{2},t_{\text{d}}\right)G_{\text{B}}^2\left(\frac{u}{2},t_{\text{d}}\right),\hspace{0.17em}n>1$$ , [4]

where $\eta ={\text{e}}^{-k{t}_{\text{d}}}/2$. Note that $G_1\left(u,0\right)$ is the initial condition at the beginning of the first cycle, and this is a user-input condition; for all results in this paper, we assumed $G_1\left(u,0\right)=1$, implying no nascent mRNA initially.

Hence, summarizing Eqs. 3 and 4 together with Eqs. 2A and 2B provides an approximate time-dependent solution of the marginal distribution of nascent mRNA numbers valid for all cell ages and cellular generations; the assumption behind our derivation was that the gene spends most of its time in the OFF state. Note that while the derivation assumed a growth-dependent transcription rate as described in point 4 of Model Specification, nevertheless, it is straightforward to derive similar results for a general time-dependent transcription rate (SI Appendix, section 10); this may be useful to describe synthetic gene-regulatory networks where the transcription rate can be arbitrarily regulated over time.

In SI Appendix, section 4, we show that an approximate time-dependent solution of the marginal distribution of mature mRNA numbers can be similarly derived, provided that one further assumes that the timescales of nascent mRNA are much shorter than those of mature mRNA. The timescales of these two types of mRNA are determined by $k$ and $d$, respectively (their elimination rates), and there is strong evidence showing $k\gg d$. For the gene c-Fos in human osteosarcoma cells, Senecal et al. (18) estimated a value of $k=1.25{\text{min}}^{-1},d=0.0462{\text{min}}^{-1}$, while for Nanog and Oct4 in mouse embryonic stem cells, Skinner et al. (19) estimated $k=0.13{\text{min}}^{-1},d=0.0022{\text{min}}^{-1}$, and $k=0.29{\text{min}}^{-1},d=0.0023{\text{min}}^{-1}$, respectively. Hence, $k$ is considerably larger than $d$ generally.

Specifically, we show using singular perturbation theory that if the gene spends most of its time in the OFF state ($\delta \gg 1$) and if nascent mRNA maturation is fast ($k\gg d$), then the marginal distribution of mature mRNA numbers within a single cell is approximately given by Eqs. 3 and 4 together with Eqs. 2A and 2B, with $k$ replaced by $d$ and with the change of variable $n_{\text{N}}\to n_{\text{M}}$. Note that under the fast-maturation assumption, the dynamics of nascent mRNA do not affect the dynamics of mature mRNA; for a detailed discussion, see SI Appendix, section 4.

Numerical Evaluation of the Accuracy of the Approximate Distributions.

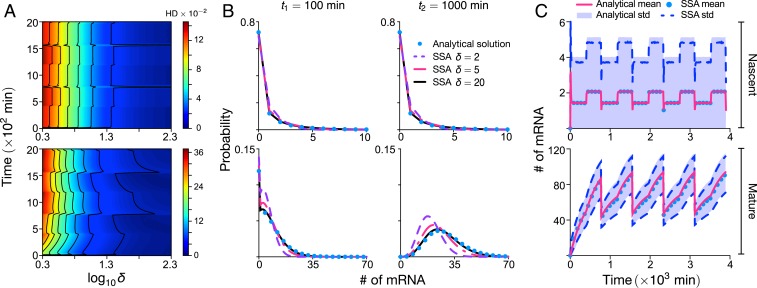
A main assumption behind our derivation is that $\delta \gg 1$ holds for many genes, but clearly this is not the case for all (Table 1). It is unclear how large $\delta$ has to be for our approximation to be accurate. Hence, we next test the accuracy of our theory by fixing $k\gg d$ (this assumption holds for all genes that we could find data for; SI Appendix, section 2) and varying parameters ${\rho }_{\text{u}}$ and ${\sigma }_{\text{b}}$ (relative to the rest which are fixed) to vary $\delta$ at constant mean burst size ${\rho }_{\text{u}}/{\sigma }_{\text{b}}$ for the case of no growth-dependent transcription ($\alpha =0$). We then quantify the accuracy of our approximation by calculating the Hellinger distance (HD) between the approximate probability distribution of nascent and mature mRNA numbers and the exact numerical solution of the chemical master equation as a function of $\delta$, which is varied over two orders of magnitude from 2 to 200. Note that the HD has the properties of being symmetric and satisfies the triangle inequality, thus implying that it is a distance metric on the space of probability distributions (unlike, e.g., the commonly used Kullback–Leibler divergence); it is also conveniently a fraction, which makes for easy interpretation.

Our approximate theory was derived by using the assumption that $\delta \gg 1$, and, hence, we expect the accuracy of the theory to increase with $\delta$. This is verified in the heatmap shown in Fig. 2A, where it is shown that the error in our approximate theory is inversely proportional to $\delta$; is a weak function of absolute time, i.e., independent of cell age and generation; and is generally small (HD $\ll 1$) for both nascent (Fig. 2 A, Upper) and mature (Fig. 2 A, Lower) mRNA. The exact probability distributions for two time points are compared with the approximate distributions in Fig. 2B for three different values of $\delta$. Note that the match between approximate analytic solution and the exact solution (using stochastic simulation algorithm [SSA]) is excellent for $\delta =20$ and acceptable for $\delta =5$ for all times; for smaller values of $\delta$, the nascent mRNA distribution still is well approximated, but the same cannot be said for the mature mRNA distribution. Hence, our theory is accurate for the majority of genes reported in Table 1.

Fig. 2.

Accuracy of the approximate analytic solution to the stochastic model of eukaryotic gene expression. The approximate probability-distribution solution for nascent mRNA numbers is given by Eqs. 3 and 4 together with Eqs. 2A and 2B; the distribution for mature mRNA numbers is given by the same equations with $k$ replaced by $d$ and $n_{\text{N}}$ replaced by $n_{\text{M}}$. Here, we investigate the accuracy of this solution relative to the exact solution, which is numerically computed by using the Finite State Projection algorithm (FSP) or the SSA; note that these simulations are of the full model (without any approximation) as described in Model Specification and SI Appendix, section 1. Upper and Lower show information for nascent and mature mRNA, respectively. (A) The heatmap for the HD (which quantifies the distance between the approximate and exact marginal distributions) for both nascent and mature mRNA as a function of absolute time and the dimensionless timescale ratio $\delta$. Note that $\delta ={\sigma }_{\text{b}}/{\sigma }_{\text{u}}^{-}$ is here varied by changing ${\sigma }_{\text{b}}$ while keeping ${\sigma }_{\text{u}}^{-}=0.0282\stackrel{-1}{min}$ and the mean burst size ${\rho }_{\text{u}}/{\sigma }_{\text{b}}=3.5$ constant; the rest of the parameter values are the same as those in Fig. 1. Due to the computational demand of producing a heatplot, the exact solution is here computed by using FSP; computations using the SSA at random points in the heatplot were indistinguishable from those using FSP. (B) Marginal distributions of the nascent and mature mRNA for two time points and three values of $\delta$ compared to those obtained from stochastic simulations using the SSA. (C) Plots of the mean and SD (std) versus time as predicted by the approximate analytical solution and exact stochastic simulations for $\delta =21.60$ using the SSA (which also agree with those using FSP). All plots show that the accuracy of the distributions and moments predicted by the approximate analytic solution is high provided $\delta$ is not too small (larger than about five). Note that $\alpha =0$ in all panels, meaning that there is no growth-dependent transcription.

In Fig. 2C, we compare the time-dependent mean and variance predicted from the approximate theory with the exact result (from SSA), showing the accuracy of the theory to capture the cyclic behavior of the moments due to the dynamic processes of replication and cell division. The theory’s accuracy remains high, even when growth-dependent transcription is turned on $\alpha >0$ (SI Appendix, Fig. S2).

Effect of Cell-Cycle-Length Variability on mRNA Distributions.

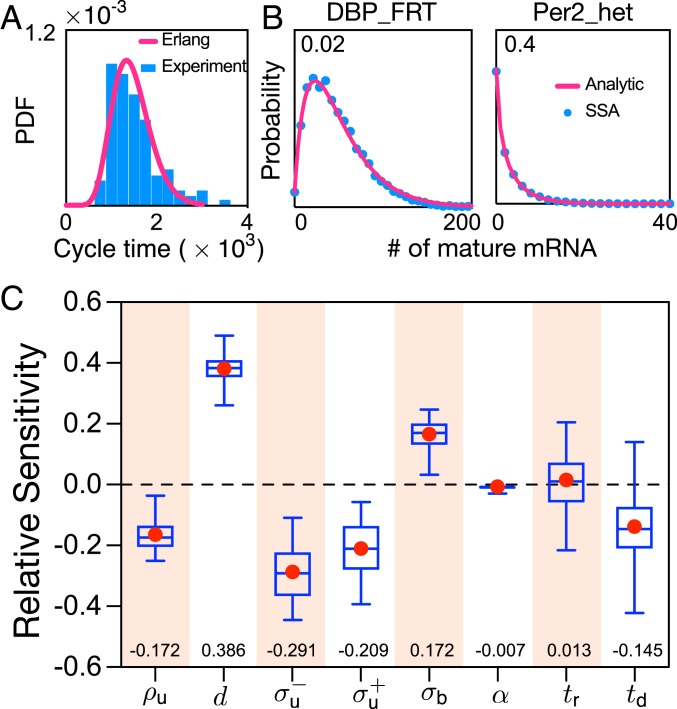
Our theory assumes a fixed cell-cycle length and synchronized cell cycles among cells. This is the case when cells are subjected to certain environmental conditions (36, 37), when the circadian clock gates the cell cycle (38, 39), and during certain phases of morphogenesis (40). However, variation in the cell-cycle length is likely common (e.g., in Fig. 3A, we show experimental data for mouse fibroblasts), which leads to asynchronous behavior. We modified the SSA such that the cell-cycle times $t_{\text{d}}$ are assumed to be random variables independently drawn from an Erlang distribution (which well approximates the experimental data in Fig. 3A) and the replication time is exactly in the middle of each cycle. Each trajectory of the algorithm corresponds to a forward lineage, i.e., either of the two daughter cells is followed with equal probability. The distribution of the number of mature mRNAs is constructed from an ensemble of these single-cell trajectories; this distribution is shown as blue dots in Fig. 3B, where the parameters are those measured for two mouse genes. The mature mRNA distribution can also be predicted by modifying our theory to take into account asynchronous cell cycles, but keeping the assumption of fixed cell-cycle length (SI Appendix, section 6); this prediction is shown as a red curve in Fig. 3B. Excellent agreement between theory and the SSA is found for 16 mouse genes (two are shown in Fig. 3B and the rest in SI Appendix, Fig. S5). As shown in SI Appendix, section 6, the implicit reason for the accuracy of the modified theory is the fact that the mRNA lifetime in mouse fibroblasts is typically much less than the average cell-cycle length; i.e., rapid degradation averages out timing fluctuations, which is in line with other recent studies (41).

Fig. 3.

(A and B) Cell-cycle-length variability and its effect on mature mRNA distributions. (A) The Erlang distribution provides a good fit to the experimentally measured cell-cycle time distribution of NIH 3T3 cells in ref. 42. PDF, probability distribution function. (B) The SSA modified such that the cell-cycle times are random variables independently drawn from an Erlang distribution is used to obtain the mature mRNA distributions (for the genes DBP_FRT and Per2_het reported in SI Appendix, Table S1) measured across an ensemble of cells (blue dots; see main text for details). The mature mRNA distributions are accurately predicted by modifying our theory (red solid lines; SI Appendix, section 6, Eq. 26) to take into account the asynchronicity of cell cycles across the population. Note that replication always occurs in the middle of a cell cycle. (C) Relative sensitivity of the cyclo-stationary coefficient of variation of mature mRNA noise averaged over the cell cycle to eight parameters. Box plots indicate the median and the 25% and 75% quantiles, with the mean marked as red dots. The median relative sensitivities are also shown as numbers at the bottom of the plot. The sensitivity analysis is carried out on 567,540 parametric combinations estimated for 1,051 genes of CAST allele data of mouse embryonic stem cells. Our results show that the degradation rate $d$ is the most sensitive parameter, followed by ${\sigma }_{\text{u}}^{-}$, while $\alpha$ is the least sensitive one. Note that there is no dependence of the coefficient of variation of mature mRNA on $k$ in the approximate theory, and, hence, $k$ is not a relevant parameter. See SI Appendix, section 11 for the specific range of parameter choice and their justification.

Sensitivity Analysis of the Coefficient of Variation of mRNA Fluctuations.

An important use of the analytic results is that we can efficiently calculate the sensitivity of the coefficient of variation of mature mRNA (SD divided by the mean) to small perturbations in the eight parameters of the model. To this end, we first used our approximate theory to calculate closed-form expressions for the cyclo-stationary mean and variance of mature mRNA, which we denote as ${\overline{⟨n_{\text{M}}⟩}}_t$ and ${\overline{\sigma }}_{n_{\text{M}},t}^2$, respectively (SI Appendix, section 5). Note that the cyclo-stationary conditions ensue in the limit of biological steady-state growth (20), which is achieved when the probability that a cell of age $t$ has a given number of molecules of certain species is independent of which generation it belongs to—i.e., setting $G_{n+1}\left(u,t\right)=G_n\left(u,t\right)$.

The cyclo-stationary coefficient of variation of mature mRNA noise averaged over the cell cycle is then given by $\overline{\text{CV}}=t_{\text{d}}^{-1}{\int }_{t=0}^{t_{\text{d}}}\sqrt{{\overline{\sigma }}_{n_{\text{M}},t}^2}/{\overline{⟨n_{\text{M}}⟩}}_{t}dt$ (which is computed numerically over 100 discrete time points evenly distributed within a cell cycle). The relative sensitivity of $\overline{\text{CV}}$ to a parameter $r$ is then given by ${\mathrm{\Lambda }}_r=\left(r/\overline{\text{CV}}\right)\partial \overline{\text{CV}}/\partial r$ (43), meaning that a $1\%$ change in the value of parameter $r$ leads to ${\mathrm{\Lambda }}_r\%$ change in $\overline{\text{CV}}$. We next computed the relative sensitivities for eight of the rate parameters for a large number of genes in mouse embryonic stem cells (10). Note that the 1,051 genes selected for this analysis are characterized by a timescale ratio $\delta \ge 5$, a value which is large enough to guarantee the accuracy of our approximate analytic solution (Fig. 2), which is used to calculate the coefficient of variation. The results illustrated by using box plots in Fig. 3C show that the most sensitive parameters were the mRNA degradation rate $d$ and the dosage-compensation parameters ${\sigma }_{\text{u}}^{-},{\sigma }_{\text{u}}^{+}$, while the least sensitive parameters were the growth-dependent transcription parameter $\alpha$ and the replication time $t_{\text{r}}$.

Effective Negative Binomial Approximation of Mature mRNA Distributions.

While our theory gives approximate distributions of nascent and mRNA molecule numbers, these distributions are complex and cannot be easily written in terms of known simple distributions. It has been frequently observed that many measured number distributions can be easily fit by the negative binomial distribution (or its continuous analog the gamma distribution). Indeed, this is one of the major reasons why the two-state model of mRNA dynamics (model M2 in Fig. 1) has become widely adopted, since in the bursty limit, the probability distribution of molecule numbers is negative binomial. Hence, we next investigate whether our approximate distributions can also be well fit by negative binomial distributions.

Assuming a negative binomial distribution (NB) for the number of molecules of mature mRNA, $P\left(n_{\text{M}}\right)\sim \text{NB}\left(r,p\right)$ with parameters $r$ and $p$, its mean and variance are given by ${⟨n_{\text{M}}⟩}_{\text{e}}=rp/\left(1-p\right),{\sigma }_{n_{\text{M}},\text{e}}^2=rp/{\left(1-p\right)}^2$. We equate these two moments to the cyclo-stationary moments from our theory: Specifically, we set ${⟨n_{\text{M}}⟩}_{\text{e}}={\overline{⟨n_{\text{M}}⟩}}_t/2$ and ${\sigma }_{n_{\text{M}},\text{e}}^2={\overline{\sigma }}_{n_{\text{M}},t}^2/2$, where the factor of $1/2$ accounts for the two independent gene copies in our model. One can then find simple expressions for $r$ and $p$:

$$r=\frac{1}{2}\frac{{\overline{⟨n_{\text{M}}⟩}}_t^2}{{\overline{\sigma }}_{n_{\text{M}},t}^2-{\overline{⟨n_{\text{M}}⟩}}_t},\hspace{0.17em}p=1-\frac{{\overline{⟨n_{\text{M}}⟩}}_t}{{\overline{\sigma }}_{n_{\text{M}},t}^2}.$$

Hence, we have constructed a negative binomial approximation $\text{NB}\left(r,p\right)$ to our model’s predicted distribution of the mature mRNA number distribution at cell age $t$ in the cyclo-stationary limit. We test the accuracy of this approximation in Fig. 4. In Fig. 4A, we compute the HD distance between the distribution solution of our model (as computed by using Eqs. 2A, 2B, 3, and 4 with $k$ changed to $d$ and $n_{\text{N}}$ changed to $n_{\text{M}}$) and the negative binomial approximation for 21 time points in the cell cycle using parameters for 1,051 genes in mouse embryonic stem cells (same as used for sensitivity analysis). Remarkably, we find the HD to be much <1 for all genes and all cell ages, implying that the negative binomial approximation is an excellent one in practice. Given the well-known fact that the negative binomial is a good approximation to the steady-state solution of the standard two-state model of mRNA dynamics in bursty conditions (8), in an indirect sense, our results in Fig. 4A also show that the cyclo-stationary distribution of our model at a particular cell age can be well approximated by the steady-state distribution of the two-state model (for a particular choice of effective parameters). This argument is further reinforced in Fig. 4B, where we show that the HD averaged over one cycle for a particular gene is roughly linearly dependent with $\mathrm{\Theta }$ in log space, where $\mathrm{\Theta }$ is the absolute difference between the uncentered third moments of the two-state model and its negative binomial approximation. Note that $\mathrm{\Theta }$ is defined in terms of the parameters ${\rho }_{\text{u}}$, ${\sigma }_{\text{u}}^{-}$, and $d$ specific to a particular gene:

$$\mathrm{\Theta }=\frac{2{\widehat{\rho }}_{\text{u}}^3{\widehat{\sigma }}_{\text{b}}{\widehat{\sigma }}_{\text{u}}^{-}\left(1+{\widehat{\sigma }}_{\text{u}}^{-}\right)}{{\left({\widehat{\sigma }}_{\text{b}}+{\widehat{\sigma }}_{\text{u}}^{-}\right)}^2{\left(1+{\widehat{\sigma }}_{\text{b}}+{\widehat{\sigma }}_{\text{u}}^{-}\right)}^2\left(2+{\widehat{\sigma }}_{\text{b}}+{\widehat{\sigma }}_{\text{u}}^{-}\right)},$$ [5]

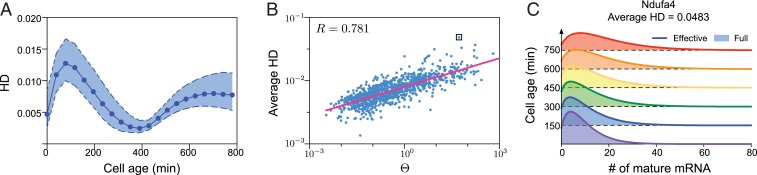
where ${\widehat{\rho }}_{\text{u}}={\rho }_{\text{u}}/\widehat{d}$, ${\widehat{\sigma }}_{\text{u}}^{-}={\sigma }_{\text{u}}^{-}/\widehat{d}$, ${\widehat{\sigma }}_{\text{b}}={\sigma }_{\text{b}}/\widehat{d}$, and $\widehat{d}=d+\ln 2/t_{\text{d}}$. For a derivation of this expression, see SI Appendix, section 7. Eq. 5 shows that the error in the negative binomial approximation is inversely proportional to the rate of promoter switching and directly proportional to the transcription rate. In Fig. 4C, we show the full versus effective negative binomial distributions as a function of cell age for the gene with the largest HD (Ndufa4)—even in this extreme case, the two distributions cannot be distinguished by eye, thus showing the high accuracy of the negative binomial approximation to our model for a large number of genes in mouse embryonic stem cells.

Fig. 4.

Effective negative binomial approximation for the mature mRNA number distribution of our model. The approximation is obtained by matching the cyclo-stationary mean and variance of our model to those of an effective negative binomial distribution. (A) We calculate the HD between the effective distribution and the full distribution for 21 equidistant time points through a whole cell cycle. Each point corresponds to the HD median for 1,051 genes in mouse embryonic stem cells (same data used for Fig. 3C), whereas the broken lines show the 25% and 75% quantiles. Note that the four parameters t_d = 780 min, $\alpha =0$, t_r = 400 min, and ${\sigma }_{\text{u}}^{+}=0.7{\sigma }_{\text{u}}^{-}$ are the same for all genes. (B) A plot of the HD for each gene averaged over 21 time points in the cell cycle versus the index $\mathrm{\Theta }$; the two quantities are linearly correlated in log space with Pearson correlation coefficient $R=0.781$. (C) The matching of the effective and full distributions in time for the gene Ndufa4, which has the largest HD in B (shown as a boxed point).

Including Protein Dynamics.

Thus far, the model only describes the stochastic mRNA dynamics. Given the increasing number of single-cell measurements of protein expression in eukaryotic cells (44–46), we next extend our theory to provide expressions for the protein distributions.

$$G_{\text{A}}\left(u,t\right)=\left\{\begin{array}{cccc}\hfill & {\left[\frac{b\left({\rho }_{\text{u}}+{\sigma }_{\text{b}}\right)u{\text{e}}^{-d_{\text{p}}t}-{\sigma }_{\text{b}}}{b\left({\rho }_{\text{u}}+{\sigma }_{\text{b}}\right)u-{\sigma }_{\text{b}}}\right]}^{\frac{{\rho }_{\text{u}}{\sigma }_{\text{u}}^{-}}{d_{\text{p}}\left({\rho }_{\text{u}}+{\sigma }_{\text{b}}\right)}},\hfill & \hfill & t\in \left[0,t_{\text{r}}\right),\hfill \\ \hfill & {\left[\frac{b\left({\rho }_{\text{u}}+{\sigma }_{\text{b}}\right)u{\text{e}}^{-d_{\text{p}}t}-{\sigma }_{\text{b}}}{b\left({\rho }_{\text{u}}+{\sigma }_{\text{b}}\right)u{\text{e}}^{-d_{\text{p}}\left(t-t_{\text{r}}\right)}-{\sigma }_{\text{b}}}\right]}^{\frac{{\rho }_{\text{u}}{\sigma }_{\text{u}}^{-}}{d_{\text{p}}\left({\rho }_{\text{u}}+{\sigma }_{\text{b}}\right)}}{\left[\frac{b\left({\rho }_{\text{u}}+{\sigma }_{\text{b}}\right)u{\text{e}}^{-d_{\text{p}}\left(t-t_{\text{r}}\right)}-{\sigma }_{\text{b}}}{b\left({\rho }_{\text{u}}+{\sigma }_{\text{b}}\right)u-{\sigma }_{\text{b}}}\right]}^{\frac{{\rho }_{\text{u}}{\sigma }_{\text{u}}^{+}}{d_{\text{p}}\left({\rho }_{\text{u}}+{\sigma }_{\text{b}}\right)}}\hfill & \hfill & t\in \left[t_{\text{r}},t_{\text{d}}\right),\hfill \end{array}\right.$$ [6A]

$$G_{\text{B}}\left(u,t\right)=\left\{\begin{array}{cccc}\hfill & 1\hfill & \hfill & t\in \left[0,t_{\text{r}}\right),\hfill \\ \hfill & {\left[\frac{b\left({\rho }_{\text{u}}+{\sigma }_{\text{b}}\right)u{\text{e}}^{-d_{\text{p}}\left(t-t_{\text{r}}\right)}-{\sigma }_{\text{b}}}{b\left({\rho }_{\text{u}}+{\sigma }_{\text{b}}\right)u-{\sigma }_{\text{b}}}\right]}^{\frac{{\rho }_{\text{u}}{\sigma }_{\text{u}}^{+}}{d_{\text{p}}\left({\rho }_{\text{u}}+{\sigma }_{\text{b}}\right)}}\hfill & \hfill & t\in \left[t_{\text{r}},t_{\text{d}}\right).\hfill \end{array}\right.$$ [6B]

The model has the same seven features as described at the beginning of Results, but with an additional two features: 1) mRNA is translated into protein at rate $\lambda$; and 2) protein decay occurs with rate $d_{\text{p}}$. Both reactions are assumed to obey first-order kinetics (6). Again, we need to make some approximation to proceed further: 1) We assume that the timescale ratio $\delta$ is large; and 2) we assume that the timescales of nascent and mature mRNA dynamics are much shorter than those of protein. The first assumption we know is satisfied for a large number of genes. The second assumption can be justified as follows. The timescales of nascent mRNA, mature mRNA, and protein are approximately given by the inverse of the elimination rates of each, i.e., $k$, $d$, and $d_{\text{p}}$, respectively. Now, as we saw earlier, $k\gg d$. Also, Schwanhäusser et al. (47) report that the median mRNA decay rate $d$ is approximately five times larger than the median protein decay rate $d_{\text{p}}$ for NIH 3T3 mouse fibroblasts (calculated over 4,200 genes); the cumulative distribution of the ratio of the two decay rates is shown in SI Appendix, Fig. S7. Similarly, for 1,962 genes in budding yeast, the median of the ratio of the mRNA decay rate to protein decay rate is approximately three (3). Hence, for a substantial number of genes, the assumption $k\gg d\gg d_{\text{p}}$ holds, and that implies that protein dynamics occurs over a much slower timescale than both nascent and mature mRNA dynamics. Given assumptions 1 and 2, we can show using perturbation theory applied to the master equation of the model (SI Appendix, section 8) that the temporal protein distribution is given by Eqs. 3 and 4 with the replacements $k\to d_{\text{p}}$ and $n_{\text{N}}\to n_{\text{P}}$ together with the generating functions given by Eqs. 6A and 6B, where $b=\lambda /d$ is the translational burst size quantifying the mean number of protein produced during the lifetime of mature mRNA. Note that this derivation is for the case of no growth-dependent transcription, i.e., $\alpha =0$.

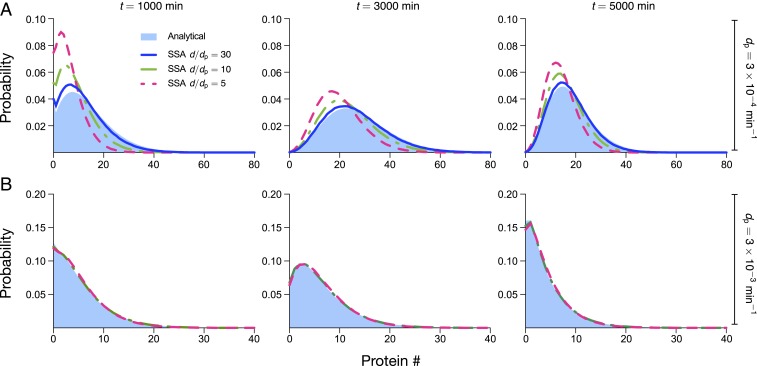
The accuracy of the approximation is tested via stochastic simulations in Fig. 5A using parameters typical of mammalian cells (47). The protein distribution obtained from theory (shown as solid blue) is compared with SSA results for the protein distribution at three different times and three different values of the ratio of mRNA to protein-decay rates $d/d_{\text{p}}$. The discrepancy between theory and simulations decreases as $d/d_{\text{p}}$ increases (as expected) and is particularly good for $d/d_{\text{p}}>10$. There is also a small increase in accuracy of the theory with increasing absolute time, though the major determinant is the decay ratio. Simulations show that the accuracy of the theory increases if we increase the protein and mRNA decay rates while keeping their ratio constant—in particular, whenever the mRNA lifetime is much less than the protein lifetime and when the latter is less than the cell-cycle length, then the agreement with theory is excellent for a wide range of values of the ratio $d/d_{\text{p}}$ (compare Fig. 5 A and B). Similarly, the accuracy of the theory also increases if we increase the cell-cycle length at constant ratio $d/d_{\text{p}}$ [note that the limit of infinite cell-cycle length corresponds to the conventional case where partitioning due to cell division is not explicitly taken into account (3)]. Hence, summarizing, our expressions for the approximate protein distributions are accurate whenever $d/d_{\text{p}}\gg 1$ and $d_{\text{p}}{t}_{\text{d}}>1$. From SI Appendix, Fig. S7, it can be deduced that about $20\%$ of proteins in mammalian cells satisfy $d/d_{\text{p}}>10$; also, analysis of the dataset in ref. 47 shows that only $30\%$ of all proteins in mammalian cells have decay lifetimes less than the cell-cycle length. Hence, while timescale separation between mRNA and protein has played an important role in the development of reduced stochastic models of gene expression in bacteria and yeast (3), it appears that the same technique should be used with care when developing reduced models of stochastic gene expression in mammalian cells.

Fig. 5.

Comparison of protein distributions predicted by theory (under the assumption of slow protein dynamics) and stochastic simulations using the SSA. (A) Using parameters typical of mammalian cells, we find that our theory agrees well with simulations for $d/d_{\text{p}}=30$, is acceptable for $d/d_{\text{p}}=10$, and performs poorly for $d/d_{\text{p}}=5$; agreement tends to be better with increasing time, but accuracy is mostly determined by $d/d_{\text{p}}$. Note that the protein lifetime is ln 2/d_p = 2,310 min, the cell-cycle duration is t_d = 1,560 min, and the mRNA lifetime is $\ln 2/d=462$, 231, and 77 min for $d/d_{\text{p}}=\mathrm{5,10,30}$, respectively. Given the value of $t_{\text{d}}$, we have that t = 1,000; 3,000; 5,000 min corresponds to cells in generations one, two, and three, respectively. (B) Parameter values as in A, except that the protein, mRNA decay, and translation rates are multiplied by 10. Note that the ratio $d/d_{\text{p}}$ is unchanged from A, but both protein and mRNA lifetimes are now 10 times smaller, meaning that they are significantly less than the cell-cycle time. This condition leads to significantly improved agreement between theory and simulations, such that they are indistinguishable for $d/d_{\text{p}}=\mathrm{5,10,30}$. See SI Appendix, section 12 for the choice of parameters.

The model can also be further extended to include bimolecular gene–protein interactions, which are common in nature (48). Specifically, we consider the case of negative feedback mediated by an auto-regulatory motif, whereby the transition from the ON to OFF state of all gene copies (i.e., the two copies prereplication and the four copies postreplication) is mediated by protein binding to the gene. Using a recently developed technique, the linear mapping approximation (LMA) (49), we show in SI Appendix, section 9 how the distributions of mRNA and protein for the model with no feedback (derived earlier) can be used to construct approximate distributions for the model with feedback.

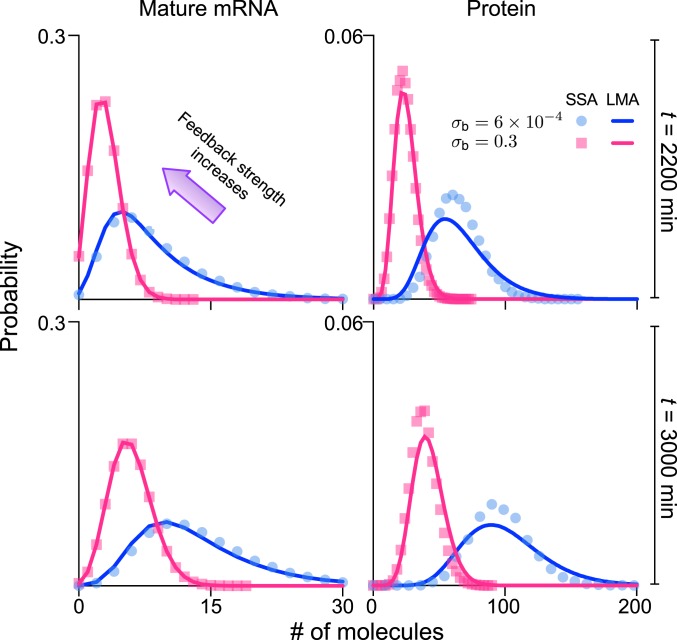
The LMA is based on two assumptions: 1) a conditional mean-field approximation which equates to assuming small protein fluctuations compared to the mean number of proteins when the promoter is unbound; and 2) a time-averaging assumption which corresponds to the first term of the Magnus expansion of the time-dependent solution of the master equation and which is uniformly valid in time, provided the protein–gene binding rates are not too large. The approximation error tends to be dominated by assumption 2. This, however, is typically small, as we show in Fig. 6, where it is clear that the LMA accurately captures the effect of negative feedback on the mature mRNA and protein distributions for both prereplication and postreplication times in the cell cycle.

Fig. 6.

LMA solution of the stochastic model with a negative-feedback auto-regulatory mechanism. The predicted distributions for mature mRNAs and proteins for time t = 2,200 min (prereplication) and t = 3,000 min (postreplication) of generation 2 are calculated from the equations for the generating functions in SI Appendix, section 9. LMA predictions for mature mRNA distributions agree with SSA results with remarkable accuracy, whereas the predictions for protein distributions agree with the SSA to an acceptable accuracy. Note that the ratio of decay rates $d/d_{\text{p}}$ is five (the median reported in SI Appendix, Fig. S7), so that the timescale separation assumption is marginally satisfied. The graphs show that increasing feedback strength ${\sigma }_{\text{b}}$ from $6\times 10^{-4}$ to 0.3 (500-fold change) substantially reduces the number of mature mRNAs and proteins. Specifically, the cell-cycle duration t_d = 1,560 min is selected to be 26 h, close to the data reported for NIH 3T3 in the supplementary information of ref. 47, the gene replication $t_{\text{r}}=800$ min occurs roughly in the middle of the cell cycle. The decay rates of mature mRNA and protein are 0.005 and 0.001 ${\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$, respectively (the half-lives are 2.3 and 11.5 h, respectively) and, hence, within the range for the same cell line reported in figure 2C of ref. 47. The other kinetic parameters are chosen as ${\rho }_{\text{u}}=0.15\hspace{0.17em}{\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$, ${\rho }_{\text{b}}=0.0075\hspace{0.17em}{\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$, $k=10\hspace{0.17em}{\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$, ${\sigma }_{\text{u}}^{-}=0.003\hspace{0.17em}{\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$, ${\sigma }_{\text{u}}^{+}=0.71{\sigma }_{\text{u}}^{-}$, $\lambda =2d$, and $\alpha =0$. See SI Appendix, section 9 for details.

Discussion

In this article, we have developed a model of gene expression in eukaryotic cells which includes a high level of biological detail compared to previous models in the literature, while remaining analytically tractable. Specifically, our model takes into account gene replication, binomial partitioning due to cell division, dosage compensation, growth-dependent transcription, promoter switching, and the translation of mature mRNA into proteins. The model also provides a description of both nascent and mature mRNA distributions, which is necessary to make sense of high-resolution experimental data (11). We have shown that by breaking this complex model into a set of simpler submodels, solving each submodel approximately using timescale-separation methods (50), and then integrating the results together, it is possible to derive closed-form expressions for the time-dependent distribution of the numbers of nascent mRNA, mature mRNA, and protein inside a single cell. Specifically, we have made use of two assumptions: 1) Nascent mRNA dynamics is much faster than mRNA dynamics, which itself is much faster than protein dynamics; and 2) the gene-inactivation rate is much larger than the gene-activation rate. We have provided experimental evidence that these assumptions are reasonable for a large number of genes in several different types of eukaryotic cells grown under different conditions, and, hence, our model provides a detailed quantitative model of eukaryotic gene expression. A major advantage of our analytic approach is that, despite the biological complexity described by the model, it leads to simple distributions (negative binomial) for the molecule numbers for all cell ages and generations. It also provides a quantitative description for both nascent and mature mRNA dynamics, both of which are measurable observables. A description in terms of the two is advantageous, since nascent mRNA closely reflects the kinetics of transcription, while mature mRNA reflects additional processes downstream of transcription.

Numerical evaluation of these distributions is far more computationally efficient than direct simulation using the SSA. This implies that the model’s behavior can be easily predicted across vast swaths of parameter space and that usually prohibitive tasks, such as stochastic sensitivity analysis, can be straightforwardly performed. Indeed, using our theory, we calculated the sensitivity of the coefficient of variation of noise (averaged over the cell cycle and in the cyclo-stationary limit) to small changes in the parameter values measured for mammalian cells. The parameters ordered according to the magnitude of their sensitivities are mRNA degradation rate, the rate of gene activation (before and after replication), rate of gene inactivation, transcription rate, cell-division time, replication time, and the parameter determining the coupling between transcription rate and cell growth. This suggests that variations in the values of the mRNA degradation rates and of the promoter-switching rates across cells are among the most significant sources of variability in gene expression across a population of cells (what is often termed extrinsic noise). Another major advantage of our closed-form expressions for the time-dependent distributions, and, in particular, their approximation by negative binomial distributions, is that they can be used to obtain the likelihood of a set of experimental observations of the molecule numbers—the likelihood can then be used within a Markov chain Monte Carlo algorithm to obtain the posterior distributions of parameters (51, 52).

Our model cannot resolve the effects of polymerase and transcription-factor fluctuations on mRNA and protein dynamics (53). It is also the case that our model cannot take into account the effect of cell-cycle-length variability on the distribution of protein numbers because the low protein degradation rates do not average out timing fluctuations (54). Lastly, the sharing of resources can potentially modify many cellular processes (55). Future work will involve extensions of the model to include these and other salient features of single-cell biology.

Data Availability.

The data used in the paper are described in SI Appendix, section 2. The simulation code is available from the corresponding author upon request.