Analysing brain networks in population neuroscience: a case for the Bayesian philosophy

Abstract

Network connectivity fingerprints are among today's best choices to obtain a faithful sampling of an individual's brain and cognition. Widely available MRI scanners can provide rich information tapping into network recruitment and reconfiguration that now scales to hundreds and thousands of humans. Here, we contemplate the advantages of analysing such connectome profiles using Bayesian strategies. These analysis techniques afford full probability estimates of the studied network coupling phenomena, provide analytical machinery to separate epistemological uncertainty and biological variability in a coherent manner, usher us towards avenues to go beyond binary statements on existence versus non-existence of an effect, and afford credibility estimates around all model parameters at play which thus enable single-subject predictions with rigorous uncertainty intervals. We illustrate the brittle boundary between healthy and diseased brain circuits by autism spectrum disorder as a recurring theme where, we argue, network-based approaches in neuroscience will require careful probabilistic answers.

This article is part of the theme issue ‘Unifying the essential concepts of biological networks: biological insights and philosophical foundations’.

1. Introduction

In network-centred research, as well as many other fields of neuroscience, drawing statistical conclusions from brain data is essential to understand the measurements of the studied phenomenon despite the presence of noise. Typical examples include inferring whether a given functional brain connection is strengthened or weakened by administering a certain environmental stimulus, or predicting a clinical diagnosis of a given individual on the basis of neuroimaging data. In this article, we argue that adopting a Bayesian perspective on network-based explanation and modelling offers several benefits, which arise from the ability to coherently handle uncertainty in developing model predictions about phenomena observed in network circuits.

Bayesian analysis and conceptualization have a long history, with origins in the eighteenth century [1]. In essence, the Bayesian framework treats all parameters in a given model as random variables and quantifies their uncertainty using Bayes' rule. For a model $\mathcal{M}$ with parameters θ, this principle indicates that the prior belief in the probability of the parameters $p(\theta |\mathcal{M})$ should be updated in the light of observed data, y, to derive the posterior distribution over the entire set of model parameters, $p(\theta |y,\mathcal{M})$

$$p(\theta |y,\hspace{0.17em}\mathcal{M})=\frac{\hspace{0.17em}p(y|\theta ,\mathcal{M})\hspace{0.17em}p(\theta |\mathcal{M})}{\hspace{0.17em}p(\theta |\mathcal{M})}.$$

The term $p(y|\theta ,\mathcal{M})$ denotes the likelihood and specifies a generative model that describes how the data may have come about. The denominator is referred to as the marginal likelihood and is obtained by integrating out the parameters $p(\theta |\mathcal{M})=\int p(y|\theta ,\mathcal{M})p(\theta |\mathcal{M})\hspace{0.17em}\text{d}\theta$. Posterior computation is typically intractable for all but the simplest models. This is why posterior parameter estimation often invites the use of numerical approximations or sampling methods [2,3]. Ready computability is probably the major hurdle for more widespread adoption of the Bayesian framework in network-based approaches.

It is important to recognize that the Bayesian philosophy of data analysis operates with a deeper and more universal concept of probability than is assumed by most of the quantitative frameworks commonly used in many areas of brain network analysis. In particular, under the frequentist paradigm [4], probability reflects long-run frequencies of repeatable events (e.g. ‘the probability of rolling a 6 on this dice is 1/6’). Under the Bayesian paradigm, probabilities reflect degrees of belief in a given proposition (e.g. ‘there is a low probability that the amygdala will increase functional connectivity 100 times more (or less) in autism vs. health’), which may not be repeatable. In a network modelling context, investigators routinely resort to frequentist notions, especially for hypothesis testing against a null distribution, for example, to define the probability that a given brain region shows more neural coupling strengths than would be expected under the null hypothesis of baseline activity.

According to the frequentist philosophy, the data-generating mechanism underlying observed network dynamics is fixed and only the observed measurements from biological networks have a probabilistic component. Inference about the model is therefore indirect, quantifying the agreement between the observed biological data and the data generated by a putative model (for example, the null hypothesis). In the Bayesian philosophy, instead, inference quantifies the uncertainty about the data-generating mechanism by the prior distribution and updates it with the data observed from biological networks to obtain the posterior distribution (figure 1). Inference about the model is therefore obtained directly as a probability statement provided by the derived posterior parameter distributions.

Figure 1.

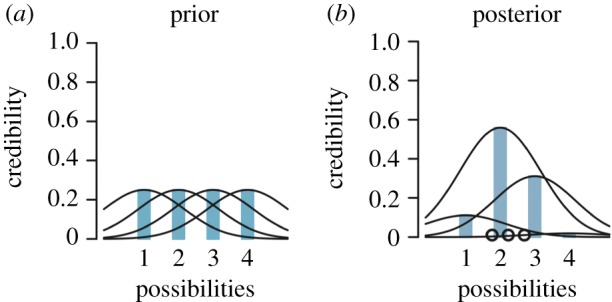
Bayesian model estimation of drug response in four autism populations based on whole-brain connectivity profiles. Suppose that a new candidate treatment for autism is being developed, such as a special psychotherapeutic intervention. The investigator now wishes to know whether there is a difference in how reliably a favourable treatment response can be estimated in four different subgroups of autism (e.g. these could correspond to male and female high-functioning and not high-functioning individuals carrying a diagnosis of autism) based on inter-subject differences in connectomic fingerprints. Before acquiring any network coupling measurements of patients about to undergo the new treatment option, the investigators pre-suppose that each of the four autism subgroups should be expected to have the exact same chance of turning out to be a treatment responder. This initial belief is reflected in four probability distributions with equal height (i.e. mean) and equal dispersion (i.e. variance) (a)—incorporating fully probabilistic expectations even before any real-world data are considered. After specifying this assumed prior knowledge of equal response probabilities, the Bayesian model is updated (parameter updating) by simultaneously integrating the observed clinical evidence collected from four different subgroups of autism patients to achieve a compromise between data-independent prior (a) and data-dependent experimental outcomes (b). In this example, the consequence is that the prior distributions are carefully adapted in shape—affecting both magnitude and uncertainty—for each autism subgroup. Importantly, the prior probability distribution of showing a favourable response to the novel therapy is re-calibrated in a subgroup-sensitive fashion. After conditioning the model on the actual clinical observations, subgroup 2 turns out to show the highest posterior parameter distribution. This model solution indicates a strongest chance for the treatment to be successful, relative to the other three considered patient subgroups. At the same time, this subgroup posterior parameter distribution features the smallest posterior variance (i.e. highest precision). The narrow dispersion of the posterior treatment effect of subgroup 2 indicates that the investigator can be more sure that the true treatment response probability is close to the estimated treatment effect (i.e. parameter mean). In stark contrast, subgroup 1 shows the widest posterior distribution, which makes explicit that the investigators should be most careful about this estimated therapy response probability. That is, we do have a specific treatment responsiveness for subgroup 1 (in form a concrete number); the interval of this posterior parameter distribution, however, also tells us that a much higher or a much lower probability is quite plausible as well, which is why the obtained parameter mean should be interpreted with caution. Note that subgroups 2 and 3 are predicted to show higher treatment response probability based on connectivity profiles than assumed under the uniform prior of equal response potential with possible implications for clinical practice, rather than succumbing to the dichotomic statement that only the posterior response probability of subgroup 2 is significant and worthy of being reported. Moreover, the conclusion of two subgroups showing evidence for treatment benefits, yet to different degrees with different uncertainty, illustrates the important advantage of Bayesian analysis to allow for fully probabilistic claims in population neuroscience studies. Adapted from [5, p. 21]. (Online version in colour.)

Over the past decade, the alternative to sampling-based approaches, namely, variational Bayes approaches, has dominated in neuroimaging analyses of (effective) connectivity. One example of this approach is dynamic causal modelling (DCM), a prominent Bayesian method for characterizing imaging time series [6,7]. Crucially, variational approaches avoid the computational cost of sampling by assuming a particular form for the posterior density [8–11]. This leads to analytic update equations that allow people to perform efficient and quick Bayesian inference on the parameters of their models. Furthermore, variational Bayes considerably finesses the problems of Bayesian model comparison, selection and reduction, to which we will return below.

Direct quantification of uncertainty is the central motif of the Bayesian framework [12]. Bayesian modelling aims to coherently incorporate uncertainty throughout the analysis such that uncertainty in the parameter estimation is carefully propagated through the generative model to form predictions about the biological system under study. Mathematical proofs show that probability theory is a unique way that this can be achieved, on the basis of a simple and common-sense set of axioms [13,14]. In short, any system of reasoning that coherently manages uncertainty for complex biological systems must be consistent with the rules of probability. As such, when carrying out Bayesian analysis of biological networks, the analyst naturally goes beyond point estimates of parameters, such as a value indicating the network connectivity strength between the amygdala and the prefrontal cortex. Rather than a single number (e.g. one Pearson correlation value of ρ = +0.27), full probability distributions are placed over all quantities in network modelling which are updated in the light of the brain data at hand. Based on the built Bayesian model, new predictions can be formed for incoming data points by averaging (i.e. integrating over) the joint posterior distribution over all model variables on the table.

A defining characteristic of the Bayesian philosophy is that this modelling regime requires the specification of a prior distribution, reflecting the beliefs about the model parameters before observing any data on brain networks. Thus, each model parameter enters with a fully specified probability distribution, whether or not biological observations have already been brought into play. If prior information is available (e.g. the topology of structural connectivity constraining functional connections, which functional connections describe intra-network versus between-network connections or whether connections between subcortical areas may be harder to measure than those between cortical areas), this can be incorporated in the model. This helps guide the parameter updates to biologically plausible ranges in the face of new observations from brain networks, while still permitting solutions that exceed the pre-set ranges to the extent supported by the data. Even in the absence of definite strong, biologically grounded a priori information, generic priors can be employed to exert a regularizing or smoothing effect on the parameter estimation (e.g. to prevent overfitting connectomic profiles of a subject sample that may not extrapolate well to the broader population). However, the specification of the priors over model parameters is often a point of criticism for Bayesian methods. This is because it can often be difficult to specify informative priors if the number of variables is large or the dependencies between them are complex, such as in many biological systems [15]. Moreover, it is often not straightforward to specify priors that convey a lack of prior knowledge [4,16]. Nevertheless, it is important to recognize that any network modelling framework is predicated on certain assumptions. The fact that the Bayesian approach forces these to be made explicit by the investigator can be viewed as a strength.

2. Notions of probability: methodological uncertainty and biological variability

The type of probability that is actually being modelled is an important distinction that is often under-appreciated across biological sciences and in network-based research on the brain in particular. Under the Bayesian conceptualization, probabilities can service multiple different purposes in network modelling [4]: probability may be treated in a ‘phenomenological’ manner to quantify natural biological variation in the brain data (e.g. how different are amygdala–prefrontal connections across subjects in the population). However, probability can also be framed in an ‘epistemological’ manner to quantify modelling uncertainty in estimating parameter values (e.g. how unsure are we about different amygdala–prefrontal connections due to finite sampling from biological networks).

This consideration reflects the distinction in statistical machine learning [17,18] between ‘aleatoric’ uncertainty, which reflects inherent variation in the measured phenomenon in biology that cannot be reduced with acquiring more observations of the biological system, and ‘epistemic’ uncertainty, which reflects uncertainty in our knowledge of model parameters and data densities can be reduced by adding more observations. Unfortunately, this nomenclature confounds the notions of variability and uncertainty described above. To simplify the discussion, we henceforth distinguish between (biological) variability and (methodological) uncertainty. For completeness, we note that in some cases it may be desirable to further decompose epistemic uncertainty (e.g. as a result of scanner noise or interpolation error).

Importantly, most dominant frequentist approaches currently used for brain network modelling conflate variability and uncertainty to a certain degree. Frequentist approaches—at best—provide post hoc estimates of model uncertainty using supplementary techniques such as bootstrapping [19]. For most network-focused applications, accurately quantifying variability is of primary explanatory interest, while minimizing or properly accounting for uncertainty. Indeed, in the physical and life sciences, uncertainty quantification is now regarded as one of the most important estimation challenges (e.g. [20–22]). This is especially the case in weather prediction and climate change [23]. It is also an important aspect of Bayesian model comparison and the way research hypotheses are tested within a Bayesian framework.

To provide a concrete example from imaging neuroscience, normative modelling is a recently introduced technique that aims to map centiles of variation, such as the functional connectivity strength between amygdala and prefrontal cortex, across a reference cohort in an analogous manner to the use of growth charts in paediatric medicine [24,25]. For example, by plotting biological parameters as a function of age (or other clinically relevant variables), normative modelling enables statistical conclusions as to where the network coupling profile of each individual participant falls within the population range. This modelling tactic can therefore be used to chart variability in biological networks relevant to many disorders including autism and detect the biological signatures of brain disorders in an anomaly detection setting [26].

In such applications, the primary interest is in modelling inter-individual variation across the cohort while accounting for modelling uncertainty such as noise intrinsic to the functional magnetic resonance imaging (fMRI) signals from brain networks. For such neuroscience applications, the ability to jointly model different sources of variation and appreciate uncertainty in the same modelling instance is an important advantage of the Bayesian culture. For example, using Bayesian methods, the investigator can use separate variance components to model variation in age-related connection strength across a population cohort and the uncertainty in that estimation, due, for example, to data sampling density (e.g. fewer female subjects, or less high-functioning patients). By contrast, classical methods may also be used for normative modelling. Confidence intervals for the centiles of variation could be derived using bootstrapping [27]. However, bootstrapped frequentist models cannot easily be used to draw probabilistic conclusions on new, unseen connectomic data. In Bayesian analysis instead, the directly estimated posterior distributions qualifying each model parameter can be readily used to form fully probabilistic predictions, such as on an individual's diagnosis for autism on the basis of connectome fingerprints.

The value of Bayesian analysis for the goal of delineating quantities of variability and uncertainty in connectivity analysis has been advertised through a body of literature (e.g. [15,28–35]). More specifically, in the context of brain networks, Bayesian methods have been applied for improving the estimation of whole-brain connectivity profiles [36,37] in finding parcellations of different brain networks [38], for causal inference in fMRI [39] and for multi-modal data fusion [40]. These existing neuroimaging applications have largely focused on datasets of modest size, for which Bayesian methods are well suited owing to the regularizing effect exerted by the imposed priors and the guidance of parameter updates by existing neuroscience knowledge. As such, generic priors can be used to de-prioritize exceedingly large model parameters to discourage unrealistic model parameter estimates. Such smooth bounding of suboptimal parameter candidates during model estimation helps guard against overfitting to seemingly coherent patterns in the connectivity fingerprints of the subjects. In addition to previous applications, we argue here that Bayesian methods also provide an excellent tool for large, population-based cohorts, which are gaining centre stage in clinical neuroimaging [41–45].

There are several reasons for the suitability of the Bayesian framework in the ‘big data’ era (cf. [46,47]): the ability to separately quantify variability and generate explainable insight in the natural phenomenon under study and uncertainty in the model under use is likely to be instrumental to understanding inter-individual variations across large cohorts (cf. above). Its importance is increasingly recognized in intelligence prediction based on connectivity fingerprints and other successful examples [24,48–50]. Bayesian methods are also appealing because they provide estimates of the plausible range of a parameter value given the brain data. By contrast, in large samples, classical null-hypothesis testing methods can easily reject the null hypothesis for nearly all values (e.g. all network nodes in a classical frequentist connection-wise analysis), even though the underlying effects are of negligible magnitude (see [31]). It should be obvious that quantifying methodological uncertainty is critical for optimal decision-making in medicine [51]. For example, for predicting an autism diagnosis on the basis of MRI scans, where uncertainty arises at multiple levels: not only in the diagnosis itself (i.e. at the level of clinical presentation), but also at the level of the underlying biology (e.g. the connectivity strength in a network modelling context).

In this paper, we will provide a conceptual overview of the aim and utility of the Bayesian modelling framework in clinical neuroscience, focusing on the use of such methods for generating explainable insights on connectomics. Functional connectivity fingerprints are particularly valuable for capturing salient characteristics of momentary states of conscious awareness and for predicting individual differences in cognition [43,48,52]. These analytical techniques are widely applicable to predicting symptomatology across many clinical populations [53,54].

3. Hierarchical Bayesian modelling: appreciating covariates of population stratification

The boundary between signal and noise is often hard to identify, let alone to know prior to data analysis. It is common practice in many empirical sciences, including network analysis in imaging neuroscience (e.g. [42,43]), to adjust for nuisance variance in the data in two separate steps. In a first modelling step, variation that can be explained by nuisance covariates is removed, typically using linear-regression-based deconfounding. In a subsequent modelling step, the remaining variation in the data is then fed into the actual statistical model of interest used to draw neuroscientific conclusions on brain network phenomena. As such, the final explanation is typically grounded in model parameter estimates from a version of the original data, in which any linear association with the considered nuisance covariates, such as age- and sex-related differences between individuals, has already been comprehensively removed beforehand. In this approach to network modelling, the implicit but critical assumption is that any target effects of interest in the brain data, such as for the goal of classifying neurotypicals from individuals with a diagnosis of autism based on connectomic fingerprints, are treated largely separately from what is measured by the nuisance covariates.

In many brain disorders, including autism, the distinction between signal and noise may be more ambiguous than established analysis workflows belie. Age, sex and motion are routinely chosen as nuisance covariates. However, the majority of autism samples include 3–5 times more males who carry a diagnosis of autism than females [55–57], reflecting differences in prevalence in the wider population. While several reasons can be brought forward [58–61], it has been speculated that the discrepant prevalence of autism may point to a more profound distinction in the aetiology of the disease, potentially linked to its triggering life events, underlying pathophysiological mechanisms, and ensuing coping strategies. Preceding removal of sex-related signal in the data can also remove information on and preclude insightful explanations about sex-specific disease pathways in autism or lead to spurious findings or incorrect conclusions [42,62]. Let us consider a hypothetical scenario where amygdala–prefrontal connectivity is pathologically increased in male patients, but pathologically decreased in female patients. Here, a preceding deconfounding step for sex would largely remove this sex-dependent aspect, which, however, truly is a characteristic of disease biology, from subsequent statistical analysis and scientific conclusion.

In a similar spirit, the age trajectories of male and female individuals with autism, including the manifestations in underlying network biology, may be different in multiple ways. For instance, a commonly described clinical feature of autism is that females are more often diagnosed later in life [61]. Better coping strategies and more successful camouflaging behaviour in women with autism is a common explanation for this age-related divergence [63]. Consequently, removing age-related variance in brain network measurements as a ‘data preprocessing’ routine, expected by peer scientists and paper reviewers in the community, may systematically withhold insights that can teach us something about the age-dependent development of autism in different strata of the population. We therefore argue that it is often more pertinent to model shared variance explicitly, such as in jointly modelling age-dependent connectivity variation and autism-dependent variation in the functional connectome, for which the Bayesian framework is well suited. For example, Bayesian analysis could answer a question such as ‘How certain are we that amygdala–prefrontal connectivity strength is similar or dissimilar in certain subgroups, such as when stratifying by sex or lifespan?’.

Rather than resorting to a deterministic decision in a black-or-white fashion, Bayesian hierarchical modelling (BHM) is a natural opportunity to quantify the separate contributions by answering which sex-, age- and motion-related components in network connectivity couplings are related to autism-related model parameters with which magnitude and how certain the investigator can be about it. A set of sources of variation in the brain data can be directly integrated in a single-model estimation, instead of carrying out initial confound and later effect analyses (cf. above). Said in yet another way, BHM allows explicit modelling of the group differences in functional brain connections in disease versus control groups as linked to the question of how much any group difference is influenced by age, sex and motion variation in the functional connectivity data by hierarchically accounting for dependencies between sources of variation.

Removing age, sex and motion-related information from the data in an isolated modelling step hides important information that can be instrumental in guiding the parameter estimation of the model actually used to gain biological insight. While this goal can also be accommodated in a non-Bayesian setting (e.g. using linear mixed effects models), the Bayesian formulation is appealing because it coherently propagates uncertainty through different levels of the model and can therefore more readily disentangle different sources of variability and uncertainty.

One prevalent form of BHM is known as parametric empirical Bayes (PEB) [64,65]. This now underwrites most of the between-subject analyses using DCM. In brief, PEB rests on a hierarchical Bayesian model in which random effects at the within- and between-subject level can be accommodated. Usually, these hierarchical models are based on general linear models at higher levels; hence they are parametric. Below, we will consider non-parametric empirical Bayesian models.

Motion during brain scanning is one of the measurements that is widely used to remove variation from connectivity data, before starting the actual functional connectivity analysis. A few years ago, neuroimaging investigators reported a seemingly distinctive pattern of maturing functional network fluctuations with weakening short-range and growing long-range connections that slowly change during child development [66,67]. Investigators speculated that these findings mean that normal children start life with prominent short-range connectivity, which then weakens over the lifespan in healthy controls, and vice versa for long-range connectivity [68]. Individuals carrying a diagnosis of autism were then found to show more short-range and fewer long-range connectivity links [69,70], especially in children. Unfortunately, it later became apparent that excessive head movements during brain scan acquisition reliably entailed artefacts with these same connectivity patterns in functional brain connectivity, previously thought to reflect impaired brain maturation [71,72], which entailed several retractions of high-profile papers (https://www.spectrumnews.org/news/movement-during-brain-scans-may-lead-to-spurious-patterns/).

On the other hand, at the behavioural level, it is well established that people with a diagnosis of autism exhibit greater degrees of movement than healthy controls [73,74]. As such, unusually high body movement can be argued to be a hallmark feature of autism, but is now recognized to also be a reason for spurious functional connectivity findings. Put differently, it is hard to give a single clear-cut answer as to which aspects of functional connectivity signals correspond to motion-related noise and which aspects correspond to biologically informative signals in functional connectivity synchronization between brain regions. With and without a given adjustment for motion-related influences, distinguishing functional connectivity fingerprints in autism reflect different statistical questions [75]. These data modelling scenarios correspond to two equally valid questions depending on the scientific purpose. Adjustment relates to partitioning a population into groups that are homogeneous according to the deconfounding variable—there may be no single right or wrong. Bayesian analysis can help in quantifying uncertainty via joint probability distributions that explicitly incorporate how body motion measurements are related to network connectivity strengths and to other measurements of interest in an integrated approach.

The inferential grip of insights about brain network coupling can thus be enhanced by findings with models acknowledging variation at different scales. In this way, BHM allows us to ask more ambitious questions using hierarchical population models of brain connectomics in strata of individuals. Young people with autism are different from old people with autism as reflected in their connectome profiles. An additional and not mutually exclusive source of variation is that male autism is different from female autism, conjointly across lifespan. We can estimate differences in network connectivity between autism and control groups by modelling hierarchical dependencies between multiple sources including covariates, like age, sex and motion, with parameters corresponding to network connectivity measurements. This multi-level modelling set-up allows partial pooling of information between measurements suspected to exert confounding influence and genuine measurements of brain signals. For instance, neuroscientists may find that increased amygdala–prefrontal connectivity in autism is particularly characteristic for females who are in early childhood and tend to move their head little in the brain scanner as part of a joint posterior parameter distribution incorporating all measured sources of variability. Additionally, sex imbalance is often encountered in population samples of autism which can reflect the population prevalence or explicit exclusion of female cases. Imbalance in the considered participants in each group can be explicitly handled by BHM, with appropriate accounting for uncertainty. To adjust for these differences in naturally occurring group size, we can avoid being misled in the way that we typically would be by common single-level models. As such, the often made a priori distinction into signal and noise, as a separate preprocessing step, can be relaxed by combining and integrating statistical evidence from disparate sources in a single probabilistic model estimation [76].

As a more concrete scenario for a key strength of flexible Bayesian hierarchical approaches, age, sex and motion may be modelled in well-defined nested relationships in order to make predictions from brain connectomic variation. It is conceivable that the tendency for body motion in the scanner is a function of age and differs by sex. As such, the investigator may wish to specify a generative model, where male and female participant prior distributions are at the top level, from which probabilistic distributions for age decades are sampled that, in turn, give rise to the (age/sex-dependent) motion covariate distributions. During model estimation, partial pooling between the age, sex and motion dependencies calibrate parameter shrinkage in a data-dependent fashion to achieve optimal prediction performance. The obtained posterior parameter distributions then allow the investigator to draw careful conclusions about the multi-level relationships between effects from several inter-dependent sources of age, sex and motion variation as to how they relate to connectome-based predictions. Importantly, such joint modelling of sources of randomness is challenging in classical (non-Bayesian) general linear models.

4. The importance of saying no: uncertainty estimates for single-subject predictions

As one of various supporting hints for the biological basis of autism, the integrity of the amygdala in the limbic network was repeatedly highlighted to differ in patients with autism, which is thought to play a role in impaired social interaction [77]. Statistically significant differences in the amygdala in autism led to varying reports in different patient samples [78,79]. Thus, this disease manifestation does not appear to be present in every single autism patient, nor is it consistently present on average in every patient sample recruited for studies that compare healthy and diagnosed individuals. Asking whether or not a strict categorical difference exists in a specific brain region in individuals on the autism spectrum may simply be a suboptimal analytical approach for the job.

Put differently, any modelling technique that is designed to give categorical black-and-white answers may be inappropriate for probing disease features that are (i) present in autism patients to varying degrees (i.e. reflecting biological variability), (ii) difficult to detect from the noisy behavioural and/or functional connectivity measurements that are available (i.e. reflecting epistemological uncertainty), or both. If these two sources of variation have played a role in amygdala studies in autism then using analysis approaches that can only make raw statements declaring presence or absence of an effect may be inherently ill-suited [80]. If the network phenomenon under study is highly variable across people and/or tricky to quantify methodologically, then investigators in one laboratory may conclude the presence of a difference in connectivity between amygdala and prefrontal cortex on their sample, while another research group studying a different patient sample with the same research question may conclude the absence of group-related connectivity differences. While the answer is seemingly certain in each of these studies, the uncertainty in whether or not an amygdala effect is present in the limbic network of autists comes out at another end [81]: lacking reproducibility across different studies that have carried out a dichotomic test for statistically significant versus insignificant amygdala alterations in autism samples [82].

In such cases, the conventional frequentist 95% confidence intervals are not the solution that many investigators desire. It is common to hear that a 95% confidence interval means that there is a probability 0.95 that the true parameter value lies within the interval; that is, that we do not have enough evidence to reject the null hypothesis of equal amygdala volume in both groups. In non-Bayesian statistical hypothesis testing, such a statement is never correct, because strict non-Bayesian inference forbids using probability to measure uncertainty about parameters like a measure of amygdala connectivity in healthy versus diseased individuals. Instead, one should say that if we repeated the study and analysis of a large number of different samples, then 95% of the computed intervals would contain the true parameter value. The classical 95% confidence interval only takes its meaning in the hypothetical long run of repeatedly analysing always new samples of controls and patients. Then we expect to be mistaken about the presence or absence of amygdala effect in only 5%, that is 1 in 20, of the conducted network connectivity studies.

A particularly clear illustration of this point is Lindley's paradox (https://en.wikipedia.org/wiki/Lindley%27s_paradox). It describes a situation in which a classical statistical analysis suggests a very significant effect, despite the fact that the Bayesian model evidence for the null hypothesis or model is far greater than the alternative. This paradox explains the dangers of over-powered studies that can become too sensitive to trivial effect sizes, while, in a Bayesian setting, they would provide evidence for the null hypothesis.

Rather than forcing definitive answers on the presence against absence of subtle amygdala effects using null-hypothesis statistical significance testing, Bayesian analysis fully embraces unavoidable variation as an integral part of model building, estimation and interpretation [2]. In the Bayesian paradigm, each component of the model has a fully specified probability distribution, before and after seeing the brain data. As a consequence, a Bayesian model estimating differences in amygdala connectivity in healthy versus autistic individuals naturally provides estimates of the degree of difference at the phenomenological level as well as estimates of the modelling uncertainty at the epistemological level. Any amount of divergence between 0 (no difference) and 1 (difference) is a possible, legitimate and interpretable result in the Bayesian posterior parameter estimate, while fully accounting for uncertainty in the parameter estimation.

In this way, the Bayesian modelling regime offers rigorous statements on how much an explanation on a given group difference in the amygdala is justified in the patient sample at hand. The width of the corresponding parameter posterior estimate can be narrow to indicate high certainty in the obtained group difference (cf. figure 1). By contrast, the posterior distribution can be widely spread out to indicate low methodological certainty and thus limited neuroscientific trustworthiness of the found parameter value reflecting amygdala coupling difference. Taken together, Bayesian modelling directly provides a confidence judgement about each quantity on the table. For example, it allows statements such as: ‘under the model, there is a 95% probability that amygdala connectivity to other networks differs between individuals with autism and controls'. If the evidence for the tested difference is ambiguous, we want this to be the result of the analysis, so that we can align the strength of our conclusions with the certainty that the model can afford.

Most modelling approaches following the frequentist philosophy have a harder time telling the investigator when the modelling result is unsure or not. For example, linear support vector classifiers or linear discriminant analysis can be applied to connectomic brain data to vote for autism, rather than control, based on a brittle 51% or a solid 98% probability for evidence of group difference in the amygdala. In other words, Bayesian analysis frameworks are a rare opportunity where the resulting model solution ‘knows when it does not know’. Moreover, in null-hypothesis statistical testing, the probability of detecting an effect (i.e. statistical power) increases with increasing sample size, even though the effect size (e.g. in terms of group differences in a point estimate for a given parameter) does not [83]. Bayesian modelling does not suffer from this shortcoming for the reasons we have outlined above.

Another key benefit of being able to say ‘None’ is that one can compare the evidence for models with and without particular parameters. This affords a very simple form of Bayesian model selection or structure learning' namely Bayesian model reduction (https://en.wikipedia.org/wiki/Bayesian_model_reduction). Using the variational procedures mentioned above, this leads to fast schemes for comparing thousands of models in which various combinations of parameters are ‘turned off’ with appropriate priors.

The ability to say ‘None’ when the investigator asks for whether a group difference either exists or not will probably turn out to be crucial in our efforts towards precision medicine [84–86]. As Bayesian models are fully probabilistic by construction, brain data from a new incoming individual, such as brain scanning yielding amygdala connectivity measures, can be propagated through the already-built model into a probabilistic prediction for the single individual at hand. Adding such information can be crucial in a variety of settings in neuroscientific research and clinical practice. First, generating single-subject predictions in a patient may yield different levels of certainty in assessments of autism symptoms related to language, motor behaviour, IQ or social interaction capacities. For example, individuals who are confidently classified may have more severe symptoms in a particular domain, while others that are less confidently classified may be more mildly affected. Separate judgements on the certainty of predictive conclusions in each of these symptom domains may turn out to characterize different types of autism in the spectrum, such as high-functioning autism. Second, along the life trajectory, different symptom dimensions of autism may turn out to be predictable based on brain network measurements with higher or lower confidence, which may turn out to be characteristic for developmental periods in autism, or specific for atypical cases or different subtypes of autism. For instance, in women with autism, typically better camouflaging of social deficits [63,87,88] may lead to social impairment predictions that have non-identical confidence in men with autism. Third, uncertainty is undoubtedly a key asset of treatment response prediction to choose therapeutic interventions tailored to single individuals. In this context, models predicting which treatment option to choose based on an individual's connectomic profile will be all the more useful in clinical practice, if such algorithmic recommendations also carry forward information on the forecasting confidence.

5. Disease subtyping: towards probabilistic intermediate phenotype discovery

A key challenge in the study of most psychiatric disorders, including autism, is that individuals with the same clinical diagnosis vary considerably from one another in terms of clinical phenotype and underlying network biology. This has led to some investigators proposing that it may be preferable to consider the ‘autisms’ [69]. Many studies have aimed to dissect the clinical phenotype of autism (e.g. [89,90]), for which functional connectivity provides promising candidate features (e.g. [91]). Moreover, since atypicalities are often complex and multifaceted, the features used for this purpose are often high-dimensional (e.g. consider even more whole-brain nodes in functional connectivity matrices) and/or multi-modal (e.g. combine measures derived from structural and functional connectivity).

In general, the goal of such connectome-based studies is to derive the latent structure underlying the clinical phenotype (e.g. partitioning the cohort into subtypes) on the basis of psychometric or biological variables, while accounting for nuisance variation. There are many ways that this can be achieved, including classical clustering techniques and matrix factorization techniques such as non-negative matrix factorization (NMF) and independent components analysis (ICA). Briefly, clustering approaches focus on finding subtype clusters in the data, whereas matrix factorization approaches focus on finding useful decompositions of a data matrix under various assumptions. This can be used, for example, to find latent factors that may overlap across individuals, in that any given individual may express multiple latent factors [92]. While these approaches are widely applied in a classical frequentist context, Bayesian variants have also been developed. In addition, highly promising Bayesian ‘non-parametric’ clustering and matrix factorization approaches have been developed such as Dirichlet process mixtures (DPMs) (Chinese restaurant processes) and the ‘Indian buffet’ process (IBP). Adopting a Bayesian approach to such problems confers many benefits, including providing good control over latent representations of the data, thereby helping to attenuate problems with high-dimensional estimation, providing predictive intervals around parameter estimates and predictions and providing flexible noise models for different forms of data. Moreover, Bayesian models are always generative in the sense that they always provide a model for how the brain connectivity measurements may have been generated. Collectively, such Bayesian approaches are increasingly applied in clinical and neuroimaging contexts [38,40,93,94].

A key problem in most classical stratification techniques is the issue of model order selection, or in other words, determining the optimal number of clusters or latent factors for the data at hand [95]. For example, ‘How many subtypes of autism can be distinguished in a given clinical dataset based on brain connectivity profiles?’. This is a notoriously difficult problem in classical statistics for which no uniquely optimal solution has imposed itself [96,97], leading to suggestions that model order selection is perhaps sometimes largely a matter of taste [98]. There are many heuristic approaches for this problem, but these are subject to difficulty in practice. Additionally, choosing between a variety of viable model order selection criteria, which are by themselves objective, still amounts to taking a subjective choice on the number of latent factors best supported by the data. Different cluster validity criteria often give different answers or do not indicate a clear preference for one model order over others [99], nor whether a given clustering solution explains the data better than a continuous model (i.e. with no clusters [100]). This has contributed to inconsistencies in the clinical stratification literature such that there are no consistently reported subtypes for autism [101] or indeed any psychiatric disorder, despite decades of effort [102].

Above, we considered parametric empirical Bayesian models [65] as prevalent examples of hierarchical Bayesian modelling. The use of Bayesian model comparison and reduction to prune these models provides an efficient way to test hypotheses about the role of any particular brain region can be associated with many other connections. A similar functionality can be afforded by Bayesian non-parametric approaches. These provide an appealing solution to this problem because they can automatically adjust the model complexity (e.g. number of clusters or latent factors) on the basis of the data at hand. In other words, non-parametric models allow the flexibility to grow with the number of data points used for model building. The simplest examples of Bayesian non-parametric models are Gaussian process models [103], which are widely used for nonlinear regression and have been used in normative modelling approaches described above. In a similar manner, DPM [104,105] and IBPs [106] provide an elegant potential solution to the problem of model order selection in clustering and matrix factorization, respectively. For example, the DPM model can be viewed as a clustering model where the number of clusters is bounded only by the sample size, effectively making the DPM an infinite mixture model [107]. This has already been shown to be useful in a recent neuroimaging study on autism [89]. As noted, a very appealing feature of this model is that it is self-calibrating in that it allows the optimal model order (i.e. the number of clusters) to be automatically derived from the data while allowing the model order to grow with more data (i.e. increasing representational capacity). In practice, the number of clusters often grows sublinearly with the number of observations [105]. At the same time, by computing (or approximating) the full posterior distribution over the model parameters, this approach helps to attenuate overfitting. This non-parametric clustering approach has clearly desirable features for the stratification of psychiatric disorders such as autism in large data cohorts. Particularly, as the size of the available datasets grows (e.g. through larger consortia), such models offer the ability to produce increasingly more fine-grained fractionations of the clinical phenotype. Similarly, in the context of brain networks, this approach has been shown to be useful for automatically parcellating brain networks into component regions [38].

A more recent addition to the Bayesian non-parametric toolbox is the ‘Indian buffet’ process (IBP) [106]. The name is derived by analogy to the ‘Chinese restaurant process' formulation of Dirichlet process mixtures (see [108]). The IBP differs in that it does not assume that a single class is responsible for generating each data point (i.e. it does not provide a hard clustering solution). Rather, it allows each data point to express multiple features simultaneously, potentially reflecting multiple causes. While this approach is yet to see extensive application in brain connectomics, IBPs have been shown to provide an elegant way to model comorbidity in psychiatric disorders, where each individual expresses multiple latent factors to varying degrees [93].

The key advantage of Bayesian techniques for model order selection in brain network modelling in health and disease is that they provide a formal framework for reasoning about model structures and deducing the plausibility of different candidate structures in view of the data at hand (e.g. [109,110]).

6. Conclusion

In this conceptual overview, we have provided a pitch for the Bayesian perspective on modelling biological network circuits in the healthy brain and their perturbation in autism spectrum disorder. There are many different ways in which adopting a Bayesian philosophy to analysis and interpretation can open new windows of explanation for neuroscience investigators building on population neuroscience initiatives like UK Biobank, CamCAN or the Human Connectome Project (e.g. [111]).

These analysis techniques provide an appealing interpretation of probability in terms of degrees of belief in a proposition, which is a more general notion than the more restricted notion of reasoning about long-run frequencies of repeatable events; they provide analytical machinery to separate (methodological) uncertainty and (biological) variability along with a calculus for reasoning about both in a coherent manner; and they usher towards avenues away from classical null-hypothesis significance testing, which is particularly valuable in data richness, and may contribute to overcoming the current reproducibility crisis in biomedicine. Finally, Bayesian methods afford estimates of uncertainty around all model parameters at play and can hence form predictions about single individuals by appropriate handling of all considered sources of variation in network approaches. Their value resides for instance in explaining brain network connectivity at different hierarchical scales in the same modelling instance. Promoting such approaches to uncovering key features of biological networks can bear further advantages in the context of data fusion, individual prediction, and subgroup stratification of cohorts, and for precisely quantifying statistical differences between experimental cohorts. We anticipate that in the coming years, the Bayesian arsenal will be endorsed for applications in network-focused neuroscience studies more than is currently the norm.

Data accessibility

This article has no additional data.

Authors' contributions

All three authors wrote and edited the manuscript.

Competing interests

The authors declare no conflict of interest.

Funding

D.B. was funded by the Healthy Brains for Healthy Lives (HBHL) initiative and by the Pan-Canada CIFAR AI Chairs programme of the Canadian Institute for Advanced Research (CIFAR). A.F.M. gratefully acknowledges funding from the Netherlands Organisation for Scientific Research under a VIDI fellowship (grant no. 016.156.415) and from the Wellcome Trust under the Digital Innovator scheme (215698/Z/19/Z).