Lossy‐Context Surprisal: An Information‐Theoretic Model of Memory Effects in Sentence Processing

Abstract

A key component of research on human sentence processing is to characterize the processing difficulty associated with the comprehension of words in context. Models that explain and predict this difficulty can be broadly divided into two kinds, expectation‐based and memory‐based. In this work, we present a new model of incremental sentence processing difficulty that unifies and extends key features of both kinds of models. Our model, lossy‐context surprisal, holds that the processing difficulty at a word in context is proportional to the surprisal of the word given a lossy memory representation of the context—that is, a memory representation that does not contain complete information about previous words. We show that this model provides an intuitive explanation for an outstanding puzzle involving interactions of memory and expectations: language‐dependent structural forgetting, where the effects of memory on sentence processing appear to be moderated by language statistics. Furthermore, we demonstrate that dependency locality effects, a signature prediction of memory‐based theories, can be derived from lossy‐context surprisal as a special case of a novel, more general principle called information locality.

1. Introduction

For a human to understand natural language, they must process a stream of input symbols and use them to build a representation of the speaker's intended message. Over the years, extensive evidence from experiments as well as theoretical considerations has led to the conclusion that this process is incremental: The information contained in each word is immediately integrated into the listener's representation of the speaker's intent. This is an integration of two parts: The listener must combine a representation r, built based on what she has heard so far, with the current symbol w to form a new representation r'. Under a strong assumption of incrementality, the process of language comprehension is fully characterized by an integration function which takes a representation r and an input symbol w and produces an output representation r'. When this function is applied successively to the symbols in an utterance, it results in the listener's final interpretation of the utterance. The incremental view of language processing is summarized in Fig. 1.

Figure 1.

A schematic view of incremental language comprehension. An utterance is taken to be a stream of symbols denoted w, which could refer to either words or smaller units such as morphemes or phonemes. Upon receiving the ith symbol w_i, the listener combines it with the previous incremental representation r_{i −1} to form r_i. The function which combines w_i and r_{i −1} to yield r_i is called the integration function.

The goal of much research in psycholinguistics has been to characterize this integration function by studying patterns of differential difficulty in sentence comprehension. Some utterances are harder to understand than others, and within utterances some parts seem to engender more processing difficulty than others. This processing difficulty can be observed in the form of various dependent variables such as reading time, pupil dilation, event‐related potentials on the scalp, etc. By characterizing the processing difficulty that occurs when each symbol is integrated, we hope to be able to sketch an outline of the processes going on inside the integration function for certain inputs.

The goal of this paper is to give a high‐level information‐theoretic characterization of the integration function along with a linking hypothesis to processing difficulty which is capable of explaining diverse phenomena in sentence processing. In particular, we aim to introduce a processing cost function that can derive the effects of both probabilistic expectations and memory limitations, which have previously been explained under disparate and hard‐to‐integrate theories. Furthermore, our processing cost function is capable of providing intuitive explanations for complex phenomena at the intersection of probabilistic expectations and memory limitations, which no explicit model has been able to do previously.

Broadly speaking, models of difficulty in incremental sentence processing can be divided into two categories. The first are expectation‐based theories, which hold that the observed difficulty in processing a word (or phoneme, or any other linguistic unit) is a function of how predictable that word is given the preceding context. The idea is that if a word is predictable in its context, then an optimal processor will already have done the work of processing that word, and so very little work remains to be done when the predicted word is really encountered (Hale, 2001; Jurafsky, 2003).

The second class of sentence processing theories is memory‐based theories: the core idea is that during the course of incremental processing, the integration of certain words into the listener's representation requires that representations of previous words be retrieved from working memory (Gibson, 1998; Lewis & Vasishth, 2005). This retrieval operation might cause inherent difficulty, or it might be inaccurate, which would lead to difficulty indirectly. In either case, these theories essentially predict difficulty when words that must be integrated together are far apart in linear order when material intervenes between those words which might have the effect of making the retrieval operation difficult.

This paper advances a new theory, called lossy‐context surprisal theory, where the processing difficulty of a word is a function of how predictable it is given a lossy representation of the preceding context. This theory is rooted in the old idea that observed processing difficulty reflects Bayesian updating of an incremental representation given new information provided by a word or symbol, as in surprisal theory (Hale, 2001; Levy, 2008a). It differs from surprisal theory in that the incremental representation is allowed to be lossy; that is, it is not necessarily possible to determine the true linguistic context leading up to the ith word w_i from the incremental representation r_{i −1}.

We show that lossy‐context surprisal can, under certain assumptions, model key effects of memory retrieval such as dependency locality effects (Gibson, 1998, 2000), and it can also provide simple explanations for complex phenomena at the intersection of probabilistic expectations and memory retrieval, such as structural forgetting (Frank, Trompenaars, Lewis, & Vasishth, 2016; Gibson & Thomas, 1999; Vasishth, Suckow, Lewis, & Kern, 2010). We also show that this theory makes major new predictions about production preferences and typological patterns under the assumption that languages have evolved to support efficient processing (Gibson et al., 2019; Jaeger & Tily, 2011).

The remainder of the paper is organized as follows. First, in Section 2, we provide background on previous memory‐ and expectation‐based theories of language comprehension and attempts to unify them, as well as a brief accounting of phenomena which a combined theory should be able to explain. In Section 3, we introduce the theory of lossy‐context surprisal and clarify its relation with standard surprisal and previous related theories. In Section 4, we show how the model explains language‐dependent structural forgetting effects. In Section 5, we show how the model derives dependency locality effects. Finally, in Section 6, we outline future directions for the theory in terms of theoretical development and empirical testing.

2. Background

Here we survey two major classes of theories of sentence processing difficulty, expectation‐based theories and memory‐based theories. We will exemplify expectation‐based theories with surprisal theory (Hale, 2001; Levy, 2008a) and memory‐based theories with the dependency locality theory (Gibson, 1998, 2000). In Section 3, we will propose that these theories can be understood as special cases of lossy‐context surprisal.

2.1. Expectation‐based theories: Surprisal theory

Expectation‐based theories hold that processing difficulty for a word is determined by how well expected that word is in context. The idea that processing difficulty is related to probabilistic expectations has been given a rigorous mathematical formulation in the form of surprisal theory (Hale, 2001, 2016; Levy, 2008a), which holds that the observed processing difficulty D (as reflected in e.g., reading times) is directly proportional to the surprisal of a word w_i in a context c, which is equal to the negative log probability of the word in context:

$$D_{\text{surprisal}}(w_i|c)\propto -\log p(w_i|c).$$ (1)

Here “context” refers to all the information in the environment which constrains what next word can follow, including information about the previous words that were uttered in the sentence. As we will explain below, this theory is equivalent to the claim that the incremental integration function is a highly efficient Bayesian update to a probabilistic representation of the latent structure of an utterance.

Why should processing time be proportional to the negative logarithm of the probability? Levy (2013, pp. 158–160) reviews several justifications for this choice, all grounded in theories of optimal perception and inference. Here we draw attention to one such justification: that surprisal is equivalent to the magnitude of the change to a representation of latent structure given the information provided by the new word. This claim is deduced from three assumptions: (a) that the latent structure is a representation of a generative process that generated the string (such as a parse tree), (b) that this representation is updated by Bayesian inference given a new word, and (c) that the magnitude of the change to the representation should be measured using relative entropy (Cover & Thomas, 2006). This justification is described in more detail in Levy (2008a).

More generally, surprisal theory links language comprehension to theories of perception and brain function that are organized around the idea of prediction and predictive coding (Clark, 2013; Friston, 2010; Friston & Kiebel, 2009), in which an internal model of the world is used to generate top‐down predictions about the future stimuli, then these predictions are compared with the actual stimuli, and action is taken as a result of the difference between predictions and perception. Such predictive mechanisms are well‐documented in other cognitive domains, such as visual perception (Egner, Monti, & Summerfield, 2010), auditory and music perception (Agres, Abdallah, & Pearce, 2018), and motor planning (Wolpert & Flanagan, 2001).

In addition to providing an intuitive information‐theoretic and Bayesian view of language processing, surprisal theory has the theoretical advantage of being representation‐agnostic: The surprisal of a word in its context gives the amount of work required to update a probability distribution over any latent structures that must be inferred from an utterance. These structures could be syntactic parse trees, semantic parses, data structures representing discourse variables, or distributed vector‐space representations. This representation‐agnosticism is possible because the ultimate form of the processing cost function in Eq. 1 depends only on the word and its context, and the latent representation literally does not enter into the equation. As we will see, lossy‐context surprisal will not be able to maintain the same degree of representation‐agnosticism.

The predictions of surprisal theory have been validated on many scales. The basic idea that reading time is a function of probability in context goes back to Marslen‐Wilson (1975) (see Jurafsky, 2003, for a review). Hale (2001) and Levy (2008a) show that surprisal theory explains diverse phenomena in sentence processing, such as effects of syntactic construction frequency, garden path effects, and antilocality effects (Konieczny, 2000), which are cases where a word becomes easier to process as more material is placed before it. In addition, Boston, Hale, Kliegl, Patil, and Vasishth (2008) show that reading times are well‐predicted by surprisal theory with a sophisticated probability model derived from an incremental parser, and Smith and Levy (2013) show that the effect of probability on incremental reading time is in robustly logarithmic over six orders of magnitude in probability. Outside the domain of reading times, Frank, Otten, Galli, and Vigliocco (2015) and Hale, Dyer, Kuncoro, and Brennan (2018) have found that surprisal values calculated using a probabilistic grammar can predict EEG responses.

Surprisal theory does not require that comprehenders are able to predict the following word in context with certainty, nor does it imply that they are actively making explicit predictions about the following word. Rather, surprisal theory relies on the notion of “graded prediction” in the terminology of Luke and Christianson (2016): All that matters is the numerical probability of the following word in context according to a latent probability model which the comprehender knows. In practice, we do not have access to this probability model, but for the purpose of calculation it has been useful to approximate this model using probabilistic context‐free grammars (PCFGs) (Hale, 2001; Levy, 2008a), n‐gram models (Smith & Levy, 2013), LSTM language models (Goodkind & Bicknell, 2018b), and recurrent neural network grammars (RNNGs) (Dyer, Kuncoro, Ballesteros, & Smith, 2016; Hale et al., 2018). The question of how to best estimate the comprehender's latent probability model is still outstanding.

Although surprisal theory has robust empirical support, as well as compelling theoretical motivations, there is a class of sentence processing difficulty phenomena which surprisal theory does not model, and in fact cannot model due to certain strong assumptions. These are effects of memory retrieval, which we describe below.

2.2. Memory‐based theories: Dependency locality effects

Another large class of theories of sentence processing difficulty is memory‐based theories. While expectation‐based theories are forward‐looking, claiming that processing difficulty has to do with predicting future words, memory‐based theories are backwards‐looking, holding that processing difficulty has to do with information processing that must be done on a representation of previous words in order to integrate them with the current word. There are many memory‐based models of processing difficulty that have been used to explain various patterns of data. In this section we will focus on a key prediction in common among various theories: the prediction of dependency locality effects, which we will derive from lossy‐context surprisal in Section 5.

Dependency locality effects consist of processing difficulty due to the integration of words or constituents that are far apart from each other in linear order.¹ The integration cost appears to increase with distance. For example, consider the sentences in (1):

(1)	a.	Bob threw out the trash.
	b.	Bob threw the trash out.
	c.	Bob threw out the old trash that had been sitting in the kitchen for several days.
	d.	Bob threw the old trash that had been sitting in the kitchen for several days out.

These sentences all contain the phrasal verb threw out. We can say that a dependency exists between threw and out because understanding the meaning of out in context requires that it be integrated specifically with the head verb threw in order to form a representation of the phrasal verb, whose meaning is not predictable from either part alone (Jackendoff, 2002). Sentences (1a) and (1b) show that it is possible to vary the placement of the particle out; these sentences can be understood with roughly equal effort. However, this symmetry is broken for the final two sentences: When the direct object NP is long, Sentence (1d) sounds awkward and difficult to English speakers when compared with Sentence (1c). This low acceptability is hypothesized to be due to a dependency locality effect: When out is far from threw, processing difficulty results (Lohse, Hawkins, & Wasow, 2004).

The hypothesized source of the dependency locality effect is working memory constraints. When reading through Sentence (1d), when the comprehender gets to the word out, she must integrate a representation of this word with a representation of the previous word threw in order to understand the sentence as containing a phrasal verb. For this to happen, the representation of threw must be retrieved from some working memory representation. But if the representation of threw has been in working memory for a long time—corresponding to the long dependency—then this retrieval operation might be difficult or inaccurate, and moreover the difficulty or inaccuracy might increase the longer the representation has been in memory. Thus, dependency locality effects are associated with memory constraints and specifically with difficulty in the retrieval of linguistic representations from working memory.

Dependency locality effects are most prominently predicted by the dependency locality theory (Gibson, 1998, 2000), where they appear in the form of an integration cost component. They are also generally predicted by activation‐based models such as Lewis and Vasishth (2005), where the retrieval of information about a previous word becomes more difficult or inaccurate with distance, due to either inherent decay or due to cumulative similarity‐based interference from intervening material (Gordon et al., 2001, 2004; Lewis, Vasishth, & van Dyke, 2006; McElree, 2000; McElree, Foraker, & Dyer, 2003; van Dyke & McElree, 2006).

Dependency locality effects plausibly underly several disparate phenomena in sentence processing. Dependency locality offers a unified explanation of PP attachment preferences, the difficulty of multiple center‐embedding, and the relative difficulty of object‐extracted relative clauses over subject‐extracted relative clauses, among other explananda.

Some of the strongest experimental evidence for locality effects comes from reading time studies such as Grodner and Gibson (2005) and Bartek, Lewis, Vasishth, and Smith (2011). In these studies, the distance between words linked in a dependency is progressively increased, and a corresponding increase in reading time on the second word (the embedded verb) is observed. Some example sentences are given below, where the words linked in dependencies are presented in boldface.

(2)	a.	The administrator who the nurse supervised…
	b.	The administrator who the nurse from the clinic supervised…
	c.	The administrator who the nurse who was from the clinic supervised…

Similar results have been shown for Spanish (Nicenboim, Logačev, Gattei, & Vasishth, 2016; Nicenboim, Vasishth, Gattei, Sigman, & Kliegl, 2015) and Danish (Balling & Kizach, 2017). The connection between dependency locality effects and working memory has been confirmed in experiments such as Fedorenko, Woodbury, and Gibson (2013), which introduce working memory interference, and Nicenboim et al. (2015), who correlate locality effects with individual differences in working memory capacity (finding a surprisingly complex relation).

While there is strong evidence for on‐line locality effects in controlled experiments on specific dependencies, evidence from a broader range of structures and from naturalistic reading time data is mixed. In sentences such as 2, there should also be a dependency locality effect on the following matrix verb, which is indeed detected by Bartek et al. (2011); however, Staub, Dillon, and Clifton (2017) find that when the dependency‐lengthening material is added after the embedded verb supervised, the matrix verb is read faster. In the realm of naturalistic reading time data, Demberg and Keller (2008a) do not find evidence for locality effects on reading times of arbitrary words in the Dundee corpus, though they do find evidence for locality effects for nouns. Studying a reading‐time corpus of Hindi, Husain, Vasishth, and Srinivasan (2015) do not find evidence for DLT integration cost effects on reading time for arbitrary words, but they do find effects on outgoing saccade length. These mixed results suggest that locality effects may vary in strength depending on the words, constructions, and dependent variables involved.

Dependency locality effects are the signature prediction of memory‐based models of sentence processing. However, they are not the only prediction. Memory‐based models have also been used to study agreement errors and the interpretation of anaphora (see Jäger, Engelmann, & Vasishth, 2017, for a review of some key phenomena). We do not attempt to model these effects in the present study with lossy‐context surprisal, but we believe it may be possible, as discussed in Section 6.

2.3. The intersection of expectations and memory

A unified theory of the effects of probabilistic expectations and memory retrieval is desirable because a number of phenomena seem to involve interactions of these two factors. However, attempts to combine these theories have met with difficulties because the two theories are stated at very different levels of analysis. Surprisal theory is a high‐level computational theory which only claims that incremental language processing consists of highly efficient Bayesian updates. Memory‐based theories are mechanistic theories based in specific grammatical formalisms, parsing algorithms, and memory architectures which attempt to describe the internal workings of the integration function mechanistically.

The most thoroughly worked out unified model is prediction theory, based on Psycholinguistically‐Motivated Lexicalized Tree Adjoining Grammar (PLTAG) (Demberg, 2010; Demberg & Keller, 2008b, 2009; Demberg, Keller, & Koller, 2013). This model combines expectation and memory at a mechanistic level of description, by augmenting a PLTAG parser with predict and verify operations in addition to the standard tree‐building operations. In this model, processing difficulty is proportional to the surprisal of a word given the probability model defined by the PLTAG formalism, plus the cost of verifying that predictions made earlier in the parsing process were correct. This verification cost increases when many words intervene between the point where the prediction is made and the point where the prediction is verified; thus, the model derives locality effects in addition to surprisal effects. Crucially, in this theory, probabilistic expectations and locality effects only interact in a highly limited way: Verification cost is stipulated to be a function only of distance and the a priori probability of the predicted structure.

Another parsing model that unifies surprisal effects and dependency locality effects is the left‐corner parser of Rasmussen and Schuler (2018). This is an incremental parsing model where the memory store from which derivation fragments are retrieved is an associative store subject to similarity‐based interference which results in slowdown at retrieval events. The cumulative nature of similarity‐based interference explains locality effects, and surprisal effects result from a renormalization that is required of the vectorial memory representation at each derivation step. It is difficult to derive predictions about the interaction of surprisal and locality from this model, but we believe that it broadly predicts that they should be independent.

To some extent, surprisal and locality‐based models explain complementary sets of data (Demberg & Keller, 2008a; Levy & Keller, 2013), which justifies “two‐factor” models where their interactions are limited. For instance, one major datum explained by locality effects but not surprisal theory is the relative difficulty of object‐extracted relative clauses over subject‐extracted relative clauses, and in particular the fact that object‐extracted relative clauses have increased difficulty at the embedded verb (Grodner & Gibson, 2005; Levy, Fedorenko, & Gibson, 2013) (though see Forster, Guerrera, & Elliot, 2009; Staub, 2010). Adding DLT integration costs or PLTAG verification costs to surprisal costs results in a theory that can explain the relative clause data while maintaining the accuracy of surprisal theory elsewhere (Demberg et al., 2013).

However, a number of phenomena seem to involve a complex interaction of memory and expectations. These are cases where the working memory resources that are taxed in the course of sentence processing appear to be themselves under the influence of probabilistic expectations.

A prime example of such an interaction is the phenomenon of language‐dependent structural forgetting. This phenomenon will be explained in more detail in Section 4, where we present its explanation in terms of lossy‐context surprisal. Essentially, structural forgetting is a phenomenon where listeners' expectations at the end of a sentence do not match the beginning of the sentence, resulting in processing difficulty. The phenomenon has been demonstrated in sentences with multiple nested verb‐final relative clauses in English (Gibson & Thomas, 1999) and French (Gimenes, Rigalleau, & Gaonac'h, 2009). However, the effect does not appear for the same structures in German or Dutch (Frank et al., 2016; Vasishth et al., 2010), suggesting that German and Dutch speakers' memory representations of these structures are different. Complicating the matter even further, Frank et al. (2016) find the forgetting effect in Dutch and German L2 speakers of English, suggesting that their exposure to the distributional statistics of English alter their working memory representations of English sentences.

The language dependence of structural forgetting, among other phenomena, has led to the suggestion that working memory retrieval operations can be more or less easy depending on how often listeners have to do them. Thus, German and Dutch speakers who are used to verb‐final structures do not find the memory retrievals involved difficult, because they have become skilled at this task (Vasishth et al., 2010). As we will see, lossy‐context surprisal reproduces the language‐dependent data pattern of structural forgetting in a way that depends on distributional statistics. Whether or not its mechanism corresponds to a notion of “skill” is a matter of interpretation.

Further data about the intersection of probabilistic expectations and memory come from studies which directly probe whether memory effects occur in cases where probabilistic expectations are strong and whether probabilistic expectation effects happen when memory pressures are strong. These data are mixed. Studying Hindi relative clauses, Husain, Vasishth, and Srinivasan (2014) find that increasing the distance between a verb and its arguments makes the verb easier to process when the verb is highly predictable (in line with expectation‐based theories) but harder to process when the verb is less predictable (in line with memory‐based theories). On the other hand, Safavi, Husain, and Vasishth (2016) do not find evidence for this effect in Persian.

To summarize, expectation‐based and memory‐based models are both reasonably successful in explaining sentence processing phenomena, but the field has lacked a meaningful integration of the two, in that combined models have only made limited predictions about phenomena involving both expectations and memory limitations. The existence of these complex phenomena at the intersection of probabilistic expectations and memory constraints motivates a unified theory of sentence processing difficulty which can make interesting predictions in this intersection.

3. Lossy‐context surprisal

Now we will introduce our model of sentence processing difficulty. The fundamental motivation for this model is to try to capture memory effects within an expectation‐based framework. Our starting point is to note that no purely expectation‐based model, as described above in Section 2.1, can handle forgetting effects such as dependency locality or structural forgetting, because these models implicitly assume that the listener has access to a perfect representation of the preceding linguistic context. Concretely, consider the problem of modeling the processing difficulty at the word out in example (1d). Surprisal theory has no way of predicting the high difficulty associated with comprehending this word. The reason is that as the amount of intervening material before the particle out increases, the word out (or some other constituent fulfilling its role) actually becomes more predictable, because the intervening material successively narrows down the ways the sentence might continue.

Lossy‐context surprisal holds that the processing difficulty of a word is its surprisal given a lossy memory representation of the context. Whereas surprisal theory is associated with the prediction problem schematized in Fig. 2a, lossy‐context surprisal theory is associated with the prediction problem in Fig. 2b. The true context gives rise to a memory representation, and the listener uses the memory representation to predict the next word.

Figure 2.

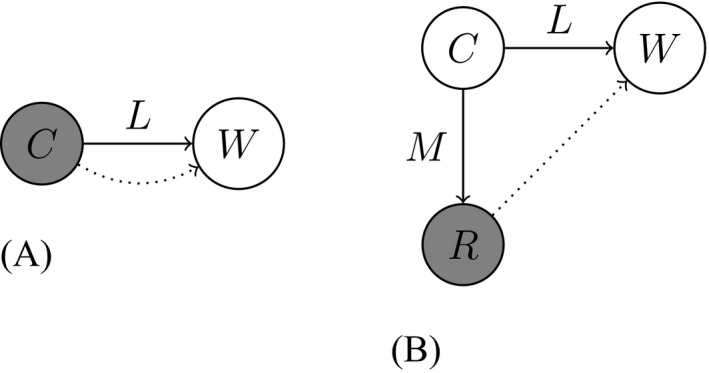
Probabilistic models associated with surprisal theory (left) and lossy‐context surprisal theory (right). Processing difficulty is associated with the problem of prediction given the shaded nodes. There is a context C, and L is the conditional distribution of the next word W given the context C, representing a comprehender's knowledge of language. In surprisal theory, we presume that C is observed, and that processing difficulty is associated with the problem of predicting W given C (indicated with the dotted line). In lossy‐context surprisal theory, we add a random variable R ranging over memory representations; M is the conditional distribution of R given C. Processing difficulty is associated with the problem of predicting W given R.

3.1. Formal statement of lossy‐context surprisal theory

Lossy‐context surprisal theory augments surprisal theory with a model of memory. The theory makes four claims:

Claim 1

(Incrementality of memory.) Working memory in sentence processing can be characterized by a probabilistic memory encoding function $m:R\times W\to R$ which takes a memory representation $r\in R$ and combines it with the current word $w\in W$ to produce the next memory representation r′ = m(r, w). We write $M(w_1,\dots ,w_i)$ to denote the result of applying m successively to a sequence of words $w_1,\dots ,w_i$.

Claim 2

(Linguistic knowledge.) Comprehenders have access to a probability model L giving the distribution of the next word w_i given a context c, where c is a sequence of words $w_1,\dots ,w_{i-1}$. In general, the probability model L may also incorporate non‐linguistic contextual information, such that L represents the comprehender's knowledge of language in conjunction with all other sources of knowledge that contribute to predicting the next word.

Claim 3

(Inaccessibility of context.) Comprehenders do not have access to the true linguistic context c; they only have access to the memory representation given by M(c).

Claim 4

(Linking hypothesis.) Incremental processing difficulty for the current word w_i is proportional to the surprisal of w_i given the previous memory representation r_{i −1}:

$$D_{\text{lc}\text{surprisal}}(w_{i}i-1)\propto -\log p(w_{i}i-1).$$ (2)

The listener's internal memory representation r_{i −1} is hidden to us as experimenters, so Eq. 2 does not make direct experimental predictions. However, if we have a probabilistic model of how context c gives rise to memory representations r, we can use that model to calculate the processing cost of the word w_i in context c based on the expected surprisal of w_i considering all the possible memory representations. Therefore, we predict incremental processing difficulty as:

$$D_{\text{lc}\text{surprisal}}(w_i|c)\propto {\mathbb{E}}_{r_{i-1}\sim M(c)}\left[-\log p(w_{i}i-1)\right].$$ (3)

The implied probability model of Claims 1–4 is shown in Fig. 2b as a Bayesian network. Eq. 3 encompasses the core commitments of lossy‐context surprisal theory: Processing difficulty for a word is proportional to the expected surprisal of that word given the possible memory representations of its context. What follows in this section is a series of deductions from these claims, involving no further assumptions. In Sections 4 and 5, we introduce further assumptions about the memory encoding function M in order to derive more concrete psycholinguistic predictions.

3.2. Modeling memory as noise

We call the memory representation r lossy, meaning that it might not contain complete information about the context c. The term comes from the idea of lossy compression, where data are turned into a compressed form such that the original form of the data cannot be reconstructed with perfect accuracy (Nelson & Gailly, 1996). Equivalently, we can see r as a noisy representation of c: a version of the true context where some of the information has been obscured by noise, in the same way that an image on a television screen can be obscured by white noise.

To make predictions with lossy‐context surprisal, we do not have to fully specify the form of the memory representation r. Rather, all we have to model is what information is lost when context c is transformed into a memory representation r, or equivalently, how noise is added to the context c to produce r. The predictions of lossy‐context surprisal theory as to incremental difficulty are the same for all memory models that have the same characteristics in terms of what information is preserved and lost. The memory representation could be a syntactic structure, it could be a value in an associative content‐addressable store, or it could be a high‐dimensional embedding as in a neural network; all that matters for lossy‐context surprisal is what information about the true context can be recovered from the memory representation.

For this reason, we will model memory using what we call a noise distribution: a conditional distribution of memory representations given contexts, which captures the broad information‐loss characteristics of memory by adding noise to the contexts. For example, in Section 5 below, we use a noise distribution drawn from the information‐theory literature called “erasure noise” (Cover & Thomas, 2006), in which a context is transformed by randomly erasing words with some probability e. Erasure noise embodies the assumption that information about words is lost at a constant rate. The noise distribution stands in for the distribution r ~ M(c) in Eq. 3.

The noise distribution is the major free parameter in lossy‐context surprisal theory, since it can be any stochastic function. For example, the noise distribution could remove information about words at an adjustable rate that depends on the word, a mechanism which could be used to model salience effects in memory. We will not explore such noise distributions in this work, but they may be necessary to capture more fine‐grained empirical phenomena. Instead, we will focus on simple noise distributions.

As with other noisy‐channel models in cognitive science, the noise distribution is a major degree of freedom, but it does not make the model infinitely flexible. One constraint on the noise distribution, which follows from Claim 1 above, is that the information contained in a memory representation for a word must either remain constant or degrade over time. Each time a memory representation of a word is updated, the information in that representation can be either retained or lost. Therefore, as time goes on, information about some past stimulus can either be preserved or lost, but cannot increase—unless it comes in again via some other stimulus. This principle is known as the Data Processing Inequality in information theory: It is impossible for a representation to contain more information about a random variable than is contained in the random variable itself (Cover & Thomas, 2006). Thus, the noise distribution is not unconstrained; for example, it is not possible to construct a noise distribution where the memory representation of a word becomes more and more accurate the longer the word is in memory, unless the intervening words are informative about the original word.

3.3. Calculation of the probability of a word given a memory representation

The question arises of how to calculate the probability of a word given a lossy memory representation. We assumed the existence in Claim 2 of a probability model L that predicts the next word given the true context c, but we do not yet have a way to calculate the probability of the next word given the memory representation r. It turns out that the problem of predicting a word given a noisy memory representation is equivalent to the problem of noisy‐channel inference (Gibson, Bergen, & Piantadosi, 2013; Shannon, 1948), with memory treated as a noisy channel.

We can derive the probability of the next word given a memory representation using the laws of probability theory. Given the probability model in Fig. 2b, we solve for the probability $p(w_i)$ by marginalizing out the possible contexts c that could have given rise to r:

$$p(w_i|r)={\mathbb{E}}_c\left[p_L(w_i|c)\right]$$ (4)

$$=\sum _{c}p(c)p_L(w_i|c).$$ (5)

Eq. 5 expresses a sum over all possible contexts c. This mathematical procedure can be interpreted in the following way: To predict the next word w_i given a memory representation r, we first infer a hypothetical context c from r, then use c to predict w_i. The distribution of likely context values given a memory representation r is represented by c|r in Eq. 4. Supposing we know the memory encoding function M, which is equivalent to a conditional distribution r|c, we can find the inverse distribution c|r using Bayes' rule:

$$p(c)=\frac{p_M(r|c)p(c)}{p(r)}.$$ (6)

Now to get the probability of the next word, we substitute Eq. 6 into Eq. 5:

$$\begin{array}{cc}p(w_i)\hfill & \propto \sum _c{p}_M(r|c)p(c)p_L(w_i|c).\hfill \end{array}$$ (7)

And recalling that a context c consists of a sequence of words $w_1,\dots ,w_{i-1}$, we have:

$$p(w_i)\propto \sum _{w_1,\dots ,w_{i-1}}{p}_M(r|w_1,\dots ,w_{i-1})p_L(w_1,\dots ,w_{i-1})p_L(w_i|w_1,\dots ,w_{i-1})$$ (8)

$$=\sum _{w_1,\dots ,w_{i-1}}{p}_M(r|w_1,\dots ,w_{i-1})p_L(w_1,\dots ,w_i),$$ (9)

where the last step comes from applying the chain rule for conditional probabilities. Eq. 9 expresses the probability for the next word given a memory representation, and does so entirely in terms of two model components: (a) the memory encoding function M (from Claim 1), and (b) and the comprehender's knowledge L of what words are likely in what contexts (from Claim 2).

3.4. Interaction of memory and expectations

The model of Eq. 3 is extremely general, yet it is still possible to derive high‐level generalizations from it using information‐theoretic principles. In particular, without making any further assumptions, we can immediately make two high‐level deductions about the interaction of memory and expectations in lossy‐context surprisal theory, both of which line up with previous results in the field and derive principles which were previously introduced as stipulations.

3.4.1. Less probable contexts yield less accurate predictions

Our theory predicts very generally that comprehenders will make less accurate predictions from less probable contexts, as compared with more probable contexts. Equivalently, comprehenders in lossy‐context surprisal theory are less able to use information from low‐frequency contexts as compared to high‐frequency contexts when predicting following words. The resulting inaccuracy in prediction manifests as increased difficulty, because the inaccuracy usually decreases the probability of the correct following word.

The intuitive reasoning for this deduction is the following. When information about a true context is obscured by noise in memory, the comprehender must make predictions by filling in the missing information, following the logic of noisy channel inference as outlined in Section 3.3. When she reconstructs this missing information, she draws in part on her prior expectations about what contexts are likely a priori. The a priori probability of a context has an influence that is instantiated mathematically by the factor $p_L(w_1,\dots ,w_{i-1})$ in Eq. 8. Therefore, when a more probable context is affected by noise, the comprehender is likely to reconstruct it accurately, since it has higher prior probability; when a less probable context is affected by noise, the comprehender is less likely to reconstruct it accurately, and more likely to substitute a more probable context in its place.

We make this argument formally in Supplementary Material A. We introduce the term memory distortion to define the extent to which the predicted processing difficulty based on lossy memory representations divergences from the predicted difficulty based on perfect memory representations. We show that memory distortion is upper bounded by the surprisal of the context; that is, less probable contexts are liable to cause more prediction error and, thus, difficulty and reading time slowdown.

We will demonstrate how this principle can explain structural forgetting effects in Section 4, where we will instantiate it via a concrete noise model to get numerical predictions.

The principle that less probable structures are decoded less accurately from memory has been proposed previously in the context of structural forgetting by Vasishth et al. (2010), who conjecture that comprehenders can maintain predictions based on high‐frequency structures more easily than low‐frequency structures, as a kind of skill. The effect arises in our model endogenously as a logical consequence of the lossiness of memory representations.

3.4.2. Lossy memory makes comprehenders regress to prior expectations

In lossy‐context surprisal, the lossiness of memory representations will usually have the effect of making the difficulty of a word in context more similar to the difficulty that would be expected for the word regardless of contexts, based on its prior unigram probability. In other words, as a comprehender's memory representations are affected by more and more noise, the comprehender's expectations regress more and more to their prior expectations. As we will see, this is the mechanism by which probabilistic expectations interact with memory effects to produce language‐dependent structural forgetting effects, elaborated in Section 4 below.

To see that our model predicts this behavior, consider the extreme case where all information about a context is lost: Then the difficulty of comprehending a word is given exactly by its log prior probability out of context (the unigram probability). On the other extreme, when no information is lost, the difficulty of comprehending a word is the same as under surprisal theory. When an intermediate amount of information is lost, the predicted difficulty will be somewhere between these two extremes on average.

We deduce this conclusion formally from the claims of lossy‐context surprisal theory in Supplementary Material A, where we show that the result holds on average over words, for all contexts and arbitrary memory models. Because this result holds on average over words, it will not hold necessarily for every single specific word given a context. Thus, it is more likely to be borne out in broad‐coverage studies of naturalistic text, where predictions are evaluated on average over many words and contexts, rather than in specific experimental items.

In fact, an effect along these lines is well‐known from the literature examining reading time corpora. In that literature there is evidence for word frequency effects in reading time above and beyond surprisal effects (Demberg & Keller, 2008a; Rayner, 1998) (cf. Shain, 2019). We have deduced that the predicted difficulty of a word in context in lossy‐context surprisal theory is on average somewhere between the prediction from surprisal theory and the prediction from log unigram frequency. If that is the case, then observed difficulty would be well‐modeled by a linear combination of log frequency and log probability in context, the usual form of regressions on reading times (e.g., Demberg & Keller, 2008a).

Further work has shown a robust effect of bigram surprisal beyond the predictions of surprisal models taking larger amounts of context into account (Demberg & Keller, 2008a; Fossum & Levy, 2012; Goodkind & Bicknell, 2018a; Mitchell, Lapata, Demberg, & Keller, 2010): these results are to be expected if distant context items are subject to more noise than local context items (an assumption which we will make concrete in Section 5). More generally, a wealth of psycholinguistic evidence has suggested that local contextual information plays a privileged role in language comprehension (Kamide & Kukona, 2018; Tabor, Galantucci, & Richardson, 2004). We leave it to future work to investigate whether these more complex local context effects can be modeled using lossy‐context surprisal.

3.5. Remarks

3.5.1. Surprisal theory is a special case of lossy‐context surprisal

Plain surprisal theory can be seen as a special case of lossy‐context surprisal where the memory encoding function M gives a lossless representation of context, for example by returning a distribution with probability mass 1 on the true context and 0 on other contexts. We will see in Section 5 that the dependency locality theory is another special case of lossy‐context surprisal, for particular values of L and M.

3.5.2. Representation agnosticism

One major advantage of surprisal theory, which is only partially maintained in lossy‐context surprisal, is that it has a high degree of representation agnosticism. It does not depend on any theory about what linguistic or conceptual structures are being inferred by the listener.

Lossy‐context surprisal maintains agnosticism about what structures are being inferred by the listener, but it forces us to make (high‐level) assumptions about how context is represented in memory, in terms of what information is preserved and lost. These assumptions go into the theory in the form of the noise distribution. While a full, broad‐coverage implementation of lossy‐context surprisal may incorporate detailed syntactic structures in the noise distribution, in the current paper we aim to maintain representation agnosticism in spirit by using only highly general noise models that embody gross information‐theoretic properties without making claims about the organization of linguistic memory.

We emphasize this remark because, as we develop concrete instantiations of the theory in sections below, we will be talking about linguistic knowledge and the contents of memory primarily in terms of rules and individual words. But words and rules are not essential features of the theory: We consider them to be merely convenient concepts for building interpretable models. In particular, the comprehender's linguistic knowledge L may contain rich information about probabilities of multi‐word sequences (Arnon & Christiansen, 2017; Reali & Christiansen, 2007), context‐dependent pragmatics, graded word similarities, etc.

3.5.3. Comparison with previous noisy‐channel theories of language understanding

Previous work has provided evidence that language understanding involves noisy‐channel reasoning: Listeners assume that the input they receive may contain errors, and they try to correct those errors when interpreting that input (Gibson et al., 2013; Poppels & Levy, 2016). For example, in Gibson et al. (2013), experimental participants interpreted an implausible sentence such as The mother gave the candle the daughter as if it were The mother gave the candle to the daughter. That is, they assumed that a word had been deleted from the received sentence, making the received sentence noisy, and then decoded the likely intended sentence that gave rise to the received sentence. The current work is similar to this previous work in that it posits a noisy‐channel decoding process as part of language comprehension; it differs in that it treats memory for context as a noisy channel, rather than treating the whole received utterance as a noisy channel.

3.5.4. Comparison with previous noisy‐channel surprisal theories

Lossy‐context surprisal is notably similar to the noisy channel surprisal theory advanced by Levy (2008b, 2011). Both theories posit that comprehenders make predictions using a noisy representation of context. Lossy‐context surprisal differs in that it is only the context that is noisy: Comprehenders are predicting the true current word given a noisy memory representation. In Levy (2011), in contrast, comprehenders are predicting a noisy representation of the current word given a noisy representation of the context. We believe that the distinction between these models reflects two sources of noise that affect language processing.

A key difference between the current work and the model in Levy (2011) is the character of the noise model investigated. Levy (2011) most clearly captures perceptual uncertainty: A reader may misread certain words, miss words, or think that certain words are present that are not really there. This view justifies the idea of noise applying to both the current word and previous words. Here, in contrast, we focus on noise affecting memory representations, which applies to the context but not to the current word. Crucially, it is natural to assume for noise due to memory that the noise level is distance‐sensitive, such that context words which are further from the current word are represented with lower fidelity. This assumption gives us a novel derivation for predicting locality effects in Section 5.

3.5.5. Relation with n‐gram surprisal

A common practice in psycholinguistics is to calculate surprisal values using n‐gram models, which only consider the previous n − 1 words in calculating the probability of the next word (van Schijndel & Schuler, 2016; Smith & Levy, 2013). Recent work has found effects of n‐gram surprisal above and beyond surprisal values calculated from language models that use the full previous context (Demberg & Keller, 2008a; Fossum & Levy, 2012; Goodkind & Bicknell, 2018a; Mitchell et al., 2010). Plain surprisal theory requires conditioning on the full previous context; using an n‐gram model gives an approximation to the true surprisal. The n‐gram surprisal can be seen as a form of lossy‐context surprisal where the noise distribution is a function which takes a context and deterministically returns only the last n − 1 words of it.

3.5.6. Relation with recurrent neural networks

Recent work has proposed to use surprisal values calculated from recurrent neural networks (RNNs) (Elman, 1990) in order to predict by‐word reading times (Frank & Bod, 2011; Frank et al., 2016; Goodkind & Bicknell, 2018b). When an RNN is used to generate surprisal values, the resulting sentence processing model can be seen as a special case of lossy‐context surprisal where the lossy memory representation is the RNN's incremental state, and where the noise distribution produces this memory representation deterministically. For this reason we do not view our model and the results presented in Section 4 to be in opposition to neural network models of the same phenomena. Rather, lossy‐context surprisal helps us explain why the neural networks behave as they do. In particular, the principles which we derived above about the interaction of memory and expectations will apply to RNN surprisal values, just as they apply to any model where words are predicted from lossy‐context representations in a rational manner.

There is also deeper connection between lossy‐context surprisal and the operation of RNNs. Lossy‐context surprisal describes processing cost in any incremental predictive sequence processing model where the representation of context is lossy and where processing is maximally efficient (Smith & Levy, 2013). Inasmuch as RNNs fulfill this description, lossy‐context surprisal can provide a high‐level model of how much computational effort they expend per integration. RNNs as currently applied do not typically fulfill the assumption of maximal efficiency, in that each integration takes a constant time, but even then lossy‐context surprisal provides a description of how much non‐redundant work is being done in each application of the integration function.

A notable exception to the claim that RNNs perform integrations in constant time is the Adaptive Computation Time network of Graves (2016). In this architecture, when a word is being integrated with a memory representation, the integration function may be applied multiple times, and the network decides before processing a word how many times the integration function will be applied. This can be seen as an implementation of the theory of optimal processing time described in Smith and Levy (2013). Thus, Adaptive Computation Time networks appear to be a straightforward practical implementation of the reasoning behind surprisal theory, and their processing time should be well‐described by lossy‐context surprisal.

3.5.7. Relation with the now‐or‐never bottleneck

In an influential recent proposal, Christiansen and Chater (2016) have argued that language processing and language structure are critically shaped by a now‐or‐never bottleneck: the idea that, at each timestep, the language processor must immediately extract as much information from the linguistic signal as it can, and that afterwards the processor only has access to lossy memory representations of preceding parts of the signal. We see lossy‐context surprisal as a particular instantiation of this principle, because lossy‐context surprisal is based on the idea that the comprehender has perfect information about the current word but only noisy information about the previous words. On top of this, lossy‐context surprisal contributes the postulate that the amount of work done at each timestep is determined by surprisal.

3.5.8. Relation with Good‐Enough processing

The idea of “Good‐Enough” processing (Ferreira & Lowder, 2016) is that the norm for linguistic comprehension and production is a kind of “shallow processing” (Sanford & Sturt, 2002) where computational operations are performed to the lowest adequate level of precision. The good‐enough principle manifests in lossy‐context surprisal in the memory encoding function, which does not store complete information about the context. A more complete analogy with Good‐Enough processing could be made for memory encoding functions which adaptively decide how much information to store about context depending on expected utility, storing as little information as possible for the desired level of utility. We discuss such adaptive noise models further in Section 6.1.

3.5.9. Relation with language production

A recent body of work has argued that language production and language comprehension—inasmuch as it relates to prediction—use the same computational system (Pickering & Garrod, 2013). In our model, linguistic prediction is embodied by the probability distribution L. Lossy‐context surprisal is agnostic as to whether L is instantiated using the same computational system used for production, but we note that it would be inefficient if the information stored in L was duplicated elsewhere in a separate system for production.

3.5.10. Digging‐in effects

A well‐known class of phenomena in sentence processing is digging‐in effects (Tabor & Hutchins, 2004), in which processing of garden path sentences becomes harder as the length of the locally ambiguous region of a sentence is increased. One surprisal‐compatible account of digging‐in effects is given by Levy, Reali, and Griffiths (2009), who posit that the relevant working memory representation is a particle‐filter approximation to a complete memory representation of a parse forest. On this theory, human comprehension mechanisms stochastically resample incremental syntactic analyses consistent with every new incoming word. The longer a locally ambiguous region, the higher the variance of the distribution over syntactic analyses, and the higher the probability of losing the ultimately correct analysis, leading to higher expected surprisal upon garden‐path disambiguation. This model is a special case of lossy‐context surprisal where the memory encoding function M represents structural ambiguity of the context (explicitly or implicitly) and performs this particle filter approximation.

4. Structural forgetting

One of the most puzzling sentence processing phenomena involving both memory and expectations is structural forgetting. Structural forgetting consists of cases where comprehenders appear to forget or misremember the beginning of a sentence by the time they get to the end of the sentence. The result is that ungrammatical sentences can appear more acceptable and easier to understand than grammatical sentences, a kind of phenomenon called a grammaticality illusion (Vasishth et al., 2010). For example, consider the sentences below.

(3)	a.	The apartment1 that the maid2 who the cleaning service3 sent over3 was well‐decorated1.
	b.	The apartment1 that the maid2 who the cleaning service3 sent over3 cleaned2 was well‐decorated1.

In acceptability judgments, English speakers reliably rate Sentence (3a) to be at least equally acceptable as, and sometimes more acceptable than, Sentence (3b) (Frazier, 1985; Gibson & Thomas, 1999). However, Sentence (3a) is ungrammatical whereas Sentence (3b) is grammatical. To see this, notice that the ungrammatical (3a) has no verb phrase corresponding to the subject noun phrase the maid. The examples in (3) involve two levels of self‐embedding of relative clauses; no structural forgetting effect is observed in English for one level of embedding. The effect is usually taken to mean that Sentence (3a) is easier to process than Sentence (3b), despite Sentence (3a) being ungrammatical.

Gibson and Thomas (1999) proposed a Dependency Locality Theory account of structural forgetting, in which the memory cost of holding predictions for three verb phrases is too high, and the parser reacts by pruning away one of the predicted verb phrases. As a result, one of the predicted verb phrases is forgotten, and comprehenders judge a sentence like (3a) with two verb phrases at the end to be acceptable.

The simple memory‐based explanation for these effects became untenable, however, with the introduction of data from German. It turns out that in German, for materials with exactly the same structure, the structural forgetting effect does not obtain in reading times (Vasishth et al., 2010). German materials are shown in the sentences (4); these are word‐for‐word translations of the English materials in (3). Vasishth et al. (2010) probed the structural forgetting effect using reading times for material after the end of the verb phrases, and Frank and Ernst (2017) have replicated the effect using acceptability judgments (but see Bader, 2016; Häussler & Bader, 2015, for complicating evidence).

(4)	a.	Die Wohnung1, die das Zimmermädchen2, das der Reinigungsdienst3 übersandte3, war gut eingerichtet3.
	b.	Die Wohnung1, die das Zimmermädchen2, das der Reinigungsdienst3 übersandte3, reinigte2, war gut eingerichtet3.

If memory resources consumed are solely a function of syntactic structure, as in the theory of Gibson and Thomas (1999), then there should be no difference between German and English. Vasishth et al. (2010) argued that listeners' experience with the probabilistic distributional pattern of syntactic structures in German—where the structures in Sentences 4a and b are more common—make it easier for listeners to do memory retrieval operations over those structures. In particular, the high frequency of verb‐final structures in German makes these structures easier to handle.

The idea that memory effects are modulated by probabilistic expectations was further supported in experiments reported by Frank et al. (2016) showing that native speakers of Dutch and German do not show the structural forgetting effect when reading Dutch or German (Dutch having similar syntactic structures to German, though without case marking), but they do show the structural forgetting effect when reading English, which is an L2 for them. The result shows that it is not the case that exposing a comprehender to many verb‐final structures makes him or her more skilled at memory retrieval for these structures in general; rather, the comprehender's experience with distributional statistics of the particular language being processed influences memory effects for that language.

4.1. Previous modeling work

The existing computational models of this phenomenon are neural network surprisal models. Christiansen and Chater (2001) and Christiansen and MacDonald (2009) find that a simple recurrent network (SRN) trained to predict sequences drawn from a toy probabilistic grammar over part‐of‐speech categories (as in Christiansen & Chater, 1999) gives higher probability to an ungrammatical sequence NNNVV (three nouns followed by two verbs) than to a grammatical sequence NNNVVV. Engelmann and Vasishth (2009) show that SRNs trained on English corpus data reproduce the structural forgetting effect in English, while SRNs trained on German corpus data do not show the effect in German. However, they find that the lack of structural forgetting in the German model is due to differing punctuation practices in English and German orthography, whereas punctuation was not necessary to reproduce the crosslinguistic difference in Vasishth et al. (2010). Finally, Frank et al. (2016) show that SRNs trained on both English and Dutch corpora can reproduce the language‐dependent structural forgetting effect qualitatively in the surprisals assigned to the final verb and to a determiner following the final verb.

In the literature, these neural network models are often described as experience‐based and contrasted with memory‐based models (Engelmann & Vasishth, 2009; Frank et al., 2016). It is true that the neural network models do not stipulate explicit cost associated with memory retrieval. However, recurrent neural networks do implicitly instantiate memory limitations, because they operate using lossy representations of context. The learned weights in neural networks contain language‐specific distributional information, but the network architecture implicitly defines language‐independent memory limitations.

These neural network models succeed in showing that it is possible for an experience‐based predictive model with memory limitations to produce language‐dependent structural forgetting effects. However, they do not elucidate why and how the effect arises, nor under what distributional statistics we would expect the effect to arise, nor whether we would expect it to arise for other, non‐neural‐network models. Lossy‐context surprisal provides a high‐level framework for reasoning about the effect and its causes in terms of noisy‐channel decoding of lossy memory representations.

4.2. Lossy‐context surprisal account

The lossy‐context surprisal account of structural forgetting is as follows. At the end of a sentence, we assume that people are predicting the next words given a lossy memory representation of the beginning of the sentence—critically, the true beginning of the sentence cannot be recovered from this representation with complete certainty. Given that the true context is uncertain, the comprehender tries to use her memory representation to infer what the true context was, drawing in part on her knowledge of what structures are common in the language. When the true context is a rare structure, such as nested verb‐final relative clauses in English, it is not likely to be inferred correctly, and so the comprehender's predictions going forward are likely to be incorrect. On the other hand, if the true context is a common structure, such as the same structure in German or Dutch, it is more likely to be inferred correctly, and predictions are more likely to be accurate.

The informal description above is a direct translation of the math in Eq. 9, Section 3.1. In order to make it more concrete for the present example, we present results from a toy grammar study, similar to Christiansen and Chater (2001) and Christiansen and MacDonald (2009). Our model is similar to this previous work in that the probability distribution which is used to predict the next word is different from the probability distribution that truly generated the sequences of words. In neural network models, the sequences of words come from probabilistic grammars or corpora, whereas the predictive distribution is learned by the neural network. In our models, the sequences of words come from a grammar which is known to the comprehender, and the predictive distribution is based on that grammar but differs from it because predictions are made conditional on an imperfect memory representation of context. Our model differs from neural network models in that we postulate that the comprehender has knowledge of the true sequence distribution—she is simply unable to apply it correctly due to noise in memory representations. We therefore instantiate a clear distinction between competence and performance.

We will model distributional knowledge of language with a probabilistic grammar ranging over part‐of‐speech symbols N (for nouns), V (for verbs), P (for prepositions), and C (for complementizers). In this context, a sentence with two levels of embedded RCs, as in Sentence (3b), is represented with the sequence NCNCNVVV. A sentence with one level of RCs would be NCNVV. Details of the grammar are given in Section 4.3.

Structural forgetting occurs when an ungrammatical sequence ending with a missing verb (NCNCNVV) ends up with lower processing cost than a grammatical sentence with the correct number of verbs (NCNCNVVV). Therefore, we will model the processing cost of two possible continuations given prefixes like NCNCNVV: a third V (the grammatical continuation) and the end‐of‐sequence symbol # (the ungrammatical continuation). When the cost of the ungrammatical end‐of‐sequence symbol is less than the cost of the grammatical final verb, then we will say the model exhibits structural forgetting (Christiansen & Chater, 2001). The cost relationships are shown below:

D(V|NCNCNVV) > D(#|NCNCNVV)	(structural forgetting, embedding depth 2)
D(#|NCNCNVV) > D(V|NCNCNVV)	(no structural forgetting, embedding depth 2)
D(V|NCNV) > D(#|NCNV)	(structural forgetting, embedding depth 1)
D(#|NCNV) > D(V|NCNV)	(no structural forgetting, embedding depth 1)

We aim to show a structural forgetting effect at depth 2 for English, and no structural forgetting at depth 1 for English, and neither depths 1 nor 2 for German. In all cases, the probability to find a forgetting effect should increase monotonically with embedding depth: We should not see a data pattern where structural forgetting happens for shallow embedding depth but not for a deeper embedding depth. (Our prediction extends to greater embedding depths as well: see Supplementary Material B.)

4.3. A toy grammar of the preverbal domain

We define a probabilistic context‐free grammar (Booth, 1969; Manning & Schütze, 1999) modeling the domain of subject nouns and their postmodifiers before verbs. The grammar rules are shown in Table 1. Each rule is associated with a production probability which is defined in terms of free parameters. These parameters are m, representing the rate at which nouns are postmodified by anything; r, the rate at which a postmodifier is a relative clause; and f, the rate at which relative clauses are verb‐final. We will adjust these parameters in order to simulate English and German. By defining the distributional properties of our languages in terms of these variables, we can study the effect of particular grammatical frequency differences on structural forgetting.²

Table 1.

Toy grammar used to demonstrate verb forgetting

Rule	Probability
S → NP V	1
NP → N	1 − m
NP → N RC	mr
NP → N PP	m(1 − r)
PP → P NP	1
RC → C NP V	f
RC → C V NP	1 − f

Nouns are postmodified with probability m; a postmodifier is a relative clause with probability r, and a relative clause is V‐final with probability f.

In figures below, we will model English by setting all parameters to $\frac{1}{2}$ except f, which is set to 0.2, reflecting the fact that about 20% of English relative clauses are object‐extracted, following the empirical corpus frequencies presented in Roland, Dick, and Elman (2007, their fig. 4). We will model German identically to English except setting f to 1, indicating the fact that all relative clauses in German, be they subject‐ or object‐extracted, are verb final. We stress that the only difference between our models of English and German is in the grammar of the languages; the memory models are identical. It turns out that this difference between English and German grammar drives the difference in structural forgetting across languages: Even with precisely the same memory model across languages, and precisely the same numerical value for all the other grammar parameters, our lossy‐context surprisal model predicts that a language with verb‐final relative clause rate f = 1 will show no structural forgetting at embedding depth 2, and a grammar with f = 0.2 will show it, thus matching the crosslinguistic data.

4.4. Noise distribution

In order to fully specify the lossy‐context surprisal model, we need to state how the true context is transformed into a noisy memory representation. For this section we do this by applying deletion noise to the true context. Deletion noise means we treat the context as a sequence of symbols, where each symbol is deleted with some probability d, called the deletion rate. Some possible noisy memory representations arising from the context NCNCNVV under deletion noise are shown in Table 2. For example, in Table 2, the second row represents a case where one symbol was deleted and six were not deleted; this happens with probability $d^1{(1-d)}^6$.

Table 2.

A sample of possible noisy context representations and their probabilities as a result of applying deletion noise to the prefix NCNCNVV. Many more are possible

Noisy Context	Probability
[NCNCNVV]	(1 − d)7
[CNCNVV]	d 1(1 − d)6
[NCCVV]	d 2(1 − d)5
[NCV]	2d 2(1 − d)3
[]	d 7

Deletion noise introduces a new free parameter d into the model. In general, the deletion rate d can be thought of as a measure of representation fidelity; deletion rate d = 0 is a case where the context is always veridically represented, and deletion rate d = 1 is a case where no information about the context is available. If d = 0, then the first row (containing the full true prefix) has probability 1 and all the others have probability 0; if d = 1, then the final row (containing no information at all) has probability 1 and the rest have probability 0. We explore the effects of a range of possible values of d in Section 4.5.

The language‐dependent pattern of structural forgetting will arise in our model as a specific instance of the generalization that comprehenders using lossy memory representations will make more accurate predictions from contexts that are higher probability, and less accurate predictions from contexts that are lower probability. This fact can be derived in the lossy‐context surprisal model regardless of the choice of noise distribution (see Supplementary Material A); however, to make numerical predictions, we need a concrete noise model. Below we describe how the language‐dependent pattern of structural forgetting arises given the specific deletion noise model used in this section.

Given the true context [NCNCNVV] and a noisy representation such as [NCV], the comprehender will attempt to predict the next symbol based on her guesses as to the true context that gave rise to the representation [NCV]. That is, the comprehender treats [NCV] as a representation of context that has been run through a noisy channel and attempts to decode the true context. Given [NCV], the possible true contexts are any contexts such that a series of deletions could result in [NCV]. For example, a possible true context is [NPNCV], which gives rise to [NCV] with probability $2d^2{(1-d)}^3$ (two deletions and three non‐deletions).

Now when predicting the next symbol, according to Bayes' rule, the hypothetical context [NPNCV]—which predicts only one more following verb—would be given weight $2d^2{(1-d)}^3{p}_L(NPNCV)$, where $p_L\left(\mathit{NPNCV}\right)$ is the probability of the sequence [NPNCV] the grammar. Hypothetical contexts with higher probability under the grammar will have more weight, and these probabilities differ across languages. For example, if the grammar disallows verb‐initial relative clauses (i.e., f = 1), then p_L(NPNCV) = 0; so this hypothetical context will not make any contribution toward predicting the next words. On the other hand, if verb‐initial relative clauses are very common in the language (i.e.,$f\approx 0$), then this hypothetical context will be influential, and might result in the prediction that the sentence should conclude with only one more verb.

In this way, different linguistic distributions give rise to different predictions under the noisy memory model. Below, we will see that this mechanism can account for the language dependence in the structural forgetting effect.

4.5. Conditions for verb forgetting

At embedding depth 2, given the default parameter values described in Section 4.3, we find lossy‐context surprisal values which reproduce the language‐dependent structural forgetting effect in reading times shown in Vasishth et al. (2010). Fig. 3a shows the difference in predicted processing cost from the ungrammatical to the grammatical continuation. When this difference (ungrammatical − grammatical) is positive, then the ungrammatical continuation is more costly, and there is no structural forgetting. When the difference is negative, then the ungrammatical continuation is less costly and there is structural forgetting. The figure shows that we predict a structural forgetting effect for English but not for German, based on the grammar parameters. Fig. 3b compares the predicted processing costs with reading time differences from the immediate postverbal region for English and German from Vasishth et al. (2010). We reproduce the language‐dependent crossover in structural forgetting.

Figure 3.

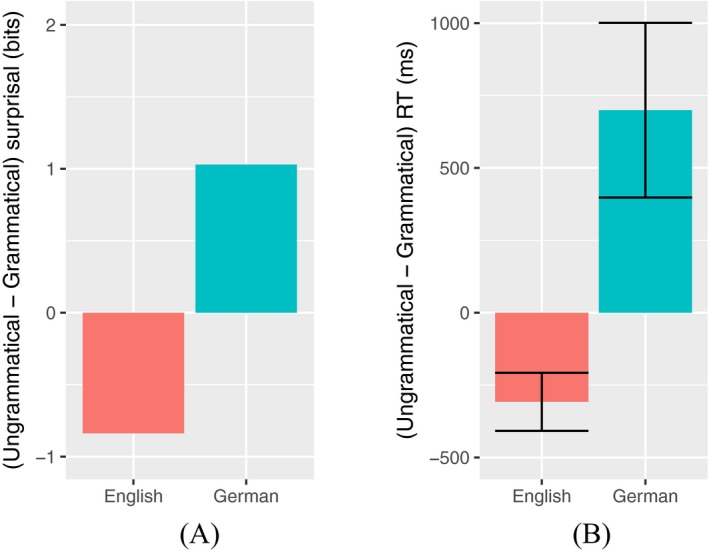
(a) Lossy‐context surprisal differences for simulated English (f = 0.2) and German (f = 1), with deletion probability d = 0.2 and all other parameters set to $\frac{1}{2}$, for final verbs in structural forgetting sentences. The value shown is the surprisal of the ungrammatical continuation minus the surprisal of the grammatical continuation. A positive difference indicates that the grammatical continuation is less costly; a negative difference indicates a structural forgetting effect. (b) Reading time differences in the immediate postverbal region for grammatical and ungrammatical continuations; data from Vasishth et al. (2010).

The results above show that it is possible to reproduce language dependence in structural forgetting for certain parameter values, but they do not speak to the generality of the result nor to the effect of each of the parameters. To explore this matter, we partition the model's four‐dimensional parameter space into regions distinguishing whether lossy‐context surprisal is lower for (G) grammatical continuations or (U) ungrammatical continuations for (a) singly embedded NCNV and (b) doubly embedded NCNCNVV contexts. Fig. 4 shows this partition for a range of r, f, m, and d.

Figure 4.

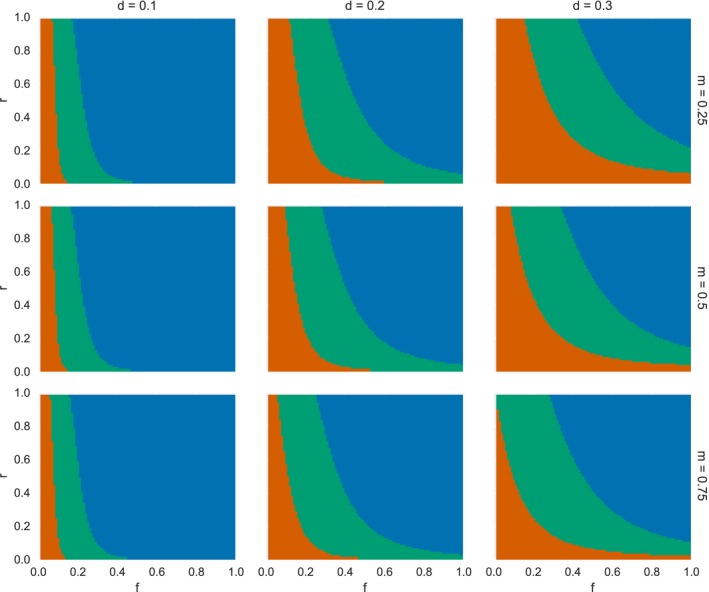
Regions of different model behavior regarding structural forgetting in terms of the free parameters d (noise rate), m (postnominal modification rate), r (relative clause rate), and f (verb‐final relative clause rate).  = U₁U₂, = G₁U₂ (like English),  = G₁G₂ (like German; see text).

In the blue region of Fig. 4, grammatical continuations are lower‐cost than ungrammatical continuations for both singly and doubly embedded contexts, as in German (G₁G₂); in the red region, the ungrammatical continuation is lower cost for both contexts (U₁U₂). In the green region, the grammatical continuation is lower cost for single embedding, but higher cost for double embedding, as in English (G₁U₂).

The results of Fig. 4 are in line with broad patterns reported in the literature. We find that no combination of parameter values ever instantiates U₁G₂ (for either the depicted or other possible values of m and d). Furthermore, each language's statistics place it in a region of parameter space plausibly corresponding to its behavioral pattern: The English‐type forgetting effect is predicted mostly for languages with low f, a fair description of English according to the empirical statistics published in Roland et al. (2007); in Fig. 4 we see that the region around f = 0.2 will have structural forgetting across a wide range of other parameter values. The German‐type forgetting pattern is predicted for languages with high f, and at f = 1 the structural forgetting pattern only obtains only for extremely low values of r (the overall relative clause rate) and high values of d (the forgetting rate). Therefore, the model robustly predicts a lack of structural forgetting for languages with f = 1, which matches standard descriptions of German grammar.

The basic generalization visible in Fig. 4 is that structural forgetting becomes more likely as the relevant contexts become less probable in the language. Thus, decreasing the postnominal modification rate m, the relative clause rate r, and the verb‐final relative clause rate f all cause an increase in the probability of structural forgetting for verb‐final relative clauses. The probability of forgetting also increases as the noise rate d increases, indicating more forgetting when memory representations provide less evidence about the true context.

Thus, lossy‐context surprisal reproduces the language‐dependent structural forgetting effect in a highly general and perspicuous way. The key difference between English and German is identified as the higher verb‐final relative clause rate (f) in German; this difference in grammar creates a difference in statistical distribution of strings which results in more accurate predictions from lossy contexts. The mechanism that leads to the difference in structural forgetting patterns is that linguistic priors affect the way in which a comprehender decodes a lossy memory representation in order to make predictions.

4.6. Discussion

We have shown that lossy‐context surprisal provides an explanation for the interaction of probabilistic expectations and working memory constraints in the case of structural forgetting.

Our model is formulated over a toy grammar over part‐of‐speech categories for ease of implementation and reasoning. We do not wish to claim that a lossy‐context surprisal account of structural forgetting requires part‐of‐speech information or that the noise model has to delete whole words at a time. Rather, the model is meant to illustrate the highly general point that, in a lossy‐context surprisal setting, contexts which are more probable in a language are more likely to produce correct predictions going forward. This is how language statistics interact with memory constraints to create language dependence in structural forgetting.

An interesting aspect of these models is that the memory representation of the key context across languages is exactly the same. The difference in model behavior arises because evidence from these noisy memory representations is combined with prior knowledge about the language to form expectations. It would be theoretically possible to create a lossy‐context surprisal implementation where the form of representation is language‐dependent and itself directly dependent on language statistics, as discussed further in Section 6.1. However, it turns out this mechanism is not necessary to explain language‐dependent structural forgetting.

Our view of structural forgetting makes some new predictions about the phenomenon. For example, if comprehenders adapt quickly to distributional statistics, then it may be possible to quickly train them to expect more verb‐final relative clauses. If the lossy‐context surprisal account of this effect is correct, then we expect that this training would reduce the structural forgetting effect in these comprehenders. Another prediction is that at higher embedding depths, even German should begin to show structural forgetting effects, because higher embedding depths create lower‐probability contexts which are harder to make predictions from. Model predictions for deeper embedding levels are given in Supplementary Material B.

One consistent result from the structural forgetting literature is that the verb that can be most easily dropped is the middle one. That is, for a sentence $N_3{N}_2{N}_1{V}_1{V}_2{V}_3$, the most acceptable ungrammatical variant is $N_3{N}_2{N}_1{V}_1{V}_3$. The particular implementation of model in this section does not provide an explanation for this phenomenon, but we believe some simple extensions could. In the implementation above, we assumed that words from the true context are missing in the memory representation with constant probability d. If this were modified so that the deletion probability increases the longer a word representation exists in memory—a natural consequence of incremental processing—then the model would instantiate a recency effect, capturing the fact that V ₁ is rarely forgotten. To capture the fact that V ₃ is rarely forgotten, there are a few options. One would be to allow the model to represent a primacy effect (Häussler & Bader, 2015); that is, the deletion probability for a word early in a sequence would increase at a slower rate than deletion probabilities for other words, such that words early in a sequence are remembered more accurately than words in the middle of a sequence. Another option, which we believe is more promising, would be to implement a subject advantage in memory in this framework, by postulating that matrix subjects are generally deleted with less probability than other words and phrases. Either a subject advantage or a primacy effect would predict the right forgetting pattern. For more discussion of extended noise models along these lines, see Section 6.1.

In this section we have shown how lossy‐context surprisal accounts for a striking interaction of expectation‐based and memory‐based phenomena. We believe this model provides an explanatory framework for understanding both human sentence processing and also the behavior of broader‐coverage black‐box models such as RNNs. Next, we will show how the same model can account for a classic memory‐based effect: dependency locality effects.

5. Deriving dependency locality from lossy‐context surprisal

A classic finding in psycholinguistics is that sentence processing difficulty increases when words linked in a syntactic dependency are distant in linear order. The effect is usually attributed to memory constraints; upon processing the second word in a syntactic dependency, it is necessary to retrieve a representation of the first word from working memory, and this retrieval may be difficult or inaccurate, with increasing difficulty or inaccuracy the longer the representation has been in memory (Gibson, 1998, 2000; Lewis & Vasishth, 2005; Vasishth, Chopin, Ryder, & Nicenboim, 2017).

In this section we aim to show how dependency locality effects emerge as a natural consequence of lossy‐context surprisal theory. This means that under appropriate conditions, lossy‐context surprisal can recover the predictions of the dependency locality theory (Gibson, 1998, 2000). However, we make predictions beyond previous theories because dependency locality effects emerge under lossy‐context surprisal as a subset of a more general, novel principle: information locality. Information locality holds that there will be relative processing difficulty when any linguistic elements which predict each other are far from each other.

Below, we show how to derive information locality as a first‐order approximation to the full predictions of lossy‐context surprisal theory (Section 5.1). Next, we give evidence that dependency locality effects can be seen as a subset of information locality effects (Section 5.2). Finally, we outline the novel predictions of information locality and survey evidence for information locality from corpus studies (Section 5.3).

5.1. Information locality from lossy‐context surprisal

In this section we will give a high‐level description of the means by which lossy‐context surprisal theory gives rise to information locality: the principle that processing difficulty should occur when words that predict each other are far from each other. A full formal derivation is found in Futrell and Levy (2017) and Supplementary Material C.

5.1.1. Sketch of the idea

We wish to know how we could model the processing difficulty at the word out in a sentence like 5b below in a lossy‐context surprisal framework:

5.	a.	Bob threw out the old trash that had been sitting in the kitchen for several days.
	b.	Bob threw the old trash that had been sitting in the kitchen for several days out.

In order to do this, we will have to assume that the memory representation of a word is affected by noise with increasing probability the longer the representation has been in memory. We call this kind of noise distribution a progressive noise distribution because the noise rate increases progressively with distance; it is illustrated in Fig. 5. A progressive noise distribution could result from decay of representations over time or the accumulation of similarity‐based interference in representations; the only assumption we make regarding noise in memory representations is that the effective noise rate increases monotonically the longer a word representation has been in memory. This assumption captures the idea that we remember gists of contexts, but rapidly lose memory of specific wordforms with time (Lombardi & Potter, 1992; Potter & Lombardi, 1990).

Figure 5.

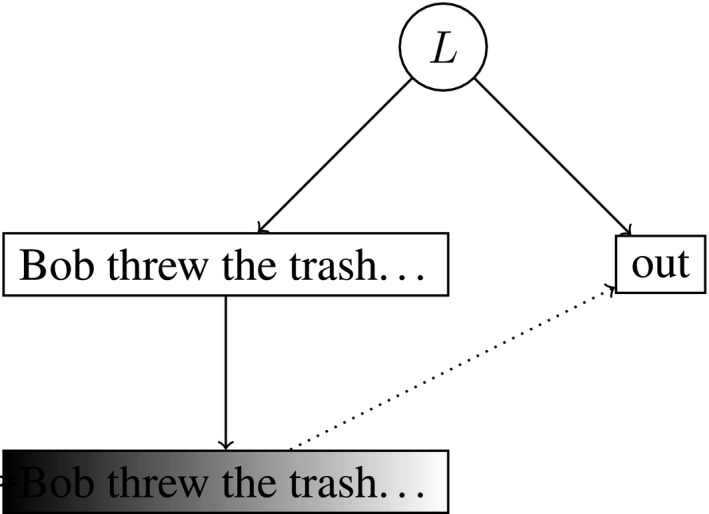
The prediction problem embodied by lossy‐context surprisal with a progressive noise distribution for the example sentence. The star indicates that the lossy memory representation is observed.

Now given a progressive noise distribution, we consider the processing difficulty at the word out in sentences like (5). When the word threw is close to the word out, as in (5a), it is likely to be represented accurately in memory and thus will be available in order to make the word out less surprising, lowering its surprisal cost. On the other hand, when the word threw is far away from out, as in (5b), it is less likely to be represented accurately in memory; in that case the comprehender will try to guess what the now‐forgotten context word was, and might guess something like removed or disposed of which would not predict out as the next word. In that case, the surprisal cost of out would increase.

This is the basic means by which dependency locality effects emerge in lossy‐context surprisal: When a word is far away from a word that it is linked to in a syntactic dependency, then when it is time to process the second word, the first word is less likely to be available in memory, and thus will fail to reduce the surprisal cost at the second word. Depending on the remainder of the context, the surprisal cost of the second word might even increase. Note that this story applies not only to words in syntactic dependencies, but to all groups of words that systematically covary and thus, predict each other.

Below, we will formalize the intuition developed in this section using concepts from information theory.

5.1.2. Decomposing surprisal

In order to make the argument clear, we will first introduce some information‐theoretic notions in the context of plain surprisal theory. To recap, surprisal theory holds that the processing cost associated with a word w_i in context $w_1,\dots ,w_{i-1}$ is proportional to its surprisal given the context, which we write below as $h(w_i|w_1,\dots ,w_{i-1})$:

$$\begin{array}{cc}{D}_{\text{surprisal}}(w_i|w_1,\dots ,w_{i-1})\hfill & \propto -\log p(w_i|w_1,\dots ,w_{i-1})\hfill \\ \hfill & \equiv h(w_i|w_1,\dots ,w_{i-1}).\hfill \end{array}$$

Technically, $h(w_i|w_1,\dots ,w_{i-1})$ is a conditional surprisal, because it is based on a conditional probability. Conditional surprisal can be thought of as measuring the information content of a word in context; that is, it measures the length in bits of an efficient binary representation of the word in context.

Our goal now is to understand the quantity $D_{\text{surprisal}}$ in terms of two parts: the inherent information contained in a word, and the modulation of that amount of information by context. We do this by rewriting it with two terms. Mathematically, it is possible to decompose any conditional surprisal $h(X|Y)$ into two terms: an unconditional surprisal $h(X)\equiv \log \frac{1}{p(X)}$ minus a term called pointwise mutual information $\text{pmi}(X;Y)\equiv \log \frac{p(X|Y)}{p(X)}$:

$$h(X|Y)=h(X)-\text{pmi}(X;Y).$$

Pointwise mutual information is the extent to which knowing the value Y lowers the surprisal of the value X. It is a correction term that changes the unconditional surprisal h(X) into the conditional surprisal $h(X|Y)$. It is also called coding gain in related literature (Agres et al., 2018).

Viewing surprisal as information content, pointwise mutual information can be thought of as measuring the number of shared bits between two representations. For example, if you know that $\text{pmi}(X;Y)=3$, then that means that when you learn Y, you can already guess the value of 3 of the bits in the representation of X. Applying this decomposition to surprisal cost, we get:

$$D_{\text{surprisal}}(w_i|w_1,\dots ,w_{i-1})\propto h(w_i)-\text{pmi}(w_i;w_1,\dots ,w_{i-1}).$$ (10)

The relation of conditional surprisal, unconditional surprisal, and pointwise mutual information is shown in Fig. 6. Pointwise mutual information is subtracted from the unconditional surprisal to yield the conditional surprisal.³

Figure 6.

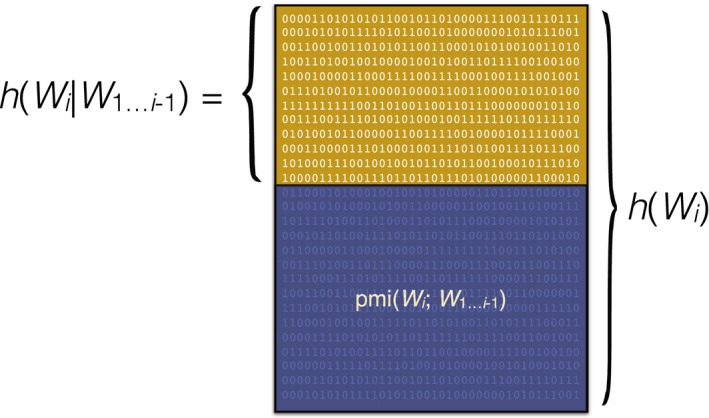
Relation of conditional surprisal $h(w_i|w_1,\dots ,w_{i-1})$, unconditional surprisal h(w_i), and pointwise mutual information $\text{pmi}(w_i;w_1,\dots ,w_{i-1})$.

5.1.3. The effect of noise

When we move to lossy‐context surprisal, where we are predicting the next word w_i given a noisy memory representation, the picture in Fig. 6 changes. On average, the noisy memory representation can only contain a subset of the information in the true context—it certainly could not contain more information than the true context. Furthermore, as a context representation is affected by more and more noise, that context representation can contain less and less about the next word. We will make this idea concrete by considering a particular kind of noise model.

In order to capture the intuition that an increasing noise rate affecting a representation means that there is less information available in that representation, we use erasure noise as a concrete model. Erasure noise is a common noise model used in information theory, where it can be a simple stand‐in for more complex underlying processes (Cover & Thomas, 2006). In erasure noise, an element of a sequence is probabilistically erased with some probability e. When an element is erased, it is replaced with an erasure symbol E. Erasure noise means that the comprehender knows some word was present in a position, but has forgotten what the word was.⁴

Furthermore, given that we want to have a progressive noise distribution, we will assume that the rate at which a word is erased increases the farther back a word is in time. Suppose we are predicting word w_i based on a memory representation of the context $w_1,\dots ,w_{i-1}$. In that case, we assume that the erasure probability for a context word w_{i − d}, which is d words back from w_i, is e_d, where e_d increases monotonically with d (so $e_{d+1}\ge e_d$ for all d). That is, the farther back a word is in context, the less information about the wordform is available. Some examples are shown in Table 3, which demonstrates possible noisy representations of the context Bob threw the trash and their probabilities.

Table 3.

Examples of noisy memory representations after progressive erasure noise, where a d‐back word is erased with monotonically increasing probability e_d

Noisy memory	Probability
Bob threw the trash	(1 − e 4)(1 − e 3)(1 − e 2)(1 − e 1)
Bob E the trash	(1 − e4)e 3(1 − e 2)(1 − e 1)
Bob threw E trash	(1 − e 4)(1 − e 3)e 2(1 − e 1)
E threw the E	e 4(1 − e 3)(1 − e 2)e 1

Erasure noise has the effect of reducing the effective pointwise mutual information. If values X and Y have pointwise mutual information $\text{pmi}(X;Y)$, and a third variable R is produced by erasing Y with probability e, then the expected pointwise mutual information between X and R is $\text{pmi}(X;R)=(1-e)\text{pmi}(X;Y)$. Erasure noise causes pointwise mutual information to decrease linearly.

Now that we have defined a concrete progressive noise model, we are ready to show that lossy‐context surprisal under this noise model exhibits information locality.

5.1.4. Information locality

Under progressive erasure noise, the lossy‐context surprisal of word w_i in context $w_1,\dots ,w_{i-1}$ can be approximated in terms of the erasure rates and the pmi values between words as the following:

$$D_{\text{lc}\text{surprisal}}(w_i|w_1,\dots ,w_{i-1})\approx h(w_i)-\sum _{j=1}^{i-1}(1-e_{i-j})\text{pmi}(w_i;w_j).$$ (11)

See Supplementary Material C for the formal argument. This expression of the cost function is schematized in Fig. 7 for the case where we are predicting out given the context Bob threw the trash. The expression is most easily understood in terms of the difference between the predictions of lossy‐context surprisal and plain surprisal. The predicted excess processing difficulty, on top of the predictions of surprisal theory, is given by:

$$D_{\text{lc}\text{surprisal}}(w_i|w_1,\dots ,w_{i-1})-D_{\text{surprisal}}(w_i|w_1,\dots ,w_{i-1})\approx \sum _{j=1}^{i-1}{e}_{i-j}\text{pmi}(w_i;w_j).$$ (12)

As words w_i and w_j become more distant from each other, the value of the erasure probability e_{i − j} must increase, so the magnitude of Eq. 12 must increase. Therefore, the theory predicts increased processing difficulty as an increasing function of the distance between w_i and w_j in direct proportion to the pointwise mutual information between them.

Figure 7.

Lossy‐context surprisal of out given Bob threw the trash, according to Eq. 11.

In order to unpack what these equations mean, let us focus on the influence of the single context word threw on the probability of the target word out. Fig. 8a shows the surprisal reduction in out due to the word threw. Now if we consider the case where the word threw is far away from out, the probability that threw is not erased decreases, because of the progressive erasure noise. Therefore, the surprisal‐reducing effect of threw is weakened, as shown in Fig. 8b.

Figure 8.

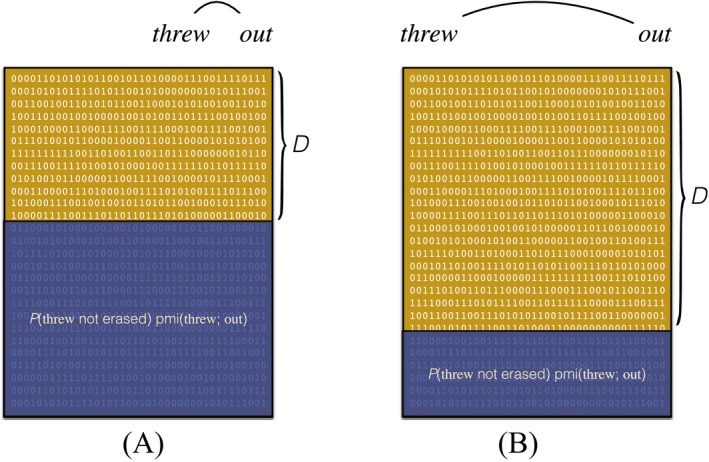
Lossy‐context surprisal of out when the context word threw is (a) close and (b) far, according to Eq. 11.

We have derived a notion of pairwise information locality: a prediction that excess processing difficulty will result whenever any pair of words that predicts each other is far from each other. This result may seem surprising given that we aim to also capture the predictions of pure surprisal models, which usually predict antilocality effects. However, as we will see in Section 5.3, the model still predicts antilocality effects depending on the nature of the intervening material.

The approximation in Eq. 11 is precise only when all context words w_j make independent contributions toward predicting the target word w_i. When two context words together make a different prediction than either word separately, then the approximation will break down. Such a scenario corresponds to the presence of interaction information among three or more words in a sequence (Bell, 2003); terms would have to be added to Eq. 11 to account for these interactions. However, the effects of these terms would be highly constrained because they will be highly penalized by noise. The reason these terms would be highly constrained is that if two words together make a different prediction than either word separately, then this prediction will only be relevant if neither of the words is affected by noise, and this is relatively unlikely.

The assumption that context words make independent contributions toward predicting the target word is necessary for Eq. 11, which expresses pairwise information locality, where processing cost results when individual word pairs that systematically covary are far from each other. However, this assumption is not necessary to show information locality in general; see Supplementary Material C for the derivation of the full form of information locality, which holds that excess difficulty will result when a word is separated from any set of context elements that jointly predict it. Pairwise information locality will be crucial, however, because we will show that it corresponds to dependency locality effects.

5.2. Relation to dependency locality

We have shown, under certain assumptions about the noise distribution, that lossy‐context surprisal gives rise to information locality: Processing is most efficient when words that predict each other are close to each other. We have not yet made an explicit link to dependency locality, the idea that processing inefficiency happens when words linked in a syntactic dependency are far from each other.

We propose that dependency locality can be seen as a subset of information locality under a particular linking hypothesis. The linking hypothesis is that those words linked in a syntactic dependency are also those words which predict each other the most in a sentence, that is, those words which have the highest pointwise mutual information. We call this the Head‐Dependent Mutual Information (HDMI) hypothesis. If it is the case that syntactically dependent words have the highest pmi, then dependency locality is an approximation to information locality where only the highest‐pmi word pairs are counted.

In some sense, the link between mutual information and syntactic dependency is definitional. Mutual information is a concept from information theory that quantifies the extent to which two random variables covary systematically. Syntactic dependency, by definition, identifies words whose covariance is systematically constrained by grammar. Based on the parallelism of these concepts, we should expect a connection between mutual information and syntactic dependency.

The HDMI hypothesis has long been assumed, often tacitly, in the literature on computational linguistics and natural language processing. Pointwise mutual information has been used in the field of computational linguistics to detect syntactic dependencies (de Paiva Alves, 1996; Yuret, 1998) and to discover idioms and collocations (Church & Hanks, 1990). The HDMI hypothesis also follows naturally from some of the probabilistic generative models that have been assumed in computational linguistics. In particular, it follows from head‐outward generative models (Eisner, 1996, 1997; Klein & Manning, 2004; Wallach, Sutton, & McCallum, 2008), in which the probability of a sentence is the product of the probabilities of dependents given heads. Therefore, inasmuch as these models have had success in unsupervised grammar induction, we have evidence for the HDMI hypothesis.

Empirical evidence for the HDMI hypothesis based on large corpora is provided by Futrell and Levy (2017) and Futrell, Qian, Gibson, Fedorenko, and Blank (2019), who also give a formal derivation of the HDMI hypothesis from an information‐theoretic interpretation of the postulates of dependency grammar.

Given the theoretical arguments and empirical evidence that words in dependencies have especially high mutual information, we can see dependency locality theory as an approximation to information locality where only the mutual information of words in dependencies is counted.

5.3. Predictions of information locality

We have given a theoretical argument for how lossy‐context surprisal predicts dependency locality effects as a subset of a new, more general principle of information locality. Here we detail some of the novel predictions of information locality about processing difficulty and about word order preferences, and give some evidence that information locality shapes the latter beyond dependency locality.

5.3.1. Word order preferences

The dependency locality theory has been used not only as a theory of on‐line processing difficulty but also as a theory of word order preferences in grammar and usage under the theory that speakers prefer to use orders that are easy to produce and comprehend (Gibson et al., 2019; Hawkins, 1994; Jaeger & Tily, 2011). In this context, it makes the prediction of dependency length minimization: In grammar and usage, the linear distance between words linked in syntactic dependencies should be minimized. This theory has had a great deal of success in explaining typological universals of word order as well as corpus data (Ferrer‐i‐Cancho, 2004; Futrell et al., 2015; Gildea & Temperley, 2010; Hawkins, 1994, 2004, 2014; Liu, 2008; Park & Levy, 2009; Rajkumar et al., 2016; Tily, 2010). For recent reviews, see Dyer (2017), Liu, Xu, and Liang (2017), and Temperley and Gildea (2018)

In the context of predicting word order preferences, information locality makes a clear prediction beyond dependency locality. It predicts that beyond the tendency for words in syntactic dependencies to be close, all words with high mutual information (which predict each other) should be close. Furthermore, words with the highest mutual information should experience a stronger pressure to be close than those with lower mutual information. The basic word order prediction is thus that mutual information between words should be observed to decrease with distance.

The prediction that linguistic units with high mutual information tend to be close has been borne out in the literature on quantitative linguistics. Li (1989) and Lin and Tegmark (2017) have shown that mutual information between orthographic letters in English text falls off as a power law. However, the relationship between mutual information and distance has not been investigated crosslinguistically at the level of words rather than orthographic letters, nor has the relationship among mutual information, distance, and syntactic dependency.

In order to test the prediction that words with high mutual information are close, beyond what is explained by dependency length minimization, we quantified mutual information among word pairs at various distances in 56 languages of the Universal Dependencies (UD) 2.1 corpus (Nivre et al., 2017). For technical reasons, we are limited to calculating mutual information based on the joint frequencies of part‐of‐speech pairs, rather than wordforms. The reason we use part‐of‐speech tags is that getting a reliable estimate of mutual information from observed frequencies of wordforms is statistically difficult, requiring very large samples to overcome bias (Archer, Park, & Pillow, 2013; Basharin, 1959; Bentz, Alikaniotis, Cysouw, & Ferrer‐i‐Cancho, 2017; Futrell et al., 2019; Miller, 1955; Paninski, 2003). The mutual information estimation problem is less severe, however, when we are looking at joint counts over coarser‐grained categories, such that there is not a long tail of one‐off forms. Therefore, we quantify mutual information over part‐of‐speech tag pairs in this section. For this reason we also do not include data from languages that have fewer than 5,000 words in their largest UD corpus.

The results of this study are shown in Fig. 9. Overwhelmingly, we find that words that are closer have higher mutual information; this is true both for arbitrary word pairs and for word pairs in syntactic dependencies. The only exception appears to be syntactic dependencies in Kazakh, which we believe is due to the small size of the corpus (8,851 words), which means the mutual information values suffer high estimation error. We quantify the relationship between mutual information and distance using the Spearman correlation coefficient rho, which is negative when mutual information falls off with distance; as seen in Fig. 9, it is negative for all cases except for head‐dependent pairs in Kazakh and head‐dependent pairs in Persian, for which it is zero.

Figure 9.

Mutual information between part‐of‐speech tag pairs at various distances across corpora. The blue line is the mutual information for all word pairs; the red line is the mutual information for word pairs in a syntactic dependency relationship. The main point of this figure is that mutual information falls off with distance, but it also gives evidence for the HDMI hypothesis; in this connection, the distances where the difference between the mutual information of all word pairs and the mutual information of syntactically dependent words is statistically significant by a Monte Carlo permutation test over observations at p < .005.

The finding that words that are close have high mutual information is evidence for information locality in word order preferences, an effect generalizing and going beyond dependency length minimization.

In addition, the results show that words in syntactic dependencies have consistently higher mutual information than general word pairs, even when controlling for distance; this provides further evidence for the HDMI hypothesis of Section 5.2.

5.3.2. On‐line processing predictions

Information locality also makes predictions beyond dependency locality in the domain of on‐line processing effects. In particular, it suggests that dependency locality effects should be moderated by the mutual information of the words involved in the syntactic dependency. In the information locality view, dependency locality effects happen when a context word that would have been useful for predicting the next word is forgotten, and thus the processing time for the next word is longer than it would have been if that context word were close. Thus, dependencies with high pointwise mutual information should be associated with strong locality effects, while dependencies with low pointwise mutual information should be associated with null or weak locality effects.

The existing literature touching on this prediction is mixed. In a reading time study, Husain et al. (2014) finds that when a final verb in a Hindi relative clause is strongly predicted by some context, then locality effects with respect to that context cannot be found; but when the context only weakly predicts the final verb, locality effects are observed. This result appears to contradict the predictions of information locality, although the effects of the intervening material would need to be taken into account.

On the other hand, Safavi et al. (2016) perform essentially the same experimental manipulation in Persian, but find no evidence that strong expectations result in an attenuated locality effect. In fact, they find in an offline sentence completion study that with increased distance before the verb, comprehenders' expectations for that verb become less sharp, indicating that they might be predicting the next word given a lossy representation of the context. This idea leads the authors to conjecture an idea similar to lossy‐context surprisal (Safavi et al., 2016, section 8.1.2). Overall they conclude that effects at the intersection of expectations and memory may be highly specific to languages and constructions. Lossy‐context surprisal theory would hold that, if there is a real difference between Hindi and Persian in their locality effects, the difference is driven by the differences in the magnitude of mutual information in the dependencies involved.

We hope that the idea of information locality creates further interest in these kinds of experiments crossing distance with prediction strength. Information locality predicts that dependencies where the two words have high pointwise mutual information will be more susceptible to locality effects. While the prediction is clear, it may prove challenging to find the effect experimentally, because it is inherently an interaction, thus requiring high power, and also because large datasets are required to get reliable estimates of pointwise mutual information from corpora.

Information locality also predicts locality effects for words that are not linked in a direct dependency. The information locality effect depends on the pointwise mutual information between words, and it is easily possible that there is nonzero pointwise mutual information among words in indirect dependency relationships, such as two words that are co‐dependent on a shared head. We predict weak locality effects involving words in such indirect dependency relationships.

5.3.3. Locality and antilocality

As a unified model of effects of expectation and memory in sentence processing, lossy‐context surprisal theory predicts locality effects in certain circumstances and antilocality effects in others. The question arises: when do we expect locality versus antilocality effects? Here we show that, typically, we expect antilocality effects when the intervening material that splits up a dependency is highly predictive of the second element of the dependency, and otherwise we predict locality effects.

Suppose we have two words: a context word C and a target word W, where C and W are linked in a dependency relationship, and there might be one or more intervening words X between them. Our goal is to predict processing difficulty for the target word W as part of two different sequences: CW versus CXW. A locality effect would mean W is harder as part of CXW; an antilocality effect would mean W is easier as part of CXW, when compared to CW. Information locality means that the predictive information in C about W might be lost if many words appear between C and W, thus making W harder in context. But if those intervening words are themselves highly predictive of W, then the information locality effect may be cancelled out.

Here we derive a basic prediction: We always predict an antilocality effect when the mutual information of W and X is greater than the mutual information between W and C.

We deduce this prediction algebraically. According to Eq. 11, the predicted processing difficulty of W preceded immediately by C is approximately:

$$D(W|C)=h(W)-(1-e_1)I_C,$$

where h(W) is the unigram surprisal of W, e₁ is the probability that an immediately preceding word is erased in the memory representation, and $I_C=\text{pmi}(C;W)$. Now we compare to the approximate predicted processing difficulty of W preceded by CX, with X an intervening word:⁵

$$D(W|CX)=h(W)-(1-e_1)I_X-(1-e_2)I_C,$$

where $I_X=\text{pmi}(X;W)$, and e₂ is the probability that a word two positions back in memory will be erased, or equivalently, the proportion of information retained in memory about the word two positions back. Locality effects correspond to $D(W|C)<D(W|CX)$—that is, processing W is harder given the additional intervening context X. Antilocality effects correspond to the opposite situation: We predict antilocality effects when $D(W|C)>D(W|CX)$.⁶ Therefore, in terms of I_C, I_X, e ₁, and e ₂, we expect a locality effect when the following condition holds:

$$\begin{array}{cc}D\left(W|C\right)\hfill & <D\left(W|CX\right)\hfill \\ h\left(W\right)-\left(1-e_1\right)I_C\hfill & <h\left(W\right)-\left(1-e_1\right)I_X-\left(1-e_2\right)I_C\hfill \\ \left(1-e_1\right)I_X\hfill & <\left(1-e_1\right)I_C-\left(1-e_2\right)I_C\hfill \\ \left(1-e_1\right)I_X\hfill & <\left(e_2-e_1\right)I_C\hfill \\ \frac{I_X}{I_C}\hfill & <\frac{e_2-e_1}{1-e_1}.\hfill \end{array}$$ (13)

Eq. 13 says that we expect an antilocality effect depending on how predictive the context word C and the intervener X are about the target word W (left‐hand side), and on a measure of the increase of information loss from context position 1 to context position 2 (right‐hand side).

We can immediately make some deductions from Eq. 13. First, we never predict a locality effect when $I_X>I_C$—that is, when the intervener X is more predictive of W than the context word C is. To see this, consider the constraints on the value of the right‐hand side of Eq. 13. Because the values e represent progressive erasure noise, we know that $e_1\le e_2\le 1$. Therefore, the numerator must be smaller than the denominator, and the value of the right‐hand side must be ≤1. But if $I_X>I_C$, then the value on the left‐hand side is greater than 1. If the value on the left‐hand side is greater than 1, then the inequality in Eq. 13 can never be satisfied. Therefore, we never predict a locality effect when $I_X>I_C$, and instead predict either an antilocality effect or no effect of intervening context.

In conjunction with the HDMI hypothesis from Section 5.2, we can make a specific prediction about how these effects relate to syntactic structure. If the intervening word X is in a direct dependency relationship with W, then it will be highly predictive of W, leading to an antilocality effect. If the intervening word X is not in a direct dependency relationship with W, then it is on average not as strongly predictive of W as C is, and therefore a locality effect is more likely—the balance will depend on the exact mutual information values and on the rate of information loss in memory representations. Konieczny and Döring (2003) provide evidence for this pattern of effects in German: The reading time at the main verb of a verb‐final clause is found to be lower when a verb is preceded by two of its dependents as opposed to one dependent followed by a grandchild. Information locality generally predicts that if there is a sufficient amount of syntactically distantly related intervening material, then locality effects will emerge even in the head‐final contexts which are typically host to antilocality effects.

5.4. Discussion

We have shown that lossy‐context surprisal gives rise to a generalization called information locality: that there will be processing cost beyond that predicted by plain surprisal theory when words that predict each other are far from each other. Furthermore, we have given evidence that dependency locality effects can be seen as a subset of information locality effects. Thus, lossy‐context surprisal provides a possible unified model of surprisal and locality. The dependency locality theory (Gibson, 2000) was originally introduced as the syntactic prediction locality theory (SPLT) (Gibson, 1998). Information locality could just as easily be called “prediction locality,” making clear how it generalizes the SPLT. Lossy‐context surprisal theory recovers the dependency locality theory exactly in the case where all head‐dependent pairs have high mutual information, all other word pairs have negligible information, and the noise rate for a memory representation increases upon processing a new discourse referent.

The idea of information locality here is similar to the idea of a decay in cue effectiveness presented in Qian and Jaeger (2012). In that work, the authors show that it is possible to predict entropy distributions across sentences under an assumption that predictive cues decay in their effectiveness, which is essentially the state of affairs described by progressive noise.

We stress that pairwise information locality as stated here is an approximation to the full predictions of lossy‐context surprisal. It relies on the assumptions that (a) the noise affecting word representations can be thought of as simply erasing information with a probability that increases monotonically with distance, and (b) that context words make independent contributions toward predicting the following word. Both of these assumptions are likely too strong, but we believe they are reasonable for the purpose of deriving broad predictions.

The evidence presented here for information locality as a generalization of dependency locality comes primarily from corpus studies of word order. Evidence from on‐line processing is mixed. This state of affairs reflects the state of affairs for dependency locality effects: While apparent locality effects have been clearly observed in controlled experiments (Balling & Kizach, 2017; Bartek et al., 2011; Grodner & Gibson, 2005; Nicenboim et al., 2015), they have proven elusive in datasets of reading time for uncontrolled, naturalistic text containing many varied syntactic constructions (Demberg & Keller, 2008a; Husain et al., 2015). On the other hand, in studies of word order preferences in corpora, dependency locality has had broad‐coverage success and enjoys strong effect sizes (Futrell et al., 2015; Rajkumar et al., 2016).

We believe the information locality interpretation of dependency locality effects may provide an explanation for why locality effects have been hard to find in naturalistic reading time datasets with broad coverage over different kinds of syntactic structures. From the view of our theory, the dependency locality theory is a kind of first‐order approximation to the full predictions of a theory of processing cost given lossy memory representations, which is only accurate when mutual information between the relevant two words in a dependency is very high, mutual information with other words is negligible, and there are no interactions between the dependent words and other words. Such cases can be engineered in experiments, but may be rare in naturalistic text.

6. Conclusion

We have proposed that sentence processing phenomena involving working memory effects can be thought of in terms of surprisal given lossy context representations. We showed two main theoretical results: first, that it is possible to use lossy‐context surprisal to model a previously puzzling phenomena at the intersection of expectations and memory, structural forgetting; and second, that it is possible to derive dependency locality effects as a subset of a new, more general prediction of information locality effects.

6.1. Toward more sophisticated noise models

Throughout the paper we have used simplified noise models which are designed to capture only the most general properties of memory: that information about individual wordforms is lost, and that the noise rate affecting a representation generally increases with time. However, more sophisticated memory models are possible, and we believe they may be useful for explaining certain phenomena.

The idea of progressive noise in Section 5 arises from the idea that a memory representation at time i is the result of successive applications of some noisy memory encoding function to words in a sequence. So a representation of word w_j (for j < i) will have had the memory encoding function applied to it i − j times. Each application of the noise increases the probability that some information about w_j is lost, hence the assumption of a progressively increasing noise rate.

While noise must logically be progressive in the sense that information about w_j will degrade over time (perhaps due to inherent decay or due to cumulative interference), it is not the case that all words will degrade at the same rate. The idea of word representations degrading at different rates raises the possibility that some positions in a sequence may enjoy a lower degradation rate than others. In that case, word representations would still contain less information the longer they have been in memory, but it would not necessarily be the case that representations of more distant words are more degraded than representations of closer words, as was assumed in Section 5. It would be possible to build these different degradation rates into an erasure noise model by holding that words are subjected to some probability of erasure at each application of the integration function, but that base probability of erasure at each function application is less for some elements compared to others.

One application of this idea could be to set a lower degradation rate for elements earlier in a sequence than for elements later in a sequence. Such a model could be used to instantiate primacy effects, the observed tendency for symbols at the beginning of a sequence to be better remembered, by assuming a lower degradation rate for elements at the beginning of a sequence.

Degradation rates could also be set adaptively. This is a means by which distributional statistics of a language could have a direct influence on memory representations. At a word, a comprehender might decide what amount of resources to devote to maintaining the representation of the current word in memory. Higher resources devoted to representing a word would correspond to that word having a lower degradation rate going forward. This resource‐allocation decision could be made rationally on the basis of predictions about the future utility of a word, which would depend on language statistics. It may be possible to use this adaptive mechanism to instantiate biases such as a subject advantage, where matrix subjects are remembered more accurately than other noun phrases in a sentence. This idea could also explain results such as those reported by Husain et al. (2014).

The proper mathematical framework for describing this resource‐allocation problem is rate–distortion theory (Berger, 2003; Sims, 2018). Within rate–distortion theory, models that optimally allocate limited memory resources to best predict the future of a sequence have been studied, under the name of the Predictive Information Bottleneck (Still, 2014). The Predictive Information Bottleneck has recently been applied to study the resource requirements required for predicting linguistic sequences by Hahn and Futrell (2019).

Another direction for the noise distribution could be to define memory representations and noise over those memory representations in terms of structured syntactic objects. Then the probability of erasure might have to do with tree topology rather than linear distance. Memory‐based theories of sentence processing have incorporated rich, syntactic notions of locality (Graf, Monette, & Zhang, 2017); syntactic memory representations and noise operations would provide a way to incorporate these distance metrics into a surprisal framework.

6.2. Prospects for a broad‐coverage model

This work has relied on mathematical derivations (Section 5) and calculations done over toy grammars (Section 4). Here we discuss what would be required to make a broad‐coverage instantiation of the lossy‐context surprisal model such that it could be applied to, for example, reading time corpora (Frank, Monsalve, Thompson, & Vigliocco, 2013; Futrell et al., 2018; Husain et al., 2015; Kennedy, Hill, & Pynte, 2003; Kliegl, Nuthmann, & Engbert, 2006; Yan, Kliegl, Richter, Nuthmann, & Shu, 2010).

There are algorithmic complexities in computing exact lossy‐context surprisal values. For each true context, it is necessary to enumerate all the possible noisy versions of the context, and for each noisy version of the context, it is necessary to enumerate all the possible true contexts that could have given rise to the noisy context. These enumerations may be infinite. The complexity of these enumerations can be brought down by dynamic programming, but it is still computationally costly in our experience. A broad‐coverage model of lossy‐context surprisal will have to either have a very simplified noise model (such as n‐gram surprisal) or compute only approximate values—which would be sensible, since lossy‐context surprisal describes the operation of a maximally efficient processor and human sentence processing is likely only an approximation to this ideal.

We believe the most promising way to instantiate lossy‐context surprisal in a broad coverage model is using RNNs with explicitly constrained memory capacity (e.g., using methods such as those developed by Alemi, Fischer, Dillon, & Murphy, 2017; Hahn & Futrell, 2019). Lossy‐context surprisal predicts that such RNNs will yield surprisal values which are more predictive of human reading times than unconstrained RNNs (though any RNN is operating under at least mild memory constraints).

6.3. Computational and algorithmic levels of description

Classical surprisal theory is stated at a fully computational level of description, meaning it describes the computational problem being solved in human sentence processing (Marr, 1982). Surprisal theory claims that human incremental sentence processing is solving the problem of updating a posterior distribution about beliefs about the sentence. The linking function from this view of sentence processing to observed processing difficulty is optimality: It is assumed that the incremental update is maximally efficient, thus yielding reading times proportional to surprisal. Memory‐based theories, on the other hand, are mechanistic models dealing with concrete representations of resources being used in the course of processing; they are algorithmic‐level models, in Marr (1982)'s terminology. Where does lossy‐context surprisal theory stand?

We think of lossy‐context surprisal theory as a computational‐level theory. It is a relaxation of the assumption in Hale (2001) and Levy (2008a) that the incremental representation of a sentence contains complete information about the previous words in a sentence. Lossy‐context surprisal theory amounts to the claim that incremental sentence processing is solving the problem of updating a posterior belief distribution given potentially noisy evidence about the previous words in the sentence. There is still an efficiency assumption, in that the time taken to do that update is proportional to surprisal. Thus, lossy‐context surprisal theory takes a computational view of the action of the sentence processor while making more realistic assumptions about the representations that sentence processor has as input and output.

6.4. Future directions

Lossy‐context surprisal provides a potential unified framework for explaining diverse phenomena, but its full predictions have yet to be fleshed out and tested. The main novel prediction about on‐line processing is information locality effects: There should be observed locality effects for words that predict each other even when they are not in syntactic dependencies, and also syntactic dependency locality effects should be moderated by the pointwise mutual information of the words in the dependency. In the domain of word order, information locality makes the broad prediction that words with high mutual information should be close, which provides potential explanations for word order universals that go beyond dependency length minimization, such as adjective ordering preferences (Futrell, 2019; Hahn, Degen, Goodman, Jurafsky, & Futrell, 2018).

It remains to be seen whether all effects of memory can be subsumed under lossy‐context surprisal. The phenomena of similarity‐based interference in agreement and anaphora interpretation remain unexplored from this perspective (Jäger et al., 2017). We hope the present work intensifies research into the intersection of expectation and memory in sentence processing.

Supporting information

Appendix A. Memory distortion: Less probable contexts result in more error in prediction.

Appendix B. Structural forgetting predictions for deeper embeddings.

Appendix C. Formal derivation of information locality.