A multidimensional array representation of state-transition model dynamics

Abstract

Cost-effectiveness analyses often rely on cohort state-transition models (cSTMs). The cohort trace is the primary outcome of cSTMs, which captures the proportion of the cohort in each health state over time (state occupancy). However, the cohort trace is an aggregated measure that does not capture information about the specific transitions among health states (transition dynamics). In practice, these transition dynamics are crucial in many applications, such as incorporating transition rewards or computing various epidemiological outcomes that could be used for model calibration and validation (e.g. disease incidence and lifetime risk). In this manuscript, we propose an alternative approach to compute and store cSTMs outcomes that capture both state occupancy and transition dynamics. This approach produces a multidimensional array from which both the state occupancy and the transition dynamics can be recovered. We highlight the advantages of the multidimensional array over the traditional cohort trace and provide potential applications of the proposed approach with an example coded in R to facilitate the implementation of our method.

State-transition models (STM) are decision models commonly used in cost-effectiveness analysis (CEA) to estimate economic and health outcomes of different strategies over time in discrete time cycles.[1, 2] In a cohort STM (cSTM), the disease dynamics are captured by distributing a closed cohort among a mutually exclusive and collectively exhaustive set of health states.[2, 3, 4] The cohort trace is the primary outcome of cSTMs, which comprises the proportion of the cohort in each health state over time (i.e., it summarizes state occupancy).[5, 1] A limitation of the cohort trace is that it does not keep track of the transitions among health states over time (i.e., the transition dynamics of the cohort). As a consequence, it can only be used to capture outcomes that result from residing in a state for a full cycle by applying the so-called state rewards and does not contain a mechanism to assign transition rewards, which are applied only when specific transitions occur. It also limits the type of epidemiological outcomes that can be obtained from cSTMs. For example, obtaining incidence of a disease requires knowledge of the proportion of the population transitioning from a subset of states without disease to the state(s) representing the disease of interest.

To overcome the limitations of the cohort trace, we propose a multidimensional array-based approach that serves as a full summary of cSTM dynamics that complements the already useful cohort trace. The proposed approach, called the dynamics-array approach, allows modelers to efficiently calculate all measures of interest that rely on transition dynamics and at the same time to aggregate all model dynamics into a standard cohort trace.

We start by providing a formal definition of cSTM components and the cohort trace. We complement this standard notation with a description of the detailed transition dynamics. Then, we introduce the multidimensional-array structure and show how it can be easily generated. In addition, we illustrate its use to compute a measure of interest that depends on transitions among health states. Finally, we demonstrate the dynamics-array approach with an illustrative example of a cSTM programmed in R [9, 10] and compare this implementation with the traditional cohort trace approach in a simulation study. The R code is provided in the supplementary material and in GitHub https://github.com/DARTH-git/state-transition-model-dynamics).

Traditional cohort trace approach

We denote the distribution of the cohort across n_s health states in a cSTM at the beginning of cycle t for all t in 0,…, n_t as the state vector m_t of dimensions 1 × n_s. That is, each element in m_t represents the proportion of the cohort in health state i = 1,…, n_s at time t. Thus, m_t is written as

$${\mathbf{m}}_t=\left[m_{[t,1]}{m}_{[t,2]}\cdots m_{[t,n_s]}\frac{}{}\right],$$ (1)

where the initial state vector m₀ contains the distribution of the cohort across all n_s health states at the start of the simulation. The simulation begins at cycle 0 and all transitions are assumed to happen at the end of each cycle. The probability of transitioning from health state i to health state j at the end of cycle t is denoted as p_[i,j,t]. This means that p_[i,j,t] determines how the population will be distributed in cycle t + 1. The collection of transition probabilities across the model states over the time horizon forms the time-dependent state transition probability matrix, P_t of dimensions n_s × n_s,

$$P_t=\left[\begin{array}{cccc}\hfill p_{[1,1,t]}\hfill & \hfill p_{[1,2,t]}\hfill & \hfill \cdots \hfill & \hfill p_{[1,n_s,t]}\hfill \\ \hfill p_{[2,1,t]}\hfill & \hfill p_{[2,2,t]}\hfill & \hfill \cdots \hfill & \hfill p_{[2,n_s,t]}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill p_{[n_s,1,t]}\hfill & \hfill p_{[n_s,2,t]}\hfill & \hfill \cdots \hfill & \hfill p_{[n_s,n_s,t]}\hfill \end{array}\right].$$ (2)

For any t, all rows of P_t must sum to one. Note that if P_t is equal for all t times, equation (2) becomes a time-homogeneous transition probability matrix, where P_t = P.

The state vector at cycle t + 1, m_t+1, is then obtained by the inner product between the state vector at cycle t, m_t, and the corresponding transition probability matrix P_t, such that

$${\mathbf{m}}_{\mathbf{t}+1}={\mathbf{m}}_{\mathbf{t}}{P}_t\text{for}t=0,\dots ,(n_t-1).$$ (3)

Stacking the state vectors by rows for all t = 0,…, n_t results in the full cohort trace matrix, M, of dimensions (n_t + 1) × n_s, where each row is a state vector (−m_t−), resulting in

$$M=\left[\begin{array}{c}\hfill -{\mathbf{m}}_0-\hfill \\ \hfill -{\mathbf{m}}_1-\hfill \\ \hfill ⋮\hfill \\ \hfill -{\mathbf{m}}_{n_t}-\hfill \end{array}\right].$$ (4)

Together, the state vectors m_t, the transition probability matrices P_t and the cohort trace M in equations (1), (2) and (4), respectively, represent the three main components of a cSTM.

Dynamics-array approach

The trace matrix M aggregates transitions from all the states to a specific state, thus loses details of the transition dynamics. We propose to use a multidimensional array, A, of dimensions n_s × n_s × (n_t + 1) to store the proportion of the cohort that transitions between any two health states in each cycle over the time horizon. This array can be thought of as a set of two-dimensional matrices stacked along a third dimension that represents time. Below, we illustrate how to compute A from the three main components, the state vector m_t, the transition probability matrices P_t and the cohort trace M, of cSTMs.

A₀ represents the first "slice" of A. We compute A₀ as a matrix containing the initial state vector m₀ in its diagonal and 0s in the off-diagonal, such that

$$A_0=\text{diag}({\mathbf{m}}_0)=\left[\begin{array}{cccc}\hfill m_{[0,1]}\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill m_{[0,2]}\hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill m_{[0,n_s]}\hfill \end{array}\right].$$ (5)

Each subsequent (t + 1)^th "slice" of A is obtained by multiplying a diagonal matrix of m_t, denoted as diag(m_t), by P_t, such that

$${\mathbf{A}}_{t+1}=\text{diag}({\mathbf{m}}_t)\cdot P_t\text{for}t=0,\dots ,(n_t-1).$$ (6)

The resulting elements of the t^th slice of A, A_t for t > 0, are

$$A_t=\left[\begin{array}{cccc}\hfill a_{[1,1,t]}\hfill & \hfill a_{[1,2,t]}\hfill & \hfill \cdots \hfill & \hfill a_{[1,n_s,t]}\hfill \\ \hfill a_{[2,1,t]}\hfill & \hfill a_{[2,2,t]}\hfill & \hfill \cdots \hfill & \hfill a_{[2,n_s,t]}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill a_{[n_s,1,t]}\hfill & \hfill a_{[n_s,2,t]}\hfill & \hfill \cdots \hfill & \hfill a_{[n_s,n_s,t]}\hfill \end{array}\right],$$ (7)

where a_[i,j,t] is the proportion of the cohort that transitions from state i to state j between cycles t – 1 and t, generated via

$$a_{[i,j,t]}=m_{[t-1,i]}{p}_{[i,j,t-1]}\text{for}t=1,\dots ,(n_t-1),$$ (8)

where m_[t–1,i] is the proportion of the cohort in state i at cycle t – 1 and p_[i,j,t–1] the corresponding transition probability of transitioning from state i to state j at the end of cycle t – 1. In other words, A stores the transition dynamics of a simulated cohort in a cSTM.

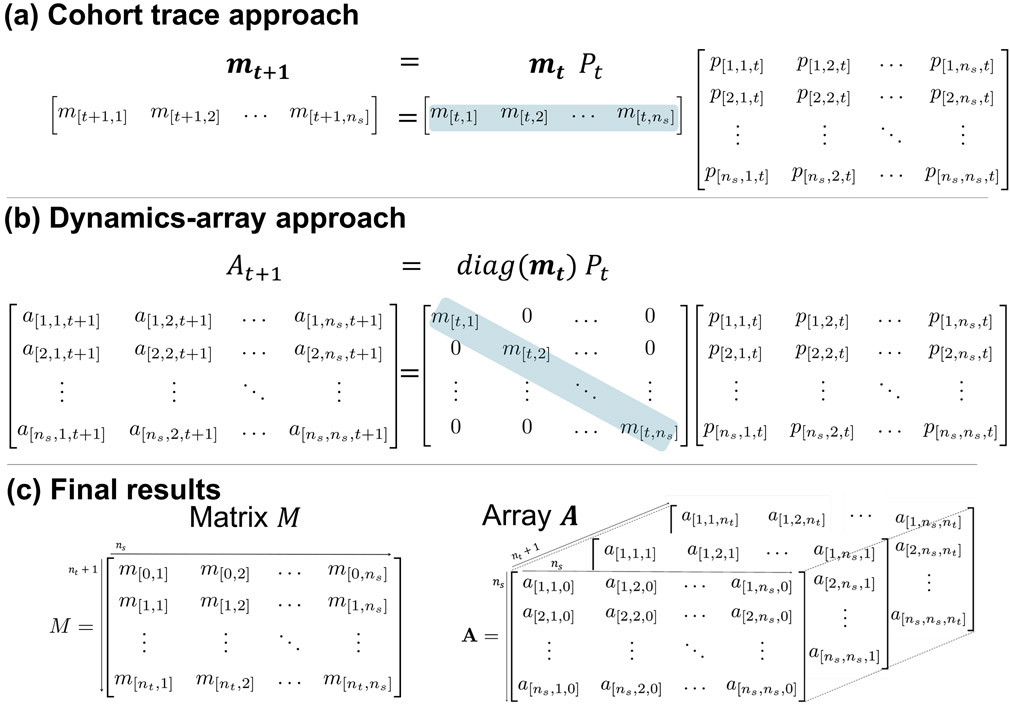
Figure 1 presents graphically the computation involved in both the traditional cohort trace approach (a) and the dynamics-array approach (b) and shows the structures of the resulting cohort trace M and dynamics-array A (c).

Figure 1:

(a) The cohort trace approach computes each row vector m_t+1 of the cohort trace M, where m_t+1 describes the distribution of the simulated cohort among the different health states at time t + 1. m_t+1 results from multiplying the state vector m_t (gray) by the transition probability matrix P_t. (b) The dynamics-array approach computes matrix A_t+1 containing information regarding the transition dynamics of the simulated cohort at time t + 1. The state vector m_t is highlighted (gray) to emphasize that the information in both approaches is identical. (c) Shows the resulting matrix M and array A of the approaches (a) and (b), respectively.

In R, it takes only a few lines of code to generate A complementary to M (Box 1).

Box 1: R code to iteratively generate the cohort trace M and the dynamics array A.

1 for (t in 1:n.t) {  # loop through the number of cycles
2   m_M [t + 1, ]     <- m_M [t, ] %*% m_P          # estimate the state vector for the next cycle (t + 1)
3   a_A [, , t + 1]   <- diag (m_M [t, ]) %*% m_P   # estimate the transition dynamics at t + 1
4 }

The cohort trace M can be computed from A by obtaining the t-th row of M, m_t, summing each of the columns of A_t as follows:

$${\mathbf{m}}_t=1^T{\mathbf{A}}_t=\left[\sum _{i=1}^{n_s}{a}_{[i,1,t]},\sum _{i=1}^{n_s}{a}_{[i,2,t]},\dots ,\sum _{i=1}^{n_s}{a}_{[i,n_s,t]}\right],$$ (9)

where 1 is a vector of ones of dimension n_s × 1. Although M can be obtained from A, we prefer to compute both M and A simultaneously. Once generated, both M and A can be exported as data objects that contain all the information about the cSTM dynamics, which can then be used in future calculation of outcomes of interest.

Applying state and transition rewards

One of the main advantages of A over M is the ability to incorporate transition rewards. Here, we demonstrate how to apply both state and transition rewards (e.g. utilities or cost) to the cSTM by using the dynamics array, A. Let R_t be a reward matrix of dimensions n_s × n_s that contains both state and transition rewards:

$$R_t=\left[\begin{array}{cccc}\hfill r_{[1,1,t]}\hfill & \hfill r_{[1,2,t]}\hfill & \hfill \cdots \hfill & \hfill r_{[1,n_s,t]}\hfill \\ \hfill r_{[2,1,t]}\hfill & \hfill r_{[2,2,t]}\hfill & \hfill \cdots \hfill & \hfill r_{[2,n_s,t]}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill r_{[n_s,1,t]}\hfill & \hfill r_{[n_s,2,t]}\hfill & \hfill \cdots \hfill & \hfill r_{[n_s,n_s,t]}\hfill \end{array}\right],$$ (10)

where r_[i,j,t] is the reward associated with transitioning from state i to state j at the end of cycle t. When j = i, r_[i,i,t] is the reward associated with staying in the i^th health state at cycle t. That is, the off-diagonal entries of R_t store the transition rewards and the diagonal of R_t stores the state rewards for cycle t. Note that if R_t is equal for all t times (i.e., neither state nor transition rewards vary over time), equation (10) becomes a time-homogeneous rewards matrix, where R_t = R.

The state and transition rewards can be applied to the model dynamics by element-wise multiplication between A_t and R_t, indicated by the ⊙ sign, which produces the matrix of outputs at cycle t, Y_t. Formally,

$$Y_t=A_t\odot R_t.$$ (11)

With this approach, the state rewards are accounted for at the beginning of the cycle and the transition rewards -assumed to happen at the end of the cycle- are accounted for at the next cycle.

In R, applying these rewards required one additional line of code compared to Box 1, as shown in line 5 of Box 2.

Box 2: R code to apply time-invariant state and transition rewards to the model dynamics stored in array A.

1 for (t in 1:n.t) { # loop through the number of cycles
2   m_M [t + 1, ] <- m_M [t, ] %*% m_P         # estimate the state vector for the next cycle (t + 1)
3   a_A [, , t +1] <- diag (m_M [t, ]) %*% m_P # estimate the transition dynamics at t + 1
4   # element-wise-multiplication of array A with the rewards matrices to apply both state and transition rewards
5   a_Y [, , t + 1] <- a_A [, , t + 1] * m_R
6 }

The total rewards for each health state at cycle t, r_t, is obtained by summing the rewards across all j = 1,…, n_s health states.

$${\mathbf{r}}_t=1^T{Y}_t=\left[\sum _{i=1}^{n_s}{Y}_{[i,1,t]},\sum _{i=1}^{n_s}{Y}_{[i,2,t]},\dots ,\sum _{i=1}^{n_s}{Y}_{[i,n_s,t]}\right].$$ (12)

Implementation in R using an illustrative example

To facilitate the implementation of the dynamics-array approach, we demonstrate its use with a stylistic healthy-sick-dead 3-state time-homogeneous cSTM example coded in R.[10] The model is used to simulate a cohort of 70-year-old individuals to compute their expected costs and quality-adjusted life years (QALYs) accrued over their remaining lifetime accounting for several transition rewards. Accounting for transition rewards with the traditional cohort trace approach is possible, however this requires creating additional temporary health states that keep track of the transitions. For our simple 3-state model this already requires two additional temporary states. In more complex models, accounting for transition rewards will result in state explosion and consequently, it is more likely to make errors while coding these models. The explanation of the state expansion and the R code for the traditional cohort trace approaches for our stylistic model can be found in the supplementary material and on GitHub (https://github.com/DARTH-git/state-transition-model-dynamics). GitHub also provides some code that shows that both approaches give identical results.

Comparison of methods using a simulation study

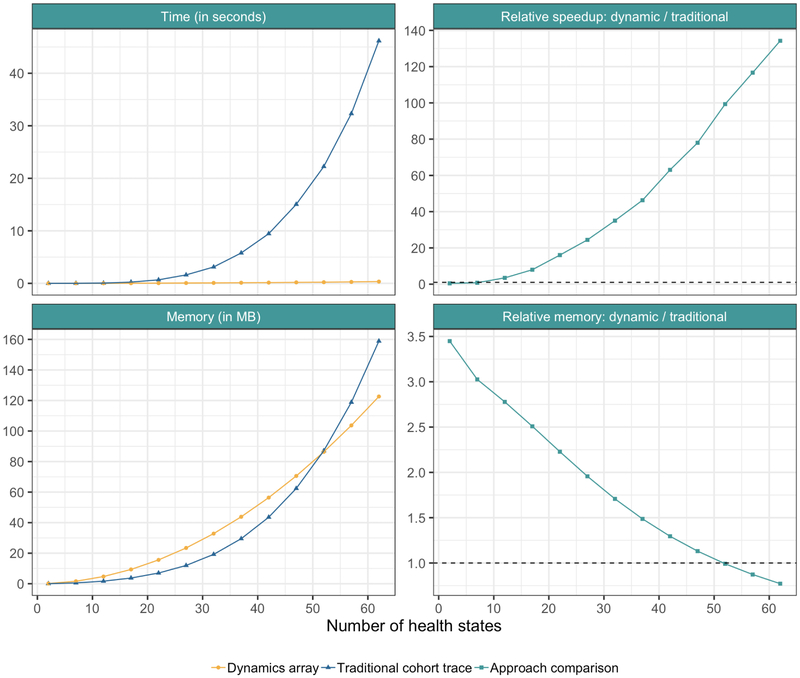
We conducted a simulation study to compare the computation time and memory requirements of the dynamics-array and traditional cohort trace approaches. We created a full factorial (13 × 110) design of experiment with the number of health states (from 2 to 62 with increments of 5 states) and the number of cycles (from 12 to 1320 with increments of 12 cycles) in a cSTM as the factors of the simulation study. We ran this full factorial experiment 10 times and took the average of the required time and memory to smooth out the variations in the computation time of R. Correcting for variation in R computation time is important, because the total required time is small (<50 seconds) and even a small variation (e.g. 3-5 seconds) could affect our results. Figure 2 shows that the dynamics-array approach is both faster (140-times with 62 health states, top part Figure 2) and requires less memory than the traditional cohort trace approach as the number of states increases (bottom part Figure 2). A more detailed description of the output of the simulation study is included in the supplementary material and the code is available on GitHub.

Figure 2:

Computation time and memory storage of the two approaches as a function of the number of states when running the model for 1,320 cycles. The top left panel shows the absolute computation time in seconds of both approaches. The top right panel shows the relative speedup of the dynamics-array approach compared to the traditional cohort trace approach. The horizontal line at y-axis equals 0 indicates when the two approached are equally fast. The bottom left panel shows the absolute memory storage in megabytes (MB) of the two approached, while the bottom right panel shows the relative required memory of the dynamics-array approach compared to the traditional cohort trace approach. The horizontal line at y-axis equals 1 indicate when both approached required the same memory storage. Above the line the traditional cohort trace requires less memory, while below the line the dynamics-array approach requires less memory. All results are based on the average of 10 simulations. This was done to smooth out the variations caused by the computation time of R.

Estimation of epidemiological measures

By obtaining A, it is possible to compute epidemiological outcomes that otherwise would not have been easily derived from M. For example, obtaining incidence and lifetime risk from M would require creating additional steps, variables or health states. Epidemiological outcomes could be used as outputs of simulation models for calibration or validation purposes. A full exposition of computing epidemiological measures from A is case-specific and is beyond the scope of this brief report. However, we illustrate the potential application of our approach with an example below.

Consider a cSTM with n_s > 3 health states. We are interested in calculating a ratio e_t of those that transition from health state 2 to health state n_s at cycle t to those that make the transition to health state n_s from health states 1, 2 and 3. Using the dynamics-array approach, the ratio e_t can be computed as

$$e_t=\frac{a_{[2,n_s,t]}}{a_{[1,n_s,t]}+a_{[2,n_s,t]}+a_{[3,n_s,t]}}\text{for}t=1,\dots ,n_t.$$ (13)

With the traditional cohort trace approach, calculating this ratio would require adding three temporary health states to distinguish those that transition to n_s from the health states 1, 2 and 3.

Discussion

We propose a multidimensional-array approach to overcome a limitation of the cohort trace produced by cSTM in not being able to store transition dynamics. The practical application of our approach involves adding a simple step to the traditional cohort trace approach that stores all transitions among health states over time in multidimensional array A. We described the multidimensional-array approach for a general cSTM where transitions are allowed from any state to others within a cycle, but our approach can also be applied to models that only allow one-state transition in a cycle (i.e., where the p_i,j,t are zero for those transitions that are not allowed).

Traditionally, researchers have dealt with this limitation of the cSTM cohort trace by creating temporary health states that collect the state-to-state transition information. However, as we showed in our method comparison section, this solution can quickly complicate a model and result in an explosion of the number of health states. Using an individual-based microsimulation STM is another alternative [1], with considerable implications on computational time.[11]

Another method that explicitly keeps track of state-to-state transitions is through a discretely integrated condition-event (DICE) simulation.[8, 7] DICE is a modeling technique that can free up some of the Markov restrictions that makes it possible to explicitly include many events occurring at various times. Although DICE simulation is a well-structured method, and the authors of the DICE papers provided very useful supplementary files to apply the method, we see the dynamics-array approach as a relatively simpler method to compute than DICE to overcome the limitation of the cohort trace on applying transition rewards and generating all the epidemiological outcomes of interest.

A potential limitation of the use of A is the additional computation needed when building the model. However, for many applications this may be a minor limitation given the matrix-based computational efficiency of current computers. Another potential limitation is the additional storage memory required to store A, which could become a limitation in systems with limited memory. This could be an issue for computationally complex models with multiple states. However, the benefit of using A for large models is that all the complexity in the model dynamics is summarized into a compact structure which makes it relatively simple to extract information or to apply new rewards without re-running the model.

In conclusion, structuring the output of cSTMs using the dynamics-array is an efficient, simple and convenient approach to summarize the model dynamics. This simple structure allows applying state and transition rewards and obtaining epidemiological measures, while still being able to obtain and display the conventional cohort trace.