Pinching a glass reveals key properties of its soft spots

Significance

Glasses form when liquids are quickly cooled. Many of the properties of glasses are universal—i.e., independent of their composition and the liquid-phase temperature $T_p$ from which they were cooled. One such property is the existence of noncrystalline soft vibrational excitations, which are highly localized in space and follow a universal vibrational frequency distribution, with a nonuniversal coefficient. We show that pinching glasses—i.e., applying local force perturbations to them—reveals dramatic variability in the physics of this coefficient with $T_p$. In particular, it reveals how the number of noncrystalline soft vibrational excitations, their size, and typical degree of softness vary with $T_p$, having major implications for the behavior of glasses in a wide variety of situations.

Abstract

It is now well established that glasses feature quasilocalized nonphononic excitations—coined “soft spots”—, which follow a universal ${\omega }^4$ density of states in the limit of low frequencies $\omega$. All glass-specific properties, such as the dependence on the preparation protocol or composition, are encapsulated in the nonuniversal prefactor of the universal ${\omega }^4$ law. The prefactor, however, is a composite quantity that incorporates information both about the number of quasilocalized nonphononic excitations and their characteristic stiffness, in an apparently inseparable manner. We show that by pinching a glass—i.e., by probing its response to force dipoles—one can disentangle and independently extract these two fundamental pieces of physical information. This analysis reveals that the number of quasilocalized nonphononic excitations follows a Boltzmann-like law in terms of the parent temperature from which the glass is quenched. The latter, sometimes termed the fictive (or effective) temperature, plays important roles in nonequilibrium thermodynamic approaches to the relaxation, flow, and deformation of glasses. The analysis also shows that the characteristic stiffness of quasilocalized nonphononic excitations can be related to their characteristic size, a long sought-for length scale. These results show that important physical information, which is relevant for various key questions in glass physics, can be obtained through pinching a glass.

Understanding the micromechanical, statistical, and thermodynamic properties of soft, nonphononic excitations in structural glasses remains one of the outstanding challenges in glass physics, despite decades of intensive research (1–19). Soft, nonphononic excitations are believed to give rise to a broad range of glassy phenomena, many of which are still poorly understood; some noteworthy examples include the universal thermodynamic and transport properties of glasses at temperatures of 10 K and lower (2, 4, 20–22); the low-temperature yielding transition in which a mechanically loaded brittle glass fails via the formation of highly localized bands of plastic strain (23, 24); and anomalous, non-Rayleigh wave-attenuation rates (25–27).

Computational studies have been invaluable in advancing our knowledge about the statistical and mechanical properties of soft, glassy excitations and in revealing the essential roles that these excitations play in various glassy phenomena. Schober and Laird (28, 29) were the first to reveal the existence of soft spots in the form of low-frequency, quasilocalized vibrational modes in a model computer glass. Soon later, Schober et al. (30) showed that relaxation events deep in the glassy state exhibit patterns that resemble quasilocalized modes (QLMs), suggesting a link between soft, glassy structures and dynamics. In an important subsequent work (31), this link was further strengthened by showing that relaxational dynamics in supercooled liquids strongly correlates with quasilocalized, low-frequency vibrational modes measured in underlying inherent states. Some years later, it was shown that plastic activity in model structural glasses and soft-sphere packings is intimately linked to nonphononic, low-frequency modes (32–34).

It was, however, only recently that the universal statistical and structural properties of soft QLMs in glasses were revealed, first in a Heisenberg spin glass in a random field (35), and later in model structural glasses (13, 14, 36–38). It is now well accepted that the density of nonphononic QLMs of frequency $\omega$ grows from zero (i.e., without a gap) as ${\omega }^4$, independently of microscopic details (13), preparation protocol (15), or spatial dimension (14). Importantly, as shown in ref. 38 and demonstrated again in this work, the ${\omega }^4$ distribution of QLMs persists, even in inherent states that underlie very deeply supercooled states—i.e., in stable computer glasses whose stability is comparable to conventional laboratory glasses. Furthermore, soft QLMs have been shown to generically feature a disordered core of linear size of a few particle spacings, decorated by long-range, Eshelby-like displacement fields, whose amplitude decays as $r^{1-d-}$ at a distance $r$ from the core, in $d-$ spatial dimensions (13, 14).

The key challenge in revealing the statistical, structural, and energetic properties of soft QLMs in computer investigations lies in the abundance of spatially extended low-frequency phonons in structural glasses (36, 39). These phononic excitations hybridize with quasilocalized excitations, as pointed out decades ago by Schober and Oligschleger (40). These hybridization processes hinder the accessibility of crucial information regarding characteristic length and frequency scales of QLMs and regarding their prevalence.

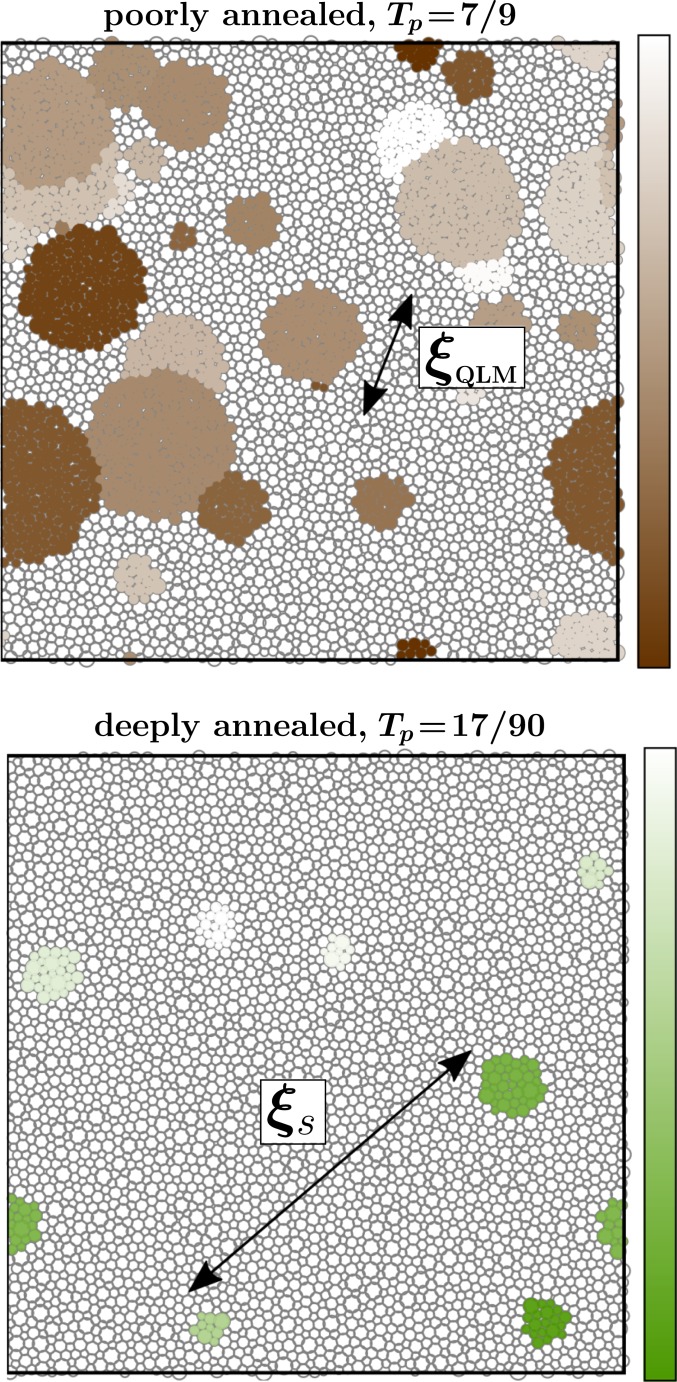
While promising attempts to overcome the aforementioned hybridization issues have been put forward (36, 40–42), a complete statistical–mechanical picture of QLMs is still lacking. In particular, recent work has revealed that annealing processes affect QLMs in three ways: Firstly, the number of QLMs appears to decrease upon deeper annealing—i.e., they are depleted—as first pointed out in refs. 15 and 43. Secondly, the core size of QLMs, ${\xi }_{\mathrm{Q}\mathrm{L}\mathrm{M}}$, was shown to decrease with deeper annealing (13, 44). Lastly, in refs. 13 and 15, it was shown that the characteristic frequencies of QLMs also increase upon deeper annealing—i.e., they stiffen—in addition to their depletion. These three effects, and other concepts discussed below, are graphically illustrated in Fig. 1.

Fig. 1.

A graphical representation of the population of QLMs in poorly annealed (Upper) and deeply annealed (Lower) two-dimensional computer glasses. Each blob represents a QLM; its size is proportional to our estimation of the mode’s core size ${\xi }_{\mathrm{Q}\mathrm{L}\mathrm{M}}$, and the color code represents the mode’s frequency, decreasing from bright to dark; the Upper (Lower) color code range is [0.18, 0.42] $\left(\left[0.54,0.74\right]\right)$, expressed in terms of $c_{\infty }/a_0$, with $c_{\infty }$ being the high-$T_p$ shear wave speed, and $a_0$ is the interparticle distance. The typical distance between QLMs, ${\xi }_s$, is also marked. Details of the calculation can be found in SI Appendix. Note that the deeply annealed case shown in Lower might be representative of laboratory molecular or metallic glasses.

In this work, we investigate the effect of very deep supercooling/annealing on the statistical, structural, and energetic properties of QLMs in a model computer glass (see Materials and Methods for details). First, we explain why information regarding the number of QLMs cannot typically be obtained from the universal vibrational density of states (vDOS) of QLMs alone. Instead, we show that the vDOS grants access to a composite physical observable, which encodes information regarding both the characteristic frequency scale of QLMs, ${\omega }_g$, and their number, $\mathcal{N}$. Then, following recent suggestions (15, 45), we use the average response of the glass to a local pinch—more formally, we use the bulk-average response of a glass to force dipoles—as a measure of ${\omega }_g$. This assumption, in turn, allows us to quantitatively disentangle the processes of annealing-induced stiffening of QLMs from their annealing-induced depletion.

Interestingly, this analysis reveals that $\mathcal{N}$ follows an equilibrium-like Boltzmann relation $\mathcal{N}\propto \exp \left(-\frac{E_{\mathrm{Q}\mathrm{L}\mathrm{M}}}{k_B{T}_p}\right)$, with $T_p$ denoting the parent temperature from which glassy states are quenched, $k_B$ is Boltzmann’s constant, and $E_{\mathrm{Q}\mathrm{L}\mathrm{M}}$ is the energetic cost of creating a QLM. That is, our results indicate that QLMs behave as “quasiparticles,” whose number is determined by equilibrium statistical thermodynamics at the parent equilibrium temperature $T_p$, and that this number is preserved when the glass goes out-of-equilibrium during a quick quench to a temperature much smaller than $T_p$. The QLMs thus appear to correspond to configurational degrees of freedom that carry memory of the equilibrium state at $T_p$, deep into the nonequilibrium glassy state, and, in this sense, $T_p$ has a clear thermodynamic interpretation as a nonequilibrium temperature. This physical picture has been, for quite some time, the cornerstone of the nonequilibrium thermodynamic Shear-Transformation-Zones (STZs) theory of glass deformation (46–48), where $T_p$ is termed a fictive/effective/configurational temperature, once QLMs are identified with STZs, i.e., with glassy “flow defects” (49).

Furthermore, we show that ${\omega }_g$ can be used to define a length that appears to match the independently determined core size of QLMs, argued to mark the cross-over between the disorder-dominated elastic response of glasses at the mesoscale and the continuum-like elastic response at the macroscale (50). Taken together, these results show that important physical information, which is relevant for various key questions concerning the formation, relaxation, and flow of glasses, can be obtained through pinching a glass.

The QLMs Depletion vs. Stiffening Conundrum

It is now established that the vDOS of QLMs, $\mathcal{D}\left(\omega \right)$, follows a universal gapless law (13, 14, 36–38)

$$\mathcal{D}\left(\omega \right)=A_g\hspace{0.17em}{\omega }^4\hspace{1em}\hspace{1em}\text{for}\hspace{1em}\hspace{1em}0\le \omega \le {\omega }_g,$$ [1]

where ${\omega }_g$ is the upper cutoff of this scaling regime, and the prefactor $A_g$ is extensively discussed below. The ${\omega }^4$ law has been rationalized by various models (1–4, 16–19) and is known to be intimately related to the existence of frustration-induced internal stresses in glasses (44), but its theoretical foundations are not yet fully developed. The prefactor $A_g$ in Eq. 1 (denoted by $A_4$ in refs. 18, 38, and 51) is a nonuniversal quantity that encodes information about a particular glassy state, most notably its composition (constituent elements, interaction potential, etc.) and its preparation protocol (15, 38, 43). The ultimate goal of this work is to explore the physical information encapsulated in $A_g$ and its dependence on the glass-preparation protocol.

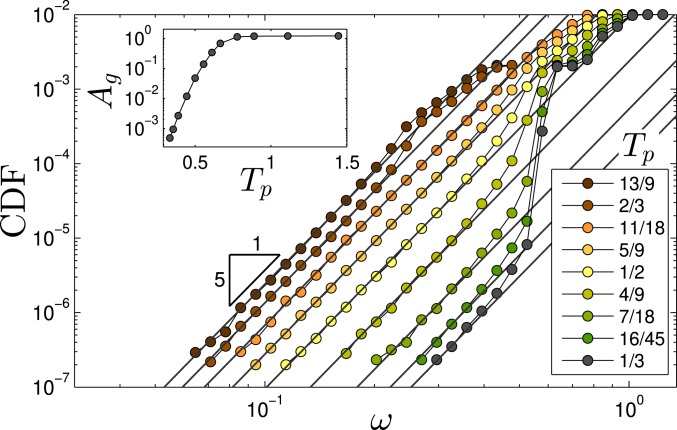
In Fig. 2, we plot the cumulative vDOS calculated for glassy samples rapidly quenched from parent equilibrium temperatures $T_p$ (as appears in the figure legend) to zero temperature. The system size was chosen so as to avoid hybridization with phonons at the lowest frequencies, as explained in ref. 13. The figure shows, in agreement with ref. 38, that the ${\omega }^4$ scaling persists all the way down to the deepest supercooled states accessible to us, $T_p=1/3$ (the units used to report $T_p$ are defined below). Fig. 2, Inset shows that the prefactor $A_g$ varies by nearly three orders of magnitude in the simulated $T_p$ range. The huge variability of $A_g$ with the preparation protocol, here quantified by the parent equilibrium temperature $T_p$, indicates dramatic changes in the resulting glassy states, despite the fact that all of them follow the universal ${\omega }^4$ law.

Fig. 2.

Cumulative density of states $\text{CDF}\equiv {\int }_0^{\omega }\mathcal{D}\left(\omega \prime \right)d\omega \prime$ for various parent temperatures $T_p$ (see values in the legend). Here, we present data measured in 10,000 glassy samples of N = 2,000 particles for $T_p\le 11/18$ and 2,000 samples of N = 16,000 particles for $T_p>11/18$. (Inset) The prefactors $A_g$ vs. $T_p$; see text for discussion.

What physics is encapsulated in $A_g$? To start addressing this question, let us first consider the dimensions of $A_g$. When $\mathcal{D}\left(\omega \right)$ is integrated over the frequency range in which Eq. 1 is valid—i.e., in the range $0\le \omega \le {\omega }_g$—one obtains an estimate for the total number of QLMs, $\mathcal{N}$. Consequently, $A_g$ has the dimensions of an inverse frequency to the fifth power, where the dimensionless prefactor is proportional to $\mathcal{N}$. Since $\mathcal{D}\left(\omega \right)$ follows a power law—i.e., it is scale-free in the range $0\le \omega \le {\omega }_g$—the only possible frequency scale that can appear in it is the upper cutoff ${\omega }_g$. Hence, we expect to have $A_g\sim \mathcal{N}{\omega }_g^{-5}$, which implies that Eq. 1 should be rewritten as

$$\mathcal{D}\left(\omega \right)\sim \mathcal{N}\hspace{0.17em}{\omega }_g^{-5}{\omega }^4\hspace{1em}\hspace{1em}\text{for}\hspace{1em}\hspace{1em}0\le \omega \le {\omega }_g.$$ [2]

We would like to note the analogy, and the fundamental difference, between Eq. 2 and Debye’s vDOS of (acoustic) phononic excitations in crystalline solids (52). The latter takes the form $D\left(\omega \right)=A_D\hspace{0.17em}{\omega }^2$ (in three dimensions), with $A_D=9N/{\omega }_D^3$, where ${\omega }_D$ is Debye’s frequency and $N$ is the number of particles. The integral over $D\left(\omega \right)$ in the range $0\le \omega \le {\omega }_D$ equals the number of degrees of freedom in the system, $3N$. The analogy between Debye’s vDOS and the glassy vDOS in Eq. 2, and between ${\omega }_g$ and Debye’s frequency, is evident. Yet, there is a crucial difference between the two cases; in Debye’s theory, the number of phononic excitations is a priori known to equal the number of degrees of freedom $3N$ (in fact, ${\omega }_D$ is precisely defined so as to ensure the latter). In the glassy case, however, there is neither an a priori constraint on the number of QLMs $\mathcal{N}$, nor on the upper-frequency cutoff ${\omega }_g$ (the total number of vibrational modes, both glassy and phononic, is, of course, still determined by the total number of degrees of freedom, but there is no a priori constraint on the fraction of QLMs out of the total number of vibrational modes). Hence, $\mathcal{N}$ and ${\omega }_g$ should be treated as independent quantities that can feature different dependencies on the glass history (preparation protocol).

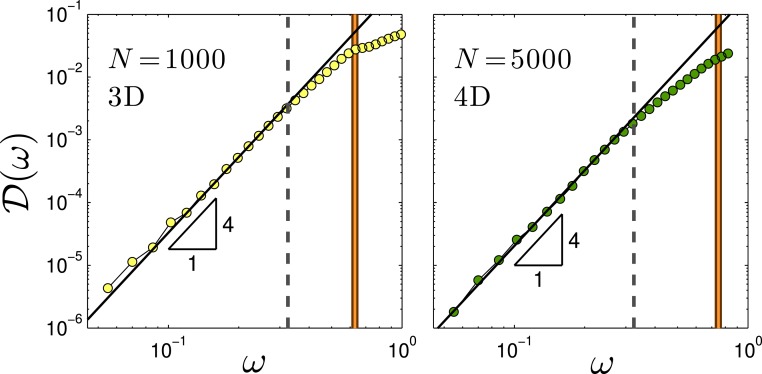
In order to disentangle the number of QLMs ($\mathcal{N}$) and their characteristic frequency (${\omega }_g$) contributions to $A_g\sim \mathcal{N}{\omega }_g^{-5}$, one needs to estimate one of them—i.e., either $\mathcal{N}$ or ${\omega }_g$—independently of $A_g$. In principle, as the characteristic frequency ${\omega }_g$ represents the upper cutoff on the ${\omega }^4$ scaling regime (as explained above), one can try to estimate it through the deviation from the universal ${\omega }^4$ law. This has been, in fact, demonstrated in ref. 14 for rapidly quenched glassy samples in a narrow range of system sizes, in three and four dimensions. Some of the data appearing in figure 2 b and c of ref. 14 are reproduced here in Fig. 3, where the lowest phononic band is shown in orange in each graph. It is observed that, in these examples, the vDOS deviates from the ${\omega }^4$ scaling at a frequency smaller than the lowest phonon frequency, which can be identified with ${\omega }_g$ (marked by the vertical dashed lines).

Fig. 3.

The vDOS $\mathcal{D}\left(\omega \right)$ of small glassy samples (the number of particles $N$ is specified in each graph) in three dimensions (3D; Left) and four dimensions (4D; Right), obtained by a rapid quench in ref. 14. The data are adapted from figure 2 b and c of ref. 14, where frequencies are normalized as detailed in SI Appendix. The vertical continuous lines indicate the position of the first phonon band, whereas the dashed lines mark the breakdown of the ${\omega }^4$ scaling regime.

In general, though, the lowest phonon frequency is, in fact, smaller than ${\omega }_g$, which obscures the identification of the latter due to hybridizations (39). Indeed, in Fig. 2, it is observed that, as $T_p$ decreases, the lowest phonon band pushes the vDOS upwards in the middle of the scaling regime, disallowing to extract ${\omega }_g$. Hence, we conclude that the vDOS alone does not allow one to distinguish between changes in the number of QLMs (e.g., a decrease, i.e., depletion) and in their characteristic frequency (e.g., an increase, i.e., stiffening). How to disentangle the $\mathcal{N}$ and ${\omega }_g$ dependence of $A_g$, and the possible depletion and stiffening of QLMs associated with them, is the question we address next.

Estimating QLMs’ Frequency Scale by Pinching a Glass

The previous discussion showed that the $T_p$ dependence of $A_g\sim \mathcal{N}{\omega }_g^{-5}$ cannot be readily used to extract the $T_p$ dependence of $\mathcal{N}$ and ${\omega }_g$ separately. Consequently, one needs additional physical input in order to disentangle the two quantities. Here, we follow the suggestion put forward in ref. 15 that the characteristic frequency ${\omega }_g$ of QLMs can be probed through pinching a glass. Formally, by pinching, we mean applying a force dipole ${\mathit{d}}^{\left(ij\right)}$ to a pair of interacting particles $i,j$ in a glassy sample. The displacement response to ${\mathit{d}}^{\left(ij\right)}$, which was shown to closely resemble the spatial pattern of QLMs (15), can be associated with a frequency ${\omega }_g^{\left(ij\right)}$ (see additional details in SI Appendix). By averaging ${\omega }_g^{\left(ij\right)}$ over many interacting pairs $i,j$ in a glassy sample, one obtains a characteristic frequency scale, which was proposed to represent ${\omega }_g$. This suggestion was discussed at length and tested, under various circumstances, in ref. 15; here, we follow it—i.e., assume that the $T_p$ dependence of the dipole response is proportional to ${\omega }_g\left(T_p\right)$. The remainder of the paper is devoted to exploring the implications of this assumption.

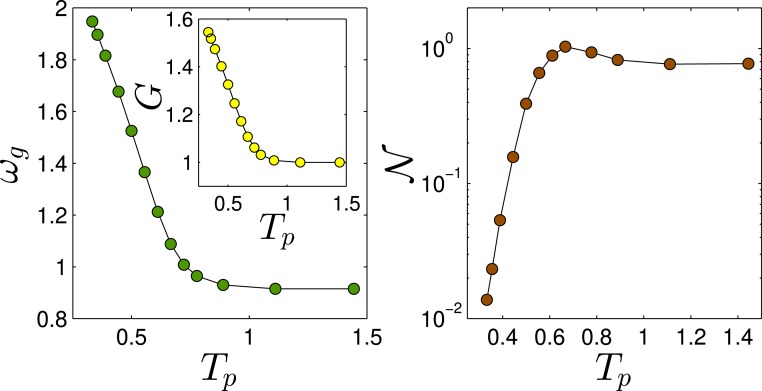
In Fig. 4, Left, we plot the characteristic frequency ${\omega }_g$ vs. the parent temperature $T_p$, where ${\omega }_g\left(T_p\right)$ is estimated by the pinching procedure just described. It is observed that ${\omega }_g$ varies by nearly a factor of two at low parent temperatures $T_p$ and reaches a plateau at higher $T_p$. We further find that the sample-to-sample mean athermal shear modulus, $G$, shown in Fig. 4, Left, Inset, also plateaus at the same $T_p$ as ${\omega }_g$ does. Consequently, in what follows, we conveniently express temperatures in terms of the onset temperature $T_{\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{e}\mathrm{t}}$ of the high-$T_p$ plateaus of $G$ and ${\omega }_g$.

Fig. 4.

(Left) The characteristic frequency ${\omega }_g$ of QLMs, estimated by the pinching procedure discussed in the text, plotted vs. the parent temperature $T_p$. (Left, Inset) The sample-to-sample mean athermal shear modulus, $G$, plotted against $T_p$. (Right) $\mathcal{N}$ is proportional to the number of QLMs and is plotted here against $T_p$.

We conclude that, in the $T_p$ range considered here, QLMs appear to stiffen by a factor of approximately two with decreasing $T_p$. Interestingly, in ref. 38, it was reported that the boson peak frequency ${\omega }_{\mathrm{B}\mathrm{P}}$ varies by approximately a factor of two over a similar range of $T_p$, suggesting that ${\omega }_{\mathrm{B}\mathrm{P}}$ and ${\omega }_g$ might be related. In ref. 45, a similar proposition was put forward in the context of the unjamming transition (53–55), where it was argued that the renowned “unjamming” frequency scale ${\omega }_{*}$ (5, 53) can be extracted by considering the frequencies associated with the responses to a local pinch. However, since ${\omega }_{*}$ and ${\omega }_{\mathrm{B}\mathrm{P}}$ may differ (10), it is not currently clear which of these frequencies is better represented by ${\omega }_g$.

The stiffening of QLMs by a factor of approximately two accounts for an approximate 30-fold variation of $A_g$, due to the ${\omega }_g^{-5}$ dependence in Eq. 2. The remaining variation is attributed to the number of QLMs, $\mathcal{N}=A_g\hspace{0.17em}{\omega }_g^5$ (note that here, we use an equality, as the $T_p$-independent prefactor is of no interest), plotted in Fig. 4, Right. The result indicates that QLMs are depleted by slightly less than two orders of magnitude in the simulated $T_p$ range. The strong depletion of QLMs upon deeper supercooling has dramatic consequences for the properties of the resulting glassy states. For example, brittle failure (56, 57) and reduced fracture toughness (58–60) are claimed to be a consequence of this depletion. It is interesting to note that the range of variability observed in Fig. 4, Right appears to be consistent with a very recent study (61) of the depletion of tunneling two-level systems in stable computer glasses, possibly indicating that a subset of the QLMs is associated with tunneling two-level systems (1, 2, 36, 62).

The results presented in Fig. 4 demonstrate that pinching a glass may offer a procedure to separate the depletion and stiffening processes that take place with progressive supercooling. Next, we aim at exploring the physical implications of disentangling $\mathcal{N}$ and ${\omega }_g$.

A Thermodynamic Signature of the QLMs

QLMs correspond to compact zones (though they also have long-range elastic manifestations), which are embedded inside a glass, and characterized by particularly soft structures. It is tempting, then, to think of them as quasiparticles that feature well-defined properties (e.g., formation energy). If true, one may hypothesize that QLMs can be created and annihilated by thermodynamic fluctuations and follow an equilibrium distribution at the parent equilibrium temperatures $T_p$. Moreover, their equilibrium thermodynamic nature might be manifested in nonequilibrium glassy states as they become frozen in during the rapid quench upon glass formation.

As we have now at hand an estimate of the number $\mathcal{N}$ as a function of $T_p$ (cf. Fig. 4, Right), we can start testing these ideas. To this aim, we plot in Fig. 5 $\mathcal{N}$ vs. $T_p^{-1}$ on a semilogarithmic scale; the outcome reveals a key result: the number of QLMs follows a Boltzmann-like law, with the parent temperature $T_p$ playing the role of the equilibrium temperature, namely,

$$\mathcal{N}\propto \exp \hspace{0.17em}\left(-\frac{E_{\mathrm{Q}\mathrm{L}\mathrm{M}}}{k_B\hspace{0.17em}{T}_p}\right).$$ [3]

A possibly related Boltzmann-like law, albeit for $A_g\left(T_p\right)$ itself, was observed in ref. 51 for reheated stable glasses (63). A corollary of Eq. 3 is that QLMs seem to feature a well-defined formation energy, $E_{\mathrm{Q}\mathrm{L}\mathrm{M}}\approx 3.3$ (in units of $k_B{T}_{\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{e}\mathrm{t}}$). It is surprising that $E_{\mathrm{Q}\mathrm{L}\mathrm{M}}$ appears to be independent of $T_p$, while the characteristic energy scale associated with ${\omega }_g$ does appear to depend on it. Future research should shed additional light on this nontrivial observation.

Fig. 5.

The density of QLMs, plotted against $1/T_p$, revealing that it is controlled by a Boltzmann-like factor $e^{-E_{\mathrm{Q}\mathrm{L}\mathrm{M}}/k_B{T}_p}$, with the parent temperature playing the role of the equilibrium temperature. We find $E_{\mathrm{Q}\mathrm{L}\mathrm{M}}\approx 3.3$, expressed in terms of $k_B{T}_{\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{e}\mathrm{t}}$.

The results in Eq. 3 and Fig. 5 indicate that QLMs might indeed correspond to a subset of configurational degrees of freedom that equilibrate at the parent temperature $T_p$ and that carry memory of their equilibrium distribution when the glass goes out of equilibrium during a quench to lower temperatures. This physical picture strongly resembles the idea of a fictive/effective/configurational temperature, which was quite extensively used in models of the relaxation, flow, and deformation of glasses (46–48, 64–67). This connection is further strengthened in light of available evidence indicating that the cores of deformation-coupled QLMs are the loci of irreversible plastic events that occur once a glass is driven by external forces (68–70).

The Boltzmann-like relation in Eq. 3, when interpreted in terms of STZs, is a cornerstone of the nonequilibrium thermodynamic STZ theory of the glassy deformation (46–48), where $T_p$ is treated as a thermodynamic temperature that characterizes configurational degrees of freedom and that differs from the bath temperature. The strong depletion of STZs with decreasing $T_p$, as predicted by the Boltzmann-like relation, was shown to give rise to a ductile-to-brittle transition in the fracture toughness of glasses (58, 59). This prediction was recently supported by experiments on the toughness of bulk metallic glasses, where $T_p$ was carefully controlled and varied (60).

It is natural to define a length scale corresponding to the typical distance between QLMs as ${\xi }_s\sim {\mathcal{N}}^{-1/d-}$, once an estimate of their number $\mathcal{N}$ is at hand. Such a “site length” ${\xi }_s$ was introduced in ref. 13, where it was related to the sample-to-sample average minimal QLM frequency $⟨{\omega }_{min}⟩$, according to $⟨{\omega }_{min}⟩\sim {\omega }_g{\left(L/{\xi }_s\right)}^{-d-/5}$. The latter implies that the lowest QLM frequency is selected among ${\left(L/{\xi }_s\right)}^{d-}\propto \mathcal{N}\hspace{0.17em}N$ possible candidates, which is directly related to the extreme value statistics of ${\omega }_{min}$ (13). The site length ${\xi }_s$ is expected to control finite-size effects in studies of athermal plasticity in stable glasses, as discussed in detail in ref. 71. Similar definitions of a site length were proposed in refs. 71 and 72; an important message here is that the disentangling of the stiffening effect from the prefactor $A_g$ is imperative for the purpose of obtaining a consistent definition of a length scale in such a setting.

A Glassy Length Scale Revealed by Pinching a Glass

What additional physics can pinching a glass reveal? Up to now, we explored the physics of the QLMs number $\mathcal{N}$; we now turn to the other contribution to $A_g$, i.e., to the frequency scale ${\omega }_g$ that characterizes the typical stiffness of QLMs. ${\omega }_g$ was shown to undergo stiffening with decreasing $T_p$ (cf. Fig. 4, Left); is this stiffening related to other properties of QLMs that vary with $T_p$? An interesting possibility we explore here is whether it might be related to a glassy length scale that is associated with QLMs.

To that aim, we construct a length scale ${\xi }_g$ as

$${\xi }_g\equiv 2\pi \hspace{0.17em}{c}_s/{\omega }_g,$$ [4]

which corresponds to the wavelength of transverse phonons propagating at the shear wave-speed $c_s$ with an angular frequency ${\omega }_g$. This length is similar in spirit to the “boson peak” length ${\xi }_{\mathrm{B}\mathrm{P}}\sim c_s/{\omega }_{\mathrm{B}\mathrm{P}}$ (73). The physical rationale behind our constructed length ${\xi }_g$ is that the emerging length scale is expected to mark a cross-over in the elastic response of a glass to a local pinch, as discussed below. In Fig. 6, we plot ${\xi }_g$ vs. the parent temperature $T_p$; we find that ${\xi }_g$ decreases upon deeper annealing by ∼40%, a manifestation of the modest stiffening of the macroscopic shear modulus compared to that of QLMs (recall that $c_s$ is proportional to the square root of the shear modulus). This decreasing length is of unique character among the plethora of glassy length scales previously put forward in the context of the glass transition, most of which are increasing functions of decreasing temperature or parent temperature (74–79).

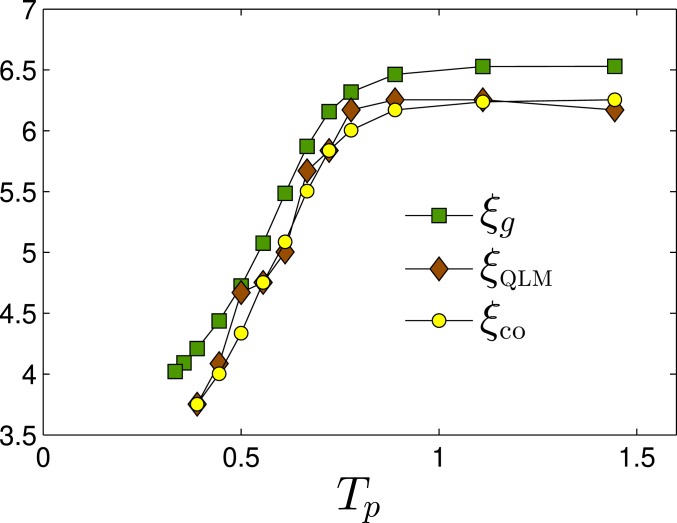
Fig. 6.

The glassy length ${\xi }_g$, the cross-over length ${\xi }_{\mathrm{c}\mathrm{o}}$, and the QLM core size ${\xi }_{\mathrm{Q}\mathrm{L}\mathrm{M}}$ (see SI Appendix for details), plotted against the parent temperature $T_p$. These lengths vary together with parent temperature $T_p$, supporting their equivalence.

In order to shed light on the physical meaning of ${\xi }_g$, we consider also $\left(i\right)$ the cross-over length ${\xi }_{\mathrm{c}\mathrm{o}}$, as observed in the displacement response to local pinches, between an atomistic-disorder-dominated response at distances $r\lesssim {\xi }_{\mathrm{c}\mathrm{o}}$ from the perturbation, to the expected continuum behavior seen at $r>{\xi }_{\mathrm{c}\mathrm{o}}$, and $\left(ii\right)$ the core size of QLMs, ${\xi }_{\mathrm{Q}\mathrm{L}\mathrm{M}}$, which is known to decrease upon annealing (38, 43, 44), as is also illustrated graphically in Fig. 1. In Fig. 6, we directly compare between ${\xi }_g$ and our measurements of ${\xi }_{\mathrm{c}\mathrm{o}}$ and ${\xi }_{\mathrm{Q}\mathrm{L}\mathrm{M}}$ (see SI Appendix for details). These three length scales feature very similar variations with $T_p$, strongly supporting their equivalence. Consequently, ${\xi }_g$—which was defined through the dipole response frequency ${\omega }_g$ (cf. Eq. 4)—seems to provide a measure of the core size of QLMs, and in light of the suggested relation between the latter and STZs, also of the size of STZs.

Additional insight may be gained by invoking the relation—established in ref. 45—between ${\omega }_g$ and the characteristic frequency ${\omega }_{*}$ that emerges near the unjamming transition (53–55). Indeed, in the unjamming scenario, the length ${\xi }_g$ (often denoted ${\ell }_c$) was shown to diverge upon approaching the unjamming point (50) and to mark the cross-over between disorder-dominated responses near a local perturbation and the continuum-like response observed in the far field, away from the perturbation. The same length was shown in ref. 80 to characterize the core size of QLMs near the unjamming point of harmonic-sphere packings. In light of the results shown in Fig. 6, we hypothesize that the fundamental cross-over length—below which responses to local perturbations are microstructural/disorder-dominated, and above which responses to local perturbations follow the expected continuum-like behavior—is, in fact, ${\xi }_g$, which, in turn, we show to agree well with the size of QLMs.

Summary and Outlook

In this work, we have employed a computer-glass model, which can be deeply annealed (81), to quantitatively study the variation of the properties of QLMs (soft spots) with the depth of annealing. Most notably, we calculated the variation of the number, characteristic frequency, and core size of QLMs with the parent temperature from which the glass is formed. This has been achieved by assuming that the characteristic frequency scale of QLMs can be estimated through the bulk-average response of a glass to a local pinch. This frequency scale, in turn, allowed us to disentangle the apparently inseparable effects of the depletion and stiffening of QLMs, which are both encoded in the prefactor of the universal ${\omega }^4$ vDOS of QLMs.

We found that the number of QLMs follows a Boltzmann-like factor, with the parent temperature—from which equilibrium configurations were vitrified—playing the role of the equilibrium temperature. Consequently, the parent temperature may be regarded as a nonequilibrium temperature that characterizes QLMs deep inside the glassy state. Furthermore, our analysis reveals that both the core size of QLMS and the mesoscopic length scale that marks the cross-over between atomistic-disorder-dominated responses near local perturbations, and continuum-like responses far away from local perturbations, can be estimated by using the characteristic frequency of QLMs—obtained by pinching the glass—and the speed of shear waves.

Our results may have important implications for various basic problems in glass physics. We mention a few of them here; first, the Boltzmann-like law of the number of QLMs may play a major role in theories of the relaxation, flow, and deformation of glasses and may support some existing approaches. Second, together with other available observations (38, 45, 80), our results may suggest that the boson-peak frequency could be robustly probed by pinching glassy samples, instead of the more involved analysis required otherwise (9, 38). Finally, the variation of the energy scale proportional to ${\omega }_g^2$ with annealing temperature appears to match very well the variation of activation barriers required to rationalize fragility measurements in laboratory glasses (compare Fig. 4, Left with figure 8 of ref. 82). If valid, our results appear to support elasticity-based theories of the glass transition (83–85) and indicate that QLMs play important roles in relaxation processes in deeply supercooled liquids (31). We hope that these interesting investigation directions will be pursued in the near future.

Materials and Methods

We employed a computer-glass-forming model in three dimensions, simulated by using the swap Monte Carlo method, explained, e.g., in ref. 81. The model consists of soft repulsive spheres interacting via a $\propto r^{-10}$ pairwise potential (with $r$ denoting the distance between the centers of a pair of particles), enclosed in a fixed-volume box with periodic boundary conditions. The particles’ sizes are drawn from a distribution designed such that crystallization is avoided (81). A comprehensive description of the model, and of all parameter choices, can be found in ref. 86, including an important discussion about how we handled large sample-to-sample realization fluctuations of particle sizes that can arise in small system sizes due to the breadth of the employed particle size distribution. Ensembles of 10,000; 1,000; and 2,000 glassy samples were made for systems of N = 2,000; 8,000; and 16,000 particles, respectively, by instantaneously quenching (to zero temperature) independent configurations equilibrated at various parent temperatures $T_p$. All data, except for those shown in Fig. 6, were calculated by using the smaller glasses. Lengths are expressed in terms of $a_0\equiv {\left(V/N\right)}^{1/\mathrm{\text{d}}-}$, where $V$ is the system’s volume. All particles share the same mass $m$, which we set as our microscopic unit of mass. Frequencies are expressed in terms of $c_{\infty }/a_0$, where $c_{\infty }\equiv \sqrt{G_{\infty }/\rho }$ is the high-$T_p$ shear wave speed, with $G_{\infty }$ denoting the high-$T_p$ sample-to-sample mean athermal shear modulus, and $\rho \equiv mN/V$ denoting the mass density. $T_p$ is expressed in terms of the cross-over temperature $T_{\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{e}\mathrm{t}}$, above which the sample-to-sample mean athermal shear modulus saturates to a high-temperature plateau, as shown in Fig. 4, Left, Inset and in ref. 86. In our model, we find $G_{\infty }{a}_0^3/k_B{T}_{\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{e}\mathrm{t}}\approx 17$. Data will be made available upon request from the corresponding author.