Estimating intracranial pressure using pulsatile cerebral blood flow measured with diffuse correlation spectroscopy

Abstract

Measuring intracranial pressure (ICP) is necessary for the treatment of severe head injury but measurement systems are highly invasive and introduce risk of infection and complications. We developed a non-invasive alternative for quantifying ICP using measurements of cerebral blood flow (CBF) by diffuse correlation spectroscopy. The recorded cardiac pulsation waveform in CBF undergoes morphological changes in response to ICP changes. We used the pulse shape to train a randomized regression forest to estimate the underlying ICP and demonstrate in five non-human primates that DCS-based estimation can explain over 90% of the variance in invasively measured ICP.

1. Introduction

The pressure environment of the brain, located in a confined space inside the skull, is driven by three volume compartments – cerebrospinal fluid (CSF), cerebral blood volume, and brain tissue. According to the Monro-Kellie Doctrine [1], intracranial pressure (ICP) remains constant if the net volume of all compartments are unchanged. This delicate equilibrium can be disrupted in diseases that alter the volume of one of the three compartments outside the limits for which the other two can compensate. For instance, the brain tissue can swell in cases of traumatic brain injury (TBI) and infections such as meningitis. Blood volume can change in hemorrhagic and ischemic stroke. Finally, CSF can be produced excessively or absorbed insufficiently in diseases such as hydrocephalus [2].

The measurement of ICP is an important diagnostic tool and regulating the level of ICP when it exceeds normal bounds has been demonstrated to improve patient outcome in brain injuries, including TBI [3–6], and hydrocephalus [7]. The measurement of ICP and the regulation thereof through external ventricular drains (EVD) can prevent the often severe consequences of intracranial hypertension, including malperfusion of the brain tissue leading to ischemia [8]. Aside from the primary use of ICP to guide interventions, secondary information can also be derived from knowledge of its value. One example that shows increasing interest and growing importance in research as well as clinical applications is the calculation of cerebral perfusion pressure (CPP) and, in combination with it, the assessment of cerebral autoregulation (CA). CPP is defined as the difference between mean arterial blood pressure (MAP) and ICP and approximates the pressure gradient between inflowing arterial blood and outflowing blood in the venous sinus. Clinical studies indicate better patient outcome when optimizing CPP to maintain intact CA [9,10]. Information about CA, which is the ability of the brain to maintain constant blood flow despite changes in CPP, is often derived from CPP or a function of it [11]. Therefore, it too relies on measurements of ICP. Lassen’s curve characterizes CA as a range of CPP in which cerebral blood flow (CBF) remains approximately constant [12]. In an autoregulated brain, a clear plateau is expected with only minor CBF changes despite changing CPP. Another metric for CA is the pressure reactivity index, which is defined as the moving correlation between ICP and MAP [13], which also requires the measurement of ICP.

Despite the benefit offered by information about ICP [14], its measurement is not free of risks. The most common instruments used to measure ICP are invasive pressure transducers placed into the parenchyma, ventricles, or just below the skull [15,16]. ICP is also often measured from an EVD that can be opened to drain CSF and closed to measure the pressure inside the EVD that corresponds to the pressure inside the cerebral ventricle [16]. All these devices allow for ICP measurements with varying precision and reliability [17], but are highly invasive in that a hole needs to be drilled into the skull and the device needs to reside inside the brain. Alternatively, ICP can be measured using lumbar puncture manometry, which measures CSF pressure in the spinal cord. This method reduces (but does not eliminate) risks for the patient but provides only a transient measurement at a distant point, and requires unobstructed cerebrospinal fluid flow in the spine [18]. Because of the high risk, ICP measurements are only considered in high risk patients, in which the benefits of measuring or regulating ICP outweigh the risk of surgery, and potential complications like hemorrhage and infection. For example, in adult TBI patients a Glasgow Coma Scale of < 8 in combination with an abnormal computer tomography scan is the recommended requirement for invasive ICP measurements [19]. For pediatric care, other guidelines apply to address the benefit to risk ratio [20]. A non-invasive alternative to current ICP monitors would reduce the risk of ICP measurements tremendously and give valuable access to additional information in less severe brain injuries that do not meet the requirements for an invasive procedure. Furthermore, it can open the field to a wealth of research in healthy volunteers to help understand the dynamics of ICP and its relationship to various disease states.

Non-invasive ICP measurement has been proposed by other research groups using a variety of approaches [21,22]. ICP changes can be indicated by impedance mismatches between the carotid artery to a peripheral artery (e.g. a finger) as measured by the dicrotic notch delay [23]. Incompressible cerebrospinal fluid carries ICP to the tympanic membrane [24] or the optical nerve sheath [25], where ICP can be measured as a displacement or diameter change, respectively. Ultrasound can be used to measure time of flight from one ear to the other across the brain [26], the blood velocity in the middle cerebral artery [27], or the pulsatility index of cerebral blood flow velocity as measured with transcranial doppler (TCD) [28,29], as well as the critical closing pressure [30]. Recently, an ultrasound based mathematical model of cerebral hemodynamics has shown potential to estimate non-invasive ICP based on pulsatile information [31]. All these ultrasound-based measurements can be correlated to ICP [28]. However, many of these examples only measure relative changes in ICP, distinguish only between highly elevated and normal ICP, or are not suited for long-term bedside measurements. The lack of precision, reliability, and ease of use of all these methods necessitate an alternative.

Previously, hemodynamic changes measured non-invasively with diffuse optical devices have been correlated to ICP or CPP [32] and first attempts to predict ICP from these measurements of hemoglobin concentrations and CBF have been presented. Using diffuse optical devices such as near-infrared spectroscopy (NIRS) [33,34] and diffuse correlation spectroscopy (DCS) [35] has the benefit of simplicity of use, given that only one probe needs to be placed on the head that can measure for hours without causing discomfort or risk to the patient. Furthermore, these devices can be portable and potentially low cost. Another significant advantage of diffuse optical methods, such as DCS, which measures changes in cerebral blood flow, is the sensitivity to the microvasculature, allowing for localized measurements as compared to global measurements using TCD. We have recently shown that a transfer function approach can translate oxygenated hemoglobin concentration changes measured with NIRS into changes in ICP [36].

Here we expand the idea of using hemodynamic changes to measure ICP and demonstrate that absolute values of ICP extraction are possible. We take advantage of changes in the cardiac pulse waveform with ICP as well as hemodynamics. Specifically, we utilize ICP pulse shape changes when the ICP baseline increases [37,38]. A similar idea has recently been proposed by Fischer and colleagues, who demonstrated a proof-of-concept of estimating ICP in infants and adults based on pulsatile CBF measurements and a recurrent neural network using a hold-out validation [39]. The pulse typically shows three distinct peaks, namely the percussion peak translated from the systolic pulse in the pulsatile arterial blood pressure (ABP), the tidal peak created as a rebound of the percussion peak (a result of intracranial compliance), and the dicrotic peak from the closure of the aortic valve. As ICP rises, the intracranial compliance changes and so does the ICP waveform, with the tidal wave increasing in height relative to the percussion wave. Here we use DCS in a non-human primate model in which ICP was experimentally manipulated to measure the cardiac pulsation of cerebral blood flow, which also shows the three descriptive peaks. Using a set of physically relevant features and advanced machine learning algorithms, we correlated the morphological changes in the CBF waveform to underlying ICP baselines. This approach permitted a highly accurate estimate of ICP from non-invasive cerebral blood flow sensing.

2. Materials and methods

To train a machine-learning algorithm to identify level of ICP from cardiac pulse waveforms, cerebral blood flow changes were recorded with DCS in combination with an electro-cardiogram (EKG) in five non-human primates (NHP) under different ICP values.

2.1. Diffuse correlation spectroscopy

Diffuse Correlation Spectroscopy (DCS) was used to measure cerebral blood flow. The working principle of DCS has been described previously [35,40,41]. A single long-coherence length laser at λ = 850 nm wavelength (DL852-050-SO, CrystaLaser, Reno, NV, USA) was used for illumination trough a 200 µm-diameter multimode fiber. The source-detector distance was 2 cm and photon counts were recorded at 2 MHz through four few-mode fibers (5.8µm core diameter) leading into a four-channel photon counting module (SPCM-AQ4C, Excelitas Technologies, Vaudreuil-Dorion, Quebec, Canada). Using software correlation, the photon intensity was auto-correlated and all four channels were averaged. The intensity auto-correlation was then converted to electric-field auto-correlation and fitted to the solution of the diffusion equation [40]. Using this technique, we achieved a sampling rate of 50 Hz, which was fast enough to resolve the cardiac pulsation. CBF was extracted as an expression of the Brownian motion diffusion coefficient αD_b (in cm²/s) and here described as a percentage change from the baseline, as ΔCBF.

A synchronization pulse was sent to the auxiliary port of the DCS at any time the 3-lead EKG registered a QRS complex in the signal. The EKG used was an in-house amplifier circuit that allowed the detection of a cardiac pulse when the electrical signal of the EKG exceeded a threshold manually set for each subject at the beginning of the experiment. This threshold was set to be exceeded during the R-peak in the QRS complex of the EKG. The thresholding approach of the EKG signal allowed for precise recording of the onset times of a cardiac pulse.

2.2. Experimental design

All procedures were approved by the Institutional Animal Care and Use Committee of the University of Pittsburgh and complied with guidelines set forth in the National Institute of Health’s Guide for the Care and Use of Laboratory Animals (2011). The measurements were conducted on five NHPs (Macaca mulatta, N=5, f/m: 0/5, 8.2 ± 1.5 years, 10.2 ± 2 kg). All animals were initially sedated using 20 mg/kg of Ketamine independently or in combination with 1 mg/kg Diazepam and 0.04 mg/kg Atropine. After placing an arterial line in the external carotid artery, the animals were ventilated and maintained under anesthesia using a combination of 10-25 µg/kg/hr Fentanyl administered intravenously and a minimal amount of Isoflurane gas (< 1%). At the same time 0.1 mg/kg/hr of Vecuronium Bromide paralytic was given. Each animal was held with its head facing forward in a stereotaxic apparatus and its stomach on the table.

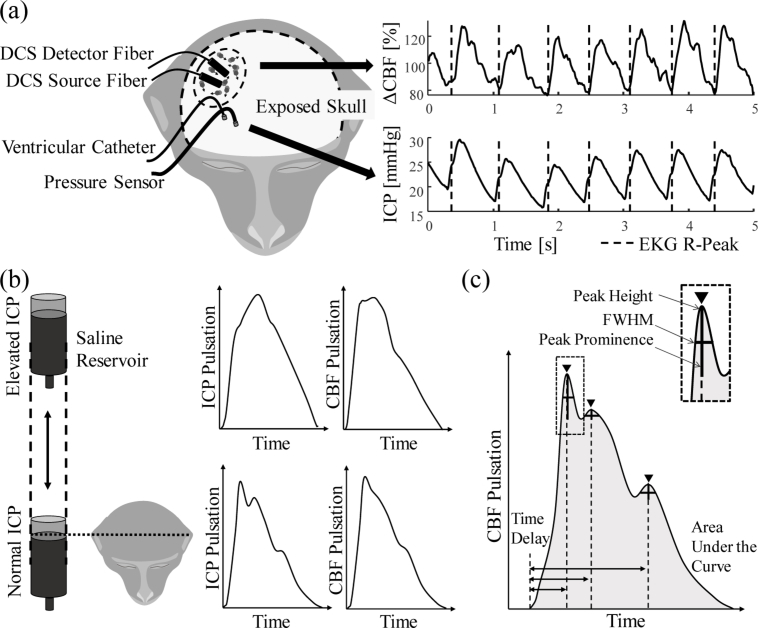
The source and detector fibers of the DCS system were placed directly on the exposed skull of the animals to reduce the influence of skin and muscle layers of the tissue. The fibers were placed laterally on the right hemisphere near anterior-posterior zero in stereotaxic coordinates (Fig. 1(a) ). For ICP monitoring and pressure manipulation, two small craniotomies were made. One permitted access to the lateral ventricle for a catheter (Lumbar catheter, Medtronic, Minneapolis MN) and the other led into the brain parenchyma for placement of the ICP sensor (Precision Pressure Catheter, Raumedic Helmbrechts, Germany). ABP was measured from the A-line and ICP from the invasive sensor at 100 Hz by a MPR1 Datalogger (Raumedic Helmbrechts, Germany). Alignment markers were sent from a central voltage source to the pressure MPR1 Datalogger and the DCS. The ventricular catheter was connected to an open saline reservoir that was lifted relative to the animal’s head height to induce fluid pressure changes (Fig. 1(b)). By maintaining a constant height, the pressure of the saline column translated to the cerebral ventricle and ICP was altered. Due to CSF absorption in the brain, the catheter was held open to allow for constant saline flow, which permitted maintenance of an ICP baseline level.

Fig. 1.

Experimental setup and data analysis. (a) shows the experimental setup with the placement of optical fibers and pressure sensor as well as the catheter on the exposed skull of the monkey. The traces at the right show an example of changes in cerebral blood flow (ΔCBF) and ICP. The dashed line marks the maximum of the QRS complex in the EKG recording. (b) shows how the saline reservoir connected to the lateral ventricle influences ICP. The left two pulses show ICP pulsation shape changes, the right two curves show similar changed in blood flow pulsation. (c) shows which morphologically relevant features were extracted from the cartoon version of an ideal ΔCBF pulse.

The first measurement for every subject was performed at the opening ICP. The ICP was then leveled to 9 mmHg for a second measurement, if the initial ICP was at or below this level. From there, the ICP was gradually raised to approximately 12 mmHg, 15 mmHg, 20 mmHg, and 30 mmHg. In three of the five subjects, the ICP was returned to a level of 9 mmHg between elevated levels (12-30 mmHg), to distinguish ICP-induced influences on the hemodynamic signal from those associated with the passage of time during the experiment. Every ICP level was held for approximately 90 minutes while ICP and ΔCBF were recorded throughout this time period.

2.3. Signal processing

General signal processing was performed using Matlab R2019a (The MathWorks Inc., Natick, MA, USA). All recorded signals were aligned with digital markers sent to the DCS and MPR1 Datalogger. EKG markers were used to measure the pulse onsets.

Over the course of several hours, laser instabilities were observed as seen in fluctuating y-axis intersection of the intensity autocorrelation curve, known as β. The presence of a laser instability was determined by any β value, averaged over 10 seconds, that showed a deviation greater than 0.01 from the median. If an instability was detected in a measurement, we removed all points in time where β deviated more than half a standard deviation from the median. Unrelated to β, some DCS pulses did not follow the canonical cardiac waveform shape, likely due to motion artifacts. These motion artifacts can be caused by human intervention for periodically filling the saline reservoir, watering the eyes of the NHP that were held open for visual stimulation of the brain in a parallel experiment, or maintenance of the anesthesia and paralytic solution syringe pumps. To exclude such pulses, we used a z-score rejection. The z-scored ΔCBF over all pulses within a measurement (a period of approximately similar ICP for 90 minutes) was calculated at each time point. Individual pulses that showed a z-score > 3 from the mean of the individual ICP baseline for individual subjects were rejected.

After rejection of data, 120 consecutive pulses were averaged to improve the signal-to-noise ratio (SNR). In our NHPs, 120 cardiac pulses corresponded to approximately 60 seconds of data, given a typical heart rate of 120 beats per minute. The invasively measured ICP was averaged over the time of these pulses to function as the ground truth for training of the machine learning approach. The average window was then shifted by 10% of the window length, or 12 pulses, and the procedure was repeated for the entire sequence of ICP data at each ICP level. This approach balanced between the need to average data to reduce measurement noise and preserve a large amount of training data for the machine learning algorithm.

The averaged pulses were then normalized to establish a consistent range across animals. The normalization was performed in both the x- and y-direction – i.e. the blood flow change across a pulse was set to be between 0 (diastolic) and 1 (systolic), and the length of a pulse was set to be 151 data points wide from diastolic to diastolic point in time by means of spline interpolation. This normalization also removed the effect of heart rate changes that can be independent of ICP changes.

To improve the SNR further, an adaptive filter was applied to the averaged pulses. Here we used a Kalman filter adaptation, which was applied consecutively to all averaged pulses. Such filtering allowed for the generation of an ideal pulse over time as an average of all previous pulses. Each pulse was compared to the ideal pulse, the difference was calculated, and the pulse was then corrected based on the error. Empirically determined constants defining the trust in the ideal pulse and the measurement determined the strength of correction, weighted by the calculated error. The ideal conception was then updated by adding the new measurement to the ideal conception calculation. As the waveform changed with increasing ICP, so did the Kalman filter. The adaptive filter permitted reduction of the noise while maintaining the cardiac pulse morphology and the ICP based changes thereof.

Given the sparsity of recorded pulses above 30 mmHg of ICP, the prediction was only performed for ICP values between 0 and 30 mmHg. The above procedures resulted in a total of 14,121 averaged pulses across all five animals.

2.4. Feature extraction

After normalization and filtering, morphological features were extracted. In Fig. 1(b) the morphological differences for both ICP and ΔCBF for low (bottom) and high (top) ICP are shown. To describe the subtle differences in the waveforms, the features shown in Fig. 1(c) were extracted using the peak finding algorithms provided by the matlab function “findpeaks”. To describe the individual waves within a cardiac pulse, peak height (pk), prominence (p) and full width at half maximum (w) were extracted. In addition, the time point of the peak relative to the prior diastolic minimum (pos), as well as the area under the curve were calculated. Further information was gained by calculating the differences between waves. A complete list of all features is shown in Table 1.

Table 1. Morphological features extracted from cardiac pulsation in ΔCBF.

Individual peak analysis		Peak to peak differences	Full pulse analysis
P1pk	P3pk	d(P1-P2)pk	Area under the curve (AUC)
P1pos	P3pos	d(P2-P3)pk	Mean arterial pressure (MAP)
P1w	P3w	d(P1-P2)pos
P1p	P3p	d(P2-P3)pos
P2pk		d(P1-P2)w
P2pos		d(P2-P3)w
P2w		d(P1-P2)p
P2p		d(P2-P3)p

P1, P2 and P3 refer to the percussion, tidal and dicrotic peaks of the pulse wave, respectively. The peak to peak differences were denoted as d(P1-P2) and d(P2-P3) and were calculated for all four single peak features. In some cases, a feature was not detectable, e.g. when the percussion and tidal peaks (P1 and P2) merged to a single peak (P1) at high ICP. In that case the dicrotic peak (normally P3) became the second detected peak (P2) and no P3 could be found. In such cases, all undetected features were set to 0, but still used in the machine learning algorithm as the lack of a peak could be a strong indicator of elevated ICP. An additional feature added to the algorithm was the averaged mean arterial pressure (MAP) over the time span of the 120 averaged pulses. This was done to avoid misinterpretation of elevated MAP for elevated ICP. Combining the 22 features created a feature set that could be used to describe the individual averaged pulse. A feature set was calculated for every averaged cardiac pulse, creating a matrix including physiologically relatable information to use for supervised machine learning.

2.5. Machine learning

To allow for training and testing of the machine learning approach, the data were first separated into training and testing data sets. The testing set, consisting of randomly sampled 20% of all available feature sets, was held out from the training process (performed on 80% of the data) and used in the final cross-validation.

The training set was then used to build a regression forest using the python toolbox scikit-learn [42]. The functionality and working principle of regression forests and random decision forests in general has been explained in detail elsewhere [43,44]. The regression forest chosen here was a bagged ensemble of 1000 individual decision tree regressors. Each decision in the decision tree was binary and described by a threshold across a single feature chosen to yield the highest information gain. Bagging describes that each individual decision tree in the ensemble was trained on a small subset of the available training data set. This reduces the risk of overfitting to the training set. Therefore, we chose to only include a randomly sampled fraction of one third of the training set in each tree. The number was chosen by empirical evaluation. No restrictions were given on the features available to every node or tree, such that all features could be used at any time.

The maximum depth of each tree was set to 15. An increased tree depth can yield better results but risks overfitting. In a decision tree regressor, the tree depth is exponentially proportional to the resolution at which ICP can be estimated – a depth of 1 can distinguish 2 ICP levels, while a depth of 3 can distinguish 8. The parameters of ensemble size and tree depth as well as bagging quantity were chosen empirically to achieve a high precision and minimize overfitting.

After training the regression forest with the training data set and the corresponding invasively measured ICP as the ground truth, the testing data set was used. A prediction of non-invasive ICP based on the feature sets of each individual pulse was generated and the correlation to the invasively measured ICP was determined.

3. Results

We successfully induced ICP baseline changes in 5 NHPs and recorded pulsatile ΔCBF throughout the experiment for multiple hours to generate a data set large enough for machine learning application.

3.1. Data acquisition

For every NHP, data were collected in sets of approximately 90 minutes per ICP baseline, with the total amount of data collected for animals varying between 9.1 and 16.6 hours. At the beginning of every set, the ICP was adjusted. The individual measurement sets were combined in post processing.

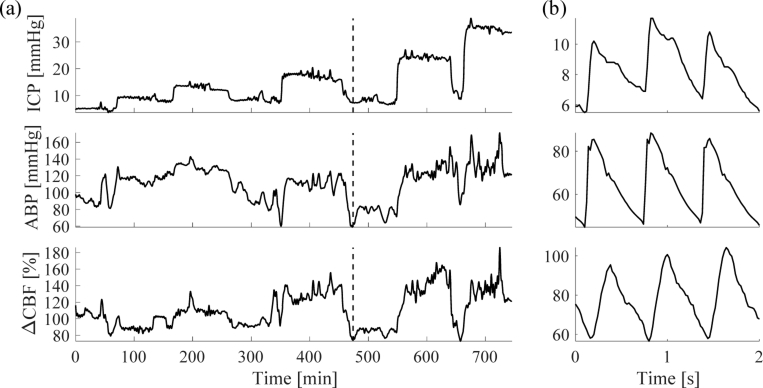
Changes in ICP translated into both changes in ABP and ΔCBF. This was especially apparent when lowering the ICP from an elevated state back down to 9 mmHg (Fig. 1(a)). By measuring ABP, ICP, and ΔCBF at high sampling rates, we were able to observe individual cardiac pulses and their characteristic peaks and valleys (Fig. 2(b)).

Fig. 2.

Example recording of data in one subject. (a) shows a full measurement from one subject, low-pass filtered (cut off frequency at 0.008 Hz) to emphasize the baseline. Dashed line indicates where figure (b) is located. In (b), a close-up of data at the dashed line is shown to see individual pulses. The pulses were filtered by a moving average of 0.1 seconds.

3.2. Waveform extraction

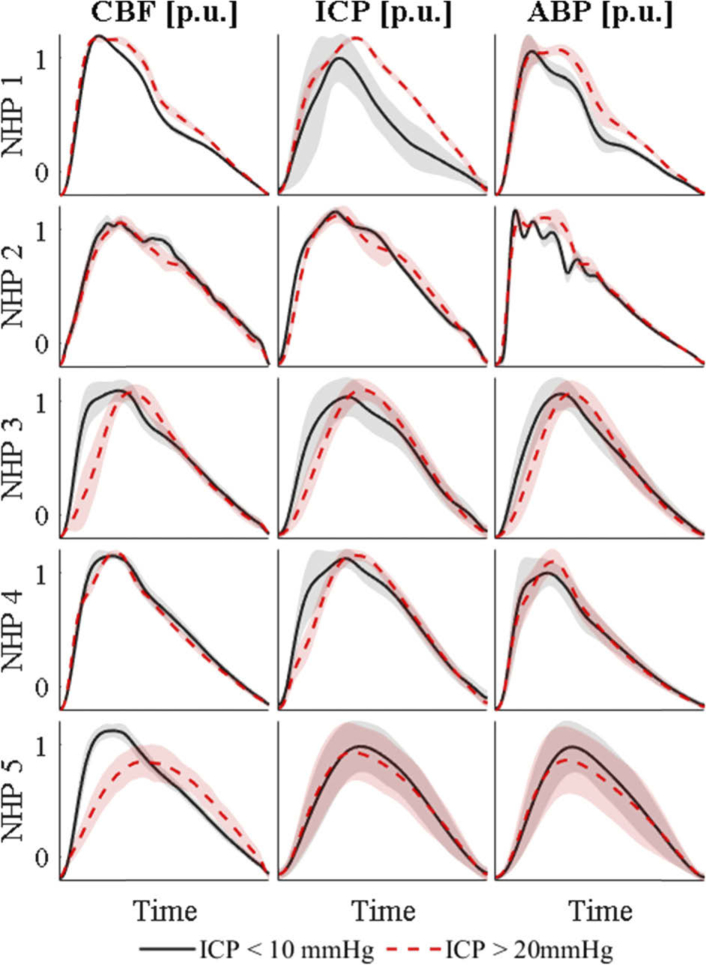
The morphological details in the ΔCBF pulsatile signal needed were apparent by comparing the pulses of low and elevated ICP baselines. Comparing pulses at ICP baseline below 10 mmHg, which is considered normal pressure, with pulses during ICP baselines above 20 mmHg, which is pathologically high, showed subtle but distinct differences (Fig. 3).

Fig. 3.

Averaged cardiac pulses of all five NHP for ΔCBF, ICP and ABP. The solid black line in each graph shows all pulses below 10 mmHg for the specific NHP. The red dashed line shows pulse averages of ICP baselines above 20 mmHg. The shaded area shows the standard deviation over all averaged pulses at each time point. The pulses were normalized in height by division of maximum, thus showing a per unit (p.u.) magnitude, and spline interpolated in time to be of the same length.

Overall, a higher ICP led to a broadening and rightward shift of the cardiac pulse compared to the previous diastolic minimum. The strength of this effect differed between subjects (rows in Fig. 3, with NHPs 2 and 4 exhibiting the least apparent changes but nonetheless subtle morphological shifts. ICP and ABP waveforms were in good agreement with the non-invasively measured ΔCBF waveform. ICP, measured through a parenchymal pressure transducer, and ABP, measured in the carotid artery through an A-line, must be measured invasively, leaving ΔCBF as the only non-invasive measurement we performed that was able to show these subtle changes.

3.3. Regression forest learner

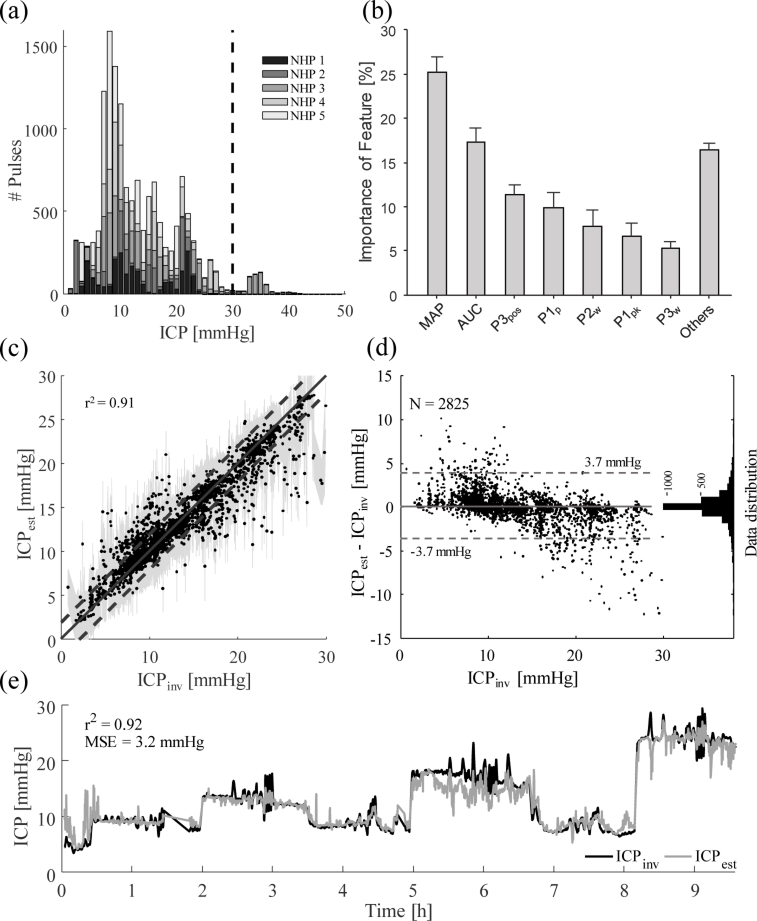
We were only able to collect a small amount of data in one animal beyond 30 mmHg (Fig. 4(a) ). Therefore, the training and testing of the regression forest was only performed for data below 30 mmHg. The held-out testing data was closely matched (r²= 0.91) between the invasively measured (ICP_inv) and estimated (ICP_est) pressure, as seen in Fig. 4(c). The shaded area shows the confidence interval of the prediction calculated using the Jackknife algorithm described by Wager et al. [45]. The dashed lines show an area of ±2 mmHg around the ideal match shown as the solid line. A mean squared error of 3.3 mmHg was calculated for this test. A good match between estimated and invasively measured ICP can be seen, especially around 10 mmHg, which is also the area with the most available data (shown in Fig. 4(a)). Further evidence for a good fit is given by the Bland-Altman plot that shows how 95% of all data points are within 3.7 mmHg of the invasive reference measurement (Fig. 4(d)).

Fig. 4.

Results of the regression forest machine learning approach. (a) shows the distribution of the available data. The dashed line marks the maximum ICP level that was fitted for at 30 mmHg. (b) shows the distribution of features used in the regression forest as a percentage of all chosen features in all decision criteria generated. The standard deviation across individual trees is shown as error bars. Nomenclature is according to Table 1. (c) shows the performance of the regression forest by plotting estimated ICP (ICP_est) over invasively measured ground truth (ICP_inv). The solid line shows the ideal fit, while the dashed lines mark an area of 2 mmHg around the ideal fit. The shaded area shows the confidence interval. (d) graphs the difference between ICP_est and ICP_inv over ICP_inv in a Bland-Altman plot. The dashed lines span a region of 95% of the distribution, corresponding to a standard deviation of 1.96. The histogram on the right of this graph shows the distribution of data points in number of samples. (e) shows a continuous estimate of ICP for NHP 3. The gray line shows the estimated ICP, and the black line the invasively measured ICP. An r² = 0.92 and a mean squared error MSE = 3.2 mmHg were achieved.

We found that the area under the curve (AUC) of the cardiac pulse and the MAP baseline value (not pulsatile shape) were the most important features in our data (Fig. 4(b)). This suggests that a measurement of MAP, for instance by blood pressure cuffs or photoplethysmography, is essential for a precise prediction of ICP. In fact, when removing MAP as a feature to the regression forest, to generate a single device approach only using information from DCS, the r² value dropped to 0.82 (data not shown). The area under the curve was the second most important feature for predicting ICP, which is confirmed by the wave broadening (Fig. 3). The time delay to the dicrotic wave, the third peak in the cardiac pulse, was the third strongest indicator of ICP. This feature is interesting as it might not be present in some averaged waveforms. Therefore, the lack of a dicrotic wave can offer valuable information to the fitting algorithm.

To simulate a continuous prediction, we ran all available waveforms for a single subject through the predictor and plotted estimates against invasive measurements. Figure 4(e) shows this example measurement, of which randomly selected 80% of the pulses were also used in the training set and only 20% held out from training representing new data points. The graphical representation over time shows good agreement between the estimated (gray colored graph) and the invasive measurement (black colored graph) and the mean square error (MSE) between the two was calculated to be 3.2 mmHg and is thus comparable to the test performed with only held out data (Fig. 4(c)).

4. Discussion

In this work, we demonstrate that changes in baseline ICP influence the shape of the cardiac pulsation observed in the ICP and ΔCBF waveforms. This effect allowed us to estimate ICP using a machine learning approach with ΔCBF data obtained from DCS. In our testing in five macaque monkeys in which we induced ICP changes with a catheter placed in the lateral ventricle, we achieved a very high similarity between estimates of ICP and the invasive measurements (r²= 0.91, cross-validated), with an estimation error of MSE = 3.3 mmHg and a 95% similarity to the invasive data within a 3.7 mmHg range. The results therefore indicate the possibility of reliable estimation of ICP in absolute numbers solely based on non-invasive measurements of MAP and ΔCBF. The addition of EKG, another non-invasive measurement, allowed for precise waveform alignment and averaging and is highly recommended in this setup, but not essential if a hypothetical clinical application would not permit its use. The invasively measured ICP was used as a validation reference, but it was not free of measurement error, due to placement location in the brain tissue and inherent device limitations, such that differences between the two can partially be explained by the limitations of the reference measurement itself.

The benefit of a feature-based machine learning approach like the regression forest lies in the information we receive about the importance for every physiological feature, i.e. how often a feature allowed for the most significant split of ICP values. This information can be used to improve the algorithm in the future or reject features to enhance performance for real-time applications. We found that MAP and area under the curve of the ΔCBF waveform were the most important features, while features that can potentially be removed without reducing the prediction performance were the derivative features showing differences in peak height, prominence, full width at half maximum and position between adjacent peaks.

Some groups have tried to predict CPP rather than ICP [30,46]. Under the assumption that CPP = MAP – ICP, we would be able to calculate ICP from the estimated CPP through a non-invasive measurement of MAP. We tried fitting to CPP directly by replacing the ground truth of invasively measured ICP with invasively measured CPP and found that CPP prediction yielded r² = 0.98. While this can be considered a good fit, deriving ICP from here, by subtracting the measured MAP value from the estimated CPP value, showed worse performance, typically overestimating the true ICP with a wider spread of ICP values and yielding r² = 0.76 (data not shown). This is likely due to the assumptions used to calculate the reference CPP values. Describing CPP as the difference between MAP and ICP is an approximation often used in the clinic, and yet it neglects the effect of vessel wall tension and assumes that venous sinus pressure is always equal to ICP. Furthermore, the MAP feature was used in over 90% of all decisions, which intuitively makes sense given that normal MAP values are approximately one magnitude larger than normal ICP values but overrules the sensitivity to ICP influences on CPP. We therefore chose the direct ICP estimation over the CPP estimation.

Despite the good performance of ICP estimation with our approach, a set of limitations apply:

Generalization and inter-subject variability

• 1.The ability of the brain to autoregulate blood flow under differing pressure conditions can vary among individuals and is one of many ways the five animals in this study differ from each other.
• 2.Despite our best efforts at maintaining inter-experimental similarity, some subject variation can be explained by slight variations in the probe placement for DCS as well as the ICP sensor and the ventricular catheter.
• 3.While our approach outperforms current non-invasive alternatives, estimates of ICP in this study were performed on held out data of the same NHP used for training. Further testing on additional NHPs (not used to train the algorithm) and testing on human subjects is needed to make a direct comparison and draw firm conclusions about the potential of clinical use.

Experimental setup

• 1.In our study, changes in ICP were induced with an open saline reservoir connected via a catheter to the lateral ventricle. These changes induced a hydrocephalus-like state in which ICP was altered, but it is unclear how this type of manipulation of ICP will relate to situations involving brain swelling or hemorrhage. Future work will be necessary to test the generality of our ICP prediction in other disease states to make application in traumatic brain injury and stroke possible.
• 2.The distribution of blood vessels and therefore blood flow as well as intracranial pressure was assumed to be equal throughout the brain. This might limit the application in certain clinical settings like local edema or hemorrhage. However, finding and comparing differences in healthy vs. impaired brain regions can be a strength of this system as well, allowing for localized ICP measurements.
• 3.Under the assumption that morphological waveform changes are a result of brain impedance changes due to elevated pressure, one must consider that the impedance to flow can be changed by other mechanisms as well, including cerebral autoregulation which influences the vasomotor tone. Influences of autoregulation are not considered artifacts in this study but rather a potential contributor to the signal.
• 4.Autoregulatory impairment and vasomotor tone can be influenced by anesthesia, which is a limitation of the study design. The isoflurane gas anesthetic, which is suspected to negatively influence autoregulation [47], was kept at a minimum through the inclusion of fentanyl. Nonetheless, the use of anesthesia may influence the generalizability of our results to measurements of ICP in awake individuals or those under different anesthesia regimes.

Signal processing

• 1.To train a regression forest, a large data set of features must be generated. This procedure can, depending on the complexity of features and amount of training data, accumulate to many hours of processing time. Once a regression forest is trained however, the application can be done in real-time, given that regression forests perform simple comparisons at each node in each tree, which require minimal computational power.
• 2.The accuracy of the regression forest prediction is dependent on the training data set size. Figure 4(c) shows an increasingly larger confidence interval with increasing ICP, which is an effect of fewer training data points at larger ICP values (as seen in the distribution in Fig. 4(a)).

Our work compares favorably to other non-invasive ICP monitors using TCD. Cardim and colleagues reported confidence intervals between 4.2 to 59.6 mmHg when comparing a large number of TCD-based approaches, with an overall confidence interval around 12 mmHg [27]. In the review by Rosenberg et al. a large portion of the discussed ICP monitoring devices used CT or Ultrasound to measure the diameter of the optical nerve sheath [21]. They only make a binary decision between elevated and normal ICP, with a cut-off pressure at 20 mmHg. Reported sensitivity for TCD ranges from 74% to 95%, with a specificity of 74-100% for 7 independent studies identifying ICP > 20 mmHg. CT approaches show similar results as they rely on the same physiological response to elevated ICP. Using our approach, a sensitivity of 88% was achieved, with a specificity of 97%, placing the DCS-based ICP estimation at the top half of the reported classification results, while having the additional advantage of allowing continuous predictions as opposed to binary decisions. This implies that our approach can potentially be used to identify cases of elevated ICP prior to EVD placement, currently estimated by enlarged ventricles in magnetic resonance imaging (MRI) or computer tomography (CT) in TBI patients.

5. Conclusions

We have demonstrated the potential of DCS to be used as a non-invasive monitor of ICP by interpreting the waveform shape of cardiac pulsation of ΔCBF. The performance of our machine learning approach relied on incorporating non-invasive measurements like EKG, for better pulse averaging, and MAP, for excluding events of elevated MAP. The regression forest reached an r² = 0.92 (cross-validated) with a mean squared error of 3.3 mmHg. In the future, a transition to human application in clinical settings is needed to test the performance of a DCS-based ICP monitor against clinically relevant invasive monitors in disease states that result in altered ICP for reasons different from the fluid pressure elevation method used here. In addition, increasing the number of subjects will be essential in future work to account for inter-subject variability and improve the generalization of the approach. Nonetheless, our method opens the door for ICP monitors in patients with less severe injuries or diseases as well as healthy patients for research purposes.

Funding

Center for Machine Learning and Health at Carnegie Mellon University; American Heart Association10.13039/100000968 (17SDG33700047); National Institutes of Health10.13039/100000002 (R21-EB024675).

Disclosures

The authors declare no conflict of interest.