Abstract
Identification of novel molecular subtypes of disease using multi-source ‘omics data is an active area of on-going research. Integrative clustering is a powerful approach to identify latent subtype structure inherent in the data sets accounting for both between and within data correlations. We propose a new integrative network-based clustering method using the non-negative matrix factorization, nNMF, for clustering multiple types of interrelated datasets assayed on same tumor-samples. nNMF utilizes the consensus matrices generated using the non-negative matrix factorization (NMF) algorithm on each type of data as networks among the patient samples. The multiple networks are then combined, and a comprehensive network structure is created optimizing the strengths of the relationships. A spectral clustering algorithm is then used on the final network data to determine the cluster groups. nNMF is a non-parametric method and therefore prior assumptions on the statistical distribution of data is not required. The application of the proposed nNMF method has been provided with simulated and the real-life datasets obtained from The Cancer Genome Atlas studies on glioblastoma, lower grade glioma and head and neck cancer. nNMF was found to be working competitively with previous methods and sometimes better as compared to previous NMF or model-based method especially when the signal to noise ratio is small. The novel nNMF method allows researchers to utilize such relationships to identify the latent subtype structure inherent in the data so that further association studies can be carried out. The R program for the nNMF will be available upon request.
Keywords: Integrative clustering, non-negative matrix factorization, cluster prediction index, network, silhouette width
1. Introduction
A large inter-patient variation in the clinical responses has been a challenge in the treatment of many cancers. Response to the treatment regimen and the disease progression vary from person to person for even the patients having same cancer diagnosis[1]. One approach to overcome this limitation has been the use of molecular profiling or clustering to determine molecular based tumor subtypes, where within these subtypes it is thought that the tumors will be more homogeneous and thus may have similar clinical response to a given therapy regimen[2]. After the discovery of high-throughput technologies such as microarray and sequencing, several types of molecular information are often being collected on the same tumor sample, resulting in correlation between features within a given data type but also across multiple data type assayed on the same subject. For example, the multi-institution collaborative project, The Cancer Genome Atlas (TCGA) has collected multiple-layers of genomic data including, genome, transcriptome, epigenome and proteome information for a large number of subjects for many cancers. Availability of such wealth of data opens up new opportunities to collectively explore the variations in genomic profiles at each layer of biological process which is critically important to understand disease etiology, drug response to treatment and progression. A part of such variation at the molecular level can be explained by identifying the disease-subtypes.
The true biological signal may or may not be present in all types of datasets. Also, there might be weak but consistent signals present across several datasets. Integrative analysis can strengthen and reveal such consistent signals more obvious. The goal of the integrative clustering analysis is to identify the subgroups of samples into a distinct classes (clusters), considering the biological phenomena at several levels including gene expression, DNA methylation, copy number variation (CNV), protein expression, etc. [3].
However, the disparity in the measurement scales of the data sets can pose challenge for such integrative analyses. The technology used to assay the data and the units of measurement create wide variation in the data. The simplest method to integrate the data is by concatenating multiple datasets after appropriate normalization (i.e. scaling of the data) into a single dataset, followed by clustering analyses on the combined data. But this approach tends to dilute the small signal to noise ratio in the multiple datasets[4]. Another approach is to manually integrate the clustering results obtained from one data at a time[5]. However, such approach can suffer from subjective bias in the subtype determination.
A few model-based[6–8] and non-parametric integrative clustering methods[4, 9] are available. Frequently used method, iCluster[6], assumes that the data follows Gaussian probability distribution. A few other examples of model-based approach are based on Gaussian mixture model and Bayesian clustering methods[7, 8]. However, integrative clustering using parametric models can be challenging in cases where the model assumptions may not be satisfied (i.e., different types of molecular data may follow different distributions). In order to overcome the limitations of the dependency on the statistical distribution assumptions, a few non-parametric methods have been proposed in recent years including integrative non-negative matrix factorization method (intNMF)[9], Similarity Network Fusion (SNF)[4] and Perturbation clustering (PINS)[10]. Arguably the state-of-art approach in the clustering analyses has been the consensus clustering based approaches[11, 12]. The integrative clustering intNMF utilizes consensus clustering in integrating the multiple types of molecular data. Another powerful method, SNF, creates the sample similarity matrices (networks) based on distance measures for each type of data and integrates those networks into a common similarity network followed by spectral clustering on the final network to partition the data. However, the kernel-based clustering of SNF has been criticized for its unstable nature of making the algorithm too sensitive to small changes in genomic assays which can create instability in the networks derived from each data[10]. Also, the choice of the distance metric can have effect on the overall clustering performance.
There are two purposes of this article. First, we propose novel network based integrative clustering method nNMF by incorporating the strengths of SNF on the intNMF. The nNMF method involves two steps: construction of stable consensus matrices for each data type using intNMF (intNMF[9] algorithm can be used for single type of data as well) and integration of those consensus matrices into a single consensus matrix using the approach proposed by SNF followed by spectral clustering. Second purpose is to compare the new nNMF method with the existing methods (intNMF, iCluster, SNF) in terms of their performances using simulated data. Lastly, nNMF is illustrated using two glioma studies and one head and neck cancer studies from TCGA.
2. Material and Methods
2.1. Network-based integrative NMF
The approach is based on the NMF[12] and the network clustering techniques[4]. We briefly review the NMF for a single data and construction of the consensus matrix before describing nNMF method.
2.1.1. NMF for a single data
NMF approach was proposed by Paatero & Tapper[13] in 1994 and its successful application in the pattern recognition problem was demonstrated by Lee & Seung[14] in 1999. The algorithm proposed by Lee & Seung was utilized by Brunet et al.[12] together with consensus clustering approach to determine the subtypes of cancer. Suppose a matrix with n subjects and p genomic features, , containing all the non-negative entries. Then NMF factorizes Xn×p into Wn×k and Hk×p, (i.e. Xn×p ≈ Wn×k Hk×p), where k is user-specified number of groups or classes. The resulting matrices Wn×k and Hk×p are also non-negative which are called matrix of basis vectors and matrix of coefficient vectors respectively.
Generally used objective function, Frobenius norm , is convex in W when H is given, or convex in H when W is given. But when W and H together are unknown the minimization problem is not convex. Therefore, in general, global minimum of the NMF problem does not exist[13, 15]. However, the beauty of NMF is that Q can be minimized using numerical optimization methods and the underlying subtype structure of the variables can be extracted using W. The “best” local minimum is achieved by running the algorithm with a large number of initializations of W and H. One local minimum is obtained at the end of each run of the algorithm. Out of many such local minima, the one for which the objective function Q converges to smallest value is chosen. In our implementation, estimation of W and H matrices are carried out using non-negative-constrained alternating least square (NNALS) algorithm[16].
Consensus matrix is computed using the matrix W. At each iteration of the algorithm, a square matrix with dimension n×n, is constructed with binary entries 1 or 0. The values 1 or 0 are assigned based on whether the samples (one on row and other on column) cluster together or not. Since the entries 1 or 0 reflect the connectivity between the samples, the matrix is also called connectivity matrix[11]. The connectivity entries keep changing for a few initial iterative steps but become stable as the algorithm progresses. When the connectivity matrix becomes stable for several consecutive iterations (say 50 iterations) without changing the values, the algorithm stops. The consensus matrix, C, is then constructed by averaging the connectivity matrices, on an element by element basis, over all the iterative steps until convergence[11]. The elements of C thus range between 0 and 1, with higher value reflecting the probability of two samples in ith row and jth column being clustered together. Details of construction of consensus matrix can be found elsewhere[9, 11, 12]. In the proposed nNMF clustering approach, we utilize such stable consensus matrix as a sample-similarity network.
2.1.2. Network based integrative clustering (nNMF)
Our proposed nNMF method involves two steps. In the first step, the stable consensus matrices Ci, i=1,2,…,m for each of m types of data are computed using intNMF algorithm[9]. Each of the n × n consensus matrices can be considered as a pairwise similarity network of subjects. By construction, each entry in the consensus matrix represents what proportion of times each pair of samples (one in row and other in column) group together over all the iterations before convergence of the algorithm. The larger elements of consensus matrix (towards 1) reflect the higher similarity between samples. In the context of graph theory, G = (V, E), the samples can be considered as vertices V and the consensus values as pairwise sample similarities edges E. In the second step, the network integration method is used on these consensus matrices in a similar way it was proposed elsewhere[4, 17]. The network integration process is based on the message-passing theory in which, networks are combined and updated making the consistent and strong signals stronger and clearer. Such an integration process helps in finding the true signal in two ways. First, the strong signals present in any data is preserved. Second, there might be a weak but consistent signals present at multiple networks. Such signals will be added up during the iterative process. On the other hand, weak signals present in any data sets will disappear which will help in filtering out the noise. The steps involved in the process is shown in Fig 1. Finally, spectral clustering is used on the integrated consensus matrix to identify the clusters and the cluster memberships to each subject [4].
Fig. 1:
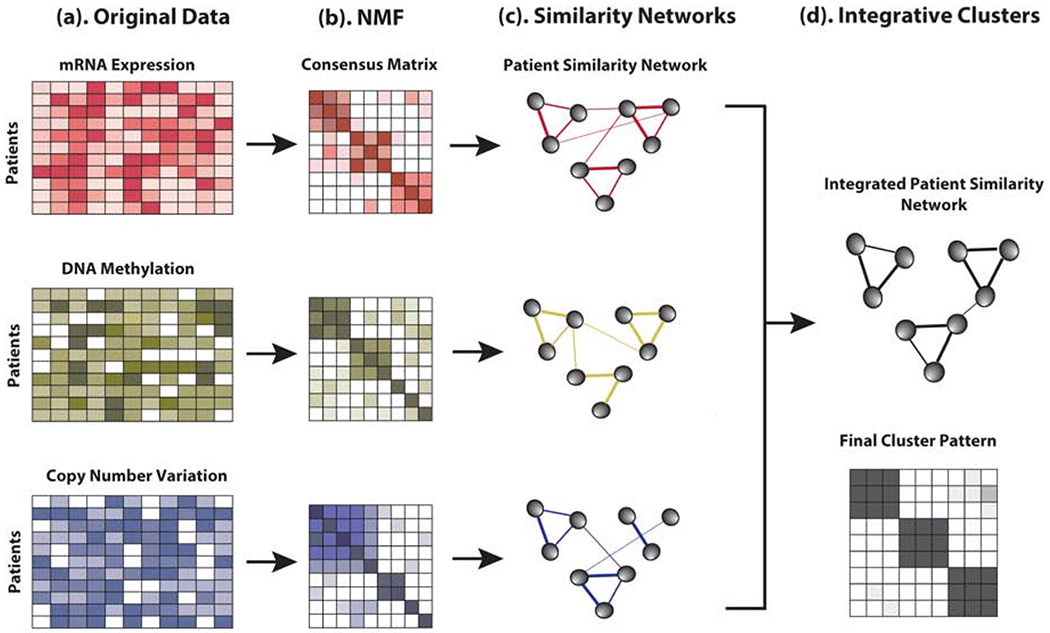
Illustration of nNMF steps: (a) Examples of the representation of multiple datasets collected at several layers of biological process from the same patient samples. (b) Consensus matrix resulting from each data separately. (c) Patient similarity network as represented by consensus matrix. Patients are represented by the nodes and the pairwise similarity are represented by the edges. (d) Single consensus matrix representing the integrated patient similarity network and cluster pattern.
This novel integrative approach has a couple of advantages over the intNMF[9] and SNF[4] method. With the intNMF, we might need to estimate and provide the weights for each data in order to better optimize the strengths across the datasets. Since the weights are generally not-known, the interpretation of the results can be difficult in the absence of correct weights if such weights are required. Also, intNMF requires that the multiple types of data be rescaled so that the data sets are comparable with respect to relative scale. Since nNMF generates separate networks from each data, no rescaling is required. Therefore, there is no possibility of loss of information due to rescaling. SNF generates a combined sample-network using a matrix-fusion method and then utilizes clustering on the fused matrix. SNF is based on the exponential kernel function to define the sample similarity matrix calculated using Euclidean or other distance-measures. However, the kernel-based clustering of SNF has been criticized for its unstable nature of making the algorithm too sensitive to small changes in genomic assays[10]. Also, the choice of the distance metric can have effect on the overall clustering performance. The proposed nNMF method does not require weights assignment to the datasets before using the algorithm and, also, does not rely on the kernel functions or any distance measures that can affect the outcomes.
The algorithm for fitting the nNMF clustering can be summarized as follows:
Randomly initialize Wi with the values generated from standard uniform distribution or by applying non-negative matrix decomposition technique[18] for each data i=1,2,…m.
- Solve for Hi given Xi and current Wi using NNALS.
(1) - Solve for Wi given Xi and current matrix Hi using NNALS.
(2) Repeat steps 2 and 3 until the algorithm converges.
During each iterative step connectivity matrices are computed as mentioned above and the consensus matrix Ci, i=1, 2, …, m is computed by averaging all those matrices after the algorithm converges.
Use the network integration algorithm[4, 17] on the Ci’s to compute the final integrated sample similarity network CF.
Use spectral clustering algorithm on CF to determine cluster numbers and clustering assignment for subjects.
3. Simulation Study
In order to meaningfully assess the ability of a new method to distinguish the cluster groups, the prior knowledge of the ground truth is required. Then we will be able to assess the performance of several clustering methods by comparing the results with the ground truth. Using the R package InterSIM [19], realistic DNA methylation (367 CpGs), gene expression (131 genes) and protein expression (160 proteins) data were generated for 500 subjects. We utilized the same simulation strategy as mentioned in Chalise el al.[9]. We first considered the null scenario in which there was no cluster groups, i.e. k=1 where effect size was set to 0. Then, we gradually increased the number of clusters, k from 2 to 6 with a sequence of effect sizes varying from 0 to 4 in the increment of 0.5. For each simulation scenario, 25% of the genomic features were considered to be differentially expressed among the assigned k cluster groups. Details of the simulation of multiple types of data having realistic within and between correlation structures can be found at Chalise et al.[19].
Before using the NMF algorithm, the simulated data requires additional transformation to make sure that the non-negativity requirement of NMF is satisfied. In our implementation, for each data, the absolute value of the smallest negative number was added to all the entries of the data. In doing so, the entries in each data will be non-negative and, also the variance of the features in the data will not be altered. Using the simulated data, the proposed nNMF was evaluated and compared with IntNMF. In addition, nNMF is also compared with one popular model-based method, iCluster and another non-parametric network-based method SNF. Optimum cluster-number was searched for each method across the specified range of k from 2 to 8. Both of the NMF based algorithms were run for 30 initializations of W. The optimality criteria for detecting the true number of clusters were measured by using Silhouette width for nNMF and default or recommended methods for other algorithms: silhouette width for SNF[4], cluster prediction index (CPI) with IntNMF[9] and proportion of deviance (POD) with iCluster[6].
4. TCGA studies on Glioblastoma, Lower Grade Glioma and Head and Neck Cancer
We implement and illustrate the nNMF method with TCGA subtype studies on two types of gliomas: Glioblastoma (GBM) and Lower Grade Glioma (LGG) and Head and Neck Squamous Cell Carcinoma (HNSCC). The first data on glioblastoma is available from data portal maintained by Genomic Data Commons (GDC) and located at https://portal.gdc.cancer.gov/ and quality controlled and processed data is also available in R package iCluster[20]. The datasets are well described and studied for integrative clustering by previous studies[9, 20]. This study was selected as they have been previously used to illustrate the iCluster[20] and IntNMF[9]. Using the data sets, we can compare the outcomes of the proposed method to that of the published papers in a real-life setting. The datasets consist of three types of genomic data assayed on 55 common subjects: DNA methylation (1515 CpGs), copy number variation (1599 genes), and gene expression (1740 genes). Based on the gene expression data alone, Verhaak et al.[21] has reported four subtypes of glioma including Classical, Proneural, Neural and Messenchymal. Also, using the three datasets, two previous integrative analytical approaches iCluster and IntNMF have reported three distinct clusters.
The second study was another glioma study from the TCGA on lower grade gliomas (grades II and III)[22, 23]. Lower grade gliomas have extremely variable clinical characteristics which cannot be predicted merely based on histologic examination alone, as some LGGs remain indolent while many others rapidly progress to glioblastoma[22]. The data used here consists of mRNA (20,330 genes), DNA methylation (25,978 CpG probes) and DNA copy number (24,776 genes) measured on 511 subjects. This data is also freely available at data portal maintained by Genomic Data Commons (GDC) https://portal.gdc.cancer.gov/. Prior to applying integrative clustering method, the dimension reduction of mRNA, methylation and CNV data were carried out by including around top 3 percentile features ranked by standard deviation in the decreasing order. This brings down the data into 584 mRNAs, 553 methylation features and 493 CNVs assayed on 511 samples which helps in reducing the noise and optimizing the computational cost. TCGA study has identified three subtypes of the LGG characterized by IDH mutation and 1p/19q co-deletion status; IDHmut-codel, IDHmut-non-codel and IDHwt[22].
The third study was from the TCGA studies on Head and Neck Squamous Cell Carcinoma (HNSCC) [24]. Head and Neck Cancer, a heterogeneous group of tumors including cancers of the oral cavity, larynx, pharynx, salivary glands and nose/nasal passages, is characterized by a common anatomic origin and most of such tumors develop from within the mucosa and are classified as Head and neck squamous cell carcinoma (HNSCC)[24]. The HNSCC TCGA data that we used in this example consists of 279 patients with clinical data, Illumina HiSeq2000 mRNA gene expression (20,149 genes), DNA Copy number variation (24,174, genes), Illumina HiSeq microRNA (1017, features) and Somatic mutation data (16566, genes). These data sets are also freely available at data portal maintained by TCGA Genomic Data Commons (GDC), https://portal.gdc.cancer.gov/. Prior to applying integrative clustering method, the dimension reduction of mRNA and CNV data were carried out by including around top 3 percentile features ranked by standard deviation in the decreasing order. The resulting data for the integrative clustering consists of 500 mRNAs and 500 CNVs assayed on 279 samples. In order to balance the number of features, 500 most varying microRNA features based on standard deviation were selected. Based on the gene expression data alone, TCGA study has identified four subtypes of the HNSCC named by; Atypical, Basal, Classical and Mesenchymal [24].
5. Results
5.1. Simulation Study
The simulated data sets were used to assess the ability of the proposed nNMF method to distinguish the true clusters (k). nNMF was also compared in terms of performance to the IntNMF method, Fig 2. In addition, the performances of the nNMF method was compared with popular iCluster method and SNF methods, Supplementary Figs. Fig 2 represents the plot of the performances of two methods nNMF and IntNMF with respect to ability to distinguish the true clusters and agreement of the resulting cluster-memberships with the true cluster memberships. The search range of k was set to 2 to 8 with the moderate effect size 3.5 (see Fig S1–S13 for complete results with all effects sizes considered in simulation). Each subplot represents the parameter values computed at each of the 30 initializations of the algorithm over the search range of k. Further, at each k, the average values are calculated and displayed as a line on the plot.
Fig. 2:
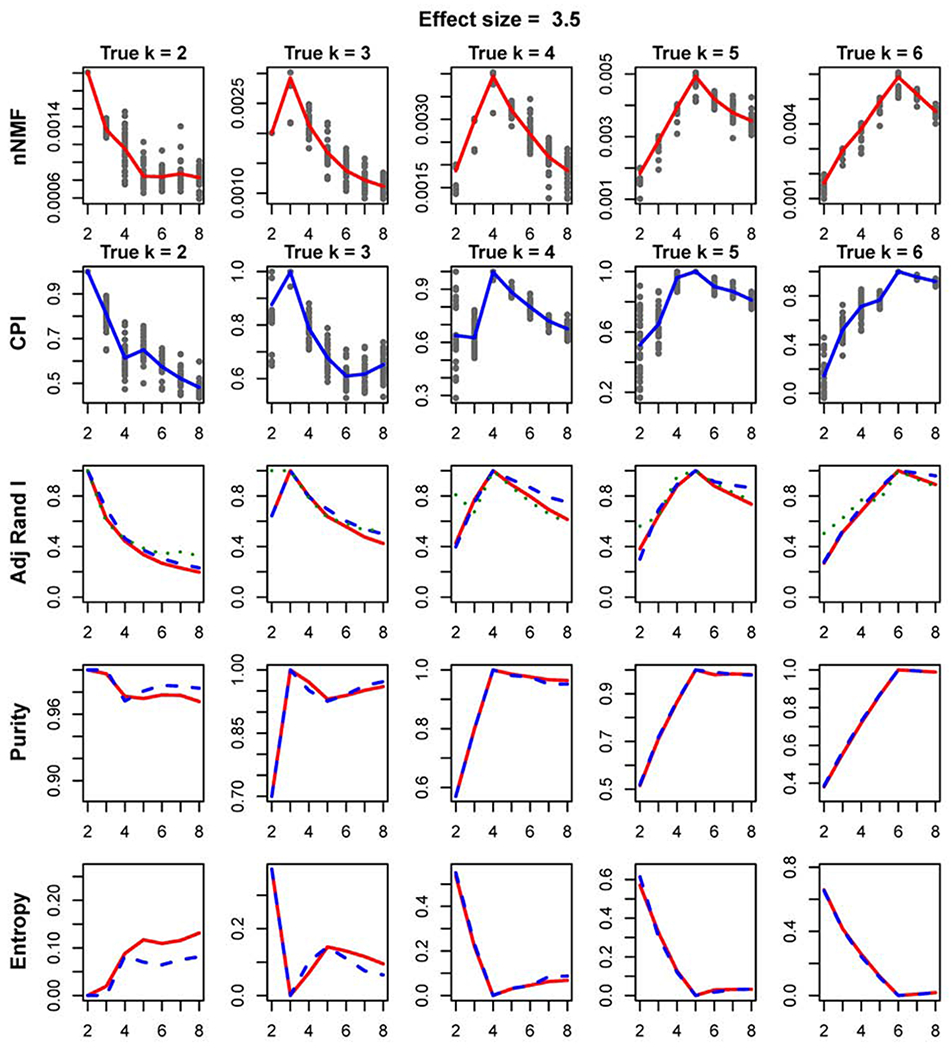
Plot showing the comparison of nNMF vs IntNMF: The plots represent the comparison of the two methods evaluated using the simulated data with moderate effect size of 3.5. The subplots on the first row show the silhouette width (nNMF) calculated over the search range of k from 2 to 8. Each column represents the true number of clusters k = 2, 3, 4, 5, and 6. The points represent the parameter values computed at each of 30 initializations of the algorithm. The averages of the parameter values at each k are calculated and displayed as lines in each subplot. CPI (intNMF) is shown in similar way in second row. Adjusted rand indices comparing (i) nNMF and Truth (red), (ii) IntNMF and Truth (blue), and (iii) nNMF and intNMF (green) are shown in third row. Fourth and fifth rows represent the cluster purity and entropy respectively.
First two rows in Fig 2 are the subplots of silhouette width and CPI, measure for nNMF and IntNMF methods, against search range of k. Both methods clearly peak at true number of clusters for each scenario of the true number of clusters. Adjusted rand index comparing true and computed cluster memberships are shown in third row of the figure. The adjusted rand index measures the agreements of the cluster memberships out of each of the two methods with true clustering assignment. The figures show that the adjusted rand index peaks at the true number of clusters and both methods agree at those peaks.
Cluster purity and entropy are other two measures of assessment of clustering performances[25]. Purity measures the proportion of the correct classification of the samples while entropy reflects any misclassification rate. Last two rows of Fig 2 represent the purity and entropy which indicate maximum purity and minimum entropy at the true number of clusters. Overall, simulation study shows that both methods are equally efficient for moderate to bigger effect sizes. nNMF performed better as compared to intNMF and iCluster in identifying the true number of clusters especially when the effect size was small, Supplementary Figures. In all other scenarios, nNMF worked competitively well with intNMF, iCluster and SNF, Supplementary Figures.
5.2. TCGA Glioblastoma, Lower Grade Glioma and Head and Neck Cancer studies
Glioblastoma data:
The nNMF identifies three optimum clusters with Glioblastoma, Fig 3. Cross-tabulation of previously identified subtypes using gene expression data[21] with the integrative subtypes identified by nNMF are shown in Table 1 and the heatmap is shown in Fig 3(a). The integrative clusters identified by nNMF strongly agreed with the previously reported clusters. The red and black colors of the heatmap displays subtypes defined using IntNMF, iCluster and SNF methods in such a way that red sample is in the cluster while black sample is not. The nNMF-C1 is made up of the Proneural type. nNMF-C2 is enriched by classical and nNMF-C3 is enriched by Messenchymal subtype. Similarly, nNMF-C1 strongly matches with iClust-C2, SNF-C1 and intNMF-C1, nNMF-C2 matches with iClust-C1, SNF-C2 and intNMF-C3, and nNMF-C3 matches with iClust-C3, SNF-C3 and intNMF-C2 (Supplementary S. Table 1). Additionally, overall survival of the patients was found to be significantly different among the three identified subtypes (p-value = 6.17×l0−3, log rank test). A few somatic mutations that were emphasized by Verhaak et al.[21] and TCGA studies[26] were examined with respect to their representation in each of the clusters identified by nNMF and are shown in Table 1. nNMF C1 that was made by Proneural is characterized by TP53-mutations, classical subtype enriched C2 is characterized by EFGR-mutations and PTEN-mutations, and the cluster C3 enriched by Mesenchymal is characterized by NF1-mutations.
Fig. 3:
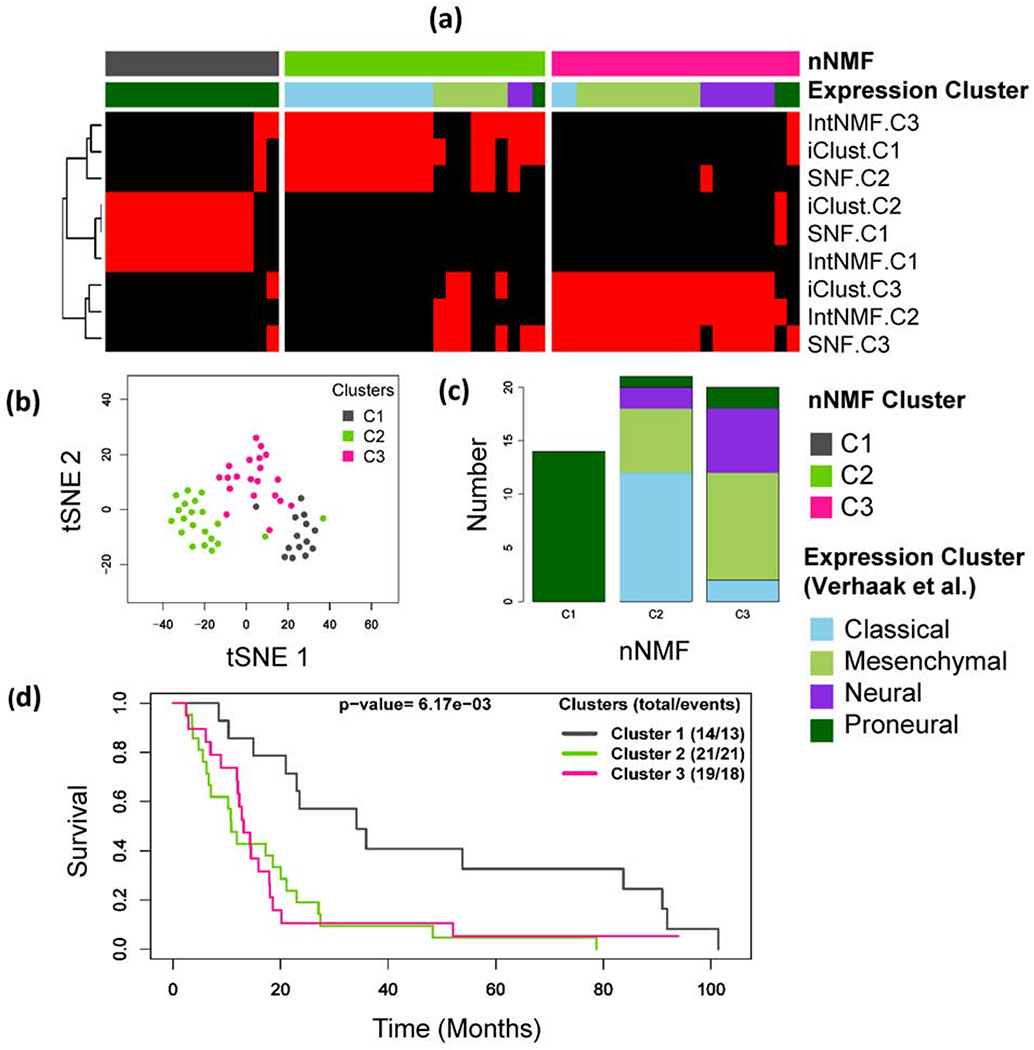
Glioblastoma example: (a) Integrative clustering of glioblastoma samples using three data types: DNA methylation, mRNA and copy number variation (CNV). The red and black panel shows subtypes identified by IntNMF, iCluster and SNF. Clusters are indicated by C1, C2 and C3. The red and black colors of the heatmap displays subtypes defined using IntNMF, iCluster and SNF methods in such a way that red sample is in the cluster while black sample is not. (b) Subgroups visualization using tSNE[27] method with colors indicating the clusters identified by nNMF. (c) Bar plot of nNMF clusters with expression subtypes indicated as segments. (d) Overall survival probability differences using Kaplan Meier method followed by log-rank test.
Table 1: Comparison of nNMF clusters with subtypes previously reported using gene expression data on Glioblastoma study.
The first panel of the table represents the cross tabular comparison of nNMF subtypes with the gene expression subtypes. Somatic mutations in a few previously highlighted genes[21, 26] are shown in second panel of Table by nNMF clusters.
|
nNMF
subtypes |
|||||
|---|---|---|---|---|---|
| C1 | C2 | C3 | Total | ||
| Expression Subtypes | Classical | 0 | 12 | 2 | 14 |
| Mesenchymal | 0 | 6 | 10 | 16 | |
| Neural | 0 | 2 | 6 | 8 | |
| Proneural | 14 | 1 | 2 | 17 | |
| Total | 14 | 21 | 20 | 55 | |
| Somatic Mutation | TP53 (%) | 64.3 | 28.6 | 31.6 | |
| NF1 (%) | 14.3 | 9.5 | 26.3 | ||
| PTEN (%) | 14.3 | 28.6 | 26.3 | ||
| EGFR (%) | 14.3 | 28.6 | 5.3 | ||
| PIK3R1 (%) | 28.6 | 14.3 | 0.0 | ||
| PIK3CA (%) | 7.1 | 4.8 | 5.3 | ||
| RB1 (%) | 7.1 | 0.0 | 15.8 | ||
| ERBB2 (%) | 14.3 | 9.5 | 15.8 | ||
Lower Grade Glioma data:
The integrative clustering with nNMF resulted in three clusters, Fig 4. The subtypes identified by nNMF were highly associated with subtypes identified by TCGA study[22]. The TCGA study classified the subtypes using a cluster-of-clusters analysis approach involving IDH mutation and 1p/19q co-deletion status by integrating cluster group assignments from the multiple individual platforms. nNMF-C1 is almost entirely made up of mutant IDH with non-codeletion, nNMF-C2 is enriched with IDH wild type, and nNMF-C3 is highly enriched with mutant IDH with codeletion (Table 2). The cross tabulation of nNMF subtypes with IDH mutation status, 1p/19q co-deletion status and histologic types and grades are presented in Table 2. The nNMF-C1 matches with the IntNMF-C3, SNF-C1 and iCluster-C2. nNMF-C2 matches with IntNMF-C1, SNF-C2 and iCluster-C1, and nNMF-C3 matches with IntNMF-C2, SNF-C3 and iCluster-C3 (Supplementary, S. Table 2). The survival probability differences across the three nNMF identified subtypes were assessed using Kaplan Meier method followed by log rank test (p-value=7.85×10−12), Fig 4(d). Consistent with TCGA study results, the survival outcome was most favorable for the patients having IDH mutation and 1p/19q codeletion (nNMF-C3).
Fig. 4:
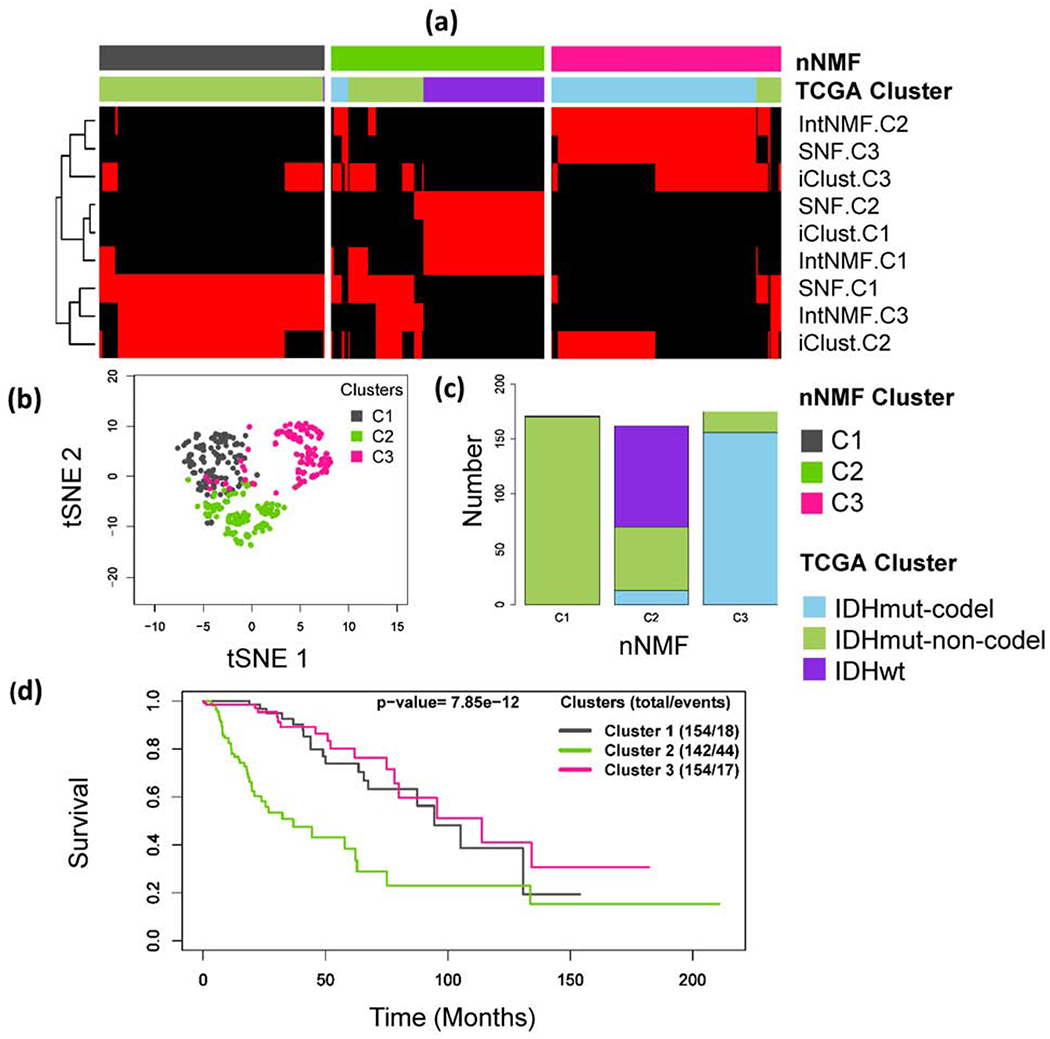
Lower Grade Glioma example: (a) Integrative clustering of subjects using three datasets: DNA methylation, mRNA expression, and copy number variation (CNV). The red and black panel shows subtypes identified by IntNMF, iCluster and SNF. Clusters are indicated by C1, C2 and C3. The red and black colors of the heatmap displays subtypes defined using IntNMF, iCluster and SNF methods in such a way that red sample is in the cluster while black sample is not. (b) Subgroups visualization using tSNE[27] method with colors indicating the clusters identified by nNMF. (c) Bar plot of nNMF clusters with expression subtypes indicated on the bars. (d) Overall survival probability differences using Kaplan Meier method followed by log-rank test.
Table 2: Comparison of nNMF clusters with TCGA subtypes on lower grade gliomas study.
TCGA study classified the subtypes based on a cluster of clusters analysis involving IDH mutation and 1p/19q co-deletion status integrating cluster group assignments from the four individual platforms (DNA methylation, mRNA, DNA copy number, and microRNA): IDH Mutation and 1p/19q Codeletion (TCGA Subtype-1), IDH Mutation and No 1p/19q Codeletion (TCGA Subtype-2) and IDH Wild Type (TCGA Subtype-3). Total of 511 subjects were used for NNMF but 3 subjects had missing IDH mutation status (First panel of table). Second panel of the table presents the IDH mutation and 1p/19q co-deletion status by nNMF cluster groups. Third panel represents histologic type and grade by cluster nNMF cluster groups.
|
nNMF
subtypes |
|||||
|---|---|---|---|---|---|
| C1 | C2 | C3 | Total | ||
| TCGA Subtypes | IDHmut-codel | 0 | 13 | 156 | 169 |
| IDHmut-non-codel | 170 | 57 | 19 | 246 | |
| IDHwt | 1 | 92 | 0 | 93 | |
| Total | 171 | 162 | 175 | 508 | |
| IDH Status | Mutant | 171 | 70 | 175 | 416 |
| Wild-type | 0 | 92 | 0 | 92 | |
| Co-deletion Status | Codel | 0 | 13 | 156 | 169 |
| Non-codel | 173 | 150 | 19 | 342 | |
| Astrocytome | |||||
| Grade II | 37 | 15 | 3 | 55 | |
| Grade III | 43 | 62 | 8 | 113 | |
| Histologic type and Grade | Oligoastrocytoma | ||||
| Grade II | 32 | 12 | 16 | 60 | |
| Grade III | 20 | 18 | 15 | 53 | |
| Oligodendroglioma | |||||
| Grade II | 20 | 18 | 60 | 98 | |
| Grade III | 3 | 18 | 52 | 73 | |
Head and Neck Squamous Cell Carcinoma (HNSCC) data:
The nNMF identifies four optimum clusters with HNSCC, Fig 5. Cross-tabulation of previously identified subtypes using gene expression data[24] with the integrative subtypes identified by nNMF are shown in Table 3 and the heatmap is shown in Fig 5(a). The nNMF-C1 is enriched by the Basal and Mesenchymal type. nNMF-C2 is enriched by Basal, netNMF-C3 is enriched by Atypical and nNMF-C4 is enriched by Mesenchymal subtype. Similarly, netNMF-C1 strongly matches with IntNMF-C2, nNMF-C2 matches with IntNMF-C3, SNF-C3 and iClust-C2, nNMF-C3 strongly matches with IntNMF-C3, SNF-C1 and iClust-C2, and nNMF-C4 strongly agrees with IntNMF-C4, SNF-C2 and entirely made up of iClust-C1 (Supplementary S. Table 3). Additionally, overall survival of the patients was found to be significantly different among the four identified subtypes (p-value = 3.43×10−2, log rank test), Fig 5d. A few somatic mutations that were emphasized by TCGA studies[24] were examined with respect to their representation in each of the identified subtypes by nNMF method and are shown in Table 3. Those genes were either significantly mutated between the tumor and normal samples or trended towards significance as reported by the TCGA studies[24]. The genes are also listed under the Catalogue Of Somatic Mutation In Cancer (COSMIC) database. nNMF-C1 that was enriched by the Basal and Mesenchymal is characterized by mutations in CDKN2A and TP53 genes, Basal enriched nNMF-C2 is characterized by CDKN2A, FAT1, CASP8, NOTCH1 and HRAS mutations. nNMF-C3 which is enriched with Atypical subtype is characterized by mutations in PIK3CA, KMT2D and NSD1 genes, and nNMF-C4 which is enriched by Mesenchymal subtype is characterized by TP53 and NOTCH1 mutations.
Fig. 5:
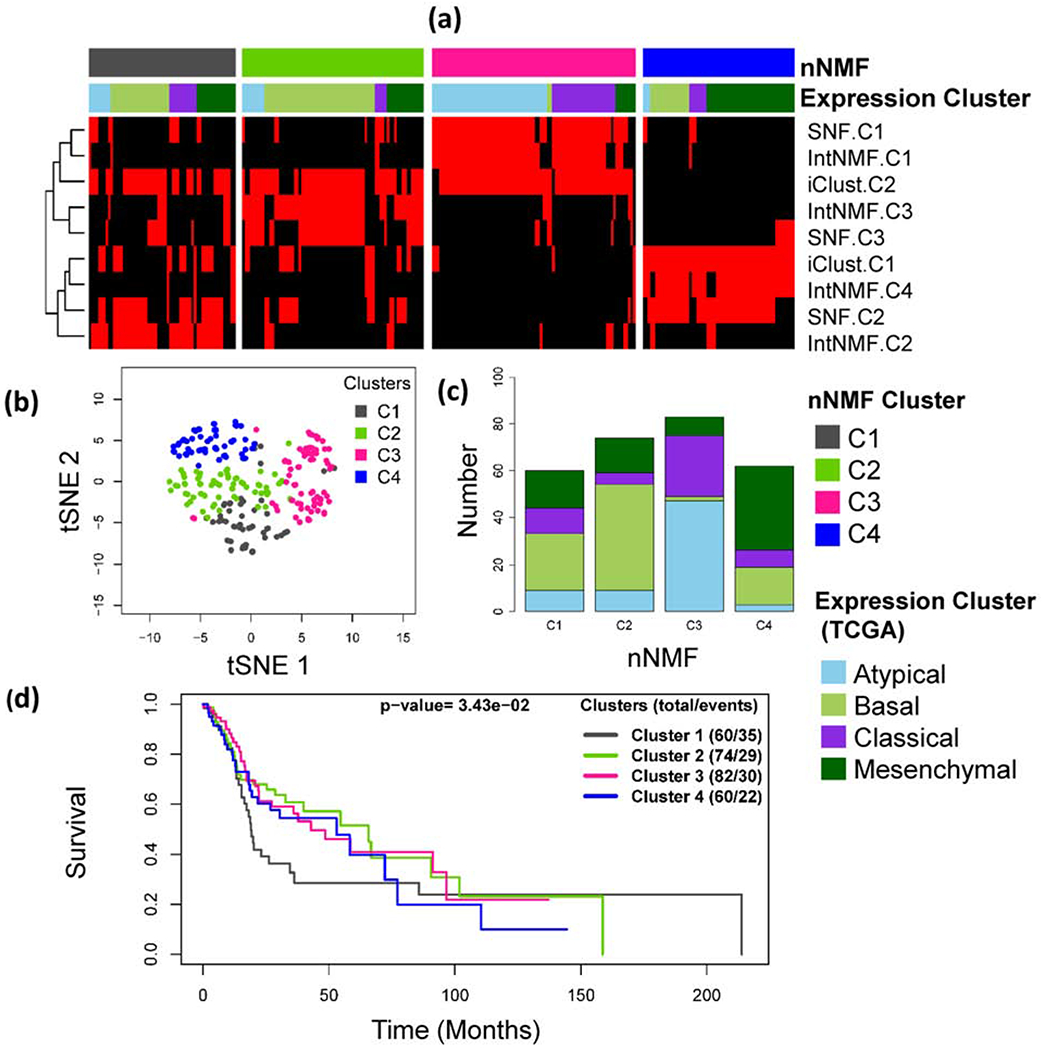
Head and Neck Squamous Cell Carcinoma (HNSCC): (a) Integrative clustering of HNSCC samples using three data types: mRNA, microRNA and copy number variation (CNV). The red and black panel shows subtypes identified by IntNMF, iCluster and SNF. Clusters are indicated by C1, C2 and C3. The red and black colors of the heatmap displays subtypes defined using IntNMF, iCluster and SNF methods in such a way that red sample is in the cluster while black sample is not. (b) Subgroups visualization using tSNE method with colors indicating the clusters identified by nNMF. (c) Bar plot of nNMF clusters with TCGA expression subtypes indicated as segments. (d) Overall survival probability differences using Kaplan Meier method followed by log-rank test.
Table 3: Comparison of nNMF clusters with subtypes previously reported using gene expression data on Head and Neck Squamous Cell Carcinoma study.
The first panel of the table represents the cross tabular comparison of nNMF subtypes with the gene expression subtypes as reported by TCGA study. Percentages of somatic mutations in a few previously highlighted genes[24] are shown in second panel of Table by nNMF clusters.
| nNMF subtypes | ||||||
|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | Total | ||
| Expression Subtypes | Atypical | 9 | 9 | 47 | 3 | 68 |
| Basal | 24 | 45 | 2 | 16 | 87 | |
| Classical | 11 | 5 | 26 | 7 | 49 | |
| Mesenchymal | 16 | 15 | 8 | 36 | 75 | |
| Total | 60 | 74 | 83 | 62 | 279 | |
| Somatic Mutation | CDKN2A (%) | 20.0 | 24.6 | 13.4 | 8.7 | |
| FAT1 (%) | 8.0 | 24.6 | 7.5 | 17.4 | ||
| TP53 (%) | 60.0 | 58.5 | 46.3 | 60.9 | ||
| CASP8 (%) | 2.0 | 15.4 | 0.0 | 6.5 | ||
| AJUBA (%) | 8.0 | 6.2 | 0.0 | 2.2 | ||
| PIK3CA (%) | 6.0 | 13.8 | 23.9 | 13.0 | ||
| NOTCH1 (%) | 16.0 | 20.0 | 6.0 | 17.4 | ||
| KMT2D (%) | 14.0 | 7.7 | 14.9 | 8.7 | ||
| NSD1 (%) | 2.0 | 6.2 | 17.9 | 4.3 | ||
| TGFBR2 (%) | 4.0 | 3.1 | 0.0 | 2.2 | ||
| HRAS (%) | 2.0 | 4.6 | 3.0 | 2.2 | ||
6. Discussion
We propose integrative clustering method nNMF to classify the data by utilizing the strengths of the non-negative matrix factorization and sample similarity networks. nNMF can handle any type of genomic data that are presented in continuous scale. The method constructs stable consensus networks for each type of the data separately. Since each consensus network is generated for each data type, the method is not affected by the varying distributions and scales of multiple data types. A common challenge of many latent subtype identification method has been the lack of prior information. In other words, the methods are generally based on unsupervised techniques which might result in overfitting or underfitting of the data. On order to partially address this issue the robust and stable consensus matrices are calculated using the resampling based cross-validation method that is built in intNMF[9] function. The method integrates the generated networks to create a robust single consensus network which is then utilized to partition the data using spectral clustering. Extensive simulation studies were completed to assess the ability of proposed nNMF method. Additionally, nNMF was applied on two glioma studies from TCGA and one head and neck cancer from TCGA. The results from these analyses have elucidated that nNMF is able to efficiently extract the latent clustering structure hidden in the data. The examples based on the simulated data and the real-life data have demonstrated that nNMF method is clearly an addition to the existing list of only a few integrative clustering methods. The results of nNMF strongly agree with the results from previous studies and methods. In addition, with the simulated data, nNMF demonstrated better ability of detecting the true clusters for small effect size.
In this manuscript, we selected three previously proposed integrative clustering methods to compare with the proposed method: IntNMF[9], SNF[4] and iCluster[6]. The main purpose of the manuscript is to demonstrate the applicability of the proposed method rather than carrying out the substantial analyses of the data. We chose IntNMF and SNF methods because the proposed method leverages the advantages of the two methods. We selected model based iCluster method because of its widespread popularity and application. Our simulation studies show that all the four methods work well for the given reasonable effect size. When the effect size is small the proposed method performs better. Since the data were simulated using the multivariate gaussian distribution, the statistical distribution assumption of the iCluster was met and it performed similar to that of non-parametric methods. But high dimensional real-life data generally does not follow the specific statistical distribution. In the two real data examples on gliomas, all four methods result in three optimum clusters while with the HNSCC example, there were differing number of clustering results, S.Tables 1–3. The results of the nNMF closely agreed with the IntNMF as measured by the adjusted Rand Index. There were least agreements of the nNMF clustering results to that of the iCluster. One reason of low performance of the iCluster is that the data does not satisfy the normality assumption which is the requirement of the method. Since the multiple types of real data can have disparate types of distributions, these results show that parametric methods are generally more robust in their applications. With the two glioma studies the survival probabilities among the identified subtypes by all methods are statistically significantly different, Fig S42 and Fig S43. But there was no significant difference in the survival probability among the two subtypes identified by iCluster with the HNSCC example, Fig S44. Overall, if the model assumptions are satisfied all the four methods perform well. But, if the model assumptions are not met, non-parametric methods perform better than the model-based methods. With the IntNMF, prior estimation and assignment of the weight for each data will be helpful in optimizing the outcomes and rescaling of the data is required. SNF is based on the exponential kernel function to define the sample similarity matrix calculated using Euclidean or other distance measures[4]. However, the kernel-based clustering of SNF has been criticized for its unstable nature of making the algorithm too sensitive to small changes in genomic assays[10]. The proposed method does not have such requirements and therefore has wider scope of application.
In summary, development of the high-throughput technologies and the reduction in cost to assay the molecular information have resulted in multiple types of high dimensional data and this trend is expected to continue for the foreseeable future. Such increasing complexities not only pose statistical challenges but have also created opportunities to develop more efficient integrative ‘omics data analysis methods to understand the biological differences between cancers and within a given cancer. Molecular clustering helps to identify the disease subtypes that the histological or morphological examinations alone cannot reveal. The comprehensive investigation of the inter- and intra- relationships in biological process and the regulatory mechanisms provide a deeper understanding of the disease mechanism which will, in turn, help in the efforts geared towards personalized and precision medicine and treatment. To this end, we propose the network based integrative clustering method using non-negative matrix factorization that allows for integrative analysis of multiple genomic data having varying distributions and scales. The computer program for the method is written in R and is available upon request.
Supplementary Material
Highlights.
Integrative approaches for the study of biological systems have gained widespread popularity.
There is lack of efficient non-parametric integrative clustering methods to assess “systems-biology”.
nNMF provides flexible non-parametric method of integrative clustering
nNMF can handle data without requiring to rescale them which adds more flexibility in the application
nNMF allows researchers to identify disease subtypes using several types of data collected on same set of patient samples.
Acknowledgements
We thank The Cancer Genome Atlas (TCGA) project for the data from Glioblastoma and Lower Grade Gliomas and Head and Neck Squamous Cell carcinoma.
Funding: This work was supported in part by the Clinical and Translational Science Award grant [UL1TR002366], University of Kansas Cancer Center [P30 CA168524] and the National Institute of Health [R21 CA182715].
Footnotes
Conflict of Interest: none declared.
References
- [1].Sørlie T, Perou CM, Tibshirani R, Aas T, Geisler S, Johnsen H, Hastie T, Eisen MB, van de Rijn M, Jeffrey SS, Thorsen T, Quist H, Matese JC, Brown PO, Botstein D, Lonning PE, Borresen-Dale A-L, Gene expression patterns of breast carcinomas distinguish tumor subclasses with clinical implications, Proceedings of the National Academy of Sciences, 98 (2001) 10869–10874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Sotiriou C, Neo S-Y, McShane LM, Korn EL, Long PM, Jazaeri A, Martiat P, Fox SB, Harris AL, Liu ET, Breast cancer classification and prognosis based on gene expression profiles from a population-based study, Proceedings of the National Academy of Sciences, 100 (2003) 10393–10398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Chalise P, Koestler DC, Bimali M, Yu Q, Fridley BL, Integrative clustering methods for high-dimensional molecular data, Translational cancer research, 3 (2014) 202–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Wang B, Mezlini AM, Demir F, Fiume M, Tu Z, Brudno M, Haibe-Kains B, Goldenberg A, Similarity network fusion for aggregating data types on a genomic scale, Nature Methods, 11 (2014) 333. [DOI] [PubMed] [Google Scholar]
- [5].The Cancer Genome Atlas Network, Comprehensive molecular portraits of human breast tumours, Nature, 490 (2012) 61–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Shen R, Olshen AB, Ladanyi M, Integrative clustering of multiple genomic data types using a joint latent variable model with application to breast and lung cancer subtype analysis, Bioinformatics, 25 (2009) 2906–2912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Lock EF, Dunson DB, Bayesian consensus clustering, Bioinformatics, 29 (2013) 2610–2616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Kirk P, Griffin JE, Savage RS, Ghahramani Z, Wild DL, Bayesian correlated clustering to integrate multiple datasets, Bioinformatics, 28 (2012) 3290–3297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Chalise P, Fridley BL, Integrative clustering of multi-level ‘omic data based on non-negative matrix factorization algorithm, PloS one, 12 (2017) e0176278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Nguyen T, Tagett R, Diaz D, Draghici A novel approach for data integration and disease subtyping, Genome Research, 27 (2017) 2025–2039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Monti S, Tamayo P, Mesirov J, Golub T, Consensus clustering: A resampling-based method for class discovery and visualization of gene expression microarray data, Mach Learn, 52 (2003) 91–118. [Google Scholar]
- [12].Brunet JP, Tamayo P, Golub TR, Mesirov JP, Metagenes and molecular pattern discovery using matrix factorization, Proceedings of the National Academy of Sciences of the United States of America, 101 (2004) 4164–4169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Paatero P, Tapper U, Positive Matrix Factorization - a Nonnegative Factor Model with Optimal Utilization of Error-Estimates of Data Values, Environmetrics, 5 (1994) 111–126. [Google Scholar]
- [14].Lee DD, Seung HS, Learning the parts of objects by non-negative matrix factorization, Nature, 401 (1999) 788–791. [DOI] [PubMed] [Google Scholar]
- [15].Berry MW, Browne M, Langville AN, Pauca VP, Plemmons RJ, Algorithms and applications for approximate nonnegative matrix factorization, Computational statistics & data analysis, 52 (2007) 155–173. [Google Scholar]
- [16].Lawson C, Hanson R, Solving Least Squares Problems, SIAM, (1995). [Google Scholar]
- [17].Pearl J, Probabilistic reasoning in intelligent systems: networks of plausible inference, Morgan Kaufmann Publishers Inc. 1988. [Google Scholar]
- [18].Boutsidis C, Gallopoulos E, SVD based initialization: A head start for nonnegative matrix factorization, Pattern Recogn, 41 (2008) 1350–1362. [Google Scholar]
- [19].Chalise P, Raghavan R, Fridley BL, InterSIM: Simulation tool for multiple integrative ‘omic datasets’, Computer Methods and Programs in Biomedicine, 128 (2016) 69–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Shen R, Mo Q, Schultz N, Seshan VE, Olshen AB, Huse J, Ladanyi M, Sander C, Integrative subtype discovery in glioblastoma using iCluster, PloS one, 7 (2012) e35236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Verhaak RGW, Hoadley KA, Purdom E, Wang V, Qi Y, Wilkerson MD, Miller CR, Ding L, Golub T, Mesirov JP, Alexe G, Lawrence M, O’Kelly M, Tamayo P, Weir BA, Gabriel S, Winckler W, Gupta S, Jakkula L, Feiler HS, Hodgson JG, James CD, Sarkaria JN, Brennan C, Kahn A, Spellman PT, Wilson RK, Speed TP, Gray JW, Meyerson M, Getz G, Perou CM, Hayes DN, Integrated Genomic Analysis Identifies Clinically Relevant Subtypes of Glioblastoma Characterized by Abnormalities in PDGFRA, IDH1, EGFR, and NF1, Cancer Cell, 17 (2010) 98–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].The Cancer Genome Atlas Network, Comprehensive, Integrative Genomic Analysis of Diffuse Lower-Grade Gliomas, New England Journal of Medicine, 372 (2015) 2481–2498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Ceccarelli M, Barthel Floris P., Malta Tathiane M., Sabedot Thais S., Salama Sofie R., Murray Bradley A., Morozova O, Newton Y, Radenbaugh A, Pagnotta Stefano M., Anjum S, Wang J, Manyam G, Zoppoli P, Ling S, Rao Arjun A., Grifford M, Cherniack Andrew D., Zhang H, Poisson L, Carlotti Carlos G., Tirapelli Daniela Pretti da C., Rao A, Mikkelsen T, Lau Ching C., Yung WKA, Rabadan R, Huse J, Brat Daniel J., Lehman Norman L., Barnholtz-Sloan Jill S., Zheng S, Hess K, Rao G, Meyerson M, Beroukhim R, Cooper L, Akbani R, Wrensch M, Haussler D, Aldape Kenneth D., Laird Peter W., Gutmann David H., Anjum S, Arachchi H, Auman JT, Balasundaram M, Balu S, Barnett G, Baylin S, Bell S, Benz C, Bir N, Black Keith L., Bodenheimer T, Boice L, Bootwalla Moiz S., Bowen J, Bristow Christopher A., Butterfield Yaron S.N., Chen Q-R, Chin L, Cho J, Chuah E, Chudamani S, Coetzee Simon G., Cohen Mark L., Colman H, Couce M, D’Angelo F, Davidsen T, Davis A, Demchok John A., Devine K, Ding L, Duell R, Elder JB, Eschbacher Jennifer M., Fehrenbach A, Ferguson M, Frazer S, Fuller G, Fulop J, Gabriel Stacey B., Garofano L, Gastier-Foster Julie M., Gehlenborg N, Gerken M, Getz G, Giannini C, Gibson William J., Hadjipanayis A, Hayes DN, Heiman David I., Hermes B, Hilty J, Hoadley Katherine A., Hoyle Alan P., Huang M, Jefferys Stuart R., Jones Corbin D., Jones Steven J.M., Ju Z, Kastl A, Kendler A, Kim J, Kucherlapati R, Lai Phillip H., Lawrence Michael S., Lee S, Leraas Kristen M., Lichtenberg Tara M., Lin P, Liu Y, Liu J, Ljubimova Julia Y., Lu Y, Ma Y, Maglinte Dennis T., Mahadeshwar Harshad S., Marra Marco A., McGraw M, McPherson C, Meng S, Mieczkowski Piotr A., Miller CR, Mills Gordon B., Moore Richard A., Mose Lisle E., Mungall Andrew J., Naresh R, Naska T, Neder L, Noble Michael S., Noss A, O’Neill Brian P., Ostrom Quinn T., Palmer C, Pantazi A, Parfenov M, Park Peter J., Parker Joel S., Perou Charles M., Pierson Christopher R., Pihl T, Protopopov A, Radenbaugh A, Ramirez Nilsa C., Rathmell WK, Ren X, Roach J, Robertson AG, Saksena G, Schein Jacqueline E., Schumacher Steven E., Seidman J, Senecal K, Seth S, Shen H, Shi Y, Shih J, Shimmel K, Sicotte H, Sifri S, Silva T, Simons Janae V., Singh R, Skelly T, SSloan Andrew E., Sofia Heidi J., Soloway Matthew G., Song X, Sougnez C, Souza C, Staugaitis Susan M., Sun H, Sun C, Tan D, Tang J, Tang Y, Thorne L, Trevisan Felipe A., Triche T, Van Den Berg David J., Veluvolu U, Voet D, Wan Y, Wang Z, Warnick R, Weinstein John N., Weisenberger Daniel J., Wilkerson Matthew D., Williams F, Wise L, Wolinsky Y, Wu J, Xu Andrew W., Yang L, Yang L, Zack Travis I., Zenklusen Jean C., Zhang J, Zhang W, Zhang J, Zmuda E, Noushmehr H, Iavarone A, Verhaak RGW, Molecular Profiling Reveals Biologically Discrete Subsets and Pathways of Progression in Diffuse Glioma, Cell, 164 (2016) 550–563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].The Cancer Genome Atlas Network, Comprehensive genomic characterization of head and neck squamous cell carcinomas, Nature, 517 (2015) 576–582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Kim H, Park H, Sparse non-negative matrix factorizations via alternating non-negativity-constrained least squares for microarray data analysis, Bioinformatics, 23 (2007) 1495–1502. [DOI] [PubMed] [Google Scholar]
- [26].The Cancer Genome Atlas Network, Comprehensive genomic characterization defines human glioblastoma genes and core pathways, Nature, 455 (2008) 1061–1068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Maaten L.v.d., Hinton G, Visualizing data using t-SNE, Machine Learning Research, 9 (2008) 2579–2605. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


