Bayesian Data Assimilation to Support Informed Decision Making in Individualized Chemotherapy

Abstract

An essential component of therapeutic drug/biomarker monitoring (TDM) is to combine patient data with prior knowledge for model‐based predictions of therapy outcomes. Current Bayesian forecasting tools typically rely only on the most probable model parameters (maximum a posteriori (MAP) estimate). This MAP‐based approach, however, does neither necessarily predict the most probable outcome nor does it quantify the risks of treatment inefficacy or toxicity. Bayesian data assimilation (DA) methods overcome these limitations by providing a comprehensive uncertainty quantification. We compare DA methods with MAP‐based approaches and show how probabilistic statements about key markers related to chemotherapy‐induced neutropenia can be leveraged for more informative decision support in individualized chemotherapy. Sequential Bayesian DA proved to be most computationally efficient for handling interoccasion variability and integrating TDM data. For new digital monitoring devices enabling more frequent data collection, these features will be of critical importance to improve patient care decisions in various therapeutic areas.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ Typically, maximum a posteriori (MAP) estimation is used to combine prior knowledge with patient‐specific monitoring data for model‐based predictions to support individualized therapy (e.g., in chemotherapy).

• WHAT QUESTION DID THIS STUDY ADDRESS?

☑ The study addresses major limitations of MAP‐based prediction for efficient and reliable clinical decision support: (i) it only provides a point estimate without associated uncertainties, (ii) it does not transform into the most probable observation (e.g., nadir concentration), and (iii) it processes data in a batch.

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

☑ Bayesian data assimilation (DA) methods are compared that allow a comprehensive uncertainty quantification by approximating the full posterior distribution. We demonstrate the advantages of uncertainty quantification in therapeutic drug/biomarker monitoring for chemotherapy‐induced neutropenia. Sequential DA methods were found to be particularly suitable for long‐run analyses as they process data sequentially.

• HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTIC?

☑ Comprehensive uncertainty quantification and recursive data processing enable reliable, efficient, and individual decision support during ongoing treatment and will become increasingly relevant with the development of novel digital monitoring devices.

In the presence of a narrow therapeutic window and large interpatient variability, therapeutic drug/biomarker monitoring (TDM) is indicated for safe and efficacious therapies. With the help of Bayesian forecasting tools, patient‐specific data are combined with prior knowledge from previous clinical studies and a drug‐specific model to enable model‐informed precision dosing (MIPD).1 Typically, only the most probable individual parameter values (i.e., the maximum a posteriori (MAP) estimates, are used to predict the individual therapy outcome without quantifying associated uncertainties.2 Thus, relevant risks associated with a dosing regimen selection (e.g., treatment inefficacy or unacceptable toxicity), are not determined hindering well‐founded therapeutic decision making.

Quantifying associated uncertainties is at the heart of making more informed decisions, not only in clinical applications. In this article, we thoroughly compare in a TDM context different Bayesian data assimilation (DA) methods that either (i) estimate the full posterior distribution (termed full Bayesian approaches) to quantify uncertainties, or (ii) estimate only its mode (MAP estimation) without uncertainty quantification. The full Bayesian approaches comprise not only methods that process patient data collected over time in a batch (i.e., all at once), like Markov Chain Monte Carlo (MCMC), sampling importance resampling (SIR), and a normal approximation (NAP) to the posterior at the MAP estimate, but also particle filters (PFs) that allow for efficient sequential data processing. PFs are well‐established in areas of application in which real‐time predictions based on online/monitoring data are required, as in navigation, meteorology, and tracking.3, 4, 5

In the context of chemotherapy‐induced neutropenia—the most frequent dose‐limiting side effect for cytotoxic anticancer drugs with substantial decrease of neutrophil granulocytes and, thus, potentially life‐threatening fever and infections6—we demonstrate the clear benefits of uncertainty quantification compared with purely MAP‐based predictions (e.g., ref. 7) using the gold‐standard model for neutropenia.8 Further, we compare the full Bayesian approaches regarding quality of uncertainty quantification and computational runtime for multiple cycle chemotherapy.9 Although MCMC, SIR, and PF all provide a reliable uncertainty quantification, the efficient data processing of the sequential approach will be clearly beneficial in a continuous monitoring context, where digital healthcare devices (e.g., wearables) allow patients to measure and report individual marker concentrations online.

Methods

First, the statistical framework of MIPD in TDM is introduced, which is used throughout the different methods described below. Then, the considered clinical application scenarios are described along with the prior knowledge from literature.

Statistical framework

TDM in the context of MIPD builds on prior knowledge in the form of a structural, observational, covariate, and statistical model. In the sequel, TDM data are considered for a single individual and, therefore, there is no running index for individuals. The structural and observational models are given as:

$$\frac{\mathrm{d}x}{\mathrm{d}t}(t)=f(x(t);\mathrm{\theta },u),x(t_0)=x_0(\mathrm{\theta })$$ (1)

$$h(t)=h(x(t),\mathrm{\theta })$$ (2)

with state vector $x=x\left(t\right)$ (including drug/biomarker concentrations), individual parameter values $\mathrm{\theta }$ (e.g., volumes and clearances), and rates of change $f(x;\mathrm{\theta },u)$ of all state variables for a given input u (e.g., dose). Because typically only a part of the state variables is observed, the function h maps x to the observed quantities $h(x,\mathrm{\theta })$ (e.g., plasma drug or neutrophil concentration), including potential state‐space transformations (e.g., log‐transformed output). The initial conditions $x_0$ are defined by the pretreatment levels (e.g., baseline values). The covariate and statistical model link the patient‐specific covariates “cov” and observations ${(t_j,y_j)}_{j=1,\dots ,n}$ to the model predictions $h_j(\mathrm{\theta })=h(x(t_j),\mathrm{\theta })$, accounting for measurement errors and possibly model misspecification.

$$Y_{j|\mathrm{\Theta }=\mathrm{\theta }}\sim p(·|\mathrm{\theta };h_j\left(\mathrm{\theta }\right),\mathrm{\Sigma }),j=1,\dots ,n\left(\text{independent}\right)$$ (3)

$$\mathrm{\Theta }\sim p_{\mathrm{\Theta }}\left(·;{\mathrm{\theta }}^{\text{TV}}\left(\text{cov}\right),\mathrm{\Omega }\right),$$ (4)

where ${\mathrm{\theta }}^{\text{TV}}(\text{cov})$ denotes the typical hyperparameter values (TV) that might depend on covariates. The dot (“·”) in a probability distribution serves as placeholder for its argument. Often, $Y_{j|\mathrm{\Theta }=\mathrm{\theta }}=h_j\left(\mathrm{\theta }\right)+{\mathrm{\epsilon }}_j$ with ${\mathrm{\epsilon }}_j{\sim }_{\mathit{iid}}\mathcal{N}\left(0,\mathrm{\Sigma }\right)$. Prior knowledge about the parameters is provided by population analyses of clinical studies, in which nonlinear mixed effect (NLME) approaches are used to estimate the functional relationship $\text{cov}\mapsto {\mathrm{\theta }}^{\text{TV}}\left(\text{cov}\right)$, and the parameters $\mathrm{\Sigma }$ and $\mathrm{\Omega }$.

The challenge in MIPD is to infer information on the individual parameter values $\mathrm{\theta }$ of a patient based on his/her covariate values and measurements. Here, a Bayesian approach is highly beneficial: the unexplained interindividual variability in the population model (Eq. 4) defines the prior uncertainty about the individual parameter values. In this context, the hyperparameters (i.e., all parameters after the semicolon in Eq. 4) are assumed to be known (fixed). As a consequence, we drop them as well as the subscripts in the notation in the sequel. As a result, the likelihood at the individual level reads $p(·|\mathrm{\theta })=p(·|\mathrm{\theta };h_j\left(\mathrm{\theta }\right),\mathrm{\Sigma })$ and the prior $p(·)=p_{\mathrm{\Theta }}\left(·;{\mathrm{\theta }}^{\text{TV}}\left(\text{cov}\right),\mathrm{\Omega }\right)$. Then, assimilating measurements $y_{1:n}={(y_1,\dots ,y_n)}^T$ into the model based on Bayes's formula:

$$p(\mathrm{\theta }|y_{1:n})=\frac{p(y_{1:n}|\mathrm{\theta })·p\left(\mathrm{\theta }\right)}{p\left(y_{1:n}\right)}$$ (5)

allows to learn about individual parameter values from the data. The remaining uncertainty of parameter values is encoded in the posterior $p(·|y_{1:n})$. Note that $p(y_{1:n}|\mathrm{\theta })=p(y_1|\mathrm{\theta })·\dots ·p(y_n|\mathrm{\theta })$ due to independence in Eq. 3. The denominator $p\left(y_{1:n}\right)$ in Eq. 5 serves as a normalization factor, denoting the probability of the data. In contrast to MAP estimation, which summarizes the posterior by its mode, Bayesian DA approaches rely on sample approximations of the posterior

$$p(\mathrm{\theta }|y_{1:n})\approx \sum _{s=1}^S{w}_n^{\left(s\right)}{\delta }_{{\mathrm{\theta }}_n^{\left(s\right)}}(\mathrm{\theta })$$ (6)

based on a sample

$${\mathbb{S}}_n:=\left\{\left({\mathrm{\theta }}_n^{(s)},w_n^{(s)}\right),s=1,\dots ,S\right\},$$

with sample parameters ${\mathrm{\theta }}_n^{\left(s\right)}$ of the posterior (Section 2.5 in ref. 10), weights $w_n^{\left(s\right)}$, which sum to one (i.e., ${\sum }_{s=1}^S{w}_n^{\left(s\right)}$=1 and point masses ${\mathrm{\delta }}_{{\mathrm{\theta }}_n^{\left(s\right)}}$ at ${\mathrm{\theta }}_n^{\left(s\right)}$). If $w_n^{\left(s\right)}=1/S$ for all s, the sample is called unweighted. Based on the posterior sample, we may also approximate quantities of interest in the observable space by solving Eqs. 1 and 2 for all elements in ${\mathbb{S}}_n$. This also serves as the basis for credible intervals (CrIs); applying subsequently the residual error model Eq. 3, the basis for prediction intervals.

Because direct sampling from the posterior is, in general, not possible, alternative approaches (described below) need to be used to generate a sample of the posterior. For a detailed description, see Section S3 –Section S7 .

MAP estimation

MAP estimation approximates the mode of the posterior distribution (i.e., the most probable parameter values given patient‐specific measurements $y_{1:n}$):

$${\widehat{\mathrm{\theta }}}_n^{\text{MAP}}=\underset{\mathrm{\theta }}{argmax}p(\mathrm{\theta }|y_{1:n}).$$ (7)

The MAP estimate ${\widehat{\mathrm{\theta }}}_n^{\text{MAP}}$ is a one‐point summary of the posterior distribution, without quantification of the associated uncertainty.

NAP

To overcome the one‐point summary limitation of the MAP estimate, the posterior $p(·|y_{1:n})$ may be approximated locally by a normal distribution located at the MAP estimate (Section 4.1 in ref. 11).

$$p(·|y_{1:n})\approx \mathcal{N}\left({\widehat{\mathrm{\theta }}}_n^{\text{MAP}},{\mathcal{I}}^{-1}\left({\widehat{\mathrm{\theta }}}_n^{\text{MAP}}\right)\right),$$ (8)

where $\mathcal{I}$ denotes the total observed Fisher information matrix (Section 2.5 in ref. 12).

$$\mathcal{I}\left(\mathrm{\theta }\right):={\mathcal{I}}^{\text{post}}\left(\mathrm{\theta }\right)=-\frac{{\mathrm{d}}^2}{\mathrm{d}{\mathrm{\theta }}^2}\log p(\mathrm{\theta }|y_{1:n})$$

of the posterior. The uncertainty in the parameters is then propagated to the observables by first sampling from the normal distribution in Eq. 8 and then solving the structural model for each sample.13 Alternatively to this sampling‐based approach, the Delta method (Section 5.5 in ref. 14) could be used, see also Section S4 and Figure S2 .

SIR

The SIR algorithm is a full Bayesian approach. It generates an unweighted sample ${\mathbb{S}}_n$ from the posterior $p(\mathrm{\theta }|y_{1:n})$ based on a sample from a so‐called importance distribution G, from which samples can easily be generated (Section 10.4 in ref. 11). SIR proceeds in three steps. S‐Step: Sampling from the importance distribution G resulting in a sample ${\tilde{\mathbb{S}}}_n$. We considered the prior as importance distribution, assuming that the patient under consideration is sufficiently well‐represented by the clinical patient populations given by the prior. I‐Step: Each sample point ${\tilde{\mathrm{\theta }}}_n^{\left(s\right)}\in {\tilde{\mathbb{S}}}_n$ is assigned an importance weight ${\tilde{w}}_n^{\left(s\right)}=p(y_{1:n}|{\tilde{\mathrm{\theta }}}_n^{\left(s\right)})$ given by the likelihood (in case G is the prior). R‐Step: After normalization of the weights $w_n^{(s)}={\tilde{w}}_n^{(s)}/{\sum }_s{\tilde{w}}_n^{(s)}$, a resampling is performed: S unweighted samples ${\mathrm{\theta }}_n^{\left(s\right)}$ are drawn from ${\tilde{\mathrm{\theta }}}_n^{\left(s\right)}$ according to weights $w_n^{\left(s\right)}$.

Note that once a new data point $y_{n+1}$ becomes available, the SIR algorithm does not simply update the present sample points ${\mathrm{\theta }}_n^{\left(s\right)}$ in ${\mathbb{S}}_n$, but re‐performs all three steps based on the updated posterior $p(·|y_{1:n+1})$ to determine ${\mathbb{S}}_{n+1}$.

MCMC

A popular alternative to SIR in Bayesian inference are MCMC methods with a wide range of different algorithms.15 MCMC generates an unweighted sample ${\mathbb{S}}_n$ from the posterior by means of a Markov chain (Section 11 in ref. 11). MCMC comprises two steps to generate sample points ${\mathrm{\theta }}_n^{\left(s\right)}$: a proposal step (generating a potential new sample point ${\mathrm{\theta }}^{\ast }$) and an acceptance step (accepting or rejecting ${\mathrm{\theta }}^{\ast }$ as a new sample point). The challenge in MCMC is to design application‐specific proposal distributions.

In TDM, MCMC was previously considered with the prior as fixed proposal distribution (independence sampler) for sparse patient monitoring data.16 We observed, however, large rejection rates with increasing number n of data points, because the posterior becomes narrower, see Section S6 . To counteract large rejection rates, we used an adaptive Metropolis‐Hastings sampler with log‐normally distributed proposal distribution (see Section S6 and Figure S4 for details).

PF

In contrast to SIR and MCMC, which process data in a batch, PF constitutes a sequential approach to DA, see 3, 17, 18 for a detailed introduction. Given a weighted sample ${\mathbb{S}}_n$ of the posterior $p(·|y_{1:n})$ and a new data point $y_{n+1}$, PF generates a weighted sample ${\mathbb{S}}_{n+1}$ of the posterior $p(·|y_{1:n+1})$ by updating ${\mathbb{S}}_n$ using a sequential version of Bayes's formula, as follows:

$$p(\mathrm{\theta }|y_{1:n+1})\propto p(y_{n+1}|\mathrm{\theta })·p(\mathrm{\theta }|y_{1:n}).$$ (9)

For $n=0$, the distribution $p(\mathrm{\theta }|y_{1:0})$ is identical to the prior $p\left(\mathrm{\theta }\right)$ (Section 3 in ref. 10). Note that $p(y_{n+1}|\mathrm{\theta })=p(y_{n+1}|y_{1:n},\mathrm{\theta })$ due to independence in Eq. 3. Analogously to the I‐step in SIR, the weights $w_n^{\left(s\right)}$ are updated proportional to the (local) likelihood: $w_{n+1}^{\left(s\right)}\propto p(y_{n+1}|\mathrm{\theta })·w_n^{\left(s\right)}$ involving, however, only the new data point $y_{n+1}$. As in SIR and MCMC, evaluation of the likelihood involves solving the structural model (1). Because the structural model is deterministic, one may either solve Eq. 1 with initial condition $x_0\left(\mathrm{\theta }\right)$ for the total timespan $\left[t_0,t_{n+1}\right]$, or with initial condition $x_n\left(\mathrm{\theta }\right)$ for the incremental timespan $\left[t_n,t_{n+1}\right]$. The latter approach requires to store for each sample point $\left({\mathrm{\theta }}_n^{\left(s\right)},w_n^{\left(s\right)}\right)$ also the corresponding state $x_n^{\left(s\right)}$ at time $t_n$, because typically the structural model cannot be solved analytically. The incremental approach makes use of the Markov property that the future state is independent of the past when the present state is known.

The resulting triple $\left({\mathrm{\theta }}_n^{\left(s\right)},w_n^{\left(s\right)},x_n^{\left(s\right)}\right)$ is called a particle. In our setting, the ensemble of particles can be interpreted as the state of a population of virtual individuals at time $t_n$, whose “diversity” represents the uncertainty about the state/parameters of the patient at time $t_n$, given the individual measurements $y_{1:n}$. The posterior $p(·|y_{1:n})$ obtained by n sequential update steps in Eq. 9 is mathematically identical to the posterior obtained in Eq. 5 by assimilating all data $y_{1:n}$ in a batch (Section 3.3.3 in ref. 19). However, the sequential update is much more efficient as it involves a reduced integration time span.

In contrast to SIR, PF does not perform resampling by default. Only if too many samples carry an almost negligible weight and the total weight is limited to only a few samples (weight degeneracy), a resampling is performed. We used a criterion based on the effective sample size

$$S_{\text{eff}}(t_n):=\frac{1}{{\sum }_{s=1}^S{\left(w_n^{\left(s\right)}\right)}^2}$$

to decide whether to resample. Starting initially with uniform weights $w_0^{\left(s\right)}=1/S$ with $S_{\text{eff}}\left(t_0\right)=S$, resampling was carried out once $S_{\text{eff}}<S/2$ (effective ensemble size half of the initial ensemble size). If resampling is performed, it is followed by a so‐called rejuvenation step3 to prevent sample impoverishment by fixation to limited parameter values:

$${\mathrm{\theta }}_n^{\left(s\right)}={\tilde{\mathrm{\theta }}}_n^{\left(s\right)}+{\mathrm{\xi }}_n^{\left(s\right)},\text{with}{\mathrm{\xi }}_n^{\left(s\right)}{\sim }_{\mathit{iid}}\mathcal{N}\left(0,\mathrm{\tau }·\left|{\tilde{\theta }}_n^{\left(s\right)}\right|\right).$$

with rejuvenation parameter $\mathrm{\tau }$, where ${\tilde{\mathrm{\theta }}}_n^{\left(s\right)}$ denotes the resampled parameters. These two steps, resampling and rejuvenation, ensure that the weighted sample ${\mathbb{S}}_n$ adequately represents areas of posterior probability, see also Figure S5 .

Biomarker data during chemotherapy for single/multiple cycle simulation studies

Two simulation studies (see below) were performed in MATLAB R2017b/2018b, see supplementary information files SCode, to analyze the approaches regarding their suitability to support MIPD.

For the single cycle study with docetaxel ($100\text{mg}/{\mathrm{m}}^2$, 1 hour infusion), we used the NLME model in ref. 20. It is based on the well‐known pharmacodynamic model in ref. 8 (Figure S6 ) and describes the effect of a single dose of the anticancer drug docetaxel based on monitoring neutrophil counts. Important model parameters are the drug effect parameter “Slope” and the pretreatment baseline neutrophil concentration “Circ0.” For inference, neutrophil concentrations were considered on a log‐scale at time points $t=0,3,\dots ,21$ days postdose, see Section S8 for full details. This simulation study aims to demonstrate the limitations of MAP estimation for a model frequently used in MIPD for TDM.7, 21 Because recursive data processing and decision‐support gain in relevance for long‐term monitoring, we performed a simulation study for multiple cycle therapy with paclitaxel using the NLME model in ref. 9. It describes the effect of the anticancer drug paclitaxel (200 mg/m², 3‐hour infusion) over six cycles of 3 weeks each, corresponding to treatment arm A of the CEPAC/TDM study.22 In ref. 9, an aggravation of neutropenia over subsequent treatment cycles is accounted for by bone marrow exhaustion9 (Figure S6 ). The model includes interoccasion variability (IOV) on pharmacokinetic parameters describing the variability between cycles within one patient. Therefore, the parameter values comprise the interindividual parameters (${\mathrm{\theta }}_{\text{IIV}}$) and a parameter for each occasion (${\mathrm{\theta }}_{\text{IOV}}$). As a consequence, the size of $\mathrm{\theta }$ increases with every occasion/cycle, $\mathrm{\theta }=\left({\mathrm{\theta }}_{\text{IIV}},{\mathrm{\theta }}_{\text{IOV}}^1,\dots ,{\mathrm{\theta }}_{\text{IOV}}^{n_c}\right)$, where $n_c$ denotes the number of cycles, see Section S9 for details. Neutrophil counts were assumed to be monitored every third day. We were interested in a setting where data become available sequentially (one‐by‐one). To this end, neutrophil count data were simulated for a virtual patient using Eqs. 3 and 4 and the corresponding model. Then the individual parameter values were inferred based on the simulated neutrophil count data available up to a certain time point, using the same model. For the statistical analysis, this procedure was repeated for $N=100$ virtual patients (with covariate characteristics mirroring the real study population underlying the NLME model).

Key characteristics for decision support in cytotoxic chemotherapy

We investigated different characteristics $T\left(·\right)$ of the neutropenia time‐course related to risk and recovery.7 Depending on the nadir (i.e., minimal neutrophil concentration), different grades of neutropenia are distinguished, see Figure 1. Neutropenia grade 4 is dose‐limiting as this severe reduction in neutrophils exposes patients to life‐threatening infections. On the contrary, neutropenia grade 0 is also undesired as it is associated with a worse overall treatment outcome.23 The time $t_{\text{nadir}}$ at which the nadir is reached is important for time management of intervention. We considered the patient out of risk at time $t_{\text{rec}2}$ when neutropenia grade 2 is reached post nadir. For the initiation of the next treatment cycle, the recovery time $t_{\text{rec}0}$ to grade 0 is important. In addition, risk is also related to the duration $t_{\text{dur}3}$ and $t_{\text{dur}4}$ of an individual being in grade 3 and 4 neutropenia, respectively.

Figure 1.

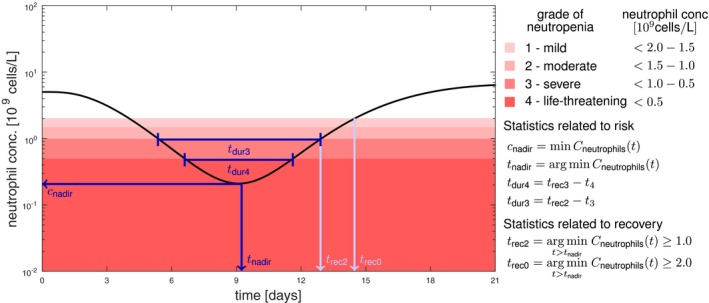
Key characteristics for decision making in cytotoxic chemotherapy related to risk (dark blue) and recovery (light blue) of neutropenia. Neutropenia grades are defined according to the Common Terminology Criteria for Adverse Events.31 Note that the shades of red are related to the increasing toxicity; however, grade 0 (white) over the whole cycle is associated with ineffective treatment. As key statistics for decision support we consider the lowest neutrophil concentration ($c_{\text{nadir}}$), the time at which the nadir is reached ($t_{\text{nadir}}$), the duration of neutropenia grade 3 and grade 4 ($t_{\text{dur3}}$ and $t_{\text{dur4}}$, respectively), as well as the times until recovery to neutropenia grade 2 and 0 ( $t_{\text{rec2}}$ and $t_{\text{rec0}}$, respectively).

Workflow in Bayesian forecasting

In full Bayesian forecasting, uncertainty is quantified on the parameter level and subsequently propagated to the observable level, possibly summarized for some key quantities of interest, see Figure 2. Prior to observing patient‐specific data, the parameter uncertainty is characterized by the prior (cmp. Eq. 4). It allows to make a priori predictions of the neutropenia time course and its uncertainty in form of a $(1-\mathrm{\alpha })$‐confidence interval. In addition, a priori predictions for quantities of interest can be derived (e.g., the neutropenia grade (Figure 2, left column)). Once patient‐specific data are assimilated into the Bayesian model, the remaining uncertainty on the parameter values is characterized by the posterior, allowing to also update the uncertainty in the observable space (CrIs) and the quantities of interest (Figure 2, middle column).

Figure 2.

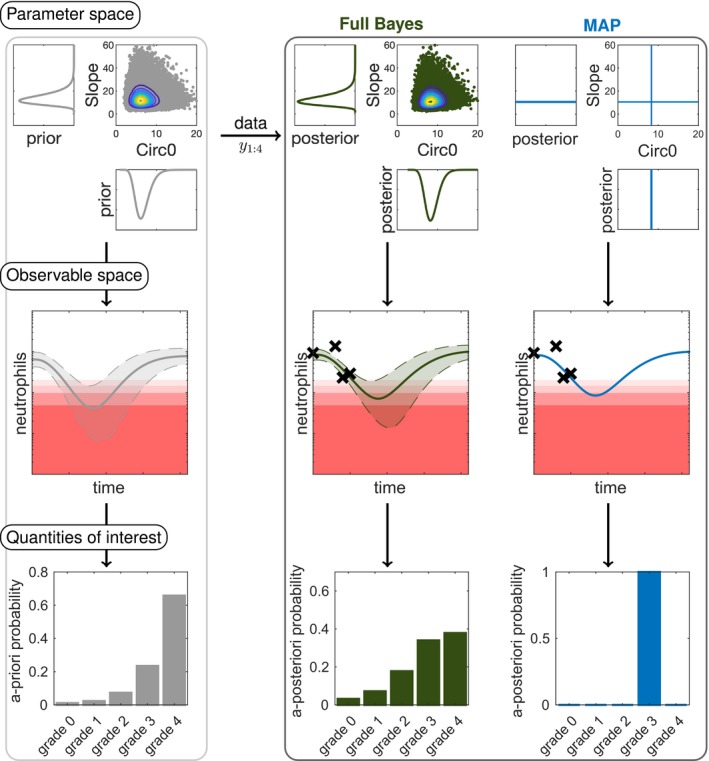
Overview of the workflow in model‐informed precision dosing comparing full Bayesian inference to maximum a posteriori (MAP)‐based prediction. In full Bayesian inference, uncertainties in the parameter values are propagated to uncertainties in the observable space and quantities of interest. The posterior $p(\mathrm{\theta }|y_{1:n})$ is displayed for the parameters “Slope” (drug effect parameter) and “Circ0” (pretreatment neutrophil concentration). For the prior and full Bayes (reference) approach (sampling importance resampling with $S={10}^6$) samples (dots) from the distributions are shown with contour levels. In the observable space, the point estimates (solid lines) are displayed with the central 90% confidence interval or credible intervals (dashed lines and shaded area) along with the therapeutic drug/biomarker monitoring data (crosses). The a priori/a posteriori probabilities are calculated for the neutropenia grades (grade 0–4). Note that $y_1$ corresponds to the measurement of baseline neutrophil counts (“Circ0”) and is taken into account in the posterior.

Forward uncertainty propagation corresponds to transforming a probability distribution (prior or posterior) under a (possibly nonlinear) mapping $T(·)$, resulting in a transformed quantity $\mathrm{\psi }=T(\mathrm{\theta })$. For illustration, we assume the one‐dimensional case with strictly increasing T and $\mathrm{\theta }=T^{-1}(\mathrm{\psi })$. Then the posterior in terms of $\psi$ is given by Section 1 in ref. 24.

$$p_{\mathrm{\Psi }}(\mathrm{\psi }|y_{1:n})=p_{\mathrm{\Theta }}(\mathrm{\theta }|y_{1:n})·\frac{\mathrm{d}{T}^{-1}(\mathrm{\psi })}{\mathrm{d}\mathrm{\psi }},$$ (10)

which is approximated in sampling‐based approaches (cf. Eq. 6) by

$${\widehat{p}}_{\mathrm{\Psi }}(\mathrm{\psi }|y_{1:n})=\sum _{s=1}^S{w}_n^{(s)}{\mathrm{\delta }}_{{\mathrm{\psi }}^{(s)}}(\mathrm{\psi }),$$

with ${\mathrm{\psi }}^{(s)}=T({\mathrm{\theta }}^{(s)})$. This allows the computation of any desired summary statistic (e.g., posterior expectation or quantiles). MAP estimation, in contrast, characterizes the posterior by a single value and allows only to make a single MAP‐based prediction by mapping the MAP estimate ${\widehat{\mathrm{\theta }}}^{\text{MAP}}$ to the quantity of interest $T\left({\widehat{\mathrm{\theta }}}^{\text{MAP}}\right)$, lacking crucial information on its uncertainty (Figure 2, right column). Importantly, for nonlinear T, this does not result in the most probable outcome, due to the Jacobian factor $\frac{\mathrm{d}\mathrm{\theta }}{\mathrm{d}\mathrm{\psi }}=\frac{\mathrm{d}{T}^{-1}\left(\mathrm{\psi }\right)}{\mathrm{d}\mathrm{\psi }}$ in Eq. 10, 25, 26: The most probable outcome is defined as the outcome with maximum posterior probability.

$${\widehat{\mathrm{\psi }}}_n^{\text{MAP}}=\underset{\mathrm{\psi }}{argmax}{p}_{\mathrm{\Psi }}(\mathrm{\psi }|y_{1:n}),$$ (11)

which satisfies (assuming for illustration that T is strictly increasing).

$$\begin{array}{cc}0=\frac{\mathrm{d}}{\mathrm{d}\mathrm{\psi }}{p}_{\mathrm{\Psi }}(\mathrm{\psi }|y_{1:n})\hfill & \stackrel{\text{Eq}.10}{=}\frac{\mathrm{d}}{\mathrm{d}\mathrm{\psi }}\left[p_{\mathrm{\Theta }}(T^{-1}\left(\mathrm{\psi }\right)|y_{1:n})·\frac{\mathrm{d}{T}^{-1}\left(\mathrm{\psi }\right)}{\mathrm{d}\mathrm{\psi }}\right]\hfill \\ \hfill & =\frac{\mathrm{d}}{\mathrm{d}\mathrm{\theta }}{p}_{\mathrm{\Theta }}(T^{-1}\left(\mathrm{\psi }\right)|y_{1:n})·{\left(\frac{\mathrm{d}{T}^{-1}\left(\mathrm{\psi }\right)}{\mathrm{d}\mathrm{\psi }}\right)}^2+p_{\mathrm{\Theta }}(T^{-1}\left(\mathrm{\psi }\right)|y_{1:n})·\frac{{\mathrm{d}}^2{T}^{-1}\left(\mathrm{\psi }\right)}{\mathrm{d}{\mathrm{\psi }}^2}.\hfill \end{array}$$ (12)

For the transformed MAP estimate, $\mathrm{\psi }=T\left({\widehat{\mathrm{\theta }}}^{\text{MAP}}\right)$, the first term in the right hand side of Eq. 12 is zero, because its first factor vanishes by definition. The second term, however, is non‐zero, because both its factors are non‐zero for nonlinear T. Therefore, the transformed MAP estimate does not satisfy the condition for the mode of the transformed posterior probability and, hence, $T\left({\widehat{\mathrm{\theta }}}^{\text{MAP}}\right)\ne {\widehat{\mathrm{\psi }}}^{\text{MAP}}$.

Method comparison

For all sampling‐based methods (NAP, SIR, MCMC, and PF) we used a sample of size $S={10}^3$. Because the posterior is analytically intractable, an extensive sample of size $S={10}^6$ was used as reference, called “full Bayes (reference)” in the sequel, which was generated by SIR and cross‐checked with MCMC (see Figure S7 , because these approaches are exact in the limit $S\to \infty$). As a statistical measure for the quality of uncertainty quantification, we considered the Hellinger distance

$$H(\widehat{P},P^{\text{ref}}):=\frac{1}{\sqrt{2}}\sqrt{\sum _{i=1}^b{\left(\sqrt{{\widehat{p}}_i}-\sqrt{p_i^{\text{ref}}}\right)}^2,}$$ (13)

which measures the difference between the discrete sampling‐based a posteriori probability distribution $\widehat{P}=\left({\widehat{p}}_1,\dots ,{\widehat{p}}_b\right)$ and the reference solution $P^{\text{ref}}=\left(p_1^{\text{ref}},\dots ,p_b^{\text{ref}}\right)$ generated with SIR $S={10}^6$ for b fixed bins.

Results

First, we show the limitations of MAP estimation for MIPD and how full Bayesian approaches can overcome these limitations (using SIR with $S={10}^6$ as reference). Next, we compare different full Bayesian approaches with reduced sample sizes regarding accuracy and computational efficiency.

Unfavorable properties of MAP‐based predictions

The first example of decision support in individualized chemotherapy uses the most frequently used model of neutropenia.8 The MAP estimate ${\widehat{\mathrm{\theta }}}_n^{\text{MAP}}$ is derived from the parameter posterior $p(·|y_{1:n})$ given experimental data $y_{1:n}={(y_1,\dots ,y_n)}^T$, see Eq. 7. In the context of TDM, it is used to predict the future time course $x\left(t;{\widehat{\mathrm{\theta }}}^{\text{MAP}}\right)$ of the patient and thereon based observables. In mathematical terms, ${\widehat{\mathrm{\theta }}}^{\text{MAP}}$ is mapped to some quantity of interest $T\left({\widehat{\mathrm{\theta }}}^{\text{MAP}}\right)$ (e.g., the nadir concentration). As pharmacometric models are generally nonlinear, this does, however, not result in the most probable outcome (see also paragraph preceding Eq. 12 in the Methods). This is due to the fact that first determining the MAP estimate and then applying a nonlinear mapping is, in general, different from first applying the mapping to the full parameter posterior and then determining its MAP estimate: $T\left({\widehat{\theta }}^{\text{MAP}}\right)\ne {\widehat{T\left(\theta \right)}}^{\text{MAP}}$, see Figure 3 for an illustration with $T\left(\mathrm{\theta }\right)=c_{\text{nadir}}\left(\mathrm{\theta }\right)$ and Figure S1 for more details.

Figure 3.

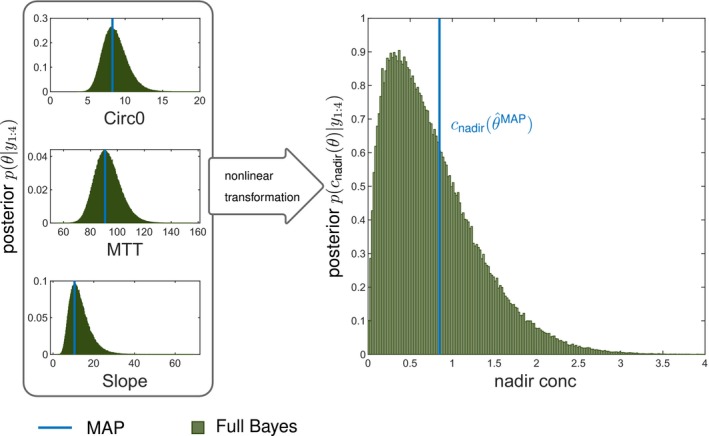
Maximum a posteriori (MAP)‐based predicted nadir concentration is not the most (a posteriori) probable nadir concentration. We considered the single cycle study docetaxel with four observed data points $y_{1:4}$ and forecasted the nadir concentration based on the posterior $p(\mathrm{\theta }|y_{1:4})$ using MAP estimation and the full Bayes (reference) approach (sampling importance resampling with $S={10}^6$), where $\mathrm{\theta }$ comprises the parameters baseline neutrophil counts (Circ0), mean transit time (MTT), and “Slope” (drug effect). The MAP estimate of the parameters coincides with the mode of the posterior distribution of the parameters (left panel), however, the mode is not preserved under nonlinear transformation (see text). Therefore, $c_{\mathit{nadir}}\left({\widehat{\theta }}^{\mathit{MAP}}\right)$ with $c_{\text{nadir}}(·)$ denoting some observable $T(·)$ does not equal the mode of the a posteriori probability $p_{T\left(\mathrm{\Theta }\right)}(·|y_{1:n})$ of the nadir concentration. Please also refer to Figure S1 for further illustration and analysis.

Thus, MAP‐based estimation lacks both, a measure of uncertainty and the feature to predict the most probable observation/quantity of interest. In addition, relevant outcomes, such as the risk of grade 4 neutropenia cannot be evaluated from the point estimate alone. MAP‐based estimation, therefore, provides a biased basis for clinical decision making. In contrast, full Bayesian inference provides access to the full posterior distribution of the parameters and correctly transforms uncertainties forward to the observables and quantities of interest, allowing to compute any desired summary statistic and relevant risks (Section 5.2 in ref. 19).

Uncertainty quantifications for more comprehensive, differentiated understanding, and better informed decision making

The first scenario served to demonstrate the limitations of MAP‐based estimations for the gold‐standard model,8 however, the model does not account for the observed cumulative neutropenia over multiple cycles. Therefore, we considered for dose adaptations a model accounting for bone marrow exhaustion over multiple cycles,9 see paragraph about the multiple cycle study paclitaxel. We exemplarily considered the dose selection for the third treatment cycle based on prior information and patient‐specific measurements during the first two cycles. The patient‐specific data together with the full Bayes (reference) model fit and prediction are shown in Figure 4 a, see also Figures S8 and S9 . The CrIs (dashed) and prediction intervals (dotted) show the uncertainty about the “state of the patient,” without and with measurement errors, respectively.

Figure 4.

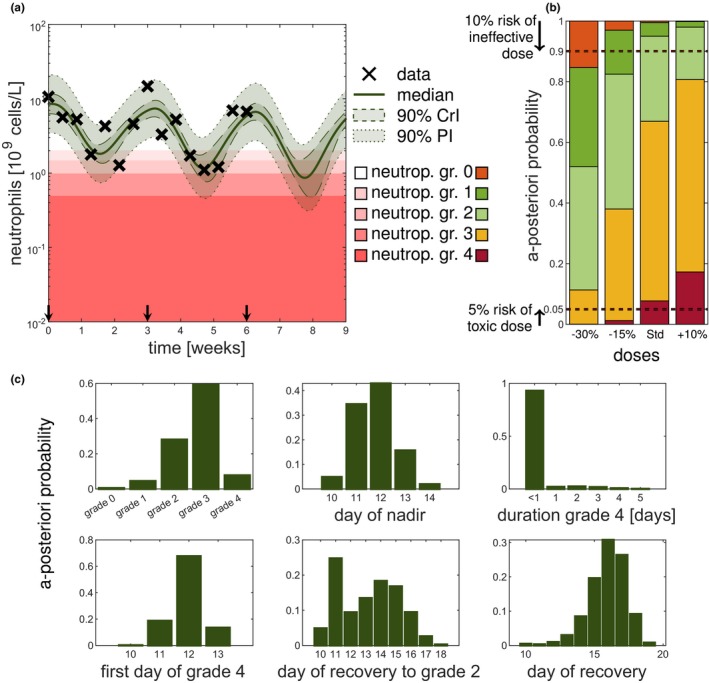
Uncertainty quantification by full Bayesian methods gives important information for therapy dosing selection. The scenario described in multiple cycle study paclitaxel is used and the results are shown for the full Bayes (reference) solution with sampling importance resampling (SIR) using $S={10}^6$ samples. (a) Forecasting the third cycle for different doses based on the patient's covariates and measurements of the first two cycles. (b) Full Bayesian inference allows for probabilistic statements of the different grades. Color coding of neutropenia grades shows trade‐off between efficacy and toxicity. No toxicity (grade 0) is associated with poorer treatment outcome (orange) but severe neutropenia (grade 3 and 4) is also not desired (yellow and red). (c) A posteriori probabilities of quantities of interest for the third cycle based on the posterior at the end of second cycle (week 6) for the standard dose. Statistics, such as day of grade 4, were computed given that grade 4 is reached. Note for all displayed forecasts the full Bayes (reference) approach (SIR with $S={10}^6$) was used. CrI, credible interval; PI, prediction interval.

For optimizing the dose of the third cycle, different dosing scenarios were considered: the standard dose and a –15%, −30%, and +10% adapted dose. Figure 4 b shows the probability of the predicted grades of the third cycle for each dose. To find an effective and safe dose, the risk of being ineffective (neutropenia grade 0) should be minimized jointly with the risk of being unsafe (neutropenia grade 4). For illustration in Figure 4 b, the dashed horizontal lines indicate a 10% and 5% level of being ineffective and unsafe, respectively. The standard dose and the increased dose have a risk of toxicity larger than 5% (lower horizontal line). A decrease in dose also leads to an increased risk of an ineffective dose (upper horizontal line). The 15% reduced dose is with 96% probability safe and efficacious (grades 13), with 3% probability ineffective (grade 0) and with 1% probability unacceptably toxic (grade 4). If grade 3 is also to be avoided, the 30% reduction would be preferable, as it is with 74% probability safe and efficacious (grades 12), with 15% probability ineffective (grade 0) and with 11% probability toxic (grades 34). Thus, the choice of an optimal dose might depend on how priority is given to the risk of inefficacy and toxicity. As both risks are described by the tails of the posterior distribution, a point estimate is not able to adequately capture them. The MAP‐based predicted grades were: grade 2 (standard dose and +10% dose), grade 1 (−15% dose); and grade 0 (−30% dose), which do not only make it difficult to distinguish between some doses, but also do not reflect the true most probable grades.

Posterior‐based predictions of important statistics related to the neutropenia time course can help to answer questions like “How probable is it that the patient will suffer from grade 4 neutropenia?” or “How probable is it that the patient will recover in time for the next scheduled dose so that the therapy can be continued as planned?” To answer such questions, Figure 4 c shows important predicted quantities of interest, illustrated for the standard dose in cycle 3. We inferred that the risk of grade 4 neutropenia is 8%, and if the patient were to reach grade 4, it would be most probable (68%) on day 12. The probability that the patient’s duration in grade 4 is a day or longer is very small (< 7%). As the probability to not have been recovered until day 21 is negligible, the administration can remain scheduled on day 21 for cycle 4. Therefore, uncertainty quantification improves the decision‐making process by quantifying the a posteriori probabilities of relevant risks and quantities of interests. Repeating the above analysis for different doses, therefore, allows for an improved distinction between dose adjustments.

Approximation accuracies comparable across different full Bayesian approaches

We next compared different established methods for uncertainty quantification with regard to their approximation accuracy. To this end, posterior inference was investigated for a patient at day 5 of the first cycle (Figure 5). Whereas the marginal posterior distribution for the parameter “Circ0” (pretreatment neutrophil concentration) is close to a normal distribution, the marginal posterior for the drug effect parameter (“Slope”) is closer to a log‐normal distribution. Accordingly, the NAP is rather reasonable for “Circ0,” but is questionable for the “Slope” parameter. In addition, sampling from the normal distribution can lead to unrealistic (negative) parameter values (Figure 5 a). In addition, NAP very clearly underestimated the patient’s risk to reach grade 4 neutropenia (Figure 5 b,c), which could possibly lead to a fatal dose selection. Considering a Student’s t distribution instead of the normal approximation, as in ref. 13, did not lead to an adequate improvement (Figure S3 ). Consequently, the NAP approach can result in overoptimistic, overpessimistic, and unrealistic predictions. In contrast, the full Bayesian methods (SIR, MCMC, and PF) adequately represent the tails and respect the positivity constraint of parameter values. The resulting CrIs are comparable to the reference CrIs. For illustration, Figure 6 a shows the approximation error for the predicted probability of neutropenia grades, measured in the Hellinger distance (see Eq. 13). Overall, SIR and PF showed the best approximation, whereas NAP resulted in the largest errors.

Figure 5.

Comparison of uncertainty quantification at the level of parameters, observables, and quantities of interest. Exemplary comparison of the different methods for one patient after having observed four data points up to day 5. (a) The posterior is shown for parameters “Slope” and “Circ0” showing the kernel density estimates of the sampling distribution univariately and as scatter plots for the bivariate sampling distributions with contour plots for the full Bayesian approach (full Bayes (reference), sampling importance resampling (SIR) with $S={10}^6$) and the normal approximation located at the maximum a posteriori (MAP) estimate. (b) On the level of the observable (neutrophil concentration) the point estimates (median or MAP) are displayed along with the 90% credible intervals (CrIs). For illustration purposes, the prediction intervals are not shown here. (c) The forecasted a posteriori probability of the different neutropenia grades (0–4) is shown for the different approximations (filled bars) in comparison with the full Bayes (reference; black outlined bars). MCMC, Markov Chain Monte Carlo; NAP, normal approximation; PF, particle filter.

Figure 6.

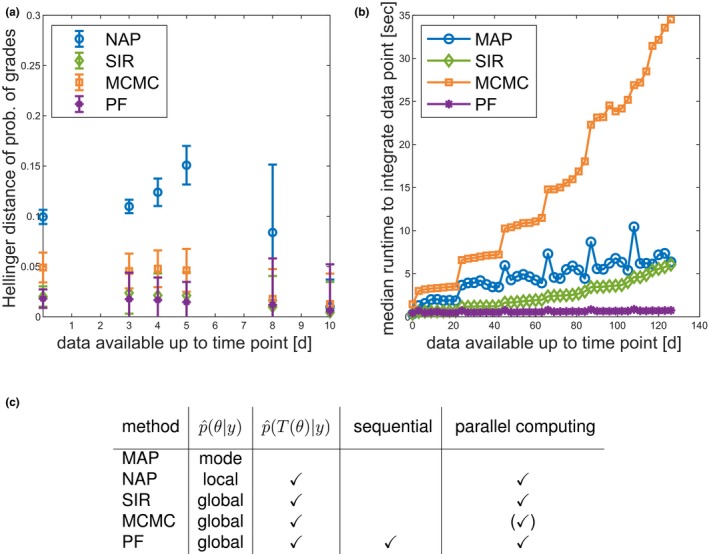
Comparison of methods regarding important aspects for model‐informed precision dosing. (a) Approximation error (measured as Hellinger distance) of the probability of neutropenia grades (“Single cycle study docetaxel”). (b) Qualitative runtime comparison to sample from the parameter posterior. Median of $N=100$ repeated analyses (“Multiple cycle study paclitaxel”). (c) Comparison of method properties. For Markov Chain Monte Carlo (MCMC) several chains could be run in parallel, however, in this study, only one chain was considered. MAP, maximum a posteriori; NAP, normal approximation; PF, particle filter; SIR, sampling importance resampling.

Sequential DA processes patient data most efficiently

The need for real‐time inference algorithms is increasing with the possibilities to more frequently collect patient‐specific data (online collection) during treatment. Sequential DA methods (e.g., PF) provide an efficient framework for real‐time data processing. At any time, all information (including associated uncertainty) is present in a collection of particles that can be interpreted as representing the current state and associated uncertainty of a patient via a virtual population. With a new datum, this information is updated. Approaches that rely on batch data analysis (i.e., MAP, SIR, and MCMC), need to redo the inference from scratch. This has impact on the computational effort as the number of data points increases. Figure 6 b shows a comparison of the computational cost to assimilate an additional data point. All approaches show some kind of increase in effort every 21 days—due to the IOV on some parameters. Clearly, PF shows lowest and almost constant costs, whereas for batch mode approaches computational costs increase over time due to an increasing number of parameters (one additional parameter for every cycle due to the IOV, see paragraph about the multiple cycle study with paclitaxel) and an increasing integration time span to determine the likelihood. This could become computationally expensive in view of long‐term treatments and higher time resolution of data points provided by new digital healthcare devices. Figure 6 c summarizes the features of the different inference approaches. Note that all sampling‐based approaches can be accelerated by parallel computing. In summary, it was found that PF processes patient monitoring most efficiently and facilitated the handling of IOV because only the IOV parameter of the current occasion needs to be considered.

Discussion

In the context of chemotherapy‐induced neutropenia, we illustrated the severe drawbacks of MAP‐based approaches for forecasting and thereon based decision making. A prediction based on the MAP estimate does neither correspond to the most probable outcome nor does it allow to quantify relevant risks as the uncertainties are not quantified. Both are highly undesirable characteristics and make MAP‐based inference difficult to interpret in a TDM setting. A normal approximation of the posterior at the MAP estimate is no alternative, as it retains the same point estimate and proved to be unsuitable in case of skewed parameter distributions. We demonstrated that full Bayesian approaches, like SIR, MCMC, or PF, provide accurate approximations to the posterior distribution, enabling comprehensive uncertainty quantification of the quantities of interest (e.g., nadir concentration). Among the three considered approaches, PF is a sequential approach that is beneficial in a more continuous monitoring context.

Uncertainty quantification in TDM is scarce. In ref. 27 the SIR algorithm was previously used in the TDM setting to construct CrIs using a Student’s t distribution located at the MAP estimate as importance function. A sequential approach in the context of MAP estimation is discussed in ref. 28 with a moving estimation horizon (window of data points that are considered). A sequential DA approach has been investigated previously for glucose forecasting,29, 30 yet, not in combination with an NLME modeling framework and without decision‐support statistics. A systematic comparison of approaches, as presented herein, is lacking.

In this study, particle filtering is applied in TDM within an NLME modeling framework to represent the current patient status via an uncertainty ensemble. A challenge in the application of PF is the potential for weight degeneracy (i.e., a gradual separation into a few large and many very small weights). A rejuvenation approach (as applied in this study) resolves this problem, but requires specification of an additional parameter (magnitude of the rejuvenation). A too large value might result in an artificially increased uncertainty, whereas a too small value might hinder exploration of the parameter space. In the present application context, however, IOV counteracts in addition to the rejuvenation step weight degeneracy.

Sequential data processing is not only computationally efficient and convenient for IOV handling, but has the additional advantage that already assimilated experimental data need not be stored to assimilate future data points. Sampling approaches allow a simple extension for hierarchical models to include the uncertainties in the population parameters for even more holistic uncertainty quantification. This would enable a continuous learning process between clinical trials from drug development (e.g., phase III) and continue during the acquisition of real‐world data after market authorization in quantifying the diverse population of patients who have taken a given drug. For a future patient, this “historic” diversity would transform into well‐quantified uncertainty in a TDM setting. The absence of need to store “historic” experimental data can also be helpful for the exchange of information among clinics, health insurances, and pharmaceutical companies. The current knowledge, present in form of a sample of particles, can easily be exchanged without the need to exchange the experimental data. The “historic” data are implicitly present in the particles.

In view of new treatments and new mobile healthcare devices (e.g., wearables) gathering data from various sources, clinicians have to deal with new challenges and an increasing complexity of treatment decision making, which demands for comprehensive approaches that integrate data efficiently and provide informative and reliable decision support. We illustrated that comprehensive uncertainty quantification can result in a more informative, reliable, and differentiated decision support, which is not only limited to individualized chemotherapy but has the potential to improve patient care in various therapeutic areas in which TDM is indicated, such as oncology, infectious diseases, inflammatory diseases, psychiatry, and transplantation patients.

Funding

Graduate Research Training Program PharMetrX: Pharmacometrics & Computational Disease Modelling, Berlin/Potsdam, Germany. Deutsche Forschungsgemeinschaft (DFG) through grant CRC 1294 Data Assimilation (associated project). Deutsche Forschungsgemeinschaft and Open Access Publishing Fund of University of Potsdam.

Conflict of Interest

C.K. and W.H. report research grants from an industry consortium (AbbVie Deutschland GmbH & Co. K.G., Boehringer Ingelheim Pharma GmbH & Co. K.G., Grünenthal GmbH, F. Hoffmann‐La Roche Ltd., Merck KGaA, and Sanofi) for the PharMetrX program. In addition C.K. reports research grants from the Innovative Medicines Initiative‐Joint Undertaking (“DDMoRe”) and Diurnal Ltd. All other authors declared no competing interests for this work.

Author Contributions

C.M., N.H., C.K., and W.H. wrote the manuscript. C.M., N.H., J.dW., C.K., and W.H. designed the research. C.M. performed the research. C.M., N.H., C.K., and W.H. analyzed the data.

Supporting information

Supplementary Material ‐ SText.pdf. Contains additional information regarding the employed methods, a detailed overview of the PK/PD models and some additional supporting analyses and figures.

Supplementary Material ‐ SCode.zip. Contains the model, implemented algorithms and figure generating MATLAB code.