Kinetic Studies of the Effect of pH on the Trypsin-Catalyzed Hydrolysis of N-α-benzyloxycarbonyl-l-lysine-p-nitroanilide: Mechanism of Trypsin Catalysis

Abstract

The pH dependence of the trypsin-catalyzed hydrolysis of N-α-benzyloxycarbonyl-l-lysine p-nitroanilide has been studied at 25 °C. k_cat/K_M was maximal at alkaline pH values but decreased with decreasing pH. k_cat/K_M was dependent on free enzyme pK_a values of 6.75 ± 0.09 and 4.10 ± 0.13, which were assigned to the ionization of the active site histidine-57 and aspartate-189, respectively. Protonation of either group abolished catalytic activity. k_cat is shown to equal the acylation rate constant k₂ over the pH range studied. k₂ decreased on the protonation of two groups with pK_a values of 4.81 ± 0.15 and 4.23 ± 0.19. We assign the pK_a of 4.23 to the ionization of the aspartate-189 residue and the pK_a of 4.81 to the oxyanion of the tetrahedral intermediate formed during acylation. We conclude that during acylation, breakdown of the catalytic tetrahedral intermediate is rate-limiting and that there is a strong interaction between the imidazolium ion of histidine-57 and the oxyanion of the catalytic tetrahedral intermediate, which perturbs their pK_a values. From the pH dependence of k₃, we conclude that deacylation depends on a pK_a of 6.41 ± 0.22 and that the ionization of the carboxylate group of aspartate-189 does not have a significant effect on the rate of deacylation (k₃). A catalytic mechanism is proposed to explain the pH dependence of catalysis.

1. Introduction

Trypsin and trypsin-like serine proteases specifically catalyze the hydrolysis of peptide bonds involving the carbonyl carbon of the α-carboxylate group of the positively charged amino acid residues lysine or arginine. Trypsin is a serine protease involved in protein digestion. Due to its high specificity for positively charged amino acid residues trypsin is widely used for peptide sequencing in proteomics.^1,2 Trypsin-like serine proteases are involved in a range of biological processes and diseases, e.g., the trypsin like enzyme urokinase plasminogen activator plays an important role in both fibrinolysis³ and cancer progression.^4,5 In this study, we utilize pH studies to investigate the catalytic mechanism of trypsin.

Catalysis by the serine proteases can be described by the minimal three-step kinetic mechanism (eq 1) below

1

where ES is the Michaelis complex and ES′ is the acyl intermediate. K_s is the disassociation constant of the Michaelis complex (K_s = k_–1/k₊₁ = [E][S]/[ES]). k₂ and k₃ are the first-order rate constants for acylation and deacylation, respectively. Catalysis obeys the Michaelis–Menten equation (d[P]/dt = k_cat[E₀][S₀]/([S₀] + K_M)). The Michaelis parameters are complex assemblies of rate constants with k_cat= k₂k₃/(k₂ + k₃) and K_M = k₃[(k_–1 + k₂)/k₊₁]/(k₂ + k₃), and if k_–1 ≫ k₂, then K_M = k₃K_s/(k₂ + k₃) and k_cat/K_M = k₂/K_s. Therefore, the mechanistic significance of the pH dependence of these Michaelis parameters is often not clear. However, pioneering studies with chymotrypsin at pH 7⁶ have shown that with ester substrates with good leaving groups (P₁) deacylation (k₃) is rate limiting and so

while with amide and anilide substrates with poor leaving groups (P₁), acylation (k₂) can be rate limiting with

Therefore, with highly reactive ester substrates, it should be possible to determine k₃ from k_cat values, while with less reactive amide or anilide substrates, it should be possible to determine k₂ and K_s values from k_cat and K_M, respectively.

At pH 2.66, the reaction of trypsin with the reactive ester substrate Z-lys-pnp was slow enough for both k₂ and k₃ to be measured and it was shown that acylation was much more rapid than deacylation (k₂/k₃ = 27.6).⁷ However, it was found that at higher pH values, the ratio k₂/k₃ decreased and k₂ was not much greater than k₃.^8,9 Therefore, it cannot be assumed that k₂ is always very much greater than k₃ with reactive ester substrates and so pH studies are essential if we are to fully understand the kinetics of catalysis at different pH values. The less reactive para-nitroanilide substrates are thought to be better models than the more reactive para-nitrophenol ester substrates for natural peptide substrates. However, a detailed kinetic analysis of the trypsin-catalyzed hydrolysis of the equivalent less reactive para-nitroanilide substrate Z-Lys-pna has not been carried out.

Therefore, in the present study a detailed study of the trypsin-catalyzed hydrolysis of the anilide substrate Z-Lys-pna has been undertaken. The effect of pH on the ratio k₃/k₂ and on values of K_M and K_s has been quantified. Also, the effect of pH on k_cat/K_M and on the rates of acylation (k₂) and deacylation (k₃) has been determined. From these studies, the pK_a values affecting catalysis in the free enzyme as well as during acylation and deacylation have been determined. In any pH study, it is difficult to dismiss the possibility that ionizations outside the active site can also affect catalytic activity. However, in this study, there is no evidence of this and all observed ionizations are assigned to active site groups.

The mechanistic significance of these results are discussed and a catalytic mechanism is proposed, which explains the pH dependence of catalysis. The mechanistic proposals and their background are briefly summarized in the following paragraph.

Some earlier studies¹⁰⁻¹⁴ have suggested that the pK_a of the catalytic histidine is decreased during acylation (pK_a < 7), while more recent studies¹⁵⁻²³ have suggested that the histidine pK_a must be raised (pK_a > 11) so that it can be an effective general base catalyst during acylation and that the pK_a of the oxyanion of the catalytic tetrahedral intermediate (THI) is lowered so that trypsin can be an effective enzyme at physiological pH values. In the present work, pK_a values of 4.8 and 4.2 were detected from the pH studies of the acylation step of catalysis (k₂ in eq 1). The pK_a of 4.8 is assigned to the oxyanion of the catalytic tetrahedral intermediate formed during acylation and not to the pK_a of the catalytic histidine that is assigned a pK_a > 11 in ES and the tetrahedral intermediate. Aspartate-189 that binds the ε-amino group of the substrate in the S₁ specificity pocket is assigned a pK_a of 4.1–4.2 and is not significantly perturbed on substrate binding or on tetrahedral intermediate formation during acylation.

2. Results

2.1. Determination of the Catalytic Parameters k_cat, k_cat/K_M, and k_cat/K_M at Different pH Values

The Michaelis parameters k_cat,K_M, and k_cat/K_M for the trypsin-catalyzed hydrolysis of Z-Lys-pna were determined by computer-fitting the initial rate data obtained at a given pH to the hyperbolic form of the Michaelis–Menten equation (d[P]/dt = V_m·[S₀]/([S₀] + K_M)) using the method of Wilkinson.²⁴

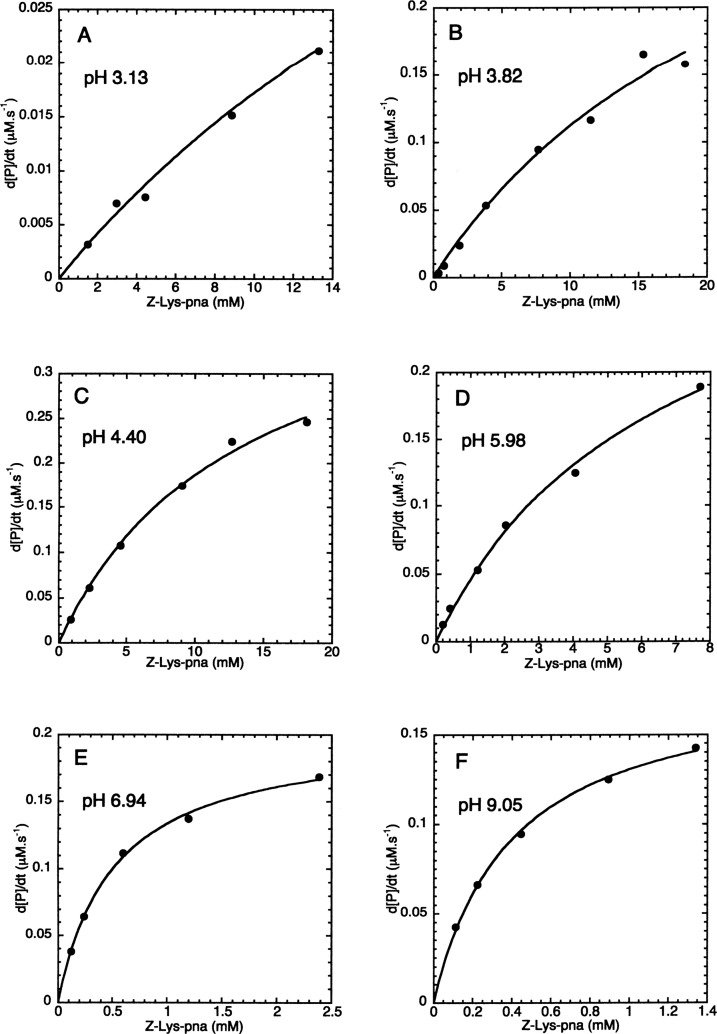
Examples of the experimental data and the fitted lines are given in Figure 1. The trypsin concentrations were increased at lower pH values to compensate for the decreases in k_cat and k_cat/K_M. K_M values increased as the pH decreased, and so higher substrate concentrations were used for determining K_M values at lower pHs (Figure 1).

Figure 1.

Determination of the catalytic parameters for the trypsin-catalyzed hydrolysis of Z-Lys-pna at different pH values. Initial rates (d[P]/dt) were fitted to eq 1 (d[P]/dt = V_m·[S₀]/([S₀] + K_M)). The pH, trypsin concentration, and the fitted values of V_m, V_m/K_M, and K_M were: (A) pH 3.13, 83.5 μM, 0.0768 ± 0.0207 μM s^–1, 2.22 ± 0.9 μs^–1, 34.6 ± 10.5 mM; (B) pH 3.82, 25.6 μM, 0.388 ± 0.094 μM s^–1, 15.8 ± 7.0 μs^–1, 24.5 ± 9.2 mM; (C) pH 4.40, 4.68 μM, 0.444 ± 0.037 μM s^–1, 32.3 ± 5.7 μs^–1, 13.8 ± 2.1 mM; (D) pH 5.98, 0.39 μM, 0.344 ± 0.029 μM s^–1, 52.8 ± 8.9 μs^–1, 6.51 ± 0.95 mM; (E) pH 6.94, 0.427 μM, 0.202 ± 0.005 μM s^–1, 395 ± 32 μs^–1, 0.512 ± 0.039 mM; (F) pH 9.05, 0.379 μM, 0.182 ± 0.005 μM s^–1, 463 ± 34 μs^–1, 0.394 ± 0.027 mM.

2.2. Effect of pH on k_cat/K_M for the Trypsin-Catalyzed Hydrolysis of Z-Lys-pna

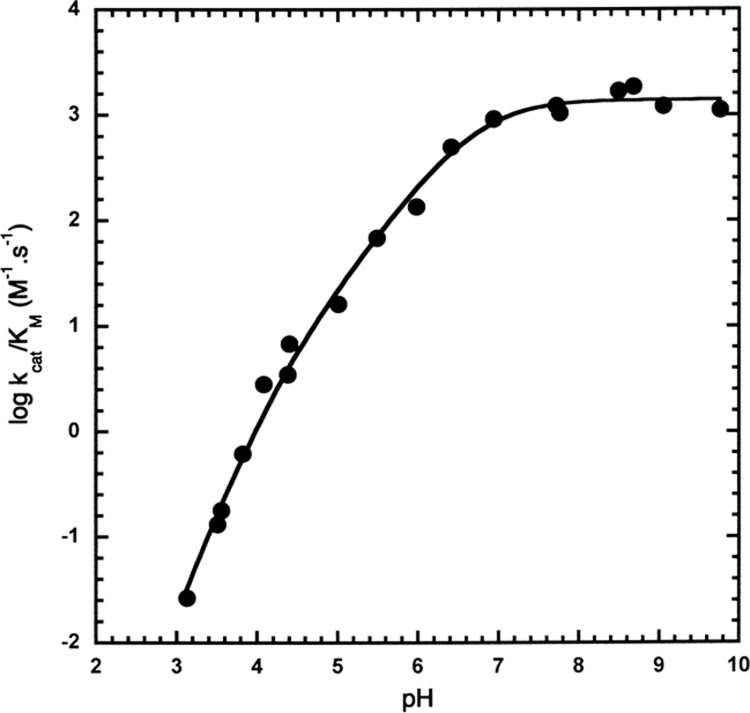
k_cat/K_M values were determined by dividing V_m/K_M values by the enzyme concentration in the reaction mixture. k_cat/K_M values were dependent on the sequential ionization of two groups (k_cat/K_M = (k_cat/K_M)_max/(1 + [H⁺]/K_b + [H⁺]²/K_a·K_b)): one with a pK_a 6.75 ± 0.09 and the other pK_b = 4.10 ± 0.13 (Figure 2). The pH dependence of k_cat/K_M reflects ionizations in either the free enzyme or the free substrate. Previous studies with other substrates have detected similar free enzyme pK_a values of ∼7 and ∼4.^9,25−30

Figure 2.

Effect of pH on log k_cat/K_M for the trypsin-catalyzed hydrolysis of Z-Lys-pna at 25 °C. The solid line was calculated using the equation k_cat/K_M = (k_cat/K_M)_max/(1 + [H⁺]/K_b + [H⁺]²/K_a·K_b), and the fitted values of (k_cat/K_M)_max = 1391 ± 72 M^–1·s^–1, pK_a = 4.10 ± 0.13 and pK_b = 6.75 ± 0.09.

2.3. Calculation of k₃ for the Trypsin-Catalyzed Hydrolysis of Z-Lys-pnp and Z-Lys-pna

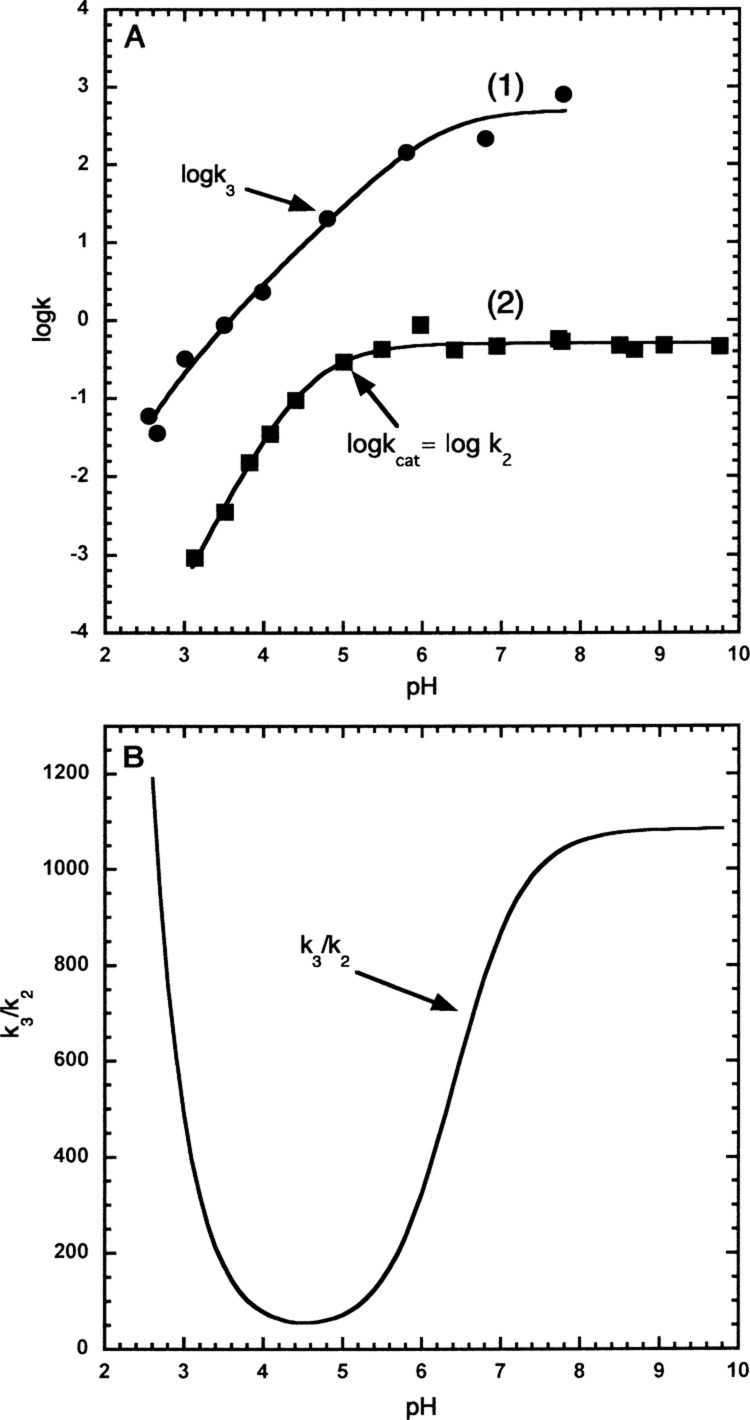
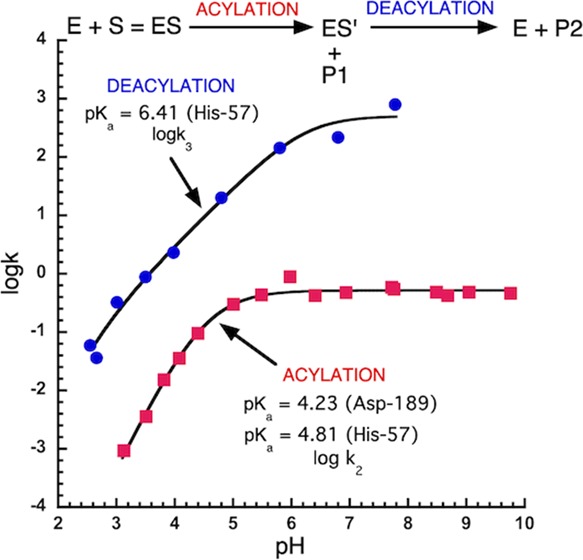
The trypsin-catalyzed hydrolysis of both Z-Lys-pna and Z-Lys-pnp proceeds via a common acyl intermediate (Z-Lys-trypsin, ES′ in eq 1 and structure d1 in Scheme 1). Therefore, both will have the same deacylation rate constant (k₃). Using pre-steady-state kinetics, the k₂ values for the trypsin-catalyzed hydrolysis of Z-Lys-pnp have been determined.²⁵ Steady-state kinetics have been used to determine k_cat values for Z-Lys-pnp.²⁵k_cat = k₂k₃/(k₂ + k₃), and this equation can be rearranged to give the equation, k₃ = k₂k_cat/(k₂ – k_cat), which has been used to calculate the k₃ values (line 1 in Figure 3A) for Z-Lys-pna and Z-Lys-pnp from the experimentally determined values of k₂ and k_cat for Z-Lys-pnp.²⁵ The experimental data was fitted to the equation, k₃ = k_3max/([1 + [H⁺]/K_b]), assuming k₃ was dependent on a single ionizing group (AH = A^– + H⁺) and the fitted values were k₃ = 561 ± 104 s^–1 and pK_a = 6.41 ± 0.22 (Figure 3A, line 1).

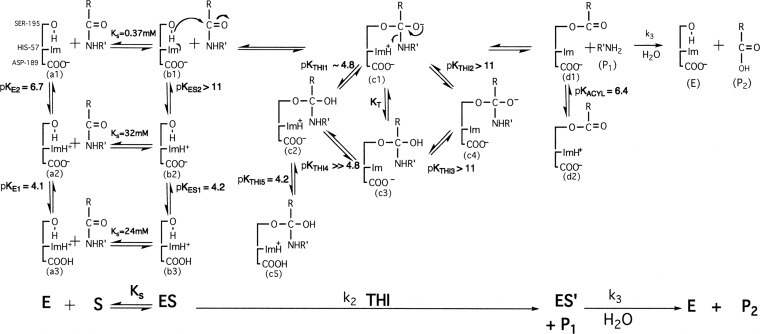
Scheme 1. Catalytic Mechanism of Trypsin.

E and S are the free enzyme and substrate. ES is the enzyme substrate complex or the Michaelis complex. THI is the catalytic tetrahedral intermediate, and ES′ is the acyl enzyme intermediate. P₁ (R′NH₂) and P₂ (RCOOH) are the first and second products, respectively, of the trypsin-catalyzed hydrolysis of the peptide RCONHR′.

Figure 3.

pH dependence of the catalytic parameters k_cat (k₂), k₃ and the ratio k₃/k₂ for the trypsin-catalyzed hydrolysis of Z-Lys-pna at 25 °C. (A) (1) The filled circles are k₃ values calculated using Z-Lys-pnp data²⁰ (see text for further details). The solid line was calculated using the equation k₃ = k_3max/([1 + [H⁺]/K_b]), and the fitted values of k_3max = 561 ± 104 s^–1, pK_b = 6.41 ± 0.22. (2) The filled squares are k_cat values (k_cat = k₂) for Z-Lys-pna, and the solid line was calculated using the equation k_cat = (k_cat)_max/([1 + [H⁺]/K_b + [H⁺]²/K_a·K_b]) and the fitted values of (k_cat)_max = 0.517 ± 0.014. s^–1, pK_a = 4.23 ± 0.19 and pK_b = 4.81 ± 0.15. (B) The ratio k₃/k₂ was calculated using the fitted values for k₂ and k₃ determined in (A). For k₃, k_3max = 561 s^–1, pK_a = 6.41. For k₂, k_2max = 0.517 s^–1, pK_a = 4.23, pK_b = 4.81.

2.4. Determination of k_cat and k₂ for the Trypsin-Catalyzed Hydrolysis of Z-Lys-pna

In the present work, k_cat values have been determined for Z-Lys-pna from pH 3.1–9.8 (Figure 3A, line 2). k_cat = k₂k₃/(k₂ + k₃), which can be rearranged to give k₂ = k₃k_cat/(k₃ – k_cat). As k₃ is the same for both Z-Lys-pnp and Z-Lys-pna, we can use the fitted parameters obtained from the pH dependence of k₃ for Z-Lys-pnp to calculate the value of k₂ for Z-Lys-pna for each value of k_cat determined for Z-Lys-pna from pH 3.1–9.8. Therefore, as k₃ and k_cat are known for Z-Lys-pna, k₂ values could be calculated for Z-Lys-pna. However, this calculation was not necessary to calculate k₂ because k₃ was 2–3 orders of magnitude greater than k₂ (Figure 3B) and so within the experimental error (<2%) k_cat = k₂. Therefore, k_cat values for the trypsin-catalyzed hydrolysis of Z-Lys-pna can be assumed to equal k₂ (Figure 3A, line 2). Experimental k_cat data (k_cat = k₂) was fitted to the equation k_cat = (k_cat)_max/(1 + [H⁺]/K_b + [H⁺]²/K_a·K_b) assuming k_cat was dependent on the sequential ionization of two ionizing groups (line 2 in Figure 3A). We conclude that k₂ has a maximal value of 0.517 ± 0.014 s^–1 and is dependent on the sequential ionization of two ionizing groups (line 2 in Figure 3A) with pK_a values of 4.81 ± 0.15 and the 4.23 ± 0.19 (Table 1).

Table 1. Catalytic Parameters for the Trypsin-Catalyzed Hydrolysis of Z-Lys-pna.

parameter	kmax	pKa	pKb	Ksa	Ksb	Ksc
kcat/KM (M–1 s–1)a	1390 ± 72	4.10 ± 0.13	6.75 ± 0.09
k2 (s–1)a	0.517 ± 0.014	4.23 ± 0.19	4.81 ± 0.15
k3 (s–1)a	561 ± 104		6.41 ± 0.22
Ks (mM)b		4.23	4.82	24.0	32.2	0.373
1/Ks (mM–1)b		4.10	6.75	24.0	32.4	0.372

^aErrors are standard errors of the fitted parameters.

^bThe K_s values used to determine pK_a, pK_b, K_sa, K_sb, and K_sc were calculated from the fitted values of k_cat and k_cat/K_M (see text for details).

2.5. Effect of pH on the Ratio k₃/k₂ for the Trypsin-Catalyzed Hydrolysis of Z-Lys-pna

The fitted values of k₂ and k₃ (lines 1 and 2 in Figure 3A) were used to calculate the ratio of k₃/k₂ from pH 2.6 to 9.8 (Figure 3B). The ratio k₃/k₂ was dependent on pH having a minimal value of ∼55 at pH 4.5 but reaching values of 1200 and 1080 at pH 2.6 and 9.8, respectively (Figure 3B). Therefore, for the trypsin-catalyzed hydrolysis of Z-Lys-pna, k₃ ≫ k₂ from pH 2.6 to 9.8 and so k₂ is rate limiting for Z-Lys-pna and the expression for K_M (K_M = K_s·k₃/(k₂ + k₃)) simplifies to K_M = K_s from pH 2.6 to 9.8. Therefore, for Z-lys-pna, K_M values are equal to K_s values.

2.6. Determination of K_s and its pH Dependence

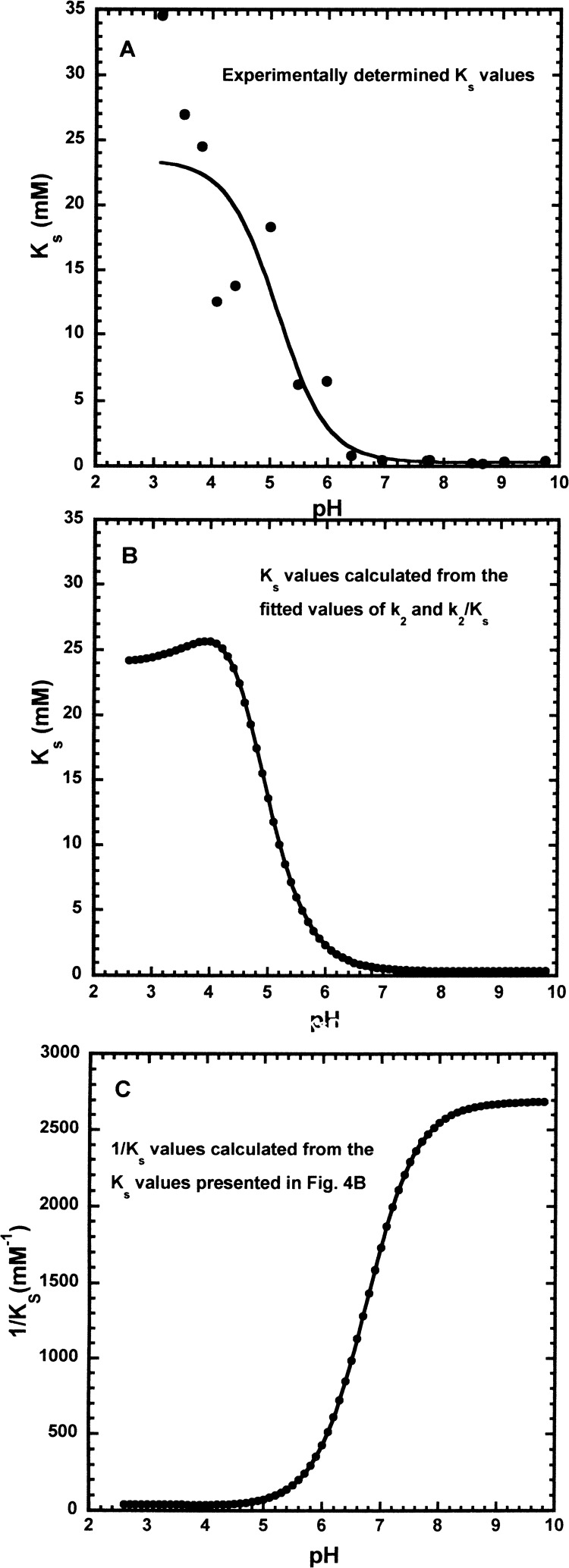
Analyzing the K_M versus pH data for dependence on one pK_a (equation K_s(obs) = K_sa/(1 + K_a/[H⁺]) + K_sb/(1 + [H⁺]/K_a)) gives a minimum K_s value of 0.333 ± 0.025 mM and a maximum K_s value of 23.5 ± 1.9 mM, with a pK_a of 5.12 ± 0.17 (Figure 4A). For optimal accuracy when determing K_M using the Michaelis–Menten equation, substrate concentrations should ideally be in the range K_M/5 to 5 × K_M to optimize accuracy. However, the maximum concentration of Z-Lys-pna was ∼20 mM and so at low pHs, substrate concentrations were similar to the K_M values and therefore accurate K_M values could not be determined (Figure 4A). In contrast, the experimental data for k_cat/K_M (Figure 2) and k_cat (k₂ in Figure 3) were both in good agreement with the fitted lines. This is because both k_cat and k_cat/K_M decrease rapidly and do not level off like K_M values to a fixed value. Consequently, k_cat and k_cat/K_M values cover a larger range of values than K_M values. The log plots of k_cat/K_M and k_cat will reflect two pK_a values, pK_E1 and pK_E2 for k_cat/K_M and pK_ES1 and pK_ES2 for k_cat. In contrast, a plot of K_M versus pH should give pK_a values of 4.2 and 4.8 (Table 1). However, the experimental K_M data (Figure 4A) is not good enough to resolve these two pK_a values and determine the pH-independent values of K_s.

Figure 4.

Effect of pH on K_s. (A) K_s values are the experimentally determined K_M values determined by fitting initial rate values to the Michaelis–Menten equation, as described in the Experimental Section. The solid line was calculated using the equation K_s(obs) = K_sa/(1 + K_a/[H⁺]) + K_sb/(1 + [H⁺]/K_a) and the fitted values of K_sa = 23.5 ± 1.9 mM, K_sb = 0.333 ± 0.025 mM, and pK_a = 5.12 ± 0.17. (B) K_s values (solid circles) were calculated at 0.1 pH intervals by dividing the fitted values for k₂ (Figure 3A) by the fitted values for k_cat/K_M (Figure 2), k_cat/K_M = k₂/K_s. The solid line was calculated using the equation K_s(obs) = (K_sa·[H⁺]² + K_sb·K_a·[H⁺] + K_sc·K_a·K_b)/([H⁺]² + K_a[H⁺] + K_a·K_b) and the fitted values K_sa = 24.0 mM, K_sb = 32.2 mM, K_sc = 0.373 mM, pK_a = 4.23, pK_b = 4.82. (C) 1/K_s values (solid circles) were calculated at 0.1 pH intervals using the values of K_s in (B). The solid line was calculated using the equation (1/K_s(obs)) = {(1/K_sa)·[H⁺]² + (1/K_sb)·K_a·[H⁺] + (1/K_sc)·K_a·K_b}/([H⁺]² + K_a·[H⁺] + K_a·K_b) and the fitted values K_sa = 24.0 mM, K_sb = 32.4 mM, K_sc = 0.372 mM, pK_a = 6.75, pK_b = 4.10.

Therefore, to obtain K_M (K_M = K_s) values consistent with the fitted values of k_cat (solid line 2 in Figure 2A) and k_cat/K_M (solid line in Figure 1), K_M values were calculated using these fitted values and the equation K_M = k_cat × K_M/k_cat. The values of K_s (K_s = K_M) were calculated at 0.1 pH intervals from pHs 2.6–9.8 (solid circles in Figure 4B).

To determine the pH-independent K_s values (K_sa, K_sb, and K_sc in Scheme 1), K_s values (K_s = K_M) were fitted (Figure 4B) to the equation for a doubly ionizing system (K_s(obs) = (K_sa·[H⁺]² + K_sb·K_a·[H⁺] + K_sc·K_a·K_b)/([H⁺]² + K_a·[H⁺] + K_a·K_b)) and this gave three pH-independent K_s values of 24 mM (K_sa), 32.2 mM (K_sb), and 0.373 mM (K_sc) (Scheme 1 and Table 1). The fitted values of pK_a and pK_b determined from the pH dependence of K_s had values of 4.23 and 4.82, in good agreement with the pK_a values obtained from the pH dependence of k₂ (Table 1). This is expected as the pH dependence of K_s (or K_M) like k_cat reflects ionizations within the ES complex or THI intermediate (Scheme 1). The pH dependence of 1/K_s like that of k_cat/K_M reflects ionizations in the free enzyme. Fitting the 1/K_s values (Figure 4C) to a doubly ionizing system gave pK_a values of 6.75 and 4.1, which, as expected, were the same as observed for the pH dependence of k_cat/K_M (Table 1), which also reflects ionizations in the free enzyme. The agreement of the pK_a values determined from the pH dependence of K_s and 1/K_s with the pK_a values obtained from the pH dependence of k_cat and k_cat/K_M, respectively, confirms that this approach should allow the determination of estimates of the pH-independent K_s values K_sa, K_sb, and K_sc that are consistent with the experimentally determined values of k_cat and k_cat/K_M used to calculate the K_s values used. This is supported by the fact that the pH-independent K_s values K_sa, K_sb, and K_sc obtained from the pH dependence of K_s and 1/K_s were essentially the same (Table 1).

3. Discussion

The pH dependence of k_cat/K_M showed that the active group was A^2– in eq 2 and that it was inctivated by protonation to form AH^– and AH₂ (eq 2)

2

The free enzyme pK_a values 6.75 ± 0.09 and pK_b = 4.10 ± 0.13 obtained from the pH dependence of k_cat/K_M and 1/K_s (Table 1) have been attributed to the trypsin residues histidine-57 and aspartate-189, respectively.^9,25−30 In both cases, it is the ionized form of these groups that are catalytically active (structure a1 in Scheme 1). Histidine-57 is part of the catalytic triad and its ionized form acts as a general base catalyst during catalysis (b1 in Scheme 1). Once it is protonated (AH^–, eq 2), it can no longer act as a general base catalyst for tetrahedral intermediate formation (b1 in Scheme 1) and so catalysis is inhibited. However, if the histidine pK_a is raised in the ES complex to a value >11 (structures b1 and b2 in Scheme 1) so that it can be an effective general base catalyst for tetrahedral intermediate formation (structures b1 to c1 in Scheme 1), then this pK_a will not be observed in our pH studies from pH 3–10. Protonation of histidine-57 in the free enzyme (structures a1 to a2 in Scheme 1) is also known to decrease substrate and inhibitor binding and so this should also contribute to substrate catalysis being inhibited with a pK_a of 6.75.^22,31,32

The negatively charged side chain carboxylate group of the aspartate-189 residue is located at the bottom of the S₁ specificity site where it can form an ion pair with the positively charged side chains of lysine or arginine substrates. pK_a values of 7.1 and 4.55 have been obtained from the pH dependence of k₂/K_s for the p-nitrophenol substrate Z-Lys-pnp with trypsin.²⁵ With the neutral substrate Z-Ala-pnp, no substrate interaction with aspartate-189 is expected and so the fact that only one pK_a value of 6.9 was obtained from the pH dependence of k₂/K_s with this neutral substrate²⁵ confirms the assignment of the pK_a value of ∼4 to aspartate-189 in the free trypsin. Likewise, the fact that pH studies of k₂ showed that the pK_a of ∼4 was detected with the lysine substrate Z-Lys-pnp but not with the neutral substrate Z-Ala-pnp also confirms the assignment of pK_a of ∼4 to aspartate-189 in the trypsin ES complex with Z-Lys-pnp.²⁵ Therefore, the pK_a values of 4.1 and 4.23 obtained from the pH dependence of k_cat/K_M and k₂ in the present study with Z-lys pna are assigned in the same way to apartate-189 in free trypsin and to the trypsin ES complex or the trypsin tetrahedral intermediate (THI in Scheme 1), respectively (Table 1).

The protonation of a group with a pK_a of 4.1 in the free enzyme and 4.23 in ES and or the trypsin tetrahedral intermediate (THI in Scheme 1) decreases the K_s from 32 to 24 mM (Table 1). Therefore, if this pK_a of 4.10–4.2 is due to ion pair formation between the substrate’s lysine side chain and aspartate-189, then ion pair formation does not increase substrate binding but instead leads to a small decrease in binding by increasing K_s from 24 to 32 mM. Small positively charged guanidines or alkylamines inhibit the hydrolysis of positively charged substrates by trypsin and they enhance the hydrolysis of neutral substrates by increasing k_cat while K_M undergoes minimal perturbation.^25,33,34 This led to the suggestion that positively charged ligands and substrates activate trypsin by binding in the S₁ specificity site.³³ Structural studies have confirmed that positively charged ligands binding to aspartate-189 in the S₁ specificity pocket induce conformational changes that activate trypsin.³⁵⁻³⁸ Replacing aspartate-189 with serine resulted in a a small 2–6-fold change in K_M but a much larger, ∼100 000, decrease in k_cat/K_M, confirming that the primary role of lysine and arginine substrates binding to aspartate-189 is to activate trypsin.³⁹ Therefore, these results show that the binding energy between the carboxylate group of aspartate-189 and the positively charged side chains of lysine or arginine substrates is mainly used to activate trypsin and has a minimal effect on K_s. This explains why protonation of aspartate-189 (pK_a 4.1–4.2) has such a small effect on K_s (42.4–24.0 mM, Table 1) and yet such a large effect on k₂, resulting in the stoichiometric inhibition of trypsin (line 2 in Figure 3A).

With the positively charged Z-Lys-pna substrate, an additional pK_a of 4.81 was obtained from the pH dependence of the acylation rate constant k₂ (eq 1). Protonation of this group led to an ∼86-fold increase in K_s from 0.37 to 32.4 mM (Table 1). A similar ∼86-fold increase in K_s was observed when histidine-57 was protonated in the free enzyme with a pK_a of 6.75 (Table 1), which would appear to suggest that the pK_a of histidine-57 changes from 6.75 in the free enzyme to 4.82 in the tetrahedral intermediate adduct (pK_THI1 in Scheme 1) and that the ∼86-fold decrease in K_M is due to binding energy being used to lower the pK_a of histidine-57 from 6.75 to 4.82. It also shows that the protonation state of histidine-57 has a major role in substrate binding. An ∼3-fold increase in K_M below pH 7 was also observed with N-benzyloxycarbonyl-l-arginine-p-toluidide and trypsin,⁴⁰ but in this case, the decrease in histidine pK_a was much smaller (pK_a 6.38). Larger 13-fold increases in K_M values have also been observed when histidine-57 in chymotrypsin is protonated with hydrazide substrates.⁴¹ It has been suggested that these decreases in binding were due to the positively charged histidine-57 interacting with the leaving group amine.¹³ As expected with trypsin and neutral p-nitrophenol substrates that do not have a leaving group amine, there is no increase in K_s when histidine-57 is protonated.²⁵ However, with chymotrypsin, decreases in inhibitor binding at low pH have also been observed with 2-p-toluidinylnaphthaline-6-sulfonate,³² proflavin,³¹ and peptide-derived glyoxal inhibitors.²² This suggests that a neutral imidazole group of the histine-57 residue is required for optimal binding of these substrates and inhibitors.

There is a considerable body of evidence that shows that the serine proteases stabilize zwitterionic tetrahedral adducts that mimic the the catalytic zwitterionic tetrahedral intermediate. These zwitterionic tetrahedral adducts refer to the negatively charged oxyanion of the tetrahedral intermediate and the positively charged imidazolium ion of histidine-57 and ignore all other charged groups on the enzyme. In these zwitterionic tetrahedral adducts, the pK_a of the majority of histidine-57 (analogous to pK_THI2 in Scheme 1) is raised^{16,18,20−22,42} and the pK_a (analogous to pK_THI1 in Scheme 1) of the majority of the oxyanion is lowered.^{16,18,19,22,43,44} Specific peptide-derived glyoxal inhibitors are tightly bound as neutral zwitterionic tetrahedral complexes (structure c1 in Scheme 1), which are thought to mimic the catalytic tetrahedral intermediate.^22,43,45 In these zwitterionic glyoxal complexes, ¹H NMR and ¹³C NMR have been used to show that the pK_a of histidine-57 is >11 and the oxyanion pK_a is ∼4.^22,43 The increase in K_i values at low pH was dependent on a pK_a of ∼4, and this pK_a was assigned to protonation of the oxyanion in the glyoxal-chymotrypsin tetrahedral adduct.²² Therefore, if the breakdown of the zwitterionic tetrahedral intermediate in the acylation step of the trypsin-catalyzed hydrolysis of Z-Lys-pna (species c1 in Scheme 1) is rate-limiting, then the pK_a of 4.81 (Table 1) in trypsin catalysis should be assigned to protonation of the oxyanion in the catalytic zwitterionic tetrahedral intermediate (pK_THI1 in Scheme 1). It also shows that tight binding of inhibitors and substrates is possible when histidine-57 is protonated provided the oxyanion is also present to neutralize the charge on the imidazolium ion of histidine-57 (ImH⁺ O^–). If the oxyanion is protonated (ImH⁺ OH), the charge on the protonated imidazolium ion will no longer be neutralized by the oxyanion and so the positively charged imidazolium ion of histidine-57 will inhibit binding. Therefore, K_i values will increase as the oxyanion is protonated, as observed with peptide glyoxal inhibitors that bind to chymotrypsin as zwitterionic tetrahedral adducts mimicking the catalytic tetrahedral intermediate.²² This also explains why K_s values with trypsin increase by essentially the same amount when histidine-57 is protonated (1/K_s in Table 1) in the free enzyme (a1 to a2 in Scheme 1) and also in the acylation complex (K_s in Table 1) when the oxyanion of the zwitterionic tetrahedral intermediate is protonated (structures c1 to c2 in Scheme 1).

It is generally accepted that the nucleophilicity of the hydroxyl group of serine-195 is enhanced by the imidazole group of histidine-57 acting as a general base catalyst (structure b1 in Scheme 1). It has been argued that as the pK_a of the serine hydroxyl group is ∼15,^{15,16,22,23,42,46} then for general base catalysis by histidine to be effective (structure b1 in Scheme 1), its pK_a should raised to a similar value of ∼15 on forming the enzyme substrate complex (ES in Scheme 1)^15,16,22,23 and not lowered to a value <7.

Earlier studies on the pH dependence of chymotrypsin catalysis appeared to contradict these results as it appeared that the pK_a of histidine-57 had been decreased to a value <7 within the ES complex.¹⁰⁻¹⁴ The reassignment of this pK_a to the oxyanion in the present work resolves this contradiction. As protonation of the oxyanion inhibits catalysis, it is essential that the oxyanion pK_a is reduced to ensure the enzyme is catalytically active at physiological pH values. This therefore explains why the serine proteases have evolved to lower the oxyanion pK_a so effectively.^{16,18,19,22,43}

When an interaction occurs between two ionizing groups, four species would be formed with four microscopic pK_a values (c1, c2, c3, c4 in Scheme 1). So, for example, if in Scheme 1 the concentrations of all species (c1, c2, c3, c4 in Scheme 1) are equal, then 50% of histidine-57 (pK_THI4 in Scheme 1) and 50% of the oxyanion (pK_THI1 in Scheme 1) will both have pK_a values of 4.8. Likewise, 50% of histidine-57 (pK_THI2 in Scheme 1) and 50% of the oxyanion (pK_THI3 in Scheme 1) will have pK_a values of >11. So this interaction could explain how histidine-57 could have microscopic pK_a values of both ∼4.8 (pK_THI4) and >11 (pK_THI2) in the THI (Scheme 1). Likewise, the oxyanion could have microscopic pK_a values of ∼4.8 (pK_THI1) and >11 (pK_THI3) in the THI (Scheme 1). However, the serine proteases preferentially stabilize zwitterionic terahedral intermediates (structure c1 in Scheme 1) and so it is expected that at least 99% of the oxyanion and the imidazolium ion of histidine-57 will have pK_a values of ∼4.8 and >11, respectively.

The deacylation rate constant (k₃, in eq 1) was dependent on a singly ionizing group (AH = A^–) with a pK_a = 6.41 ± 0.22, which we assign to histidine-57. Therefore, we can conclude that the ionization of aspartate-189 does not appear to have a significant effect on the pH dependence of deacylation.

3.1. Mechanism for the pH Dependence of the Trypsin-Catalyzed Hydrolysis of Z-Lys-pna

The proposed mechanism is summarized in Scheme 1. In the free enzyme (a1, a2, and a3 in Scheme 1), the imidazole group of histidine-57 has a pK_a of 6.75 and the carboxylate group of aspartate-189 (Scheme 1) that binds the side chains of the lysine or arginine residues of substrates or inhibitors has a pK_a of 4.1. Binding of the substrate to form the enzyme–substrate complex (ES in Scheme 1) causes a strong interaction between the carboxylate group of aspartate-102 of the catalytic triad and the imidazolium group of histidine-57,^16,18,22,47 which perturbs the pK_a values of these groups to values <3 and >11, respectively, so they are no longer detected in pH studies. This increase in the pK_a (pK_a > 11) of the imidazolium group of the histidine-57 enables it to act as an effective general base catalyst (structure b1 in Scheme 1) for deprotonation of the hydroxyl group of the catalytic serine group (pK_a ∼ 15), promoting its reaction with the substrate to form a zwitterionic tetrahedral intermediate (structure c1 in Scheme 1). The positively charged imidazolium group of histidine-57 helps lower the pK_a of the oxyanion stabilizing the zwitterionic tetrahedral intermediate. A small reorientation the imidazole ring⁴⁸ will then allow histidine-57 to act as general base catalyst for breakdown of the tetrahedral intermediate (structure c1 in Scheme 1) to form the acyl intermediate (structure d1 in Scheme 1). The rate-limiting step in acylation (k₂) is this breakdown of this zwitterionic tetrahedral intermediate (structures c1 to d1 in Scheme 1). Protonation of the oxyanion with a pK_a value of 4.8 (pK_THI1 in Scheme 1) will decrease the concentration of the catalytic zwitterionic intermediate (c1 in Scheme 1), inhibiting catalysis, and so k₂ decreases with a pK_a of 4.8. Protonation of aspartate-189 (pK_THI2 in Scheme 1) with a pK_a of 4.2 disrupts its ion pair interaction with the ε-amino group of the substrate deactivating trypsin and promoting substrate disassociation from trypsin. This inhibits catalysis, and so k₂ also decreases with a pK_a of 4.2.

Deacylation (k₃ step in Scheme 1) like acylation is also expected to proceed via a tetrahedral intermediate(not shown in Scheme 1). The imidazole group of histidine-57 has the potential to act as a general base catalyst for formation of the zwitterionic tetrahedral intermediate and as a general acid catalyst for its breakdown. As the rate of deacylation (k₃) increases with increasing pH with a pK_a of 6.4 (Figure 3A), this suggests the imidazole group is acting as a general base catalyst for tetrahedral intermediate formation. However, as water has a pK_a value of 15.74, an imidazole group with a pK_a of 6.4 would not be expected to be an effective general base catalyst. Aldehyde inhibitors of chymotrypsin form zwitterionic tetrahedral adducts with chymotrypsin where the oxyanion has a pK_a ∼ 7 and histidine-57 has a pK_a ∼ 8.⁴⁹ It has been argued that the histidine pK_a of ∼8 can be explained by the fact that these inhibitor adducts of chymotrypsin-like acyl intermediates do not have a large leaving group that can fix the catalytic histidine in position and raise its pK_a > 11.⁴⁹ If breakdown of this zwitterionic tetrahedral intermediate is rate limiting for deacylation, then another possibility is that the pK_a of 6.4 reflects formation of the oxyanion of the zwitterionic tetrahedral intermediate as proposed for the acylation reaction. However, as the carboxylate group of the product of deacylation (P₂) is a good leaving group, formation and not breakdown of the zwitterionic tetrahedral intermediate is expected to be rate limiting in the deacylation reaction. Also, as there is a very good leaving group in the deacylation step, a concerted reaction becomes a possibility.¹⁷

4. Experimental Section

4.1. Materials

Trypsin (type III, 2× crystalized, salt free from bovine pancreas) and all other reagents were obtained from Sigma-Aldrich Chemical Co., Gillingham, Dorset, U.K. Trypsin was 72% fully active by active site titration with p-nitrophenyl p-guanidobenzoate,⁵⁰ as described by Malthouse et al.¹⁹ Z-Lys-pna was synthesized as described by Mackenzie et al.⁵¹

4.2. Kinetic Studies

The trypsin -catalyzed hydrolysis of Z-Lys-pna was studied at 25 °C in 3 mL volumes and 0.1 M ionic strength buffers.⁵² The buffers used were pH 3.13–4.38 (sodium formate), pH 4.40–5.49 (sodium acetate), 5.98–7.72 (potassium phosphate), 7.76–8.68 (Tris–HCl), pH 9.05 (sodium borate), and pH 9.76 (sodium carbonate). pH measurements were made either with a Radiometer combination electrode (GK 2401C) or by using a Beckman combination electrode model number 39522. Stock solutions of Z-Lys-pna were made up in 1 mM HCl (maximum solubility ∼18 mM) and quantified using E₃₁₄ = 13 900 M^–1·cm^–1, as described by Mackenzie et al.⁵¹ Primary stock solutions of ∼1 mM fully active trypsin were prepared in 1 mM HCl, and this solution was diluted in 1 M HCl to prepare appropriate concentrations for the pH studies. A typical assay contained 1 mL of buffer (I = 0.3 M), 1.9–x mL of 1 mM HCl, and x mL of substrate in 1 mM HCl. Different substrate concentrations were obtained by adding different amounts of the stock substrate (x mL). Catalysis was initiated by adding 0.1 mL trypsin in 1 mM HCl. The concentration of trypsin was kept constant when determining the catalytic parameters at a given pH. However, fully active enzyme concentrations were increased (0.35–83.6 μM) as the pH was decreased to help compensate for the decrease in k_cat and k_cat/K_M as the pH decreased. The fully active trypsin concentrations used in the assays were 11–84 μM (pH 3.1–5.0), 3.7–4.4μM (pH 4.4–5.5), and 0.35–0.39μM (pH 6.0–9.8). Initial rates of hydrolysis of Z-Lys-pna were followed by determining the amount of p-nitroaniline (E₄₁₀ = 8800 M^–1·cm^–1) released over a 5–15 min period. It was ensured that there was always at least a 15-fold excess of the substrate over enzyme when initial rates were determined. k_cat/K_M data at pHs 3.56 and 4.38 were determined from initial rates obtained when [S₀] ≪ K_M. The effect of pH on the catalytic parameters was determined by fitting experimental data to the appropriate function as described by Cleland.⁵³

Glossary

Abbreviations

Z

benzyloxycarbonyl

pna

p-nitroanilide

pnp

p-nitrophenyl ester

Accession Codes

The UniProtKB accession ID for bovine trypsin is P00760.

The author declares no competing financial interest.