graphDelta: MPNN Scoring Function for the Affinity Prediction of Protein–Ligand Complexes

Abstract

In this work, we present graph-convolutional neural networks for the prediction of binding constants of protein–ligand complexes. We derived the model using multi task learning, where the target variables are the dissociation constant (K_d), inhibition constant (K_i), and half maximal inhibitory concentration (IC₅₀). Being rigorously trained on the PDBbind dataset, the model achieves the Pearson correlation coefficient of 0.87 and the RMSE value of 1.05 in pK units, outperforming recently developed 3D convolutional neural network model K_deep.

1. Introduction

The majority of marketed drugs act via non-covalent binding to a macromolecular target in a human organism, such as protein molecules or nucleic acids.¹ The binding affinity is one of the major determinants along with absorption, distribution, metabolism, and excretion properties of the dose necessary to achieve a biological response and, consequently, the additional off-target impact on the organism. Many efforts are made to develop robust and powerful binding affinity prediction models.² With the substantial growth of atomic structures in the Protein Data Bank (PDB³), now it is possible to derive reliable scoring functions.⁴⁻¹¹ Depending on the formulation of the optimization problem, the scoring functions aim (i) to identify correct (near-native) binding pose amongst conformations of modeled putative binding candidates or (ii) to rank a given set of chemical compounds (ligands) with respect to its binding affinity to a particular target.¹² These task-specific SFs should combine the high speed of computation with accuracy,¹³ and usually, the parameters of the recent scoring functions were obtained without affinity information.¹⁴ SFs can be divided into three categories based on the way parameterization: (1) force-field-based SFs were designed from physical principles based on the theoretical representation of interatomic potentials;¹⁵ (2) empirical SFs, which utilize force-field based canvas with the parameter set, were tuned to reproduce experimental affinity measurements;^4,8,9 (3) knowledge-based SFs trained with experimental structural data to approximate interatomic potentials as arbitrary functions defined by piece-wise linear interpolation or in the other way.^7,11

1.1. Machine Learning Approaches for Protein–Ligand Scoring Functions

The majority of the mentioned approaches basically utilize a linear regression approach to account for different terms describing intermolecular interactions such as hydrogen bonding, π–π stacking, π–cation interactions, entropic contribution, van der Waals interactions, and so forth⁴ for the sake of efficiency and are easy to interpret because of the possibility of per atom decomposition of the score value. Ain et al. reported² the possible improvement in performance when the scoring function is not constrained to a predefined functional form. These machine learning approaches¹⁶ were applied for both classification and regression tasks in the different areas of science and technology. One of the most known machine learning-based SF for the evaluation of protein–ligand interactions is the RF-score¹⁰ that utilizes the ensemble of decision trees to approximate binding affinity using the receptor–ligand interatomic interactions counts as the descriptors. Some authors customized this methodology by training target-specific scoring functions using AutoDock Vina scoring terms as descriptors.^17,18

1.2. Sampling Approaches to Binding Affinity Estimation

It should be noted that because of the peculiarities of the common drug discovery pipelines, hit identification and hit to lead optimization are considered to be separate stages, and fast scoring is used for the former and the sophisticated molecular simulations are performed for the latter. The free energy perturbation (FEP) technique¹⁹ is based on the alchemical transformations and allows us to achieve in some cases good results for the affinity ranking in a series of closely related compounds. The end-state free energy approaches (MM-PB(GB)SA)²⁰ being not so demanding for computational resources can be considered as a cheaper but a less accurate alternative to FEP.²¹ While the chemical space exploration^22,23 leads to creation of enormous virtual databases, there is a strong demand to assess for better techniques that are faster than ensemble methods (FEP, MM-PBSA) and more accurate than scoring functions developed for virtual screening.

1.3. Progress in Applications of Deep Learning for Chemical Problems

Deep neural networks (DNN) are powerful machine learning models with broad applicability to different regression and classification tasks. Progress in hardware and software development for large-scale training of convolutional neural networks (CNN)²⁴ and recurrent neural networks (RNN)²⁵ resulted in great achievements in computer vision, natural language and signal processing, and other related problems²⁶ The promising results obtained in computational chemistry^27,28 structure generation tasks^29,30 and QSPR/QSAR^31,32 by means of DNN, demonstrate that the application of DNN undoubtedly has a strong potential to growth in the area of the computer-aided molecular design.

1.4. 3D Convolutional Neural Networks for Protein–Ligand Scoring Functions

Recently it was shown that 3D convolutional neural networks (3D CNN) can be applied to derive scoring functions for binding affinity prediction.^33,34 Current approaches use voxelized representation of a molecular complex, where voxel channels encode physicochemical properties, similar to the RGB channels in images. Molecular representations for processing by 3D CNN can be constructed in several ways: each atom or a group of atoms can be represented either by a separate channel or a channel which can represent some kind of superposition of atoms. For example, one can calculate interactions with a probe atom to construct 3D molecular field or use some physicochemical or DFT (3D electron density) calculations as 3D filed representations.^31,35 Both of these approaches have limitations: atom-to-channel representation leads to dramatic increase in the number of input channels, which are crucial for memory consumption. It is also inefficient because many channels are empty or sparse. The use of molecular fields, in turn, results in losing information. The balance between the quality of representation and memory requirements is a fundamental problem with 3D CNNs. This fact motivates us to search for new ways and architectures for 3D deep learning in molecular science. K_deep(33) trained using PDBbind data and aimed at predicting absolute binding affinities takes a set of 3D grids representing map of certain structural features (hydrophobic, aromatic, h-bond acceptors, and so forth.) as the input data. Also, the model developed by Ragoza et al.³⁴ with the goal to improve virtual screening results act as a classification model which operates with 3D maps defined by smina (scoring and minimization with AutoDock Vina) atom types.³⁶ However, the performance of these models can still be improved. The major drawback of 3D CNN is the enormous number of parameters, which results in high-demand of computational resources and GPU memory; meanwhile, GPU memory is limited.³⁷ Interestingly, a special architecture which is applied simultaneously for two maps representing similar ligands was used to predict differences in affinity to input ligands and achieved better results compared to MM-GBSA and QSAR in blind predictions.³⁸

1.5. Geometric Deep Learning and Tasks of This Work

The limitations of 3D CNN architectures motivated researchers to search more natural ways of processing chemical structures. Geometric deep learning is a bunch of approaches which aim to generalize neural network to non-Euclidian manifolds, in particular, to graphs.³⁹ Simultaneously, molecules can be represented as labeled and weighted graphs in chemoinformatics, and the idea of the applications of geometric deep learning seems to be natural and can lead to very promising results.^40,41 One of the graph convolutional architectures (PotentialNet⁴²) was trained on PDBBind 2007⁴³ and applied to the affinity prediction problem. Authors use gated graph neural network architectures which utilizes RNN for the update stage. PotentialNet can perform graph convolution operations for both covalent and non-covalent interactions; in other words, authors include in an initial graph the nearby residues.

The goal of this work is the design of the scoring function with a possibility to predict binding free energy for a diverse set of chemical compounds and protein targets based on subclass of graph CNN—message passing neural networks which demonstrated very promising results in approximation of DFT electron energies²⁸ for the QM9 small molecule data set.⁴⁴ We assess its performance on different data sets and compare it with the existing tools. We showed that the message passing neural network (MPNN) can be a very efficient tool for modeling protein–ligand interactions.

2. Results and Discussion

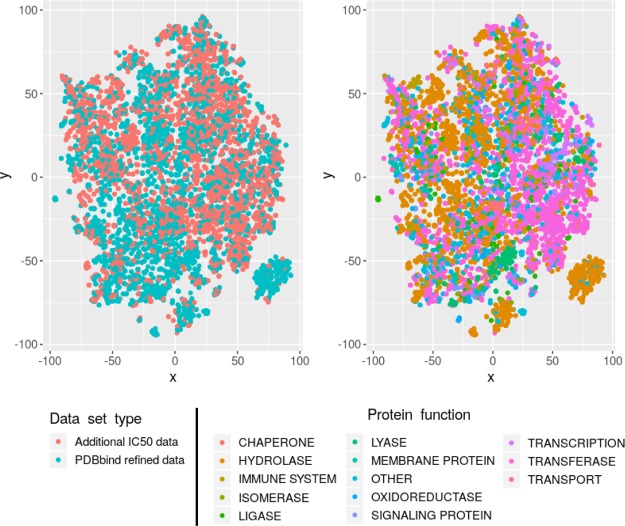
The thorough description of the training set properties is necessary for the applicability domain definition of a scoring function. The extended training set obtained by IC₅₀ data addition contains more druglike molecules (Figure S1) than the initial data set. It may indicate that the optimal applicability domains of the model are structures which fall into line with Lipinski’s rule of five. To analyze the distributions of protein targets, we performed a t-SNE⁴⁵ mapping (by scikit-learn 0.19.1 package) of protein–ligand interaction descriptors⁴⁶ into a 2D space using an Open Drug Discovery Toolkit⁴⁷ (ODDT). The obtained distribution is shown in Figure 1. It should be noted that the usage of the additional IC₅₀ data improves the representation of the known types of interactions rather than introduce completely undescribed binding modes. The additional data, in general, describe the interaction with transferase and hydrolase enzymes, which appeared to be the most representative class of proteins in the current data set.

Figure 1.

Results of t-SNE mapping of ligand protein interactions represented by SILIRID⁴⁶ fingerprints: (left) blue color mark complexes that consist the initial PDBbind refined set while the red one represents the additional data; (right) color scheme is based on protein functions.

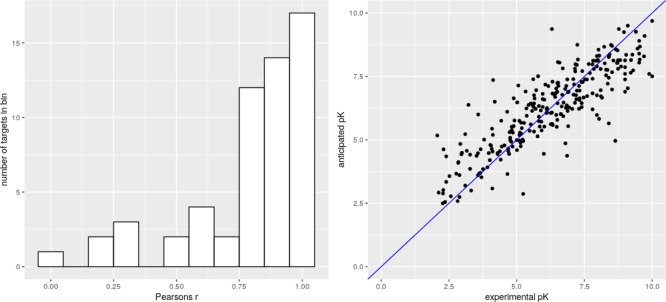
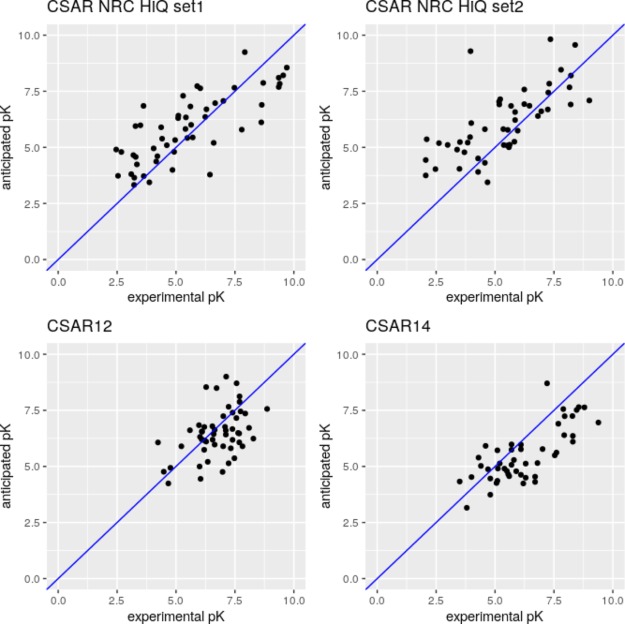
The trained MPNN scoring function demonstrates very good results for the CASF2016 test set composed of the X-ray structures significantly outperforming both K_deep and RF score in terms of Pearson R. Unfortunately, it is difficult to accurately compare RMSE because of the unavailability of the raw data from K_deep and RF-score. The authors of the K_deep mentioned that the inclusion of the low-quality data to the training set did not improve the results, probably because of the excessive noise contribution to the model. In this work, we showed that the inclusion of the IC₅₀ subset with a similar structural quality can improve the model and speed up model training when multi task learning is used. The neural network can predict a set of properties simultaneously, and the prediction of IC₅₀ and K_d, which are strongly correlated but still slightly differs, significantly improves the CASF2016 prediction results at 1000 epochs of training. At the same time, the multi task model trained for 2000 epochs appeared to be slightly overtrained compared to the single task model, which demonstrated the best performance for CASP2016 among all the used models. The results are presented in Table 2. The distribution of Pearson correlation coefficients computed for each target from CASF2016 demonstrates the improvement compared to K_deep: the number of Pearson r < 0.75 is 14 for graphDelta and is 32 (more than the half of targets) for K_deep and the number of Pearson r < 0.0 is zero for graphDelta and is six for K_deep (Figure 4). graphDelta (single task, 2000 epochs) demonstrates the best prediction rates for CASF2016 compared to the RF-score (one-tailed, z = −2.78, P = 0.0027) and K_deep (one-tailed, z = −2.09, P = 0.018) in terms of Pearson correlation coefficients. The single task graphDelta model trained for 2000 epochs outperforms K_deep or yields the similar results in terms of RMSE and Pearson correlation coefficients for CASF2016 and CSAR sets, except CSAR NRC HiQ set2, while RF-score yields better results than graphDelta in CSAR NRC HiQ set2 and CSAR14 (RMSE) and for CSAR NRC HiQ set1, CSAR NRC HiQ set2, CSAR14 (Pearson r). In average, graphDelta outperforms K_deep for these four data sets and yields practically similar results as the RF-score in terms of Pearson r and outperforms it in terms RMSE (Table 2).

Table 2. Results of graphDelta Evaluation on the CSAR Data Compared to K_deep and RF-Score^a.

			graphDelta		Kdeep(33)		RF-score33
dataset	epochs	MT/ST	r	RMSE	r	RMSE	r	RMSE
CASP2016	500	true	0.82	1.22	0.82	1.27	0.80	1.39
	500	false	0.84	1.17
	1000	true	0.86	1.11
	1000	false	0.84	1.16
	2000	true	0.84	1.17
	2000	false	0.87	1.05
CSAR NRC HiQ set1	500	true	0.74	1.67	0.72	2.08	0.77	1.99
	500	false	0.64	1.81
	1000	true	0.71	1.70
	1000	false	0.71	1.66
	2000	true	0.74	1.59
	2000	false	0.74	1.59
CSAR NRC HiQ set2	500	true	0.60	1.86	0.65	1.91	0.75	1.66
	500	false	0.59	1.72
	1000	true	0.56	1.92
	1000	false	0.71	1.52
	2000	true	0.64	1.73
	2000	false	0.71	1.53
CSAR12	500	true	0.52	1.16	0.37	1.59	0.46	1.00
	500	false	0.41	1.37
	1000	true	0.59	0.94
	1000	false	0.54	1.11
	2000	true	0.52	1.10
	2000	false	0.48	1.14
CSAR14	500	true	0.72	1.40	0.61	1.75	0.80	0.87
	500	false	0.66	1.51
	1000	true	0.65	1.34
	1000	false	0.59	1.67
	2000	true	0.70	1.32
	2000	false	0.74	1.22
average	500	true	0.68	1.46	0.62	1.72	0.72	1.38
	500	false	0.63	1.52
	1000	true	0.67	1.40
	1000	false	0.68	1.42
	2000	true	0.69	1.38
	2000	false	0.71	1.31

^aBold font is used to stress the best correlation coefficient and RMSE for the selected data set.

Figure 4.

Results of prediction (graphDelta, 2000 epochs, single task) for the CASF2016 data set: (left) histogram of correlation coefficients computed for all targets from CASF2016, (right) the depiction of the prediction results with the trend line.

To compare the obtained results with PotentialNet,⁴² we trained our model on PDBbind v.2007 which is about eight times less in size compared to the initial training set. PotentialNet for the smaller training sets yields better results (r = 0.82) than GraphDelta (r = 0.38) possibly because of the small size of the training set. It should be noted that the learning procedure was accompanied by fast overtraining and leaps to the prediction of the mean value.

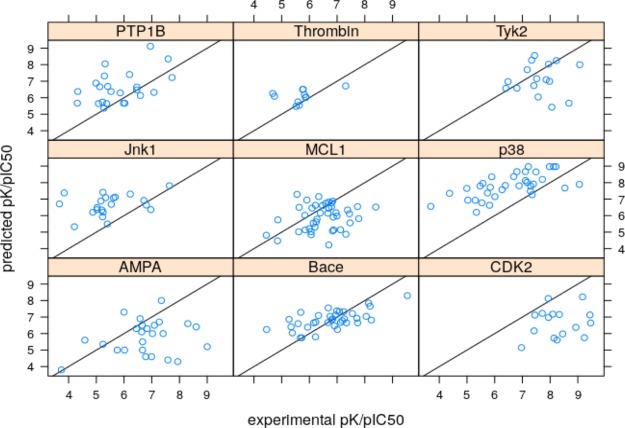
The graphDelta evaluation on the FEP and MM-PBSA data sets demonstrated worse results compared to the other SF where K_deep demonstrated the best results in terms of the Pearson correlation coefficient and RF-score shows the best RMSE (Table 3). The application of the MPNN scoring function (multi task, 2000 epochs of training) yields better results among ML scoring functions only for two subsets of the FEP data set: p38 and BACE. This dataset consists presumably of hydrolase (PTP1B, thrombin, Bace) and kinase (Tyk2, Jnk1, p38, CDK2) targets, and multi task demonstrated better results because of the extended training set by these types of proteins. The other graphDelta models yielded even worse results in terms of RMSE and Pearson r (see Table S1 and Figures S7–S11; Supporting Information). However, it should be noted that all examined SF gave poor results for this set of closely related structures.

Table 3. Results of graphDelta Evaluation on the Data Set Used for FEP and MM-PBSA Evaluation (graphDelta, 2000 Epochs, Multi Task)^a.

	graphDelta		Kdeep		RF-score		FEP or MM-PBSA
subset	r	RMSE	r	RMSE	r	RMSE	r	RMSE
p38	0.64	1.56	0.36	1.57	0.48	0.9	0.6	1.03
PTP1B	0.46	1.22	0.58	0.93	0.26	0.9	0.80	1.22
thrombin	0.39	0.74	0.58	0.44	0.08	0.71	0.71	0.93
Tyk2	0.17	1.08	0.05	1.23	0.41	0.94	0.89	0.93
Bace	0.65	0.78	–0.06	0.84	–0.14	0.65	0.78	1.03
CDK2	0.19	1.94	0.69	1.26	–0.23	1.05	0.48	0.91
JNK1	0.33	1.53	0.69	1.18	0.61	0.5	0.85	1.00
MCL1	0.22	1.12	0.34	1.04	0.52	0.99	0.77	1.41
AMPA	0.39	1.37	0.74	1.32	0.38	1.71	0.78	0.62
average	0.35	1.31	0.41	1.07	0.26	0.92	0.75	1.00

^aBold font is used to stress the best correlation coefficient and RMSE for the selected data set. MM-PBSA data are provided for AMPA receptor ligands, while FEP data are provided for other targets.

In this work, our goal was to develop a novel tool for scoring of protein–ligand interactions based on graph-CNN. Despite the performance improvement in CASF2016 and some other X-ray data sets, both the RMSE and correlation coefficient decreases for some data sets obtained by docking. We believe that the performance improvement is caused by the addition of high-quality IC₅₀ data to the training set which allowed the increase of the training set size in more than two times. This data set extension allowed us to train the model obtaining similar results faster (1000 epochs vs 2000 for Single task model). Noteworthy, the additional IC₅₀ data may introduce a skew performing better on kinases and hydrolases which are the main content of the cleaned IC₅₀ data set. This fact may be confirmed by the better performance of the multi task model on the docked data (Tables 3 and S1). At the same time, the performance of the examined models is still worse than trajectory-based approaches (FEP, MM-PBSA). Although trajectory-based approaches work well for some systems, sometimes, deep-learning-based models surpass their results.³⁸ It should be noted that trajectory-based affinity prediction methods works in the case of sufficient sampling which may be tricky for some types of proteins.⁴⁸ Modest results obtained for the complexes obtained by docking suggest the necessity of model improvement. We suggest two ways to accomplish this task. The first one is the application of this model to molecular dynamics trajectories or Monte-Carlo ensembles of structures which may be even slower than the trajectory-based approaches. The other possible approach is to apply proper data augmentation scheme which is not a straightforward task. Augmentation techniques which are often for 3D-CNN such as a shift of the box center and random rotations around are not suitable for graph CNN. We made available this scoring function at http://mpnn.syntelly.com/.

3. Computational Methods

3.1. Data Sets

The main source of data for the current work was PDBbind⁴⁹ (v.2018) containing 16151 protein–ligand complexes derived from Protein Data Bank (PDB) accompanied with their binding data in terms of dissociation (K_d) and inhibition (K_i) constants and half maximal inhibitory concentration (IC₅₀). A smaller “refined” set (4463 complexes) was compiled based on the following rules: the structure resolution less than 2.5 Å, an R-factor less than 0.25, ligand should be bound noncovalently and without steric clashes (any distance between pairs of ligand–protein atoms is more than 2.0 Å), pK is inside the range from 2 to 12, and complexes labeled only by IC₅₀ are eliminated. The reason for the latter action is the substrate concentration dependence of IC₅₀ (Cheng–Prusoff eq 1, where [S] and K_m are the substrate concentration in the experiment and Michaelis constant, respectively) and cannot be in union with the K_i/K_d subset. However, in practice, the pIC₅₀ values (logarithmically transformed IC₅₀) are usually less and within one logarithmic value compared to pK_i/pK_d. This bias can be easily learned using the model in the multi task learning mode⁵⁰ when the last layer simultaneously predicts both pK and pIC₅₀. Thus, we prepared a novel subset containing both pIC₅₀ and pK in all other quality criteria identical to the mentioned “refined” subset yielding 8766 complex structures. The idea to extend PDBbind refined set by low-quality data was also reported by Li et al.⁵¹ A core set (285 items) used for critical assessment of scoring¹² (CASF) 2016 was not changed compared to the previous version of the database, facilitating the performance matching with the other scoring functions. Additional test sets were used for comparison with other available models: two subsets of CSAR NRC-HiQ containing after removing intersections with training data 53 and 49 complexes (csardock.org), and CSAR12 and CSAR14 sets downloaded from D3R (drugdesigndata.org) were prepared according to Jiménez et al.³³ Finally, we considered a bunch of data set serving as benchmarks^52,53 for the ensemble methods (FEP, MM-PB(GB)SA) developed for binding free energy estimation.

1

3.2. Descriptors

The choice of the descriptor set which reflects the atomic environment in the relevant manner was influenced by a success of electron energy approximation by neural network potentials. The good representation of an atomic environment should be invariant to the permutation, rotational, reflection, and translation symmetries. It is worth mentioning that Behler–Parrinello symmetric functions (BPS)⁵⁴ made a basis for the first transferable NN potential and smooth overlap of atomic positions,⁵⁵ which defines a similarity metric for direct comparison of atomic environments. In this work, we employed BPS to describe the atomic environment in a binding site.

It is natural to prioritize local environment defining a cut-off function f_c(r_ij) (eq 2)⁵⁶ which smoothly decreases the weights of atoms outside the proximal environment and assigns the zero weight for atoms outside the cut-off distance. In the present work, a cutoff of 12 Å had been used. Table S2 (Supporting Information) lists the parameters defining BPS descriptors used in this study.

BPSF contains terms which depend only on the distance to the neighboring atoms and terms which are based on angles formed by all atom pairs in the environment and the central atom as an angle vertex. Functions with the radial symmetry are constructed as follows (eq 3) with the sum of Gaussian functions. Their role is to indicate the existence of certain atom approximately at distance r_s.

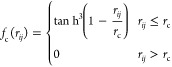2

3

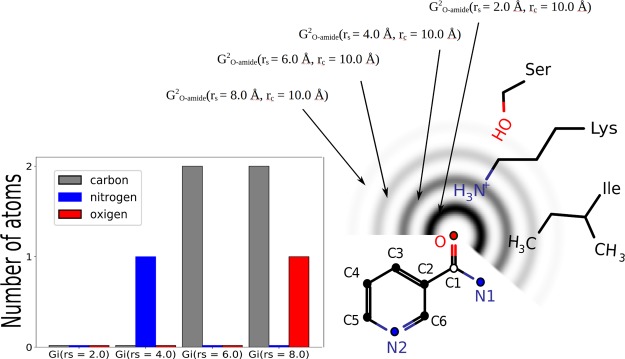
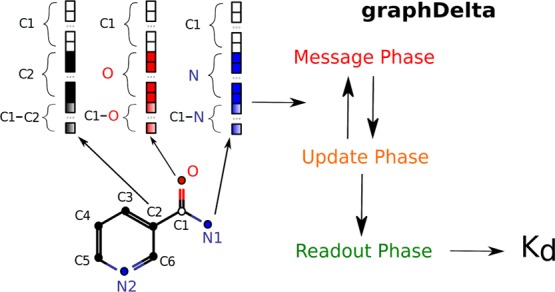
It is to be noted that that radial symmetry functions take into account only pair-wise atom interactions. We illustrated the G_i² computation procedure as a simple example (Figures 2, 3, 5 and 6) which shows nicotinic acid amide schematically surrounded by three amino acid residues (Ser, Lys, and Ile), and the descriptors are computed for its oxygen atom. The BPS functions are denoted by concentric circles with decreasing intensity which is caused by the f_c function application. The bar plot on the left part of Figure 2 shows the number of atoms which contribute to the G_O–amideⁱ values for different r_s parameter values; taking into account triplewise interactions, we compute the angular dependent function (eq 4)

4

where r_ij corresponds to the distance between i and j atoms. All angles θ_jik are defined with atom i as the central one and atoms j and k are the atoms from the environment. The η value control the guassian sharpness, while the role of parameter ζ is to provide angular resolution. High ζ values produce a narrower range of nonzero symmetry function values. The parameter λ can take values +1 or −1 allows to shift the maximum value of the cosine part from π (+1) to 0 (−1) and describe the atomic environment in a better way. It should be noted that G_i² and G_i³ represent two-body and three-body interactions and can be expanded to high-order terms, but they are not used in the current work.

Figure 2.

Illustration of the G_i² computation.

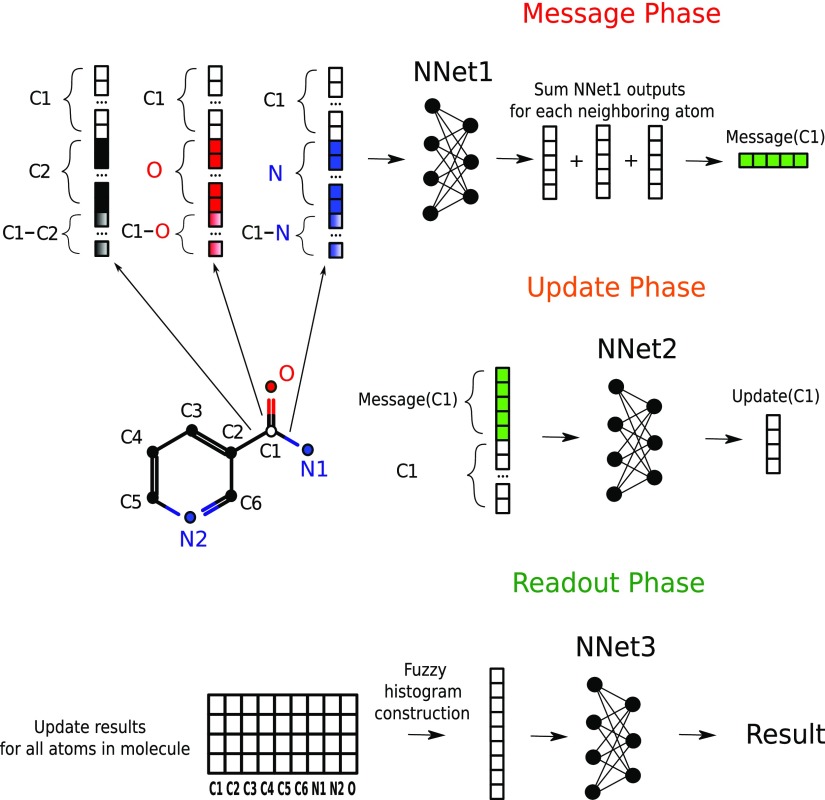
Figure 3.

General description of the MPNN forward pass with interaction net architecture.

Figure 5.

Results of prediction (graphDelta, 2000 epochs, single task) for CSAR data sets.

Figure 6.

Results of prediction (graphDelta, 2000 epochs, multi task) for data sets used to assess FEP⁵² and MM-PBSA⁵³ performance.

The parameter set used to compute descriptors can be found in Table S2 (Supporting Information), and all possible combinations of parameters yielded 52 descriptors of the atomic environment. We defined several atom types representing the most common elements which can be found in the protein structure: C, O, N, S, P, M1, M2, where M1 and M2 represent single charged metal ions and metal ions in the other charged state, respectively. BPS computed for each atom type of the protein environment leads to 364 environmental descriptors and combined with one-hot encoded ligand atom type gives 373 descriptors calculated for each atom of the ligand molecule. Ligand atom types (C, O, N, S, P, F, Cl, Br, I) were selected by their relative occurrence in the data set. Hydrogen atoms were ignored to reduce the memory requirements. It should be noted that boron atoms were considered to be included in this set, but the majority of boron-containing ligands contain carborane substructures difficult to describe using the standard valence model or boronic acids which usually form a covalent bond with certain protein atoms.

3.3. Neural Network Architecture

Chemical structures are naturally represented as undirected graphs, where nodes and edges correspond to atoms and bonds, respectively. Recently Gilmer et al. designed the MPNN framework,⁵⁷ that operates with chemical graphs, and which is invariant to graph isomorphism.^28,41,58 In this study, we consider a chemical graph G with node features x_v and edge features e_vw where v and w are node indexes. According to Gilmer et al., the forward pass consists of two main stages: (i) the message passing phase and (ii) the readout phase. The message passing phase can be divided into T stages, which are performed sequentially, and at each time step, two functions are carried out on the graph elements: message function (M_t) and update function (U_t). The message and update functions are learned differentiable functions with fixed length input and output. To perform the message phase, first, for each node v of graph G, we select neighboring nodes of v and denote them N(v). Then, for each pair v and w, where w ∈ N(v), we concatenate two node descriptor vectors h_v^t and h_w with edge descriptor vector e_vw, and the obtained vector of fixed length becomes an input for a message function M_t. Then, we summarize all these outputs (eq 5), yielding the m_v^t+1 vector of the fixed length finishing the message phase. The update phase is performed for each node v as a result of application of an update function (eq 6) to the concatenation of the hidden state vector h_v and the newly computed message vector m_v^t+1.

5

6

7

One can imagine this iterative process as information flooding across the graph from node to node. It should be noted that in our implementation vector, h_v¹ is initialized as the BPS node descriptor vector calculated to represent the atomic environment. Vector e_vw is added for all time steps without changes. The readout phase consists of an application of the readout function (eq 7) to a set of hidden states h_v obtained at the final update step yielding the target variable. The readout function is constructed to be invariant to the node permutations which make the designed MPNN invariant to chemical graph isomorphisms. The simplest way to achieve this property is to summarize all hidden state vectors reducing N (number of nodes) vectors of length L (number of resulting features) to one vector of length L. Unfortunately, this approach leads to the significant information loss. That is why we followed Kearnes et el.⁴¹ and applied a fuzzy histogram approach⁵⁹ to capture the distribution of each L features.

To construct histograms, we apply a set of membership functions of length equals to the number of predefined bins to the data. Each membership function returns one, if the data element is in the current bin and zero otherwise. For the fuzzy histogram approach, the normalized Gaussian membership function (eq 8) was used where i is a bin index and K is the number of bins, respectively. Each fuzzy membership function is defined by the bin center x_i where x denotes the current data element. In this work, 11 fuzzy membership functions centered at −2.75, −2.0, −1.35, −0.8, −0.35, 0, 0.35, 0.8, 1.35, 2.0, and 2.75 were used with all σ_i² equals to 0.5. Then, the summation performed over all nodes yields 11 × L permutationally invariant descriptors.

8

The choice of message, update, and readout functional forms were inspired by Battaglia et al.,⁵⁸ where each of the function is a multilayer fully connected perceptron with a specific architecture defined in Table 1. Batch normalization⁶⁰ was applied for each layer of all neural networks except the output layer. We found that the dropout technique significantly increased the training time; thus, we did not use it to obtain the final model.

Table 1. Network Architecture of Message, Update, and Readout Functions^a.

		message function			update function			readout function
T	layer	in	out	BN	in	out	BN	in	out	BN
1	1	751	200	yes	473	200	yes
	2	200	100	yes	200	100	yes
	3	100	100	no	100	100	no
2	1	205	200	yes	200	200	yes
	2	200	100	yes	200	100	yes
	3	100	100	no	100	100	no
3	1	205	200	yes	200	200	yes	1100	300	yes
	2	200	100	yes	200	100	yes	300	200	yes
	3	100	100	no	100	100	no	200	100	yes
	4							100	2	no

^a“In” and “Out” means the number of input and output neurons in the current layer, and “BN” denotes the application of the batch normalization layer.

3.4. Error Metrics and Training Details

We used the Pytorch 0.4 framework for DNN training and networkx 2.1 and rdkit 2018.03.1 for molecular graph processing and chemoinformatics routines. It should be noted that reading of some sdf files in database yields an error by rdkit. The most common issue is the lack of positive charge on tertiary amine nitrogen atoms. These structures were corrected manually using MarvinSketch 18.10 (http://www.chemaxon.com). The detailed description of the training procedure is given in the Supporting Information. Because scoring function training was reformulated as a multi task learning problem, we should describe in more detail the loss function and quality metrics. The loss function is the modified MSE loss (eq 9), where N and T are the number of complex in a batch multiplied by two (for both pIC₅₀ and pK predictions) and the number of available activities for the batch, respectively. The root-mean-square error (RMSE) and the mean average error, as well as the Pearson correlation coefficient (r) and the Spearman rank correlation coefficient (ρ) were computed for the performance comparison.

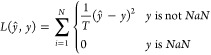9

It was stressed in the literature that the usage of the train and test split provided by the PDBbind tends to provide too optimistic results.^61,62 Thus, we performed fivefold cross-validation, selecting the best pool of models and subsequently assessing their performance on the selected test sets by averaging the prediction results from all of the five models. Our scoring model is available at http://mpnn.syntelly.com.

Glossary

Abbreviations

MPNN

message passing neural network

NN

neural networks

DNN

deep neural networks

FEP

free energy perturbation

BPS

Behler–Parrinello symmetric function

SOAP

smooth overlap of atomic positions

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.9b04162.

• Training details, basic molecular properties of the training sets, results of prediction for data sets, learning curves for the refined set and refined set + IC₅₀ data, results of graphDelta evaluation on the data set used for FEP and MM-PBSA evaluation; and the parameter set used to compute BPS functions (PDF)

The authors declare the following competing financial interest(s): Maxim Fedorov and Sergey Sosnin are co-founders of Syntelly LLC.