Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2020 Mar 9;5(10):5318–5325. doi: 10.1021/acsomega.9b04339

Predictions of High-Order Electric Properties of Molecules: Can We Benefit from Machine Learning?

Tran Tuan-Anh †,*, Robert Zaleśny ‡,*
PMCID: PMC7081434  PMID: 32201820

Abstract

graphic file with name ao9b04339_0007.jpg

There is an exigency of adopting machine learning techniques to screen and discover new materials which could address many societal and technological challenges. In this work, we follow this trend and employ machine learning to study (high-order) electric properties of organic compounds. The results of quantum-chemistry calculations of polarizability and first hyperpolarizability, obtained for more than 50,000 compounds, served as targets for machine learning-based predictions. The studied set of molecular structures encompasses organic push–pull molecules with variable linker lengths. Moreover, the diversified set of linkers, composed of alternating single/double and single/triple carbon–carbon bonds, was considered. This study demonstrates that the applied machine learning strategy allows us to obtain the correlation coefficients, between predicted and reference values of (hyper)polarizabilities, exceeding 0.9 on training, validation, and test set. However, in order to achieve such satisfactory predictive power, one needs to choose the training set appropriately, as the machine learning methods are very sensitive to the linker-type diversity in the training set, yielding catastrophic predictions in certain cases. Furthermore, the dependence of (hyper)polarizability on the length of spacers was studied in detail, allowing for explanation of the appreciably high accuracy of employed approaches.

1. Introduction

Screening and discovering of new materials have been playing a crucial role in the development of various fields, including physics, chemistry, material technology, biology, and medicine, to name a few. In vitro high-throughput systems and in silico approaches (e.g., quantum mechanics-based calculations and molecular dynamics) seem to be incapable of exploring sufficiently the chemical space of potential candidates because of the huge number of possible compounds. For example, combinations of up to only 17 atoms (C, N, O, S, and halogens) could lead to a data set of 166 billion molecules1 which, unfortunately, accounts for a minor portion of the chemical universe. Characterizing properties of these compounds could be challenging, time consuming, and requires a vast amount of resources.

Among various rapidly developing fields, nonlinear optics (NLO) occupies a privileged spot because of a plethora of technology-related applications. As demonstrated by developments made during the last two decades, the bottom-up engineering of materials for NLO applications is a powerful and effective strategy.2−7 Electric susceptibility tensors (χ) describe the strengths of light–matter interactions at a macroscopic level, while at the molecular scale, linear and nonlinear optical properties are governed by the electric dipole polarizability (α) and first (β) and second (γ) hyperpolarizabilities.8 Pinpointing factors that determine the magnitudes of the (hyper)polarizabilities are essential to model new molecules and host–guest complexes characterized by large nonlinear optical responses, which are required for optoelectronic and photonic applications. Quantum-chemistry tools, from a historical perspective, contributed significantly to the establishment of structure–property relationships, both for nonresonant and resonant nonlinear optical processes.9−26 As the complexity of the systems studied using sophisticated experimental techniques increased in the last decade, this has stimulated the efforts of theoreticians to develop computational protocols capable of treating molecular properties at nanoscale.27−32 In particular, there are very successful attempts to describe (non)linear optical properties in complex systems (e.g., heterogeneous environments) using quantum mechanics/molecular mechanics methods (QM/MM).28−32 One of the approaches that could be potentially employed to study the nonlinear properties of molecules and their aggregates, thus allowing for exploring larger chemical space, is machine learning (ML).

The ML approach comprises a collection of prediction, clustering, and optimization methods which can capture the complex inter-relationships among variables to yield high performance models. Once trained, a ML model can rapidly screen desired molecular properties, and this is the rationale behind its increasing popularity in the field of computational chemistry.33,34 Many studies have employed ML in molecular modeling, especially in material technology35 and pharmaceutical science.36,37 However, the number of studies applying ML to predict NLO properties is scarce.38−42 These attempts were either conducted using computational methods on small data sets,38−40 which reduced the confidence in the final results, or exhibited low predictive power.43 It is fair to mention that low-order electric properties (e.g., dipole moment and polarizability) were studied much more extensively.42,44−46

Multivariate linear regression was commonly used to construct a quantitative structure–property relation (QSPR) model for predicting NLO responses of materials,38,39,43 but the assumption of linearity is not always satisfied in practice. Alternatively, the neural network, which is an appropriate approach for analysis of data with a nonlinear structure, was utilized to predict the hyperpolarizability of alkalides.40 In that work, the authors made a successful attempt to predict high-order electric properties at a higher level (MP2) based on the properties computed at the lower level (HF).

The concept of the neural network was inspired by the structure of the human brain in that a neural network contains several hidden layers of connected hidden nodes representing for neural cells. According to the universal approximation theory,47,48 neural networks can precisely fit continuous functions as it is considered to be able to capture the complexity and the interrelation of predictors as well as predictor–target correlation. Besides neural network, random forest is one of the well-known ML algorithms which are applicable for regression tasks.49 Random forest is a robust method to outliers and is considered a correction of decision/regression tree which is a weak learner constructed by a set of if-then-else rules. The method was used to predict physical properties of polymers,35 partial charges derived from quantum calculation,50 and electronic ground-state properties of organic molecules.50

The present study aims at contributing to these efforts and is devoted to the application of ML to predict molecular (hyper)polarizabilities of organic compounds by exploiting a neural network and random forest combined with three different fingerprints/descriptors.

2. Theory and Computational Details

In the presence of an external electric field F, the a’th Cartesian component of the total molecular dipole moment, μa, may be expressed as a Taylor series which takes the form51

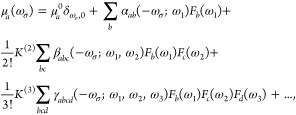2. 1

where μa0 is the a’th component of the permanent dipole moment; αab(−ωσ; ω1), βabc(−ωσ; ω1, ω2) and γabcd(−ωσ; ω1, ω2, ω3) are components of the linear polarizability, first hyperpolarizability, and second hyperpolarizability, respectively; ωσ is the sum of the external field frequencies ωi, and K(2) and K(3) are factors required for all hyperpolarizabilities of the same order to have the same static limit. The static polarizability (α(0; 0)) and first hyperpolarizability (β(0; 0, 0)) are central to this study. Orientationally averaged polarizability and first hyperpolarizability were calculated according to the following formulae

2. 2
2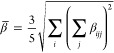. 3

where αij and βijk are tensor components in the Cartesian coordinate system. For the sake of brevity, the fields will be omitted and the symbols α and β will be used instead to denote rotationally-averaged static properties.

High-throughput generation of chemical compounds was performed using an in-house computer code written in PYTHON programming language. Chemical structures and fragments were drawn using CS ChemDraw Ultra software. Quantum-chemical calculations were performed using Gaussian 09 program,52 and preoptimization was done with the aid of OpenBabel53 program with MMFF94s force field. Logarithmic log10 scale was used to improve the performance of ML methods and to ease further analysis. In this study, we used two hidden-layer neural networks54 and the random forest55 algorithms. Feature extraction was done by PaDEL program.56 R and Matlab programming languages were employed for the data analysis. Briefly, regression by the neural network and random forest was performed using Matlab Statistic and ML toolbox and Neural Network toolbox, respectively. Data visualization, including principal component analysis (PCA), and scatter plot were exploited using “vegan”57 and “ggplot2”58 R package. In order to evaluate the accuracy of the ML models, correlation coefficient of predicted values and actual values of (hyper)polarizabilities (α and β) was computed as

2. 4

where Ypredicted is the predicted value, Yactual is the actual value of (hyper)polarizability, E(·) is statistical expectation, μ is mean, and σ is standard deviation.

3. Results and Discussion

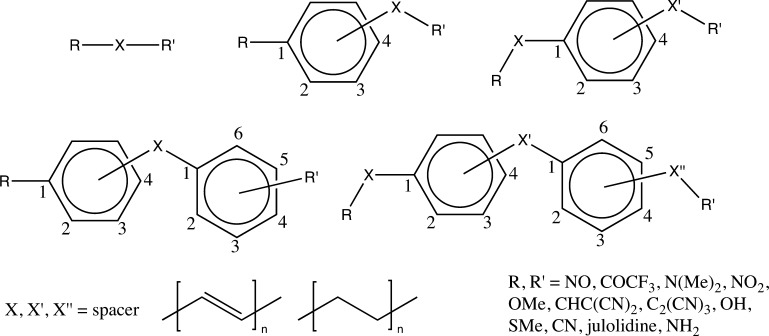
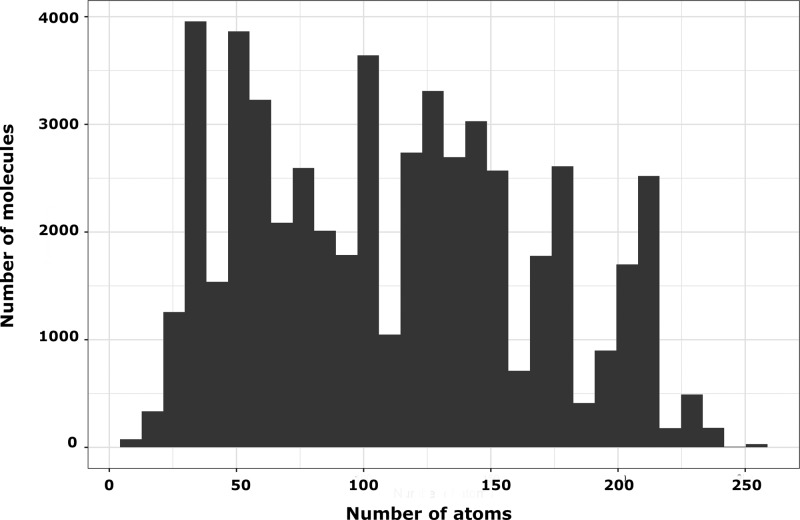
In order to study the performance of the ML approach in predicting the electric properties of molecules, we generated more than 50,000 molecular geometries by combining chemical fragments depicted in Figure 1. The choice of these one-dimensional (1D) donor–acceptor (D–A) systems stems from their popularity in the field of molecular NLO. For example, in late 70s of past century, Oudar and Chemla proposed a two-level model which predicted that push–pull systems are good candidates for second-order NLO.9 Since then, these systems have been extensively studied both on theoretical and experimental basis.11−13,17,18,23,59−69 It should be highlighted that some of the structures studied in this work, that is, with short linkers, were synthesized, and their nonlinear optical properties were characterized experimentally.59,70 The geometries of molecules shown in Figure 1 were preoptimized using molecular mechanics-based approach and used in subsequent quantum-chemical calculations using the AM1 method. After elimination of unsuccessful attempts to locate stationary points on potential energy hypersurfaces, we obtained in total 51,461 optimal geometries. The geometries fell into 10,656 unique families, which contained up to five members each. A family was defined as a group of geometries that share the same structure and only differ in total length of spacers. For the very same set, we computed polarizability and first hyperpolarizability. Likewise, the AM1 method was used to that end. The choice of this method stems from the significant size of the studied systems, as shown in Figure 2. As it will be shown at the end of this section, the AM1 Hamiltonian satisfactorily predicts the property trends for extended π-conjugated systems. The first hyperpolarizability was transferred into a logarithmic (with base 10) scale to center the histogram and reduce the skewness of data, which would improve the predictive performance of ML models (see Figure S1 in Supporting Information). The outputs from quantum-chemical calculations were further postprocessed by PaDEL program for features extraction, including Pubchem and Klekota–Roth71 fingerprints (hereafter abbreviated as Klekota), and 1D/2D descriptors. Single-value features were removed from further analysis, resulting in 272 features of Pubchem fingerprint, 296 features of Klekota fingerprint, and 1098 features of 1D/2D descriptors. Finally, the preprocessed features served as inputs for ML methods to predict α and β. The whole data set was randomly divided into training, validation, and test set with a ratio of 50:25:25, respectively. The results of these analyses are gathered in Table 1 (polarizability, α) and Table 2 (first hyperpolarizability, β).

Figure 1.

Figure 1

Open in a new tab

Studied systems.

Figure 2.

Figure 2

Open in a new tab

Size distribution for studied molecules.

Table 1. Correlation Coefficient of Predicted and Computed (Using AM1 Method) Polarizability on Traning, Validation, and Test Set Corresponding to ML Methods and Descriptors/Fingerprint.

ML methods descriptors/fingerprint training validation test
random forest 1D and 2D 0.99 0.99 0.99
  Pubchem 0.84 0.82 0.82
  Klekota 0.99 0.99 0.99
neural network 1D and 2D 0.99 0.99 0.99
  Pubchem 0.83 0.82 0.82
  Klekota 0.99 0.99 0.99
Open in a new tab

Table 2. Correlation Coefficient of Predicted and Computed (Using AM1 Method) Values of the First Hyperpolarizability (log10 Scale) on Traning, Validation, and Test Set Corresponding to ML Methods and Descriptors/Fingerprint.

ML methods descriptors/fingerprint training validation test
random forest 1D and 2D 0.99 0.96 0.97
  Pubchem 0.95 0.92 0.92
  Klekota 0.98 0.96 0.95
neural network 1D and 2D 0.98 0.96 0.97
  Pubchem 0.95 0.93 0.93
  Klekota 0.98 0.97 0.97
Open in a new tab

By and large, the performances of random forest and the neural network in predicting polarizability are similar regardless of the feature sets. Klekota fingerprint and 1D/2D descriptors yielded the highest correlation coefficient on the test set equal to 0.99. The combination of ML methods and Pubchem fingerprint resulted in rather a low value of the correlation coefficient (0.82). In the case of hyperpolarizability, the correlation coefficients obtained for ML methods and fingerprint/descriptors exceed 0.92 (see Table 2). A much higher value, that is, as large as 0.97, can be obtained employing either random forest or neural network methods coupled with 1D/2D descriptors or Klekota fingerprint. Pubchem fingerprint yields the lowest accuracy regardless of the ML method employed.

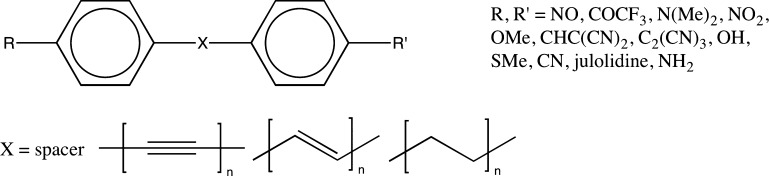
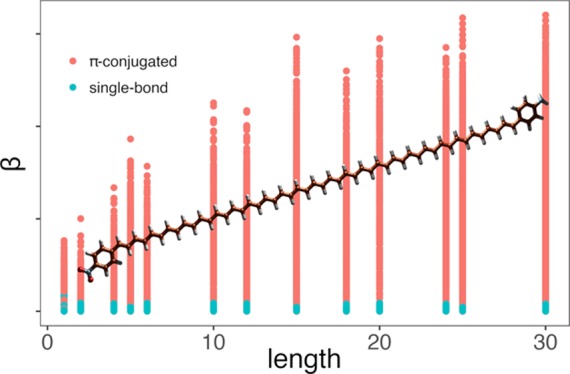
Aiming at the testing of the performance of ML methods applied to new types of data, we generated three groups of compounds from a subset of the studied systems, which is shown in Figure 3. Each group was composed of molecules with spacers containing single, alternating single/double, or single/triple carbon–carbon bonds. First hyperpolarizability was obtained, as above, using the AM1 method. The final sets included 1,907, 2,142, and 1,789 compounds with spacers containing single, double, and triple carbon–carbon bonds, respectively. A neural network with Klekota fingerprint was trained based on the training set for compounds with particular spacer type and subsequently tested based on the test sets for all three groups of molecules (i.e., with three different spacer types). The analysis of the results leads to an interesting observation. For example, as expected based on the conclusions drawn in the preceding paragraphs, the correlation coefficient is high, provided the training and the test sets were composed of the molecules from the very same group. In such case, the corresponding values are in the range 0.98–0.99 (see Table 3). In contrast, the neural network trained on one particular group (i.e., containing molecules with specific type of spacer) cannot accurately predict hyperpolarizability for the members of the other groups. In qualitative sense, this result falls into expectation, but the corresponding small values of correlation coefficient are quite striking. The only exception is found for a neural network trained on the set of compounds with linkers containing double carbon–carbon bonds. In that event, one finds an average correlation of 0.46 for the test set encompassing molecules with linkers composed of alternating single/triple carbon–carbon bonds. For the rest of the cases, the neural network showed correlation coefficient values not exceeding 0.25. In order to investigate the poor performance of the neural network in these cases, PCA were utilized on data extracted from the three groups of geometries (Klekota–Roth fingerprints were used), and the results are shown in Figure S2 (see Supporting Information). We found that compounds containing single bonds segregated from compounds containing alternating single/π-conjugated carbon–carbon bonds, which suggested a high degree of dissimilarity in data patterns between the two groups. Presumably, this explains why neural networks trained on a single-bond group failed to predict hyperpolarizability on a π-conjugated-bond group and vice versa. Compounds containing alternating single/triple carbon–carbon bonds fall into the transition region of the two groups, which is a likely explanation that testing performance on the triple-bond group was higher than that of the rest.

Figure 3.

Figure 3

Open in a new tab

Three groups of compounds for cross-system testing.

Table 3. Cross-System Testing of the Hyperpolarizability (log10 Scale) Prediction Model Based on the Neural Network Combined with Klekota Fingerprint.

  test system
training system single-bond spacer single/double bond spacer single/triple bond spacer
single bond spacer 0.99 –0.12 0.25
single/double bond spacer 0.08 0.99 0.46
single/triple bond spacer –0.05 –0.18 0.98
Open in a new tab

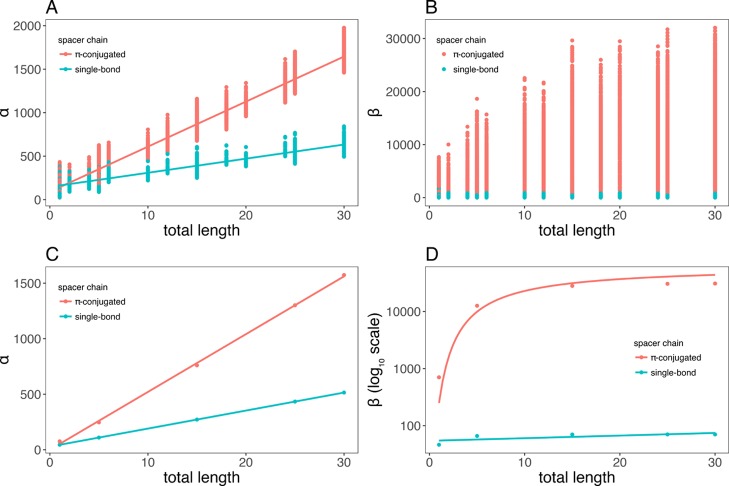
In order to shed light on the relationship between (hyper)polarizability and the total spacer length (n), we prepared a scatter plot for a subset of molecules with spacers containing either single or alternating single/double bonds, and the results are shown in Figure 4. In general, the (hyper)polarizability of compounds with linkers containing alternating single/double carbon–carbon bonds is significantly higher than those for molecules presenting linkers with single bonds only. There is a substantial qualitative difference in the pattern of polarizability and hyperpolarizability. While polarizability is linearly dependent on the length of spacers (see Figure 4A,C), the relation between hyperpolarizability and the spacer length is nonlinear (Figure 4B,D). We observed a trend of saturation on hyperpolarizability (log10 scale), and we modeled this behavior using the following equation

3. 5

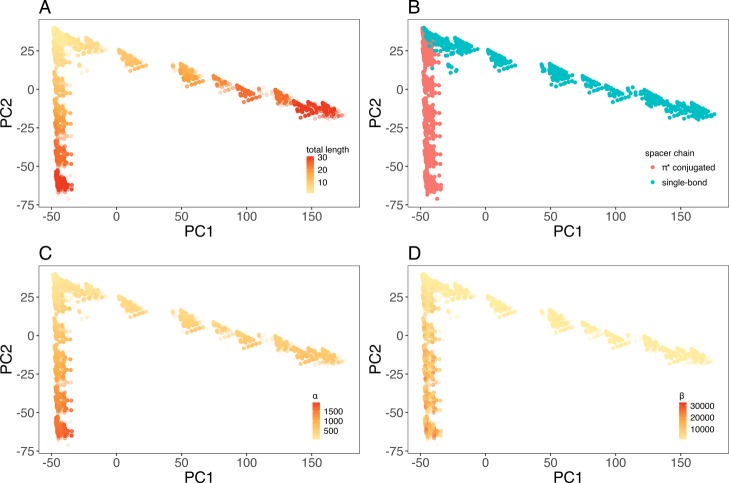
where n is the length of spacers. We used nonlinear least squares regression to fit the eq 5 to data points and to determine the βmax coefficient. Families with less than four compounds and with correlation coefficient less than 0.9 were eliminated, resulting in 23,591 π-conjugated compounds with corresponding estimated βmax. Random forest and neural networks were employed with Pubchem fingerprint, Klekota fingerprint, and 1D/2D descriptor to predict the estimated βmax coefficient. The results are shown in Table 4. Generally, the proposed methods could accurately predict βmax coefficient of different families of compounds with correlation of at least 0.88, regardless of the spacer length. Neural network overperformed random forest, except the combination with 1D/2D descriptors, and exhibited the highest correlation of 0.94 (Klekota). Regarding the random forest method, the three fingerprint/descriptors showed almost equivalent correlation. To investigate structures of data generated by Klekota fingerprint, we used PCA to project the data into a two-dimensional (2D) space by selecting two principal components corresponding to the highest eigenvalues (Figure 5). The variation of the data was 98% explained by the principal components, which indicated the confidence of PCA plot for further analysis. It was obvious that the data were segregated into two separate clusters composed of molecules with alternating single/double (denoted as π-conjugated) and single carbon–carbon bonds (Figure 5B). Among each cluster, data tended to cluster based on the spacer length (Figure 5A) and polarizability (Figure 5C), while the segregation by hyperpolarizability remained uncertain (Figure 5D).

Figure 4.

Figure 4

Open in a new tab

Correlation between polarizability (A,C)/hyperpolarizability (B,D), and total length of spacer.

Table 4. Correlation Coefficient of Predicted and Computed (Using AM1 Method) Values of the Maximum of Hyperpolarizability (log10 Scale) on Traning, Validation, and Test Set Corresponding to ML Methods and Descriptors/Fingerprint.

ML methods descriptors/fingerprint training validation test
random forest 1D and 2D 0.98 0.92 0.91
  Pubchem 0.95 0.90 0.92
  Klekota 0.97 0.92 0.91
neural network 1D and 2D 0.95 0.90 0.88
  Pubchem 0.96 0.93 0.93
  Klekota 0.96 0.95 0.94
Open in a new tab

Figure 5.

Figure 5

Open in a new tab

PCA plot of Klekota fingerprint of studied systems corresponding to (A) spacer length, (B) type of spacers, (C) polarizability, and (D) hyperpolarizability.

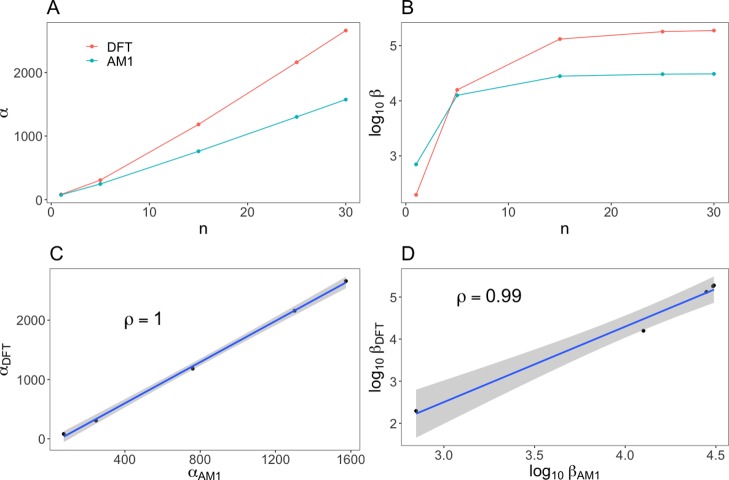
In order to safeguard the conclusions drawn based on the AM1 results, we have performed more advanced electronic-structure calculations using density functional theory. To this end, we used CAM-B3LYP functional which was proved to be reliable in the case of nonlinear optical properties of π-conjugated systems.72,73 Property trends were calculated at AM1 and CAM-B3LYP/cc-pVDZ levels of theory for the family shown in Figure 3 with single/double bond linker and COCF3 and NMe2 substituents. The cc-pVDZ basis set was used to avoid linear-dependency issues during property calculations for the largest molecules. It is well known that diffuse functions are needed to accurately predict high-order electric properties of molecules. However, earlier studies demonstrate that the polarized basis sets are sufficient to reproduce property trends (α and β) for donor−π–acceptor molecules. The comparison is presented in Figure 6 and demonstrates that there is satisfactory trend reproduction in the case of the AM1 method. It holds both for polarizability and first hyperpolarizability. Finally, it should not be overlooked that the recent study of Lu et al. on predictions of first hyperpolarizability of solvated donor−π–acceptor molecules demonstrates very good correlations between calculated and experimental trends in the case of range-separated functionals.74

Figure 6.

Figure 6

Open in a new tab

Comparison of property [polarizability—(A,C) and hyperpolarizability—(B,D)] trends calculated at AM1 and CAM-B3LYP/cc-pVDZ levels of theory for the family shown in Figure 3 with single/double bond linker and COCF3 and NMe2 substituents.

4. Summary and Conclusions

In the present work, the ML was utilized to predict high-order electric properties of donor–acceptor-substituted organic compounds. To this end, we studied polarizability and hyperpolarizability of more than 50,000 compounds using quantum-chemistry methods and ML approaches. As far as the latter property is concerned, this is the first investigation for such large and diverse set of compounds. Large-scale data analysis contributed to the much higher confidence and accuracy of the results presented herein, in comparison with previous attempts.38−40,43 Particularly, random forest and neural networks, two of the most appreciated ML methods for regression, were able to capture the correlation between three fingerprints/descriptors and α and β computed using quantum tools, and yielded QSPR models with considerable accuracy. Additionally, we found that the high quantity of data was sufficient but not enough to train high-performance ML predictors. A high degree of data diversity is also a key ingredient, complementing to data quantity, in application of ML in predicting high-order electrical properties. The hyperpolarizability dependence on the spacer length was also investigated, and it can be concluded that the ML approaches can reliably capture the trends for different families of compounds with correlation of at least 0.88, regardless of the spacer length. With an appropriate data set, that is, covering wide palette of linker/conjugation patterns, the proposed methods could be presumably extended to predict other nonlinear optical properties for the purpose of fast and efficient material screening and design.

Acknowledgments

This work was supported by a statutory activity subsidy from the Polish Ministry of Science and Higher Education for the Faculty of Chemistry of Wroclaw University of Science and Technology. Quantum-chemical calculations were performed at the Wroclaw Center for Networking and Supercomputing.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.9b04339.

  • Histograms of hyperpolarizability and the results of PCA for compounds containing single, alternating single/double, and single/triple carbon–carbon bonds (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao9b04339_si_001.pdf (424.5KB, pdf)

References

  1. Ruddigkeit L.; van Deursen R.; Blum L. C.; Reymond J.-L. Enumeration of 166 Billion Organic Small Molecules in the Chemical Universe Database GDB-17. J. Chem. Inf. Model. 2012, 52, 2864–2875. 10.1021/ci300415d. [DOI] [PubMed] [Google Scholar]
  2. Sullivan P. A.; Dalton L. R. Theory-Inspired Development of Organic Electro-optic Materials. Acc. Chem. Res. 2010, 43, 10–18. 10.1021/ar800264w. [DOI] [PubMed] [Google Scholar]
  3. Castet F.; Rodriguez V.; Pozzo J.-L.; Ducasse L.; Plaquet A.; Champagne B. Design and Characterization of Molecular Nonlinear Optical Switches. Acc. Chem. Res. 2013, 46, 2656–2665. 10.1021/ar4000955. [DOI] [PubMed] [Google Scholar]
  4. Chen K. J.; Laurent A. D.; Jacquemin D. Strategies for Designing Diarylethenes as Efficient Nonlinear Optical Switches. J. Phys. Chem. C 2014, 118, 4334–4345. 10.1021/jp412071e. [DOI] [Google Scholar]
  5. Jaunet-Lahary T.; Chantzis A.; Chen K. J.; Laurent A. D.; Jacquemin D. Designing Efficient Azobenzene and Azothiophene Nonlinear Optical Photochromes. J. Phys. Chem. C 2014, 118, 28831–28841. 10.1021/jp510581m. [DOI] [Google Scholar]
  6. Alam M. M.; Chattopadhyaya M.; Chakrabarti S.; Ruud K. Chemical Control of Channel Interference in Two-Photon Absorption Processes. Acc. Chem. Res. 2014, 47, 1604–1612. 10.1021/ar500083f. [DOI] [PubMed] [Google Scholar]
  7. Schulze M.; Utecht M.; Hebert A.; Rück-Braun K.; Saalfrank P.; Tegeder P. Reversible Photoswitching of the Interfacial Nonlinear Optical Response. J. Phys. Chem. Lett. 2015, 6, 505–509. 10.1021/jz502477m. [DOI] [PubMed] [Google Scholar]
  8. Kurtz H. A.; Dudis D. S.. Reviews in Computational Chemistry; Wiley-VCH, 1998; Vol. 12, pp 241–279. [Google Scholar]
  9. Oudar J. L.; Chemla D. S. Hyperpolarizabilities of the Nitroanilines and Their Relations to the Excited State Dipole Moment. J. Chem. Phys. 1977, 66, 2664–2668. 10.1063/1.434213. [DOI] [Google Scholar]
  10. Marder S. R.; Gorman C. B.; Tiemann B. G.; Perry J. W.; Bourhill G.; Mansour K. Relation Between Bond-Length Alternation and Second Electronic Hyperpolarizability of Conjugated Organic Molecules. Science 1993, 261, 186–189. 10.1126/science.261.5118.186. [DOI] [PubMed] [Google Scholar]
  11. Lu D.; Chen G.; Perry J. W. Valence-Bond Charge-Transfer Model for Nonlinear Optical Properties of Charge-Transfer Organic Molecules. J. Am. Chem. Soc. 1994, 116, 10679–10685. 10.1021/ja00102a037. [DOI] [Google Scholar]
  12. Chen G.; Lu D. Valence-Bond Charge-Transfer Solvation Model for Nonlinear Optical Properties of Organic Molecules in Polar Solvents. J. Chem. Phys. 1994, 101, 5860–5864. 10.1063/1.467302. [DOI] [Google Scholar]
  13. Barzoukas M.; Runser C.; Fort A.; Blanchard-Desce M. A Two-State Description of (Hyper)Polarizabilities of Push-Pull Molecules Based on a Two-Form Model. Chem. Phys. Lett. 1996, 257, 531–537. 10.1016/0009-2614(96)00586-6. [DOI] [Google Scholar]
  14. Cronstrand P.; Luo Y.; Ågren H. Generalized Few-State Models for Two-Photon Absorption of Conjugated Molecules. Chem. Phys. Lett. 2002, 352, 262–269. 10.1016/s0009-2614(01)01454-3. [DOI] [Google Scholar]
  15. Cronstrand P.; Norman P.; Luo Y.; Ågren H. Few-States Models for Three-Photon Absorption. J. Chem. Phys. 2004, 121, 2020–2029. 10.1063/1.1767516. [DOI] [PubMed] [Google Scholar]
  16. Dirk C. W.; Cheng L.-T.; Kuzyk M. G. A Simplified Three-Level Model Describing the Molecular Third-Order Nonlinear Optical Susceptibility. Int. J. Quantum Chem. 1992, 43, 27–36. 10.1002/qua.560430106. [DOI] [Google Scholar]
  17. Blanchard-Desce M.; Barzoukas M. Two-Form Two-State Analysis of Polarizabilities of Push-Pull Molecules. J. Opt. Soc. Am. B 1998, 15, 302–307. 10.1364/josab.15.000302. [DOI] [Google Scholar]
  18. Bishop D. M.; Champagne B.; Kirtman B. Relationship Between Static Vibrational and Electronic Hyperpolarizabilities of π-Conjugated Push-Pull Molecules Within the Two-State Valence-Bond Charge-Transfer Model. J. Chem. Phys. 1998, 109, 9987–9994. 10.1063/1.477665. [DOI] [Google Scholar]
  19. Bartkowiak W.; Zaleśny R.; Leszczynski J. Relation Between Bond-Length Alternation and Two-Photon Absorption of Push-Pull Conjugated Molecules: A Quantum-Chemical Study. Chem. Phys. 2003, 287, 103–112. 10.1016/s0301-0104(02)00982-5. [DOI] [Google Scholar]
  20. Zaleśny R.; Bartkowiak W.; Styrcz S.; Leszczynski J. Solvent Effects on Conformationally Induced Enhancement of the Two-Photon Absorption Cross Section of a Pyridinium-N-Phenolate Betaine Dye. A Quantum-Chemical Study. J. Phys. Chem. A 2002, 106, 4032–4037. 10.1021/jp0142684. [DOI] [Google Scholar]
  21. Pati S. K.; Marks T. J.; Ratner M. A. Conformationally Tuned Large Two-Photon Absorption Cross Sections in Simple Molecular Chromophores. J. Am. Chem. Soc. 2001, 123, 7287–7291. 10.1021/ja0033281. [DOI] [PubMed] [Google Scholar]
  22. Albota M.; Beljonne D.; Brédas J.-L.; Ehrlich J.; Fu J.-Y.; Heikal A.; Hess S.; Kogej T.; Levin M.; Marder S.; McCord-Maughon D.; Perry J.; Röckel H.; Rumi M. Design of Organic Molecules with Large Two-Photon Absorption Cross Sections. Science 1998, 281, 1653–1656. 10.1126/science.281.5383.1653. [DOI] [PubMed] [Google Scholar]
  23. Kogej T.; Beljonne D.; Meyers F.; Perry J. W.; Marder S. R.; Brédas J. L. Mechanism for Ehancement of Two-Photon Absorption in Donor-Acceptor Conjugated Chromophores. Chem. Phys. Lett. 1998, 298, 1–6. 10.1016/s0009-2614(98)01196-8. [DOI] [Google Scholar]
  24. Alam M. M.; Chattopadhyaya M.; Chakrabarti S. Enhancement of Twist Angle Dependent Two-Photon Activity through the Proper Alignment of Ground to Excited State and Excited State Dipole Moment Vectors. J. Phys. Chem. A 2012, 116, 8067–8073. 10.1021/jp304456w. [DOI] [PubMed] [Google Scholar]
  25. Alam M. M.; Chattopadhyaya M.; Chakrabarti S. Solvent Induced Channel Interference in the Two-Photon Absorption Process - a Theoretical Study with a Generalized Few-State-Model in Three Dimensions. Phys. Chem. Chem. Phys. 2012, 14, 1156–1165. 10.1039/c1cp22849h. [DOI] [PubMed] [Google Scholar]
  26. Alam M. M.; Chattopadhyaya M.; Chakrabarti S.; Ruud K. High-Polarity Solvents Decreasing the Two-Photon Transition Probability of Through-Space Charge-Transfer Systems - A Surprising In Silico Observation. J. Phys. Chem. Lett. 2012, 3, 961–966. 10.1021/jz300198y. [DOI] [PubMed] [Google Scholar]
  27. Hu Z.; Jensen L. A Discrete Interaction Model/Quantum Mechanical Method for Simulating Plasmon-Enhanced Two-Photon Absorption. J. Chem. Theory Comput. 2018, 14, 5896–5903. 10.1021/acs.jctc.8b00893. [DOI] [PubMed] [Google Scholar]
  28. Zahariev F.; Gordon M. S. Nonlinear Response Time-Dependent Density Functional Theory Combined with the Effective Fragment Potential Method. J. Chem. Phys. 2014, 140, 18A523. 10.1063/1.4867271. [DOI] [PubMed] [Google Scholar]
  29. Jensen L. L.; Jensen L. Electrostatic Interaction Model for the Calculation of the Polarizability of Large Noble Metal Nanoclusters. J. Phys. Chem. C 2008, 112, 15697–15703. 10.1021/jp804116z. [DOI] [Google Scholar]
  30. Murugan N. A.; Apostolov R.; Rinkevicius Z.; Kongsted J.; Lindahl E.; Ågren H. Association Dynamics and Linear and Nonlinear Optical Properties of an N-Acetylaladanamide Probe in a POPC Membrane. J. Am. Chem. Soc. 2013, 135, 13590–13597. 10.1021/ja407326n. [DOI] [PubMed] [Google Scholar]
  31. Nielsen C. B.; Christiansen O.; Mikkelsen K. V.; Kongsted J. Density Functional Self-Consistent Quantum Mechanics/Molecular Mechanics Theory for Linear and Nonlinear Molecular Properties: Applications to Solvated Water and Formaldehyde. J. Chem. Phys. 2007, 126, 154112. 10.1063/1.2711182. [DOI] [PubMed] [Google Scholar]
  32. Silva D. L.; Murugan N. A.; Kongsted J.; Rinkevicius Z.; Canuto S.; Ågren H. The Role of Molecular Conformation and Polarizable Embedding for One- and Two-Photon Absorption of Disperse Orange 3 in Solution. J. Phys. Chem. B 2012, 116, 8169–8181. 10.1021/jp3032034. [DOI] [PubMed] [Google Scholar]
  33. von Lilienfeld O. A. Quantum Machine Learning in Chemical Compound Space. Angew. Chem., Int. Ed. 2018, 57, 4164–4169. 10.1002/anie.201709686. [DOI] [PubMed] [Google Scholar]
  34. Rupp M. Machine Learning for Quantum Mechanics in a Nutshell. Int. J. Quantum Chem. 2015, 115, 1058–1073. 10.1002/qua.24954. [DOI] [Google Scholar]
  35. Venkatraman V.; Alsberg B. Designing High-Refractive Index Polymers Using Materials Informatics. Polymers 2018, 10, 103. 10.3390/polym10010103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Hughes T. B.; Miller G. P.; Swamidass S. J. Modeling Epoxidation of Drug-Like Molecules with a Deep Machine Learning Network. ACS Cent. Sci. 2015, 1, 168–180. 10.1021/acscentsci.5b00131. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Stephenson N.; Shane E.; Chase J.; Rowland J.; Ries D.; Justice N.; Zhang J.; Chan L.; Cao R. Survey of Machine Learning Techniques in Drug Discovery. Curr. Drug Metab. 2019, 20, 185–193. 10.2174/1389200219666180820112457. [DOI] [PubMed] [Google Scholar]
  38. Öberg K.; Berglund A.; Edlund U.; Eliasson B. Prediction of Nonlinear Optical Responses of Organic Compounds. J. Chem. Inf. Comput. Sci. 2001, 41, 811–814. 10.1021/ci000402q. [DOI] [PubMed] [Google Scholar]
  39. Xu J.; Chen B.; Xu W.; Zhao S.; Yi C.; Cui W. 3D-QSPR Modeling and Prediction of Nonlinear Optical Responses of Organic Chromophores. Chemom. Intell. Lab. Syst. 2007, 87, 275–280. 10.1016/j.chemolab.2007.03.006. [DOI] [Google Scholar]
  40. Wang J.-N.; Xu H.-L.; Sun S.-L.; Gao T.; Li H.-Z.; Li H.; Su Z.-M. An Effective Method for Accurate Prediction of the First Hyperpolarizability of Alkalides. J. Comput. Chem. 2012, 33, 231–236. 10.1002/jcc.21969. [DOI] [PubMed] [Google Scholar]
  41. Liang C.; Tocci G.; Wilkins D. M.; Grisafi A.; Roke S.; Ceriotti M. Solvent Fluctuations and Nuclear Quantum Effects Modulate the Molecular Hyperpolarizability of Water. Phys. Rev. B 2017, 96, 041407. 10.1103/physrevb.96.041407. [DOI] [Google Scholar]
  42. Grisafi A.; Wilkins D. M.; Csányi G.; Ceriotti M. Symmetry-Adapted Machine Learning for Tensorial Properties of Atomistic Systems. Phys. Rev. Lett. 2018, 120, 036002. 10.1103/physrevlett.120.036002. [DOI] [PubMed] [Google Scholar]
  43. Katritzky A. R.; Pacureanu L.; Dobchev D.; Karelson M. QSPR Modeling of Hyperpolarizabilities. J. Mol. Model. 2007, 13, 951–963. 10.1007/s00894-007-0209-4. [DOI] [PubMed] [Google Scholar]
  44. Browning N. J.; Ramakrishnan R.; von Lilienfeld O. A.; Roethlisberger U. Genetic Optimization of Training Sets for Improved Machine Learning Models of Molecular Properties. J. Phys. Chem. Lett. 2017, 8, 1351–1359. 10.1021/acs.jpclett.7b00038. [DOI] [PubMed] [Google Scholar]
  45. Bereau T.; Andrienko D.; von Lilienfeld O. A. Transferable Atomic Multipole Machine Learning Models for Small Organic Molecules. J. Chem. Theory Comput. 2015, 11, 3225–3233. 10.1021/acs.jctc.5b00301. [DOI] [PubMed] [Google Scholar]
  46. Bleiziffer P.; Schaller K.; Riniker S. Machine Learning of Partial Charges Derived from High-Quality Quantum-Mechanical Calculations. J. Chem. Inf. Model. 2018, 58, 579–590. 10.1021/acs.jcim.7b00663. [DOI] [PubMed] [Google Scholar]
  47. Cybenko G. Approximation by Superpositions of a Sigmoidal Function. Math. Control, Signals, Syst. 1989, 2, 303–314. 10.1007/bf02551274. [DOI] [Google Scholar]
  48. Hornik K. Approximation Capabilities of Multilayer Feedforward Networks. Neural Network. 1991, 4, 251–257. 10.1016/0893-6080(91)90009-t. [DOI] [Google Scholar]
  49. Wang R. Significantly Improving the Prediction of Molecular Atomization Energies by an Ensemble of Machine Learning Algorithms and Rescanning Input Space: A Stacked Generalization Approach. J. Phys. Chem. C 2018, 122, 8868–8873. 10.1021/acs.jpcc.8b03405. [DOI] [Google Scholar]
  50. Bleiziffer P.; Schaller K.; Riniker S. Machine Learning of Partial Charges Derived from High-Quality Quantum-Mechanical Calculations. J. Chem. Inf. Model. 2018, 58, 579–590. 10.1021/acs.jcim.7b00663. [DOI] [PubMed] [Google Scholar]
  51. Shelton D. P.; Rice J. E. Measurements and Calculations of the Hyperpolarizabilities of Atoms and Small Molecules in the Gas Phase. Chem. Rev. 1994, 94, 3–29. 10.1021/cr00025a001. [DOI] [Google Scholar]
  52. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; Li X.; Caricato M.; Marenich A.; Bloino J.; Janesko B. G.; Gomperts R.; Mennucci B.; Hratchian H. P.; Ortiz J. V.; Izmaylov A. F.; Sonnenberg J. L.; Williams-Young D.; Ding F.; Lipparini F.; Egidi F.; Goings J.; Peng B.; Petrone A.; Henderson T.; Ranasinghe D.; Zakrzewski V. G.; Gao J.; Rega N.; Zheng G.; Liang W.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Throssell K.; Montgomery J. A. Jr.; Peralta J. E.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Keith T.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Millam J. M.; Klene M.; Adamo C.; Cammi R.; Ochterski J. W.; Martin R. L.; Morokuma K.; Farkas O.; Foresman J. B.; Fox D. J.. Gaussian 09, Revision D.01; Gaussian Inc: Wallingford CT, 2009.
  53. O’Boyle N. M.; Banck M.; James C. A.; Morley C.; Vandermeersch T.; Hutchison G. R. Open Babel: An Open Chemical Toolbox. J. Cheminf. 2011, 3, 33. 10.1186/1758-2946-3-33. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Mitchell T.Machine Learning; McGraw-Hill International Editions; McGraw-Hill, 1997. [Google Scholar]
  55. Breiman L.Classification and Regression Trees; Routledge, 2017. [Google Scholar]
  56. Yap C. W. PaDEL-descriptor: An Open Source Software to Calculate Molecular Descriptors and Fingerprints. J. Comput. Chem. 2011, 32, 1466–1474. 10.1002/jcc.21707. [DOI] [PubMed] [Google Scholar]
  57. Dixon P. VEGAN, a Package of R Functions for Community Ecology. J. Veg. Sci. 2003, 14, 927–930. 10.1111/j.1654-1103.2003.tb02228.x. [DOI] [Google Scholar]
  58. Wickham H.ggplot2: Elegant Graphics for Data Analysis; Springer, 2016. [Google Scholar]
  59. Cheng L. T.; Tam W.; Stevenson S. H.; Meredith G. R.; Rikken G.; Marder S. R. Experimental Investigations of Organic Molecular Nonlinear Optical Polarizabilities. 1. Methods and Results on Benzene and Stilbene Derivatives. J. Phys. Chem. 1991, 95, 10631–10643. 10.1021/j100179a026. [DOI] [Google Scholar]
  60. Champagne B.; Perpète E. A.; Jacquemin D.; van Gisbergen S. J. A.; Baerends E.-J.; Soubra-Ghaoui C.; Robins K. A.; Kirtman B. Assessment of Conventional Density Functional Schemes for Computing the Dipole Moment and (Hyper)Polarizabilities of Push–Pull π–Conjugated Systems. J. Phys. Chem. A 2000, 104, 4755–4763. 10.1021/jp993839d. [DOI] [Google Scholar]
  61. Lu S.-I.; Chiu C.-C.; Wang Y.-F. Density Functional Theory Calculations of Dynamic First Hyperpolarizabilities for Organic Molecules in Organic Solvent: Comparison to Experiment. J. Chem. Phys. 2011, 135, 134104. 10.1063/1.3644336. [DOI] [PubMed] [Google Scholar]
  62. Marder S. R.; Gorman C. B.; Tiemann B. G.; Cheng L. T. Stronger Acceptors Can Diminish Nonlinear Optical Response in Simple Donor-Acceptor Polyenes. J. Am. Chem. Soc. 1993, 115, 3006–3007. 10.1021/ja00060a071. [DOI] [Google Scholar]
  63. Marder S. R.; Perry J. W.; Tiemann B. G.; Gorman C. B.; Gilmour S.; Biddle S. L.; Bourhill G. Direct Observation of Reduced Bond Length Alternation in Donor/Acceptor Polyenes. J. Am. Chem. Soc. 1993, 115, 2524–2526. 10.1021/ja00059a067. [DOI] [Google Scholar]
  64. Bourhill G.; Bredas J.-L.; Cheng L.-T.; Marder S. R.; Meyers F.; Perry J. W.; Tiemann B. G. Experimental Demonstration of the Dependence of the First Hyperpolarizability of Donor-Acceptor-Substituted Polyenes on the Ground-State Polarization and Bond Length Alternation. J. Am. Chem. Soc. 1994, 116, 2619–2620. 10.1021/ja00085a052. [DOI] [Google Scholar]
  65. Meyers F.; Marder S. R.; Pierce B. M.; Bredas J. L. Electric Field Modulated Nonlinear Optical Properties of Donor-Acceptor Polyenes: Sum-Over-States Investigation of the Relationship Between Molecular Polarizabilities (α, β and γ) and Bond Length Alternation. J. Am. Chem. Soc. 1994, 116, 10703–10714. 10.1021/ja00102a040. [DOI] [Google Scholar]
  66. Meyers F.; Brédas J.; Pierce B.; Marder S. Nonlinear Optical Properties of Donor-Acceptor Polyenes: Frequency-Dependent Calculations of the Relationship Among Molecular Polarizabilities, α, β, and γ, and Bond-Length Alternation. Nonlinear Optic. 1995, 14, 61–71. [Google Scholar]
  67. Marder S. R.; Cheng L.-T.; Tiemann B. G.; Friedli A. C.; Blanchard-Desce M.; Perry J. W.; Skindhoj J. Large First Hyperpolarizability in Push-Pull Polyenes by Tuning of the Bond Length Alternation and Aromaticity. Science 1994, 263, 511–514. 10.1126/science.263.5146.511. [DOI] [PubMed] [Google Scholar]
  68. Kim H.-S.; Cho M.; Jeon S.-J. Vibrational Contributions to the Molecular First and Second Hyperpolarizabilities of a Push-Pull Polyene. J. Chem. Phys. 1997, 107, 1936–1940. 10.1063/1.474545. [DOI] [Google Scholar]
  69. Zaleśny R. Anharmonicity Contributions to the Vibrational First and Second Hyperpolarizability of Para-Disubstituted Benzenes. Chem. Phys. Lett. 2014, 595–596, 109–112. 10.1016/j.cplett.2014.01.041. [DOI] [Google Scholar]
  70. Cheng L. T.; Tam W.; Marder S. R.; Stiegman A. E.; Rikken G.; Spangler C. W. Experimental Investigations of Organic Molecular Nonlinear Optical Polarizabilities. 2. A Study of Conjugation Dependences. J. Phys. Chem. 1991, 95, 10643–10652. 10.1021/j100179a027. [DOI] [Google Scholar]
  71. Klekota J.; Roth F. P. Chemical Substructures That Enrich for Biological Activity. Bioinformatics 2008, 24, 2518–2525. 10.1093/bioinformatics/btn479. [DOI] [PMC free article] [PubMed] [Google Scholar]
  72. Limacher P. A.; Mikkelsen K. V.; Lüthi H. P. On the Accurate Calculation of Polarizabilities and Second Hyperpolarizabilities of Polyacetylene Oligomer Chains Using the CAM–B3LYP Density Functional. J. Chem. Phys. 2009, 130, 194114. 10.1063/1.3139023. [DOI] [PubMed] [Google Scholar]
  73. Baranowska-Łączkowska A.; Bartkowiak W.; Góra R. W.; Pawłowski F.; Zaleśny R. On the Performance of Long-Range-Corrected Density Functional Theory and Reduced-Size Polarized LPol-n Basis Sets in Computations of Electric Dipole (Hyper)Polarizabilities of π-Conjugated Molecules. J. Comput. Chem. 2013, 34, 819–826. 10.1002/jcc.23197. [DOI] [PubMed] [Google Scholar]
  74. Lu S.-I.; Chiu C.-C.; Wang Y.-F. Density Functional Theory Calculations of Dynamic First Hyperpolarizabilities for Organic Molecules in Organic Solvent: Comparison to Experiment. J. Chem. Phys. 2011, 135, 134104. 10.1063/1.3644336. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao9b04339_si_001.pdf (424.5KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES