Evaluation of Fluid Resuscitation Control Algorithms via a Hardware-in-the-Loop Test Bed

Abstract

Objective:

This paper presents a hardware-in-the-loop (HIL) testing platform for evaluating the performance of fluid resuscitation control algorithms. The proposed platform is a cyber-physical system that integrates physical devices with computational models and computer-based algorithms.

Methods:

The HIL test bed is evaluated against in silico and in vivo data to ensure the hemodynamic variables are appropriately predicted in the proposed platform. The test bed is then used to investigate the performance of two fluid resuscitation control algorithms: a decision table (rule-based) and a proportional-integral-derivative (PID) controller.

Results:

The statistical evaluation of test bed indicates that similar results are observed in the HIL test bed, in silico implementation, and the in vivo data, verifying that the HIL test bed can adequately predict the hemodynamic responses. Comparison of the two fluid resuscitation controllers reveals that both controllers stabilized hemodynamic variables over time and had similar speed to efficiently achieve the target level of the hemodynamic endpoint. However, the accuracy of the PID controller was higher than the rule-based for the scenarios tested in the HIL platform.

Conclusion:

The results demonstrate the potential of the HIL test bed for realistic testing of physiologic controllers by incorporating physical devices with computational models of physiology and disturbances.

Significance:

This type of testing enables relatively fast evaluation of physiologic closed-loop control systems to aid in iterative design processes and offers complementary means to existing techniques (e.g., in silico, in vivo, and clinical studies) for testing of such systems against a wide range of disturbances and scenarios.

I. Introduction

FLUID therapy is extensively used to restore blood volume (BV) and optimize cardiac function in hypovolemic scenarios such as hemorrhage, burns, and trauma. Closed-loop fluid resuscitation systems, sometimes called automated fluid resuscitation control, monitor patients’ hemodynamic variables (e.g., BV, blood pressure (BP), etc.) and adjust the infusion rate of fluids (e.g., crystalloids, colloids or blood) based on an embedded algorithm that targets optimizing cardiac variable(s) [1]-[4]. Such automated systems have the potential benefit to reduce the incidence of human errors in clinical settings [5], provide relatively-accurate infusion rates to avoid under and over resuscitation [6], and allow more patients to receive adequate supportive care, for example during mass casualty incidents [1].

Physiologic closed-loop controlled systems are medical systems that employ computational control algorithms along with physiological sensors and actuators to automatically adjust a physiologic variable [7]. Closed-loop fluid management systems may incorporate a variety of control algorithms, including rule-based (decision table) [3], [4], [8], proportional-integral-derivative (PID) [4], fuzzy [1], or model-based control approaches [9]. They may also use different hemodynamic endpoints such as cardiac output (CO) [2] or mean arterial pressure (MAP) [1]. Due to the complexity of human cardiopulmonary system as well as the variety of disturbances occurring in a clinical environment (e.g., concomitant therapies, sensor noise), fluid resuscitation controllers must undergo significant testing to ensure that they can achieve the necessary performance under the variety of disturbances they may encounter [10]. Pre-clinical safety and performance testing of fluid resuscitation controllers have been reported based on either in silico studies in computer simulated environments [9] or pilot animal studies [11], [12]. Both types of testing have their benefits and usage in pre-clinical testing: inclusion of real physiologic variability and physical devices in animal studies and ability to perform large numbers of simulations with in silico studies over ranges not possible with animal subjects. However, animal studies are usually limited, costly, and time-consuming, while in silico testing may not be representative of when control commands are applied to actual hardware. Hardware-in-the-loop (HIL) testing that integrates physical devices with computational models of physiologic variables may provide a realistic environment to demonstrate resuscitation scenarios and test the performance of automated fluid resuscitation controllers, compared to pure in silico testing. In addition, a HIL testing approach provides a platform to test the safety and performance of actual devices within the closed-loop control system, which is not feasible in a simulated environment. At the same time, HIL testing can maintain the benefit of enabling additional relatively-expensive testing iterations without the high costs associated with animal studies

This paper presents a cyber-physical system as a potential testing platform for automated fluid resuscitation systems. The developed platform, called HIL test bed, integrates devices (e.g., infusion pump) with computational patient models (e.g., BV and hemodynamic response model) and computer-based algorithms (e.g., BP waveform generator) for automated fluid administration testing. The HIL test bed is first evaluated against in silico and in vivo data to verify its accuracy and then leveraged to assess the performance of fluid resuscitation controllers. The proposed platform delivers the controlled signal within the desired sample period due to its real-time design and could potentially improve and accelerate the non-clinical testing of automated fluid resuscitation control algorithms.

The rest of this paper is organized as follows: In Section 2, the testing platform for automated fluid resuscitation systems is described, and example scenarios are provided as potential use cases. In Section 3.a, the methods used for comparing the testing platform to in vivo and in silico data are explained, and in Section 3.b, the methods used for comparing fluid resuscitation control algorithms based on the testing platform are described in detail. Section 4.a describes the results for the testing of the system and section 4.b describes the results for the comparison of control algorithms. Discussions along with limitations and conclusions are presented in Section 5.

II. Hardware-in-the-Loop Test Bed

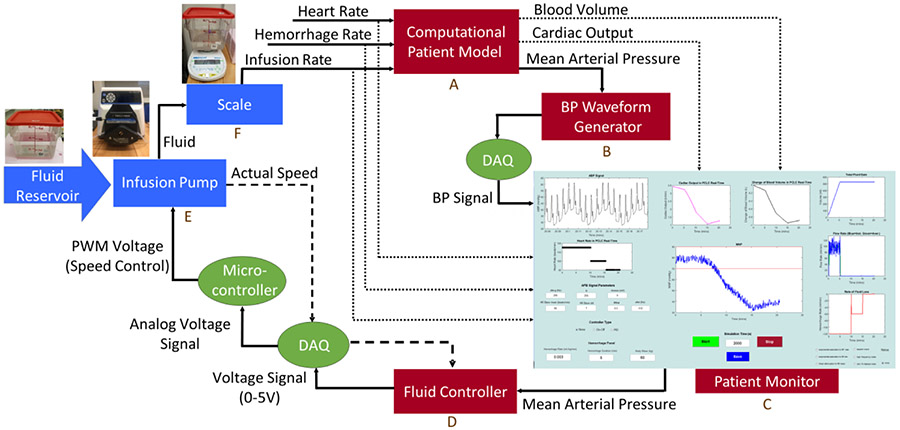
A HIL test bed was designed for testing closed-loop control algorithms for fluid resuscitation. The platform consists of software components, including a patient model, a BP waveform generator, a patient monitor, and fluid resuscitation controllers, hardware components, including an infusion pump and scale, and hardware-software interfaces, including data acquisition (DAQ) cards and microcontroller, as shown in Fig. 1.

Fig. 1.

Hardware-in-the-loop testing platform consisting of hardware components in blue (infusion pump and scale), software component in red (patient model, blood pressure waveform generator, patient monitor, and fluid resuscitation controller), and hardware-software interfaces in green (DAQ cards and microcontroller)

A. System Description

The HIL test bed works as follows: The computational model computes the cardiac functions, including BV, CO, and MAP, based on the current values of heart rate, fluid infusion rate, and hemorrhage rate. MAP is used as an input to a BP waveform generator that is then displayed on the patient monitor along with other measurements and physiological variables. A fluid resuscitation control algorithm was incorporated into the HIL test bed to control the pump flow rate based on the value of MAP. The controller output (voltage signal) is converted to a pulse width modulation signal by a microcontroller and sent to the pump, which is used to deliver the fluid infusion to a container placed on the scale. The scale measures delivered fluid which is then translated to the infusion rate fed to the patient model, representative of the fluid infused to a patient. Major components of the HIL test bed are described below.

Computational patient model:

The patient model (Box A in Fig. 1) is a recently-developed control-oriented physiological model [5] capable of reproducing hemodynamic responses to BV perturbations. The hemodynamic model uses a proportional integral (PI) control model to relate change of BV response to fluid gain (i.e., infusion) and fluid loss (i.e., hemorrhage) and then predicts CO as well as BP using the estimated BV response, heart rate (as an input), and model-predicted total peripheral resistance. The PI control model represents the dynamics of the intravascular fluid compartment equipped with a fluid shift mechanism (valve) between the intravascular and extravascular compartments. The discrepancy between target versus actual BV change is reflected as a function of valve opening (see [5] for more information about the model). The model was chosen for this work, since it is i) mathematically simple yet accurate to be utilized in the design of closed-loop fluid controllers, ii) computationally fast to be deployed in a real-time platform, and iii) physiologically transparent to provide legitimate hemodynamic outcomes.

BP waveform generator:

The designed BP waveform generator (Box B in Fig. 1) takes an arterial blood pressure template beat and updates its parameters based on current cardiac values including MAP and heart rate. This waveform is then sent to a simulated patient monitor represented by a graphical display. The dynamics of the signal can also be modified to include low and high frequency modulations as well as heart rate variations to represent beat-to-beat variability in timing and morphology of the BP signal [13]. A more detailed description of the BP waveform model is provided in Supplementary Information.

The BP waveform can be enhanced to include representative noise and artifacts that can be expected to occur during invasive BP monitoring mainly due to transducer flushing, catheter clotting, movement artifact, etc. These artifacts frequently corrupt the BP waveform and cause the monitor to display inaccurate values of MAP and sometimes generate false alarms. To this end, various types of previously reported artifact models reflecting noise sources in a clinical environment [13] were incorporated into the system. Six generic types of artifacts, identified as the common types of phenomenological BP artifacts, were: 1) rapid saturation to some maximal BP, 2) rapid saturation to some minimal BP, 3) rapid saturation to the current mean BP, 4) high-amplitude square wave artifact, 5) high-frequency noise, and 6) highly-transient impulse-like artifact. Each artifact was synthetically generated using the mathematical model described in [13] and incorporated into the HIL test bed.

Patient monitor:

A graphical user interface (Box C in Fig.1)was designed in MATLAB R2018a (The Mathworks, Natick, MA) representative of a patient monitor. In the current iteration of the HIL testing platform, this also serves as the interface for the testing environment. All necessary measurements, including fluid gain and infusion rate, as well as physiological parameters, including heart rate, CO, BV, and MAP, are displayed in the interface. In addition, the interface communicates with other components of the closed-loop system to alter the configuration of the HIL platform. For example, the features of BP signal, type of measurement noise, fluid resuscitation control algorithm, hemorrhage scenario, and simulation time can all be modified through the interface in real time.

Control algorithm:

The outputs of the hemodynamic model used in the current work are BV, CO, and MAP. Fluid resuscitation control algorithms that use any of these hemodynamic variables as their design endpoint can be incorporated in the current HIL platform. For simplicity and consistency, MAP was chosen as the design endpoint throughout this work. The control algorithm (Box D in Fig. 1) determines the input voltage of the infusion pump. The voltage range is 0 to 5 volts corresponding to the fluid infusion rate of 0 to 130 ml/min.

Two fluid resuscitation control algorithms, previously reported in the literature [1], [4], were implemented in the system for the current work: An empirical rule-based algorithm (look-up table) [1] and a proportional-integral-derivative (PID) controller [4]. Both controllers were previously designed and tested in an animal study [1], [4] to restore and maintain a MAP of 90 mmHg by controlling the infusion rate of Lactated Ringer’s solution (LR). We implemented the controllers in MATLAB based on the available information and integrated into the HIL test bed to regulate the fluid infusion rate based on the updated value of MAP obtained from the real-time simulation. The rule-based controller adjusts the fluid infusion rate based on the different levels of MAP. For MAP values less than 50 mmHg, the maximum infusion rate of 100 ml/min per 70 kg is applied. If MAP is between 50 mmHg to 55 mmHg, the infusion rate is 80% of the maximum rate. Similarly, 60%, 30%, and 10% of the maximum infusion rate will be applied for 55 mmHg ≤ MAP < 60 mmHg, for 60 mmHg ≤ MAP <80 mmHg, and for 80 mmHg ≤ MAP < 90 mmHg, respectively. The infusion stops if MAP becomes higher than 90 mmHg. For the PID controller, the reference MAP is set to 90 mmHg, and PID gains were the same values as reported in [4].

Infusion pump:

The infusion pump in the current iteration of the system (Box E in Fig. 1) is a precision digital drive (Masterflex L/S, Cole-Parmer, Vernon Hills, IL) providing the speed of 0.1 to 600 rpm corresponding to 0.021 to 130 ml/min flow rate with L/S 14 silicone tubing. The pump is employed in a remote continuous mode for which a pulse width modulation (PWM) signal is used as a speed control signal. The speed control signal (voltage) set by the control algorithm is transformed into a PWM signal using a microcontroller and transmitted to the pump along with the pump start/stop command. The infusion pump delivers fluid from the reservoir to a container placed on the scale.

Scale:

The scale (Box F in Fig. 1) is used to measure fluid mass in the HIL platform (AE Adams Nimbus, Adam Equipment, Oxford, CT). The scale’s mass reading is then converted to the fluid infusion rate fed to the patient model, representative of the fluid infused to a patient.

B. Example Resuscitation Scenarios in HIL Test Bed

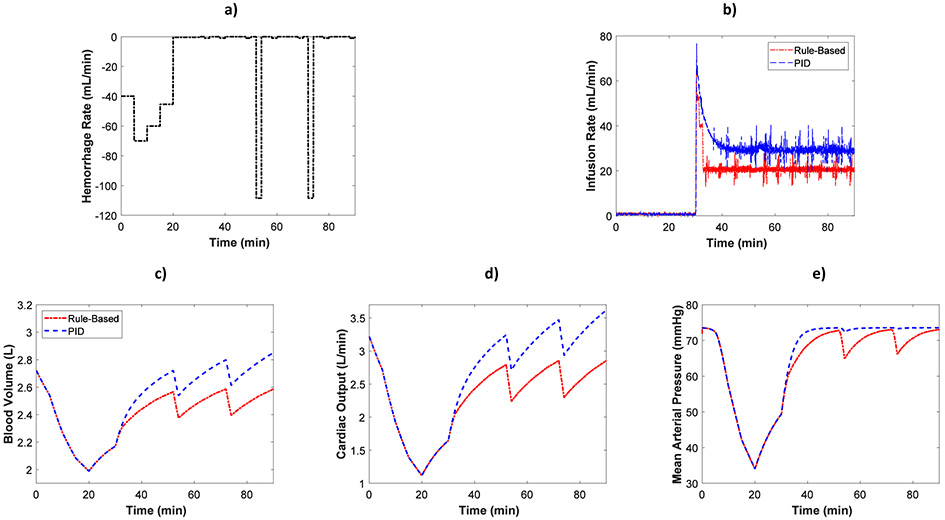
A fluid resuscitation scenario is demonstrated in the HIL test bed. The scenario, adopted from [1], includes high and medium hemorrhage rates. The scenario was run twice with fluid controlled with the rule-based and then the PID controller. The simulation time was set to 90 minutes. The hemorrhage scenario is shown in Fig. 2a. Hemorrhage rate starts at 40 ml/min, increases to 70 ml/min and 60 ml/min after 5 and 10 minutes, respectively, and then decreases to 45.4 ml/min after 15 minutes from the start of the simulation. No hemorrhage is applied to the rest of the simulation except at t=52 min and t=72 min when a high hemorrhage rate of 108.5 ml/min is applied for two minutes.

Fig. 2.

Example of hemorrhage/resuscitation scenario implemented in HIL test bed along with the hemodynamic measurements of the system a) Hemorrhage profile b) Fluid infusion rates c) Model-predicted blood volume d) Model-predicted cardiac output e) Mean arterial pressure measured from the patient monitor

Fig. 2b shows infusion profiles adjusted by the rule-based and PID controller in this example scenario. BV, CO, and MAP measurements computed in the closed-loop HIL platform are shown in Figs. 2c, 2d, and 2e, respectively. During the hemorrhage, BV, CO, and MAP decrease and begin to recover due to fluid shift in the computational hemodynamic model when the hemorrhage ends after 20 minutes. The fluid resuscitation controllers turn on at t=30 min, where the infusion rates can be seen to start high while precipitously decreasing as MAP recovers.

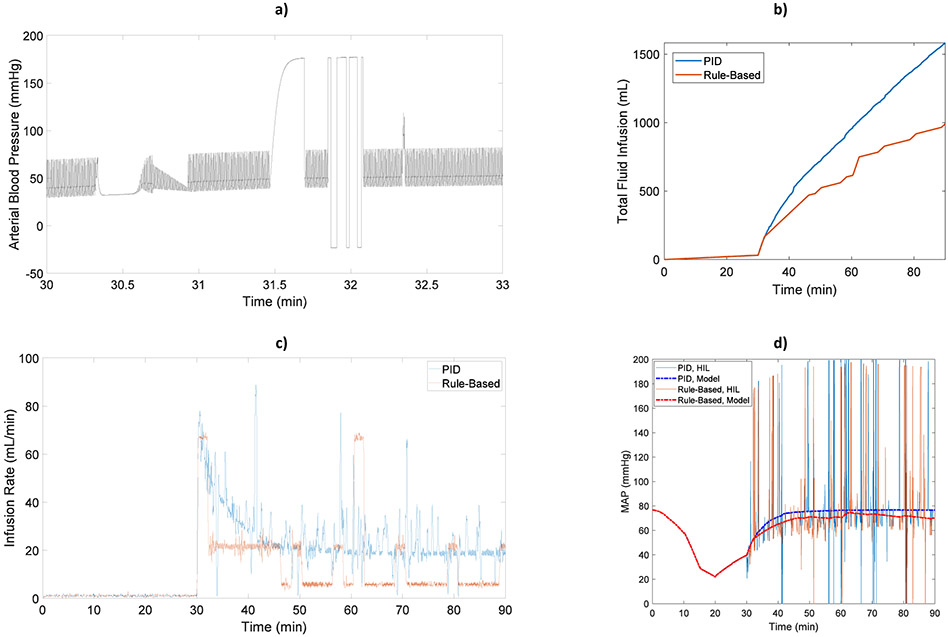
Another example use case, Fig. 3, demonstrates how disturbances can be added into the system. The six types of BP artifacts described in [13] were incorporated in a 90-minute scenario. As in the previous case, no artifact was present from t=0 to t= 30 min. However, from t= 30 min to t= 90 min, artifacts were randomly selected from the six models at each iteration of BP signal generation, which was around 23 seconds. 50% of the 23 second BP signal generation period included the artifacts, and the BP signals were artifact-free for the rest of the period. The total amount of fluid infusion and the instantaneous infusion rates from each controller are shown in Figs. 3.b and 3.c, respectively. MAP responses for the HIL test bed (thin lines in Fig. 3d) were computed from the patient monitor and included BP disturbances (Fig. 3a) incorporated in BP waveform generator. In contrast, MAP responses for the model (thick lines in Fig. 3d) were computed directly from the hemodynamic model before adding disturbances.

Fig. 3.

Example scenario combining all 6 types of BP artifacts: a) Generated BP signal with 6 types of artifacts added, b) Cumulative fluid delivered by rule-based and PID controllers, c) Infusion rates, and d) MAP response measured from the patient monitor (thin line) and predicted by the model (thick line)

III. Methods

A. Evaluation of HIL Test Bed

To evaluate the HIL test bed, the infusion input recorded from an animal study was used as the input to the HIL test bed as well as an in silico implementation of the system, so that all three methods (in vivo, in silico, and HIL test bed) can be evaluated with the same inputs and disturbance profiles. The in silico implementation was performed by disabling all of the HIL components except the physiologic model, then applying model inputs and recording hemodynamic measurements (model outputs) offline. The hemodynamic responses were then compared between these methods using the same protocols.

1). Experimental Animal Data

The animal study was previously reported and described in detail in [11]. The animal data was collected by the Resuscitation Research Laboratory at the University of Texas Medical Branch with the study protocol approved by its Institutional Animal Care and Use Committee [11]. The experimental data includes hemorrhage scenarios, infusion profiles, and hemodynamic measurements for 9 adult sheep that underwent intravenous blood loss and fluid infusion. The sheep were hemorrhaged a total of 35 ml/kg over three separate bleeds. The initial hemorrhage rate of 25 ml/kg started at the beginning and lasted for 15 minutes, representative of a major hemorrhage scenario. The second and third hemorrhage rates (5 ml/kg each) occurred after 50 and 70 minutes from the beginning of the study and each lasted for 5 minutes. These two bleeds were considered to represent hemorrhage occurring during patient transportation to medical facilities. The fluid resuscitation was performed by lactated Ringer’s (LR) as a standard crystalloid solution. The infusion started after 30 minutes from the beginning of the study and continued until the end of the study. For each animal, the duration of study was 180 minutes. The infusion rate during the studies was controlled by two different types of automated algorithms described in Section 2.a: rule-based (decision table) and PID controller. The controllers used MAP as the hemodynamic endpoint to regulate the LR infusion rate.

2). Comparative Analysis

To evaluate the HIL test bed, we removed the control algorithm from both the HIL platform and in silico implementation and instead applied the same infusion rate collected during the animal study. The same hemorrhage scenario along with the experimentally measured heart rate profiles were applied to each animal subject in the test bed. BV, CO, and MAP were compared every 5 minutes over each 180 minute trial between the three methods, i.e., HIL test bed, in silico and in vivo. The root-mean-square error (RMSE) was calculated between the HIL test bed and animal data, as well as between the HIL test bed and in silico results.

B. Comparison of control algorithms

1). Simulation Description

The HIL test bed was leveraged to assess the performance of two previously-reported fluid resuscitation controllers [1], [4] against a set of subject-specific models [5] representing digital twins of a pre-clinical animal study. In fact, model parameters were uniquely determined and optimized for each animal subject [5], so the hemodynamic model could reflect the performance of its corresponding animal twin. The controllers’ performance was investigated in two different conditions: with and without BP artifacts. The fluid resuscitation controllers were rule-based and PID controllers that adjust the infusion rate based on the value of MAP. A brief description of the controllers was given in Section 2.a. Although we followed the general designs described in [1], [4], [11], the actual implementation of these control algorithms in our HIL test bed were not necessarily identical to those used in the previous experimental work. Nine computational subjects representing conscious sheep for which the hemodynamic model was previously determined [5] were considered in this study. A hemorrhage rate of 25 ml/kg was applied to each subject for the first 15 minutes from the beginning of the study. The closed-loop controllers were turned on 30 minutes after the beginning of each trial and continued until the end of the trial (90 minutes). The target (desired) MAP for the controllers was considered to be 90 mmHg.

2). Performance Measures

The performance of fluid resuscitation controllers was evaluated with respect to dynamic performances, measurement errors, and input and output responses (i.e. infusion rate, total infusion, and MAP response).

Dynamic performances of the closed-loop HIL system with integrated controllers followed the IEC 60601-1-10 standard for physiologic closed-loop controllers recommended performances metrics [7]. The performance indicators that were measured included response time, settling time, and relative overshoot. Response time, also called rise time, is the amount of time required for the step response of MAP to rise from its initial value to 90% of the MAP steady-state value. Settling time is the time taken for the MAP response to be within a specified tolerance of its steady-state value without subsequently deviating from it by that amount. The amount of tolerance is considered to be 95% of MAP steady-state value. Relative overshoot is defined as the maximum transient deviation of MAP response from its steady-state value and is shown by the percentage overshoot, the difference between the steady-state value and maximum value divided by the steady-state value. For each of the dynamic measures, the initial value was considered to be the hemodynamic measure at the time the controller was turned on and the steady-state value was considered to be the final value of hemodynamic response at t=90 min.

Different measurement errors were considered for the performance assessment of closed-loop control systems. Steady-state error (SSE) is the error between the target MAP and steady-state MAP. Root-mean-square error (RMSE) is calculated as the square root of the mean square of the difference between the target MAP and instantaneous MAP, when the controller is on (from t=30 min to t=90 min). Performance error (PE) is the percent difference between the achieved and target MAP. Bias, i.e., the median performance error (MDPE), inaccuracy, i.e., the median absolute performance error (MDAPE), wobble, i.e., the median absolute difference between PE and MDPE, and divergence, i.e., the slope of linear regression of absolute PE against time, were computed following the methods in [14], which are often referred to as Varvel measures.

3). Controller Comparison during BP Artifact Disturbances

The simulation described in Section 3.b.i was repeated with artifacts added to the BP waveform. Artifacts were synthetically generated using the mathematical models described in [13] and added to the BP waveform starting from t=30 min (when controller turns on) until t=90 min (end of the study). BP waveforms were constantly updated during the real-time simulation in ~23 second segments, and the percentage of artifacts in each segment was randomly selected from 20%, 40%, 60%, 80%, and 100%.

C. Statistical Analysis

Analysis of Variance (ANOVA) with repeated measurements was used to statistically compare the HIL test bed performance against the in silico implementation and in vivo data. Hemodynamic measurements BV, CO, and MAP were compared between the methods. α was set to 0.05. The normality assumption for residuals were checked and the Box-Cox transformation of dependent variable was used wherever appropriate. To check whether or not the performance of the HIL test bed was equivalent to the in vivo data as well as the in silico implementation, an equivalence test was conducted. In the pair-wise equivalence test, the null hypothesis was that the population mean of each hemodynamic variable obtained from each method was different from another population mean and the alternative hypothesis assumed the means were equal. The equivalence test was performed with α = 0.05 and the equivalence interval considered to be ±5% of the in vivo hemodynamic response means.

Performance of the two control algorithms were compared using paired T-test for normally-distributed data or Wilcoxon signed-rank (WSR) test for non-normal data, whichever was appropriate. Normality assessment was performed with Anderson-Darling test with α = 0.1.

IV. Results

A. HIL Verification

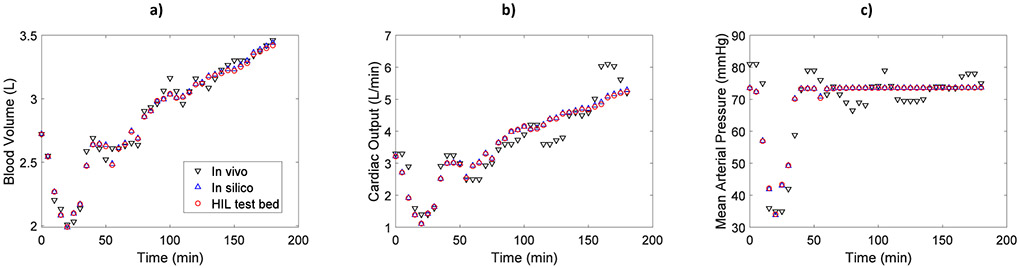
Fig. 4 demonstrates the hemodynamic responses of a representative subject from the HIL test bed, in silico implementation, and in vivo data. Differences between the in silico simulation and HIL test bed results are minimal compared with in vivo data. This is consistent with remaining animals, so only RMSE between the hemodynamic results of HIL test bed and in vivo data are shown in Table 1. Individual RMSE values for all three comparisons are shown in Supplementary Information Table 1.

Fig. 4.

a) Blood volume, b) Cardiac output, and c) Mean arterial pressure for a representative subject from three different methods: HIL test bed, in silico, and in vivo

Table 1.

Root-mean-square error (RMSE) for hemodynamic responses between the HIL test bed and in vivo data along with the ANOVA results

		BV	CO	MAP
RMSE	Mean (SD)	0.08 (0.03) L	0.62 (0.33) L/min	8.85 (3.45) mmHg
	Mean % (SD %)	4.29 % (2.08 %)	16.17 % (6.76 %)	11.57 % (3.69%)
ANOVA P-Value	Time	<0.001	<0.001	<0.001
	Subject (Random)	<0.001	<0.001	<0.001
	Method	0.089	0.077	0.204

Time, a covariate (continuous variable) in the experiment, had a significant effect on the results since the infusion and hemorrhage—and therefore the hemodynamic responses—changed over time during the experiment (ANOVA results in Table 1). In addition, the inter-subject variability was significant in this study, as the animals’ hemodynamic responses varied among the subjects. ANOVA results indicate that the method (i.e., HIL test bed, in silico model, and in vivo data), did not significantly affect the measured BV, CO or MAP responses. Equivalency results in Table 2 demonstrate that the difference between the HIL test bed and in vivo data for each hemodynamic variable was within the pre-defined equivalency margin of 5%. Similar equivalency results were achieved when comparing the HIL test bed with the in silico implementation, demonstrating the integrated hardware-software design of the proposed HIL platform did not affect the performance (this comparison is not shown here to avoid redundancy).

Table 2.

Results of equivalence test comparing blood volume, cardiac output, and mean arterial pressure from HIL test bed and in vivo data

	95% CI	Equivalence Interval	Null Hyp.	P-Value
BV	(0, 0.0388)	(−0.12, 0.12)	Difference ≤ −0.12	0.000
			Difference ≥ 0.12	0.000
CO	(0, 0.162)	(−0.166, 0.166)	Difference ≤ −0.166	0.000
			Difference ≥ 0.166	0.040
MAP	(−0.27, 1.438)	(−4.12, 4.12)	Difference ≤ −4.12	0.000
			Difference ≥ 4.12	0.000

B. Control Algorithm Comparison

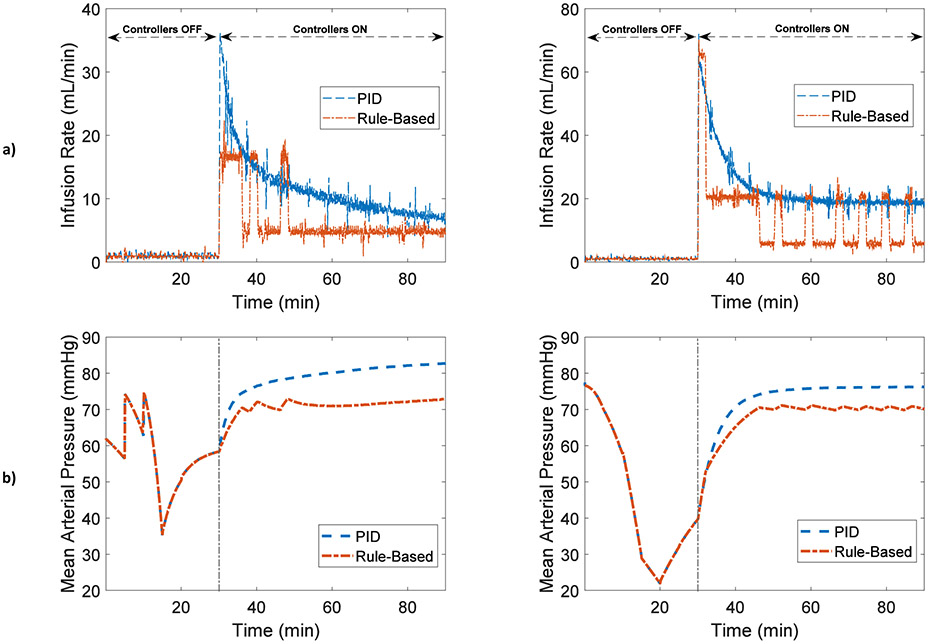
MAP and fluid infusion responses measured from the HIL test bed for two representative subjects are shown in Fig. 5. MAP decreases during the hemorrhage and begins to recover after the hemorrhage ends due to fluid shift mechanisms in the hemodynamic model. The controllers are turned on at t=30 min, at which time both control algorithms deliver high infusion rates initially that decrease over time. Infusion and MAP responses for all experiments are presented in Supplementary Information.

Fig. 5.

a) Infusion rate and b) Mean arterial pressure for two representative subjects during closed-loop fluid administration for PID and rule-based controllers

Assessment of the fluid resuscitation control algorithms indicate that dynamic performances of PID and rule-based controllers, including response time (P=0.850), settling time (P=0.562), and relative overshoot (P=0.636), were similar, as shown in Table 3. However, the measurement errors, including SSE, RMSE, PE, MDPE, and MDAPE, of the PID controller were significantly smaller than the rule-based controller (P<0.001 for all). This implies that while both controllers had similar speed in terms of reaching their steady-state level, the accuracy of the PID controller was superior to that of the rule-based controller in terms of approaching the target MAP.

Table 3.

Comparison of PID and rule-based fluid resuscitation controllers

		PID	Rule-Based	P-value
Dynamic Performance	Response Time [0 to 90%] (min)	25.73 ± 14.53	27.56 ± 20.63	P=0.850 (T)*
	Settling Time [5%] (min)	39.08 ± 14.88	40.65 ± 17.01	P=0.562 (T)
	Relative Overshoot (%)	1.90 ± 5.52%	3.08 ± 4.23%	P=0.636 (T)
Measurement Errors	SSE (%)	2.84 ± 6.00	9.79 ± 4.37	P<0.001 (T)*
	RMSE (%)	9.17 ± 4.70	13.01 ± 5.95	P=0.002 (T)*
	PE (%)	−6.20 ± 8.08	−12.23 ± 7.16	P<0.001 (WSR)**
	Bias (%)	−4.59 ± 6.21	−11.10 ± 5.33	P<0.001 (T)*
	Inaccuracy (%)	6.61 ± 3.76	11.29 ± 4.89	P=0.003 (T)*
	Wobble (%)	1.15 ± 0.89	1.51 ± 0.94	P=0.239 (T)*
	Divergence (% h−1)	−9.09 ± 8.01	−9.38 ± 7.44	P=0.885 (T)**
Infusion and MAP Response	Infusion Rate (mL/min)	17.46 ± 9.06	10.51 ± 7.51	P<0.001 (WSR)
	Total Infusion (mL)	1048 ± 472	631 ± 312	P<0.001 (T)
	MAP Response (mmHg)	75.04 ± 6.46	70.22 ± 5.73	P<0.001 (WSR)

^*Paired T-test

^**WSR: Wilcoxon Signed-Rank Test

Wobble, a measure of the total intra-individual variability in PEs, which is directly related to the ability to achieve the stable MAP, is similar in both controllers (P=0.239). The low value of wobble in Table 3 (1.15 ± 0.89 % for PID or 1.51 ± 0.94 % for rule-based) suggests a low intra-subject variability among the performance errors of subjects, meaning that both controllers maintained a stable value of MAP over time. Divergence, a measure of the expected systematic time-related changes in performance—that is, the tendency towards the narrowing or the widening over time of the gap between measured and target MAP in a given subject— is similar in both controllers (P=0.885). The relatively-high negative divergence implies that the gap between measured and target MAP decreases with time and the measured MAP converges to target MAP for each controller (more negative value indicates that convergence is more pronounced).

The infusion rate (P<0.001) as well as the total amount of infusion (P<0.001) of the PID controller was higher than the rule-based controller, while the MAP response of the PID controller was notably closer to target level than the rule-based controller (P<0.001), Table 3. The higher level of fluid infusion delivered by the PID controller resulted in the controller being more effective in terms of reaching the MAP target, compared to the rule-based controller.

C. Evaluation of Fluid Resuscitation Controllers in Presence of BP Disturbances

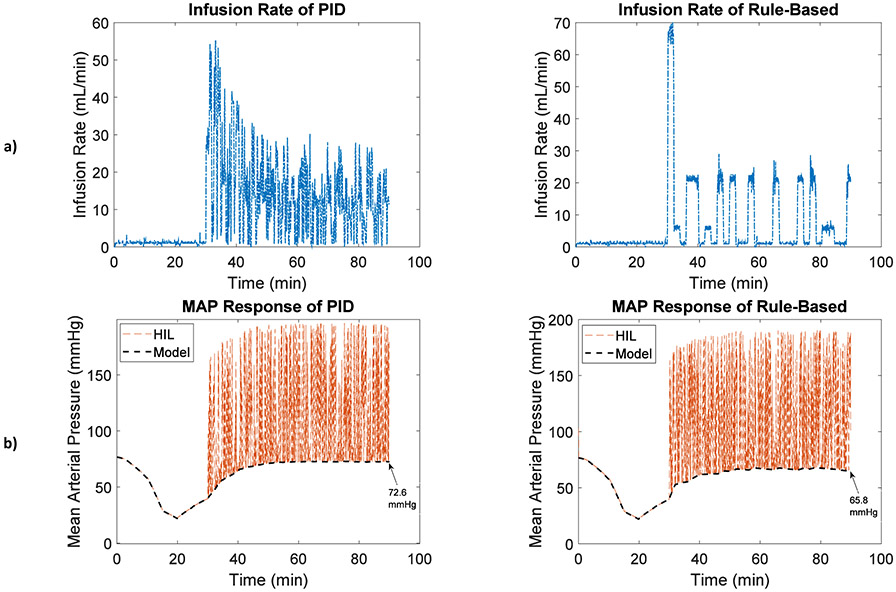
By augmenting BP signals with the type 1 artifact (rapid saturation to maximal BP), Fig. 6, the infusion rate (P<0.001), total infusion (P<0.001), and MAP response (P<0.001) of the two controllers were still significantly different, Table 4. The measured MAP response representative of the physiologic MAP in addition to the simulated artifacts (HIL MAP, orange dashed lines) was shown alongside the physiologic value of MAP, which was the output of the computational patient model (Model MAP, black dashed lines) in Fig. 6b. The type 1 artifact causes the MAP response measured from the HIL test bed to saturate to the maximal BP, as demonstrated in Fig. 6b.

Fig. 6.

a) Fluid infusion rate and b) MAP responses of the PID and rule-based controllers in the presence of blood pressure disturbances (type 1 artifact: rapid saturation to maximal BP)

Table 4.

Infusion rate, total infusion, and MAP response of controllers for the type 1 artifact: rapid saturation to maximal BP

	PID	Rule-Based	P-value
Inf. Rate (mL/min)	10.8 ± 8.5	6.6 ± 8.4	P<0.001 (WSR)
Total Inf. (mL)	651 ± 254	397 ± 179	P<0.001 (T)
MAP (mmHg)	114.8 ± 43.8	109.9 ± 43.4	P<0.001 (WSR)

Other BP artifact models described in Section 2.a were also tested, and depending on the type of artifact, the fluid infusion and MAP responses of the same controller could potentially vary from the no-artifact scenario. For instance, in both controllers, the MAP response was notably higher with the type 1 artifact than without artifact due to BP saturation to a maximal value at random times (see MAP responses in Table 3 and 4). Comparing the controllers’ results when all six types of artifacts were combined reveals the same trend of fluid infusion and MAP responses as they were with each separate artifact case, as in the example case in Fig. 3 (compare the measured MAP with the simulated artifacts, thin lines in Fig. 3d, with the true value of MAP, thick lines in Fig. 3d). While requiring higher level of infusion, the PID controller could achieve more accurate MAP results (closer to target) in the presence of BP artifact disturbances, compared to its rule-based counterpart.

V. Discussion

The focus of this work was to design a HIL test bed for physiologic closed-loop control fluid resuscitation systems. The HIL test bed incorporates a computational hemodynamic model, an arterial BP waveform generator, a patient monitor and a simulation interface, a fluid infusion pump, a scale, and control algorithms. Although its current iteration has limitations as discussed below, the system has been designed to be modular so that the various pieces can be substituted as needed. This type of system allows realistic testing of physiologic closed-loop controllers by incorporating physical devices with computational models of physiology as well as disturbances, such as the BP artifacts demonstrated in this work.

Our evaluation of the HIL test bed indicated that, given the same fluid infusion profile, similar hemodynamic responses were observed in the HIL test bed, in silico implementation, and the in vivo data.

This gives confidence that the HIL test bed including the physiologic model adequately predicts the hemodynamic measures for the tested scenarios. It can be seen from Fig. 4 that the comparison between the in vivo data and HIL test bed are not identical and more variability occurs in the animal data. The need to include such variability in the testing results may depend on the objective of the test, and more complex computational models of the physiologic response to blood loss could potentially be incorporated to enable more variability in the system. Similarly, the equivalency test as well as the 5% equivalency interval margin used could be modified depending on what is necessary to demonstrate before using the HIL test bed for a specific test.

The HIL test bed enabled us to compare the performance of two physiologic closed-loop fluid controllers under various testing iterations. We found that the two controllers had similar speed for reaching the target MAP (dynamic performance, Table 3) and maintained a stable value of MAP (wobble, Table 3) that converged to the target value over time (divergence, Table 3). However, the measurement errors, including SSE, RMSE, PE, MDPE, and MDAPE, for the PID controller were significantly smaller than the rule-based control algorithm (measurement errors, Table 3). While the infusion rate of the PID controller was higher than its rule-based counterpart, it maintained MAP closer to the target value than the rule-based controller, Fig. 5. Overall, the accuracy of the PID controller was higher than the rule-based controller for various scenarios tested in the HIL test bed. The results of controller assessment were limited to the subject-specific models determined from the conscious sheep [5], which should be considered before making any generalization of the results.

The control algorithms implemented in this work were based on fluid resuscitation controllers previously developed and validated in an animal study [1], [4]. The MAP target level for the controllers (90 mmHg) was previously set as part of the design for those studies and we did not modify the controllers’ parameters or their MAP target level in our study. We implemented them in MATLAB based on the available information and integrated into the HIL test bed in an attempt to replicate the original fluid controllers. Depending on the implementation of the controllers in the animal study, or whether the controller parameters were modified during the animal study, there might be differences between the results of the original controllers and those reported in this study. Our objective of using these controllers was to demonstrate and evaluate how the HIL test bed can be leveraged to thoroughly investigate the performance of fluid resuscitation control algorithms. We compared the controllers against each other but have not considered how their performance compares to any levels that may need to be achieved for clinical use. That said, it must be emphasized that the test bed is not limited to function with the controllers described in this work. A variety of control strategies that use different target levels for blood pressures, fluids, or different types of design endpoints such as CO or BV could be evaluated in the HIL test bed.

The BP artifact testing demonstrates how the HIL test bed can be used to examine various disturbances and their impact on physiologic closed-loop controllers. Comparing MAP responses of the hemodynamic model with those of the HIL test bed (with type 1 artifact) demonstrated that MAP responses were disturbed by the artifact for both PID and rule-based controllers, Fig. 6. The high values and frequent variations of MAP seen in Figs 3d and 6b are due to the simulated artifacts that were added to the BP signals. One of the advantages of using this type of testing is that it allows us to examine the differences between the measured MAP with the artifacts and the predicted physiologic MAP from the patient model. This is in contrast to animal or clinical testing where we would only be able to observe the MAP measured with the artifacts but not the true physiologic value.

In addition, the steady-state MAP response for the PID controller was still closer to the target MAP in the presence of artifacts, confirming the superior accuracy of the PID compared to the rule-based controller, Table 4. Although the disturbance scenario represented in this work has been an extreme case with repeating saturation of the BP waveform, more clinically realistic scenarios can be designed and implemented to test the control algorithms under normal as well as representative worst-case conditions. BP artifacts represent just one type of disturbance that could be included in simulations using the HIL test bed. Disturbances could also be added to the fluid infusion (such as blockage of the fluid line) or as intra-patient variability by adding time-variance to certain physiologic parameters to mimic changes in an individual’s physiology. Assessing the performance of physiologic closed-loop control algorithms during such disturbances is an important step in demonstrating their safety during expected clinical scenarios. By using computational models, we can simulate different scenarios relatively easily, and by incorporating the physical devices in the testing, such as in our HIL test bed, we can examine if the system will respond safely.

A significant factor of any testing result that uses computational models is the credibility of the model for its proposed purpose in testing [10]. In the current study, we used a previously-reported model of hemodynamic response during hemorrhage and fluid infusion [5]. We selected this model because it allowed us to implement the HIL test bed with a set of digital twins from a pre-clinical animal study. It should be noted that the data used to develop and parameterize the model was the same as the scenarios implemented in this study. While this allowed us to have some confidence in the model validity for that purpose, the validity of the model for different simulations may be less clear. In addition, the current model requires heart rate as an input. The heart rate values were assumed to be the same as those obtained from the animal study for the HIL evaluation as well as the first 30 minutes of the controller assessment (when controllers are off) and were considered constant from t=30 min to t=90 min (end of the study). While physiologically conscious sheep may have very different responses to hemorrhage that vary over time [15], we had to make some assumptions about the heart rate response in the current study for the model to function.

In the current study we did not incorporate an actual BP transducer and patient monitor, but rather incorporated the patient monitor into part of our simulation system. However, we did generate an analog voltage signal of the arterial BP waveform and received that back through our implementation of a patient monitor. In future studies, a pressure pulse generator can be incorporated to generate a physical pressure BP signal, to which transducer and patient monitor can be connected. One of the advantages of a HIL system approach is that the components can be modular, so that we can substitute computational models and physical devices as necessary depending on the testing objectives.

While the HIL testing approach can enable accelerated evaluation of control algorithms, system interactions, and disturbance scenarios with potentially lower costs compared to animal and clinical studies, it has an inherent limitation of not including the real physiology. The specific model we used in this study does not attempt to model, for example, changes in individual cardiac properties or interactions between physiologic systems that may affect the response to changes in blood volume in clinical scenarios. This limits the types of questions that the HIL system incorporating the current model will be suitable to address. As a result, it is not intended to replace other types of testing, but to serve a complementary role in the comprehensive evaluation of physiologic closed-loop control systems. For example, HIL testing could be used to verify the functionality of fallback modes in the system design so that patients are not exposed to unsafe conditions during clinical testing. To expand the types of questions that can be answered with the HIL systems incorporating physiologic models, there is a need to i) incorporate more complex physiologic models into the system, such as [16], and ii) establish the credibility of such models for the questions they will be used to address [17].

VI. Conclusion

Physiologic closed-loop control systems are complex cyber-physical systems that involve interactions between patient monitors, therapeutic devices, complex patient physiology, and clinical users. In each of these, there are sources of variability and disturbances that can challenge the design and evaluation of physiologic closed-loop controllers. A variety of types of test methods are available for physiologic closed-loop control systems that can be leveraged to demonstrate the performance of these systems depending on the testing needs. Here, we have designed and demonstrated the use of a HIL test bed for automated fluid resuscitation systems that enables incorporation of computational models of physiology with physical devices. The main advantage of this type of testing is to enable realistic evaluation of control algorithms and system interactions with lower costs, compared to the existing methods. Our HIL test bed was designed to be modular so that various pieces can be substituted, as needed. For instance, other complex models that incorporate different variations of human physiology can be incorporated, as a future extension of the use space of the test bed. The HIL testing approach serves a complementary role alongside purely in silico, pre-clinical animal, and clinical studies in the evaluation of physiologic closed-loop control systems.