Multiple Predictively Equivalent Risk Models for Handling Missing Data at Time of Prediction: with an Application in Severe Hypoglycemia Risk Prediction for Type 2 Diabetes

Abstract

The presence of missing data at the time of prediction limits the application of risk models in clinical and research settings. Common ways of handling missing data at the time of prediction include measuring the missing value and employing statistical methods. Measuring missing value incurs additional cost, whereas previously reported statistical methods results in reduced performance compared to when all variables are measured. To tackle these challenges, we introduce a new strategy, the MMTOP algorithm (Multiple models for Missing values at Time Of Prediction), which does not require measuring additional data elements or data imputation. Specifically, at model construction time, the MMTOP constructs multiple predictively equivalent risk models utilizing different risk factor sets. The collection of models are stored and to be queried at prediction time. To predict an individual’s risk in the presence of incomplete data, the MMTOP selects the risk model based on measurement availability for that individual from the collection of predictively equivalent models and makes the risk prediction with the selected model. We illustrate the MMTOP with severe hypoglycemia (SH) risk prediction based on data from the Action to Control Cardiovascular Risk in Diabetes (ACCORD) study. We identified 77 predictively equivalent models for SH with cross-validated c-index of 0.77±0.03. These models are based on 77 distinct risk factor sets containing 12-17 risk factors. In terms of handling missing data at the time of prediction, the MMTOP outperforms all four tested competitor methods and maintains consistent performance as the number of missing variables increase.

Graphical Abstract:

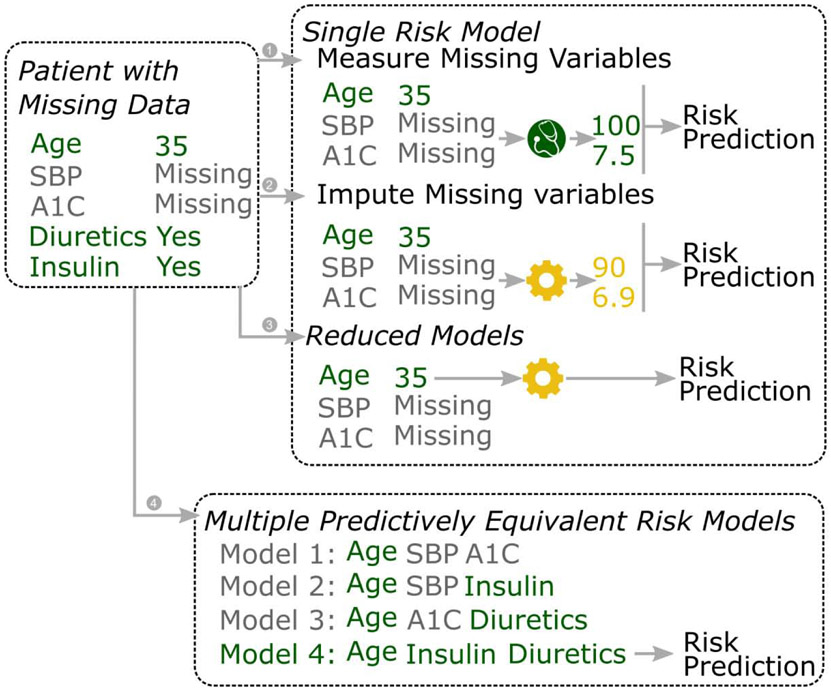
Consider a scenario where we want to predict SH risk for a patient with SBP and A1C missing. When we only have one (hypothetical) risk model based on age, SBP and A1C, we could handle the missing SBP and AIC by (1) measuring the missing variables, or (2) imputing the missing variables. (3) When we employ the reduced model technique, a reduced model (only containing age as a predictor) of the original model with be used. When we have multiple predictively equivalent risk models available (e.g. model 1-4), we could handle the missing data by (4) find the risk model that matches the data availability of the patient.

1. Introduction

In recent years, many risk prediction models has been developed for various diseases and disorders. High quality risk models hold great promise in improving quality of care and clinical research. In the clinical setting, deploying high quality risk models at the point of care as decision support tools could enhance the effectiveness and efficiency of care. In research based on electronic health record (EHR) data, these risk prediction models could be useful for risk adjustment and stratification. Many factors influence the effectiveness of the risk models in the situations described above (1). One of them is the missing data problem. Simply put, if a patient has a missing variable in the risk model, the outcome risk cannot be computed without addressing the missing data first. Missing data is omnipresent in the clinical setting and in the EHR, due to issues such as limited data sharing among different health services, under-documentation, and insufficient data extraction from unstructured data fields (e.g. clinical notes) (2-5). A survey of common risk factors for severe hypoglycemia (SH, the outcome of interest for our demonstration study described in section 4) in the Fairview EHR reveals large proportions (13% to 75% depending on the measurement) of missing data (supplemental table 1).

Several strategies exist for handling missing data at the time of prediction. One obvious strategy is to collect the missing variables. This can certainly be done if the risk prediction is needed during a clinical encounter; however, logistics, costs and time may present significant barriers. Moreover, in the case of retrospective analysis of the EHR data, measuring the missing data is impossible.

Another strategy for handling missing data is to apply statistical methods. Typically, missing data at time of prediction is handled by imputation methods (3,5,6), where missing data are “filled in” with different statistical techniques. The performance of imputation methods, however, depends on whether the assumptions (e.g., most methods assume data are missing at random) of these methods are satisfied, which could be difficult to determine in practice (3,6,7). Also, some imputation methods, such as the multiple imputation by chained equations (MICE), is computationally expensive to apply at the time of prediction. More recently, attention is called to the often overlooked reduced models method (8,9). The reduced models methods uses a collection of reduced models to handle missing data at the time of prediction. Specifically, an original model is first derived, this is model contains the full set of predictors and is used when there is no missing data. To make predictions in the presence of missing data, the reduced models method construct a reduced model with only the available predictors in the original model. The reduced models method has demonstrated superior performance compared to imputation in a benchmark study over many datasets (9). It is worth noting that, many missing value methods only handles missing values at the time of model construction, i.e. missingness in training data, such as the full information maximum likelihood and expectation maximization (7,10). These methods do not apply to missing variables at the time of prediction.

In the present study, we introduce a new strategy for handling missing data at the time of prediction. Our method, the MMTOP (Multiple models for Missing value at the Time Of Prediction) leverages multiple predictively equivalent risk models for handling missing data at the time of risk prediction. Multiple predictively equivalent models are defined as a set of risk models for the outcome based on distinct set of risk factors with statistically indistinguishable predictive performances. Our strategy is depicted in Figure 1, part (3): We first construct multiple predictively equivalent risk models utilizing different risk factor sets. To predict a patient’s risk for SH in the presence of incomplete data, we select the risk model based on measurement availability for that patient from our collection of predictively equivalent models and make the risk prediction with the selected model. This strategy does not require measuring additional data elements or data imputation, if the patient's available data can be matched with a predictively equivalent risk model.

Figure 1.

Handling missing data at the time of prediction with different methods.

Consider a scenario where we want to predict SH risk for a patient with SBP and A1C missing. When we only have one (hypothetical) risk model based on age, SBP and A1C, we could handle the missing SBP and AIC by (1) measuring the missing variables, or (2) imputing the missing variables. (3) When we employ the reduced model technique, a reduced model (only containing age as a predictor) of the original model with be used. When we have multiple predictively equivalent risk models available (e.g. model 1-4), we could handle the missing data by (4) find the risk model that matches the data availability of the patient.

Our strategy relies on the presence of multiple predictively equivalent models for the outcome of interest and the ability to construct them. The presence of multiple predictively equivalent models has long been recognized in machine learning. It was first coined as the “Rashomon Effect” by Leo Breiman (11) and later mathematically formalized as target information equivalence (12). Intuitively, multiple predictively equivalent models stem from the presence of overlapping or redundant information in candidate predictors regarding the outcome of interest. In biomedicine, overlapping or redundant information often manifests as co-occurring symptoms in multiple organs and systems, concurrent abnormal lab values from different lab tests, and simultaneously disturbed molecular pathways (13-16). Because of the redundancy, one could obtain multiple models with distinct risk factor sets that predict patient risk equally well. Several algorithms exist for deriving multiple Markov boundaries, including the TIE*(17), the SES(18), and the MB-DEA(19). The TIE* algorithm has mathematically proven theoretical properties and has been benchmarked on various datasets intensively (17). Moreover, the application of the TIE* algorithm to various datasets in the general domain as well as biomedicine (11,17,20,21) has resulted in collections of highly accurate and predictively equivalent risk models. The TIE* algorithm is also flexible and can be adapted to work with various distribution families. Given the demonstrated success of TIE*, we chose to use TIE* to derive multiple predictively equivalent models.

In the following sections, we first introduce the necessary statistical concepts and the theoretical underpinning of multiple predictively equivalent models (section 2). We than describe the MMTOP algorithm for handling missing data at the time of prediction (section 3). Next, in section 4, we demonstrate the application of the MMTOP algorithm on the ACCORD dataset for severe hypoglycemia risk prediction. We compared the performance of the MMTOP algorithm to four competitor methods. Finally in section 5, we discuss practical considerations when applying MMTOP and future directions.

This study contributes to the field of biomedical informatics by introducing a new strategy for handling missing data at the time of prediction. We demonstrate this strategy by applying the MMTOP algorithm in the ACCORD dataset for the risk prediction of SH. In our empirical evaluation, the MMTOP outperforms all four tested competitor methods.

2. Notations and Definitions

In this section, we provide the definition of essential concepts and analytical tools used in subsequent sections of the paper. All the definitions and theoretical results have been previously reported elsewhere, we include them in this section so the paper is relatively self-contained. We choose to include the minimal set of theoretical tools for brevity, and encourage the interested readers to follow the references for more details.

Unless specifically mentioned, we use uppercase letters to denote a variable (e.g. X,Y), bold uppercase letters to denote a variables set (e.g. Z), lowercase letters to denote instantiations or values of the corresponding uppercase variables (e.g. x is a instantiation of X).

For all the discussion below, we use the following common notations. V = {V₁,V₂,…,V_p} denotes all measured variables. T denotes the target of interest. p(V,T) denotes the joint distribution over of all variables in V ∪ T.

2.1. Optimal Variable Set and Markov Boundary Theory

Since we are concerned about clinical grade risk models, it would be ideal to be able to construct models with optimal performance. Therefore, we first introduce the Markov boundary theory, which formalizes the statistical relationship between the optimal variable (risk factor) set, other measured variables, and the target of interest.

Definition: optimal variable set (17,22). Given a data set D sampled form p(V,T) for variables V, a learning algorithm $\mathbb{L}$, and a performance metric $\mathbb{M}$, variable set V_opt is an optimal variable set of T if applying $\mathbb{L}$ on V_opt maximizes the performance metric $\mathbb{M}$ for predicting T.

To put it plainly, the optimal variable set V_opt for predicting T is a subset of variables that produces a model that maximizes the predictive performance T. This definition is intuitive but not very useful, since it does not provide a way to identify V_opt. We next introduce the Markov Blanket theory and related concepts, since it describes the statistical characteristics of the optimal variable set and provides the theoretical foundation for deriving the optimal variable set.

To define Markov blanket and Markov boundary, we first define conditional independence (23,24).

Definition: Conditional Independence. Let V be a set of variables and p(V) be the joint distribution over V, ∀ X ⊂ V, Y ⊂ V, Z ⊂ V, X and Y are conditionally independent given Z, if p(X ∣ Y,Z) = p(X∣Z), where p(Z) > 0.

In other words, variables in Y do not provide additional information regarding X once Z is available. And therefore including variables in Y in a model for predicting variables in X is redundant, when Z is part of the model. We use the symbol “ ⊥ ” to represent independence and symbol “∣” to represent conditioning. The statement “X and Y are conditionally independent given Z” is expressed as X ⊥ Y∣ Z.

Definition: Markov blanket (23,24). A Markov blanket X of the response variable T in the joint probability distribution p(V,T) is a set of variables conditioned on which all other variables are independent of T, that is, ∀ Y ∈ V − {X,T}, T ⊥ Y∣X.

Definition: Markov boundary (23,24). If no proper subset of Markov blanket X of T satisfies the definition of Markov blanket of T, then X is a Markov boundary (MB) of T.

The correspondence between Markov blanket and optimal feature set of T was established in the theorem below.

Theorem 1 (17,25): If $\mathbb{M}$ is a performance metric that is maximized only when p(T∣V −{T}) is estimated accurately, and $\mathbb{L}$ is a learning algorithm that can approximate any conditional probability distribution, then variable set M is a Markov blanket of T if and only if it is an optimal feature set of T.

Similarly, under the condition of the above theorem, a Markov boundary of T is a minimal optimal feature set of T.

2.2. Target Information Equivalence and Multiple Markov Boundaries

If there is only one unique Markov boundary of T, there is only one irreducible variable set that result in optimal performance for predicting T. Given Theorem 1, any other variable set that do not include all variables of the Markov boundary will result in suboptimal predictive performance. In this case, our strategy for handling missing data with predictively equivalent models would not work, since there is no predictively equivalent optimal models with an alternative risk factor set. In other words, our proposed method for using predictive equivalent models to handle missing variable depends on having multiple Markov Boundaries.

The uniqueness of Markov boundary is guaranteed under the faithfulness condition, more specifically when the intersection property (23) is satisfied (17). Under faithfulness, the unique Markov boundary of T have structure property with respect to the data generation process (a faithful Bayesian network). It correspond to the parents, children and parents of the children of T (25). When the intersection property is violated, there can exist multiple Markov boundaries for the target T. The multiple Markov boundaries of T are Target information equivalent (12,17). One of the many Markov boundaries of T would correspond to the parents, children and parents of the children of T (17,26).

Definition: Target information equivalence. Two subsets of variables X ⊂ V and Y ⊂ V contain equivalent information about a variable T iff the following conditions hold: T ⊥ X, T ⊥ Y, T ⊥ X∣Y, T ⊥ Y∣X.

Multiple Markov boundaries is a specific form of target information equivalence, where there exist multiple distinct and irreducible variable sets that produces predictively optimal models for target T.

3. The MMTOP Algorithm

In this section, we present the MMTOP algorithm for handling missing data at the time of prediction. MMTOP consists of two parts: the model construction procedures and the prediction time procedures. The model construction procedures produce predictively equivalent models. At prediction time, given the missing data pattern in the observation (e.g. a patient) to be predicted, the prediction time procedures select the appropriate models and make a prediction.

3.1. Model Construction Procedures

The first procedure in the model construction procedures is TIE*: TIE* derives all Markov boundaries of a target T. TIE* (previously described in detail in (17)) is a generative algorithm, which describes a family of algorithms that have the same underlying algorithmic principle. Here, we describes the instantiation of TIE* that is used in our demonstration study in section 4. For the generative TIE*, other potential instantiations, computational complexity, and proof of correctness, see (17). The generative nature of TIE* makes it flexible and able to handle different distributions (e.g. particular outcome distribution and/or time dependent relationship among variables).

A high level summary of our instantiation of the TIE* is the following: (i) the entire data are partitioned into two non-overlapping subsets, one for the identification of risk factor sets that are candidate Markov boundaries (training set), the other for determining target information equivalence (validation set). This separation obtains unbiased performance estimation for multiple Markov boundary induction. (ii) In the training set, we first learn the 1^st Markov boundary of T using the generalized local learning algorithm, GLL (27,28) (line 2). (iii) To construct other Markov boundaries, we removed one or more risk factors from the already derived Markov boundaries from the data, and applied GLL to identify risk factors that could potentially substitute for the removed risk factors, resulting a new risk factor set (line 5,6). (iv) The new risk factor set is considered predictively equivalent if its predictive performance is comparable to that of the 1^st Markov boundary risk factor set in the validation set (line 7-9). Steps (iii) and (iv) are repeated until all Markov boundaries have been identified (line 4-11).

The second model construction procedure is GenerateEquivalentModels, this simple procedure constructs models for target T based on the multiple Markov boundaries identified by TIE*, a dataset D, and a learning algorithm $\mathcal{L}$. The choice of the learning algorithm is mainly influenced by the distribution of target T. For our demonstration study in section 4, since our target of interest is time-to-event, we choose the Cox proportional hazard (coxph) (29,30) as our learning algorithm. In general, any learning algorithm that is compatible with the distribution of the target could be used here. If several possible learning algorithms are available, model selection can be conducted via standard protocol such as nested cross validation to optimize predictive performance (not shown in pseudo code below).

Procedure TIE*(D_t,D_v,T)

/* generates multiple Markov boundaries */

Inputs:

• Dataset D_t sampled from p(V,T), training set for identifying candidate Markov Boundary sets.

• Dataset D_v sampled from p(V,T), validation set for evaluating target information equivalence.

Output: Set MMB, containing all Markov boundaries of T

1. MMB = {}

2. Use GLL to learn a Markov boundary MB of T from the training set D_t

3. MMB = MMB ∪ {MB}

4. Repeat

5. Generate a dataset $D_t^e=D_t(\mathit{V}\setminus \mathit{G})$ by removing from the full set of variables V the smallest subset G ⊂ ∪MMB, such that:

   1. G was not considered in the previous iterations of this step, and
   2. G does not include any subset of variables that was found not to be a Markov boundary of T (per step 9)

6. Use GLL to learn a Markov boundary MB_new of T on $D_t^e$

7. On validation set D_v, compute predictive performance of model based on MB_new for T

8. On validation set D_v, compute predictive performance of model based on MB for T

9. If the performance based on MB_new is not statistically worse compared to that of MB

10. MMB = MMB ∪ {MB_new}

11. Until all dataset D^e generated in step 5 are considered.

Procedure GenerateEquivalentModels(D,MMB,$\mathcal{L}$)

/* Generates multiple predictively equivalent models */

Inputs:

• Dataset D sampled from p(V,T)

• Set MMB containing multiple Markov boundaries derived by procedure TIE*

• Learning algorithm $\mathcal{L}$ to learn function T = m(X), X ⊂ V

Output: Set PEM, contains predictively equivalent models based on MMB for T

1. PEM = {}

2. for MB ∈ MMB

3. Use $\mathcal{L}$ to learn model m based on variables in MB from D for T

4. PEM = PEM ∪ m

3.2. Prediction Time Procedures

To predict an observation with missing values given a collections of predictively equivalent models (procedure PredictWithMissing), we need to specify what subset of models among all predictively equivalent models are applicable (procedure ModelSelect) and how to arrive at a single prediction if multiple models are applicable (procedure IntegratePredictions). There are many ways to achieve the two tasks above. We show below our implementation the demonstration study in section 4.

Briefly, to select applicable models (procedure ModelSelect), we simply take any model where all predictors in the model are measured. To obtain a single prediction from the collection of models selected by ModelSelect (procedure IntegratePredictions), we choose one model at random and make prediction with that model. Alternative instantiations of these procedures are discussed in section 5.

Procedure PredictWithMissing(d, PEM)

/* Handles missing data at the time of prediction leveraging predictively equivalent models */

Inputs:

• Vector d = {v₁,v₂,…,v_i,…} representing available variables for the observation (e.g. a patient) for predicting T

• Set PEM, containing all predictively equivalent models of T, derived by Procedure GenerateEquivalentModels.

Output: Prediction for T given available data d = {v₁,v₂,…,v_i,…}

1. M = ModelSelect(PEM, d)

2. prediction = IntegratePredictions(M,d)

Procedure ModelSelect(d, PEM)

/*selects appropriate models for risk prediction according to availability of data*/

Inputs:

• Vector d = {v₁,v₂,…,v_i,…} representing available variables for the observation (e.g. a patient) for predicting T

• Set PEM, containing all predictively equivalent models of T, derived by Procedure GenerateEquivalentModels.

Output: M ⊆ PEM can be applied to d = {v₁,v₂,…,v_i,…}

1. M = {}

2. for m in PEM

3. if predictors in m are all present in d

4. M = M ∪ m

Procedure IntegratePredictions(M,d)

/*Produce a single prediction for T given d and multiple models in M */

Inputs:

• M, a collection of models for predicting T given sets of elements in d

• Vector d = {v₁,v₂,…,v_i,…} representing available variables for the observation (e.g. a patient) for predicting T

Output: Prediction for T given d

1. Randomly select model m ∈ M

2. prediction = m(d)

4. Demonstration of MMTOP

In this section, we demonstrate the application of MMTOP using data from the ACCORD dataset. We first derive multiple predictively equivalent models for severe hypoglycemia risk in the training set. We than systematically introduced missingness in the testing set by dropping out variables at varying rates to simulate missing data at time of prediction. We compared the performance of MMTOP vs. four competitor methods for handling missing data at the time of prediction.

4.1. Type II Diabetes and Severe Hypoglycemia

More than 20 million Americans have type 2 diabetes (T2DM) (31), an acknowledged public health burden. Although intensive glucose control to lower HbA1c to near-normal levels has established benefits in patients with T2DM, including reduction in microvascular disease (32-34) and possibly macrovascular events (32,35), fear of hypoglycemia commonly limits intensification of glycemic control (36). Many clinical risk factors for hypoglycemia have been identified. These include older age, diabetes duration, burden of co-morbidities, glycemic treatment intensification, current insulin treatment, duration of insulin treatment and use of other T2DM medications (37-42). Risk models predicting short-term (2-12 months) (43-48) and long-term (5 years) (49) hypoglycemia have been developed. However, the application of these risk models to the clinical setting is limited.

4.2. Data

4.2.1. The ACCORD Dataset

The Action to Control Cardiovascular Risk in Diabetes (ACCORD) study was a randomized, multicenter, double 2x2 factorial design study in patients with pre-existing T2DM (50). The ACCORD study examined the effects of glycemic control (Intensive vs. Standard), blood pressure control and lipid control on cardiovascular (CV) morbidity and mortality (51).

All study participants (n=10,251) had a clinical diagnosis of T2DM, defined using the 1997 ADA criteria, and were on stable diabetes treatment program for at least 3 months. In addition, all study participants either had a history of diagnosed CV disease or at least 2 CV risk factors in addition to diabetes. Exclusion criteria included the following: self-reported or previously diagnosed type 1 diabetes, secondary causes of diabetes, or gestational diabetes. All participants were randomized to standard glycemic treatment [HbA1c target 7.0-7.9%(53-63 mmol/mol)] or intensive glycemic treatment [HbA1c target < 6.0%(42 mmol/mol)]. Due to higher mortality in the intensive treatment group, participants receiving intensive treatment were transitioned to standard treatment partway through the study (median follow up: 3.7 years) (52).

The ACCORD study has rigorously documented risk factors, defined follow-up, and adjudicated SH outcomes. The wealth of information collected prospectively within the ACCORD study provides a rich dataset, enabling the identification of multiple predictively equivalent models.

Deidentified data from the ACCORD study were obtained from BioLINCC (https://biolincc.nhlbi.nih.gov/) in June, 2017.

4.2.2. Outcome

The outcome of this analysis was the time to the first severe hypoglycemia (SH) event. SH was defined as an episode of hypoglycemia requiring medical assistance and either blood glucose less than 50 mg/dL or requiring the administration of glucose. Hypoglycemia events were assessed by clinic staff at each visit based on self-report by the participant and then adjudicated by the ACCORD study.

4.2.3. Candidate Risk Factors

We extracted 91 variables as candidate risk factors for SH analysis within ACCORD (Table 1 and Supplemental Table 2). Table 1 contains all variables that are significantly associated with the outcome (48 out of 91), whereas Supplemental Table 2 contains all 91 variables. These risk factors span the following sources: demographics, lab values, medications, physical exam findings and mental health evaluations. Some candidate risk factors were only collected at baseline, others were collected at baseline and over varying intervals during ACCORD follow-up. Frequency of these measurements are reported in Table 1 and Supplemental Table 2. Candidate risk factors measured at multiple time points, including the discontinuation of the intensive hypoglycemic treatment, were treated as time-varying covariates in our models.

Table 1:

Candidate risk factors and their univariate relationship with the outcome variable time to SH. HR=hazard ratio; CI=confident interval; Only risk factors that are univariately significantly associated with time to SH are shown (48 out of 91). See supplemental table 1 for all candidate risk factors.

Variable Name	Description	measurement time	Univariate Relationship with SH
			HR	CI (95%)		P- Value
Glycemia	Glycemia Trial Status: 1=active, 0=inactive	every 2 weeks in the first three month; monthly afterwards	2.83	1.51	5.29	0.001
Intensive Tx	Intensive Hypoglycemia treatment	baseline	2.52	2.15	2.96	<0.001
Black	Black Race	baseline	1.81	1.54	2.13	<0.001
White	White Race	baseline	0.79	0.68	0.92	0.002
Age	Age (yrs) at Randomization	baseline	1.05	1.04	1.06	<0.001
Education	Highest level of education	baseline	0.79	0.74	0.85	<0.001
DBP	Diastolic Blood Pressure (mmHg)	Monthly in the 1st four month; every two month afterwards	0.96	0.96	0.97	<0.001
Serum Creatinine	Serum creatinine (mg/dL)	quarterly	1.93	1.76	2.12	<0.001
eGFR	eGFR from 4 variable MDRD equation (ml/min/1.73 m2)	quarterly	0.98	0.98	0.98	<0.001
Urine Protein	Urinary albumin to creatinine ratio (mg/g)	every two years	1	1	1	<0.001
CVD History	CVD History at Baseline: 0=No, 1=Yes	baseline	1.31	1.13	1.52	<0.001
Ulcer	foot ulcer requiring antibiotics	baseline	0.63	0.47	0.84	0.002
UACR	protein in urine	baseline	0.81	0.68	0.96	0.016
Years Diab	year of diabetes diagnosis	baseline	1.06	1.05	1.06	<0.001
# Recent Hypoglycemia	# of hypoglycemic episodes (SMBG <70 mg/dL or <3.9mmol/L) in last 7d	monthly	1.34	1.29	1.38	<0.001
Visual Acuity (R)	visual acuity score, right eye	baseline	0.99	0.99	0.99	<0.001
Visual Acuity (L)	visual acuity score, left eye	baseline	0.99	0.98	0.99	<0.001
Retinopathy	participant had retinopathy	annually	0.48	0.39	0.59	<0.001
Vision Loss	vision loss	annually	0.62	0.5	0.76	<0.001
Ankle Reflexes	ankle reflexes	annually	1.31	1.12	1.54	0.001
# hypoglycemia hospitalization	hypoglycemia requiring hospitalization, emergency care without hospital admission, or medical assistance without emergency care or hospitalization, number of times since last call	monthly	15.4	10.9	22	<0.001
HUI3	Health Utilities Index Mark3 (HUI3);	baseline; 12m; 36m; 48m and Exit visit	0.48	0.37	0.62	<0.001
HUI2	Health Utilities Index Mark2 (HUI2);	baseline; 12m; 36m; 48m and Exit visit	0.4	0.27	0.6	<0.001
Loop	Loop diuretics	annually	2.12	1.78	2.53	<0.001
Thiazide	Thiazide diuretics	annually	1.25	1.08	1.45	0.003
Ksparing	Ksparing diuretics	annually	1.54	1.1	2.15	0.012
Potassium	Potassium supplements	annually	1.19	1.03	1.38	0.022
Ace Inibitos	Ace inhibitors	annually	1.18	1.02	1.37	0.025
DHP CCD	Dihydropyridine calcium channel blockers	annually	1.34	1.08	1.66	0.008
Alpha-Blocker	Peripheral alpha-blockers	annually	1.45	1.08	1.96	0.014
Beta-Blocker	Beta-blockers	annually	1.48	1.27	1.71	<0.001
Antiarrhythmic	Anti-arrhythmics	annually	1.96	1.05	3.65	0.035
Nitrates	Nitrates	annually	1.4	1.05	1.86	0.02
Other CV Meds	Other cardiovascular drugs	annually	1.94	1.07	3.51	0.03
Sulfonylurea	Sulfonylureas	annually	0.6	0.52	0.7	<0.001
Biguanide	Biguanides	annually	0.58	0.5	0.67	<0.001
Meglitinide	Meglitinides	annually	1.36	1.11	1.67	0.003
NPH/L Insulins	NPH or L Insulins	annually	3.49	2.94	4.14	<0.001
TZD	Thiazolidinediones	annually	1.43	1.23	1.66	<0.001
Reg Insulin	Regular Insulins	annually	2.52	1.95	3.26	<0.001
Lisprot/Aspart Insulin	Lispro or Aspart Insulins	annually	2.43	2.08	2.84	<0.001
Other Bolus Insulin	Other Bolus Insulins	annually	0.23	0.07	0.77	0.018
Premixed Insulins	Premixed Insulins	annually	1.56	1.31	1.86	<0.001
Anti Coag	Oral anitcoagulants (warfarin, coumadin, anisindione)	annually	1.44	1.04	2	0.029
Platelet Agi	Inhibitors of platelet aggregations (except aspirin)	annually	1.35	1.03	1.76	0.029
Thyroid	Thyroid agents	annually	1.35	1.07	1.72	0.013
Fluid Retention	Diuretic for fluid retention	annually	2.58	1.22	5.44	0.013
Other Meds	Any other prescribed medication	annually	1.4	1.21	1.62	<0.001

4.3. Analytical Procedure

4.3.1. Application of MMTOP

MMTOP was instantiated as in section 3. Since our target of interest time-to-SH, for several procedures, we use their variants that are designed for time-to-SH. Specifically, in TIE* line 2 and 6, we used a version of GLL that accommodates the time-to-event outcome, a similar implementation was reported here (53). In TIE* line 7 and 8, we used the coxph model to compute predictive performance. In GenerateEuivalentModels, we used coxph as the learning algorithm for deriving multiple predictively equivalent models. Also, in TIE* line 9, we operationally define “not statistically worse” as achieving a c-index greater than the c-index (see 4.3.2) of the model built from the 1^st Markov boundary minus 1 standard deviation of the c-index. The standard deviation of the c-index is estimated from all the cross validation runs.

4.3.2. Performance Estimation for Predictively Equivalent Models

We first evaluated the model construction procedures of MMTOP, in other words, we evaluated the performance of predictively equivalent models without the presence of missing data. We performed 10-fold cross-validation, in which participants were randomly split into ten outcome stratified non-overlapping subsets, each containing about 10 percent of the participants. The TIE* was applied in nine of these ten data subsets (where eight subsets were used as training set and one subset was used as validation set) to identify predictively equivalent risk factor sets. Coxph models were built for each of the identified risk factor sets and tested in the remaining tenth subset (testing set) to serve as an independent performance estimation. This procedure was conducted iteratively, resulting in each of the ten data subsets being used once for testing of the models. We repeated the 10-fold cross validation procedure five times to account for splitting variance, resulting in 50 repetitions of model construction and performance estimation. This procedure, repeated balance nested cross validation, has been shown to produce robust and unbiased performance estimation for predictive models (54-56).

We used the concordance index (c-index) as the performance metric for the models (29). Concordance is defined as probability of agreement for any two randomly chosen observations, where agreement means that the observation with the shorter survival time also has the larger risk score. The c-index ranges from 0 to 1. A c-index of 1 indicate perfect agreement, a c-index of 0.5 indicate agreement of random chance.

4.3.3. Comparing the Performance of MMTOP with Competitor Methods

We then evaluated the prediction time procedures of MMTOP. We quantitatively compared MMTOP to three other widely adopted imputation methods as well as the reduced models method (9) for handling missing data at the time of prediction in the presence of missing data. The three imputation methods were median value imputation (6), Multivariate Imputation by Chained Equations (MICE)(57), and k nearest neighbor imputation (KNN, with k=5)(58).

We conducted this analysis using the ACCORD dataset and systematically introduced missingness by dropping out variables at varying rates. Specifically, we tested dropping out 1 through 5 randomly selected variables.

Risk models were derived from training data where values for all variables were available, and evaluated on the testing data where missingness was introduced. To make a prediction with MMTOP, we randomly selected an equivalent model where the missing variables were not risk factors. To make a prediction using imputation methods, we assumed that only the 1st risk model was available to us and applied the 1st risk model to the imputed test data to obtain risk predictions. To make a prediction using the reduced models method, we compared the available data element to the 1^st risk model, made a reduced model based on what is available in the 1^st risk model and applied the reduced model to obtain risk predictions. Note that as suggested in (9), an alternative would be to compute and store the reduced models for all possible patterns of missingness at model construction time and query the reduced models at prediction time.

The above analytical procedure was repeated 50 times to assess the variability in performance while randomly dropping different variables. We also embedded the procedure in five repeat ten-fold cross validation to ensure unbiased performance estimation. We used the paired t-test to compare the predictive performance between MMTOP and the competitor methods and applied Bonferroni correction to correct for multiple comparisons.

4.3.4. Analysis Software

We used the survival package in R for the coxph model (59,60). We used the mice package and the DMwR package for MICE and KNN imputation respectively. For reduced models method and MMTOP custom scripts were created in R (17). The Majority of the analysis was performed on the super computers provided by Minnesota Supercomputing Institute.

4.4. Results

4.4.1. Identification of Multiple Predictively Equivalent Risk Models

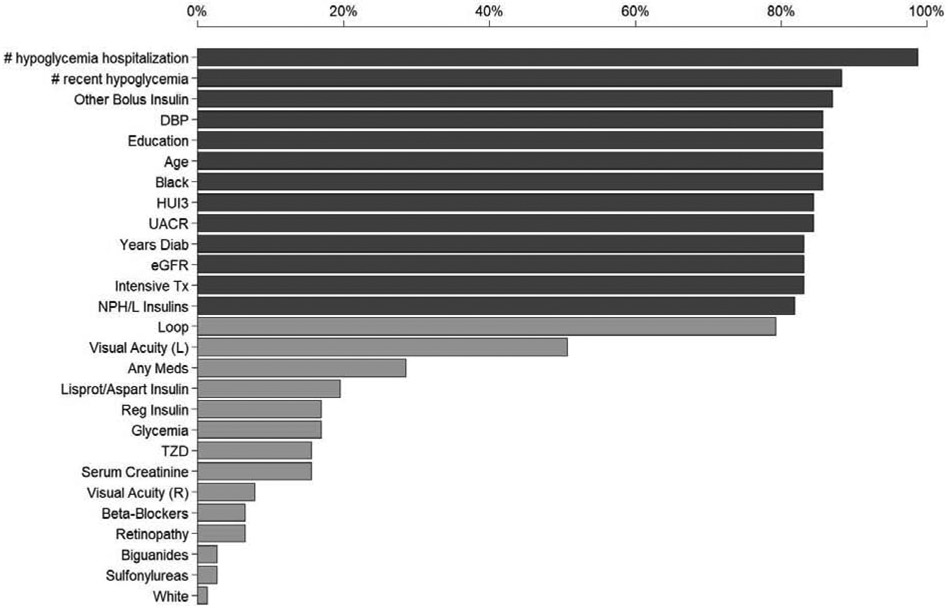
By applying TIE* on the full dataset, we identified 77 Markov boundary risk factors sets which result in predictively equivalent models. The cross-validated c-index of the predictively equivalent risk models are 0.77+/−0.03 (mean+/−std), estimated by 5 repeat 10 fold cross validation. The number of risk factors in each risk factor set ranged from 12 to 17 (median 14 variables). Out of the 91 candidate risk factors, 27 are present in at least one risk factor set. Table 2 shows the 77 predictively equivalent risk factor sets and corresponding risk models. Figure 2 shows the percentage of time that a given variable appears in all identified predictively equivalent risk factor sets.

Table 2.

Predictively equivalent risk models. Seventy-seven predictively equivalent risk models (columns) were discovered. The c-index of individual models and the coefficients of risk factors are shown. The blank cell indicate a variable is not part of the predictive equivalent feature set. See table 1 for description of variables.

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
c-idx	0.79	0.78	0.77	0.77	0.77	0.77	0.78	0.78	0.78	0.78	0.79	0.79	0.79	0.78	0.79	0.79	0.78	0.79	0.79	0.78
Glycemia		1.73									0.96	1.42	1.20	0.86	0.99	0.97	0.98	0.97	0.95	1.17
Intensive Tx	0.62	0.90	0.76	0.75	0.76		0.75	0.76	0.76	0.75	0.61	0.65	0.64		0.63	0.64	0.65	0.65	0.64	0.63
Black	0.70	0.68	0.66	0.54	0.60	0.68	0.64	0.63	0.69	0.63	0.71	0.60	0.67	0.73	0.70	0.69		0.74	0.70	0.69
White
Age	0.19	0.17	0.24	0.24	0.25	0.22	0.16		0.19	0.18	0.20	0.21	0.23	0.28	0.14		0.15	0.17	0.15	0.17
Education	−0.12	−0.14	−0.13	−0.13	−0.13	−0.14	−0.13	−0.13		−0.13	−0.14	−0.14	−0.14	−0.15	−0.14	−0.14	−0.18		−0.14	−0.15
DBP	−0.18	−0.20	−0.22	−0.22		−0.19	−0.20	−0.23	−0.28	−0.23	−0.26	−0.19		−0.17	−0.17	−0.20	−0.16	−0.19	−0.18	−0.18
Serum Creatinine				0.41								0.49
eGFR	−0.12	−0.13	−0.13		−0.13	−0.12	−0.13	−0.14	−0.12	−0.13	−0.12		−0.12	−0.11	−0.12	−0.12	−1.00	−0.11	−0.11	−0.12
UACR	0.25	0.24	0.26	0.24	0.23	0.27		0.24	0.26	0.25	0.26	0.24	0.24	0.28		0.24	0.25	0.26	0.25	0.25
Years Diab	0.27	0.27		0.25	0.28	0.28	0.25	0.26	0.23	0.25		0.23	0.27	0.21	0.24	0.24	0.24	0.23	0.23	0.24
# Recent Hypoglycemia	0.19										0.19	0.19	0.19	0.22	0.18	0.19	0.18	0.19	0.19	0.18
Visual Acuity (R)
Visual Acuity (L)	−0.57							−0.58	−0.53		−0.57	−0.55			−0.55	−0.60	−0.57	−0.58	−0.58
Retinopathy			−0.31								−0.27
# hypoglycemia hospitalization		2.25	2.37	2.34	2.28	2.44	2.29	2.33	2.29	2.32	2.26	2.24	2.24	2.32	2.24	2.26	2.32	2.21	2.24	2.18
HUI3	−0.36	−0.34	−0.37	−0.33	−0.33	−0.34	−0.31		−0.36		−0.44	−0.40	−0.39	−0.44	−0.38	−0.33	−0.31	−0.49		−0.39
Loop	0.25			0.26		0.28	0.24				0.27	0.30	0.24	0.34	0.28	0.25	0.24	0.25	0.27	0.25
Beta-Blocker													0.24
Sulfonylurea
Biguanide
NPH/L Insulins	0.88		0.93	0.93	0.94	0.93	0.98	0.90	0.93	0.92
TZD						0.49								0.45
Reg Insulin		0.89									0.95	0.84	0.82	0.82	0.83	0.80	0.81	0.88	0.82	0.76
Lisprot/Aspart Insulin		0.57	0.21			0.31					0.54	0.49	0.46	0.60	0.46	0.44	0.41	0.46	0.46	0.45
Other Bolus Insulin	−2.39	−2.52	−2.66	−2.69	−2.67	−2.62	−2.65	−2.66	−2.68	−2.67	−2.58	−2.63	−2.60	−2.56	−2.55	−2.59	−2.55	−2.62	−2.58
Other Meds		0.14			0.15			0.17		0.16						0.13	0.13		0.15
	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40
c-idx	0.78	0.78	0.78	0.79	0.78	0.79	0.78	0.78	0.79	0.79	0.78	0.78	0.78	0.79	0.78	0.79	0.78	0.78	0.79	0.78
Glycemia
Intensive Tx	0.55	0.55		0.55	0.55	0.56	0.58	0.55	0.56	0.55	0.55	0.59		0.58	0.59	0.60	0.60	0.60	0.59	0.58
Black	0.58	0.64	0.68	0.67	0.67	0.68		0.72	0.67	0.68	0.67	0.53	0.58	0.55	0.55	0.56		0.61	0.56	0.56
White
Age	0.26	0.30	0.22	0.19		0.20	0.20	0.21	0.20	0.28	0.20	0.31	0.27	0.22		0.24	0.22	0.24	0.23	0.24
Education	−0.13	−0.13	−0.13	−0.13	−0.13	−0.12	−0.17		−0.13	−0.13	−0.14	−0.13	−0.14	−0.14	−0.14	−0.14	−0.17		−0.14	−0.14
DBP	−0.21		−0.20	−0.19	−0.24	−0.27	−0.18	−0.27	−0.26	−0.24	−0.26		−0.18	−0.18	−0.23	−0.19	−0.17	−0.19	−0.19	−0.19
Serum Creatinine	0.42											0.44	0.39	0.55	0.42	0.43	0.45	0.40	0.40	0.47
eGFR		−0.13	−0.12	−0.13	−0.13	−0.13	−1.00	−0.12	−0.12	−0.12	−0.12
UACR	0.27	0.25	0.29		0.26	0.28	0.27	0.29	0.28	0.28	0.27	0.23	0.26		0.23	0.26	0.24	0.26	0.25	0.24
Years Diab												0.25	0.28	0.22	0.23	0.21	0.23	0.24	0.22	0.22
# Recent Hypoglycemia	0.20	0.20	0.23	0.19	0.19	0.19	0.19	0.19	0.19	0.19	0.19	0.20	0.22	0.19	0.19	0.19	0.18	0.19	0.19	0.18
Visual Acuity (R)										−0.39				−0.37		−0.40	−0.38		−0.48
Visual Acuity (L)	−0.63		−0.59	−0.56	−0.69	−0.63	−0.57	−0.66	−0.66		−0.62				−0.62			−0.59
Retinopathy		−0.36		−0.27			−0.28
# hypoglycemia hospitalization	2.32	2.31	2.37	2.30	2.34	2.29	2.41	2.29	2.30	2.32	2.21	2.32	2.46	2.30	2.36	2.34	2.39	2.29	2.34	2.56
HUI3	−0.41	−0.43	−0.41	−0.37	−0.37	−0.38	−0.36	−0.42		−0.39	−0.37	−0.38	−0.42	−0.38	−0.35	−0.38	−0.35	−0.40		−0.37
Loop	0.29	0.27	0.33	0.27	0.26			0.25	0.27	0.25	0.24	0.27	0.36	0.30	0.32		0.25	0.28	0.29	0.28
Beta-Blocker												0.20
Sulfonylurea
Biguanide							−0.18
NPH/L Insulins	0.94	0.92	0.97	0.90	0.89	0.93	0.91	0.92	0.92	0.92	0.86	0.85	0.92	0.85	0.82	0.87	0.85	0.85	0.85	0.80
TZD			0.41										0.42
Reg Insulin
Lisprot/Aspart Insulin
Other Bolus Insulin	−2.74	−2.75	−2.74	−2.71	−2.73	−2.73	−2.72	−2.76	−2.73	−2.75		−2.75	−2.73	−2.73	−2.75	−2.77	−2.75	−2.77	−2.76
Other Meds						0.14			0.15							0.13			0.15
	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60
c-idx	0.78	0.78	0.78	0.77	0.78	0.78	0.78	0.78	0.78	0.78	0.77	0.78	0.78	0.78	0.79	0.79	0.78	0.79	0.79	0.78
Glycemia
Intensive Tx		0.57	0.59	0.59	0.58	0.58	0.58								0.57	0.58	0.58	0.58	0.58	0.57
Black	0.64	0.63	0.61		0.68	0.62	0.62	0.67	0.67	0.67		0.72	0.66	0.67	0.66	0.66		0.80	0.65	0.65
White
Age	0.28	0.23		0.24	0.28	0.24	0.26	0.18		0.22	0.29	0.21	0.19	0.22		0.16	0.16	0.17	0.14	0.15
Education	−0.14	−0.14	−0.14	−0.17		−0.14	−0.13	−0.13	−0.14	−0.13	−0.18		−0.14	−0.14	−0.14	−0.13	−0.17		−0.14	−0.14
DBP								−0.17	−0.28	−0.17	−0.15	−0.18	−0.18	−0.18	−0.20	−0.18	−0.15	−0.17	−0.17	−0.17
Serum Creatinine
eGFR	−0.12	−0.13	−0.14	−0.12	−0.12	−0.12	−0.13	−0.12	−0.12	−0.12	−0.18	−0.11	−0.11	−0.12	−0.13	−0.13	−0.20	−0.12	−0.12	−0.12
UACR	0.26		0.22	0.25	0.25	0.25	0.24		0.26	0.28	0.27	0.28	0.28	0.27
Years Diab	0.22	0.25	0.26	0.26	0.24	0.25	0.24	0.19	0.20	0.20	0.27	0.18	0.19	0.19	0.22	0.21	0.23	0.28	0.21	0.28
# Recent Hypoglycemia	0.22	0.19	0.19	0.18	0.19	0.19	0.19	0.21	0.22	0.22	0.21	0.22	0.21	0.21	0.18	0.18	0.18	0.18	0.19	0.18
Visual Acuity (R)																	−0.38
Visual Acuity (L)			−0.55					−0.53	−0.57			−0.57	−0.55		−0.58	−0.54		−0.59	−0.57	−0.54
Retinopathy
# hypoglycemia hospitalization	2.39	2.25	2.30	2.37	2.28	2.27	2.23	2.34	2.46	2.48	2.48	2.36	2.37	2.12	2.29	2.25	2.38	2.25	2.25	2.00
HUI3	−0.40	−0.37	−0.29	−0.34	−0.41		−0.38	−0.38	−0.36	−0.43	−0.37	−0.42		−0.40	−0.34	−0.39	−0.33	−0.39		−0.34
Loop	0.37	0.29	0.25		0.26	0.27		0.33	0.32		0.37	0.38	0.33	0.32	0.27		0.25	0.26	0.27	0.25
Beta-Blocker	0.19						0.26			0.19
Sulfonylurea
Biguanide
NPH/L Insulins	0.90	0.84	0.80	0.86	0.84	0.84	0.79	0.90	0.88	0.91	0.98	0.91	0.90	0.85	0.87	0.85	0.83	0.83	0.83	0.78
TZD	0.45							0.49	0.48	0.49	0.42	0.43	0.42	0.44
Reg Insulin
Lisprot/Aspart Insulin
Other Bolus Insulin	−2.71	−2.72	−2.74	−2.72	−2.77	−2.74		−2.68	−2.80	−2.70	−2.70	−2.73	−2.77		−2.73	−2.70	−2.74	−2.73	−2.72
Other Meds			0.15	0.15		0.16							0.14						0.14
	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77
c-idx	0.78	0.79	0.79	0.78	0.78	0.78	0.78	0.78	0.79	0.78	0.79	0.78	0.79	0.79	0.79	0.78	0.78
Glycemia													1.14	0.92
Intensive Tx	0.59	0.59	0.58	0.58	0.58	0.59	0.58	0.58	0.59	0.59	0.57	0.58	0.70	0.61	0.62	0.59
Black		0.76	0.66	0.66					0.73	0.70	0.66	0.65	0.66	0.69	0.72	0.59	0.67
White					−0.41
Age					0.22	0.17	0.18	0.18	0.19	0.19	0.18	0.16	0.14	0.16	0.16	0.25	0.19
Education	−0.17		−0.14	−0.14		−0.17	−0.17	−0.17			−0.14	−0.14	−0.14	−0.14	−0.14	−0.13	−0.14
DBP	−0.19	−0.21	−0.28	−0.21	−0.17	−0.16	−0.16	−0.17	−0.19	−0.19	−0.18	−0.18	−0.17	−0.17	−0.18	−0.20	−0.18
Serum Creatinine
eGFR	−0.12	−0.12	−0.13	−0.12	−0.15	−0.99	−0.15	−0.18	−0.11	−0.12	−0.11	−0.11	−0.12	−0.12	−0.12		−0.11
UACR	0.26	0.26	0.25	0.24	0.27	0.27	0.26	0.26	0.28	0.28	0.26	0.26	0.25	0.26	0.26	0.29	0.26
Years Diab	0.23	0.22	0.23	0.22	0.27	0.22	0.23	0.21	0.25	0.23	0.22	0.26	0.27	0.26	0.23	0.22	0.18
# Recent Hypoglycemia	0.18	0.18	0.18	0.18	0.19	0.18	0.18	0.18	0.18	0.18	0.18	0.18	0.20	0.19	0.20	0.19	0.22
Visual Acuity (R)
Visual Acuity (L)	−0.63	−0.64		−0.58		−0.59		−0.58	−0.62	−0.60		−0.56
Retinopathy
# hypoglycemia hospitalization	2.41	2.31	2.34	2.38	2.35	2.38	2.39	2.17	2.28	2.13	2.36	2.89	2.20	2.21	2.24	2.32	2.42
HUI3	−0.30	−0.37	−0.36	−0.32	−0.37		−0.34	−0.34		−0.48			−0.35	−0.39	−0.38	−0.35	−0.36
Loop		0.24	0.26	0.24	0.24	0.24	0.24		0.25		0.27	0.24	0.32	0.29	0.27	0.33	0.26
Beta-Blocker
Sulfonylurea													−0.24	−0.23
Biguanide																−0.23
NPH/L Insulins	0.82	0.86	0.85	0.76	0.84	0.83	0.84	0.85	0.83	0.80	0.84	0.78				0.83	0.89
TZD
Reg Insulin													0.63		0.79
Lisprot/Aspart Insulin														0.34	0.48
Other Bolus Insulin	−2.80	−2.76	−2.75		−2.75	−2.71	−2.72		−2.76		−2.74		−2.59	−2.54	−2.62	−2.79	−2.74
Other Meds	0.15				0.14	0.15			0.15			0.14	0.13

Figure 2.

Frequency of a variable being present in a predictively equivalent risk factor set. See Table 1 for description of variables. Dark gray bar indicate a variable is selected in more than 80% of the predictively equivalent risk factor sets.

The following risk factors were consistently selected by TIE* into most predictively equivalent risk factor sets (appears in more than 80% of risk factor sets): 1) number of hypoglycemia episodes requiring hospitalization or emergency care or medical assistance in the previous visit period, 2) number of hypoglycemia episodes in the past 7 days, 3) other bolus insulin use, 4) diastolic blood pressure, 5) highest level of education 6) age, 7) black race, 8) Health Utilities Index Mark3, 9) urinary albumin to creatinine ratio, 10) duration of diabetes 11) renal function (Glomerular filtration rate: eGFR) 12) intensive hypoglycemia treatment, 13) NPH or L Insulin use.

Many of the risk factors underlying the multiple predictively equivalent models derived in the present study (such as previous hypoglycemia, intensive hypoglycemia treatment, black race, diastolic blood pressure, age, education, years of diabetes, eGFR, and insulin use) are in concordance with previously reported risk factors in SH literature (38) as well as previous work based on the ACCORD study(40).

Examination of the derived predictively equivalent models reveals information regarding information equivalence among sets of risk factors with respect to SH. For example, our model suggests that eGFR and retinopathy contain the same information content regarding SH as serum creatinine in conjunction with years of diabetes given a set of 15 other variables (See table 2, comparing risk factor set 11 with risk factor set 12). Another example (table 2, compares risk factor set 42 with risk factor set 46) is HUI and other medication contain the same information regarding SH as UACR in the presence of other 11 other risk factors. Understanding which risk factors contain overlapping information could provide mechanistic insights regarding the disease.

4.4.2. Comparing the Performance of MMTOP with Competitor Methods

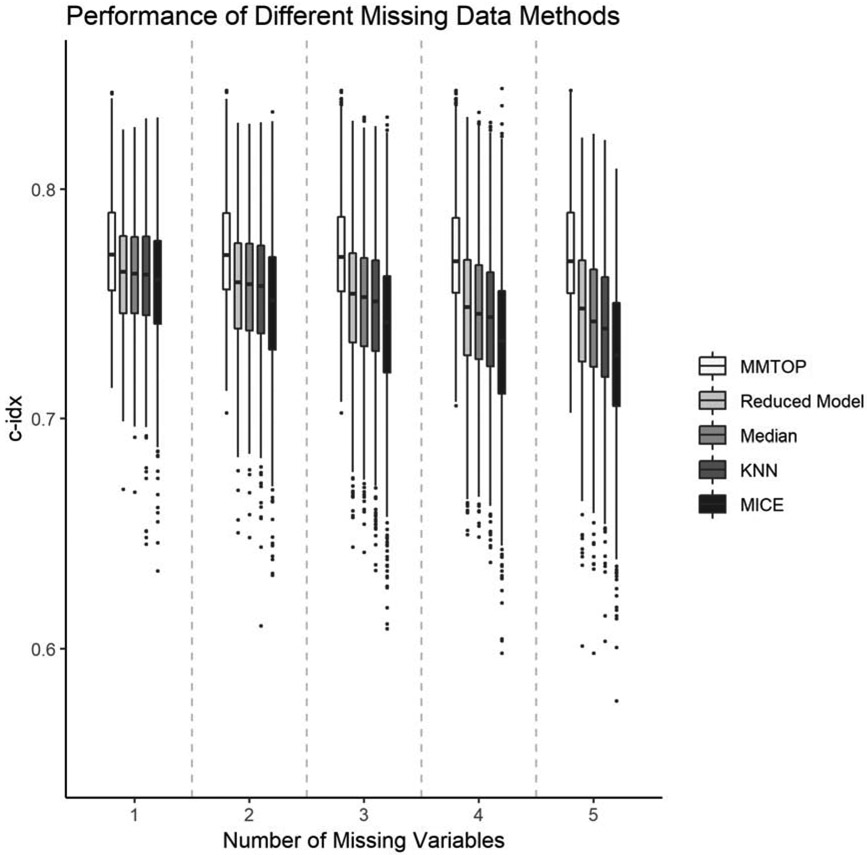
Figure 3 and supplemental table 3 illustrates the performance of MMTOP compared to four competitor methods for handling missing data at the time of prediction. Paired t-tests showed statistically significant superiority of the MMTOP vs the competitor methods for all examined rates of missingness (all p-values<0.001 after adjusting for multiple comparisons). As expected, the number of missing variables did not affect the performance of the MMTOP, since predictively equivalent models were used for all predictions. The c-index for MMTOP is 0.77+/−0.03 for all rates of missingness tested. As the number of missing variables increased, the performance of all competitor methods deteriorated. When only one variable is missing, the average c-index for all competitor methods was 0.76+/−0.03. When five variables are missing, the c-index for the reduced models method is 0.75+/−0.03, the c-index for KNN and median imputation is 0.74+/−0.03, and the c-index for MICE is 0.73+/−0.03.

Figure 3.

Predictive performance of different methods for handling missing data at the time of prediction.

5. Discussion and future work

The present study extends the current literature by illustrating a novel strategy for making risk prediction in the presence of missing data. Our strategy leverages multiple predictively equivalent risk models and makes risk predictions based on models that match the available data. We demonstrated the successful application of this strategy on SH risk prediction. We showed that, the performance of the MMTOP methods is not influenced by the presence of missing data, it achieved the same performance compared to when it was operating on the complete dataset, whereas the performance of all tested competitor methods deteriorated as number of missing variables increased.

There are several considerations for deploying this strategy in the clinical setting. First, the number of predictive equivalent models could be reduced based on knowledge of clinical workflow (modification to procedure ModelSelect). For example, certain variables such as age, education, race, years of diabetes, and blood pressure can be measured with little cost and/or burden during a clinical encounter, therefore, we could consider predictively equivalent models that utilize these risk factors. This reduces the number of models from 77 to 30. Second, the measurement quality of different risk factors in the clinical setting should be taken into consideration. Our predictively equivalent models were derived from ACCORD, a clinical trial, where measurement quality of certain variables (e.g. number of recent hypoglycemic events) are likely higher compared to what can be obtained in routine clinical setting. The models utilizing these variables may result in suboptimal risk prediction when applied to the clinical setting. Therefore, one should either prioritized models constitutes of risk factors with high measurement quality (modification to procedure IntergateModels by weighting models based on measurement quality) or consider improving measure quality of these variables. Third, the prediction time procedures of MMTOP could be linked to the EHR so that our missing data strategy could be incorporated into the clinical workflow. Fourth, it is possible that in certain clinical situation, we may not want the optimal risk prediction models (e.g. risk factors in optimal risk model is too expensive to collect), and are happy with risk models with performance that are higher than a certain threshold. In this case, procedure TIE* can be swapped with a procedure that output all risk factor sets that result in models with performance greater than the specified threshold.

In summary, the primary strength of our study is the novel approach of leveraging multiple predictively equivalent models to handle missing data at the time of prediction. This approach accommodates missing data by presenting alternative, equivalent models that do not require measuring the missing data elements or imputation.

The future direction of this work is to evaluate the performance of our missing value strategy on data collected through routine clinical practice and to design a clinical decision support system that incorporate the multiple predictive equivalent models into the clinical workflow.

Highlights.

• We introduce a new strategy, predictively equivalent models, to address the missing data issue at the time of prediction

• Its application in severe hypoglycemia risk prediction for Type 2 Diabetes is demonstrated.

• The predictively equivalent models outperformed all tested competitor methods methods when applied to data with missing values.