Abstract
Physical models of biological systems can become difficult to interpret when they have a large number of parameters. But the models themselves actually depend on (i.e., are sensitive to) only a subset of those parameters. This phenomenon is due to parameter space compression (PSC), in which a subset of parameters emerges as “stiff” as a function of time or space. PSC has only been used to explain analytically solvable physics models. We have generalized this result by developing a numerical approach to PSC that can be applied to any computational model. We validated our method against analytically solvable models of a random walk with drift and protein production and degradation. We then applied our method to a simple computational model of microtubule dynamic instability. We propose that numerical PSC has the potential to identify the low-dimensional structure of many computational models in biophysics. The low-dimensional structure of a model is easier to interpret and identifies the mechanisms and experiments that best characterize the system.
Significance
Computational models are integral to many domains of science. But are these models overly complex? Von Neumann quipped that only four parameters can fit an elephant, and five can make its trunk wiggle. Here, we show how to compress the parameter space of computational models, which allows us to discover their underlying structure and to extract key parameters. We validate our method against two analytically solvable models. We then compress a well-known computational model of microtubule dynamic instability, which is the nonequilibrium switching of tubulin polymers between phases of growth and shrinkage. We show that only two effective parameters are sufficient to describe dynamic instability. Our work opens the door to the rigorous analysis of any computational model in biophysics.
Introduction
A central goal of biophysics is to develop mathematical and computational models that describe biological systems. These models can operate at different temporal and spatial scales. In the case of the microtubule cytoskeleton, models range from molecular dynamics simulations of αβ-tubulin heterodimers (1) to Monte Carlo simulations of microtubule dynamic instability (2, 3, 4) to analytical theories that treat the mitotic spindle as a nematic liquid crystal (5). These models vary in their degree of complexity, i.e., in the number of parameters they use.
A central problem in biophysical modeling is defining the “right” number of parameters to explain and predict experimental data, which we refer to as observables. We prefer simple models; in the well-known quip from Von Neumann, four parameters are sufficient to fit an elephant, and five can make its trunk wiggle (6), as was indeed later demonstrated (7). More parameters can sometimes improve a model’s performance—namely, its ability to reproduce observables—but too many can be a problem. Unnecessary parameters obfuscate those that determine the model’s output and render the model less interpretable—all without any gain in predictive power (8). In other words, complex models can be black boxes. Thus, we need a rigorous way to define which parameters determine the performance of any model.
The behavior of a model can be described within a so-called parameter space, which has as many dimensions as there are parameters. Moving within this parameter space (by changing the values of parameters) should change a model’s output of observables. But usually a given observable significantly changes along only a few directions in parameter space (9). In other words, most directions in parameter space are irrelevant. To make sense of complex models, an important scientific problem is to reliably extract relevant directions in parameter space, defining the true, lower-order “dimensionality” of the model. There are several ways to solve this problem. In the 1980s, classical principal-component analysis was proposed as a method to reduce ordinary differential equations (ODE)-based models of biochemical systems (10). More recently, the manifold boundary approximation method has been developed to fit data while minimizing dimensionality (11); similarly, fitness-based asymptotic parameter reduction can extract the “core working module” of a model (12). Other machine-learning approaches can develop realistic models with a minimal number of parameters, e.g., using Bayesian information criterion (13). These methods are focused on ODE-based models, however, so there is an acute need for universal methods that are applicable to stochastic computational models as well.
Recently, parameter space compression (PSC) (14) has been proposed as the reason why fundamental models in physics operate successfully with simple parameter sets (15). PSC is related to the properties of the Fisher information matrix (FIM), which quantifies the relative significance of a model’s parameters. More specifically, for a generic dynamical physical system, the eigenvalues of the FIM change over time to identify combinations of parameters that become “stiff” (viz, those with strong effects on model outputs) versus others that become “sloppy” (those with very weak effects) (16). The sloppy parameters or parameter combinations are thus “compressed away” to reveal the simpler dimensionality that underlies a model’s performance (17). In other words, most parameters are sloppy and thus irrelevant; this sloppiness is the main reason why coarse-grained models in physics provide such satisfying descriptions of the natural world (15).
PSC explains how the predictive, low-dimensional structure of a model emerges (14), but currently PSC has been applied to a very limited number of analytically solvable physics models because of the difficulty of generalizing PSC to other contexts. To study the phenomenon of dimensional reduction via PSC in more general contexts, we developed a numerical PSC method, allowing us to explicitly study stochastic biophysical systems. To validate our method, we recovered the analytical results of a simple one-dimensional random walk model (14) and its perturbations. We further tested our method on an analytically solvable model of protein production and degradation. To test our method on a bona fide computational model, we applied numerical PSC to a classic Monte Carlo model of microtubule dynamic instability. In all three test cases, we show that the eigenvalues of the FIM provide critical insights into the behavior of a model and the importance of its parameters. Thus, our numerical PSC method opens the door to an analysis of computational models in biophysics that reveals the minimal yet predictive descriptions of living systems.
Materials and Methods
Mathematical formulation
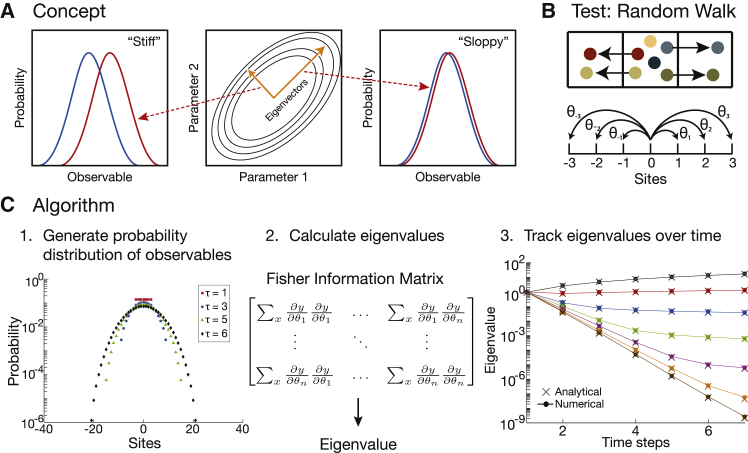
Our approach implements numerically the theoretical ideas of Machta and colleagues on the computation of the FIM to describe parameter space compression (14,16,17). We thus study the distribution of an observable x and its sensitivity to a vector of parameters . The central idea is that changes in an important parameter will result in larger changes in the probability distributions relative to changes in a less important one (Fig. 1 A). Thus, the important parameters will dominate the eigenvalues and eigenvectors of the FIM. Dominating eigenvalues define directions in parameter space where observables vary significantly. We call these directions “effective parameters.” In general, the effective parameters of a model are not the original parameters but rather combinations of them (see below). Thus, the goal of PSC is to identify these dominating eigenvalues and eigenvectors, which will define the most important directions in parameter space and the effective parameters defining the distribution of observable x (16,17). In particular, for a dynamical system, we expect that a hierarchy of eigenvalues will appear for the FIM of as time t progresses, such that only a few effective parameters define the observed dynamics at any given time. These few effective parameters are sufficient to completely describe the system.
Figure 1.
Numerical PSC. (A) Shown is a schematic of a stiff parameter versus a sloppy parameter in parameter space. The stiff parameter changes the observable more significantly than a sloppy one. Note: the red and blue curves are probability distributions when shifting different parameters by the same amount. (B) Shown is a schematic of one-dimensional random walk with parameters , the probability of jumping to neighboring sites. (C) Shown are the three steps of our numerical PSC method: 1) generate the probability distributions of the observables needed (see the plot of particle density at different time steps), 2) calculate the finite derivatives for the Fisher information matrix and its corresponding eigenvalues, and 3) repeat at each time step of the simulation and track the eigenvalues over time. Our numerical PSC reproduces the analytical result from (14). Note: each color corresponds to the same eigenvalue tracked over time. To see this figure in color, go online.
As shown in (14), with being the probability distribution of observable x with parameters , the FIM at any given time t can be rewritten with standard assumptions as a simple “metric”:
| (1) |
where y can be evaluated as a function of time t. Notice that then becomes a simple function of the Jacobian with respect to its parameters. A detailed derivation adapted from (14) is provided in Appendix 1 in the Supporting Material. We independently consider several observables x and, for each x, compute the FIM of distribution and its eigenvalues as a function of time t by summing over the entire observable landscape.
Scaling and algorithm
A challenge in analyzing computational models, especially in biology, is that the parameters have different units and scales. Some parameters are energies (e.g., the of bond formation), and some are kinetic rate constants (e.g., the rate constant of a GTP hydrolysis reaction). Because rate constants are exponentially distributed to thermal energy , we choose to rescale the parameters to express them all in terms of energies when calculating the FIM. Energies are more fundamental quantities, and their variations are easier to interpret physically. We thus define newly rescaled parameters, , so that for parameters that are energies and for rate constants (with an implicit conversion factor to remove units, which normalizes the different parameters, equivalent to the common procedure of taking the derivatives with respect to the log of the parameter, as done previously (9)). Therefore, Eq. 1 becomes
| (2) |
where if is an energy and if is a rate constant.
To calculate the FIM numerically using Eq. 2, we developed a three-step algorithm, shown in Fig. 1 C. First, we numerically compute the probability distributions of each observable x at any time t for incremental variations of parameters . We then compute finite derivatives to evaluate (corresponding to the Jacobian), which implies that we need to generate probability distributions for each observable x for a model with N parameters. Second, we evaluate each element of the FIM using the probability distributions that we generated. Therefore, Eq. 2 becomes
| (3) |
Using Eq. 3, we sum over the entire observable landscape for each element of the FIM and then calculate the eigenvalue of the FIM at a given time. Third, we track the eigenvalues of the FIM over time. In general, the eigenvalues of the FIM are logarithmically distributed (16). The important feature of the eigenvalues is not their absolute values but rather their relative values, which is to say that the largest eigenvalue points to the most important direction in parameter space.
When evaluating the finite derivatives in Eq. 3, the choice of is arbitrary. It is clear that very large changes in parameter values will cause numerical instability when calculating the finite derivatives. Rather, the issue is whether small changes in parameter values are nevertheless large enough to cause meaningful changes in the distributions of observables. In our experience, very small changes cause the eigenvalues and eigenvector components of the FIM to become noisy. Therefore, we recommend = 0.05 (leading to a change of for corresponding rate constants; see Appendix 2 in the Supporting Material) as a robust choice to avoid numerical instability while keeping significant changes in model output. The best value of may be be model dependent. The consequences of small changes in the parameters (e.g., 0.01 ) will be demonstrated below.
Computational costs mostly come from running enough simulations to generate good probability distributions. For the microtubule study, we ran independent simulations of microtubule growth per parameter set, which represents a bit less than 1 h of computation on a single 3.6-GHz core. As mentioned above, for N parameters, we need simulations to compute derivatives from Eq. 3. Thus, for five parameters, roughly 10 core hours of computation are needed. Computation can be easily parallelized because simulations of individual microtubules are independent, and distributions of all observables can be obtained from the same set of simulations.
Results
Test case: one-dimensional random walk
To test our numerical PSC method, we benchmarked our algorithm by simulating a model for which an analytical solution is available. We chose the one-dimensional random walk model introduced in Machta et al. (14), which is the model used to develop the concept of PSC. The parameters of the model are the probabilities of a particle jumping to one of six neighboring sites (Fig. 1 B); the observable x of the model is the position of a particle, and is the distribution of particle positions as a function of time (viz, the particle density in a mean-field approximation when there are many particles). We simulated the random walk and plotted the eigenvalues of the FIM over time (Fig. 1 C), and our results precisely match those derived from the analytical expression (see Appendix 2 in the Supporting Material). In particular, the eigenvalues start at unity; as time progresses, the distribution of eigenvalues expands, establishing a clear hierarchy of eigenvalues at later times.
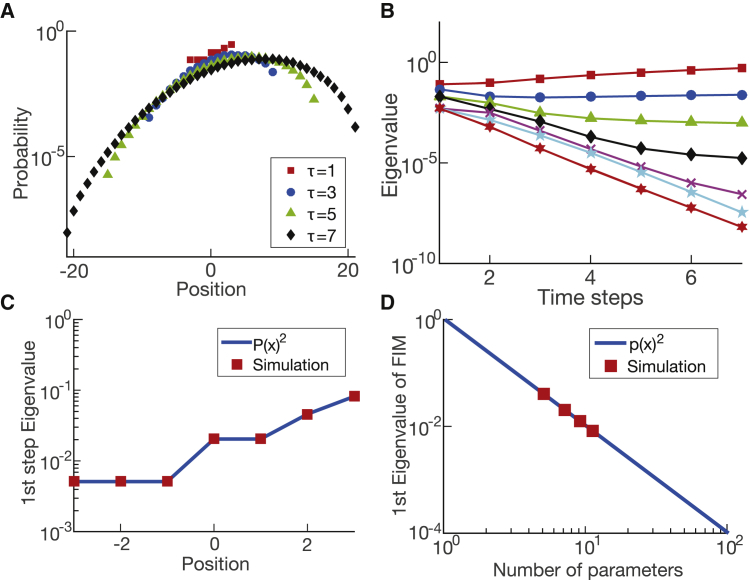
As pointed out in Machta et al. (14), the first two eigenvalues can be interpreted as a drift term and a diffusion coefficient, respectively; the spreads of the eigenvalues are enough to reproduce most of the data in an effective theory (as discussed in (14)). We further tested the correspondence between our numerical results and the analytical theory by introducing drift into the random walk, which was not done previously. The particle density over time is shown in Fig. 2 A. The eigenvalues of the FIM over time for the perturbed random walk are shown in Fig. 2 B. The result is similar to uniform diffusion in the sense that a hierarchy of eigenvalues appears as time progresses. We are able to show that the eigenvalues are proportionally defined by the probabilities of particles jumping to neighboring sites (the derivation is shown in Appendix 3 in the Supporting Material). Most importantly, our numerical results precisely match the analytical solutions we derived for a random walk with drift and a uniform random walk with different numbers of parameters (see Fig. 2, C and D, respectively). Thus, our numerical PSC method successfully compressed this classical system and its variations.
Figure 2.
Random walk and random walk with drift. (A) Shown is the particle density for a nonuniform one-dimensional random walk over time (with probability higher to the right side of the space). (B) Shown are the eigenvalues for the nonuniform one-dimensional random walk. The eigenvalues at the first step of the simulation are not at unity contrary to the uniform random walk. (C) At the first step of the simulation for the one-dimensional random walk, the eigenvalue is equal to the squared rate given for the nonuniform simulation. This result is universal for any rates given. (D) The eigenvalues at the first step of a uniform simulation are also equal to the squared rate of the simulation, i.e., squared of one over the number of parameters. To see this figure in color, go online.
Test case: a simple protein production and degradation system
Having benchmarked our algorithm against the random walk model, we next wondered how our numerical PSC method would handle a model in biophysics, in which the distributions of observables are often complex. Therefore, we applied our numerical PSC method to a textbook biophysical model of protein production and degradation. The model has only two parameters, the production rate ρ and the degradation rate δ (see Fig. 3 A). The observable x of the model is the number of proteins in the system at any given time. Importantly, the stationary distribution of protein number is a Poisson distribution of the parameter combination (representing the expectation value for the number of proteins) (18). Using this stationary distribution, we can analytically solve for the dominating eigenvalue of the corresponding FIM in the continuous limit:
| (4) |
The derivation of the eigenvalues and the expression for Eq. 4 can be found in Appendix 4 in the Supporting Material.
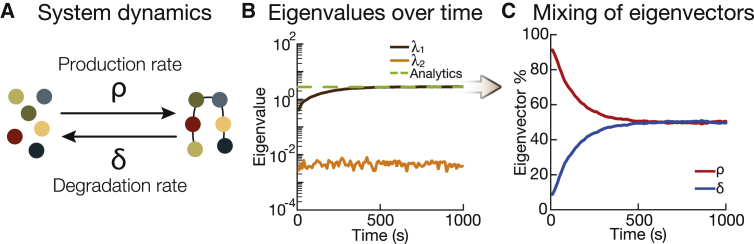
Figure 3.
Protein production and degradation. (A) Shown is a schematic of a simple protein production-degradation system with production rate ρ and degradation rate δ. (B) Shown is a plot of eigenvalues over time for the protein production-degradation system. There is one dominating eigenvalue, and it matches the analytical result. (C) Shown is the plot of eigenvector percent from the dominating eigenvalue of (B). The production rate ρ dominates at early time points, but at stationarity, the production rate and degradation rate contribute equally. Note: the eigenvector percent is the absolute value of the parameter component. To see this figure in color, go online.
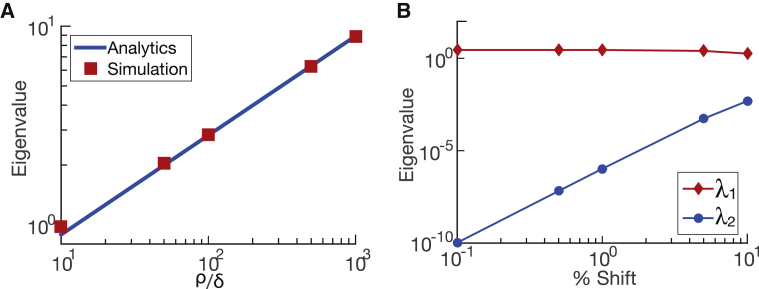
Starting from an initial condition with no proteins, we simulated this process using the Gillespie algorithm (19) and computed the eigenvalues of the system over time (Fig. 3 B). One eigenvalue is always over two orders of magnitude larger than the other, indicating that the system is governed by one effective parameter, which is to say that there is only one relevant direction in parameter space that determines the model’s output. Looking at the relative contribution of the eigenvector components of the dominating eigenvalue in Fig. 3 C, we can see that during the early stages of the simulation, the production rate ρ dominates, corresponding to the net production of proteins from the initial condition. The system then reaches stationarity, at which point the eigenvector components of the dominating eigenvalue are an equal mix of the production rate ρ and degradation rate δ, as expected from our derivation (Fig. 3 C). We checked that our method recovers the analytical result of Eq. 4 (in the asymptotic limit) for different ratios of production rate over degradation rate (see Fig. 4 A). Thus, our numerical PSC method is able to compress out irrelevant directions and extract the effective parameter defining the distribution of protein number (here, a Poisson distribution).
Figure 4.
Generalization of protein system and understand numerical limitations. (A) The dominating eigenvalue for the protein production-degradation system is shown to be a ratio of the production rate over the degradation rate times some constant. The simulations of different ratios match the analytic solution. (B) The second eigenvalues for the protein production and degradation rate are nonzero during simulation because of the limitation of the physical system itself. At steady state, the average number of proteins is 100 proteins, which means that the smallest shift for probability to calculate the finite derivatives is one protein (1% of the average number), which gives a nonzero eigenvalue. To see this figure in color, go online.
In the continuous limit, the second eigenvalue of the system goes to 0. In a discrete simulation, however, it is impossible for the second eigenvalue to reach 0 because of the limitations of numerical precision and the physical definition of the system. For example, for a production rate and a degradation rate , we know that the steady-state solution will have a peak at proteins. However, this means that when calculating the finite derivatives, any shift smaller than will result in a change of less than one protein, which is nonphysical. We show that even using analytical values of the Poisson distribution, we will not be able to reach 0 when calculating finite derivatives (see Fig. 4 B).
Microtubule dynamics: a complex biophysical system
Having fully characterized our method, we applied it to a biophysical system that cannot be solved analytically—namely, the dynamic instability of microtubules (20). Microtubules are polymers of αβ-tubulin, and dynamic instability is the nonequilibrium behavior in which the polymers stochastically switch between periods of growth and shrinkage. This complex, nonequilibrium phenomenon was first simulated numerically in the 1980s (21,22) and has remained a subject of considerable interest for computational biologists, who have developed increasingly sophisticated models (3,4,23,24). The long-term goal of these collective efforts is to develop a powerfully predictive yet minimal model that can be used to explain microtubule physiology. Our numerical PSC method has the power to determine whether existing models have an underlying low-dimensional structure.
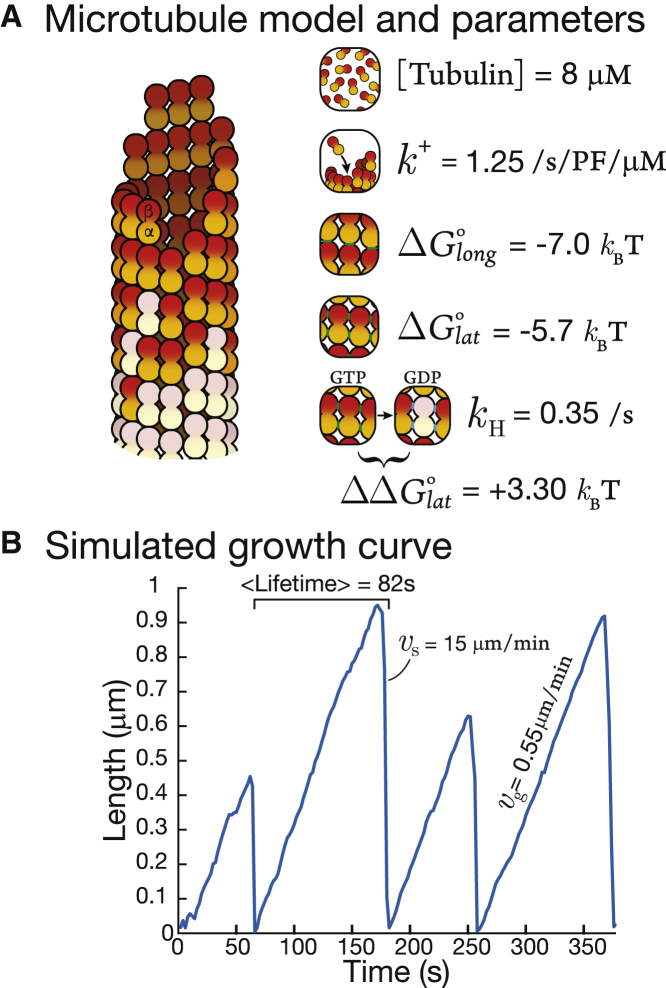
Our model is based on VanBuren et al. (2) (see Fig. 5 A); a similar model is used by Ayaz et al. (25). We chose this model because it is a classic and because understanding its underlying dimensionality will inform ongoing modeling work on microtubules. Briefly, tubulin subunits associate head-to-tail to create protofilaments (pfs), forming longitudinal bonds described by an energy parameter . In our model, 13 pfs are connected by lateral bonds between adjacent subunits with an energy parameter (26). The rate at which tubulin binds to pf ends is described by an association rate constant, . Because tubulin is a GTPase, these incoming tubulin subunits contain GTP in the tubulin nucleotide pocket. This GTP becomes hydrolyzed after 1) the subunit incorporates into the polymer and 2) another GTP-tubulin binds on top of it, contributing catalytic residues that complete the nucleotide pocket (27). The rate of GTP hydrolysis is described by a rate constant parameter . GTP hydrolysis and phosphate release converts GTP-tubulin to GDP-tubulin and weakens the bonds between tubulin subunits in the polymer (28,29). After VanBuren, this weakening of energies is described by an energy parameter, , which is assigned to the lateral bonds of the new GDP-tubulin subunit.
Figure 5.
Microtubule dynamics. (A) Shown is the base model of our microtubule simulation after VanBuren et al. (2). (B) Shown is a plot of length versus time from our microtubule simulation. To see this figure in color, go online.
We performed a parameter sweep and arrived at parameter values similar to Castle et al. ((4), see Fig. 5 A). Using these parameters, our simulation produces microtubule growth curves that correspond reasonably with measurements from multiple labs using 8 μM brain tubulin (e.g., (30), see Fig. 5 B). More specifically, microtubules grow as long as their ends are protected by a “cap” of GTP-tubulin (31). If this GTP cap is “lost,” the polymer switches to rapid shrinkage in an event known as a “catastrophe,” the hallmark of dynamic instability (20).
There are many subtleties and caveats to models of dynamic instability. For example, which bonds are weakened by GTP hydrolysis is not well established (32,33), and the transition from GTP-tubulin to GDP-tubulin may have substeps (33). These subtleties are discussed in Appendix 5 in the Supporting Material. We used the direct method of the Gillespie algorithm (19), which is a different implementation than the one in VanBuren et al. (2) and Ayaz et al. (25). To validate our Gillespie algorithm, we used the parameters found in Ayaz et al. (25) and confirmed that our simulation produces identical results. The details of our simulation method and the benchmarking of our algorithm against published data can be found in Appendix 5 in the Supporting Material and Fig. S2.
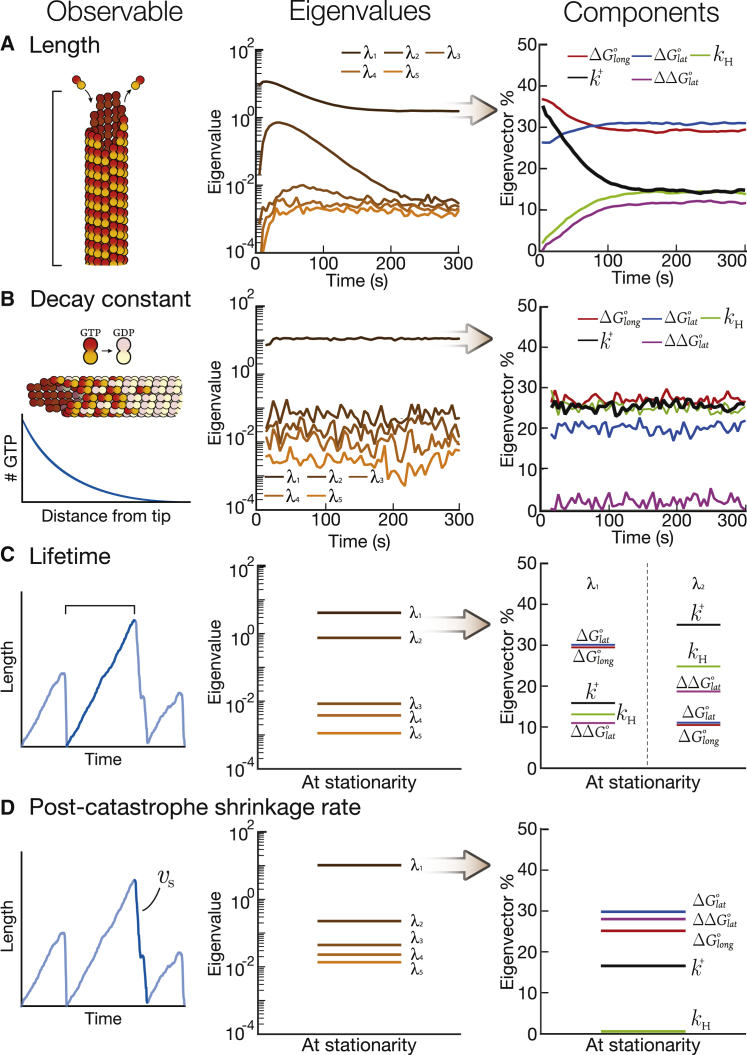
To compress our model, we varied all five parameters (, , , , and ) around their initial values. We measured four independent observables of the simulations that correspond to the experimental data used in our parameter sweep (30): 1) the length of the microtubule (Fig. 6 A); 2) the decay constant that describes the conversion of GTP-tubulin into GDP-tubulin (“GTP cap size,” Fig. 6 B) (34); 3) the microtubule lifetime (Fig. 6 C); and 4) the postcatastrophe shrinkage rate (Fig. 6 D). Two of these observables can be tracked continuously over the time course of the simulation—namely, the length of microtubule and the decay constant. The second column of Fig. 6, A and B shows the eigenvalues over time for these observables. The other two observables—namely, microtubule lifetimes and the postcatastrophe shrinkage rate—are not tracked continuously because they require postsimulation analysis to determine when catastrophes occurred (see Appendix 6 in the Supporting Material). The second column of Fig. 6, C and D shows the eigenvalues for these observables at the conclusion of the simulation, when the distributions have reached stationarity. This framework allowed us to apply our numerical PSC method to our model of microtubule dynamic instability.
Figure 6.
Numerical PSC for the five-parameter bovine microtubule model. (A–D) Eigenvalues and eigenvector components (percent) for four observables: (A) length (the exact number of dimers in each microtubule), (B) decay constant of GTP from the tip, (C) average lifetime of the microtubule, and (D) postcatastrophe shrinkage rate. Note: the eigenvector percent is the absolute value of the parameter component. To see this figure in color, go online.
For three out of four observables, one eigenvalue dominates the others by at least one order of magnitude (note the log-scale for eigenvalues). This dominance implies that the distribution of these observables is determined by a single effective parameter. This result is not obvious: one expects that the mean and the variance of any given distribution are described by independent parameters, as was the case for the random walk (14). Rather, three of our microtubule observables are similar to the number of proteins in the protein production/degradation model, in which both the mean and variance of the distributions are determined by a single effective parameter. The only exception we observe to this rule is the microtubule lifetime distribution; even though one eigenvalue strongly dominates this distribution, a second eigenvalue is a bit less than one order of magnitude below the first one. This smaller difference suggests that although the lifetime distribution is mostly determined by one effective parameter, another parameter mildly modulates it.
As for the protein production/degradation case, the single effective parameter determining the distribution of each observable is a priori a complex function of the initial parameters. As before, the relative influence of each initial parameter is given by the eigenvector components of the dominant eigenvalue (see column three of Fig. 6, A–D; for the lifetime distribution, we also show the eigenvector components for the second eigenvalue). Importantly, we can also see which parameters are not important for a given observable because these parameters will be insignificant components of the dominating eigenvalue.
The important components for microtubule length are the lateral bond, , followed closely at later times by the longitudinal bond, . These components are not surprising considering that the bond energies are what drive polymerization. The important components for the decay constant are more interesting. In addition to the obvious parameter of the GTP hydrolysis rate constant, , the decay constant is also determined by and . A simple interpretation of this result is that a microtubule that forms stronger bonds (and hence grows faster) will have a larger GTP cap. Consistently, microtubules that grow faster have larger GTP caps when end-binding proteins are used as reporters of GTP cap size (34). The lifetime distribution depends on the two bond energies and is further modulated by and via the second eigenvalue. However, for the postcatastrophe shrinkage rate, the most important parameter is the lateral bond , followed closely by and . Table 1 summarizes the parameters that are important for each observable.
Table 1.
This Table Demonstrates the Importance of Parameters on Different Observables
| Observables | Ranking |
||
|---|---|---|---|
| Important | Intermediate | Less Important | |
| Length | NA | ||
| Decay constant | |||
| Lifetime | NA | ||
| Postcatastrophe shrinkage rate | |||
As explained in Scaling and Algorithm, we calculated the FIM by varying our parameters by 0.05 . When we used smaller variations (0.01 ), the results were similar in magnitude but clearly noisier (see Fig. S6) because the distributions of observables were shifted to a lesser extent.
The results above used a parameter set that reproduces data from mammalian microtubules using tubulin purified from brain tissue (e.g., (30)). We wondered whether a different parameter set would give the same results in terms of the number of dominating eigenvalues and their components. In other words, do our results apply only to a local region of parameter space, or do they apply globally? To answer this question, we used a parameter set that reproduces different data—namely, the dynamic instability of Caenorhabditis elegans microtubules (30). C. elegans microtubules are among the most divergent measured to date in that they grow faster and have shorter lifetimes than microtubules from several other species (35, 36, 37). Our PSC predicts that faster growth requires more negative values for and , and indeed, the C. elegans parameter set is shifted accordingly (see Fig. S4).
With this C. elegans parameter set, we performed PSC on our model. The results were quite similar; e.g., as with the bovine parameter set, the length distribution, decay constant, and postcatastrophe shrinkage rate had one dominating eigenvalue (see Fig. S4), indicating that these observables are controlled by a single effective parameter. Similarly, the lifetime distribution had two dominating eigenvalues (see Fig. S4). Indeed, the eigenvector components of these eigenvalues were nearly identical in every case, indicating that the low-dimensional structure of our model is conserved between the brain and C. elegans parameter sets. The one difference we observed was in the eigenvector components that describe the effective parameter for the postcatastrophe shrinkage rate (see Fig. S4). In the C. elegans case, the association rate constant is a significant component. We interpret this result in light of our previous observation that C. elegans tubulin is more “active” in solution (30): a more active dimer may influence the rate of shrinkage through its binding to microtubule ends. Despite this difference, the PSC results for brain microtubules and C. elegans microtubules are broadly similar. We conclude that our PSC results are weakly dependent on specific parameter values and/or the local position in parameter space.
Parameter dependencies of distributions
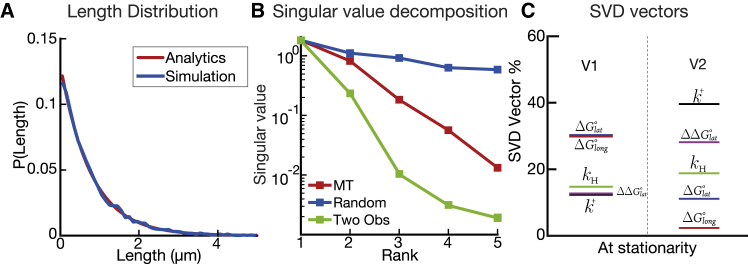
As shown above, the distribution of most observables can be described by a single effective parameter, which is specified by the eigenvector components of the dominating eigenvalue. We can illustrate this phenomenon by plotting the distribution of microtubule lengths (Fig. 7 A); the distribution is a nearly perfect exponential (as predicted from simple analytical models (38,39)). Exponential probability distributions are described by one parameter, which in the microtubule case is the average length, , thus defining the effective parameter.
Figure 7.
Identifying the dimensionality of the models. (A) Shown is the probability of length plot for our simulation versus analytic expression from (38,39). (B) Shown is the plot of the singular values for three different cases: in red, our five parameter microtubule model; in blue, five random five-dimensional vectors; in green, length and decay constant observables. (C) The first column is the leading vector for the highest singular value for the microtubule system. The lateral bond and longitudinal bond are the controlling parameters. The second column is the leading vector for the second highest singular value for the microtubule system. The on-rate constant and the energy penalty after hydrolysis are the controlling parameters. Note: the SVD vector percent plotted is the absolute value of the parameter component. To see this figure in color, go online.
In contrast to the length distribution, the microtubule lifetime distribution should be controlled by two parameters according to our analysis. Consistent with this idea, it has been suggested that this lifetime follows a -distribution (40). We thus plotted our computed lifetime distribution (Fig. S3). We indeed observe an increase followed by an exponential tail (consistent with a multistep process as proposed in (40)), but our distribution rises slightly faster than the best -fit. To visualize the effects of the two effective parameters, we follow the two eigendirections, as illustrated in Fig. S3 B. To compare properly the shapes of the distribution, 1) we further rescale the distributions by their maximal probability, and 2) we adjust the magnitude of the changes so that the most probable lifetime is the same in both directions. It is then very clear that although the leftmost part of the distribution is similar, the exponential tail differs. Contrary to the length case above, we thus cannot define the distribution with only one parameter (such as the most probable lifetime) because the tail of the distribution clearly requires another parameter.
Estimating the dimensionality of the system
Our eigenvector components tell us which directions matter in parameter space, similar to the “hyper-ribbon” notion described in (17). But is the important direction for microtubule length, e.g., the same direction that is important for the other observables? Or do we need five orthogonal directions to describe the full model? For three of our observables, the eigenvector components are very similar, suggesting a common effective parameter. More specifically, , , and are dominating eigenvector components for microtubule lengths, lifetimes, and the postcatastrophe shrinkage rates. In contrast, the decay constant has a significant eigenvector component from , indicating that its effective parameter may differ from the others. So what is the true dimensionality of our model?
To perform a rigorous estimation of the dimensionality, we computed the singular value decomposition (SVD) on all the eigenvectors of all the observables. The number of large singular values in an SVD analysis indicates how many dimensions are sufficient to describe the original matrix with good precision. To perform our SVD analysis, we rescaled the eigenvectors proportionally to their respective eigenvalues so that the largest eigenvalue for each observable has a weight of 1 (41). This rescaling allows us to capture the global sensitivity with respect to parameters of all observables simultaneously. We compared the SVD computation of our model with two cases: 1) five random vectors in five directions and 2) combinations of eigenvectors for the length and lifetime observables in our microtubule system. The singular values for these computations are shown in Fig. 7 B. The random case gives a baseline for what might be expected from a five-dimensional system: random vectors are almost orthogonal, so we obtained five large singular values. The two-observable case gives us a baseline for a low-dimensional system: the singular values decay rapidly from the first large singular value, indicating that only one effective parameter defines the distributions of these two observables.
SVD for the full model shows an intermediate result with a sloppy distribution of singular values: there is one large singular value, a second singular value roughly three times smaller, and three even smaller singular values at least one order of magnitude below. It is also visually clear that the relative positions of the first two singular values are roughly comparable to the first two singular values of the random case, indicating that the system is close to two-dimensional.
Thus, the presence of two large singular values means that two effective parameters are essentially enough to fit the data. A standard estimation of the precision of this dimensional reduction can be done by computing ratios of Frobenius norms of the singular matrix , where are singular values ordered from top to bottom rank (42). The closer to 1, the better the reduction, and a good rule of thumb is . For , one finds , whereas for , one finds , indicating an excellent dimensional reduction if we keep the first two modes.
Our SVD analysis demonstrates rigorously that the full dimensionality of our model is essentially equal to two. The vectors that correspond to the two dominating singular values are shown in Fig. 7 C. The first vector is primarily composed of the lattice bond energies. The second vector combines parameters associated with the binding and unbinding of tubulin dimers, with major contributions from and . We observed similar results for an SVD analysis of our model when we used our C. elegans parameter values (Fig. S5). The C. elegans model was also two-dimensional, but the second singular value included a significant contribution from , which is consistent with our PSC results for the worm model described above. Thus, our results generalize to different parameter sets while revealing how new parameter dependencies can appear.
Discussion
As biophysicists, we want to capture the complexity of biology in the simplest possible terms, even if those terms are themselves quite complex. Our work has demonstrated the power of numerical PSC as a method for identifying the essential parameters and low-dimensional structure of complex models. We first validated our method against two analytically solvable models and then applied it to a well-known computational model of microtubule dynamic instability. Thus, our method opens the door to the simplification of many computational models in biophysics. Computation of effective parameters is made rigorous and possible by the use of our approach. PSC of microtubule dynamics is very reminiscent of classical examples, such as random walks (14), in which a sloppy distribution of eigenvalues is also observed and two effective parameters naturally appear (drift and diffusion, Fig. 1 C). It is remarkable that a biological phenomenon as complex as dynamic instability can be compressed into a two-parameter system as well.
Our analysis of microtubule dynamic instability revealed that almost all data simulated here can be described with only two effective parameters: 1) a “polymerization” parameter, which includes and , and 2) a GTP cap parameter, which includes , , and . These two parameters form a two-dimensional “ribbon” within the five-dimensional space of parameters (16). The polymerization parameter makes physical sense if most of the binding sites at the end of a microtubule are shaped like “corners,” where the incoming tubulin subunit will form one longitudinal bond and one lateral bond. Because these bonds are formed at the same time in the model, they are strongly coupled, as our analysis shows. The GTP cap parameter makes physical sense because it couples the size of the GTP cap (determined by and ) and the strength of the GTP cap (determined by , which encodes the extra bond strength found in the cap versus the lattice).
This ribbon structure also provides direct insight into catastrophe dynamics. For example, we were surprised to find that had a lesser influence on the lifetime distribution than and . This suggests that catastrophe might be more efficiently prevented by making stronger bonds rather than by slowing down hydrolysis. Our interpretation is that stronger bonds help prevent pfs from losing their terminal GTP-tubulin dimers, which would cause the pf to become “fully uncapped.” Bowne-Anderson et al. argued that uncapping of pfs is the irreversible event that leads to catastrophe (43). Similarly, poisoning of pf ends with the drug eribulin has a very strong effect on catastrophe frequency (44). Therefore, our results showing the importance of and are consistent with the emerging concept that “pf destabilization” is a root cause of catastrophe. Our results may also explain why depolymerases and catastrophe factors work by disrupting lattice bonds rather than acting as GTPase activating proteins, which are common in the regulation of other GTPases.
From the modeling standpoint, our results imply that a basic quantitative understanding of dynamic instability might not require many parameters but, rather, only the effective ones. This simplified structure is illustrated by the one-parameter fit of the length distribution in Fig. 7 A. But one limitation of PSC is the lack of a universal method for converting these discoveries into a coarse-grained model (e.g., a two-parameter simulation or analytical model). Machine-learning approaches and principal component analysis face a similar problem: how to interpret the lower-dimensional model or principal components. In the microtubule PSC case, we have made our best effort to interpret our results in physically meaningful ways that will facilitate the development of simpler models.
It is important to point out that the addition of new parameters might add new dependencies on the corresponding eigenvectors/eigenvalues, meaning that those parameters would matter (in the sense that they influence the effective parameters). However, they might change neither the nature nor the number of the effective parameters controlling the dynamics. A more interesting situation would be when adding a new biochemical parameter also adds a new effective parameter to the system, increasing the net dimensionality from two and three. Additionally, we can add new observables to our analysis (e.g., the “taper length” that describes the difference in length between the shortest and longest profotilaments). These new observables may demand new effective parameters. Our approach could help experimentalists identify the types of data that are necessary and sufficient to define such effective parameters. Which parameters of a model are stiff and which are sloppy depends critically on the observables that the model attempts to reproduce.
Our ability to distinguish between models in science is always limited by the availability of hard data. In biophysics, the rigor of physical modeling collides against the complexity of biological interactions. A coupling of theory and experiment is necessary to disentangle this complexity. PSC tightens this coupling by improving the interpretability of models, which in turn identifies the key experiments that drive theory forward.
Author Contributions
G.J.B. and P.F. conceptualized the project. C.-T.H. did all simulations, calculations, and analysis. C.-T.H., G.J.B., and P.F. wrote the manuscript. G.J.B. and P.F. administered and supervised the project.
Acknowledgments
The authors thank Sami Chaaban, Claire Edrington, Dr. Hadrien Mary, Félix Proulx-Giraldeau, Thomas Rademaker, Laurent Jutras-Dubé, and Dr. Adrien Henry for feedback on this project and comments on the manuscript.
C.-T.H. acknowledges support from the Milton Leung fund in McGill Physics and from Fonds de recherche du Quebec - Nature et technologies (FRQNT) Bourse. G.J.B. is supported by the Canadian Institutes of Health Research (137055 and PJT-148702) and the Natural Sciences and Engineering Research Council of Canada (372593). P.F. is supported by a Simons Foundation fellowship in Mathematical Modelling of Biological Systems and NSERC (2016-06501). Lastly, this work was supported by a FRQNT Projet de Recherche en Equipe (FRQ-NT191128).
Editor: David Sept.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.01.023.
Contributor Information
Gary J. Brouhard, Email: gary.brouhard@mcgill.ca.
Paul François, Email: paul.francois2@mcgill.ca.
Supporting Material
References
- 1.Mitra A., Sept D. Taxol allosterically alters the dynamics of the tubulin dimer and increases the flexibility of microtubules. Biophys. J. 2008;95:3252–3258. doi: 10.1529/biophysj.108.133884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.VanBuren V., Odde D.J., Cassimeris L. Estimates of lateral and longitudinal bond energies within the microtubule lattice. Proc. Natl. Acad. Sci. USA. 2002;99:6035–6040. doi: 10.1073/pnas.092504999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.VanBuren V., Cassimeris L., Odde D.J. Mechanochemical model of microtubule structure and self-assembly kinetics. Biophys. J. 2005;89:2911–2926. doi: 10.1529/biophysj.105.060913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Castle B.T., McCubbin S., Odde D.J. Mechanisms of kinetic stabilization by the drugs paclitaxel and vinblastine. Mol. Biol. Cell. 2017;28:1238–1257. doi: 10.1091/mbc.E16-08-0567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Brugués J., Needleman D. Physical basis of spindle self-organization. Proc. Natl. Acad. Sci. USA. 2014;111:18496–18500. doi: 10.1073/pnas.1409404111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dyson F. A meeting with Enrico Fermi. Nature. 2004;427:297. doi: 10.1038/427297a. [DOI] [PubMed] [Google Scholar]
- 7.Mayer J., Khairy K., Howard J. Drawing an elephant with four complex parameters. Am. J. Phys. 2010;78:648–649. [Google Scholar]
- 8.Gunawardena J. Models in biology: ‘accurate descriptions of our pathetic thinking’. BMC Biol. 2014;12:29. doi: 10.1186/1741-7007-12-29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gutenkunst R.N., Waterfall J.J., Sethna J.P. Universally sloppy parameter sensitivities in systems biology models. PLoS Comput. Biol. 2007;3:1871–1878. doi: 10.1371/journal.pcbi.0030189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Vajda S., Valko P., Turányi T. Principal component analysis of kinetic models. Int. J. Chem. Kinet. 1985;17:55–81. [Google Scholar]
- 11.Transtrum M.K., Qiu P. Model reduction by manifold boundaries. Phys. Rev. Lett. 2014;113:098701. doi: 10.1103/PhysRevLett.113.098701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Proulx-Giraldeau F., Rademaker T.J., François P. Untangling the hairball: fitness-based asymptotic reduction of biological networks. Biophys. J. 2017;113:1893–1906. doi: 10.1016/j.bpj.2017.08.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Daniels B.C., Nemenman I. Automated adaptive inference of phenomenological dynamical models. Nat. Commun. 2015;6:8133. doi: 10.1038/ncomms9133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Machta B.B., Chachra R., Sethna J.P. Parameter space compression underlies emergent theories and predictive models. Science. 2013;342:604–607. doi: 10.1126/science.1238723. [DOI] [PubMed] [Google Scholar]
- 15.Waterfall J.J., Casey F.P., Sethna J.P. Sloppy-model universality class and the Vandermonde matrix. Phys. Rev. Lett. 2006;97:150601. doi: 10.1103/PhysRevLett.97.150601. [DOI] [PubMed] [Google Scholar]
- 16.Transtrum M.K., Machta B.B., Sethna J.P. Geometry of nonlinear least squares with applications to sloppy models and optimization. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2011;83:036701. doi: 10.1103/PhysRevE.83.036701. [DOI] [PubMed] [Google Scholar]
- 17.Transtrum M.K., Machta B.B., Sethna J.P. Perspective: sloppiness and emergent theories in physics, biology, and beyond. J. Chem. Phys. 2015;143:010901. doi: 10.1063/1.4923066. [DOI] [PubMed] [Google Scholar]
- 18.Ross S.M. Introduction to Probability Models. Academic Press; 2019. The exponential distribution and the poisson process; pp. 293–374. [Google Scholar]
- 19.Gillespie D.T. Exact stochastic simulation of coupled chemical reactions. J. Chem. Phys. 1977;81:2340–2361. [Google Scholar]
- 20.Mitchison T., Kirschner M. Dynamic instability of microtubule growth. Nature. 1984;312:237–242. doi: 10.1038/312237a0. [DOI] [PubMed] [Google Scholar]
- 21.Chen Y.D., Hill T.L. Monte Carlo study of the GTP cap in a five-start helix model of a microtubule. Proc. Natl. Acad. Sci. USA. 1985;82:1131–1135. doi: 10.1073/pnas.82.4.1131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bayley P., Schilstra M., Martin S. A lateral cap model of microtubule dynamic instability. FEBS Lett. 1989;259:181–184. doi: 10.1016/0014-5793(89)81523-6. [DOI] [PubMed] [Google Scholar]
- 23.Zakharov P., Gudimchuk N., Grishchuk E.L. Molecular and mechanical causes of microtubule catastrophe and aging. Biophys. J. 2015;109:2574–2591. doi: 10.1016/j.bpj.2015.10.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.McIntosh J.R., O’Toole E., Gudimchuk N. Microtubules grow by the addition of bent guanosine triphosphate tubulin to the tips of curved protofilaments. J. Cell Biol. 2018;217:2691–2708. doi: 10.1083/jcb.201802138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ayaz P., Munyoki S., Rice L.M. A tethered delivery mechanism explains the catalytic action of a microtubule polymerase. eLife. 2014;3:e03069. doi: 10.7554/eLife.03069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ledbetter M.C., Porter K.R. Morphology of microtubules of plant cell. Science. 1964;144:872–874. doi: 10.1126/science.144.3620.872. [DOI] [PubMed] [Google Scholar]
- 27.Löwe J., Li H., Nogales E. Refined structure of alpha beta-tubulin at 3.5 A resolution. J. Mol. Biol. 2001;313:1045–1057. doi: 10.1006/jmbi.2001.5077. [DOI] [PubMed] [Google Scholar]
- 28.Mandelkow E.M., Mandelkow E., Milligan R.A. Microtubule dynamics and microtubule caps: a time-resolved cryo-electron microscopy study. J. Cell Biol. 1991;114:977–991. doi: 10.1083/jcb.114.5.977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Maurer S.P., Fourniol F.J., Surrey T. EBs recognize a nucleotide-dependent structural cap at growing microtubule ends. Cell. 2012;149:371–382. doi: 10.1016/j.cell.2012.02.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Chaaban S., Jariwala S., Brouhard G.J. The structure and dynamics of C. elegans tubulin reveals the mechanistic basis of microtubule growth. Dev. Cell. 2018;47:191–204.e8. doi: 10.1016/j.devcel.2018.08.023. [DOI] [PubMed] [Google Scholar]
- 31.Carlier M.F., Pantaloni D. Kinetic analysis of guanosine 5′-triphosphate hydrolysis associated with tubulin polymerization. Biochemistry. 1981;20:1918–1924. doi: 10.1021/bi00510a030. [DOI] [PubMed] [Google Scholar]
- 32.Zhang R., Nogales E. A new protocol to accurately determine microtubule lattice seam location. J. Struct. Biol. 2015;192:245–254. doi: 10.1016/j.jsb.2015.09.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Manka S.W., Moores C.A. The role of tubulin-tubulin lattice contacts in the mechanism of microtubule dynamic instability. Nat. Struct. Mol. Biol. 2018;25:607–615. doi: 10.1038/s41594-018-0087-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bieling P., Laan L., Surrey T. Reconstitution of a microtubule plus-end tracking system in vitro. Nature. 2007;450:1100–1105. doi: 10.1038/nature06386. [DOI] [PubMed] [Google Scholar]
- 35.Katsuki M., Drummond D.R., Cross R.A. Mal3 masks catastrophe events in Schizosaccharomyces pombe microtubules by inhibiting shrinkage and promoting rescue. J. Biol. Chem. 2009;284:29246–29250. doi: 10.1074/jbc.C109.052159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Vemu A., Atherton J., Roll-Mecak A. Structure and dynamics of single-isoform recombinant neuronal human tubulin. J. Biol. Chem. 2016;291:12907–12915. doi: 10.1074/jbc.C116.731133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Walker R.A., O’Brien E.T., Salmon E.D. Dynamic instability of individual microtubules analyzed by video light microscopy: rate constants and transition frequencies. J. Cell Biol. 1988;107:1437–1448. doi: 10.1083/jcb.107.4.1437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Verde F., Dogterom M., Leibler S. Control of microtubule dynamics and length by cyclin A- and cyclin B-dependent kinases in Xenopus egg extracts. J. Cell Biol. 1992;118:1097–1108. doi: 10.1083/jcb.118.5.1097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Dogterom M., Leibler S. Physical aspects of the growth and regulation of microtubule structures. Phys. Rev. Lett. 1993;70:1347–1350. doi: 10.1103/PhysRevLett.70.1347. [DOI] [PubMed] [Google Scholar]
- 40.Gardner M.K., Zanic M., Howard J. Depolymerizing kinesins Kip3 and MCAK shape cellular microtubule architecture by differential control of catastrophe. Cell. 2011;147:1092–1103. doi: 10.1016/j.cell.2011.10.037. [DOI] [PubMed] [Google Scholar]
- 41.Wall M.E., Rechtsteiner A., Rocha L.M. Singular value decomposition and principal component analysis. In: Berrar D.P., Dubitzky W., Granzow M., editors. A Practical Approach to Microarray Data Analysis. Springer US; 2003. pp. 91–109. [Google Scholar]
- 42.Golub G.H., Van Loan C.F. Johns Hopkins University Press; Baltimore, MD: 1966. Matrix Analysis. [Google Scholar]
- 43.Bowne-Anderson H., Zanic M., Howard J. Microtubule dynamic instability: a new model with coupled GTP hydrolysis and multistep catastrophe. BioEssays. 2013;35:452–461. doi: 10.1002/bies.201200131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Doodhi H., Prota A.E., Steinmetz M.O. Termination of protofilament elongation by eribulin induces lattice defects that promote microtubule catastrophes. Curr. Biol. 2016;26:1713–1721. doi: 10.1016/j.cub.2016.04.053. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.