Combining Multiple Biomarker Models in Logistic Regression

Summary.

In medical research, there is great interest in developing methods for combining biomarkers. We argue that selection of markers should also be considered in the process. Traditional model/variable selection procedures ignore the underlying uncertainty after model selection. In this work, we propose a novel model-combining algorithm for classification in biomarker studies. It works by considering weighted combinations of various logistic regression models; five different weighting schemes are considered in the article. The weights and algorithm are justified using decision theory and risk-bound results. Simulation studies are performed to assess the finite-sample properties of the proposed model-combining method. It is illustrated with an application to data from an immunohistochemical study in prostate cancer.

1. Introduction

Biomarkers play an important role in medical research (Biomarkers Definitions Working Group, 2001). Using novel genomic and proteomic technologies, new biomarkers are constantly being discovered. It is becoming increasingly clear that one single biomarker will not be sufficient to serve as an optimal screening device for early detection or prognosis for many diseases (Sidransky, 2002). It has been suggested that a combination of multiple biomarkers will potentially lead to more sensitive screening rules for detecting cancer (Etzioni et al., 2003). One example comes from ovarian cancer, where multiple serum markers from patients are being used to assess disease (Bast et al., 2005). A combination of two markers, Mesothelin and HE4, produces an improved receiver-operating characteristic (ROC) curve relative to that for either marker individually. The resulting composite marker can improve sensitivity without losing specificity. Therefore, the natural answer to improve the clinical performance of a single biomarker is to combine the information from multiple markers. As Bast et al. (2005) argue, new statistical methods must be developed to facilitate multiple marker analysis and improve clinical performance compared with the evaluation of individual markers.

We consider a data set from an immunohistochemical study in prostate cancer conducted at the University of Michigan with eight biomarkers: ECAD, MIB1, P27, TPD52, BM28, MTA1, AMACR, and XIAP. The biomarkers have been selected from previous gene expression studies in the literature on prostate cancer. The data have a two-level structure. The upper level is the patient level, where a group of patients are followed to observe their recurrence time to prostate cancer. The lower level is the core level within each patient. The tumor sample of each patient is divided into several fractions. The core is a fraction of the tumor sample. Each biomarker is measured at each core on a continuous scale of protein-staining intensities using the method developed in Bauer et al. (2000). The tissue microarray is used as a high-throughput tool to assess the protein-staining at the core level. The goal of the study is to establish relationships between the protein staining intensities of the eight biomarkers and the clinical outcomes. The clinical outcome of interest in this article is the diagnostic status of the tumor sample being cancerous or not at the core level, which is binary. The eight biomarkers serve as continuous independent predictors. We are interested in combining multiple biomarkers in order to achieve better prediction in the context of logistic regression models for binary data.

There has been much recent work developing methods for combining multiple biomarkers. Su and Liu (1993) and Pepe and Thompson (2000) considered linear combinations of biomarkers to optimize measures of diagnostic accuracy. McIntosh and Pepe (2002) noted the optimality of the likelihood ratio. Etzioni et al. (2003) proposed developing screening rules based on the consideration of logical combinations of biomarker measurements.

The methods described in the previous paragraph all attempt to find the best combination of all available biomarkers, which we term a full model approach. However, there are plenty of biomarkers being discovered through genomic and proteomic technologies. This necessitates selecting biomarkers and leads to the problem of variable/model selection. When multiple plausible models are present, the traditional approach is to use a model selection criteria to select a “best” model. This selected model is then used for subsequent inference and prediction. A large amount of work has been done on the topic of model selection. These procedures ignore the uncertainty in model selection. This could lead to poor prediction and diagnostic accuracy on independent data sets.

Because the natural objective in these studies is prediction, an alternative approach is to combine predications from multiple models. These procedures have been considered from a Bayesian viewpoint (Hoeting et al., 1999) as well as a frequentist one (Yang, 2001). We consider the latter approach here. In this article, we extend the algorithm of Yuan and Yang (2005), called adaptive regression by mixing with screening (ARMS), to logistic regression. We propose several weighting schemes for combining biomarker logistic models and compare their prediction performance with that of a full model and Akaike information criteria (AIC; Akaike, 1973)-selected model. In addition, we develop both risk-bound results as well as a decision-theoretic framework to theoretically justify the algorithm.

The article is organized as follows. In Section 2, we outline the model and describe the ARMS algorithm. A risk-bound result for the algorithm, Theorem 1, is also presented here. In Section 3, we propose various weighting methods for the algorithm and describe a decision-theoretic framework for the justification of certain weights. In Section 4, we study the finite-sample performance of the proposed algorithm. Simulation studies are performed to compare ARMS with Bayesian model averaging (BMA; Hoeting et al., 1999) and model selection methods in logistic regression. In addition, we apply the proposed methodology to the previously mentioned tissue microarray data from the immunohistochemical study in prostate cancer. We conclude with some discussion in Section 5.

2. Proposed Methodology

2.1. Data and Model Setup

Suppose we have p biomarkers available in a biomarker study on n individuals. The data are (D_i, $X_i^{*}$), i = 1, … , n, independent and identically distributed (i.i.d.) observations from (D, X*), where D is the indicator of disease and X* is the p-dimensional biomarker profile. Let X = ($1_n^{\prime }$, X*) be the design matrix in the logistic regression model. We consider logistic regression models of the following form:

$$\text{logit}P\left(D_i=1|X_i\right)=f\left(X_i,\beta \right)=X_i\beta ,$$

where f(·) is the true regression function and β = (β₀, β₁, … , β_p). For estimating f, there will be 2^p models (including the trivial intercept-only model) to be considered as candidates. Let Γ denote the set of all candidate models being considered. The kth model is given by

$$\text{logit}P\left(D_i=1|X_i\right)=f_k\left(X_{ki},{\beta }_k\right)=X_{ki}{\beta }_k,i=1,\dots ,n,$$

where X_k is a subset of X.

The goal of model selection is to find a “best” f_k(X_ki, β_k) that fits the data; by contrast, that of model combining is to combine multiple plausible good models with appropriate weights.

2.2. ARMS for Logistic Regression

Yang (2001) proposed ARM (adaptive regression by mixing), a method for combining linear regression models. He examined its theoretical convergence properties and empirically demonstrated its adaptation ability (having the best convergence rate under a global L₂ loss over various scenarios) in nonparametric estimation with a small number of candidate procedures. To deal with a large number of candidate linear regression models, Yuan and Yang (2005) proposed an improved ARM with a model-screening step (ARMS) in linear regression. They did not include all candidate models for combining. Instead, (AIC; Akaike, 1973) and Bayes information criteria (BIC; Schwarz, 1978) criteria were used to find good candidate models for combining. They showed that the reduction of the number of models for combining substantially reduces the computation cost and also is advantageous from a theoretical point of view.

In this article, we extend ARMS to the binary outcome setting. There are three main steps involved for the new version of ARMS. In the first step, half of the sample is used as a training set to estimate the parameters for each model; the other half is used as a test set. The second step consists of using AIC to select the number of most promising candidate models for combining, namely, a screening step. At the third step, the response values in the test set are predicted using the fitted models obtained from the training set and the prediction performance is assessed by comparing the predicted values with the true ones. Then the models are weighted according to the prediction performance assessment. The following is the ARMS algorithm for logistic regression:

1. Randomly permute the order of the observations and let r denote the rth permutation. For simplicity, assume that the sample size n is even. Split the data into two parts Q^(1,r) = (D_i, X_i), 1 ≤ i ≤ n/2 and Q^(2,r) = (D_i, X_i), n/2 + 1 ≤ i ≤ n.

2. Define Γ to be the entire model space or the set of all possible candidate models. Estimate β_k by ${\widehat{\beta }}_{k,n/2}^r$ using maximum likelihood based on Q^(1,r) for each candidate logistic model k in Γ. Compute the AIC values for each model k based on Q^(1,r) and keep the top m models with the smallest AIC values. Let ${\Gamma }_s^r$ denote the screening set of the selected models, where $\text{dim}\left({\Gamma }_s^r\right)=m$. This step is called AIC model screening.

3. Assess the accuracies of the models in ${\Gamma }_s^r$ based on the second half of the data Q^(2,r). For each model $k\in {\Gamma }_s^r$, compute a model accuracy measurement $B_k^r$ using a weighting method that we present in Section 3.1.

4. Compute the weight for each model $k\in {\Gamma }_s^r$ based on $B_k^r$ in step 3:

   $$W_k^r=\frac{B_k^r}{\sum _{j\in {\Gamma }_s^r}{B}_j^r}.$$

   Note that ${\sum }_{k\in {\Gamma }_s^r}{W}_k^r=1$.

5. Repeat steps 1–4 (n_p − 1) more times and obtain an average weight ${\widehat{W}}_k=n_p^{-1}{\sum }_{r=1}^{n_p}{W}_k^r$ for each model k over n_p permutations. The parameter n_p is chosen to be 20 in our work. Let ${\Gamma }_s=\cup {\left\{{\Gamma }_s^r\right\}}_{r=1}^{n_p}$ denote the union of the screening sets over n_p permutations.

6. Let ${\widehat{f}}_{k,n}(x)={\widehat{f}}_k\left(x;{\widehat{\beta }}_{k,n}\right)=x_k{\widehat{\beta }}_{k,n}$ be the estimator of the regression function f_k =x_k β_k of the logistic model k based on all data, where x_k is a subset of x. The final ARMS combined estimator of the regression function f is

   $${\widehat{f}}_n(\text{x})=\sum _{k\in {\Gamma }_s}{\widehat{W}}_k{\widehat{f}}_{k,n}(\text{x}).$$

Note that our final estimator combines the union of the models selected across the permutations.

Screening by AIC can remove some very poor models, which would affect the performance of the combined estimator of the ARMS method. Of course, other model selection criteria could also be used for screening, such as BIC. The purpose of model screening is to get a list of plausible candidate models and remove other very poor models. So in this article, we decide to stick to AIC model screening for the purpose of illustration and simplicity.

Ideally, the number of models, $\text{dim}\left({\Gamma }_s^r\right)=m$, to include in the procedure should strike a balance between the number of models and the variability in the resulting predictions. This is very similar to the bias-variance tradeoff in other areas of statistics (Liu and Brown, 1993; Low, 1995). Here, we take m to be 20.

Although we fit logistic regression models in the algorithm, we do not require the assumption that the true model is logistic. The algorithm will adaptively obtain a combined estimator that gives a good estimate of the true model even if the true model is not of the logistic form.

2.3. Risk Bound of the ARMS under Bernoulli Likelihood Weights

Regarding the ARM method of combining procedures, Yang (2001) gave a risk-bound result and an improvement was made in Yuan and Yang (2005) for ARMS. Those papers dealt with linear regression. No known results exist for logistic regression models. In this section, we show that the ARMS estimator under Bernoulli likelihood weights in logistic regression provides adaptivity among all possible candidate models and its L₂ risk is bounded by the minimum L₂ risk of all candidate models plus a small penalty.

Suppose we have K available candidate models for combining. Let $\widehat{f}\left(x_i\right)=Pr\left(D_i=1|x_i\right)$ be the probability of having disease; let ${\widehat{f}}_j\left(x_i\right)$ be the maximum likelihood estimate of f(x_i) for model j. Define $P_f\left(d_i\right)=\widehat{f}{\left(x_i\right)}^{d_i}{\left(1-\widehat{f}\left(x_i\right)\right)}^{1-d_i}$ and $P_{{\widehat{f}}_j}\left(d_i\right)={\widehat{f}}_j{\left(x_i\right)}^{d_i}{\left(1-{\widehat{f}}_j\left(x_i\right)\right)}^{1-d_i}$. Similar to Yang (2001), for the theoretical result, we study a slightly different combined estimator from the one we defined in the ARMS algorithm. Let λ_j be a set of positive numbers satisfying ${\sum }_{j=1}^K{\lambda }_j=1$. They are prior weights of the candidate models. One natural choice is uniform prior weights, that is, λ_j = 1/K. Let W_j,i be the weights for model j based on the first i observations and let ${\tilde{W}}_j$ be the modified weight for model j. For i = n/2 + 1, let W_j,i = λ_j and for n/2 + 1 ≤ i ≤ n, let

$$\begin{gathered} W_{j,i}=\frac{{\lambda }_j\prod _{s=n/2+1}^{i-1}\left\{{\left({\widehat{f}}_j\left(x_s\right)\right)}^{d_s}{\left(1-{\widehat{f}}_j\left(x_s\right)\right)}^{1-d_s}\right\}}{\sum _l\left\{{\lambda }_l\prod _{s=n/2+1}^{i-1}\left\{{\left({\widehat{f}}_l\left(x_s\right)\right)}^{d_s}{\left(1-{\widehat{f}}_l\left(x_s\right)\right)}^{1-d_s}\right\}\right\}} \\ =\frac{{\lambda }_j\prod _{s=n/2+1}^{i-1}{P}_{{\widehat{f}}_j}\left(d_s\right)}{\sum _l\left\{{\lambda }_l\prod _{s=n/2+1}^{i-1}{P}_{{\widehat{f}}_l}\left(d_s\right)\right\}}. \end{gathered}$$

Then let ${\tilde{f}}_i\left(x_s\right)={\sum }_j{W}_{j,i}{\widehat{f}}_j\left(x_s\right)$ be a combined estimator based on the first i observations. Then the modified estimator is

$${\widehat{f}}_n^{*}(x)=\frac{1}{n/2}\sum _{i=n/2+1}^n{\tilde{f}}_i(x).$$

Note that ${\widehat{f}}_n^{*}$ depends on the order of observations. For applications (as in the ARMS algorithm), we can randomly permute the order a number of times and average ${\widehat{f}}_n^{*}$ over the permutations to average out the order effect, which results in the estimator ${\widehat{f}}_n$ of the ARMS algorithm (Yang, 2001). Thus the risk-bound results certainly apply to the improved estimator ${\widehat{f}}_n$ using permutations. For the theoretical development, we focus on ${\widehat{f}}_n^{*}$.

For an estimator $\widehat{f}$ of f, let $\Vert f-\widehat{f}{\Vert }^2={\int \left(f\left(x\right)-\widehat{f}(x)\right)}^{2}d\mu (x)$. The theorem on the risk-bound results requires the following conditions.

Condition 1:

We assume that for each model j, the estimators of the probabilities are uniformly bounded away from 0 and 1, that is, there exists constants 0 ≤ A_j ≤ 1/2 such that $A_j\le {\widehat{f}}_j\left(x_s\right)\le 1-A_j$ for all x_s.

Condition 2:

Let Γ denote the set of all candidate models in the model space before screening. There exists a constant τ ≥ 0 such that with probability one, we have

$$su{p}_{j\in \Gamma }\Vert f-{\widehat{f}}_j\Vert \le \sqrt{\tau }.$$

Theorem 1:

Let Γ_s denote the union set of the models screened by AIC and let K_s denote the size of Γ_s. Let λ_j be λ_j = 1/K_s. Assuming that conditions 1 and 2 are satisfied, then for any j ∈ Γ, the L₂ risk of ${\widehat{f}}_n^{*}$ using ARMS satisfies

$$\begin{gathered} E{\Vert f-{\widehat{f}}_n^{*}\Vert }^2 \\ \le \tau P\left(j\notin {\Gamma }_s\right)+2\left\{\frac{\text{log}\left(K_s\right)}{n/2}+\frac{2}{A_j^2}E{\Vert f-{\widehat{f}}_j\Vert }^2\right\}P\left(j\in {\Gamma }_s\right) \\ \le \tau P\left(j\notin {\Gamma }_s\right)+2\left\{\frac{\text{log}(K)}{n/2}+\frac{2}{A_j^2}E{\Vert f-{\widehat{f}}_j\Vert }^2\right\}{B}_0, \\ \le \tau P\left(j\notin {\Gamma }_s\right)+\frac{4B_0\text{log}(K)}{n}+\frac{4B_0}{A_j^2}E{\Vert f-{\widehat{f}}_j\Vert }^2, \end{gathered}$$

where we assume that P(j ∈ Γ_s) is upper bounded by a constant B₀, and K denotes the size of the model space Γ.

The proof of Theorem 1 is given in Web Appendix A, available in the Supplementary Materials at the Biometrics website. From Theorem 1, K₀, B₀, A, and τ are finite constants. Guyon and Yao (1999) and Zhang (1993) showed that $P\left(j\cancel{\in }{\Gamma }_s\right)\le c_1{e}^{-c_2{n}^{c}3}$ for some positive constants c₁, c₂, c₃ for a model selection criterion of a penalized log-likelihood term with penalty term λ_n p. Therefore the ARMS-combined estimator ${\widehat{f}}_n^{*}$ converges automatically at the best rate of convergence in terms of L₂ risk among the estimators ${\left\{{\widehat{f}}_j\right\}}_{j\in \Gamma }$ of all candidate models. In addition, for ARMS, we do not require that the set of candidate models contains the true model. The risk-bound result for ARMS holds regardless of whether the true model exists in the model space.

3. Combining Weights in ARMS

3.1. Description

Yuan and Yang (2005) used the normal likelihood to construct weights for linear regression models. In the logistic regression models for binary data, we propose five different methods to construct weights. For the definition of the weights, k indexes the model being fitted.

1. Bernoulli likelihood weights

   The analog of the normal likelihood-based weights from Yuan and Yang (2005) in the current setting would be those based on a Bernoulli likelihood:

   $$B_k^L\equiv L_k=\prod _{i=1}^n\left[{\widehat{f}}_k{\left(X_i\right)}^{D_i}{\left\{1-{\widehat{f}}_k\left(X_i\right)\right\}}^{1-D_i}\right],$$

   where $B_k^L$ is called model accuracy measure. Then weights are constructed to be proportional to the likelihood:

   $$W_k^L=\frac{B_k^L}{\sum _{j\in {\Gamma }_s}{B}_j^L}.$$

2. AIC weights

   We use an exponentiated function of AIC as the model accuracy measure:

   $$B_k^{AIC}\equiv \text{exp}\left(-AI{C}_k\right)=L_k\text{exp}\left(-p_k\right),$$

   where p_k is the number of parameters in model k. Note that it is a product of the Bernoulli likelihood and the penalty term from the AIC criterion. The corresponding weights are constructed proportional to $B_k^{AIC}$.

3. Generalized degrees of freedom weights

   Ye (1998) proposed a notion of the generalized degrees of freedom (GDF) in a linear model setup. The definition of GDF was extended to a general exponential family by Shen, Huang, and Ye (2004). Ye (1998) argued that the GDF can be used as a measure of the complexity or cost of a general modeling procedure. Thus we use the generalized degrees of freedom GDF_k to replace p_k in the AIC weights:

   $$B_k^{GDF}\equiv L_k\text{exp}\left(-GD{F}_k\right),$$

   where GDF_k is the GDF of model k. The GDF in logistic regression is calculated using data perturbation technique (see Web Appendix B in the Supplementary Materials at the Biometrics website for details). The corresponding weights are constructed proportional to $B_k^{GDF}$.

4. Absolute prediction error weights

   Absolute prediction error is often used in practice to indicate how well the model fits; it is defined as $d_{abs}-d_{abs,x}^k$, where $d_{abs}=2{\sum }_{i=1}^n\left|D_i-{\widehat{f}}_0\right|/n$, ${\widehat{f}}_0$ is the estimated intercept-only model, and $d_{abs,x}^k={\sum }_{i=1}^n\left|D_i-{\widehat{f}}_k\left(X_i\right)\right|/n$. One can construct weights using the following model accuracy measure:

   $$B_k^{APE}\equiv \left(d_{abs}-d_{abs,x}^k\right)/d_{abs}.$$

5. Standardized residual weights

   A common goodness-of-fit diagnostic for a model is the residuals. They can be used to construct weights as well. In particular, we define model accuracy measurement as the inverse of the sum of squared standardized residuals:

   $$B_k^{\mathit{\text{RESID}}}\equiv \frac{1}{\sum _i{e}_{ki}^2},$$

   where $e_{ki}=\left(D_i-{\widehat{f}}_k\left(x_i\right)\right)/{\left\{{\widehat{f}}_k\left(x_i\right)\left(1-{\widehat{f}}_k\left(x_i\right)\right)\right\}}^{1/2}$. Note that e_ki is the standardized Pearson residual for the kth model and the ith subject.

The intuitive idea of weight assignment is that models with good prediction performance will be given larger weight, whereas those with worse prediction performance will be given smaller weight. All of the above weighting methods are used in step 4 of the ARMS algorithm to compute the model accuracy measure B_k. We will compare their performance in Section 2.4 in simulation studies and the real data example.

3.2. Weights for ARMS: Decision Theory Framework

Yuan and Yang (2005) pointed out that their weights can be interpreted as posterior probabilities of the models after observing the second part of the data with the uniform prior on the linear regression estimates from the first part of the data.

Three of our weighting methods have posterior probabilities interpretation with different corresponding priors. The Bernoulli likelihood weight corresponds to the posterior likelihood with a uniform prior. The AIC weight and GDF weight correspond to the posterior likelihood with priors exp(−p_k) and exp (−GDF_k), respectively.

We now provide an informal justification that the posterior probabilities have an optimal model-ranking property in a decision theory framework. A related result was derived by Müller et al. (2004) for a microarray problem for genes ranking. We consider a model space in which some models are good approximations to the true model, whereas the remaining models are not. We refer to the former class of models as good models; note that we are being loose with the terminology. The goal is to make decisions on whether each model i in the model space is a good model or not. We let e_i ∈ {0, 1} denote an indicator of being a good model for model i. Let v_i ≡ P(e_i = 1 | D) denote the marginal posterior probability of being a good model for model i. The decision to be made is whether the ith model is selected as a good one (denoted by s_i = 1) or not (denoted by s_i = 0). We have m decisions to make if we have m candidate models in the model space. We let $S\equiv {\sum }_{i=1}^m{s}_i$ denote the number of positive decisions, where the positive decision is defined to be a decision of selecting model i as a good model. Then we let

$$FD(s,e)\equiv \sum _{i=1}^m{s}_i\left(1-e_i\right)$$

$$FN(s,e)\equiv \sum _{i=1}^m\left(1-s_i\right)e_i$$

denote the number of realized false-positive decisions and false-negative decisions. Conditioning on S and marginalizing with respect to D, we obtain the posterior expected count of false-positive decisions and false-negative decisions:

$$\widehat{FD}(s,v)=\sum _{i=1}^m{s}_i\left(1-v_i\right),$$

$$\widehat{FN}(s,v)=\sum _{i=1}^m\left(1-s_i\right)v_i.$$

We consider the following posterior expected loss for our decision framework,

$$L_N(s,v)=c\widehat{FD}+\widehat{FN},$$

where c is a constant parameter used to balance the importance of false-positive decisions and false-negative decisions. If both are equally important, then c = 1. We now state the following theorem.

Theorem 2:

Under the loss function L_N (s, v), the optimal decision takes the form

$$s_i=I\left\{v_i\ge t^{*}\right\},$$

where t* = c/(c + 1).

Proof. Subject to a fixed total number of positive decisions $S\equiv {\sum }_{i=1}^m{s}_i$,

$$L_N(s,v|S)=cS-(c+1)\sum _{i=1}^m{s}_i{v}_i+\sum _{i=1}^m{v}_i.$$

The last term does not involve the decisions. For any fixed S, the quantity is minimized by setting s_i = 1 for the S largest v_i. In other words, for any S, the optimal rule is of the type s_i = I(v_i ≥ t*), where t* is the (m − S)th order statistic of (v₁, … , v_m). Thus the global minimizer must be of the same form. Some straightforward algebra shows that the minimum is achieved for t* = c/(c + 1).

Because Theorem 2 shows that the decision based on the posterior probabilities v_i ≡ P(e_i = 1 | D) is optimal and minimizes the loss function, this provides an informal motivation for using the posterior probabilities or posterior likelihood to assign weights in our model-combining method. The Bernoulli likelihood weights, AIC weights, and GDF weights all have posterior likelihood interpretation with certain priors. Thus we expect that these three weights should give good performance from a decision-theoretic point of view, compared with other forms of weights.

4. Numerical Examples

4.1. Simulation Studies

We perform extensive simulation studies in order to assess the finite-sample properties of the proposed ARMS method. Sample sizes of 100 and 400 are considered; the number of random permutations for ARMS is set to be 20. The estimation methods are evaluated based on several criteria: L₂ risk, L₁ risk, error probability (EP), and the area under ROC curve (AUC) based on 1000 simulations. Note that better prediction is associated with lower EP, L₁, and L₂ values but higher AUC values. In simulation studies, because we know the true model, we generate an independent data set to compute the L₂, L₁, EP, and AUC values.

For simplicity, we refer to the ARMS methods with Bernoulli, AIC, GDF, absolute prediction errors, and standardized residuals weights as ARMS-LIKELI, ARMS-AIC, ARMS-GDF, ARMS-APE, and ARMS-RESID, respectively.

In addition, because the BMA method (Hoeting et al., 1999) can often produce better prediction results than any single model, we also compare our ARMS method with BMA in simulation. The BMA is implemented by using the BMA package in R, available at the following website: http://www.research.att.com/~volinsky/bma.html. Default parameter settings for the BMA software are used in the simulations. The assumption that all candidate models are equally likely a priori is used (a uniform prior on the model space); normal conjugate priors are used for the coefficients of each candidate model. The hyperparameters in the normal priors of coefficients are estimated using the summary statistics of the data under each candidate regression model.

In the simulation studies, because we know the true model, we generate an independent data set to compute the L₂ risk, L₁ risk, EP, and AUC values. We generate a panel of eight biomarkers X* ≡ (X₁, … , X₈) from multivariate normal distribution with zero mean, unit variance, and correlation 0.3. Then the binary responses are generated from the prespecified underlying true model.

Because of space limitations, we only present one set of simulation results; others can be found in Web Appendix C of the Supplementary Materials, available from the Biometrics website. Here, we study the following case:

Case 1:

We use the following true model relating biomarkers with disease status:

$$\text{logit}P(D=1)=1.0+0.1X_1+0.2X_2+0.3X_3+0.4X_4\text{+}0.5X_5\text{+}{X}_1{X}_2.$$

Note that we only consider the models with main effects in the ARMS algorithm so that the true model is not in the space of candidate models for combining in this case. The results are shown in Table 1 and Table 2. Among all ARMS methods, we find that the ARMS methods with the GDF, AIC, and Bernoulli likelihood weights perform better than others and the ARMS method with the GDF weight performs the best. For the sample size of 100, the ARMS-LIKELI, ARMS-AIC, and ARMS-GDF methods have 10–14% smaller prediction risks and 7–10% higher AUC values than the AIC-selected model. For the sample size of 400, the ARMS-LIKELI, ARMS-AIC, and ARMS-GDF methods still have smaller prediction risks and higher AUC values than the AIC-selected model, although the discrepancy is reduced. Sample size affects the difference between the AIC-selected model and the ARMS methods. This is because the data with smaller sample size exhibit more instability with respect to model selection procedures. Model combining thus performs better than selection when sample size is 100 compared with sample size 400. For both sample sizes, the ARMS-GDF method has better prediction performance than the BMA method. ARMS-GDF shows bigger gains at the sample size of 100 relative to the sample size of 400.

Table 1.

ARMS simulation results of case 1 with n = 100^*

Method	L2 risk	L1 risk	EP	AUC
ARMS-LIKELI	0.087	0.191	0.391	0.771
	(0.002)	(0.003)	(0.007)	(0.007)
ARMS-AIC	0.085	0.188	0.385	0.773
	(0.002)	(0.003)	(0.007)	(0.007)
ARMS-GDF	0.082	0.181	0.372	0.792
	(0.002)	(0.003)	(0.006)	(0.007)
ARMS-APE	0.093	0.203	0.411	0.744
	(0.002)	(0.003)	(0.007)	(0.008)
ARMS-RESID	0.093	0.201	0.409	0.742
	(0.002)	(0.003)	(0.007)	(0.008)
BMA	0.090	0.196	0.401	0.751
	(0.002)	(0.003)	(0.007)	(0.008)
AIC	0.096	0.211	0.418	0.718
	(0.002)	(0.003)	(0.007)	(0.008)
Full	0.099	0.218	0.426	0.709
	(0.002)	(0.003)	(0.007)	(0.008)
True	0.063	0.143	0.328	0.865

^*The Bernoulli, AIC, GDF, absolute prediction errors, and standardized residuals weights as ARMS-LIKELI, ARMS-AIC, ARMS-GDF, ARMS-APE, and ARMS-RESID, respectively. Number in parentheses is standard error over 1000 simulations.

Table 2.

ARMS simulation results of case 1 with n = 400^*

Method	L2 risk	L1 risk	EP	AUC
ARMS-LIKELI	0.0181	0.101	0.379	0.811
	(0.0002)	(0.001)	(0.003)	(0.004)
ARMS-AIC	0.0178	0.099	0.375	0.816
	(0.0002)	(0.001)	(0.002)	(0.004)
ARMS-GDF	0.0172	0.096	0.368	0.827
	(0.0002)	(0.001)	(0.002)	(0.004)
ARMS-APE	0.0186	0.103	0.389	0.798
	(0.0002)	(0.001)	(0.003)	(0.004)
ARMS-RESID	0.0188	0.105	0.392	0.793
	(0.0003)	(0.001)	(0.003)	(0.004)
BMA	0.0182	0.102	0.384	0.809
	(0.0002)	(0.001)	(0.003)	(0.004)
AIC	0.0191	0.107	0.397	0.775
	(0.0003)	(0.001)	(0.003)	(0.005)
Full	0.0198	0.110	0.403	0.768
	(0.0003)	(0.001)	(0.004)	(0.005)
True	0.0141	0.076	0.333	0.879

^*See footnote in Table 1.

The Bernoulli, GDF, and AIC-based weights tend to give better prediction performance in the simulation studies relative to the other weights considered across the scenarios considered here. Intuitively, these methods are approximating the posterior model probabilities better than the other weights. The decision theory framework described in Section 3.2 gives some justification for these three weights being optimal.

To explore the robustness of our biomarker combining methods, we also used multivariate t distributions to generate data. We found a similar pattern of results to those presented here (data not shown).

4.2. Prostate Cancer Real Data Example

In this section, we apply the ARMS combining method to the real data set from an immunohistochemical study in prostate cancer described in the Introduction. The binary response is the diagnostic status of the cancer sample being cancerous or not at the core level. The predictors are eight biomarkers in the data: ECAD, MIB1, P27, TPD52, BM28, MTA1, AMACR, and XIAP. They are normalized and standardized to be nonskewed and approximately normal variables. Logistic regression models are fit in the analysis. There are five blocks of data. Only the first block of data is considered here. We exclude the observations with missing values on either response or predictors. This results in n = 200 complete observations (139 cases and 61 controls).

Boxplots comparing intensity measurements of each marker between two disease groups (cancer versus non-cancer) are shown in Figure 1. Seven of the eight biomarkers have higher mean intensity in the cancer group and the other one has higher mean intensity in the noncancer group. Among them, AMACR shows the largest difference and P27 shows the smallest difference. However, we observe that there is substantial overlap between the boxes of two groups, which implies that using any individual biomarker might not be sufficient for the purposes of prediction. We apply our ARMS combining methods on the data and compare it with the full model, the AIC-selected model and the best univariate (AMACR) model.

Figure 1.

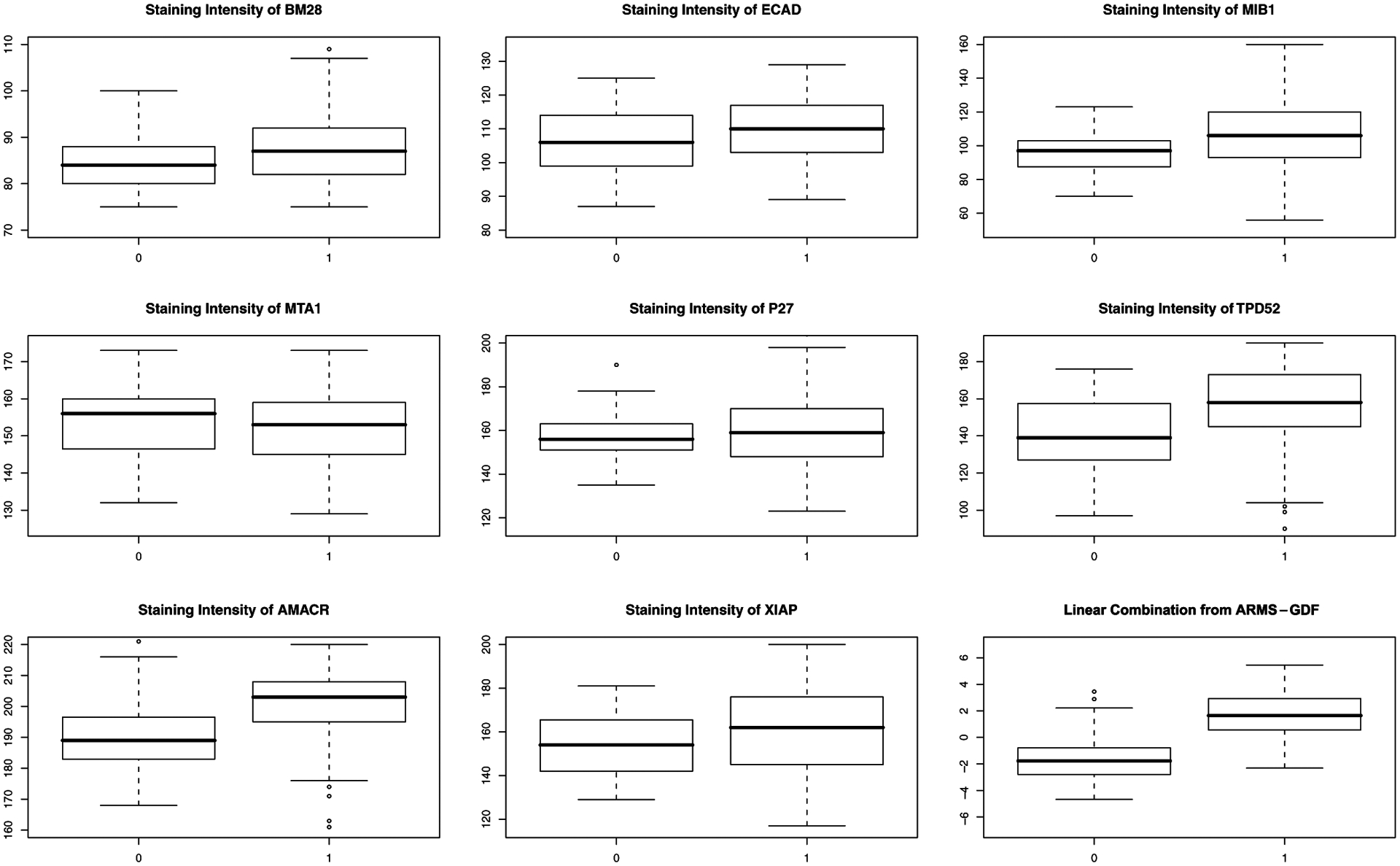
Boxplots of the staining intensities of eight biomarkers and their linear combination from the ARMS-GDF method in prostate cancer data classified by the cancer (1) group versus the non-cancer (0) group.

The performance comparison is done as follows. First, we split the data into two parts: Ω⁽¹⁾ with n₁ = 134 observations and Ω⁽²⁾ with n − n₁ = 66 observations. The first part data Ω⁽¹⁾ is used for estimation, whereas the second part data Ω⁽²⁾ serves as the validation set for performance assessment. Second, we apply the ARMS algorithm on the first part data Ω⁽¹⁾ to get the combined estimator. Third, we compute the L₂, L₁, EP, and AUC values of the combined estimator based on the second part data Ω⁽²⁾. Finally, we randomly permute the order of the observations in the data 1000 times and repeat steps 1–3 to obtain the average L₂, L₁, EP, and AUC values over the 1000 permutations. The results are given in Table 3. The results show that even the best univariate model has much higher prediction risks and much lower AUC values than any other multivariate methods. Again, the ARMS methods with the GDF, AIC, and Bernoulli weights perform better than both the AIC-selected model and the full model; the ARMS-GDF method performs the best among all. Therefore we exhibit gains in predictive accuracy using the ARMS methods compared with either the full model or the AIC-selected model. The separation achieved by the ARMS procedure is shown in Figure 1 as well.

Table 3.

A comparison of ARMS with AIC, full, and best univariate models in logistic regression for prostate cancer data (n = 200) under 1000 random permutations

Method	L2 risk	L1 risk	EP	AUC
ARMS-LIKELI	0.083	0.169	0.388	0.79
	(0.002)	(0.004)	(0.006)	(0.01)
ARMS-AIC	0.082	0.166	0.382	0.80
	(0.002)	(0.004)	(0.006)	(0.01)
ARMS-GDF	0.078	0.159	0.373	0.82
	(0.002)	(0.004)	(0.006)	(0.01)
ARMS-APE	0.087	0.175	0.398	0.77
	(0.003)	(0.005)	(0.007)	(0.01)
ARMS-RESID	0.088	0.177	0.401	0.76
	(0.003)	(0.005)	(0.007)	(0.01)
AIC	0.089	0.179	0.405	0.76
	(0.003)	(0.005)	(0.007)	(0.01)
Full	0.095	0.193	0.418	0.73
	(0.003)	(0.005)	(0.007)	(0.01)
Univariate (AMACR)	0.106	0.214	0.439	0.70
	(0.003)	(0.006)	(0.008)	(0.01)

Although the focus of the ARMS combining method has been on assessing prediction performance, it is also possible to select biomarkers based on their average weights across models. From the ARMS combining estimator ${\widehat{f}}_n(x)$, we have

$$\begin{gathered} {\widehat{f}}_n(x)=\sum _{k\in {\Gamma }_s}{\widehat{W}}_k{\widehat{f}}_k\left(x;{\widehat{\beta }}_k\right)=\sum _{k\in {\Gamma }_s}{\widehat{W}}_k\sum _{j=1}^p{\widehat{\beta }}_{kj}{x}_j \\ =\sum _{j=1}^p\left\{\sum _{k\in {\Gamma }_s}\left({\widehat{W}}_k{\widehat{\beta }}_{kj}\right)\right\}{x}_j, \end{gathered}$$

where we assume ${\widehat{\beta }}_{kj}=0$ if biomarker x_j is not selected in the model k. Thus the average weights for each biomarker is actually ${\sum }_{k\in {\Gamma }_s}\left({\widehat{W}}_k{\widehat{\beta }}_{kj}\right)$. The results are shown in Table 4, which include both the average weights of each biomarker and the prediction results of its corresponding univariate analysis. We see that the ranking tends to be concordant across the univariate and multivariate analyses. The biomarkers that are more discriminatory from the univariate analyses tend to have larger weights. The two biomarkers, AMACR and TPD52, are assigned by the weights 0.76 and 0.84, respectively, which are approximately four times the weight of P27.

Table 4.

Biomarker weights for prostate cancer data and corresponding univariate prediction performance results: the first row are the final weights assigned to each biomarker predictor by ARMS algorithm; second to fourth rows are prediction results of L₂, L₁, and AUC from fitting univariate logistic models of disease status on each biomarker.

Method	BM28	ECAD	MIB1	MTA1	P27	TPD52	AMACR	XIAP
Weights	0.60	0.57	0.65	0.25	0.21	0.76	0.84	0.31
L2 risk	0.123	0.125	0.122	0.137	0.139	0.115	0.106	0.134
L1 risk	0.249	0.251	0.245	0.271	0.278	0.235	0.214	0.267
AUC	0.66	0.66	0.67	0.61	0.59	0.68	0.70	0.62

Originally, we used AIC as a screening criterion. The current implementation requires a complete searching to identify the top 20 models with smallest AIC values. When the dimension of the data or model is large, complete searching is not feasible computationally. In Web Appendix D of the Supplementary Materials, available on the Biometrics website, we describe some data analyses using an adaptive penalty for model selection (Shen et al., 2004). The results appear promising and definitely merit further research.

5. Conclusion

In this article, we propose a model-combining method with an AIC model-screening procedure, called ARMS, for logistic regression models in biomarker studies and propose five different weights for combining logistic models. The adaptive-risk-bound results show that the resulting combined estimator from ARMS has the best rate of convergence in terms of L₂ risk among the estimators of all candidate models. We perform simulations studies for comparing our proposed ARMS method with the AIC-selected model and the full model; then apply it to a real data set from an immunohistochemical study in prostate cancer. The results from both simulation examples and the real data example show that the ARMS combining methods have lower prediction risks and higher AUC values than those based on the AIC-selected model or the full model when the uncertainty of model selection in estimation is not ignorable. Among five weighting methods we proposed, GDF, Bernoulli likelihood, and AIC weights perform better than others and the ARMS method with GDF weights performs the best. All those three weights have posterior likelihood interpretations. We showed in Section 3.2 that the decision by the posterior probabilities v_i ≡ P(e_i = 1 D) is optimal in terms of minimizing the posterior loss function. The framework we have used for justification of ranking using posterior probabilities is greatly different from the theoretical results developed in Yuan and Yang (2005).

Comparison between BMA and our ARMS-GDF method is also done in simulation studies. Our ARMS-GDF method performs significantly better than BMA method when there is large instability, whereas it performs closely as BMA method when the instability is small or the size of underlying true model is small. In addition, when there is data instability, GDF weights performs better than the Bernoulli likelihood and AIC weights in the ARMS algorithm. This suggests that GDF is a more accurate model accuracy criterion than AIC. Differences in BMA and ARMS might reflect this difference in estimation, along with the fact that the current implementation of BMA for logistic regression in R uses the (BIC; Schwarz, 1978) as an approximation to the posterior probability of a good model (B_k in the notation of Section 3.1). In that sense, the R implementation of BMA is a special case of the framework we have proposed in this article. A comparison with the method of Hoeting et al. (1999), which uses fully Bayesian inference Markov chain Monte Carlo methods, would be useful.

What is done in much of statistical practice is to select a model and to do inference and predictions using the model. Our study raises the possibility that combining results from multiple models might be useful for prediction purposes or from a diagnosis point of view when the uncertainty of selection procedure is large or not ignorable for the given data. In practice, it would be quite simple to use the model-combining algorithm. Based on the initial study for validating the panel of biomarkers, one would save the results of the multiple models used for combining and prediction. Given new samples, one could predict the probability of disease using the previously saved output.