The Benefits of Transmission Dynamics Models in Understanding Emerging Infectious Diseases

Abstract

Factors associated with the emergence and transmission of infectious diseases often do not follow the assumptions of traditional statistical models such as linearity and independence of outcomes. Transmission dynamics models are well suited to address infectious disease scenarios that do not conform to these assumptions. For example, these models easily account for changes in the incidence rates of infection as the proportions of susceptible and infectious persons change in the population. Fundamental concepts relating to these methods, such as the basic reproductive number, the effective reproductive number and the susceptible-infected-recovered compartmental models, are reviewed. In addition, comparisons and contrasts are made between the following concepts: microparasites and macroparasites, deterministic and stochastic models, difference and differential equations and homogeneous and heterogeneous mixing patterns. Finally, examples of how transmission dynamics models are being applied to factors associated with emerging infectious diseases, such as zoonotic origins, microbial adaption and change, human susceptibility and climate change, are reviewed.

There is an extensive literature on factors contributing to the emergence and reemergence of infectious diseases. One of the seminal works in this field is the report of Institute of Medicine of the United States National Academies on emerging infectious diseases.¹ A central piece of this work is their convergence model that describes factors that contribute to the emergence of infectious diseases. These include microbial adaption and change, human susceptibility to infection, climate and weather, changing ecosystems, economic development and land use, human demographics and behavior, technology and industry, international travel and commerce, breakdown of public health measures, poverty and social inequality, war and famine, lack of political will and intent to harm. Each of these factors requires complex data collection to be addressed in an epidemiologic study aimed at understanding the emergence of a given infection.

One set of methods that epidemiologists use to better understand emerging infections is mathematical transmission dynamics models. These models describe the transmission of an infectious agent between hosts (humans, animals and/or vectors) in a population. One historical example of their usefulness in furthering our understanding of infections is Sir Ronald Ross’ (1857–1932) hypothesis and mathematical model that a community could eliminate malaria by sufficiently reducing the size of the mosquito population.² Transmission dynamics models such as Sir Ross’ are known to be highly nonlinear³ and cannot be captured with traditional statistical models, requiring instead a range of calculus-based methods. However, the fundamental concept of keeping a model as simple as possible, while accounting for only the most important factors, is similar to what is done in traditional statistical models.³ For example, consider the series of images in Figure 1 . All the panels are sketches of a bull. The simplest sketch lacks detail and could possibly be confused with other animals, such as a cow or a buffalo. As additional detail is added to the sketches, it becomes readily apparent that the sketch is truly a bull. However, to describe how an infectious agent is transmitted between hosts in a large population, a model as rough as the simplest sketch may be sufficient. Despite the science and mathematics involved in developing infectious disease transmission dynamics models, there is also a certain amount of art entailed; and perhaps surprisingly, usually less is more. Chief among many reasons to keep the model simple is to make it easily comprehensible to a wide audience, including both scientists and policy makers.4., 5.

Figure 1.

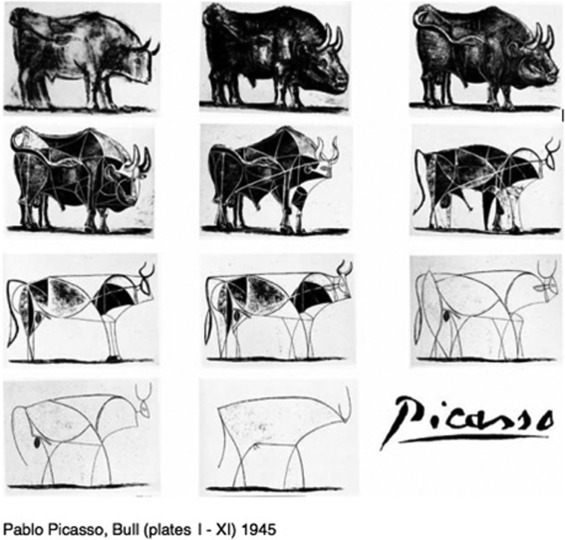
A series of sketches of a bull by Pablo Picasso.

Reprinted with permission from Pablo Picasso/Artists Rights Society (ARS), New York. © 2010 Estate of Pablo Picasso/Artists Rights Society (ARS), New York.

Thus, infectious disease clinicians/epidemiologists are placed in a paradox. The transmission of emerging infections is often complex, involving several hosts and important small population clusters, yet, the most desirable models to describe the transmission are simple. In addition, most clinicians and public health professionals are not exposed to approaches in which theory (in contrast to data) is the base of developing a model. The theory-based model is used to simulate scenarios of transmission and control, which may be later verified by field data. This approach may provoke a sense of unease and skepticism among the uninitiated researcher or clinician. The purpose of this article is to provide a brief overview of some of the common methods used in transmission dynamics models and illustrate their uses in the context of emerging infectious diseases. Ultimately, our goal is to demonstrate that transmission dynamics models can be helpful in better understanding how emerging and reemerging infections are being transmitted and how best to control them.

TRANSMISSION DYNAMICS MODELS AND METHODS

There are a few critical differences between traditional statistical methods (eg, regression) used by most public health professionals and transmission dynamics models. All these differences are related to the different set of assumptions needed for infections that are transmissible from person to person and those that are not.

Differences Between Transmissible and Nontransmissible Diseases

Absence of Independence Between Individuals

Transmissible diseases, such as emerging infections, are different from nontransmissible diseases because the occurrence of 1 case of disease will impact the occurrence of disease in the people with whom this case has been in contact. For example, it is easy to conceive that, if a case of severe acute respiratory syndrome (SARS) is introduced into a household, the household members of that case are more likely to become infected than people who are not in direct contact with that case. In statistics, this phenomenon is called clustering or nonindependence of outcomes and requires the use of specific methods. This would not be true for diseases such as cancer or heart disease in which there is no transmission of an infectious agent. Thus, transmission dynamics models are designed to describe and explain how transmission occurs between contacts.

Nonconstant Incidence Rates

An incidence rate is defined as the number of new cases of a disease occurring divided by the number of people susceptible for that disease during a specific period of time. In nontransmissible disease epidemiology, the number of susceptibles in a population is often fairly constant because the outcome is rare (eg, some cancers and heart disease). In addition, the incidence rate is independent from the number of people affected by the disease in the population. With infectious diseases, the number of individuals infected at any point in time influences the chance that a susceptible individual will contact an infected person. Therefore, the incidence rate of infection is not constant through time and can vary from day to day.

Concept of Threshold of Susceptible

Most infectious agents of humans require human or other animal cells to replicate. Therefore, most infectious agents require a minimum number of hosts to invade to survive. Thus, the most efficient prevention programs will typically rely on vaccines to reduce the number of susceptible hosts and prevent the agent from surviving. When the proportion of the population who is susceptible is reduced below the “threshold of susceptible,” herd immunity is reached, and the agent will become extinct. No such concept exists for nontransmissible diseases.

Fundamental Concepts in Transmission Dynamics Models

Although there is ample literature discussing the concepts of transmission dynamics models,3., 6., 7. we will provide a brief review of some of the fundamentals in the context of microparasitic infections using a deterministic model. First is the basic reproductive number (R ₀). The basic reproductive number is the average number of secondary cases of an infection that will occur once an infectious individual is introduced into a population that is completely susceptible to infection.⁷ There are multiple mathematical definitions for R ₀, depending on the context and model; some definitions use algebraic principles and some use calculus.⁸ One straightforward, algebraic formula is as follows⁷:

$$R_0=\text{number}\text{of}\text{contacts}\text{per}\text{unit}\text{time}\times \text{transmission}\text{probability}\text{per}\text{contact}\times \text{duration}\text{of}\text{infectiousness}=\text{c}\times \text{p}\times \text{d}$$

The application of R ₀ in a given epidemic is short lived, because, after the first infectious individual has transmitted infection to the susceptible contacts, the population is no longer completely susceptible. Thus, to understand the number of subsequent infections from the second generation of infective individuals, another, yet highly related term is needed, called the effective reproductive number (R). Similar to R ₀, R is influenced by the number of contacts per unit time, the transmission probability per contact and duration of infectiousness; however, as the number of susceptibles in the population decreases, so will the number of individuals who can be infected by each case. Thus, R is always a proportion of R ₀ and will continuously change as the proportion of susceptibles changes in the population.

These concepts are combined using a framework for transmission dynamics models in a susceptible-infected-recovered compartmental model (Figure 2 ),⁹ in which S(t) represents the number of susceptible individuals in the population at time t, I(t) represents the number of infectious individuals in the population and R(t) represents the number of people who are recovered from (or immune to) infection. The simplest approach is to begin with a closed population of size N, where there are no births or deaths affecting the size of the population (including deaths from infection). These models are helpful in counting the flow of individuals through the compartments over the course of time of an epidemic. That is, at time t, the rate at which susceptibles move from S to I is equal to c×p×(I/N), and the rate at which people move from I to R is equal to 1/d, where d represents the average duration of infectiousness. The following set of algebraic equations is used to solve for the number of individuals in each of the compartments at time t.

$$\begin{array}{c}S\left(\text{t}+1\right)=S\left(\text{t}\right)-cp\left(\text{I}/\text{N}\right)\times S\left(\text{t}\right)\\ I\left(\text{t}+1\right)=I\left(\text{t}\right)+cp\left(\text{I}/\text{N}\right)\times S\left(\text{t}\right)-\left(1/\text{d}\right)\times I\left(\text{t}\right)\\ R\left(\text{t}+1\right)=R\left(\text{t}\right)+\left(1/\text{d}\right)\times I\left(\text{t}\right)\end{array}$$

Figure 2.

A simple susceptible-infected-recovered compartmental model. S is the number of susceptibles, I is the number of infectious individuals, R is the number of recovered (or immune) individuals, c is the number of contacts per unit time, p is the transmission probability per contact, N is the size of the total population and d is the duration of infectiousness.⁷

By using these equations, it is easy to approximate the number of susceptible, infectious and recovered individuals in the population at each point of time. This information is particularly useful in estimating how long it will take for the epidemic to run out of susceptibles. When applying this information to more realistic scenarios, such as accounting for an open population in which births in the population are replenishing the pool of susceptibles, we can estimate when a vaccine, for example, should be implemented to prevent transmission to the new pool of susceptibles.

TYPES OF TRANSMISSION DYNAMICS MODELS

The field of transmission dynamics modeling is complex and growing increasingly sophisticated. Although the following description and categorization of these models is perhaps overly simplistic, we believe it is instructive for the purposes of a brief introduction. Types of transmission dynamics models often come in pairs, for example, macroparasite versus microparasite, deterministic versus stochastic models, models using difference equations versus differential equations and homogeneous versus heterogeneous mixing assumptions.

Macroparasites Versus Microparasites

In transmission dynamics models, the major difference between microparasites and macroparasites is in the outcome being modeled. In general, for microparasites (ie, bacteria, viruses, fungi, protozoa and prions), the outcome is the number of infected hosts, whereas for macroparasites (ie, helminths and ectoparasites), the outcome is the number of viable female offspring produced. This is important because the intensity of infection (ie, number of parasites infecting the host) impacts the infectiousness of the host. Some additional differences between macroparasites and microparasites are the following: the generation time for macroparasites is longer than for microparasites; hosts rarely develop full immunity to reinfection with macroparasites; and the death rates of macroparasites have greater variability than those observed in microparasites. These factors can be accommodated using increasingly complex compartmental models.¹⁰ Even though a large number of macroparasites are considered as reemerging, the majority of emerging infectious diseases in the United States are microparasites (Table 1 ); thus, most of the examples will be those of microparasites.

Table 1.

Selected pathogens that have emerged since 1980

Year Identified	Pathogen
1981	Human immunodeficiency virus
1982	Escherichia coli O157:H7
1986	Ehrlichia chaffeensis
1992	Bartonella henselae
1993	Sin Nombre virus
1996	Prions (variant Creutzfeldt-Jakob disease)
1996	Avian influenza virus
1998	Nipah virus
1999	Ehrlichia ewingii
2001	Human metapneumovirus
2002	SARS coronavirus
2005	Human bocavirus
2009	2009 swine-origin H1N1 influenza virus

Deterministic Versus Stochastic Models

The fundamental difference between deterministic models, where fixed mathematical operations are allowed to “determine” the course of the model (ie, you get the same results every time) and stochastic models, where probabilities determine the likelihood of obtaining a certain outcome (but the outcome itself is determined randomly), is deciding whether to allow chance an opportunity to play a role in the model. In deterministic models, the size of each compartment is influenced by fixed rates of emigration (going out) and immigration (coming in), which can result in fractions of people being assigned to a given compartment. In contrast, stochastic models incorporate the role of chance in determining whether an event occurs (eg, that transmission occurs given an exposure) and, thus, either an event occurs or it does not. Fractions of people are not allowed to enter compartments, and thus stochastic models attempt to better model reality in transmission of infectious disease scenarios. However, because stochastic models are usually run through thousands of iterations to identify the average probability of observing the modeled event, the results from deterministic and stochastic models are often similar when applied to large populations.⁷ However, by running a stochastic model through many iterations, a distribution of outcomes is obtained, which is more informative than the average result obtained from a deterministic model.4., 11. Stochastic models have at least 2 advantages over deterministic models. First, they are better at modeling the probability of an epidemic running a course through extinction.⁷ Second, they do not require the assumption of a large sample size (which may be unrealistic in some settings) that deterministic models need.⁶

There are 2 primary obstacles to developing stochastic models. One is a lack of computing power necessary to run increasingly complex models through the necessary number of iterations, and the other is the increased intellectual difficulty demanded in incorporating the stochastic components. Computing power is rapidly becoming more available to the average infectious disease clinician/epidemiologist.⁵ The decision to overcome the second obstacle is a personal decision. Thus, our recommendation to the novice modeler is to start with deterministic models and work into stochastic models as competence and interest dictates.

One of the most important ways of balancing between an overly simplistic model and overly complex model is to start simple and state as many of the assumptions as possible, both implicit and explicit. Then, find ways to relax those assumptions imposed by the model/method.⁴

Difference Versus Differential Equations

As discussed above, in the use of compartmental models, the population moves between compartments at specified rates and predefined time steps. The choice of using difference or differential equations is thus influenced by whether the time steps are defined discretely or continuously. That is, difference equations can be used to model discrete changes in time, whereas differential equations use calculus-based principles to model continuous changes in time.¹¹ The chained binomial probability (eg, the Reed-Frost model) is a well-known example of the use of discrete time events modeled using the compartmental model structure.¹² Because infection transmission occurs on a continuous time-scale, differential models are often preferred. However, the straightforward nature of difference equations can provide useful approximations without intimidating less proficient mathematicians.

Homogeneous Versus Heterogeneous Mixing

Fundamental to the transmission of infections is the way in which susceptible and infectious persons interact, because how that interaction occurs is going to largely determine whether or not transmission can occur. The types of interactions necessary for transmission of measles (transmitted via the airborne route) are vastly different from those necessary to transmit genital herpes. In addition, there are complex patterns that dictate how people within populations interact with each other. For example, while typical school-aged children spend the majority of their time mixing with other children of their same age, the parent of that child likely mixes with a much broader age range of individuals in the same community because of activities related to work, hobbies, etc. Despite the obvious complex pattern of mixing among individuals, basic transmission dynamics models assume that individuals within a population mix homogeneously.⁷ That is, the probability of a given individual coming into sufficient contact to transmit infection is equal in every other individual in that population, regardless of age, gender or social status.

Despite the unrealistic nature of this homogeneous mixing assumption, some early models of infections transmitted via the airborne and droplet modes were helpful in predicting transmission and identifying effective methods to control spread. Furthermore, relatively simple adaptations were made to models of sexually transmitted infections (ie, differentiating between males and females) that were able to move this class of models forward. A major advance in transmission dynamics models has been the development of methods to account for heterogeneous mixing patterns. These methods typically rely on matrices in which the columns and rows represent the characteristics of the subpopulations and individual cells are estimates of probabilities of contact or contact rates between each subpopulation as shown in Table 2 .12., 13.

Table 2.

An example of a matrix in which the columns and rows represent the characteristics of the subpopulations (age group) and individual cells are estimates of probabilities of contact or contact rates between each subpopulation sufficient for transmission to occur (β)

	0–4 yr	5–18 yr	19–64 yr	65 + yr
0–4 yr	β1	β2	β3	β4
5–18 yr		β5	β6	β7
19–64 yr			β8	β9
65 + yr				β10

Another method to account for heterogeneous mixing patterns is the use of social networks,¹³ for example, areas where public transportation is common in contrast to areas where most individuals use their own transportation. This summarizes some of the basic concepts in the structure of transmission dynamics models. The dichotomy of methods and assumptions illustrates the choice that the modeler must make in determining the complexity of the model and hopefully facilitates the reading of this type of research. We also provided guidance regarding factors to consider when choosing which type of model or assumption to pursue.

APPLYING TRANSMISSION DYNAMICS MODELS TO EMERGING INFECTIOUS DISEASES

Recently, there has been an important increase in technology that can be incorporated into developing transmission dynamics models. In addition, there has been a tremendous amount of information devoted to understanding factors associated with the emergence (and reemergence) of infectious diseases. Thus, this next section will succinctly assess the latest technology and risk factors that need to be considered in the development of transmission dynamics models.

There are a number of challenges in developing transmission dynamics models. The first is that the majority of emerging infectious diseases are vector borne and/or zoonotic. Thus, in addition to modeling human-to-human transmission (which can be as difficult as the matrices used to describe the mixing patterns of the population), it may be necessary to model both the population dynamics of the vectors and the interaction between the vector and the human host. As technology advances, more factors can be incorporated into transmission dynamics models. For example, considerable advances have been made in molecular techniques that help us better understand microbial adaption and change and human susceptibility to infection, and the use of remote sensing technology has advanced climate change science.

Zoonoses

Zoonoses are infectious diseases of humans that have an animal reservoir. Zoonoses not only account for approximately 75% of all emerging infections¹⁴ but also have been responsible for some of the most devastating pandemics in world history [ie, plague, Spanish influenza and human immunodeficiency virus (HIV)/AIDS].¹⁵ Most of the zoonotic pathogens that have been modeled are viruses (with influenza and SARS accounting for almost half of all zoonotic models).¹⁵ Modeling infection transmission accounting for spread from the animal reservoir is often an important step in understanding the relevant dynamics. However, the impact of including animal reservoirs in the model is as varied as each zoonotic infection. For example, while HIV can be considered a zoonotic infection in the strictest sense of the word, ongoing spread from the animal reservoir plays an insignificant (if any) role in the overall spread of HIV, which is principally spread person to person. In contrast, tick-borne infections, such as Lyme disease, are not known to be transmitted person to person, and therefore modeling infection transmission from the reservoir is critical. In between these 2 ends of the transmission spectrum are infections such as Escherichia coli O157:H7, which is primarily spread by escaping the animal host (by contaminated food products) but can also be spread person to person via the fecal-oral route.

Microbial Adaption and Change

Among the pathogenic agents that have recently emerged, several have been RNA viruses (eg, HIV, Sin Nombre virus, Nipah virus, SARS coronavirus, human metapneumovirus and avian influenza). RNA viruses are among the most adaptable pathogens, because the structure of their genome is prone to mutations during replication. Models have shown the dynamic nature of these RNA pathogens as they expertly coevolve with their hosts.¹⁶ Our ability to account for microbial adaption and change in transmission models has advanced given the increased availability of viral genome sequences and the growth in computing power.¹⁷ Reasons for modeling microbial adaption include estimating probabilities of emergence from the reservoir, resistance to antimicrobials, geographic diversity across different populations and rate of global spread.¹⁷

Human Susceptibility to Infection

One of the fundamental principles of sustaining a pathogen in a population is the replenishment of susceptibles.¹² One of the demographic characteristics of the modern era is the population explosion that has occurred.¹ Hence, with the world being more populous than ever, the potential for having a large pool of susceptibles is high. Another important factor in facilitating infection transmission is creating opportunities for infectious and susceptible individuals to interact with each other. International travel is a primary method of introducing infectious individuals into highly susceptible populations,¹⁸ as has been modeled with SARS,19., 20. influenza²¹ and intentional release of smallpox.²²

Climate Change

Changes in weather and climate have been identified as important factors in the emergence of infectious diseases.²³ Advancements in technology, such as satellites for remote sensing, have been used to explore associations between climate change and emerging infections. One specific example is that of Sin Nombre virus, the cause of hantavirus pulmonary syndrome, in the 4-corners region of the United States in 1993²⁴ and, more recently, in Europe and parts of Africa.²⁵ To date, the models used for this purpose in humans have used traditional methods such as logistic regression,²⁶ but transmission dynamics models have been used in emerging infections among other animal species, such as nematode infection of muskoxen in the Arctic.²⁷

CONCLUSIONS

In the past 30 years, since the onset of the HIV epidemic, many other pathogens have emerged as new threats to human populations. During this same period of time, advancement in transmission dynamics models has improved our ability to predict the impact of these emerging infections on our health. Specifically, advancements have increased our ability to understand microbial adaption and change, the aspect of zoonoses escaping their reservoir, climate change and changes in human behavior that facilitate mixing between infectious and susceptible individuals. As these advancements have been made, so have the sophistication and complexity of the models advanced to account for these factors. These models will likely play an increasingly important role in understanding the dynamics of emerging infectious diseases, and thus the importance for infectious disease clinicians and epidemiologists to understand these methods cannot be overstated.