Abstract
The interim guidance issued by the World Health Organization during the West Africa 2014 Ebola outbreak provides guidelines on the use of convalescent blood from Ebola survivors for transfusion therapy. Here we develop a novel mathematical model, based on the interim guidance, to examine the nonlinear transmission–treatment–donation–stockpile dynamics during an Ebola outbreak and with a large scale use of the transfusion therapy in the population. We estimate the reduction of case fatality ratio by introducing convalescent blood transfusion as a therapy, and inform optimal treatment–donation–stockpile strategies to balance the treatment need for case fatality ratio reduction and the strategic need of maintaining a minimal blood bank stockpile for other control priorities.
MSC: 92D25, 92D30, 37N25
Keywords: Population dynamics, Ebola treatment, Convalescent blood transfusion
Highlights
-
•
A novel model for the large-scale use of the convalescent blood transfusion therapy.
-
•
Based on WHO׳s interim convalescent treatment guidance in 2014 Ebola outbreak.
-
•
Estimate the reduction of case fatality ratio by introducing convalescent therapy.
-
•
Inform optimal treatment-donation-stockpile strategies.
-
•
Guide convalescent blood transfusion services in future emerging disease outbreaks.
Passive immune therapy (also called as convalescent therapy, antibody infusion and serum therapy) refers to an infectious disease treatment that transfuses convalescent blood product from survivors to other patients. This treatment has been widely applied in the pre-antibiotic era (1890–1930s) (Leider et al., 2010). Modern use of convalescent therapy consists of blood products in the forms of screened whole blood, convalescent plasma, hyperimmune globulins (HIG/IVIG), and monoclonal antibody (MoAb), where HIG and MoAb are both derived from plasma through rigorous medical processes. HIG has been actively applied in the treatment of many bacterial and viral diseases, such as tetanus, hepatitis A/B, rabies, measles, complications of smallpox vaccination (Keller and Stiehm, 2000). In addition, convalescent therapy has a strong track record of success in treating emerging infections such as H1N1, Spanish Influenza, severe acute respiratory syndrome (SARS), and Chikungunya (Kreil et al., 2012, Luke et al., 2006, Mair-Jenkins et al., 2014, Couderc et al., 2009), and is considered as a potential treatment option for H5N1, middle east respiratory syndrome (MERS), and Ebola (Luke et al., 2006, BRN, 2015, WHO, 2014b).
Convalescent blood transfusion was used with success as a treatment in a group of 8 Ebola patients during the 1995 Kikwit Ebola outbreak (Mupapa et al., 1999): after the treatment, only 1 patient (12.5%) died. With no licensed medicine or vaccine for Ebola, convalescent blood transfusion was the only treatment approved by World Health Organization (WHO) and there are increasing interests in its use (Gulland, 2014, WHO, 2014b, WHO, 2014a, Casadevall and Pirofski, 2015).
In September 2014, WHO (2014b) issued an interim guidance on use of convalescent whole blood or plasma collected from Ebola virus disease survivors for transfusion during outbreaks, and provided detailed guidelines on donor selection, screening, donation and handling of blood and plasma units, and transfusion therapy. This interim guidance points out a dynamic treatment–donation–stockpile positive feedback cycle: transfused patients survive from Ebola, convalescent survivors become donors and make donation to the blood bank, the blood bank storage is affected by the current blood usage and donation, and the blood bank level in turn determines the number of transfused patients.
Modeling the use of passive-immunotherapy during an infectious disease outbreak was previously studied in Wu et al. (2009), in which a differential equation model was formatted to investigate the logistical feasibility of collecting convalescent plasma to treat severe cases of pandemic influenza in Hong Kong. This study assumes that only 0.5% of all infected cases are severe cases who are not expected to make donation after recovery, so the blood donation must be obtained from survivors of non-severe cases. Unlike pandemic influenza, Ebola is a fatal disease with a death ratio of 70% (Kucharski and Edmunds, 2014) and all cases receiving palliative care are severe. Therefore, with an urgent need of convalescent treatment in a large-scale population, all survivors are considered as potential donors. Moreover, for some developing countries with limited resources such as those in West Africa, blood donations are likely to expire quickly with underrated storage condition. With these concerns, we propose a model for convalescent treatment in a population that is applicable in epidemic outbreaks when no other treatment strategies are available.
We develop a mathematical model that incorporates the treatment–donation–stockpile dynamics, and addresses two important questions relevant to a potential large scale Ebola outbreak and convalescent blood transfusion treatment: to what extent the case fatality ratio (CFR) can be reduced by using convalescent blood transfusion as the empiric therapy; and what would be an optimal treatment–donation–stockpile strategy that can sustain a rapid and effective implementation of treatment plans (WHO, 2014a).
The transmission dynamics of 2014–2015 West Africa Ebola outbreak have been well studied in WHO-Ebola-Response-Team (2014), Chowell et al. (2004), Chowell and Nishiura (2014), Nishiura and Chowell (2014), Towers et al. (2014), Meltzer et al. (2014), Fisman et al. (2014), Althaus (2014), and Gomes et al. (2014). Possible containment and surveillance strategies have been modeled and evaluated (Chowell et al., 2015, Webb et al., 2015). Gutfraind and Meyers (2015) proposed a model to evaluate the large-scale use of convalescent therapy, but the model is different from ours. Comparisons between the two models will be discussed in Section 5.
An objective of our study here is to inform a rational distribution strategy of inadequate resource in order to balance between reducing the CFR and maintaining a reasonable level of convalescent blood bank storage for other priority considerations. Our model simulations show that in a setting similar to the 2014–2015 Ebola outbreak in Guinea (with a total population of 12-million, a final case count of 3810, and an overall CFR of 67% (CDC, 2014), if the public health system is well developed to be able to handle a total of 200 patients with convalescent blood transfusion as an empiric therapy, then at the end of an outbreak, the Ebola CFR can be reduced to less than 57%. Our simulation also shows that the efficiency in switching from palliative care to blood transfusion treatment is essential for the treatment outcome: a 10-day delay increases the overall CFR by more than 5%.
1. The model
To model the treatment–donation–stockpile dynamics, we assume that the convalescent therapy is initiated as the empirical therapy at the beginning of an Ebola outbreak, and the community has a developed public health system for complete isolation in hospitals and proper handling of dead bodies both inside and outside hospitals. These assumptions can be relaxed, as will be discussed later, to allow more complicated transmission dynamics than we model in this paper. We assume further that Ebola patients become contagious upon onset of symptoms.
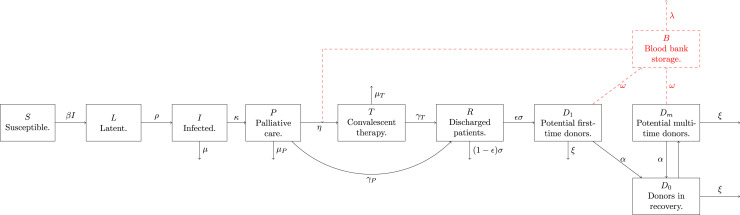
To establish the model, we first classify the population into the following 9 classes (Fig. 1 ): susceptible (S), infected in latent period (L), infectious and symptomatic but still unidentified (I), identified patients receiving palliative care (P), identified patients receiving convalescent therapy (T), convalescent patients discharged from hospital (R), first-time and multi-time potential donors who can immediately make donations ( and ), and potential donors in recovery period after their latest donation ().
Fig. 1.
Flow diagram of transmission–treatment-donation-stockpile dynamics. Susceptible people become infected. Identified infectives are isolated and treated with palliative care. Each patient in palliative care is considered to switch to blood transfusion therapy at a constant rate η, and the percentage of those who are selected to receive blood transfusion depends on the blood bank stockpile and the blood bank stockpile usage strategy. Patients under blood transfusion and palliative care have different probabilities to survive. Convalescent patients discharged from hospitals need to wait for an average of days to be considered as potential donors. Donors will be considered again as potential donors τ days after their latest donation.
Our transmission–treatment–donation–stockpile dynamics model, given in the Appendix, follows the schematic diagram in Fig. 1 and tracks the blood bank stock level (B). Previous modelling studies on Ebola outbreaks mainly considered the infection dynamics in systems involving the 3 compartments (left boxes of Fig. 1) or their variations. Our model focuses on the treatment–donation–stockpile dynamics, which involves the remaining compartments in Fig. 1.
The three compartments S(t), L(t), and I(t) form a subsystem about the disease transmission dynamics. We take into consideration of the fact that the disease transmission rate is reduced due to the enforcement of a series of public health interventions (other than convalescent treatment) throughout the outbreak (Althaus, Webb and Browne, 2015), and we set the transmission rate at time t from the beginning of the outbreak as in Eqs. (1), (2) in the section of Appendix. We will discuss the choice of this transmission rate and its relationship to the basic and effective reproduction numbers in the following section.
We shall use the standard assumptions provided in the WHO׳s interim guidance (WHO, 2014b):
-
•
On average, convalescent therapy takes one unit of blood donation to treat one Ebola patient.
-
•
Potential donors are defined as those Ebola survivors who have been discharged from hospitals for more than a certain number of days (28 days as suggested by WHO, 2014b).
-
•
After each donation, the donor is required to wait for a certain number of days for next donation.
-
•
There is a constant loss rate of donors for various reasons such as donors׳ health conditions, and loss of contacts.
-
•
Blood donation in the blood bank has a constant storage expiration rate.
To develop specific strategies on the deployment of blood transfusion therapy, we further assume the following:
-
•
Identified infected individuals will be hospitalized, and then first receive palliative care. All the patients in palliative care request for convalescent therapy, but only part of them will receive the therapy according to daily blood bank stock levels and the deployment strategy adopted.
-
•
Blood bank storage might be inadequate at any stage, specially at the beginning of the outbreak, so the ratio of patients switching to the convalescent therapy is affected by the stock level and given by at time t, where K is the threshold level of the stock when half of the patients receive the therapy – a higher value of K corresponds to a more conservative use of the stockpile.
We emphasize that this model framework is appropriate when the public health system is enhanced to ensure that the assumed isolation, treatment and stockpile measures can be implemented. Possible variations of the model setting in the case when this assumed public health enhancement is not met will be discussed in the final discussion section.
Under an outbreak scenario, we use the model to evaluate how the following aspects are determined by different treatment policies including initial blood stockpile: (1) daily patient population under convalescent therapy and palliative care – the requirement on hospital facility and personnel; (2) cumulative CFR – the effectiveness of convalescent therapy; (3) daily blood bank levels and the minimum level during the entire outbreak – number of stockpiles available for other control priorities; and (4) loss of blood donation due to expiration – storage waste.
2. Parameters in the model
We categorize the parameters involved in our model based on the disease epidemiology, implementation logistics and their impact on final outcomes.
Disease transmission parameters: Parameters N (total population), β (infection transmission rate function), ρ (transition rate from latent to infectious period), κ (case identification rate), and μ (death rate of unidentified individuals) are related to the epidemiological characteristics of the disease spread.
We adopt the results in Althaus (2014), with the assumption that the transmission rate decays exponentially at rate r due to public health interventions, and set , where β 0 is the initial transmission rate. From our model equations (1), (2), (3) in the section of Appendix, which are the same as in Althaus (2014), the basic reproduction number of the disease is given by , and the effective reproduction number at any time is given by .
Treatment strategy parameters: The management of the two available treatments, convalescent therapy and palliative care, depends on the values of parameters: η (rate of switching treatment from palliative care to convalescent therapy), K (a parameter relevant to the stockpile usage strategy), and (discharge rates of patients under blood transfusion and under palliative care, respectively), and (death rates of patients under blood transfusion and under palliative care, respectively). The initial stockpile level will be treated as a parameter, which affects the initial treatment strategy and the subsequent potential donors from the first generation of disease cases.
We explain more about the parameter η here. Depending on the current blood bank level, only a portion of the patients under palliative care can be switched to blood transfusion treatment. In reality, η reflects the rate of blood bank storage update and blood delivery to hospitals. For example, means a daily update of blood bank storage and delivery of blood units. Hence, the patients under palliative care are considered to switch to blood treatment everyday, but only some can be switched based on the daily blood bank level and the stockpile usage strategy.
Blood donation parameters: Parameters relevant to blood collection and expiration policies are σ (transition rate from discharged patients to potential donors), ϵ (percentage of survivors who are qualified for donation), α (blood donation rate of donors), ω (inflow rate of donation to blood bank), ξ (loss rate of donors), τ (donor recovery period between donations), and λ (expiration rate of donated blood).
3. Methods for simulation of the model
We set up the model parameters (relevant to transmission dynamics) and initial conditions to closely mimic the actual Ebola outbreak in Guinea with a total population of 12 millions, that is, . Since we have used the decaying transmission rate to reflect the impact of other intervention measures on transmission dynamics, we will focus on the impact of convalescent treatment on CFR reduction when all infected cases are identified and receive palliative care. Hence the death rate μ of unidentified cases is assumed to be zero. As reported in WHO (2014b), the mean time from symptom onset to case identification is around 5 days, so we let .
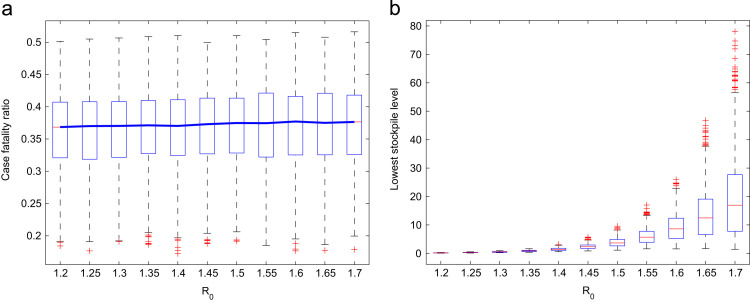
We use the estimation results for Guinea in Althaus (2014): the basic reproduction number R 0 is estimated to be 1.51, and the rate r=0.0023 at which control measures reduce transmission. The value of β 0 and the transmission rate function β are determined by R 0, r, κ, and μ in the above settings. The robustness of the results is discussed via sensitivity analysis in Fig. 8.
Fig. 8.
Sensitivity analysis for the variations in the final CFR and minimal stockpile level based on different values of R0. We here fix . We sample the parameters in larger ranges: death ratio of blood treatment (5–30%), death ratio of palliative care (60–80%), average length of hospital stay after blood treatment (10–40 days), average length of hospital stay with palliative care (15–40 days), and percentage of survivors who are qualified for donation (20–80%).
There is no evidence shown that successful blood transfusion can shorten the recovery period of a patient. Hence, we assume that the average time for hospitalization is 20 days, which coincides with that of Mupapa et al. (1999). If the hospitalization period of a patient with palliative care alone is , then for patients switch from palliative care to convalescent therapy, we can use the equation to estimate the value . In our simulations, we will also set to reflect the death ratios under two different treatments, one is 70% for palliative care (Kucharski and Edmunds, 2014) and the other is 12.5% for blood transfusion treatment (Mupapa et al., 1999).
We assume , which means that all donated blood are handled properly and the wasted blood is solely due to the expiration. The ranges of and ξ are obtained by estimating possible ranges of the corresponding daily percentages of donors who make donations, and donors who lost contact, as shown in Table 1 .
Table 1.
Parameter values for Fig. 2, Fig. 3, Fig. 4, Fig. 5, Fig. 6, Fig. 7, Fig. 8. Most of the fixed parameters are taken from the references (Althaus, Mupapa et al., 1999, WHO, 2014b, WHO-Ebola-Response-Team, 2014, Chowell and Nishiura, 2014, Eichner et al., 2011, Kucharski and Edmunds, 2014).
| Transmission | Value | Treatment | Value | Donation | Value |
|---|---|---|---|---|---|
| N | 0.053 | σ | 1/28 | ||
| 0.05 | α | ||||
| 11.4 days | ω | Same as α | |||
| κ | 0.2 | ξ | |||
| μ | 0.0 | η | 1.0 | 90%a | |
| R0 | 1.51 | K | 1–500 unitsa | 10%a | |
| B(0) | 0–200 unitsa | 56 days to 16 wks for CWB | |||
| 2 wks for CP | |||||
| 35 days for CWB | |||||
| 40 days for CP | |||||
| ϵ | 50%a |
CWB: convalescent whole blood; CP: convalescent plasma.
Assumed values.
As an illustration, we show how to estimate the value α. We consider a group of donors, denoted by D(t) at time t, who never lose contacts, and the only loss rate is due to donation. Hence, for and . It follows that the percentage of donors who donate in a certain day from time t to is and .
4. Simulation results
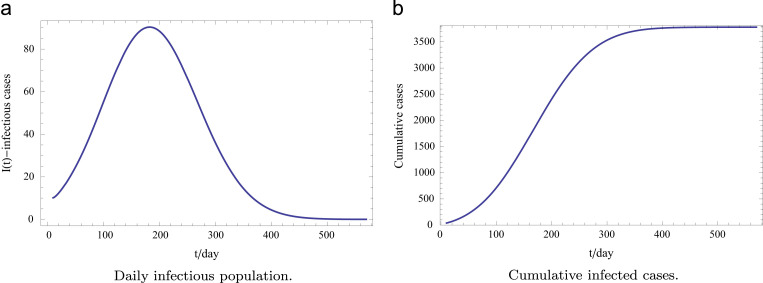
We fit the transmission dynamics of Ebola in Guinea in Fig. 2 , with initially 21 infectious cases, and 1 recovered case. Note that the transmission dynamics is not affected by the treatment, but the case fatality will be subject to the treatment–donation–stockpile dynamics. All simulations are performed under the assumption that the use and collection of convalescent blood starts at the beginning of the outbreak.
Fig. 2.
A fitted outbreak scenario for Guinea. Assume 21 initial infectious case, and 1 recovered case. The transmission dynamics is not affected by the treatment, but the case fatality will be subject to the treatment–donation–stockpile dynamics. (a) Daily infectious population. (b) Cumulative infected cases.
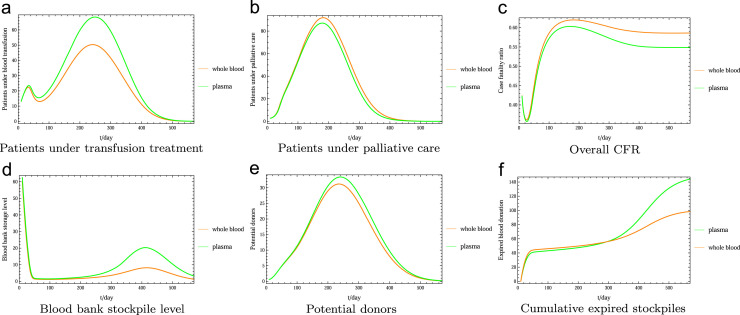
Convalescent whole blood or plasma: Fig. 3 compares the blood collection and storage in two different forms: convalescent whole blood (CWB) and convalescent plasma (CP), as suggested in WHO (2014b). We set the donor recovery period for CWB as 56 days – the shortest recommended period for whole blood donors, and for CP as 14 days; the blood collection expiration period is 35 days for CWB and 40 days for CP. The simulation clearly shows substantial advantage of convalescent plasma treatment in terms of reducing the CFR (Fig. 3c) and increasing the blood bank stockpile (Fig. 3d). Logistic consideration of different therapies will need a further cost–benefit study based on our model formulation. Note that a significant difference in the amount of expired stockpiles (Fig. 3f) is mainly caused by the higher amount of blood donation in the form of CP (Fig. 3d) since there will be more recovered patients and donors from the CP therapy.
Fig. 3.
Comparison of the use of convalescent whole blood (CWB) and convalescent plasma (CP): (1) the donor recovery period is 56 days for CWB donors and 14 days for CP donors; and (2) the blood collection expiration period is 35 days for CWB and 40 days for CP. The simulation clearly shows substantial advantage of convalescent plasma treatment in terms of reducing the CFR (Fig. 3c) and increasing the blood bank stockpile (Fig. 3d). (a) Patients under transfusion treatment. (b) Patients under palliative care. (c) Overall CFR. (d) Blood bank stockpile level. (e) Potential donors. (f) Cumulative expired stockpiles.
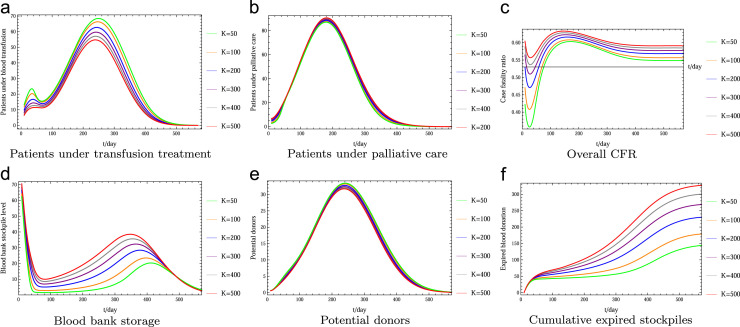
Initial stockpile and blood stockpile usage strategy: Fig. 4 examines the impact on CFR and implication for the need of capacity of the public health system to implement different stockpile usage strategies by varying K, where larger K corresponds to more conservative use of stockpiles. This simulation is based on convalescent plasma therapy and the assumption that a blood stockpile of 100 units is available at the beginning of the outbreak. Aggressive use of blood storage indeed leads to lower CFR throughout the outbreak (Fig. 4c), but also results in low blood storage level for a long time (Fig. 4d). Conservative use of stockpile maintains higher blood bank levels for most of the time, but leads to large amount of donation waste (Fig. 4f). So in either case, it might be also necessary to utilize and process the expiring donations into HIG blood product for use during emergency events.
Fig. 4.
Comparison among different stockpile usage strategies–variations of K. Recall that a large K value means more conservative usage of the stockpile. This simulation is based on convalescent plasma therapy and the assumption that a blood stockpile of 100 units is available at the beginning of the outbreak. Fig. 4c shows that more conservative use of blood storage leads to higher CFR in the early stage of the outbreak, and the CFR decreases faster later on due to more stockpiles become available. (a) Patients under transfusion treatment. (b) Patients under palliative care. (c) Overall CFR. (d) Blood bank storage. (e) Potential donors. (f) Cumulative expired stockpiles.
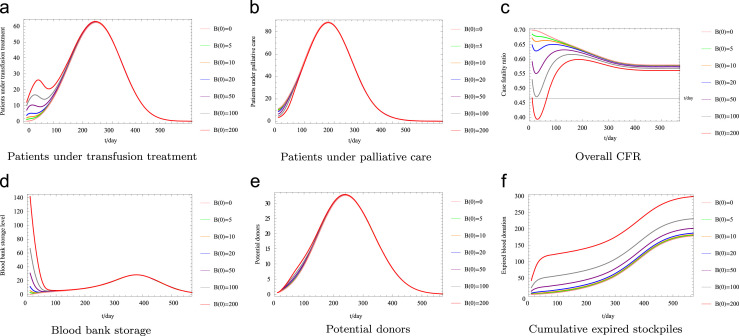
In Fig. 5 , we illustrate the impact of initial stockpiles . The simulation is based on convalescent plasma therapy and on the assumption that a stockpile preservation policy with threshold of 200 stockpiles under which half of the patients will switch to blood transfusion. In a large-scale convalescent therapy program, the availability of more stockpiles at the beginning leads to lower CFR during the early stage of the outbreak, but the overall CFR is not affected much. However, impact of insufficient initial stockpile could be different from outbreaks in a small population, to address this small-scale outbreak requires agent-based simulations in a future study.
Fig. 5.
Comparison among different initial stockpiles– variations of . The simulation is based on convalescent plasma therapy and on the assumption that a stockpile preservation policy with threshold of 20 stockpiles under which half of the patients will switch to blood transfusion. (a) Patients under transfusion treatment. (b) Patients under palliative care. (c) Overall CFR. (d) Blood bank storage. (e) Potential donors. (f) Cumulative expired stockpiles.
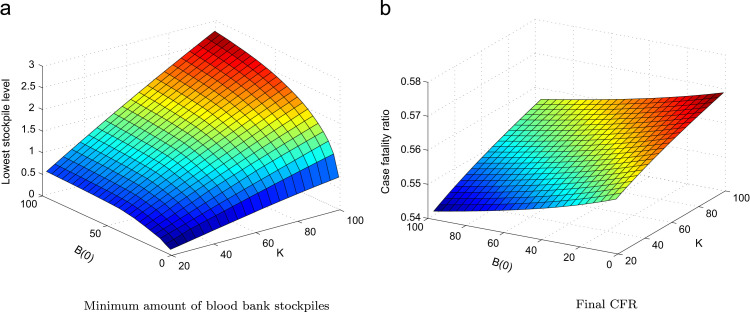
In Fig. 6 , we consider the impact on CFR when the values K and are changed. We note that the final CFR over the entire period of the outbreak is not considerably affected by either of the two aspects, and the minimal stockpile number is small in all cases. The above results suggest us to investigate the impacts of the blood collection parameters on reducing CFRs and maintaining blood bank levels.
Fig. 6.
Impact of varying K and on the CFR and minimum stockpile. We fix all other parameters as in Table 1 for CP therapy, except K and . We report the cumulative CFR and the minimum stockpile throughout the outbreak. (a) Minimum amount of blood bank stockpiles. (b) Final CFR.
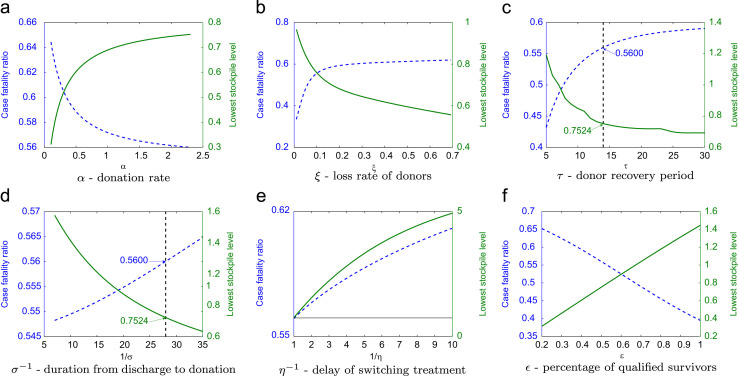
Management of blood collection services: We vary the parameter values relevant to blood donation policy and service in Fig. 7 one by one, while keeping all other parameters fixed as in Table 1 and consider the treatment and collection in the form of plasma. Parameters suggested in the WHO guideline are marked in the figures. Efficient reduction of the CFR depends significantly on the following aspects: enhancing the policy and service on donation, encouraging and recruiting donors, keeping good track of donor contacts, frequently updating stockpile information and rapid delivery, shortening the donor recovery period, and reducing the transition duration from discharge to first donation. We note that the outcomes are very sensitive to the parameter α, ξ, and ϵ. Hence in real applications of this model, these parameters should be carefully estimated from local blood donation data.
Fig. 7.
Impact of different levels of blood donation policies and implementation – variations of blood donation relevant parameters. We report the simulations based on convalescent plasma with . Parameters suggested in the WHO guideline are marked in the figures. Great reductions of the CFR depend significantly on the following aspects: enhancing the policy and service on donation, encouraging and recruiting donors, keeping good track of donor contacts, frequently updating stockpile information and rapid delivery, shortening the donor recovery period, and reducing the transition duration from discharge to first donation. (a) α – donation rate. (b) ξ – loss rate of donors. (c) τ – donor recovery period. (d) – duration from discharge to donation. (e) – delay of switching treatment. (f) ϵ – percentage of qualified survivors.
However, similar to the results in Fig. 6b, the lowest blood bank levels are not essentially affected by the blood collection parameters and always stay at a low level. Therefore, following our simulation results, to save a sufficient amount of stockpiles for other control priorities, one needs to either hold the stockpiles at a certain threshold level until additional donations are made by recovered patients, or make use of the expiring blood donations.
5. Summary and discussions
At the initial stage of an emerging infectious disease like Ebola, convalescent therapy is a major treatment option in the absence of licensed medicine or vaccine. Public health authorities should plan with caution about blood transfusion services and develop an informed optimal strategy to both reduce the CFR and maintain the blood bank level that meets the need of other control priorities.
Managing effective blood transfusion services during an outbreak when requires comprehensive understanding of the complex treatment–donation–stockpile dynamics: the use of donated blood for treatment reduces the blood stockpile immediately, but the treatment increases the chance for patient recovery, and the recovered patients increase the donation to the blood bank for future treatments. We have developed a mathematical model to examine the outcome of the treatment–donation–stockpile dynamics under different blood service strategies including that described in the WHO interim guidance.
We conclude in our simulations that the use of blood transfusion can significantly reduce the CFR if the use and collection of convalescent plasma start at the beginning of the outbreak. Providing such service does not require a large amount of hospital beds in our setting when other interventions have already reduced the number of infectious cases under palliative care. In our simulations, the number of patients receiving treatment at the peak time is less than 200 (Fig. 3, Fig. 4, Fig. 5). The efficiency of implementing blood transfusion treatment and blood collection, and keeping track of donors is of importance for the outcome (Fig. 7). Establishing sufficient initial stockpile helps with reducing CFR at the early stage of the outbreak, but the overall outcome is not sensitive to the initial amount of stockpiles (Fig. 5). Aggressive use of blood donations would definitely help achieve the lowest overall CFR, but the blood bank storage level may remain at very low levels in the first half of the outbreak (Fig. 4), so we may have to consider the use of the expiring blood donations into products as HIG for emergency use.
In our sensitivity analysis shown in Fig. 8 , our aforementioned observations are shown to be valid for a range of basic reproduction numbers (1.2–1.7), death ratio of blood treatment (5–30%), death ratio of palliative care (60–80%), average length of hospital stay after blood treatment (10–40 days), average length of hospital stay with palliative care (15–40 days), and percentage of survivors who are qualified for donation (20–80%).
Our modeling analysis is based on a homogeneous population and we assume that every identified patient has equal chance of switching from palliative care to convalescent therapy. Detailed information about disease progression in individuals is needed to guide the model design with further stratification of the population into finer compartments to develop the priority list of patients for the blood transfusion treatment. Again, this issue needs to be considered within the complex treatment–donation–stockpile dynamics.
We conclude that convalescent plasma treatment is more efficient in reducing the CFR and boosting blood bank storage than convalescent whole blood treatment. Additionally, we should note that there will be logistic consideration for each treatment option or their combination which requires a further cost–benefit study. We stress that convalescent whole blood treatment is effective for reducing the CFR as shown in Fig. 3, and every effort should be made to implement this if convalescent plasma treatment is difficult to achieve.
Our modeling framework assumes an improved public health system for effective identification and isolation, so as to identify symptomatic patients at an early stage. Modifications of the framework are needed to address disease transmission and management scenarios in countries where this assumption is not met (Gao and Feng, 2014, Burnouf et al., 2014, Bausch and Schwarz, 2014, Fauci, 2014, Briand et al., 2014, Ozer et al., 2014). Compared with the work in Gutfraind and Meyers (2015), our model possesses the following features of the blood transfusion dynamics. (1) Our model contains a treatment decision period upon hospital admission, and reflects the fact that every hospitalized patient can be considered for blood transfusion regardless of their current length of stay. In this way, the probability for a patient to receive blood transfusion depends on the blood bank level during the whole period of their hospital stay. (2) We model the recovery time from the most recent donation by the delay suggested by WHO (2014b), so that the period between the current and forthcoming donation could follow a distribution of lags with a lowest value of τ days. (3) More importantly, the strategy for distributing blood stockpiles is modeled with a function involves both of the up-to-date blood bank level and a measurement of the decision on preserving stockpiles for emergency purposes. This function can be easily modified with specific stockpile deployment policies, and our model is suitable for evaluating relevant future treatment plans.
As asymptomatic close contacts might provide a potential resource for convalescent blood donation (Bellan et al., 2014), contact tracing and surveillance should be enhanced. As other infection control measures including isolation, contact tracing (Webb et al., 2015) and early diagnosis (Chowell et al., 2015) all contribute to shortening the switching time from palliative care to blood transfusion treatment, an integrated strategy of Ebola control must incorporate the consideration of blood transfusion services. All of these infection control measures are implicitly incorporated into the decaying transmission rate of the model (Althaus, 2014) we have adopted. Incorporating these measures explicitly in our model will only require appropriate modifications in the disease transmission dynamics -components.
The use of convalescent serum has a long history (Leider et al., 2010, Lu, 2014), and blood transfusion can be the first available treatment option when little is known about an emerging infectious disease. We believe that our study can also be used with necessary modifications to inform integrated control programs for many other emerging and re-emerging infectious diseases.
Acknowledgments
We acknowledge the two anonymous reviewers for their comments.
X.H. is supported by the Faculty of Science at Ryerson University and York University. X.S. is supported by the National Natural Science Foundation of China (NSFC 11571273), and by the China Scholarship Council (grant no. 201406280058). K.L. is supported by the Natural Sciences and Research Council of Canada (NSERC). J.W. is supported by the Natural Sciences and Research Council of Canada (NSERC 105588-2011-RGPIN), Canadian Institute for Health Research (CIHR 289907), the Canada Research Chair Program (CRC), and the International Development and Research Centre (IDRC) through its IDRC-CRC International Research Chair Program.
Appendix A. Model equations
The mathematical model we establish is governed by the following system of 10 first-order differential equations. The first three equations describe the disease transmission dynamics only involving compartments in Fig. 1.
| (1) |
| (2) |
| (3) |
The last 7 equations model the treatment–donation–stockpile dynamics, where a delayed subsystem is introduced and contains a delay τ (days) for survived patients to make subsequent donations.
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
References
- Althaus C.L., Estimating the reproduction number of Zaire ebolavirus (ebov) during the 2014 outbreak in West Africa, PLOS Curr. Outbreaks, 2014 Sep 2, Edition 1. 10.1371/currents.outbreaks.91afb5e0f279e7f29e7056095255b288 [DOI] [PMC free article] [PubMed]
- Bausch D.G., Schwarz L. Outbreak of ebola virus disease in guinea: where ecology meets economy. PloS Negl. Trop. Dis. 2014;8:e3056. doi: 10.1371/journal.pntd.0003056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bellan S.E., Pulliam J.R.C., Dushoff J., Meyers L.A. Ebola control: effect of asymptomatic infection and acquired immunity. Lancet. 2014;384:1499–1500. doi: 10.1016/S0140-6736(14)61839-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Briand S., Bertherat E., Cox P., Formenty P., Kieny M.P., Myhre J.K., Roth C., Shindo N., Dye C. The international ebola emergency. N. Engl. J. Med. 2014;371:1180–1183. doi: 10.1056/NEJMp1409858. [DOI] [PubMed] [Google Scholar]
- BRN, W.B.R.N., 2015. Position Paper on Collection and Use of Convalescent Plasma or Serum as an Element in Middle East Respiratory Syndrome Coronavirus Response.
- Burnouf T., Emmanuel J., Mbanya D., El-Ekiaby M., Murphy W., Field S., Allain J.P. Ebola: a call for blood transfusion strategy in sub-Saharan Africa. Lancet. 2014;384:1347–1348. doi: 10.1016/S0140-6736(14)61693-7. [DOI] [PubMed] [Google Scholar]
- Casadevall A., Pirofski L. The ebola epidemic crystallizes the potential of passive antibody therapy for infectious diseases. PLoS Pathog. 2015:11. doi: 10.1371/journal.ppat.1004717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- CDC, 2015. 2014 Ebola Outbreak in West Africa—Case Counts. 〈http://www.cdc.gov/vhf/ebola/outbreaks/2014-west-africa/case-counts.html〉. (last accessed 9 November 2015).
- Chowell D., Castillo-Chavez C., Krishna S., Qiu X., Anderson K.S. Modelling the effect of early detection of ebola. Lancet. 2015;15:148–149. doi: 10.1016/S1473-3099(14)71084-9. [DOI] [PubMed] [Google Scholar]
- Chowell G., Hengartner N.W., Castillo-Chavez C., Fenimore P.W., Hyman J.M. The basic reproductive number of ebola and the effects of public health measures: the cases of congo and uganda. J. Theor. Biol. 2004;229:119–126. doi: 10.1016/j.jtbi.2004.03.006. [DOI] [PubMed] [Google Scholar]
- Chowell G., Nishiura H. Transmission dynamics and control of ebola virus disease (evd): a review. BMC Med. 2014;12:1–16. doi: 10.1186/s12916-014-0196-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Couderc T., Khandoudi N., Grandadam M. Prophylaxis and therapy for chikungunya virus infection. J. Infect. Dis. 2009;200:516–523. doi: 10.1086/600381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eichner M., Dowell S.F., Firese N. Incubation period of ebola hemorrhagic virus subtype zaire. Osong Public Health Res. Perspect. 2011;2:3–7. doi: 10.1016/j.phrp.2011.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fauci A.S. Ebola-underscoring the global disparities in health care resources. N. Engl. J. Med. 2014;371:1084–1086. doi: 10.1056/NEJMp1409494. [DOI] [PubMed] [Google Scholar]
- Fisman D., Khoo E. and Tuite A., Early epidemic dynamics of the west africanAfrican 2014 ebola outbreak, estimates derived with a simple two-parameter model, PLOS Curr. Outbreaks, 2014 Sep 8, Edition 1. 10.1371/currents.outbreaks.89c0d3783f36958d96ebbae97348d571 [DOI] [PMC free article] [PubMed]
- Gao G.F., Feng Y. On the ground in Sierra leone. Science. 2014;346:666. doi: 10.1126/science.346.6209.666. [DOI] [PubMed] [Google Scholar]
- Gomes M.F., Piontti A.P., Rossi L., Chao D., Longini I., Halloran M.E., Vespignani A. Assessing the international spreading risk associated with the 2014 West African ebola outbreak. PLOS Curr. Outbreaks. 2014:1–17. doi: 10.1371/currents.outbreaks.cd818f63d40e24aef769dda7df9e0da5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gulland A. First ebola treatment is approved by who. BMJ. 2014;349:g5539. doi: 10.1136/bmj.g5539. [DOI] [PubMed] [Google Scholar]
- Gutfraind A., Meyers L.A. Evaluating large-scale blood transfusion therapy for the current ebola epidemic in liberia. J. Infect. Dis. 2015:211. doi: 10.1093/infdis/jiv042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller M., Stiehm E. Passive immunity in prevention and treatment of infectious diseases. Clin. Microbiol. Rev. 2000;13:602–614. doi: 10.1128/cmr.13.4.602-614.2000. PMCID:PMC88952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kreil T., Vey J.M., Lei L. Preparation of commercial quantities of a hyperimmune human intravenous immunoglobulin preparation against an emerging infectious disease: the example of pandemic h1n1 influenza. Transfusion. 2012;52:803–809. doi: 10.1111/j.1537-2995.2011.03347.x. [DOI] [PubMed] [Google Scholar]
- Kucharski A.J., Edmunds W.J. Case fatality rate for ebola virus disease in west Africa. Lancet. 2014;384:1260. doi: 10.1016/S0140-6736(14)61706-2. [DOI] [PubMed] [Google Scholar]
- Leider J., Brunker P., Ness P. Convalescent transfusion for pandemic influenza: preparing blood banks for a new plasma product? Transfusion. 2010;50:1384–1398. doi: 10.1111/j.1537-2995.2010.02590.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu S. Using convalescent whole blood or plasma as passive immune therapy for the global war against ebola. Emerg. Microbes Infect. 2014;3:e80. doi: 10.1038/emi.2014.86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luke T., Kilbane E., Jackson J., Hoffman S. Meta-analysis: convalescent blood products for Spanish influenza pneumonia: a future h5n1 treatment? Ann. Intern. Med. 2006;145:599–609. doi: 10.7326/0003-4819-145-8-200610170-00139. [DOI] [PubMed] [Google Scholar]
- Mair-Jenkins J., Saavedra-Campos M., Baillie J. The effectiveness of convalescent plasma and hyperimmune immunoglobulin for the treatment of severe acute respiratory infections of viral etiology: a systematic review and exploratory meta-analysis. J. Infect. Dis. 2014;211:80–90. doi: 10.1093/infdis/jiu396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meltzer, M.I., Atkins, C.Y., Santibanez, S., Knust, B., Petersen, B.W., Ervin, E.D., Nichol, S.T., Damon, I.K., Washington, M.L. 2014. Estimating the future number of cases in the ebola epidemic – liberia and sierra leone, 2014–2015. MMWR Surveill. Summ. , 2014–2015. [PubMed]
- Mupapa K., Massamba M., Kibadi K., Kuvula K., Bwaka A., Kipasa M., Colebunders R., Muyembe-Tamfum J. Treatment of ebola hemorrhagic fever with blood transfusions from convalescent patients. J. Infect. Dis. 1999;179(Suppl 1):S18–23. doi: 10.1086/514298. [DOI] [PubMed] [Google Scholar]
- Nishiura, H., Chowell, G., 2014. Early transmission dynamics of ebola virus disease (evd), west africa, march to august 2014. Eurosurveillance 19, 20894. http://dx.doi.org/10.2807/1560-7917.ES2014.19.36.20894. [DOI] [PubMed]
- Ozer P., Thiry A., Fallon C., Blocher J., Longueville F.D. Containment in sierra leone: the inability of a state to confront ebola? Lancet. 2014;384:e47. doi: 10.1016/S0140-6736(14)61594-4. [DOI] [PubMed] [Google Scholar]
- Towers, S., Patterson-Lomba, O., Castillo-Chavez, C., 2014. Temporal variations in the effective reproduction number of the 2014 West Africa ebola outbreak. PLOS Curr. Outbreaks (September) 1–12. http://dx.doi.org/10.1371/currents.outbreaks.9e4c4294ec8ce1adad283172b16bc908.Abstract. [DOI] [PMC free article] [PubMed]
- Webb G., Browne C. A model of the ebola epidemics in West Africa incorporating age of infection. J. Biol. Dyn. 2015:10. doi: 10.1080/17513758.2015.1090632. [DOI] [PubMed] [Google Scholar]
- Webb G., Browne C., Huo X., Seydi M., Seydi O., Magal P. A model of the 2014 ebola epidemic in west africa with contact tracing. PLOS Curr. Outbreaks. 2015;(January):1–14. doi: 10.1371/currents.outbreaks.846b2a31ef37018b7d1126a9c8adf22a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- WHO, 2014a. Experimental Therapies: Growing Interest in the Use of Whole Blood or Plasma from Recovered Ebola Patients(convalescent therapies). World Health Organization September.
- WHO, 2014b. Use of Convalescent Whole Blood or Plasma Collected from Patients Recovered from Ebola Virus Disease for Transfusions, as an Empirical Treatment during Outbreaks. World Health Organization, September, 1–19.
- WHO-Ebola-Response-Team Ebola virus disease in West Africa—the first 9 months of the epidemic and forward projections. N. Engl. J. Med. 2014;371:1–15. doi: 10.1056/NEJMoa1411100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu J., Lee C., Cowling B., Yuen K. Logistical feasibility and potential benefits of a population-wide passive-immunotherapy program during an influenza pandemic. Proc. Natl. Acad. Sci. USA. 2009;107:3269–3274. doi: 10.1073/pnas.0911596107. [DOI] [PMC free article] [PubMed] [Google Scholar]