Applications of a deep learning method for anti-aliasing and super-resolution in MRI

Abstract

Magnetic resonance (MR) images with both high resolutions and high signal-to-noise ratios (SNRs) are desired in many clinical and research applications. However, acquiring such images takes a long time, which is both costly and susceptible to motion artifacts. Acquiring MR images with good in-plane resolution and poor through-plane resolution is a common strategy that saves imaging time, preserves SNR, and provides one viewpoint with good resolution in two directions. Unfortunately, this strategy also creates orthogonal viewpoints that have poor resolution in one direction and, for 2D MR acquisition protocols, also creates aliasing artifacts. A deep learning approach called SMORE that carries out both anti-aliasing and super-resolution on these types of acquisitions using no external atlas or exemplars has been previously reported but not extensively validated. This paper reviews the SMORE algorithm and then demonstrates its performance in four applications with the goal to demonstrate its potential for use in both research and clinical scenarios. It is first shown to improve the visualization of brain white matter lesions in FLAIR images acquired from multiple sclerosis patients. Then it is shown to improve the visualization of scarring in cardiac left ventricular remodeling after myocardial infarction. Third, its performance on multi-view images of the tongue is demonstrated and finally it is shown to improve performance in parcellation of the brain ventricular system. Both visual and selected quantitative metrics of resolution enhancement are demonstrated.

1. Introduction

In many clinical and research applications, MR images with high resolution and high signal-to-noise ratio (SNR) are desired. However, acquiring such MR images takes a long time, which is costly, lowers patient throughput, and increases both patient discomfort and motion artifacts. A common compromise in practice is to acquire MRI with good in-plane resolution and poor through-plane resolution. With a reasonable acquisition time, the resulting elongated voxels have good SNR and one viewpoint (the in-plane view) with good resolution in two directions that yields acceptable diagnostic quality. Though they are acceptable in diagnosis, these elongated voxels are not ideal for automatic image processing software, which is generally focused on 3D analysis and needs isotropic resolution. A common first step in automatic analysis is to interpolate (nearest neighbor, linear, b-spline, zero-padding in k-space, etc.) the data into isotropic voxels. Unfortunately, since interpolation does not restore the high frequency information that was not acquired in the actual scan itself, the interpolated images have blurry edges in the through-plane direction. Also, for 2D MRI acquisitions the low sampling rate in the through-plane direction causes aliasing artifacts which appear as unnatural high-frequency textures that cannot be removed through interpolation.

To address the problem of low through-plane resolution, researchers have developed a number of super-resolution (SR) techniques, including multi-image SR and single-image SR methods, that attempt to restore the missing and attenuated high frequency information. Multi-image SR methods reconstruct a high resolution (HR) image from the acquisition of multiple low-resolution (LR) images each with degraded resolution in a different direction [1, 2], such that the methods can combine high-frequency information from multiple orientations. Although multi-image SR methods [1, 2] can be effective, there are two major disadvantages. First, it takes extra time to acquire the multiple images, which is costly and inconvenient. Second, the images must be registered together, an operation that is prone to errors because of differences in both image resolution and geometric distortions (both caused by differences in the orientations of the acquired images). Single-image SR, on the other hand, only involves one acquired LR image, which solves the problem of acquisition time and focuses our attention on the SR algorithms. The most successful algorithms for single-image SR in MRI have been learning-based including sparse coding [3], random forests [4], and convolutional neural networks (CNNs) [5, 6, 7]. The basic strategy of these methods is to learn a mapping from LR atlas images (also called training images or examplars) to HR atlas images and apply the learned mapping to the acquired LR subject images (also called testing images). Methods like sparse coding and random forests need a manually designed feature as the input for the mapping. On the other hand, CNNs take either images or patches directly as input, and learn the features automatically during training. Some CNNs are trained with aliased LR images [7, 8]. These networks do anti-aliasing and super-resolution at the same time.

Many of these learning-based methods provide good results, especially the state-of-the-art methods CNNs [9, 10]. In NTIRE CVPR 2017 [11, 12] and PIRM ECCV 2018 super-resolution challenge [13], a variety of SR methods were evaluated. Among them, generative adversarial network (GAN)-based models provide results with better visual quality, while a CNN model called Enhanced Deep Residual Network (EDSR) [9] achieves the best accuracy, which is more important than visual quality for medical imaging. Although these SR methods provide far better results than interpolation, they have not been universally adopted in MRI for two major reasons. First, training data requires paired LR and HR MR images which can be difficult to obtain, primarily because high-SNR HR MR images take a long time to acquire and may suffer from motion artifacts. Second, to avoid overfitting in deep networks, the tissue contrast of external training images must closely match with the subject data, but this is difficult because MRI has no standardized intensity scale. Because of these two reasons, it is highly desirable for SR in MR to avoid external atlases.

SR methods that do not require external atlases have been developed in the past. Methods include total variation methods [14, 15], non-local means [16, 17], brain hallucination [18], and self super-resolution methods (SSR) [19, 20, 21, 22]. These methods all have features that make them non-optimal. For example, total variation SR methods are essentially image enhancement methods designed to strengthen edges and suppress noise, where the parameters need to be carefully tuned to decide how much high frequency information to be restored. Non-local means SR assumes that small patches repeat themselves at different resolutions within the same image, which may not be true in medical images. Brain hallucination assumes that the LR/HR properties in a T1-weighted image are the same as those in a T2-weighted image, which may not be true. Self super-resolution methods, with the exception of [22], assume that images obey a spatial self-similarity wherein the LR/HR relationship at a coarse scale applies to that at a finer scale. The SR method presented in Jog et al. [22] is the first SR method to improve resolution in the through-plane direction using the higher resolution data that is already present in the in-plane directions. Our method is motivated by and improves upon this prior work, which we refer to as JogSSR in this paper.

We previously developed an SSR algorithm called Synthetic Multi-Orientation Resolution Enhancement (SMORE) [23, 8]. SMORE does not use external training data, there are no parameters to tune, there is no intensity smoothing or regularization, and the only pre-processing that is required is N4 intensity inhomogeneity correction [24]. SMORE takes advantage of the fact that the in-plane slices have high resolution data and can be used to extract paired LR/HR training data by downsampling. For 3D MRI, SMORE uses the state-of-the-art network EDSR as the underlying SSR CNN [23]. For 2D MRI, SMORE uses a self anti-aliasing (SAA) deep CNN that precedes the SSR CNN, also using EDSR as the underlying CNN model [8]. We have already demonstrated that SMORE can give results with better SR accuracy than competing methods, including standard interpolation and JogSSR. Also Dewey et al. [25] have demonstrated that SMORE can be used to improve the performance of image synthesis and white matter lesion segmentation.

In this paper, we use four applications to demonstrate the potential of SMORE in both research and clinical scenarios. The first application is on T2 FLAIR MR brain images acquired from multiple sclerosis (MS) patients. MS is an auto-immune disease in which myelin, the protective coating of nerves, is damaged and can be visualized as hyperintense lesions in FLAIR images. We show that visualization of MS lesions using SMORE is better than that obtained using cubic b-spline interpolation and JogSSR. The second application is on cardiac MRI where we explore the visualization of myocardial scarring from cardiac left ventricular remodeling after myocardial infarction. Characterizing such scarring is important factor in assessing the long-term clinical outcome after myocardial infarction [26] and it is challenging due to the competing requirements of high-resolution imaging and rapid scanning due to cardiac motion and breathing. We show improved visualization of such scars when using SMORE.

The third application of SMORE is on multi-orientation MR images of the tongue in tongue tumor patients. Because of the involuntary requirement to swallow during lengthy MR scans, acquisition times are very limited–less than 3 minutes—in tongue imaging. A previous approach to obtaining super-resolution in the tongue used a computational combination of axial, sagittal, and coronal image stacks, each obtained in a separate stationary phase and registered together [2]. We demonstrate how the use of SMORE on a single acquisition is comparable to the result of combining three acquisitions. The fourth application of SMORE is on brain ventricle labeling in subjects with normal pressure hydrocephalus (NPH). NPH is a brain disorder usually caused by disruption of the cerebrospinal fluid (CSF) flow, leading to ventricle expansion and brain distortion. Having accurate parcellation of the ventricular system into its sub-compartments could potentially help in diagnosis and surgical planning in NPH patients [27]. Both visual and selected quantitative metrics of resolution enhancement are demonstrated.

In this paper, we make three important contributions about the implementation and utility of SMORE. First, we give a complete explanation of the method (previously described more briefly in conference publications [23, 8]) in Sec. 2.1. Second, in order to show the versatility of SMORE, we present results on four MRI datasets from different pulse sequences and different organs, with three of them being real acquired LR MR datasets. Finally, we demonstrate that the proposed SR algorithm yields improvements not only in apparent image quality but, in the fourth experiment, show quantitative improvements when SMORE is applied as a preprocessing step for a segmentation task.

2. Material and Methods

2.1. Overview of SMORE

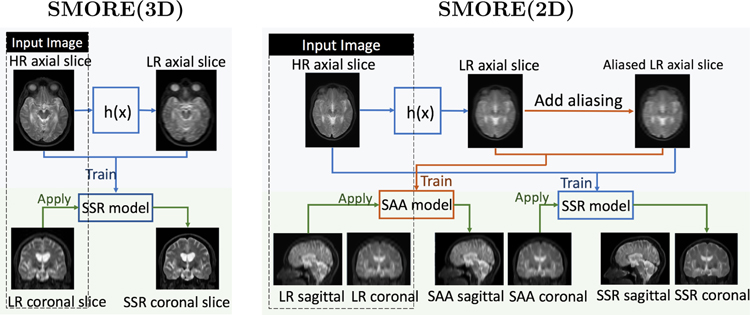
Fig. 1 shows the workflow of SMORE for MRI acquired with 3D and 2D protocols assuming that axial slices are in-plane slices. For 3D MRI, SMORE(3D) simulates LR axial slices from HR axial slices by applying a filter h(x) consisting of a rect filter as well as an anti-ringing filter in k-space that yields the through-plane resolution, and then uses the paired LR/HR data to train a self super-resolution (SSR) network. This trained network is applied on LR coronal slices to improve through-plane resolution, resulting in a HR volume. Details can be found in [23], with a modification that the anti-ringing filter is changed to a Fermi filter to better mimic the behavior in scanners. SMORE(2D) uses the same general concept as SMORE(3D), but adds a self anti-aliasing (SAA) network trained with aliased axial slices. The aliased slices are created by first applying the filter h(x), which in this case mimics the through-plane slice profile, and then a downsampling/upsampling sequence that produces aliasing at the same level as that found in the through-plane direction. We first apply the trained SAA network on sagittal slices to remove aliasing in the sagittal plane. We then apply the trained SSR network on the coronal plane to both remove aliasing in the coronal plane and improve through-plane resolution, resulting in an anti-aliased HR volume. Details can be found in [8]. For both SMORE(3D) and SMORE(2D), we only apply the trained networks in one orientation instead of two (or more) as described in our previous conference papers [23, 8]. This reduces computation time from 20 min to 15 min for SMORE(3D), and from 35 min to 25 min for SMORE(2D) on a Telsa K40 GPU, with only a minor impact on performance. Also we omit SAA network and directly apply SSR network to the LR image to further reduce time cost from 25 min to 15 min for SMORE(2D) if the ratio r between through-plane and in-plane resolution is less than 3, since the aliasing is empirically not severe in this case.

Figure 1: Overview of SMORE.

Workflow of SMORE for MRI acquired with 3D protocols and 2D protocols, referred as SMORE(3D) and SMORE(2D). They are simplified version of algorithms described in our previous conference papers [23, 8].

The SAA and SSR neural networks currently used in SMORE are both implemented using the state-of-the-art super-resolution EDSR network [9]. In this paper, we implement patch-wise training with randomly extracted 32×32 patches. Training on small patches restricts the effect receptive field [28] to avoid structural specificity so that this network can better preserve pathology. It also reduces spatial correlation of the training data, which can accelerate convergence in theory [29]. To reduce training time, the networks are fine-tuned from pre-trained models that were trained from arbitrary data. When applying the trained networks, we apply them to entire coronal or sagittal slices (depending on whether it is SAA or SSR) rather than just 32 × 32 patches. This is possible since EDSR is a fully convolutional network (FCN) which allows an arbitrary input size [30].

2.2. Application to visual enhancement for MS lesions

In this experiment, we test whether super-resolved T2 FLAIR MR images can give better visualization of white matter lesions in the brain than the acquired images. The T2 Flair MR images were acquired from multiple sclerosis (MS) subjects using a Philips Achieva 3T scanner with a 2D protocol and the following parameters: 0.828 × 0.828 × 4.4 mm, TE = 68ms, TR = 11s, TI = 2.8s, flip angle = 90°, turbo factor = 17, acquisition time = 2m56s. We performed cubic b-spline interpolation, JogSSR [22], and SMORE(2D) on the data using a 0.828 × 0.828 × 0.828 mm digital grid. We show a visual comparison on the regions of white matter lesions in axial, sagittal, and coronal slices for the three methods. We also plot 1D intensity profiles of the three methods across selected paths through different lesions.

2.3. Application to visual enhancement of scarring in cardiac left ventricular remodeling

In this experiment, we test whether super-resolved images can give better visualization of the scarring caused by left ventricular remodeling after myocardial infarction than the acquired images. We acquired two T1-weighted MR images from an infarcted pig, each with a different through-plane resolution. One image, which serves as the HR reference image, was acquired with resolution equal to 1.1 × 1.1 × 2.2 mm, and then it was sinc interpolated on the scanner (by zero padding in k-space) to 1.1 × 1.1 × 1.1 mm. The other image was acquired with resolution equal to 1.1 × 1.1 × 5 mm. Both of these images were acquired with a 3D protocol, inversion time = 300ms, flip angle = 25°, TR = 5.4 ms, TE = 2.5 ms, and GRAPPA acceleration factor R = 2. The HR reference image has a segmented centric phase-encoding order with 12 k-space segments per imaging window (heart beat), while the LR subject image has 16 k-space segments.

In our experiment, we performed sinc interpolation, JogSSR, and SMORE(3D) on the 1.1 × 1.1 × 5.0 mm data using a 1.1× 1.1× 1.1 mm digital grid. These images were then rigidly registered to the reference image for comparison. We are interested in the regions of thinning layer of midwall scar between the endocardial and epicardial layers of normal myocardium and the thin layer of normal myocardium between the scar and epicardial fat. These two regions of interest are cropped and zoomed to show the details.

2.4. Application to multi-view reconstruction

In this experiment, we test whether a super-resolved image from a single acquisition can give a comparable result to a multi-view super-resolution image reconstructed from three acquisitions. MR images of the tongue were acquired from normal speakers and subjects who had tongue cancer surgically resected (glossectomy). Scans were performed on a Siemens 3.0 T Tim Treo system using an eight-channel head and neck coil. A T2-weighted Turbo Spin Echo sequence with an echo train length of 12, TE = 62ms, and TR = 2500ms was used. The field-of-view (FOV) was 240 × 240 mm with a resolution of 256 × 256. Each dataset contained a sagittal, coronal, and axial stack of images containing the tongue and surrounding structures. The image size for the high-resolution MRI was 256 × 256 × z (z ranges from 10 to 24) with 0.9375 × 0.9375 mm in-plane resolution and 3 mm slice thickness. The datasets were acquired at a rest position and the subjects were required to remain still for 1.5–3 min for each orientation. For each subject, the three axial, sagittal, and coronal acquisitions were interpolated onto a 0.9375 × 0.9375 × 0.9375 mm digital grid and N4 corrected [24].

We applied both JogSSR and SMORE(3D) on single acquisitions to compare to the multi-view super-resolution reconstruction. The multi-view reconstruction algorithm we used for comparison is an improved version of the algorithm described in Woo et al. [2]. This approach takes three interpolated image volumes, aligns them using ANTs affine registration [31] and SyN deformable registration [32], and then uses a Markov random field image restoration algorithm (with edge enhancement) to reconstruct a single HR volume.

2.5. Application to brain ventricle parcellation

This experiment demonstrates the effect of super-resolution on brain ventricle parcellation and labeling using the Ventricle Parcellation Network (VParNet) described in Shao et al. [33]. In particular, we test whether super-resolved images can give better VParNet results than images from either interpolation or JogSSR. The data for this experiment are from an NPH data set containing 95 T1-w MPRAGE MRIs (age range: 26–90 years with mean age of 44.54 years). They were acquired on a 3T Siemens scanner with scanner parameters: TR = 2110 ms, TE = 3.24 ms, FA = 8°, TI = 1100 ms, and voxel size of 0.859 × 0.859 × 0.9 mm. There are also 15 healthy controls from the Open Access Series on Imaging Studies (OASIS) dataset involved in this experiment. All the MRIs were interpolated to a 0.8 × 0.8 × 0.8 mm digital grid, and then pre-processed using N4-bias correction [24], rigid registration to MNI 152 atlas space [34], and skull-stripping [35].

VParNet was trained to parcellate the ventricular system of the human brain into its four cavities: the left and right lateral ventricles (LLV and RLV), and the third and the fourth ventricles. It was trained on 25 NPH subjects and 15 healthy controls (not involved in the evaluations). In the original experiment of Shao et al. [33], the remaining 70 NPH subjects were used for testing. In this experiment, we downsampled the 70 NPH subject images first so that we could study the impact of super-resolution. In order to remove the impact of pre-processing, we downsampled the 70 pre-processed test datasets instead of the raw datasets. In particular, we downsampled the data to a resolution of 0.8 × 0.8 × 0.8r mm following a 2D acquisition protocol, where r is the through-plane to in-plane resolution ratio. The slice number of the HR images happens to be a prime number. Since the downsampled images must have integer slice numbers, the downsample ratio r which is also the ratio between the slice number of HR images and downsampled images must be non-integers. In the experiment, we choose ratio r of 1.50625, 2.41, 3.765625, 4.82, 6.025. The downsampled images have voxel length (0.8r mm) in z-axis of 1.205 mm, 1.928 mm, 3.0125 mm, 3.856 mm, 4.82 mm. To apply VParNet, which was trained on 0.8 × 0.8 × 0.8 mm images, to these downsampled images, we used cubic b-spline interpolation, JogSSR, and SMORE(2D) to produce images on a 0.8 × 0.8 × 0.8 mm digital grid. These images were then used in the same trained VParNet to yield ventricular parcellation results.

The HR NPH images have physical resolution in z-axis of 0.9 mm. We used them as ground truth and evaluated the accuracy of super-resolved images using the Structural Similarity Index (SSIM) and the Peak Signal to Noise Ratio (PSNR) within brain masks. As for the ventricle parcellation performance, we evaluated the automated parcellation results using manual delineations. We computed Dice coefficients [36] to evaluate the parcellation accuracy of the same network on different super-resolved and interpolated images. By comparing the parcellation accuracy, we can evaluate how much improvement we get from SMORE(2D) compared with interpolation.

3. Results

3.1. Application to visual enhancement for brain white matter lesions

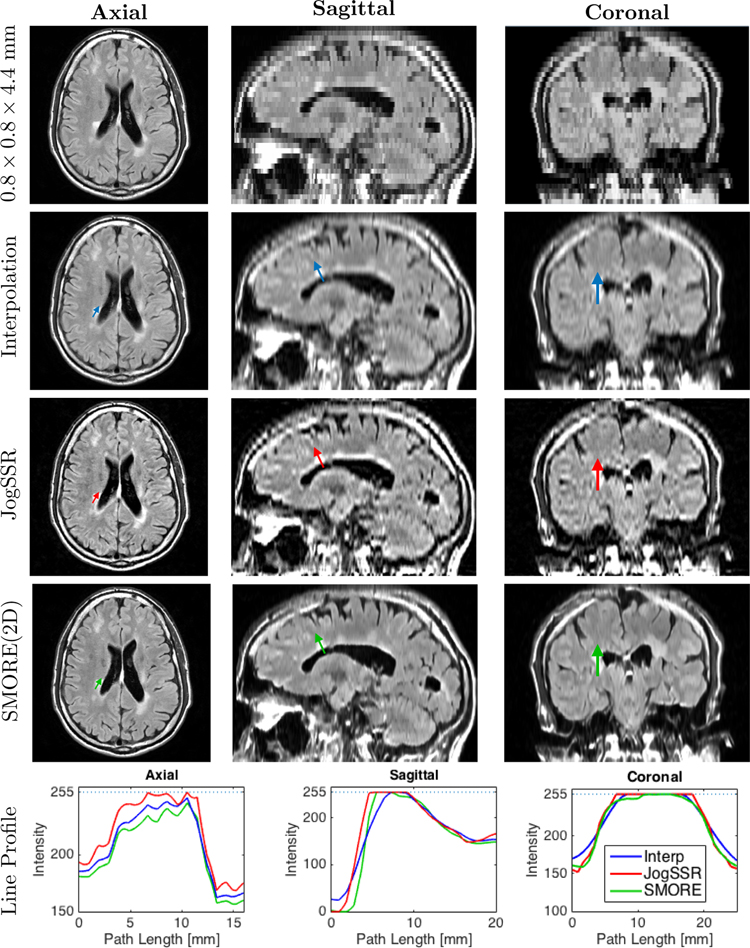
Fig. 2 shows an example of T2 FLAIR images reconstructed from the acquired resolution of 0.828 × 0.828 × 4.4 mm input image onto a 0.828 × 0.828 × 0.828 mm digital grid using cubic-bspline interpolation, JogSSR, and SMORE(2D). On these images, MS lesions appear as bright regions in the brain’s white matter. We can see that both JogSSR and SMORE(2D) give sharper edges than interpolation and the SMORE(2D) result looks more realistic than JogSSR. This is in part because JogSSR does not carry out anti-aliasing, which allows aliasing artifacts, which are seen in the original and interpolated images, to remain. We note that in Fig. 2, SMORE also enhances resolution in the axial slice slightly, which is originally 0.828 × 0.828 mm HR. Although we apply super-resolution in the through-plane, structures like edges that pass through-plane slices obliquely also gets enhanced, permitting in-plane edges to also be enhanced.

Figure 2: T2 Flair MRI from an MS subject:

Axial, sagittal, and coronal views of the acquired 0.828 × 0.828 × 4.4 mm image, and the reconstructed volumes with 0.828 × 0.828 × 0.828 mm digital grid through cubic b-spline interpolation, JogSSR, and SMORE(2D). In each view, we pick a path across lesions, shown as colored arrows in the images, and plot the line profiles of the three methods in the same plot on the bottom of each view.

Aside from the visual impression of performance differences gleaned from looking at the images directly, we also examined selected intensity profiles within the images. Each reconstructed image in Fig. 2 contains a small colored arrow. These arrows depict the line segment and direction over which intensity profiles shown in the bottom row of the figure are extracted. For example, the three colored arrows in the axial images of the first column yield the profiles on the bottom right graph. These axial profiles show that other than some differences in overall intensity, the resolutions of the methods appear to be very similar. This is to be expected since the axial image already has good resolution. The profiles through the ventricle and lesion in the sagittal orientation, however, show significant differences. Both super-resolution approaches show a steeper edge than the interpolated image (although the JogSSR result is inexplicably shifted relative to the true position of the edge). The profiles from the lesion in the coronal images show a similar property—steeper edges from the super-resolution approaches. Overall, the selected intensity profiles suggest resolution enhancement from both SMORE(2D) and JogSSR.

3.2. Application to visual enhancement for scarring in cardiac left ventricular remodeling

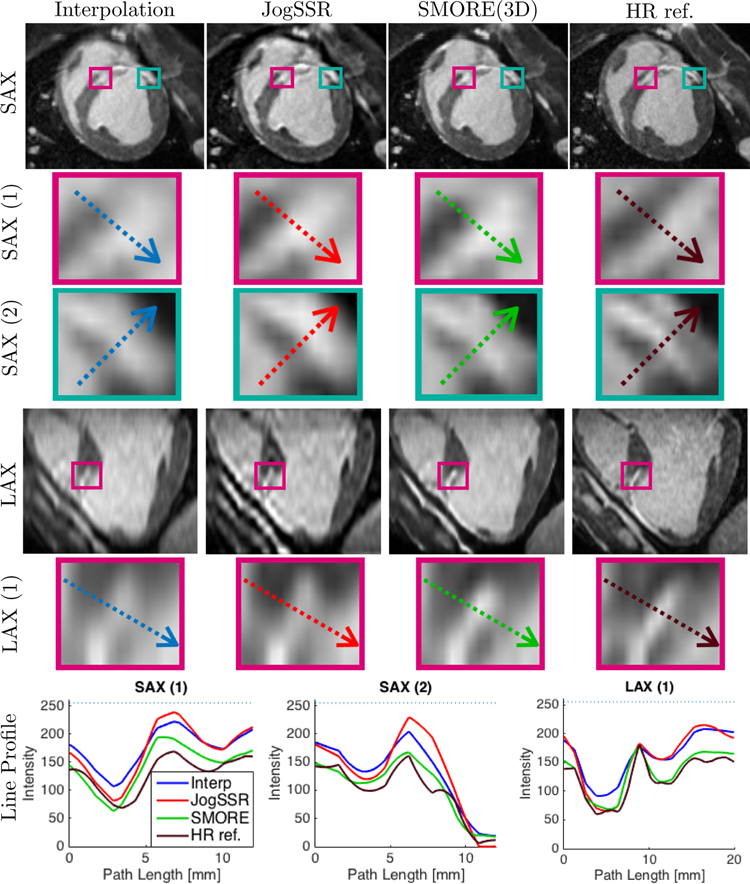
Cardiac imaging data that were acquired with a resolution of 1.1 × 1.1 × 5.0 mm are shown in Fig. 3 after application of interpolation (zero-padding in k-space), JogSSR, and SMORE(3D) applied on a 1.1 × 1.1 × 1.1 mm digital grid. A thin layer of the midwall scar between the endocardium and and epicardium of normal myocardium appears as bright strip in the megenta boxes. A thin layer of normal myocardium between scar and epicardial fat appears as dark strip in the cyan boxes. They are zoomed in to show the details below the short-axis (SAX) slices with acquired resolution of 1.1 × 1.1 mm and long-axis (LAX) slices with originally acquired resolution of 1.1 × 5 mm for the first three columns, or 1.1 × 2.2 mm for the column of ”HR ref.”. Each zoomed box contains a colored arrow which depicts a line segment. The corresponding line profiles are shown on the bottom.

Figure 3: Late gadolinium enhancement (LGE) from an infarct swine subject:

Short-axis (SAX) and long-axis (LAX) views arranged in columns using 1.1 × 1.1 × 1.1 mm digital grid: output of 1) sinc-interpolation, 2) JogSSR and 3) SMORE(3D) for the subject LR image acquired at 1.1 × 1.1 × 5 mm; 4) sinc-interpolated HR reference image for comparison acquired at 1.1 × 1.1 × 2.2 mm. SAX(1) and LAX(1) boxes contain a thinning layer of enhanced midwall scar between endo- and epi layers of normal myocardium (hypo-intense). SAX(2) boxes contain a thin layer of normal myocardium (hypo-intense) between scar and epicardial fat (both hyper-intense). In each box, we pick a path across the region of interest, shown as colored arrows, and plot the profiles in the last row.

As seen in the long-axis (LAX) images and zoomed regions, the borders between normal myocardium, enhanced scar and blood are significantly clearer in SMORE(3D) compared with JogSSR and interpolation. The intensity profile of SMORE(3D), the green line shown in the magenta box marked ”LAX (1)”, very closely matches that of the HR reference image. For the short-axis (SAX(1) and SAX(2)), the resolution was already high and there is less to be gained. Nevertheless, it is apparent that the image clarity is slightly improved by SMORE(3D) while faithfully representing the patterns from the input images.

Furthermore, we computed the SSIM and PSNR between each method and HR reference image. The SSIM for interpolation, JogSSR, and SMORE results are 0.5070, 0.4770, and 0.5146, correspondingly. The PSNR for interpolation, JogSSR, and SMORE are 25.8816, 24.4142, and 25.3002, correspondingly. SMORE gives best SSIM, yet worse PSNR than sinc interpolation. Note that the registration cannot be perfect among different sets of cardiac images, due to motion or changing physiological state. When computing SSIM, images are prefiltered. Therefore, SSIM is less sensitive to image distortion. On the other hand, PSNR is a measure of noise level. SMORE does not consider noise reduction. This might be the reason why the SMORE result has better SSIM but worse PSNR. Also this evaluation is done on only one pair of LR/HR data, and is not very informative statistically.

3.3. Application to multi-frame reconstruction

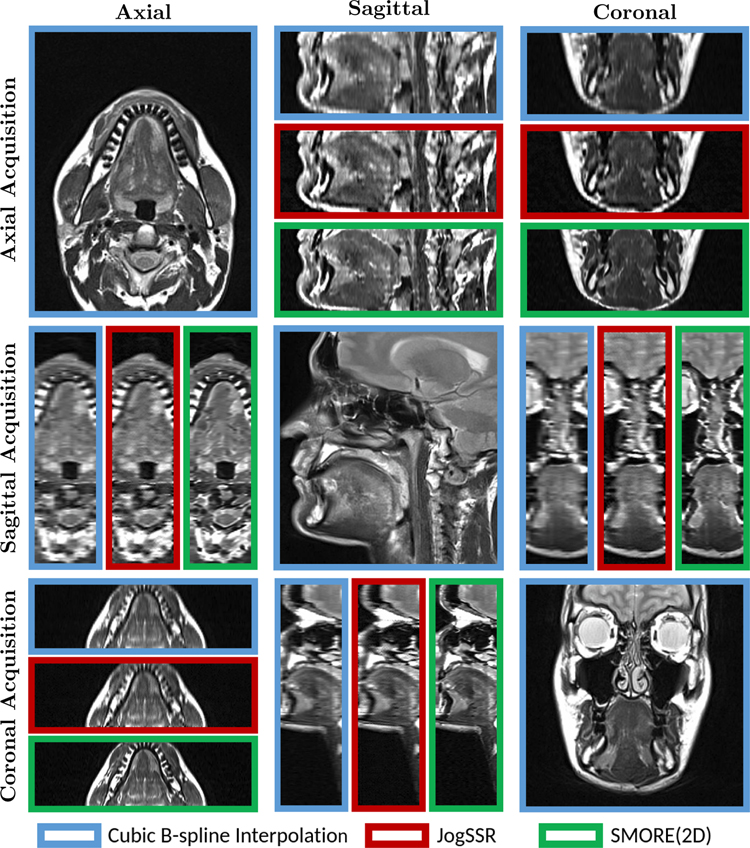
Tongue data with 0.9375 × 0.9375 mm in-plane resolution and 3 mm through-plane resolution were acquired with in-plane view of axial, sagittal, and coronal. They are shown in Fig. 4 on a 0.9375 × 0.9375 × 0.9375 mm digital grid after both cubic b-spline interpolation (blue boxes) interpolation, JogSSR (red boxes), and SMORE(2D) (green boxes). The in-plane views are only shown for interpolation since they are already HR slices. In through-plane views, SMORE(2D) always gives visually better results than both interpolation and JogSSR. In particular, we can see the edges are sharper in SMORE(2D) and no artificial structures are created.

Figure 4: T2w MRI from a tongue tumor subject:

Axial, Sagittal, and Coronal views of the three acquisitions in Axial, Sagittal, and Coronal planes (not registered). We show the through-plane views of the resolved volumes with isotropic digital resolution that result from cubic b-spline interpolation (blue boxes), JogSSR (red boxes), and our SMORE(2D) (green boxes). The in-plane views are only shown with interpolation results since they are already HR slices.

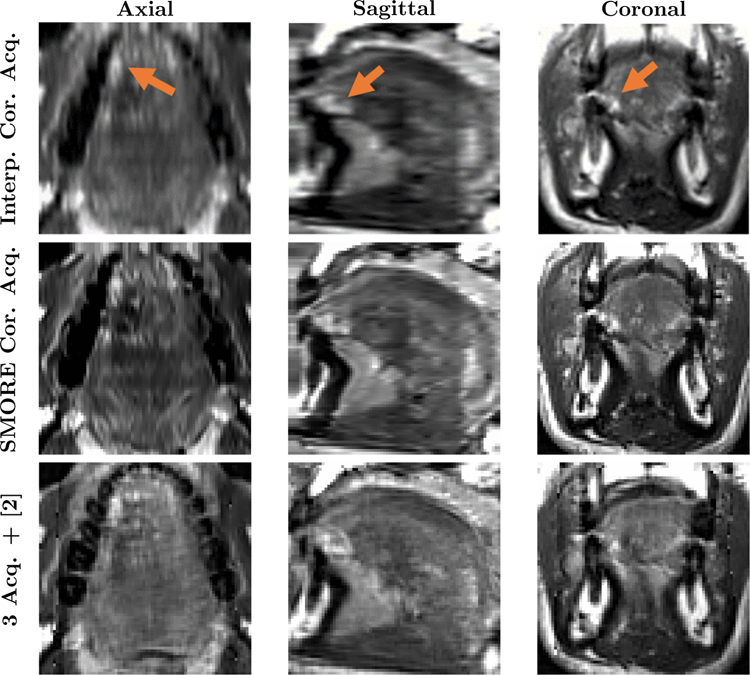
A comparison of interpolation and SMORE(2D) (where each used only the coronal image) and the multi-view reconstruction (which used all three images) is shown in Fig 5. The arrows point out at the bright pathology region—i.e., scar tissue formed after removing a tumor. We can see that SMORE has visually better resolution than the interpolated image, but several places within the multi-view reconstruction have visually better detail. On the other hand, the pathology region in the multi-view reconstruction appears to be somewhat degraded in appearance over both the SMORE(2D) and interpolation result. We believe that this loss of features may be caused by regional mis-registration between the three acquisitions.

Figure 5: Comparison between SMORE(2D) and multi-view reconstruction for a tongue tumor subject:

Axial, Sagittal, and Coronal views of the tongue region in cubic b-spline interpolation and SMORE(2D) results for a single coronal acquisition, and multi-view reconstructed image [2] using three acquisitions. The arrows point out the bright looking scar tissue from a removed tumor.

3.4. Application to brain ventricle parcellation

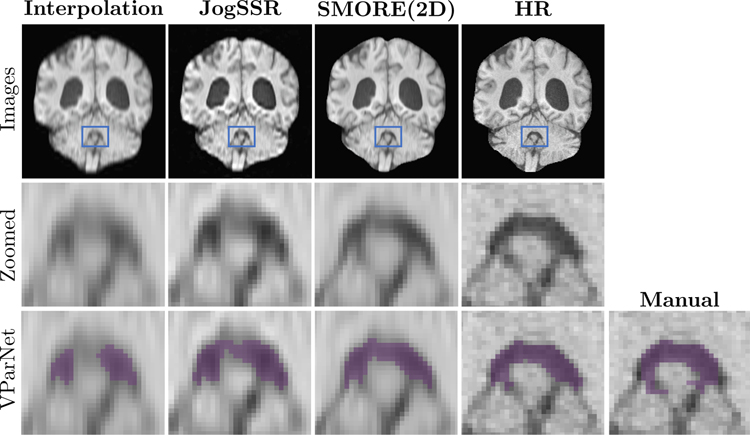
Example images from an NPH subject, all reconstructed on a 0.8 × 0.8 × 0.8 mm digital grid, are shown in Fig. 6. The LR image depicted using cubic-bspline interpolation has resolution 0.8 × 0.8 × 3.856 mm LR while the ground truth image has resolution 0.859 × 0.859 × 0.9 mm. The JogSSR and SMORE(2D) results are also shown. To reveal more detail, the second row shows zoomed images of the 4th ventricle, where the zoomed region is shown using blue boxes in the first row. The VParNet [33] parcellations as well as the manually delineated label of the 4th ventricle are shown using purple voxels on the third row. Visually, of all the results derived from the LR data, SMORE(2D) gives the best super-resolution and parcellation results. In particular, the VParNet parcellation on the SMORE(2D) result is very close to the VParNet on the HR image.

Figure 6: Coronal views of brain ventricle parcellation on an NPH subject:

The volumes with digital resolution of 0.8 × 0.8 × 0.8 mm that resolved from 0.8 × 0.8 × 3.856 mm LR image using cubic-bspline interpolation, JogSSR, SMORE(2D), and the interpolated 0.8 × 0.8 × 0.9 mm HR image. The patches in blue boxes are zoomed in the second row to show details of the 4th ventricle. The last row shows the VParNet [33] parcellation results and the manual labeling for the 4th ventricle.

We also evaluated these results quantitatively. The mean values of SSIM and PSNR are shown in Table 1. Paired two-tail Wilcoxon signed-rank tests [37] were performed between results from interpolation, JogSSR, and SMORE(2D). The ‘*’ (p < 0.005) and ‘†’ (p < 0.05) indicate the method is significantly better than the other two methods. We can see that the SR results from SMORE(2D) are always significantly more accurate than interpolation and JogSSR, with SSIM and PSNR as accuracy metrics. For images with thickness of 1.205 mm, the significance is weak, indicating that the improvement is not dramatic. For images with thicker slices, the significance is strong, and therefore the improvement is large. The Dice coefficient of the parcellation results of the four cavities (RLV, LLV, 3rd, 4th) and the whole ventricular system are also shown in Table 1. From the table, we can find that for example, VParNet on SMORE(2D) results of thickness 4.82 mm is better than interpolation results of 3.856 mm, while the later needs 56.25% longer scanning time. It shows the potential of reducing scanning time by using SMORE.

Table 1:

Evaluation of brain ventricle parcellation on 70 NPH subjects. We performed paired two-tail Wilcoxon signed-rank tests between interpolation, JogSSR, and SMORE.

Metrics	Thickness	Interp.	JogSSR	SMORE	HR(0.9 mm)
SSIM	1.205 mm	0.9494	0.9507	0.9726*	1*
	1.928 mm	0.9013	0.9106	0.9389*
	3.0125 mm	0.8290	0.8400	0.8893*
	3.856 mm	0.7677	0.7812	0.8387*
	4.82 mm	0.7003	0.7170	0.7817*
PSNR	1.205 mm	35.0407	34.0472	39.5053*
	1.928 mm	31.9321	30.6444	35.7429*
	3.0125 mm	29.2785	27.4384	31.9878*	–
	3.856 mm	27.7562	25.7118	29.6050*
	4.82 mm	26.4127	24.2377	28.1593*
Dice(RLV)	1.205 mm	0.9704	0.9705	0.9712†	0.9715*
	1.928 mm	0.9678	0.9690	0.9706*
	3.0125 mm	0.9610	0.9635	0.9693*
	3.856 mm	0.9527	0.9578	0.9648*
	4.82 mm	0.9405	0.9498	0.9629*
Dice(LLV)	1.205 mm	0.9710	0.9709	0.9715†	0.9717†
	1.928 mm	0.9690	0.9693	0.9710*
	3.0125 mm	0.9638	0.9641	0.9699*
	3.856 mm	0.9571	0.9585	0.9663*
	4.82 mm	0.9469	0.9510	0.9638*
Dice(3rd)	1.205 mm	0.9149	0.9149	0.9163†	0.9174*
	1.928 mm	0.9095	0.9097	0.9141*
	3.0125 mm	0.8945	0.8940	0.9073*
	3.856 mm	0.8779	0.8761	0.8937*
	4.82 mm	0.8560	0.8545	0.8832*
Dice(4th)	1.205 mm	0.8954	0.8941	0.8973*	0.8983*
	1.928 mm	0.8891	0.8851	0.8947*
	3.0125 mm	0.8741	0.8657	0.8878*
	3.856 mm	0.8550	0.8463	0.8753*
	4.82 mm	0.8254	0.8216	0.8629*
Dice(whole)	1.205 mm	0.9690	0.9690	0.9696†	0.9699*
	1.928 mm	0.9665	0.9672	0.9690*
	3.0125 mm	0.9602	0.9614	0.9675*
	3.856 mm	0.9524	0.9552	0.9632*
	4.82 mm	0.9408	0.9470	0.9607*

The ‘*’ (p < 0.005) and ‘†’ (p < 0.05) indicate the method is significantly better than the other two methods. For the column of ‘HR’, they indicate that HR images give significantly better parcellation results than resolved images from the three methods with thickness of 1.205 mm.

We wondered whether the parcellation results from HR images are significantly better than SMORE(2D) from images with thickness 1.205 mm. In the column of ‘HR’ of Table 1, we show results of paired two-tail Wilcoxon signed-rank tests between HR and the results from the three methods. The ‘*’ and ‘†’ indicate that HR images give significantly better evaluation values than SMORE(2D) for thickness of 1.205 mm. The strong significance always holds, except for the Dice of LLV for which only weak significance holds. It shows that acquiring HR images with adequate SNR gives better parcellation results than LR images, even with SMORE(2D) applied to improve spatial resolution. However, if the acquired data are already limited to be anisotropic LR, which is common in clinical and research, SMORE(2D) can give better parcellation than interpolation.

4. Discussion and Conclusions

This paper demonstrates the applications of a self super-resolution (SSR) algorithm, SMORE, on four different MRI datasets, and shows the improved MRI resolution both visually and quantitatively. The methodology of SMORE has been introduced in our previous conference papers [23, 8]. While in this paper, we make important contributions about the implementation and utility of SMORE, which are useful and necessary to appreciate that SMORE can be reliably and widely used in practice. First, this paper provides a complete explanation of SMORE, while previous conference papers have been incomplete due to their required brevity. Second, this paper shows the application of SMORE on MR images produced from different pulse sequences and contrasts, in different organs. To our best knowledge, no other published deep-learning SR method has been demonstrated for improvement of such diverse MRI data sets without training data. Finally, we have demonstrated how SMORE can improve segmentation accuracy, a result which shows there are quantifiable improvements from using SMORE, in additional to the visual improvement in image quality.

In this paper, we demonstrate the applications of SMORE in real world scenarios for MR images. First of all, we consider an important distinction between general SR on natural images and SR on real acquired MR images. Although the general SR problem has been discussed a lot in computer vision application, the common SR problem setting requires well-established LR/HR paired external training data. In contrast to natural images, such external training data is much more difficult to obtain for MR images. In this paper, we develop SMORE to be a SSR algorithm, which requires no external training data; in other words, what it needs is only the input subject image itself. This makes SMORE more applicable in real world scenarios. Second, SMORE is developed for a common type of MRI acquisition which has high in-plane resolution but low through-plane resolution (thick slices). This type of MRI is widely acquired in clinical and research applications. Third, the four experiments in this paper are performed on four different MRI datasets, with three out of them being real acquired LR datasets. From a visual comparison, we find that SMORE enhances edges but does not create structures out of nothing; this reduces the risk of wrongly altering anatomical structures. Finally, the experiment in Sec. 3.4 shows that SMORE is not only visually appealing, it also gives quantitative improvements on SSIM and PSNR. More importantly, applying SMORE as a preprocessing step significantly improves ventricular segmentation accuracy on this brain MRI dataset. Furthermore, we note that sometimes lower resolution images processed with SMORE yield better segmentation results than those from higher resolution images processed with interpolation. This suggests that SMORE post-processing may allow shorter scan times.

The SMORE method has limitations. First, we use EDSR as the SR deep network in SMORE, since it was evaluated as one of the state-of-the-art SR architecture by extensive comparisons [11, 13]. We note that these evaluations were performed on natural images, not MR images, and it is possible that there might be another SR network that performs better on MR images. Fortunately, EDSR can be easily replaced under the framework of SMORE if a better SR network becomes available. Second, the best resolution that can be achieved by SMORE is limited to the in-plane resolution. Because of this, for example, there is no way to use SMORE to enhance images that have been acquired with isotropic resolution. Also, SMORE does not consider cases where resolution differs in three orientations. Third, SMORE does not address motion artifacts. Finally, both SMORE(2D) and SMORE(3D) require knowledge of h(x), the point spread function (or slice profile), which may not be known accurately in some cases. Future work should address these issues.

In conclusion, SMORE produces results that are not only visually appealing, but also more accurate than interpolation. More importantly, applying it as a preprocessing step can improve segmentation accuracy. All these SMORE results were obtained without collecting any external training data. This makes SMORE a useful preprocessing step in many MRI analysis tasks.