An Inverse Eikonal Method for Identifying Ventricular Activation Sequences from Epicardial Activation Maps

Abstract

A key mechanism controlling cardiac function is the electrical activation sequence of the heart’s main pumping chambers termed the ventricles. As such, personalization of the ventricular activation sequences is of pivotal importance for the clinical utility of computational models of cardiac electrophysiology. However, a direct observation of the activation sequence throughout the ventricular volume is virtually impossible.

In this study, we report on a novel method for identification of activation sequences from activation maps measured at the outer surface of the heart termed the epicardium. Conceptually, the method attempts to identify the key factors governing the ventricular activation sequence – the timing of earliest activation sites (EAS) and the velocity tensor field within the ventricular walls – from sparse and noisy activation maps sampled from the epicardial surface and fits an Eikonal model to the observations.

Regularization methods are first investigated to overcome the severe ill-posedness of the inverse problem in a simplified 2D example. These methods are then employed in an anatomically accurate biventricular model with two realistic activation models of varying complexity – a simplified trifascicular model (3F) and a topologically realistic model of the His-Purkinje system (HPS). Using epicardial activation maps at full resolution, we first demonstrate that reconstructing the volumetric activation sequence is, in principle, feasible under the assumption of known location of EAS and later evaluate robustness of the method against noise and reduced spatial resolution of observations.

Our results suggest that the FIMIN algorithm is able to robustly recover the full 3D activation sequence using epicardial activation maps at a spatial resolution achievable with current mapping systems and in the presence of noise. Comparing the accuracy achieved in the reconstructed activation maps with clinical data uncertainties suggests that the FIMIN method may be suitable for the patient- specific parameterization of activation models.

1. Introduction

Computational models of cardiac electrophysiology already show high promise not only as clinical research tools, but also as a modality for assisting in diagnosis [1] and treatment planning [52]. To gain further clinical utility, however, personalization of the models to a given patient’s electrophysiology is required based ideally on non- or minimally invasive acquired routine clinical data. Personalization procedures must also be sufficiently fast and automated to be compatible with clinical workflows and time scales.

As the key driver controlling cardiac function, personalization of the ventricular electrical activation sequence is of pivotal importance. It is known that initiation of the ventricular activation sequences begins at subendocardial coupling sites between the His-Purkinje system (HPS) and the ventricular muscle [30] typically referred to as Purkinje-Ventricular junctions (PVJs). Furthermore, the conduction velocity (CV) of electrical depolarization wavefronts within the ventricular wall is characterized by a spatially varying orthotropic tensor field [23, 34]. Thus, to determine the ventricular activation sequence the locations and relative timings of earliest activation sites (EAS), representing initiation sites mediated by PVJs, as well as the orthotropic velocity tensor field must be identified.

Currently, however, 3D mapping of the activation sequence through the entire myocardial volume of the ventricles is infeasible due to limitations in spatial resolution of 3D mapping systems [15] and ambiguities in the interpretation of extracellularly-recorded electrograms [13]. Even with advanced massively invasive experimental mapping techniques [33], only a relatively coarse panoramic view of the complete, volumetric activation sequence can currently be obtained. Therefore, minimally invasive mapping procedures are routinely performed that record activation maps for both the interior and exterior surfaces of the heart, termed endo- and epicardium respectively, at increasingly higher spatio-temporal resolutions [70]. Non-invasive inverse methods that indirectly infer epicardial activation maps from measurements taken at the body surface [54] have also been developed, but have not yet gained significant clinical relevance.

In general, such techniques, referred to as non-invasive electrocardiographic imaging (ECGi), attempt to reconstruct the spatio-temporal behavior of the electrical sources of the heart from electrocardiograms (ECGs) recorded from the body surface by solving the inverse problem of electrocardiography [29]. Solving this inverse problem is complicated by the non-uniqueness of the relation between myocardial sources and their signature outside the heart, recorded in the form of extracellular electrograms. The vast body of research found in the literature can be broadly categorized based on the regularization techniques used to rule out solutions that are unlikely on physiological grounds [66] and the model used for representing the cardiac sources, with the predominant source models being transmembrane voltage-based [32, 71], extracellular-potential based [61, 7] and activation/recovery-based [68, 24, 31, 35]. Such models have pros and cons in terms of verifiability with experimental data, the domains in which sources can be reconstructed (i.e. on endo- and epicardial surfaces or transmurally throughout the myocardial wall), and their accuracy in pathological scenarios such as the presence of infarcts [72] or more complex non-physiological activation patterns such as arrhyhthmias [60]. For a comprehensive overview of these aspects of ECG imaging we refer to the recent review of Cluitmans et al [17].

Biophysically-detailed forward models based on mono- or bidomain reaction-diffusion equations are able to capture all known electrophysiological details of depolarization wavefront propagation. While these models are routinely used in electrophysiological organ-scale models representing anatomy at a high degree of geometric fidelity [50, 10], they are, in general, computationally too demanding to be feasible in higher dimensional parameter exploration studies [45, 56]. In such applications, techniques based on the Eikonal equation [18] have been preferred as these models are substantially less costly to evaluate and their solution directly yields activation maps. Owing to the superior computational efficiency, the anisotropic Eikonal model appears a suitable choice for exploring the high-dimensional parameter space governing the ventricular activation sequence. Eikonal models have been successfully used to recreate activation maps from clinical surface recordings by constructing feasible HPS networks[20, 47] and assuming global constant conduction velocity.

In this study we develop methodology for identifying the ventricular activation sequence from limited sparse and noisy data sampled from the epicardial surface. We investigate the feasibility of the method using a ground truth forward model representing the ventricular activation by the anisotropic Eikonal equation. For evaluation, we rely on the computed, synthetic data rather than clinical data which are not yet available and may not be suitable at this point in terms of resolution for evaluation of the algorithm’s performance. A Fast Iterative Method (FIM) solver [27] was employed for solving the forward problem and a novel Fast Iterative Method Minimization (FIMIN) algorithm for solving the corresponding inverse problem was developed for identifying the governing input parameters of the forward model – the initiation timings of EAS’s and the velocity tensor field – which optimally fit the epicardial mapping data. An anatomically accurate human biventricular (BiV) model was used, either with a simplified trifascicular HPS representing only the main fascicles of a HPS or a topologically realistic HPS network, to generate high fidelity reference activation sequences. Using epicardial surface data extracted from the forward model at full resolution, we first demonstrate that a reconstruction of the 3D activation sequence is, in principle, feasible. The robustness of the method is then evaluated by reducing spatial resolution and adding noise. Our study results demonstrate that the FIMIN algorithm is able to fully recover 3D activation sequences from sparse epicardial activation maps within the margins of error of clinical data uncertainty. Considering the uncertainties in clinical data, the accuracy achieved suggests that the method may be suitable for the patient-specific parameterization of in silico models of ventricular activation in future clinical applications.

2. Methods

2.1. Preliminaries/Definitions

The anisotropic Eikonal equation is given by the non-linear Partial Differential Equation:

$$\begin{array}{cc}\begin{array}{ll}\parallel \nabla \varphi \left(\mathbf{x}\right){\parallel }_{2,D\left(\mathbf{x}\right)}& =\sqrt{\nabla \varphi \left(\mathbf{x}{)}^{T}D\right(\mathbf{x})\nabla \varphi (\mathbf{x})}=1\end{array}& \forall \mathbf{x}\in \Omega \\ \begin{array}{ll}\varphi \left({\mathbf{x}}_0\right)& =g\left({\mathbf{x}}_0\right)\end{array}& \forall {\mathbf{x}}_0\in S\subset \Omega \end{array}$$ (1)

on a domain Ω, where ||·||_2,D(x) is the norm in the metric D(x), ϕ is the first arrival time for each point in space, and S are the initiation sites or EAS, from where wavefronts emanate at a time prescribed by g ∈ ℝ^k for k being the number of initiation sites. For the tensor field D, we need D ∈ 𝒮 for well-posedness, where 𝒮 the set of symmetric positive definite tensors fields over the whole domain Ω. The special case D(x) = c(x)I for c ∈ ℝ with I being the identity matrix, is called the isotropic Eikonal equation. Throughout the paper, the 12-norm will be defined as ||·||₂ = ||·||_2,I. The The metric D(x) ∈ ℝ^n×n makes the anisotropic Eikonal equation not only dependent on the location of the wave, but also on its direction. In the case of electrical propagation in the heart, D(x) ∈ ℝ^3×3 is commonly referred to as the 3D conductivity metric or diffusion tensor. It is given by

$$D(\mathbf{x}):={\upsilon }_f^2(\mathbf{x})\mathbf{f}(\mathbf{x})\otimes \mathbf{f}(\mathbf{x})+{\upsilon }_s^2(\mathbf{x})\mathbf{s}(\mathbf{x})\otimes \mathbf{s}(\mathbf{x})+{\upsilon }_n^2(\mathbf{x})\mathbf{n}(\mathbf{x})\otimes \mathbf{n}(\mathbf{x}),$$ (2)

and encodes the squared conduction velocities along the tissue’s eigenaxes where f(x), s(x) and n(x) are the fiber, sheet and normal vectors respectively and ν_f(x), ν_s(x) and ν_n(x) encode their respective propagation velocities.

Computing ϕ(x) given g(x) and D(x) is called the forward anisotropic Eikonal problem. In contrast, computing g(x) and or D(x) from data ϕ(x) observed on a subdomain Ω_O is called the inverse anisotropic Eikonal problem. As conduction velocities in the ventricular myocardium are known to be orthotropic with velocity ratios of υ_f : υ_s : υ_n ≈ 0.6 : 0.4 : 0.2 m/s, the focus of this study will be solely on the anisotropic inverse Eikonal problem. Except for very restricted cases, the general inverse Eikonal problem is considered ill-posed.

To find D or g, we start with a common optimization approach

$$\begin{array}{l}\underset{D,g}{\text{min}}{\displaystyle {\int }_{{\Omega }_{\text{o}}}{\left(\varphi (\mathbf{x})-\widehat{\varphi }(\mathbf{x})\right)}^2\text{dx}}\\ \begin{array}{ll}\text{s}.\text{t}.:D(\mathbf{x})\in S_{++}^n,{\Vert \nabla \varphi (\mathbf{x})\Vert }_{2,D(\text{x})}=1\hfill & \forall \mathbf{x}\in \Omega \hfill \\ \varphi ({\mathbf{x}}_0)=g({\mathbf{x}}_0)\hfill & \forall {\mathbf{x}}_0\in S\hfill \end{array}\end{array}$$ (3)

where Ω_O refers to the observation domain and $\hat{\varphi }\left(\mathbf{x}\right)$ are the observed arrival times in Ω_O. Eq. (3) states that we want to minimize the squared distance of computed arrival times $\varphi \left(\mathbf{x}\right)-\hat{\varphi }\left(\mathbf{x}\right)$ over the observable domain Ω_O, assuming that activation times ϕ(x) are compatible with the anisotropic Eikonal condition in (1) and that D(x) is in the set of symmetric positive definite matrices on the whole domain Ω:

$$S_{++}^n=\left\{D\right(\mathbf{x})\mid \forall \mathbf{z}\in {ℝ}^n\backslash \mathbf{0}:{\mathbf{z}}^{T}D(\mathbf{x})\mathbf{z}>0\}$$ (4)

2.2. Forward Problem - The Fast Iterative Method

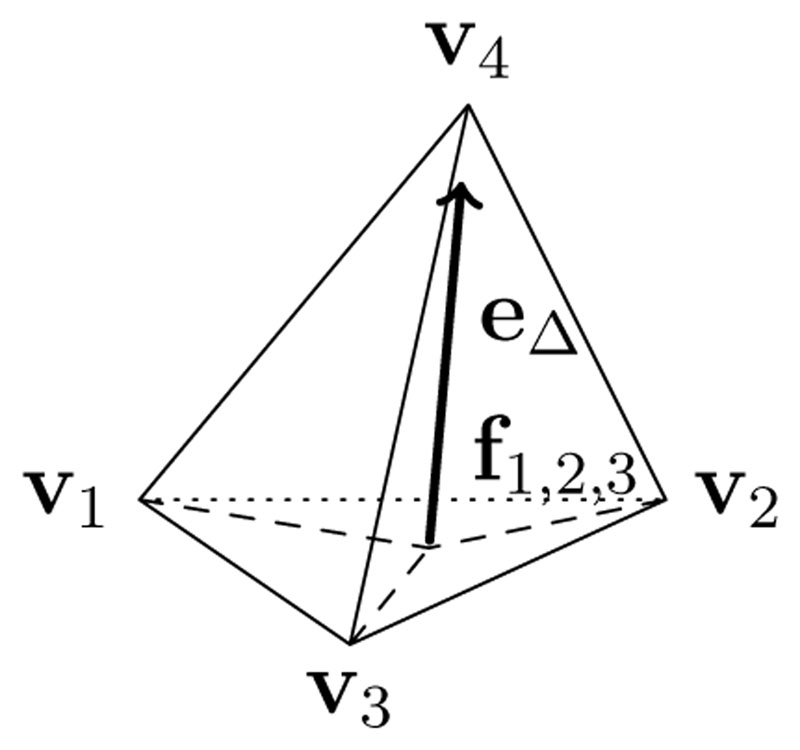
For finding the solution to the anisotropic Eikonal forward problem, ϕ(x), the FIM algorithm of Fu et al. proposed in [27], was implemented as an efficient method for computing an approximate solution of the anisotropic Eikonal equation from Eq. (1). As details of the FIM implementation matter with regard to the inverse FIMIN method, we briefly summarize the underlying key concepts here. At the heart of the FIM is the local update rule, computing a vertex value given the three other vertex values inside a tetrahedron.

For this purpose, the 3D-domain Ω is approximated by a Mesh M = {V, T}, consisting of a discrete set of vertices V = ∪_i v _i ∈ ℝ³, combined with a discrete set of tetrahedra T = ∪_j T_j, consisting of four vertices each T_j = (v _j1, v _j2, v _j3, v _j4). As basis functions, we assume Lagrangian 𝑝 ₁ elements, i.e. ϕ is linear inside each element, values are defined at the vertices spanning the tetrahedra, the gradient ∇ϕ and the Diffusion tensors are piecewise constant over the whole domain Ω. There is exactly one constant diffusion Tensor D_j associated with each T_j. For convenience the minimum arrival time associated to a vertex v _i is written as ϕ(v _i) = ϕ_i.

Barycentric coordinates are then used to define an arbitrary point inside the simplex Δ_k(triangle k = 3, or tetrahedron k = 4 in our case):

$${\Delta }_k=\left\{{({\lambda }_1,\dots ,{\lambda }_k)}^T|\sum _{i=1}^k{\lambda }_i=1\wedge {\lambda }_i\ge 0\right\}$$ (5)

Using λ ∈ Δ₄, the parametric definition of ϕ(x) inside an assumed linear tetrahedron T_j = (v ₁, v ₂, v ₃, v ₄) is therefore:

$$\mathbf{x}=\sum _{i=1}^4{\lambda }_i{\mathbf{v}}_{i,}\varphi (\mathbf{x})=\sum _{i=1}^4{\lambda }_i{\varphi }_i$$

This way, we can compute at any point f _1,2,3, its associated value ϕ _1,2,3 on the triangle spanned by v ₁, v ₂, v ₃ and the vector e _Δ from this point to v₄ as:

$${\mathbf{f}}_{1,2,3}=\sum _{i=1}^3{\lambda }_i{\mathbf{v}}_{i,}{\varphi }_{1,2,3}=\sum _{i=1}^3{\lambda }_i{\varphi }_i,{\mathbf{e}}_{∆}={\mathbf{v}}_4-\sum _{i=1}^3{\lambda }_i{\mathbf{v}}_i$$

The local update rule inside one tetrahedron, which defines the travel time from any point on the face f _1,2,3 to the vertex v ₄, is given by

$${\varphi }_4-{\varphi }_5={\Vert {\mathbf{\text{v}}}_4-{\displaystyle \sum _{i=1}^3{\lambda }_i{\mathbf{\text{v}}}_i}\Vert }_{2,D_i}=\sqrt{{\mathbf{\text{e}}}_{\Delta }^T{D}_j{\mathbf{\text{e}}}_{\Delta }>0}$$

In order to update a single node v ₄, given all other vertex values inside a single tetrahedron ϕ ₁, ϕ ₂, ϕ ₃, we want to find the point f _1,2,3that minimizes the travel time from the face, to the vertex v ₄ in the metric D_j. This can be formulated as the minimization problem:

$${\varphi }_4^I({\varphi }_1,{\varphi }_2,{\varphi }_3)=\underset{\lambda }{min}\sum _{i=1}^3{\lambda }_i{\varphi }_i+\sqrt{{\mathbf{e}}_{\Delta }^T{D}_j{\mathbf{e}}_{\Delta }},\text{s}.\text{t}.:\lambda \in {\Delta }_3$$ (6)

The computation is visualized in Fig. 1. If we set λ₃ = 1 − λ₁ − λ₂ and solve Eq. (6) w.r.t. one λ_i, while the other barycentric coordinate is called λ_k, then the optimal solution to the unconstrained problem is the solution to the quadratic problem

$${\lambda }_{i_{1,2}}=\frac{-p_{1,2}\pm c\sqrt{\frac{p_{1,1}{p}_{2,2}-p_{1,2}^2}{p_{1,1}-c^2}}}{p_{1,1}}$$ (7)

with

$$\begin{array}{l}{\mathbf{\text{w}}}_1={\mathbf{\text{v}}}_3-{\mathbf{\text{v}}}_1;{\mathbf{\text{w}}}_2={\mathbf{\text{v}}}_3-{\mathbf{\text{v}}}_2;{\mathbf{\text{w}}}_3={\mathbf{\text{v}}}_4-{\mathbf{\text{v}}}_3\hfill \\ {\mathbf{\text{z}}}_1={\mathbf{\text{w}}}_i-\frac{{\mathbf{\text{w}}}_2^{T}D({\mathbf{\text{w}}}_2({\varphi }_1-{\varphi }_3)-({\varphi }_2-{\varphi }_3){\mathbf{\text{w}}}_1)}{{\mathbf{\text{w}}}_j^{T}D({\mathbf{\text{w}}}_2({\varphi }_1-{\varphi }_3)-({\varphi }_2-{\varphi }_3){\mathbf{\text{w}}}_1)}{\mathbf{\text{w}}}_j\hfill \\ {\mathbf{\text{z}}}_2={\mathbf{\text{w}}}_3-\frac{{\mathbf{\text{w}}}_3^{T}D({\mathbf{\text{w}}}_2({\varphi }_1-{\varphi }_3)-({\varphi }_2-{\varphi }_3){\mathbf{\text{w}}}_1)}{{\mathbf{\text{w}}}_j^{T}D({\mathbf{\text{w}}}_2({\varphi }_1-{\varphi }_3)-({\varphi }_2-{\varphi }_3){\mathbf{\text{w}}}_1)}{\mathbf{\text{w}}}_j\hfill \\ c={\varphi }_i-{\varphi }_3-\frac{{\mathbf{\text{w}}}_i^T{D}_j({\mathbf{\text{w}}}_2({\varphi }_1-{\varphi }_3)-({\varphi }_2-{\varphi }_3){\mathbf{\text{w}}}_1)}{{\mathbf{\text{w}}}_j^T{D}_j({\mathbf{\text{w}}}_2({\varphi }_1-{\varphi }_3)-({\varphi }_2-{\varphi }_3){\mathbf{\text{w}}}_1)}\\ p_{\mathit{a},\mathit{b}}={\mathbf{\text{z}}}_a^T{D}_{\mathit{j}}{\mathbf{\text{z}}}_b\hfill \end{array}$$ (8)

Figure 1.

Local update of the FIM solver within one tetrahedron. The update is computed using the linear distance formulation e _Δ from the point f_1,2,3 on the face between nodes v ₁, v ₂, v ₃ to the point v ₄ to be computed.

Once we found λ_i, computing λ_k for k ≠ i becomes:

$${\lambda }_k=-\frac{{({\mathbf{w}}_3+{\lambda }_i{\mathbf{w}}_i)}^T{D}_j({\mathbf{w}}_2({\varphi }_1-{\varphi }_3)-({\varphi }_2-{\varphi }_3){\mathbf{w}}_1)}{{\mathbf{w}}_j^T{D}_j({\mathbf{w}}_2({\varphi }_1-{\varphi }_3)-({\varphi }_2-{\varphi }_3){\mathbf{w}}_1)}$$ (9)

The derivation that arrives at this conclusion is given in the Appendix in Sec. A.2. The actual minimal solution of λ₁ and λ₂ in Eq. (6) is a constrained quadratic minimization problem, for which special cases may arise when solving it unconstrained according to Eq. (7) as Fu et al. already stated:

If no root exists, or if λ₁ or λ₂ falls outside the range of [0,1] (that is, the characteristic direction does not reside within the tetrahedron), we then apply the 2D local solver used in [26] to the faces Δ_1,2,4, Δ_1,3,4 and Δ_2,3,4 and select the minimal solution from among the three.

([27])

where the mentioned root refers to the root term in Eq. (7). The referenced solution for the 2D-case over all faces can be defined as

$${\varphi }_4^{II}({\varphi }_1,{\varphi }_2,{\varphi }_3)=\underset{(i,k)\in \left\{(1,2),(2,3),(3,1)\right\}}{min}\underset{\lambda }{min}{\lambda }_i{\varphi }_i+{\lambda }_k{\varphi }_k+{\parallel v_4-({\lambda }_i{v}_i+{\lambda }_k{v}_k)\parallel }_{2,D_j},s.t.:\lambda \in {\Delta }_2$$ (10)

We can distinguish between all possible cases therefore:

$${\varphi }_4^{\ast }=\{\begin{array}{ll}{\varphi }_4^I({\varphi }_1,{\varphi }_2,{\varphi }_3)& \text{if}\lambda \in {\Delta }_3\text{according}\text{to}\text{Eq}\cdot \left(7\right)\text{and}\left(9\right)\\ {\varphi }_4^{II}({\varphi }_1,{\varphi }_2,{\varphi }_3)& \text{if}\lambda \in {\Delta }_2\\ {\min }_{i\in \{1,2,3\}}{\varphi }_i+{\parallel {\mathbf{\text{v}}}_4-{\mathbf{\text{v}}}_i\parallel }_{2,D_j}& \text{else}\end{array}$$ (11)

v ₄ is in most cases part of multiple tetrahedra and the minimum arrival time ϕ ₄ is therefore the minimum arrival time over all tetrahedra T_j that v ₄ is a vertex of (v ₄ ∈ T_j):

$${\varphi }_4=\underset{j}{min}{\varphi }_4^{\ast }({\varphi }_1,{\varphi }_2,{\varphi }_3)\text{s}.\text{t}.:{\mathbf{v}}_1,{\mathbf{v}}_2,{\mathbf{v}}_3,{\mathbf{v}}_4\in T_j$$ (12)

To globally compute the Eikonal solution, FIM initializes all vertices with starting times to their value and adds their neighbors to the active list (AL), while all other arrival times are set to ∞. The active list (AL) keeps track of all points to be updated according to Eq. (12) in the next iteration. Converged points are removed from the active list, while points are added that received an update. If one or more of ϕ ₁, ϕ ₂ and ϕ ₃ are not yet computed (meaning their value is still ∞ from the initialization), Eq. (6) and (12) still work if we define 0 ·∞ = 0 for this sake. Once the value ϕ₄ has been updated, all points sharing a tetrahedron with υ₄ are recomputed using Eq. (12) and are added to the AL if their activation time decreased. The convergence property of the FIM alg. removes a point from the AL if the change between two subsequent iterations, k and k + 1, is smaller than ε: FIM can be efficiently computed on single instruction, multiple data (SIMD) architectures, such as GPUs, thanks to the easy parallelization of the updates of all points in the AL. However, the values needed for the update of each vertex need to be buffered to avoid race conditions. This can lead to multiple necessary subsequent updates of the same nodes until convergence is reached, resulting in a sublinear speedup of the algorithm.

$$\left|{\varphi }_4^k\left(\mathbf{\text{x}}\right)-{\varphi }_4^{k+1}\left(\mathbf{\text{x}}\right)\right|<\mathit{ϵ}$$ (13)

Relaxing constraints on ϵ can be used to reduce computational costs at the expense of precision, or to avoid small rounding errors due to limited floating point precision. However, with regard to the inverse FIMIN algorithm we introduce in Sec. 2.3, the choice of e is crucial. An outline of the computations done by the FIM are given in Alg. 1. We define the computed solution of the FIM algorithm, given a mesh M, starting points S, their respective initiation timings g(x) and diffusion tensors D(x) as:

$$\varphi \left(\mathbf{\text{x}}\right)=\text{FIM}\left(D,g,M,S\right)\left(\mathbf{\text{x}}\right)$$ (14)

Since we are using these local Eikonal updates in each finite element, the final solution converges to the true Eikonal solution and thus the Eikonal condition in Eq. (1) holds up to a finite error once the FIM algorithm has converged.

2.3. Inverse Problem - Gradient Computation

For the inverse solution of the Eikonal equation, where the unknown values for g(x) and S are solved from a known solution ϕ(x), the gradient of FIM is required. Additionally, the local update rules Eq. (6) and Eq. (7) for each point must be further considered. In order to derive the gradient w.r.t. an optimizable variable y, we define all nodal values ϕ_i(y) and diffusion tensors D_j (y) as functions of y Given the optimal choice of λ₁ and λ₂, the derivative of (6) w.r.t. y and a diffusion tensor function D(x, y) = D_j of the tetrahedron x ∈ T_j becomes:

$$\frac{\partial {\varphi }_4}{\partial y}({\varphi }_1,{\varphi }_2,{\varphi }_3)=\{\begin{array}{ll}\sum _{i=1}^3\left(\frac{\partial {\lambda }_i}{\partial y}{\varphi }_i+{\lambda }_i\frac{\partial {\varphi }_i}{\partial y}\right)+\frac{1}{2\sqrt{{\mathbf{\text{e}}}_{\Delta }^T{D}_j{\mathbf{\text{e}}}_{\Delta }}}\left(2\frac{\partial {\mathbf{\text{e}}}_{\Delta }^T}{\partial y}{D}_{\mathit{j}}{\mathbf{\text{e}}}_{\Delta }+{\mathbf{\text{e}}}_{\Delta }^T\frac{\partial D_{\mathit{j}}}{\partial y}{\mathbf{e}}_{\Delta }\right)& \text{if}\lambda \in {\Delta }_3\\ \sum _{i=1}^2\left(\frac{\partial {\lambda }_i}{\partial y}{\varphi }_i+{\lambda }_i\frac{\partial {\varphi }_i}{\partial y}\right)+\frac{1}{2\sqrt{{\mathbf{\text{e}}}_{\Delta }^T{D}_j{\mathbf{\text{e}}}_{\Delta }}}\left(2\frac{\partial {\mathbf{\text{e}}}_{\Delta }^T}{\partial y}{D}_{\mathit{j}}{\mathbf{\text{e}}}_{\Delta }+{\mathbf{\text{e}}}_{\Delta }^T\frac{\partial D_{\mathit{j}}}{\partial y}{\mathbf{\text{e}}}_{\Delta }\right)& \text{if}\lambda \in {\Delta }_2\\ \frac{\partial {\lambda }_i}{\partial y}{\varphi }_i+\frac{1}{2\sqrt{{\mathbf{\text{e}}}_{\Delta }^T{D}_j{\mathbf{\text{e}}}_{\Delta }}}\left(2\frac{\partial {\mathbf{\text{e}}}_{\Delta }^T}{\partial y}{D}_j{\mathbf{\text{e}}}_{\Delta }+{\mathbf{\text{e}}}_{\Delta }^T\frac{\partial D_j}{\partial y}{\mathbf{\text{e}}}_{\Delta }\right)& \text{else}\end{array}$$ (15)

with $\frac{\partial {\mathbf{e}}_{∆}}{\partial y}={\mathbf{v}}_4-\sum _{i=1}^3\frac{\partial {\lambda }_{\mathit{i}}}{\partial y}{\mathbf{v}}_{\mathit{i}}$. In order to derive Eq. (7), we may need to derive each variable of the quadratic problem, assuming dependency of each variable on y. The exact derivations of each of the variables can be found in Sec. A.3.

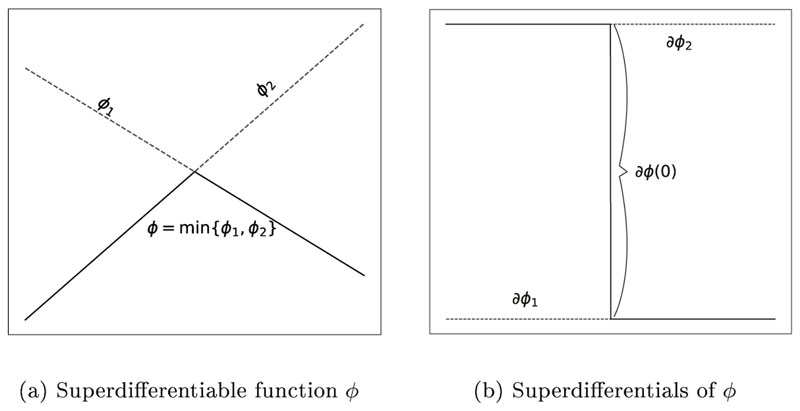
The derivation (∂ϕ_i)/(∂y) is recursively acquired by applying the chain rule (i.e. backpropagation) along the path of updates we computed in the forward FIM solution, until we computed all necessary updates. For the case that the solution of Eq. (12) of several tetrahedra share the same arrival time, there is no single unique solution for $\frac{\partial {\lambda }_{\mathit{i}}}{\partial y}$ Our optimization uses the superdifferential in these cases, which is the supporting hyperplane above the minimum functions in (12). The superdifferential is the inverse of the subdifferential as defined in [57] (p. 300 ff), which is needed since we are using the minimum function:

Algorithm 1: Fast Iterative Method (FIM) [36].

Input : Diffusion Tensors D, Starting Points S, Mesh M with Neighborhood Operator 𝒩 Initiation Timings Function g(v)

Output: First arrival times ϕ, FIM Updates FIM_U

∀v ₀ ∈ V(S): ϕ(v ₀) := g(v ₀)

∀v ∈ V(M) \ S : ϕ(v) := ∞

$\mathbf{AL}=\underset{\forall {\mathbf{v}}_{\mathbf{0}}\in V\left(S\right)}{\cup }𝒩\left({\mathbf{v}}_0\right)$

FIM_U = ϕ

while AL ≠ ϕ do

      for v _i ∈ AL do

          v _j, v _k, v _l ∈ 𝒩 (v _i)

          ϕ _new,i := ϕ ₄ (ϕ_j, ϕ_k, ϕ_l) // Compute local eikonal solution (Eq. (12))

          ϕ _old,i := ϕ(v _i)

          ϕ(v _i) := ϕ _new,i

          FIM_U = FIM_U ∪ (ϕ _new,i, v ₄, λ)

          //If point has converged

          if |ϕ _new,i − ϕ _old| < ε then

              AL = AL \ v ₄ // Remove converged from AL

              // Check if neighboring points are converged

              for ∀v _n ∈ 𝒩 (v _i) do

                  v _j, v _k, v _l ∈ 𝒩 (v _i)

                  ϕ _new,n := ϕ ₄ (ϕ_j, ϕ_k, ϕ_l) // Eq. (12)

                  if |ϕ _new,n − ϕ(v _n)| ≥ ε Λ ϕ _new < ϕ(v _n) then

                      AL = AL ∪ v _n // Add to AL if not converged

                  end

              end

          end

      end

end

$$\partial \varphi \left(\mathbf{\text{x}}\right)=\{\mathbf{\text{v}}\in {ℝ}^N\mid \varphi (\mathbf{\text{z}})\le \varphi (\mathbf{\text{x}})+⟨\mathbf{\text{v}},\mathbf{\text{z}}-\mathbf{\text{x}}⟩\forall \mathbf{\text{z}}\in \mathrm{dom}\varphi \}$$ (16)

Fig. 2 demonstrates how the superdifferential looks like for an 1D-minimum function, where the function is not continuously differentiable. Any choice of superdifferential $\partial \tilde{\varphi }\in \partial \varphi$ is feasible for the optimization. These superdifferentials become relevant inside elements where multiple wavefronts arrive at the same time.

Figure 2.

Exemplary depiction of a superdifferential of a 1D minimum function. The superdifferential is uniquely defined at points x ≠ 0, whereas the superdifferential at x = 0 is the set ∂ϕ(x = 0) = [∂ϕ₂, ∂ϕ ₁].

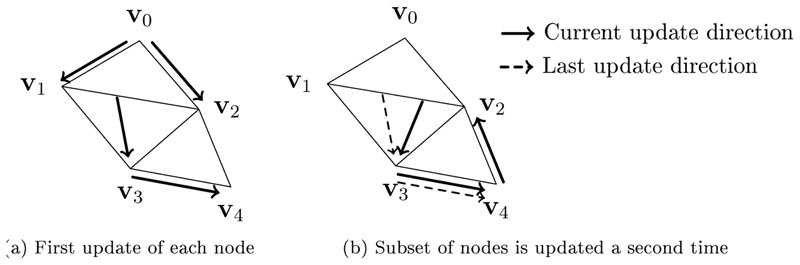
The FIM Alg. is a Gauss-Seidel method, meaning that nodes will be updated multiple times until the final, minimum arrival time is calculated. Up until now, we only considered this final value, which is sufficient for the forward problem. However, for the differentiation of ϕ ₄ in Eq. (15), non-trivial cases may occur that might require the results of previous updates of ϕ ₄. Consider a simple example 2D-mesh with 3 triangles and 4 nodes υ ₁ through υ ₄ and their respective arrival times ϕ ₁ through ϕ ₄, visualized in Fig. 3. In Fig. 3a, the update directions (similar to e _Δ in Eq. (6), but in 2D) are marked as arrows for the first update of each node. In Fig. 3b, we now assume that ϕ ₂ receives an update from ϕ ₄, which can happen for very non-smooth and anisotropic D_s. This update of ϕ ₂ will result in possibly additional updates of ϕ₃, ϕ ₄ and subsequently ϕ ₂, until convergence according to Eq. (13) is reached. If we assume $D\in S_{++}^2$ for all triangles, then the update directions can never form a full circle, since for any update direction it holds that ∀e _i,j ≠ 0: ||e _i,j||_2,D > 0. To derive $\frac{\partial {\varphi }_2}{\partial y}$ properly, we need to distinguish between different updates of ϕ ₂. Let ${\varphi }_i^k$ denote the k-th update of ϕ_i and f(ϕ_i, ϕ_j) = Eq. (6) (FIM Update). Then (assuming ${\varphi }_0^1=0$):

$${\varphi }_2^2=f({\varphi }_3^1,{\varphi }_4^1)=f(f({\varphi }_1^1,{\varphi }_2^1),f({\varphi }_2^1,{\varphi }_3^1))=f(f({\varphi }_1^1,f(0,{\varphi }_1^1)),f(f(0,{\varphi }_1^1),{\varphi }_3^1))$$ (17)

Figure 3.

Visualization of an exemplary update sequence of the FIM algorithm that demonstrates the necessity to distinguish between nodal values of different iterations. The arrows visualize the update directions similar to e _Δ in Eq. (6). the High anisotropies may lead to multiple updates of nodes with an update direction that is dependant on itself. For such cases, we need to remember the earlier computations of the same node. Note that the update directions can never form a full circle if all diffusion tensors are symmetric and positive definite.

To this end, we use a forward method of differentiation, beginning from the starting points x ₀ ∈ S and applying the gradient in the same update order as the original computation of ϕ_j to compute $\frac{\partial {\varphi }_j}{\partial y}$. This way, all ϕ_j-values reflect the exact values and differentials at any given iteration of the algorithm. Instead of computing the forward solution a second time, we remember 250 Gauss-Seidel iterations for this purpose by using ring-buffers, which was sufficient for all experiments conducted. To avoid duplicate evaluation, we remember the values of λ_i from Eq.(6) for each point and the vertices υ _j as well as their values ϕ _j at the time of the minimal evaluation. The backpropagation starts at the starting points v ₀ and applies the chain rule along the path of updates we computed in the forward FIM solution. Remembering the Gauss-Seidel updates increases the required memory, but in return speeds up the computation. This however may lead to very high memory consumption for large meshes, in which case an implementation that computes the forward solution and all derivatives jointly would be preferrable.

2.4. Optimization

Moving from the continuous optimization problem in Eq.(3) to the discrete domain, we define our main optimization problem using an arbitrary given function $\hat{\varphi }$ on a measurable discrete surface Ω_O:

$$\begin{array}{l}\underset{D,g}{min}\frac{1}{2}{\displaystyle \sum _{\mathbf{\text{v}}\in {\Omega }_o}(\varphi (\mathbf{\text{v}})-\hat{\varphi }(\mathbf{\text{v}}){)}^2+\gamma 𝓡(D,g)}\\ \text{s}.\text{t}.:D(\mathbf{\text{x}})\in S_{++}^n,\varphi (\mathbf{\text{x}})=\text{FIM}(D,g,M,S)(\mathbf{\text{x}})\end{array}$$ (18)

where ϕ(y) and $\hat{\varphi }$ are the vector of nodal vertex values ϕ _i from the current model and reference respectively and R is a regularizing function, penalizing unlikely solutions. We refer to the sum as the sum of squared errors (SSE).

To properly derive all final points $\frac{\partial {\varphi }_i}{\partial y}$, we apply all saved updates FIM_U in their original order and derive each updated value using Eq. (15). The computation takes only a fraction of the original time of the FIM algorithm, since a lot of computations in the original FIM algorithm are dedicated to checking if the values of vertices have converged. An outline of the procedure is given in Alg. 2.

All that is left for our optimization in Eq. (18) to work, is to define a proper regularization function 𝓡. The proper choice of 𝓡 has been a long debated topic in multiple fields for inverse problems, but we used an arguably very popular choice for regularzing the diffusion tensors D, that has been successfully used in many inverse problems, such as image denoising: The Huber regularization [59], a smoothed Total-Variation function, $\left(𝓡\left(D,\mathbf{g}\right)={||\nabla D||}_{H,\alpha }\right)$, where ||·||_H,α denotes the Huber norm defined as:

$$\parallel \mathbf{\text{x}}{\parallel }_{H,\alpha }=\{\begin{array}{ll}\frac{1}{2}\parallel \mathbf{\text{x}}{\parallel }^2& \text{if}\parallel \mathbf{\text{x}}\parallel \le \alpha \\ \alpha (\parallel \mathbf{\text{x}}\parallel -\frac{1}{2}\alpha )& \text{else}\end{array}$$

To compute ∇D we use Gauss’ theorem since D is defined as a piecewise constant function. Details how we approximated this gradient are given in the Appendix Sec. A.4.

Several algorithms are suitable to optimize our objective function in (18), but the number of iteration steps within a given amount of time is severely limited by the size of the mesh and the number of parameters. The original problem in Eq. (18) can be reformulated as the non-linear least squares problem, given the parameter set y ∈ C, where C is a convex constraint set:

$$\underset{\mathbf{\text{y}}\in \mathbf{\text{C}}}{\text{min}}\frac{1}{2}\parallel \varphi (\mathbf{\text{y}})-\hat{\varphi }{\parallel }_{2,{\Omega }_0}^2+\frac{\gamma }{2}\sum _{j=1}^{\left|T\right|}{\parallel (\nabla 𝒟\mathbf{\text{y}}{)}_j\parallel }_{H,\alpha }=\underset{\mathbf{y}\in \mathbf{\text{C}}}{\text{min}}\frac{1}{2}\parallel \mathbf{\text{r}}(\mathbf{\text{y}}){\parallel }_{2,{\Omega }_0}^2+\frac{\gamma }{2}\sum _{j=1}^{\left|T\right|}{\parallel (\nabla 𝒟\mathbf{\text{y}}{)}_j\parallel }_{H,\alpha }$$ (19)

with γ being the regularization weight. Only errors on the measurement domain Ω₀ contribute to the norm ${||·||}_{2,{\Omega }_O}^2=\sum _{\mathbf{v}\in {\Omega }_O}{\left(·\right)}^2·𝒟$ is our linear diffusion tensor assembly operator, creating the tensors D from the elements in the parameter vector y. We define the gradients on the diffusion tensors as the sum of variation of the tensor’s elements:

$${\left(𝒟\left(\mathbf{\text{y}}\right)\right)}_j=\left[\begin{array}{lll}a\hfill & d\hfill & e\hfill \\ d\hfill & b\hfill & f\hfill \\ e\hfill & f\hfill & c\hfill \end{array}\right]\Vert \left(\nabla 𝒟\left(\mathbf{\text{y}}\right)\right)\Vert ={\displaystyle \sum _{\xi \in \left\{a,\dots ,f\right\}}\Vert \nabla \xi \Vert }$$

where j denotes the diffusion tensor D_j of T_j and each element is a function of y.

We use a constrained Gauss-Newton method to optimize Eq. (19), by linearizing the function around the current value y _k using a first-order Taylor series expansion and discarding higher order terms:

$$\underset{\mathbf{\text{y}}\in \mathbf{\text{C}}}{\text{min}}\frac{1}{2}\parallel \mathbf{\text{r}}(\mathbf{\text{y}}){\parallel }^2+\frac{\gamma }{2}\sum _{j=1}^{\left|T\right|}{\parallel (\nabla 𝒟(\mathbf{\text{y}}){)}_j\parallel }_{H,\alpha }\approx \underset{\mathbf{\text{y}}\in \mathbf{\text{C}}}{\text{min}}\frac{1}{2}{\parallel \mathbf{\text{r}}\left({\mathbf{\text{y}}}_{\mathbf{\text{k}}}\right)+\mathbf{\text{J}}\left({\mathbf{\text{y}}}_k\right)(\mathbf{\text{y}}-{\mathbf{\text{y}}}_k)\parallel }^2+\frac{\gamma }{2}\sum _{j=1}^{\left|T\right|}{\parallel (\nabla 𝒟(\mathbf{\text{y}}){)}_j\parallel }_{H,\alpha }$$ (20)

where J(y _k) denotes the Jacobian matrix of r at the point y_k.

The size of the Jacobian easily exceeds the available memory, but since only few of the activation times are dependant on single variables and diffusion tensors, the Jacobian matrix can be represented in a memory-efficient sparse matrix format.

Algorithm 2: Compute FIM Gradients.

Input : Diffusion Tensor Operator 𝒟(y), Starting Points S, Mesh M

            Activation Times ϕ

            Differential Operator ∂𝒟

            FIM Updates (Eq. (12)) FIM_U

Output: Activation Times Derivation $\frac{\partial \varphi }{\partial 𝒟}$

∀v _j ∈ M \ S : ϕ_j := ∞

∀v _j ∈ M : $\frac{\partial {\varphi }_j}{\partial y_i}$:= 0

for ϕ_u, v _n, λ ∈ FIM_U do

    ϕ_n :=ϕ_u // Reapply Update

    $\frac{\partial {\varphi }_n}{\partial 𝒟}:=f\left(\frac{\partial D}{\partial y_i},D\left(y\right),\varphi ,\frac{\partial \varphi }{\partial y_i},\lambda \right)$ // Calculate f = Eq. (15)

end

Alg. 2 is also applicable to optimize the activation timings g if the operator D(y) is swapped with g(y). The constrained Gauss-Newton optimization problem in Eq. (20) is a convex problem, which we solve by using a bounded limited-memory BFGS (L-BFGS) method [12]. In Alg. 3, the activation times derivation and the constrained Gauss-Newton method are combined to iteratively adapt the parameter set to the minimize Eq. (18). The step-size parameter β is found by using the Armijo backtracking line search [2].

Algorithm 3: FIMIN.

Input : Initial Parameter set y ₀ ∈ ℝ^K

            Diffusion Tensor Operator 𝒟(y)

            Convex Constraint Set C

            Differential Operator $\frac{\partial 𝒟}{\partial y}$

            Desired Activation Map $\hat{\varphi }$

Output: Optimized Parameter Set y _n

while not converged do

    r(y_k) = ϕ (𝒟(y _k)) − $\hat{\varphi }$ // Compute Residuals

    i ∈ V(M) : J _i,j(y _k) = $\frac{\partial {\varphi }_i}{\partial y_j}$ // Build Jacobian using Alg. 2

    ${\hat{\mathbf{y}}}_{k+1}=\underset{\mathbf{y}\in \mathbf{C}}{\min }\frac{1}{2}{||\mathbf{r}\left({\mathbf{y}}_{\mathbf{k}}\right)+\mathbf{J}\mathbf{\left(}{\mathbf{y}}_{\mathbf{k}}\mathbf{\right)}(\mathbf{y}-{\mathbf{y}}_{\mathit{k}})||}_{2,{\Omega }_O}^2+\frac{\gamma }{2}\sum _{j=1}^{\left|T\right|}{||{(\nabla \mathrm{𝒟y})}_j||}_{H,\alpha }$ // Constr. Gauss-Newton

    y _k+1 = y _k − β (y _k − ${\hat{\mathbf{y}}}_{k+1}$)

end

The L-BFGS method is limited to box constraint sets C _b, but the problem can also be solved for any convex constraint C with an unconstrained optimization algorithm by defining the Moreau- enveloped problem of Eq. (20) as:

$$f(\overline{\mathbf{\text{y}}}):=\underset{\mathbf{\text{y}}}{min}\frac{1}{2}\parallel K\mathbf{\text{y}}-\mathbf{\text{b}}{\parallel }_{2,{\Omega }_O}^2+{\delta }_{\mathbf{\text{C}}}\left(\mathbf{\text{y}}\right)+\frac{1}{2}\parallel \mathbf{\text{y}}-\overline{\mathbf{\text{y}}}{\parallel }_{2,M}^2+\frac{\gamma }{2}\parallel A\mathbf{\text{y}}{\parallel }_2^2$$ (21)

where δ _C(x) is the indicator function on C and $M=\frac{1}{\tau }I-K^{T}K-\gamma A^{T}A$. The Huber regularization can not be used for the regularization term $\frac{\gamma }{2}{||A\mathbf{y}||}_2^2$ without any modifications. For this purpose, we approximate the Huber H function locally around the current point y _k by defining

$$\parallel \mathbf{\text{x}}{\parallel }_{H_{k,\alpha }}=\{\begin{array}{ll}\frac{1}{2}\parallel \mathbf{\text{x}}{\parallel }^2& \text{if}\parallel {\mathbf{\text{x}}}_k\parallel \le \alpha \\ \alpha (\frac{\parallel \mathbf{\text{x}}{\parallel }^2}{\parallel {\mathbf{\text{x}}}_k\parallel }-\frac{1}{2}\alpha )& \text{else}\end{array}$$

Our total regularization operator is therefore $A=H_k\nabla D$. Since we require $M\in S_{++}^n$ (see Eq. (4)), τ needs to be chosen depending on A and J. To ensure positive definiteness of M, we chose τ = (||K^TK|| + γ||A^TA||)^-1. The optimal choice of y in Eq. (21), yields a proximal point algorithm returning a feasible point:

$$\widehat{\mathbf{\text{y}}}={\text{proj}}_{\tau \mathbf{\text{C}}}(\overline{\mathbf{\text{y}}}-\tau K^T(K\overline{\mathbf{\text{y}}}-\mathbf{\text{b}}{)}_{{\Omega }_o}-\tau \gamma A^{T}A\overline{\mathbf{\text{y}}})$$

where proj_τC is the projection operator on the convex set C. The gradient direction of this Moreau-envelope is:

$$\nabla f\left(\overline{\mathbf{\text{y}}}\right)=\overline{\mathbf{\text{y}}}-\widehat{\mathbf{\text{y}}}$$

By setting K = J(y _k) and b = J(y _k)y _k − r(y _k), we can use Eq. (21) together with a proper step-size backtracking to optimize the original problem in Eq. (20) for convex constraints C. More details about the Moreau-enveloped problem can be found in [14] (p. 29 ff).

2.5. Benchmarks

Performance of the proposed optimization method was evaluated by solving a series of benchmark problems of increasing complexity. Fully characterized reference solutions $\hat{\varphi }$ for ventricular activation sequences for a given domain Ω were generated by defining an orthotropic diffusion tensor $\hat{D}$ and initial activation Ŝ with initial timings g. Data observed at the outer surface of the domain (Ω_O ⊂Ω) were used then as inputs for the inverse FIMIN-based optimization. Starting from various default assumptions we attempted to identify either the eigenvalues υ _f, υ _s and υ _n of the velocity tensor D, as well as initiation timings ϕ(v ₀) on S, or both.

Two setups were considered. First, a simple computationally inexpensive 2D tissue sheet was generated that allowed for sufficiently short simulation cycles useful in identifying fundamental algorithmic issues and devising strategies of how to address these. Secondly, an anatomically accurate human biventricular (BiV) model with physiologically realistic activation sequences was utilized to evaluate the method’s ability to identify the parameters governing the ventricular activation sequence from limited observations recorded from the epicardial surface.

2.5.1. 2D tissue sheet

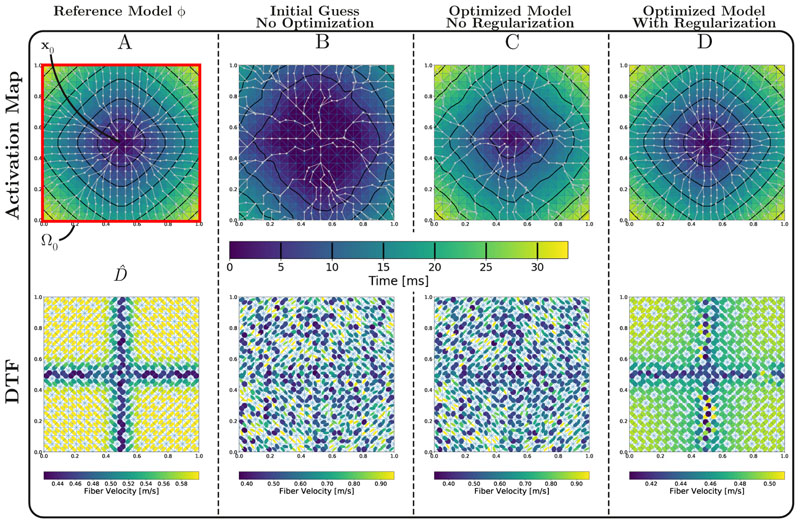
A simple 2D sheet of size 2 × 2cm² was discretized at 1mm resolution, yielding a small grid, which was triangulated using Delaunay triangulation into 722 triangles (see Fig. 4 A)). In [25] it was shown that, using an Eikonal model, a spatial resolution of 1mm is capable of capturing the most important features of wavefronts for anisotropy ratios found in cardiac applications. An arbitrary, but smooth, diffusion tensor field $\hat{D}$ with EAS at the tissue’s center was used for generating a reference activation sequence $\hat{\varphi }$ by solving Eq. (18) using FIM for triangular domains. Data along the boundary of the domain Ω_O were used to identify D(x) by optimizing according to Eq. (18).

Figure 4.

A) 2D benchmark setup showing domain Ω, EAS x ₀ in the sheet’s center, the reference activation map $\tilde{\varphi }$ diffusion tensor field $\hat{D}\left(\mathit{x}\right)$ and the measurement domain Ω₀. Note that the velocity colormap is slightly different for each of the diffusion tensor field due to high variation of fiber velocities between experiments. B) Initial solution before optimization. C) Solution for optimizing Eq. (18) with no regularization (γ = 0). The SSE of activation times is practically 0, but the resulting D is highly anisotropic and non-smooth. Many geodesic paths (grey lines) collapse into one. D) Solution for optimizing Eq. (18) with γ = 5 · 10^-3. The energy is still very low, but the regularization yields a smoother D and avoids high anisotropies. Geodesic paths are spread over more points and the contour lines are very close to the desired solution.

2.5.2. Human biventricular model

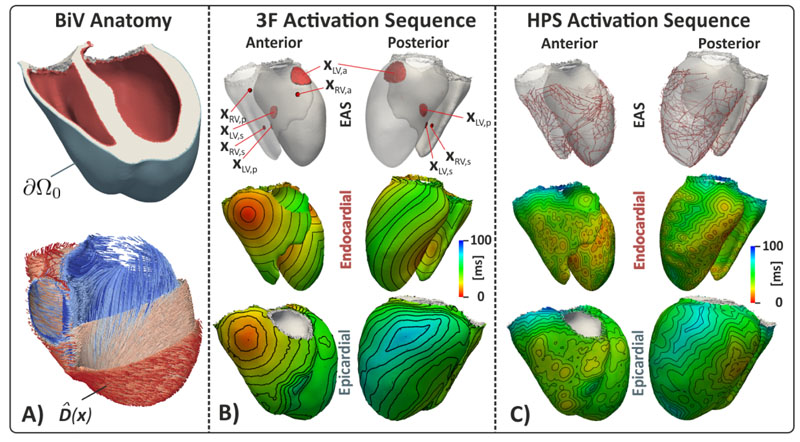
A human biventricular (BiV) anatomy model was reconstructed from an end diastolic 3D balanced steady state free precession (SSFP) cardiac magnetic resonance imaging acquisition in a sagittal orientation with whole-heart coverage and an isotropic resolution of 1.3 mm. Details on the model building process have been reported previously elsewhere [3, 19],but are briefly summarized here. A tetrahedral finite element mesh was generated [53] from a segmented image stack at an average resolution of 880μm (Fig. 5 A, top panel). Fiber architecture was incorporated assuming a linear rotation of fiber angles from — 60° at the epicardium to -60° at the endocardium using a rule-based method[4] (Fig. 5 A, bottom panel). This resulted in a BiV model consisting of ~ 5 · 10⁵ nodes and ~ 2.6 · 10⁶ tetrahedral elements. To ease computational load, the original model was downsampled to an approximate resolution of about 1.3mm with ~ 1.1 · 10⁵ nodes and ~ 5.8 · 10⁵ tetrahedral elements.

Figure 5.

Biventricular benchmark setups showing domains Ω, earliest activation sites x ₀ (EAS), diffusion tensor field $\hat{D}\left(\mathbf{x}\right)$ and the domain boundary Ω₀ from which observed data are recorded. A) Biventricular anatomy highlighting endocardial and epicardial surface (top panel) and fiber arrangement (bottom panel). B) and C) show trifascicular (3F) and HPS initiated activation sequence, driven by EAS activating at prescribed ϕ(x ₀) (top panels).

Reference Solutions

The forward model for generating the ventricular activation sequence was based on the following considerations. Both anatomical [21, 46] and experimental [23] mapping studies that utilize ex vivo human hearts provide evidence that the electrical activation of the ventricles is initiated by the HPS [30] with EAS occuring at PVJs. PVJs within a healthy human LV can be approximated by a tri-fascicular conduction system [58] consisting of three major fascicles located high on the anterior paraseptal wall, x _LV,a, in a central area at the septal endocardium, x _LV,s, and in a posterior paraseptal area at about one third of the LV long axis above the apex, x _LV,p. Similarly, in the RV fascicles were assumed to be located low on the the septal endocardium, x _RV,s, at the base of the pulmonary trunk, x _LV,p, and at area high on the anterior wall near the junction of the right atrium, x _RV,a. Spread of activation from EAS occurs at much higher CVs within the subendocardial layer than in the bulk myocardial wall due to the fast-conducting properties of the Purkinje network [22] or by a more abundant expression of sodium channels in subendocardial myocytes [55]. Tissue patches surrounding EAS are asumme to activate instantaneously.

Size, location, and timings of the EAS determining S and g are therefore key determinants shaping the activation sequence of the LV, as well as the prescribed orthotropic CVs within the domain. Thus, two different activation sequence models were used that both approximated the HPS with different degrees of fidelity: a topologically realistic model of the HPS with a larger number of PVJs (BiV- HPS), and a simpler trifascicular model (BiV-3F) comprising of only the three main fascicles in LV and RV. The BiV-HPS topolgy was obtained by starting with a manually delimited, scanner-based rabbit HPS and transferring it to the human mesh with universal ventricular coordinates[6]. Sizes and locations of EAS in S are indicated in Fig. 5 B-C. The six distinct EAS, x _LV,a, x _LV,s, x _LV,p, x _RV,a, x _RV,s, x _RV,p, consisted of ~ 230 discrete nodes.

Reference solutions for BiV-HPS and BiV-3F model were generated using a set of default parameters that produce physiological activation patterns in line with measurements in humans [23]. In both cases, CVs were chosen homogeneously with υ _f = 0.6 m/s, υ _s = 0.4 m/s,υ _n = 0.2 m/s, respectively, except for a subendocardial layer where a higher isotropic CV was prescribed with υ _f = υ _s = υ _n = 1.5 m/s. In the BiV-HPS model, endocardial activation is governed by the topology of the HPS network, subendocardial and myocardial definitions of CV within the orthotropic diffusion tensor D, and transduction delays across PVJs when thin essentially 1D fibers of the HPS network initiate propagation in the large mass of the ventricular myocardium [11]. Initiation timings of PVJs therefore ranged from 0.58 ms up to 38.76 ms. Activation of the BiV-3F model was initiated by prescribing EAS timings, in the LV at t ₀ = 0 ms, 7 ms and 3 ms to x _LV,s, x _LV,a and x _LV,p fascicle, respectively, and in the RV at t ₀ = 1 ms 9 ms and 15 ms to x _RV,s, x _RV,a and x _RV,p fascicle, respectively.

Optimization

Unlike for the 2D sheet, no attempts were made to identify eigenvectors and eigenvalues of D for all elements in the mesh as the high dimensionality of this problem would render the optimization prohibitively expensive. Rather, we subdivided the mesh into N partitions and identified in each partition i a set of CVs υ_fi, υ_si, υ_ni. That is, the eigenvectors f j, s _j, n _j of all D_j were considered given in each tetrahedral element j and optimization was performed only w.r.t. to the CVs in one partition i, i.e. the optimized CVs in a tetrahedron j υ_j,fi, υ_j,si, υ_j,ni were identical for all tetrahedra in partition i. The velocity tensor D in tetrahedra j of partition i is given then as

$$D_{i,j}={\upsilon }_{f_i}^2{\mathbf{\text{f}}}_j\otimes {\mathbf{\text{f}}}_j+{\upsilon }_{s_i}^2{\mathbf{\text{s}}}_j\otimes {\mathbf{\text{s}}}_j+{\upsilon }_{n_i}^2{\mathbf{\text{n}}}_j\otimes {\mathbf{\text{n}}}_j$$

where D_j belongs exactly to one partition i. In addition, to limit the amount of anisotropy introduced during optimization, constraints were imposed on the admissible minimum and maximum CVs chosen as υ_min = 0.10m/s and υ_max= 1.75m/s. This limited the maximum possible ansiotropy ratio $\left({\displaystyle \frac{{\upsilon }_{\text{max}}}{{\upsilon }_{\text{min}}}}\right)$ to < 17.5. Additionally, the Huber regularization for this example is calculated on the conduction velocities, i.e. we regularize ∇_{υ f/s/ni} The optimization problem for the BiV model is therefore

$$\begin{gathered} \underset{{\upsilon }_{f_i},{\upsilon }_{s_i},{\upsilon }_{n_i},\mathbf{\text{g}}}{min}\frac{1}{2}{\parallel \varphi ({\upsilon }_{f_i},{\upsilon }_{s_i},{\upsilon }_{n_i},\mathbf{\text{g}})-\hat{\varphi }\parallel }_{2,{\Omega }_O}^2+\frac{\gamma }{2}\sum _{j=1}^{\left|T\right|}{\parallel \nabla {𝒟}_j({\upsilon }_{f_i},{\upsilon }_{s_i},{\upsilon }_{n_i})\parallel }_H \\ \text{s}.\text{t}.:D\in S_{++}^n,\varphi (\mathbf{\text{x}})=\text{FIM}(D({\upsilon }_{f_i},{\upsilon }_{s_i},{\upsilon }_{n_i}),M,S(\mathbf{\text{g}}\left)\right)(\mathbf{\text{x}}), \\ {\upsilon }_{\text{min}}<{\upsilon }_i<{\upsilon }_{\text{max}} \end{gathered}$$ (22)

The epicardial surface Ω_O of the BiV model was spanned by ≈ 1.4 · 10⁴ discrete nodes. Optimization of the initiation timings ϕ(x ₀) of PVJs in the BiV-3F was performed for each discrete node separately.

The partitioning between BiV-3F and BiV-HPS models differed. In the BiV-3F model only N = 2 partitions were used, the endocardium and the remainder of the heart, whereas in the BiV-HPS model N = 100 partitions of equal size were used that were randomly located throughout the domain Ω. Partitioning in the BiV-HPS case was performed by converting the tetrahedral mesh into an unweighted dual-graph, where an edge is equal to a face connecting two tetrahedra, and applying then the min-edge-cut algorithm as implemented in the METIS library [37].

2.5.3. Robustness

Real world measurements are limited in terms of spatio-temporal resolution and afflicted by uncertainties. With regard to measuring epicardial activation patterns, spatial location of recording sites, electrogram fractionation and associated difficulties in reliably deriving a marker representing the instant of local activation, and noise are the main sources of error. To probe the robustness of the FIMIN algorithm against these errors, the BiV benchmarks were repeated in presence of measurement errors and with undersampled data. Original reference data $\hat{\varphi }$ were perturbed in two different ways:

1. Undersampled data were generated by selecting a subset of observed points on Ω_O, ${\hat{\Omega }}_O\subset {\Omega }_O$. The remainder of points on Ω₀ were generated from ${\hat{\Omega }}_O$ by inverse distance weighting.

2. Measurement errors were introduced by perturbing observed data by adding a normal distributed random noise with zero mean and σ standard deviation:

   $$\forall \mathbf{v}\in {\hat{\Omega }}_0:\tilde{\varphi }(\mathbf{v})=\hat{\varphi }(\mathbf{v})+𝒩(0,\sigma ).$$ (23)

where σ was chosen at the order of typically used temporal sampling intervals up to 8 ms.

3. Results

3.1. 2D-Sheet

To demonstrate the general applicability of the FIMIN algorithm, we allowed the maximum degree of freedom by optimizing each element of every D seperately with no constraints other than D being required to be a metric (see Eq. (18)). Data at the observation domain were generated by initiating a wavefront at the tissue center with D defined by the eigenvectors illustrated in Fig. 4 A and a homogeneous set of CVs υ_f and υ_s given as 0.6 and 0.34 m/s. To provide a more realistic and continuous scenario, D was slightly smoothed to ease optimization. Additionally, the 2D experiments also considered the eigenaxes of D to be unknown and optimizable. We optimized D by using the FIMIN Alg. 3 and completely random initial CVs within the range υ_f,0, υ_s,0, ∈[0.15, 0.98]m/s. The initial random D and the corresponding initial activation sequence without optimization is shown in Fig. 4 B. Optimization with the FIMIN, without any regularization (γ = 0) yielded an optimal, zero energy solution, but with a highly anisotropic and non-smooth D (Fig. 4 C). This can be attributed to the fact that FIM gradients track the wavefront and compute the influence of changing D on each vertex of the domain along the geodasic paths from an initial starting point. Since the gradient is propagated along the geodesic paths and there is no cost associated with errors outside Ω_O, many geodesic paths collapsed into a single path. Diffusion tensors that did not fall on any geodesic path were not updated as no gradients were propagated across them. Such highly anisotropic and non-smooth D _s are a rather unlikely solution to the problem, even though they may perfectly approximate the target function $\hat{\varphi }$ on Ω_O.

As shown in Fig. 4 D, already with a low value of γ = 5 · 10^-3 the resulting D provides a much smoother solution closer to the original diffusion tensor field (compare Fig. 4 C and D).

The 2D toy example demonstrated that the ill-posedness of the problem could not be overcome without a good regularization of the objective function. While still not perfect, the regularized solution in Fig. 4D provides a less complex and much more likely D than the unregularized optimal solution in Fig. 4C and demonstrates the viability of our approach. We tried two other, probably more physiological plausible, 2D experiments that can be seen in the Appendix, Sec. A.1, Fig. A1 and Fig. A2.

3.2. Biventricular Models

In the BiV anatomy model with a given fiber and sheet architecture (Fig. 5A) reference activation sequences were generated with the BiV-3F and BiV-HPS configuration (see Fig. 5B-C), respectively. Using FIMIN we attempted to identify the timings ϕ(x ₀) and velocities υ _f, υ _s and υ _n in each of the N partitions of the myocardium from measurements of ϕ, taken at the epicardial surface Ω₀ only. Eigenvectors of the D, f (x), s(x) and n(x), were considered given.

FIMIN was initialized assuming that activation is initiated at all EAS at the same time, i.e. ϕ(x ₀) = 0 ms was chosen. The initial velocities for all partitions were set to 0.93 m/s, 0.66 m/s and 0.54 m/s for υ _f,i, υ _s,i andυ _n,i respectively. Note that these initial velocities differed significantly from those used for computing the reference solution in terms of both magnitudes as well as the ratios between them. Further, no distinction was made between the orthotropic myocardium (0.6, 0.4 and 0.2 m/s for υ _f, υ _s and υ _n, respectively) and the much faster conducting isotropic subendocardial layer (1.5 m/s).

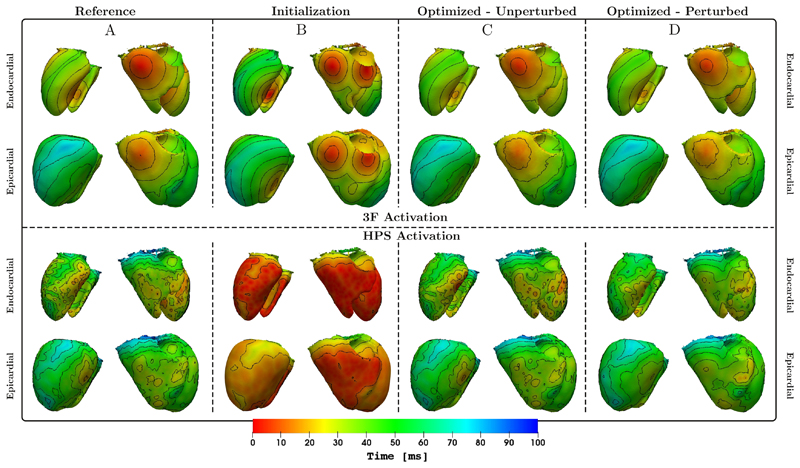
Optimizing Eq. (22) w.r.t. velocities υ _f,i, υ _s,i and υ _n,i and EAS timings ϕ(x ₀) proved to successfully reduce the error on both epicardium Ω₀ and myocardium Ω. A comparison of activation isochrones of initial and optimized model to the reference model is shown in Fig. 6 for both 3F and HPS model. The activation sequence ϕ _HPS(x) is significantly more complex than ϕ _3F(x). Owing to the larger number and the smaller sizes of EAS’s in the HPS model wave fronts amalgamated inside the myocardial wall well before breaking through at the epicardium. Thus, the number of epicardial breakthrough sites was much smaller than the number of endocardial initiation sites, as evident by comparing endocardial and epicardial isochrone patterns in the HPS case (see Fig. 6). This rendered the estimation of timings ϕ(x ₀) and velocities υ _f,i, υ _s,i and υ _n,i a challenging task. Similar to the 2D example in Sec. 3.1, the proper choice of γ in Eq. (18) played an equally important role in keeping the optimization from overfitting onto the epicardial data Ω_O.

Figure 6.

Top panels: Shown are endocardial and epicardial activation isochrones of ϕ _3F from a posterior and anterior viewpoint for the reference ${\hat{\varphi }}_{3F}$ (A), the solution ϕ _3F using initial (B) and optimized (C) parameters. Additionally we show the result when optimizing against ${\tilde{\varphi }}_{3F}$ from Eq. (23) with the strongest tested perturbation (D) (see Sec. 3.3, Tab. 1, bottom right cell). Bottom panels: The same comparison is shown for ϕ _HPS.

In Fig. 7, the comparison of the isochrones of our optimized model (black), versus the reference model (white) at a fixed time is shown, for both the 3F and HPS model and the epi-, as well as the endocardium. The overlap of both isochrones on the epicardium show that FIMIN is able to effectively adjust the conduction velocity parameters to minimize the distance of the activation times of the model and reference on the epicardium to a high - and on the endocardium to a lesser, but still significant - degree.

Figure 7.

Comparison of the isochrones at a certain time for the optimized model (black), versus the reference model (white).

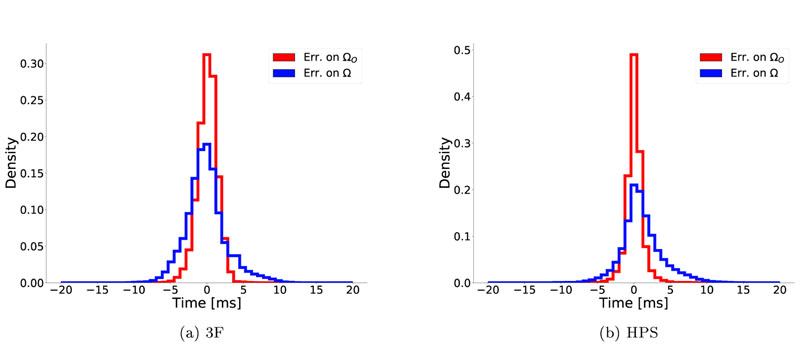
The effect of optimization on reducing the variation of errors ${∆}_{\varphi }=\hat{\varphi }-\varphi (y)$ is shown in Fig. 8, considering only Δ_ϕ in the range [—20, 20] ms. After optimization, errors on Ω_O were significantly reduced, following a normal distribution with μ _Δ= —1.3ms, σ_Δ = ±2.6 ms and μ _Δ = 0.7ms, σ_Δ = ±3.7ms for 3F and HPS, respectively. Over the domain Ω, hidden to the optimization function, the overall behavior was comparable, with errors also converging close to a zero mean, albeit with a slightly skewed distribution. These results suggest that the hidden SSE function can be optimized over the whole ventricular domain Ω using data observed on the epicardium Ω_O only.

Figure 8.

Effect of optimization on the distributions of errors Δ_ϕ in (a) 3F and (b) HPS model. Blue traces show Δ_ϕ on the epicardium Ω_O only, whereas red traces consider the whole domain Ω. The error distributions on Ω can be very well approximated by a normal distribution, albeit slightly skewed. Means and standard deviations were (a) μ _Δ = -1.3ms, σ _Δ = ±2.6ms and (b)μ _Δ = 0.7ms σ _Δ = ±3.7ms for 3F and HPS model, respectively.

Optimization results with regard to conduction velocities are shown in Fig. 8. For the less complex activation sequence ϕ _3F where Ω was partitioned into two velocity domains only - myocardium and subendocardial layer the optimized CV triplets of 0.68/0.29/0.18 m/s and 1.69/1.68/1.25 m/s were close to the true values of 0.6/0.4/0.2 m/s and 1.5/1.5/1.5 m/s (compare Sec. 3.2). In contrast, for the more complex activation sequence ϕ _HPS, where 100 partitions were used, a higher variability in optimized conduction velocities was witnessed, as shown in Fig. 9. The optimized velocity distributions were centered around the reference velocities, but outliers existed, particularly in the distribution of υ _f.

Figure 9.

Distribution of optimized velocities υ_f, υ_s and υ_n of the HPS model. The bars represent the actual, narrow distributions, which can be attributed to splitting the mesh into 100 partitions. The lines show the envelope of the corresponding bars with the same color. Reference velocities were 0.6/0.4/0.2${\displaystyle \frac{m}{s}}$ for υ_f, υ_s and υ_n, respectively.

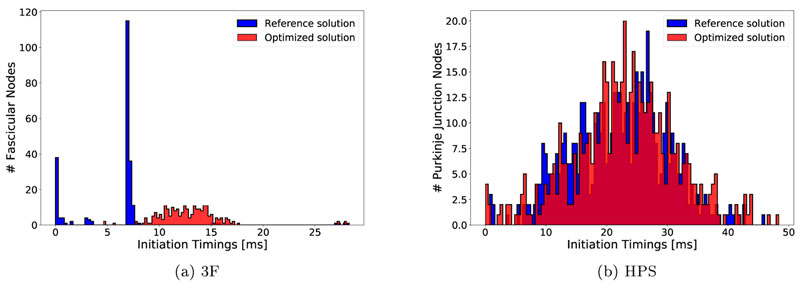
A comparison between true and optimized EAS timings ϕ(x ₀) is given in Fig. 10. For both sequences ϕ _3F and ϕ _HPS true and optimized EAS timings largely overlap, but the distribution of optimized timings is more spread out which is a consequence of optimizing each discrete node of the EAS regions independently. Moreover, an apparent bias towards later timings is observed which was particularly pronounced for the ϕ _3F sequence.

Figure 10.

Distribution of reference $\hat{\varphi }\left(\mathbf{x}0\right)$ in blue versus opimized ϕ(x0) EAS timings in red.

The observed spread in both CVs and EAS timings could be mitigated by increasing the value of γ in Eq. (22), leading to a more narrow velocity distribution. However, errors in ϕ at the epicardium Ω_O were compensated by the optimization by shifting the initiation timings ϕ(x ₀) which were not subjected to regularization (data not shown).

3.3. Robustness

To gauge the potential of the FIMIN algorithm under real world conditions, input data on Ω_O were perturbed by reducing spatial sampling and adding noise, as detailed in Sec. 2.5.3. A qualitative comparison in terms of activation isochrones between BiV-3F and BiV-HPS models with maximum perturbation $\left(\frac{\left|{\widehat{\Omega }}_o\right|}{\widehat{\Omega }}=0.7\%,\sigma =8ms\right)$ relative to the reference and unperturbed optimization is also shown in Fig. 6. While minor deviations were visible in the BiV-3F case, there was a high level of agreement in isochronal patterns suggesting that the overall structure of the BiV-3F model was captured despite coarse spatial sampling and high noise levels.

In the BiV-HPS case, discrepancies were more pronounced as details of the fine-grained HPS- mediated break-through patterns were lost. Nonetheless, even under these severely perturbed conditions the model approximated the overall epicardial activation patterns with sufficient accuracy for real world applications.

As shown in Fig. 8 for the noise-free model, the optimization reduces the errors of activation times and usually converges to a normal distribution with near-zero mean. Noisy and undersampled input data followed a sirniliar normal distribution of error (data not shown) as shown in the noise-free model Fig. 8. Deterioration due to noise and undersampling, can therefore be characterized by computing mean and standard deviation of total errors relative to the known reference solution. Results for all scenarios considered are summarized in Tab. 1. As evident from inspection of data in Tab. 1, relative to the optimal case in absence of noise and undersampling (upper left corner in Tab. 1 with ${\hat{\Omega }}_O={\Omega }_O$ and σ = 0 ms), errors increased with increasing noise and decreasing spatial sampling, but the chosen regularization kept the FIMIN algorithm from overfitting to the epicardial activation times.

Table 1.

Shown are the means and standard deviations of total errors ∆_ϕ in ms over the whole do main Ω between reference and optimized solutions for varying degrees of noise σ and spatial undersampling ${\hat{\Omega }}_O$. Initial errors of 3F and HPS model were μ _Δ = −1.4ms, σ_Δ = ±11.3ms and μ _Δ = −23.0ms, σ_Δ = ±8.3ms for 3F and HPS model, respectively.

		3F-Model			HPS-Model
$\left|{\hat{\Omega }}_O\right|$	σ	0 ms	4 ms	8 ms	0 ms	4 ms	8 ms
${\hat{\Omega }}_O={\Omega }_O$		−0.1 ± 2.8	1.7 ± 3.0	0.4 ± 4.2	1.0 ± 3.5	1.5 ± 3.6	0.5 ± 3.6
1 · 103		− 1.2 ± 3.7	−0.3 ± 2.8	−0.9 ± 3.8	4.0 ± 5.4	3.5 ± 5.4	1.8 ± 6.4
1 · 102		1.2 ± 3.9	− 1.6 ± 4.4	− 1.2 ± 3.5	5.3 ± 6.9	4.8 ± 6.5	2.1 ± 7.2

4. Discussion

This study reports on the development of a novel FIMIN algorithm for solving an inverse Eikonal problem. Conceptually, the method attempts to identify the key factors governing the ventricular activation sequence - location and timing of EAS and the velocity tensor field D - from sparse and noisy activation data $\hat{\varphi }$ sampled from the epicardial surface.

The overall feasibility and limitations of the method were investigated in silico. An anatomically accurate human BiV model was used to generate high fidelity reference activation sequences ϕ(x) as ground truth solutions - either the simplified ϕ _3F sequence initatiated by a trifascicular HPS, or, the ϕ _HPS sequence driven by a topologically more realistic HPS network - by solving the anisotropic Eikonal equation. Using activation times sampled from the forward solution over the epicardial surface and assuming the location of EAS’s were known, the corresponding inverse problem was solved using the FIMIN algorithm to identify the governing input parameters of the forward model that optimally fit the epicardial activation map.

Using the epicardial activation map at full resolution we first demonstrated that a reconstruction of activation sequence in 3D is, in principle, feasible under the assumption of known location of EAS. The robustness of the method under closer to real world conditions was evaluated by reducing the spatial resolution of the observed epicardial activation map and by adding noise. Our results suggest that the FIMIN algorithm is able to recover the full 3D activation sequence even under these more realistic conditions with spatial resolutions that are achievable with currently used clinical mapping systems. Contrasting the uncertainties in clinical data with the accuracy achieved in reconstructing ϕ(x) suggests that the FIMIN method may be suitable for the patient-specific parameterization of activation models in future clinical applications.

4.1. Identifying the ventricular activation sequence

The identification of the ventricular activation sequence ϕ(x) from measurements taken from the body surface - as in a standard inverse electrocardiographic imaging problem - or from the outer epicardial surface of the ventricles - as suggested in this study - constitutes a severely ill-posed problem. Any attempt to address this kind of problem depends therefore critically on the use of a-priori knowledge to constrain the problem and appropriate regularization techniques to enforce the constraints. Conceptually, the ventricular activation sequence ϕ(x) is governed by three factors only, the location of EAS, their timings, ϕ(x ₀), and the conduction properties of the tissue as encoded in the velocity tensor field D(x). This problem, in its most general interpretation, can be considered extremely high dimensional. In this study, three simplifying assumptions were made to reduce the dimensionality of the problem and to keep the FIMIN-based optimization tractable: i) the location of EAS’s were assumed to be known; ii) the eigenaxes of D(x) were prescribed on a per-rule basis [5] informed by anatomical studies [23], only the tensor eigenvalues representing anisotropic velocities were considered unknown; and, iii) the spatial variation of the eigenvalues of D(x) was regularized by partitioning the ventricles into N domains and enforcing velocity triplets υ_f,i,υ_s,i and υ_n,i to be constant throughout a partition i.

Under these assumptions FIMIN was able to find parameter sets comprising ϕ(x ₀) and υ_f,i,υ_s,i and υ_n,i which approximated ϕ(x) quite well at the epicardial surface Ω_O where activation maps predicted by the FIMIN model ϕ were compared to observations $\hat{\varphi }$, but also over the entire myocardial volume Ω where data on $\hat{\varphi }$ were hidden to the optimization.

In general, results tended to be more accurate for the ϕ _3F than for the ϕ _HPS sequence due to the more direct relationship between EAS and epicardial breakthrough sites, as well as the lower complexity of the optimization model. In the ϕ _HPS case there was a larger number of EAS’s in each ventricle. These initiated numerous wavefronts at the endocardium which merged within the ventricular myocardium, thus yielding a reduced number of epicardial breakthrough sites.

A notable deviation of optimized CVs from the reference CVs was wittnessed in the BiV-HPS case which can be attibuted to a number of factors. First, the high number of EAS’s is likely to lead to a multimodal problem where the errors Δ_ϕ can be compensated by both changes in initiation timings as well as changes of the CVs. Second, the gradient of velocities is not uniformly distributed over the domain, favoring optimization of the partitions closer to the epicardium as their gradient tends to have a higher magnitude. The Huber regularization mitigates this behavior up to a certain degree, but increasing γ amplifies the first mentioned problem, favoring the optimization of initiation timings over conduction velocities. Partitioning the mesh into regions of constant conduction velocities significantly reduced the computation load, but the regularity of conduction velocities across the whole domain is more effectively driven by our choice of γ.

This activation time which was earlier relative to the actual PVJ activation times in the reference model (see Fig. 10). Thus the initial activation sequence leads the reference sequence throughout the entire domain Ω, i.e. Δ_ϕ < 0. Both optimized BiV-3F and BiV-HPS models yielded a normal distribution of errors on Ω_O, which is a common effect when optimizing using the SSE function. In the case of not perfectly optimizable functions, the SSE function will lead to a normal distribution of errors with zero mean, as can be seen in Fig. 8.

Finding the correct velocities by optimization was complicated by the fact that initiation timings ϕ(x ₀) were also assumed to be unknown. This biased the optimized solution towards later initiation timings ϕ(x ₀) (see Fig. 10) which were compensated by higher conduction velocities (see Fig. 9).

4.2. Robustness

In view of potential applications of FIMIN in an experimental or clinical context, the robustness with regard to spatial resolution and distortions due to noise is of pivotal importance as current modalities for measuring ϕ(x) suffer from a number of limitations. With regard to spatial undersampling and noise FIMIN-based reconstructions of ϕ(x) were shown to be surprisingly robust. Reconstructed isochronal patterns appeared low-pass filtered when compared to unperturbed reconstructions, but the overall structure of the solution was retained, even under the most severe conditions where only 100 epicardial data points were used and the noise added to arrival times was normally distributed with a standard deviation of 8ms. The undersampling corresponded to approximately 0.7% of the available epicardial points, with an average spacing of 14.2 mm between the measurement points.

In general, it can be observed from Tab. 1 that the final error after the optimization is mostly dependant on the undersampling (vertical) rather than the noise added to the observed data (horizontal). This can be attributed mainly to our cost function: We chose a mean-squared-error function in our problem formulation (see Eq. (18)), which is an appropiate assumption to mitigate the effects of Gaussian noise. Although mean and standard deviation vary between most of the experiments in horizontal direction of Tab. 1, the final mean-squared error is very similar for all of these experiments.

Robustness of FIMIN-based reconstructions of the activation sequence must be viewed in the context of data uncertainty of measured activation maps. In general, a highly accurate observation of ϕ(x) at the organ scale throughout Ω is not feasible with currently available technology. Owing to the physics of propagating depolarization wavefronts which is governed by fast transients (< 1ms) that translate into steep wavefronts (< 1mm), mapping technologies for an accurate registration of ϕ(x) would be required that offered the ability to measure wavefront arrival times with sub-millimeter and sub-millisecond resolution throughout the entire ventricular myocardium. Such measurements are massively invasive and only applicable in an experimental setting, but even the most advanced mapping techniques do not meet these requirements. Optical mapping techniques provide better spatial resolution, at least in theory, but are affected by a number of significant artifacts related to signal distortion due to integration effects mediated by photon scattering [9]. Further, optical measurements are confined to superficial tissue layers as they are not able to record, in a reliable fashion, any information from the depth of the tissue. While panoramic imaging systems exist, the typical field of view of mapping systems is limited and cannot cover the entire epicardial surface Ω_O. Finally, while cardiac tissue is often considered a functional syncytium, it is a discrete structure which inevitably results in wavefront fractionation, even in perfectly healthy tissue. These deviations from a continuum are reflected in signal fractionation which often renders the determination of arrival times ambiguous.

4.3. Related Algorithmic Work

The Eikonal equation is a widely used method to approximate wave propagation through different media. The approximation is useful if one is interested in determining the first instant in time when a wavefront passes a given point in space. A special case is the isotropic Eikonal equation, i.e. D(x) = cI for c ∈ ℝ with I being the identity matrix. The isotropic Eikonal equation can be efficiently solved as has been shown in both [65] and [67]. Both papers propose concepts which can solve this problem with a runtime complexity of 𝓞(n log n) for a grid of size n. We will refer to these concepts as Fast Marching Methods (FMM).

The anisotropic Eikonal equation (see Eq. (1)) represents a more general form where the wave speed is not only dependent on the location of the wave, but also on its direction of propagation. This renders anisotropic Eikonal problems harder to solve than isotropic ones since anisotropies may change the characteristic directions needed for solving, as stated in [64]. In cardiac tissue anisotropies play a fundamental role. Due to the discrete structure and the organization of tissue in fibers and laminar layers three distinct eigendirections exist [39]. The conduction velocities along the eigendirections vary, being about three times faster along the fiber direction than along the slowest eigendirection normal to the laminar sheets. Therefore, these properties of cardiac conduction prompted for the use of the anisotropic Eikonal equation.

In [64] the concept of the FMM was extended to cover the exact amount of neighbors that need to be considered to compute anisotropic Eikonal solutions. The runtime complexity for this method referred to as Ordered Upwind Method (OUM) is 𝓞(k ² n log n) where κ is the maximum anisotropy. Similar to the FMM, it is a one-pass algorithm that fixes the value of one vertex per each iteration.

In contrast, in the FIM [36] as used in this study a Gauss-Seidel method was proposed to solve the anisotropic Eikonal equation on the whole domain by iteratively computing the minimum arrival time locally for each grid point. Unconverged points on the active list are updated in each iteration until the local solution converges. Their neighbors are then added to the active list if their value changed in the last iteration. The runtime-complexity of the FIM is worse, but due to the high parallelization capacity, its performance is comparable or the FIM may even outperform similar algorithms, as has been shown in various examples [36]. In our study the FIM was preferred over OUM since, in practice in our implementation, the FIM appeared to be computationally more efficient.

The extension of Eikonal solvers to compute inverse Eikonal problems is a non-trivial roblem. The study [8] analyzed the inverse isotropic Eikonal problem of a solution obtained by FMM. It was shown that the inverse problem is non-convex, but can be solved in many practical applications such as landscape design, traffic congestion equilibria and travel time tomography. The resulting runtime of 𝓞(n ² log n) holds only for isotropic media. This approach is not applicable to anisotropic media without modifications, since larger neighborhoods would need to be considered, depending on the maximum anisotropy which is again dependent on the optimizable parameters. The required number of iterations of the FIM is likewise dependent on the anisotropy of the model, but implicitly encoded in Alg. 1 and therefore also taken into account in the FIMIN optimization (compare Alg. 3).

Inverse Eikonal problems emerge in a variety of fields, including optimal trajectory optimization under constraints in two player games [43], estimating reaction-based tumor growth [38], transient elastography [41], [42], or inverse seismic problems [40]. In these problems the same parameters have to be estimated, but the constraints on estimated parameter sets, as well as the problem setups differ markedly. Most of these mentioned problems are usually inverse isotropic Eikonal problems, but could also be optimized using the FIMIN approach presented in here.

4.4. Relation to inverse ECG imaging problems

The FIMIN method for relating epicardial arrival times to the ventricular activation sequence is a non-standard ECGi problem. Instandard ECGi problems electrical potentials in the form of electrocardiograms or body surface potential maps are used as observations to infer different aspects of the ventricular activation sequence. In physical terms, inverse ECGi yields information on transmembrane voltages [32, 71], extracellular potentials [61, 7] or local activation/recovery times [68, 24, 31, 35]. which are, typically, reconstructed on the epicardial surface, but methods for endocardial or transmural reconstructions also exist. That is, the observations used as input in this study are often considered the solution in ECGi problems. As such the FIMIN is not directly applicable to ECGi problems without further extensions as the FIMIN, in its current form, accepts activation times from the epicardial surface as inputs, but not electrical potentials. However, coupling of FIM-based activation models with forward predictions of electrical potentials at the body surface can be done very efficiently, as has been shown by us [44] and others [73, 49]. In particular, Eikonal solvers in combination with appropriate source models and a lead-field approach [28, 51] as used in [49] can be solved in a computationally highly efficient manner. Such methods yield body surface potentials which are essentially equivalent to ground truth solutions computed with an expensive fullblown bidomain formulation [51]. To construct an ECGi method based on the FIMIN one could use a FIM-based forward model [44] to compute transmembrane voltage maps throughout the myocardium, V_m(x, t). In the simplest case a fixed action potential shape U(t) may be used and shifted by the computed activation times ϕ(x) to compute the source term V_m(x, t) = U(t - ϕ(x)). Using precomputed lead fields Z(x) for each electrode pair at the body surface, body surface potentials can be recovered by solving

$$V(t)={\int }_{{\Omega }_O}\nabla Z(\mathbf{x})\cdot \mathbf{\sigma }(\mathbf{x})\nabla V_m(\mathbf{x},t).$$

where σ is the intracellular conductivity tensor. Thus, the cost function given in (3) could be replaced by

$$\underset{D,g}{min}{\int }_{{\Omega }_O}(V(\varphi (\mathbf{x}))-\hat{V}(\mathbf{x}){)}^2\text{d}\mathbf{\text{x}}$$ (24)

to relate computed and measured body surface potentials V and $\hat{\mathit{V}}$, respectively, to the parameters D and g which govern the activation sequence in the FIM.

4.5. Related Cardiac Eikonal Application

A related problem was addressed in [16] and [63] where potentials measured at the endocardium during radio-frequency ablation procedures were used to generate endocardial activation maps, where either anisotropic [16] or isotropic propagation[63] was assumed. These were then used to estimate endocardial velocity parameters using an Eikonal-diffusion or Eikonal-curvature equation. Endocardial fiber directions were assumed to be known and were fixed to +60° [16]. The method was validated on patients with a Left Bundle Branch Block pathology, as well as on patients with scarred tissue. For the latter, regions of low propagation velocity were linked to scarred tissue. The solution of the inverse problem using only measurement data was shown to be able to locate the scar tissue by comparing computed solution to magnetic resonance images.

Another successful use of the Eikonal approach in activation time determination has been to construct feasible Purkinje networks that recreate measured surface activation times using a minimal set of PVJs[20, 48, 69, 47]. These approaches rely on optimiziation, and, hence, profited from the reduced computation. They have generally considered propagation velocities to be global, unlike our approach.

4.6. Importance of ϵ

Initial experiments with the 2D sheet model demonstrated that appropriately choosing ϵ for Eq. (13) in the FIM algorithm is of pivotal importance. This can be exemplified in a simple perturbation experiment with the BiV model from Sec. 2.5.2, with a single CV triplet (υ_f,υ_s and υ_n) for the whole domain. Increasing ϵ decreased the runtime to compute the FIM solution, but the resulting surfaces of the inverse optimization problem and the obtained gradients were significantly less smooth as compared to using a smaller ϵ (see Fig. 11). In this example, only a weakly anisotropic D was used with the optimal choice of CVs being υ_f - υ ₁ = 1 and υ_s = υ ₂ = 1.5. It is worth noting that this effect was amplified by increasing anisotropy ratio ${\displaystyle \frac{{\upsilon }_1}{{\upsilon }_2}}$ (not shown).

Figure 11.

Energy landscapes for different values of ∈ in the FIM Algorithm. Contour lines visualize the cost function from Eq. (18) we seek to minimize, with the global minimum being located at υ ₁ = 1 and υ ₂ = 1.5. Arrows indicate the normalized gradient descent direction obtained by using Alg. 2. Smaller ∈ yields a smoother energy landscape which benefits optimization.

4.7. Computational Costs

Computational costs of the FIMIN algorithm were significant. For instance, finding the optimal parameters in the BiV-HPS model last for ≈ 12 hours using 30 cores of an Intel(R) Xeon(R) CPU E5-2640 v4 CPU running a clock rate of 2.40 Ghz. The BiV models consisted of ~ 1.1·10⁵ nodes and ~ 5.7· 10⁵ tetrahedral elements. The FIM and the computation of the Jacobian in Alg. 2 were implemented in C++, while the remainder of the optimization used Python/Numpy. As a stopping criterion for the FIMIN a maximum number of iterations of 1000 or a slowdown in the rate of convergence was used. Prolonged execution times could be attributed to the increasing anisotropy of the optimized model as well as to the small value of e that was needed for the FIM algorithm to efficiently optimize the FIM function. The two major contributors to overall execution time were the FIM algorithm and the Jacobian computation.

Increasing ∈, lowering the maximum number of iterations or further decreasing spatial resolution are viable ways to achieve shorter execution cycles. However, these measures are likely to increase errors due to lower precision or premature convergence. Constraining the maximum permissible anisotropy by regularization could also be beneficial, but this has not been investigated in this study. Finally, further speedups may be gained from optimized implementations. For instance, the computationally expensive parts of the FIM algorithm are well suited for a SIMD-architectures such as a GPU, albeit the size of the model and, consequently, its Jacobian would require a GPU with a large memory or a multi-GPU implementation.

4.8. Limitations

Owing to the severe degree of ill-posedness of the problem, a number of simplifying modeling assumptions were made that may restrict the applicability of FIMIN to real world clinical problems. First and most importantly, epicardial activation maps were used as inputs. While the acquisition of such maps is clinically feasible with minimally invasive techniques, such procedures are non-standard. To be of wider utility, non-invasive input data such potential maps from the body surface should be considered within a more standard inverse ECG imaging setting [17]. Secondly, the location of the various EAS were assumed to be known. There is currently no straight-forward way, in which the location of the EAS could be integrated as an optimizable parameter into the optimization problem in Eq. (18), using only epicardial data. While endocardial mapping studies to reveal EAS are performed routinely in the clinic, the acquisition of endocardial maps relies on an invasive procedure. From an applied point of view, the location of EAS should therefore be considered unknown and must be identified with FIMIN as part of the optimization procedure. Clinically acquired endocardial activation maps are valuable for validation, but should not be used for inferring location of EAS a priori.

Another potential drawback is the choice of the number of partitions in which the conduction velocity is kept constant for the 3D-cases. This reduces complexity and therefore expressibility of the model. To model local heterogeneity of conduction velocities, like found in scarred regions, current methods utilize technologies relying on image-based modalities, e.g. [1]. If these are available, the partitions could be adapted to include the scarred regions in single partitions.

In the absence of this data, the partition size would need to be chosen smaller than the region of interest, to have a chance of finding the regions by the model alone. Excessively chosen partitions will not be able to express the desired local heterogeneity of conduction velocities, but rather average the found conduction velocity over the area/volume. In contrast, small partition sizes will lead to longer computational times, more needed optimization iterations and prohibitively large Jacobian-matrices for the Gauss-Newton updates. While the latter, memory drawback can be mitigated by using sparse matrix formats, the two former problems can only be addressed by by efficient parallelization, either on a cluster, or an efficient GPU implementation.

5. Conclusion & Future Work

This study reports on the development of a novel FIMIN algorithm for solving an inverse Eikonal problem. We demonstrated that FIMIN is able to identify the key factors governing the ventricular activation sequence - the timing of EAS and the velocity tensor field D - throughout the myocardial volume from sparse and noisy activation data sampled from the epicardial surface. The accuracy achieved in reconstructing ϕ(x) relative to uncertainties in clinical data suggests that the FIMIN method may be suitable for the patient-specific parameterization of activation models in future clinical applications.

Future work will address the various limitations of this first implementation of FIMIN. Specifically, these are the assumption of known EAS’s, the prescription of fiber and sheet architecture and the use of epicardial activation data instead of potential recordings from the body surface. FIMIN will be extended to also optimize parameters of rules for describing fiber architecture [5] and embedded in an inverse ECG imaging setting which defines the cost as difference between computed and observed body surface potential recordings.

Further algorithmic improvements will be attempted to better deal with the high computational complexity and to further improve the reconstruction accuracy. Possible efforts include the use of proper regularization of EAS timings which takes into account spatio-temporal relations between EAS’s or the use of subgradient methods which may prove beneficial in complex models like the HPS model where the multitude of colliding wavefronts renders the problem hard to optimize globally.