Abstract
Patterson’s D, also known as the ABBA-BABA statistic, and related statistics such as the ƒ4-ratio, are commonly used to assess evidence of gene flow between populations or closely related species. Currently available implementations often require custom file formats, implement only small subsets of the available statistics, and are impractical to evaluate all gene flow hypotheses across datasets with many populations or species due to computational inefficiencies. Here we present a new software package Dsuite, an efficient implementation allowing genome scale calculations of the D and ƒ4-ratio statistics across all combinations of tens or hundreds of populations or species directly from a variant call format (VCF) file. Our program also implements statistics suited for application to genomic windows, providing evidence of whether introgression is confined to specific loci, and it can also aid in interpretation of a system of ƒ4-ratio results with the use of the ‘ƒ-branch’ method. Dsuite is available at https://github.com/millanek/Dsuite, is straightforward to use, substantially more computationally efficient than comparable programs, and provides a convenient suite of tools and statistics, including some not previously available in any software package. Thus, Dsuite facilitates the assessment of evidence for gene flow, especially across larger genomic datasets.
Keywords: ABBA-BABA, D statistic, f4-ratio, gene flow, introgression, software
Introduction
Admixture between populations and hybridisation between species are common and a bifurcating tree is often insufficient to capture their evolutionary history (Green et al. 2010; Patterson et al. 2012; Tung & Barreiro 2017; Kozak et al. 2018; Malinsky et al. 2018). Patterson’s D statistic, first used to detect introgression between modern human and Neanderthal populations (Green et al. 2010; Durand et al. 2011), has been widely applied across a broad range of taxa (Fontaine et al. 2015a; vonHoldt et al. 2016; Tung & Barreiro 2017; Kozak et al. 2018; Malinsky et al. 2018). The D statistic and the related estimate of admixture fraction ƒ, referred to as the ƒ4-ratio (Patterson et al. 2012), are simple to calculate and well suited for taking advantage of genomic-scale datasets, while being robust under most demographic scenarios (Durand et al. 2011).
The D and ƒ4-ratio statistics belong to a class of methods based on studying correlations of allele frequencies across populations and were developed within a population genetic framework (Patterson et al. 2012). However, the methods can be successfully applied for learning about hybridisation and introgression within groups of closely related species, as long as common population genetic assumptions hold – namely that (i) the species share a substantial amount of genetic variation due to common ancestry and incomplete lineage sorting; (ii) recurrent and back mutations at the same sites are negligible; and (iii) substitution rates are uniform across species (Patterson et al. 2012; Pease & Hahn 2015).
While the results of other methods such as PCA (Patterson et al. 2006), STRUCTURE (Pritchard et al. 2000), and ADMIXTURE (Alexander et al. 2009) may be hard to interpret historically because they do not explicitly fit a historical model or unrealistically assume that all populations have radiated from a single ancestral group, the use of the D and ƒ4-ratio statistics involves fitting a simple explicit phylogenetic tree model to a quartet of populations or species (Fig. 1a, b) and provides a formal test for a history of admixture in that context (Patterson et al. 2012). The treemix method (Pickrell & Pritchard 2012), on the other hand, can fit a complex historical graph model of a tree with migration edges for a dataset of many populations, but does not provide a rigorous test for whether any proposed migration edges are correct (Pickrell & Pritchard 2012; Patterson et al. 2012). Finally, methods based on detailed population genetic models, such as dadi (Gutenkunst et al. 2009), fastsimcoal2 (Excoffier et al. 2013), or IMa2 (Hey 2010) can be used to infer demographic history that includes events such as population size changes, population splits and joins, and migration. However, these methods require data from multiple individuals per population or species, and, despite recent improvements in efficiency (Kamm et al. 2019), are computationally very demanding, limiting their application to a small number (generally < 10) of populations or species.
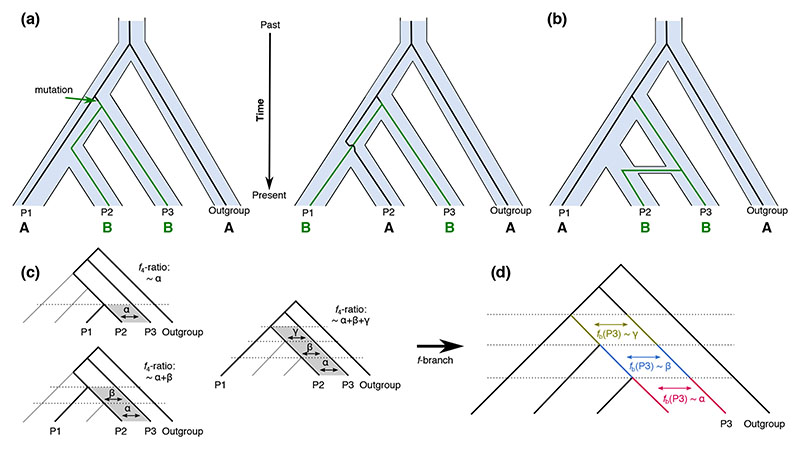
Figure 1. Basic principles behind the D and ƒ-branch statistics.
(a) Example genealogies showing the sharing of derived (B) alleles between populations P2 and P3 (the ABBA pattern) and between P1 and P3 (the BABA pattern) as a result of incomplete lineage sorting. In a scenario without gene flow, both patterns are assumed to be equally likely [but see (Eriksson & Manica 2012) for exceptions]. (b) Gene flow between P2 and P3 introduces additional loci with ABBA patterns, which would lead to a positive D statistic. (c) An example illustrating interdependences between different ƒ4-ratio scores, which can be informative about the timing of introgression. In this example, different choices for the P1 population provide constraints on when the gene flow could have happened. (d) Based on relationships between ƒ4-ratio results from different four taxon tests, the ƒ-branch, or ƒb statistic, distinguishes between admixture at different time periods, assigning signals to different (internal) branches in the population/species tree.
With more genomic data becoming available, there is a need for handling datasets with tens or hundreds of taxa. Applying the D and ƒ4-ratio statistics has the advantage of computational efficiency and is powerful even when using whole genome data from only a single individual per population (Green et al. 2010). On the other hand, as each calculation of D and ƒ applies to four populations or taxa, the number of calculations/quartets grows rapidly with the size of the dataset. The number of quartets is , i.e. n choose 4, where n is the number of populations. This can present challenges in terms of increased computational requirements. Moreover, the resulting test statistics are correlated when quartets share an (internal) branch in the overall population or species tree, which may make a system of all possible four taxon tests across a dataset difficult to interpret.
Because pinpointing specific introgression events in datasets with tens or hundreds of populations or species remains challenging, the ƒ-branch or ƒb(C) metric was introduced in Malinsky et al. (2018) to disentangle correlated ƒ4-ratio results and assign gene flow evidence to specific, possibly internal, branches on a phylogeny. The ƒ-branch metric builds upon and formalises verbal arguments employed by Martin et al. (2013) to assign gene flow to specific internal branches on the phylogeny of Heliconius butterflies. Thus, the ƒ-branch statistic can be seen as an aid for formulating gene flow hypotheses in datasets of many populations or species.
Patterson’s D and related statistics have also been used to identify introgressed loci by sliding window scans along the genome [e.g. (Heliconius Genome Consortium 2012; Fontaine et al. 2015b)], or by calculating these statistics for particular short genomic regions. Because the D statistic itself has large variance when applied to small genomic windows and because it is a poor estimator of the amount of introgression (Martin et al. 2015), additional statistics which are related to the ƒ4-ratio have been designed specifically to investigate signatures of introgression in genomic windows along chromosomes. These statistics include ƒd (Martin et al. 2015), its extension ƒdM (Malinsky et al. 2015), and the distance fraction df (Pfeifer & Kapan 2019).
Programs for calculating Patterson’s D and related statistics include ADMIXTOOLS (Patterson et al. 2012), HyDe (Blischak et al. 2018), ANGSD (Paul et al. 2011; Soraggi et al. 2018), PopGenome (Pfeifer et al. 2014; Pfeifer & Kapan 2019), and Comp-D (Mussmann et al. 2019). However, a number of factors call for an introduction of new software. First, most of the existing programs cannot handle the variant call format (VCF) (Danecek et al. 2011), the standard file format for storing genetic polymorphism data produced by variant callers such as samtools (Li 2011) and GATK (DePristo et al. 2011). Second, the computational requirements of these programs in terms of either run time or memory (or both) make comprehensive analyses of datasets with tens or hundreds of populations or species either difficult or infeasible. Third, the programs implement only a subset of the statistics discussed above, and there are some statistics, namely ƒdM, and ƒ-branch, which have not yet been implemented in any publicly available software package.
To address these issues, we introduce the Dsuite software package. Dsuite brings the calculation of different related statistics together into one software package, combining genome-wide and sliding window analyses, and downstream analyses aiding their interpretation (Table 1). Dsuite has a user-friendly straightforward workflow and uses the standard VCF format, thus generally avoiding the need for format conversions or data duplication. Moreover, Dsuite is computationally more efficient than other software in the core task in calculating the D statistics, making it more practical for analysing large genomewide datasets with tens or even hundreds of populations or species. Finally, Dsuite implements the calculation of the ƒdM and ƒ-branch statistics for the first time in publicly available software. While researchers can implement these and other statistics in their own custom scripts, the inclusion of the whole package of statistics in Dsuite facilitates their use and reproducibility of results.
Table 1. Statistics calculated by Dsuite and overlap with other software packages.
| Software | VCF input | Genome-wide tests/statistics | Sliding window statistics | |||||
|---|---|---|---|---|---|---|---|---|
| D | f 4-ratio | f-branch | D | f d | f dM | df | ||
| ADMIXTOOLS | ✓ | ✓ | ||||||
| ANGSD | ✓ | |||||||
| Comp-D | ✓ | |||||||
| HyDe | ✓ | |||||||
| PopGenome | ✓ | ✓ | ✓ | ✓ | ✓ | |||
| Dsuite | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
Methods
The D and ƒ4-ratio statistics
The D and ƒ4-ratio statistics can be presented as applying to biallelic SNPs across four populations or taxa: P1, P2, P3, and O, related by the rooted tree (((P1,P2),P3),O), where the outgroup O defines the ancestral allele, denoted by A, and the derived allele is denoted by B (Green et al. 2010; Durand et al. 2011; Pease & Hahn 2015). The site patterns are ordered such that the pattern BBAA refers to P1 and P2 sharing the derived allele, ABBA to P2 and P3 sharing the derived allele, and BABA to P1 and P3 sharing the derived allele. Under the null hypothesis, which assumes no gene flow, the ABBA and BABA patterns are expected to occur due to incomplete lineage sorting with equal frequencies, and a significant deviation from that expectation is consistent with introgression between P3 and either P1 or P2. See Fig. 1, (Patterson et al. 2012) and (Durand et al. 2011) for more detail.
While simple site pattern counts can be computed for single sequences, most implementations, including Dsuite, work with allele frequency estimates, so that multiple individuals can be included from each population or taxon. Denoting the derived allele frequency estimate at site i in P1 as , and similarly and for populations P2 and P3, the following sums are calculated across all n biallelic sites:
| (1a) |
| (1b) |
| (1c) |
where we assume that the outgroup is fixed for the ancestral allele (i.e., ). The D statistic is then simply a normalised difference between the ABBA and BABA patterns of the form
| (2) |
If the frequency of the derived allele in the outgroup is not zero, the results of Dsuite correspond to the D and ƒ4-ratio statistics as defined by Patterson et al. (2012), who present the statistics as applying to an unrooted four taxon tree, with O being simply a fourth population rather than an outgroup. Their D definition is:
| (3) |
In this case, the ancestral vs. derived allele assignment is not necessary and the A and B labels can be assigned arbitrarily; the BAAB site pattern is equivalent to ABBA, ABAB to BABA, and AABB to BBAA. Therefore, the Patterson et al. (2012) definition of D corresponds to changing the right-hand side of equations (1a–c) to:
| (4a) |
| (4b) |
| (4c) |
We note that this definition is different from the one used by Durand et al. (2011) and Martin et al. (2014), which implicitly assumes that the outgroup is fixed for the ancestral allele and should only be used in such cases. While with the above formulas (eq. 3 and eq. 4a–c) it is technically not necessary for O to represent an outgroup, the current implementation of Dsuite makes this assumption in order to streamline the analysis and downstream interpretation of the results.
Calculating the ƒ4-ratio requires that P3 be split into two subsets, P3a and P3b, which is done in Dsuite by randomly sampling alleles from P3 at each SNP but is possible even if the dataset contains only one diploid individual from P3, in which case the two alleles are both sampled from that one individual. The results in Dsuite then correspond to the Patterson et al. (2012) definition:
| (5) |
The ƒ-branch statistic
The number of possible gene flow donor-recipient combinations increases rapidly with the number of populations or species. A unified test for introgression has been developed for a five taxon symmetric phylogeny, implemented in the DFOIL package (Pease & Hahn 2015). However, no such framework currently exists for datasets with six or more taxa. A common approach is to perform the D and ƒ4-ratio analyses on all four taxon subsamples from the dataset [e.g. (Green et al. 2010; Martin et al. 2013; vonHoldt et al. 2016; Kozak et al. 2018; Malinsky et al. 2018)]. However, the number of analyses that need to be performed grows very quickly. Even with a fixed outgroup, the number of combinations is , i.e. n choose 3, where n is the number of taxa. For example, there are 1,140 different combinations of ((P1, P2), P3) in a dataset of 20 taxa, growing to 161,700 combinations in a dataset with 100 taxa. Interpreting the results of such a system of four taxon tests is not straightforward; the different subsets are not independent as soon as the taxa share drift (that is, they share branches on the phylogeny) and, therefore, a single gene flow event can be responsible for many elevated D and ƒ4-ratio results. At the same time, the correlations, especially of the ƒ4-ratio scores, can be informative about the timing of introgression events and about the specific donor-recipient combinations.
The ƒ-branch or ƒb metric was introduced in Malinsky et al. (2018) to disentangle correlated ƒ4-ratio results and assign gene flow evidence to specific, possibly internal, branches on a phylogeny by building upon the logic developed by Martin et al. (2013), as illustrated in Fig. 1. Given a specific tree (with known or hypothesised relationships), the ƒb(P3) statistic reflects excess sharing of alleles between the population or species P3 and the descendants of the branch labelled b, relative to allele sharing between P3 and the descendants of the sister branch of b.
Formally:
| (6) |
where B refers to the populations or taxa descending from the branch b, and A refers to descendants from the sister branch of b. The calculation is over all positive ƒ4-ratio results which had A in the P1 and B in the P2 positions.
Sliding window statistics
A number of statistics have been developed specifically for application to genomic windows. They can be used to assess whether the admixture signal is confined to specific loci and to assist in locating any such loci. The D statistic itself has large variance when applied to small genomic windows and it is a poor estimator of the amount of introgression (Martin et al. 2015). However, statistics related to the ƒ4-ratio have been found to perform better. The Dsuite package implements three of these statistics (Table 1). The first is ƒd (Martin et al. 2015), which is defined as
| (7) |
where S(P1,P2,P3,O) stands for the numerator of D (i.e. nABBA — nBABA) and S(P1, Pd, Pd, 0) denotes the equivalent calculation but with Pd = P2 or Pd = P3, depending on which of these two populations has the higher frequency of the derived allele. While the ƒd statistic may be useful to localise genomic regions introgressed between P2 and P3, it is not meaningful in cases of excess sharing of alleles between P1 and P3 and can take arbitrarily large negative values in those cases (ƒd < —1). To address this issue, Malinsky et al. (2015) developed a modified version of the ƒd statistic which: (i) under the null hypothesis of no introgression is symmetrically distributed around zero; and (ii) can equally quantify shared variation between P3 and P2 (positive values) or between P3 and P1 (negative values). They called this modified ƒd statistic ƒdM. The calculation of ƒdM further depends on the frequency of the derived allele in P1 and P2. If the frequency of the derived allele in P2 is higher or equal to P1 then fdm = fd. However, if the derived allele frequency is higher in P1, then
| (8) |
The final sliding window statistic implemented in Dsuite is the distance fraction df of (Pfeifer & Kapan 2019), which is derived by combining the approach of studying correlation of allele frequencies (as in the other statistics presented here) with the concept of genetic distance. Specifically,
| (9) |
where is an estimate of the genetic distance at variable sites between populations x and y, so is the distance between P1 and P3 at site i. This can be formulated as a function of allele frequencies in the form
| (10) |
and equivalently for P2 and P3. The distance fraction d f shares the advantages of ƒdM of being symmetric and bounded on the interval [-1,1], while it may provide a more accurate estimate of the amount of introgression, being less sensitive to the timing of gene flow (Pfeifer & Kapan 2019). However, a thorough comparison of the advantages and disadvantages of all three sliding window statistics across a broad range of historical scenarios is lacking - therefore, it may be beneficial to consider the evidence provided by the combination of all three statistics.
Implementation
The statistics described above are implemented in a set of programs and utilities within the Dsuite package. The first program, Dtrios calculates the sums in equations (4a–c) and outputs genome-wide statistics including the D, its associated p-value, and the ƒ4-ratio statistic, for all trios of populations or species. This enables the assessment of evidence for gene-flow across the entire dataset. Next, Dinvestigate calculates the sliding window statistics (ƒd, ƒdM, and d f) for particular trios specified by the user. These programs take as input a VCF file (Danecek et al. 2011), whereby allele frequencies for each biallelic SNP and each population are calculated by default from the called genotypes (the GT field). In addition, we provide an option to use genotype probabilities (GP field) produced for example by phasing and imputation software such as BEAGLE (Browning & Browning 2007), or genotype likelihoods (either GL or PL fields) produced by variant callers such as GATK (DePristo et al. 2011). More details are provided in Supplemental Information. Using genotype likelihoods or probabilities instead of relying solely on called genotypes can be especially useful for low coverage data and can be taken advantage of by choosing the new -g option to Dtrios and Dinvestigate. Missing genotypes (./.) or likelihoods/probabilities are handled as follows. When data are missing from a subset of samples from a population or species, the allele frequency is estimated from the remaining samples; if genotypes are missing in all individuals from the population or species then the site is ignored for all trios which contain that population or species. Although primarily designed for whole genome analyses, being based on allele frequencies, the programs are in principle also applicable to restriction-site-associated DNA sequencing (RADseq) data (Andrews et al. 2016) and other multi-locus genomic data in VCF format. Results from Dtrios can be further processed using the Fbranch program and associated plotting utilities for the ƒ-branch statistic, facilitating interpretation of the results. Finally, the utilities DtriosCombine and DtriosParallel enable analyses of large datasets by parallelisation of the workflow across different compute nodes or across CPU cores on a single compute node.
The Dtrios program
Dtrios does not require a priori knowledge of population or species relationships, only the outgroup has to be specified. Instead, the command produces three types of output. For the first, in a file with the “BBAA.txt” suffix, Dtrios attempts to infer the population or species relationships: it orders each trio assuming that the correct tree is the one where the BBAA pattern is more common than the discordant ABBA and BABA patterns, which are assumed to result from incomplete lineage sorting or from introgression. The second type of output is the D min score, the minimum D for each trio regardless of any assumptions about the tree topology. There is no attempt to infer the true tree; instead, the trio is ordered so that the difference between nABBA and nBABA is minimized. This output is in a file with the “Dmin.txt” suffix and can be used to set a lower bound on the amount of “non-treeness” in the dataset as in Malinsky et al. (2018). Finally, there is also an option for the user to supply a tree in Newick format specifying known or hypothesized relationships between the populations or species. An output file with the “tree.txt” suffix then contains D and ƒ4-ratio values for trios ordered in a way consistent with this tree. This has to be done if the user later wants to calculate the ƒ-branch statistic, because the statistic relies on a particular tree hypothesis. In all three types of output, we order P1 and P2 so that nABBA >= nBABA. As a result, the D statistic is always positive and all the results, including the ƒ4-ratio and other statistics reflect evidence of excess allele sharing between P3 and P2 for each trio.
To assess whether D is significantly different from zero, Dtrios uses a standard blockjackknife procedure as in Green et al. (2010) and Durand et al. (2011), obtaining an approximately normally distributed standard error. For all three types of output, Dtrios calculates the Z-scores as Z = D/std_err(D), and outputs the associated p-values. However, when testing more than one trio, users should take into account the multiple testing problem and adjust the p-values accordingly. Although the different D statistics calculated on the same dataset are not independent, a straightforward conservative approach is to consider them as such and to control for overall false discovery rate.
The Dinvestigate program
The program Dinvestigate can provide further information about trios for which the D statistic is significantly different from zero by assessing whether the admixture signal is confined to specific loci and to assist in locating any such loci. For each trio specified by the user, the program outputs overall ƒd, and ƒdM, and also produces a text file which contains the values of ƒd, ƒdM, and d f in sliding windows.
The size of the windows is specified by the user and refers to a fixed number of ‘informative’ SNPs, i.e. SNPs that change the numerator of these statistics for any particular trio. We prefer this approach rather than specifying windows of fixed physical size (e.g. in kb), because equally sized physical windows can have vastly different amounts of information and the overall pattern of the results then tends to be driven by statistical noise - windows with fewer informative SNPs have more variance for all the calculated statistics.
The Fbranch program
Given the “tree.txt” output of Dtrios or DtriosCombine and the same Newick format tree specifying known or hypothesized relationships between the populations or species, the Fbranch program outputs a matrix with ƒ-branch statistic values for each branch on the tree, including internal branches, reflecting excess allele sharing with each valid population or species P3. The ƒ-branch statistic results can be visualised by plotting this matrix using the dtools.py script, which we provide with the package. When calculating the ƒ-branch statistic, it makes sense to set ƒ4-ratio results which are not statistically significant to zero, because ƒ4-ratio calculations for trios of nearly-equally closely related populations or species can produce large but non-significant values even in the absence of gene flow. Per default, our implementation sets all ƒ4-ratio values to zero where the p-value of the associated D statistic for that trio is > 0.01. This threshold can be changed by the user.
The DtriosCombine utility
It is common practice, especially for larger datasets, that VCF files are divided into smaller subsets by genomic regions, e.g. per chromosome. This facilitates the parallelization of computational workflows. The DtriosCombine program enables parallel computation of the D and ƒ4-ratio statistics across genomic regions, by combining the outputs of multiple Dtrios runs, summing up the counts in equations (4a–c) and the denominator of the ƒ4-ratio. It also calculates overall block-jackknife standard error across all regions to produce overall combined p-values for the D statistic.
The DtriosParallel utility
We provide a convenient wrapper script for parallel Dtrios computation on a single computer or a compute node. The script optimally divides the Dtrios runs across the VCF file into a number of chunks which correspond to the number of available compute cores supplied by the used with the --cores option. The script waits for all the runs to complete and then automatically executes DtriosCombine to generate a single set of output files for the entire VCF dataset.
Results
We assessed the performance of Dsuite using three datasets (Malinsky et al. 2020): 1) variants mapping to the largest Metriaclima zebra reference genome scaffold (∼16Mb) from a dataset comprising 73 species of Lake Malawi cichlid fishes, which was published in Malinsky et al. (2018); 2) a small simulation dataset comprising 20 species and 20Mb of sequence generated using the msprime (Kelleher et al. 2016) software; 3) a large simulation dataset with 100Mb of sequence and 100 species. To confirm the validity of Dsuite results, D statistics and associated p-values from analysis of the Malawi cichlid dataset were compared against the output of ADMIXTOOLS. The D values were found to be >99.99% correlated between the two programs, and the p-values showed >99% correlation. The results are thus qualitatively the same-the small differences in D include rounding errors, and for the p-values, the slightly larger differences are expected because of the stochasticity of the jackknife standard error estimation with different block sizes. In the simulated data, directional admixture events were simulated at randomly selected time points, with uniform distribution between the initial split time and the present, between a randomly selected pair of branches coexisting at that time point, and with admixture proportions drawn from a beta distribution rescaled to be between 0% and 30% with a maximum density around 5% to 10%. Diploid samples were produced by combining two independently simulated haploid sequences. Further details about the datasets and the parameters used in the simulations are outlined in Table 2 and in the Supplemental Information document online.
Table 2. An outline of datasets used to evaluate the performance of Dsuite.
| Dataset | Species | Samples | Trios | Sequence length | SNPs | Simulation parameters | |||
|---|---|---|---|---|---|---|---|---|---|
| μ ρ†(10-8) | Ne(103) | Gene flow events | Age(generations) | ||||||
| Malawi scaffold_0 | 73 | 131 | 62,196 | 16Mb | 612,889 | -----------Empirical data----------- | |||
| Simulation small | 20 | 40 | 1,140 | 20Mb | 4,342,771 | 1 | 50 | 5 | 1 million |
| Simulation large | 100 | 200 | 161,700 | 100Mb | 97,201,601 | 1 | 50 | 10 | 1 million |
μ - per generation mutation rate
ρ - per-generation recombination rate
Computational efficiency
To assess computational efficiency of Dsuite, we calculated D statistics for all combinations of trios with four other software packages: ADMIXTOOLS, HyDe, Comp-D, and PopGenome. ANGSD was not included in the comparisons because, unlike all the other programs, it uses read alignments instead of genotypes as a starting point of the analyses. For the Malawi cichlids and for the large simulated datasets, Dsuite was by far the most efficient of the programs in terms of both memory requirements and run time. For the small simulated dataset, Dsuite was still the most memory efficient, but ADMIXTOOLS, HyDe, and especially PopGenome were faster. PopGenome also performed well on the large simulated dataset-although slightly slower than Dsuite, it was the only other program competitive in both the run time and the memory requirement. The remaining programs required a lot of memory for the analysis of the large simulated dataset-ADMIXTOOLS and Comp-D required over 1 Terabyte of RAM and HyDe over 18 Gigabytes, while the Dsuite run required less than 223MB. The difference in memory efficiency between Dsuite and especially ADMIXTOOLS and Comp-D remained more than two orders of magnitude also for the two other datasets. In terms of speed, Comp-D stood out as being substantially slower across all analyses. We cancelled all the Comp-D runs after 24hours with only a small proportion of the trios completed. Among Dsuite, ADMIXTOOLS, and HyDe the run time differences were up to ∼2-3 fold depending on the dataset. The full results are shown in Table 3. We suggest that in addition to facilitating analyses of large datasets, improvements in computational efficiency may also facilitate the future inclusion of D and ƒ4-ratio as summary statistics within Approximate Bayesian Computation (ABC) inference frameworks (Beaumont et al. 2002; Jay et al. 2019).
Table 3. A comparison of Dsuite and a number of other tools in terms of computational efficiency of D statistic estimation.
| Dataset | Software | Options | Peak memory | Run time |
|---|---|---|---|---|
| Malawi scaffold_0 | Dsuite Dtrios | --no-f4-ratio | 92MB | 74m59s |
| Admixtools qpDstat | blgsize: 0.01 | 27,212MB | 125m2s | |
| HyDe run_hyde.py | none | 178MB | 231m38s | |
| Comp-D† | -d -H -b10 | 8,300MB | 24hours+ | |
| PopGenome | do.df=F block.size=1000 | 1,170MB | 24hours+ | |
| Simulation small (20 species) | Dsuite Dtrios | --no-f4-ratio | 8MB | 28m18s |
| Admixtools qpDstat | blgsize: 0.01 | 17,100MB | 13m59s | |
| HyDe run_hyde.py | none | 258MB | 19m38s | |
| Comp-D† | -d -H -b10 | 22,100MB | 24hours+ | |
| PopGenome | do.df=F block.size=1000 | 440MB | 1m50s | |
| Simulation large (100 species) | Dsuite Dtrios | --no-f4-ratio | 223MB | 215m52s (×100‡) |
| Admixtools qpDstat | blgsize: 0.05 | 1,117,314MB | 331m39s (×100‡) | |
| HyDe run_hyde.py | none | 18,716MB | 576m32s (×100‡) | |
| Comp-D† | -d -H -b10 | 1,000,185MB+ | 24hours+ (×100‡) | |
| PopGenome | do.df=F block.size=1000 | 470MB | 274m53s (×100‡) |
Comp-D cannot use allele frequencies calculated across multiple individuals, so only one individual per species included.
Because of the size of the dataset, we divided the analysis into 100 equally sized jobs to run in parallel; the run time and memory requirements are given for the first job
While the Dsuite and PopGenome analyses were run directly on the VCF file, all other software required format conversion. For ADMIXTOOLS, we first obtained data in the PED format using VCFtools v0.1.12b (Danecek et al. 2011) with the --plink option, and then translated these into the software-specific EIGENSTRAT format using the convertf program, which is included in the ADMIXTOOLS package. Data conversion into the PHYLIP input format for HyDe and Comp-D was done using the vcf2phylip script (Ortiz 2019). The additional run and set-up time needed for these conversions was excluded from the run times shown in Table 3.
Example and interpretation
In this section we use the small simulated dataset to illustrate the outputs of Dsuite and some topics related to the interpretation of the results. The results for the Malawi cichlid dataset are discussed in Malinsky et al. (2018).
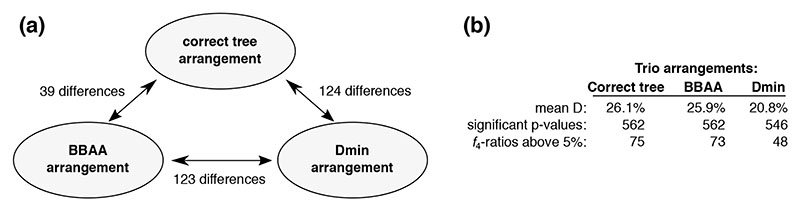
We found tens of differences among the trio arrangements in the three output files produced by Dsuite Dtrios (Fig. 2A). The “BBAA” trio arrangements differed from the correct tree in 39 cases (3.4% of the trios), which illustrates that sister species do not always share the most derived alleles in the presence of gene flow, even in the absence of rate variation. However, unlike for the simulation, the correct tree is not known for most real-world datasets and the frequency of the “BBAA” pattern may then be a useful guide regarding the population relationships. The “Dmin” arrangements differed from the correct tree in 124 trios (10.9%).
Figure 2. Summary of Dtrios output for the small simulated dataset (20 species, 1,140 trios, 5 gene flow events).
(a) The number of differences in trio arrangements between the three different output files. (b) A brief summary comparing the results with the three alternative arrangements.
Keeping in mind that only five gene flow events were simulated, it is notable that almost half of the D statistics were significantly elevated, e.g. 546 (47.9%) even in the “Dmin” arrangement which provides a lower bound on the D value for each trio (Fig. 2B). Using the ƒ4-ratio measure, we found that admixture proportions above 5% were estimated for at least 48 trios. This demonstrates that D and ƒ4-ratio statistics are correlated and that a significantly elevated result for a trio does not necessarily pinpoint the populations involved in a gene flow event.
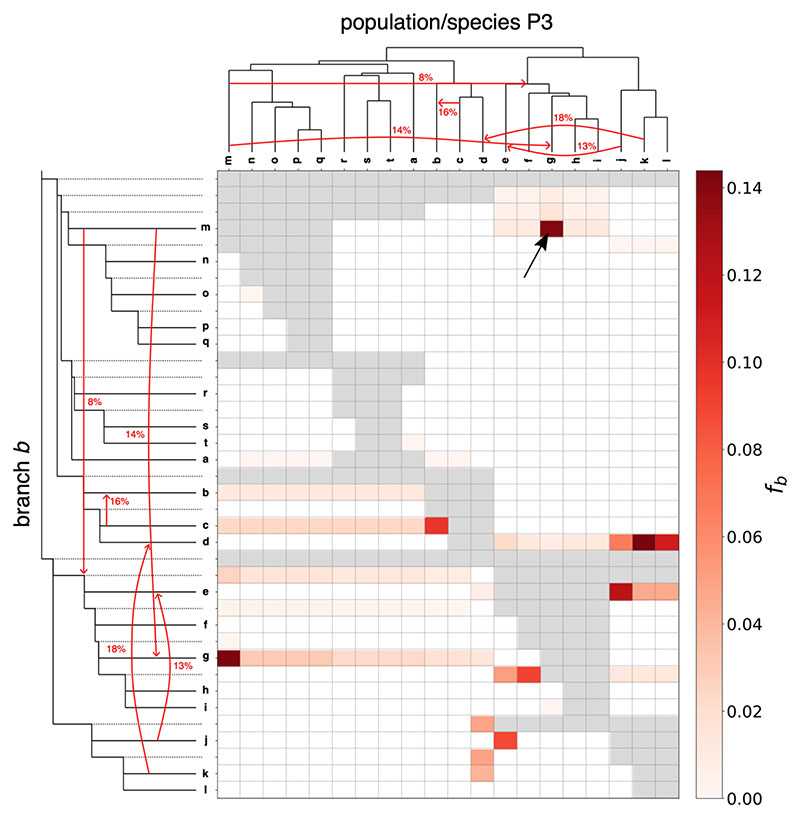
The tree in Fig. 3 shows the true simulated relationships between the 20 species together with the five gene flow events and their admixture proportions. The output of Dsuite Fbranch inference is then plotted in the inset heatmap, revealing how the ƒ-branch statistic is useful in guiding the interpretation of correlated ƒ4-ratio results. Ten out of the 568 f-branch (fb) signals are stronger than 5%, much fewer than the 73 signals identified from the raw trio analysis with the “BBAA” trio arrangements.
Figure 3. Results of Fbranch for the small simulated dataset.
The true species tree, which was used as input for simulating the data, is shown along the sides. The red arrows correspond to the simulated gene flow events and true admixture proportions. The tree is displayed in an ‘expanded’ form along the y axis, so that each branch, including internal branches, points to a corresponding row in the matrix with inferred ƒ-branch statistics. The values in the matrix thus refer to excess allele sharing between the branch b identified on the expanded tree on the y axis (relative to its sister branch) and the species P3 identified on the x axis. As an example, the cell highlighted by the black arrow refers to excess allele sharing between species g and the branch leading to species m, relative to its sister, the internal branch above species n, o, p, and q.
The reduction of information and the visualization provided by ƒ-branch facilitates narrowing down the number of possible acceptor and donor lineages involved in a gene flow event and should be seen as an aid for formulating specific gene flow hypotheses in a large data set that can be followed up individually by other methods, for example in a more richly parametrised model-based inference framework by software such as fastsimcoal2 (Excoffier et al. 2013) or δaδi (Gutenkunst et al. 2009). In particular, the ten ƒ-branch signals stronger than 5% correctly identify seven out of the nine branches involved in gene flow events. Six of these signals correctly pinpoint both branches involved in gene flow events ((d, k), (e, j), (m, g), (c, b)). However, a single gene flow event between two branches can still produce more than one ƒ-branch signal. For example, the gene flow event from m into g above produces elevated values for both ƒb=g(P3=m), i.e. the branch leading to g and species m, and its ‘mirror image’ ƒb=m(P3=g), branch leading to m and species g. While such mirror images are a common feature of the ƒ-branch, we note that the statistic is not designed to be symmetric, because the ƒ4-ratios themselves, and the trees on which the statistics are based, are not symmetric with respect to switching P2 and P3. Furthermore, the gene flow from m into g produces correlated signals between g and lineages related to m (e.g. n, o, p, q) because of the shared ancestry between these lineages and m. This generally manifests in horizontal lines of correlated signals in the ƒ-branch plots as shown in Fig. 3. Finally, note that an ƒ-branch result in itself does not indicate directionality of gene flow. We suggest using 5-taxon tests, when possible, for inferring directionality (Pease & Hahn 2015; Svardal et al. 2019).
Assessment of ƒ-branch accuracy
Malinsky et al. (2018) first introduced the ƒ-branch statistic and tested its behaviour on a simple simulated dataset of eight species, comparing its behaviour against inference with the treemix software (Pickrell & Pritchard 2012; Patterson et al. 2012). They found the ƒ-branch statistic to be more robust in detecting branches involved in hybridisation events in cases where gene flow was particularly strong. Here we provide an additional assessment of ƒ-branch inference accuracy on a simulated dataset of 20 species, reflecting the focus on Dsuite and the overall trend towards analyses of larger datasets.
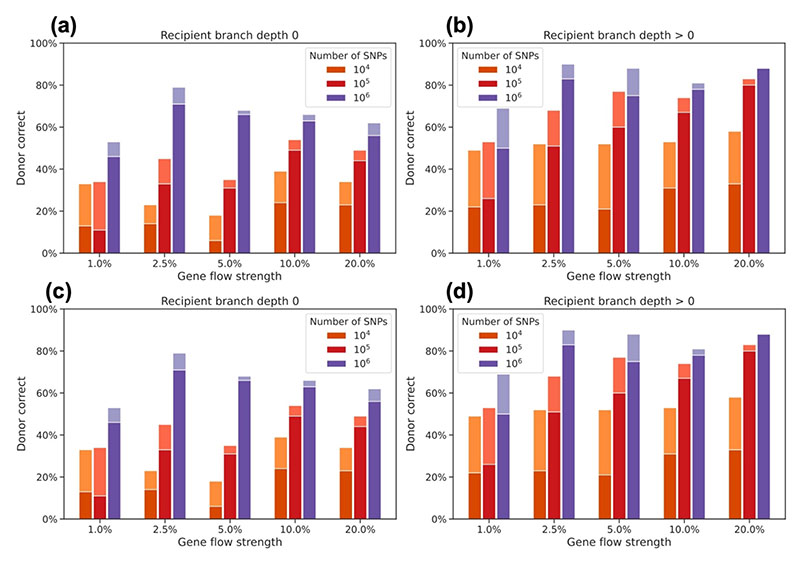
We examine how often the strongest inferred ƒ-branch signal corresponds to the correct gene flow donor and recipient branches within the species tree in a scenario with one gene flow event, depending on gene flow strength and the number of SNPs used as input for the inference. For this, we selected numbers whose magnitude approximates common sequencing strategies: 104 SNPs corresponding to RADseq experiments, 105 SNPs corresponding to transcriptome sequencing or exome capture studies, and 106 SNPs which corresponds in magnitude to the size of datasets obtained by whole genome (re-)sequencing experiments. The results are shown in Fig. 4. See Supplemental Information for more details about how these simulations and inference were performed.
Figure 4. Simulation based assessment of ƒ-branch accuracy.
The barplots show the proportion of cases where the strongest inferred ƒ-branch signal corresponds the correct simulated gene flow recipient and donor branches. We simulated a single gene flow event randomly placed on a 20 species tree. The lighter shaded areas of each bar correspond to cases where rather than the actual recipient/donor branches their sister branches showed the strongest signal. (a)-(b) Proportion of times that the branch b of the strongest ƒ-branch signal corresponds to the true recipient of gene flow, in cases where the recipient branch is (a) a terminal or (b) an internal branch. (c)-(d) Proportion of times that P3 of the strongest ƒ-branch signal corresponds to the true donor of gene flow or to a descendant branch of it for cases where the recipient branch is (c) a terminal or (d) an internal branch.
We found that with 106 SNPs, ƒ-branch inference was accurate in the majority of cases for both donor and recipient branches in all cases where the simulated gene flow was stronger than 2.5%. Inference for gene flow on internal branches, which is a key benefit of the ƒ-branch statistic, was more accurate than for terminal branches (compare Fig. 4a,c against Fig. 4a,d). We note that performance depends on the number of SNPs used. The inferences corresponding to RAD-seq were accurate in only < 40% of the simulations, even when the simulated gene flow strength was substantial. Therefore, while RAD-seq data can be used successfully to estimate D statistics and the ƒ4-ratio, the simulations suggest that ƒ-branch results should be treated with caution for this data type. The inferences corresponding to transcriptome or exome capture data performed better and inferred internal donor and recipient branches correctly in the majority of the cases, as long as the simulated gene-flow was > 1%. A further improvement is seen with whole genome data, where ƒ-branch can deliver good accuracy for both internal and external branches in 20-species trees, as long as gene flow proportions are over 1%.
Conclusions
The Dsuite software package brings together a number of statistics for learning about admixture history from patterns of allele sharing across populations or closely related species. In particular, by being computationally efficient, it facilitates the calculation of the D and ƒ4-ratio statistics across tens or even hundreds of populations, meeting the needs of ever-growing genomic datasets. Correct interpretation of the results of a system of D and ƒ4-ratio tests remains challenging and is an active area of research. In real datasets, imbalances in allele sharing that lead to significantly elevated D and ƒ4-ratio statistics can result from specific scenarios involving ancestral population structure (Durand et al. 2011; Eriksson & Manica 2012) and variation in substitution rates (Pease & Hahn 2015). Even when all allele sharing imbalances are caused by introgression, more work remains to be done to reliably pinpoint all introgression events and infer the networks of gene flow that may characterise relationships between many populations or closely related species. Dsuite implements tools that aid the interpretation of the results, including the ƒd, ƒdM, and d f statistics suited for applying to genomic windows and the ƒ-branch statistic which aids in assigning the gene flow to particular branches on the population or species tree.
Supplementary Material
Acknowledgements
We would like to thank Richard Durbin and Walter Salzburger for useful discussions and comments. This work has been supported by the EMBO grant ALTF 456-2016 to MilMal, the Norwegian Research Council grant 275869 to MicMat, and the Swiss National Science Foundation (SNSF) grant 176039 to Walter Salzburger. HS was supported by the Flemish University Research Fund. Conflict of Interest: none declared.
Footnotes
Data accessibility statement
The Malawi cichlid data and the simulated data used in this manuscript are available through the Dsuite GitHub repository (https://github.com/millanek/Dsuite). They are also archived, together with a snapshot of the Dsuite code, on DataDryad under https://doi.org/10.5061/dryad.tdz08kpxt.
Author contributions
MilMal developed the Dsuite software package with assistance from MicMat regarding tree-based operations. HS conceived the ƒ-branch statistics, coded the plotting function for it, and performed the simulations. HS also wrote the DtriosParallel script. MilMal wrote the manuscript with contributions from HS and MicMat. All authors approved the manuscript.
References
- Alexander DH, Novembre J, Lange K. Fast model-based estimation of ancestry in unrelated individuals. Genes & development. 2009;19:1655–1664. doi: 10.1101/gr.094052.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrews KR, Good JM, Miller MR, Luikart G, Hohenlohe PA. Harnessing the power of RADseq for ecological and evolutionary genomics. Nature reviews Genetics. 2016;17:81–92. doi: 10.1038/nrg.2015.28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beaumont MA, Zhang W, Balding DJ. Approximate Bayesian computation in population genetics. Genetics. 2002;162:2025–2035. doi: 10.1093/genetics/162.4.2025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blischak PD, Chifman J, Wolfe AD, Kubatko LS. HyDe: A Python Package for GenomeScale Hybridization Detection. Posada D, editor. Systematic Biology. 2018;67:821–829. doi: 10.1093/sysbio/syy023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Browning SR, Browning BL. Rapid and accurate haplotype phasing and missing-data inference for whole-genome association studies by use of localized haplotype clustering. American journal of human genetics. 2007;81:1084–1097. doi: 10.1086/521987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danecek P, Auton A, Abecasis G, et al. The variant call format and VCFtools. Bioinformatics Oxford England. 2011;27:2156–2158. doi: 10.1093/bioinformatics/btr330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DePristo MAM, Banks EE, Poplin RR, et al. A framework for variation discovery and genotyping using next-generation DNA sequencing data. Nature Genetics. 2011;43:491–498. doi: 10.1038/ng.806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durand EY, Patterson N, Reich D, Slatkin M. Testing for ancient admixture between closely related populations. Molecular Biology and Evolution. 2011;28:2239–2252. doi: 10.1093/molbev/msr048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eriksson A, Manica A. Effect of ancient population structure on the degree of polymorphism shared between modern human populations and ancient hominins. Proceedings of the National Academy of Sciences of the United States of America. 2012;109:13956–13960. doi: 10.1073/pnas.1200567109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Excoffier L, Dupanloup I, Huerta-Sanchez E, Sousa VC, Foll M. Robust demographic inference from genomic and SNP data. Akey JM, editor. PLoS genetics. 2013;9:e1003905. doi: 10.1371/journal.pgen.1003905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fontaine MC, Pease JB, Steele A, et al. Extensive introgression in a malaria vector species complex revealed by phylogenomics. Science (New York, N.Y.) 2015a;347 doi: 10.1126/science.1258524. 1258524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green RE, Krause J, Briggs AW, et al. A draft sequence of the Neandertal genome. Science (New York, N.Y.) 2010;328:710–722. doi: 10.1126/science.1188021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutenkunst RN, Hernandez RD, Williamson SH, Bustamante CD. Inferring the joint demographic history of multiple populations from multidimensional SNP frequency data. McVean G, editor. PLoS genetics. 2009;5:e1000695. doi: 10.1371/journal.pgen.1000695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heliconius Genome Consortium. Butterfly genome reveals promiscuous exchange of mimicry adaptations among species. Nature. 2012;487:94–98. doi: 10.1038/nature11041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hey J. Isolation with migration models for more than two populations. Molecular Biology and Evolution. 2010;27:905–920. doi: 10.1093/molbev/msp296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jay F, Boitard S, Austerlitz F. An ABC Method for Whole-Genome Sequence Data: Inferring Paleolithic and Neolithic Human Expansions. Hernandez R, editor. Molecular Biology and Evolution. 2019;36:1565–1579. doi: 10.1093/molbev/msz038. [DOI] [PubMed] [Google Scholar]
- Kamm J, Terhorst J, Durbin R, Song YS. Efficiently Inferring the Demographic History of Many Populations With Allele Count Data. Journal of the American Statistical Association. 2019;155:1–16. doi: 10.1080/01621459.2019.1635482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelleher J, Etheridge AM, McVean G. Efficient Coalescent Simulation and Genealogical Analysis for Large Sample Sizes. PLoS Computational Biology. 2016:e1004842. doi: 10.1371/journal.pcbi.1004842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozak KM, McMillan WO, Joron M, Jiggins CD. Genome-wide admixture is common across the Heliconius radiation. bioRxiv. doi: 10.1093/gbe/evab099. 414201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H. A statistical framework for SNP calling, mutation discovery, association mapping and population genetical parameter estimation from sequencing data. Bioinformatics Oxford England. 2011:2987–2993. doi: 10.1093/bioinformatics/btr509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H. A statistical framework for SNP calling, mutation discovery, association mapping and population genetical parameter estimation from sequencing data. Bioinformatics Oxford England. 2011;27:2987–2993. doi: 10.1093/bioinformatics/btr509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malinsky M, Challis RJ, Tyers AM, et al. Genomic islands of speciation separate cichlid ecomorphs in an East African crater lake. Science (New York, N.Y.) 2015;350:1493–1498. doi: 10.1126/science.aac9927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malinsky M, Matschiner M, Svardal H. Dsuite - fast D-statistics and related admixture evidence from VCF files, Dryad, Dataset. 2020 doi: 10.5061/dryad.tdz08kpxt. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malinsky M, Svardal H, Tyers AM. Whole-genome sequences of Malawi cichlids reveal multiple radiations interconnected by gene flow. Nature Ecology & Evolution. 2018;457:830. doi: 10.1038/s41559-018-0717-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin SH, Dasmahapatra KK, Nadeau NJ, et al. Genome-wide evidence for speciation with gene flow in Heliconius butterflies. Genome Research. 2013;23:1817–1828. doi: 10.1101/gr.159426.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin SH, Davey JW, Jiggins CD. Evaluating the use of ABBA-BABA statistics to locate introgressed loci. Molecular Biology and Evolution. 2015;32:244–257. doi: 10.1093/molbev/msu269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mussmann SM, Douglas MR, Bangs MR, Douglas ME. Comp-D: a program for comprehensive computation of D-statistics and population summaries of reticulated evolution. Conservation Genetics Resources. 2019;16:1–5. [Google Scholar]
- Ortiz EM. vcf2phylip v2.0: convert a VCF matrix into several matrix formats for phylogenetic analysis. 2019 [Google Scholar]
- Patterson N, Moorjani P, Luo Y, et al. Ancient admixture in human history. Genetics. 2012;192:1065–1093. doi: 10.1534/genetics.112.145037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson N, Price AL, Reich D. Population structure and eigenanalysis. PLoS genetics. 2006;2:e190–e190. doi: 10.1371/journal.pgen.0020190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paul JS, Albrechtsen A, Song YS. Genotype and SNP calling from next-generation sequencing data. Nature reviews Genetics. 2011;12:44–451. doi: 10.1038/nrg2986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pease JB, Hahn MW. Detection and polarization of Introgression in a five-taxon phylogeny. Systematic Biology. 2015;64:651–662. doi: 10.1093/sysbio/syv023. [DOI] [PubMed] [Google Scholar]
- Pfeifer B, Kapan DD. Estimates of introgression as a function of pairwise distances. BMC bioinformatics. 2019;20:207–11. doi: 10.1186/s12859-019-2747-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeifer B, Wittelsbürger U, Ramos-Onsins SE, Lercher MJ. PopGenome: an efficient Swiss army knife for population genomic analyses in R. Molecular Biology and Evolution. 2014;31:1929–1936. doi: 10.1093/molbev/msu136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pickrell JK, Pritchard JK. Inference of population splits and mixtures from genome-wide allele frequency data. PLoS genetics. 2012;8:e1002967. doi: 10.1371/journal.pgen.1002967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155:945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soraggi S, Wiuf C, Albrechtsen A. Powerful Inference with the D-Statistic on Low-Coverage Whole-Genome Data. G3 Bethesda Md. 2018;8:551–566. doi: 10.1534/g3.117.300192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svardal H, Quah FX, Malinsky M, et al. Ancestral hybridisation facilitated species diversification in the Lake Malawi cichlid fish adaptive radiation. Molecular Biology and Evolution. 2019 doi: 10.1093/molbev/msz294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tung J, Barreiro LB. The contribution of admixture to primate evolution. Current Opinion in Genetics & Development. 2017;47:61–68. doi: 10.1016/j.gde.2017.08.010. [DOI] [PubMed] [Google Scholar]
- vonHoldt BM, Cahill JA, Fan Z, et al. Whole-genome sequence analysis shows that two endemic species of North American wolf are admixtures of the coyote and gray wolf. Science Advances. 2016;2:e1501714. doi: 10.1126/sciadv.1501714. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.