Polarity of uncertainty representation during exploration and exploitation in ventromedial prefrontal cortex

Abstract

Environments furnish multiple information sources for making predictions about future events. Here we use behavioural modelling and fMRI to describe how humans select predictors that might be most relevant. First, during early encounters with potential predictors, participants’ selections were explorative and directed towards subjectively uncertain predictors (positive uncertainty effect). This was particularly the case when many future opportunities remained to exploit knowledge gained. Then, preferences for accurate predictors increased over time, while uncertain predictors were avoided (negative uncertainty effect). The behavioural transition from positive to negative uncertainty-driven selections was accompanied by changes in representations of belief uncertainty in ventromedial prefrontal cortex (vmPFC). The polarity of uncertainty representations (positive or negative encoding of uncertainty) changed between exploration and exploitation periods. Moreover, the two periods were separated by a third transitional period in which beliefs about predictors’ accuracy predominated. VmPFC signals a multiplicity of decision variables, the strength and polarity of which vary with behavioural context.

Introduction

Humans and other animals are often presented with multiple information sources in the environment that can predict different outcomes such as reward. Selecting the right predictor to guide behaviour towards a particular outcome requires determining the predictors’ relevance in forecasting that outcome^1,2. Biases in information seeking can lead to mistaken beliefs about the relationships that prevail in the world^3,4. It has been argued that animals should attend either to certain predictors⁵ or, on the contrary, to uncertain predictors⁶. Certain predictors might be relevant as they deliver an outcome with known prediction accuracy, while attending to uncertain predictors might turn out to be more beneficial in the long-term.

We propose that which type of predictor should be considered most relevant changes during different phases of the learning process. When selecting between multiple predictors for the first time, selections should maximize information about available predictors. Selections should be “explorative” and directed towards “uncertain” predictors. The degree of exploration should also be determined by the time horizon. The time horizon is the remaining time in the current context (or block in the current experiment)^7,8: exploration is beneficial in longer compared to shorter time horizons as the knowledge gained can be used in later predictor selections. Once an estimate about a predictor’s accuracy has formed, selections should be “exploitative” and guided by the “accuracy” and “certainty” of predictors in line with reward maximization. This perspective draws on both previously formulated hypotheses in the field of learning theory^5,6. Predictors should be selected based on the learner’s uncertainty about predictors’ accuracy during exploration and on the learner’s certainty about predictors’ accuracy during exploitation. Our first aim in the current study was to examine whether this was the case.

Evidence for uncertainty-guided exploration has, however, recently been questioned⁹. It has been argued that behaviour may sometimes appear exploratory but on closer inspection the decisions that people make can be understood as having been guided by noisy estimates of the values of the choices that are formed during learning. In other words, when people appear exploratory, they may in fact be attempting to make exploitative decisions, but their exploitative decisions are informed by noisy estimates of choice values. Our second aim was to ascertain whether people genuinely engage in exploratory behaviour. This can be tested by comparing rates of exploratory behaviour when past experience is held constant, but the length of the future time horizon is manipulated; a longer future time horizon should elicit more exploration even when previous learning opportunities are the same. Moreover, the appropriateness of computational models of exploratory behaviour can also be tested by obtaining more direct empirical indices of participants’ subjective uncertainty; we obtained such measures in our experiment. In addition, the computational model can be used to identify trials in which exploratory behaviour appears to be guided by information seeking in order to reduce uncertainty and trials in which exploratory behaviour simply reflects randomness in the response selection or learning process⁹.

Our third aim was to examine neural activity related to exploratory and exploitative modes of decision making. Many previous studies have shown that vmPFC activity reflects information relevant for making value-guided decisions between choices. When making a decision between choice options, vmPFC activation covaries with the decision variable that guides the decision – the difference in value between the choice taken as opposed to the choice rejected^10–18. If, as has been argued, such vmPFC activity changes reflect allocation of attention to a choice option^19–21, then it is possible that vmPFC activity also reflects selection of a predictor to guide behaviour and the reason why it is being selected to guide behaviour: either because of its predictive accuracy, because of the certainty of its prediction, or because of the uncertainty of its prediction.

We use a combination of behavioural analysis, computational modelling, and functional magnetic resonance imaging (fMRI) to investigate at both behavioural and neural levels which predictors are classified as informative, uncertain or certain, as a function of time horizon, and the current behavioural mode (exploration, exploitation, or the period of transition from exploration to exploitation). We designed a novel task in which participants selected between multiple predictors which gave partial information about the location of a target that the participants were asked to find. During the course of multiple experimental blocks, participants encountered a series of potential predictors while transitioning through time horizons of different lengths, inducing explorative and exploitative selections. We used a Bayesian model to extract trial-by-trial estimates of participants’ beliefs about both the accuracy of predictors and their subjective uncertainty in those beliefs. This allowed us to test their independent and complementary impact on selection behaviour and their neural representations.

We found predictor selections are made as a function of time in two important ways. They change as a function of the time that has elapsed since learning began and they change as a function of the remaining time horizon – the time period over which the learner expects the current conditions to prevail. These changes occur in tandem with the evolution of predictor-related activity patterns in vmPFC. Activity in vmPFC was sensitive to participants’ uncertainty in their beliefs about predictors but the polarity of uncertainty representations (positive or negative encoding of uncertainty) changed with the behavioural mode: a positive uncertainty decision signal was present in vmPFC during exploration, while activity in the same region signalled negative uncertainty during exploitation. By contrast, other brain areas such as anterior cingulate cortex (ACC) and other dorsomedial frontal cortical areas, signalled uncertainty only during explorative phases. We also found that exploration and exploitation modes were separated by a transitional period in which beliefs about predictors’ accuracy predominated in their impact on vmPFC activity. These results show that a predictor’s relevance for guiding behaviour is not defined by a single attribute (accuracy, positive or negative uncertainty), but rather it is dynamically modulated by the behavioural modes of exploration, exploitation, and their transition. We show that vmPFC carries similar information, representing a multiplicity of predictor selection variables, the strength and polarity of which vary according to their relevance for the current behavioural mode.

Results

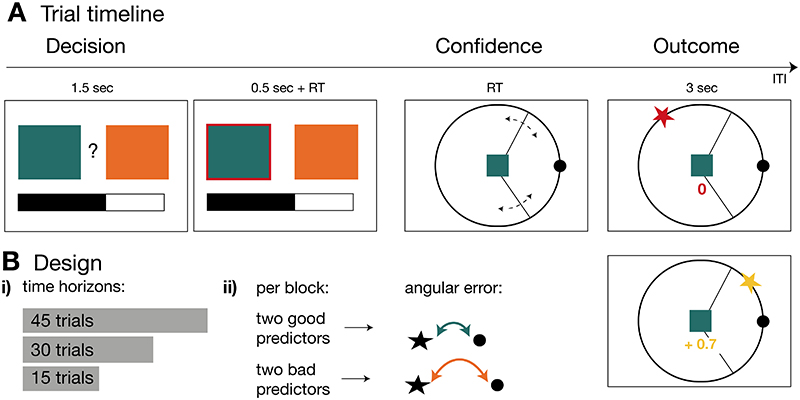
On each trial of the experiment (Figure 1A), participants made two decisions. First, they made a binary choice between two predictors to find a target’s location on a circle (decision phase). Participants knew that the target location changed constantly on every trial and could not be predicted directly from previous observations of its location. The only way to infer the target’s location was through learning how well each predictor predicted the target location. Participants learned how well a predictor predicted the target by observing the distance between the location estimated by the selected predictor and the true target location (which we refer to as “angular error”). Importantly, predictors differed in how well they estimated the target location (see S1 for details on the cover story). Selecting a better predictor led to more rewards at the time of a second decision in the trial. During the second decision, the predictor’s estimate of the target location was revealed, and participants expressed their confidence in it (confidence phase). They did this by adjusting the size of an interval around the predictor’s estimate such that the true target location would fall within this interval. At the end of a trial, the true target location and possible points were revealed (outcome phase). Participants gained points when the target fell within the chosen interval and the amount of points increased when the interval size was small. This payoff scheme incentivised selecting predictors with smaller angular errors in the first place. In addition to being informed about whether they had won or lost, the outcome phase enabled participants to update their beliefs about how well the chosen predictor estimated the target by observing the angular error. Participants took part in two versions of the task that differed in their framing aspect (social/non-social framing). Here, we collapsed data across versions after finding that versions did not differ in the results depicted here (see details on task versions in Supplementary Information).

Figure 1. Experimental Task and Design.

(A) Trial timeline. In each trial, participants made two choices. First, a binary choice between two predictors (coloured boxes; decision phase) to receive information about a target’s location on a circle. The goal was to choose predictors that accurately predicted the target location. The length of a black bar at the bottom of the screen informed participants about the number of remaining trials in the current block. Second, participants indicated their belief in the accuracy of the chosen predictor by modifying the size (dotted lines) of an interval symmetrical around the reference point (confidence phase). In the outcome phase, the target location (star) and any points earned were indicated. Two possible example outcomes are illustrated. In the above case, the participant’s prediction was incorrect as the target fell outside the interval, resulting in a null payoff. In the bottom case, the target fell within the interval, resulting in a positive payoff. Positive payoffs increase with narrower intervals as long as the target falls within the interval. (B) Design. (B-i) Participants transitioned through blocks of different numbers of trials (time horizons). (B-ii) Each time horizon introduced four new predictors (illustrated as boxes) that were categorised into two good (green and yellow boxes) and two bad predictors (orange and blue boxes) according to how well they predicted the target. The quality of predictions was determined by the angular error between target and reference location with a smaller angular error representing better target predictions.

The value of exploration lies in revealing more accurate predictors, but this is only useful if the time horizon (the amount of trials remaining) offers sufficient opportunity to exploit the newly discovered predictors⁷. To test this idea, participants transitioned through blocks of different lengths (45, 30 and 15 trials) each with a unique set of four predictors (Figure 1B-i). This made it possible to examine the balance between exploration and exploitation as a function of time horizon. Time horizon and current progress were explicitly cued on each trial. Each block comprised two good predictors with a relatively low average angular error between predicted reference point and target and two bad predictors with a higher angular error (Figure 1B-ii).

Dissociable effects of uncertainty and accuracy on predictor selections and subjective confidence judgments

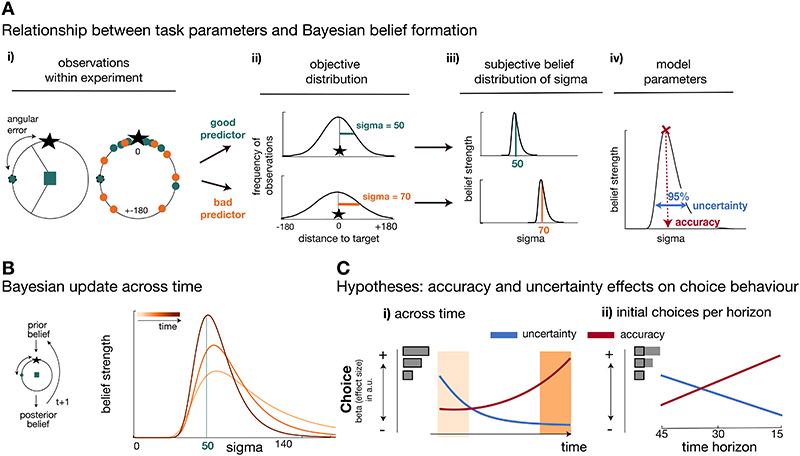
Exploration should not only be guided by one’s belief in the predictor’s accuracy, but also by one’s own uncertainty in that belief. For this reason, we used a Bayesian model to capture participants’ belief distribution over the angular error between the reference point and the true target location (Figure 2A-i). The trial-by-trial angular errors were derived from a normal distribution centred on the true target location. Predictors’ normal distributions varied in their standard deviations (referred to here as sigma), making some predictors better in estimating the target location (lower sigma value) and other predictors worse (higher sigma value). Hence, by tracking the angular errors of a predictor, participants could estimate the sigma value associated with each predictor’s distribution (see Figure 2A-ii). We used the Bayesian model to capture participants’ beliefs in the sigma value after observing the angular error of the chosen predictor at each trial (Figure 2A-iii;2B). This belief distribution allowed us to derive two independent model-based estimates that we hypothesized to influence choice in parallel: first, an estimate in the “accuracy” of a predictor (a point-estimate derived by the mode of the belief distribution, representing the sigma believed to be the most likely of that of the chosen predictor):

$$\text{accuracy}=\text{max}[\text{belief}\text{distribution}]\ast (-1)$$ (1)

Figure 2. Task statistics, Bayesian model, and choice hypotheses.

(A) Panels depict the mapping between observations during the task (i), their statistical properties (ii), and subjective beliefs about these properties derived with Bayes’ rule (iii;iv). (A-i) A predictor’s performance can be evaluated by the angular error at each trial (left panel), and by comparing angular errors between predictors across observations (right panel). Better predictors have on average smaller angular errors (green is better than orange). (A-ii) Predictors’ angular errors were derived from normal distributions centred on the true target location. Critically, the normal distributions for good and bad predictors differed in their standard deviation (sigma): smaller sigma’s reflected smaller angular errors, i.e. more accurate predictions of the true target location. Learning about a predictor’s angular error across time corresponded to forming beliefs about a predictor’s sigma value. (A-iii) To capture this learning process, we used Bayesian modelling and derived trial-wise belief distributions over sigma for each predictor. In other words, we estimated a probability density function that expressed the belief strength in each possible sigma over a large range of sigmas, and that was updated with each new observation via Bayes’ rule. The coloured vertical lines indicate the true underlying sigmas of the predictors and the black distributions reflect the Bayesian approximation after extensive training. (A-iv) We captured two separable estimates about participants’ beliefs concerning predictors: an estimate of the accuracy of a predictor (the mode of the distribution indicated by the position of the vertical line on the abscissa) and the uncertainty in that belief (width of the belief distribution). (B) In all panels, light to dark orange represents earlier and later trials, respectively, in a block. Left: Prior beliefs are updated after observing the angular error in the trial’s outcome phase, resulting in a posterior belief. The posterior belief forms the prior for the next encounter with the same predictor. Right: Belief distribution when selecting the same predictor multiple times. Across time, the belief distribution will converge towards the true value of sigma (here, true sigma is 50). (C) Experimental hypotheses. Note that panels depict an illustration of hypothesized effect sizes of accuracy and uncertainty on choice akin to logistic GLM analyses of choice. (C-i) Participants’ patterns of explore/exploit choices should systematically change over the course of the blocks. At the beginning of a block (light orange area), participants should pursue the more uncertain predictor, that is choices should be driven by a positive uncertainty effect, but this tendency should reverse over time. Accurate predictors should be sought out throughout (positive accuracy effect), but particularly towards the end of the block (dark orange area) when the value of exploration diminishes. (C-ii) At the time of initial choices (indicated by black boxes in inset), the value of exploration should be modulated by the time horizon and choices towards uncertain predictors should systematically increase if there are more trials remaining in which to exploit the knowledge gained, i.e. in longer horizons (vice versa for accuracy-driven choices).

Note that a higher accuracy value denoted in Eq.(1) indicates bigger deviations of the target from the reference point. To derive an accuracy estimate that can be interpreted intuitively, the sign of Eq.(1) is reversed so that positive values can be interpreted as higher accuracy.

Second, an estimate of the “uncertainty” in that predictor (variability around the accuracy estimate, representing the uncertainty) (Figure 2A-iv):

$$\text{uncertainty}={\widehat{\sigma }}_{(\text{cumulative}\text{belief}\text{distribution}=97.5\%)}-{\widehat{\sigma }}_{(\text{cumulative}\text{belief}\text{distribution}=2.5\%)}.$$ (2)

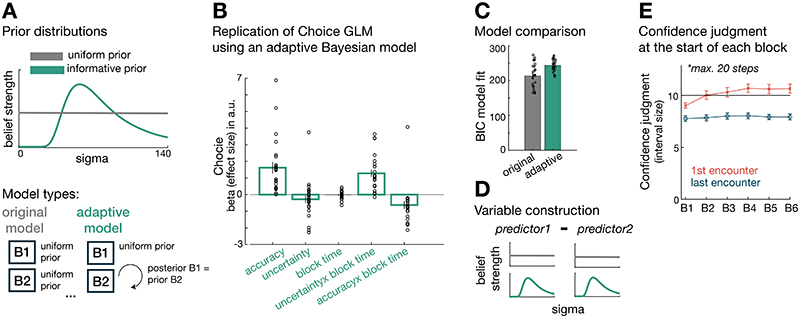
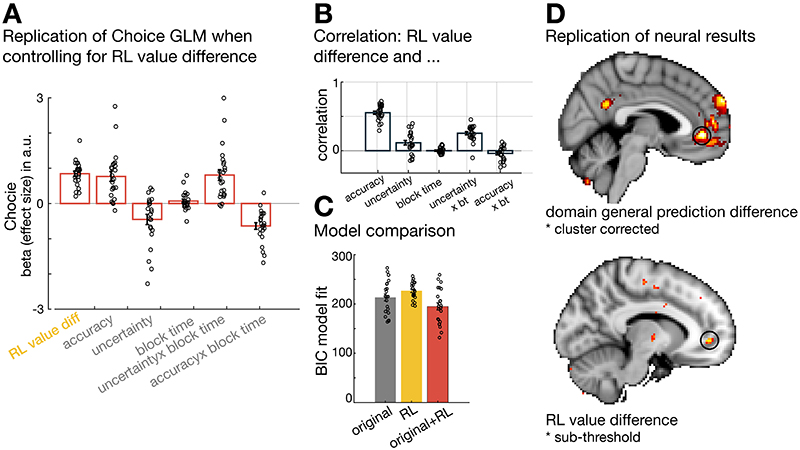
The terms “accuracy” and “uncertainty” will from now onwards refer to the model-derived parameters defined in Eq. (1) and (2), respectively (Figure 2A-iv). We used a Bayesian model that assumed uniform prior beliefs for all four predictors at each block start. However, we compared this Bayesian model to two competing models: a Bayesian model using informative priors (Extended Data Figure 1) and a reinforcement learning (RL) model tracking payoff history (Extended Data Figure 2). The Bayesian model with uniform priors provided a better model fit to choice behaviour compared to either of the other models (see Method; Supplementary Information: alternative computational models; Extended Data Figures 1 and 2).

We measured the degree to which participants were exploiting accurate predictors and the degree to which they were exploring uncertain predictors. We hypothesized, first, that uncertainty drives exploration between choices at the beginning of a block and so choices might be directed to uncertain predictors. Then, over the course of a block, participants should become increasingly uncertainty avoiding in other words, choices should be directed towards certain predictors (negative uncertainty effect) (Figure 2C-i). Second, we hypothesized that the initial choice pattern in a block should depend on how many more trials were still to be encountered in the block (effect of time horizon). Longer blocks favour more uncertainty-driven exploration and less accuracy-driven exploitation compared to shorter blocks (Figure 2C-ii).

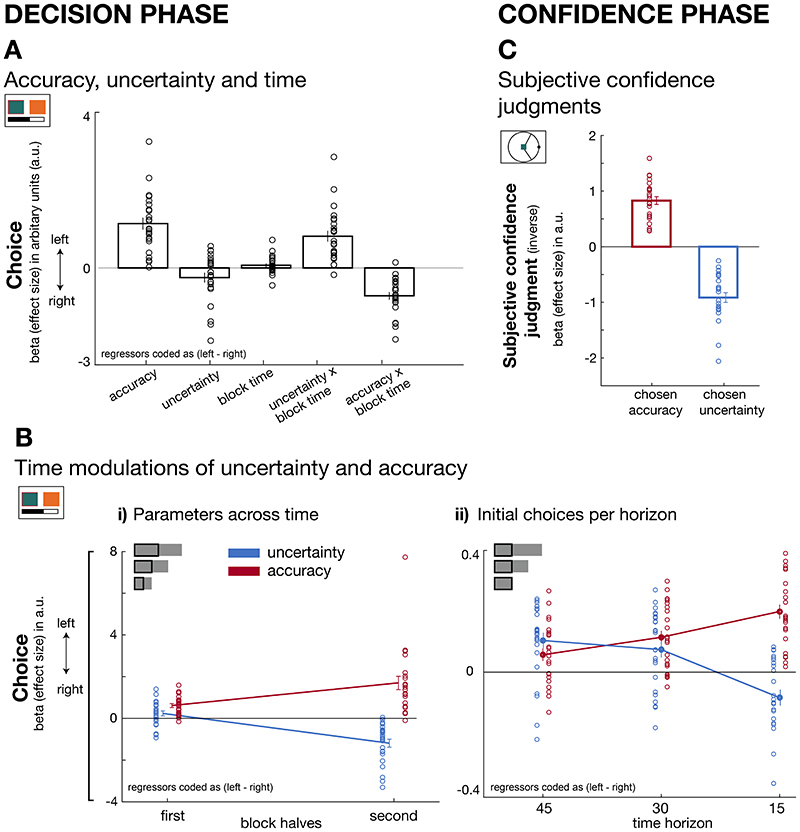
To test the first hypothesis, we applied a logistic general linear model (GLM, see GLM1 in Methods) to participants’ selections during the decision phase and then averaged beta weights across participants (Figure 3A, Supplementary Figure 1). Regressors of interest (accuracy and uncertainty) were coded as the difference between left and right predictors to predict leftward selections. As would be expected if participants were attempting to maximize payoff, participants generally sought out accurate predictors (main effect of accuracy: t(23)=7.5, p<0.001, d=1.53, 95% confidence interval=[0.82 1.45]). There was no credible evidence that uncertainty impacted choice behaviour (t(23)=-1.9, p= 0.07, d=-0.39,95% confidence interval=[-0.51 0.018], Bayes factor₁₀=1.05, %error=1.1017e-4). Next, to examine the time-dependent effect of uncertainty and accuracy on selection, we included the percentage of trials remaining in a block (referred to as ‘block time’) into the GLM model and examined its interaction with accuracy and uncertainty. Participants alternated between behavioural modes of exploration and exploitation by integrating information about the remaining trials into their predictor selections: a positive interaction term between uncertainty and block time (t(23)=5.8, p<0.001, d=1.18,95% confidence interval=[0.53 1.1]) showed that uncertain sources were explored when many trials remained. By contrast, a negative interaction term between accuracy and block time indicated that, as time passed, choices were increasingly directed towards accurate predictors (accuracy × block time interaction: t(23)=7.5, p<0.001, d=-1.53,95% confidence interval=[-0.91 -0.52]; Figure 3A).

Figure 3. Dissociable effects of accuracy and uncertainty on predictor selections and subjective confidence judgments.

(A) Decision phase. By using logistic GLM analyses we predict leftward predictor selection as a function of several variables (coded as left minus right). In general, participants preferred accurate predictors (accuracy: t(23)=7.5, p<0.001, d=1.52,95% confidence interval=[0.8 1.45]). There was no credible evidence for an uncertainty effect on behaviour (t(23)=-1.9, p= 0.07, d=-0.39,95% confidence interval=[-0.51 0.018], Bayes factor₁₀=1.05, %error=1.1017e-4). However, uncertainty and accuracy exerted different effects depending on when choices were made: uncertain predictors were explored when many trials remained (positive interaction term with percentage of remaining trials, i.e. block time; t(23)=5.8, p<0.001, d=1.18,95% confidence interval=[0.53 1.1]), whereas decisions were accuracy-driven as the end of a block approached (negative interaction effect with block time; t(23)=7.5, p<0.001, d=-1.53,95% confidence interval=[-0.91 -0.52]). (B) Decision phase. (B-i) Trials were binned into first and second halves of each block (independent of time horizon length) to examine the interaction effects shown in panel A. Earlier choices (i.e. first half) were more uncertainty-driven compared to later (i.e. second half) choices when uncertainty was avoided (paired-test early vs late: t(23) = -8.1, p<0.001, d=1.66, 95%confidence interval=[1.06 1.8]). In contrast, accuracy determined choices throughout both early and late block halves, but increasingly so in the second half (paired t-test early vs late: t(23) =-4.2, p<0.001, d=-0.85,95%confidence interval=[-1.63 -0.55]). Both accuracy and uncertainty changed differently across block halves (paired t-test between differences of block halves for accuracy and uncertainty: t(23) = -8.1, p<0.001, d=-1.7, 95% confidence interval =[-2.27 -1.02]). (B-ii) Accuracy and uncertainty effects on choice also varied as a function of how many trials still remained within a block: differences in the initial choice patterns (first 15 trials; see inset) across horizons showed that the exploration of uncertain predictors was more pronounced when horizons were longer while shorter horizons demanded more rapid exploitation of predictors estimated as most accurate (3x2 ANOVA: F(2,46)=36.7, p<0.001, η²=0.62). (C) Confidence phase. Trial-by-trial confidence judgments increased (i.e. the confidence interval size decreased) when selecting predictors that were believed to be accurate (t(23)=11.7, p<0.001, d=2.4, 95%confidence interval=[0.66 0.98]) but decreased when predictors were believed to be uncertain according to the Bayesian model (t(23)=-10.4, p<0.001, d=-2.12,95% confidence interval=[-1.1 -0.73]. Note that we used the inverse of the confidence interval such that a greater confidence index also represents higher confidence. (n = 24; error bars are SEM across participants).

In a follow-up analysis, we further examined the interaction effects. We binned trials into those that occurred in the first and second halves of each time horizon (Figure 3B-i). A logistic GLM with accuracy and uncertainty as regressors was fitted to both halves of each block’s trials. Once again we found that decisions were influenced by both factors but in dynamically distinct ways (paired t-test between the differences of block halves for accuracy and uncertainty: t(23) = -8.1, p<0.001, d=-1.7, 95% confidence interval =[-2.27 -1.02]; Figure 3B-i). Uncertain predictors were more likely to be sought out early compared to late in a block (paired t-test early vs late: uncertainty (t(23)=-8.1, p<0.001, d=1.66,95% confidence interval=[1.06 1.8]): while during the first half there was only anecdotal support for the interpretation that participants sought out uncertain predictors (positive uncertainty effect in half 1: t(23)=2, p =0.057, d=0.41, 95% confidence interval=[-0.007 0.48], Bayes factor₁₀=1.18, %error=9.954e-5), during the second half of blocks, uncertain predictors were avoided (negative uncertainty effect in half 2: t(23)=-6.2, p<0.001, d=-1.27,95% confidence interval=[-1.59 -0.79]). Accurate predictors were preferred to inaccurate ones and this was increasingly the case in the second half of the blocks (paired t-test early vs late time points accuracy: t(23)=-4.2, p<0.001, d=-0.85,95% confidence interval=[-1.63 -0.55]). These results replicated when regressors were normalised across or within blocks.

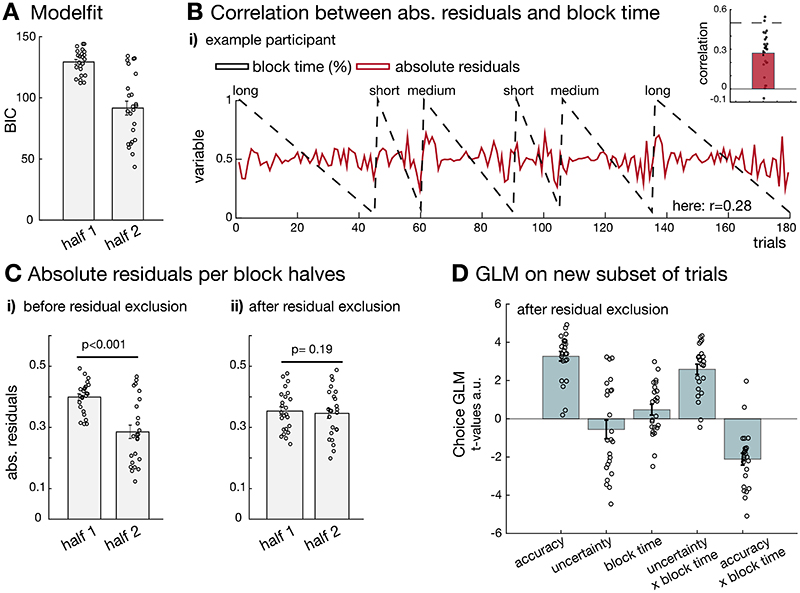
In response to the reviewers’ comments, we considered the possibility that such a result might have arisen because the overall model fit was better for either the first or second half of the block. It is important to consider differences in model fit across sets of trials (or participants) because a poor model fit might indicate that the model is not appropriate for the behaviour under investigation in one part of the data. However, a priori such an argument would predict that an effect, such as uncertainty, would be stronger in the part of the data that was better fit by the model than in the part worse fit by the model; it cannot predict a polarity change in the uncertainty prediction effects when moving from exploration (earlier trials) to exploitation (later trials). We excluded trials on the basis of the trial wise choice residuals so that both first and second block halves were no longer different in their residual variance (Extended Data Figure 3). Even under such conditions, we were able to replicate evidence for the same pattern of results (Extended Data Figure 3D). Moreover, below we show that several brain regions only represent uncertainty prediction difference during exploration and not exploitation (Supplementary Figure 7, in particular 7B) even though model fits were better for later compared to earlier phases.

Next, we tested our second hypothesis that the degree of exploration during initial choices should be stronger in longer time horizons, i.e. if subsequent encounters with the same predictor are expected to be more frequent. We compared choices during the first 15 trials across all time horizons by fitting a linear robust GLM to data from each time horizon. The first 15 trials in all three horizons were identical in their order presentation and importantly, their trial-by-trial target estimates were drawn from a Gaussian distribution with the same parameters (sigma of either 50 or 70). As predicted, participants adjusted their behavioural strategy in the initial trials according to the horizon type: participants explored more in longer than shorter horizons and in a complementary manner, shorter horizons led to a rapid convergence onto accurate predictors (3x2 repeated measures ANOVA with horizon (long, medium, short) and variable (accuracy, uncertainty); horizon × variable interaction: F(2,46)=36.7, p<0.001, η²=0.61, assumption of sphericity is met with Mauchly’s test: x²(2)=0.28, p=0.87; Figure 3B-ii). Uncertain predictors were particularly sought out during initial trials within long and medium time horizons (long horizon: t(23)=4, p<0.001, d=0.8,95% confidence interval=[0.053 0.164]; medium horizon: t(23)=2.8, p=0.009, d=0.56,95% confidence interval=[0.02 0.13]).

So far we have shown that model-derived estimates of the accuracy and uncertainty determined participants selections between predictors. Next, we examined whether participants also relied on both of these estimates when making their subjective confidence report during the second phase of each trial (the confidence phase in Figure 1A). Accuracy reflects a point-estimate of the most likely angular error between target and the predictor’s estimate and should therefore have an impact on the interval size the participants use to indicate their subjective confidence during the confidence phase. Indeed, participants indicated higher confidence for predictors that were believed to be accurate (t(23)=11.7, p<0.001, d=2.4,95% confidence interval=[0.66 0.98]). The Bayesian model also suggests that participants form a representation about other possible angular errors that might underlie a predictor’s distribution (i.e. the width of the belief distribution). If participants are very uncertain in their point-estimate of the angular error (i.e. if the Bayesian belief distribution is very wide), then they should report a larger interval size to guarantee that the target falls within the interval. In tandem with above effect of accuracy, participants were less confident and selected a larger interval size when they evaluated predictors they believed were uncertain (uncertainty: t(23)=-10.4, p<0.001, d=-2.12,95% confidence interval=[-1.1 -0.73]; Figure 3C).

In summary, accuracy, uncertainty, and a time modulation of both effects influenced participants’ predictor selections. Early selections were uncertainty-driven explorative selections and occurred particularly when time horizons were longer. Later selections were of exploitative selections, directed towards accurate and away from uncertain predictors. The exploratory behaviour we identify cannot simply be the result of noise in the learning process⁹; people are more exploratory when the future time horizon is longer even if learning opportunities are identical. Moreover, we show that our model-derived estimates of participants’ beliefs about the accuracy of a predictor and uncertainty about those beliefs correspond to features of their subjective confidence judgments.

Polarity of uncertainty decision signal in vmPFC changes from exploration to exploitation

Our behavioural analyses show that participants incorporated the uncertainty in their beliefs when selecting between two predictors. We went on to examine the coding of uncertainty in the brain during predictor selection (fMRI-GLM1, see Methods). Our variable of interest was the difference in uncertainty (as captured by our model) between the chosen and unchosen predictors, i.e. “uncertainty prediction difference”. This is similar to studies of value-guided decision-making, where the difference in value between the option chosen and the option rejected is regressed against the BOLD signal. A value difference signal often prominently implicates the vmPFC in decision making processes^10–14,17.

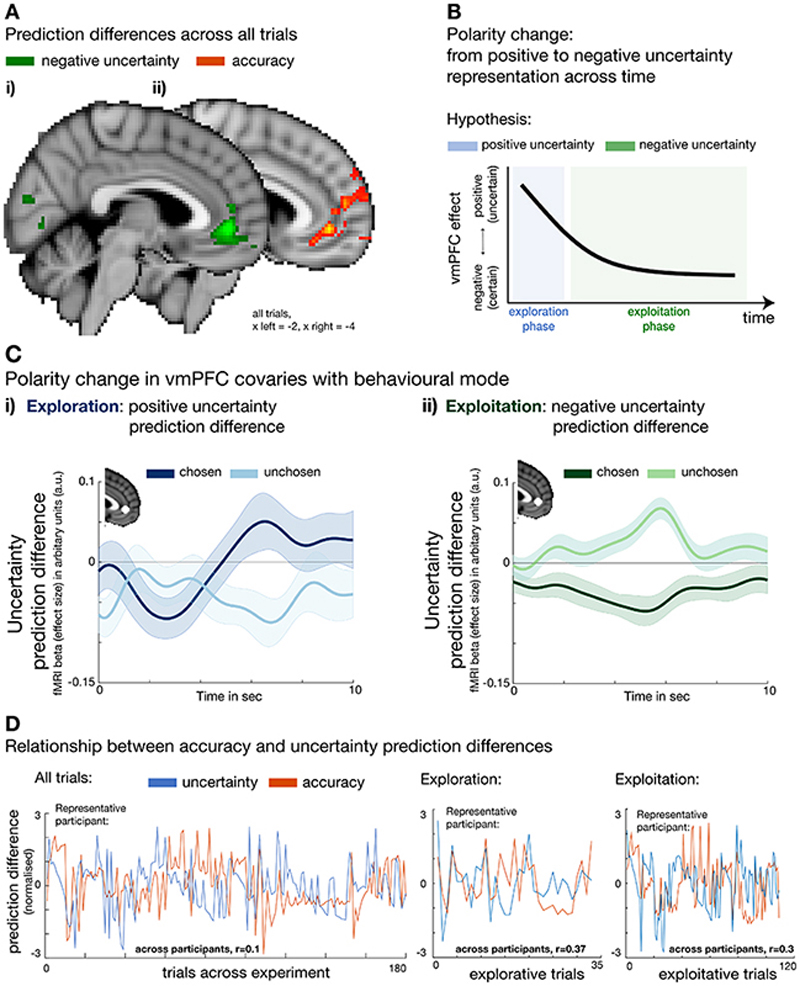
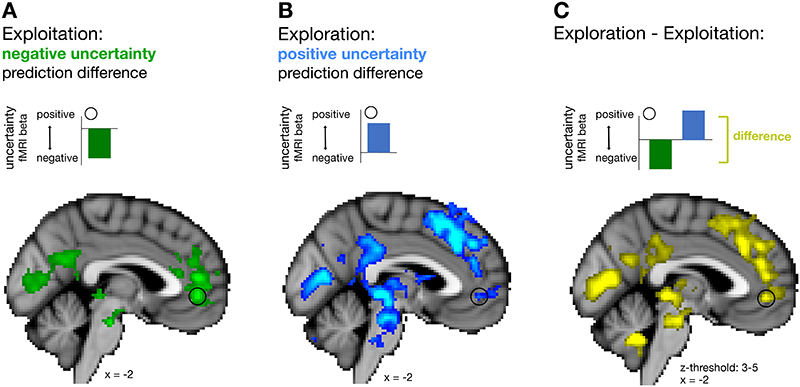
When testing for an uncertainty prediction difference signal across all trials, we found a negative uncertainty prediction difference in vmPFC (whole brain cluster-corrected; Figure 4A-i, Supplementary Table 1). This neural effect was in line with the negative effect uncertainty exerted on choice behaviour towards the end of a block when participants avoided uncertain predictors or in other words, sought out certain predictors. In addition, we also found an “accuracy prediction difference” in a similar anatomical location in vmPFC (Figure 4A-ii, Supplementary Table 1). Again, this accords with participants’ general preference for selecting accurate predictors to help them find the target location. To additionally show that both accuracy and uncertainty prediction differences were encoded in a similar anatomical region, we derived a domain general prediction difference by first, calculating the mean across both absolute contrasts “((chosen uncertainty – unchosen uncertainty) + (chosen accuracy – unchosen accuracy))” and second, by deriving a conjunction between both absolute contrasts (Supplementary Figure 3A, 3B, respectively, and Supplementary Table 3). A domain general prediction difference peaked within vmPFC. Accuracy and uncertainty prediction differences are independent variables sharing across all trials, on average, 0.01% of their variance (0.137% and 0.09 % of their variance is shared when exploration and exploitation trials are each considered separately; Figure 4D) suggesting both variables have independent effects on activity but within the same part of vmPFC (for more details on regressor correlations, see Supplementary Figures 1,2). These findings underline the role of vmPFC in guiding predictor selection as a function of both the differences in accuracy and uncertainty of the predictors.

Figure 4. Modulation of uncertainty prediction difference in vmPFC according to behavioural mode.

(A) Across all trials, a negative uncertainty (i) and positive accuracy (ii) prediction differences covaried with activation in vmPFC. (B) We found a polarity change in the impact uncertainty exerted on predictor selection at a behavioural level; initial trials in longer horizons were more likely to be explorative and directed towards more uncertain predictors while behaviour in later trials was more exploitative and directed away from uncertain predictors, in other words they selected certain predictors (see labels on y-axis). We tested for a neural uncertainty polarity change in vmPFC comparing behavioural modes of exploration and exploitation, respectively, representing a positive and then negative uncertainty prediction difference. (C) Time courses extracted from vmPFC for both chosen and unchosen components of an uncertainty prediction difference signal during exploration (i) and exploitation (ii). VmPFC BOLD activity changed in accordance with the behavioural results; it transitioned from activity positively related to uncertainty prediction difference (positively encoding the uncertainty of the chosen predictor as opposed to the unchosen predictor) during initial choices to activity negatively related to uncertainty prediction difference (negatively encoding the uncertainty of the chosen predictor as opposed to the unchosen predictor) in later trials. All effects were time-locked to the decision phase. (n = 24; error bars are SEM across participants; whole-brain effects family-wise error cluster corrected with z > 2.3 and p < 0.05). (D) The relationship between accuracy and uncertainty prediction differences used for all neural analyses across all trials (left) exploration trials (centre), and exploitation trials (right). Average correlations between accuracy and uncertainty prediction differences across all participants are reported at the bottom of each panel, while panels show variables across time taken from a representative participant for each analysis. Accuracy and uncertainty prediction differences are similarly decorrelated in all other analyses (for details on correlation, see Supplementary Figure 1, 2).

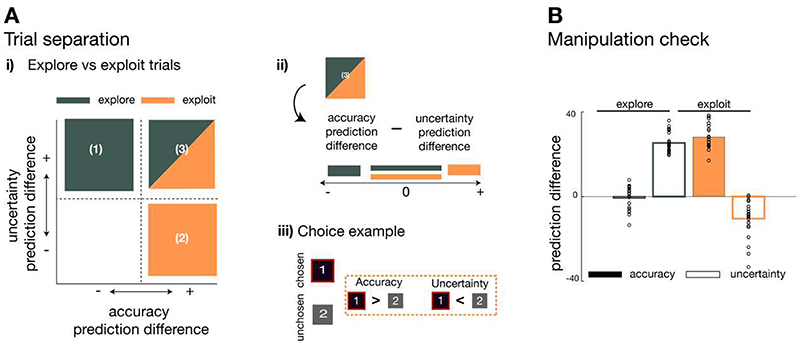
Having identified vmPFC as representing a negative uncertainty prediction difference across all trials, we then went on to test whether this signal was modulated by distinct behavioural modes of exploration and exploitation. We have shown that uncertainty tended to drive exploration of predictors at the beginnings of blocks; at that time, selections were directed to uncertain predictors (i.e. there was a positive effect of uncertainty during the first 15 trials in medium and long horizons, Figure 3B-ii). Then, over the course of the block, participants became increasingly uncertainty avoiding shown by a negative effect of uncertainty on choice behaviour. We refer to this pattern of change as an “uncertainty polarity change”. We investigated whether there was a brain region with similar characteristics: transitioning from encoding a positive to negative uncertainty-based prediction difference as participants switched from exploration to exploitation (Figure 4B). To test this hypothesis, we made use of the fact that our computational model allowed us to classify individual trials into exploration or exploitation according to the selection made on each trial: an exploitative selection was defined as one in which the more accurate and less uncertain predictor was selected while a directed uncertainty-guided explorative selection was defined as the opposite: a trial in which the more inaccurate and uncertain predictor was chosen (Extended Data Figure 4). Importantly this is distinct to other types of decision that might initially appear exploratory, because the less accurate predictor was chosen, but which may simply be due to noise in the learning or decision process^9,22. On such trials, selection is not just of the less accurate predictor but are also made with certainty (Supplementary Figure 4A).

To test for a neural polarity change of uncertainty prediction difference, we extracted time courses from an independent region of interest (ROI) associated with the accuracy prediction difference effect across all trials. This ensured that we did not bias the analysis towards finding an effect in an area that was previously associated with the uncertainty prediction difference. First, we used a time course analysis to extract both components of the uncertainty prediction difference signal (variance in activity related to the chosen predictor and variance in activity related to the unchosen predictor) during exploration and exploitation. Activation in vmPFC covaried with a decision signal that changed its polarity depending on the current behavioural mode: during exploitation, vmPFC carried a decision signal that reflected a negative uncertainty prediction difference (negatively encoding the uncertainty of the chosen predictor as opposed to the unchosen predictor; Figure 4C-ii); in exploration, when behaviour was guided by uncertainty, vmPFC activity carried a positive uncertainty prediction difference (positively encoding the uncertainty of the chosen predictor as opposed to the unchosen predictor; Figure 4C-i). Given that the same variable is reflected in both increase and decrease in activity at different task stages suggests an important change in the nature of the representation. In response to reviewers’ comments, we verified the robustness of these results when the precise criteria for drawing boundaries between exploration/ exploitation categories were modified (Supplementary Figure 8). It might be argued that the vmPFC activity pattern simply reflects absolute uncertainty differences between the presented predictors irrespective of behavioural mode (exploration versus exploitation). We repeated the analysis and included the absolute uncertainty prediction difference as an additional regressor. Nevertheless, we replicated the uncertainty polarity change across modes in vmPFC (Supplementary Figure 5).

The trials we define as uncertainty-guided exploration trials are comparable to trials that have previously been described as directed explorative choices⁷. They are, however, hypothesized to be distinct to apparently random choice selections that may result simply from noise in the decision process²² or the learning process⁹. In the current experiment, random exploration trials were defined as ones on which participants selected predictors that they believed to be inaccurate with certainty (i.e. negative uncertainty) (Supplementary Figure 4A). While it is not possible to be sure that all uncertainty-guided exploration and all noise-based exploration trials are classified correctly, on average the classification should capture a potential difference in exploration type that may be associated with different neural mechanisms. To test this possibility we therefore, in addition examined vmPFC activity on random exploration trials. We extracted a time course from vmPFC associated with the previous cluster of accuracy prediction difference and tested for an uncertainty prediction difference during random exploratory trials. We tested beta weights extracted from the time course with a leave-one-out procedure and found that unlike on uncertainty-guided exploratory trials, there was no credible evidence that vmPFC represented uncertainty prediction difference during these random exploratory selections (Supplementary Figure 4B).

We have shown that behavioural modes were associated with different polarities of uncertainty representation in vmPFC. Next, we were interested in whether the different behavioural modes were associated with any distinct neural networks. We performed a whole-brain GLM of exploration and exploitation trials and focused again on the uncertainty prediction difference during the decision phase (fMRI-GLM2). During exploitation, we observed activity centred on vmPFC related to a negative uncertainty prediction difference (Figure 5A; Supplementary Table 2), confirming our previous findings. During exploration, a positive uncertainty prediction difference signal was represented in vmPFC, but also across an extensive network of brain regions, including dorsomedial frontal areas (Figure 5B). A direct contrast of activation patterns in exploration and exploitation trials confirmed these differences between behavioural modes (compare panels A, B, and C of Figure 5). Dorsal ACC (dACC) in particular has been associated with exploratory²² and foraging behaviour²³. We show that dACC represents uncertainty prediction differences during directed exploration (Figure 5B, Supplementary Figures 6, 7A-iii), but there was no credible evidence for such a representation during random exploration (Supplementary Figure 4B) or, unlike vmPFC, exploitation (Supplementary Figure 7B-iii). We also observed an uncertainty prediction difference in frontopolar cortex and dorsolateral prefrontal cortex (dlPFC), replicating results of previous exploration studies^24,25 (Supplementary Figure 7A). However, like dACC and other dorsomedial frontal areas, both dlPFC and frontopolar cortex have distinct profiles compared to vmPFC, as there was no credible evidence for a representation of uncertainty prediction difference during exploitation and hence unlike vmPFC did not show an uncertainty polarity change across behavioural modes (Supplementary Figure 7B).

Figure 5. Whole brain maps for uncertainty prediction difference during exploration and exploitation.

Illustrations above whole-brain images clarify the polarity (positive or negative) of the uncertainty prediction difference signal represented in vmPFC (indicated by the black circle) during exploitation, exploration and their contrast. (A) During exploitation, activity related to an uncertainty prediction difference was restricted to a region centred on vmPFC and was represented with a negative polarity (see inset). (B) However, during exploration uncertainty prediction difference was represented with a positive polarity and associated with an extended network including vmPFC but also dorsomedial frontal areas peaking in dorsal anterior cingulate cortex (dACC) (see also Supplementary Figure 6). (C) Difference in uncertainty prediction difference between exploration and exploitation. Contrasting activations between the behavioural modes of exploration and exploitation confirmed the presence of mode-specific (e.g. dACC) and mode-general (e.g. vmPFC) activations. Note that the sign of activation patterns resulting from a contrast between exploration and exploitation need to be interpreted with reference to the levels of activity found in the exploration and exploitation phases with respect to baseline (see illustration above each whole-brain map) (n = 24; whole-brain effects family-wise error cluster corrected with z > 2.3 and p < 0.05).

In summary, we have shown a polarity change in the influence that uncertainty in one’s belief exerts not just on behaviour but also on vmPFC activity. During exploitative modes, when differences in predictor certainty are the key decision variable, vmPFC reflects negative uncertainty prediction difference, but when participants are in an explorative mode, vmPFC activity reflects positive uncertainty prediction differences. During exploration, vmPFC is co-active with an extensive network of regions carrying a similar uncertainty-related signal.

Uncertainty-related signals in subcortical structures during exploration and exploitation

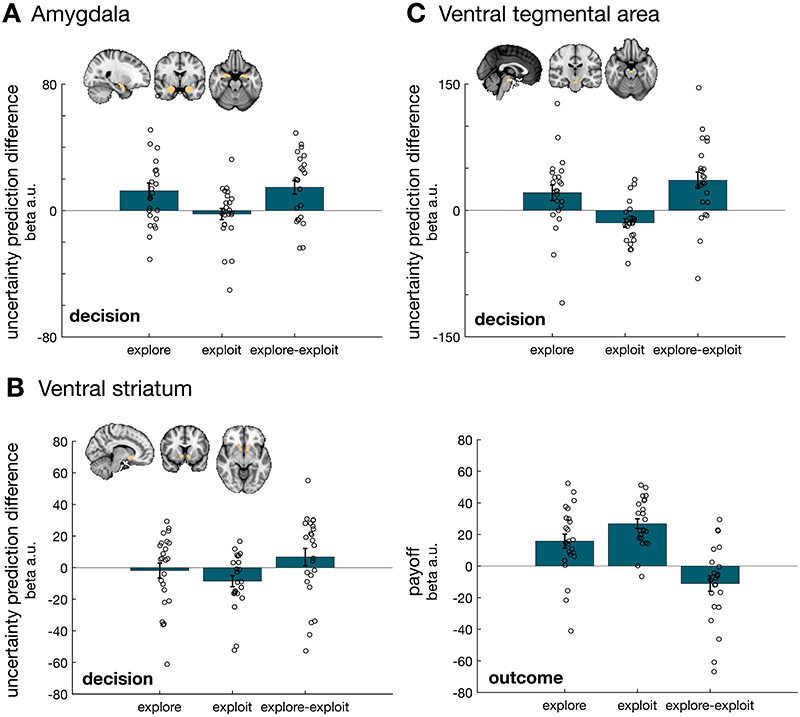
We used a region-of-interest approach to test for an uncertainty prediction difference in subcortical structures during both behavioural modes. We focused on amygdala and ventral striatum as they have been previously associated with modes of exploration and exploitation²⁶. We also focused on ventral tegmental area (VTA) which exhibited cluster-corrected positive and negative uncertainty prediction difference during exploration and exploitation respectively (Figure 5). All three subcortical regions represented uncertainty prediction difference during at least one behavioural mode – either exploration or exploitation – but with a different pattern of activation in each case: amygdala predominantly represented uncertainty prediction difference during exploration (Extended Data Figure 5A), while VS (Extended Data Figure 5B) activation was most apparent during exploitative phases when it reflected a negative uncertainty prediction difference. VTA activity suggested a representation of uncertainty prediction difference during both, exploration and exploitation in the decision phase (Extended Data Figure 5C). These patterns show that a network of areas including multiple cortical and subcortical areas represent uncertainty-related information during both exploration and exploitation. While it was not identical, the pattern in the VTA most closely resembled that seen in the vmPFC; it carried uncertainty signals that reversed in polarity between exploration and exploitation but there was no credible evidence for an accuracy-related signal during the transition phase between exploration and exploitation (see paragraph on transition between exploration and exploitation; t(23) = -0.97, p=0.35, d=-0.197,95% confidence interval=[-0.07 0.026], Bayes factor₁₀=0.325,%error=0.037). These analyses were conducted in response to the reviewers’ comments.

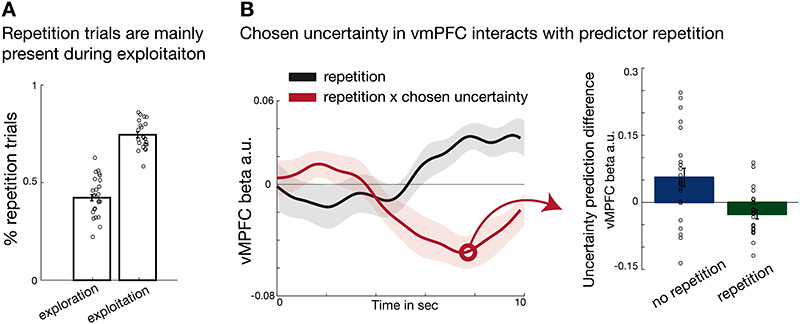
Uncertainty representation in vmPFC scales with predictor repetition

We have shown a polarity change in the effect of uncertainty on guiding behaviour and influencing vmPFC activity when comparing exploratory and exploitative behavioural modes. One possible way to interpret the negative uncertainty representation during exploitation is that vmPFC encodes a default choice^21,23,27. In the context of the current task, an effective default choice is repetition of previously made choices particularly when there has been certainty about the predictor’s accuracy. We therefore asked whether there was evidence of a higher frequency of choice repetition on exploitation as opposed to exploration trials; this was indeed the case (paired t-test explore vs exploit: t(23)=-16.2, p <0.001, d= -3.3,95% confidence interval = [-0.36 -0.28]; Figure 6A). Moreover, activity in the same location in vmPFC reflected whether, on each trial, participants would repeat a choice they had made the last time it was offered. There was more activity in vmPFC when participants were repeating a choice made previously (repetition: t(23) = 4, p <0.001, d= 0.8,95% confidence interval=[0.017 0.06]; Figure 6B, grey time course). In addition, the effect was greater when there was a stronger negative uncertainty signal (repetition × chosen uncertainty: t(23) = -3.4216, p =0.002, d= -0.7,95% confidence interval=[-0.07 -0.02], Figure 6B, red time course): in other words, the repetition signal was greater when there was more certainty about the selected predictor during repetitive trials compared to non-repetitive trials during which they switched to a new choice that had not been made on a previous trial, a behaviour more likely to occur during exploration (Figure 6A), then vmPFC had the opposite polarity (positively related to uncertainty; Figure 6B, right panel).

Figure 6. Interaction of repetition and uncertainty representation in vmPFC.

(A) The percentage of choice repetitions during exploitation was significantly higher than during exploration (paired t-test explore vs exploit: t(23)=-16.2, p <0.001, d= -3.3,95% confidence interval = [-0.36 -0.28]). Also note that within the two phases, this indicates a relative predominance of repetitions versus no repetitions in exploitation, but a relative predominance of no repetition choices versus repetitions in exploration. (B) VmPFC activity increased when participants repeated the same predictor selection as they had made on the last encounter with the predictor (grey time course; repetition is coded as “repeat – no repeat”; t(23) = 4, p <0.001, d= 0.8,95% confidence interval=[0.017 0.06]). Moreover, we found a significant interaction effect of repetition × chosen uncertainty (red time course; t(23) = -3.4, p =0.002, d= -0.7,95% confidence interval=[-0.07 -0.02]). The interaction effect is illustrated in the right panel by decomposing it into the binned effects of chosen uncertainty during “repetition” and “no repetition” trials at the time of the interaction effect time course peak. This indicates that the increase in BOLD response accompanying choice repetition was even stronger if participants were very certain about their choice (i.e. negative uncertainty during repetition; green bar in right panel); whereas in case of switching choices, the BOLD signal increased as a function of chosen uncertainty (i.e. positive uncertainty; blue bar in right panel). Note that the statistical test comparing the blue and green bars was performed in the leftward panel of B by testing the interaction effect against zero (n = 24; error bars are SEM across participants).

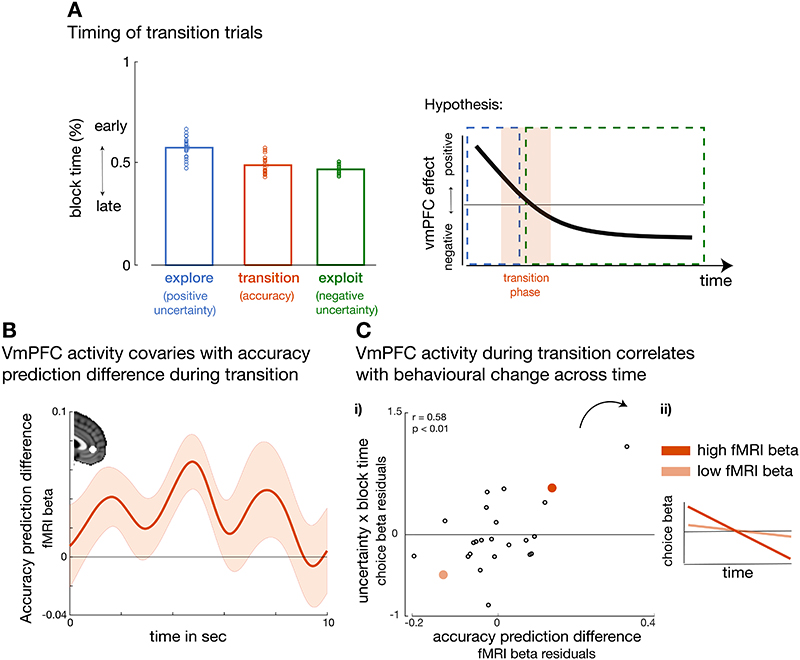
The transition from positive to negative uncertainty representations is accompanied by the processing of accuracy between predictors

So far we have shown that the transition from exploration to exploitation and choice repetition behaviour is accompanied by a change in the polarity of uncertainty signals and emergence of choice repetition signals in vmPFC. However, it remains unclear how the transition between directing behaviour towards uncertain and then certain predictors occurs as the behavioural mode shifts from exploration to exploitation. It is possible that, after initial exploration but before repetitively choosing certain predictors there might be a phase in which participants focus on how well – how accurately – each predictor estimates the target’s location (Figure 7A, see illustration). Such a period might naturally precede a period when the most accurate predictors are identified and continuously chosen. During such a transition period, one would expect neural activity correlating with an accuracy prediction difference, the difference between the accuracy estimates associated with the chosen and unchosen predictors. Moreover, because participants are transitioning from positive to negative uncertainty-guided behaviour, the accuracy estimates held by participants for the chosen and unchosen predictors should be close in value. This would suggest that participants have no strict preference between predictors yet, as they are still learning about them. We identified a new subset of trials by selecting trials with accuracy prediction differences close in value (Supplementary Figure 9A). We hypothesized that vmPFC computes decision variables that are most relevant for guiding choice behaviour in the current context, therefore when the accuracy difference is small in value, participants need to carefully compare accuracy estimates between predictors to make their choice. First, we tested whether these trials occurred in time between the exploration and exploitation periods that we had previously identified. Indeed, these transition trials occurred later in time compared to previously defined explorative choices (paired t-test, explore vs. transition: t(23)=6, p<0.001, d =1.2, 95%confidence interval= [0.056 0.12]) and earlier in time compared to exploitative choices (paired t-test, exploit vs. transition: t(23)=-2.8, p=0.01, d =-0.57, 95%confidence interval= [-0.04 -0.006]) (Figure 7A).

Figure 7. Accuracy processing mediates uncertainty polarity change from exploration to exploitation.

(A)Transition trials (Supplementary Figure 9A) occurred later than exploratory selections and earlier than exploitative selections (left panel) (explore vs transition: t(23)=6, p<0.001, d=1.2, 95%confidence interval= [0.056 0.12]; transition vs exploit: t(23)=-2.8, p=0.01, d=-0.57, 95%confidence interval= [-0.04 -0.006]). We hypothesized activation in vmPFC to be correlated with positive uncertainty, accuracy and negative uncertainty prediction differences between predictors, but at different times during the experiment (see illustration, right panel). (B) During transition trials, activation in vmPFC covaried with the difference in the accuracy between the chosen and unchosen predictor, i.e. accuracy prediction difference (t(23) = 3.5, p= 0.002, d=0.71,95% confidence interval=[0.03 0.1]. (C-i) Participants who showed a stronger vmPFC accuracy prediction difference during the transition period (variability around time course peak from panel b), also integrated more drastically the uncertainty between predictors across time into their choice behaviour (uncertainty × block time from Figure 3A; r= 0.58, p= 0.007, 95% confidence interval=[0.23 0.8]). (ii) For illustration, this means that participants with stronger accuracy-related vmPFC activation had a stronger change in integrating uncertainty across time, i.e. a stronger slope in the uncertainty × block time effect. The illustration depicts two example participants, dark orange indicates a subject with both a strong vmPFC accuracy activation and pronounced behavioural change in how uncertainty was used to drive choice behaviour. By contrast, the participant indicated in light orange shows a weak vmPFC BOLD accuracy effect and only a small change in how uncertainty was used over time. These findings support the idea that the transition between positive uncertainty-driven exploration to negative uncertainty-driven exploitation is mediated by representing the accuracy between predictors. (n = 24; error bars are SEM across participants).

We then examined whether vmPFC activity reflected the accuracy prediction difference during this transitional period. To test for this effect, we chose an independent ROI in vmPFC extracted from the cluster-corrected uncertainty prediction difference effect across all trials (Figure 4A). As predicted, activation in vmPFC correlated with an accuracy prediction difference during this transitional phase (t(23) = 3.5, p= 0.002, d=0.71,95% confidence interval=[0.03 0.1]; Figure 7B). In further support of the suggestion that accuracy processing is especially prominent during this transition phase (in which chosen and unchosen predictors have similar accuracy values), we found no credible evidence of an accuracy prediction difference signal in vmPFC when very inaccurate predictors (accuracy prediction difference: t(23) = -0.84, p =0.41, d=-0.17, 95%confidence interval=[-0.13 0.055], Bayes factor₁₀=0.296,%error=0.037; Supplementary Figure 9B-i) or very accurate predictors were selected (accuracy prediction difference: t(23) = -1.3, p =0.21, d=-0.27, 95% confidence interval=[-0.06 0.02], Bayes factor₁₀=0.447,%error=1.178e-4; Supplementary Figure 9B-ii). This pattern of results suggests that the periods in which vmPFC activity reflects first positive and then negative uncertainty prediction difference are separated by a transition period in which vmPFC reflects the accuracy estimate of the predictor chosen to guide behaviour.

We tested whether activation during the transition phase was related to behavioural changes across time – from positive to negative uncertainty-driven behaviour – when selecting between predictors. As the transition phase bridges exploration (positive uncertainty) to exploitation (negative uncertainty), we tested whether accuracy-related vmPFC activation during the transition period was related to a behavioural effect of uncertainty that changes across time, i.e. the interaction term uncertainty × block time (see behavioural choice GLM, Figure 3A). We used a partial correlation analysis to examine the relationship between each individual’s accuracy-related vmPFC activity extracted from the vmPFC cluster (accuracy prediction difference effect across all trials) and the behavioural transition from positive to negative uncertainty-driven predictor selection. In the same analysis, we controlled for all other behavioural variables included in the previous GLM1 (Figure 3A). We found that accuracy prediction difference-related activity in vmPFC during the transition period was positively correlated with uncertainty × block time (r= 0.58, p= 0.007, 95% confidence interval= [0.23 0.8]; Figure 7C-i). That is, the larger the vmPFC signature encoding accuracy prediction difference during the transition period, the stronger the behavioural transition from positive to negative uncertainty-driven behaviour over the course of a block (Figure 7C-ii). Notably, these results were not confounded by variation across participants’ in the number of transition trials that were identified; a partial correlation that controlled additionally for the number of transition trials remained significant (r=0.57, p=0.01, 95% confidence interval= [0.22 0.79]).

This result suggests that a transition phase during which the accuracy between predictors is represented in vmPFC may facilitate a neural polarity change from first representing positive uncertainty when selections are exploratory to later, representing negative uncertainty when repeatedly selecting the same certain predictor during exploitation (Figure 8). Participants exhibiting stronger predictor accuracy signals in vmPFC during the transition period exhibited a more drastic change from positive to negative uncertainty-driven behaviour.

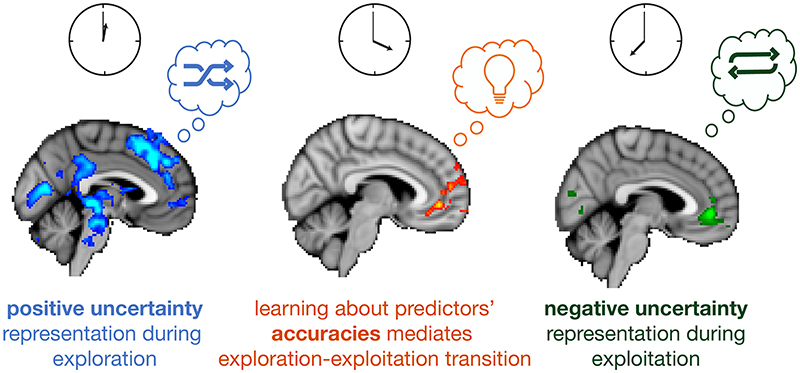
Figure 8. Summary. From exploration to exploitation: polarity of subjective uncertainty in vmPFC changes with behavioural mode.

At the beginning of a block, choices are exploratory and directed towards uncertain predictors (like a shuffle mode when playing music, left panel). VmPFC and an extended network centred in dACC represent the difference in uncertainty between the predictors that might be selected. With time passing, participants learn about the predictors’ accuracy through observing how well they predict an outcome. A participant’s belief in the accuracy of the predictors exerts the predominant influence on vmPFC activity during this transition phase (middle panel). Towards the end of a block, vmPFC activity represents the difference in negative uncertainty, in other words the certainty between predictors. In this exploitative period, choices are repeatedly directed towards certain predictors (like a repeat mode, right panel). We show that vmPFC carries information about a multiplicity of decision variables, the strength and polarity of which vary according to their relevance for the current context of exploration, exploitation or their transition.

Discussion

Humans select between multiple information sources that can predict outcomes in an adaptive manner that enables them efficiently both to gather information about the predictors and to use that information to make choices. Using Bayesian modelling, we derived estimates of two kinds of beliefs that simultaneously influenced choice and neural activity. To select between predictors, participants integrated beliefs about how accurately a predictor predicted the target (“accuracy”) and beliefs about the uncertainty in that estimate (“uncertainty”). How much these beliefs influenced predictor selection depended on how many opportunities participants had had to learn about the predictors already⁷. Behaviourally, participants initially gathered information about available predictors by selecting more uncertain predictors, while over time they converged towards accurate and certain (i.e. the negative uncertainty effect) predictors. However, importantly the influence of accuracy beliefs and their uncertainty depended on the future time horizon; participants explored uncertain predictors more during initial phases of a block when they knew that they had a longer time horizon remaining to exploit the knowledge gained. Behaviour that initially appears uncertainty-directed and exploratory in nature may simply reflect noise in the decision process²² or the learning process⁹ but in the present study behaviour is uncertainty seeking and exploratory in nature because it manifests to a greater degree when the future time horizon is longer even when the decision context and past learning opportunities remain the same.

Similar flexibility was also observed on a neural level. VmPFC activity reflected different decision variables at different times in a manner that reflected their relevance for the current context of exploration or exploitation. Behaviour and neural activity in vmPFC were not determined by only exploration or exploitation, but rather it reflected several different variables but only when they were relevant to the current mode.

Our findings are related to studies of attention during the learning of cue-outcome relationships. Here, two influential models have made opposite predictions: one model suggests that selective attention is driven by cues that are most predictive of reward^2,5, reminiscent of the accuracy-driven, repetition-driven, and certainty-driven predictor selections in the present study. The second model assumes that the uncertainty of a predictor is crucial for selective attention⁶. By using a Bayesian model to dissociate participants’ beliefs about accuracy and uncertainty, we were able to show that in fact, both are important to determine whether a predictor will be selected to guide behaviour. Importantly, the magnitude of their influence on predictor selection depends on their relevance to the current context which varies across time.

In accordance with the behavioural results, we found that neural activity reflected predictor differences. Activity in vmPFC reflected the difference between the selected and rejected predictor, in terms of the key feature that was currently of relevance for guiding behaviour: first positive uncertainty, then accuracy, and then negative uncertainty. Previous studies have often focused on the manner in which activation in vmPFC is correlated with differences in the reward values of chosen and rejected choices^11,28,29. In such studies, differences in the reward values associated with the choices constitute the evidence in favour of taking one choice rather than the other. Although we focus on vmPFC’s role in representing information-based belief estimates of accuracy and uncertainty, on sub-threshold vmPFC also represented the difference in expected value between predictors (Extended Data Figure 2). Here, we show when selecting between predictors to guide behaviour, multiple types of information, rather than just a single one, can be of importance. This can be linked to the idea that vmPFC integrates a diverse set of variables that are currently choice-relevant³⁰ and to recent evidence that exploitation and exploration are not simply behaviours that are controlled by completely separate neural circuits but rather they are, at least in part, controlled by changes in mode within neural structures²⁶. An alternative interpretation could be that vmPFC’s signal represents variables that are relevant for long-term reward expectation: early uncertainty-driven exploration is beneficial for reward maximization during later exploitative phases. Although we do not differentiate between immediate or long-term representations, other studies have shown that dACC in particular represents value expectations modulated by different timescales^8,31–33.

Our results also suggest that vmPFC does not guide behaviour in isolation, but that there are additional broader differences in the recruitment of choice-relevant brain networks between exploration and exploitation. Although activation associated with negative uncertainty prediction difference during exploitation was mainly present in vmPFC, positive uncertainty prediction difference during exploration was associated with a wider network including areas such as dACC, dlPFC, and frontopolar cortex that have previously been associated with exploration^24,25. Activation in dACC has often been related to behavioural adaptation and the search for better alternatives, for example during foraging^{8,22,23,33–40}and to the update of internal models during environmental changes^41–43. Our results may therefore suggest that in some cases during exploration wider updates in decision networks occur that encompass both vmPFC, dACC and prefrontal areas in a similar fashion. Nevertheless, it is important to remember that the pattern of activity in vmPFC, when considered across both behavioural modes, is different from that seen in dACC, dlPFC, and frontopolar cortex where activity only reflects uncertainty during exploration while the change in the polarity of positive to negative uncertainty-related activation, between exploration and exploitation, only occurs in vmPFC. Additionally, vmPFC did not carry a clear uncertainty signal during random exploration as opposed to uncertainty-guided exploration. An important new finding is that effective exploratory behaviour may simply emerge from noise in the learning process⁹ and this may impact on activity in brain areas such as dACC that reflect choice value learning at multiple time scales^31,33,44. However, the current findings suggest that an uncertainty signal is also carried in these areas when it is relevant for behaviour.

A related line of research supports the notion that vmPFC not only represents the value difference between choice options, but also a second-order representation, that is one’s own confidence in a choice^13,45. These results are compatible with our finding that both accuracy and uncertainty are represented in vmPFC. However, we show in addition that the polarity of the uncertainty representation (which is a second-order representation similar to confidence) in vmPFC changes depending on the behavioural mode. This suggests that in some cases second-order representations in vmPFC are themselves choice-guiding and highly context sensitive. The change in signal in vmPFC from signalling positive to negative uncertainty prediction differences, i.e. uncertainty polarity change in vmPFC, might be related to the presence of a learning phase during which predictors’ accuracies are compared. We identified a transition phase between exploration/exploitation periods, when no clear preference had yet been formed for predictors. At that point, we observed that vmPFC most prominently reflected participants’ accuracy estimates for the predictors. Notably, the accuracy effect in vmPFC during the transition phase was related to the degree of change from positive to negative uncertainty-driven behaviour exhibited by each participant: participants exhibiting stronger accuracy-related vmPFC activation during the transition period also showed more drastic behavioural changes.

Although predictor selections were accuracy-guided throughout the task, we did not observe an accuracy prediction difference in vmPFC during the final exploitation stages of predictor selection. This is similar to the way in which vmPFC activity related to value comparison during choice selection has been shown to be stronger during earlier compared to later phases of a task²⁸. A predictor accuracy representation was present in vmPFC during the transition phase between exploration and exploitation when accuracy estimates between predictors were close in value, meaning that a careful comparison between predictors was required to guide predictor selections successfully. In comparison, during exploitative trials participants established which predictors were accurate resulting in repeated selections of the same predictors. At that point vmPFC activity reflected this repetitive mode of decision making and it did so in a manner that interacted with the representation of certainty (i.e. negative uncertainty) about the predictor.

Summary

In summary, the combination of computational modelling and fMRI made it possible to show that beliefs concerning the accuracy of predictors and the uncertainty of those beliefs inform predictor selection to guide behaviour. Their influence on both behaviour and activity in vmPFC changed and transitioned in tandem. The vmPFC carried information about a multiplicity of decision variables (uncertainty, accuracy and repetition), the strength and polarity of which varied according to their relevance for the current context.

Methods

Participants

Thirty participants took part in the experiment. Participants were excluded because they fell asleep repeatedly during the scan (N=2), exhibited excessive motion during the scan (N=1), or because of premature termination of an experimental session (N=3) (final sample: 24 participants; 14 female, age range:19-35, mean age:25.6, standard deviation:4). No statistical methods were used to pre-determine sample sizes but our sample sizes are larger to those reported in previous publications^31,33. Moreover, participants took part in two versions of the task which were averaged within participant and thereby statistical power was increased. The study was approved by the Central Research Ethics Committee (MSD-IDREC-C1-2013-13) at the University of Oxford. All participants gave informed consent.

Experimental Procedure

Participants took part in two magnetic resonance imaging (MRI) sessions on separate days (Supplementary Information, details on task versions). We collapsed participants data across two versions of the task (social/non-social) as the presented results did not show differences between versions. The order of task version was counterbalanced across participants. Stimuli used in each version were randomized across participants. Data collection and analysis were not performed blind to the conditions of the experiments. Each session lasted approximately two hours, including one hour of scanning. Participants received £15 per hour and a bonus based on task performance (per session: £5 - £7).

Before each scanning session, participants were instructed about the task and performed seven practice trials outside the scanner. After completion of both sessions, participants filled in a questionnaire that assessed their understanding of the study.

Experimental design

On every trial, participants made decisions to maximise rewards over the course of the experiment. The experiment was subdivided into six blocks. Each block included four new predictors associated with four new stimuli. Although each predictor was unique, every block comprised two good and two bad predictors. After selecting between a pair of predictors, the chosen predictors suggested the location of a target. The true target location varied from trial to trial and could not be predicted directly. The only way to estimate the target location was to learn about the distance, in terms of the angular error, between true target location and the predictor-suggested target location. The goal was to identify and exploit the good predictors in each block. On every trial, at the first stage, participants made a binary choice between the two presented predictors pseudo-randomly drawn from the four-predictor set (decision phase). Choosing better predictors at this first stage of each trial led potentially to more rewards through a decision that was made in the second stage of each trial (confidence phase). The predictors’ estimates varied around a true target location according to a normal distribution with a given standard deviation. Better options were characterised by a smaller standard deviation of the normal distribution. At the second stage, participants expressed their confidence by changing the size of an interval (symmetric interval around the predicted target location) and were rewarded if the target fell within the selected area (Figure 1A). The payoff scheme was such that participants earned most if they indicated a small angular error and the target appeared within the selected area in the subsequent outcome phase. Therefore, choosing a better predictor in the decision phase allowed participants to earn more rewards in the long run.

Overall, each MRI session comprised 180 trials, subdivided into 6 blocks, and lasted approximately one hour. The length of a block (time horizon) was either short (15 trials), medium (30 trials), or long (45 trials) (Figure 1B-i). Each time horizon was presented twice and their order was pseudo-randomised with the constraint that blocks of the same horizon did not succeed each other directly. Note that there was only one temporal order of predictor presentation: the order for short and medium horizons were extracted from the long horizon such that the first 15 trials were identical across horizons. The order of predictors was carefully constructed such that variables of interest, model-derived estimates of accuracy and uncertainty, were decorrelated statistically and across time. As shown in the Figure 4D, the critical correlations between accuracy and uncertainty prediction differences are r= 0.1 (95% confidence interval=[-0.32 0.48]) across all trials, r= 0.37 (95% confidence interval=[-0.04 0.67]) within exploration and r= 0.30 (95% confidence interval=[-0.12 0.63]) within exploitation, on average across participants. This means that the maximum shared variance in these conditions is 0.14 (in exploration). For more information on how experimental design features helped to further decorrelate accuracy and uncertainty estimates across time, see Supplementary Figure 2. In response to the reviewers’ comments, we simulated a scenario during which accuracy and uncertainty are correlated across time and show that this scenario does not exist in the current study because of multiple precautions that were taken when designing the experiment. One of the main precautions was the order of predictors across time. We created the sequence of predictors in each block such that all possible binary combinations of high/low uncertainty and high/low accuracy predictors were likely to occur irrespective of the particular choice pattern of the participant. To achieve this, we introduced two of the four predictors at slightly later times in each block, making them more uncertain compared to the earlier presented predictors. We determined the precise order of predictors in behavioural pilot experiments.

How good a predictor was, was determined by how well it estimated the target in the confidence phase. Estimations followed a Gaussian distribution centred on the true target location (Figure 1B-ii). Values, x, for each predictor were drawn from a Gaussian distribution and represented the difference between the true target location and the predictor’s estimate:

$$x\sim \text{N}(\mu ,\sigma )\text{with}-180<x<180$$ (1)

where at a given trial, value x was derived from a normal distribution with mean of μ = 0 and sigma of either σ = 50 for good predictors or σ = 70 for bad predictors. Note that sigma determined the distance (i.e. the angular error) between the true target location and the target position indicated by the predictor. Averaging across all observations of the angular error allowed participants to estimate the sigma associated with each predictor (see Figure 2A for detailed mapping between task space and belief estimates). As participants learned about the predictor’s performance through observing the angular error, they learned about the sigma of each predictor’s distribution.

Participants maximized their points by decreasing the interval size during the confidence phase (Figure 1A). Participants changed the interval size with a precision of up to 20 steps on each side of the reference location, that is a maximum of 40 steps as the interval was set symmetrically. A step size was derived by dividing the circle size (6.3 radians) by the maximum number of possible steps, resulting in a step size of approximately 0.16 radians. The interval size was determined like follows:

$$\text{Interval}\text{size}=(\text{number}\text{of}\text{steps}\times 2)/40$$ (2)

When the target fell within the interval set by the participant, the magnitude of the payoff was determined by subtracting the interval size from 1. However, if the target fell outside the confidence interval, it resulted into a null payoff. This meant that the payoff per trial ranged between 0 and 1.

$$\text{Payoff}=\{\begin{array}{ll}(1-\text{interval}\text{size})\hfill & \text{if}\text{target}\text{is}\text{included}\hfill \\ 0\hfill & \text{if}\text{target}\text{is}\text{excluded}\hfill \end{array}$$ (3)

Trial structure

Each trial included a decision, confidence, and outcome phase (Figure 1A). Trials started with the presentation of two options, a time bar, and question mark (1.5 sec on screen, decision phase). The time bar indicated the amount of trials left in the current block; it decreased after each trial until the end of a block. At the start of a new block, the type of horizon was identifiable by inspecting the time bar. After the question mark disappeared, participants chose between two predictors to receive information about the location of the target on the circle. The chosen predictor was marked with a red box (0.5 sec). In the confidence phase, the chosen predictor was shown in the centre of a circle and an interval was depicted around a reference point (i.e., predictor’s suggested target location) which was indicated by a dot. The interval covered a portion of the circle symmetrically around the reference point. The interval size was randomly initiated on each trial between a minimum of one and a maximum of 20 steps (one step corresponds to one button press) away from the predictor’s estimated target location. After participants made a choice how to set the interval size, a black frame appeared around the chosen predictor to indicate their response (0.5 sec). The duration of the confidence phase was determined by the participant’s reaction time. Finally, a second marker appeared on the circle representing the true target location and the number of points (between zero and one) below the predictor (3 sec, outcome phase).

To decorrelate variables of interest between trial phases, short intervals were included between trials (inter-trial-intervals) and randomly, but equally allocated to either the transition between decision- and confidence phase or confidence- and outcome phase. The duration of an interval was drawn from a Poisson distribution with the range of 4s to 10s and a mean of 4.5s. During these intervals, a fixation cross was shown on the screen.

Bayesian Model

We used a Bayesian model to estimate the beliefs participants might optimally hold about the sigma (σ) characterising the normal distribution of each predictor. Sigma (σ) refers to the standard deviation of the normal distribution from which observations of the angular error were drawn, i.e. distance between target and reference location at each trial. Participants learn about how well a predictor predicts the target location across time and by doing so, they implicitly estimate the sigma value (σ) of the distribution (see Figure 2 for detailed mapping between task parameters and subjective estimates). Using a Bayesian model, we derived subjects’ beliefs about the sigma value (σ) of each predictor’s distribution, resulting in sigma-hat ($\widehat{\sigma }$) that denotes participants’ estimated sigma. Before a belief can be formed, participants selected a predictor and then made an observation x of how good the predictor was on a given trial, defined by the angular error between the true target location and the predictor-estimated location (reference location):

$$\text{x}\left(\text{angular}\text{error}\right)=\text{reference}\text{location}-\text{true}\text{target}\text{location},$$ (4)

where the reference location indicated the predictor’s prediction of the target location. Key features of beliefs can be captured by a probability density function (pdf) over sigma (Figure 2A-iii,iv; 2B). The parameter space comprised possible sigma values that could be estimated by the participant. The parameter space of sigma was bound between 1 and 140 degrees to allow a broad range of sigma values considering the circle shape.

Following Bayes’ rule, a belief is updated by multiplication of a prior belief and a likelihood distribution resulting in a posterior belief, i.e. belief update (Figure 2B). Before the very first observation, participants’ belief in sigma, $\widehat{\sigma }$, was assumed to be uniformly distributed across parameter space, i.e. possible sigma values in parameter space were predicted to occur with equal probability:

$$\text{p}(\widehat{\sigma })=\text{U}(1,140).$$ (5)

A likelihood function was then calculated that described the probability of the observation x given each possible sigma value:

$$\text{p}(\text{x}\mid \widehat{\sigma })=\text{N}(\text{x}\mid \mu =0,\widehat{\sigma }).$$ (6)

With Bayes rule, we derived a trial-by-trial posterior distribution that was proportional to the multiplication of a prior distribution and likelihood:

$$p(\widehat{\sigma }\mid \text{x})\propto p(\text{x}\mid \widehat{\sigma })p(\widehat{\sigma })$$ (7)

where,

1. $\text{p}(\widehat{\sigma })$ is the prior distribution.

2. $\text{p}(\text{x}\mid \widehat{\sigma })$ is the likelihood function.

3. $\text{p}(\widehat{\sigma }\mid \text{x})$, is the posterior pdf across parameter space. The posterior pdf is the updated belief across sigma space and is used as prior for the next trial of the same predictor.

Each posterior was normalised to ensure that probabilities across all sigma values added up to one:

$$p(\widehat{\sigma }\mid \text{x})=\frac{p(\widehat{\sigma }\mid \text{x})}{\sum p(\widehat{\sigma }\mid \text{x})}$$ (8)

Model parameters

We used features of an option’s prior distribution on every trial to approximate participants’ estimates of the accuracy of the predictor and their uncertainty in those accuracy estimates. The mode (peak of distribution) of the prior pdf was used to define “accuracy”, while a 95% interval around the mode was used to define “uncertainty”. Note that both variables depended on choices made by participants, because feedback was only provided for the chosen predictor and hence only beliefs for the chosen predictor could be updated. On trial i, variables of interest were defined as follows (Figure 2A-iv):

$$\text{accuracy}=\text{max}[\text{p}(\widehat{\sigma })]\ast (-1)$$ (10)

Note that a higher $\text{max}\left[\text{p}(\widehat{\sigma })\right]$ of the pdf indicated bigger deviations of the target from the reference point. To derive an accuracy estimate that can be interpreted intuitively, the sign of $\text{max}\left[\text{p}(\widehat{\sigma })\right]$ is reversed (multiplication with (-1)) so that positive values can be interpreted as higher accuracy. The accuracy estimate represents a point-estimate of a subject’s belief distribution in sigma-hat ($\widehat{\sigma }$). This means it represents the subject’s belief in the sigma value associated with the predictors’ distribution.

To derive a trial-wise uncertainty estimate from the distribution, we identified a percentage (2.5%) of the lower and upper tail of the prior pdf, representing the distribution around the believed sigma value ($\widehat{\sigma }$). We extracted the estimated sigma value ${\widehat{\sigma }}_{\text{high}}$ and ${\widehat{\sigma }}_{\text{low}}$ at each of the two positions. The difference of both sigma values constituted the estimated “uncertainty” variable:

$$\begin{array}{c}{\widehat{\sigma }}_{\text{high}\leftarrow }\text{cumulative}(\text{p}(\widehat{\sigma }))=97.5\%\\ {\widehat{\sigma }}_{\text{low}\leftarrow }\text{cumulative}(\text{p}(\widehat{\sigma }))=2.5\%\\ \text{uncertainty}={\widehat{\sigma }}_{\text{high}}{-\widehat{\sigma }}_{\text{low}}\end{array}$$ (11)

From now onwards, the terms of accuracy and uncertainty refer to the model-derived estimates defined in equations (10) and (11) respectively.

Alternative computational models

We used a Bayesian model with uniform priors at the start of each block for all four predictors, assuming participants do not have prior knowledge about the underlying distributions associated with predictors. We refer to this model as ‘the original model’ because it is the model used elsewhere in this study. We compared the original model to two alternative computational models: a Bayesian model with informative priors (Extended Data Figure 1) and a reinforcement learning (RL) model which tracks the payoff history of each predictor (Extended Data Figure 2). We explain in detail the rationale behind each computational model, their construction and the results in the Supplementary Information (Section 2: Alternative computational models). The results demonstrate that a Bayesian model using uniform priors had a better model fit compared to a Bayesian model with informative priors or an RL model. However, a combination of the original Bayesian model with uniform priors and value-based variables derived from an RL model showed the best model fit to choice behaviour. In conclusion, RL value terms complement the Bayesian model but do not substitute for the Bayesian model terms as an explanation of behaviour; participants’ beliefs in the accuracy and uncertainty of a predictor explained additional variance in choice behaviour above and beyond that explained by their choice value estimates. These analyses were conducted in response to the reviewers’ comments.

Behavioural Analyses

We applied a set of general linear models (GLM) to the behavioural data. All GLM analyses were applied to both versions (social and non-social) of the experiment separately. The resulting beta weights for each subject were first averaged across versions and then across participants. We used two-tailed statistical tests for all analyses. Additionally, we report effect size as Cohen’s d (d) for t-tests and eta squared (η²) for ANOVAs, a 95% confidence interval and Bayes factors for non-significant results.

Decision Phase

We analysed the trial-wise impact of Bayesian-derived estimates of accuracy, uncertainty, and their modulations across time in a block on choice behaviour. Our first analysis aimed to show that the belief in the accuracy of a predictor (“accuracy”) and the uncertainty in that belief (“uncertainty”) influenced choice behaviour. Moreover, we focused on how these effects changed with the percentage of remaining trials in a block (referred to as block time), suggesting a transition between exploration and exploitation as time within a block pass. We used a logistic general linear model (GLM) to investigate these effects across all trials on choice behaviour (Choice GLM1). For all GLM analyses, regressors were normalised across all trials (mean of 0 and standard deviation of 1). The first GLM comprised the following regressors.

Choice GLM1 (Figure 3A)

• accuracy difference (left – right),

• uncertainty difference (left – right),

• block time,

• accuracy difference (left – right) × block time,

• uncertainty difference (left – right) × block time.

The dependent variable was whether or not participants made a leftward choice on the current trial. Accordingly, for each regressor (except block time), we calculated the difference in the variable for the left and right option. To calculate the interaction term, we multiplied the normalised uncertainty and accuracy variables with the normalised block time variable and then normalised this interaction term again. Note that we use the accuracy and uncertainty regressors as defined in the “ Bayesian model” section.

To further examine how the influence of uncertainty and accuracy on choice changed over time in a block, we binned trials within a given time horizon into first and second halves (Figure 3B-i). We fitted a logistic GLM on each half with uncertainty and accuracy as regressors, irrespective of the overall time horizon length of the block. Although we normalise regressors here within blocks, results replicate when regressors are normalised across blocks.

Time GLM 1 (Figure 3B-i):

• accuracy difference (left – right)

• uncertainty difference (left – right)

Next, we predicted an effect of time horizon (Figure 3B-ii) on the first trials of a block. We fitted a robust linear GLM on the first 15 trials (a multiple of all horizons, which were 15, 30 and 45) with accuracy and uncertainty as regressors to investigate whether a variable’s effect covaried with the amount of remaining trials.

Time GLM 2, for the first 15 trials within horizons (Figure 3B-ii):

• accuracy difference (left – right)

• uncertainty difference (left – right)

We used a linear robust regression to better estimate effects given the small amount of trials included in the analysis. The first 15 trials were identical across horizons in terms of their predictor order and statistical properties (apart from the specific choice sequence taken by participants). All significant results reported in Figure 3B-ii remained significant when basing the statistical tests on the t-stats of the effect sizes obtained from a logistic regression (reported interaction effect: 3×2 repeated measures ANOVA with horizon (long, medium, short) and variable (accuracy, uncertainty); horizon × variable interaction: F(2,46)=27.6, p<0.001, η²=0.965, 95% confidence interval [0.052 1.13], assumption of sphericity is met with Mauchly’s test: x²(2)=0.26, p=0.88; reported main effects: positive uncertainty during long horizon: t(23)=4.7, p<0.001, d=0.96, 95%confidence interval=[0.51 1.3]; medium horizon: t(23)=2.6, p=0.017,d=0.5,95%confidence interval=[0.1 1]).

Confidence phase

We analysed the effect of accuracy and uncertainty on confidence judgments reported at the second phase of a trial (Figure 1A). Confidence judgments were indicated by modifying the interval size around the chosen predictor with a smaller interval representing higher confidence. To make this measure intuitive, we sign-reversed their relationship such that a higher confidence index represents greater confidence in the chosen predictor. We analysed the trial-by-trial confidence judgements by applying the following linear GLM:

• Confidence GLM1 (Figure 3C):

  • chosen accuracy,
  • chosen uncertainty.

Exploration, exploitation and transitional trials

We subdivided trials into exploration and exploitation trials to compare neural signals between both behavioural modes. For each subject, we categorized trials based on the predictor selections during the decision phase (Extended Data Figure 3). On each trial, we calculated the difference between chosen and unchosen accuracy and chosen and unchosen uncertainty. Exploitative trials were defined by a positive “accuracy prediction difference” (chosen predictor had higher accuracy than unchosen ones) and negative “uncertainty prediction differences” (the chosen predictor was the predictor participants were more certain about). Vice versa, exploration trials were defined by a negative accuracy prediction difference and positive uncertainty prediction differences (the more uncertain predictor is picked even though it has yielded less accurate results in the past). Trials with both positive accuracy prediction difference and uncertainty prediction difference (i.e. that were both accuracy and uncertainty guided) were allocated to either the exploitative or the exploratory bin depending on the relative predominance of the accuracy prediction difference or the uncertainty prediction difference. For example, if the chosen predictor and the unchosen predictor differed more in the uncertainty of their predictions as opposed to the accuracy of their predictions (the chosen predictor was more uncertain than the unchosen predictor and the chosen predictor was, to a smaller degree, more accurate in its predictions than the unchosen predictor) then the predictor selection on that trial was labelled as exploratory.

Finally, trials with differences between both accuracy and uncertainty close to zero (absolute difference of 5) were assigned to both categories. We elaborate on the robustness of the current classification and compare it to those used in previous studies in the Supplementary information (Supplementary Figure 8).

Furthermore, we defined a new subset of trials to understand the transition from positive uncertainty prediction difference signals (exploration) to a negative uncertainty prediction difference signal (exploitation) in vmPFC. Because predictor selections are not driven by uncertainty alone, we tested whether accuracy prediction difference signals were particularly prominent in a transitional phase between exploration and exploitation in vmPFC. We defined a threshold in a range of accuracy prediction difference values between [5 20] that classified trials into the transition period. We chose this subset such that it would comprise trials that are close in accuracy values for both options and at the same time predictor selection would still be guided rationally by accuracy. Moreover, this window resulted in a sufficiently large sample for analysis (approximately 20% of the trials in the range of positive accuracy prediction difference). The threshold is arbitrary and slightly smaller or greater ranges (compromising positive values) did not alter the results. To show that the transition period was characterized by learning about predictors, and that periods outside this transition were defined by the processing of either positive uncertainty or negative uncertainty, we defined two separate subsets of trials (Supplementary Figure 9A). One subset included extreme positive accuracy-driven trials [accuracy values > 20] (Supplementary Figure 9A-ii), while a second subset contained extreme negative accuracy-driven [accuracy values < -5] trials (Supplementary Figure 9A-i).

FMRI data acquisition and data processing

Imaging data were acquired with a Siemens Prisma 3T MRI using a multiband T2*-weighted echo planar imaging sequence with acceleration factor of two and a 32-channel head-coil. Slices were acquired with an oblique angle of 30 ° to the PC-AC line to reduce signal dropout in frontal pole. Other acquisition parameters included 2.4×2.4×2.4 mm voxel size, TE = 20 ms, TR = 1030 ms, 60° flip angle, a 240 mm field of view and 60 slices per volume. For each session, a fieldmap (2.4×2.4×2.4mm) was acquired to reduce spatial distortions. Bias correction was applied directly to the scan. A structural scan was obtained with slice thickness = 1 mm; TR = 1900 ms, TE = 3.97 ms and 1×1×1 mm voxel size.

Imaging data was analysed using FMRIB’s Software Library (FSL)⁴⁶. Preprocessing stages included motion correction, correction for spatial distortion by applying the fieldmap, brain extraction, high-pass filtering and spatial smoothing using full-width half maximum of 5mm. Images were co-registered to an individuals’ high-resolution structural image and then nonlinearly registered to the MNI template using 12 degrees of freedom⁴⁷.

FMRI Data analysis

MRI whole-brain analyses

We used FSL FEAT for first-level analysis⁴⁶. First, data was pre-whitened with FSL FILM to account for temporal autocorrelations. Temporal derivatives were included into the model. We used two GLMs to analyse fMRI data across the whole brain. FMRI-GLM1 was applied to all trials and fMRI-GLM2 was fitted separately to trials that had been identified as exploration and exploitation trials. Results were calculated using FSL’s FLAME 1 with a cluster-correction threshold of z>2.3 and p<0.05, two-tailed. To analyse BOLD changes associated with the processing of uncertainty and accuracy across participants, a second-level analysis was applied in a two-step approach: data was first average across both versions within subject (fixed-effect analysis) and then sessions were analysed across participants (FLAME1). We included all three phases of a trial (decision, confidence and outcome) into the fMRI-GLM. Each phase included a constant regressor, which was the onset of each phase as well as parametric regressors that were modelled as stick functions (i.e. duration of zero) time-locked to the relevant phase onset.

The decision phase began at the time the predictor appeared and lasted until a selection was made by the participant (Figure 1A). The decision phase was modelled as a constant and was accompanied by the following parametric regressors:

• fMRI-GLM 1, decision phase:

  • chosen uncertainty,
  • unchosen uncertainty,
  • chosen accuracy,
  • unchosen accuracy,

All regressors were normalised before inclusion into the analysis. We calculated the difference between chosen and unchosen predictors for both accuracy and uncertainty to derive prediction differences. To derive a “domain general prediction difference”, we calculated the mean across absolute uncertainty and accuracy prediction differences: ((chosen – unchosen uncertainty) + (chosen – unchosen accuracy)) (Supplementary Figure 3A) and calculated a conjunction between both cluster-corrected maps of accuracy and uncertainty prediction differences with a cluster-correction of z>2.3 and p<0.05 (Supplementary Figure 3B). For the conjunction analysis, we used the provided FSL script ‘easythresh_conj’ with z>2.3 and p<0.05.

The confidence phase was defined from the onset of circle and interval presentation (Figure 1A) until a decision about the interval size was made. It included a constant and the following parametric regressors:

• fMRI-GLM 1, confidence phase:

  • chosen uncertainty,
  • chosen accuracy,
  • block time,
  • chosen uncertainty × block time,
  • chosen accuracy × block time.

All regressors were normalized before, and, where relevant, after building the interaction term (chosen accuracy/ uncertainty × block time). We only included the chosen predictor, as participants evaluated their uncertainty and accuracy estimates according to the predictor they selected during the decision phase.

The outcome phase was defined by the onset of the target and payoff presentation and lasted for a fixed duration of three seconds. In addition to the constant regressor, we included the following parametric regressors:

• fMRI-GLM 1, outcome phase:

  • chosen accuracy,
  • chosen uncertainty,
  • payoff (as defined in equation 3).

In the second fMRI-GLM2, trials were binned into exploratory and exploitative trials as described above. For this purpose, we included decision, confidence and outcome phases for exploratory and exploitative trials separately. This meant that, in total, there were six phases within the fMRI-GLM2. We included the same set of regressors in the exploratory and exploitative phases. The constants for each phase was modelled as in the previous GLM, but we used separate constants for exploration and exploitation phases.

fMRI-GLM 2, decision phase (for explore and exploit separately):

• uncertainty prediction difference (i.e., chosen – unchosen)

• accuracy prediction difference (i.e., chosen – unchosen)

fMRI-GLM 2, confidence phase (for explore and exploit separately):

• chosen accuracy

• chosen uncertainty

fMRI-GLM 2, outcome phase (for explore and exploit separately):

• chosen accuracy

• chosen uncertainty

• payoff.

To test whether the uncertainty prediction difference significantly differed between exploration and exploitation, we built a contrast comparing uncertainty prediction differences between exploration and exploitation (Figure 5C).

In addition, fMRI-GLM1 contained one regressor time-locked to all button presses, modelled as a stick function. For fMRI-GLM2, two regressors were time-locked to the button presses: one relating to the exploration phase and the other related to the exploitation phase.

Region of Interest (ROI) analyses

We calculated ROIs with a radius of three voxels that were centred on the peak voxel of significant clusters derived from whole brain fMRI-GLM1 and fMRI-GLM2. The selected ROI was transformed from MNI space to subject space and the pre-processed BOLD time courses were extracted for each participant’s session. Time courses were averaged across volumes, then normalized and oversampled by a factor of 20 for visualisation. Time courses were time-locked to the onsets of each phase consistent with timings used in whole-brain fMRI-GLMs (decision, confidence or outcome). Then, a GLM was applied to each timepoint to derive beta weights per time point for each regressor. For analyses across versions, we used the same principle as applied to the whole-brain fMRI-GLMs and our behavioural analyses: first, we averaged the time course within a subject across both social and non-social versions, then we averaged across participants. For all ROI analyses, regressors were normalized (mean of zero and standard deviation of one).

To illustrate positive and negative uncertainty in exploration and exploitation phases, respectively, we included the following regressors:

• ROI-GLM 1, decision phase (for explore and exploit separately), Figure 4C:

  • chosen uncertainty,
  • unchosen uncertainty,
  • chosen accuracy,
  • unchosen accuracy.

Effects of ROI-GLM1 were extracted from the whole-brain cluster corrected accuracy prediction difference effect in vmPFC to allow for an unbiased test.

Next, we tested whether the uncertainty effect changed when repeating the same predictor as on the last encounter. We used a ROI analysis to test for a main effect of repetition and interaction effect between repetition and chosen uncertainty. We used ROI-GLM1 and additionally included the following regressors:

• ROI-GLM 2, decision phase (across all trials), Figure 6:

  • additional regressors to ROI-GLM1:
  • repetition (1= repetition of the same predictor as during last encounter with same predictor;
  • 0=no repetition of the same predictor)
  • repetition × chosen uncertainty,
  • repetition × chosen accuracy.

Then, we split trials into repetition and no-repetition categories to investigate the simple effect of chosen uncertainty per category (ROI-GLM3). We used ROI-GLM1, but now applied separately to repetition and no-repetition trials (Figure 6). For both ROI-GLM2 and 3, we used an unbiased ROI extracted from the whole-brain cluster corrected accuracy prediction difference effect across all trials in vmPFC.

Next, we applied a ROI analysis to show activation for accuracy prediction difference during the transitional phase (Figure 7) in vmPFC, using fMRI-GLM2. We were interested whether the accuracy prediction difference effect occurred in the transition between the previously observed positive and then negative uncertainty prediction differences. Because we hypothesized that the accuracy prediction difference effect would occur in the same ROI as the uncertainty prediction difference effects, we used an independent ROI based on the cluster-corrected accuracy prediction difference effect across all trials (fMRI-GLM 1). The same ROI and GLM was used to test extreme positive and negative accuracy-driven trials (Supplementary Figure 9B).

ROI-GLM 4, decision phase (transition trials and extreme positive and negative accuracy trials), Figure 7B; Supplementary Figure 9B:

• see fMRI-GLM2.

Leave-one-out procedure

A leave-one-out procedure was used to test the unbiased significance of the time courses extracted from ROI-GLM2,3. For every participant (n = 24), we extracted the average time course based on the 23 remaining participants. We identified the peak of the group time course in a time window between 4-8 seconds and then extracted the beta value for the excluded subject at the time of the group peak. This procedure was repeated for all participants which resulted in individual peak values that were independent from the subject to be analysed. The extracted peak values were tested with a one-sample t-test against zero.

Correlations between neural and behavioural beta weights

To calculate the correlation between the time course of neural activations and behavioural beta values, we used neural beta weights extracted from the group peak. We calculated a partial correlation between the vmPFC accuracy prediction difference effect during the transition phase and the behavioural interaction term of uncertainty × block time (Figure 7C), controlling for all other behavioural variables (main effects of accuracy, uncertainty, block time (in percentage) and the interaction between block time and accuracy, see behavioural GLM1). A second partial correlation additionally included the number of individual transition trials.

Extended Data

Data availability

We have deposited all choice raw data used for the analyses in an OSF repository. The accession code is: https://osf.io/d5qzw/?view_only=037ea3b875914623a06999cef97ac57f.

We have deposited unthresholded fMRI maps of all contrasts depicted in the manuscript on Neurovolt. The accession code is: https://identifiers.org/neurovault.collection:8073.

The source data underlying Figure 3,6,7 and Extended Data Figure 1,2,3,5 are provided as a Source Data file.

Code availability

The above OSF repository includes the full Bayesian modelling pipeline. Relevant behavioural and neural regressors were derived from this pipeline. We also provide the code for behavioural GLMs shown in Figure 3. Please follow the README file inside the repository for details of its use: https://osf.io/d5qzw/?view_only=037ea3b875914623a06999cef97ac57f.