Fast Local Phase Velocity Based Imaging (LPVI): Shear Wave Particle Velocity and Displacement Motion Study

Abstract

Fast and precise noninvasive evaluation of tissue mechanical properties is of high importance in ultrasound shear wave elastography. In this study we present an updated, faster version of the local phase velocity based imaging (LPVI) method used to create images of local phase velocity in soft tissues. The updated LPVI implementation uses one-dimensional Fourier transforms in spatial dimensions separately in comparison to its original implementation. A directional filter is applied upon the shear wave field to extract the left-to-right (LR) and right-to-left (RL) propagating shear waves. A local shear wave phase velocity map is recovered based on both LR and RL waves. Finally, a two-dimensional shear wave velocity map is reconstructed by combining the LR and RL phase velocity maps. LPVI performance for shear wave displacement and velocity wave motion data is examined. A study of LPVI used for only one data acquisition with multiple focused ultrasound push beams is presented. The lesion placement with respect to the pushes and whether two sequential pushes provided different results from two simultaneous radiation force pushes was investigated. The addition of white Gaussian noise to the wave motion data was also tested to examine the LPVI method’s performance. Robust and accurate shear wave phase velocity maps are reconstructed using the proposed LPVI method using numerical tissue mimicking phantoms with inclusions. Results from the numerical phantom study showed that the reconstructed, asymmetric inclusions, for various axial locations, are better preserved for shear wave particle velocity signals compared to particle displacement motion data.

I. Introduction

EVALUATION of soft tissue mechanical properties can be performed with various techniques in the field of elasticity imaging [1]. Shear wave elastography (SWE) is one of the methods that has been utilized in a clinical setting for evaluation of liver, breast, thyroid, skeletal muscle, kidney, prostate, among other organs [2]–[4]. SWE methods typically use a focused ultrasound ”push” beam that transfers momentum to the medium through the acoustic radiation force (ARF) mechanism [5], [6]. Application of the ARF causes displacement of the tissue at the focus of the push beam. The displacement at the focus causes shear waves to propagate within the medium. Fast ultrasound imaging is then used to capture data that can be used to estimate the motion of the shear waves [7], [8].

Different clinical implementations of SWE use the particle displacement or particle velocity for estimation of the group velocity in the time-domain [9]. Algorithms for tracking the time-of-flight of the propagating shear waves have been proposed that either use correlation or peak tracking [10]–[15]. Estimating a group velocity assumes that the medium is linear, elastic, isotropic, and locally homogeneous. However, it is known that soft tissues are viscoelastic and so additional measures are needed for full characterization.

One method that has been employed for viscoelastic characterization is measurement of phase velocity dispersion, or variation of the shear wave velocity with frequency [16], [17]. By fitting the dispersion characteristic to frequency dependent relationships for rheological models, viscoelastic properties such as elasticity and viscosity can be estimated. Additionally, using a phase velocity at a particular frequency for characterizing a medium could provide a standardized approach for comparing data from different patients in a study [18].

In recent years, several methods have been developed to perform two-dimensional (2-D) imaging of phase velocity. Budelli, et al., used a phase gradient within a sliding window to estimate the phase velocity in a local fashion over the whole region-of-interest (ROI) to construct a 2-D image [19]. A method proposed by van Sloun, et al., used model fitting of the measured motion to evaluate the local shear wave velocity and viscosity [20], [21]. Lastly, a new method called local phase velocity imaging (LPVI) was proposed by Kijanka and Urban which uses Fourier decomposition and a moving window to create 2-D phase velocity images at various frequencies [22], [23].

While developing the LPVI method we have observed performance differences that we will address in this paper. One of the limitations of the LPVI method that was proposed by Kijanka and Urban was the long computational time [22], [23]. For each image, it takes on the order of ~56 seconds for the reconstruction at each frequency (as will be discussed later in Sec. IV). This can be prohibitive for reconstruction of many phase velocity images. Additionally, when using LPVI in viscoelastic media we determined that wavenumber filtering was necessary to reconstruct accurate phase velocity images [23]. In the original LPVI work, we used two separate ARF pushes to reconstruct images and then combined the two images. We sought to evaluate using multiple simultaneous pushes as utilized in the comb-push ultrasound shear elastography (CUSE) method [8], [24], [25]. Lastly, in our original work we used particle velocity as the motion source for performing the reconstructions. As some scanners use particle displacement or particle velocity, we wanted to evaluate the performance for both cases.

The rest of the article is organized as follows. First, we present an updated, faster Local Phase Velocity based Imaging (LPVI) method as applied for the shear wave phase velocity mapping. This method employs one-dimensional (1-D) Fourier transforms in spatial dimensions separately in comparison to its original implementation where a 2-D Fourier transform was used for segmented wave motion data. The LPVI method was tested on data from numerical simulations twofold. Firstly, for a single push beam excitation generated once on the left side and once on the right side of the probe. Secondly, for two, simultaneous focused ultrasound push beams generated on both sides of the probe. The robustness of the method was tested for shear wave particle velocity and displacement motion data in numerical tissue mimicking phantoms. In addition, we evaluated the algorithm with different levels of added noise. In this paper we use simulations with inclusions that are softer and stiffer than the background material to address the clinically relevant problem of cancerous lesion characterization. Results from these phantoms will be presented. The results are followed with a discussion and conclusions.

II. Materials and Methods

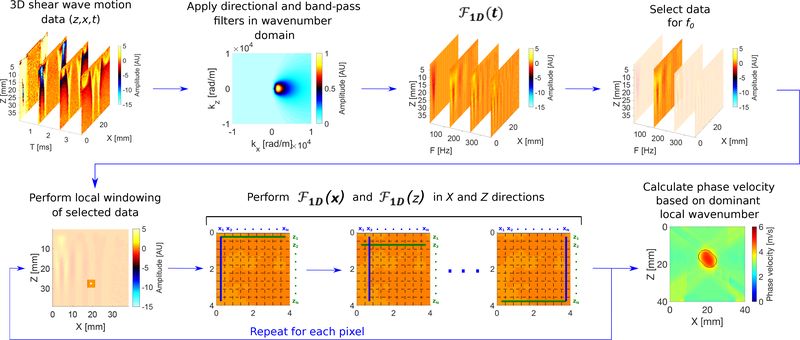
In this section, a modified LPVI method is presented for 2-D shear wave phase velocity estimation. The reconstruction capabilities are tested with the local interaction simulation approach (LISA) numerical elastic models for shear wave displacement and velocity signals, respectively [26]–[28]. Computation efficiency is also studied and compared with its original implementation [22]. Major steps of the method are presented in a flow chart, in Fig. 1. A description of the numerical LISA elastic phantoms is described in Sec. II-B. Examples for various inclusions locations and with added white Gaussian noise are provided.

Fig. 1:

Flow chart of the proposed LPVI approach for double-sided push. Principal steps of the LPVI can be summarized as follows: (I) acquire a 3D shear wave velocity data set; (II) apply directional and band-pass filters to the data in a wavenumber domain; (III) transform the spatio-temporal data into a frequency domain; (IV) choose the spatial spectrum at a particular frequency f₀; (V) select a short space domains data; (VI) execute 1-D Fourier transforms in X and Z directions on the windowed wavefield regions; (VII) calculate spatial distribution of the phase velocity of the shear wave motion for the specified frequency and select ROI. Repeat previous steps for shear wave velocity data for the second push. Average resulting LPVI data for ROI’s from two pushes.

A. Local-Phase-Velocity-based Imaging Approach

The LPVI method, used to measure tissue phase velocity, was originally proposed in [22]. The LPVI approach reconstructs local shear wave velocity for a single frequency or selected frequency band. In contrast to the work presented in [22] a band-pass filter in the wavenumber domain combined with a directional filter is added in this manuscript. Moreover, a 2-D Fourier transform $\left({\mathcal{F}}_{2D}\right)$ is replaced with a combination of 1-D Fourier transforms $\left({\mathcal{F}}_{1D}\right)$ in the x- and z- directions, respectively. This step allows for reducing computation time in comparison to the original implementation developed in [22], where a 2-D Fast Fourier transform was used. The steps of the modified, faster LPVI method are shown in a flow chart in Fig. 1.

First, the directional and band-pass filters in a 2-D wavenumber domain are used on the shear wave field to extract the left-to-right (LR) and right-to-left (RL) propagating shear waves and remove shear wave interferences [29]. A first order Butterworth band-pass filter is applied to each frame to remove spatial wavelengths representing shear wave velocities outside a predetermined range (0.5 – 10 m/s). Shear wave components propagating in the axial direction are reduced by the directional filter using a wedge filter with smooth roll-off in the k_z direction [30]. This process is given as the product between the spectrum in the frequency-wavenumber domain, $\tilde{V}\left(k_z,k_x,f\right)$, of the particle motion and a filter function in the form

$${\tilde{V}}_w\left(k_z,k_x,f\right)=\tilde{V}\left(k_z,k_x,f\right)\cdot B_k\left(k_z,k_x\right),$$ (1)

where B_k(k_z, k_x) denotes the 2-D filter in the k_z −k_x domain and ${\tilde{V}}_w\left(k_z,k_x,f\right)$ is the filtered spectrum. Then, the filtered spectrum is converted back into the frequency-space domain using an inverse ${\mathcal{F}}_{2D}$ resulting in ${\tilde{V}}_w\left(z,x,f\right)$. With the acquired spectrum data, a wavefield can be obtained for a particular frequency f₀ or frequency band f_band.

Next, a short space ${\mathcal{F}}_{2D}$ is applied in the x and z spatial domains in order to break down the ${\tilde{V}}_w\left(z,x,f_0\right)$ wavefield into small segments over the spatial dimensions, using e.g., a 2-D cosine-tapered window. During this process windowed wavefield regions, ${\tilde{V}}_w^{*}\left(\overline{z},\overline{x},f_0\right)$, are generated. For more details about this step readers are referred to [22].

Then, ${\mathcal{F}}_{1D}$ operations are executed in the z and x directions, for each row and column, separately. This results in a set of a 1-D wavenumber spectra for the particular frequency f₀. Mathematically it is written as

$${\tilde{\tilde{V}}}_z\left(k_z,1:{\overline{x}}_N,f_0\right)={\int }_{-\infty }^{+\infty }{\tilde{V}}_w^{*}\left(\overline{z},1:{\overline{x}}_N,f_0\right)\cdot e^{-i\left(k_z\overline{z}\right)}dz,$$ (2)

for the z direction and

$${\tilde{\tilde{V}}}_x\left(1:{\overline{z}}_N,k_x,f_0\right)={\int }_{-\infty }^{+\infty }{\tilde{V}}_w^{*}\left(1:{\overline{z}}_N,\overline{x},f_0\right)\cdot e^{-i\left(k_x\overline{x}\right)}dx,$$ (3)

for the x direction, respectively. N is the number of scanning lines in the z and x directions. The resulting spectra are stored in vectors for each direction. Afterwards, a wavenumber magnitude is computed as

$$|\mathbf{k}{|}_{(1:N)}=\sqrt{k_{z(1:N)}^2+k_{x(1:N)}^2},$$ (4)

and k_z(1:N) and k_x(1:N) arguments are found using

$$k_{z(1:N)}=\underset{k_z}{\arg \max }\left\{{\tilde{\tilde{V}}}_z\left(k_z,1:{\overline{x}}_N,f_0\right)\right\},$$ (5)

for the z direction and

$$k_{x(1:N)}=\underset{k_x}{\arg \max }\left\{{\tilde{\tilde{V}}}_x\left(1:{\overline{z}}_N,k_x,f_0\right)\right\},$$ (6)

for the x direction, respectively.

Next, the spatial distribution of the phase velocity of the shear wave motion for the frequency f₀ is calculated. From the ${\tilde{\tilde{V}}}_z\left(k_z,1:{\overline{x}}_N,f_0\right)$ and ${\tilde{\tilde{V}}}_x\left(1:{\overline{z}}_N,k_x,f_0\right)$ spectra, for all spatial locations, the phase velocity is calculated as

$$c_{ph(z,x)}\left(f_0\right)=\frac{2\pi f_0}{\frac{1}{N}{\sum }_{i=1}^N|\mathbf{k}{|}_i},$$ (7)

Based on Eq. (7) the full field-of-view (FOV) of phase shear wave velocity image is reconstructed. Similar, as it was described in [22], the frequency f₀ can be a single frequency value as well as a frequency band (f_band) centered about f₀ (f₀ − f_b, …, f₀, …, f₀ + f_b). The phase velocity at each location over a selected frequency band can be given as

$$c_{ph(z,x)}\left(f_{band}\right)=\frac{1}{N}\sum _{i=1}^N{c}_{ph(z,x)}\left(f_i\right),$$ (8)

where f_i (i = 1,2, …, N) is a frequency band centered about f₀. When f_band = f₀, Eq. 8 simplifies to Eq. 7.

The above procedure has been implemented in MATLAB (Mathworks, Natick, MA) on a standalone computer equipped with Windows 7 Professional operating system and the Intel(R) Xeon(R) CPU E5–2683 v4 @2.10 GHz processor to show and evaluate the modified LPVI approach performance. The FFT length in time and spatial dimensions z and x was 1024. We conducted tests using this new method on phantoms containing asymmetric inclusions in different locations. LISA numerical phantom data were used for our studies. A clean shear wave motion data set and a set with added white Gaussian noise at various levels were studied. Shear wave particle displacement and velocity signals were examined.

B. Numerical LISA Phantoms Description

To produce digital phantoms of elastic materials with inclusions for which the mechanical properties are known, we used a 2-D LISA models, similar as it was used in [22]. LISA can be used for shear wave propagation in any heterogeneous material of arbitrary shape and complexity [26]–[28]. The LISA algorithm is a finite difference (FD) based approach which incorporates the local interaction nature of boundaries in the model for wave propagation. The sharp interface model (SIM) is used to average physical properties at interface grid points which represent intersections of four elementary cells [31]. SIM allows for a more physical and unambiguous treatment of interface discontinuities for different layers of material in comparison to standard FD schemes. Physical parameter smoothing across material interfaces is applied, leading to more precise results when treating wave propagation problems in complex media at interfaces and discontinuities.

The LISA technique for an elastic, isotropic, homogeneous, and nearly incompressible model for soft tissue is described by Navier’s equation

$$(\lambda +2\mu )\nabla (\nabla \cdot \mathbf{u})+\mu \nabla \times (\nabla \times \mathbf{u})+\mathbf{F}=\rho \frac{\partial }{\partial t}\mathbf{u},$$ (9)

where, λ and μ are the first Lamé parameter and shear modulus, respectively, and ρ is the density. u is the local particle displacement, F is the induced body force, and t is the time.

We used a parallelized version of the LISA algorithm by adopting parallel computation technology - offered by modern graphics processing units (GPUs) and compute unified device architecture (CUDA) used in low-cost graphical cards - for computation of the LISA equations.

The acoustic radiation force push beam, for the numerical models, was simulated using Field II [32], [33]. A linear array with 32 active elements, with element width of 0.283 mm, element height of 7 mm, element of 0.35 mm, elevation focus of 25 mm was simulated with a center frequency of 4.0 MHz, and using a medium attenuation, α, of 0.5 dB/cm/MHz and sound velocity, c, of 1540 m/s. The intensity, I, was calculated as I = ⟨p⟩²/ρc, to be used in the body force defined by F = 2αI/c where, p is the pressure. A focal depth of 20 mm was used for the push beams with a fixed f-number (F/N) of 2.21.

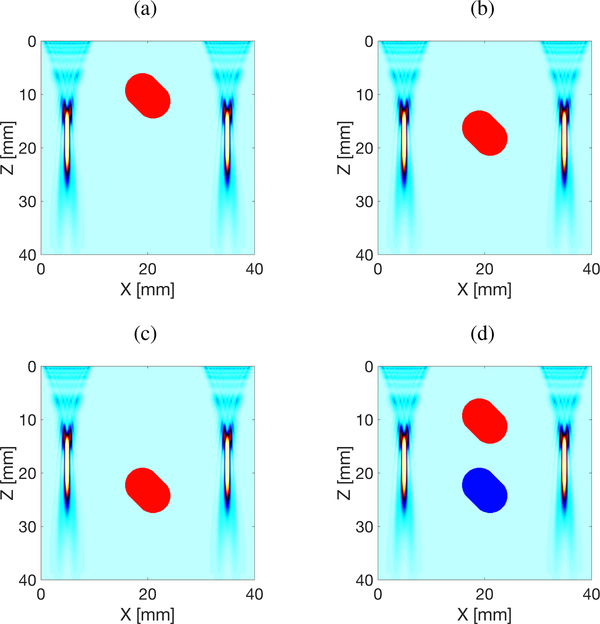
The elastic domains were uniformly spatially sampled at 0.1 mm. The dimensions of the simulated domain are x = ±40 mm in the lateral direction and z = 40 mm in the axial dimension. Four different models were simulated presented in Fig. 2. Models A, B and C contain a single inclusion positioned at various axial locations, as can be seen in Figs. 2a–2c. Model D instead, includes two inclusions with varying stiffnesses. The background Young’s modulus was set to 23.52 kPa for all four models. The inclusion’s Young’s modulus was equal to 75 kPa for Models A, B, and C, respectively. Model D had two inclusions with Young’s modulus of 75 kPa, for the upper inclusion (D_H), and 9.72 kPa, for the lower inclusion (D_L), respectively. The density was set to 1000 kg/m³ for all materials, i.e. background and the inclusions, respectively.

Fig. 2:

Local Interaction Simulation Approach (LISA) numerical configurations used for shear wave velocity simulation. The inclusion’s Young’s modulus was equal to 25 kPa for (a) Model A, (b) Model B, and (c) Model C. Model D (d) has two inclusions with Young’s modulus of 25 kPa, for the upper inclusion, and 3.24 kPa, for the lower inclusion, respectively. The background Young’s modulus was set to 7.84 kPa for all four models. A focal depth of 20 mm was used for the push beams with a fixed f-number (F/N) of 2.21.

For each investigated model three simulations were performed, i.e. (1) for a single ultrasound focused push beam located on the left side of the probe; (2) for a single ultrasound focused push beam located on the right side of the probe; and (3) for two, simultaneous ultrasound focused push beams located on both sides of the probe. Shear wave displacement and velocity signals were acquired with a sampling frequency of 10 kHz for each scenario.

C. The Final Image Reconstruction

The data sets (shear wave particle displacement and shear wave particle velocity) were then processed as described in Sec. II-A, in order to obtain 2-D estimates of the local shear wave phase velocity.

Resulting 2-D maps for the single ultrasound push beams (SP) located once on the left side and once on the right side (numerical simulations scenarios no. 1 and 2) were averaged in order to get a final 2-D shear wave phase velocity reconstruction (similar to the work presented in [22]). For the two simultaneous focused push beams (MP) (numerical simulation scenario no. 3) shear waves propagating left-to-right (LR) and right-to-left (RL) were extracted by changing the orientation of the directional filter. A final 2-D shear wave phase velocity reconstruction was obtained by combining both LR and RL velocity maps.

The spatial window size, $W_{z,x}(\overline{z},\overline{x})$, used within the LPVI approach was set to 45 × 45 pixels, resulting in 4.5 × 4.5 mm. The 2-D estimates of shear wave phase velocity were performed for a ”clean” (without any additional noise) data set as well as in the presence of noise (as added white Gaussian noise). The white Gaussian noise was generated in MATLAB software and then manually added into shear wave time-domain particle displacement and velocity signals for each spatial position. The power of the wave motion was measured. Subsequently, white Gaussian noise was added to the time-domain vector signal. Here, a signal-to-noise ratio (SNR) for the noise-added models was set to vary between 20 and 5 dB.

We used different processing scenarios for 2-D shear wave phase velocity reconstructions and compared all results in Sec. III. For clarity we define the LPVI processing scenarios used in our study in Table I.

TABLE I:

LPVI processing scenarios used for 2-D shear wave phase velocity maps reconstructions.

Processing scenario	Acquisitions	Directional and band-pass filters	Motion data type
I	Double*	Inactive	Displacement
II	Double*	Inactive	Velocity
III	Double*	Active	Displacement
IV	Double*	Active	Velocity
V	Single**	Active	Displacement
VI	Single**	Active	Velocity

^*Double acquisitions stand for a single ultrasound focused push beam (SP).

^**Single acquisition corresponds to multiple ultrasound focused push beams (MP).

III. Results

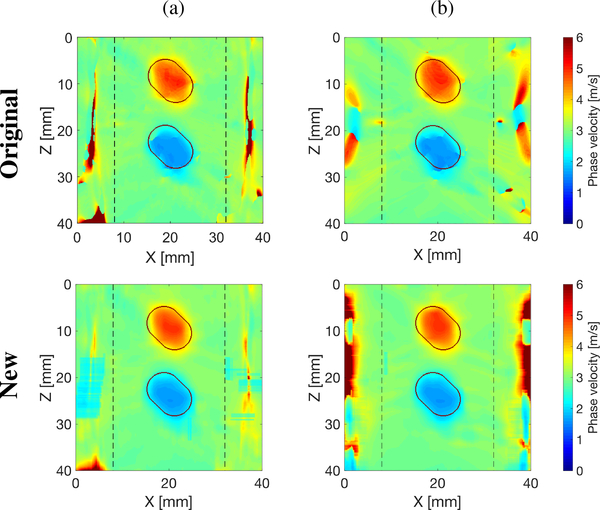
Figure 3 shows comparison of 2-D shear wave phase velocity image reconstructions with an SNR of 20 dB, using the original LPVI method developed in [22] (top row) and modified, new LPVI technique presented in this manuscript (bottom row). Results for the processing scenarios no. II (the same as was used in [22]) and no. VI are presented in Figs. 3a and 3b, respectively. The velocity maps were reconstructed for spatial window size of 4.5 × 4.5 mm, and selected frequency f₀ = 1000 Hz. It can be seen that the modified LPVI approach provides very similar results compared to the original implementation, but is capable to reconstruct inclusions with a better preserved shape. This is more visible for the softer inclusion.

Fig. 3:

Two-dimensional shear wave phase velocity image reconstructions for Model D with an SNR of 20 dB, using the original (top row) and the modified, new (bottom row) LPVI technique. The spatial window size was 4.5 × 4.5 mm, and selected frequency, f₀ = 1000 Hz. Results for shear wave particle velocity signal as an input signal, with (a) inactive directional and wavenumber filters, for a single ultrasound focused push beam, and (b) active directional and wavenumber filters, for multiple ultrasound focused push beams. Vertical, dashed lines separate regions where the focused ultrasound push beams were located.

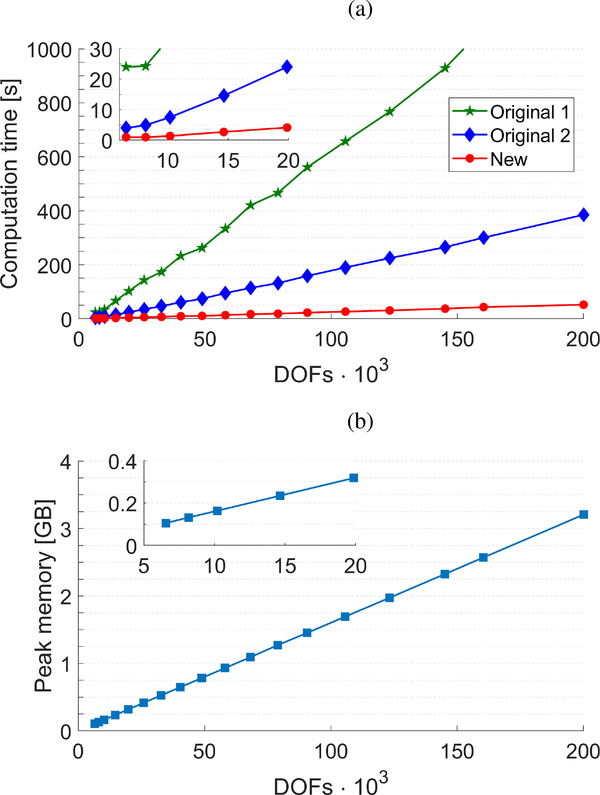
Figure 4a shows the computation time for reconstruction of a final 2-D shear wave phase velocity map for a particular frequency, based on the LR and RL waves, for the original implementation of the LPVI method and the modified approach proposed in this manuscript. The original LPVI method was studied twofold: by adopting a built-in fft2(·) function in MATLAB (Original 1, green curve), and by using dual fft(·) functions (Original 2, blue curve), for calculating ${\mathcal{F}}_{2D}$. Results are presented against number of degrees-of-freedom (DOFs) corresponding to the number of pixels present in a 2-D spatial wavefield data (z and x). Processing scenario no. VI was selected for this study and the resulting computation time was estimated. For example, reconstruction of a 2-D shear wave phase velocity map for a region-of-interest of 30 × 30 mm with axial and lateral resolution of 0.154 mm (~40 · 10³ DOFs) takes ~212 seconds for the original 1 and ~56 seconds for the original 2 implementations, respectively. At the same time the modified approach proposed in this manuscript requires ~8.5 seconds for calculations.

Fig. 4:

Computation time (a) for reconstruction of a final 2-D shear wave phase velocity map based on the LR and RL waves, for the original implementation of the LPVI method proposed in [22] (green and blue curves) and the modified, new approach proposed in this manuscript (red curve). Original 1 stands for adopting a built-in fft2(·) function in MATLAB whereas, Original 2 represents data for using dual fft(·) functions, respectively. Peak memory requirements, for all implementations, is marked as a dashed, square line in (b). Results are presented against number of DOFs corresponding to the number of pixels present in the spatial wavefield data (z and x). Calculations were performed on a standalone computer equipped with Windows 7 Professional operating system and the Intel(R) Xeon(R) CPU E5–2683 v4 @2.10 GHz processor. Padding factor of 1024 was used in the directions z and x, as well as, in the time domain.

Figure 4b shows peak memory requirements for reconstruction of a final 2-D shear wave phase velocity map for a particular frequency, based on the LR and RL waves. Results for the original implementation of the LPVI method and the modified approach proposed in this manuscript are presented as a mean curve because they are almost the same. For instance, a difference of the peak memory requirements between the ”Original 1” and ”New” implementations is at the level of a few megabytes (MB) for more than 100·10³ DOFs.

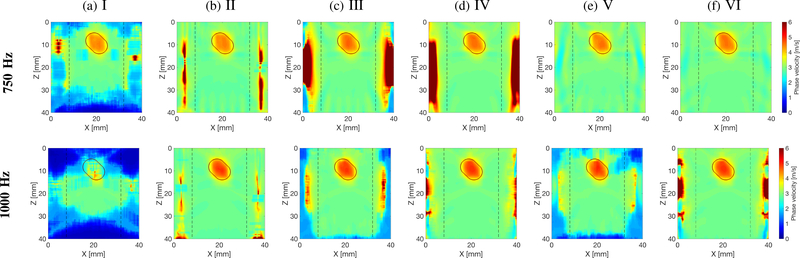
Figure 5 presents final 2-D shear wave phase velocity images for Model A (Fig. 2a), using the new LPVI approach with an SNR of 20 dB. The final images were obtained by averaging reconstructed intermediate maps from two acquisitions (single focused push beam), for the shear wave particle displacement (Figs. 5a, and 5c, processing scenarios no. I and III), and for the shear wave velocity (Figs. 5b, and 5d, processing scenarios no. II and IV) signals, respectively. Reconstructed maps for a single acquisition (multiple focused push beams) are also presented for the shear wave particle displacement (Fig. 5e, processing scenario no. V), and for the shear wave particle velocity (Fig. 5f, processing scenario no. VI) signals. For the single focused push beam two configurations of the LPVI approach were studied. Namely, the directional and band-pass filters were appropriately ”off” (processing scenarios no. I and II) and ”on” (processing scenarios no. III-VI) for 2-D shear wave phase velocity maps reconstructions. Maps for two different frequencies are presented. Vertical, dashed lines separate regions where the focused ultrasound push beams were located.

Fig. 5:

Two-dimensional shear wave phase velocity image reconstructions for Model A with an SNR of 20 dB, using the proposed LPVI technique. The spatial window size was 4.5 × 4.5 mm, and selected frequencies, f₀ = 750 and 1000 Hz. Results for shear wave (a) particle displacement signal as an input signal, with inactive directional and wavenumber filters, for a single ultrasound focused push beam (SP); (b) particle velocity signal as an input signal, with inactive directional and wavenumber filters, for a single ultrasound focused push beam (SP); (c) particle displacement signal as an input signal, with active directional and wavenumber filters, for a single ultrasound focused push beam (SP); (d) particle velocity signal as an input signal, with active directional and wavenumber filters, for a single ultrasound focused push beam (SP); (e) particle displacement signal as an input signal, with active directional and wavenumber filters, for multiple ultrasound focused push beams (MP); (f) particle velocity signal as an input signal, with active directional and wavenumber filters, for multiple ultrasound focused push beams (MP). Vertical, dashed lines separate regions where the focused ultrasound push beams were located.

Some differences between all reconstructed shear wave phase velocity maps can be distinguished. One can observe that the 2-D phase velocity reconstructions based on the shear wave displacement signal, without the directional and wavenumber filters (processing scenario no. I), are much noisier than the other ones. The inclusion for f₀ = 1000 Hz was not detected at all in this case, as can be seen in Fig. 5a. Other processing configurations were able to generally reconstruct the inclusion.

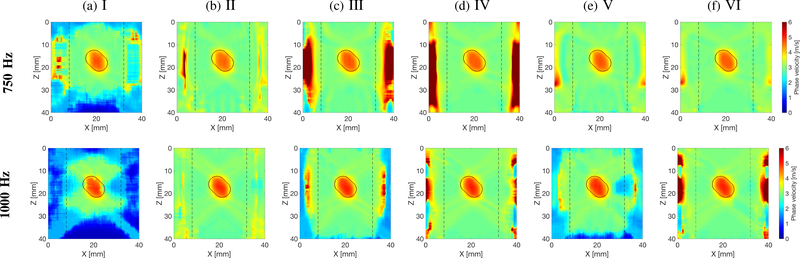
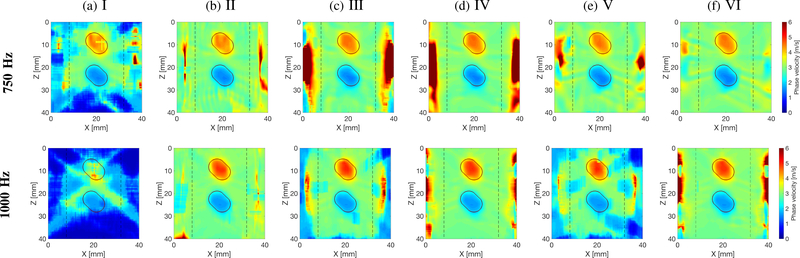
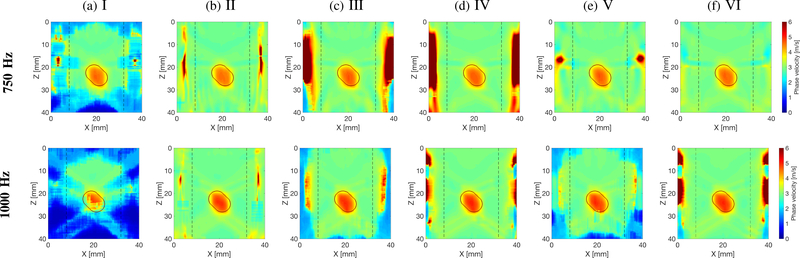
Figures 6–8 present similar 2-D shear wave phase velocity reconstructions for Models B, C and D (Figs. 2b–2d), respectively. For the inclusion situated within the main focused push beam energy (z ~ 13 – 22 mm), the inclusion was reconstructed for all processing scenarios investigated, as can be seen in Fig. 6. However, the surrounding background, outside the main focused push beam energy, was not recovered for inactive directional and wavenumber filters, and the shear wave particle displacement signal (processing scenario no. I). Similar phenomena can be observed for other inclusions locations in Figs. 7a and 8a.

Fig. 6:

Two-dimensional shear wave phase velocity image reconstructions for Model B with an SNR of 20 dB, using the proposed LPVI technique. The spatial window size was 4.5 × 4.5 mm, and selected frequencies, f₀ = 750 and 1000 Hz. Results for shear wave (a) particle displacement signal as an input signal, with inactive directional and wavenumber filters, for a single ultrasound focused push beam (SP); (b) particle velocity signal as an input signal, with inactive directional and wavenumber filters, for a single ultrasound focused push beam (SP); (c) particle displacement signal as an input signal, with active directional and wavenumber filters, for a single ultrasound focused push beam (SP); (d) particle velocity signal as an input signal, with active directional and wavenumber filters, for a single ultrasound focused push beam (SP); (e) particle displacement signal as an input signal, with active directional and wavenumber filters, for multiple ultrasound focused push beams (MP); (f) particle velocity signal as an input signal, with active directional and wavenumber filters, for multiple ultrasound focused push beams (MP). Vertical, dashed lines separate regions where the focused ultrasound push beams were located.

Fig. 8:

Two-dimensional shear wave phase velocity image reconstructions for Model D with an SNR of 20 dB, using the proposed LPVI technique. The spatial window size was 4.5 × 4.5 mm, and selected frequencies, f₀ = 750 and 1000 Hz. Results for shear wave (a) particle displacement signal as an input signal, with inactive directional and wavenumber filters, for a single ultrasound focused push beam (SP); (b) particle velocity signal as an input signal, with inactive directional and wavenumber filters, for a single ultrasound focused push beam (SP); (c) particle displacement signal as an input signal, with active directional and wavenumber filters, for a single ultrasound focused push beam (SP); (d) particle velocity signal as an input signal, with active directional and wavenumber filters, for a single ultrasound focused push beam (SP); (e) particle displacement signal as an input signal, with active directional and wavenumber filters, for multiple ultrasound focused push beams (MP); (f) particle velocity signal as an input signal, with active directional and wavenumber filters, for multiple ultrasound focused push beams (MP). Vertical, dashed lines separate regions where the focused ultrasound push beams were located.

Fig. 7:

Two-dimensional shear wave phase velocity image reconstructions for Model C with an SNR of 20 dB, using the proposed LPVI technique. The spatial window size was 4.5 × 4.5 mm, and selected frequencies, f₀ = 750 and 1000 Hz. Results for shear wave (a) particle displacement signal as an input signal, with inactive directional and wavenumber filters, for a single ultrasound focused push beam (SP); (b) particle velocity signal as an input signal, with inactive directional and wavenumber filters, for a single ultrasound focused push beam (SP); (c) particle displacement signal as an input signal, with active directional and wavenumber filters, for a single ultrasound focused push beam (SP); (d) particle velocity signal as an input signal, with active directional and wavenumber filters, for a single ultrasound focused push beam (SP); (e) particle displacement signal as an input signal, with active directional and wavenumber filters, for multiple ultrasound focused push beams (MP); (f) particle velocity signal as an input signal, with active directional and wavenumber filters, for multiple ultrasound focused push beams (MP). Vertical, dashed lines separate regions where the focused ultrasound push beams were located.

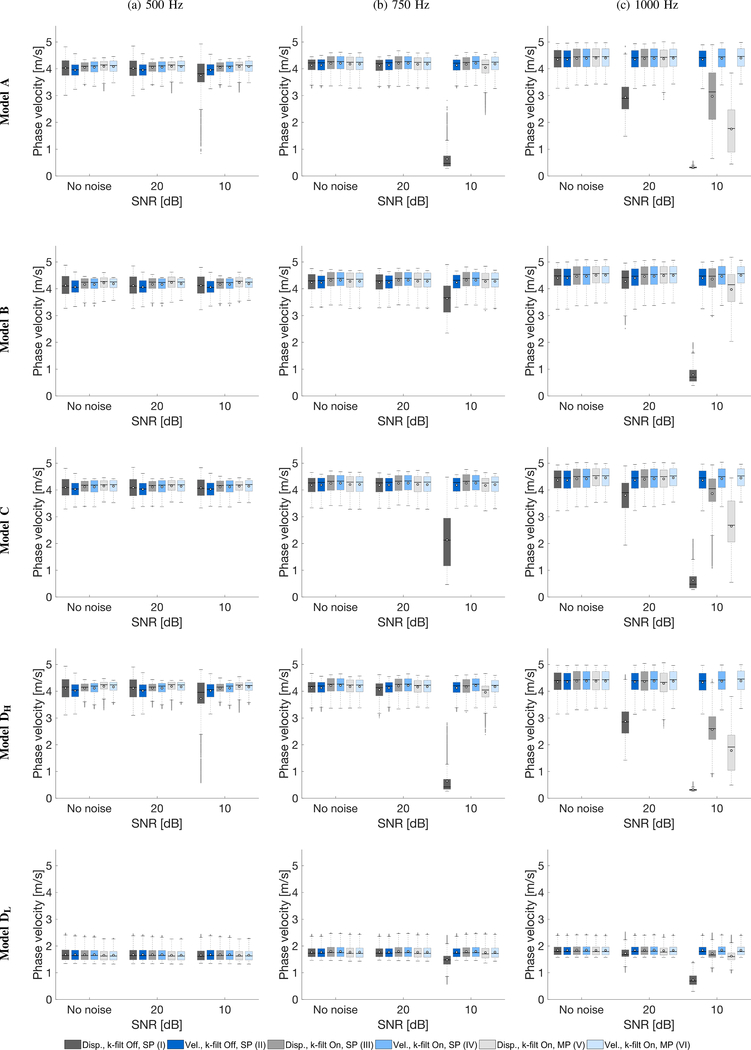
Boxplots of the phase velocity within inclusions, for the four models investigated, were calculated for the clean data and with an SNR of 20 and 10 dB. Results are summarized in Fig. 9. The bottom and top edges of the box indicate the 25^th and 75^th percentiles, respectively. White circles represent mean values of the phase velocity whereas, a solid line within each box corresponds to a median value. Outliers were also plotted if values are greater than q₃ + w(q₃ − q₁) or less than q₁ − w(q₃ − q₁), where w is the maximum whisker length, and q₁ and q₃ are the 25^th and 75^th percentiles of the sample data, respectively. w was selected to be 1.5. IQR quantitative evaluation can be made by calculation of a difference between 25^th and 75^th percentiles of the sample data as IQR = q₃ − q₁. Results for three different frequencies of 500, 750 and 1000 Hz are presented in Figs. 9a, 9b and 9c, respectively. Additionally, 50^th percentile for each model and six selected frequencies (500, 600, 700, 800, 900, and 1000 Hz) are summarized in Tables II–VI in the Appendix. Similar tabulated summaries for the 25^th, and 75^th percentiles are presented in the Supplementary Material. Moreover, similar boxplots however, for an SNR of 15 and 5 dB are also shown in the Supplementary material.

Fig. 9:

Boxplots of phase velocity, of the inclusion for various numerical LISA models data and noise levels. White circles represent mean values whereas, a solid line within the box corresponds to a median value. Results were calculated for various LPVI processing scenarios tabulated in Table I. Analogous boxplots for an SNR of 15 and 5 dB are presented in the Supplementary material in Fig. S1.

TABLE II:

The 50^th percentile phase velocity of the inclusion for Model A and various LPVI processing scenarios. Values are presented in the unit of m/s.

Noise level [dB]	Processing	Frequency [Hz]
		500	600	700	800	900	1000
No noise	I	4.03	4.04	4.11	4.29	4.31	4.42
	II	3.96	4.01	4.16	4.26	4.32	4.41
	III	4.09	4.16	4.21	4.32	4.40	4.44
	IV	4.11	4.15	4.23	4.31	4.39	4.45
	V	4.14	4.13	4.19	4.30	4.40	4.45
	VI	4.12	4.15	4.20	4.29	4.39	4.46
20	I	4.02	4.03	4.11	4.24	3.95	2.90
	II	3.96	4.01	4.16	4.27	4.32	4.41
	III	4.10	4.16	4.21	4.33	4.39	4.45
	IV	4.11	4.15	4.23	4.31	4.39	4.45
	V	4.14	4.16	4.20	4.30	4.37	4.43
	VI	4.12	4.15	4.20	4.29	4.39	4.45
15	I	4.00	4.01	3.42	2.25	1.02	0.60
	II	3.96	4.01	4.16	4.26	4.32	4.41
	III	4.10	4.13	4.20	4.30	4.37	4.30
	IV	4.11	4.15	4.23	4.31	4.39	4.44
	V	4.13	4.16	4.19	4.20	4.26	3.85
	VI	4.12	4.14	4.20	4.30	4.39	4.45
10	I	3.82	2.48	0.69	0.40	0.33	0.32
	II	3.96	4.01	4.16	4.25	4.31	4.42
	III	4.10	4.14	4.18	4.14	4.12	3.14
	IV	4.10	4.15	4.23	4.31	4.39	4.45
	V	4.14	4.11	4.13	3.84	3.01	1.77
	VI	4.12	4.14	4.20	4.29	4.41	4.46
5	I	1.20	0.37	0.24	0.24	0.26	0.27
	II	3.96	3.99	4.16	4.27	4.31	4.35
	III	4.05	4.08	3.98	3.22	2.06	0.92
	IV	4.11	4.15	4.22	4.31	4.39	4.44
	V	4.06	4.09	3.39	1.47	0.76	0.61
	VI	4.11	4.15	4.20	4.29	4.38	4.44

TABLE VI:

The 50^th percentile phase velocity of the inclusion for Model D_L and various LPVI processing scenarios. Values are presented in the unit of m/s.

Noise level [dB]	Processing	Frequency [Hz]
		500	600	700	800	900	1000
No noise	I	1.65	1.68	1.71	1.74	1.76	1.80
	II	1.64	1.68	1.70	1.74	1.77	1.79
	III	1.65	1.69	1.73	1.73	1.76	1.80
	IV	1.65	1.69	1.73	1.73	1.76	1.80
	V	1.63	1.70	1.72	1.72	1.77	1.80
	VI	1.63	1.70	1.72	1.72	1.77	1.80
20	I	1.65	1.68	1.71	1.71	1.69	1.68
	II	1.64	1.68	1.70	1.74	1.76	1.80
	III	1.65	1.69	1.73	1.72	1.76	1.80
	IV	1.65	1.69	1.73	1.72	1.76	1.80
	V	1.63	1.70	1.71	1.72	1.77	1.78
	VI	1.63	1.70	1.72	1.72	1.77	1.80
15	I	1.64	1.68	1.70	1.63	1.50	1.31
	II	1.64	1.68	1.70	1.74	1.76	1.80
	III	1.65	1.69	1.72	1.72	1.75	1.79
	IV	1.65	1.69	1.73	1.73	1.76	1.80
	V	1.63	1.70	1.72	1.73	1.77	1.73
	VI	1.63	1.69	1.72	1.73	1.77	1.79
10	I	1.62	1.66	1.58	1.31	1.07	0.69
	II	1.65	1.68	1.71	1.74	1.76	1.79
	III	1.64	1.69	1.73	1.70	1.70	1.67
	IV	1.65	1.69	1.73	1.72	1.76	1.80
	V	1.63	1.70	1.70	1.65	1.67	1.61
	VI	1.63	1.70	1.72	1.72	1.77	1.79
5	I	1.54	1.44	1.05	0.70	0.41	0.33
	II	1.64	1.68	1.71	1.74	1.75	1.77
	III	1.65	1.69	1.71	1.59	1.55	1.45
	IV	1.65	1.69	1.73	1.72	1.76	1.80
	V	1.63	1.69	1.67	1.48	1.42	1.19
	VI	1.63	1.70	1.72	1.72	1.76	1.79

Shear wave phase velocity within the inclusion for the clean data, for all models investigated, give similar interquartile range (IQR) estimates for various LPVI processing scenarios. There is no abrupt change for the evaluated phase velocity. Nevertheless, larger IQRs are present when the shear wave particle displacement motion data are used with inactive directional and wavenumber filters (processing scenario no. I), in comparison to the shear wave velocity motion and the same type of processing (processing scenario no. II). This is observed for the frequency of 500 Hz, and the inclusions being stiffer than the surrounding background (Models A, B, C, and D_H, respectively). For higher frequencies, i.e. 750 and 1000 Hz, estimated IQRs stabilize for the shear wave displacement and velocity signals (processing scenarios no. I and II). For the softer inclusion in Model D (Fig. 9, bottom row, Model D_L), all evaluated IQRs ranges are at nearly the same level for 500 Hz and the clean data.

When noisy data are analyzed, the LPVI method provides larger errors for shear wave particle displacement signals in comparison to the velocity wave motion data. For an SNR of 20 dB and frequencies of 500 and 750 Hz, all processing scenarios give similar IQRs, for all numerical models investigated, as can be seen in Figs. 9a, and 9b, respectively. For 1000 Hz however, processing scenario no. I fails to give reasonable results (Fig. 9c).

IQRs for the inclusions reconstructed for an SNR of 10 dB and frequency 750 Hz miss estimates for the processing scenario no. I. Moreover, for higher frequency, i.e. 1000 Hz, processing scenarios I, III and V fail to give an approximate solution. A common feature of these processing scenarios is that they use the shear wave displacement particle motion instead of the particle velocity.

IV. Discussion

In this work we present a modified, faster version of the LPVI approach, which was originally proposed in [22], for the 2-D shear wave phase velocity imaging in soft tissues. LPVI is based on a frequency-domain approach. Unlike the ${\mathcal{F}}_{2D}$ used in the original implementation, our updated technique utilizes 1-D Fourier transforms in the z and x spatial dimensions separately. This modification of LPVI reduced the computation time several times as can be seen in Fig. 4a. The reconstructions are ~25 and ~6.5 times less computationally expensive in comparison to the original 1 and original 2 implementations, respectively, as can be seen in Fig. 4a. The computational comparison was made using MATLAB and a single CPU processor. Moreover, it is expected that an optimized implementation in C/C++ with a GPU technology will reduce the processing time significantly. Hence, one of the limitations of the LPVI approach was reduced in this study.

The speedup comes from the way the Fourier transform is calculated. In our study the shear wave particle motion signals were padded with trailing zeros. A padded length of 1024 was used. For this scenario a 1D FFT returns a 1024-point DFT whereas, the 2-D FFT returns 1024·1024 = 1048576-point DFT. Evaluating a few 1024-point DFTs (done in parallel) is faster than computing one 1048576-point DFT. Moreover, numerical operations performed in 1D, by their nature, are faster than done in 2-D since the problem is reduced by one dimension. If the padding factor of a higher value was used (e.g. 2048) the speedup for the new implementation will be higher than presented in Fig. 4a.

By looking at Eq. (7) of the local phase velocity, it can be observed that the denominator simply represents a mean value of the wavenumber magnitude vector. One can appreciate that the mean value can be replaced with a median or any other mathematical expression. This in turn, can facilitate inclusions cross section profiles improvement by, for example, adopting a weighted function. In the original implementation of LPVI this additional step could not be performed in a straightforward manner.

We examined LPVI feasibility for a scenario where two shear waves were produced and processed simultaneously. This was not investigated in our previous work [22]. Numerical inclusion phantom experiments show that LPVI is able to provide good estimates for the inclusion. The results indicate that LPVI is not sensitive to relative positions of the inclusion at three axial positions. It is also capable to reconstruct more than one inclusion at a time. The inclusion can be reconstructed well if shear wave particle velocity signals are used or directional and wavenumber filters are active. Applying directional and band pass filters play an important role when using the shear wave displacement signals for LPVI reconstructions, particularly in the case when simultaneous push beams are used to generate the shear waves. For these configurations LPVI gives stable estimates for an SNR of 20, and 15 dB. For an extreme case of noise presence, i.e. SNR of 10 dB, and higher frequencies the shear wave particle velocity motion data provide stable and reasonable estimates. Additionally, phase velocity reconstructions of the inclusions for an SNR of 5 dB give comparable outcomes to those obtained for higher SNR values, for the shear wave particle velocity data (see Fig. S1 in the Supplementary material). The results indicate that LPVI is more robust for the shear wave particle velocity signals than the particle displacement. This is pronounced for higher frequencies where temporal frequency content of the shear wave is weaker and affected by noise for the displacement signal. It should be noted that to arrive a particle velocity, a temporal derivative is taken, which in the frequency domain equates to a multiplication by iω so the magnitude distribution is shifted towards higher frequencies. Moreover, we found that an appropriate design of spatial filters overcomes this difficulty.

The inclusion was designed to be asymmetric in order to better mimic possible real life case met in clinical situations. Focused push beams were used with a limited depth penetration (~13 – 22 mm) and yet LPVI was able to reconstruct inclusions outside this region. The best reconstructions of the full FOV were obtained for the shear wave velocity motion data.

Shear wave phase velocity reconstructions for the surrounding background, outside the focused ultrasound push beams regions, were consistent for a SNR of 20 dB and the processing scenarios II, III, IV, and VI, as can be seen in Figs. 5–8, respectively. The processing scenario I fails completely with shear wave velocity estimation of the background. On the other hand, the processing scenario V exhibits inconsistency for higher frequencies (1000 Hz). Additionally, some heterogeneity was observed for the processing scenario no. III in Fig. 8 for 1000 Hz. In contrast to processing scenarios I, III, and V, where the shear wave particle displacement was considered, processing scenarios II, IV, and VI give best shear wave phase velocity estimates for the surrounding background.

Based on position of the inclusion various levels of IQR were observed. Values for the 25^th and 75^th percentiles are summarized in the Supplementary Material for each model and processing scenarios investigated in this work. For example, considering the case with an SNR of 20 dB and the processing scenario no. VI (as the most relevant for clinical applications), corresponding IQR is on the level of 0.29, 0.27, 0.27, 0.31, and 0.16 m/s, for Models A, B, C, D_H, and D_L, respectively, and for the frequency of 1000 Hz. Inclusions positioned above the focused ultrasound push beam location (z = 20 cm) provided higher IQR in comparison to the inclusions located at or below the focused axial point. This is more likely caused by diffraction of shear wave produced by the focused ultrasound push beam. Moreover, the lowest IQR was observed for the softer inclusion (Model D_L) in comparison to the stiffer ones. In this case the mechanical impedance mismatch between the surrounding background and the inclusion plays an important role. As can be observed, a ratio in material’s stiffness between the background and the stiffer inclusion is in the order of ~3.19 whereas, for the softer inclusion it is ~2.42.

The presented study shows that only one data acquisition is required for LPVI. This is very beneficial from a clinical point of view since an acquisition time can be highly reduced. Data acquisition time has to be enough to allow the shear wave from the left-most push beam to propagate to the right-most push beam and vice versa. In addition, for reconstructing images at frequencies ranging from 500–1000 Hz it is important to tailor the acoustic radiation force push for generating shear waves with large bandwidth. Neglecting post-processing time the acquisition should be sufficient to reconstruct tissue mechanical properties in near real time.

LPVI when used for a single acquisition with multiple ultrasound focused push beams (case scenario no. VI) requires usage of directional and wavenumber filters in order to remove shear wave interferences due to reflection and refraction. A spatio-temporal directional filter applied as a pre-processing step can separate interfering waves so they can be processed separately. The wavenumber filter instead, is responsible for removing spatial wavelengths representing shear wave velocity outside a predetermined range. Hence, depending on a clinical application, the wavenumber filter may require tuning of its parameters, especially, when LPVI is used for shear wave phase velocity reconstructions in viscoelastic tissues [23].

The SNR values of displacement and velocity signals reconstructed from ultrasound data widely differ in practice. This depends on many factors such as acoustic radiation force magnitude and ultrasound echo SNR [34]. In a previous paper from our group, we explored group velocity estimation methods and differentiated cases with high SNR as 20 dB and above and low SNR as 10 dB or lower [35]. In our work, we adopted the white Gaussian noise for the numerical, tissue mimicking models in order to better mimic a real situation. This may not be the best representative of real noise encountered in SWE motion estimation. However, previous experiments in tissue-mimicking phantoms have yielded similar results to those obtained in numerical models [22]. Nevertheless, a plane wave compounding method is typically used to improve the signal-to-noise-ratio of shear wave displacement tracking. Moreover, the band-pass filter in the wavenumber domain, present in the LPVI method, additionally reduces the noise from the shear wave motion particle measurements. Future work will be dedicated towards evaluating these methods for in vivo applications.

V. Conclusions

This paper introduces a modified, faster version of the LPVI approach used for 2-D shear wave phase velocity imaging. The reconstructions were reduced ~25 and ~6.5 times in comparison to the original 1 and original 2 implementations, respectively. Results from numerical phantoms show that LPVI is able to accurately reconstruct 2-D shear wave phase velocity maps for the single and multiple pushes. Moreover, the lesion placement with respect to the pushes did not affect the overall quality of the reconstructions. Our method is also capable of reconstructing more than one inclusion at a time. In addition, LPVI is capable to reconstruct inclusions for data with an SNR of 5 dB when particle velocity signals are used. It was also observed that using particle velocity and appropriate directional and wavenumber filters provided the most reliable phase velocity reconstructions.

TABLE III:

The 50^th percentile phase velocity of the inclusion for Model B and various LPVI processing scenarios. Values are presented in the unit of m/s.

Noise level [dB]	Processing	Frequency [Hz]
		500	600	700	800	900	1000
No noise	I	4.10	4.13	4.27	4.34	4.41	4.48
	II	4.05	4.13	4.28	4.35	4.40	4.47
	III	4.24	4.29	4.36	4.42	4.48	4.54
	IV	4.24	4.29	4.36	4.42	4.48	4.53
	V	4.27	4.26	4.30	4.41	4.51	4.57
	VI	4.26	4.27	4.31	4.41	4.51	4.56
20	I	4.10	4.12	4.27	4.35	4.41	4.42
	II	4.05	4.12	4.27	4.35	4.40	4.47
	III	4.25	4.30	4.36	4.42	4.48	4.54
	IV	4.24	4.30	4.36	4.43	4.48	4.54
	V	4.28	4.27	4.31	4.41	4.49	4.55
	VI	4.25	4.27	4.31	4.41	4.51	4.56
15	I	4.09	4.11	4.24	4.34	4.10	2.89
	II	4.04	4.12	4.28	4.35	4.40	4.47
	III	4.25	4.30	4.35	4.43	4.48	4.51
	IV	4.23	4.29	4.36	4.43	4.48	4.54
	V	4.28	4.26	4.29	4.41	4.47	4.51
	VI	4.26	4.26	4.31	4.41	4.52	4.56
10	I	4.12	4.10	4.02	3.06	1.80	0.70
	II	4.05	4.12	4.27	4.35	4.40	4.47
	III	4.24	4.29	4.35	4.39	4.46	4.47
	IV	4.23	4.30	4.36	4.42	4.48	4.54
	V	4.28	4.26	4.30	4.41	4.47	4.15
	VI	4.25	4.26	4.31	4.42	4.51	4.56
5	I	4.07	3.93	1.59	0.59	0.38	0.32
	II	4.05	4.11	4.27	4.34	4.40	4.44
	III	4.24	4.29	4.33	4.40	4.29	3.20
	IV	4.23	4.29	4.36	4.43	4.47	4.53
	V	4.28	4.24	4.27	4.23	3.51	2.18
	VI	4.25	4.26	4.31	4.42	4.50	4.55

TABLE IV:

The 50^th percentile phase velocity of the inclusion for Model C and various LPVI processing scenarios. Values are presented in the unit of m/s.

Noise level [dB]	Processing	Frequency [Hz]
		500	600	700	800	900	1000
No noise	I	4.09	4.08	4.21	4.32	4.37	4.46
	II	4.04	4.07	4.24	4.32	4.36	4.45
	III	4.18	4.22	4.29	4.37	4.44	4.50
	IV	4.18	4.24	4.30	4.37	4.43	4.50
	V	4.19	4.20	4.24	4.35	4.46	4.53
	VI	4.20	4.21	4.25	4.35	4.45	4.53
20	I	4.08	4.08	4.20	4.32	4.23	3.90
	II	4.03	4.07	4.24	4.32	4.36	4.45
	III	4.17	4.22	4.30	4.39	4.43	4.49
	IV	4.18	4.24	4.30	4.37	4.44	4.50
	V	4.20	4.21	4.23	4.34	4.45	4.50
	VI	4.20	4.21	4.26	4.35	4.45	4.53
15	I	4.08	4.08	4.19	4.01	2.65	1.78
	II	4.04	4.07	4.24	4.32	4.36	4.45
	III	4.18	4.23	4.30	4.36	4.43	4.46
	IV	4.18	4.23	4.31	4.37	4.43	4.50
	V	4.20	4.19	4.25	4.33	4.36	4.33
	VI	4.20	4.21	4.25	4.35	4.45	4.53
10	I	4.06	4.00	3.04	1.28	0.57	0.48
	II	4.03	4.07	4.23	4.31	4.36	4.45
	III	4.17	4.22	4.26	4.34	4.35	4.05
	IV	4.18	4.24	4.31	4.37	4.44	4.50
	V	4.19	4.20	4.24	4.20	3.99	2.69
	VI	4.20	4.22	4.25	4.35	4.44	4.53
5	I	3.69	1.81	0.51	0.33	0.29	0.30
	II	4.04	4.07	4.23	4.33	4.36	4.42
	III	4.17	4.20	4.30	3.98	3.54	2.02
	IV	4.17	4.23	4.31	4.37	4.43	4.50
	V	4.15	4.14	4.17	3.59	1.61	1.07
	VI	4.18	4.21	4.25	4.33	4.46	4.54

TABLE V:

The 50^th percentile phase velocity of the inclusion for Model DH and various LPVI processing scenarios. Values are presented in the unit of m/s.

Noise level [dB]	Processing	Frequency [Hz]
		500	600	700	800	900	1000
No noise	I	4.16	4.03	4.10	4.25	4.25	4.40
	II	4.05	3.99	4.12	4.24	4.26	4.40
	III	4.15	4.16	4.22	4.31	4.35	4.42
	IV	4.19	4.15	4.23	4.30	4.35	4.43
	V	4.24	4.19	4.19	4.26	4.34	4.42
	VI	4.24	4.19	4.20	4.25	4.33	4.43
20	I	4.15	4.02	4.06	4.21	3.41	2.86
	II	4.05	3.99	4.12	4.24	4.25	4.40
	III	4.16	4.16	4.21	4.30	4.34	4.39
	IV	4.19	4.15	4.23	4.30	4.35	4.43
	V	4.25	4.19	4.20	4.26	4.31	4.33
	VI	4.24	4.19	4.20	4.25	4.34	4.43
15	I	4.16	4.03	3.29	2.13	0.97	0.64
	II	4.04	3.99	4.11	4.24	4.25	4.39
	III	4.16	4.14	4.22	4.29	4.27	4.30
	IV	4.20	4.15	4.23	4.30	4.35	4.43
	V	4.26	4.17	4.18	4.22	4.18	3.86
	VI	4.24	4.18	4.21	4.25	4.32	4.43
10	I	3.96	2.40	0.54	0.37	0.32	0.31
	II	4.05	3.99	4.11	4.24	4.25	4.39
	III	4.15	4.16	4.22	4.22	3.99	2.60
	IV	4.19	4.15	4.24	4.31	4.34	4.42
	V	4.23	4.14	4.11	3.94	2.59	1.92
	VI	4.21	4.19	4.20	4.25	4.32	4.45
5	I	1.44	0.34	0.24	0.25	0.25	0.27
	II	4.02	4.00	4.11	4.24	4.19	4.29
	III	4.18	4.12	3.99	3.21	1.40	0.82
	IV	4.19	4.15	4.23	4.31	4.34	4.41
	V	4.19	4.06	3.73	2.19	0.66	0.63
	VI	4.22	4.19	4.19	4.23	4.31	4.38

Appendix

Tables II - VI present the 50^th percentiles of the sample data for the reconstructed shear wave phase velocity, using the new implementation of LPVI, for the clean data and with an SNR of 20, 15, 10, and 5 dB. Results for six different frequencies of 500, 600, 700, 800, 900, and 1000 Hz are summarized. Models, A, B, C, and D are investigated, respectively.