Automated calculation of spectral-reflectance marker-points to enable analysis of plant colour-signalling to pollinators

Abstract

A spectral reflectance curve for a coloured surface can be constructed from a set of radiation reflectance value measurements made across the spectrum at discrete wavelengths. The curve gives an indication of the pattern of light entering the eye of an organism viewing an illuminated object. Marker points represent the positions along a reflectance curve at which sharp transitions in reflectance occur, these being potentially important to visual perception, for instance by insects discriminating between two flowers, each of a different colour. Consequently, methods of marker point analysis have been applied in several studies evaluating flower colours. These studies have sometimes required researchers to place marker points on reflectance curves by eye, or they have used algorithms written as unreleased software. To automate the process systematically and provide open access, we implemented special-purpose software in C++. Below we provide a summary of the approach adopted in our implementation and made available online in a port to TypeScript. The main benefits of our method are summarized as being:

• •Automation and repeatability.
• •Standardisation, cross-platform compatibility and Open Access.
• •Interactive exploration of the effects of parameter variation.

Graphical abstract

Specification Table

Subject Area:	• Agricultural and Biological Sciences
More specific subject area:	• Colour perception and software analysis of natural surface spectral reflectance
Method name:	Spectral-MP: Software-based spectral reflectance curve markerpoint placement
Name and reference of original method:	Chittka, L and R Menzel, The evolutionary adaptation of flower colors and the insect pollinators' color vision systems. Journal of Comparative Physiology A, 1992. 171: p. 171-181.
Resource availability:	https://ecosim.infotech.monash.edu/SpectralMP/,https://github.com/Monash-Ecological-Simulation/SpectralMPDOI: to be determined once the method approaches publication.

Method details

To understand how organisms visually perceive an environment, it is important to know the spectral reflectance properties of the surfaces they perceive. These may be documented in the form of spectral reflectance curves. These curves are plots of the percentage of incident radiation reflected at each wavelength across the region of the spectrum relevant to the visual system of the organism under study [Fig. 1]. An organism may perceive variations in reflection across the spectrum as differences in surface colour or brightness, depending on its perceptual physiology and cognitive system [8]. This article introduces a new tool to automatically calculate key features of spectral reflectance, marker points, that enable us to unravel the complexity of the interactions between evolved colour signals, such as flowers, and the animals they target as pollinators.

Fig. 1.

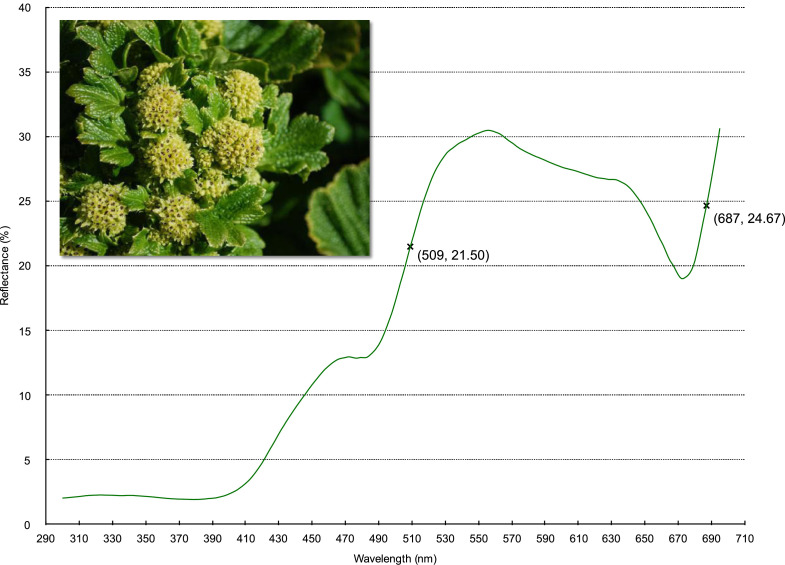
Reflectance spectrum of a sample cream-green flower, Stilbocarpa Polaris (Araliaceae). Crosses indicate marker points calculated with Spectral-MP parameters: Amplitude=10%, Range=50 nm, Lookahead=5, Smoothing=0. [Inset image © Copyright Natalie Tapson 2014, RTBG Tasmania. Used with permission.]. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Any location on a surface's spectral reflectance curve where rapid changes in reflectance occur, is potentially helpful in understanding colour perception of the surface by organisms [4,13]. The centers of these sharp reflectance steps have been termed inflection points [11,13] and marker points [2,14]. In this article, we call them by the latter name. We provide a brief overview of the value of marker points, before explaining our algorithm, and online Spectral-MP interactive software, for calculating their positions.

Marker point analysis has often been applied in studies evaluating the interactions between animal pollinators and flower colours – their analysis has been valuable in understanding colour vision of flowers in Hymenoptera (bees, wasps, ants etc.), Lepidoptera (butterflies, moths), and even avian pollinators [4,5,[11], [12], [13]. As floral signaling to pollinators is the application for which we expect our software to be most widely used, we shall explain the concept of marker points briefly within this context. For further detail, see [4,13].

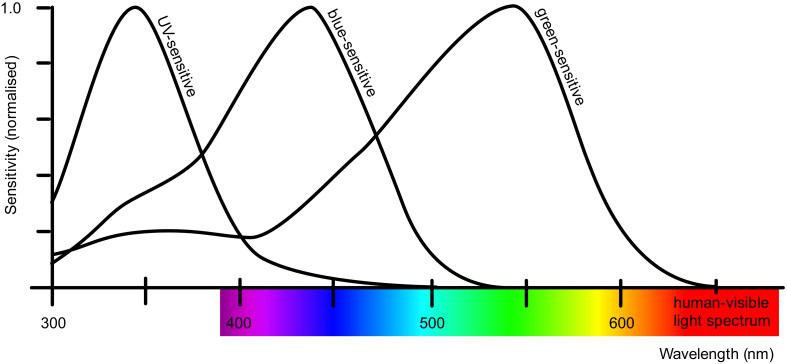
Colour vision systems incorporate photoreceptors that convert captured light into signals made available to an organism's brain for processing. These photoreceptors most effectively capture light within particular wavelength bands, and, because of the principle of univariance [6,9], can be conveniently described by reference to locations of maximal sensitivity to spectral radiation [Fig. 2]. Bee colour vision is phylogenetically constrained [1] and thus, all bees are trichromats – their 3 types of photoreceptor are centered at 344 nm (UV region), 436 nm (“blue” region) and 544 nm (“green” region). Humans are also trichromats, but our 3 photoreceptor types are most sensitive at 420 nm (“blue” region), 534 nm (“green” region) and 564 nm (“red” region). In practical terms, this means that bees and humans do not view the world in the same way. Bees see more towards the UV end of the spectrum than we do [7].

Fig. 2.

The sensitivities of the three honeybee (worker) photoreceptors are approximated with solid black lines in the figure: UV-sensitive (max. sens. 344 nm), blue-sensitive (max. sens. 436 nm) and green-sensitive (max. sens. 544 nm) receptors [8, Table 2 and Fig. 6a]. The human-visible spectrum is illustrated in the x-axis colour bar (~380 – ~740 nm) to enable comparison. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

The regions of peak sensitivity of an organism's photoreceptors do not directly tell us about an organism's ability to distinguish colours however. Colour perception depends on the relative position of photoreceptors, since colour is a result of the comparison by an organism's brain of signals from two (or more) photoreceptors [7,8]. Organisms are most sensitive to the differences between colours (they can make the finest colour discriminations) where surface reflectance changes rapidly in regions of overlapping photoreceptor sensitivity, allowing the organism's brain to compare the signals from at least two different types of photoreceptor. Honeybees and bumblebees for example, are sensitive to colours with rapid reflectance change around 400 nm and/or 500 nm (see [15]), regions either side of their “blue”-sensitive photoreceptor that are overlapped by the UV- and “green-” sensitive receptors respectively [3,8].

Since coloured flowers are plants’ signals to their animal pollinators, the locations of rapid change in reflection on the spectral reflectance curves of their petals is informative. These are the locations our algorithm identifies as marker points. Marker point positions can, for instance, help us to tell which pollinators are most likely to be the target for a specific flower, and they can help us to predict which flower colours an animal is likely to struggle to distinguish. Generally speaking, we can use marker points to help unravel the complexity of visually-guided plant-pollinator interactions [13], even in cases where we do not have a lot of detail on the visual system of the organism under study, or when we are studying two organisms with different visual systems [10].

To date, some studies have relied on the human eye to place marker points on spectral reflectance curves [4], or used algorithms written in Mathcad [11, Appendix S1] or R [2]. To automate the process systematically so that it can be applied to large datasets quickly, reliably, and easily, and so that the method can be applied consistently across multiple studies in the future, we have implemented special-purpose software in C++ which we have called Spectral-MP. We have ported Spectral-MP to TypeScript to make it available in an accessible online and interactive form, further simplifying the process of exploring the implications of marker points of varying parameters. The details of our algorithm are explained below.

Data format

Spectral reflectance readings of a surface measured using a spectrophotometer are taken, ideally in replicate, prior to the use of our software and stored in a single CSV file with an optional header-row. Measurements should be made at uniform wavelength increments and stored in monotonic increasing order. The file may be formatted in one of two ways: (1) Single-wavelength format has the first column holding the wavelength values against which the subsequent columns contain multiple replicate measurements of reflectance at that wavelength [Table 1a]; (2) Multi-wavelength format stores pairs of wavelength/reflectance replicate measurements across a row. All replicates in the multi-wavelength format file on a single row still correspond to measurements made at the same wavelength, as they do in the single-wavelength format. However, the wavelength value is repeated in every second column of the multi-wavelength format file [Table 1b].

Table 1a.

Example single-wavelength file format.

Wavelength (nm),	Reflectance (%),	Reflectance (%),	…,	Reflectance (%)
400.5,	50.001,	50.003,	…,	50.002
400.75,	50.011,	50.020,	…,	50.019

Table 1b.

Example multi-wavelength file format.

Wavelength (nm),	Reflectance (%),	Wavelength (nm),	Reflectance (%),	…,	Wavelength (nm),	Reflectance (%)
400.5,	50.001,	400.5,	50.003	…,	400.5,	50.002
400.75,	50.011,	400.75,	50.020	…,	400.75	50.019

Replicate averaging and data-clipping

Our software averages replicate values between 0 and 100% reflectance at each data-point to generate a single new curve representing the spectral reflectance of the surface. If no valid replicates at a data point fall above 2.0%, the reflectance at that wavelength is clipped at 2.0%; this being the reflectance of black coal, a very dark natural surface. If no valid replicates at a data point fall below 100.0%, the reflectance at that wavelength is capped at 100.0%. This is the theoretical maximum reflective value for natural surfaces such as flower petals.

Algorithm overview

The algorithm is composed of two main functions to process the spectral reflectance curves. The first detects monotonically increasing or decreasing sub-curves. The second tests the gradient of these, and possibly sub-divides them further, to determine if their reflectance amplitude changes within the wavelength range required to meet the criteria specified for marker point placement.

Function 1: sub-curve detection

A sub-curve is an ordered series of monotonically increasing or decreasing DataPoints (λ,%), each with a wavelength λ (independent variable) and reflectance reading% (dependent variable). Each sub-curve is delimited by a StartPoint (λ,%) and EndPoint (λ,%). The sub-curve detection algorithm "grows" a sub-curve by pushing its Endpoint out from its StartPoint in the direction of increasing λ, until an inflection point on the curve is reached. (N.B., by inflection point, here we mean a change in the direction of the curve's slope – the conventional use of the term; this is not to be confused with the earlier use of inflection point (discussed above) to denote what we are calling here a marker point.) When an inflection point is encountered, a sub-curve is concluded. The concluded sub-curve is tested by our second function (below) for marker point potential. The sub-curve detection process restarts from the DataPoint immediately following the Endpoint of the previous sub-curve and continues to sub-divide the curve until the last of the useable DataPoints is processed.

Function Sub-curve detection

Data:

// Curve stored as a list of DataPoints[1..N](wavelength λ, reflectance%)

//   DataPoints are ordered according to increasing λ.

// Look-ahead distance LA, specified in data point indices.

//   LA is used to check curve slope in the direction of increasing λ.

// DataPoint[x] (λ), the wavelength value of DataPoint[x].

// DataPoint[x] (%), the reflectance value of DataPoint[x].

Initialisation:

CurStartPoint          ← DataPoint[1](λ,%)

FinalEndPoint          ← DataPoint[N-LA](λ,%)

PreviousSlopeDirection ← Rising

Algorithm:

For each DataPoint[i] in range CurStartPoint (exclusive) .. FinalEndPoint (inclusive) in the sequence

Set CurEndPoint ← DataPoint[i]

// Compute the mean reflectance from CurEndPoint out to a distance of [i+LA]

μ% ← ComputeAverage (DataPoints[i, i+1 .. i+LA](%))

If μ% < CurEndPoint (%)

Then SlopeDirection ← Falling        // The curve is falling ahead

Else if μ% > CurEndPoint (%)

Then SlopeDirection ← Rising         // The curve is rising ahead

Else

SlopeDirection ← PreviousSlopeDirection   // Treat the curve as “unchanged” ahead

|

| If (PreviousSlopeDirection NOT-EQUAL-TO SlopeDirection) OR (CurEndPoint EQUAL-TO FinalEndPoint)

| |

| | Then // This is an inflection point or end of data, a monotonic sub-curve is concluded.

| |      // Test the concluded sub-curve's marker point suitability.

| |     MarkerPointSuitabilityTest (CurStartPoint, CurEndPoint)

| |

| |     // Continue the loop to identify the next sub-curve

| |     CurStartPoint ← CurEndPoint[i+1](λ,%) // Start at the DataPoint after CurEndPoint

| |     PreviousSlopeDirection  ← SlopeDirection

| |

| Else

| | Continue // Continue with the loop, pushing CurEndPoint another step from CurStartPoint

Function 2: steepness test

This method processes each monotonically increasing or decreasing sub-curve detected by the algorithm above. We check if the sub-curve meets the user-specified amplitude threshold within the user-specified wavelength range limit. If it does, then the entire sub-curve warrants marker point placement. If an entire sub-curve contains a sufficiently high reflectance step, but fails the wavelength limit test (i.e. the reflectance step is spread across a wide wavelength range), we divide the sub-curve into further sub-sections for individual assessment. A section of sub-curve is delimited by SectionStartPoint .. SectionEndPoint. We scan these in order of increasing wavelength and stop the scan if the steepness criteria are met, in which case a central marker point can be placed on the sub-curve, or the end of the sub-curve is reached.

Function Steepness test

Input parameters:

StartPt, the first point of the monotonically increasing or decreasing sub-curve to be tested

EndPt, the last point of the monotonically increasing or decreasing sub-curve to be tested

Data:

// Curve stored as a list of DataPoints[1..N](wavelength λ, reflectance%)

//   DataPoints are ordered according to increasing λ.

// Δ%-min, a minimum reflectance change (i.e. a reflectance threshold).

// Δλ-max, a maximum wavelength change (i.e. a wavelength limit).

// SectionStartPt, the beginning of a sub-section of the input segment under analysis.

// SectionEndPt, the end of a sub-section of the input segment under analysis.

Algorithm:

// Exit if the entire sub-curve cannot surpass Δ%-min.

If absoluteValue (EndPt(%) - StartPt(%)) < Δ%-min

Then Exit

// Search if we have a sub-section to satisfy Δ%-min and Δλ-max.

For Each DataPoint SectionStartPt such that (SectionStartPt<EndPt)

| For Each DataPoint SectionEndPt such that (SectionEndPt>SectionStartPt) AND (SectionEndPt≤EndPt)

| |

| | SectionAmplitude ← absoluteValue (SectionEndPt(%)- SectionStartPt(%))

| |

| | If SectionAmplitude ≥ Δ% // If section reflectance change meets the threshold criterion

| | |

| | Then SectionRange    ← (SectionEndPt(λ)-SectionStartPt(λ))

| | |

| | |    If SectionRange < Δλ-max // If section wavelength change falls within the limit

| | |    |

| | |    Then  // We have a valid sub-section so the whole sub-curve requires marker placement

| | |    |     MarkFullSubcurve (StartPoint, EndPoint)

| | |    |     Return

| | |    |

| | |    else  // The current section is already too wide given a valid Δ%-min.

| | |    |     // Hence, continue with the outer loop, starting a new sub-section.

| | |    |     Break

| |

|

Curve sub-segment detection

Since marker points occur on sections of the curve where sharp steps in reflectance occur, the data is processed to establish which data points lie on monotonically increasing or decreasing sub-segments. To achieve this, the curve's slope is assessed at each data-point by looking towards increasing wavelengths an amount specified as a “look-ahead” distance specified in data-points. This allows computation of the projected trend in the curve at a data point in a way that cushions the calculation of segment gradient from the smoothing parameter specified using the Spectral-MP software (see below), or any offline pre-smoothing process applied. The approach also acts as an intermediary between gradient calculation and small-scale noise or micro-fluctuations in the data that would not, using manual marker-point placement, have been detected by the naked eye at a practical level of curve magnification. Additionally, the look-ahead enables the user to ensure that the algorithm for marker point placement does not act on what are believed by the user to be imperceptible or irrelevant curve features for hymenopteran, avian or human viewers, depending on their subject; i.e. micro-fluctuations in reflectance over wavelengths of the order of some specified threshold.

The look-ahead value is specified in data points (rather than nm) to ensure the user explicitly considers the resolution of their data and does not inadvertently request an estimate of the gradient at a scale less than is justified by the resolution of their data. For instance, if the file contains reflectance readings at 5 nm intervals, or contains even a little noise, it would make no sense to compute sub-sample gradient estimations over 0.5 nm intervals. Even an estimate over a 5 nm interval would be unreliable. However, this would, in our system, be specified as a “1 step” look-ahead, which, from the user's perspective, is clearly insufficient as a reliable measure of projected trend, especially in noisy data.

Curve sub-segment threshold calculation

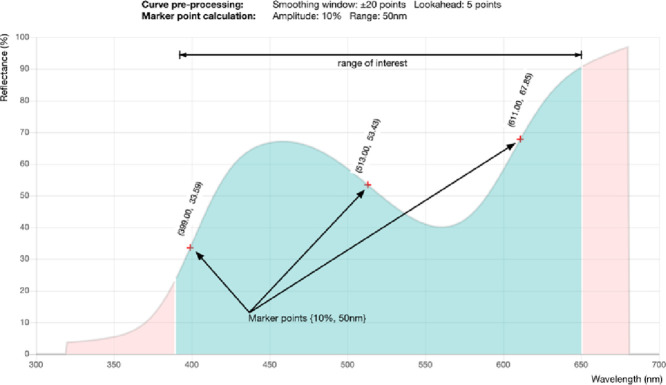
Our algorithm, and marker point placement methods in general, attempt to locate markers only on curve sections exceeding a specified gradient threshold. The software assesses each monotonically increasing or decreasing curve sub-segment identified above to determine if it contains a change in amplitude beyond a specified percentage total reflectance (perhaps 10%) and a horizontal span less than a maximum specified wavelength range (such as 50 nm). If these criteria are met, all data points within the sub-segment are, at this point in the process, tagged as potential markers.

Any curve segments failing the wavelength range limit, but meeting the reflectance change threshold, are exhaustively subdivided to the level of individual data-points, to test if any sub-segments meet the required criteria. If these sub-segments then qualify, the data points lying along the entire monotonically increasing or decreasing sub-curve on which they lie may potentially be marker points. Consequently, all of the points on the curve segment, not just those in the part of it that met the criteria, are individually tagged as potential markers for the next stage of the process.

Marker-point placement

Any data points lying on any curve segments that meet the required reflectance amplitude change within the required wavelength range identified above are potentially suitable as marker point locations. The algorithm will, finally, tag any of these data points as marker points if, and only if, they contain the closest reflectance reading on their sub-segment to the sub-segment's vertical center.

Smoothing

Data files may be smoothed using any standard approaches prior to loading into the Spectral-MP software. However, for convenience, if raw data is loaded into the software, the curve may be smoothed within the Spectral-MP interface by applying uniformly weighted averaging across a user-specified range of data points centered on the value being smoothed. Note that smoothing will potentially impact on marker point placement and this parameter should be recorded with all data/results. For instance, considering the curve in Fig. 1, if the smoothing is increased, the slight dip in the reflectance around 470 nm could be “smoothed away”. In this case, the entire region from 390 nm - 550 nm would become a single monotonically increasing sub-section to be considered against the user-specified steepness criteria. With this dip present, the two sub-sections lying either side of it are instead considered individually by the algorithm.

Software input/interface/output/licensing

The Spectral-MP software allows online web-based drag-and-drop loading of multiple files in CSV format. Interactive tools are provided for basic uniform smoothing of uploaded data, and specification of the algorithm's essential parameters. Marker points and other curve data are displayed in real-time and plotted immediately in wavelength bins for bulk data analysis. Data, including graphics files of the marker and curve visualisations, and the binned data, are available for immediate bundled ZIP-archive download via the web interface.

• •The software is available online under an ISC license: https://ecosim.infotech.monash.edu/SpectralMP/ and for download: https://github.com/Monash-Ecological-Simulation/SpectralMP.
• •For use in published research, cite by reference to this paper.
• •For software (re)use specifically:

Copyright 2019 Alan Dorin and Matthieu Herrmann

Permission to use, copy, modify, and/or distribute this software for any purpose with or without fee is hereby granted, provided that the above copyright notice and this permission notice appear in all copies.

THE SOFTWARE IS PROVIDED "AS IS" AND THE AUTHOR DISCLAIMS ALL WARRANTIES WITH REGARD TO THIS SOFTWARE INCLUDING ALL IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS. IN NO EVENT SHALL THE AUTHOR BE LIABLE FOR ANY SPECIAL, DIRECT, INDIRECT, OR CONSEQUENTIAL DAMAGES OR ANY DAMAGES WHATSOEVER RESULTING FROM LOSS OF USE, DATA OR PROFITS, WHETHER IN AN ACTION OF CONTRACT, NEGLIGENCE OR OTHER TORTIOUS ACTION, ARISING OUT OF OR IN CONNECTION WITH THE USE OR PERFORMANCE OF THIS SOFTWARE.

Declaration of interests

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.