How migratory populations become resident

Abstract

Migratory behaviour is rapidly changing in response to recent environmental changes, yet it is difficult to predict how migration will evolve in the future. To understand what determines the rate of adaptive evolutionary change in migratory behaviour, we simulated the evolution of residency using an individual-based threshold model, which allows for variation in selection, number of genes, environmental effects and assortative mating. Our model indicates that the recent reduction in migratory activity found in a population of Eurasian blackcaps (Sylvia atricapilla) is only compatible with this trait being under strong directional selection, in which residents have the highest fitness and fitness declines exponentially with migration distance. All other factors had minor effects on the adaptive response. Under this form of selection, a completely migratory population will become partially migratory in 6 and completely resident in 98 generations, demonstrating the persistence of partial migration, even under strong directional selection. Resident populations will preserve large amounts of cryptic genetic variation, particularly if migration is controlled by a large number of genes with small effects. This model can be used to realistically simulate the evolution of any threshold trait, including semi-continuous traits like migration, for predicting evolutionary response to natural selection in the wild.

1. Introduction

Every year, billions of animals travel between their breeding and non-breeding areas. These migratory movements are highly adaptive, as they allow migrants to reproduce in seasonal environments that have a high abundance of food only during a short period of time. For migration to confer an adaptive advantage, migratory movements need to be synchronized with the periods of favourable conditions in the areas of reproduction and passage, and in the non-breeding areas [1,2]. Yet if environmental conditions change, migratory organisms need to re-adjust migration schedules, distances and routes in order to persist. The mechanisms underlying changes in migratory behaviour have been particularly well studied in birds: while some long-lived species (e.g. cranes, storks) modify migratory behaviour predominantly by learning and following experienced individuals [3,4], most migratory populations show little flexibility, suggesting that an adaptive adjustment of migration can only be achieved by evolutionary change [5–7].

In the last two decades, the response of migratory birds to global change has been of major interest [2,6,7]. It is predicted, and has been observed, that an important adaptive response of migrants to the increase in global temperatures is the shift of non-breeding areas towards the areas of reproduction. This not only reduces energetic costs by shortening migration distance but also allows birds to readjust the timing of their lifecycle to the phenological shifts in the breeding area by advancing spring arrival [8–10]. While it is well established that global warming will favour residency, it is largely unknown which populations of migrants have the potential to adapt and whether adaptive changes will be rapid enough, and persist for sufficient time, to keep track with environmental changes. These predictions can only be made by modelling the evolutionary response to selection favouring residency, and identifying the factors that affect adaptation.

In recent years, some effort has been made to elucidate how environmental conditions may affect the fitness of residents and migrants, particularly in partially migratory populations [11–13]. Yet none of these models of the evolution of migration, or the persistence of partial migration, accounted for what we currently know on the genetics of migratory behaviour (i.e. that it is a polygenic threshold trait, controlled by many genes with small effects [6,8,14]). As it is unknown how this may have affected the reliability of models, there is an urgent need for an evolutionary model of migration, which incorporates these findings and is tested against empirical data. The threshold model of migration, which is strongly supported by studies in a variety of organisms [6,15–19], assumes that there is a normally distributed polygenic liability trait that influences an individual's migratory behaviour. Individuals with a liability equal to or below the migration threshold are resident and those with a liability above the threshold are migratory. In every migrant, migratory liability is phenotypically expressed as migratory activity, a continuous behavioural trait in which higher values correspond to a stronger migratory urge that is associated with migrating larger distances [15,19]. In birds, migratory activity can be quantified in captivity by measuring its proxy, migratory restlessness [6–8,19]. This semi-continuous pattern of expression of migratory behaviour differs from the one expected for ‘typical’ threshold traits, which are dichotomous [20–22]. We may expect selection responses in semi-continuous threshold traits to be stronger than in dichotomous traits, since selection may act on both the categorical (migrant or resident) and the continuous (amount of migratory activity) aspect of the trait at the same time [8,15,19].

Currently, the most comprehensive data on the evolution of avian migration are available for the Eurasian blackcap, a small passerine bird species, which is a model species for the study of the genetics and evolution of bird migration [6–8,14]. The results of a selection experiment and the observed reduction in migratory activity in the wild suggested that a completely migratory blackcap population could become resident in response to selection for lower migratory activity in a few decades [8]. The wealth of information provided by this experiment makes it possible to build an evolutionary model and to validate it by direct comparison with empirical data.

Here, we present an individual-based simulation model for the evolution of semi-continuous threshold traits, which we fitted to published data on evolutionary changes in migratory activity of the blackcap. The aim of this study was firstly to assess the importance of the parameters that are likely to affect evolutionary change in migratory behaviour, like the strength and form of selection, the number of genes, mutational variance, environmental effects or assortative mating. A second aim was to build a model that will allow us to better understand and predict the rate, direction and limitations of adaptive evolutionary changes in migration.

2. Material and methods

(a). Simulation model

Like the models by Roff [21,22], which we used as a starting point, our model is an individual-based simulation model of threshold trait evolution, where the genetics is modelled explicitly. We considered the semi-continuous expression of migration, and made it more flexible to allow variation in allelic effects, environmental effects, mutational variance and assortative mating. Our model allows adjusting parameters (e.g. phenotypic and genetic variance) to those found in natural populations, which made it possible to generate predictions that could be compared directly with empirical data. For a full description of the model and the R code [23], see electronic supplementary material. Briefly, individuals are diploid at each of n loci, and every allele is characterised by a single value that corresponds to its contribution to migratory liability. The sum of all the allelic values of an individual gives its genetic value for migratory liability, such that alleles are co-dominant. The phenotypic value of migratory liability of an individual is the sum of its genetic value and a random environmental effect. We assume that if individuals have migratory liabilities above the threshold value, which is zero, they are migrants; the amount of migratory activity is given by their value of migratory liability [6,15,19]. If liabilities are equal or below zero, individuals are resident and show no migratory activity. The model proceeds in discrete time-steps such that in each generation the population is made up of individuals with these characteristics.

After initialisation (see below), the following processes were repeated every generation: (i) selection, (ii) reproduction, (iii) mutation, (iv) computation of genetic values and liabilities, and, if thresholds were variable, (v) assignation of individual threshold values (electronic supplementary material, figure S1).

(i). Submodels

Selection. We imposed selection through fitness functions that determined an individual's relative survival probability from its migratory behaviour. Individuals with zero or negative liability all had the same fitness. For individuals with liabilities above the threshold, we calculate fitness from their amount of migratory activity. These relative fitness values then determined an individual's probability of being sampled into the surviving fraction of the population (for the specific fitness functions used, see below).

Reproduction. To simulate random mating, the selected individuals were paired at random. Each pair produced a fixed number of offspring, such that the population size remained constant. The allele effects of the offspring at each locus were obtained by randomly sampling an allele from each parent at this locus.

To simulate assortative mating, we used the folded normal distribution mating-preference function [24], which determines the mating probability of two individuals based on the difference between their phenotypic values. To increase the strength of assortative mating, we modified the parameter values of this function to give a higher mating probability to individuals with more similar levels of migratory activity (see electronic supplementary material).

Mutation. We assumed a continuum-of-alleles mutation model. At every generation, each allele had a certain probability of mutating, in which case its new value was given by the original value plus a random deviate sampled from a normal distribution of mean zero. This is a commonly used mutation model in quantitative genetics which, unlike the house-of-cards mutation model, is not biased towards a particular state [25].

Computation of individual migratory liability. For every individual, migratory liability was calculated as the sum of the genetic value and an environmental effect, which was randomly sampled from a normal distribution with a mean of 0. The variance of the environmental effects, which is assumed to remain fixed over time, was the one required to generate a population with a specific initial phenotypic variance and heritability (see below).

Threshold variance. To explore the effect of variance in threshold values, we introduced a step in the simulation process where individuals were randomly assigned a threshold value which was sampled from a normal distribution. This allowed us to simulate a situation where individual threshold values depend on random variation in the environment [19].

(b). Simulation of the evolution of residency in a migratory bird population

(i). Initialisation and fixed parameters

To simulate the evolution of migration, we used published data on the migratory blackcap population of southern Germany [8]. The purpose of initialisation was to create populations resembling this population in 1988, so that simulation results could be compared with empirical data for the following years. Thus, the initial mean and standard deviation in migratory activity were set at 1045 and 376 half-hour intervals with activity, respectively, and the initial heritability of migratory activity was set at 0.432 (electronic supplementary material, table S1; see [8] for details). To generate populations with these characteristics, we assumed that the population initially was in mutation–selection–drift equilibrium. Thus, we first allowed populations to evolve under stabilizing selection imposed by a Gaussian fitness function that was centred at an optimum of 1045. The initial genetic variance was manipulated by adjusting the width of the fitness function and, thus, the strength of stabilizing selection. Mean migratory activity, genetic variance, the distribution of allele effects and the number of alleles per locus stabilized after approximately 4000 generations, yet we run this ‘burn-in’ for a total of 15 000 generations to discard any effect of initial conditions (see electronic supplementary material).

Throughout the simulations, the number of offspring per pairing was set to 5, in agreement with the modal clutch size in this population [26]. Population size was fixed at 1000. Although the population of Eurasian blackcaps is very large [27], we expect this to be a good approximation since the species is philopatric and dispersal is limited [26], which reduces deme size. Moreover, increasing the population size beyond this point is unlikely to affect the equilibrium genetic variance, allele frequencies and phenotype frequencies for a threshold trait under selection [22].

(ii). Tested parameters

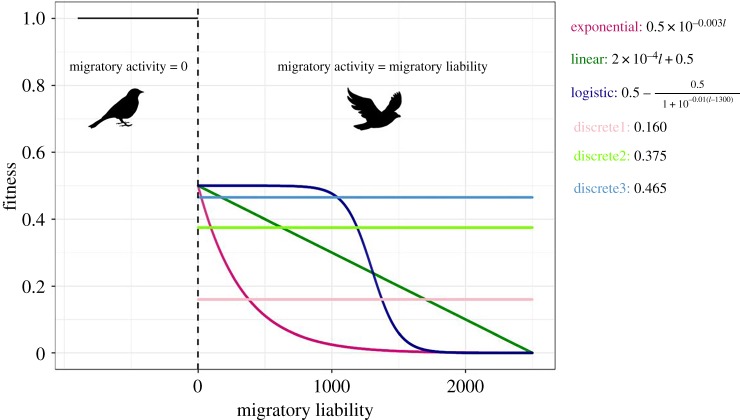
Strength and form of selection. We designed fitness functions that (i) simulated selection regimes that are biologically plausible for migratory birds, and (ii) that were sufficiently distinct from each other to allow exploring a large range of selection effects. In all functions, we assumed that the fitness of migratory individuals is reduced by at least 50% compared to resident individuals. This is a realistic assumption since migrants leave the breeding territories after reproduction, and, therefore, every spring, they must obtain a new territory. The best territories, however, are occupied by residents, which have the advantage of prior residency [28,29]. Furthermore, a number of studies have shown that residents have higher fitness than (short-distance) migrants [30–32], and that birds with longer migration distance have lower fitness [33,34]. Based on these findings, we designed three continuous fitness functions: one where the decline in fitness with increasing migratory activity is exponential, one where it is linear and one that follows a logistic relationship (figure 1).

Figure 1.

Relationship between fitness and migratory liability for the fitness functions used in the simulations (distinguished by colour). The dashed line represents the migration threshold. Migratory liability of residents is smaller than this value, in migrants it is larger. Note that residents are given a fitness of 1 (horizontal line) under all fitness functions. (Online version in colour.)

To distinguish the effect of selection on the dichotomous trait (migratory status) from the effect of selection on the continuous trait (migratory activity), we compared each of the three fitness functions to a discrete function (figure 1). Each discrete function was generated by giving all migrants the same fitness value, which equals the mean fitness of migrants in the continuous function (electronic supplementary material, table S2).

Genetic architecture. The only locus so far found to be associated with migratory activity in blackcaps explains approximately 6–8% of the additive genetic variance for this trait [35]. Thus, if other migration genes have a similar effect, we would expect migratory activity to be controlled by about 12–16 loci. Genome-wide association studies (GWAS) and gene expression studies found 4–18 loci differing between birds with differences in migratory behaviour [36–38]. However, recent theoretical and empirical studies indicate that most quantitative traits are controlled by a large number of genes with very small effects [39,40]. This was also suggested in a GWAS analysis of the control of migration in fish [41]. In order to cover this range of potential values, we ran all simulations with either 10 or 200 loci.

The input of genetic variation for quantitative traits by mutation may be described by the mutational heritability, which is the mutational variance scaled by environmental variance $(h_m^2=\text{VM/VE) }$. Since this parameter has not yet been estimated for migratory activity, we used the median value that has been estimated for other quantitative traits ($h_m^2=0.00184$; see [25]). Much less is known about the parameters underlying mutational variance, such as the per locus mutation rate and the distribution of effects of new mutations. The per locus mutation rate could range between 10⁻⁶ and 10⁻⁴ for standard quantitative trait loci, but may be as high as 10⁻² for STR loci, which are expected to provide an important contribution to genetic variance [25,42]. To obtain the same mutational heritability under 10 and 200 loci, we assumed that the rate and effect of new mutations were higher if the trait is governed by fewer loci (10 loci: σ_α = 86 and µ = 10⁻³; 200 loci: σ_α = 61 and µ = 10⁻⁴). We chose this combination of parameters because it assumes per locus mutation rates which are within the expected range and sufficient for genetic variation to be maintained at the levels observed in the blackcap population under mutation-selection-drift equilibrium.

Assortative mating. To test the effect of assortative mating, we compared simulations assuming random mating with those obtained under two levels of assortative mating. A common way of quantifying the strength of assortative mating is measuring the correlation r between parental phenotypic values. Although direct estimates are unavailable, we covered the range of values that are realistic for migration in blackcaps [43], by running simulations with r = 0.25 and r = 0.70. This range includes 95% of the values reported for birds in a meta-analysis of assortative mating [44].

Threshold variance. To test the effect of environmental variance in threshold positions, we compared results obtained assuming a fixed threshold with simulations ran with a standard deviation in the threshold position of 100 and 300 half-hour intervals with activity. Although there are no empirical estimates of threshold variance, we expect these values to be reasonable because they are similar in magnitude to the environmental variance in migratory activity. To evaluate if the influence of environmental variance depends on the form of selection, we ran these simulations with both the exponential and the corresponding discrete fitness functions.

(c). Analysis of simulation results

For each combination of parameters, we ran 20 replicate simulations for 100 generations. For every generation, we computed the mean, variance and heritability of migratory liability, and the proportion of resident individuals averaged across all replicate simulations. Heritability was calculated as the variance in genetic values divided by the variance in migratory liability values.

We compared the changes in migratory activity predicted under different combinations of parameters with observed values in German blackcaps between 1988 and 2002 [8]. Empirical values were obtained by measuring migratory restlessness in a common garden experiment and are given in half-hour intervals where birds show activity at night (see [8], for details). In the simulations, migrants have a value of migratory activity that equals their individual migratory liability (see above). It is given in the same unit as migratory restlessness. To compare predicted and observed changes over time, we converted generations of selection into years, assuming a mean generation time for blackcaps of 2 years [26]. For each combination of parameters, we computed a loess line of best fit for the relationship between time (in years) and migratory activity (in half-hour intervals with migratory activity) using the loess function in R v. 3.4.1 [23]. For a quantitative assessment of fit, we generated yearly predictions of mean migratory activity from the lines of best fit and estimated the variance explained by cross validation (VEcv) and mean absolute error (MAE) by contrasting them with the observed values of mean migratory activity [45].

3. Results

(a). Effects of selection and genetic architecture

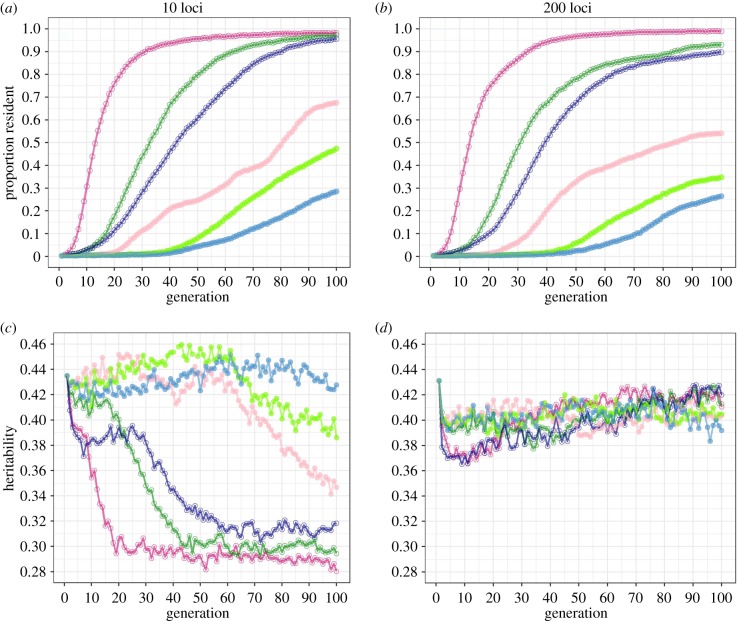
Semi-continuous fitness functions (i.e. those that imposed differential selection on migratory activity) always led to a faster evolution towards residency than their corresponding discrete functions (figure 2a,b). In fact, the model predicts that the evolution of residency without selection on migratory activity would be very slow. Even when the fitness of migrants was 16.5% that of residents, substantial increases in the frequency of resident individuals occurred only in a few simulations (electronic supplementary material, figure S5), and the mean proportion of resident individuals remained below 70% after 100 generations. By contrast, semi-continuous fitness functions led to a fast increase in the frequency of residents, with most populations approaching complete residency within 100 generations. Among these, the exponential fitness function lead to the fastest response (figure 2a,b).

Figure 2.

Evolutionary response (a,b) and heritability (c,d) in a migratory population selected for residency under six different fitness functions, assuming 10 (a,c) or 200 loci (b,d). Different fitness functions are distinguished by colour (figure 1). Filled points give discrete fitness functions, open points semi-continuous functions. Each point represents the mean of 20 simulations. (Online version in colour.)

The number of loci assumed to affect migratory liability had little impact on the rate at which residency evolved but greatly affected the reduction of heritability for migratory liability (figure 2c,d). With 200 loci there was little change in heritability over time, except for a slight decrease with continuous fitness functions followed by an increase towards initial levels. With 10 loci, however, heritability decreased from 0.432 to about 0.30 in populations that evolved under continuous fitness functions and, therefore, had shown strong evolutionary change. If selection led to weak responses (discrete2 and discrete3), heritability remained virtually unchanged (figure 2c,d). Therefore, a substantial loss in heritability occurred only when the number of loci was small and the selection response was strong.

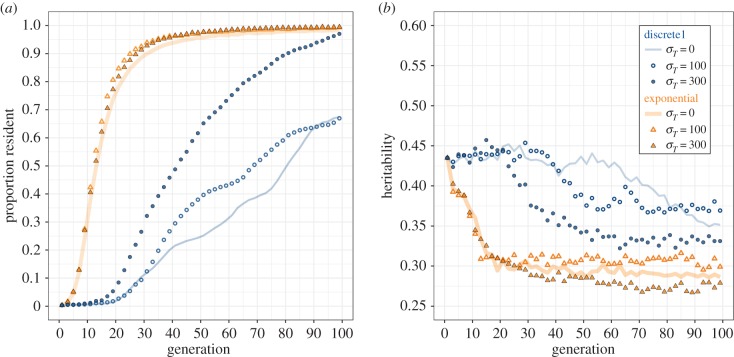
(b). Environmental effects on threshold

When selection was imposed by an exponential fitness function, environmental threshold variance did not affect the evolutionary response or heritability (figure 3a,b). Yet, it had strong effects in populations with a discrete fitness function: the higher the threshold variance the faster the increase in the proportion of residents. After 100 generations, most populations became fully resident if threshold variance (σTr) was 300, but, if it was 0, populations remained partially migratory with about 60% residents. With a variable threshold and a discrete fitness function, heritability remained roughly constant for approximately 20 generations before dropping abruptly. After 100 generations, heritabilities were slightly higher than those observed under the exponential fitness function.

Figure 3.

Effect of environmental variance σ_T on the evolutionary response (a) and heritability (b) in a migratory population selected for residency under the exponential (orange) and corresponding discrete1 fitness function (blue). (Online version in colour.)

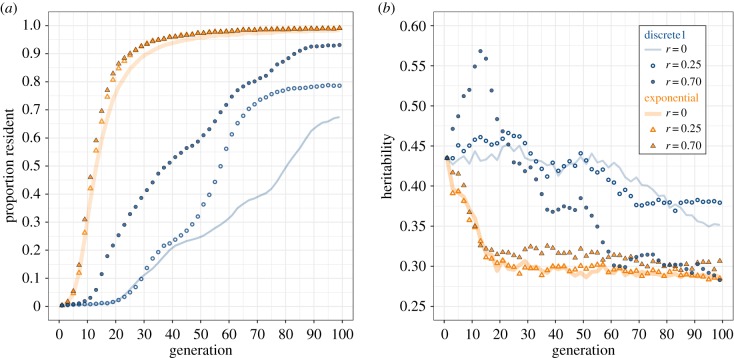
(c). Effect of assortative mating

The effects of assortative mating were similar to those of threshold variance: if evolutionary changes were driven by a semi-continuous fitness function, the strength of assortative mating did neither affect the rate at which residency evolved, nor the rate of loss in heritability.

Under a discrete fitness function, however, assortative mating led to a faster increase in the proportion of residents (figure 4a). Most populations became fully resident only in the presence of strong assortative mating. With random mating or weak assortative mating, heritability remained roughly constant for approximately 50 generations, before dropping towards a value of 0.35 after 100 generations. Under strong assortative mating (r = 0.70, discrete1), heritability first increased to over 0.55 after 20 generations of selection and then dropped abruptly to reach final mean heritability values similar to those resulting from selection by the exponential fitness function (h^{2 =} 0.25; figure 4b).

Figure 4.

Effect of the strength of assortative mating (r) on evolutionary response (a) and heritability (b) in a migratory population selected for residency under the exponential (orange) and corresponding discrete1 (blue) fitness function. (Online version in colour.)

(d). Prediction of evolutionary response in the blackcap

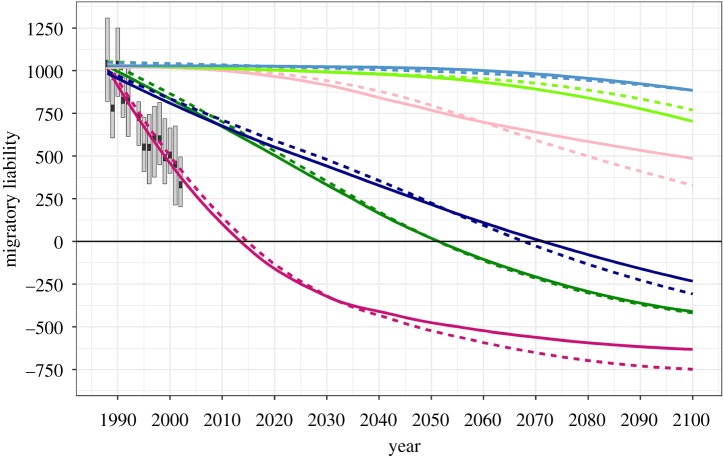
The fitness function that best predicted evolutionary change in migratory activity in southern German blackcaps was the exponential fitness function (figure 5; electronic supplementary material, table S3). All other forms of selection led to predictions that were less accurate than would be obtained by simply using the mean migratory activity over the study period (VEcv < 0). Predictions for the study period were very similar if 10 or 200 loci were assumed but some divergence was evident for long-term predictions. With the exponential fitness function, the response after 100 generations was slightly stronger if more loci were assumed (figure 5).

Figure 5.

Observed [8] and predicted changes in migratory liability of the blackcap population of southern Germany. Migratory liability equals migratory activity (given in half-hour intervals with activity) in migrants. Boxplots illustrate the yearly distribution of migratory liability values (box: median and interquartile range). Coloured lines represent the loess smoothed lines of best fit for the simulated data under five different fitness functions (figure 1), assuming 10 (solid lines) and 200 (dashed lines) loci. (Online version in colour.)

The time expected for this migratory blackcap population to become sedentary strongly depended on the fitness function: With the exponential function, the model predicts that the population will become 95% resident after 42 (bootstrapped 95% CIs: 32–46) and 99% resident after 98 (83–112) generations of selection. With the linear and logistic functions, 95% residency would evolve after at least 60 generations (electronic supplementary material, table S4). If discrete functions are assumed, the decrease is expected to be very slow, and residency not achieved within 100 generations (figure 5).

4. Discussion

There is currently great interest in knowing the potential of migratory populations to adapt to climate change. Here, we developed a genetic model, based on the threshold model of migration [8,17]. This allowed us to identify the most important variables determining the response to selection of threshold traits, to reconstruct evolutionary change in a migratory bird population and to make predictions on the rate and direction of future evolutionary changes in migratory behaviour.

Our study suggests that the strength and form of selection are the key determinants of evolutionary change in migratory behaviour, and that the number of genes, environmental effects or assortative mating are of minor importance. It further demonstrates that the observed reduction in migratory activity in migratory populations is most likely not only the result of fitness differences between migrants and residents, as assumed in all previous models, but also of strong directional selection acting on differences in the amount of migratory activity. Thus, migration should be treated as a semi-continuous threshold trait, in which the resident fraction of the population is phenotypically uniform, but the migratory fraction of the population shows phenotypic variation. Our simulations clearly indicate that the dynamics of evolutionary change in semi-continuous threshold traits is different from that of classical threshold traits, which have been modelled by Roff [21,22]. If selection not only favours resident individuals but also migrants travelling shorter distances, the response to selection is much faster. The expected rate of evolutionary change in migratory behaviour predicted by this model is in accord with that observed in the southern German blackcaps [8]. How variation in migration activity relates to fitness depends on the balance between the costs and benefits of migrating shorter or longer distances. The recent evolutionary change towards residency [8] in blackcaps is most consistent with a scenario in which residents have the highest fitness, and fitness declines exponentially with increasing migratory distance. Hence, in the blackcap, the potential advantages of wintering at, or close, to the breeding site are clearly higher than the costs of migration, and outweigh the advantages of wintering more to the south under more favourable winter conditions. The exponentially increasing fitness cost of migration in this species may be due to the importance of territory quality and the prior residency effect. The maintenance of breeding home-ranges throughout the year in resident blackcaps is in line with this idea [46]. Identifying the factors that contribute to the form of the fitness function will allow us to understand the adaptive process and to make specific predictions about the rate of change and which fraction of a population will benefit most from changing environmental conditions. We predict, for instance, that if the selection observed between 1988 and 2002 persists, this migratory blackcap population may become 99% sedentary in 98 generations, which would be around the year 2184.

Our simulations further suggest that evolutionary changes from a completely migratory to a resident population will be very rapid in the beginning, but greatly slow down once the proportion of residents in the population is greater than 90% (figure 2a,b). Therefore, partially migratory populations, particularly those with a low proportion of migrants, may prevail in natural populations, as assumed by Berthold [47] and predicted using a simple, single-locus threshold model [13]. In southern German blackcaps, for instance, the population will remain partially migratory for about 200 years, if the selection observed between 1988 and 2002 persists see above. Yet if selection fluctuates or becomes weaker, the population will remain partially migratory much longer. Interestingly, this evolutionary inertia due to this pattern of phenotypic expression has hitherto not been considered in phenotypic evolutionary models of partial migration [18]. These models generally assume that for partial migration to persist the fitness of migrants and residents should be approximately equal over time, which is at odds with empirical findings [32]. Our model demonstrates that even in the presence of large fitness differences, partially migratory populations may evolve rapidly and persist during a long period of time, as a consequence of the evolutionary dynamics of semi-continuous threshold traits. This could also be an explanation for the maintenance of other alternative phenotypes [20], like wing dimorphisms in insects, if the expression of these phenotypes is semi-continuous.

Another important result of our study is that, if we assume that migration is a polygenic trait, for which there is strong empirical evidence [6,14], knowing the exact number of genes controlling migration is not crucial for predicting short-term evolutionary change. We simulated two extremes: migration being controlled by few genes with large effects or by many genes with very small effects. Yet the evolutionary response to selection for residency was very similar under both assumptions, and in all models considerable amounts of genetic variation was preserved, as cryptic genetic variation [48]. However, with 10 genes the loss of genetic variation was much larger (44%) than with 200 genes (11%), particularly under the strongest selection regimes (figure 2; electronic supplementary material, table S4). This agrees with the findings of Roff [21,22], and is not surprising given that the larger the number of loci, the lower the per-locus selection coefficients and fixation probabilities. Thus, if we assume that migratory activity is controlled by a large number of genes, for which there is some empirical evidence [35–38,41], genetic variation for migration liability would be present in all populations, including resident populations that evolved under strong selection for residency (electronic supplementary material, table S4).

Environmental effects on migratory behaviour have been considered an important factor in the evolutionary transition from migration to residency and from residency to migration [19]. Yet in our simulations, environmental effects on the threshold had no major effect on the response to selection or on heritability, if a semi-continuous threshold trait was assumed. However, if migration was simulated to be dichotomous, as assumed in the classical threshold model [20–22], environmental variation in the migration threshold increased selection response. This is probably due to environmental effects causing some individuals with low migratory activity to become resident and, as a consequence, have a higher fitness. The environmental variance could thus induce faster evolution by increasing variation in migratory behaviour. Environmental effects on the position of the threshold may be particularly important in accelerating the evolution of migration in resident populations. Since in this process, resident individuals with high migration liability may become migratory, if the environmental effect ‘pushes’ them across the threshold. Once there are migrants in the population, selection may increase mean liability in the population by selecting the migrants with the highest activity. Thereafter, the proportion of individuals with liability values above the threshold will rapidly increase, completing a process of genetic accommodation [19].

It has been proposed that assortative mating may be important for maintaining variation in migratory behaviour within populations, as a consequence of habitat segregation [49] or allochrony [43]. Our simulations indicate that assortative mating, even when it is very strong, generally may have little impact on evolutionary responses. However, if there are only fitness differences between migrants and residents, assortative mating could accelerate the rate of adaptive evolution. Overall, the conditions under which assortative mating may impact on selection responses are similar to those previously described for environmental effects on the threshold: When there is a discrete fitness function and in the evolution from a resident to a migratory population. In this selection process, we would expect strong assortative mating to particularly accelerate the increase in the frequency of migrants when they are rare.

5. Conclusion

Our model confirms that threshold traits follow particular evolutionary trajectories [21,22]: under strong directional selection, evolutionary responses rapidly decelerate when one of the phenotypes is close to fixation, and large amounts of cryptic genetic variation are preserved. However, semi-continuous traits, like migration, respond more rapidly to selection than dichotomous traits. Moreover, their evolutionary response is more predictable (electronic supplementary material, figure S5), depending primarily on the fitness function and being less affected by assortative mating or environmental effects. It is likely that many ‘classical’ threshold traits, like mental disorders, wing dimorphisms or dispersal, which are considered dichotomous [20], actually evolve as semi-continuous traits. In each of these traits, it could be necessary to test whether the frequency of incidence of a trait is genetically correlated to the trait value in the phenotype in which the trait is expressed [15]. The flexibility of our genetic model makes it possible to simulate the evolution of any dichotomous or semi-continuous threshold trait by integrating all available knowledge on genetic architecture, demography, mating system and selection. This approach will help us to obtain more realistic evolutionary models, which can then be compared to empirical data collected in experiments or the wild.

However, to make accurate predictions on the rate of adaptation to environmental change, we will need much more and better data on the fitness of different phenotypes under different environmental conditions in a variety of species. Ultimately, we would need to be able to translate climate change prediction into predictions of changes of selection in wild populations. This may be possible if we understand the central mechanisms linking environmental change to changes in fitness and phenotypic change (see, for instance, [50]). Yet also our model needs improvement: One limitation of our model is that fitness functions are assumed to be fixed. In natural populations, however, selection is likely to fluctuate over time, depending on changes in population dynamics and ecological conditions in the breeding and wintering areas, making evolutionary responses hard to predict [51,52]. Similarly, to obtain a more realistic model we would need to measure and consider phenotypic plasticity, directional changes of environmental effects, and genetic correlations with other traits that are under selection [53]. Rapidly accumulating genomic data, will provide specific estimates of gene numbers, allelic effects, mutation rates and mutational variance for migration and other threshold traits, which could be considered in future models.

In conclusion, although we present a flexible, empirically validated genetic model of the evolution of migration, more empirical data, particularly, on selection and demography in different species, will be required to test the model and to predict how different populations will respond to global change.

Data accessibility

The code for running the simulation models is provided in the electronic supplementary material.

Authors' contributions

T.d.Z. and F.P. designed the study and developed the model. T.d.Z. carried out the simulations and data analysis. T.d.Z. and F.P. wrote the manuscript.

Competing interests

We declare we have no competing interests.

Funding

We received no funding for this study.