Imaging local genetic influences on cortical folding

Significance

Major gaps remain in our understanding of mechanisms that underlie the folding of the human cerebral cortex. Stereotyped folding in specific cortical locations could be explained by a corresponding anatomical pattern of genetic influences on cortical development, but no direct evidence supports this explanation. Here, we use high-resolution brain MRI to show the existence of the predicted pattern of genetic influences on the thickness of the cerebral cortex, leveraging the prediction that shared genetic influences during development create covariability of cortical thickness in adult neuroanatomy. Anatomically local covariability in cortical thickness has a genetic basis, is symmetric between cortical hemispheres, shows consistency across independent datasets, and may influence patterns of surface folding on the human brain.

Abstract

Recent progress in deciphering mechanisms of human brain cortical folding leave unexplained whether spatially patterned genetic influences contribute to this folding. High-resolution in vivo brain MRI can be used to estimate genetic correlations (covariability due to shared genetic factors) in interregional cortical thickness, and biomechanical studies predict an influence of cortical thickness on folding patterns. However, progress has been hampered because shared genetic influences related to folding patterns likely operate at a scale that is much more local (<1 cm) than that addressed in prior imaging studies. Here, we develop methodological approaches to examine local genetic influences on cortical thickness and apply these methods to two large, independent samples. We find that such influences are markedly heterogeneous in strength, and in some cortical areas are notably stronger in specific orientations relative to gyri or sulci. The overall, phenotypic local correlation has a significant basis in shared genetic factors and is highly symmetric between left and right cortical hemispheres. Furthermore, the degree of local cortical folding relates systematically with the strength of local correlations, which tends to be higher in gyral crests and lower in sulcal fundi. The relationship between folding and local correlations is stronger in primary sensorimotor areas and weaker in association areas such as prefrontal cortex, consistent with reduced genetic constraints on the structural topology of association cortex. Collectively, our results suggest that patterned genetic influences on cortical thickness, measurable at the scale of in vivo MRI, may be a causal factor in the development of cortical folding.

Human brain folding—which vastly increases cortical surface area relative to the cranium—is subject to increasingly rigorous experimental investigation. Primate tract tracing provided early evidence of a mechanistic role for axonal tension (1). However, biomechanical experiments have shown that the tension theory (2) is unlikely to be a sufficient generic explanation for folding (3). Alternatively, folding may result from different neurodevelopmental rates of expansion of superficial and deep cortical layers (4). A remarkable series of theoretical and biomechanical studies have shown that, in the setting of such differential expansion, simple variations in the relative rigidity of superficial and deep layers can produce a biologically plausible pattern of folding in an in silico cortical model (5–8).

However, biomechanical theories to date have not explained the partly stereotyped locations of folding, which are extremely consistent across primary sulci (sulci that are formed earliest in utero and are most stable across species) and less so across secondary and tertiary sulci (9, 10). Given the stereotyped map of how cortical folds emerge during prenatal life (11, 12), it may be predicted that the cortical sheet shows highly constrained regional differences in expandability, stiffness, or thickness [which directly affects folding (13)]. Such differences may in turn be mediated by regional differences in cortical microstructure and “tethering” to molecular signaling gradients (14), such that early programs for cortical arealization arise within an expanding sheet of variegated susceptibility to folding. It is reasonable to hypothesize that such early constraints would be partially due to genetic patterning of the cortical sheet prior to the late fetal phase of dramatic cortical expansion and folding (15, 16). The role of genetic patterning is also supported by highly penetrant genetic mutations that disrupt both folding and cortical thickness (17).

As comprehensive spatial maps of cytoarchitecture and gene expression from the human cortex during prenatal life do not yet exist, neuroimaging studies have provided a critical source of information about human cortical arealization and its relationship to folding that complements other sources of evidence (18). Analysis of brain MRI data has quantified human variability in sulcal locations; the relationship between morphological phenotypes such as sulcal depth, curvature, and cortical thickness; and the heritability of these and other morphological features (19–22). A putative genetic basis for stereotyped patterns of folding may be reflected in regionally varying genetic influences on morphological features such as thickness that influence folding (4, 23–25). Overlap in interregional genetic influences on thickness can be quantified by the genetic correlation (the shared genetic basis for the phenotypic correlation between two traits), which is likely due to pleiotropy. Indeed, it is known that shared genetic influences account for a great deal of interregional correlations in morphology at the phenotypic level (which has also been called “structural covariance”) (26–30).

Despite this progress, what might be called “local” patterns in phenotypic or genetic correlations—the shared genetic influences on adjacent, small areas of brain and how these vary across the cortex—have not yet been a focus of investigation, significantly limiting the informativeness of prior studies. The paucity of investigations at this resolution is particularly unfortunate because local genetic patterning is likely to be important for folding, a local phenomenon that occurs at an intraregional scale. Shared (or distinct) genetic influences at the centimeter or subcentimeter scale more plausibly influence folding than do long-distance genetic correlations between regions separated by multiple gyri and sulci. If the hypothesized relationship between local genetic influences and folding does exist, then we would expect a neuroanatomical correspondence between maps of local correlation and maps of folding, the latter of which can be quantified by the measurement of curvature (18, 31). Moreover, correlations along the sulcal or gyral axis may have different strengths than correlations that are tangential to these axes in the direction of cortical folding. The present study tests these hypotheses by developing and applying analytic methods to two large in vivo genetically informative neuroimaging datasets totaling over 2,500 scans. Our study discovers profoundly variegated patterns of local genetic correlations in cortical thickness. The spatial patterning of these local genetic correlations is intimately related to sulcal/gyral topology—providing evidence for a patterned genetic influence on cortical folding.

Results

The methodologies developed for this study successfully identified maps of covariability in cortical thickness within local “neighborhoods” of the cerebral cortex (Fig. 1). This covariability was found to have a basis in genetic influences. The strength of these local genetic influences varied markedly across different areas of cortex and was robustly related to cortical folding. These maps of patterned local influences on cortical thickness, identifiable in the adult human brain, may reflect molecular signaling gradients, cellular variation, and laminar features that influence neurodevelopmental cortical folding.

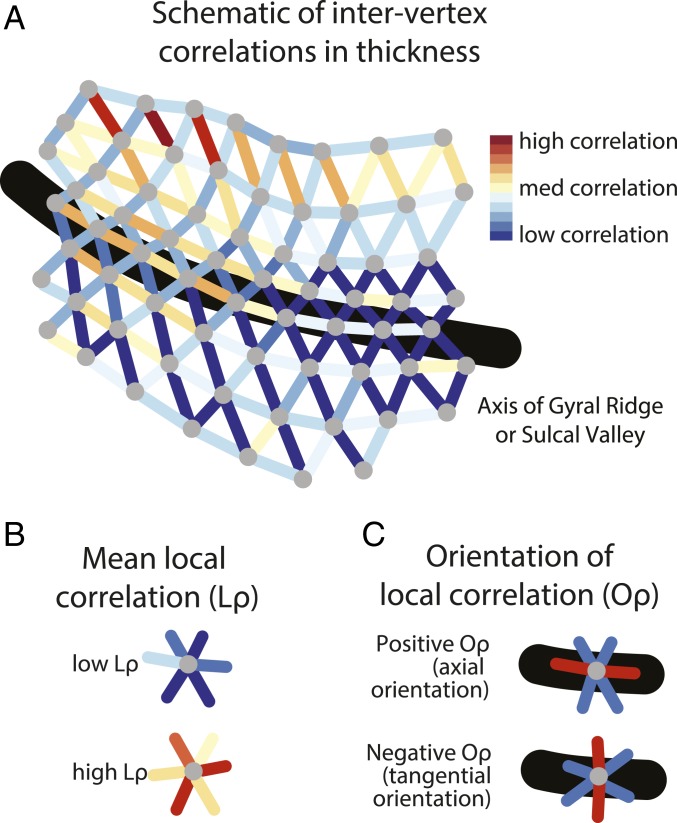
Fig. 1.

Schematic of methodological approaches. (A) An illustration of a patch of triangular mesh fit to the cortical surface. Vertices are colored gray. Edges between two vertices are colored in accordance with the correlation in the interindividual variation in the cortical thickness of the two vertices. (B) Mean local correlation Lρ is the average of the correlation in the interindividual variation of the vertex with that of its neighbors. (C) Correlation orientation (Oρ) is the difference between the axial correlation (parallel or close-to-parallel to the long axis of the local gyrus or sulcus) and the tangential correlation (perpendicular or close-to-perpendicular to this axis).

The Genetic Basis of Local Phenotypic Correlations.

In theory, the strength of local phenotypic correlations could be homogenous throughout the cortex, or any heterogeneity could be driven exclusively by nongenetic factors. In order to reject these null hypotheses, we used data from both the Genetics of Brain Structure and Function Study (GOBS) (1,443 individuals) and the Human Connectome Project (HCP) (1,113 individuals) (30, 32–34), processed with FreeSurfer to yield maps of cortical thickness (the distance between the gray–white surface and the pial surface) at ∼10,000 vertices per hemisphere. Spatially varying maps of local correlations in cortical thickness were identified in both of these two large neuroimaging datasets, supporting the conclusion that local phenotypic correlations in cortical thickness were not homogenous throughout the cortex (Fig. 2). Univariate heritability was also reasonably high throughout the cortex (SI Appendix, Fig. S1), indicating that a nontrivial amount of the phenotypic variance was accounted for by genetic factors.

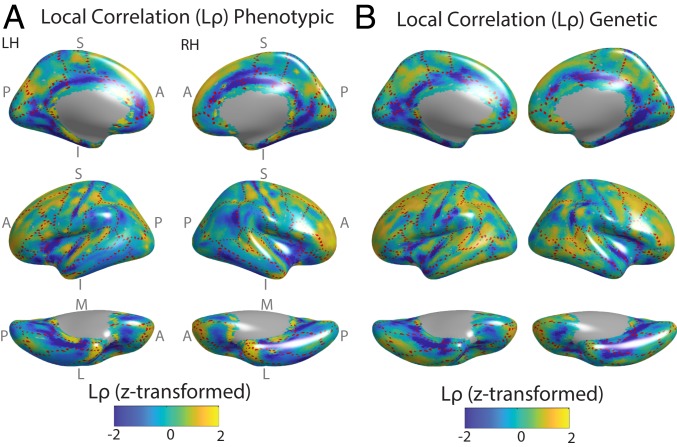
Fig. 2.

Shared, local genetic influences on the pattern of cortical thickness across the cortex, in the GOBS datasets. (A) For all subjects, thickness was estimated at ∼10,000 vertices of the triangular mesh fit to the left and right cortical surface, and the interindividual variation of each vertex was correlated with the interindividual variation of each of its neighbors (here, adjacent vertices on the cortical mesh) to yield the phenotypic correlation. After regressing out the nonlinear relationship between the anatomical distance between vertices and these correlations, the local correlation (Lρ) of each vertex was calculated as the mean of its correlations with its neighbors. For purposes of visualization, Lρ was z-transformed within each cortical map. The dashed red lines mark boundaries between gyral regions of FreeSurfer’s Desikan atlas (38), such that the dashed lines generally occur within sulcal fundi. (B) The phenotypic correlation was decomposed into environmental (SI Appendix, Fig. S2) and genetic components based on the subjects’ extended pedigree structure. Genetic Lρ was then calculated analogously to A. There is a strong and statistically significant anatomical correspondence between these maps (SI Appendix, Fig. S3). A, anterior; I, inferior; L, lateral; LH, left hemisphere; M, medial; P, posterior; RH, right hemisphere; S, superior.

In addition, the pattern of average local phenotypic correlations between neighboring vertices (phenotypic Lρ) recapitulated the pattern of the average local genetic correlation (genetic Lρ, isolated based on the extended pedigree structure in the GOBS, which is optimized for genetic analyses). For both phenotypic and genetic correlations, relatively low Lρ occurred in the fundus of the central sulcus, the circular sulcus of the insula, superior and inferior temporal sulci, cingulate sulcus, and the anterior portion of the calcarine sulcus. In contrast, relatively high Lρ was present in the postcentral and precentral gyri, the short insular gyrus, and the superior and middle temporal gyri. Lρ was also moderately high throughout prefrontal cortex (Fig. 2). The observed genetic–phenotypic correspondence was statistically significant (Pearson’s correlation coefficient, r = 0.64; P_spin < 0.001) per a randomization procedure (the “spin test”) based on a null model of random alignment of the cortical surface (35). Importantly, the between-sample genetic–phenotypic correspondence was also high (r = 0.55, between GOBS genetic Lρ and HCP phenotypic Lρ; P_spin < 0.001).

This set of results supported the existence of cortically patterned genetic influences on cortical thickness that were shared within local anatomical neighborhoods. Moreover, the genetic–phenotypic correspondence in Lρ suggests that phenotypic correlations are a reasonable proxy of genetic correlations in these data. Demonstrated here in the context of brain morphology, genetic–phenotypic correspondence in Lρ is in line with past theoretical and empirical predictions that phenotypic correlations can in general be used a proxy for genetic correlations (26, 36) (SI Appendix, Results I and II and Fig. S2). This correspondence is also of large practical importance, as even with high-performance parallel computing, it would be intractable to estimate the genetic component of the millions of phenotypic correlations considered below.

Consistency across Datasets, Symmetry across Hemispheres, and Robustness to Methodological Approaches.

Given the large number of potential confounds and divergent methodological choices involved in any neuroimaging study, replicability is a necessary condition to conclude that findings may reflect underlying biology as opposed to technical confounds. Critically, when other variables were held constant, there was a high anatomical correspondence between phenotypic $L\rho$ based on analyses of HCP or GOBS datasets (r = 0.70, P_spin < 0.001; see SI Appendix, Fig. S4). (Given the high observed similarity between genetic and phenotypic correlations, comparisons between different datasets and methodological pipelines were in general made based on the phenotypic correlations for computational reasons.) The high degree of consistency across datasets indicated that findings did not depend on scanner type or differences in data quality. A supplemental analysis in children aged 8 to 9 from the Philadelphia Neurodevelopmental Cohort (PNC) further confirmed the stability of the results across age ranges (SI Appendix, Results III and IV and Fig. S5).

Since left–right homologs share developmental precursors, a high degree of left–right symmetry is also expected in neuroanatomical phenotypes with early developmental origins. Such left–right symmetry was observed in maps of $L\rho$. Quantitatively, this symmetry was demonstrated using phenotypic $L\rho$ projected on the CIVET surface, which unlike FreeSurfer has a one-to-one mapping from left hemisphere vertices to right hemisphere. Across vertices, the left–right correspondence was substantial (r = 0.79; P_spin < 0.001). Zooming in on the “local correspondence” (37) (the correlation within a demarcated region spanned by a 10-mm geodesic distance), there were large areas where $r\cong 1$ (SI Appendix, Fig. S6) and no areas where local correspondence was consistently negative—although local correspondence was lower in prefrontal cortex and the temporal-parietal junction, and higher on average in sulci compared to gyri. The high degree of observed left–right symmetry was suggestive of early developmental origins of the biological processes that drive local correlations in cortical thickness.

The pattern of $L\rho$ was also robust to methodological choices in the data analysis pipeline (see SI Appendix, Fig. S4). There was reasonably high anatomical correspondence between maps of $L\rho$ regardless of the degree of anatomical smoothing used during image processing (25- vs. 10-mm full-width at half-maximum smoothing kernels in FreeSurfer; r = 0.36, P_spin < 0.001). Similarly, there was a reasonable correspondence between alternative preprocessing pipelines (FreeSurfer vs. CIVET), indicating a robustness to the diverse subroutines used in these pipelines (r = 0.31, P_spin < 0.006). The largest differences between the pipelines were located in the precuneus ($L\rho$ lower in CIVET) and in the inferior occipitotemporal gyri ($L\rho$ lower in FreeSurfer). Finally, the pattern of $L\rho$ was robust to two approaches for quantifying a vertex’s local neighborhood, whether the neighborhood comprised the six adjacent vertices on the cortical mesh or all of the vertices within a 10-mm geodesic distance (r = 0.68, P_spin < 0.001). Because it is based on a larger amount of data, the distance-based neighborhood is expected to have a higher signal-to-noise ratio. Subsequent results are therefore based on phenotypic $L\rho$ calculated using FreeSurfer processing of HCP data with a 25-mm smoothing kernel and a 10-mm geodesic neighborhood. Overall, the degree of replicability in the pattern of results increases our confidence that our findings do reflect an underlying biological process.

Relationship with Gyral–Sulcal Patterns.

If the cortical pattern of shared genetic influences on cortical thickness did relate to cortical folding, we would predict an anatomical correspondence between these maps and folding patterns. As hypothesized, the pattern of $L\rho$ corresponded with sulcal/gyral organization, especially in primary somatomotor, superior temporal/insular, and cingulate areas. In other words, relatively homogeneous areas of high or low $L\rho$ appeared to occur along anatomical regions demarcated by sulcal or gyral boundaries (38), with greater variability in $L\rho$ when transversing sulcal or gyral boundaries. Moreover, peaks and valleys of local correlations tended to occur in sulcal fundi or gyral crests, indicating a relationship between $L\rho$ and folding. Visual verification of this relationship was confirmed via highly magnified projections onto cortical flat maps at the regional level (Fig. 3). Quantitatively, this result was confirmed when modeling folding via mean curvature (which is positive in outwardly curved sulci and negative in inwardly curved gyri). There was a global correspondence between $L\rho$ and mean curvature (r = −0.28, P_spin < 0.001), indicating that $L\rho$ tended to be lower in sulci and higher in gyri (Fig. 4 A and B). The relationship with curvature was also preserved in a childhood sample from the PNC (r = −0.32, P_spin < 0.001; SI Appendix, Results IV and Fig. S5) and when using a “center-ring” alternative to smoothing, where the average thickness within 5 mm of a vertex was correlated with the average thickness at a distance of 5 to 7 mm to estimate Lp (r = −0.30, P_spin < 0.001; SI Appendix, Results II and Fig. S7). This anatomical correspondence is consistent with the hypothesis that patterned genetic influences on cortical thickness influence patterns of cortical folding in the developing brain.

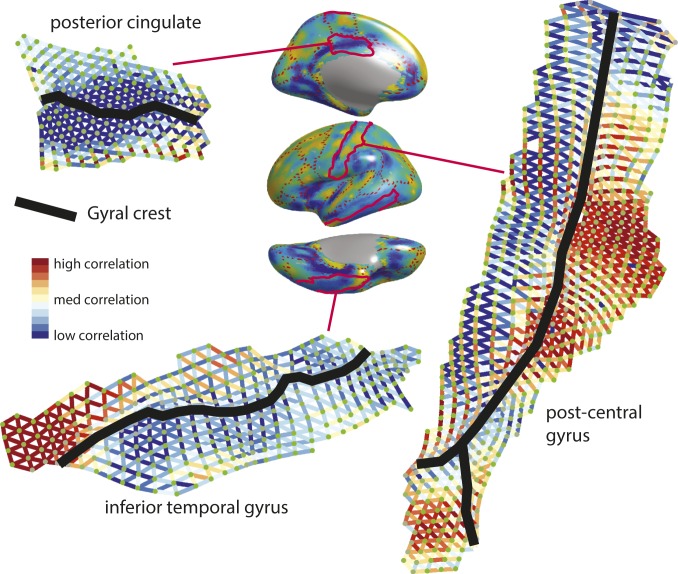
Fig. 3.

Flattened surfaces showing the phenotypic correlations between adjacent vertices, which are the basis for the brain maps of average local correlation (Lρ) and orientation of local correlation (Oρ). Phenotypic Lρ is shown on the surface plot in the center (as per Fig. 1), with three anatomical gyri outlined in red. Flat maps of these gyri are shown, clockwise from center: postcentral gyrus, inferior temporal gyrus, and posterior cingulate. A relationship between phenotypic correlation and the location of the gyral crest within these gyri can be observed in each of these cases.

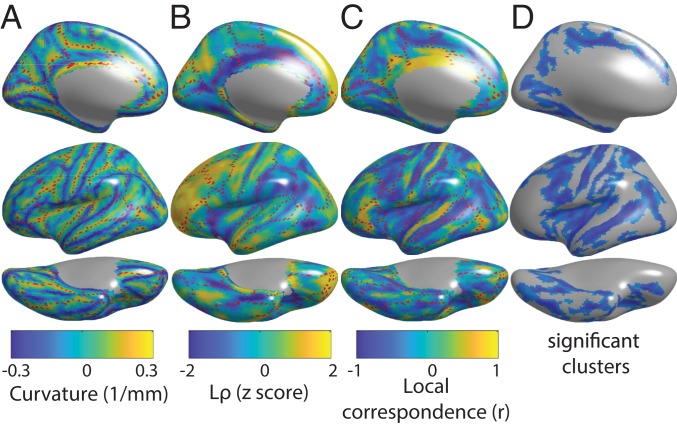
Fig. 4.

Mean phenotypic local correlation $\left(L\rho \right)$ and its relationship with gyral–sulcal organization as measured by mean curvature. (A) Map of mean curvature. Sulci are positively curved, while gyri are negatively curved. (B) Map of Lρ. (C) Map of local correspondence between mean curvature and Lρ. (D) Significant clusters of local correspondence based on the spin test. See SI Appendix, Fig. S8 for analogous maps showing both cerebral hemispheres.

Since the locations of folding are stereotyped only in a subset of sulci, with greater intersubject variability in the locations of other sulci thought to be under looser genetic control, the degree of anatomical correspondence between folding and $L\rho$ should also be spatially heterogenous. This spatial heterogeneity was captured by the local correspondence, which showed specific areas of high-magnitude correspondence between mean curvature and $L\rho$ (Fig. 4 C and D). This correspondence tended to be negative in sulci, indicating lowest $L\rho$ in the sulcal valley where mean curvature is most positive. Using a cluster-based implementation of the spin test, seven clusters bilaterally were statistically significant (P < 0.05, familywise correction for multiple comparisons). All of these clusters were composed of negative correspondence within sulci. Prefrontal cortex, an area of the brain enriched for relatively high intersubject variability in sulcal locations, was notable in having relatively low local correspondence with mean curvature. On visual inspection, this finding is consistent with the observation that $L\rho$ in prefrontal cortex is relatively high but also relatively spatially uniform within this area of cortex, without the kind of sulcal–gyral variability observed elsewhere in the brain.

Orientation of Local Correlations.

In theory, spatial heterogeneity in local correlation could be limited to the average strength of local correlations. Alternatively, a relationship with folding would be supported by differential strength of correlations in different directions relative to sulcal fundi or gyral crests. These differences in the local “correlation orientation” $\left(\mathrm{O}\rho \right)$ were quantified relative to the sulcal/gyral axis (SGA) at each vertex, which was defined as the axis of minimum change in sulcal depth. This axis provided a consistent frame of reference relative to folding throughout the cortical mantle. Axial correlations were parallel to (“along”) this axis, tangential correlations were perpendicular to (“across”) this axis, and $\mathrm{O}\rho$ was defined as the normalized difference between axial and tangential correlations. Local correlations along the sulcal or gyral axis differed in strength compared to local correlations tangential to these axes, reflected by a remarkable pattern of variation in $\mathrm{O}\rho$ across the cortex (SI Appendix, Fig. S9 A and B). Overall, anatomical correspondence was low between $\mathrm{O}\rho$ and mean curvature (r = 0.05, P_spin > 0.5). The spatial heterogeneity in anatomical correspondence between $\mathrm{O}\rho$ and mean curvature was captured by local correspondence, which showed significant clusters of positive local correspondence bilaterally in the central sulcus and precentral gyrus, suggesting relatively a greater axial orientation in sulcal fundus. In addition, there was a significant cluster of negative local correspondence along the marginal sulcus in the left hemisphere, suggesting relatively higher tangential orientation in the sulcal fundus; SI Appendix, Fig. S9 C and D). Overall, $\mathrm{O}\rho$ had a complex spatial neuroanatomical profile.

Discussion

The colocalization of folding with local genetic influences on cortical thickness is a significant contribution to existing models of cortical folding, which have difficulty in explaining the stereotyped location of certain gyri and sulci (17). Patterned, local correlations in cortical thickness may capture the genetic coordination of microstructural properties that constrain cortical folding. The importance of such local correlations in cortical thickness is predicted by previous neuroimaging studies, but prior investigations of thickness covariability focus on correlations between regions across the entire brain (39, 40). At this scale, shared genetic influences tend to be much stronger on average at short distances (30), consistent with the prediction that evolutionary pressure decreases distances between highly connected brain areas to decrease metabolic and wiring costs (41). The topographical variation of local correlations reported in the present study greatly expands upon these prior results.

We propose that the observed differences in local correlations track differences in the development of cortical thickness, which may contribute to the emergence of stereotyped cortical folding. There is prior support for the fact that genetic correlations in cortical thickness, and the phenotypic correlations to which they are closely related, reflect coordinated changes in thickness in neurodevelopment (42, 43) and arise from spatial gradients of signaling molecules (29). At the cellular level, thickness may relate to the size of and number of neurons in cortical columns, which partially dictate the function of different cortical areas (1, 44, 45). Moreover, biomechanical models have clearly demonstrated that thickness influences folding, with increased average thickness expected to result in wider folds (13). To our knowledge, the biomechanical effect of stereotyped spatial variation in thickness is unexplored but could plausibly influence the localization of folding in neurodevelopment; the latter comprises a testable prediction for future biomechanical studies. Zones of low average correlation may reflect gradient boundaries in terms of different growth factors influencing alternative development of cortical thickness on either side of the boundary. These boundaries represent plausible anchor points for folding, which is supported by their correspondence with primary sulci in the present work. The plausibility of the proposal that different factors influence thickness in sulci vs. gyri is consistent with differences in the laminar basis of sulcal and gyral thickness; gyri are on average thicker than sulci, and this increased thickness disproportionately stems from expansion of deep cortical layers that disproportionately project to subcortex as opposed to other cortical areas (1, 44).

It is important to note possible alternative explanations for our empirical findings. We argue that the physical effects of thickness on a folding surface may anchor folding patterns. However, thickness also reflects aspects of cellular composition and the extracellular matrix (46), which may independently affect cortical stiffness and thereby folding (13). Finally, the observed correspondence could result from an alternative influence of folding on thickness, or a third variable that emerges subsequent to cortical folding in neurodevelopment. Critically, we demonstrate that the correspondence between local correlations and curvature is preserved in a childhood sample aged 8 to 9, supporting the hypothesis that this correspondence results from coordinated development prior to maturity. However, as folding is complete before age 8, an alternative approach to confirm the role of cortical thickness variation in the formation of sulci and gyri would be to directly map the temporal dynamics of changes in thickness and local thickness covariance relative to changes in folding in utero—an approach that is increasingly possible using recent prenatal imaging resources (47, 48). Of note, our results do not imply that folding is only under genetic control in the subset of sulci where there is correspondence with local thickness covariance; a role for genetic factors that influence thickness in no way precludes the many other factors that are expected to influence curvature in a regionally heterogenous fashion.

The normative model we propose provides a framework for how alterations of cortical patterning may underpin neuropsychiatric risk for disorders such as schizophrenia. In schizophrenia, thickness is decreased (49), folding is disrupted (50), and structural covariance and functional connectivity are altered especially at anatomically local spatial scales (51, 52). Histologically, pyramidal neuron dendritic spine density is decreased (53–55). This set of findings is compatible with a disruption of the model of early developmental cortical patterning described in this paper. Empirical predictions follow, including the disruption of local correlations in cortical thickness in schizophrenia, and a role for schizophrenia risk genes in driving normative cortical patterning.

It is also important to address methodological issues related to the present study. One limitation is the use of phenotypic correlation as a proxy for genetic correlation in some of the analyses, for computational reasons, although this practice is supported by prior studies (26, 36) and we show that these patterns of correlation strongly correspond with one another in our data. In addition, smoothing by image processing pipelines is expected to inflate phenotypic correlations in cortical thickness. A nonbiological basis of the results such as an image processing confound must be considered, but is less plausible (although not ruled out entirely) given the correspondence of results between different image processing pipelines and different datasets.

In summary, this study provides evidence for patterned genetic influences on cortical thickness, which are shared within local cortical neighborhoods less than 1 cm apart on the cortical surface and correspond anatomically with cortical folding in the adult human brain. These patterned maps may reflect local signaling gradients that provide a spatial template for cortical folding patterns during early development, by influencing cortical thickness and the biomechanical properties of local tissue. Disruption of these gradients may in turn underlie folding disruption in developmental neuropsychiatric disorders.

Materials and Methods

Study Sample, Image Acquisition, and Data Availability.

The GOBS, HCP, and PNC datasets have been described in detail in prior publications (30, 32–34). Briefly, the GOBS consisted of high-resolution MRI in 1,443 individuals (836 females; age mean, 40.7; SD, 15.5; range, 18 to 85) from randomly ascertained extended pedigrees of Mexican American individuals living in San Antonio, Texas. The HCP is a publicly available resource and consists of MRI data from 1,113 individuals (606 females; age mean, 28.8 y; SD, 3.7; range, 22 to 37) from 457 unique families. Image processing used FreeSurfer, version 5.3 (56–58). Cortical thickness was calculated as the distance between the gray–white and pial surfaces at each vertex. Mean curvature, a measure of cortical folding, was defined as the average of the principal curvatures at each vertex (31). For comparison, the Montreal Neurological Institute CIVET pipeline (version 1.1.10) was also used to calculate cortical thickness on the HCP sample, as previously described (59). For fidelity of comparison to FreeSurfer surfaces, this mesh was down-sampled to 9,895 uniform cortical regions by merging triangular faces into single regions (where the thickness of each region was the average of the thickness of the vertices within the region). See SI Appendix, Methods I and Results IV for further details.

The HCP data used in this study are available to investigators deemed to have a legitimate research use according to the Restricted Access Data Use Terms described at https://www.humanconnectome.org. The PNC data are available through dbGaP (phs000607.v1.p1). The genotype data for GOBS participants are available through dbGap (phs001215.v2.p2). The GOBS imaging phenotypes used in this study are available from the National Institute of Mental Health Repository (https://www.nimhgenetics.org). Alternatively, data from the GOBS cohort can be applied for by contacting D.C.G. (david.glahn@childrens.harvard.edu) or J.B. (john.blangero@utrgv.edu). Access to data by qualified investigators is subject to ethical and scientific review (to ensure the data are being requested for valid scientific research) and must comply with all relevant guidelines. The completion of a material transfer agreement signed by an institutional official will be required. All GOBS participants provided informed consent, and the study was approved by institutional review boards at Yale University and the University of Texas Health Science Center at San Antonio. Code used for analyses presented in this paper is available at https://github.com/aaronab.

Local Correlations of Cortical Thickness.

Informed by familial information from extended pedigrees, SOLAR (60) was used to confirm significant heritability of cortical thickness at each vertex, as well as to decompose the phenotypic correlation $\left(\rho \right)$ into the environmental correlation $\left({\rho }_E\right)$ and the genetic correlation $\left({\rho }_G\right)$ between neighboring vertices on the cortical mesh. $\rho$ is equivalent to the “structural covariance” between vertices, while ${\rho }_G$ is an estimate of the proportion of the shared variance due to shared genetic factors (see SI Appendix, Methods II–III for further details). Age, age², sex, and total brain volume were also included as covariates in these models.

Two methods were used to determine a vertex’s local neighborhood: in the first method, adjacent vertices on the triangular cortical surface (∼6 neighbors per vertex); in the second method, vertices within 10 mm of a vertex, calculated using geodesic distance on the triangular mesh (∼30 neighbors per vertex). The nonlinear relationship between the local correlations between neighboring vertices and the anatomical distance between these vertices across the cortex was regressed from the strength of these correlations (after r-to-z transformation) using generalized additive models in the R package gam (61), and the residuals after this step were used in all subsequent analysis. This regression step is necessary as smoothing is imposed by image processing pipelines for the purposes of spatial normalization, which could result in spurious correlations (see SI Appendix, Results II for further details). The correlation between an individual vertex and each of the vertices in its neighborhood was averaged to yield $L\rho$.

The Orientation of Local Correlations.

We also quantified a measure of anisotropy in a vertex’s $L\rho$ (higher correlations along a specific directional axis), which we labeled the “orientation of correlation” $\left(O\rho \right)$ (Fig. 1C). To find $O\rho$ at each vertex, v, we first estimated the orientation of the SGA at v. The SGA provided a biologically meaningful frame of reference throughout the cortical mantle, whereby directions parallel to (“along”) the SGA at a vertex are defined as axial, while directions perpendicular to (“across”) the SGA are defined as tangential. Then, the axial correlation $\left(L{\rho }_{ax}\right)$ is the correlation in the axial direction, quantified as the average of correlations within 30 degrees of SGA; the tangential correlation $\left(L{\rho }_{tan}\right)$ is the correlation in the tangential direction, quantified as the average of the correlations within 30 degrees of the direction that is orthogonal to SGA. The vertex’s orientation is defined as follows: $O\rho =\left(L{\rho }_{ax}-L{\rho }_{tan}\right)/sd\left(L\rho \right)$, where $sd\left(L\rho \right)$ is the SD of all of the vertex’s correlations. Intuitively, a highly positive $O\rho$ corresponds to a vertex with an axial orientation, a highly negative $O\rho$ corresponds to a vertex with a tangential orientation, and $O\rho \cong 0$ corresponds to a relatively isotropic orientation. See SI Appendix, Methods III for further information.

Statistical Testing of Anatomical Correspondence.

The global anatomical correspondence between two maps, such as those of genetic and phenotypic $L\rho$, was quantified using a previously described randomization procedure (the “spin test”) (35). Here, the null hypothesis is that the observed correspondence is due to a random alignment between the maps that is not greater than is expected by chance. This null is operationalized by randomly rotating one map relative to the other map and recalculating the measure of correspondence. See SI Appendix, Fig. S3 for an illustration of this procedure. Local correspondence was quantified using a method similar to the previously described approach of “local cortical coupling” (37). In brief, this procedure quantifies the correspondence between two surfaces, within a demarcated local area around each vertex—a sliding 10-mm geodesic window only including points within 10 mm of that vertex. The statistical significance of local correspondence was quantified using cluster-based version of the spin test, which rejects the null hypothesis of no local correspondence for clusters of vertices while controlling for multiple comparisons. See SI Appendix, Methods IV for further information.