Correction for multiple testing in candidate-gene methylation studies

Abstract

Aim:

We compared the performance of multiple testing corrections for candidate gene methylation studies, namely Sidak (accurate Bonferroni), false-discovery rate and three adjustments that incorporate the correlation between CpGs: extreme tail theory (ETT), Gao et al. (GEA), and Li and Ji methods.

Materials & methods:

The experiment-wide type 1 error rate was examined in simulations based on Illumina EPIC and 450K data.

Results:

For high-correlation genes, Sidak and false-discovery rate corrections were conservative while the Li and Ji method was liberal. The GEA method tended to be conservative unless a threshold parameter was adjusted. The ETT yielded an appropriate type 1 error rate.

Conclusion:

For genes with substantial correlation across measured CpGs, GEA and ETT can appropriately correct for multiple testing in candidate gene methylation studies.

DNA methylation is the attachment of methyl groups to a cytosine guanine dinucleotide in DNA molecules, which most often occurs at CpG sites in the genome. Differences in methylation levels (the proportion of DNA which is methylated) can be correlated with differences in gene expression. DNA methylation patterns have been used as biomarkers of traits such as cancer, suicide, premature aging and smoking [1–4]. For studies in humans, the primary method for assessing DNA methylation across the genome has been commercially available DNA-methylation BeadChips. Recently, Illumina released their Infinium MethylationEPIC BeadChip (EPIC chip) that measures the proportion of methylated DNA (denoted β) at more than 850,000 CpG sites, supplanting their older Infinium HumanMethylation450 BeadChip (450K chip) that examines the levels of methylation at nearly 500,000 sites [5]. However, methylation levels at many of these sites are essentially constant across samples in a particular tissue [6].

Candidate gene studies of methylation that assess association between a phenotype and methylation of CpG sites within a particular gene or region, can be motivated by associations observed with genetic variation (base-pair changes) or from studies indicating differential expression of a particular gene. Studies of this type can yield important information about the potential mechanism of action of both associated genetic variants and environmental exposures. However, in candidate gene or gene region studies, failure to properly account for the number of CpG sites examined can lead to a high rate of type 1 errors (false positives). One approach to addressing this problem is the Bonferroni correction, which requires that the observed p-values be less than the specified significance level (α) divided by the number of tests (K), and sets the experiment-wide type 1 error rate at α. Equivalently, the p-values themselves can be adjusted and compared with the specified significance level. That is, a statistic can be said to be significant according to a Bonferroni correction when the corrected p-value p_cor = p × K < α. This is slightly more conservative than the similar, but more precise, Sidak correction, in which the corrected p-value is p_{cor Sidak} = 1-(1-p)^K. Both approaches limit the experiment-wide type 1 error rate to the specified α level but also have a well-known weakness: they are overly conservative when the multiple tests are correlated. Alternately, the Benjamini-Hochberg false-discovery rate (FDR) procedure [7] controls the expected proportion of false positives to a specified cutoff rather than limiting the overall probability of at least one false positive. The FDR procedure can also be formulated as an adjustment to the observed single test p-values through the computation of the Q-values [8]. Accepting as significant all sites for which Q < α limits the expected FDR to α. It also controls the type 1 error rate in the sense that, when all tests are under the null, limiting the FDR to some level α also yields a family-wise type one error rate of α [7]. Like the Bonferroni correction, the FDR procedure is based on the assumption that the multiple test statistics are independent, and in the case of correlated test statistics, the FDR method is overly conservative in its control of the expected false-positive rate.

Methods to address correlated loci are well established in the context of genetic association studies focused on SNPs. In a genetic association study, the gold standard approach to multiple testing correction is a permutation-based adjustment in which the genotype data are permuted among subjects in a way that preserves the correlation among the variants, but removes any association between the genetic variants and the phenotype (see, e.g., the Max(T) procedure in PLINK [9,10]). The permutations are performed repeatedly (typically tens-of-thousands of times) to determine the distribution of the minimum p-value of the test statistics under the null hypothesis of no association between the trait and the set of genetic variants. The percentile of an observed p-value in the permutation-based minimum p-value distribution then represents a corrected p-value with the appropriate type 1 error rate accounting for the correlation among the variants. One substantial downside of permutation methods is the computational time necessary to simulate an adequate minimum p-value distribution. Additionally, it is not always possible to design an appropriate permutation for correlated samples, such as in the case of family studies.

Beyond permutation, several less computationally intensive alternatives have been proposed including the extreme tail theory (ETT) method [11], and several methods that compute an effective number of tests which can then be used in a Bonferroni/Sidak correction including the Cheverud method [12], the Nyholt method [13], the Li and Ji (LJ) method [14], the Galwey method [15] and the Gao et al. (GEA) method [16]. One study that compared these approaches found that all of them were successful at limiting false positives to some degree, but the LJ, GEA and the ETT methods maintained the type 1 error rate closest to the specified significance level [17]. In some ways, the ETT is optimal, because it is based on an explicit calculation of the type 1 error rate given the correlation between the observed test statistics. However, this approach, like permutation, requires access to the individual-level data, and it is not appropriate when there is correlation among the samples. This contrasts with the GEA and LJ methods which can be applied in cases where only summary statistics are available, for example, in the context of a meta-analyses where only summary results from contributing dataset are examined. Therefore, the GEA and LJ methods remain useful in practice as they can be applied in cases when the permutation and ETT methods cannot.

There are several inherent differences in the nature of the data and approach to association analysis for SNP versus methylation data. First, in regression models of methylation data, methylation is traditionally the response, while the trait of interest is one of several predictors. Second, when coded numerically, genotypes are usually coded as 0, 1 and 2 to represent the number of minor alleles or the number of nonreference alleles, while the proportion of DNA methylation at a site, β, is a value between 0 and 1, which is usually log-2 logit transformed into an M-value (i.e., $M={log}_2\left(\frac{\text{β}}{1-\text{β}}\right)$) prior to analysis. Thus, it is important to assess the ability of the multiple testing adjustment methods to control type 1 error in this context. In this study, we examined the correlation of methylation values observed within a gene, evaluated the performance of the LJ method, the GEA method and the ETT method in candidate gene methylation studies and compared the degree to which each method achieved their stated type 1 error rate relative to a Sidak correction, an FDR correction and a permutation-based adjustment. We accomplished this through a series of simulations based on whole-blood methylation data generated using both the Illumina EPIC and 450K BeadChips.

Correction methods

We examined two methods that establish a correction by estimating the effective number of independent tests: the GEA and LJ methods. An effective number of tests paradigm for correction estimates a correction value k* such that applying a Sidak correction based on k* tests yields an appropriate type 1 error rate. Both the LJ and GEA methods take as input the correlation matrix for the SNPs as proposed for the genetic association case, or here the correlation matrix for the M-transformed methylation proportion for the K probes within a gene. Then, the K eigenvalues of this correlation matrix are computed (e_i), which give some indication of the proportion of variance explained by underlying components of variance, as from a principal components analysis. Note that different correlation measures can be used to construct this correlation matrix. This was explicitly discussed in the paper proposing the LJ method [14] in which the correlation between genotypes was calculated based on measures of entropy and mutual information [18]. As M-values are continuous, we here utilize a Pearson correlation to compute the correlation between each pair of sites to construct the correlation matrix.

The LJ method

Based on the intuition that a fixed number of correlated identical tests c will result in an eigenvalue of c >1, the LJ method decomposes the eigenvalues into their integer and fractional components. If I(x) is the indicator function, which is 1 if the proposition is true and 0 if it is false, and [x] the floor function, which is the largest integer smaller than x, then the LJ estimated effective number of independent tests (eff_LJ) is then computed by the formula:

$${\text{eff}}_{\text{LJ}}={\sum }_{\text{i}=1}^{\text{K}}\text{f}(|{\text{e}}_{\text{i}}|)$$

where $\text{f}(\text{x})=\text{I}(\text{x}\ge 1)+(\text{x}-[\text{x}]),\text{x}\ge 0$.

Investigations of the performance of the LJ method when applied to genetic association studies have found it to be modestly anticonservative [17], in other words, yielded greater than the nominal type 1 error rate.

The GEA method

For the GEA method, k* is defined as the number of eigenvalues required to exceed some specified proportion of the sum of the eigenvalues, usually 99.5%. That is, if e_i is the i^th eigenvalue, k* is the minimum value such that $\frac{{\sum }_{\text{i}=1}^{\text{k}*}{\text{e}}_{\text{i}}}{{\sum }_{\text{i}=1}^{\text{K}}{\text{e}}_{\text{i}}}$ >0.995, although the authors indicate that this cutoff may need to be adjusted in situations where the correlation structure may differ substantially. Here, we evaluate corrected significance by the GEA method using the 0.995 level as specified in the original publication (p_Gao) [16] but also at a grid of values from the 0.99 level (p_Gao99) to the 0.95 level (p_Gao95).

The ETT method

The ETT method was proposed based on the observation that under the null hypothesis, for linear models, the correlation between multiple test statistics can be computed based on the correlation from multiple responses (methylation loci in this case) and multiple predictors. That is, when examining the association between a batch of sites and some response, the resulting joint test statistic distribution of all m statistics T₁, T₂,…, T_m is approximately multivariate normal with the same correlation structure. Also, based on this, there is a closed form solution to the correlation of the test statistics for linear models that we denote Σ that can be computed from the correlation of the multiple predictors or even the correlation of multiple predictors and multiple responses being modeled. Then, with the asymptotic multivariate normal distribution of test statistics T = (T₁, T₂,…, T_m) ∼ N(0, Σ), the probability of observing at least one p-value as small as P_min under the null hypothesis is that there is no association for two sided test as:

$$P_{ETT}=1-P\{max(\left|T_1\right|,\left|T_2\right|,\dots ,\left|T_m\right|)<{\Phi }_{\sum }^{-1}(1-\frac{P_{min}}{2})\}$$

where Φ is the multivariate normal probability density function, and this P_ETT is taken as the corrected significance level.

Datasets

The datasets used for this study are summarized in Table 1. The first dataset we assessed was from a cohort ascertained at the Translational Research Center for TBI and Stress Disorders (TRACTS), a VA Rehabilitation Research and Development (RR&D) National Center for TBI Research at VA Boston Healthcare System. Assessment of methylation in blood samples from the TRACTS study was performed with both 450K (n = 326) and EPIC BeadChips (n = 330), with a large proportion of samples overlapping (n = 177). Cleaning and processing of the BeadChip data for TRACTS has been described in detail elsewhere [6,19] and followed the protocol outlined in a large-scale posttraumatic stress disorder (PTSD)-epigenetics consortium [20]. To ensure that our observed results were not dataset specific, we also utilized data from several other cohorts. We examined data from the National Center for PTSD (NCPTSD) sample (n = 487) that we had previously used in a genome-wide association study of PTSD [21]. For this dataset, methylation in blood was assessed with 450K BeadChips. The cleaning and processing of the 450K data for the NCPTSD cohort is described in detail elsewhere [22] and followed the same pipeline used for the TRACTS cohort. We also examined the performance of these methods using multiple publicly available datasets from the Gene Expression Omnibus (GEO; https://www.ncbi.nlm.nih.gov/geo/) (Table 1). Results of the methods applied to the NCPTSD and publicly available datasets are presented primarily in the Supplementary Materials, and will only be briefly summarized in the text.

Table 1. . Datasets used in this paper.

Name	Chip	Normalization	Batch effect correction	Sample size	Available covariates†	URL
TRACTS	450K/EPIC	BMIQ	ComBat	N = 326/N = 330	Age, sex, three PCs for ancestry, cell types	N/A
NCPTSD	450K	BMIQ	ComBat	N = 487	Age, sex, three PCs for ancestry, cell types	N/A
GSE56046	450K	Quantile normalization, background subtraction with lumi	Random assignment of samples to Chip & position, but no post-hoc correction	N = 1202	Age, sex, cell types	https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE56046
GSE112611	EPIC	Background subtraction, not normalized	None	N = 402	Age, sex, cell types	https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE112611
GSE103397	EPIC	Stratified quantile normalization with minfi R package	None	N = 20	Age, sex, cell types	https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE103397

^†Cell-type proportions computed from the methylation data itself were included for all datasets.

BMIQ: Beta-mIxture quantile dilation; N/A: Not applicable; NCPTSD: National center for PTSD; PC: Principal components; TRACTS: Translational research center for TBI and stress disorder.

Analysis

We used standard linear regression with M-values as the response and a simulated dichotomous trait as the predictor along with additional selected variables as available for each dataset. Across cohorts, this minimally included sex and age, but may have included adjustments for study site, sample composition, principal components for population stratification, etc. (Table 1). We included covariates for estimated white blood cell proportions (that is CD4 cells, CD8 cells, NK cells, B cells, NK cells, monocytes) in all analyses to account for cell-type heterogeneity. These covariates were estimated from the methylation data itself using the R minfi package [23,24]. Analyses were performed using the Bioconductor limma package [25]. Limma’s default pipeline includes a Bayesian-adjusted standard error estimate, but in this case, the significance of parameters was computed from the unadjusted standard errors. As recently noted [6], the low degree of variation of many probes on both the EPIC and 450K chip when assessing the methylation of blood samples can lead to low correlation across chips and poor reliability of samples measured on a single chip, due to a low signal-to-noise ratio. That publication recommended excluding low variation SNPs (observed β range <0.1) prior to analysis to increase replicability of findings and to reduce the multiple testing burden. Thus, we analyze our simulations twice, once including the full complement of sites passing the QC pipeline, and once again in the ‘trimmed’ dataset where the low-variation sites have been removed.

Simulation method

To assess type 1 error, we simulated null phenotypes by generating random dichotomous trait data to accompany real methylation data with a case:control ratio of 1:1. We additionally explored the effect of an unbalanced case:control ratio (9:1). For each gene, the simulated trait data were permuted and reanalyzed 10,000-times to get a null distribution for the minimum p-value across the gene for use in the permutation correction. Then, the simulated trait was permuted another 2000-times to assess the type 1 error rate of the correction methods. First, the percentile of the minimum p-value for each replicate in the null distribution was computed and taken as our estimate of permutation-based significance. We take this as our gold standard. For each replicate we also computed the corrected significance using a Sidak correction, an FDR correction, the LJ correction, the GEA correction across a grid of threshold parameters and the ETT correction.

We used the Illumina annotation for the 450K and the EPIC chip to assign CpG sites to genes, specifically the Illumina’s Infinium MethylationEPIC v1.0 B4 manifest for the EPIC chip data and the Illumina’s Infinium HumanMethylation450 v1.2 manifest for the 450K chip data. We here used gene annotation as a way to group probes and to quickly examine a large pool of candidate regions that varied in terms of size and correlation structure. However, to ensure that these results would apply to other region-based analyses, we also performed a simulation in the TRACTS 450K data where we only examined the sites in each gene that were identified as regulatory according to the BIOS QTL browser cis-meQTL database (https://genenetwork.nl/biosqtlbrowser/). We also performed a region-based analysis of the TRACTS EPIC data in which we examined regions made up of 50 consecutive probes, regardless of gene boundaries. In order to quantify the extent of correlation between probes within a gene/region, we first computed the adjusted methylation for each probe that was the residual from a linear model of the methylation value adjusted for all covariates. Then, we computed the average absolute correlation (AAC), which is the average absolute pairwise correlation for each possible adjusted probe pair in the gene. The extent of correlation is categorized into four levels: no correlation for 0< AAC ≤0.1, low correlation for 0.1< AAC ≤0.2, medium correlation for 0.2< AAC ≤0.3, and high correlation for AAC >0.3. A natural cubic spline with 3 degrees of freedom fit with R package spline 3.4.0 [26] was used to illustrate the relationship between AAC and type 1 error rate for the Sidak and FDR methods. For the purposes of discussion, we define ‘conservative’ as a gene-wide type 1 error rate less than 4.75% when the expected rate is 5% – that is 5% fewer type 1 errors than expected. In order to evaluate the performance of the correction methods for genes with different levels of innate correlation, we computed the type 1 error rate simulation for 100 genes randomly chosen from each of the no correlation, low correlation, medium correlation, and high correlation categories. We examine the effect of gene size by randomly sampling 100 genes from each of six bins: 2–4 probes, 5–10 probes, 11–20 probes, 21–50 probes, 51–100 probes and more than 100 probes per gene. When examining the regulatory probes within a gene, we computed AAC based only on the regulatory probes in TRACTS 450K data that were identified by the cis-meQTL data based on BIOS QTL browser, and sampled 100 genes from each correlation category. When examining the 50 consecutive probe regions we computed AAC for all possible consecutive probes regions with length of 50, and randomly sampled 100 regions from each correlation category (no correlation, low correlation, medium correlation and high correlation). When looking at the effect of gene size on the type 1 error rate, we focused our attention on genes with higher levels of within-gene correlation, specifically those genes within the medium- and high-correlation groups. Hendricks et al. have shown that breaking-up large regions into subregions in candidate gene association studies could yield corrected type 1 error rate closer to the desired levels [17] for the GEA and LJ methods. That is, a gene could be split into subregions and the M_eff could be computed within each block, and then summed across blocks to be the final M_eff for that gene. For genes in the more than 100 probe category, we evaluated a similar procedure, dividing a large gene into blocks of size 30, which we refer to as binning. To examine the effect of sample size, we examined the type 1 error rate for random subsets of the TRACTS EPIC data with sample size, n = 20, 50, 100 and 150 subjects. To examine the performance of these methods in a meta-analysis setting, where perhaps the BeadChip used might vary between cohorts, we performed a simulation where probes passing QC in both the TRACTS EPIC data and the NCPTSD 450K data were meta-analyzed and multiple-testing corrections were based on correlation patterns observed in the TRACTS EPIC data. Meta-analysis was performed using the ‘sample-size’ method with METAL software [27] that converts the direction of effect and p-values for each cohort into Z-scores and combines them in a weighted sum to compute meta-analysis significance.

Example genes

To demonstrate the range of performance of these methods, we have picked several ‘example genes’ (from EPIC chip data) that varied in number of probes and AAC. The C22orf27 gene is an example of a high-correlation gene according to our classification scheme outlined above in the 11–20 probe size bin (AAC = 0.53 across 13 probes), RPL0P2 gene is an example of a gene in the low correlation and 11–20 probe bins (but still at the 89.14th percentile of the AAC distribution, AAC = 0.016 across 16 probes), and BRSK2 is an example of a larger gene (>100 probe bin) with low correlation (AAC = 0.14 across 124 probes).

Results

Number & correlation of probes per gene

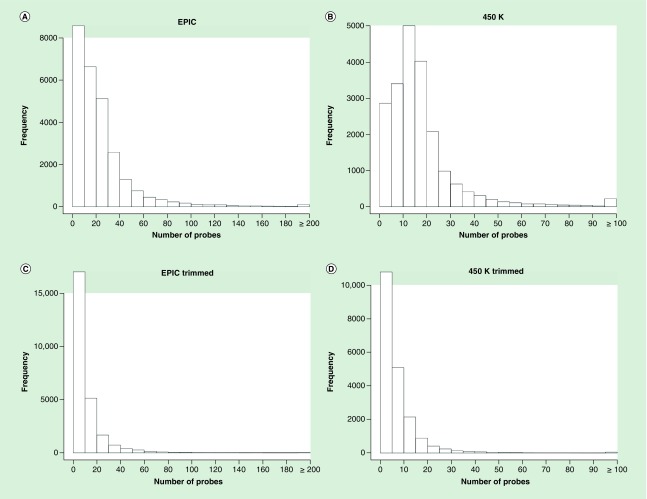
For TRACTS cohort EPIC chip data, a total of 820,670 probes passed quality control, and 590,921 of these probes were annotated by Illumina’s Infinium MethylationEPIC v1.0 B4 manifest to 26,795 genes. The distribution of the number of probes per gene is represented in Figure 1A. The number of probes per gene ranged from 1 to 1398. The median number of probes is 18 and the mean was 24.4. The distribution was highly skewed. There were 1071 genes for which methylation was only measured with a single probe. There were 631 genes with over 100 probes, 90 genes had more than 200 probes and only 6 genes had more than 500 probes. After trimming, 272,011 probes remained (46.03% of the annotated probes) mapping to 25,663 genes. Figure 1C shows the distribution of the number of probes for EPIC after trimming, the mean number of probes is 11.61 (standard deviation [SD] = 17.23). The 95th percentile of number of probes per gene is 71 before trimming and 37 after trimming.

Figure 1. . Histogram of number of probes per gene for EPIC and 450K pre- and post-trimming.

For the TRACTS 450K chip data, a total of 453,747 probes passed quality control, and 348,238 of these were annotated by Illumina’s Infinium HumanMethylation450 v1.2 manifest to 20,816 genes. The distribution of the number of probes per gene is represented in Figure 1B. The number of probes per gene ranged from 1 to 1218 and the distribution was also highly skewed. After trimming, 144,883 probes remained (41.60% of the annotated probes) mapping to 20,075 genes. Figure 1D shows the distribution of number of probes for the TRACTS 450K chip data after trimming, the mean number of probes is 7.95 (SD = 12.58). The 95th percentile of number of probes per gene is 46 before trimming and 22 after trimming.

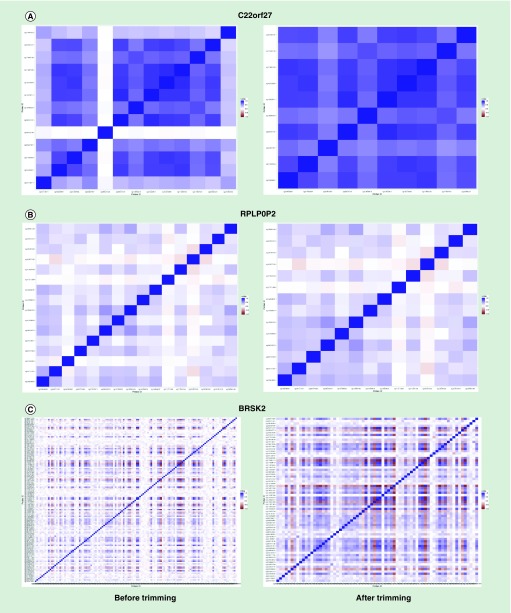
Figure 2A–C presents the pairwise correlations for probes in the example genes and the effects of trimming the low variation probes. The AAC of the high correlation/11–20 probe bin example gene C22orf27 increases from 0.53 to 0.75 after dropping three probes. For the low correlation/11–20 probe bin example gene RPLP0P2, the AAC increases from 0.16 to 0.18 after dropping two low variation probes. For the low correlation/more than 100 probe bin example gene BRSK2, the AAC increases from 0.14 to 0.17 after dropping 53 low variation probes.

Figure 2. . Heat map of correlation for sample genes.

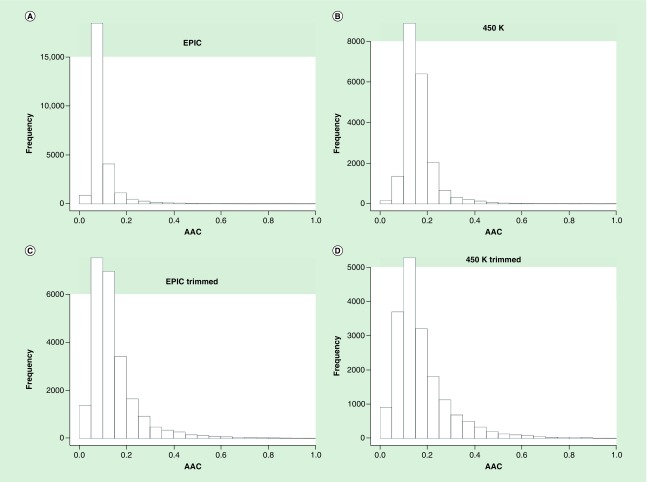
The increase of AAC as a result of trimming low-range probes observed in our example genes was broadly similar in the EPIC and 450K data. Table 2 presents the number and proportion of the 20,861 genes assessed by EPIC and 450K chip by number of probes and AAC before and after trimming low range probes. Figure 3A–B shows the distribution of AAC for the EPIC and 450K chip before trimming. The mean AAC for the EPIC chip before trimming is 0.0943 (SD = 0.0610), and for the 450K chip it is 0.1632 (SD = 0.0693). Figure 3C–D shows the distribution of the AAC for EPIC and 450K chip after trimming. The mean AAC for the TRACTS EPIC chip data after trimming is 0.1438 (SD = 0.1017), and for 450K chip it is 0.1749 (SD = 0.1202). For both the EPIC and 450K chips, the dropping of these low variation probes decreases the average number of probes per gene and increases the AAC. The lower AAC for EPIC chips apparent in Table 2 and Figure 3 is consistent with the design of that chip, where newly added probes were targeted at previously untargeted regions rather than simply added to give higher coverage to regions assessed on the 450K chip [27]. As noted in Pidsley et al., the new sites added on the EPIC chip were designed to target regulatory elements far away from the TSS (likely enhancers identified by the ENCODE and FANTOM5 projects), and the vast majority of these distal sites (93%) are only targeted by a single probe. Based on the Illumina annotations, the distance to the closest flanking marker actually increased in the EPIC chip compared with the 450K chip: for autosomal loci assessed by the EPIC chip, the median distance to the closest flanking probe is 207 bp, while for the autosomal loci assessed by the 450K chip, the median distance to the closest flanking probe is 133 bp.

Table 2. . Number of probes and average absolute correlation per gene for the Translational Research Center for TBI and Stress Disorder EPIC and 450K data before and after trimming of low variation probes.

	Number of genes (%)		EPIC trimmed	450K trimmed
	EPIC	450K
Number of probes
[2, 4]	2930 (11.39)	1759 (8.66)	6504 (27.76)	7033 (38.63)
(4–10]	4586 (17.83)	4023 (19.8)	8294 (35.40)	6985 (38.37)
(10–20]	6636 (25.80)	9062 (44.59)	5145 (21.96)	3020 (16.59)
(20–50]	8996 (34.97)	4635 (22.81)	2775 (11.84)	984 (5.41)
(50–100]	1945 (7.56)	641 (3.15)	581 (2.48)	128 (0.7)
(>100)	631 (2.45)	201 (0.99)	130 (0.55)	54 (0.3)
Adjusted AAC
No [0–0.1]	19,323 (75.12)	1514 (7.45)	8901 (38.00)	4598 (25.26)
Low (0.1–0.2]	5217 (20.28)	15,269 (75.14)	10,376 (44.29)	8484 (46.61)
Median (0.2–0.3]	739 (2.87)	2702 (13.3)	2573 (10.98)	2936 (16.13)
High (>0.3)	445 (1.73)	836 (4.11)	1579 (6.74)	2186 (12.01)

AAC: Average absolute correlation.

Figure 3. . Histogram of average absolute correlation for genes from the EPIC and 450K pre- and post-trimming.

Multiple testing correction

Type 1 error rate for Sidak & FDR

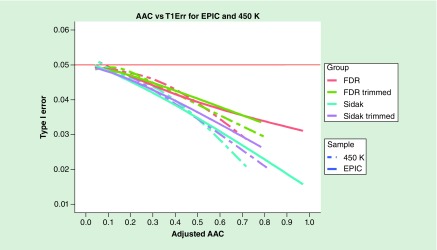
First, we examined the type 1 error rate for the Sidak and FDR methods as a function of the AAC to determine the proportion of genes with high-enough correlation between probes to cause them to be conservative (according to our 5% fewer type 1 error criterion). Figure 4 presents the type 1 error rate of the Sidak and FDR methods from null simulations based on the EPIC and 450K data from the TRACTS study. Based on the cubic spline curve, the type 1 error rate drops below 4.5%, the point at which there are 10% fewer significant genes under the null than expected given the nominal α level when the AAC is around 0.26 regardless of the chip or whether the data are trimmed. The type 1 error rate drops below 4% (20% fewer significant probes than expected) when the AAC is around 0.42, again regardless of the chip used. However, the proportion of genes that have a particular AAC level differ across chips and is shifted by trimming. The Sidak and FDR methods are not conservative when the AAC is less than 0.16. This includes 88.16 and 65.34% of genes measured by the EPIC chip pre- and post-trimming, respectively, and 57.91 and 53.30% of genes measured by the 450K chip pre- and post-trimming, respectively. Hence, for the majority of genes examined, the Sidak and FDR corrections are sufficient to control for experiment-wide type 1 error rate across the probes of the gene without being overly conservative.

Figure 4. . Type 1 error rate of false-discovery rate and Sidak for genes as a function of average absolute correlation for EPIC and 450K pre- and post-trimming.

AAC: Average absolute correlation; FDR: False-discovery rate.

Type 1 error rate across multiple testing correction methods

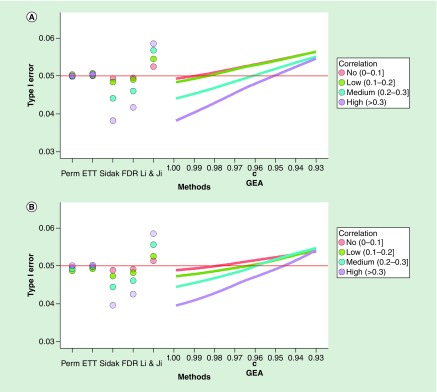
We then examined the type 1 error rate across different methods for both the EPIC and 450K chip before and after trimming. Changing the case:control ratio to 1:9 had no effect, so for simplicity we forgo presenting the simulations with an unbalanced ratio, and all presented simulations assumed an equal number of cases and controls. Figure 5A presents type 1 error rate across methods by correlation groups for EPIC chip before trimming. Consistent with the results presented above, the Sidak and FDR methods had near the correct nominal type 1 error rate in no correlation (AAC ≤0.1) and low correlation (0.1 <AAC ≤0.2) gene groups. As the AAC increased, these two methods became more conservative. The Sidak had a type 1 error rate around 0.045 for medium AAC genes and around 0.04 for high AAC genes, while FDR correction was slightly less conservative. The ETT method achieved close to the nominal (0.05) type 1 error rate regardless of AAC. The LJ method became increasingly anticonservative as the AAC increased, with a type 1 error rate of 0.057 in the medium AAC category and around 0.059 in the high AAC category. GEA with the parameter set at c = 0.995 as originally recommended by GEA gave type 1 error rate very close to Sidak, which was increasingly conservative as the AAC increased. As c was adjusted downward, the type 1 error rate increased and regained the nominal α = 0.05 at 0.985 in the no and low correlation categories, at around 0.96 in the medium correlation genes, and at around 0.95 in the high correlation genes. Although the effect of trimming shifted the number of genes in each of the correlation categories, the trimming itself did not appear to alter the pattern observed within each correlation category Figure 5B. We observed similar results for the TRACTS and NCPTSD 450K data and across the GEO datasets (see Supplementary Figures 1–5).

Figure 5. . Type 1 error rate by correlation group.

Type 1 error rate across methods for genes in different correlation groups based on EPIC data from the TRACTS sample (A) and after trimming low variation probes (B).

FDR: False-discovery rate; GEA: Gao et al.; ETT: Extreme tail theory.

Number of probes

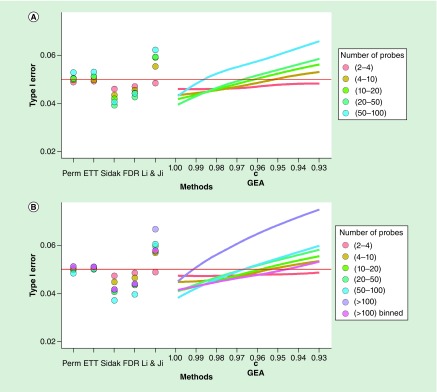
We also examined the effect of number of probes among genes with medium and high correlation. Figure 6 presents the type 1 error rate across methods by number of probes groups for EPIC chip before and after trimming. The ETT correction yields a type 1 error rate close to 0.05 regardless of the number of probes per gene, similar to what was observed for the permutation method. For the Sidak and FDR methods, the type 1 error rate dropped, becoming more conservative as the number of probes increased. The LJ method became more liberal as the number of probes increased. GEA was overly conservative (close to Sidak) when the original c = 0.995 was used. The type 1 error rate for GEA increased as c decreased, and the rate of increase (slope) was higher for genes with a greater number of probes. However, for genes with a small number of probes (≤4) it remained conservative regardless of c. We note that c = 0.96 yielded a type 1 error rate near 0.05 for all except the largest gene categories in both the pre- and post-trimmed results. However, we note that there are very few genes with both high correlation and a large number of probes. That is, there were no genes with AAC >0.20 and >100 probes in the EPIC data prior to trimming and there are only five genes in that category post-trimming, so that the extreme inflation observed after even a small adjustment in c for the GEA method may be partially because of instability in the estimate due to the small number of genes examined. Nevertheless, we found that splitting large genes into smaller subregions of size 30 and summing the effective number of tests, reduced the type 1 error rate for the GEA and LJ methods down to the range observed for the smaller genes (see Figure 6B).

Figure 6. . Type 1 error rate by number of probes.

Type 1 error rate across methods for genes as a function of the number of probes based on EPIC data before (A) and after trimming low variation probes (B).

ETT: Extreme tail theory; GEA: Gao et al.; FDR: False-discovery rate.

The results for the evaluation of the effect of number of probes per gene for the other cohorts (NCPTSD GEO datasets) including both 450K and EPIC data are presented in Supplementary Figures 6–10. These results are similar in that the Sidak and FDR corrections were too conservative with a type 1 error rate around 0.04 for genes with more than ten probes, and the LJ correction was too liberal with type 1 error rate around 0.06 for genes with a large number of probes. The GEA method had a type 1 error rate that increased as the GEA parameter c was decreased, achieving a type 1 error rate around 0.05 when c = 0.96.

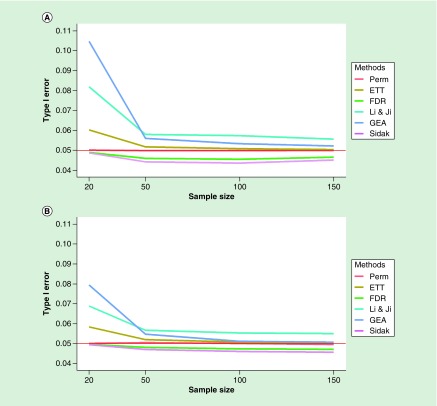
The effect of sample size

To determine the effect of sample size on our findings, we selected subsamples of n = 20, 50, 100 and 150 from the TRACTS EPIC dataset and compared them with the results for the entire cohort (n = 300). We found that the sample size of the dataset strongly affected the type I error rate for the LJ and GEA methods, and even the ETT method had excess type I error when the sample size was low (Figure 7; see Supplementary Figures 11 & 12 for detailed results). The inflation for the LJ and GEA methods appears to be due to the poor estimation of correlations in the small samples, as when the correlation estimates from the full TRACTS dataset were used in computing the effective number of tests, the type I error rate was reduced (Supplementary Figure 13). This was confirmed in the EPIC dataset GSE103397 (n = 20) dataset, where there was substantial inflation for the LJ and GEA methods, but this was eliminated when we applied the effective number of test corrections based on correlations computed from the GSE112611 dataset (n = 402) to the GSE103397 dataset (Supplementary Figure 14). That is, using more accurate correlation estimates from an external source can reduce the inflated type 1 error rate for the LJ and GEA methods when applied to samples with small n.

Figure 7. . Type 1 error rate by sample size.

Type 1 error rate for genes across methods as a function of sample size before (A) and after trimming low variation probes (B).

ETT: Extreme tail theory; FDR: False-discovery rate; GEA: Gao et al.

Type 1 error rate in meta-analyses

Supplementary Figure 15 presents the results of a meta-analysis of overlapping EPIC and 450K data using the TRACTS and NCPTSD datasets, using correlation estimates from the TRACTS EPIC dataset. Since individual data were not combined, and would not necessarily be available in a large-scale consortium setting, there are no results for the PERM and ETT methods, which require individual-level data. The results for the LJ and GEA methods are broadly similar to those obtained for the single-cohort analyses.

Other region-based analyses

Supplementary Figures 16 and 17 present the results for simulations based on only the regulatory probes in each gene and also for 50 consecutively measured CpG sites at a time, regardless of gene boundary. These results for these simulations are consistent with the gene-based results we previously obtained. This demonstrates that our results are not specifically applicable only to gene boundaries as identified in the Illumina annotation, but could be applied to other region-based tests as well. That is, the relevant factor is the number of probes and the degree of correlation between them rather than their attribution to a single gene.

Discussion

In this paper, we examined the patterns of correlation of methylation across genes as measured by Illumina BeadChips. We found that for most of the genes assessed by the chips, the AACs were less than 0.16 (about 88% before trimming and 65% after trimming for EPIC chip and about 57% before trimming and 53% after trimming for 450K chip), and a Bonferroni, Sidak or FDR correction would all work approximately well and not be excessively conservative for a majority of genes. However, for a substantial proportion of the genes, there will be a moderate level of correlation, and the type 1 error rate will be less than the expected α = 0.05 under the null. This lower rate of type 1 error also implies lower than expected significance for truly associated sites, which is not desirable. Additionally, we noted that dropping low-variability probes had the effect of increasing the average correlation across the genes for both chips and consequently increased the number of genes for which the Sidak and FDR corrections were conservative. As one of the motivations for trimming is reducing the multiple-testing correction burden, it is unfortunate that simply applying a FDR correction for the remaining probes still yields a correction that is more stringent than necessary and leaves some of the potential increase in power due to trimming unrealized.

This motivated us to examine other methods that can yield a type 1 error rate closer to the specified α level and hence retain power for candidate examination of genes with a high level of correlation between adjacent probes, including the LJ method, the GEA method and the ETT method. We evaluated these methods on data generated using the Illumina 450K and EPIC BeadChips to assess methylation in several ‘in-house datasets’ as well as publicly available data from GEO to increase the chance that our recommendations would be suitably robust. We found that the LJ method tended to produce higher than expected type 1 error rates (0.055–0.06) for genes with AAC larger than 0.2. The ETT method was very stable and consistently achieved type 1 error rate similar to the gold standard permutation correction across various datasets, except for very small sample sizes. The GEA method yielded a lower than expected type 1 error rate when applied to methylation data when the initially proposed parameter c = 0.995 was used, very close to the performance of the Sidak correction. As this parameter was reduced, the type 1 error rate increased, achieving the intended .05 type 1 error rate around c = 0.96 for genes with medium correlation levels (Figure 5). For genes with low correlation levels (AAC <0.2) a 0.05 type 1 error rate was observed when c was around 0.985, and GEA was slightly anticonservative (type 1 error rate around 0.053) when c = 0.96 was used. We also noticed that adjusting the c make GEA anticonservative when applied to large genes (>50 probes) with moderate-to-high correlation (Figure 6), but that binning, in other words, splitting the gene up into smaller intervals and summing the effective number of tests across them, can correct this (Supplementary Figure 12).

Which correction method is optimal for an analysis depends on the availability of individual-level data, the characteristics of the gene and type of analysis. For analyses where the investigator has access to the raw data, the permutation test and ETT method can be used and yield the correct type 1 error rate. However, we note that ETT depends on the use of a linear model with uncorrelated errors across subjects, and indeed performs such an analysis within the software itself. However, permutation and ETT may be inappropriate when the data are clustered, for example, in family studies, repeated measures studies, longitudinal studies, studies from large consortia with several participating sites where site level variation is expected to occur. For these studies, the assumption of uncorrelated errors in ETT would not be appropriate, and in such cases it may be difficult or potentially impossible to design a permutation scheme that preserves the correct correlation structure. In such cases, a Bonferroni, Sidak or FDR test will be suitable when the genes have AAC less than 0.2, which is over half of the genes assayed by the EPIC and 450K chips. For genes with higher AAC and less than 50 probes, we could consider using GEA with c = 0.96. Larger genes may exhibit inflation with the c set at this level, but this can be counteracted by dividing the probes into several blocks and computing an M_eff that is the sum of the GEA effective number of tests across the blocks. When computing the GEA estimate for a dataset with small sample size (n < 100), the type 1 error rate can be inflated. Using a larger reference dataset to estimate the correlation among probes used to compute the GEA M_eff and applying this M_eff to the small sample can help mitigate this inflation. This also highlights the distinct advantages of effective number of test-based corrections. That is, if suitable between probe correlation estimates are available from another source, they can be applied to a candidate gene analysis even when the data used for the analysis are not readily available. This is often very useful when calculating significance of post hoc candidate tests of results from large-scale meta-analysis consortia, for example. In such cases, it is often true that only summary results have been aggregated, and no large-scale cross-site dataset has been assembled. In that case, it is not possible to use ETT and permutation for multiple testing correction. However, the two M_eff options presented here are still feasible to apply and our meta-analysis simulation condition indicates that their performance in meta-analyses will be similar to their performance in single-cohort analyses. However, care should be taken to ensure that the dataset used to compute the correlation used for M_eff calculation applied to the meta-analysis results is suitably representative of the samples that were meta-analyzed, that is, from the same tissue, from a similar population and a used pipeline for processing, normalization and batch correction.

There are several limitations to our work. We have focused exclusively on performance in terms of type 1 error rate, but in the future, other quantities such as power could be evaluated. Additionally, we have examined the FDR with the justification that when all tests are under the null, the FDR is equivalent to the type 1 error rate. However, a more in-depth investigation of the impact of nonindependence between tested hypotheses could evaluate the degree to which the nonindependence impacts the FDR directly. We have exclusively used Pearson correlation estimates in the calculation of the M_eff corrections, and it might be possible that some other robust nonparametric correlation estimates might be more effective in certain conditions, for example, when variation in DNA methylation in the gene is driven by nearby genetic variation. We did not investigate surrogate variable analysis that can be used to correct for batch effects and other underlying sources of sample heterogeneity because of the underlying computational complexity of the method and the need to recompute the surrogate variables for each simulated replicate. However, we expect that the methods evaluated here would perform similarly for analyses incorporating surrogate variable analysis, as long as the correlation structure within the candidate region is adjusted for the surrogate variables that are included as covariates. Another limitation is the exclusive focus on BeadChip data. The performance of these methods might differ for data generated via pyrosequencing or whole-genome bisulfite sequencing as the CpG site density and the patterns of correlation would differ.

Conclusion

In our study, we have critically examined the correlation patterns of two of today’s most popular BeadChips used for the assessment of DNA methylation and evaluated several methods for computing a corrected significance for candidate gene examinations using these data. We find that the ETT method performs well in all cases, its performance in terms of experiment-wide control of type 1 error and data requirements are similar to that needed for permutation-based multiple testing correction. For situations where individual level data are not available, a suitable GEA effective number of test correction can be constructed which is less conservative than an FDR or a Bonferroni/Sidak method. These results can guide researchers looking to perform candidate gene studies of DNA methylation data from BeadChips. When applied to regions with a high amount of correlation across CpG sites, use of these methods could lead to increased power to detect association.

Future perspective

Utilizing correlation-aware multiple testing correction methods will continue to be important in DNAm candidate-gene and candidate-region studies. First, we anticipate the number of CpG sites assessed to increase, both through an increase in the number of sites assessed on commercial BeadChips and through the increased use of whole-genome bisulfite sequencing. This increased density of sites assessed will eventually increase the average correlation between nearby sites, and hence increase the conservativeness of Bonferroni/Sidak and FDR adjustments. These methods can also be incorporated into other analyses and platforms, and have utility beyond candidate gene studies. For example, gene set enrichment analyses can be biased when genes are not equally likely to be included in the candidate list [28]. One potential cause of this bias is the differential number of sites (genetic variants in genetic association studies or CpGs in DNAm studies) assessed per gene. Methods have been developed to counter this bias by estimating the probability that a gene is detected based on the number of probes assessed (see, e.g., the gometh function from the R missMethyl package [29]). However, these bias corrections could potentially be improved via the use of an effective number of test calculation, for example, using the GEA method, which could incorporate a gene’s correlation pattern and yield a more accurate estimate of the chance that a particular gene appears in a gene set. The methods discussed here could also be used in the online presentation of large-scale genomic analysis results as supplied by genomic consortia. Currently, there are databases in which a researcher might pull out all of the GWAS results for a particular gene which they would like to examine with a particular trait, for example, the Oxford BIG server (http://big.stats.ox.ac.uk) that presents genome wide association study (GWAS) results for neuroimaging variables and other traits from the UK Biobank cohort [30,31] (http://www.nealelab.is/uk-biobank/). We anticipate that in the future online repositories for presentation of consortia genome-wide DNAm results will become prevalent. It would be quite feasible to automate the incorporation of the ‘effective number of tests methods’ of multiple testing correction, such as the LJ and GEA methods, into such a website. For example, if a researcher were to look up results for a particular gene, a multiple testing correction might automatically be applied to results within this gene based on a precomputed GEA correction. It would even be feasible to implement the automatic generation of an appropriate GEA correction for an arbitrary set of queried probes by precomputing the correlation between probes using a representative cohort. Hence, continued development of multiple testing correction methods will remain an interesting and important area of inquiry in the future with application to genomic studies in general and DNAm studies in particular.

Summary points.

• Candidate gene methylation studies are often useful to follow-up on evidence from genetic association or gene expression studies. However, when examining several CpG sites within a gene for association with a trait, multiple testing correction is necessary to limit the overall type 1 error rate to some specified level.

• The common methods to perform multiple testing correction, the false-discovery rate (FDR) correction and the Bonferroni or Sidak (more accurate Bonferroni) correction are based on the assumption that all of the tests examined are independent, and will be conservative when this is not the case.

• In a series of simulations using both Illumina 450K and EPIC BeadChip data, we compared the performance of the FDR and Sidak corrections to three methods that take the correlation between CpGs into account when performing candidate gene methylation studies: The extreme tail theory (ETT) method, the Li and Ji (LJ) method and the Gao et al. (GEA) method. The performance of these three methods has not previously been assessed when applied to DNA methylation studies.

• We find that most genes have low levels of correlation when assessed by EPIC and 450K chips. The EPIC chip has lower average across gene correlation than the 450K chip, which is consistent with Illumina’s stated design goal of targeting new regions with the added probes.

• Dropping probes that have low variability as they may be unreliable (Logue et al., Epigenomics 2017) has the effect of increasing the average level of correlation within genes for both the EPIC and 450K data.

• We found that when the correlation between probes in a gene is moderate to high, FDR and Sidak methods were conservative, the ETT method yielded a correct type 1 error rate, the LJ method had an inflated type 1 error rate and the GEA method tended to be conservative unless a parameter inherent in this method was adjusted.

• The performance of the different methods varied as a function of the within gene correlation, but did not differ depending on whether the data were generated using the EPIC or the 450K chip.

• While ETT performed well across simulations, there is no ‘one size fits all’ method to be used for candidate gene studies, as the ETT method requires access to the individual-level data and it requires that standard linear model assumptions (independent error terms) apply. Hence, it is not appropriate or feasible in all studies. When ETT cannot be used, a GEA adjustment may be implemented that yields an appropriate type 1 error rate, but the performance of this correction can depend on the sample size and the size of the gene examined.

• Using the recommendations presented here can yield less conservative candidate gene methylation study corrections, and hence will increase power to detect truly associated sites.